A Population Pharmacokinetic Analysis of the Penetration of the Prostate by Levofloxacin

Abstract

Prostatitis has remained a pathological entity that is difficult to treat. Part of the difficulty revolves about the putative offending pathogens. For acute prostatitis, members of the Enterobacteriaceae, particularly Escherichia coli, play a central role, while intracellular pathogens such as Chlamydia are more frequently seen in chronic prostatitis. Consequently, a drug needs to be able to penetrate to this specialized site in both the acute and chronic infection forms of the disease and also have potent activity against the most common causative pathogens, both intracellular and extracellular. Levofloxacin has such an activity profile. We wished to document its ability to penetrate to the site of infection. Patients undergoing prostatectomies were administered 500 mg of levofloxacin orally every 24 h for 2 days prior to surgery, and then on the day of surgery, 500 mg was administered as an hour-long, constant-rate intravenous (i.v.) infusion. A set of blood samples was obtained as guided by stochastic optimal design theory. Prostate biopsy times were determined by randomizing subjects into one of four groups, based on the interval after the i.v. dose. All plasma and prostate drug concentrations were comodeled by a population modeling program, BigNPEM, implemented on the Cray T3E Supercomputer housed at the Supercomputer Center at the University of California at San Diego. Penetration was determined as the ratio of the area under the concentration-time curve (AUC) of levofloxacin in the prostate to the plasma levofloxacin AUC. When calculated from the mean population parameters, this penetration ratio was 2.96. We also performed a 1,000-subject Monte Carlo simulation from the mean parameter vector and covariance matrix. The mean penetration ratio here was 4.14 with a 95% confidence interval of 0.20 to 19.6. Over 70% of the population had a penetration ratio in excess of 1.0. Levofloxacin adequately penetrates a noninflamed prostate and should be evaluated for the therapy of prostatitis.

Prostatitis, particularly chronic prostatitis, is often difficult to treat. Part of the difficulty revolves around defining the infecting pathogen. Another aspect of the problem lies in the protected nature of the prostate with regard to antimicrobial penetration. The causative pathogen can be extracellular (e.g., as in acute or chronic prostatitis due to Escherichia coli) or intracellular (e.g., as in chronic prostatitis due to Chlamydia). Consequently, the agent chosen for therapy should have a spectrum that is appropriate for the suspected pathogen and should penetrate well into the protected space of the prostate.

Levofloxacin is an agent that has good microbiological activity against the pathogens that cause the vast majority of infections of the prostate (9). Because it is a fluoroquinolone, one would, on first principles, believe that it would have excellent penetration properties into extracellular fluid as well as into cells. However, it is important to validate the penetration properties of an agent before testing the drug in the clinical trial arena.

It was our intent, then, to examine the penetration of levofloxacin into prostatic tissue. Because of the ethical issues involved in obtaining penetration data during an acute infection, we chose to look at penetration in the noninflamed situation, when patients were undergoing prostatic surgery for other reasons.

Most penetration studies performed with patients can only obtain a single sample of the drug's concentration at the desired site because of the invasive or destructive nature of sampling. This leads to difficulties in analyzing the data. Most often, paired plasma and peripheral site samples are obtained, and the ratio between the two is calculated. This is problematic because in most instances, system hysteresis exists, so that the ratio between plasma and peripheral site concentrations continuously changes, and the value for penetration obtained depends on the sampling time. Obviously, such a result is suboptimal. In this evaluation, we wished to handle the data in a more reasonable way so as to be able to obtain the best estimate of drug penetration into the prostate. This involved making sure that tissue samples were obtained throughout the 24-h dosing interval for levofloxacin and also ensuring that a robust plasma sampling schedule was in place for each patient. With such a data set, we applied population pharmacokinetic modeling as the analytic tool to allow calculation of the area under the concentration-time curve (AUC) of the drug both in plasma and in the prostate. The ratio of these AUC determinations was our estimate of prostate penetration.

MATERIALS AND METHODS

Patients.

Patients in three medical centers were studied. Patients who were undergoing prostatic surgery for benign prostatic hypertrophy and were 18 years of age or older were selected (age range, 47 to 94 years). Heights and weights ranged from 63 to 73 inches and from 107 to 253 pounds, respectively. Patients were of either Caucasian or Hispanic origin. Written informed consent was obtained from all patients according to institutional guidelines. Exclusions included (i) the presence of an indwelling Foley catheter for ≥4 days prior to surgery, (ii) an oral temperature in excess of 38°C or other evidence of infection within 24 h of surgery, (iii) administration of a fluoroquinolone other than the study drug from 72 h prior to surgery through the end of the period of sample acquisition, (iv) allergy to the fluoroquinolone class of antimicrobials, (v) a serum creatinine level of >2.0 or estimated (Cockcroft-Gault) creatinine clearance of <50 ml/min, (vi) an acute systemic illness, (vii) presence of a seizure disorder or any condition requiring the administration of major tranquilizers, (viii) use of any investigational drug or device within 30 days of study entry, and (ix) classification as a poor surgical risk.

Drug and drug administration.

Levofloxacin, 500 mg, was administered orally once daily starting 2 days prior to surgery. On the day of surgery, levofloxacin was administered as a 500-mg dose intravenously (i.v.) over 1 h. Actual infusion times were recorded.

Prostate sampling.

Patients were randomly assigned to receive their levofloxacin i.v. infusion in one of four time intervals: (i) 0 to 0.5 h prior to surgery (estimated), (ii) 3.75 to 4.25 h prior to surgery, (iii) 7.5 to 8.5 h prior to surgery, or (iv) 22 to 24 h prior to surgery. Protaste samples (3 to 10 g) were well timed during surgery and obtained with a paired plasma sample. The prostate sample was carefully blotted dry of all blood contamination and weighed prior to being frozen for subsequent levofloxacin concentration determination.

Plasma sampling.

The plasma sampling schedule was designed employing stochastic optimal design theory for use in population modeling. We had available a prior population pharmacokinetic model for levofloxacin derived from a large (n = 272) population of patients (7). This database had been analyzed with the NPEM program of Schumitzky and Jelliffe (8). Part of the output of this program is the MATLAB.M file, which provides the parameters for the discrete support points in the population distribution as well as the estimate of the probability of that particular support point in the population distribution. Consequently, this provides m parameter vectors and their associated probabilities (where m usually approximates the population, n). We did not consider parameter vectors with P values of <0.0001. All other parameter vectors were entered into the Optimal Sampling module of the ADAPT II package of programs of D'Argenio and Schumitzky (6). D optimality was the design criterion employed. The optimal sampling schedule for each parameter vector was recorded, along with its probability. These were then plotted on a frequency histogram employing 15-min intervals and corrected for probability. This provided a plot of the system information over time. This was used to select sampling times. The final sampling schedule was predose, near the end of infusion (it was requested to allow 1 to 2 min to elapse to avoid mixing transients), and 1.5, 2, 3.75, 5, and 6 h postinfusion. In addition, as noted above, a plasma sample was obtained from patients at the time of prostate biopsy.

Prostate and plasma levofloxacin concentration determinations.

Samples of plasma and prostatic tissue had levofloxacin concentrations determined by a well-validated high-performance liquid chromatography procedure (4). Separate standard curves were developed for plasma and prostate drug levels. Within- and between-day coefficients of variation were developed at low, middle and high concentrations of levofloxacin and were less than 5%. Plasma drug concentrations were expressed in micrograms per milliliter. Prostate drug concentrations were expressed in micrograms per gram of tissue.

Population pharmacokinetic modeling.

All plasma and prostate samples were subjected to simultaneous population analysis. There were 156 plasma samples available from 22 subjects (7.1 samples per patient). There were 20 prostate samples available for analysis. One patient's sample was lost. Another patient had a prostate drug concentration that was quite low. A plasma drug concentration obtained simultaneously from this patient was also quite low. A regularly scheduled plasma drug sample had been taken 42 min later that had a >7-fold-higher concentration. Because of this, we chose not to employ this plasma-prostate sample pair in the analysis.

Because we wished to employ an algorithm of demonstrated mathematical consistency and because multiple outputs were required, we employed the BigNPEM program of Jelliffe and Schumitzky. This program resides on the Cray T3E Supercomputer at the University of California, San Diego, Supercomputer Center, and access is available over the internet.

We employed a three-compartment open model with zero- or first-order input and first-order elimination. One compartment also had an explicit second volume, which served as the prostate equivalent compartment. This volume is a virtual volume and represents the rapidly exchangeable volume attendant to the prostate. The differential equations for the model and the output equations are displayed below:

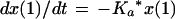1

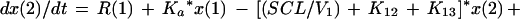2

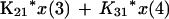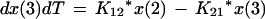3

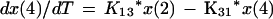4

For model outputs, plasma concentration = x(2)/V₁; prostate concentration = x(4)/V₂. The differential equations provide the rate of change of the amount of levofloxacin in the absorptive compartment (equation 1), plasma (equation 2), the peripheral compartment (equation 3), and the prostate (equation 4). R is the piecewise input function for levofloxacin i.v. administration, K_a is the absorption rate constant for oral levofloxacin administration, SCL is the clearance, V₁ and V₂ are the volume terms for the plasma and prostate, respectively, and all other K terms are first-order intercompartmental transfer rate constants.

We assumed that assay variance was the major component of total observation variance. We modeled the assay error with zero-through second-order polynomials. The final models for plasma and prostate were as follows:

plasma standard deviation = 0.00318 + 0.03259 × concentration + 0.00277 × concentration²

prostate standard deviation = 0.14018 + 0.00043*concentration + 0.00142*concentration²

The convergence criterion was 99.9999% of the true maximum-likelihood estimate.

Maximum a posteriori probability Bayesian parameter estimates for each patient were obtained employing the population of one utility of BigNPEM for both plasma and prostate outputs. These were employed to predict plasma and prostate drug concentrations at specified times for each patient.

Monte Carlo simulation.

The mean parameter vector and covariance matrix from the output of BigNPEM were embedded in SUBROUTINE PRIOR of the ADAPT II package of D'Argenio and Schumitzky (6). A log-normal distribution as well as a normal distribution was assumed. The distributions were differentiated on the basis of their ability to recreate the original mean parameter values. A 1,000-subject Monte Carlo simulation was performed with seven outputs: (i) plasma drug concentration, (ii) prostate drug concentration, (iii) plasma drug AUC, (iv) prostate drug AUC, (v) prostate drug AUC/plasma drug AUC ratio, (vi) amount of drug in plasma, and (vii) amount of drug in the prostate. The prostate drug AUC/plasma drug AUC ratio was depicted in a frequency histogram. The 95% confidence interval (as well as other statistics) was developed directly from the Monte Carlo simulation.

RESULTS

Demographics.

These patients are older than would be seen in a normal volunteer trial (see above). As levofloxacin is approximately 90% renally cleared, it is therefore understandable that one would expect plasma drug clearances that were lower than those seen in normal volunteer trials.

Pharmacokinetic parameter values.

The mean parameter values, median parameter values, and standard deviations are shown in Table 1, and the covariance matrix from the output is displayed in Table 2. As can be seen, the serum drug clearance is 7.27 ± 2.83 liters/h, and the volume of distribution of drug in the central compartment is 41.38 ± 25.97 liters. The prostate volume of drug distribution was 0.78 kg.

TABLE 1.

Pharmacokinetic parameter values from the population analysis of penetration of the prostate by levofloxacin

Measurement	Parameter
	V1 (liters)	SCL (liters/h)	K12 (h−1)	K21 (h−1)	K13 (h−1)	K31 (h−1)	V2 (kg)
Mean	41.38	7.27	13.42	18.56	2.887	51.77	0.779
Median	28.17	7.24	8.469	4.566	1.600	64.60	0.832
Standard deviation	25.97	2.83	9.20	24.32	2.869	26.18	0.252

TABLE 2.

Covariance matrix values

Parameter	Parameter
	V1	SCL	K12	K21	K13	K31	V2
V1	674.255
SCL	−19.6130	8.01426
K12	−20.7243	9.56949	84.6419
K21	552.551	−12.2919	54.4699	591.646
K13	−45.7275	4.09659	9.63338	−30.1985	8.23102
K31	63.7342	−25.8258	16.0352	78.0667	−7.65091	685.517
V2	2.31842	0.183003	0.0717147	1.08513	0.037635	−2.18603	0.06322

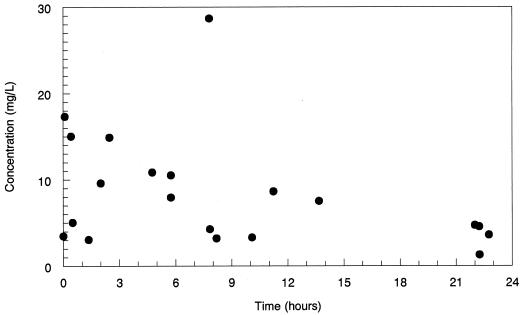
The actual prostate drug concentrations for 20 patients are displayed in Fig. 1. These values are timed with respect to the end of the i.v. infusion of levofloxacin.

FIG. 1.

Concentrations of levofloxacin in the prostate as determined by high-performance liquid chromatography. Times are after the end of the actual administration of the intravenous infusion are shown. ●, concentration of drug in prostate.

The results of the maximum a posteriori probability Bayesian estimation for the 156 plasma data points showed that the plot of observed versus predicted values had a regression line with an intercept of −0.008 and a slope of 1.041. The r² of this regression is 0.930 (r = 0.964), P ≪ 0.0001. The mean error (predicted versus observed values) was employed as a measure of bias and was −0.17 μg/ml. The mean squared error was used as a measure of precision and was 0.44 (μg/ml)².

The predicted versus observed values regression for the 20 prostate data points has an intercept of 0.09 and a slope of 0.996. The r² of this regression is 0.992 (r = 0.996), P ≪ 0.0001. The mean error was 0.059 μg/ml. The mean squared error was 0.161 (μg/ml)².

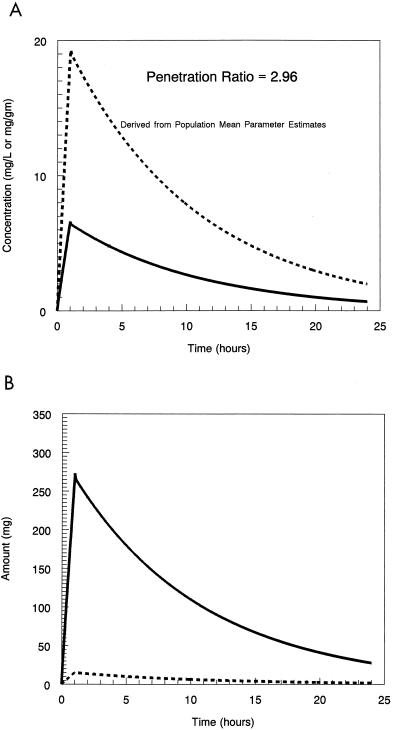
The concentration-time curves for drug in the plasma and prostate as simulated from the mean parameter values only are displayed in Fig. 2A. The penetration ratio for this is 2.96. The amount-time curve for drug in the plasma and prostate is displayed in Fig. 2B.

FIG. 2.

(A) Simulation from the mean parameter vector of the plasma and prostate concentration-time profiles of levofloxacin. (B) Simulation from the mean parameter vector of the plasma and prostate amount-time curves of levofloxacin. Dotted line, drug concentration in prostate; solid line, drug concentration in plasma.

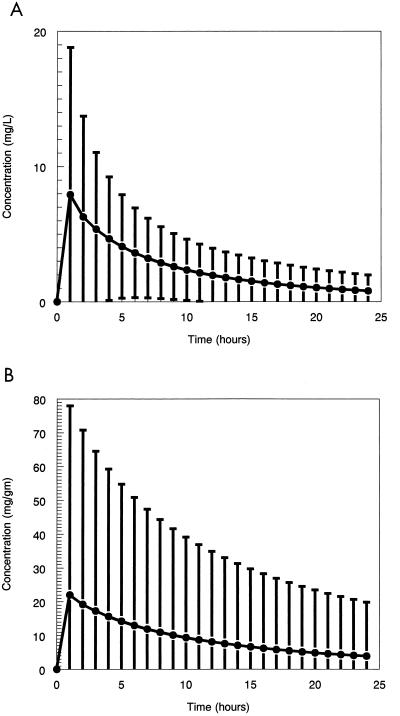
The Monte Carlo simulation using the log-normal distribution best recreated the initial mean values for the system parameters. This was used to create the mean curve of the 1,000-subject simulation and the 95% confidence interval about the mean for both the plasma and prostate samples. These are displayed in Fig. 3.

FIG. 3.

(A) Mean concentration-time curve in plasma and the 95% confidence interval derived from a Monte Carlo simulation. ●, drug concentration in plasma. (B) Mean concentration-time curve in the prostate and the 95% confidence interval derived from a Monte Carlo simulation. ●, drug concentration in prostate.

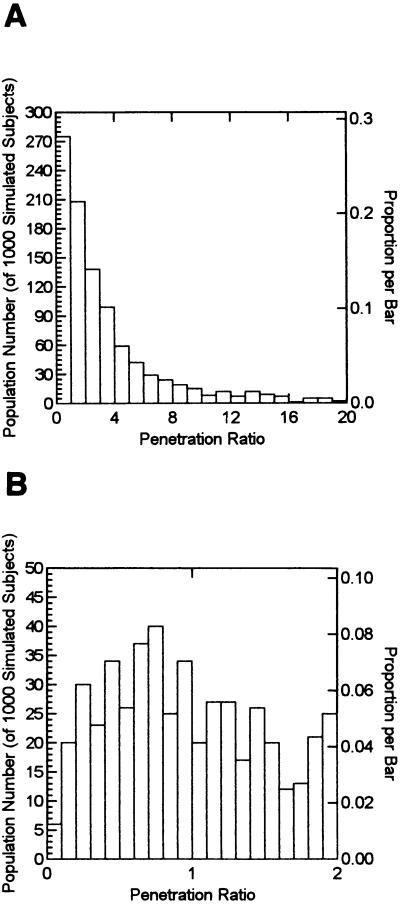
The mean, median, standard deviation, and 95% confidence interval of the observation values for the drug penetration ratio as calculated from the Monte Carlo simulation were 4.14, 2.08, 6.94, and 0.197 to 19.63, respectively.

In order to understand the true variability of drug penetration as might be seen in the clinical trial arena, we display this Monte Carlo simulation in Fig. 4. Figure 4A displays the full variability of drug penetration, with a penetration ratio range that exceeds 20. The largest penetration ratio was 95.30. This and 23 other values exceeding 20 were not displayed on the histogram for clarity. Figure 4B demonstrates how many subjects were at the low end for penetration. Of the simulated subjects, 72.5% had a penetration ratio that was 1.0 or greater.

FIG. 4.

(A) Histogram of a 1,000-subject Monte Carlo simulation of the AUC_prostate/AUC_plasma of levofloxacin. (B) As in panel A, but with only the range of the ratio of 0 to 2 displayed.

DISCUSSION

In order for an antibiotic to cure an infection, the antibiotic must be able to penetrate to the primary infection site. In most instances, this is not a problem, as most sites demonstrate the rapid exchange of drug from the central compartment to the peripheral site of infection (e.g., in lung tissue in pneumonia and skin in skin structure infection). However, there are several specialized sites where it is important to check drug penetration before initiating clinical trials. Certainly, cerebrospinal fluid, the vitreous of the eye, and the prostate must rank as the most important sites to delineate penetration before clinical trials (2).

Many penetration studies are flawed by their methods of analysis. Since obtaining serial samples is difficult to impossible in protected sites like those listed above, one must examine only a single sample from each site of interest from each patient. Using a site/plasma drug concentration ratio at a single time point as a measure of drug penetration is problematic, as there is often system hysteresis that causes the ratio to change nearly continuously with time. While straightforward to perform as a study and also straightforward to analyze, such investigations may give biased estimates of drug penetration, depending on the sampling time.

Consequently, we decided to approach this problem from the viewpoint of population pharmacokinetic modeling. We decided it was important to have information from all parts of the concentration-time curve obtained from the prostate samples. Therefore, we randomized patients as to when their prostate sample would be collected with regard to the dosing interval of 24 h.

The approach worked well, with the plots of predicted versus observed values demonstrating excellent regression relationships (r² = 0.930 and 0.992 for plasma and prostate, respectively), particularly for the prostate drug concentrations. Consequently, the results may be viewed with some degree of confidence.

The parameter values are likewise concordant with our expectations. The estimate of a mean clearance of 7.27 liters/h is to be expected from patients in the age range observed. The mean values for clearance and volume of drug distribution in the central compartment as well as marginal distributions fit well into the larger population of patients that our group has studied previously (7). It should be noted that the estimate of prostate volume was 0.779 kg. This should not be taken to indicate that the true prostate volume was this large, any more than one should assume from the volume of distribution of the central compartment of 41.38 liters that the circulating blood volume is this size. Rather, the central compartment represents the rapidly exchangeable compartment for plasma, and the prostate volume represents the rapidly exchangeable compartment size about the prostate.

When we calculate the penetration drug ratio, either from the mean parameters (2.96 [Fig. 2A]) or from the mean of a 1,000 subject Monte Carlo simulation (4.14), it is clear that much higher levofloxacin concentrations are present in the prostate, on average, than are present in the plasma. This seems to be an impossible finding. The answer is provided in Fig. 2B. The amount of drug present in the plasma always exceeds that present in the prostate. It is only because the volume of prostate distribution is much smaller that the concentrations become so great. The physiology that supports this finding is that fluoroquinolones, like levofloxacin, are able to take on a net charge at intracellular pH, rendering them subject to ion trapping intracellularly (1).

As we sampled only whole tissue, it is likely that the majority of the three- to fourfold increase in prostate drug concentrations seen here represents intracellular drug. If one examines levofloxacin penetration into other tissues representing interstitial fluid (5), it is clear that AUC ratios approximate 1.0. If this is also true for the interstitial fluid for the prostate, this means that extracellular concentrations would approximate those seen in plasma (AUCs are equal). The intracellular drug concentrations (which should constitute approximately 80% of the volume of a whole tissue biopsy [3]) should be approximately 3.8- to 4.8-fold that of the plasma drug concentration by AUC ratio.

On average, then, levofloxacin concentrations in either the extracellular space or the intracellular environment should be sufficient to provide a high probability of good clinical and microbiological outcomes when one considers the MICs for the target pathogens.

Figures 3 and 4 provide us with some insight into biological variability. When we administer a fixed dose of drug to a large number of patients, we often carry around a mental picture of the mean plasma or tissue drug concentration-time profile. The reality is much different. Figure 3 provides an idea of how variable the concentration-time profiles can be when administered to a large group of patients. Figure 4 allows us to see how the overall penetration of the drug varies.

Two things should be stated clearly. One is that levofloxacin is a drug that behaves very predictably. The coefficients of variation are quite small when one considers that patients are being studied under clinical conditions, making the results more predictable than with many other agents. The second is that the vast majority of patients had an excellent drug penetration into tissue, with over 70% of patients having an AUC ratio that exceeded 1.0. So, even if one considers the full range of variability, given the distribution of MICs for target pathogens (9), excellent clinical results can be expected. Finally, it should be emphasized that these penetration figures are minimal estimates, as none of our patients had any inflammation. Target patients with prostatitis should have sufficient inflammation to boost penetration considerably, adding to the degree of confidence engendered by these findings.

In summary, we have examined the penetration of the prostate by levofloxacin in a mathematically robust way, so as to obtain the most precise estimates of whole tissue penetration based on AUC ratios. We have also expanded this investigation to examine the full range of variability expected in a Monte Carlo simulation. The outcome of this study is clear. Given levofloxacin's profile of microbiological activity against target pathogens seen in prostatitis, its penetration to this protected site makes it likely that clinicians will find excellent clinical and microbiological outcomes in infected patients subsequent to its use. Clinical trials of this agent in prostatitis are warranted.