Dose-Dependent Pharmacokinetics of Amphotericin B Lipid Complex in Rabbits

Abstract

Amphotericin B lipid complex (ABLC) was recently approved by the Food and Drug Administration for treatment of patients with invasive fungal infections who are intolerant of or refractory to conventional amphotericin B therapy. Little is known, however, about the pharmacokinetics of this new antifungal compound. We therefore investigated the pharmacokinetics of ABLC in comparison with those of conventional desoxycholate amphotericin B (DAmB) in rabbits. The pharmacokinetics of DAmB in a rabbit model were similar to those previously reported in humans. The pharmacokinetics of ABLC differed substantially from those of DAmB. Plasma amphotericin B levels following ABLC administration were 10 times lower than those following administration of an equal dosage of DAmB. The levels of ABLC in whole blood were approximately 40 times greater than those in plasma. The ABLC model differed from the DAmB model by (i) a dose- and time-dependent uptake and return between the plasma compartment and apparent cellular components of the blood-sediment compartment and (ii) time-dependent tissue uptake and return to plasma from serially connected compartments. Following infusion of ABLC, there was a nonlinear uptake into the apparent cellular components of the blood-sediment compartment. This uptake was related to the reciprocal of the integral of the total amount of drug infused (i.e., the more drug infused the greater the fractional uptake between 0.5 and 5 mg/kg of body weight for ABLC). The transfer of drug from plasma to the cellular components of the blood-sediment compartment resulted in initial uptake followed by rapid redistribution back to the plasma. The study describes a detailed model of the pharmacokinetics of ABLC and characterizes a potential role of the cellular components of the blood-sediment compartment in the distribution of this new antifungal compound in tissue.

Invasive fungal infections have emerged as important causes of morbidity and mortality in immunocompromised hosts (14, 15). Desoxycholate amphotericin B (DAmB) remains the treatment of choice for treatment of many life-threatening opportunistic mycoses. However, dose-limiting nephrotoxicity often compromises the ability to administer DAmB, resulting in therapeutic failures. Certain lipid formulations of amphotericin B can be administered at higher dosages with reduced nephrotoxicity (6, 9, 13, 17).

Amphotericin B lipid complex (ABLC or Abelcet; The Liposome Company, Princeton, N.J.) was developed to reduce the toxicity and maximize the therapeutic utility of amphotericin B in the treatment of invasive fungal infections (10). The preparation of ABLC consists of amphotericin B complexed with two lipids in a 1:1 drug-to-lipid molar ratio. These lipids, dimyristoylphosphatidylcholine (DMPC) and dimyristoylphosphatidylglycerol (DMPG), are present in a 7:3 molar ratio.

Amphotericin B lipid complex was recently approved by the Food and Drug Administration for treatment of patients with invasive fungal infections who are intolerant of or refractory to conventional amphotericin B therapy. Despite its clinical availability, little is known about the pharmacokinetics of ABLC. As ABLC becomes more widely used, increased understanding of its optimal modes of administration, distribution, and clearance mechanisms becomes more imperative. We therefore investigated the pharmacokinetics of ABLC in comparison with those of conventional amphotericin B in rabbits in order to more clearly define the relationships of dosage, distribution, and clearance of this new agent.

A series of studies with conventional DAmB and ABLC were conducted with rabbits. The studies with DAmB were used to develop a compartmental model that with appropriate modifications would also describe the kinetics of DAmB after administration as the lipid complex (ABLC). As ABLC may be used over a range of dosages, its pharmacokinetics were studied at doses of 0.5 to 10 mg/kg of body weight.

When preliminary analysis of these single-dose data revealed a dose-related rapid disappearance of ABLC from plasma, we sought to identify a readily sampled tissue(s) responsible for this initial distribution. Therefore, cellular components of blood-sediment which may equilibrate with ABLC (3) were studied by sampling whole blood.

Finally, because the drug is most often chronically administered, a study with repeated dosing for 27 days was performed to evaluate the performance of the single-dose model in predicting the results of chronic administration. The data from each study with ABLC were fitted by using a nonlinear pharmacokinetic model constructed to explain the study data.

MATERIALS AND METHODS

Animals.

Female New Zealand White rabbits (weight, 2.5 to 3.5 kg) were used throughout these experiments. Animals were individually housed and were provided food and water ad libitum, following National Institutes of Health guidelines on the care and use of laboratory animals. Silastic venous catheters were surgically placed under sterile operative conditions for nontraumatic venous access, as described previously (16). The central silastic venous catheter facilitated parenteral administration of medications and withdrawal of blood for pharmacokinetics.

Antifungal compounds.

DAmB (Fungisone; Bristol-Myers Squibb, Princeton, N.J.) was reconstituted with distilled water, maintained at 4°C, and diluted 1:5 (by volume) with sterile 5% dextrose in water immediately prior to use. ABLC (The Liposome Company) was provided as a 5-mg/ml solution. The stock solution of ABLC was diluted 1:5 (by volume) with sterile 5% dextrose in water to yield an infusion solution of 1.0 mg/ml for ABLC.

Administration of antifungal compounds and plasma sampling.

DAmB (0.5 to 1.5 mg/kg) was administered by constant infusion over 5 min with subsequent sampling of plasma. Sampling times were at 0, 5, 10, 15, 30, and 60 min and 2, 3, 4, 6, 8, 12, 24, 48, and 72 h postinfusion. Infusion of DAmB at dosages of 0.5 to 1.0 mg/kg is well tolerated by rabbits. However, DAmB at 1.5 mg/kg is poorly tolerated by intravenous infusion over times that range from 5 to 15 min. Approximately one-half of the rabbits that receive DAmB at 1.5 mg/kg will sustain ventricular fibrillation, presumably due to the extracellular efflux of potassium due to amphotericin B-induced myocardial membrane injury during infusion through the central silastic venous catheter. Thus, the ability to study DAmB at 1.5 mg/kg was limited by the mortality induced by the drug at this dosage.

ABLC (0.5, 1.0, 2.5, 5.0, and 10.0 mg/kg) was administered by constant infusion over 5 min, with subsequent sampling of plasma. Four additional animals were given an infusion of the 5.0-mg/kg dose over 5 min, with whole blood then sampled. There was no intolerance of infusion of ABLC. The sampling times were the same as those for DAmB.

Analytical methods.

Amphotericin B levels in plasma were assayed by high-pressure liquid chromatography based upon a modification of the method developed by Granich et al. (8). Calibration curves were prepared with plasma with low (25 to 1,000 ng/ml) and high (1 to 20 μg/ml) concentration ranges. The resulting curves were linear, with correlation coefficients of 0.998. Assay sensitivity was 25 ng/ml, with intraday variabilities of 10.2 and 5.4% at concentrations of 75 and 1,000 ng/ml, respectively. Interday variabilities at these respective concentrations were 12.4 and 6.2%. Assay accuracy was 92%.

Whole-blood samples that contained ABLC were analyzed by extraction with dimethyl sulfoxide-methanol, after an aliquot had been removed for analysis of plasma, with the resulting supernatant being quantitatively injected onto a high-pressure liquid chromatograph for analysis by UV detection. The assay did not use an internal standard. Standard calibration curves prepared with whole blood were constructed in the ranges of 50 to 100 ng/ml and 1 to 30 μg/ml. Intraday variability at concentrations of 50 ng/ml and 20 μg/ml were 6.5 and 3.2%, respectively, with interday variabilities at the same concentrations being 7 and 5.1%, respectively. Assay accuracy was 95%, and drug recovery was 90%.

Data analysis.

Plasma and cellular components of blood-sediment data were fitted simultaneously by using CONSAM. (The CONSAM software is available at no cost from Peter Greif at the National Cancer Institute, Building 10, Room 6B13, Bethesda, MD 20892 [(301) 496-8915], or by e-mail [Greif@SAAM.NCI.NIH.GOV] or anonymous FTP [ftp@SAAM.NCI.NIH.GOV].) When the final model was developed, the parameters were adjusted individually for each rabbit by nonlinear least-squares techniques to obtain a best fit of the data, as judged visually both by the sum of squared deviations of the model-calculated values from the observed data and by the magnitude of the percent coefficient of variation for the estimated parameters. Clearance from plasma was estimated as the quotient of the administered dose and the fitted area under the plasma concentration-time curve.

Model validation.

Model validation was done by external validation (4), with the single-dose data for the 5-mg/kg dose with sampling of whole blood used as the training data set and the data from the chronically infused rabbit, from which only plasma was sampled, used as the validation data set. Both sets of data were analyzed by use of the full model.

RESULTS

DAmB model.

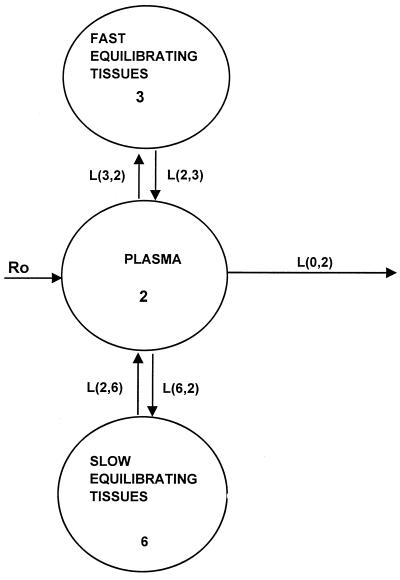
The reported pharmacokinetic properties of DAmB include multicompartmental kinetics, a half-life of 24 to 48 h, excretion via urine and bile, partitioning into hydrophilic environments, and binding to cellular components of blood-sediment and plasma proteins. In order to account for these properties and the present observations, a previously proposed model for DAmB (2) which included separate equilibrium distributions of drug in plasma with fast compartments (interstitial fluid of tissues with discontinuous capillaries [liver, spleen, and intestine]) with small distribution volumes, slowly equilibrating tissues (interstitial fluid of muscles and blood cells), and elimination from plasma was used to describe the data (Fig. 1).

FIG. 1.

Model for DAmB showing all linear transfers with equilibrium between compartment 2 and compartments 3 and 6.

The rate constants L(3,2) and L(2,3) (for intercompartmental transfer between fast equilibrating tissues and plasma, respectively), L(2,6) and L(6,2) (for intercompartmental transfer between slowly equilibrating tissues and plasma, respectively), and L(0,2) (elimination of drug from plasma) were estimated from the best fit of the data. All kinetic transfers were first order, and the volume of plasma in the rabbit was estimated to be 38.8 ml/kg (T. J. Walsh, T. Whitcomb, and P. A. Pizzo, Abstr. Am. Soc. Microbiol. Conf. Candida and Candidiasis. Biology, Pathogenesis, and Management, abstr. 1341, 1996), while the volume of the cellular components of blood-sediment was 16.8 ml/kg (18). The differential equation used to describe the concentration of drug in the central compartment is given in the Appendix.

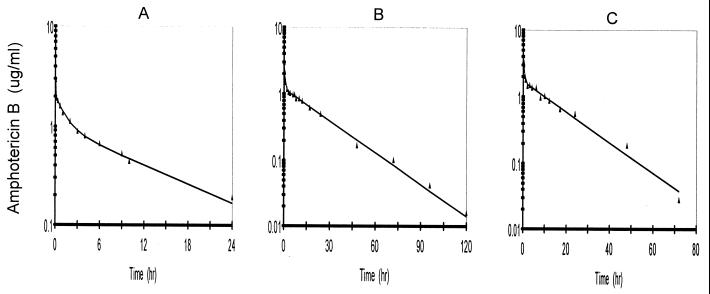
The fitted data for individual rabbits that received doses of 0.5, 1.0, and 1.5 mg/kg are presented in Fig. 2. Model parameters based upon the fitted data are given in Table 1. The fitted parameters for equilibration between compartments 2 and 6 were similar for all three doses. However, the rate constants L(3,2) and L(2,3) for equilibration with compartment 3 were larger for the 1.5-mg/kg dose but smaller for the 1.0- and 0.5-mg/kg doses. The area under the plasma concentration-time curve as a function of dose presented in Table 1 exhibits an apparent loss in dose proportionality after administration of the 1.0-mg/kg dose.

FIG. 2.

Best-fit curves for amphotericin B in rabbits that received 0.5 mg (n = 3) (A), 1.0 mg (n = 3) (B), and 1.5 mg (n = 2) (C) of DAmB per kg via a 5-min infusion.

TABLE 1.

Parameter values for the rabbits dosed with DAmB at 1.5, 1.0, and 0.5 mg/kg via a 5-min infusion based on the best fit of the curves for concentrations determined in plasma^a

Parameter	1.5 mg/kg	1.0 mg/kg	0.5 mg/kg
L(3,2) (h−1)	2,653 [5,000–306]b	111.9 (33) [154.4–86.4]	136.2 (16) [149–110.6]
L(2,3) (h−1)	301.2 [558–44]	13.3 (80) [25.5–6.6]	28.0 (21) [31.5–21.2]
L(0,2) (h−1)	1.26 [1.26–1.16]	0.97 (20) [1.2–0.7]	0.89 (2.7) [0.9–0.8]
L(2,6) (h−1)	0.69 [0.9–0.4]	1.14 (91) [2.3–0.4]	1.22 (61) [1.6–0.4]
L(6,2) (h−1)	8.64 [10.7–6.5]	6.01 (55) [9.7–3.3]	8.77 (69) [12.3–1.8]
Clearance (ml/h)	124	80 (46)	77 (50)
AUCc (μg · h/ml)	31.78	28.5 (18)	17.2 (27)

^aValues are means (±coefficients of variation) for three rabbits for all doses except the 1.5-mg/kg dose, for which only the mean for two rabbits is presented. 

^bValues in brackets are the rate constant range. 

^cAUC, area under the concentration-time curve. 

ABLC model.

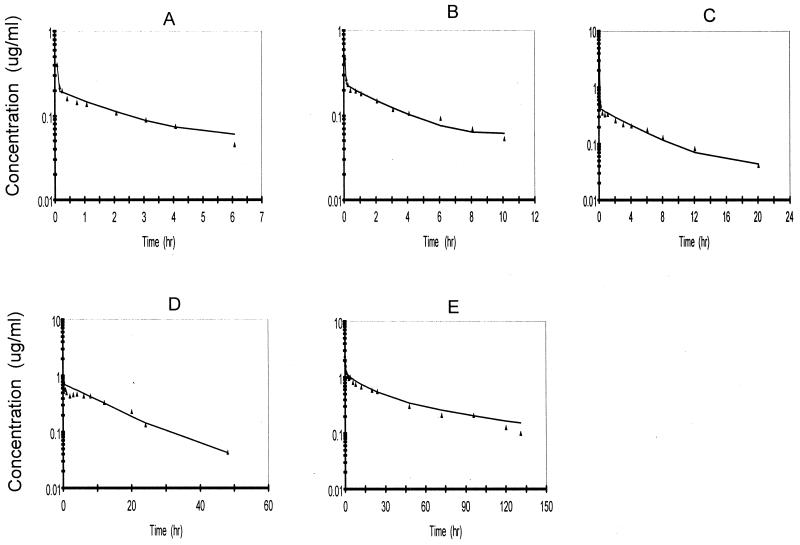
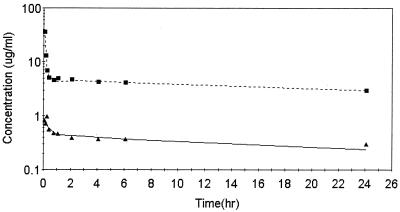
The a priori model used to begin the development of a suitable model to describe the pharmacokinetics of ABLC in rabbits was based upon several changes in that for DAmB. The DAmB model was modified to account for observations at doses between 2 and 10 mg/kg. It was apparent from preliminary examination of the data for the amphotericin B concentration in plasma (Fig. 2) following DAmB administration that they were much higher following the 5-min infusion than following administration of the equivalent dose of ABLC (Fig. 3). This apparent drug formulation effect was investigated with an additional study with four rabbits that received 5 mg/kg, with sampling of whole blood to determine if significant levels of ABLC were associated with blood compartments. From this supplemental study it was apparent that the uptake (association with) of ABLC by cellular components of blood-sediment occurred during the infusion period, resulting in levels in cellular components of blood-sediments 40-fold higher than the levels in plasma at the end of the infusion (Fig. 4). This information was used to modify the DAmB model to describe ABLC by including the following factors: (i) dose- and time-dependent uptake by (association with) and return from cellular components of blood-sediment and (ii) time-dependent tissue uptake and delayed return to plasma.

FIG. 3.

Best-fit curves for amphotericin B with the ABLC model for rabbits following administration of ABLC at doses of 0.5 mg/kg (n = 4) (A), 1.0 mg/kg (n = 4) (B), 2.5 mg/kg (n = 4) (C), 5.0 mg/kg (n = 4) (D), and 10.0 mg/kg (n = 3) (E) via a 5-min infusion.

FIG. 4.

Best-fit of amphotericin B levels in red cell-sediment (A) and plasma (B) for rabbit B, which received 5 mg of ABLC per kg, with the ABLC model.

The transfer of drug from cellular components of blood-sediment to plasma, L(2,6), was described by a function (see equation A3 in the Appendix) whose sign at the beginning is negative, indicating that initially the net transfer of drug is only from plasma to cellular components of blood-sediment. At some point during infusion, L(2,6) switches to a positive value. The values for L(2,6) during infusion are related to the reciprocal of the cumulative amount of drug infused. Thus, the larger the amount of drug infused per unit of time, the higher the total dose, the slower the increase of L(2,6) toward zero, and the smaller the positive value of L(2,6) prior to the end of the infusion at 5 min. During the infusion period, the larger the infusion rate, the greater the amount of drug accumulated by (associated with) the cellular components of blood-sediment at the end of the infusion period. This function was turned off at 5 min (i.e., the end of infusion) via a step function, u(t − a) (equation 1).

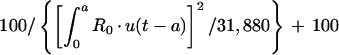1

where t is time elapsed since initiation of drug input, a is the length of infusion, u(t − a) is equal to 1 for t less than a, and u(t − a) is equal to 0 for t greater than a, and R₀ is the amount infused over 5 min.

In other words, the amount of ABLC within the apparent cellular components of the blood-sediment compartment is dependent on the balance between the rates of association and disassociation with the cellular components of blood-sediment. As these rates cannot be independently determined from this study design, we chose to make the fractional rate of accumulation constant and build the nonlinearity and time dependence into the rate of dissociation of ABLC from the cellular components of blood-sediment. However, during infusion, prior to collection of data, we modeled L(2,6) so that it was negative (i.e., double arrow in Fig. 5). This not only allowed control of efflux from the cellular components of the blood-sediment but also facilitated a very rapid influx of drug to the cellular components of the blood-sediment compartment to describe the observed high levels in blood at the end of the infusion as a function of the ABLC dose (Fig. 3).

FIG. 5.

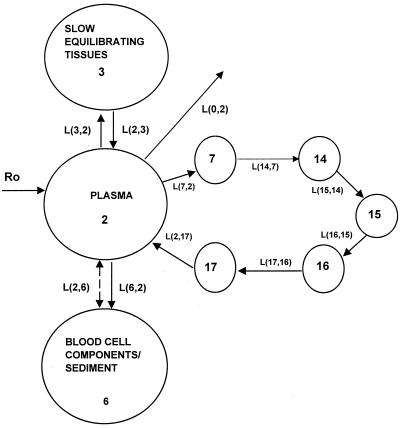
Model for amphotericin B in rabbits following ABLC administration. The model consists of red blood cells (compartment 6) and plasma (compartment 2). The model has a nonlinear return from red blood cells to plasma, a time-dependent uptake of drug into compartment 7 with a delayed return to plasma, an equilibrium with compartment 3, and nonlinear elimination from the central compartment.

The final model was determined from the sampling of whole blood after administration of the 5-mg/kg dosage to rabbits. This dosage is that which is currently approved by the Food and Drug Administration for treatment of invasive aspergillosis in humans. The amphotericin B levels in the cellular components of blood-sediment were estimated from the concentrations in whole blood on the basis of the rabbits' hematocrits and the concentrations in plasma.

Similar to DAmB, there was an equilibrium of ABLC with a peripheral compartment. However, unlike DAmB, ABLC required a slow time-dependent uptake into peripheral compartment 7, with a delayed return to plasma. The return of drug from compartment 7 to plasma was first order. The rate constants for the delayed uptake into the peripheral compartments, L(14,7), L(15,14), L(16,15), L(17,16), and L(2,17), were all set equal to the same value to allow each to contribute to drug delay equally.

Elimination of drug from the central compartment, L(0,2), was dependent upon the quotient of the concentration in plasma and the cumulative area under the curve to 5 min (see equation A2 in the Appendix), which resulted in the elimination of a decreasing fraction of drug with time. The final model is presented in Fig. 5.

The results of the fits for the rabbits from which plasma and whole blood were sampled are given in Table 2. The results reveal very large rate constants for transfer of drug from plasma to compartment 3 and also from plasma to the cellular components of blood-sediment.

TABLE 2.

Parameter values for four rabbits dosed with 5 mg of ABLC per kg via a 5-min infusion based on best-fit curves from concentrations determined in whole blood and plasma

Parameter	Rabbit A	Rabbit B	Rabbit C	Rabbit D	Mean (CVc)
L(3,2) (h−1)	1,600	3,200	4,812	2,260	2,968 (47)
L(2,3) (h−1)	10.84	16.49	10.60	5.06	10.74 (43)
L(6,2) (h−1)	163.2	297	342	188	247.6 (34)a
P(2)b	1.97	3.70	4.68	1.97	3.08 (32)a
P(3) (h−1)	9.9 × 10−4	8.0	9.9 × 10−4	9.9 × 10−4	2.02 (197)
P(4) (h−1)	1,678	96.14	1.36	1,678	847.9 (108)
P(6) (h−1)	2.8 × 10−3	2.3 × 10−2	2.8 × 10−3	2.3 × 10−2	0.014 (93)a
P(10) (h−1)	1.62 × 10−5	4.72	1.62 × 10−5	1.62 × 10−5	1.18 (199)
P(12) (h−1)	63	58.04	51.51	52.1	56.2 (9.7)
P(13) (h−1)	12.5	12.0	17.87	17.75	15.0 (21)a

^aThe mean values of the parameters from these fits were used to define the red blood cell compartment for the animals from which whole blood was not collected. 

^bNo units. 

^cCV, coefficient of variation. 

Although most of the values were similar for the four rabbits that received 5 mg/kg and from which whole blood was sampled, the parameters related to tissue uptake and delayed return to plasma, i.e., P(3), P(4) [the exponential and intercept in equation A3 in the Appendix that define L(7,2)], and P(10) (P values are unassociated nonlinear estimated parameters in SAAM [simulation, analysis, and modeling]), did exhibit large interanimal differences.

This was a result of the fact that the values for these tissue parameters were estimated solely from concentrations in plasma. Therefore, P(10), P(3), and P(4) were highly variable, as indicated by their high coefficients of variation.

The mean blood-sediment parameters for the rabbits from which whole blood was sampled was used to define the cellular components of the blood-sediment compartment for those animals from which only plasma was sampled. Parameters L(2,3), L(3,2), P(10), P(4), and P(3), related to uptake by other tissue, were allowed to vary to fit the data for the rabbits from which only plasma was sampled. Although the same mean cellular components of the blood-sediment parameters were used for each dose, the dose effect was reflected in L(2,6) by the magnitude of R₀ (i.e., the amount of drug infused), as defined by equation A3 in the Appendix, during the 5-min infusion.

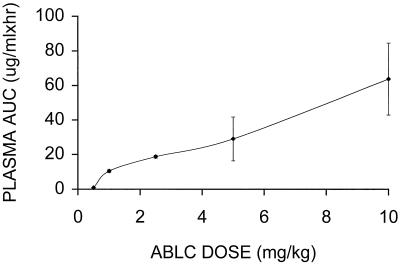
The dose effect seen for the rabbits on the basis of the analysis of plasma is presented in Fig. 3, which gives representative individual fits for curves for concentrations in plasma after administration of 0.5, 1.0, 2.5, 5.0, and 10.0 mg/kg. A nonlinear response to dose is indicated by the 10-fold increase in initial levels in plasma following a 20-fold increase in the dose. The values of the parameters from the fits are given in Table 3. The parameters for plasma did not exhibit a trend related to dose. However, there was some indication of nonlinearity in the area under the plasma concentration-time curve versus dose (Fig. 6) above 5 mg/kg. This was supported by the 95% confidence interval (i.e., 4.8 to 2.4) for the mean slope calculated by using a power model (7).

TABLE 3.

Parameter values for rabbits dosed with ABLC at 10, 5, 2.5, 1.0, and 0.5 mg/kg on the basis of the best-fit curves determined from concentrations in plasma^a

Parameter	10 mg/kg	5 mg/kg	2.5 mg/kg	1.0 mg/kg	0.5 mg/kg
L(3,2) (h−1)	4,071.7 (88) [7,806–580]b	10,153 (163) [35,000–1,137]	3,425.2 (72) [6,854–1,563]	1,218.5 (34) [1,832–899]	784 (28) [1,100–605]
L(2,3) (h−1)	32.6 (130) [81.4–2.9]	61.6 (165) [21.4–6.6]	31.6 (84) [70–13]	13.2 (15) [15.8–11.3]	13.6 (3) [17.9–11.4]
P(10)c	19.2 (148) [52–0.04]	0.13 (38) [0.18–0.09]	0.71 (122) [2–0.2]	0.5 (46) [0.75–0.2]	0.003d
P(4)	672.6 (84) [1,000–17]	25 (40) [40–20]	23.5 (65) [46–12]	11.7 (22) [15.5–9.5]	10.9 (22) [13–7.9]
P(3)	1.74 (94) [3.3–0.03]	0.10 (156) [0.35–0.02]	10.7 (87) [23–0.06]	30d	30d
Clearance (ml/h)	476.2 (75)	523.2 (47)	415.2 (8.5)	248.7 (8.0)	1,918 (12)
Red blood cell area (μg · h/ml)e	448,100 (71)	111,566 (92)	34,700 (83)	19,275 (37)	10,925 (3)

^aOnly plasma was sampled from these animals. Values are mean (±coefficient of variation) for four rabbits for all doses except the 10-mg/kg dose, for which the values are for three rabbits. 

^bThe rate constant range is given in brackets. 

^cAll delay rate constants [i.e., L(7,2), L(14,7), L(15,14), L(16,15), L(17,16), and L(2,17)] for the nonlinear tissue uptake were set equal to P(10) for each rabbit, the slowest turnover time. 

^dThe value was fixed at a lower dose; therefore, no percent coefficient of variation is reported for these doses. 

^eRBC areas were derived from the best-fit curves for ABLC concentrations plasma. 

FIG. 6.

Plot of area under the plasma concentration-time curve (AUC) (± standard deviation) for amphotericin B versus dose based upon the best-fit curves for plasma for the rabbits that received ABLC at 0.5 to 10 mg/kg.

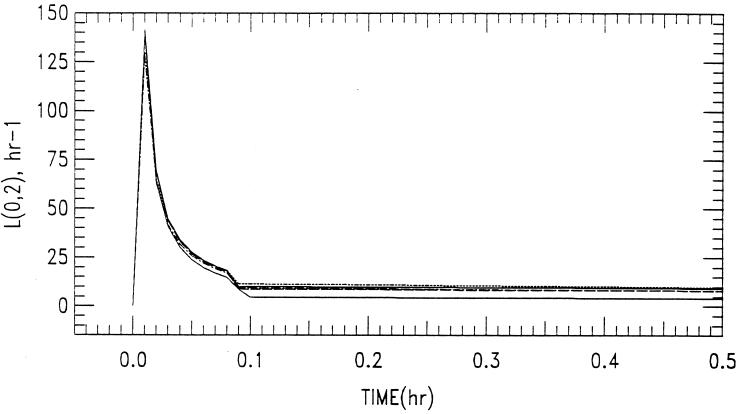
The maximum capacity for an association between the cellular components of blood-sediment and ABLC was achieved with doses of between 5 and 10 mg/kg, as indicated by the unexpected increase in the initial postinfusion concentration to 4 μg/ml for a dose of 10 mg/kg compared to the low initial postinfusion values (1 μg/ml) for doses of between 0.5 and 5 mg/kg. The change in the rate constant for the elimination of ABLC from the central compartment with respect to dose and time, L(0,2), is given in Fig. 7. Figure 7 shows that as time increases, there is a decrease in the rate constant for the elimination of amphotericin B following ABLC dosing, L(0,2).

FIG. 7.

Rate constant for elimination from the central compartment, L(0,2), plotted as a function of dose versus time. ABLC was administered at 0.5 mg/kg (.....), 1.0 mg/kg (–––), 2.5 kg/kg (–.–.–), 5.0 mg/kg (-----), and 10.0 mg/kg (——) (curves from top to bottom, respectively) via a 5-min infusion.

Model validation.

The mean values for the variable parameters L(3,2), L(2,3), P(10), and P(4) from the data obtained after administration of a single dose of 5 mg/kg in Table 2 were used to fit the data obtained after administration of multiple doses by allowing these parameters to deviate by no more than 10% from the mean. The resulting fit indicated that the parameters related to the recycling of ABLC from the single-dose model would have to be quite different to adequately predict the multiple-dose data.

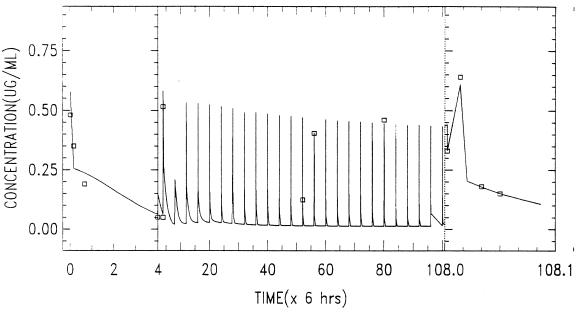
Further testing and application of the model was done by fitting the data from the multiple-dose study by allowing the parameters L(3,2), L(2,3), P(10), P(3), and P(4) to vary as required to best fit the data. The best fit of the validation data following chronic administration of 5 mg/kg for 27 days is given in Fig. 8. Visual inspection of the data indicates that the single-dose model adequately predicts the effects of administration of multiple doses of ABLC to rabbits but requires a different set of parameter values related to tissue recycling of drug. On the other hand, the nonlinear functions related to the cellular components of blood-sediment and elimination were predictive for the multiple-dose data. Best-fit parameters (and their respective coefficients of variation) were as follows: L(3,2), 3,997 h⁻¹ (11.8 h⁻¹); L(2,3), 8.42 h⁻¹ (1.69 h⁻¹); P(10), 0.073 h⁻¹ (60 h⁻¹); P(3), 1.6 × 10⁻³ h⁻¹ (86 h⁻¹); and P(4), 1.29 × 10³ h⁻¹ (112 h⁻¹).

FIG. 8.

Data obtained following the chronic administration of ABLC at 5 mg/kg/day for 27 days via a daily 5-min infusion to a rabbit. The levels in plasma following chronic administration were fit by using the model presented in Fig. 5.

DISCUSSION

The data obtained in this study demonstrate differences in the pharmacokinetics of amphotericin B when it is infused as DAmB (a mixed micellar dispersion) or as ABLC (a ribbon-like lipid structure which is not a true liposome). Pharmacokinetic data for DAmB appeared to be linear to 1 mg/kg, as has been reported previously (2). As illustrated in Fig. 1, the model developed by Atkinson and Bennett (2) to describe the data for the concentration in plasma included equilibrium with a fast and a slowly equilibrating tissue. The pharmacokinetics of DAmB in a rabbit model was similar to that in humans (2). All transfers and elimination from the central compartment were linear. The equilibrium with compartment 6 was speculated to represent interaction with cellular components of blood-sediment on the basis of the large uptake of AmB when it is given as the lipid complex (ABLC). The previously reported nonlinearity above 1 mg/kg was not further investigated, but it is possible that it may also be related to an interaction with cellular components of blood-sediment (2, 3).

Administration of amphotericin B as ABLC resulted in significant changes in the pharmacokinetics of the parent compound. The most notable changes in pharmacokinetics were the substantially smaller plasma amphotericin B concentrations after the administration of 10-mg/kg doses of ABLC compared to those seen after administration of the largest DAmB dose (1.5 mg/kg). This difference appears to be the result of the nonlinear uptake of ABLC by (association with) the cellular components of blood-sediment and/or cell membranes. This greater proportional amount of drug delivered to tissues may have important implications for the greater efficacy of higher dosages against severe infections.

The nonlinear uptake of ABLC by tissue was related to the reciprocal of the integral of the total amount of drug infused over 5 min, as described in equation 1. Consequently, the greater the amount infused the smaller the rate constant L(2,6) for the transport of amphotericin B from cellular components of blood-sediment to plasma during the 5-min infusion. During the 5-min infusion, the value for L(2,6) is initially negative and becomes positive, which would not be considered physiologically possible. Although alternative models without negative rate constants that describe the data during infusion exist, it would be difficult to definitively establish an appropriate model during the infusion since samples were not collected during the 5-min infusion. The change in sign is a technique that allows the nonlinear process to be attributed to the transfer of drug from cellular components of blood-sediment to plasma. However, this does not preclude the possibility that the transfer from plasma to cellular components of blood-sediment is also nonlinear. The procedure that we chose allows the appropriate accumulation of drug by (association with) the cellular components of the blood-sediment compartment to simulate the observed datum points for cellular components of blood-sediment and plasma at the conclusion of the 5-min infusion. Conversely, the smaller the amount of ABLC infused over time, the greater the amount of drug delivered to plasma, thus permitting the drug to reach other tissues. Thus, a slow rate of infusion may permit improved delivery to noncellular components of blood-sediment tissue compartments (i.e., interstitial fluid of tissues with discontinuous capillaries [liver, spleen, and intestine]).

Figure 6 shows the nonlinear relationship between the area under the concentration-time curve and dose for plasma following dosing with ABLC. Initially, little drug escapes the blood-sediment, resulting in low levels in plasma which increase with dose and result in an apparent nonlinearity between 0.5 and 1 mg/kg. The derived area under the curve data for blood-sediment in Table 3 shows nonlinearity for doses between 5 and 10 mg/kg, although it is not clearly seen for the concentration in plasma since the concentration in plasma is in equilibrium with those in several other tissues and plasma is not the tissue of origin for the nonlinearity. On the other hand, the area under curve data for plasma in Table 1 show that some possible nonlinearity for DAmB occurs at a dose of 1.5 mg/kg, although the small sample size precludes a definitive conclusion.

Approximately 2 to 5% of the administered DAmB has been reported to be excreted unchanged in urine and bile each (1, 2, 4,5). No metabolites have yet been identified in plasma or urine. The model used to describe the kinetics of amphotericin B after the administration of DAmB has linear elimination. However, the elimination rate constant L(0,2) becomes nonlinear when AmB is administered as ABLC. This change is dependent on both the time following infusion and the total dose infused and suggests diminished renal or hepatic function with time during infusion.

As ABLC is used over a number of dosages, understanding of its pharmacokinetic parameters may further facilitate improved approaches to administering this novel agent. ABLC is approved for use for the treatment of invasive aspergillosis at 5.0 mg/kg/day. However, higher dosages (7.5 to 10 mg/kg/day) are sometimes used to treat profoundly immunocompromised patients whose infections fail to respond to 5.0 mg/kg/day (9). A lower dosage of 2.5 mg/kg/day was administered for 6 weeks for the successful treatment of hepatosplenic candidiasis in children (Walsh et al., Abstr. Am. Soc. Microbiol. Conf. Candida and Candidiasis).

The role of cellular components of blood-sediment in serving as a major compartment carries several pathophysiological implications. This interaction occurs in the apparent absence of hemolysis. First, the improved therapeutic index afforded by the DMPG-DMPC (3:7) lipid complex protects cellular components of blood-sediment from high concentrations of AmB, in contrast to the effect observed with DAmB, in which hemolysis occurs at relatively low concentrations (11). Second, immunocompromised patients receiving ABLC for treatment of life-threatening mycoses are often anemic, with hematocrit values 25 to 50% below normal baseline values. The implications of anemia on the pharmacokinetics of ABLC have yet to be explored; however, anemic states may allow transfer of ABLC to noncellular components of blood-sediment membrane sites that otherwise would not be involved in patients with normal hematocrit values. Third, the impact of acquired or inherited membrane defects in cellular components of blood-sediment that result in altered binding or interaction sites could further influence the distribution of ABLC (12).

The transfer of ABLC into noncellular components of blood-sediment tissue compartments occurs predominantly in reticuloendothelial system (RES) tissues, particularly the liver and spleen. The slow time-dependent uptake into peripheral compartment 7 with a delayed return to plasma may reflect this uptake by RES tissues. This distribution into RES tissues provides a compelling pharmacodynamic rationale for treatment of hepatosplenic (chronic disseminated) candidiasis. These properties have led to the use of ABLC in a protocol for children with hepatosplenic candidiasis (17; Walsh et al., Abstr. Am. Soc. Microbiol. Conf. Candida and Candidiasis). All patients in that study responded to ABLC with complete or partial resolution of physical findings and lesions of hepatosplenic candidiasis. During the course of ABLC infusions and monitoring, there was no progression of hepatosplenic candidiasis, breakthrough fungemia, or posttherapy recurrence. Hepatic lesions continued to resolve after completion of administration of ABLC, reflecting the high concentrations in the liver and spleen.

The physiological entities which comprise the cellular components of blood-sediment compartment are red blood cells, leukocytes, platelets, lipoproteins, and nonlipoprotein plasma proteins. This was presented as the rapidly equilibrating compartment since clear definition of the component which interacts with ABLC and which results in high blood ABLC levels would require the analysis of washed red blood cells to be certain that the reported levels are a result of drug that has partioned into the red blood cell and not merely the result of an association with the cellular components of blood-sediment.

In summary, this study is the first to our knowledge to describe a detailed model of the pharmacokinetics of ABLC and the first to characterize a possible role of the cellular components of the blood-sediment compartment in the distribution of this novel antifungal compound in tissue.

Appendix

Model equations for amphotericin B in the central compartment (C_P):

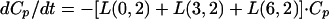A1

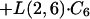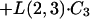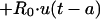where C₆ and C₃ are amounts in compartments 6 and 3, respectively.

Model equations for ABLC in the central compartment:

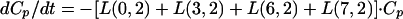A2

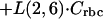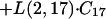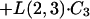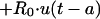where C_rbc is the red blood cell sediment compartment.

Model equation for cellular components of blood-sediments:

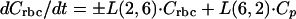A3

where

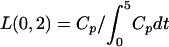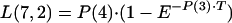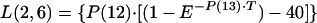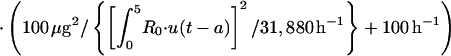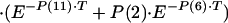where E is exponential function for natural log, P(11) is 1.0 h⁻¹, and T is time.