Abstract
The human gait can be described as the synergistic activity of all individual components of the sensory–motor system. The central nervous system (CNS) develops synergies to execute endpoint motion by coordinating muscle activity to reflect the global goals of the endpoint trajectory. This paper proposes a new method for assessing temporal dynamic synergies. Principal component analysis (PCA) has been applied on the signals acquired by wearable sensors (inertial measurement units, IMU and ground reaction force sensors, GRF mounted on feet) to detect temporal synergies in the space of two-dimensional PCA cyclograms. The temporal synergy results for different gait speeds in healthy subjects and stroke patients before and after the therapy were compared. The hypothesis of invariant temporal synergies at different gait velocities was statistically confirmed, without the need to record and analyze muscle activity. A significant difference in temporal synergies was noticed in hemiplegic gait compared to healthy gait. Finally, the proposed PCA-based cyclogram method provided the therapy follow-up information about paretic leg gait in stroke patients that was not available by observing conventional parameters, such as temporal and symmetry gait measures.
Keywords: gait, gait cycle, ground reaction force, inertial measurement unit, principal component analysis, stroke, synergy, wearable device
1. Introduction
The central nervous system (CNS) controls many degrees of freedom (DOFs) of the musculoskeletal system, coordinating many muscle activities on many joints. Human movements can have different trajectories, speeds, and accelerations even when they achieve the same goal. To control so many DOFs, it becomes necessary for the CNS to have a complex and delicate organizational structure [1]. Different mathematical approaches for modeling realistic multi-joint movements were suggested in the literature, based on the various optimization functions such as minimum jerk [2,3], minimum torque change [4], minimum effort [5], as well as more complex functions [6,7]. An organizational approach based on activities of functional groups (called synergies) was also suggested [8]. Synergies represent patterns of body segment coactivations. Researchers have hypothesized that the nervous system activates synergies by a neural signal and creates a set of temporal–spatial synergy modules. These modules represent a smaller dimensional space than the space formed by individual DOFs. Synergies can be found at various levels, such as joint coordinates or muscles [9,10]. Kinematic synergies may result from muscle synergies, i.e., as a consequence of muscle activity [11,12]. In addition, researchers have suggested that CNS develops synergies to execute endpoint motion [13,14]. Motor intra-limb coordination is the ability to coordinate segments in a sequence [15]. This coordination can be accomplished by controlling the endpoint trajectory.
The human gait can be described as a synergistic activity of all individual components of the human sensory–motor system. Different mathematical models of muscle synergies are known in the literature: invariant temporal (“temporal synergies”), spatial (“synchronous synergies”), and spatiotemporal (“time-varying synergies”) [16]. All of these approaches reduce the dimensionality of the movements, but they are not equivalent to each other.
Temporal muscle synergies imply the existence of a set of temporal components common to different activation tasks [17,18]. Ivanenko et al. [19] showed that there is a basic set of five temporal components extracted from recorded electromyography (EMG) signals in controls and patients with a spinal cord injury (SCI). The consistent timing of motor patterns across various walking tasks was shown even with considerable variation of muscle coactivation. These temporal components represent the timings of the intersegmental coordination and may reflect a neural strategy for coordination in a low dimensional set of patterns that facilitate control of gait. Furthermore, these timings are argued to represent a control variable in central pattern generators [20]. Furthermore, it was reported that the nervous system’s activation pattern during walking does not depend on walking speed, including running [21].
However, EMG analysis has certain limitations; for example, adipose tissue can affect EMG recordings. There is also the problem of muscle crosstalk and a lack of deep muscles reliability [22]. Furthermore, it was shown that the synergy structure is dependent on the number and choice of muscles [23]. On the other hand, the intermediate dynamic representation is a logical connection between highly variable muscle activity and whole-body mechanics [20].
The synergism in people without sensorimotor impairment differs from patients with sensorimotor disorders. Injury to the CNS, such as stroke, leads to changes in gait modality and synergism [24]. These differences can be observed concerning the parameters that characterize gait. Characteristics of gait in stroke hemiplegic patients are: decreased speed, decreased and asymmetrical step length, decreased stance and single support times on the affected side, changes in joint kinematics, and overall asymmetry in different metrics [25]. The rehabilitation process restores the gait, i.e., retrains the patient to stand and walk with reduced sensory–motor resources and to walk in the way most similar to the gait before the disorder. During rehabilitation, it is essential to objectively quantify the success of the applied protocols and therapies on gait performance.
The gold standard for quantitative gait analysis implies the usage of high cost, space, and time-consuming 3D motion capture systems and force platforms [26,27]. Recently, the development of wearable technology enabled the usage of alternative low-cost approaches for gait assessment based on inertial measurement units (IMU) and ground reaction force (GRF) sensors [28,29]. These portable, wireless systems are suitable for clinical and home monitoring [30]. They are easy to use, non-invasive, small, compact, and robust enough to provide valuable information for the objective evaluation of the gait performance of people with neurological disorders [31,32]. Conventionally, the prerequisite for quantitative gait analysis is gait segmentation. Several algorithms were developed to tackle this problem in IMU-based systems, such as zero-crossing and threshold methods [33,34]. However, these algorithms usually have lower accuracy in pathological gait [35]. The gold standard for gait phase partitioning is the measurement signal of the direct contact between the foot and the ground. For this reason, some wearable systems, in addition to the IMUs, also contain foot pressure insoles in shoes. However, gait phases’ detection accuracy and reliability also depend on the location of the GRF sensors [36]. It is difficult to determine the heel-strike events automatically in the recordings of the person after a stroke, precisely because of the problem with the drop foot [37]. Thus, a gait analysis methodology that does not need the segmentation process is preferred.
The principal component analysis (PCA) has been widely used to discover “hidden” patterns in the high dimensional space of human gait signals in healthy and pathological gait [19,38,39]. Many researchers used PCA to identify muscle [21] and limb synergies [40], which are proposed to be building blocks for motor behavior [19]. Recently, it was shown that the space of two-dimensional PCA cyclograms allows simple assessment of gait performance in stroke hemiplegic patients [41].
This study aims to evaluate whether invariant (temporal) features of synergies can be extracted by analyzing foot (endpoint) dynamics (kinetics and kinematics) acquired by a wearable device, without the need for gait segmentation and need of EMG data acquisition. PCA was applied on the signals acquired by wearable sensors (IMU and GRF integrated into shoe insoles and mounted on feet) to detect temporal synergies in the space of two-dimensional PCA cyclograms. The idea of invariant temporal components “hidden” in motion dynamics signals was explored, as shown in the literature for EMG signals [19]. To test the hypothesis about invariant temporal dynamic synergies, the gait was analyzed at different speeds in healthy subjects. The gait of stroke hemiplegic patients before and after the rehabilitation therapy was also analyzed. The differences between healthy and pathological gait patterns were observed concerning the parameters which define the temporal dynamic synergies. Additionaly, it was investigated whether the method for detecting temporal dynamic synergies from IMU and GRF signals has an additional practical value for the paretic side recovery follow-up of stroke patients compared to the conventional gait analysis results, such as symmetry and temporal gait parameters.
2. Materials and Methods
2.1. Subjects
Nineteen subjects took part in this study: 14 healthy persons (without sensory–motor deficiency) and five hemiplegic stroke patients in the subacute phase (4–6 months after stroke). Subject characteristics are shown in Table 1. The patients could follow instructions from clinicians. The patients could walk with or without cane support.
Table 1.
Subject characteristics.
| Variable | Mean ± SD | |
|---|---|---|
| Healthy Subjects (n = 14) | Patients (n = 5) | |
| Age (years) | 34.8 ± 12.6 | 61 ± 5.1 |
| Gender | 8 male, 6 female | 1 male, 4 female |
| Total body mass (kg) | 73.3 ± 12.7 | 78.4 ± 9.2 |
| Height (m) | 1.78 ± 0.08 | 1.7 ± 0.05 |
| BMI (kg/m2) | 23 ± 2.18 | 28.18 ± 3.6 |
| Affected side | - | 4 left, 1 right |
The patients participated in functional electrical stimulation (FES)-based therapy. The effectiveness of FES therapy for the drop foot correction was assessed by observing the neuroplasticity changes using electroencephalography examination. Eight-channel MOTIMOVE electronic stimulator (3F—FIT FABRICANDO FABER, Belgrade, Serbia, [42]) was used for FES therapy, augmenting the patient’s pedaling (OMEGO® Plus, Graz, Austria, [43]). The duration of the rehabilitation protocol was four weeks. The healthy subjects did not participate in the FES therapy.
The experimental design was approved by the ethical review board of the Rehabilitation Clinic “Dr Miroslav Zotović” in Belgrade. Participants were well-informed about the noninvasive protocol and they signed informed consent forms prior to gait assessment.
2.2. Instrumentation
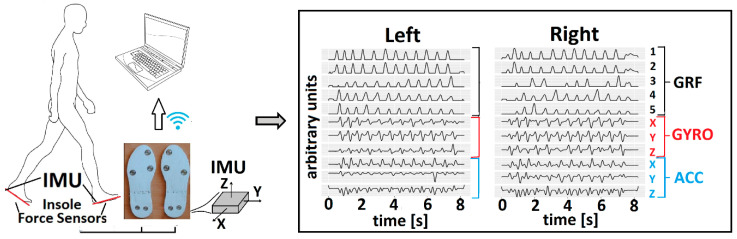
The Gait Teacher (RehabShop, Belgrade, Serbia) [44] was used in the study. This system comprises 10 GRF sensors (five per foot insole) that measure vertical forces and two IMUs (MPU6050 module) with integrated three-axis accelerometers and gyroscopes into the insoles. Each foot insole has two piezoresistive GRF sensors in the heel zone (medial heel—HeelM, lateral heel—HeelL), two sensors in the metatarsal (medial metatarsal—MetaM, lateral metatarsal—MetaL), and one sensor in the toes zone (Toe). Each sensor can estimate pressure up to 3.5 MPa. The characteristics of GRF sensors are: linearity < ±0.25% FS, BFSL, repeatability < ±0.075% FS, hysteresis < ±0.05% FS, zero thermal error < 0.75% FS, @35 °C, span thermal error < 0.75% FS, @35 °C, and stability error < ±0.2% FS/year. The gyroscope and accelerometer specifications within IMU are: supply voltage 2.3–3.4 V, consumption 3.9 mA, calibration tolerance ±3%, I2C interface support, and operating temperature −40 °C to −85 °C. The IMU can measure the 3D acceleration (range of ±4 g) and the 3D angular velocity (range of ±500 deg/s). The 3D directions in the IMU are as follows: the z-axis directs up from the insole, the x-axis directs ahead, and the y-axis directs medially. The direction of angular velocity ωx is from heel to toe. This angular rate is perpendicular to the insole (frontal plane). The rate ωy is also orthogonal to the insole and directed laterally. The angular rate ωz is in the plane of the insole pointing up. Each insole is wirelessly connected to the computer. Eleven signals from each insole are transferred at a sampling rate of 100 Hz. The acquisition software was built in LabView (National Instruments, Austin, TX, USA). The built-in software synchronizes IMU and GRF sensors. The system provides data with a time delay of 20 ms. Data are stored in text format (.txt) for further offline analysis (Figure 1). In conclusion, the data obtained with the Gait Teacher are a set of five GRF time series and six-time series of angular velocities and accelerations per insole. The output is a large matrix with 22 components [41].
Figure 1.
Gait Teacher instrumentation and output signals from both insoles.
2.3. Experiment Protocol
The Gait Teacher insoles were fitted to the subjects’ shoes. First, the outputs from GRF sensors were zeroed: a participant raised the left foot and then the right and held it in the air for about 2 s (no load) while the clinician pressed the set button on the host computer. The IMU signals were zeroed while the participant stood on both feet for about 2 s.
Healthy subjects walked on a flat surface 10 m long. Before the recording, the respondent practiced walking for a few minutes. Signals from all sensors were recorded from three consecutive sessions. They walked at different speeds: 0.4 m/s, 0.8 m/s, 1 m/s, 1.6 m/s, and 2 m/s. The lowest speed was chosen to mimic the speed of the patients after stroke in the subacute phase ~0.4 m/s [45]. The highest speed was set to be the highest speed of the oldest participant. The oldest participant in the study was a healthy individual, 70 years old, and the maximal speed for this age is ~2 m/s [46]. Different speeds were recorded to address the diversity of different gaits and therefore generalize results from temporal synergies detection as much as possible, controlling for speed. To ensure a particular gait speed on the ground (avoiding the treadmill effect on the gait performance [47]), the subject followed the sound of the metronome, which signaled the cadence depending on the desired walking speed (Table 2). Markers were placed at one of the predefined distances: 0.5, 0.75, and 1 m, Figure 2. The markers were not moved between consecutive gait sessions of one participant for the same walking speed. This distance between markers was changed depending on the height or walking speed of the participant, so that the subject feels comfortable while walking. For higher subjects or higher speeds, markers were set at a greater distance. The metronome signaled the beginning of each stride, which occurred at specific markers on the floor. Table 2 shows the cadences required for different speeds, on a path of 10 m, for three possible stride lengths (the most suitable one for a particular respondent, heuristically chosen depending on the subject’s height and the specified speed).
Table 2.
Cadence for various speeds and stride lengths on a path of 10 m (SPM = strides per minute).
| SPM | |||||
|---|---|---|---|---|---|
| 0.5 m | 240 | 192 | 120 | 96 | 48 |
| 0.75 m | 160 | 128 | 80 | 64 | 32 |
| 1 m | 120 | 96 | 60 | 48 | 24 |
Figure 2.
An example of the experimental setup.
The patients were asked to walk at a self-selected preferred speed. Signals from all sensors were recorded from three consecutive sessions. The rest between runs was about 1 min long. The clinician could monitor the signals on the computer screen during the recording. Signals recorded from sensors mounted on the paretic leg before therapy (p.b.), nonparetic leg before therapy (np.b.), paretic leg after therapy (p.a.), and nonparetic leg after therapy (np.a.) were separately analyzed. The number of strides performed by healthy subjects was 534, 534, 400, 366, and 300, respectively for speeds: 0.4 m/s, 0.8 m/s, 1 m/s, 1.6 m/s, and 2 m/s. The number of strides performed by patients was 110 before and 168 after therapy.
2.4. Data Preprocessing
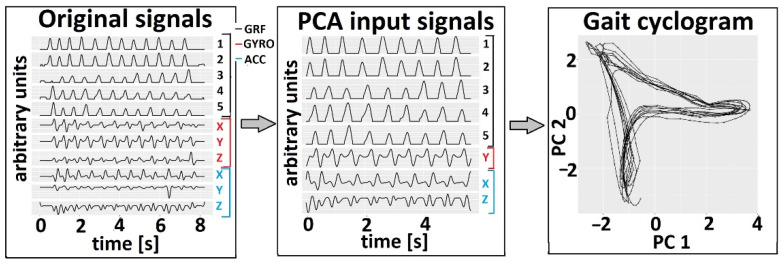
The first and last strides were excluded from the gait analysis since the person needs to adapt the gait speed to the sound of a metronome. The signals were filtered by a low-pass Butterworth filter, third order, with a cut-off frequency of 5 Hz [48]. Signals obtained by sensors from different legs were analyzed separately. The input for PCA included five signals from five GRF sensors, angular velocity in the sagittal plane, Gyro_Y, and accelerations in the frontal plane, Acc_X, and transverse plane, Acc_Z, (in total, eight signals per leg, Figure 3). They are chosen heuristically because the gait is predominant in the profile plane. All PCA and statistical analyses were done in the R software environment, version 3.5.1.
Figure 3.
PCA cyclogram generation in the first two principal components space. Example data are from a person with no known sensory–motor impairment. The original signals were acquired by the Gait Teacher system (left panel). The subset of signals from the whole gait session (middle panel) was used to form a cyclogram (PC2 vs. PC1, right panel).
2.5. Detection of Temporal Synergies
PCA was used to find common temporal components hidden in the waveforms of dynamics’ signals. The PCA input signals were normalized to have unit variance. Bartlett’s sphericity test showed that the signals were suitable for PCA [49]. The PCA allowed the mapping of original data into the orthogonal space, where the principal axis is the direction of the data’s maximal variance [50].
The analysis included calculating the correlation matrix, extracting the principal component of the varimax rotation, and calculating factor scores. These factor scores can be interpreted geometrically as the projections of the observations onto the principal components [49]. The whole preprocessed gait session (gait cyclogram) per subject was input for PCA. Therefore, the standardization across subjects with a different range of motions (subjects may engage in different walking strategies) was avoided [41]. After PCA, no stride segmentation was performed. Consequently, there was no need for the time interpolation of the signals for separate gait cycles.
The proposed method uses 2D gait cyclograms to represent recorded foot dynamics in the space of the first two principal components, PC1 and PC2 (Figure 3). The repetitive nature of near-cyclic events resulted in the overlapped cyclogram (cyclograms of gait cycles were overlapped) [41]. The calculation of principal components’ quantitative parameter of cyclogram, introduced in [41], is shown in Equation (1) and expressed as an angle θ in each time point (observation).
| (1) |
where PC1 and PC2 are the coordinates of the observations on the first two principal components (PC).
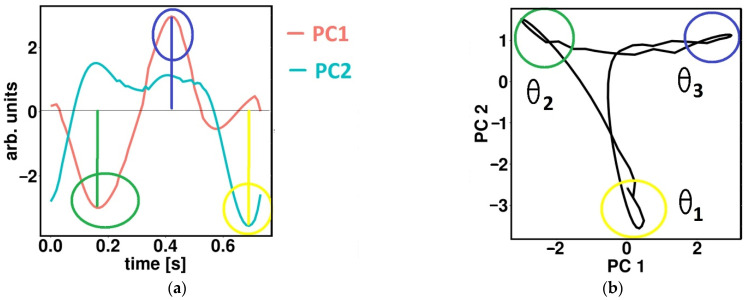
Figure 4a shows examples of specific time points where three temporal components exist during the single gait cycle by different colors (green, blue, yellow). These points correspond to the local extremums of PC1 or PC2. In Figure 4b the corresponding points of temporal synergy are presented in gait cyclogram using the same colors as in Figure 4a. The corresponding angles θ of observations that belong to each of three temporal components are marked by θ1, θ2, and θ3.
Figure 4.
Representation of temporal synergies on the first two components on: (a) time PC signals; (b) PCA gait cyclograms. Time activations of temporal synergies are displayed using different colors (green, blue, yellow).
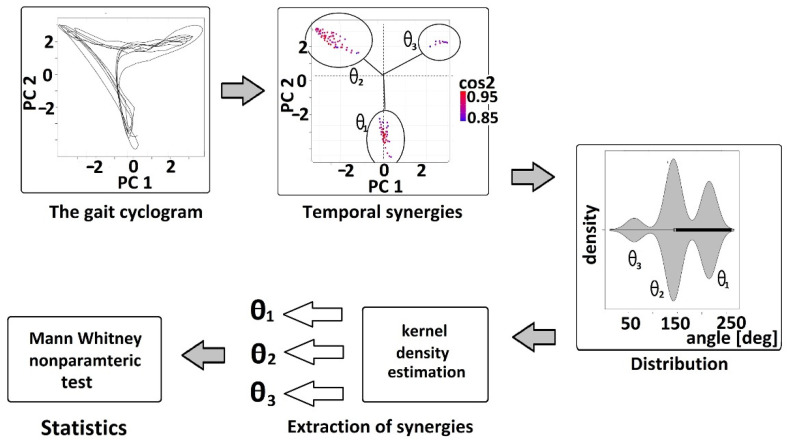
The overall schema of the performed methodology on the PCA gait cyclogram is shown in Figure 5, and it includes:
Figure 5.
Temporal synergies detection from the PCA gait cyclograms.
(1) Thresholding of gait cyclograms—Only observations (points in time) where principal components contribute significantly have been extracted and analyzed; namely, the threshold values for the squared cosine of the angle θ which was set heuristically to 0.8 ( and ).
(2) Estimation of the distribution density applying nonparametric kernel density estimation (KDE) [51] on the angle θ (obtained after thresholding in the last stride)—KDE was obtained for nine groups of data separately: H2, H1.6, H1, H0.8, H0.4 (both legs analyzed together for healthy subjects with the following walking speeds: , , , , , respectively), Pp.b and Pp.a (patients’ paretic legs before and after therapy), Pnp.b and Pnp.a (patients’ nonparetic legs before and after therapy). Shapiro–Wilk normality test [52] was used to check the (non)normality of the distributions.
(3) Clustering of distribution density to three clusters θ1, θ2, and θ3 (related to three temporal components) for each of nine groups—distribution density was smoothed by the bandwidth parameter. The bandwidth of the kernel is a free parameter that exhibits a strong influence on the resulting estimate; it is the real positive number that defines the smoothness of the density plot. The formula used to calculate optimal bandwidth parameter bw for each group is shown in Equation (2) [53].
| (2) |
where n is the number of observations of X, Var(X) is its variance, and IQR(X) is the interquartile range. Cluster limits were extracted as local minimums of the bandwidth smoothed distribution density.
(4) Statistical analysis—Mann–Whitney U nonparametric test was performed to determine whether the same clusters (detected temporal synergies) differ statistically between patients and healthy groups [54]. Wilcoxon test for partially matched two sample data (the combination of Wilcoxon signed-rank statistics for paired data and Mann–Whitney U statistics) was used to compare healthy groups for different speeds [55]. The same test was used to compare patients before and after therapy. Finally, it was analyzed whether the statistically significant results before and after therapy can be assessed based on temporal synergism and compared the effects to conventional parameters (Section 2.6). The significance level was p = 0.001 for estimating the statistically significant differences.
2.6. Conventional Gait Analysis
The threshold method extracted the swing and stance phases for each gait session. The threshold was set to be 5% of the sum of all GRF signals in each insole divided by the number of force sensors, which was 5. The signals were filtered by a low-pass Butterworth filter, third order, with a cut-off frequency of 5 Hz. For each stride, stance and swing durations were calculated as a percentage of the gait cycle. In addition, since gait after stroke is characterized by high asymmetry, four symmetry measures were calculated for both the swing and stance phase, as in Equations (3)–(6). These measures were used to assess therapy impact on stroke patients [56,57].
| (3) |
| (4) |
| (5) |
| (6) |
where is the duration of the specific gait phase (stance or swing) for the left leg, and is the duration of the specific gait phase (stance or swing) for the right leg.
Whether statistically significant results could be assessed before vs. after therapy was assessed using the Wilcoxon test for partially matched two-sample data. The significance level was p = 0.001 for estimating the statistically significant differences.
3. Results
3.1. PCA Cyclograms
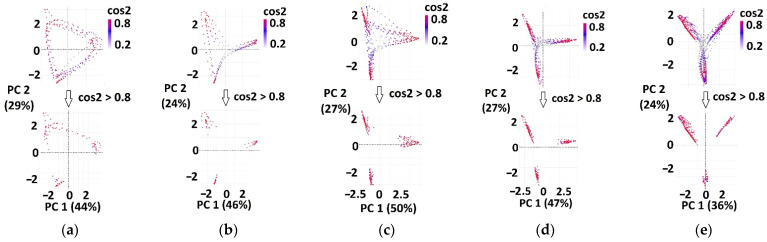
Figure 6 (top) presents an example of overlapped cyclograms in a healthy subject for gait sessions with different gait speeds. For healthy subjects, the signals from sensors mounted on left and right feet were analyzed together. Figure 6 (bottom) shows thresholded cyclograms ( and , as explained in Section 2.5) that contain observations where temporal synergies are activated.
Figure 6.
Examples of overlapped cyclograms for one healthy subject’s gait session (top) and thresholded cyclograms (bottom). Extracted (red) observations on thresholded cyclograms correspond to temporal synergies in PCA space, for the following gait speeds: (a) ; (b); (c) ; (d); (e). In brackets, the percentages of explained variance of the specific principal component (PC1 or PC2) are shown.
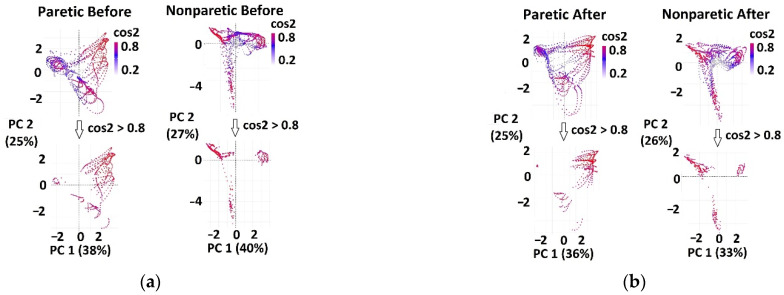
Cyclograms for patients’ paretic and nonparetic sides, before and after therapy, were separately analyzed (Figure 7).
Figure 7.
Examples of overlapped cyclograms for one patient (top) and thresholded cyclograms (bottom). Extracted (red) observations on thresholded cyclograms correspond to temporal synergies in PCA space: (a) before therapy (the paretic leg is in the left column, the nonparetic leg is in right column), and (b) after therapy (the paretic leg is in the left column and the nonparetic leg is in right column). In brackets, the percentages of explained variance of the specific principal component (PC1 or PC2) are shown.
Angles θ were calculated by Equation (1) for each observation on thresholded cyclograms (for red points in Figure 6 bottom and Figure 7 bottom). Arrays of angles’ values for each of nine groups (H2, H1.6, H1, H0.8, H0.4, Pp.b, Pnp.b, Pp.a, Pnp.a) were further used as an input for KDE.
3.2. Temporal Synergies Extracted by KDE
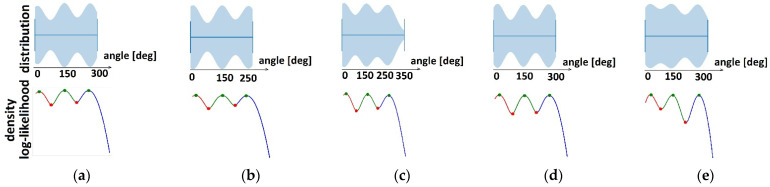
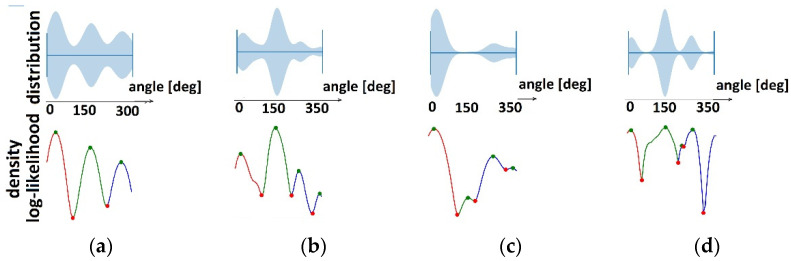
KDE was used to detect temporal synergies (clusters in time) for each of the nine groups. The cluster limits were estimated (Table 3) as local minimums in bandwidth-smoothed density distribution plots (red dots in Figure 8 and Figure 9).
Table 3.
Cluster limits (temporal components) in distribution density of angle values θ1, θ2, and θ3, mean ± standard deviation, all expressed in degrees.
| Healthy Subjects | Patients before Therapy |
Patients after Therapy |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H2 | H1.6 | H1 | H0.8 | H0.4 | Pp.b | Pnp.b | Pp.a | Pnp.a | ||
| cluster limits | [198–360] | [198–360] | [198–360] | [206–360] | [213–360] | [257–360] | [235–360] | [191–360] | [206–360] | |
| mean ± SD | 265 ± 14.9 | 262 ± 15.7 | 266 ± 7.9 | 271 ± 15.8 | 276 ± 12.8 | 318 ± 24.4 | 295 ± 38.6 | 291 ± 40.3 | 272 ± 27.6 | |
| cluster limits | [73–197] | [73–197] | [73–197] | [88–205] | [81–212] | [110–256] | [110–234] | [118–190] | [59–205] | |
| mean ± SD | 138 ± 8.9 | 138 ± 7.5 | 140 ± 9.7 | 147 ± 14 | 147 ± 22.6 | 183 ± 26.1 | 172 ± 18.4 | 162 ± 4.3 | 152 ± 11.7 | |
| cluster limits | [0–72] | [0–72] | [0–72] | [0–87] | [0–80] | [0–109] | [0–109] | [0–117] | [0–58] | |
| mean ± SD | 16 ± 7 | 13 ± 5.2 | 13 ± 8.3 | 21 ± 12.9 | 23 ± 16.7 | 36 ± 18.9 | 39 ± 12.7 | 25 ± 12.7 | 12 ± 6.9 | |
Figure 8.
Clustering of temporal components in healthy subjects for the following gait speeds (red dots are cluster limits): (a) ; (b); (c) ; (d); (e). Top graphics represent distribution densities, and bottom graphics represent bandwidth-smoothed distribution densities.
Figure 9.
Clustering of temporal components (red dots are cluster limits) in patients for: (a) Paretic legs before therapy; (b) Nonparetic legs before therapy; (c) Paretic legs after therapy; (d) Nonparetic legs after therapy. Top graphics represent distribution densities, and bottom graphics represent bandwidth-smoothed distribution densities.
In Table 3, cluster limits in distribution density of angle values θ1, θ2, and θ3 are shown in degrees for healthy subjects and patients before and after therapy.
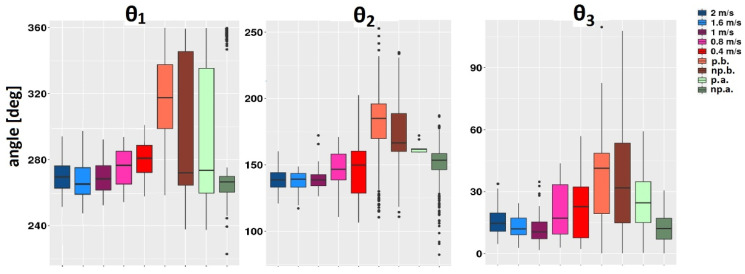
Based on Equation (1), the mean values and standard deviations of the θ1, θ2, and θ3 angles in cyclograms (i.e., the significant contribution of activation of the first two principal components) are shown in Table 3 for all patients and healthy subjects with different speeds. It could be noticed that the angles were shifted in time by approximately one-third of the walking cycle. These angles quantify temporal activations of gait synergies.
3.3. Comparison of Synergies between Different Speeds in Healthy Subjects
No significant differences were found between H2, H1.6, H1, H0.8, H0.4 groups for θ1, θ2, and θ3 (p > 0.001).
3.4. Comparison of Synergies between Patients and Healthy Subjects
Table 4 shows the results of statistic tests between healthy groups (H2, H1.6, H1, H0.8, H0.4) and patients (Pp.b, Pnp.b, Pp.a, and Pnp.a). Significant differences were found in all angles (θ1, θ2, and θ3) between all healthy groups and paretic leg gait before therapy (Pp.b). After therapy, the shift in the angle towards a healthy angle can be found in some angles, specifically for the lowest gait speed (), which is the most similar to the speed of the patient’s gait after stroke [58].
Table 4.
Statistical differences between healthy and patient groups (before and after therapy).
| Patients | Pp.b. | Pnp.b. | Pp.a. | Pnp.a. | ||
|---|---|---|---|---|---|---|
| Healthy | ||||||
| 0 * | 0 * | 0 * | 0 * | |||
| 0 * | 0 * | 0 * | 0 * | |||
| 0 * | 0 * | 0 * | 0.008 | |||
| 0 * | 0 * | 0 * | 0 * | |||
| 0 * | 0 * | 0 * | 0 * | |||
| 0 * | 0 * | 0 * | 0.332 | |||
| 0 * | 0 * | 0.001 | 0.115 | |||
| 0 * | 0 * | 0 * | 0 * | |||
| 0 * | 0 * | 0 * | 0.594 | |||
| 0 * | 0 * | 0.022 | 0.045 | |||
| 0 * | 0 * | 0 * | 0.004 | |||
| 0 * | 0 * | 0.024 | 0.002 | |||
| 0 * | 0.588 | 0.301 | 0.001 | |||
| 0 * | 0 * | 0.008 | 0.138 | |||
| 0 * | 0.002 | 0.190 | 0.001 | |||
* p < 0.001.
3.5. Comparison of Synergies between Patients before and after Therapy
The significant differences in patients before and after therapy were found in all angles θ1, θ2, and θ3 (p < 0.001). The boxplots for each angle θ1, θ2, and θ3 for all nine groups are shown in Figure 10. The temporal synergies (angles) shift can be observed after therapy towards healthy synergies.
Figure 10.
Temporal synergies (angles θ1, θ2, and θ3) for all groups.
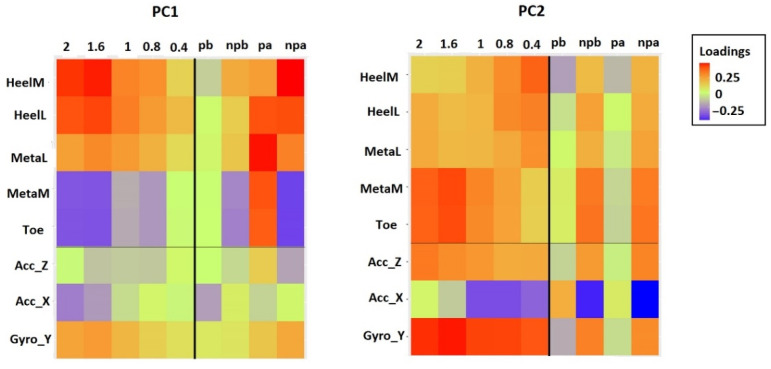
Additionally, it is important to consider the relative weight of each dynamic’s signal, which is called loading. Loadings from the first two principal components are interpreted as the coefficients of the linear combination of the input variables from which the principal components are constructed. The relative strength of the effect of each factor on an input signal is given by this weighting coefficient. For each input signal, the mean weighting coefficients (loadings) of the first two components were obtained by averaging the values across all subjects for specific gait speed [19]. Figure 11 shows average weighting coefficients for all nine groups. Some input variables loaded highly on the specific component, such as angular velocity Gyro_Y on PC2. Most of the input variables are loaded on both components. The noticeable gradual change of weightings with gait speed can be noticed in loadings on both PC1 and PC2. For patients, it could be noticed that loadings in PC1 are approaching values from healthy subjects’ gaits.
Figure 11.
Weighting coefficients of the PC1 and PC2 for all groups. Coefficients are plotted on a color-coded scale.
3.6. Comparison with Conventional Methods
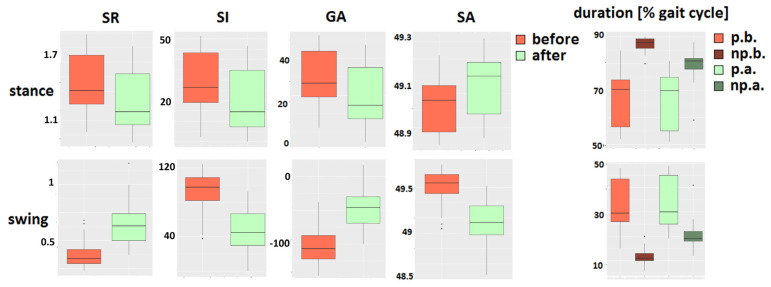
In Figure 12, boxplots for symmetry (SR, SI, GA, SA) and temporal (duration) parameters of stance and swing gait phases are shown.
Figure 12.
Boxplots of symmetry and temporal parameters for all patients’ groups.
No significant differences between gait before and after therapy with the paretic leg could be found in swing or stance duration (p = 0.94). A significant difference has been found in swing and stance durations in nonparetic leg gait. Furthermore, this significant difference was reflected in swing symmetry parameters since it is proportional to the ratio of paretic and nonparetic leg parameters (p < 0.001) but not in the stance symmetry parameters (p = 0.017–0.019).
Unlike temporal parameters for the paretic leg, by observing the temporal synergies parameters (Equation (1)), the statistically significant differences for the paretic leg after therapy were found compared to before therapy (p < 0.001, Figure 10).
4. Discussion
This paper proposes a new method for detecting temporal gait synergies in dynamic space using PCA without recording muscle activity. The foot trajectory has been represented with respect to time in the PCA cyclogram space. The foot dynamics reflect the muscle activity but in a more straightforward way. Analyzing the dynamics of the endpoint—i.e., foot—is important since it is assumed that the control of limb dynamics, instead of muscle activity, would help ensure whole-body mechanical stability and energy [59]. The control of limb segment motion may happen by encoding the limb endpoint dynamics.
The inputs for PCA were GRF signals measured at the lateral and medial heel, lateral and medial metatarsal, and toe on each foot, as well as the accelerations and angular velocities measured at the rear part of each foot. The Gait Teacher system is easy to use, wearable, and relatively cheap compared to EMG-based and other gait analysis systems. It can be used in everyday life, not just in a hospital environment [60,61]. The clinician does not need the training to manage the system, unlike EMG equipment, where electrode montage and data acquisition are more time-consuming. The system’s set-up comes down to putting on shoes with insoles and following the simple interface. Due to the high level of impairment of patients in the subacute phase of stroke [62], it is crucial to provide fast and straightforward screening to make the gait evaluation more comfortable and effortless for patients.
PCA used whole preprocessed gait session recordings as an input. There was no gait segmentation before or after PCA; therefore, there was no loss of information due to the interpolation to the specific time base or incorrect stride segmentation. The problem of gait phase detection accuracy and reliability was bypassed by observing the whole gait session and evaluating the sequence at once. Unlike when calculating symmetry and temporal parameters, valuable data were lost due to incorrect gait event detection.
In this paper, three temporal activations of synergies were extracted (three modules, related to angles θ1, θ2, and θ3). Statistical tests proved the differences between healthy and patient gait before therapy and confirmed that the temporal synergies are invariant in healthy gait, regardless of different gait speeds, Table 4. These temporal activations are shifted 30% in time, which agrees with previous studies. Researchers have also claimed that three main temporal components from a set of five are also shifted by approximately 30% in time. Additionally, the existence of three synergies was statistically confirmed. The time shift of synergies was not significantly different in healthy gait for different speeds, which was not aligned with the observation from the literature [19].
The rehabilitation helps recovery of cortical neuronal networks controlling gait, and the re-emergence of healthy synergies can be noticed [63]. In this paper, synergies have been analyzed before and after therapy for stroke patients, and synergies were also compared to healthy subjects. Before the therapy, there were significant differences in all three temporal synergies compared to healthy gait. This can be explained by a change in double limb support and single limb support duration [64]. After therapy, the temporal activations ‘moved’ closer (i.e., cyclogram has rotated towards healthy cyclogram orientation) to the activations of lower speed healthy gait. The time-shift of specific synergies towards healthy values was statistically confirmed for synergies because of the FES therapy, Table 4. To the best of our knowledge, no prior studies have statistically compared temporal synergies from dynamics perspective between stroke hemiparetic gait before and after therapy with different healthy gait speeds.
On the other side, an observation can be reported about the second module related to the angle θ2 in the paretic leg before and after therapy, indicating less complex locomotor control of the affected side (Figure 7). The reduction in observations for the second module could be noticed because the same amount of variance can be explained with fewer synergies. These results agree with previous findings of the relation between less complex control and poorer walking performance [17]. A decreased number of synergies (‘disappearing’ of the second module, from three to two synergies) in the paretic leg can be explained by the merging of synergies [17,65,66]. This decrease is explained by the greater cohesion between the parts of the body and the generally reduced complexity of movement due to injury. The merging of synergies was shown in paretic gait after the therapy, indicating the possible development of abnormal synergies [17,67].
The difference in the distribution of weightings reflects complex motor coordination, although the temporal synergies are consistent (Figure 11). This means that even though the input variables had a different contribution to each PC, the activations of PCs in time remained the same. It could be noticed that some weightings in the paretic leg after therapy became more exaggerated than in a healthy one, such as lateral metatarsal force weighting on PC1 (Figure 11). This aligns with the possible development of abnormal synergies (merging of synergies) but needs further investigation.
By applying PCA, it was possible to characterize better the specific features of gait disorders in relation to commonly used techniques [40]. Therefore, the conventional temporal and symmetry parameters were also calculated. The proposed method was more advantageous than conventional gait analysis since the statistical test proved the significant difference in the paretic leg, which was not observed in temporal or symmetry parameters (Figure 12). After the therapy, symmetric gait may not be the only measure of therapy success and may not reveal the complete picture [68]. On the other hand, maximal gait variability was preserved by using PCA, and variability is a complementary way of quantifying locomotion and monitoring rehabilitation effects [69,70,71].
Other studies have examined the possibilities for follow-up of stroke patients based on the analysis of temporal muscle synergies [72]. Abnormal patterns of muscle synergies were used to provide additional measures for clinicians during various therapy sessions, such as robotic-assisted, conventional gait, or FES-cycling training [73,74]. Whether temporal synergies indicate the gait recovery of stroke patients is still arguable [65,73,74,75]. The present study showed significant changes in the temporal synergies during the rehabilitation from a dynamics perspective without considering muscle synergies.
The detection of temporal synergies from a dynamic perspective is helpful for gait assessment. Visually monitoring 2D cyclograms is a robust and straightforward qualitative measure for clinicians. The values of the proposed θ angles—i.e., temporal synergies—are quantitative measures of gait performance. The rotation of a 2D cyclogram (the change in temporal synergy) is a direct and simple measure that clinicians can use to assess gait performance by comparing values with healthy temporal synergies. As a result, clinicians will better understand and follow up with the therapy’s effect on gait after a stroke. Whether the gait synergies represent an input or an output of neuromuscular control is still a point of debate [76,77]. Nevertheless, defining changes in gait from a dynamic systems perspective can be useful in rehabilitation for clinical gait assessments [41,78].
The performed study has several limitations. First, the COVID-19 pandemic restrictions caused a lack of participants following the rehabilitation protocol, and for that reason, a limited number of stroke patients were included in the study. Future studies will include a larger patient population. Additionally, for the therapy efficiency assessment, data could be acquired before and after different therapy protocols [73]. Second, the study was underpowered when comparing healthy subjects and patients since they were unmatched by confounding factors, such as age and gender. Future studies will also include matched healthy and patient groups by confounding factors. Third, the wearable device used in the study has lower accuracy and reliability than the gold standard optoelectronic systems with force platforms. However, the trade-off between good performance characteristics and high cost should also be considered [79]. Finally, the question may be asked whether data loss due to PCA affects the results. Even though the initial dataset of 11 signals per leg contains more information than two PCs, the valuable information about the gait variability is kept using PCs. This dimensionality reduction imitates the problem of neural control, where many input signals fire one control signal [41]. More synergies could be observed, and more data information could be kept by adding additional components and creating three-dimensional cyclograms. Nonetheless, observing cyclograms in 2D coordinate frames (and monitoring only θ angles) is more convenient for the clinician than monitoring the higher dimensionality graphs and parameters. The presented concept of 2D PCA-based temporal synergies assessment is suitable for near real-time monitoring purposes and can be used to improve the current clinical tools for gait assessment in the future.
5. Conclusions
In this paper, an innovative method for directly observing the limb’s endpoint dynamics and detecting temporal synergies during walking with different speeds is proposed, without stride extraction, and without using EMG recordings. Furthermore, the hypothesis about invariant temporal dynamic synergies was statistically confirmed, and the potential use of this information in practical gait assessment during rehabilitation after stroke was highlighted.
Acknowledgments
We would like to thank Dejan B. Popović for his initial advice in this research. We also thank Ljubica Konstantinović and Suzana Dedijer-Dujović, for providing gait data for patients who participated in the FES therapy (MOTIMOVE electronic stimulator, https://www.3-x-f.com/ (accessed on 20 February 2022)) augmenting the pedaling (OMEGO® Plus, https://tyromotion.com/en/products/omegoplus/ (accessed on 20 February 2022)).
Author Contributions
Conceptualization: M.M.G. and M.M.J.; Methodology: M.M.G.; Software: M.M.G.; Validation: M.M.G. and M.M.J.; Formal analysis: M.M.G.; Investigation: M.M.G.; Resources: M.M.G. and M.M.J.; Data curation: M.M.G.; Writing—original draft preparation: M.M.G. and M.M.J.; Writing—review and editing: M.M.G. and M.M.J.; Visualization: M.M.G. and M.M.J.; Supervision: M.M.J.; Project Administration: M.M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Science and Technological Development of the Republic of Serbia (No 175016).
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the ethics committee of the Rehabilitation Clinic “Dr Miroslav Zotović” in Belgrade, Serbia.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bernstein N. The Coordination and Regulation of Movements. Pergamon; Oxford, UK: 1967. [Google Scholar]
- 2.Flash T., Hogan N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985;5:1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Embry K.R., Villarreal D.J., Macaluso R.L., Gregg R.D. Modeling the Kinematics of Human Locomotion Over Continuously Varying Speeds and Inclines. IEEE Trans. Neural Syst. Rehabil. Eng. 2018;26:2342–2350. doi: 10.1109/TNSRE.2018.2879570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Uno Y., Kawato M., Suzuki R. Formation and control of optimal trajectory in human multijoint arm movement. Biol. Cybern. 1989;61:89–101. doi: 10.1007/BF00204593. [DOI] [PubMed] [Google Scholar]
- 5.Hasan Z. Optimized movement trajectories and joint stiffness in unperturbed, inertially loaded movements. Biol. Cybern. 1986;53:373–382. doi: 10.1007/BF00318203. [DOI] [PubMed] [Google Scholar]
- 6.Rosenbaum D.A., Meulenbroek R., Vaughan J., Jansen C. Posture-based motion planning: Applications to grasping. Psychol. Rev. 2001;108:709–734. doi: 10.1037/0033-295X.108.4.709. [DOI] [PubMed] [Google Scholar]
- 7.Oguz O.S., Zhou Z., Wollherr D. A Hybrid Framework for Understanding and Predicting Human Reaching Motions. Front. Robot. AI. 2018;5:27. doi: 10.3389/frobt.2018.00027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.d’Avella A., Saltiel P., Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- 9.Oshima H., Aoi S., Funato T., Tsujiuchi N., Tsuchiya K. Variant and Invariant Spatiotemporal Structures in Kinematic Coordination to Regulate Speed During Walking and Running. Front. Comput. Neurosci. 2019;13:63. doi: 10.3389/fncom.2019.00063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Popovič M., Popovic D. Cloning biological synergies improves control of elbow neuroprostheses. IEEE Eng. Med. Biol. 2001;20:74–81. doi: 10.1109/51.897830. [DOI] [PubMed] [Google Scholar]
- 11.Tagliabue M., Ciancio A.L., Brochier T., Eskiizmirliler S., Maier M.A. Differences between kinematic synergies and muscle synergies during two-digit grasping. Front. Hum. Neurosci. 2015;9:165. doi: 10.3389/fnhum.2015.00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Esmaeili S., Karami H., Baniasad M., Shojaeefard M., Farahmand F. The association between motor modules and movement primitives of gait: A muscle and kinematic synergy study. J. Biomech. 2022;134:110997. doi: 10.1016/j.jbiomech.2022.110997. [DOI] [PubMed] [Google Scholar]
- 13.Ivanenko Y.P., Cappellini G., Dominici N., Poppele R.E., Lacquaniti F. Modular Control of Limb Movements during Human Locomotion. J. Neurosci. 2007;27:11149–11161. doi: 10.1523/JNEUROSCI.2644-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huang B., Xiong C., Chen W., Liang J., Sun B.-Y., Gong X. Common kinematic synergies of various human locomotor behaviours. R. Soc. Open Sci. 2021;8:210161. doi: 10.1098/rsos.210161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cech D., Martin S. Functional Movement Development Across the Life Span. 3rd ed. Elsevier; Amsterdam, The Netherlands: 2012. [Google Scholar]
- 16.Chiovetto E., Berret B., Delis I., Panzeri S., Pozzo T. Investigating reduction of dimensionality during single-joint elbow movements: A case study on muscle synergies. Front. Comput. Neurosci. 2013;7:11. doi: 10.3389/fncom.2013.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Clark D.J., Ting L.H., Zajac F.E., Neptune R.R., Kautz S.A. Merging of Healthy Motor Modules Predicts Reduced Locomotor Performance and Muscle Coordination Complexity Post-Stroke. J. Neurophysiol. 2010;103:844–857. doi: 10.1152/jn.00825.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chvatal S.A.P., Ting L.H.P. Common muscle synergies for balance and walking. Front. Comput. Neurosci. 2013;7:48. doi: 10.3389/fncom.2013.00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ivanenko Y.P., Grasso R., Zago M., Molinari M., Scivoletto G., Castellano V., Macellari V., Lacquaniti F. Temporal Components of the Motor Patterns Expressed by the Human Spinal Cord Reflect Foot Kinematics. J. Neurophysiol. 2003;90:3555–3565. doi: 10.1152/jn.00223.2003. [DOI] [PubMed] [Google Scholar]
- 20.Lacquaniti F., Grasso R., Zago M. Motor patterns in walking. Physiology. 1999;14:168–174. doi: 10.1152/physiologyonline.1999.14.4.168. [DOI] [PubMed] [Google Scholar]
- 21.Ivanenko Y.P., Poppele R.E., Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2004;556:267–282. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kuiken T.A., Lowery M., Stoykov N.S. The effect of subcutaneous fat on myoelectric signal amplitude and cross-talk. Prosthetics Orthot. Int. 2003;27:48–54. doi: 10.3109/03093640309167976. [DOI] [PubMed] [Google Scholar]
- 23.Steele K.M., Tresch M.C., Perreault E.J. The number and choice of muscles impact the results of muscle synergy analyses. Front. Comput. Neurosci. 2013;7:105. doi: 10.3389/fncom.2013.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fox E.J., Tester N., Kautz S., Howland D.R., Clark D.J., Garvan C., Behrman A.L. Modular control of varied locomotor tasks in children with incomplete spinal cord injuries. J. Neurophysiol. 2013;110:1415–1425. doi: 10.1152/jn.00676.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Woolley S.M. Characteristics of Gait in Hemiplegia. Top. Stroke Rehabil. 2001;7:1–18. doi: 10.1310/JB16-V04F-JAL5-H1UV. [DOI] [PubMed] [Google Scholar]
- 26.Akhtaruzzaman M.D., Shafie A.A., Khan M.R. Gait analysis: Systems, technologies, and importance. J. Mech. Med. Biol. 2016;16:1630003. doi: 10.1142/S0219519416300039. [DOI] [Google Scholar]
- 27.do Carmo Vilas-Boas M., Choupina H.M., Rocha A.P., Fernandes J.M., Cunha J.P. Full-body motion assessment: Concurrent validation of two body tracking depth sensors versus a gold standard system during gait. J. Biomech. 2019;87:189–196. doi: 10.1016/j.jbiomech.2019.03.008. [DOI] [PubMed] [Google Scholar]
- 28.Benson L.C., Clermont C.A., Bošnjak E., Ferber R. The use of wearable devices for walking and running gait analysis outside of the lab: A systematic review. Gait Posture. 2018;63:124–138. doi: 10.1016/j.gaitpost.2018.04.047. [DOI] [PubMed] [Google Scholar]
- 29.Kokolevich Z.M., Biros E., Tirosh O., Reznik J.E. Distinct Ground Reaction Forces in Gait between the Paretic and Non-Paretic Leg of Stroke Patients: A Paradigm for Innovative Physiotherapy Intervention. Healthcare. 2021;9:1542. doi: 10.3390/healthcare9111542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Petraglia F., Scarcella L., Pedrazzi G., Brancato L., Puers R., Costantino C. Inertial sensors versus standard systems in gait analysis: A systematic review and meta-analysis. Eur. J. Phys. Rehabil. Med. 2019;55:265–280. doi: 10.23736/S1973-9087.18.05306-6. [DOI] [PubMed] [Google Scholar]
- 31.Panero E., Digo E., Dimanico U., Alberto Artusi C., Zibetti M., Gastaldi L. Effect of Deep Brain Stimulation Frequency on Gait Symmetry, Smoothness and Variability using IMU; Proceedings of the 2021 IEEE International Symposium on Medical Measurements and Applications (MeMeA); Lausanne, Switzerland. 23–25 June 2021. [Google Scholar]
- 32.Vienne A., Barrois R.P., Buffat S., Ricard D., Vidal P.-P. Inertial Sensors to Assess Gait Quality in Patients with Neurological Disorders: A Systematic Review of Technical and Analytical Challenges. Front. Psychol. 2017;8:817. doi: 10.3389/fpsyg.2017.00817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gouwanda D., Gopalai A.A., Khoo B.H. A Low Cost Alternative to Monitor Human Gait Temporal Parameters–Wearable Wireless Gyroscope. IEEE Sens. J. 2016;16:9029–9035. doi: 10.1109/JSEN.2016.2616163. [DOI] [Google Scholar]
- 34.Mei C., Gao F., Li Y. A Determination Method for Gait Event Based on Acceleration Sensors. Sensors. 2019;19:5499. doi: 10.3390/s19245499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pérez-Ibarra J.C., Williams H., Siqueira A.A., Krebs H.I. Real-time identification of impaired gait phases using a single foot-mounted inertial sensor: Review and feasibility study; Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob); Enschede, The Netherlands. 26–29 August 2018; pp. 1157–1162. [Google Scholar]
- 36.Lyons G., Sinkjaer T., Burridge J., Wilcox D. A review of portable FES-based neural orthoses for the correction of drop foot. IEEE Trans. Neural Syst. Rehabil. Eng. 2002;10:260–279. doi: 10.1109/TNSRE.2002.806832. [DOI] [PubMed] [Google Scholar]
- 37.Beckerman H., Becher J., Lankhorst G.J., Verbeek A. Walking ability of stroke patients: Efficacy of tibial nerve blocking and a polypropylene ankle-foot orthosis. Arch. Phys. Med. Rehabil. 1996;77:1144–1151. doi: 10.1016/S0003-9993(96)90138-0. [DOI] [PubMed] [Google Scholar]
- 38.Chau T. A review of analytical techniques for gait data. Part 1: Fuzzy, statistical and fractal methods. Gait Posture. 2001;13:49–66. doi: 10.1016/S0966-6362(00)00094-1. [DOI] [PubMed] [Google Scholar]
- 39.Daffertshofer A., Lamoth C.J., Meijer O.G., Beek P.J. PCA in studying coordination and variability: A tutorial. Clin. Biomech. 2004;19:415–428. doi: 10.1016/j.clinbiomech.2004.01.005. [DOI] [PubMed] [Google Scholar]
- 40.Milovanović I., Popovic D.B. Principal Component Analysis of Gait Kinematics Data in Acute and Chronic Stroke Patients. Comput. Math. Methods Med. 2012;2012:649743. doi: 10.1155/2012/649743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gavrilović M., Popović D.B. A principal component analysis (PCA) based assessment of the gait performance. Biomed. Tech. 2021;66:449–457. doi: 10.1515/bmt-2020-0307. [DOI] [PubMed] [Google Scholar]
- 42.3F-FIT FABRICANDO FABER. [(accessed on 20 February 2022)]. Available online: https://www.3-x-f.com/
- 43.Robotic Gait Therapy | OMEGO® Plus | Tyromotion. [(accessed on 20 February 2022)]. Available online: https://tyromotion.com/en/products/omegoplus/
- 44.REHAB SHOP. [(accessed on 20 February 2022)]. Available online: https://www.rehabshop.rs.
- 45.Fulk G.D., Echternach J.L. Test-Retest Reliability and Minimal Detectable Change of Gait Speed in Individuals Undergoing Rehabilitation after Stroke. J. Neurol. Phys. Ther. 2008;32:8–13. doi: 10.1097/NPT0b013e31816593c0. [DOI] [PubMed] [Google Scholar]
- 46.Bohannon R.W. Comfortable and maximum walking speed of adults aged 20–79 years: Reference values and determinants. Age Ageing. 1997;26:15–19. doi: 10.1093/ageing/26.1.15. [DOI] [PubMed] [Google Scholar]
- 47.Asmussen M.J., Kaltenbach C., Hashlamoun K., Shen H., Federico S., Nigg B.M. Force measurements during running on different instrumented treadmills. J. Biomech. 2018;84:263–268. doi: 10.1016/j.jbiomech.2018.12.025. [DOI] [PubMed] [Google Scholar]
- 48.Crenna F., Rossi G., Berardengo M. Filtering Biomechanical Signals in Movement Analysis. Sensors. 2021;21:4580. doi: 10.3390/s21134580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bartlett M.S. Proceedings of the Royal Society of London. Volume 160. Royal Society; London, UK: 1937. Properties of sufficiency and statistical tests; pp. 268–282. (Series A-Mathematical and Physical Sciences). [Google Scholar]
- 50.Milovanović I. Ph.D. Thesis. Faculty of Electrical Engineering University of Belgrade; Belgrade, Serbia: 2013. Synergy Patterns of Stroke Subjects While Walking: Implications for Control of FES Assistive Devices. [Google Scholar]
- 51.Rosenblatt M. Remarks on Some Nonparametric Estimates of a Density Function. Ann. Math. Stat. 1956;27:832–837. doi: 10.1214/aoms/1177728190. [DOI] [Google Scholar]
- 52.Shapiro S.S., Wilk M.B. An analysis of variance test for normality (complete samples) Biometrika. 1965;52:591–611. doi: 10.1093/biomet/52.3-4.591. [DOI] [Google Scholar]
- 53.Silverman B.W. Density Estimation for Statistics and Data Analysis. Chapman and Hall; London, UK: 1986. [Google Scholar]
- 54.Mann H.B., Whitney D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947;18:50–60. doi: 10.1214/aoms/1177730491. [DOI] [Google Scholar]
- 55.Fong Y., Huang Y., Lemos M.P., McElrath M.J. Rank-based two-sample tests for paired data with missing values. Biostatistics. 2017;19:281–294. doi: 10.1093/biostatistics/kxx039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gavrilović M. Gyroscope based method for evaluation of gait symmetry; Proceedings of the 5th IcETRAN; Palić, Serbia. 11–14 June 2018. [Google Scholar]
- 57.Błażkiewicz M., Wiszomirska I., Wit A. Comparison of four methods of calculating the symmetry of spatial-temporal parameters of gait. Acta Bioeng. Biomech. 2014;16:29–35. doi: 10.5277/abb140104. [DOI] [PubMed] [Google Scholar]
- 58.Wing K., Lynskey J.V., Bosch P.R. Walking speed in stroke survivors: Considerations for clinical practice. Top. Geriatr. Rehab. 2012;28:113–121. doi: 10.1097/TGR.0b013e31823d9cba. [DOI] [Google Scholar]
- 59.Pearson K.G. Common Principles of Motor Control in Vertebrates and Invertebrates. Annu. Rev. Neurosci. 1993;16:265–297. doi: 10.1146/annurev.ne.16.030193.001405. [DOI] [PubMed] [Google Scholar]
- 60.Rinehart N.J., Tonge B.J., Iansek R., McGinley J., Brereton A.V., Enticott P.G., Bradshaw J.L. Gait function in newly diagnosed children with autism: Cerebellar and basal ganglia related motor disorder. Dev. Med. Child Neurol. 2006;48:819–824. doi: 10.1017/S0012162206001769. [DOI] [PubMed] [Google Scholar]
- 61.Winter D.A. Chapter 9: Kinesiological Electromyography. In: Winter D.A., editor. Biomechanics and Motor Control of Human Movement. 3rd ed. John Wiley & Sons, Inc.; Hoboken, NJ, USA: 2005. [Google Scholar]
- 62.Frenkel-Toledo S., Ofir-Geva S., Mansano L., Granot O., Soroker N. Stroke Lesion Impact on Lower Limb Function. Front. Hum. Neurosci. 2021;15:27. doi: 10.3389/fnhum.2021.592975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Maguire C.C., Sieben J.M., De Bie R.A. Movement goals encoded within the cortex and muscle synergies to reduce redundancy pre and post-stroke. The relevance for gait rehabilitation and the prescription of walking-aids. A literature review and scholarly discussion. Physiother. Theory Pract. 2018;35:1–14. doi: 10.1080/09593985.2018.1434579. [DOI] [PubMed] [Google Scholar]
- 64.Goldie P.A., Matyas T.A., Evans O.M. Gait after stroke: Initial deficit and changes in temporal patterns for each gait phase. Arch. Phys. Med. Rehabil. 2001;82:1057–1065. doi: 10.1053/apmr.2001.25085. [DOI] [PubMed] [Google Scholar]
- 65.Gizzi L., Nielsen J.F., Felici F., Ivanenko Y., Farina D. Impulses of activation but not motor modules are preserved in the locomotion of subacute stroke patients. J. Neurophysiol. 2011;106:202–210. doi: 10.1152/jn.00727.2010. [DOI] [PubMed] [Google Scholar]
- 66.Bowden M.G., Clark D.J., Kautz S.A. Evaluation of Abnormal Synergy Patterns Poststroke: Relationship of the Fugl-Meyer Assessment to Hemiparetic Locomotion. Neurorehabilit. Neural Repair. 2009;24:328–337. doi: 10.1177/1545968309343215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Van Criekinge T., Vermeulen J., Wagemans K., Schröder J., Embrechts E., Truijen S., Hallemans A., Saeys W. Lower limb muscle synergies during walking after stroke: A systematic review. Disabil. Rehabil. 2020;42:2836–2845. doi: 10.1080/09638288.2019.1578421. [DOI] [PubMed] [Google Scholar]
- 68.Krasovsky T., Levin M.F. Review: Toward a Better Understanding of Coordination in Healthy and Poststroke Gait. Neurorehabilit. Neural Repair. 2009;24:213–224. doi: 10.1177/1545968309348509. [DOI] [PubMed] [Google Scholar]
- 69.Hausdorff J.M. Gait variability: Methods, modeling and modeling meaning. J. Neuroeng. Rehab. 2005;2:19. doi: 10.1186/1743-0003-2-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Keklicek H., Kirdi E., Yalcin A., Topuz S., Ulger O., Erbahceci F., Sener G. Comparison of gait variability and symmetry in trained individuals with transtibial and transfemoral limb loss. J. Orthop. Surg. 2019;27 doi: 10.1177/2309499019832665. [DOI] [PubMed] [Google Scholar]
- 71.Kim W.-S., Choi H., Jung J.-W., Yoon J.S., Jeoung J.H. Asymmetry and Variability Should Be Included in the Assessment of Gait Function in Poststroke Hemiplegia with Independent Ambulation During Early Rehabilitation. Arch. Phys. Med. Rehabil. 2020;102:611–618. doi: 10.1016/j.apmr.2020.10.115. [DOI] [PubMed] [Google Scholar]
- 72.Rosa M.C.N., Marques A., Demain S., Metcalf C.D. Lower limb co-contraction during walking in subjects with stroke: A systematic review. J. Electromyogr. Kinesiol. 2014;24:1–10. doi: 10.1016/j.jelekin.2013.10.016. [DOI] [PubMed] [Google Scholar]
- 73.Tan C.K., Kadone H., Watanabe H., Marushima A., Hada Y., Yamazaki M., Sankai Y., Matsumura A., Suzuki K. Differences in Muscle Synergy Symmetry Between Subacute Post-stroke Patients With Bioelectrically-Controlled Exoskeleton Gait Training and Conventional Gait Training. Front. Bioeng. Biotechnol. 2020;8:770. doi: 10.3389/fbioe.2020.00770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Ambrosini E., Parati M., Peri E., De Marchis C., Nava C., Pedrocchi A., Ferriero G., Ferrante S. Changes in leg cycling muscle synergies after training augmented by functional electrical stimulation in subacute stroke survivors: A pilot study. J. Neuroeng. Rehabil. 2020;17:35. doi: 10.1186/s12984-020-00662-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Den Otter A.R., Geurts A.C.H., Mulder T.H., Duysens J. Gait recovery is not associated with changes in the temporal patterning of muscle activity during treadmill walking in patients with post-stroke hemiparesis. Clin. Neurophysiol. 2006;117:4–15. doi: 10.1016/j.clinph.2005.08.014. [DOI] [PubMed] [Google Scholar]
- 76.Tresch M.C., Jarc A. The case for and against muscle synergies. Curr. Opin. Neurobiol. 2009;19:601–607. doi: 10.1016/j.conb.2009.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Cheung V.C.K., Seki K. Approaches to revealing the neural basis of muscle synergies: A review and a critique. J. Neurophysiol. 2021;125:1580–1597. doi: 10.1152/jn.00625.2019. [DOI] [PubMed] [Google Scholar]
- 78.Singh R.E., Iqbal K., White G., Hutchinson T.E. A Systematic Review on Muscle Synergies: From Building Blocks of Motor Behavior to a Neurorehabilitation Tool. Appl. Bionics Biomech. 2018;2018:3615368. doi: 10.1155/2018/3615368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zhou L., Fischer E., Tunca C., Brahms C.M., Ersoy C., Granacher U., Arnrich B. How We Found Our IMU: Guidelines to IMU Selection and a Comparison of Seven IMUs for Pervasive Healthcare Applications. Sensors. 2020;20:4090. doi: 10.3390/s20154090. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.