Abstract
We demonstrated a fiber optic distributed acoustic sensor based on a double Sagnac interferometer, using two wavelengths separated by CWDM modules. A mathematical model of signal formation principle, based on a shift in two signals analysis, was described and substantiated mathematically. The dependence of the sensor sensitivity on a disturbance coordinate and frequency was found and simulated, and helped determine a low sensitivity zone length and provided sensor scheme optimization. A data processing algorithm without filtering, appropriate even in case of a high system noise level, was described. An experimental study of the distributed fiber optic sensor based on a Sagnac interferometer with two wavelengths divided countering loops was carried out. An accuracy of 24 m was achieved for 25.4 km SMF sensing fiber without phase unwrapping.
Keywords: Sagnac interferometer, fiber optic sensor, disturbance localization, sensitivity
1. Introduction
Distributed fiber optic sensors (FOS) have become quite popular for pipeline monitoring and perimeter security, etc., due to their ability to interrogate a long sensor length at a high spatial resolution and sampling rate. For recording high-frequency vibration influences, the most popular scheme is a phase-sensitive reflectometer, which provides a high accuracy of disturbance localization but has disadvantages such as a complex scheme and a high cost of components. A distributed sensor based on a Sagnac interferometer (SI) is gaining popularity due to its simple optical scheme, signal processing, and low dependency on laser phase noise [1]. In contrast with reflectometers, the possibility of using distributed measurements in schemes involving SI is not a default method. Such sensors are currently developing rapidly and there are three main ways to implement distributed sensing. The first is the “null frequencies” method, based on the position of the minima in the spectrum of the recorded signal from one loop of the interferometer [2]. The second is the expected time delay method, based on the correlation of arrays generated from two signals from loops of different known lengths or with another variant of delay [1]. The third method uses the time delay method between oppositely directed sensory loops [3]. However, the literature does not cover the issue of studying the sensitivity features of such systems. Moreover, creating a system with a sensor length of more than 20 km, which demonstrates a disturbance localization error of less than 0.1% of a total sensing length, especially in the case of a high noise level, requires using expensive components, and applying phase unwrapping and filtering. This makes data processing more complex and increases the cost of a sensor. Therefore, the issue of implementing a system with a simple optical scheme and low-cost components, which does not employ a complex data processing algorithm, and can operate at a high noise level, remains relevant.
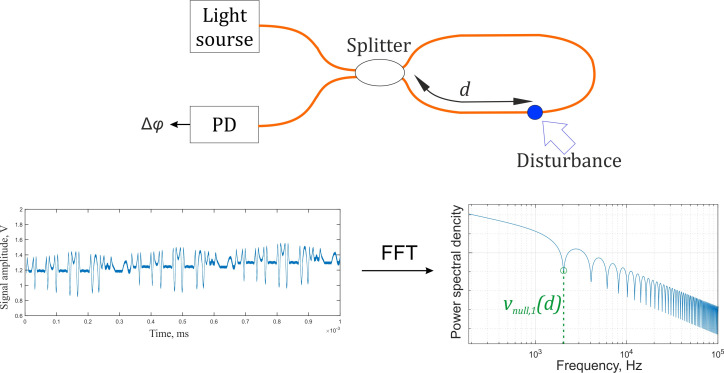
The “null frequency” method is based on signal spectrum analysis from the sensor and the determination of a disturbance location using the low spectral density points’ positions. They appear in a spectrum in the presence of an acoustic disturbance due to a time delay between clockwise (CW) and counterclockwise (CWW) radiation. This method can be implemented based on one fiber loop [2], demonstrated in Figure 1, or in more complex schemes [4,5] such as the double Sagnac scheme [6], or another scheme in which a linear section and a Faraday rotator mirror (FRM) form at the output of the imbalanced Mach-Zehnder interferometer (MZI), with a laser coherence length less than the MZI arms’ difference [7,8,9,10]. In addition, the “null frequency” method was mentioned as an example for comparison in [1,5]. In [8], to reduce localization errors, the authors proposed a modified “null frequency” method, which consisted of applying the second Fourier transform to the signal spectrum in order to determine a periodicity of “null frequency” points instead of searching for individual ones. The error presented by the authors is 100 m for a sensor length of 50 km. A great disadvantage of these methods is that localization error strongly depends on a system noise level. Even after filtration, these methods are not appropriate for practical use, since the obtained spectra are distorted and unreliable. It is extremely difficult to determine the position of the low spectral density points or to find out the periodicity of spectrum modulation in the case of high noise. To provide good localization it is necessary to have some prior information about the position of the “null frequency” points, which is possible in a laboratory setup with a stated disturbance position assembled [3] or if the disturbance position can be obtained as a result of a numerical simulation [5].
Figure 1.
Diagram of a “null frequency” method principle.
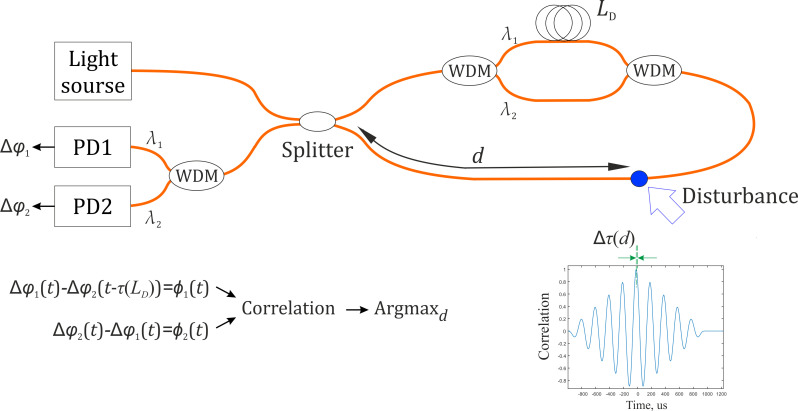
The second method of implementing a distributed acoustic FOS based on a Sagnac interferometer is a time delay estimation. This requires a scheme with two loops that differ from each other by an fixed length amount LD. The scheme includes a MZI at one end of the loop [11,12,13], as shown in Figure 2, or a linear section with a mirror at the opposite edge [14,15], formed using couplers or WDM modules. The formed MZIs have a length difference LD between the arms that exceeds the coherence length of a laser source. Therefore, they do not create an interference signal and are only applied to separate optical paths and form two loops of different lengths. When using WDM modules, instead of splitters, radiation with a wavelength of λ1 and λ2 will propagate through the first and second loops [16,17]. Signals from the two loops are shifted relative to each other by a time delay, which is determined by the length LD. Since the loops have different lengths, each of the CW and CCW beams receives a phase shift from disturbance at different times. A demodulation data processing algorithm includes phase unwrapping of the signals from the two loops followed by correlation. Therefore, it is possible to determine the beginning moments of a disturbance in interference signals in each loop, calculate a time delay, and use it to find the location of the disturbance. A method of time delay introduction, implemented based on a scheme with one unbalanced MZI, allows the creation of a sensor with a length of 180 m [12] to 120 km [11]. In different studies, a disturbance position error was approximately a few hundreds of meters for a sensor length of 10 km (1% of the sensor length) [13], and up to 60 m for a sensor length of 120 km (0.05% of the sensor length) [11]. However, the method of time delay introduction has disadvantages. One disadvantage is a high noise level in a MZI due to an environmental influence, such as temperature fluctuations and vibrations. In addition, since in most cases a disturbance in the loop is quite intense, it becomes necessary to unwrap a signal phase. It requires at least two photodetectors for each loop, which increases the cost of the sensor and makes a data processing algorithm more complex.
Figure 2.
Diagram of a time delay estimation method principle.
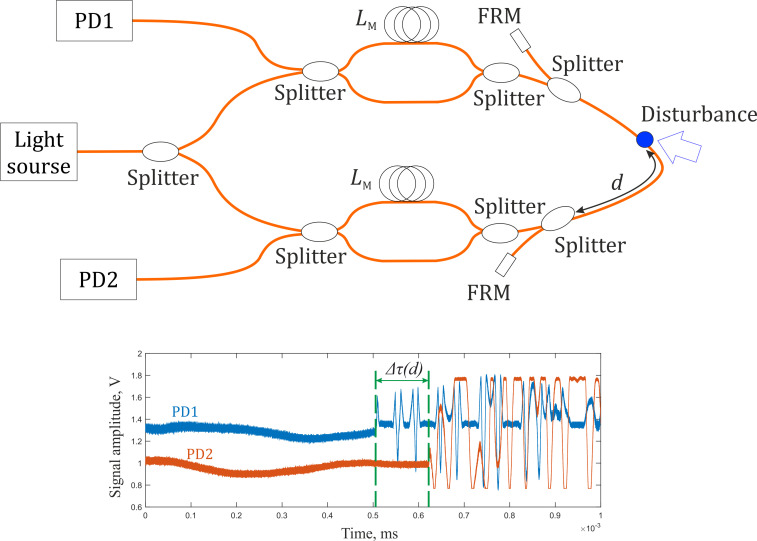
One more method for disturbance localization is based on determining a time delay between signals from two counter loops of the same lengths. Two loops of a SI are formed, using MZIs with a difference LM between the arms that exceeds the coherence length of a radiation source, and Faraday mirrors (FRM) [3,18], as shown in Figure 3, or by using light polarization state multiplexing [19,20]. Thus, two SI loops are formed based on linear sections, which are located oppositely. As a result, in the presence of an acoustic disturbance on the common sensory fiber along which the radiation of both interferometers passes, a change in the interference signal is detected at time moments which differ from each other, which is the time delay. The value of the time shift between the signals is calculated by a correlation algorithm. However, the scheme with light polarization state multiplexing has significant disadvantages, as it includes expensive optical components, such as polarization-maintaining fibers, which contribute to the overall high cost and make it impractical for use on objects with a long perimeter. The scheme with a MZI and SI combination based on FRM has a great disadvantage of high loss. It has 4 fiber splitters that lead to a dynamic range of 18 dB (Att = 3 dB · 3 (couplers) · 2 (passes)), which can affect nonlinearity in propagating radiation and decrease signal power.
Figure 3.
Diagram of a counter loops method principle.
In this article, we proposed a distributed fiber sensor scheme based on a double Sagnac interferometer. The directions were separated by CWDM splitters that formed opposite loops of the Sagnac interferometer with equal lengths. These loops included two common fibers, one of which was a sensor, and the other a reference. The proposed scheme was promising in avoiding the disadvantages described above, as it was simple and did not need to use expensive fibers or a narrow-band laser. It demonstrated high disturbance localization accuracy even in the case of high noise level, and without phase unwrapping.
2. Theory of a Disturbance Localization Method
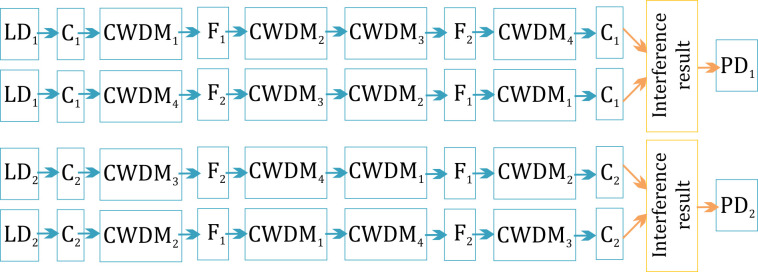
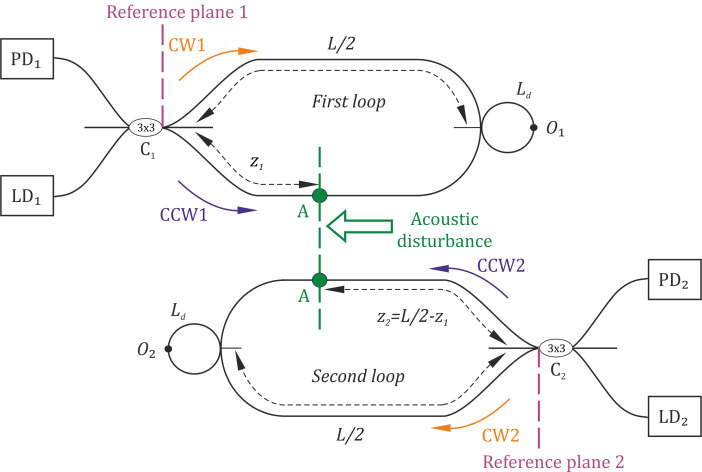
The scheme of the proposed setup is shown in Figure 4. The principle of the sensor’s operation is as follows. Radiation from a continuous light source (LD1), with wavelength (λ1) in a range of 1540–1560 nm, enters the x-shaped fiber splitter (C1), and is divided into two equal parts. We used a 3 × 3 splitter to avoid the Sagnac mirror effect that occurs when using a 2 × 2 splitter. Moreover, the 3 × 3 splitter provided a 2π/3 phase shift, which might be convenient for phase unwrapping in the scheme extension. One part of the light remaining after passing through splitter C1 propagated CW, and passed through CWDM1, the sensor fiber F1 in the 1→2 direction, CWDM2, CWDM3, the second reference fiber F2 in the 3→4 direction, and CWDM4. It then returned to the C1 splitter. The second part of the radiation, with a wavelength range of Δλ1 = 1540–1560 nm and central wavelength λ1 = 1550 nm, passed through the interferometer loop CCW. It then passed through CWDM4, the F2 reference fiber in the 4→3 direction, CWDM3, CWDM2, the sensor fiber F1 in the 2→1 direction, and CWDM1, then passed through splitter C1, where interference occurred between the two parts of radiation with a wavelength λ1. After that, the interference result entered photodetector PD1. Similarly, in the second loop, radiation from a continuous light source (LD2), with a wavelength range Δλ2 = 1560–1580 nm and central wavelength λ2 = 1570 nm, entered the splitter C2 and was divided into two equal parts. One of the parts propagated CW through CWDM3, the reference fiber F2 in the 3→4 direction, CWDM4, CWDM1, sensor fiber F1 in the 1→2 direction, and CWDM2. The second part passed CCW through CWDM2, the F1 sensor fiber in the 2→1 direction, CWDM1, CWDM4, the F2 fiber in the 4→3 direction, and CWDM3. Then, both parts arrived at the C2 splitter. Following this process, photodetector PD2 detected the interference result. Due to signal forming features in a Sagnac interferometer, a point of low sensitivity arose at the half-length of each loop [21]. To move the points of low sensitivity outside the sensory region, we included an additional length Ld in fiber F2. The lengths of fibers l1 − l6 were negligibly small in comparison with L and Ld and were neglected in further calculations. Possible light propagation paths are shown in Figure 5.
Figure 4.
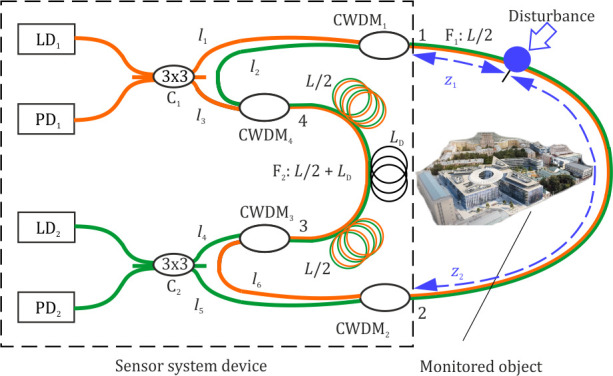
Structural scheme of Sagnac-based sensor system with two counter loops.
Figure 5.
Possible light propagation paths.
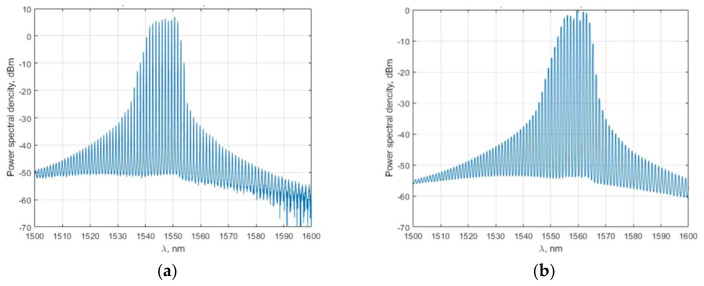
Laser phase noise did not affect the interference significantly in SI compared to other types of distributed fiber sensors [10]. A narrow-bandwidth light source was not needed. In our scheme, we used 15 mW and 9 mW Fabry-Perot laser diodes with central wavelengths at 1550 nm and 1570 nm, respectively, for a 51,800 m loop. The spectra are shown in Figure 6. The CWDM modules had a channel spectral bandwidth of 20 nm, and the SLD transmission spectrum is shown in Figure 7. We did not achieve a perfect match between the laser emission and the CWDM transmission spectra but the power received was enough to achieve a signal-to-noise ratio (SNR) of up to 50 and to detect impacts.
Figure 6.
Spectra of Fabry-Perot laser diodes used in a system.
Figure 7.
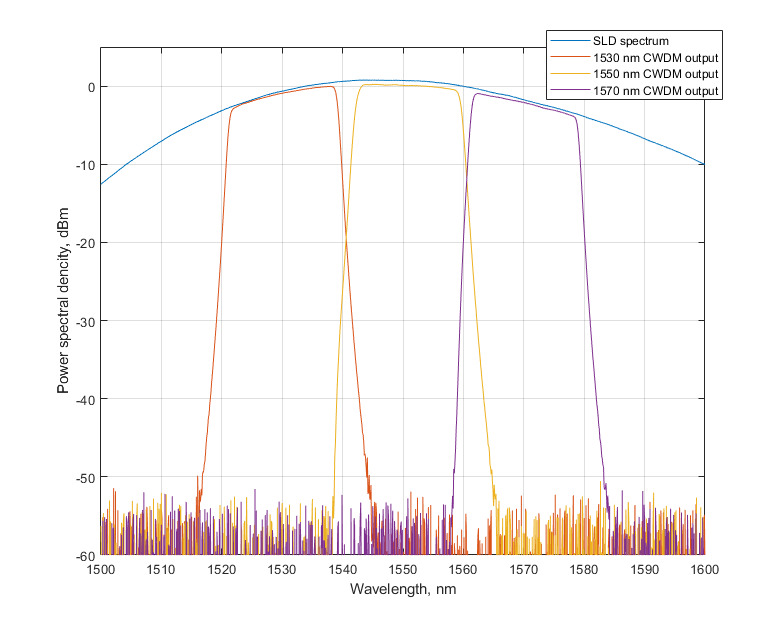
SLD transmission spectra of CWDM modules.
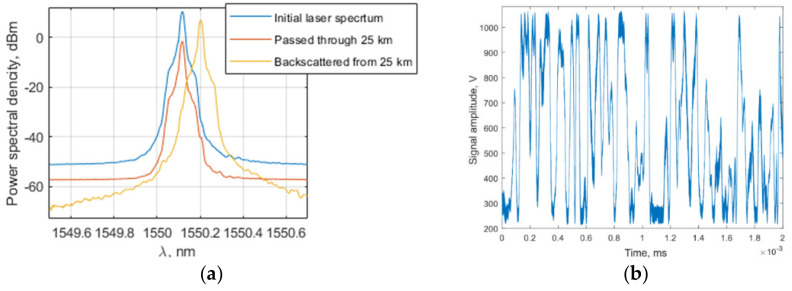
The usage of DWDM modules may narrow down the required spectral range. However, experiments using a narrow-band laser and DWDM modules show a quick nonlinear growth of Brillouin scattering. Figure 8a demonstrates the spectra of narrow-band 2 kHz laser radiation, the radiation passed through 25 km of fiber, and the Brillouin scattering gathered in experiments. This effect leads to signal fluctuations, which made position detection impossible, as shown in Figure 8b.
Figure 8.
(a) Spectra of narrow-band 2 kHz laser radiation, radiation passed through 25 km of fiber and Brillouin scattering, (b) Plot of a signal with high Brillouin scattering.
For a better understanding, the scheme shown in Figure 4 can also be presented as two separate loops, as shown in Figure 9. Light spread with wavelengths λ1 and λ2 in the first loop and the second loop, respectively. Light beams in CW and CCW directions interfered at the splitters. We considered C1 to be in the first reference plane, and C2 to be in the second reference plane. The central points O1 and O2 were located in half-length of loops.
Figure 9.
Two-loop diagram for sensitivity analysis.
As two counter Sagnac interferometers were used, a disturbance influenced both loops simultaneously, producing signal phase deviation, which led to interference changes. A disturbance influenced the first loop at a point located at a distance of z1 from the first reference plane. At the same time, it influenced the second loop at a point located at a distance of z2 from the second reference plane. These two distances are related to total loop length L as follows:
| (1) |
External disturbance added a signal phase deviation φ(t), and the resulting phase difference at the photodetectors from the first and the second loop can be determined as follows:
| (2) |
| (3) |
where φCW, φCCW is the phase deviation of light propagated in CW and CCW directions; τCW1, τCCW1 shows the time during which the radiation travelled in the first loop in CW and CCW directions, respectively, from the disturbance location point to the first reference plane; and τCW2, τCCW2 shows the time during which the radiation travelled in the second loop from the disturbance location point to the second reference plane in two directions.
As one can see, at the points of half-loop length, O1 and O2, the phase deviations in CW and CCW directions were equal . Therefore, there was zero phase deviation in the output of the loops . It means that a low sensitivity region occurred closer to the center of the loop, the so-called “dead zone”. By including an additional length Ld in the loops, we moved the points O1 and O2 outside the sensory region.
The indicated delays are important for signal forming process and can be determined from the lengths in Figure 1:
| (4) |
| (5) |
The light with gathered phase deviation from point A came to the first reference plane after time delays τCW1 and τCCW1, and in both these moments optical power variations occurred at the photodetector, which were the interference signal changes. For the second loop, the interference signal changes occurred in the moments after the τCW2 and τCCW2 time delay, when the light came from point A to the second reference plane. Due to a sensor configuration, it is obvious that for any coordinate of point A, the condition (L/2 + Ld) > L/2 ≥ zi, i = 1,2 is satisfied. Therefore, the inequalities τCW1 > τCCW1 and τCW2 < τCCW2 are always correct. Consequently, the interference signal reached the photodetectors PD1 and PD2 at times τCCW,1 and τCW,2, which were the earliest moments of interference signal changes in both loops. The shift between them is as follows:
| (6) |
This value allowed us to calculate a coordinate of point A as its position towards the first reference plane:
| (7) |
Expression (7) is the final equation for determining the disturbance coordinate. As one can see, for disturbance localization it is necessary to gather two interference signals at the outputs of the loop, find the time delay value Δτ between them, and then calculate the distance from the disturbance point to the first reference plane z1.
3. Simulation of a Sensor Sensitivity Distribution
To study sensitivity distribution over the loop of SI, phase change occurring due to acoustic disturbance can be expressed as follows:
| (8) |
where is the disturbance envelope, we used is a constant that determined the magnitude of the disturbance, is an acoustic signal attenuation, is the time of impact beginning, is the impact duration, and is the disturbance frequency.
The phase difference in the first loop output is:
| (9) |
where a time delay can be calculated as follows:
| (10) |
For the second loop, the same phase difference can be written as:
| (11) |
where a time delay can be calculated as follows:
| (12) |
Three parts can be highlighted in these expressions. A(t) is the envelope of the external impact and determines the main form of the interference pattern. It has slow changes in time, so . The component has the highest frequency and is responsible for the oscillations of the interference pattern with the frequency of the external impact . When registering a signal, the intensity of this component will pass through the entire range from minimum to maximum, from −1 to 1. An additional amplitude coefficient for the phase difference and, consequently, the amplitude of the interference pattern at the receiver, is the component. It becomes zero when the argument is:
and becomes the maximum when:
Thus, the sensitivity graph is a two-dimensional oscillation field, and the maxima, and the minima on the axes of the impact coordinates and frequency will change according to a hyperbolic dependence:
| (13) |
| (14) |
Taking into account the fact that signals usually have a wide spectrum, low impact frequencies and sensor areas close to the middle of the loops are critical for sensing applications
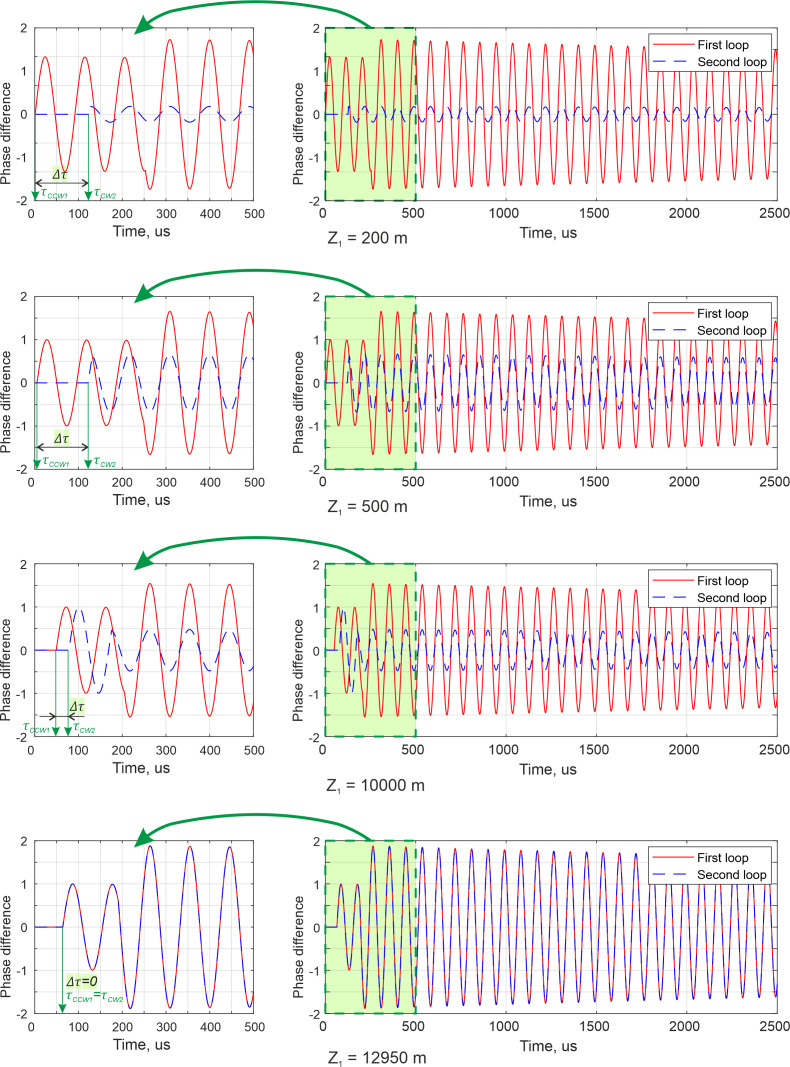
Due to the principles of SI signal formation, a phase difference at the sensor loops output differs if the same disturbance influences the loops at points with different coordinates z1. We considered the sensitivity of the sensor as a maximum phase difference amplitude at the output of the loop, in the presence of an acoustic disturbance. In order to investigate sensitivity distribution through loops and define zones of low sensitivity, where disturbance localization is difficult, we simulated phase difference at the loop outputs ∆φ1(t,∆τ1), ∆φ2(t,∆τ2), in a case when a disturbance influences the loops at different distances z1 from the first reference plane. Figure 10 presents diagrams of the phase difference at the output of the first and the second loops, with a length of L = 51,800 m, that arises when a disturbance influences the loops at points distanced for z1 = 200 m, 500 m, 10,000 m, and 12,950 m from the first reference plane. We assumed that a disturbance had a frequency of ft = 11 kHz and produced a phase shift with an amplitude of 2 radians. The ADC sampling frequency was vD = 25 MHz, the observation time was 2.5 ms, and the loops included additional coils with a length of Ld = 1000 km in its half-length, in order to move “dead zones” outside the sensory region. The first diagram for z1 = 200 m shows that this disturbance point is close to the “dead zone” of the first loop. A phase difference amplitude φA1 = max{∆φ1(t,∆τ1)}-min{∆φ1(t,∆τ1)} was too small in such a case, so the interferential signal amplitude was also small, and the moment when the signal started to change due to a disturbance cannot be distinguished. On the contrary, the phase difference in the second loop was large because the disturbance point was close to the second reference plane, but we needed a start time in both loops for disturbance localization. The point located at a distance of z1 = 500 m is on the edge of the “dead zone”, as the second diagram shows. The amplitude of the phase difference and an interferential signal amplitude increased, which made it possible to determine the moment when the signal started to change due to a disturbance both in the second loop and in the first loop. The third diagram, showing the point with coordinate z1 = 10,000 m, shows that phase differences both in the first loop and in the second one are sufficient to localize the disturbance. The fourth diagram shows that for the point with coordinate z1= L/4 = 12,950 m, phase differences at the output of the first and second loops become the same and both are sufficient for disturbance localization. Moreover, in such a case, zero time delay exists (∆τ = 0), which is consistent with (7). With a further increase in z1, when a disturbance point shifts closer to the first loop half-length, the phase difference amplitude increased for the first loop and decreased for the second loop, until the “dead zone” of the second loop was reached, closer to its half-length.
Figure 10.
Simulated signal plots for two loops.
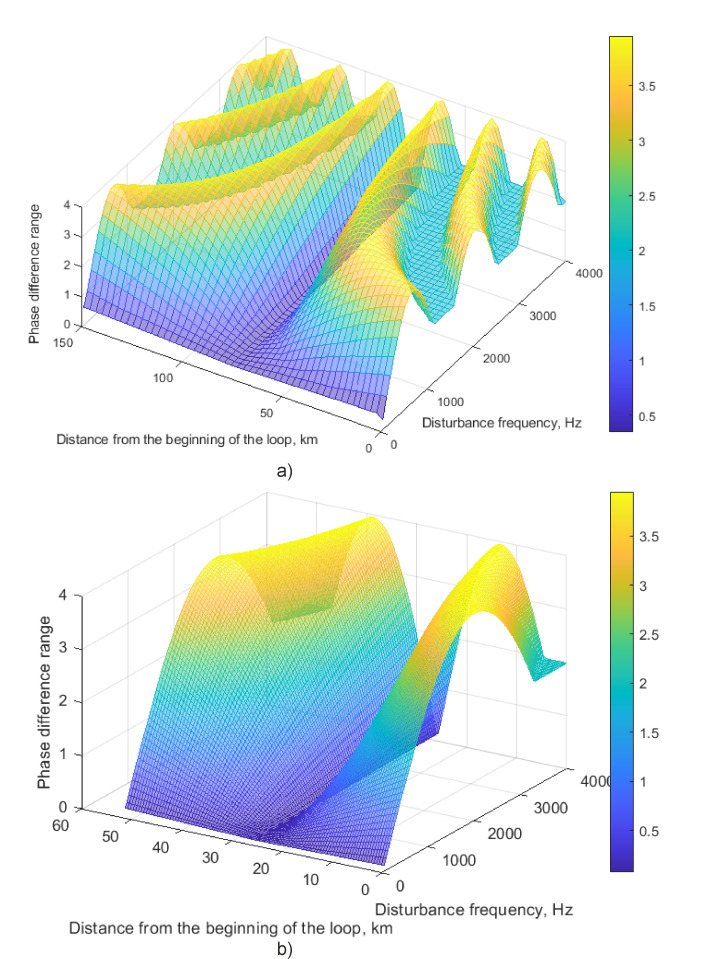
The phase difference range φA1 in the first loop output, depending on a disturbance position z1 along the first loop, and its frequency ft were studied. For this purpose, several disturbances were simulated. Each of them had a fixed frequency and a position along a sensing loop. The time duration was similar to the plots in Figure 10. A simulation of the sensitivity distribution along the first SI loop was carried out depending on two parameters: the coordinate of the disturbance relative to the first reference plane z1, and the disturbance frequency ft. For the loop length L = 150 km, 50 values of the disturbance coordinate were selected in a range of 0 km to 150 km with a uniform step, as well as 50 values of the disturbance frequency in a range of 40 Hz to 4 kHz with a uniform step. The results are presented in Figure 11a,b.
Figure 11.
Phase different range depending on disturbance frequency and position: (a) L = 150 km, (b) L = 51.8 km.
The sensitivity has a periodical distribution, with a shorter period at high disturbance frequencies, which is consistent with (9) and (11). A “dead zone” is located in the center of the loop, at a distance of d1 = L/2 = 75 km. If a loop has a shorter length, a plot is limited by the length values. When applied to the loop with a length of 51,800 m, the plot from Figure 11a includes only its central region, as shown in Figure 11b. To avoid a low sensitivity region, we used an additional Ld = 1000 m fiber spool that moved the “dead zone” outside of the sensory region. Thus, the ±500 m “dead zone” close to the half-length of the loop was inside the additional coil and throughout the rest of the loop, along the entire sensory region, the disturbance was localized easily. We carried out experimental studies at the coordinate ž = 24,500 m with a total loop length of (L + Ld) = 51,800 m.
However, the disturbance localization error depends not just on impact spectra, which are determined by the signal shape. It is necessary to take into account the SNR and the ADC sampling rate. To study a mutual dependence of disturbance localization error on these three parameters, an experimental setup was assembled. A series of experiments, with a certain impact shape, were conducted to obtain a coordinate of the disturbance determined by the sensor system.
4. Experiment
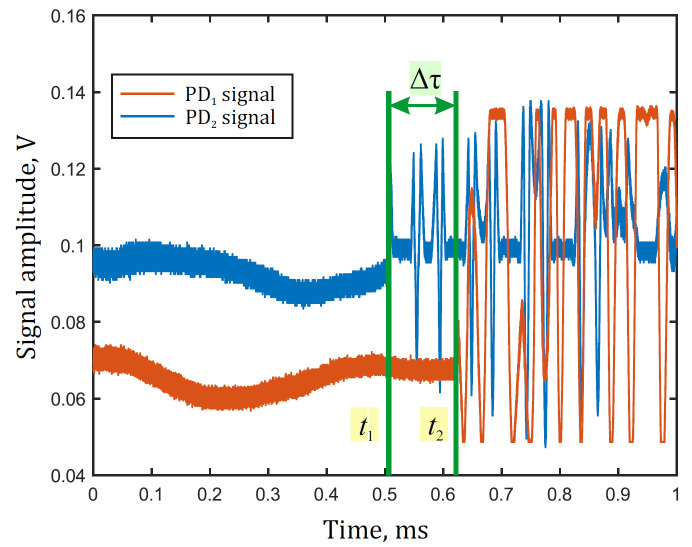
An experimental setup of the sensor model shown in Figure 4 was assembled to implement the method and analyze disturbance localization error. A piezoelectric transducer (PZT) wound with 20 m of fiber was used to emulate a disturbance. It was positioned at the coordinate z0 = 25,450 m from the first reference plane, which was measured using a reflectometer. In further experiments, we defined z0 as a true value of the disturbance coordinate. The sensor measured the value of z1, so we compared z1 with z0 to calculate an error of disturbance localization. The total length was L = 51,800 m, considering both the coils’ length Lc = 25,400 m and the delay fiber length Ld = 1000 m. Pulses from a signal generator with a width of 10 μs produced a deformation with 4 μm amplitude for 20 m of wounded fiber, which were supplied to the PZT. Two FEMTO HCA-S-200M-IN were used as photodetectors. A LeCroy WaveRunner 620Zi oscilloscope operated in the system as an ADC and delivered acquired data to a computer for processing in MATLAB, which was carried out according to the specified method. To investigate the accuracy with which the system identifies localized disturbances, 100 data realizations were acquired and processed. An example of a single data realization obtained from the sensor with vD = 25 MHz sampling frequency is shown in Figure 12.
Figure 12.
Measured signal plots for two loops.
For disturbance localization, we used an adaptive threshold method, consisting of determining the moments of the interference signal modulation beginning with the outputs of loops and . The moments were determined using a signal that exceeded a threshold level, and the time difference, defined as Δτ = t1 − t2, is used in (7).
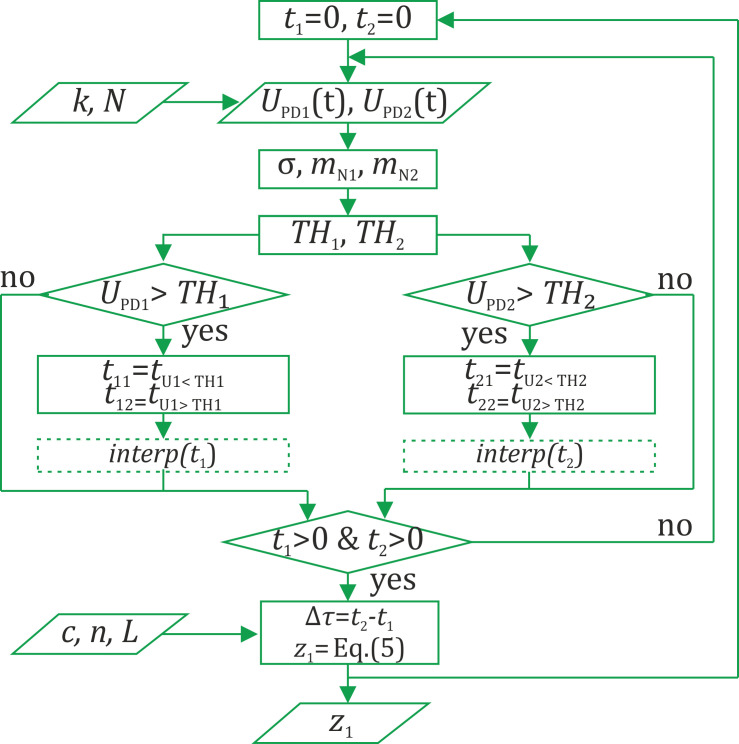
In the data processing algorithm diagram shown in Figure 13, UPD1,2 is the level of the signal gathered from PD1,2, TH is the threshold level, t1,2 is the beginning moment of interference signal modulation for the first and the second loops, and z1 is the determined disturbance position.
Figure 13.
Data processing algorithm.
TH level is defined as follows:
| (15) |
where σ is the standard deviation, calculated from 100 sample points, and mN1,2(νD) is the expected value calculated from sample points for both data realizations. The number of points N(νD) depends on sampling frequency νD, as well as k(νD), which refers to a proportional coefficient. Adjusting the adaptive threshold level allowed us to consider noise level changes and interference signal range changes due to photodetector noise, environmental influence, and polarization instability [8]. Thus, a timely response to disturbances was insured. The moments t1,2 were determined by linear interpolation between two successive signal points: one occurred before the threshold exceeding, and the other after it, as shown in Figure 14a.
Figure 14.
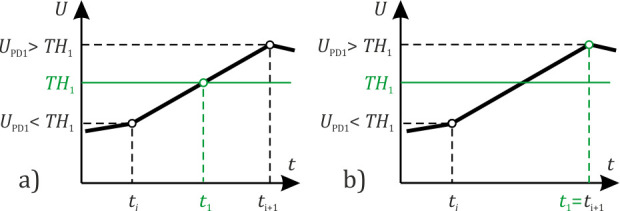
Determination of the detected moments at which the signal exceeds the threshold (a) with and (b) without interpolation.
When using an algorithm for defining a time delay ∆τ, by determining when the moments of the interference signal modulation begin as specified above, a method for defining these moments is essential. If a time delay ∆τ is defined improperly, it causes errors of disturbance localization. A theoretical minimum error of sensor disturbance localization is theoretical spatial resolution δz, which can be determined using the sampling rate of the formula δz = c/(n νD). In a case when a realization is obtained using low sampling frequency, disturbance can be localized with error, limited by SNR in a realization analyzed by the sensor and by a signal shape. Therefore, in practice, an error of disturbance localization is greater than the theoretical spatial resolution due to system noise, and it depends on both SNR and sampling frequency. Implementing interpolation makes it possible to improve the accuracy of determining the interference signal modulation beginning moments when the SNR is high enough, but in a case of a high noise level, this is not enough to overcome the limitations of the algorithm, and interpolation does not provide high-precision results. The SNR value depends on both system state and experimental conditions. The SNR particularly depends on the sampling frequency of ADC. We investigated the SNR dependence on sampling frequency and a disturbance localization error of our system, using the algorithm with and without interpolation for different SNR, i.e., for different sampling frequency values. It allowed us to discover if interpolation is excessive for realizations with high noise and it is appropriate to save computing resources by excluding this stage.
Experiments were carried out with ADC sampling frequencies ranging from 1 to 25 MHz. For each sampling frequency, 100 data realizations with a duration of 1 ms were acquired. First of all, we defined an SNR in a realization as follows:
| (16) |
where σN is noise standard deviation, and S is signal amplitude.
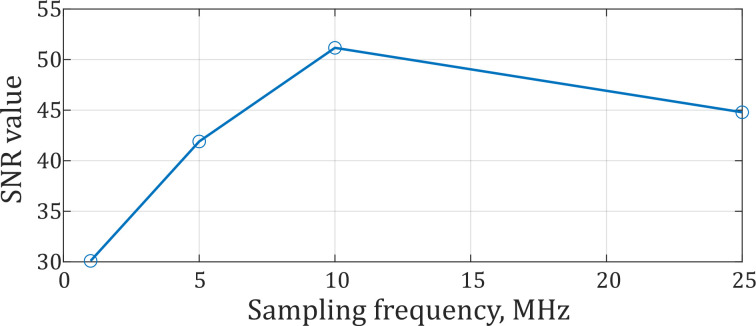
Signal amplitudes were calculated as a difference between the maximum and the minimum of optical power in the photodetector values when it is modulated due to an acoustic disturbance. Noise standard deviation values were calculated by 162, 829, 1662, and 4162 points for 1, 5, 10, and 25 MHz respectively, which refers to a duration of (1/6) μs. For each certain value of sampling frequency, the SNR was calculated for each realization, and then averaged over 100 realizations. The result is shown in Figure 15. As one can see, the SNR reached the maximum value at vD = 10 MHz. This value will affect spatial resolution as described in the following.
Figure 15.
The SNR averaged over 100 realizations for different sampling frequencies.
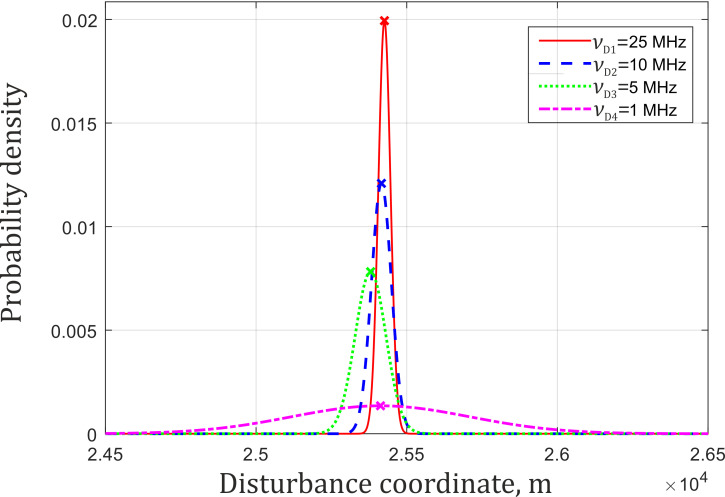
For each sampling frequency, 100 data realizations were processed according to the specified algorithm with interpolation. For every sampling frequency value, coordinate distribution histograms were plotted. An example of a histogram for the 25 MHz sampling frequency with its Gaussian approximation is shown in Figure 16.
Figure 16.
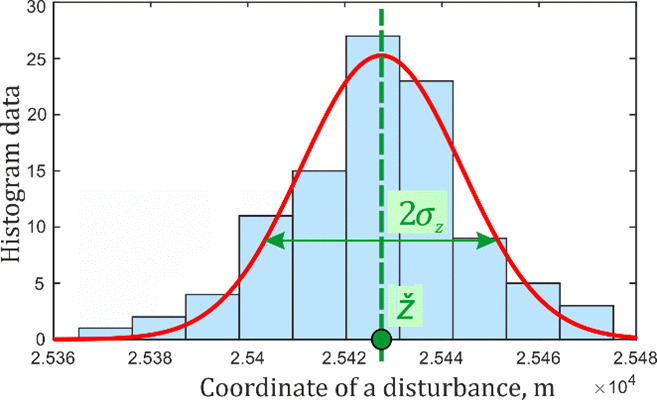
Coordinate determination histogram at νD = 25 MHz.
The histogram envelopes of the determined coordinates for the different sampling rates are shown in Figure 17. Table 1 shows values calculated from the results of the experiments performed. Standard deviation σz represents the coordinate determination error for 100 measurements. The expected value ž is the average coordinate value for all realizations, ∆z is its deviation from the true value z0.
Figure 17.
Gaussian approximation of z1 obtained using interpolation algorithm for different νD values.
Table 1.
System parameters in case of interpolation.
| νD, MHz | N(νD) | k(νD) | δz, m | 2σz, m | ž, m | ∆z, m |
|---|---|---|---|---|---|---|
| 1 | 32 | 5 | 200 | 296 | 25,413 | 37 |
| 5 | 64 | 7 | 40 | 51 | 25,380 | 33 |
| 10 | 64 | 11 | 20 | 33 | 25,416 | 34 |
| 25 | 128 | 11 | 8 | 20 | 25,426 | 24 |
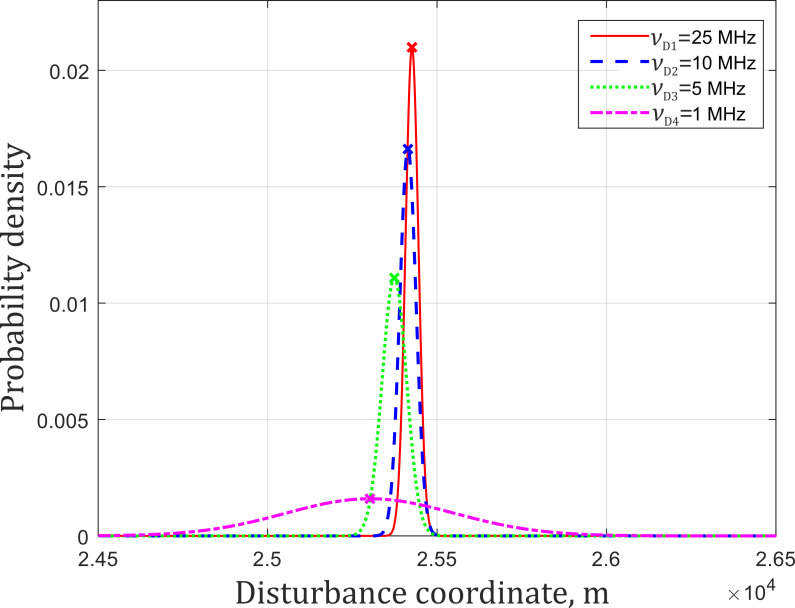
The results indicate that when the sampling frequency grows, the coordinate determination error decreases. However, it increases the theoretical value of δz. At νD = 25 MHz, it exceeds the theoretical limit by 2.5 times. Under such conditions, interpolation for coordinate determination is inappropriate. This was verified on the same data using the algorithm from which the interpolation stage was excluded. The obtained results are presented in a similar form in Figure 18 and Table 2.
Figure 18.
Gaussian approximation of z1 obtained without interpolation for different νD.
Table 2.
System parameters without interpolation.
| νD, MHz | δz, m | 2σz, m | ž, m | Δz, m |
|---|---|---|---|---|
| 1 | 200 | 250 | 25,302 | 148 |
| 5 | 40 | 36 | 25,374 | 76 |
| 10 | 20 | 24 | 25,414 | 36 |
| 25 | 8 | 19 | 25,426 | 24 |
The results show that at low sampling rates, ∆z and σz increase, but at high sampling rates, they become similar to the equivalent values obtained when using interpolation. Overall assessment can be carried out based on the graphical presentation of the tables in Figure 19.
Figure 19.
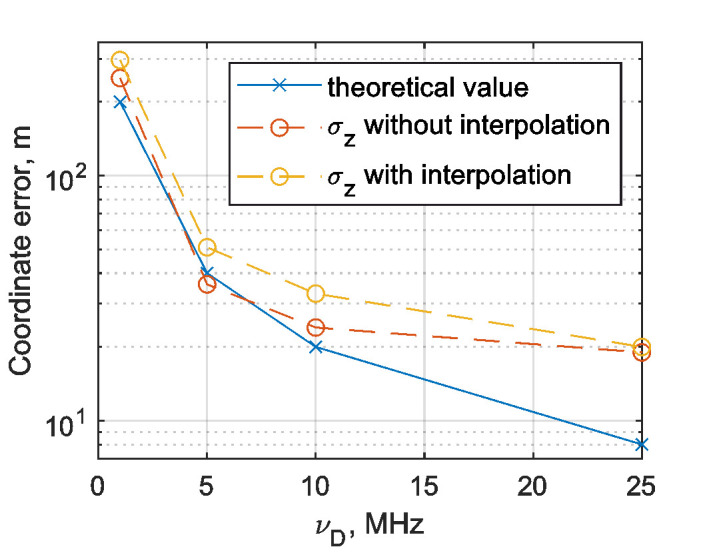
Dependence of disturbance localization error on sampling frequency.
5. Discussion
Usually, the coordinate determination error σz is comparable to the theoretical expectation for sampling frequencies of up to 10 MHz. Figure 15 and Figure 19 presented that the SNR, for a fixed time duration, has a correlation with the critical value of the coordinate determination error σz. The SNR stopped growing at νD = 10 MHz, and at the same sampling frequency σz started to exceed its theoretical limit significantly, which demonstrates that the SNR value influences the disturbance localization error critically. Nevertheless, SNR depends on νD, as we have a number of points for the SNR calculation for different νD values, as shown in Equation (16). At νD = 25 MHz, the error in the coordinate determination is significantly higher than the theoretical value, because of the SNR limitation. However, the coordinate determination error decreases when increasing the sampling frequency, and disturbance localization error Δz for νD = 25 MHz is lower than the result for νD = 10 MHz. It means that SNR is not the only limiting factor. Therefore, to achieve a small enough error of disturbance localization in the proposed scheme, it is advisable to use an ADC with a sampling rate of at least 10 MHz and SNR > 44. In addition, in the case of a low sampling rate, interpolation can reduce the average value of Δz, but it is not stable, as shown in Table 1 and Table 2.
In the proposed version of the scheme and algorithm, data processing does not require signal phase unwrapping, so there is no need to use several photodetectors and ADCs at the output of each loop. A disturbance’s coordinates can be determined in other ways, including using correlation, for which it is necessary to restore the original disturbance signal shape. In this case, it is possible to detect the radiation coming from the C1 and C2 splitter outputs, which are not used in the scheme in Figure 1. Phase restoration can be performed, for example, according to the algorithm [22].
A comparison with previously described sensor configurations is presented in Table 3.
Table 3.
Comparison of system parameters for reviewed schemes.
| Used method | Coordinate Determination Error | Sensor Length | Comments | Ref. |
|---|---|---|---|---|
| Combination of Michelson and Sagnac interferometers | 160 m for 120 km sensor (0.14%) | 120 km | [23] | |
| Combination of Mach-Zehnder and Sagnac interferometers | 60 m for 61 km sensor (0.1%) | 61 km | [24] | |
| SI based on TDE | 10 m for a 50 km sensor (0.02%) | 50 km | Requires phase unwrapping scheme | [17] |
| SI based on “null frequencies” | 100 m for 50 km sensor (0.2%) | 50 km | Highly sensitive to noise | [4] |
| SI based on TD between countering loops | 15 m for a 5 km sensor (0.9%) | 5 km | Losses on couplers or Requires PM-fiber |
[18,19,20] |
| Suggested scheme | 24 m for 25.4 km sensor (0.1%) | 25.4 km |
Results show that the suggested scheme does not require phase unwrapping, filtering, and high-cost components such as special fibers, but it demonstrates good localization accuracy, and is competitive with the best existing schemes.
6. Conclusions
In this article, we proposed a new scheme for a distributed fiber optic sensor based on a double Sagnac interferometer, and explored its sensitivity for different disturbance frequencies and coordinates, and measured disturbance localization accuracy. We proposed a simple algorithm for determining the coordinates of the disturbance and have confirmed its high-accuracy operation with several experiments. In the laboratory setup, a 25 km sensor fiber was used. A disturbance with stated parameters was localized with different sampling rates and SNR values. The results show that the SNR value is important for reaching a minimal error of disturbance localization. However, increasing the sampling rate allowed the obtention of better accuracy, even with lower SNR. For example, in our setup, we achieved 34 m accuracy (at νD = 10 MHz and SNR = 52) and 24 m accuracy (at νD = 25 MHz and SNR = 44) which is less than 0.1% of the sensing fiber length. This scheme can be used to implement distributed acoustic fiber monitoring systems.
Author Contributions
Conceptualization, A.A.Z. and T.V.C.; methodology, A.A.Z. and T.V.C.; software, T.V.C.; validation, A.A.Z. and K.I.K.; formal analysis, A.O.C. and T.V.C.; investigation, T.V.C. and A.A.Z.; resources, A.B.P. and V.E.K.; data curation, K.V.S. and A.A.Z.; writing—original draft preparation, T.V.C. and A.A.Z.; writing—review and editing, K.V.S., A.O.C., V.E.K. and K.I.K.; visualization, T.V.C., A.A.Z. and K.V.S.; supervision, A.B.P.; project administration, A.B.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 22-29-01577.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Yuan W., Pang B., Bo J., Qian X. Fiber optic line-based sensor employing time delay estimation for disturbance detection and location. J. Lightwave Technol. 2014;32:1032–1037. doi: 10.1109/JLT.2013.2296617. [DOI] [Google Scholar]
- 2.Hoffman P.R., Kuzyk M.G. Position determination of an acoustic burst along a Sagnac interferometer. J. Lightwave Technol. 2004;22:494. doi: 10.1109/JLT.2004.824455. [DOI] [Google Scholar]
- 3.Wang Y., Li P., Zhang J., Liu X., Bai Q., Wang D., Zhang M., Jin B. Distributed optical fiber vibration sensor using generalized cross-correlation algorithm. Measurement. 2019;144:58–66. doi: 10.1016/j.measurement.2019.04.092. [DOI] [Google Scholar]
- 4.Song Q., Peng H., Zhou S., Zhou P., Xiao Q., Jia B. A novel weak-scattering Michelson interferometer based on PBS for long-distance disturbance localization. J. Lightwave Technol. 2020;38:1543–1548. doi: 10.1109/JLT.2019.2953134. [DOI] [Google Scholar]
- 5.Huang J., Chen Y., Song Q., Peng H., Zhou P., Xiao Q., Jia B. Distributed fiber-optic sensor for location based on polarization-stabilized dual-Mach-Zehnder interferometer. Opt. Express. 2020;28:24820–24832. doi: 10.1364/OE.399640. [DOI] [PubMed] [Google Scholar]
- 6.Zhang G., Liang Y.J., Xi C., Zuo H.G. Dual-Sagnac Optical Fiber Sensor Used in Acoustic Emission Source Location; Proceedings of the 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference; Harbin, China. 26–30 July 2011. [Google Scholar]
- 7.Fang N., Wang L., Jia D., Shan C., Huang Z. Walking intrusion signal recognition method for fiber fence system; Proceedings of the 2009 Asia Communications and Photonics conference and Exhibition (ACP); Shanghai, China. 2–6 November 2009. [Google Scholar]
- 8.Wang H., Sun Q., Li X., Wo J., Shum P.P., Liu D. Improved location algorithm for multiple intrusions in distributed Sagnac fiber sensing system. Opt. Express. 2014;22:7587–7597. doi: 10.1364/OE.22.007587. [DOI] [PubMed] [Google Scholar]
- 9.Ye Z., Wang J., Wang C., Jia B. A positioning algorithm realized multilateration for distributed fiber-optic sensor. Microw. Opt. Technol. Lett. 2016;58:2913–2917. [Google Scholar]
- 10.Hang L., He C., Wu B. Novel distributed optical fiber acoustic sensor array for leak detection. Opt. Eng. 2008;47:054401. doi: 10.1117/1.2920390. [DOI] [Google Scholar]
- 11.Huang J., Chen Y., Peng H., Zhou P., Song Q., Huang P., Xiao Q., Jia B. A 150 km distributed fiber-optic disturbance location sensor with no relay based on the dual-Sagnac interferometer employing time delay estimation. Opt. Commun. 2021;479:126420. doi: 10.1016/j.optcom.2020.126420. [DOI] [Google Scholar]
- 12.Fang X. A variable-loop Sagnac interferometer for distributed impact sensing. J. Light. Technol. 1996;14:2250–2254. doi: 10.1109/50.541215. [DOI] [Google Scholar]
- 13.Xu W., Zhang C., Liang S., Li L., Lin W., Yang Y. Fiber-optic distributed sensor based on a Sagnac interferometer with a time delay loop for detecting time-varying disturbance. Microw. Opt. Technol. Lett. 2009;51:2564–2567. doi: 10.1002/mop.24672. [DOI] [Google Scholar]
- 14.Fang X. Fiber-optic distributed sensing by a two-loop Sagnac interferometer. Opt. Lett. 1996;21:444–446. doi: 10.1364/OL.21.000444. [DOI] [PubMed] [Google Scholar]
- 15.Ruan L., He C., Wua B. Security monitoring system based on a line structure Sagnac interferometer with 3 × 3 coupler. Opt. Eng. 2016;55:064108. doi: 10.1117/1.OE.55.6.064108. [DOI] [Google Scholar]
- 16.Russell S., Brady K., Dakin J. Real-time location of multiple time-varying strain disturbances, acting over a 40-km fiber section, using a novel dual-Sagnac interferometer. J. Light. Technol. 2001;19:205–213. doi: 10.1109/50.917882. [DOI] [Google Scholar]
- 17.Hu Y., Chen Y., Song Q., Zhou P., Shen L., Peng H., Xiao Q., Jia B. An asymmetrical dual Sagnac distributed fiber sensor for high precision localization based on time delay estimation. J. Light. Technol. 2021;39:6928–6933. doi: 10.1109/JLT.2021.3105299. [DOI] [Google Scholar]
- 18.Wang Y., Guo M., Liu X., Bai Q., Wang D., Zhang M., Jin B. Distributed acoustic sensor based on improved minimum control recursive average algorithm. Opt. Fiber Technol. 2019;50:125–131. doi: 10.1016/j.yofte.2019.03.012. [DOI] [Google Scholar]
- 19.Teng F., Yi D., Hong X., Li X. Distributed fiber optics disturbance sensor using a dual-Sagnac interferometer. Opt. Lett. 2019;44:5101–5103. doi: 10.1364/OL.44.005101. [DOI] [PubMed] [Google Scholar]
- 20.Teng F., Yi D., Hong X., Li X. Optimized localization algorithm of dual-Sagnac structure-based fiber optic distributed vibration sensing system. Opt. Express. 2021;9:13696–13705. doi: 10.1364/OE.421569. [DOI] [PubMed] [Google Scholar]
- 21.Szustakowski M., Zyczkowski M., Ciurapinski W.M., Palka N. Sensitivity of perimeter sensor based on Sagnac interferometer; Proceedings of the Lightguides and their Applications II; Krasnobród, Poland. 9–11 October 2003. [Google Scholar]
- 22.Koo K.P., Tveten A.B., Dandridge A. Passive stabilization scheme for fiber interferometers using (3 × 3) fiber directional couplers. Appl. Phys. Lett. 1982;41:616–618. doi: 10.1063/1.93626. [DOI] [Google Scholar]
- 23.Song Q., Zhou P., Peng H., Hu Y., Xiao Q., Wu H., Jia B. Improved localization algorithm for distributed fiber-optic sensor based on merged Michelson-Sagnac interferometer. Opt. Express. 2020;28:7207–7220. doi: 10.1364/OE.384728. [DOI] [PubMed] [Google Scholar]
- 24.Ma C., Liu T., Liu K., Jiang J., Ding Z., Pan L., Tian M. Long-range distributed fiber vibration sensor using an asymmetric dual Mach-Zehnder interferometers. J. Lightwave Technol. 2016;34:2235–2239. doi: 10.1109/JLT.2016.2532877. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.