Abstract
A biphasic computational model of a growing, vascularized glioma within brain tissue was developed to account for unique features of gliomas, including soft surrounding brain tissue, their low stiffness relative to brain tissue, and a lack of draining lymphatics. This model is the first to couple non-linear tissue deformation with porosity and tissue hydraulic conductivity to study the mechanical interaction of leaky vasculature and solid growth in an embedded glioma. The present model showed that leaky vasculature and elevated interstitial fluid pressure produces tensile stress within the tumor in opposition to the compressive stress produced by tumor growth. This tensile effect was more pronounced in softer tissue and resulted in a compressive stress concentration at the tumor rim that increased when tumor was softer than host. Aside from generating solid stress, fluid pressure driven tissue deformation decreased the effective stiffness of the tumor while growth increased it, potentially leading to elevated stiffness in the tumor rim. A novel prediction of reduced porosity at the tumor rim was corroborated by direct comparison with estimates from our in vivo imaging studies. Antiangiogenic and radiation therapy were simulated by varying vascular leakiness and tissue hydraulic conductivity. These led to greater solid compression and interstitial pressure in the tumor, respectively, the former of which may promote tumor infiltration of the host. Our findings suggest that vascular leakiness has an important influence on in vivo solid stress, stiffness, and porosity fields in gliomas given their unique mechanical microenvironment.
Keywords: glioma, brain, mechanical model, poroelasticity, biphasic theory, porous media, antiangiogenesis
1. Introduction
The mechanical microenvironment plays an important role in brain tumor progression and treatment. Both solid and fluid mechanical phenomena are present and interact with each other in vivo. Solid elements of tissue include the cellular cytoskeleton and extracellular matrix, which develop mechanical stress as the tumor grows and displaces host tissue. High tumor interstitial fluid pressure (IFP) caused by leaky tumor vasculature produces interstitial flow from the tumor and deforms the solid structure to produce an abnormal stress state in the tumor and surrounding host tissue. An elevated mechanical stress surrounding nodular brain tumors embedded in mice reduced blood vessel size and deformed neuronal nuclei, leading to apoptosis in the host tissue (Seano et al. 2019). External mechanical compression of mouse brain tissue in vivo with a bolt apparatus recapitulated the effects of nodular tumors, confirming that these effects are a direct consequence of mechanical changes (Seano et al. 2019).
Numerous in vitro studies indicate that brain tumor cells are sensitive to such mechanical cues as stress and substrate stiffness. Compression of glioma cells in vitro reduced proliferation and encouraged metastasis via upregulation of Growth Differentiation Factor-15 (GDF15) and the MEK1/Erk1 signaling pathway (Kalli et al. 2019). Glioma cells cultured on stiff substrates proliferated faster than those on softer substrates and showed an increase in Epidermal Growth Factor Receptor (EGFR) and Phosphoinositide-3 Kinase (PI3K) expression (Ulrich et al. 2009; Umesh et al. 2014). Glioma cell lines became non-spherical by extending F-actin rich lamellipodia and were more mobile on stiffer substrates (Grundy et al. 2016; Kim et al. 2014; Ulrich et al. 2009). Glioma 3D tumor spheroids in stiffer substrates invaded their surroundings more readily than in softer substrates (Ananthanarayanan et al. 2011; Grundy et al. 2016). At the tissue level, compressive stress increased the stiffness of ex vivo glioma tissue samples due to compaction. This effect was purely mechanical and could not be attributed to such biochemical changes in the extracellular matrix as increased fiber deposition or cross-linking caused by living cells (Pogoda et al. 2014). Together these results suggest that the mechanical compressive stress that develops within a growing glioma can increase tissue stiffness and promote infiltration of host tissue. However, the question of how to relate stress and stiffness levels that influence glioma cell behavior in vitro to the in vivo mechanical state and their influence on tumor progression remains.
Mechanical changes in the tumor microenvironment are also a consequence of cancer therapies, such as antiangiogenic and radiation therapy. Antiangiogenic therapy reduces the leakiness of tumor vessels which in turn may increase the transvascular pressure gradient and reduce the characteristic elevated IFP of vascularized tumors (Chauhan et al. 2012; Jain et al. 2014; Tong et al. 2004). Restoration of the transvascular pressure gradient has been used to explain the improved extravasation of therapeutic nanoparticles in a size-selective manner that was observed in a preclinical model (Chauhan et al. 2012). Another common therapy, radiotherapy, also induces such mechanical perturbations as cell swelling and changes in tumor blood flow (Brown et al. 2015). Since these changes signal changes in tissue strains and flows, they will presumably signal changes in mechanical stresses. Notably, radiotherapy has also demonstrated synergy with antiangiogenic therapy in animal models (Elmghirbi et al. 2017; Mikkelsen et al. 2009). However, the effects of both antiangiogenic and radiation therapies on tumor mechanics are not entirely clear, although these effects may relate to their therapeutic efficacy.
The study of brain tumor mechanics is hampered by the challenge of measuring mechanical stress and interstitial fluid flow in vivo. Computational models can yield useful insights into in vivo mechanics by providing estimates of stress, interstitial flow, and stiffness fields in the tumor and surrounding host. These models can also be used to predict the effect of changing material properties due to progression or therapy. Computational tumor modeling is a rich field consisting of varied approaches including discrete cell models (Rejniak 2007), reaction-diffusion models (Hogea et al. 2008; Hormuth et al. 2015), and multiphase flow models (Byrne et al. 2003; Tosin and Preziosi 2010). A more comprehensive overview of tumor mathematical modeling can be found in reviews by Lowengrub et al. (2010), Sciume et al. (2013), and Stylianopoulos (2017). A class of continuum models have considered the tumor a deformable solid porous medium saturated with interstitial fluid (Byrne and Preziosi 2003; Roose et al. 2003). In vascularized tumors, computational models of this type have simulated high tumor IFP, outward interstitial fluid flow at the tumor boundary, and growth-induced compressive stress in the tumor (Sarntinoranont et al. 2003; Stylianopoulos et al. 2013). This stress can collapse blood vessels and thus limit the delivery of oxygen, immune cells, and drugs to the tumor (Jain et al. 2014). High IFP also reduces drug transport across vessel walls, and drugs that enter the interstitial space are carried away from the tumor by radial flow. The biphasic mechanical modeling approach has been applied specifically to glioma in a series of studies based on human magnetic resonance imaging (MRI) data (Angeli et al. 2018; Angeli and Stylianopoulos 2016). The simulated glioma developed high IFP and compressive stress within the surrounding brain tissue.
The glioma microenvironment has unusual mechanical characteristics that distinguish it from other tumor types that have been studied with computational modeling. The brain itself is an especially soft organ (Cheng et al. 2008; Franze et al. 2013), and in vivo magnetic resonance elastography (MRE) measurements have indicated that gliomas tend to be softer than surrounding brain tissue (Jamin et al. 2015). In such a soft tissue, stresses and deformations caused by interstitial fluid, normally ignored in stiffer tissues, can provide a more significant contribution. This contribution may be especially pronounced in brain tissue, given the absence of lymphatic vessels in brain parenchyma to help drain fluid that exudes from tumor vasculature (Abbott 2004). Previous models have not accounted for the low stiffness of glioma relative to brain tissue or the absence of draining lymphatics (Angeli et al. 2018; Angeli and Stylianopoulos 2016; Feng et al. 2019). Furthermore, the sensitivity of this fluid-driven solid stress contribution to properties such as vascular leakiness, stiffness or tissue hydraulic conductivity in glioma has not been investigated. The stiffness distribution is also expected to depend on both tumor growth and vascular leakiness because tissue stiffness generally varies under large deformation (Fovargue et al. 2020; Pogoda et al. 2014; Voutouri et al. 2014). Given the challenge of measuring stress in vivo, there is a need for a mechanical model that accounts for characteristics that are specific to gliomas and estimates changes in stiffness that accompany tumor progression. To do this, we have built upon previous biphasic models by our group (Magdoom et al. 2012; Pishko et al. 2011) and included spatial gradients and nonlinear coupling of mechanical and fluidic properties.
Interstitial volume fraction, or porosity, is another tissue property that influences tumor mechanics, especially of the fluid phase. Porosity influences tumor tissue hydraulic conductivity and affects IFP and interstitial flow. These in turn affect both tumor solid stress and transport of species such as therapeutics and growth factors through the tumor. In fact, estimates of interstitial flow and porosity derived from dynamic contrast enhanced MRI (DCE-MRI) showed that outward flow at the tumor rim correlates closely with rim porosity (Ewing et al. 2015). Porosity estimates from this study also showed a lower porosity in the tumor rim compared to the tumor interior or host tissue. Despite the potential importance of this tissue property, previous computational brain tumor models have not examined porosity closely, especially how a spatially varying porosity field might arise from tissue deformation and its consequences for fluid transport (Angeli et al. 2018; Angeli and Stylianopoulos 2016; Feng et al. 2019).
Considering the unique features of glioma, specifically their low stiffness and lack of draining lymphatics, a biphasic computational model was developed to determine how the solid stress produced by leaky vasculature and solid growth interact in an embedded tumor. This model is the first to couple tissue deformation, hydraulic conductivity, and porosity to demonstrate how leaky vasculature may contribute to tumor rim porosity reductions that have been observed in vivo with DCE-MRI. The model was used to further investigate the effect of very soft mechanical properties on the microenvironment. Changes in the spatial distribution of stiffness associated with elevated IFP and growth induced deformations were also considered. In addition, parametric sweeps of vascular leakiness and tissue hydraulic conductivity were conducted to predict the effects of antiangiogenic therapies (reduction in vascular leakiness) and radiation therapies (reduction in tissue hydraulic conductivity).
2. Methods
A spherical biphasic tumor model was developed that accounts for leaky vasculature and tumor growth. The tissue was modeled as a deformable porous medium in which the solid phase consisted of tumor cells, vasculature, and extracellular matrix, and the fluid phase was interstitial fluid (Fig. 1a).
Fig. 1.
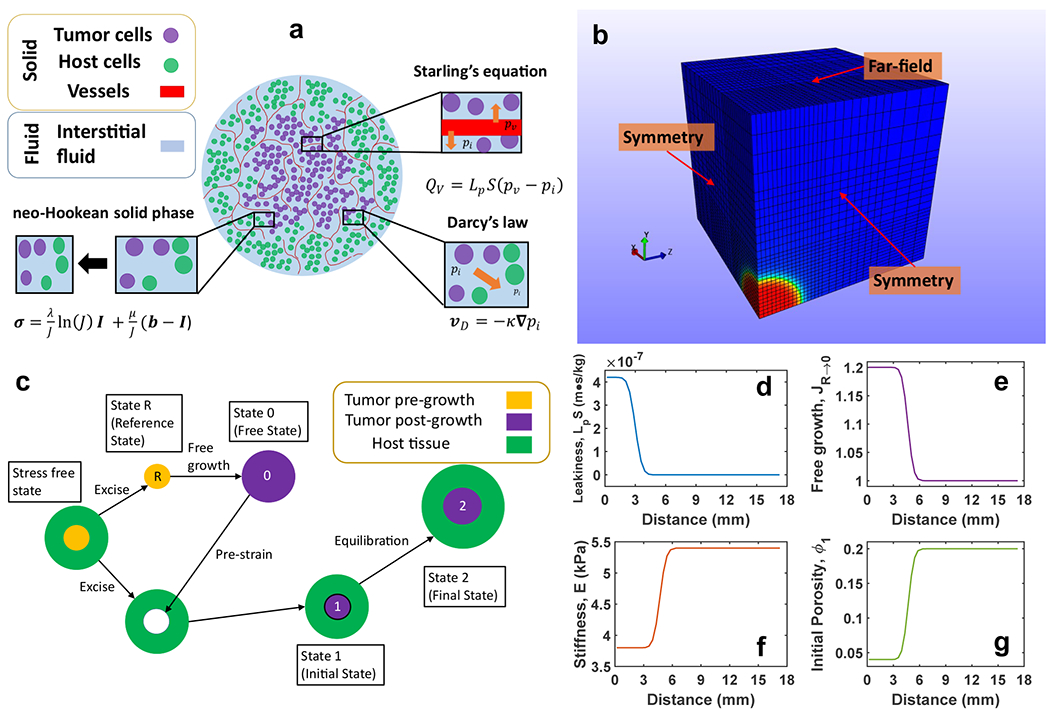
Mechanical model. (a) Diagram of the biphasic spherical tumor model that accounts for vascular fluid production, interstitial fluid transport, as well as solid phase deformation and stress. The legend indicates the constituents of each phase and cutouts describe important model features and their associated equations. (b) Model geometry, finite element mesh, and boundary conditions. The modeled geometry consisted of a 3 mm radius tumor centered at the origin and surrounding host tissue that extended at least five radii beyond the tumor boundary. The model was implemented on a rectilinear mesh with 21,952 elements. (c) Deformation states of the pre-strain technique to model isotropic tumor growth. Beginning with a hypothetical stress-free state, the excised tumor tissue underwent unhindered growth from State R to State 0 before a pre-strain was applied to return the tumor to its original size back inside host tissue (State 1). The tumor tissue then mechanically equilibrated with host tissue while accounting for vascular leakiness (State 2). (d-g) Smooth radial variation of model input parameters such as (d) vascular leakiness LpS, (e) free growth Jacobian JR→0, (f) elastic modulus E and (g) porosity ϕ1 according to Eq. 13
2.1. Mathematical Model
The momentum balance for static equilibrium in the absence of body forces included both solid matrix stress and fluid pressure,
| (1) |
where σ, σs, and pi are the mixture stress tensor, the solid stress tensor, and the IFP, respectively (Bowen 1980). A non-linear neo-Hookean constitutive relation was used for the solid phase which, in general, prescribes a decrease in stiffness for an increase in volume (dilatation) and an increase in stiffness for a decrease in volume (contraction).
| (2) |
Here λ and μ are Lame’s first and second stiffness parameters and J is the Jacobian of deformation which is defined as the determinant of the deformation gradient tensor F. The tensor b is the left Cauchy-Green deformation tensor (Bonet and Wood 1997). A fiber-reinforced neo-Hookean relation for the solid phase has successfully modeled creep indentation experiments in rat brain slices (Lee et al. 2014; Wang and Sarntinoranont 2019) and a simple neo-Hookean relation has been used in previous rat brain mechanical models (Angeli et al. 2018; Angeli and Stylianopoulos 2016). Lame’s stiffness parameters are related to the elastic modulus E and Poisson’s ratio ν as follows (Boresi and Chong 1987):
| (3a) |
| (3b) |
Superficial fluid velocity, or Darcy’s velocity, was proportional to the gradient of IFP by Darcy’s law, where the constant of proportionality is the hydraulic conductivity of the tissue.
| (4) |
Here vD and κ are the superficial velocity and hydraulic conductivity, respectively (Bear 1972). Hydraulic conductivity was assumed independent of direction and thus reduced to a scalar. The superficial velocity is the volumetric flow rate per unit cross section of tissue and is related to the interstitial fluid velocity vi by vD = ϕvi where ϕ is the fluid volume fraction or porosity. Herein, superficial velocity, interstitial flux, and interstitial flow are used interchangeably. Fluid production by leaky tumor vessels within the tumor was proportional to the difference between vascular and interstitial fluid pressure by Starling’s equation.
| (5) |
Here QV is the volumetric fluid production rate per unit volume and pv is the effective vascular pressure (Jain 1987; Netti et al. 1995). The constant of proportionality, LpS, known as the filtration coefficient or vascular leakiness, is the product of the vascular surface area per unit volume, S, and vessel hydraulic conductivity, Lp (Jain 1987). Starling’s equation typically includes a term for osmotically driven fluid production, σ(πi – πv), but because the osmotic pressure difference tends to be small in tumors given the free exchange of most blood proteins across tumor blood vessels (Baxter and Jain 1989) and because rapid osmotic changes were not simulated, this term was subsumed along with vascular pressure into pv. This simplification has been made in previous brain tumor mechanical models (Angeli et al. 2018; Angeli and Stylianopoulos 2016; Netti et al. 1995). A fluid sink term was not included for the host tissue given the lack of draining lymphatics in brain parenchyma (Abbott 2004). Vascular leakiness in healthy brain was set to zero because the intact blood brain barrier greatly restricts fluid and solute transport across brain capillaries compared to capillaries in other organs (Abbott 2004; Fenstermacher and Johnson 1966; Jain 1987). The baseline values for the material parameters used in simulations are in Table 1.
Table 1 –
Material parameters for tumor and host tissue. Tumor and host values are denoted by “T” and “H”, respectively.
| Parameter | Symbol | Value (Baseline; Range) |
|---|---|---|
| Elastic modulus | E | T: (3.8;1.9 – 11.4) kPa (Jamin et al. 2015; Stewart et al. 2017) H: (5.4; 2.7 – 16.2) kPa (Cheng et al. 2008; Franze et al. 2013; Jamin et al. 2015) |
| Vascular leakiness | LpS | T: (4.2; 2.1 – 8.4) × 10−7 m1s1kg−1 (Baxter and Jain 1989; Pishko et al. 2011) H: 0 m1s1kg−1 |
| Specific wetted surface area | Sw | T: (1.4; 0.7 – 2.8) × 106 m−1 H: (1.4; 0.7 – 2.8 × 106 m−1 (Elmghirbi et al. 2018) |
| Poisson’s ratio | ν | T: 0.35 H: 0.35 (Kaczmarek et al. 1997; Wang and Sarntinoranont 2019) |
| Tissue hydraulic conductivity | κ | T: Model dependent H: 2.33 × 10−13 m3s1kg−1 (Elmghirbi et al. 2018; Pishko et al. 2011; Wang and Sarntinoranont 2019) |
| Porosity | ϕ | T: Model dependent H: 0.2 (Sykova and Nicholson 2008) |
| Effective vascular pressure | pv | T: 6 mmHg H: 6 mmHg (Elmghirbi et al. 2018) |
| Fluid dynamic viscosity | μf | T: 3.5 × 10−3 kg1m−1s−1 (Chen et al. 1998; Elmghirbi et al. 2018; Yao et al. 2012) |
| Karman-Cozeny constant | CKC | 5 (Happel and Brenner 1983; Truskey et al. 2009) |
| Tissue transition center | c | (3 – 4.7) × 10–3 m (This study) |
| Tissue transition gradient | s | 0.75 × 10−3 m (This study) |
Isotropic tumor growth was modeled using a pre-strain technique that involved contracting tumor tissue that has undergone unhindered growth and allowing it to reach mechanical equilibrium with the host tissue. An illustration of the states of deformation associated with the pre-strain technique can be found in Fig. 1c. The tumor and host were assumed to begin in a hypothetical reference state (State R) devoid of mechanical stress with the same porosity ϕR as healthy brain tissue, 0.2 (Sykova and Nicholson 2008). The tumor was “excised” and allowed to grow freely (State 0) by adding solid mass due to cell proliferation while preserving normal brain porosity such that ϕR = ϕ0. The amount of growth is quantified by the free growth Jacobian of deformation JR→0, the ratio of State 0 to State R tissue volume. The enlarged tumor was returned to its original size and re-embedded in the host by a pre-strain deformation that resulted in stresses within the tumor that were not balanced by the host (State 1). Assuming the tumor solid volume did not change during the pre-strain tumor tissue deformation, State 1 porosity ϕ1 is related to State 0 porosity ϕ0 by the Jacobian of deformation J0→1 (Eq. 6a). The host tissue must deform and develop stress to mechanically equilibrate with the tumor (State 2). Leaky vasculature was introduced at State 1 and contributed to the deformation and stress field at State 2. As before, State 2 porosity ϕ2 is related to State 1 porosity ϕ1 by the Jacobian of deformation J1→2 (Eq. 6b). By tracking volume changes through the stages of deformation, the final porosity ϕ2 that resulted from constrained growth of tumor tissue with originally normal porosity could be estimated. This approach does not assume a tumor growth rate or track changes over time, but rather predicts the mechanical state for a specified amount of free growth and tissue properties.
| (6a) |
| (6b) |
The State 1 tissue hydraulic conductivity κ1 was related to porosity ϕ1 by the Karman-Cozeny relation.
| (7) |
Here μf is the fluid dynamic viscosity of the interstitial fluid and Sw is the specific wetted surface area of tissue. Sw is a property of porous media which refers to the surface area of contact between the solid and fluid phases normalized by the tissue volume. CKC is a constant which has been shown to approximately equal 5 for porosity less than 0.7 in randomly oriented fiber matrix materials (Happel and Brenner 1983; Truskey et al. 2009).
A strain-dependent hydraulic conductivity formulation related the hydraulic conductivity of the tissue to the Jacobian of deformation.
| (8) |
Here α and M are fitting parameters (Holmes and Mow 1990). κ1 changes by a factor that is a function of J1→2 and ϕ1. This formulation was chosen because it closely mimics the Karman-Cozeny equation relating κ1 and ϕ1 for particular values of α and M. Despite any physical interpretation of these parameters, if M = 0 and α varies with ϕ1 as follows
| (9) |
then Eq. 8 approximates the Karman-Cozeny equation for the range of J1→2 simulated within 10 percent. In other words, this α value results in a functional relationship between κ2 and ϕ2 that is close to Eq. 7. This approximation was used because the Karman-Cozeny equation was not available as a native strain-dependent hydraulic conductivity relation in FEBio, the finite element software employed (Maas et al. 2012). The α value selected also ensures that the hydraulic conductivity of the growing tumor and the reference/host tissue are equal if their porosities are equal. Further development of Eq. 7–9 is found in Appendix 1.
The non-linear neo-Hookean constitutive relation for the solid phase accounts for tissue stiffness that varies with deformation. To quantify the changes in stiffness caused by tumor growth and leaky vasculature, a metric termed effective elastic modulus Eeff was developed which estimated the response of the deformed tissue to further applications of small stresses and strains. Eeff was derived from the effective Lame parameters for a neo-Hookean material (Bonet and Wood 1997)
| (10a) |
| (10b) |
By re-writing Eq. 3a and 3b in terms of effective quantities, an expression for Eeff in terms of E, ν, and J0→2 was derived.
| (11a) |
| (11b) |
To quantify the relative magnitude of Eeff with respect to E, a normalized effective elastic modulus ENeff was defined as
| (12) |
2.2. Computational Methods
Because the tumor was spherical, only an octant of the 3 mm radius tumor (Elmghirbi et al. 2018) surrounded by a host tissue layer five times the tumor radius was modeled (Fig. 1b). A rectangular prism or box geometry with a mesh of rectangular trilinear hexahedral elements (21,952 elements) where the tumor tissue occupied a corner of the box was selected because this mesh style facilitates the transition to realistic tumor geometries derived from imaging data. The mesh was made coarser with increasing distance from the tumor tissue to save computation time because sharp gradients were not expected far from the tumor. The element side lengths ranged from 0.375 mm in the tumor to 1.5 mm in the far-field. A mesh refinement analysis indicated that the model was mesh independent in steep gradient regions near the tumor boundary for elements with side lengths smaller than 0.9 mm. A comparison of the spherical model in a rectangular domain and spherical domain did not show significant differences because the far field boundaries were located at least 5 tumor radii from the tumor edge. No fluid flux was permitted through the three interior boundaries intersecting the tumor and these could only deform in plane due to geometric symmetry. Fluid could pass through the three far field boundaries where IFP was set to zero, and these surfaces were allowed to deform freely. An open source finite element solver designed specifically for biological applications, FEBio (Maas et al. 2012), was used to solve the biphasic governing equations with the stated boundary conditions. Tumor growth was prescribed as a pre-strain deformation gradient from State 0 to State 1 using the FEBio PreStrain plugin (Maas et al. 2016).
To ensure a smooth transition in material properties from tumor to host tissue, MATLAB (MATLAB v. 9.4.0.813654 (R2018a), The Mathworks, Inc., Natick, MA) code was developed to produce custom input files in which material properties were assigned to each element in the mesh. Specifically, vascular leakiness LpS, elastic modulus E, and pre-stretch ratio λ0→1, varied radially within tumor and host tissue by Eq. 13 (Fig. 1d & 1f). For isotropic growth, the deformation gradient tensor F0→1 = λ0→1I and the free growth Jacobian (Fig. 1e). State 1 porosity ϕ1 was computed based on as in Eq. 6a (Fig. 1g).
| (13) |
The variable A(r) represents any of the spatially varying properties mentioned above. The constants Ah and At are the nominal values for this property in the host and tumor tissue, respectively. The constant c is the center position of the transition region between tumor and host values. The constant s is inversely related to the slope of this transition region at its center position. The values for c and s were selected to produce uniform tumor properties up to the nominal tumor radius and a smooth transition to normal tissue beyond this radius. This is intended to reflect the poorly defined boundaries of brain lesions which are often infiltrative. The LpS curve began its transition at a smaller radius so that substantial leakiness does not extend into the transition region outside the nominal tumor radius. This was motivated by in vivo MRI data which show that contrast agent enhancement due to leaky vasculature first occurs in the tumor proper before extravascular contrast agent is driven into the surrounding transition region by interstitial flow (Ewing et al. 2015). Background gradients presented in the results figures extend from 3 mm to 6 mm which corresponds to the transition/infiltrative region between the nominal tumor radius (indicated with a vertical line) and the healthy host tissue.
2.3. Parameter Sensitivity and Comparison with Experiment
A parametric analysis was performed in which mean stiffness Eμ, stiffness ratio ER, vascular leakiness LpS, and specific wetted surface area Sw, were varied. Three levels for each parameter were considered: twice the baseline, baseline, and half the baseline for four free growth values. Mean stiffness and stiffness ratio were defined as the average and ratio of tumor Et and host Eh elastic moduli, respectively.
| (14a) |
| (14b) |
Variations in vascular leakiness and specific surface area were intended to reflect changes in tissue properties that result from antiangiogenic and radiation therapy thus providing insight into the effect of these therapies on the mechanical state of the tumor and host tissue. In the sweep of LpS, a 50 percent reduction in the baseline value is justified by in vivo estimates of a roughly 50 percent maximum reduction in tumor Ktrans following Avastin administration (Nagaraja et al. 2021). A sensitivity analysis of material property profile alignment, centering c, and inclination s is included in Appendix 2.
Simulated porosity and velocity fields were compared with in vivo estimates of porosity and interstitial fluid flux made in embedded rat cerebral tumors using DCE-MRI (Ewing et al. 2015). These data were derived from 16 athymic rats bearing U251 MG tumors with maximum diameter ranging from 3.11 mm to 8.26 mm (5.21 ± 1.55 mm). The 6 mm diameter of the simulated spherical tumor fell within one standard deviation of the mean maximum diameter. This value was considered reasonable given that the in vivo tumors were not perfectly spherical. Two imaging studies at 7 T were performed for each animal 24 hrs apart and are herein referred to as Exp 1 and Exp 2. A dual-echo spoiled gradient-recalled sequence was used to acquire an image with 2 mm slices every 4 seconds for 10 min. Further details about the experimental procedures can be found in previous publications (Aryal et al. 2014a; Aryal et al. 2014b; Ewing et al. 2015). A reduction in porosity at the tumor boundary was quantified by taking the ratio of contrast agent distribution volume fraction estimates in the normal rim and the tumor interior, Rϕ. A one-tailed t-test with a significance level of 0.05 was used to determine whether the population mean was less than unity. A Lilliefors test with significance level 0.05 failed to reject the null hypothesis (p = 0.089) that the Rϕ data were sampled from a distribution in the normal family (Lilliefors 1967). Despite this, given the small sample size, a non-parametric one-tailed sign test with significance level 0.05 was also used to determine whether the population median was less than unity. Separate estimates of fluid flux through the tumor rim from the two studies per animal were compared with the simulated velocity at the tumor boundary. The coefficient of determination R2 was computed for ten simulated rim fluid velocity versus porosity data points. All statistical tests and correlation analyses were performed in MATLAB (MATLAB v. 9.4.0.813654 (R2018a), The Mathworks, Inc., Natick, MA).
3. Results
Fluid exudation from tumor vasculature and tumor growth both affected the mechanical state of the tumor and surrounding host tissue. Leaky vasculature produced an elevated tumor IFP that declined sharply near the tumor boundary resulting in outward interstitial fluid flow (Fig. 2a – 2b; Fig. 3b). High IFP expanded the tissue and stretched the solid phase to produce radial and hoop tension within the tumor and host tissue (Fig. 2c – 2d). In contrast, solid phase tumor growth had a compressive effect in the tumor and reduced predicted intra-tumor tension. Tumor growth displaced the surrounding host tissue, producing radial compression and also increasing hoop tension in regions adjacent to the tumor rim (Fig. 2c–2d). Fluid driven tissue expansion drives increases in tissue porosity inside the tumor, but at the tumor rim this was counteracted by growth driven tissue compression which reduced porosity, producing a radial porosity profile with a notable dip in value at the tumor boundary for JR→0 > 1.1 (Fig. 3a). Reduced porosity at the tumor boundary has been previously measured with DCE-MRI (Ewing et al. 2015). The ratio of host to tumor porosity estimates at the boundary, Rϕ, in that study were significantly less than unity (Fig. 3c; n = 16; t-test p < 1.21 x 10−5; Sign test p < 2.59 x 10−4) indicating a similar decrease in porosity in the tumor periphery. Interstitial flow was greatest at the tumor boundary and decreased with increasing growth (Fig. 3b). Additionally, a strong positive correlation between interstitial flow and porosity at the tumor boundary was present in both our model predictions (R2 = 0.84) and in vivo measurements (R2 = 0.9) (Ewing et al. 2015) (Fig. 3b, 3d). The 0.5 SW case is shown in Fig. 3d because the magnitude and slope of the model output data were the best match to the experimental data although model outputs with other SW values also showed a positive trend.
Fig. 2 –

Mechanical stress in host and tumor with leaky vasculature at various free growth levels. (a-b) IFP color map (a) and line plot (b) where the horizontal axis is distance from the tumor center. (c-d) Line plots of solid phase radial (c) and hoop (d) stress. Each growth level is denoted by its free growth Jacobian JR→0 value, up to 20% free growth (See legend in Panel b). The background gradient indicates the smooth transition from tumor to host (left to right). The vertical line marks the nominal tumor boundary. Refer to Table 1 for baseline values of vascular perfusion pressure and leakiness
Fig. 3 –

Porosity and interstitial flow in host and tumor with leaky vasculature at various free growth levels. (a-b) Line plots of porosity (a) and superficial fluid velocity (b) where the horizontal axis is distance from the tumor center. Each growth level is denoted by its free growth Jacobian JR→0 value, up to 20% free growth (See Legend in b). The vertical line marks the nominal tumor boundary. (c) Ratio of host to tumor porosity estimates at the boundaries of U251 tumors implanted in sixteen rats adapted from (Ewing et al. 2015). A one-tailed t-test accepts with p < 1.21 × 10−5. A one-tailed sign test accepts with p < 2.59 x 10−4. (d) Scatter of tumor rim superficial velocity against porosity from mechanical modeling and in vivo experiments adapted from (Ewing et al. 2015). Results from two DCE-MRI experiments are plotted as free points (Exp 1 and Exp 2) whereas model outputs for the growth levels considered in panels (a) and (b) at two boundary locations are plotted as connected points (Sw set to half the baseline value Sw = 1.4 × 106 m−1). The approximate maximum tumor diameter in the experiments ranged from 3.11 mm to 8.26 mm (5.21 ± 1.55 mm) (Ewing et al. 2015). Refer to Table 1 for baseline values of vascular perfusion pressure and leakiness
Effects of growth were isolated by modeling solid phase growth in the tumor without vascular exudation. Growth generated compressive stress in the tumor and hoop tension in the host tissue rim (Fig. 4). If fluid exudation and growth were absent, tumor and host remained stress free. When the mean value of tumor and host stiffness Eμ was decreased, both compressive stress in the tumor and hoop tension in the tumor rim decreased (Fig. 4a–4b). Varying the ratio of tumor to host tissue stiffness ER had a much smaller effect on the stress state (Fig. 4d – 4e). A stiffer tumor (2ER case) does experience greater growth-induced compressive stress at State 1 than a softer tumor (0.5ER case), but the former equilibrates with a softer surround than the latter resulting in similar compressive stress magnitudes at State 2. Conversely, the stiffness ratio affected the tumor porosity whereas mean stiffness did not (Fig. 4c & 4f). When tumor was softer than host tissue, the host tissue more effectively resisted tumor expansion, which led to a decrease in porosity as the growing solid phase displaced the fluid phase within the tumor.
Fig. 4 –
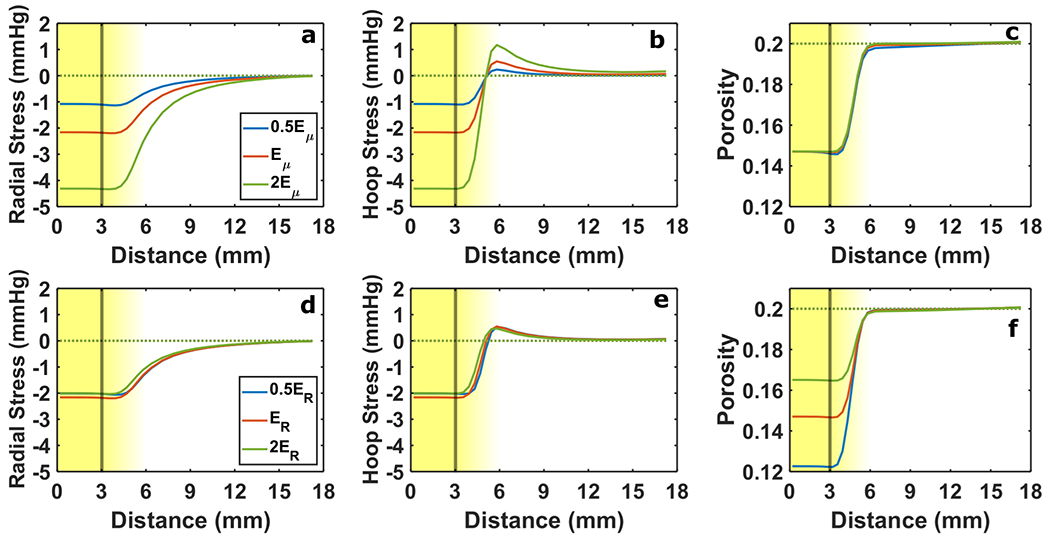
Solid stress and porosity response to changes in stiffness without vascular leakiness. In (a-c) the average of tumor and host stiffness Eμ was varied and in (d-f) the ratio of tumor to host stiffness ER was varied. Radial stress (a & d) and hoop stress (b & e) are presented alongside tissue porosity (c & f). The line color distinguishes each level of Eμ and ER considered (See Legend in Panel a and Panel d). Solid lines indicate 20% free growth (JR→0 = 1.2), and dashed lines indicate no growth. The background gradient indicates the smooth transition from tumor to host (left to right). The vertical line marks the nominal tumor boundary. Baseline values were Eμ = 4.6 kPa and ER = 0.7
Effects of leaky vasculature alone were also isolated. As with growth alone, the solid stress was sensitive to Eμ. Lower Eμ resulted in lower tissue tension and greater porosity in both the tumor and host (Fig. 5a – 5c). Higher porosity corresponded with higher tissue hydraulic conductivity which increased superficial fluid velocity out of the tumor. With the inclusion of solid phase tumor growth, tension in the tumor was reduced and resulted in compressive stress for higher stiffness levels while increasing hoop tension outside the tumor boundary (Fig. 5a–5b). Softer tissue ameliorated the compressive effect of tumor growth in the tumor (Fig. 5a–5b) and increased tumor porosity (Fig. 5c).
Fig. 5 –
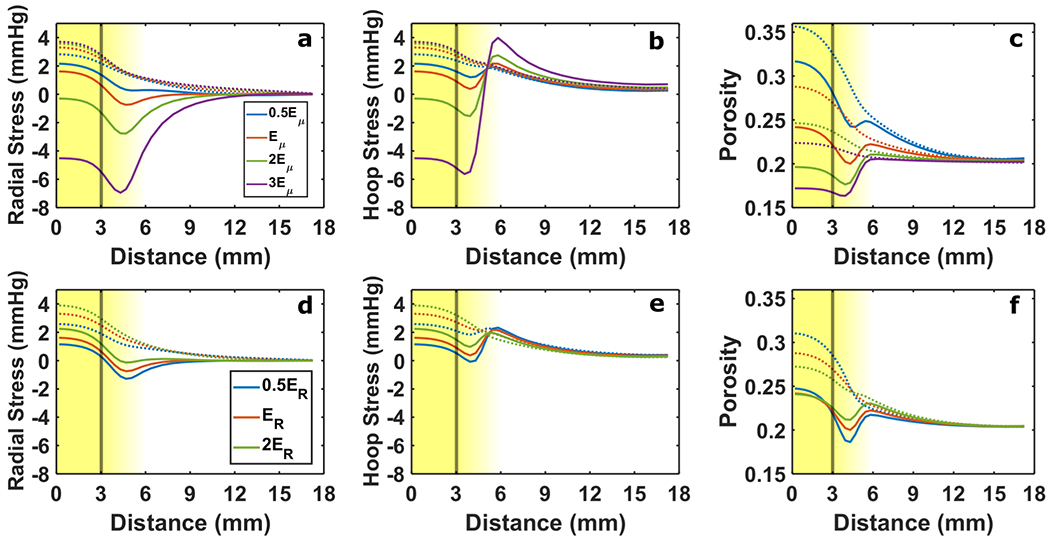
Solid stress and porosity response to changes in stiffness with vascular leakiness. In (a-c) the average of tumor and host stiffness Eμ was varied and in (d-f) the ratio of tumor to host stiffness ER was varied. Radial stress (a & d) and hoop stress (b & e) are presented alongside tissue porosity (c & f). The line color distinguishes each level of Eμ and ER considered (See legends in Panel a and Panel d). Solid lines indicate 20% free growth (JR→0 = 1.2), and dashed lines indicate no growth. The vertical line marks the nominal tumor boundary. The background gradient indicates the smooth transition from tumor to host (left to right). Baseline values were Eμ = 4.6 kPa and ER =0.7
When tumor tissue was softer than the surrounding host, lower tumor tension and higher porosity developed as a result of leaky vasculature compared to higher tumor stiffness (Fig. 5d–5f). Porosity at the rim, however, was similar between these three cases, reducing variation in peak superficial fluid velocity. Growth increased tumor compression and hoop tension at the rim, becoming more pronounced for a lower stiffness ratio (Fig. 5d – 5e). A more significant reduction in rim porosity due to growth was evident for softer tumor tissue (Fig. 5f) which was also present with growth alone (Fig. 4f).
Variation in fluid phase parameters such as vascular leakiness and tissue hydraulic conductivity affected solid phase stresses and porosity. Higher vascular leakiness led to more fluid exudation and consequently higher tension and porosity within the tumor (Fig. 6c – 6e). Superficial fluid velocity also increased (Fig. 6b). Tumor growth decreased tumor tension and increased normal rim hoop tension, but the extent to which stress was affected by growth did not depend on vascular leakiness since the separation between curves remained relatively constant before and after growth (Fig. 6c – 6d). The same observation can be made about the effect of vascular leakiness and growth on porosity (Fig. 6e).
Fig. 6 –
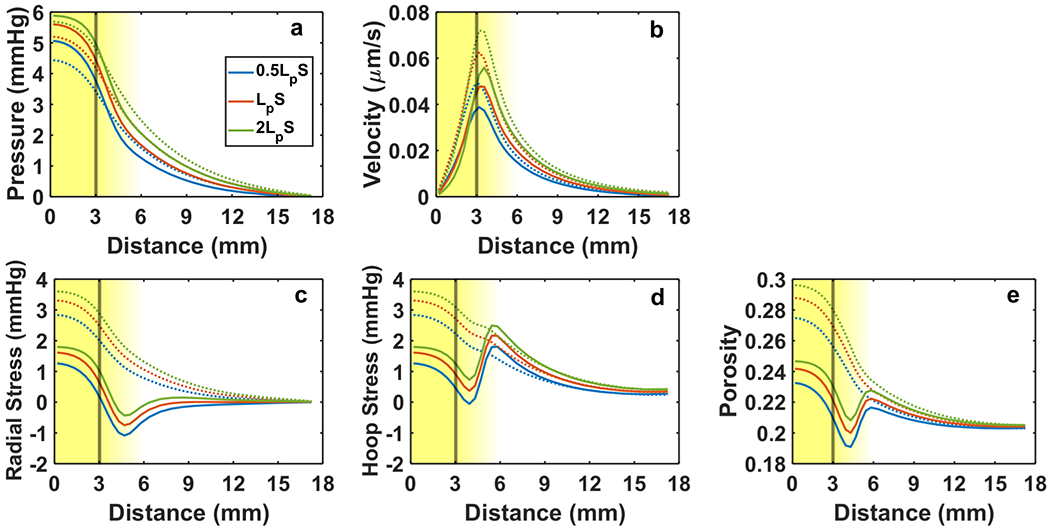
Mechanical response of tumor and host to changes in vascular leakiness LpS. Fluid phase variables include IFP (a) and superficial fluid velocity (b). Solid phase variables include radial stress (c), hoop stress (d), and porosity (e). Solid lines indicate 20% free growth (JR→0 = 1.2), and dashed lines indicate no growth. The line color distinguishes each level of LpS considered (legend in Panel a). The vertical line marks the nominal tumor boundary. The background gradient indicates the smooth transition from tumor to host (left to right). Baseline was LpS = 4.2 × 10−7 m1s1kg−1
Increased specific wetted surface area Sw lead to greater viscous resistance to flow of the fluid phase through the solid matrix and a decrease in tissue hydraulic conductivity. Consequently, higher wetted surface area reduced superficial fluid velocity (Fig. 7b). Because lower tissue hydraulic conductivity inhibited the fluid phase’s ability to exit the tumor, higher pressure developed within the tumor (Fig. 7a) causing more expansion and higher tumor tension and porosity (Fig. 7c – 7e). Similar to variation in vascular leakiness (Fig. 6), growth decreased tumor tension and produced compression for the smallest Sw simulated (Fig. 7c – 7d). Tumor growth was also responsible for the reduction in porosity at the tumor rim below the host tissue level (Fig. 7e).
Fig. 7 –
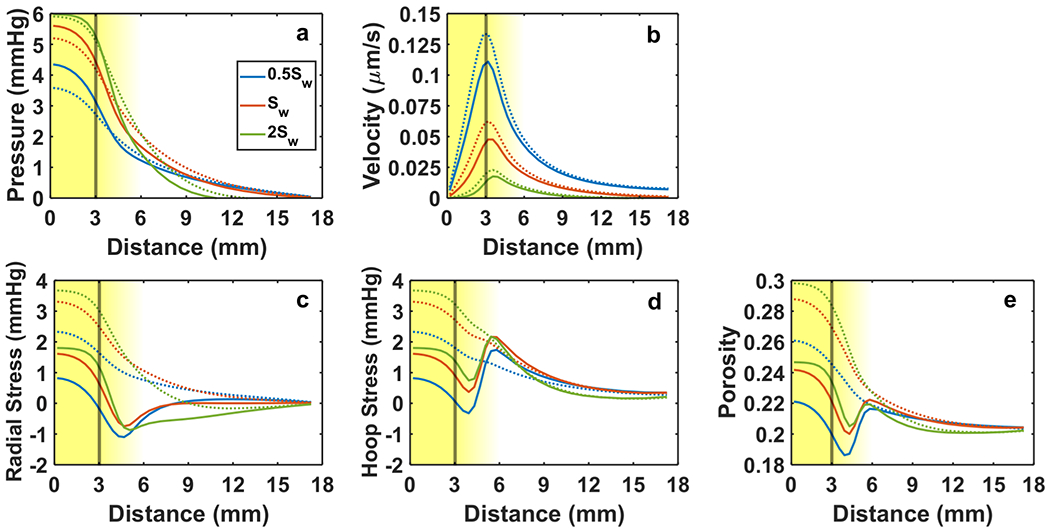
Mechanical response of tumor and host to changes in tissue specific wetted surface area Sw. Fluid phase variables include IFP (a) and superficial fluid velocity (b). Solid phase variables include radial stress (c), hoop stress (d), and porosity (e). Solid lines indicate 20% free growth (JR→0 = 1.2), and dashed lines indicate no growth. The line color distinguishes each level of Sw considered (legend in Panel a). The vertical line marks the nominal tumor boundary. The background gradient indicates the smooth transition from tumor to host (left to right). Baseline was Sw = 1.4 × 106 m−1
Tumor tissue compression caused by growth increased the effective elastic modulus Eeff of the tumor by roughly the same factor as the tumor free growth JR→0 (Fig. 8a). A 20 percent increase in JR→0 corresponded to approximately a 20 percent increase in Eeff (Fig. 8b). In contrast, increased vascular leakiness produced tissue expansion and a decrease in tumor and host Eeff (Fig. 8a). When vascular leakiness was present, the stiffening effect of tumor growth was most pronounced in the region just outside the tumor where Eeff was nearly equal to the nominal elastic modulus E (Fig. 8b).
Fig. 8 –

Deformation-induced changes in tissue stiffness. Line plots of (a) effective elastic modulus Eeff and (b) normalized effective elastic modulus ENeff. Results presented for leakiness without growth (JR→0 = 1), growth without leakiness (JR→0 = 1.2; LpS = 0), and growth with leakiness (JR→0 = 1.2). The lines labeled “State R” correspond to Eeff prior to deformation, Eeff = E (See legend in Panel a). The vertical line indicates the nominal tumor boundary. The nominal elastic modulus values are Et = 3.8 kPa and Eh = 5.4 kPa
4. Discussion
A computational model was developed to study the mechanical state of a growing, vascularized spherical tumor within brain tissue. The model was based on biphasic mechanical theory, which can account for interactions between the fluid and solid phases in the tumor microenvironment due to leaky vasculature and tissue growth. Similar models have been published that simulate IFP and solid stress for tumors generally (Sarntinoranont et al. 2003; Stylianopoulos et al. 2013), and brain tumors specifically (Angeli et al. 2018; Angeli and Stylianopoulos 2016). The novelty of the present model is that it considered properties that are specific to gliomas, including very soft host tissue, evidence of lower tumor stiffness compared to the host tissue (Jamin et al. 2015), and the absence of draining lymphatic vessels (Abbott 2004).
4.1. Solid Phase Effects: Stress and Stiffness
As in previous tumor mechanical models, vascular leakiness resulted in elevated tumor IFP that nearly equaled the microvascular perfusion pressure (Baxter and Jain 1989; Netti et al. 1995; Sarntinoranont et al. 2003). The simulated pressure drop at the tumor boundary resulted in a peak pore fluid velocity at the rim in the approximate range of 0.2 μm/s to 0.3 μm/s similar to previous estimates based on DCE-MRI (Fig. 2a–2b,3b)(Elmghirbi et al. 2018; Ewing et al. 2015). This range was computed for the baseline case by dividing the superficial fluid velocity at the tumor rim in Fig 3b by the rim porosity in Fig 3a. By simulating vascular leakiness and a range of solid tumor growth, the present model distinguished the opposing effects of these features on tumor stress. Pressurization due to leaking vasculature and the absence of draining lymphatics expanded the tumor and surrounding host, producing tension. This effect of pressure-driven tissue expansion or how it contributes along with tumor growth to in vivo stress at the tumor rim has not been previously studied. Given that in vitro studies have focused on glioma cell response to compressive stress, the potential direct effects of tensile stress on a cell’s tendency to proliferate or infiltrate the host are unknown. Inside the tumor, tension is counteracted by the compressive effect of tumor growth, resulting in a region of lower tension and greater compression at the rim (Fig. 2c–2d). This compressive stress concentration at the tumor rim could stimulate infiltration as has been observed in vitro (Kalli et al. 2019). It is important to note that this stress profile was only present when growth and leakiness were modeled, and that it became more prominent when tumor was softer than host (Fig. 5d–5e). The lower the mean stiffness, the greater the tumor tension observed for the same amount of growth (Fig. 5a–5b). This is especially relevant in brain, a notably soft organ (Franze et al. 2013; Pogoda et al. 2014), and in light of recent MRE measurements that suggest gliomas may be softer than their host (Jamin et al. 2015). Other potential consequences of pressure-driven tumor expansion stem from its reduction of growth-induced compression. When the tensile effect was curbed by decreasing vascular leakiness, IFP decreased but, paradoxically, greater compression in the tumor and tumor rim developed (Fig. 6c–6d). This is somewhat counter-intuitive because the decrease in IFP represents a “normalization” of the tumor microenvironment, but the concomitant increase in solid compression drives the tumor tissue further from “normal” tissue conditions. This may help explain some indications that reducing vascular leakiness in vivo with antiangiogenic therapy can promote tumor infiltration in preclinical models (Kunkel et al. 2001; Paez-Ribes et al. 2009) and human patients (de Groot et al. 2010; Narayana et al. 2009; Norden et al. 2008).
A handful of tumor mechanical models built on biphasic theory that account for both leaking vasculature and growth indicate that the solid stress within the tumor is compressive both radially and circumferentially. This is mainly due to both the higher growth strains and tissue stiffness used in these models. Our results indicate that solid stress in the tumor becomes less tensile and more compressive with increasing growth and stiffness (Fig 2c, 2d; Fig 5a, 5b). Angeli et al. 2016 report a growth stretch of λG = 8 which corresponds to a very large growth Jacobian JG = 512 and a stiffness of 35 kPa in the tumor. This corresponds to mean tumor solid stress of −13 kPa (Angeli and Stylianopoulos 2016). In Fraldi and Carotenuto (2018), a Jacobian of JG = 2 leads to radial and hoop stresses of approximately −6.5kPa. In our model, the scenario with the highest mean stiffness (13.8 kPa), JG = 1.2 corresponds to tumor solid stress on the order of −0.5 kPa. Smaller JG values were used in our model because they are not interpreted as growth from a small tumor seed, but rather the degree of unconstrained growth that reduces tumor porosity from healthy levels to typical tumor levels when constrained by normal tissue (from 0.2 to 0.15 in the no leakiness case, Fig 4c). Analysis of tumor volume change in MR images of rat gliomas indicate that JG for most of the volume is less than 4 (Feng et al. 2019). Despite this growth strain limitation our conclusions regarding the opposing stress effects of leakiness and growth, the concentrated effects at the boundary, and the trends observed when varying parameters should be significant at the larger growth strains estimated in Feng et al. (2019) given the innate softness of brain tissue and that the tumors remain softer than their host. While the implications of pressure-driven tumor tension on progression are not clear, our results show this is an important factor in the mechanics of glioma given their unique properties.
Because tissue stiffness influences the tumor stress state, it is important to consider that stiffness in brain tissue tends to change as the tissue deforms (Pogoda et al. 2014), e.g. strain hardening with tissue compaction. This non-linear property implies that the deformations related to tumor progression such as those associated with growth or leaky vasculature affect in situ or in vivo stiffness. Deformation-induced changes in stiffness have been investigated as a source of bias in stiffness estimates made with MRE (Fovargue et al. 2020), but could also serve as an indicator for the extent of deformation the tumor has undergone and thus its progression. The present model showed that while leaky vasculature and tumor growth both lead to enlargement of the tumor from State 1 to State 2 (J1→2 > 1), the former reduced the effective tumor stiffness Eeff and the latter increased it (Fig. 8). This softening effect may contribute to the low estimates for glioma stiffness in vivo. Moreover, the normalized stiffness ENeff plots show that growth and leakiness together could result in a region of higher effective stiffness near the tumor rim than in the tumor interior or host tissue (Fig. 8b). This is important because increased substrate stiffness has been shown to stimulate infiltration in numerous 2D and 3D in vitro studies.
4.2. Fluid Phase Effects: Porosity and Velocity
Our model demonstrated that leakiness-driven tissue expansion increased tumor porosity above the host value, but growth decreased porosity, especially at the tumor rim (Fig. 3a). This dip in porosity at the tumor rim matches with in vivo porosity estimates made with DCE-MRI (Ewing et al. 2015)(Fig. 3c) and has not been predicted by previous computational tumor models. Without accounting for vascular leakiness, tumor growth was expected to decrease porosity by increasing solid volume fraction and resulted in uniformly lower porosity within the tumor (Fig. 4c & 4f). Thus, our modeling suggests that these in vivo porosity profiles are a consequence of leakiness and growth, not growth alone. As with rim compressive stress, the peri-tumoral dip in porosity becomes more pronounced with the decreasing tumor-to-host stiffness ratio characteristic of glioma. Another factor contributing to observed in vivo porosity profiles may be an increase in central tumor porosity because of necrotic edema observed in vascularized tumors (Jain et al. 2014), which was not accounted for in our model. Our model also showed a positive correlation between rim porosity and superficial fluid velocity, in agreement with in vivo estimates (Ewing et al. 2015) (Fig. 3d). As with solid stress, porosity was also sensitive to variations in stiffness ratio and mean stiffness. Fluid pressure-driven tissue expansion resulted in the highest tumor porosity when mean tissue stiffness and tumor to host stiffness ratio were lowest (Fig. 5c & 5f). In contrast, tumor growth produced the greatest decrease in tumor porosity when tumor was softer than host (Fig. 4f). Growth-induced reduction of porosity could explain how vascularized in vivo gliomas that are softer than the surrounding tissue could have lower porosity than normal brain and produce a marked decrease in porosity in the adjacent normal tissue. Accounting for spatially varying porosity is important because changes in this parameter affect the transport of nutrients, drugs and signaling molecules through the tumor extracellular space and can be an indirect indicator of mechanical compression or expansion.
4.3. Therapeutic implications: vascular normalization and radiotherapy
Variation in fluid phase parameters such as vascular leakiness and tissue hydraulic conductivity also affected solid phase stresses. Antiangiogenic therapy represses the production of new tumor vasculature and decreases vascular leakiness (Gerstner et al. 2020; Jain et al. 2014) In agreement with previous computational models and in vivo DCE-MRI observations, lower vascular leakiness reduced IFP (Chauhan et al. 2012; Tong et al. 2004) and interstitial flow out of the tumor (Nagaraja et al. 2021) (Fig. 6a–6b). While this, in turn, decreased the hoop tension that has been associated with collapse of peripheral blood vessels (Stylianopoulos et al. 2013), our model also predicted increased tumor compression due to reductions in pressure-driven tissue expansion (Fig. 6c–6d). An unintended consequence of antiangiogenic therapy could therefore be further compression of tumor cells which has been shown to encourage metastasis in vitro in certain glioma cell lines (Kalli et al. 2019).
Radiation is a common cancer therapy that can acutely cause tumor cell swelling (Brown et al. 2015). This leads to an inference that cell swelling can alter tissue hydraulic conductivity by affecting porosity and wetted surface area. Increasing wetted surface area and decreasing tissue hydraulic conductivity will result in an increased IFP and decrease in radial flow out of the tumor (Fig. 7a & 7b). Preliminary experimental evidence indicates a decrease in tumor rim porosity, a parameter which is highly correlated with radial flow (Ewing et al. 2015), following high dose radiotherapy in rats (Elmghirbi et al. 2015). Higher wetted surface area also reduces tumor compression caused by solid growth but results in higher hoop tension in the normal tissue rim (Fig. 7c & 7d). This could cause a spatially varying effect in which peripheral vessels, especially those oriented circumferentially, become more prone to collapse than interior tumor vessels. This may contribute to the decrease in tumor blood flow observed in the early hours after single high-dose radiation in brain tumor-bearing rats (Brown et al. 2015). However, radiotherapy induces a complex time-dependent biological cascade involving long-term changes in cell density and tumor cell proliferation rate (Lima et al. 2017) that could result in an increase in tissue hydraulic conductivity and potential increases in radial interstitial flow (Fig. 7b) and tumor blood flow at later times (Brown et al. 2015). While radiotherapy likely affects more than a single property, varying SW provides insight into the possible effects of changes in hydraulic conductivity following radiotherapy. Another structural property, tumor stiffness, is expected to change following radiotherapy. MRE studies have reported tumor softening both with and without treatment but only significant host stiffening without treatment (Feng et al. 2016). Radiation may thus attenuate the decrease in tumor to host stiffness ratio observed in the untreated group and also decrease mean tissue stiffness. While changes in the stiffness field following radiation are likely complex and patient-specific, our results indicate a decrease in mean tissue stiffness and a greater stiffness ratio would decrease growth induced compression in the tumor and tumor rim (Fig. 5).
4.4. Advantages and Limitations
While the present model accounted for solid and fluid mechanical factors that influence the tumor microenvironment, it did not account for the full spatial heterogeneity characteristic of in vivo tumors. Gliomas can have irregular geometries and vascular density, leakiness, and porosity distributions. However, considering a spherical tumor with uniform growth facilitated the interpretation of results because the effects of local property gradients which would obscure the underlying interaction of growth and leakiness were not present. Given the spatial distribution of phenotypes comprising a proliferative rim and quiescent/necrotic core is tumor specific, this study involves an idealized geometry to establish baseline behavior to compare with future studies that will account for image-based material property heterogeneity. The authors expect that growth restricted to a proliferative rim as opposed to uniform tumor growth would further enhance the local increases in stress and stiffness and decreases in porosity present at the rim in the uniform growth scenario. The far-field fluid pressure in the present model was set to zero because the objective was to study stresses in the tumor and its immediate surroundings in the general context of embedded brain tumors. The consequences of elevated cerebrospinal fluid pressure, fluid drainage via the arachnoid villi and lymphatics at the brain periphery (Louveau et al. 2015), or the proximity of the tumor to cerebrospinal fluid spaces (Orozco et al. 2020) will be studied in future image-based models that account for subject-specific geometries and boundary conditions. These models will incorporate MRI data on a voxel-to-element basis where each voxel is associated with a hexahedral element of the same size and shape. Such an approach has been shown to perform well against more traditional models in which features in MRI images are segmented and subsequently meshed (Magdoom et al. 2012).
The present model assumed changes in porosity and stiffness that were based solely on tissue deformation and did not consider cell biochemical signaling that could potentially alter tissue stiffness or porosity without an associated tissue-level deformation. However, because ex vivo glioma and brain tissue exhibit strain stiffening behavior (Pogoda et al. 2014) in vitro and are fluid saturated, these properties can be expected to respond to deformation in a similar manner in vivo. Although cell-level effects including necrosis and infiltration of host tissue were not modeled, our continuum estimates of spatial stress and stiffness variations can inform the stress-based growth rules employed in previous continuum models (Mpekris et al. 2018) and models that combine continuum mechanics and cell behavior (Carotenuto et al. 2018). The opposing effects of leakiness and growth on solid stress in this study motivate careful consideration of the particular stress quantity (mixture stress, solid stress, some measure of mean stress, stress components, etc.) used to modulate cell growth in future models.
Our approach does not model cell proliferation driven growth over time because including the numerous dynamic phenomena that affect cell proliferation such as nutrient distribution, angiogenesis, and cellular competition as well as their sensitivity to mechanical stress would result in a mechanical model that is difficult to validate with available in vivo data for glioma. Anticipating the availability of robust estimates of vascular exudation and tissue porosity via DCE-MRI, our modeling framework was designed to ultimately estimate a growth field that could result in the measured porosity distribution and predict the corresponding in vivo tissue stress state without modeling the prior stress evolution. This is a practical approach since useful imaging data are generally unavailable for early stages of tumor growth because (1) sufficient tumor vascularization has not occurred to enhance the lesion with contrast agent, (2) other sources of contrast such as edema are absent, or (3) patient symptoms have not developed to prompt imaging diagnostics.
The model also assumed that material properties such as stiffness and tissue hydraulic conductivity were isotropic, but evidence from MRE suggests that in vivo tumors and their surroundings develop stiffness anisotropy (Fovargue et al. 2020). Future models will consider the stiffness non-uniformities and anisotropy that could develop from deformation associated with leaky vasculature and growth.
5. Conclusions
A biphasic computational model of a growing, vascularized glioma within brain tissue was developed to account for unique features of glioma, including the soft surrounding brain tissue, their low stiffness relative to brain tissue, and the lack of draining lymphatics. Unlike previous mechanical models, the present model showed that leaky vasculature and elevated IFP produce tensile stress in opposition to the compressive stress produced by tumor growth. This tensile effect was more pronounced in softer tissue and resulted in a compressive stress concentration at the tumor rim that increased when tumor was softer than host. Fluid-solid coupling revealed how growth and leakiness together can produce reduced porosity profiles at the tumor rim observed in previous in vivo DCE-MRI studies (Ewing et al. 2015). Antiangiogenic and radiation therapy were simulated by varying vascular leakiness and tissue hydraulic conductivity. Decreasing vascular leakiness reduced IFP and interstitial flow, but led to greater solid compression in the tumor which may promote tumor cell infiltration of host tissue and vessel compression. Our findings suggest that vascular leakiness has an important influence on in vivo solid stress, stiffness, and porosity fields in gliomas given their unique mechanical microenvironment.
Supplementary Material
Funding:
National Institutes of Health R01CA135329 and R01CA218596
Footnotes
Conflicts of interest: None
Code availability: FEBio (Maas et al. 2012); MATLAB v. 9.4.0.813654 (R2018a); Available upon request.
Availability of data and material:
Upon request
6. Bibliography
- Abbott NJ (2004) Evidence for bulk flow of brain interstitial fluid: significance for physiology and pathology Neurochem Int 45:545–552 doi: 10.1016/j.neuint.2003.11.006 [DOI] [PubMed] [Google Scholar]
- Ananthanarayanan B, Kim Y, Kumar S (2011) Elucidating the mechanobiology of malignant brain tumors using a brain matrix-mimetic hyaluronic acid hydrogel platform Biomaterials 32:7913–7923 doi: 10.1016/j.biomaterials.2011.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angeli S, Emblem KE, Due-Tonnessen P, Stylianopoulos T (2018) Towards patient-specific modeling of brain tumor growth and formation of secondary nodes guided by DTI-MRI NeuroImage-Clin 20:664–673 doi: 10.1016/j.nicl.2018.08.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angeli S, Stylianopoulos T (2016) Biphasic modeling of brain tumor biomechanics and response to radiation treatment Journal of Biomechanics 49:1524–1531 doi: 10.1016/j.jbiomech.2016.03.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aryal MP et al. (2014a) Intratumor distribution and test-retest comparisons of physiological parameters quantified by dynamic contrast-enhanced MRI in rat U251 glioma NMR Biomed 27:1230–1238 doi: 10.1002/nbm.3178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aryal MP et al. (2014b) Dynamic Contrast Enhanced MRI Parameters and Tumor Cellularity in a Rat Model of Cerebral Glioma at 7 T Magn Reson Med 71:2206–2214 doi: 10.1002/mrm.24873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baxter LT, Jain RK (1989) TRANSPORT OF FLUID AND MACROMOLECULES IN TUMORS .1. ROLE OF INTERSTITIAL PRESSURE AND CONVECTION Microvasc Res 37:77–104 doi: 10.1016/0026-2862(89)90074-5 [DOI] [PubMed] [Google Scholar]
- Bear J (1972) Dynamics of Fluids in Porous Media. Dover Publications, Inc., New York, NY, USA [Google Scholar]
- Bonet J, Wood R (1997) Nonlinear continuum mechanics for finite element analysis. Cambridge University Press, New York, NY, USA [Google Scholar]
- Boresi AP, Chong KP (1987) Elasticity in Engineering Mechanics. Elsevier Science Publishing Co., Inc., New York, New York, USA [Google Scholar]
- Bowen RM (1980) INCOMPRESSIBLE POROUS-MEDIA MODELS BY USE OF THE THEORY OF MIXTURES Int J Eng Sci 18:1129–1148 doi: 10.1016/0020-7225(80)90114-7 [DOI] [Google Scholar]
- Brown SL et al. (2015) MRI-Tracked Tumor Vascular Changes in the Hours after Single-Fraction Irradiation Radiat Res 183:713–721 doi: 10.1667/rr13458.1 [DOI] [PubMed] [Google Scholar]
- Byrne H, Preziosi L (2003) Modelling solid tumour growth using the theory of mixtures Math Med Biol 20:341–366 [DOI] [PubMed] [Google Scholar]
- Byrne HM, King JR, McElwain DLS, Preziosi L (2003) A two-phase model of solid tumour growth Appl Math Lett 16:567–573 doi: 10.1016/s0893-9659(03)00038-7 [DOI] [Google Scholar]
- Chauhan VP et al. (2012) Normalization of tumour blood vessels improves the delivery of nanomedicines in a size-dependent manner Nat Nanotechnol 7:383–388 doi: 10.1038/nnano.2012.45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CT, Malkus DS, Vanderby R (1998) A fiber matrix model for interstitial fluid flow and permeability in ligaments and tendons Biorheology 35:103–118 doi: 10.1016/s0006-355x(99)80001-8 [DOI] [PubMed] [Google Scholar]
- Cheng S, Clarke EC, Bilston LE (2008) Rheological properties of the tissues of the central nervous system: A review Med Eng Phys 30:1318–1337 [DOI] [PubMed] [Google Scholar]
- de Groot JF, Fuller G, Kumar AJ, Piao Y, Eterovic K, Ji YJ, Conrad CA (2010) Tumor invasion after treatment of glioblastoma with bevacizumab: radiographic and pathologic correlation in humans and mice Neuro-Oncology 12:233–242 doi: 10.1093/neuonc/nop027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmghirbi R et al. (2018) Toward a noninvasive estimate of interstitial fluid pressure by dynamic contrast-enhanced MRI in a rat model of cerebral tumor Magn Reson Med 80:2040–2052 doi: 10.1002/mrm.27163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmghirbi R et al. (2017) Acute Temporal Changes of MRI-Tracked Tumor Vascular Parameters after Combined Anti-angiogenic and Radiation Treatments in a Rat Glioma Model: Identifying Signatures of Synergism Radiat Res 187:79–88 doi: 10.1667/rr14358.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmghirbi RM et al. (2015) MRI tracked tumor physiology in the hours after 20 Gy single-fraction radiation. Paper presented at the Proceedings of the International Society of Magnetic Resonance in Medicine, 2015 [Google Scholar]
- Ewing JR et al. (2015) Peritumoral tissue compression is predictive of exudate flux in a rat model of cerebral tumor: an MRI study in an embedded tumor NMR Biomed 28:1557–1569 doi: 10.1002/nbm.3418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng XZ, Hormuth DA, Yankeelov TE (2019) An adjoint-based method for a linear mechanically-coupled tumor model: application to estimate the spatial variation of murine glioma growth based on diffusion weighted magnetic resonance imaging Computational Mechanics 63:159–180 doi: 10.1007/s00466-018-1589-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y, Clayton EH, Okamoto RJ, Engelbach J, Bayly PV, Garbow JR (2016) A longitudinal magnetic resonance elastography study of murine brain tumors following radiation therapy Physics in Medicine and Biology 61:6121–6131 doi: 10.1088/0031-9155/61/16/6121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenstermacher JD, Johnson JA (1966) FILTRATION AND REFLECTION COEFFICIENTS OF RABBIT BLOOD-BRAIN BARRIER Am J Physiol 211:341-+ [DOI] [PubMed] [Google Scholar]
- Fovargue D, Fiorito M, Capilnasiu A, Nordsletten D, Lee J, Sinkus R (2020) Towards noninvasive estimation of tumour pressure by utilising MR elastography and nonlinear biomechanical models: a simulation and phantom study Sci Rep 10:13 doi: 10.1038/s41598-020-62367-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraldi M, Carotenuto AR (2018) Cells competition in tumor growth poroelasticity J Mech Phys Solids 112:345–367 doi: 10.1016/jjmps.2017.12.015 [DOI] [Google Scholar]
- Franze K, Janmey PA, Guck J (2013) Mechanics in Neuronal Development and Repair. In: Yarmush ML (ed) Annual Review of Biomedical Engineering, Vol 15, vol 15. Annual Review of Biomedical Engineering. pp 227–251. doi: 10.1146/annurev-bioeng-071811-150045 [DOI] [PubMed] [Google Scholar]
- Gerstner ER et al. (2020) Bevacizumab Reduces Permeability and Concurrent Temozolomide Delivery in a Subset of Patients with Recurrent Glioblastoma Clinical Cancer Research 26:206–212 doi: 10.1158/1078-0432.ccr-19-1739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grundy TJ et al. (2016) Differential response of patient-derived primary glioblastoma cells to environmental stiffness Sci Rep 6 doi: 10.1038/srep23353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happel J, Brenner H (1983) Low Reynolds number hydrodynamics with special applications to particulate media. Martinus Nijhofff Publishers, The Hague, The Netherlands [Google Scholar]
- Hogea C, Davatzikos C, Biros G (2008) An image-driven parameter estimation problem for a reaction-diffusion glioma growth model with mass effects J Math Biol 56:793–825 doi: 10.1007/s00285-007-0139-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes MH, Mow VC (1990) THE NONLINEAR CHARACTERISTICS OF SOFT GELS AND HYDRATED CONNECTIVE TISSUES IN ULTRAFILTRATION Journal of Biomechanics 23:1145–1156 doi: 10.1016/0021-9290(90)90007-p [DOI] [PubMed] [Google Scholar]
- Hormuth DA, Weis JA, Barnes SL, Miga MI, Rericha EC, Quaranta V, Yankeelov TE (2015) Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data Physical Biology 12 doi: 10.1088/1478-3975/12/4/046006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain RK (1987) TRANSPORT OF MOLECULES ACROSS TUMOR VASCULATURE Cancer Metastasis Rev 6:559–593 doi: 10.1007/bf00047468 [DOI] [PubMed] [Google Scholar]
- Jain RK, Martin JD, Stylianopoulos T (2014) The Role of Mechanical Forces in Tumor Growth and Therapy. In: Yarmush ML (ed) Annual Review of Biomedical Engineering, Vol 16, vol 16. Annual Review of Biomedical Engineering. Annual Reviews, Palo Alto, pp 321–346. doi: 10.1146/annurev-bioeng-071813-105259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamin Y et al. (2015) Exploring the Biomechanical Properties of Brain Malignancies and Their Pathologic Determinants In Vivo with Magnetic Resonance Elastography Cancer Res 75:1216–1224 doi: 10.1158/0008-5472.can-14-1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaczmarek M, Subramaniam RP, Neff SR (1997) The hydromechanics of hydrocephalus: Steady-state solutions for cylindrical geometry Bulletin of Mathematical Biology 59:295–323 [DOI] [PubMed] [Google Scholar]
- Kalli M, Voutouri C, Minia A, Pliaka V, Fotis C, Alexopoulos LG, Stylianopoulos T (2019) Mechanical Compression Regulates Brain Cancer Cell Migration Through MEK1/Erk1 Pathway Activation and GDF15 Expression Frontiers in Oncology 9:17 doi: 10.3389/fonc.2019.00992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SN et al. (2014) ECM stiffness regulates glial migration in Drosophila and mammalian glioma models Development 141:3233–3242 doi: 10.1242/dev.106039 [DOI] [PubMed] [Google Scholar]
- Kunkel P et al. (2001) Inhibition of glioma angiogenesis and growth in vivo by systemic treatment with a monoclonal antibody against vascular endothelial growth factor receptor-2 Cancer Res 61:6624–6628 [PubMed] [Google Scholar]
- Lee SJ, King MA, Sun J, Xie HK, Subhash G, Sarntinoranont M (2014) Measurement of viscoelastic properties in multiple anatomical regions of acute rat brain tissue slices J Mech Behav Biomed Mater 29:213–224 doi: 10.1016/j.jmbbm.2013.08.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lilliefors HW (1967) ON KOLMOGOROV-SMIRNOV TEST FOR NORMALITY WITH MEAN AND VARIANCE UNKNOWN J Am Stat Assoc 62:399-+ doi: 10.2307/2283970 [DOI] [Google Scholar]
- Lima E et al. (2017) Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data Computer Methods in Applied Mechanics and Engineering 327:277–305 doi: 10.1016/j.cma.2017.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louveau A et al. (2015) Structural and functional features of central nervous system lymphatic vessels Nature 523:337-+ doi: 10.1038/nature14432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowengrub JS et al. (2010) Nonlinear modelling of cancer: bridging the gap between cells and tumours Nonlinearity 23:R1–R91 doi: 10.1088/0951-7715/23/1/r01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA (2012) FEBio: Finite Elements for Biomechanics J Biomech Eng-Trans ASME 134:10 doi: 10.1115/1.4005694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas SA, Erdemir A, Halloran JP, Weiss JA (2016) A general framework for application of prestrain to computational models of biological materials J Mech Behav Biomed Mater 61:499–510 doi: 10.1016/j.jmbbm.2016.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magdoom KN, Pishko GL, Kim JH, Sarntinoranont M (2012) Evaluation of a Voxelized Model Based on DCE-MRI for Tracer Transport in Tumor J Biomech Eng-Trans ASME 134:9 doi: 10.1115/1.4007096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikkelsen T et al. (2009) Radiation sensitization of glioblastoma by cilengitide has unanticipated schedule-dependency International Journal of Cancer 124:2719–2727 doi: 10.1002/ijc.24240 [DOI] [PubMed] [Google Scholar]
- Nagaraja TN et al. (2021) Imaging acute effects of bevacizumab on tumor vascular kinetics in a preclinical orthotopic model of U251 glioma NMR Biomed:11 doi: 10.1002/nbm.4516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayana A et al. (2009) Antiangiogenic therapy using bevacizumab in recurrent high-grade glioma: impact on local control and patient survival J Neurosurg 110:173–180 doi: 10.3171/2008.4.17492 [DOI] [PubMed] [Google Scholar]
- Netti PA, Baxter LT, Boucher Y, Skalak R, Jain RK (1995) TIME-DEPENDENT BEHAVIOR OF INTERSTITIAL FLUID PRESSURE IN SOLID TUMORS-IMPLICATIONS FOR DRUG-DELIVERY Cancer Res 55:5451–5458 [PubMed] [Google Scholar]
- Norden AD et al. (2008) Bevacizumab for recurrent malignant gliomas-Efficacy, toxicity, and patterns of recurrence Neurology 70:779–787 doi: 10.1212/01.wnl.0000304121.57857.38 [DOI] [PubMed] [Google Scholar]
- Orozco GA, Smith JH, Garcia JJ (2020) Three-dimensional nonlinear finite element model to estimate backflow during flow-controlled infusions into the brain Proc Inst Mech Eng Part H-J Eng Med 234:1018–1028 doi: 10.1177/0954411920937220 [DOI] [PubMed] [Google Scholar]
- Paez-Ribes M et al. (2009) Antiangiogenic Therapy Elicits Malignant Progression of Tumors to Increased Local Invasion and Distant Metastasis Cancer Cell 15:220–231 doi: 10.1016/j.ccr.2009.01.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pishko GL, Astary GW, Mareci TH, Sarntinoranont M (2011) Sensitivity Analysis of an Image-Based Solid Tumor Computational Model with Heterogeneous Vasculature and Porosity Ann Biomed Eng 39:2360–2373 doi: 10.1007/s10439-011-0349-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pogoda K et al. (2014) Compression stiffening of brain and its effect on mechanosensing by glioma cells New Journal of Physics 16:15 doi: 10.1088/1367-2630/16/7/075002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejniak KA (2007) An immersed boundary framework for modelling the growth of individual cells: An application to the early tumour development J Theor Biol 247:186–204 doi: 10.1016/j.jtbi.2007.02.019 [DOI] [PubMed] [Google Scholar]
- Roose T, Netti PA, Munn LL, Boucher Y, Jain RK (2003) Solid stress generated by spheroid growth estimated using a linear poroelasticity model Microvasc Res 66:204–212 doi: 10.1016/s0026-2862(03)00057-8 [DOI] [PubMed] [Google Scholar]
- Sarntinoranont M, Rooney F, Ferrari M (2003) Interstitial stress and fluid pressure within a growing tumor Ann Biomed Eng 31:327–335 doi: 10.1114/1.1554923 [DOI] [PubMed] [Google Scholar]
- Sciume G, Gray WG, Ferrari M, Decuzzi P, Schrefler BA (2013) On Computational Modeling in Tumor Growth Archives of Computational Methods in Engineering 20:327–352 doi: 10.1007/s11831-013-9090-8 [DOI] [Google Scholar]
- Seano G et al. (2019) Solid stress in brain tumours causes neuronal loss and neurological dysfunction and can be reversed by lithium Nature Biomedical Engineering 3:230-+ doi: 10.1038/s41551-018-0334-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart DC, Rubiano A, Dyson K, Simmons CS (2017) Mechanical characterization of human brain tumors from patients and comparison to potential surgical phantoms PLoS One 12 doi: 10.1371/journal.pone.0177561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stylianopoulos T (2017) The Solid Mechanics of Cancer and Strategies for Improved Therapy J Biomech Eng-Trans ASME 139 doi: 10.1115/1.4034991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stylianopoulos T, Martin JD, Snuderl M, Mpekris F, Jain SR, Jain RK (2013) Coevolution of Solid Stress and Interstitial Fluid Pressure in Tumors During Progression: Implications for Vascular Collapse Cancer Res 73:3833–3841 doi: 10.1158/0008-5472.can-12-4521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sykova E, Nicholson C (2008) Diffusion in brain extracellular space Physiol Rev 88:1277–1340 doi: 10.1152/physrev.00027.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong RT, Boucher Y, Kozin SV, Winkler F, Hicklin DJ, Jain RK (2004) Vascular normalization by vascular endothelial growth factor receptor 2 blockade induces a pressure gradient across the vasculature and improves drug penetration in tumors Cancer Res 64:3731–3736 doi: 10.1158/0008-5472.can-04-0074 [DOI] [PubMed] [Google Scholar]
- Tosin A, Preziosi L (2010) Multiphase modeling of tumor growth with matrix remodeling and fibrosis Mathematical and Computer Modelling 52:969–976 doi: 10.1016/j.mcm.2010.01.015 [DOI] [Google Scholar]
- Truskey GA, Yuan F, Katz DF (2009) Transport phenomena in biological systems. Pearson Prentice Hall bioengineering, 2nd edn. Pearson Prentice Hall, Upper Saddle River, N.J. [Google Scholar]
- Ulrich TA, Pardo EMD, Kumar S (2009) The Mechanical Rigidity of the Extracellular Matrix Regulates the Structure, Motility, and Proliferation of Glioma Cells Cancer Res 69:4167–4174 doi: 10.1158/0008-5472.can-08-4859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umesh V, Rape AD, Ulrich TA, Kumar S (2014) Microenvironmental Stiffness Enhances Glioma Cell Proliferation by Stimulating Epidermal Growth Factor Receptor Signaling PLoS One 9:8 doi: 10.1371/journal.pone.0101771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voutouri C, Mpekris F, Papageorgis P, Odysseos AD, Stylianopoulos T (2014) Role of Constitutive Behavior and Tumor-Host Mechanical Interactions in the State of Stress and Growth of Solid Tumors PLoS One 9 doi: 10.1371/journal.pone.0104717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang RZ, Sarntinoranont M (2019) Biphasic analysis of rat brain slices under creep indentation shows nonlinear tension-compression behavior J Mech Behav Biomed Mater 89:1–8 doi: 10.1016/j.jmbbm.2018.08.043 [DOI] [PubMed] [Google Scholar]
- Yao W, Li YB, Ding GH (2012) Interstitial Fluid Flow: The Mechanical Environment of Cells and Foundation of Meridians Evid-based Complement Altern Med:9 doi: 10.1155/2012/853516 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Upon request


