blitzGSEA: efficient computation of gene set enrichment analysis through gamma distribution approximation

Abstract

Motivation

The identification of pathways and biological processes from differential gene expression is central for interpretation of data collected by transcriptomics assays. Gene set enrichment analysis (GSEA) is the most commonly used algorithm to calculate the significance of the relevancy of an annotated gene set with a differential expression signature. To compute significance, GSEA implements permutation tests which are slow and inaccurate for comparing many differential expression signatures to thousands of annotated gene sets.

Results

Here, we present blitzGSEA, an algorithm that is based on the same running sum statistic as GSEA, but instead of performing permutations, blitzGSEA approximates the enrichment score probabilities based on Gamma distributions. blitzGSEA achieves significant improvement in performance compared with prior GSEA implementations, while approximating small P-values more accurately.

Availability and implementation

The data, a python package, together with all source code, and a detailed user guide are available from GitHub at: https://github.com/MaayanLab/blitzgsea.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Transcriptomics analysis aims to unravel the molecular mechanisms underlying physiological and pathological cellular phenotypes. Identifying differential activity of pathways and biological processes can be inferred by gene set enrichment analysis (GSEA). GSEA is the most popular statistical test used to compare differential expression signatures with sets of annotated genes (Subramanian et al., 2005, 2007). GSEA calculates an enrichment score (ES) using a weighted Kolmogorov–Smirnov (WKS) test (Hung et al., 2012). To calculate a P-value from an observed ES, GSEA performs permutations of either the samples or the gene labels. In practice, gene label shuffling is used most often due to the lack of sufficient number of replicates. By default, 1000 permutations are calculated resulting in 1000 ES. The P-value is then calculated by comparing the observed ES to the 1000 shuffled ES values. Instead of performing permutations, an analytical background distribution can be estimated. However, it leads to less accurate small P-values. Multiple hypotheses testing correction methods are also challenging to compute for very small P-values. For example, multiple hypotheses testing correction methods such as Bonferroni (Dunn, 1961) or Benjamini–Hochberg (Benjamini and Hochberg, 1995) fail when P-values become very small. Here, we present a novel method to accurately model the ES null distribution, improving computational performance and accuracy of GSEA.

2 Materials and methods

blitzGSEA calculates a background distribution analytically for the WKS statistic described in GSEA-P and fGSEA using the gene set shuffling methodology (Korotkevich et al., 2021; Subramanian et al., 2007). The ES distribution depends on the values/weights of the input signature and the number of genes in the gene set. All gene sets with equal number of genes share the same null distribution. A signature with positive and negative values, such as fold change, typically results in a bimodal ES distribution that can be accurately approximated by two gamma distributions, where one distribution models the negative ES values and the other the positive ES values (Fig. 1a). To calculate null distributions, blitzGSEA requires the generation of permutations just like GSEA-P. The sampled ES values are then used to fit two parameters: alpha (shape) and beta (scale) of the gamma distribution. Since accurate fitting requires a large sample randomized ES score, the process is computationally costly. To avoid calculating permutations for each possible gene set size, only a subset of calibration anchor gene set sizes are chosen, i.e. A = {a₁, a₂, …., a_N}. The parameters of the estimated gamma distributions, relative to the gene set size, follow monotonous functions. Alpha increases linearly relative to the number of genes in a gene set, while beta decreases. This enables precise estimation calculated from the anchor points (Supplementary Fig. S2). The missing gene set sizes are interpolated by first applying locally estimated scatterplot smoothing (LOESS) fit applied to the anchors. The LOESS fit reduces small errors that may arise by the calculation of the anchors. Following the LOESS fit, corrected parameters for missing gene set sizes are derived from the anchors by linear interpolation.

Fig. 1.

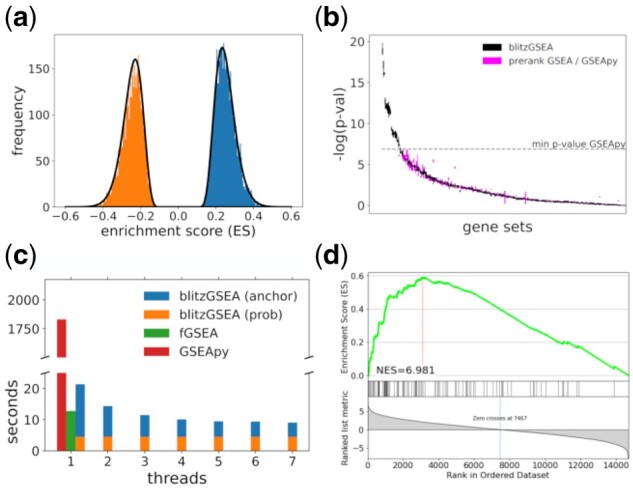
(a) Sampled ES distribution for gene sets of size 50 and estimated gamma distributions for negative and positive ES values. (b) Comparing the accuracy of small P-values computed by blitzGSEA and GSEApy. (c) Comparing execution speed for blitzGSEA, fGSEA and GSEApy on a single thread, and improvements of blitzGSEA execution speed when implemented as a multithreaded application. (d) Example, GSEA plot generated by blitzGSEA plotting submodule

Fitted anchor distributions are tested for goodness of fit using a KS test. Sampled ES are compared to the theoretical distribution of the positive and negative gamma distributions. After parameter fitting for all possible gene set sizes, blitzGSEA calculates ES for each gene set for a given gene set library. The corresponding P-value is then calculated with the respective gamma distributions.

3 Results

To test whether the gamma distributions accurately estimate sampled ES distributions, we performed a KS test for 10 000 sampled ES for a gene set size of 50. The KS test does not find any significant differences between the fitted gamma distributions for negative and positive ES, with P = 0.726 and P = 0.213 (Supplementary Fig. S1) suggesting an appropriate choice for the distribution function type. blitzGSEA does not suffer from P-value saturation, in which P-values reaching a certain level of significance become zero. The reference implementation of GSEA-P in Python, GSEApy (Fang, 2020), reduces small P-values to 0 when no random permutation is more extreme than the observed ES. Additionally, GSEApy suffers from higher level of noise for low P-values (Fig. 1b and Supplementary Fig. S3). This limits GSEApy’s ability to order gene sets by significance and apply multiple hypotheses correction. By modeling ES distributions more accurately, blitzGSEA is not limited by the P-value accuracy. The randomization of permutation-based enrichment analysis methods introduces some variation in P-value estimation; with the same number of permutations blitzGSEA produces higher reproducibility of P-values when repeatedly calculated on the same gene set library compared the GSEApy (Supplementary Fig. S3). blitzGSEA achieves higher self-consistency compared to fGSEA at >1250 permutations and uses 2000 permutations as the default setting. In addition, blitzGSEA outperforms GSEApy and fGSEA in execution time (Fig. 1c). We tested the runtime on an Intel Core i7-8750H machine with 32 GB. In single-threaded mode, blitzGSEA outperforms GSEApy by a factor of 73. To calculate enrichment for Gene Ontology Biological Processes (The Gene Ontology Consortium, 2019), which contains 6021 gene sets in Enrichr (Kuleshov et al., 2016), GSEApy requires 30 min, while blitzGSEA requires 21 s. Of these 21 s, about 17 s is spent calculating the gamma distribution from the anchors, while the rest of the time (4.5 s) is spent calculating the ES for the gene sets. Using more than two threads, blitzGSEA outperforms fGSEA, which only supports single threaded operation. Multithreading with blitzGSEA can half the required compute time (Fig. 1c). To enable access to a large repository of gene set libraries, blitzGSEA supports programmatic access to the Enrichr libraries. The blitzGSEA Python package includes plotting functions for standard publication-ready visualization of GSEA results (Fig. 1d). The blitzGSEA package supports running sum plots in normal and compact modes, as well as a top table plot showing the most significant gene sets in one table (Supplementary Fig. S4). While maintaining the same statistical framework of the running sum statistic of the original GSEA algorithm, blitzGSEA outperforms existing implementations in accuracy and computational speed.

Funding

This work was partially supported by the National Institutes of Health [U24CA224260, U54HL127624, R01DK131525 and OT2OD030160].

Conflict of Interest: none declared.