Learning Structures: Predictive Representations, Replay, and Generalization

Abstract

Memory and planning rely on learning the structure of relationships among experiences. Compact representations of these structures guide flexible behavior in humans and animals. A century after ‘latent learning’ experiments summarized by Tolman, the larger puzzle of cognitive maps remains elusive: how does the brain learn and generalize relational structures? This review focuses on a reinforcement learning (RL) approach to learning compact representations of the structure of states. We review evidence showing that capturing structures as predictive representations updated via replay offers a neurally plausible account of human behavior and the neural representations of predictive cognitive maps. We highlight multi-scale successor representations, prioritized replay, and policy-dependence. These advances call for new directions in studying the entanglement of learning and memory with prediction and planning.

1-. Introduction

As we navigate the world we learn and update the relational structure of experienced events. The idea that relational representations are used as internal maps for navigation and planning was popularized by Tolman, as ‘cognitive maps’ [1]. Early theories of cognitive maps localized them in the hippocampus of various species and proposed that these maps were spatial, allocentric, and Euclidean in nature [2], but did not provide a learning mechanism that could explain how cognitive maps represent the structure of the environment. In the decades that followed, a wealth of neural findings provided pieces to this larger puzzle. Place cells signalled the current location of an animal, entorhinal grid cells tiled spaces into grids, and the environment was further summarized in representations that each served a purpose: boundary vector cells, head direction cells, reward cells, object vector cells, etc [3]. Simulated experience during offline replay can update cognitive maps [4], e.g., piecing together current experience with memory to make inferences about unseen links or integrating structural knowledge and rewards to update action policies [5,6]. Some of these findings contradict predictions of earlier cognitive map theories. For instance, inconsistent with merely spatial structures, place and grid fields capture non-spatial state spaces as well [7–9]. Counter to a merely Euclidean representations, it has been shown that place field representations are path-dependent [10] and skew asymmetrically toward goal locations [11], sequential trajectories to goal locations twist around obstacles [10,12–14]. Furthermore, entorhinal grid fields are shown to capture principle components or basis sets of state spaces [15,16], and these grid fields can get over-represented or warped near the locations of goals and rewards [17,18] (section 3).

The disagreement of some findings with earlier neural theory poses a larger puzzle: how does the brain learn and update cognitive maps and how do they represent and generalize structures? Solving the cognitive map puzzle calls for a theoretical and computational framework that can capture decades of cumulative evidence, is biologically plausible, and makes testable behavioral and neural predictions. Various theoretical proposals have attempted to solve the puzzle with computational frameworks such as manifolds and neural networks [19,20], topological models [21,22], relational learning [23], and reinforcement learning [15]. While these frameworks are not mutually exclusive, this review focuses on representation learning using a reinforcement learning (RL) framework to solve the cognitive map puzzle by learning structures of the state spaces (spatial or non-spatial).

Representation learning in RL refers to learning the structure of a state space. The states can be spatial locations, experimental stimuli, associated memory items, or task states [24]. The RL framework can be used to learn mappings between observed perceptual features and states [25], compact representations of relational and associative structures of the state space [15,23,26], as well as abstractions enabling transfer between tasks and environments [27,28]. While in classic model-based RL learning the structure of states implies learning the probabilities of transition between adjacent states [29], other RL approaches can learn compact representations of the multi-step and multi-scale structure of states [5,15]. This review is focused on learning compact representations of the structure of states that are multi-step, multiscale, and path-dependent using successor representations and replay in the RL framework.

In what follows, we briefly review how representation learning and replay help acquire multiscale predictive cognitive maps (section 2), how predictive representations are learned and the role of policy-dependence in learning representations (section 3), how the content and prioritization of memory replay updates these representations (section 4), and emerging computational directions in generalization and transfer (section 5). In short, learning predictive representations of structures using policy-dependent SR and replay accounts for neural evidence (path-dependent and non-spatial) that disagrees with earlier (euclidean and spatial) cognitive map theory. This calls for further work on learning compact and generalized representations of structures and updating our notions of cognitive maps.

2-. Learning predictive representations of structures

The reinforcement learning problem is typically that of an agent flexibly learning paths to reward and avoiding death in a dynamic environment [30]. Many RL problems require planning over long time scales, latent learning (used by Tolman to support the idea of a cognitive map), and inference in complex environments with sparse rewards. Planning in such problems requires remembering the relational structure of the environment. While RL is famous for reward-based learning, it offers a framework for learning representations in absence of rewards. There are different notions of learning and memory for structures. You can remember the specific structure of your childhood home, or the abstract structure of rooms in any house. Here we review evidence that the RL framework can capture both notions and their neural implementations.

Why use the RL framework to study how biological agents learn structures? There are at least two reasons for using RL for structure learning. First, RL is biologically plausible and offers testable hypotheses about the neural implementation of structure learning and their correspondence to behavior. This is an advantage over Bayesian cognitive models that have been more commonly used to study structure learning and causal inference, but cannot offer an adequate account of neural implementation [31]. Second, while model-free RL is more broadly known, RL representation learning principles can acquire compact and predictive representations of structures in absence of rewards. This review highlights how representation learning using the RL framework can account for learning predictive representations of the structure of states, generalization and transfer, and their neural implementation.

Let us briefly review two RL agents prominent in cognitive neuroscience: model-free and model-based RL, and why they do not offer satisfactory solutions to the cognitive map puzzle. A model-free agent (MF) takes actions, observe the running average of outcomes, and stores (caches) the discounted expected value of actions. This cached value can be learned via temporal difference (TD) learning and prediction errors. MF agents act fast and are computationally cheap, but have no memory of structures or the relationship among states; they only store expected value of actions in given states (see Equation 1). Model-based agents (MB), on the other hand, store a relational representation of the environment in terms of probabilities of 1-step transitions between states. This model is later used to compute action policies that maximize expected value. Classic MB agents learn a representation of relationships between states that are one step apart, which is formalized as a one-step Transition matrix denoted as T. When faced with a decision, MB iteratively unfolds consecutive states taking mental actions, one step at a time, in order to simulate different trajectories and compute and compare their expected value. Thus, MB agents can flexibly compute expected value (long-term cumulative reward) for each possible sequence, but do so at a high computational cost of iteration [29].

In short, MF agents are fast and cheap but have no knowledge of structures and are hence inflexible, and MB agents are flexible but their representation of structures requires iterations that makes their use computationally expensive – even intractable for realistically large decision trees [32]. Therefore, neither can sufficiently capture flexible and efficient cognitive map use in mammals. An alternative RL approach offers a computationally efficient intermediate solution between MB and MF: the flexibility of MB behavior without the intractable costs. This is the successor representation (SR) [26,32,33]. SR enables representation learning and uses abstractions to acquire relationships between a state and all its successor states, multi-steps away (Figure 1C). Note that this representation captures non-adjacent dependencies, unlike model-based RL’s one-step probability matrix (Figure 1B). Combining SR and replay can also precompute multi-step and multi-scale dependencies offline, increasing efficiency [26,32].

Figure 1. Successor representation and empirical evidence.

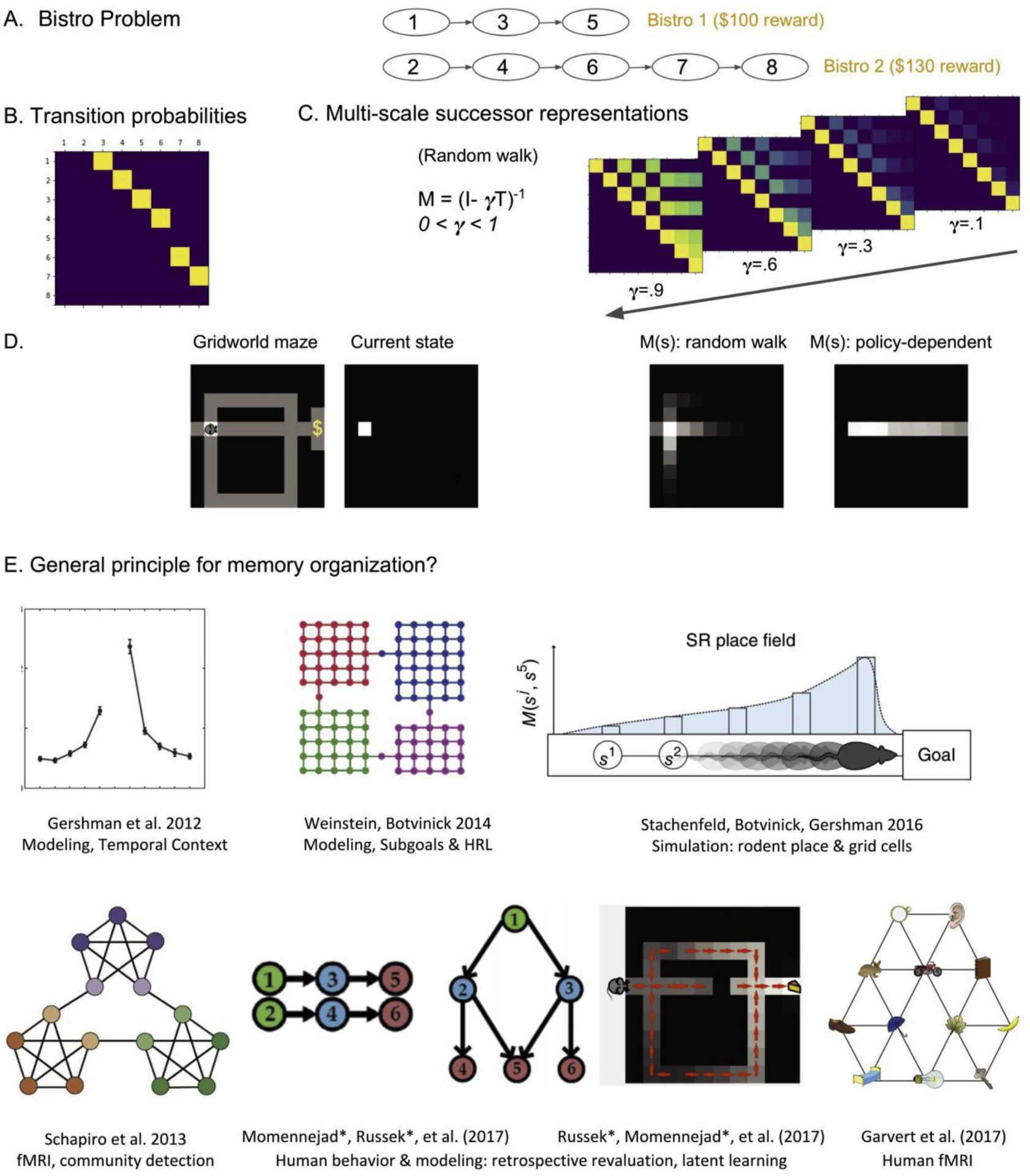
(A) Illustration of the bistro problem [5], an RL problem where there are two bistros and the further bistro is more rewarding. The agent needs to choose between state 1 and 2. The environment is represented as a graph of states and associated rewards. (B) The corresponding 1-step transition matrix (T) of the Bistro problem. (C) Multi-scale successor representations of the Bistro environment across a number of scales. Note that these are policy-independent or random-walk SRs. The interesting property of the bistro problem is that an SR with a scale of .1 does not capture the relationship between state 2 and 8. When combined with the reward vector, a single SR matrix with a small predictive horizon may fail to recognize state 2 as the optimal starting state. (D) A maze similar to those used in rodent experiments is depicted as a grid-world, where every location corresponds to a square [26]. The RL problem is to navigate to a reward in the location on the right side. Assume that an agent is in the location depicted in the second matrix from the left. Two possible successor representations for this state are depicted to the right. Random-walk SR represents the structure of the maze regardless of the reward. Policy-dependent SR over-represents the states on the trajectory to the goal. In both cases, the SR for state s, M(s), activates the representation of successor states within a given predictive horizon of the current state. (E) Computational support and empirical evidence from rodents and humans behavior, fMRI, and electrophysiology. The successor representation may offer a general principle for the organization of memory representations. (Figures in E are reprinted from cited papers [15,26,32,34–37]. Note that these are schematic summaries and readers should refer to the original papers for detail.)

What is the successor representation and how is it learned?

If an environment has n states, think of SR as a nXn matrix of state-state relations. SR captures relational structures by learning expected future visitations among states. For instance, consider the 2nd row of SR matrices in Figure 1C: the expected future visitations from state 2 to all other states are captured within each predictive horizon. This predictive horizon or scale of SR, i.e., the furthest successor state that is ‘visible’ from every starting state, depends on a discount parameter (0< γ <1).

SR can be gradually learned via temporal difference (TD) of the counts of visit among states and their successor states within the given horizon (Equation 2) [26]. For an intuitive understanding, recall that TD learning can be used for model-free learning of cached value using reward prediction errors (Equation 1). However, while MF learning stores discounted expected future value (running average of rewards), SR learning stores discounted expected future visitations from one state to another state (mean count visits). We address SR learning in more detail in section 3.

In short, the successor representation is a count-based compact representation: it does not store transition probabilities (which are <=1, Figure 1B) like MB agents, but the mean discounted counts of future visitations (can be >1, Figure 1C and D). Consider again the SR in Figure 1C. The 4th row of the learned SR matrix (M) stores the discounted average count of expected future visitations to any successor state of 4, in the columns of M(4). Therefore, when an agent is in state 4, the successor representation of state 4 is not only one state (i.e., not merely a matrix cell), but the entire 4th row of the SR matrix. This is why the structure of SR is inherently predictive: it offers predictive representations that can solve inference and planning, and makes predictions about the structure of underlying neural representations.

Empirical evidence for the successor representation

A series of empirical and computational studies have tested and found support for the proposal that relational maps are organized in memory according to the principles of the successor representation [15,26,32,37]. Human behavioral evidence comes from two studies specifically designed to compare the predictions of MF, MB, SR, and hybrid models to human performance on varieties of retrospective revaluation (reward revaluation, transition revaluation, policy revaluation). Human behavior was best captured by a model that learned successor representations via both direct and replayed experience [32]: SR-Dyna (see section 4). A normative study [26] showed that SR-Dyna class of algorithms combining SR and replay outperform other normative models. It has also been shown that SR helps discover subgoals for planning in hierarchical reinforcement learning (HRL) problems [36].

Capturing structures and spectral clustering.

The successor representation has theoretically rich properties. In linear algebra, dimensionality reduction, and graph theory, the SR matrix is mathematically equivalent or related to concepts such as the matrix dissolvant, fundamental matrix, communicability distance, and the inverse of the graph Laplacian (see Equation 3, the graph Laplacian is shown the be captured by I-T). In graph theory, the eigenvectors of the graph Laplacian are widely used across the sciences for spectral clustering, graph diffusion, and community detection [38]. Intuitively, eigenvectors factorize directions in the relational space, where every other state vector can be captured as a linear combination of them. Matrix compression for compact and abstract representations, can be achieved if eigenvector components with small eigenvalues (less influence) are set to zero and ignored. If we consider the state space a graph of connected states, the SR approximates the inverse of the graph laplacian. Mathematically, the eigenvectors of SR tile the state space into grid-like representations. The linear combination of these grids can help solve problems involving the partitioning and chunking of experience, subgoal discovery, graph diffusion, and communicability in graphs and complex networks [39]. This lends well to understanding hippocampal cognitive maps, discussed next.

Neural implementation of the successor representation

How is the SR implemented in the brain? What is the correspondence between learned SR and neural representation? Recall that the sth column of SR represents the predecessors of state s: what predicts this current state, its past. Now when the agent is in state s, the sth row of SR is the cached representation of the discounted successors of state s: what state s predicts, its future. This idea makes predictions about the neural similarity relationships among different states.

Let us return to hippocampal cognitive maps, and consider place fields. A place field is activated when the agent is in the field’s preferred location or is approaching it within a given horizon. A recent study compared rodent hippocampal and entorhinal electrophysiology results with SR, and shows that SR’s columns simulate place fields. Moreover, they showed that SR’s eigenvectors look like grid field representations [15]. Recall that eigenvectors of a matrix are linearly uncorrelated principal axes of the state space, or a smaller state space within which all information in the matrix can be captured as the linear combination of these axes. It has thus been suggested that entorhinal grid cells encode a low-dimensional basis set that extracts the multi-scale structure of predictive representations for hierarchical planning and subgoal processing [16]. section 5 notes further advances of these topics in generalization and transfer.

There are two other properties of place fields that any sufficient computational account needs to capture. The first is the observation that place fields fire asymmetrically and are skewed towards goal locations [11,15]. This asymmetry would be expected of predictive representations as well. Since SR-Dyna learns visitation-counts during experience and prioritizes replay of trajectories toward goals, it will learn higher expected future visitations for locations that are expected to be visited more often (Figure 1D, rightmost). This property can capture the asymmetry of place fields, and is related to policy-dependent representations discussed in section 3. The second property that any account of place fields needs to capture is that they are on average larger along the hippocampal long axis towards the anterior (or ventral) hippocampus. Multi-scale successor representations (MSR), learned simultaneously with different discount parameters and corresponding to different predictive horizons (Figure 1C) can capture this property [5]. Furthermore, the derivative of the multi-scale ensemble of SR matrices can be used to reconstruct an entire trajectory of future states and account for path-dependent distance to goal representations in the medial temporal lobe [5].

Can SR’s predictions about the structures of neural similarities be tested using functional magnetic resonance imaging (fMRI)? A number of studies have compared hypothesis similarity structures with the similarity among fMRI patterns associated with different states. Consistent with predictions, SR could account for fMRI pattern similarity in statistical learning [35] and learning non-spatial relational concepts [37]. A recent fMRI study has shown that during planned hierarchical navigation, predictive horizons of small to medium lengths are represented along the long axis of the hippocampus (with longer horizons in anterior hippocampus of humans, corresponding to ventral hippocampus in rodents) and the prefrontal cortex (PFC) hierarchy [40,41]. The largest horizons were represented in gradually more anterior regions of the rostral and orbital prefrontal cortex, corresponding to Brodmann areas 10 and 11 [40,41](Figure 2). As noted in Sections 3 and 5, prefrontal representations are not merely representations of larger scales. Similar regions have been reported in the representation of prospective tasks in human fMRI [86, 87]. Prefrontal and entorhinal representations may compute and represent generalization of structures, basis sets, grid fields, and schema [3,23,42].

Figure2. Multiscale successor representations.

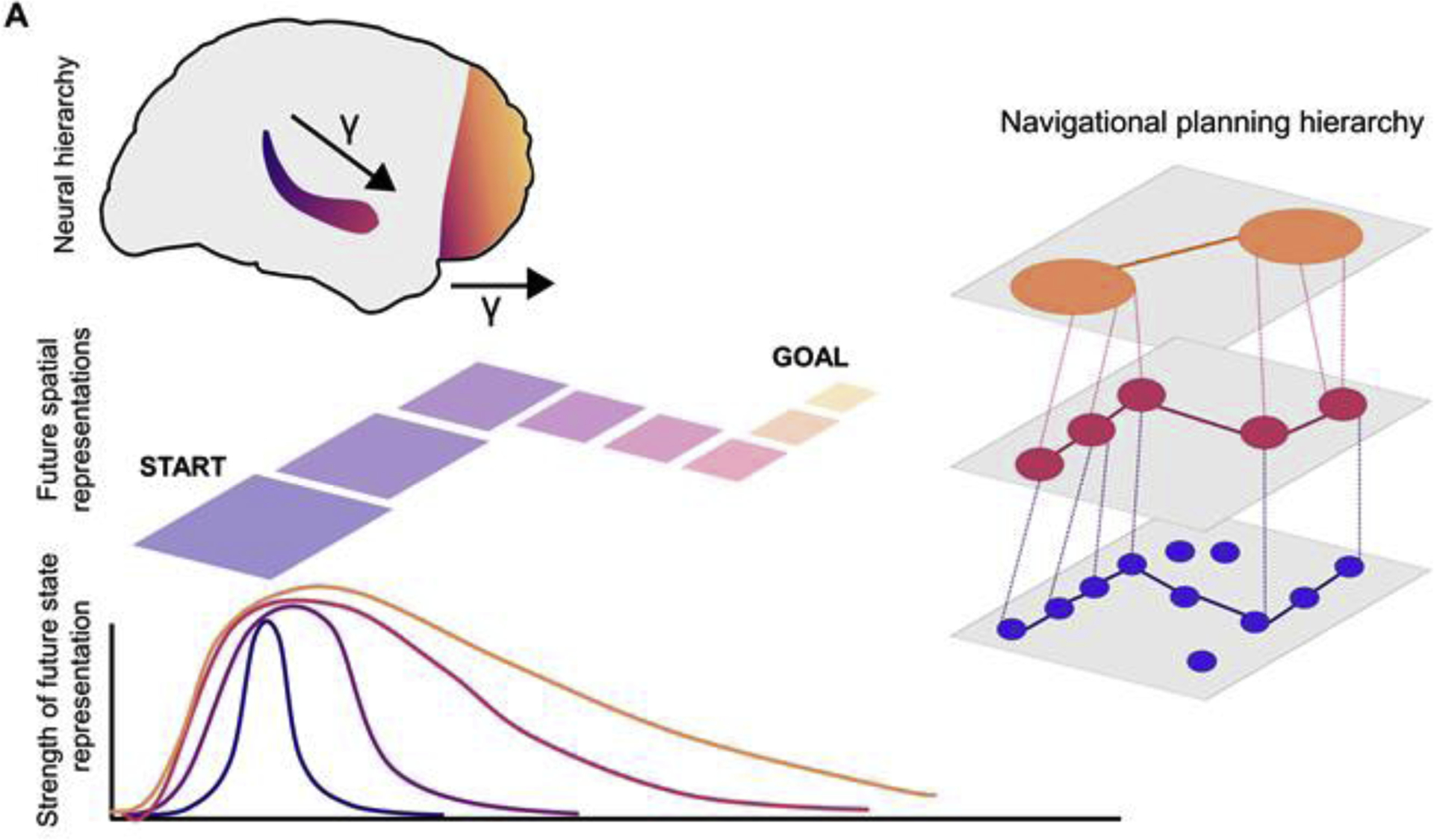
Successor representations with different predictive horizons from start to goal are depicted with different colors. Predictive horizons are represented in cold-warm color shades (blue-orange) along the hippocampal long axis as well as the prefrontal cortex (PFC). The horizon of spatial representations are depicted with squares of different sizes: when the agent is in the start state, nearby successor states are represented in blue shades and further successors are in warmer shades. Their size of the spatial tiles capture the discount applied to states further away. Corresponding shades are used in the graph depiction of abstraction across the scales of representation. Such a multi-scale predictive structure in the agent’s representations of the environment readily enables hierarchical planning: planning at larger horizons uses the large scale PFC representations, while fine-grained plans are hierarchically unfolded backward down to the smallest horizon of place fields in posterior hippocampus. Note that prefrontal and entorhinal representations are not merely representations of larger scales, but may compute and represent generalized structures, such as grid fields and schema (see Sections 3 and 5). Reprinted from Brunec, Momennejad (2019)[40].

These and other empirical evidence have been taken to suggest the successor representation as a principle for memory organization and temporal context (Figure 1E) [34]. However, there are a variety of algorithms for learning the structure of state-spaces using the SR, and they generate different behavioral and neural predictions depending on at least three factors. The first is whether SR acquired during goal-directed experience is different from SR computed analytically or with random walks (section 3). This determines the policy-dependence of the learned representations. The second regards whether and how memory replay updates SR offline, stitching together distal experiences to infer and update unseen relations (section 4).

3-. Learning structures and policy-dependence

How does an agent learn the graph structure of the state space while navigating it? A temporal difference (TD) learning approach, which is typically used to learn and update state-action values, can be applied to learning and updating state-state structures irrespective of rewards. Before showing how, let us recall how TD learning can update cached value in model-free RL in Equation 1:

$$V\left(s\right)=V\left(s\right)+\alpha \left(R_{\mathit{\text{observed}}}+{}_{\text{γ}}V\left(s_{\mathit{\text{new}}}\right)-V\left(s\right)\right)$$ 1)

Model-free RL: TD gradually updates cached value for state s.

Equation 1 shows how the value of state s is gradually learned using a simple value-based TD update [30]: a learning rate is applied to the observed reward it leads to plus the prediction error (i.e., the difference between the discounted value of the next state and the present state). TD learning can also be used to gradually update expected counts of visits from a state to its successors. Equation 2 shows how the SR can be gradually learned using a simple count-based TD update. Each time the agent starts from a starting state s, and arrives to a new state s_new, the count of expected visitations to the new state and its successors are updated. As such, gradually a “successor representation” is learned: a predictive matrix of how often we expect to visit s_new and its successors if we are currently in s (Figure 1). TD updates require a discount parameter (0 < γ < 1) that determines the scale or predictive horizon of the SR, and a learning rate (0 < α < 1) applied to the successor prediction error (the difference between the expected successors of s and the discounted successors of the new state), as follows [26,43].

$$M\left(s\right)=M\left(s\right)+\alpha \left(\mathit{\text{onehot}}\left(s_{new}\right)+{}_{\text{γ}}M\left(s_{\mathit{\text{new}}}\right)-M\left(s\right)\right)$$ 2)

Representation learning: TD gradually updates the successor representation for state s.

Here M denotes the successor representation matrix (or predictive representation) at scale. Here onehot(s_new) is a vector of all zeros with a 1 for successor state s_new. When the agent starts from s and visits state s_new, onehot(s_new) adds one visit to the count of visits to s_new in the s’th row of M (learning rates apply). The subtraction of the discounted successors of state s_new (s_newth row of M) from the successors of the current state (sth row of M) is the “successor prediction error”: used for temporal difference learning of SR. Gradually, the SR matrix is updated via TD learning. Due to more visitation counts to states that fall on the reward policy, successor states along the trajectory to rewards and bottlenecks gain higher SRs (mean expected discounted visits).

As mentioned earlier, a key difference in successor representation learning methods is whether the learning is policy-dependent or policy-independent. Intuitively, policy-independent learning of a graph structure (e.g., during navigation) is like learning by taking random walks on a graph in all directions (Figure 1). The agent has no reason to prefer a policy that favors one direction or trajectory more than another, and hence the structure of the graph as a whole is learned. If rewards were present, a random walk would emerge while exploring and learning in an open field where rewards are uniformly distributed. Given enough experience, policy-independent or random-policy SR can be learned directly from the transition matrix as in Equation 3 (Figure 1). Thus, SR can be either gradually learned or computed from an MB learner’s transition matrix T.

$$M={\left(I-{}_{\text{γ}}T\right)}^{-1}$$ 3)

Random-walk policy SR can be computed using the transition matrix.

Note that when rewards are not uniformly distributed across the state space, or when there are obstacles, or when the agent visits some states more than others, the successor representation gradually learned via TD in Equation 2 no longer converges to Equation 3. In other words, when the agent’s policy is to visit rewarded locations and bottleneck states (such as doors) more often than others, the SR can no longer be computed as if the agent were taking a random walk.

Policy-dependence and path-dependence

An important property of policy-dependent SR is that, consistent with path-dependent representations reflected in behavior and the hippocampus [10], its estimate of distance to goal would be non-Euclidean. This bears other predictions about vectorial and distance to goal representations [44]. Namely, policy-dependent goal-vectors, unlike previous suggestions, would not point to the goal location through a wall that obstructs it, but twist around barriers. This is consistent with recent findings in vectorial goal-representations in the hippocampus of flying bats [12]. This may be related to the behavioral finding that circumnavigation led to underestimating travel times and expanding spatial distance [45]. Furthermore, recall that SR can capture place fields and SR’s eigenvectors capture grid fields that tile the state space [15]. These eigenvectors can compress representations, encoding a low-dimensional basis set of predictive representations of the state space [16]. Notably, in some cases the eigenvectors of policy-independent and policy-dependent SR could potentially be different, making the prediction that the grid fields of policy-dependent and random-policy SR may be different. Policy-dependent SR values increase as an agent approaches bottlenecks and goal locations. As such, the eigenvectors of the policy-dependent SR may lead to grid fields that over-represent often-visited states, tiling “more space” near highly visited locations. This prediction is consistent with recent evidence showing grid fields are attracted to reward locations [17,18]. Future studies and reviews are required to test and compare these predictions to neural and behavioral findings.

As we will see in the next section, prioritized replay as well contributes to policy-dependence. Even when the number of visitations to all locations are empirically controlled [32], replay prioritization can simulate goal-related states (e.g., reward location, subgoals and doors, locations on the path to reward) more often than others. Preferential replay of goal-related states leads to higher number of virtual visitations to those states during replay cycles. Since the agent is learning and updating SR during offline replay, a policy-dependent SR map emerges [26], over-representing goal-directed states even though the agent’s experience is controlled.

4-. Learning structures via replay and prioritization

Often learning the relational structure of the environment requires combining current experience with our memory of past experiences. This can be mediated by memory replay [4,46]. Rodent electrophysiology shows that while animals rest, or eat, there are brief high-frequency network oscillations in the hippocampus known as ripples [47], accompanied by neural activity patterns that sweep trajectories of place cells forwards and backwards at compressed time-scale [48,49]. These replayed trajectories are not merely memories of recent experience: they are task-related prospective trajectories to remembered goals [50] that are replayed backward when they encounter prediction errors [49], to capture the structure of the environment and support learning, prediction, inference, and planning [21,51–53].

In reinforcement learning, the proposal of planning as learning from memory replay has been captured in a family of models called Dyna [30,43], in which an RL agent is trained during both direct experience as well as simulated experience during offline replay. Replay here is simulation of experience by replaying past episodes stored in memory, or reconstructing experience from a matrix of transitions. Table 1 summarizes four replay-based learning algorithms, including Dyna-Q [43], Dyna-Q+ [30], prioritized sweeping [6,54,55], and SR-Dyna [26,32]. In Dyna-Q, a model-free Q learner agent learns cached values of actions both during experience, and offline via replayed trajectories from a model-based transition matrix. Dyna-Q+ gives a bonus to sampling states that have not been recently explored. This enables shortcut discovery, a caveat in Dyna-Q as it greedily maximizes value missing the opportunity to discover new shortcuts. In prioritized Dyna replay priority is given to experiences where prediction errors occurred, their predecessors, and successors. In SR-Dyna, SR’s predictive representations are learned both online during direct experience and offline via memory replay.

Table 1.

Replay-based (Dyna) algorithms in reinforcement learning.

Algorithm	Learning and prioritization	Advantage	Caveat
Dyna-Q [43]	MF Q-learner learns and acts during experience, is trained by offline replay of random states using MB	Fast, but flexible	New shortcuts
Dyna-Q+ [30]	Dyna-Q, but not random: bonus for exploring states that have not been visited for a while	Finds new shortcuts	Needs many samples, HRL
Prioritized sweeping [6,54,55]	Events with unsigned prediction error (PE) during experience put in a priority queue. Later, states on trajectories leading to and from the PE-tagged state are given priority for replay.	HRL solutions	Large decision trees
SR-Dyna [26,32]	learns successor representations through experience and updates SR via offline episodic replay, prioritizes recent experience	Human-like retrospective revaluation	Discrete states, future: feature based

Empirically it has been shown that SR-Dyna outperforms MF, MB, MF-MB, Dyna-Q(+), prioritized Dyna, and SR without replay in capturing human retrospective revaluation behavior [26,32]. One human fMRI study in particular focused on how prioritizing replay by prediction errors affected planning behavior. Consistent with any prioritized Dyna model, larger unsigned prediction errors were followed by more offline replay, and offline replay of predecessors of states tagged with PE was correlated with future revaluation behavior [6]. The correlation between fMRI evidence of replay and revaluation behavior was more pronounced in the condition with higher reward variance, or uncertainty. In the real world, rewards and transition structures often vary as well: your favorite food truck moves elsewhere, and the subway maps rewire more often than desired. Future studies are required to better understand the role of uncertainty and volatility of rewards and transition structures on offline replay and prioritization.

Notably, the direction of replay sequences as well as their optimal prioritization can be computed using the successor representation itself. In Figure 1C, the SR matrix’s 5th column represents its predecessors or states that predict it (its past, states 1 and 3), and the 2nd row represents the successors of state 2 or the states that 2 predicts (its future, states 4, 6, 7, 8). Note that depending on the scale of the SR matrix, the horizons of past and future within which predecessors and successors are represented differ. A recent model of prioritized forward and reverse replay leverages these properties and consults SR to compare the value of taking different mental actions during planning in order to determine what replay content maximizes planning outcomes [56].

Offline replay is also a key memory process contributing to generalization and consolidation [57,58]. Human and animal neural evidence supports a role for wake and sleep memory replay in generalization and community detection [59,60], inference [52,61] especially of unseen relations among states, problem solving, and memory consolidation [62,63]. Deep learning algorithms also benefit from prioritized replay in generalization, discovery, and adversarial self-learning [64–66]. Different replay algorithms differ with regards to the storage or model from which they generate the experience, how far into the past memories are replayed (e.g., an exponential decay may prioritize replaying more recent memories, or replay may be limited to the past 2000 episodes), and whether replayed memories are in sequential or random order. Future experiments with hierarchical structures, uncertainty, and sparse rewards are required to test different replay and sampling prioritization methods against human and animal performance. Furthermore, future modeling work is required to capture the relationship between hippocampal and cortical replay, sharp wave ripples and neural oscillations, and behavioral outcomes.

5-. Abstraction, generalization, and transfer

Humans learn structures at different levels of abstraction. We can remember the specific structure of our childhood home, as well as the generalized structure of a house or an airport. We also use abstract structures to learn and discern new environments faster. Upon looking at an outlandish indoor scene in a sci fi movie, we can typically guess if it is a kitchen or an airport. Such higher levels of structural abstraction are sometimes discussed as schema, and have been studied in the medial prefrontal cortex [67]. Learning structures with the RL framework can capture both memory of specific structures and memory for generalized structures as well as their neural implementations. Here we briefly review a number of ways in which compression of predictive representations can benefit abstraction and transfer.

Successor feature abstraction and transfer

Most RL approaches assume learning from discrete states. However, we experience the world as a continuous series of dynamic features rather than discrete states. Different tasks and goals depend on different dynamic features of the same environment. An important challenge for RL algorithms concerns decomposing complex task structures to learn relevant feature weights and generalizing predictive feature representations to improve the learning of unseen tasks [68]. Successor feature learning offers a solution. If different tasks can be done in the same environment (e.g., at home), decoupling the dynamics of the environment (e.g. doors open to rooms, obstacles block passage) from specific goals and rewards (e.g., food in the kitchen) enables the algorithm to consider not one but a set of policies during policy improvement [28]. Other than transfer across tasks with different reward functions [27], successor features have been shown to support behavior shown by classic model-based and model-free reinforcement learning models as well [69]. A recent model shows that hippocampal place cell firing can be captured using successor features. Place cells are learned from a basis set of known neurobiological features (i.e., boundary vector cells and grid cells) that offer low-dimensional representations of successor features [70].

Options

While successor feature learning enables generalization and transfer over features, the most challenging RL problems regard hierarchically structured environments in which rewards are sparse. A benchmark example is Atari’s Montezuma’s revenge, which most deep learning models fail to solve [71]. A series of solutions come from the options framework in hierarchical reinforcement learning (HRL). Through options, agents can abstract policies: temporally extended series of primitive actions (e.g., move one square left) are abstracted into “options” that simplify hierarchical goal discovery (e.g., “go forward until wall”, “climb ladder up”, “find the key”, “use key to open door”) [72–74]. Recent evidence shows the use of options in human behavior in hierarchical tasks and transfer [75]. However, discovering a useful set of options is a challenging problem. One way to identify useful options and subgoals is via states that are frequently visited [72]. This is why count-based representation learning, such as deep successor representation learning and successor feature learning, have been shown to support option discovery [28,76,77]. As discussed earlier, the eigen-decomposition of count-based predictive representations can give us the basis sets for the entire state space. Similarly, the eigendecomposition of options leads to “eigen-options”, or compact abstracted options that factorize temporarily extended policies. Eigen-options simplify planning in complex environments into more manageable components. They allow transfer of learned structures as well: solutions to different tasks can be captured as their linear combinations [76,78,79].

Intrinsic motivation

Learning in the real world often takes place without a specific goal and with sparse rewards that are not immediately reinforced. Such learning requires intrinsically motivated information seeking and structure discovery [80]. Intrinsic motivation has been an active topic in machine learning and RL, discussed in terms of “proto-value function”, intrinsic reward, intrinsic value, drive, and curiosity-driven learning [81,82]. It has been shown that intrinsic motivation qua proto-value function can be computed via Laplacian eigenmaps (shown to be the equivalent of the eigenvectors of SR and linear slow feature analysis) [15,76,83]. When computing the proto-value function, an environment is decomposed into basis functions of successor features and options, the linear combinations of which could compute any given task’s value function and hence serve as intrinsic motivation [79,84]. It has been shown that approximating proto-value function using eigen-options (mentioned above) serves as intrinsic motivation to solve problems such as Montezuma’s revenge [85]. These emerging directions open up exciting new directions for studying the role of structure discovery in planning in uncertain environments. Such an endeavor can lead to a novel computational understanding of the link between learning and memory processes and intrinsic motivation.

While RL approaches to structure learning successfully capture behavioral and neural evidence for learning relational and statistical associations, one open question is how they can account for causal inference. Another open question is: what kinds of structures or graphs can a given learning algorithm learn and what are its limits of structure learning? How do these limits compare to the limits of human structure learning? A possible angle to approach these questions from is using the successor feature and eigen-option framework in RL.

6-. Conclusion

Flexible memory and planning behavior rely on learning compact representations of environmental structures. This review focuses on using reinforcement learning for learning the structure of state spaces – irrespective of rewards. As an agent navigates an environment, a count-based representation learning approach can gradually learn compact representation of relationships in the graph of states (by learning how often a state leads to its successor states). This learned predictive representation of successor states can be updated via prioritized offline replay of past experience, enabling inference of unseen relationships among states. Factorization of this predictive representation offers abstract properties of the relational structure such as grids, bottlenecks, subgoals, etc. We summarized evidence that predictive representation learning and replay capture cumulative neural and behavioral evidence. We noted emerging topics in generalization and transfer. This rich body of studies calls for further computational work on structure learning, matched experimental work, and a computational update to earlier cognitive map theory.