Matching Methods for Confounder Adjustment: An Addition to the Epidemiologist’s Toolbox

Abstract

Propensity score weighting and outcome regression are popular ways to adjust for observed confounders in epidemiologic research. Here, we provide an introduction to matching methods, which serve the same purpose but can offer advantages in robustness and performance. A key difference between matching and weighting methods is that matching methods do not directly rely on the propensity score and so are less sensitive to its misspecification or to the presence of extreme values. Matching methods offer many options for customization, which allow a researcher to incorporate substantive knowledge and carefully manage bias/variance trade-offs in estimating the effects of nonrandomized exposures. We review these options and their implications, provide guidance for their use, and compare matching methods with weighting methods. Because of their potential advantages over other methods, matching methods should have their place in an epidemiologist’s methodological toolbox.

INTRODUCTION

In epidemiology, the frequent inability to randomly assign participants to various exposure statuses makes establishing the causal effects of those exposures challenging. For example, Samples et al. (1) sought to characterize the effect of opioid misuse on suicidal behaviors, but it would be implausible to randomly assign exposure to opioid misuse. One of these challenges is that of confounding, the circumstance in which the exposure and outcome of interest share common causes. Statistical methods exist to adjust for confounding when the relevant variables have been measured; these methods include some that involve modeling the outcome (analysis-based methods), such as regression and g-computation; others that involve mimicking the balancing qualities of randomized trials (design-based methods), such as inverse probability weighting; and combinations of the 2 approaches.

A set of methods in the second class are matching methods, which involve the reorganization or selection of units in the sample so the exposure is independent of the measured covariates in the matched sample (2). The most typical use of matching involves finding a subset of the unexposed sample with a covariate distribution similar to that of the exposed sample and discarding the rest, leaving a matched sample from which a causal effect can be estimated (ideally) without confounding. As a design-based method, matching is conceptually similar to inverse probability weighting in that it operates on the sample without reference to the outcome, which offers it some advantages in terms of robustness and transparency over analysis-based methods like outcome regression (3, 4). Design-based methods have the advantage of allowing extensive diagnostics without invalidating inferences because the potential effectiveness of a method in a specific data set can be assessed before estimating the exposure effect (5). When used effectively, design-based methods can reduce the dependence of results on specific modeling choices made by the analyst (6).

Although matching is popular in several research disciplines, including medicine, education, political science, and economics, it is used less in epidemiology, where inverse probability weighting is more common. An exception is in pharmacoepidemiology, where matching has been used to examine the effects of medical products on health outcomes (7–9). Matching can have some advantages over weighting, including robustness to model misspecification and methods of customization that can increase precision and robustness to violations of certain assumptions (5). The purpose of this article is to provide an introduction to matching methods for epidemiologists, highlighting several of the ways to customize a matching analysis and their statistical implications. Our goal is not to be comprehensive but rather to present contemporary perspectives on matching and orient readers to the large literature on matching methods.

MATCHING PRELIMINARIES

Assumptions for causal inference

Matching is used primarily when examining the effect of a point exposure (i.e., at a single time point) that has 2 exposure levels (e.g., exposed and unexposed). (Extensions to multicategory exposures exist but are not discussed here; see Lopez and Gutman (10) for a review.) The problem matching is used to solve is confounding by measured covariates, represented by the directed acyclic graph in Figure 1, with A being the exposure, Y the outcome, and X the confounding covariates (i.e., confounders). Confounders are variables that cause selection into exposure status and the outcome (see VanderWeele and Shpitser (11) for a more formal definition); this manifests as covariate imbalance: differences in the covariate distributions between the exposed and unexposed. The bias in an exposure effect estimate is a function of the imbalance in covariates that cause the outcome. The goal of matching is to reduce this bias by reducing imbalance in the matched sample.

Figure 1.

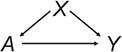
A directed acyclic graph demonstrating classic confounding of the exposure (A)–outcome (Y) relationship by covariates (X).

A critical assumption for matching to produce estimates of the exposure effect that can be interpreted validly as causal is no unmeasured confounding, known variously as conditional exchangeability (12), ignorability (13, 14), or satisfaction of the backdoor criterion (15). This assumption requires that all relevant confounders have been measured, which, in practice, may be hard to satisfy, though sensitivity analyses exist for when this assumption is in doubt (16, 17). Other necessary assumptions include positivity—that the probability of being either exposed or unexposed is nonzero for all individual in the analysis (12, 18)—and the stable unit treatment value assumption, which requires that outcomes for individuals not depend on the exposure status of other individuals (19, 20). These assumptions, along with the assumption of no unmeasured confounding, are not unique to matching and are common to most methods that rely on controlling for confounding using observed variables, including regression adjustment and inverse probability weighting.

Although causal assumptions are often invoked when using matching, matching is simply an adjustment method that can be used regardless of whether these assumptions are met; it is the interpretation of the estimated effect after matching as causal that requires these assumptions (21). In this sense, the methods described here can also be used to form “balanced comparisons” where the goal is to compare outcomes between 2 groups that have been “equated” on a set of covariates, without a causal interpretation, such as when analyzing disparities between groups (22).

Performing a matching analysis

Here we describe the basic steps of a standard matching analysis, with more details in the sections that follow. Matching can involve subset selection (i.e., selecting units from the sample to retain and dropping the rest) or stratification (i.e., assigning units to pairs or strata containing both exposed and unexposed units); some methods, like pair matching, involve both. The outputs of a matching specification are a set of matching weights and stratum identifiers, which are used in estimating the exposure effect. In 1:1 pair matching, in which each exposed unit is paired with an unexposed unit and any unpaired units are discarded, the matching weights are 1 for those paired and 0 for those dropped, and the pairs form the strata. Over time, the matching literature has expanded to include a much broader set of methods with different characteristics, strengths, and limitations. In the section Matching Methods, we describe the specifics of a broad variety of these approaches to help readers understand the spectrum of options and what may be most appropriate for a particular analysis.

After matching, one must assess the quality of the matching specification, which includes assessing covariate balance and other properties of the resulting matched sample. If the matched sample is of unacceptable quality or if its quality can be improved (as we discuss in the section Evaluating Matches), elements of the matching specification should be changed and the matching performed again. This process continues until a high-quality matching specification is found. This process, though, should maintain the separation of design and analysis by not estimating the exposure effect until the final matching specification is selected (4). We describe how to assess the quality of the matches in the section Evaluating Matches.

Once a high-quality matching specification has been found, the exposure effect can be estimated in the matched sample. This typically involves fitting a regression model of the outcome on the exposure (and, optionally, the covariates), incorporating the matching weights and strata into the estimation of the model coefficients and standard errors. We describe this process in the section Estimation and Inference After Matching.

Quantity estimated

The quantity matching is most often used to estimate (i.e., the estimand) is the average exposure effect among those who were exposed, also known as the average treatment effect on the treated, which is the average difference between the observed outcomes for those exposed and their counterfactual outcomes had they not been exposed. This is the same quantity estimated using weighting by the odds. Some matching methods allow estimation of the average exposure effect in the population, the same quantity estimated with inverse probability weights. The choice of estimand depends on the desired target population of interest, which should be specified before the analysis, and matching methods appropriate for that estimand should be used (Table 1). Desai and Franklin (23) present considerations for making this choice. Some matching methods, described in more detail in the section Matching Methods, can change the estimand by discarding exposed units; these methods should be used with caution if one has a specific target population in mind (24).

Table 1.

Matching Methods Corresponding to Estimands

Estimand	Matching Method
Average exposure effect in the exposed	Pair matching without a caliper
	Full matching
	Propensity score stratification
Average exposure effect in the population	Full matching
	Propensity score stratification
Average exposure effect in the matched sample	Pair matching with a caliper
	(Coarsened) exact matching
	Cardinality matching

Measuring the similarity between units

Matching requires a notion of the similarity between units to determine how strata or pairs should be formed and how close units are to each other. Given that the goal of matching is to attain balance on the covariates, the covariates themselves can be used directly to determine the similarity between units. When many covariates need to be controlled for, however, such as in the analysis of large health-care databases containing many potential proxies for confounders (25), it may be impossible to use covariates directly because of the curse of dimensionality (5): the more covariates there are, the harder it is to find units similar on all covariates (26, 27). Instead, one can use methods that summarize the covariates into a lower-dimensional measure, such as the propensity score, the predicted probability of exposure given the covariates (13). Propensity scores are often estimated as the predicted values resulting from a logistic regression of exposure status on the covariates, though more sophisticated and flexible optimization- and machine learning–based methods increasingly are being used (28–30).

Within strata defined by the true propensity score, exposure status is independent of the covariates; in this sense, the propensity score is a balancing score, making it ideal as a measure of similarity (13). Although this property does not imply that units with the same propensity score will have identical covariate values, it does allow matching on the propensity score to yield groups of exposed and unexposed units balanced on the measured covariates. However, because propensity scores must be estimated, their theoretical properties may not hold in a given specification, and the quality of the resulting matched sample must be evaluated (5).

Overlap and common support

There are sometimes regions of the covariate space where the distributions of the exposed and unexposed do not overlap; in these scenarios, restricting the analysis sample to a region of common support can prevent extrapolation. Common support can be assessed by examining the overlap between the distributions of covariates and the propensity score before matching (5). Methods of restricting the sample to a region of common support include trimming on the basis of a set values or quantiles of the propensity score (24, 31, 32), discarding units outside the convex hull of the covariates (33), and using covariate cutoffs to mimic the selection criteria of a clinical trial (34). In some cases, common support restrictions can reduce unmeasured confounding that occurs in the extremes of the propensity score distribution (31). However, restricting the sample can change the estimand by shifting the distribution of the covariates in the remaining sample toward a population with clinical equipoise (i.e., where either exposure status is somewhat likely for all included units), and this should be indicated in the interpretation of the resulting effect (24).

MATCHING METHODS

Broadly, matching methods involve grouping units that are similar to each other but differ in their exposure status, which is accomplished by subset selection and/or stratification. In this section, we describe these methods in more detail, providing examples of how to customize a matching specification to achieve good statistical performance and fully take advantage of the robustness properties matching has to offer. We then discuss how to assess the quality of matches to decide which options should be used for the final matching specification in which the exposure effect is estimated. A schematic of matching methods is displayed in Figure 2.

Figure 2.

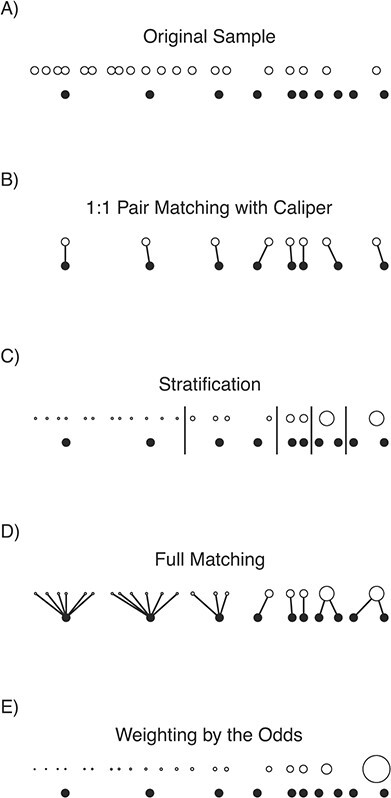
A visual demonstration of matching and weighting for the average exposure effect in the exposed on a toy data set. Exposed units (filled circles) and unexposed units (unfilled circles) are aligned horizontally by their propensity score. The size of the dots corresponds to the value of the resulting matching weights for the matching methods and propensity score weights for weighting by the odds. Links between units represent pairs, and long vertical lines represent stratum boundaries. Notice that only 8 of the original 10 exposed units remain after 1:1 pair matching with a caliper, changing the estimand. In this example, the best balance and effective sample size were found with full matching and stratification; the worst balance and effective sample size were found with weighting by the odds, due to the extreme weight for the rightmost unexposed unit.

Subset selection and pairing

Subset selection can be thought of as extracting from the original sample a subsample that looks like it could have been obtained through random exposure assignment, at least with respect to the observed covariates (5). This feature makes subset selection methods transparent, easy to explain to nontechnical audiences, and compatible with any analysis that could be used with data from a randomized trial. The most common method of subset selection is pairing, which involves finding pairs of similar units that differ in their exposure status and are otherwise close, where closeness is measured using a quantifiable distance metric. Exposed units are paired with unexposed units on the basis of this distance, and any unpaired units are discarded. The output of a subset selection method includes a matching weight for each unit, typically 1 if remaining in the sample and 0 if dropped, though some matching methods can yield matching weights taking on other values. If pairing is used, pair membership is also included.

There are many ways to customize a pair-matching specification to increase the precision of the estimated effect, improve balance, and improve its robustness to potential misspecification of any explicit or implied models. In the following subsections, we describe these options and their implications, which are summarized in Table 2.

Table 2.

Methods of Customizing a Pair-Matching Specification and Their Implications

Option	Benefits	Cautions
Matching on the covariates directly (e.g., Mahalanobis distance matching)	Can better balance the joint distribution of covariates; does not require an exposure model	May not perform well with many covariates, due to curse of dimensionality
Matching on the propensity score	Requires matching only on a single dimension; has theoretical balancing properties; tends to perform well empirically	Relies on specification of exposure model, pairs may not be close on covariates
Restrictions on closeness of matches	Can improve balance; yields close pairs; improves robustness to assumptions about outcome model	Dropping units decreases precision and can change the target population/estimand
Matching with replacement	Better balance than without replacement; good with small unexposed samples or when ratio of exposed to unexposed is high	Reusing units decreases precision; increases reliance on a few units
k:1 matching	Retains more units, thereby increasing precision	Balance can be worse

Distance measure used.

With pairing, a distance measure must be defined for each potential pair of units. This distance can be constructed directly from the covariates (e.g., as the Mahalanobis distance (35) or its rank-based robust variant (36)). Pairing on these distance measures can often allow imbalance to remain, due to the curse of dimensionality, so an alternative is to use the difference between values of a covariate summary measure, like the propensity score, to pair. Pairing on the propensity score tends to yield well-balanced samples, due to its status as a balancing score (13), though, as previously mentioned, a given pair of units may not be close on any specific covariates. Matching methods that combine propensity scores with covariate-based measures, such as Mahalanobis distance matching with restrictions on the propensity score distance between pairs, often perform better than each alone (35).

Matching with or without replacement.

When matching without replacement, once an unexposed unit has been paired with an exposed unit, it cannot be paired with any other exposed unit. This can sometimes yield low-quality matched samples if few unexposed units are close to the exposed units or if the pool of unexposed units is small. Instead, matching can be done with replacement, where each unexposed unit can be paired with multiple exposed units. This may yield improved balancing performance because exposed units are no longer competing for unexposed units. Reusing the same unexposed units can, however, decrease the precision of the effect estimate and cause it to rely heavily on a few frequently reused units (4, 37), akin to the problem of extreme weights in inverse probability weighting. Estimating the exposure effect after matching with replacement requires special methods to account for the fact that some unexposed units are selected multiple times and are members of multiple pairs (38, 39).

Order of matches.

Greedy pair matching involves finding an unexposed unit to pair with each exposed unit, 1 exposed unit at a time. The order in which the units are matched can affect the properties of the matched sample, and evidence is mixed on the preferred order (2, 37). Optimal matching eschews this problem by choosing the matches in such a way that the total distance between paired units is minimized (40). In practice, however, the difference in performance between optimal and greedy matching tends to be slight (37, 41).

k:1 matching.

When there are many more unexposed units than exposed units, it can be beneficial to pair more than 1 (i.e., k) unexposed units to the same exposed unit. Increasing the ratio of unexposed to exposed units in the matched sample can improve the precision of an estimate by retaining a greater number of units, though the marginal benefits in precision decrease with higher k (42), and some evidence suggests a preference for using k = 2 (43). In addition, there is a bias-variance trade-off in choosing k: with k > 1, balance may degrade (and thus bias may increase) because the second (and third, and so on) closest unexposed units to each exposed unit will necessarily be farther away (44). In practice, researchers may want to attempt 2:1 and 3:1 matching and examine how much the balance degrades; if the differences in balance are not substantial, then the higher ratios may be preferred. One can also perform variable ratio matching, in which different numbers of unexposed units are paired with each exposed unit; doing so can improve balance relative to fixed ratio matching at the cost of some precision (45).

Restricting the closeness of matches.

To control how far apart members of a pair can be, one can use a caliper or exactly match on a subset of covariates. A caliper defines the maximum distance 2 units can be from each other for them to be allowed to be paired with each other (46). Any exposed units with no remaining unexposed units within its caliper are dropped from the matched sample. One can also require that paired units are exactly matched (i.e., have identical values) on certain covariates. It can be beneficial to set a caliper or exact matching restriction on a subset of covariates believed to be most prognostic of the outcome or that are challenging to balance otherwise. Calipers are often applied to the propensity score, which can (sometimes dramatically) improve the balancing performance of a matching specification (35, 37). A common caliper size is 0.2 standard deviations of the logit of the propensity score (47). Restrictions on the closeness of matches should be used with caution, however: matching within propensity score calipers can actually worsen balance in some cases (6) (though there is doubt about the relevance of this finding for epidemiologic research (48)), and when matching restrictions cause exposed units to be dropped from the sample (i.e., because they were unable to be matched), the estimand will no longer correspond to the original target population, which can affect the generalizability of the effect estimate (49).

Improving matching through optimization.

Given that the goal of matching is to produce a well-balanced matched sample, optimization methods can help achieve those goals without the repeated manual respecification of certain matching options. Genetic matching finds a specification of the distance measure for pairing that optimizes balance in the resulting matched sample (50). Cardinality matching maximizes the size of a matched sample satisfying user-specified balance requirements and does so by selecting the matched sample directly without first finding pairs of units (51, 52). Other methods optimize a measure of balance subject to constraints on the remaining sample size (53–55). Although optimization-based methods often perform better than standard methods in simulation studies (56, 57), they are used less frequently than traditional matching methods and require specification of some particular balance metric to optimize.

Stratification

Stratification methods involve the creation of strata (i.e., bins) to which exposed and unexposed units are assigned. An early example of stratification was the creation of age strata to examine the link between smoking and lung cancer (58). The idea of stratification is to create strata such that, within strata, the distribution of covariates is independent of exposure, eliminating imbalance. Exact matching, the most robust way of forming the strata, involves assigning units to strata on the basis of the unique combinations of all covariate values so that all units within a stratum are identical with respect to all of the covariates. Units within strata that do not contain both exposed and unexposed units are dropped from the matched sample. Forming strata in this way can be thought of as a generalization of the method of standardization long used in epidemiologic research (12). The benefit of exact matching is that the resulting full joint distribution of covariates is identical in the matched exposure groups, eliminating imbalance without any assumptions on the exposure or outcome models.

Coarsened exact matching.

When there are continuous covariates or categorical covariates with many values, exact matching can be challenging, given the number of potential strata. In that case, coarsened exact matching (59), which involves splitting continuous covariates into categories and possibly combining levels of categorical variables before exact matching, can be used as an alternative and has seen some recent use in epidemiology (60). With many covariates, however, the curse of dimensionality may still be present; it is often the case that there are few or no matches, even after heavy coarsening of the covariates, leading to imprecise inferences based solely on the few units that remain, if any (35). In addition, discarding units that do not have matches, even if some matches remain, can change the target population (61). These features can cause coarsened exact matching to yield erratic and spurious results when used improperly (62).

Propensity score stratification.

An alternative to (coarsened) exact matching on the covariates is propensity score stratification (27, 63), in which units are assigned to strata on the basis of their propensity score values, often defined by user-specified quantiles of the propensity score. This avoids the curse of dimensionality, because stratification occurs only on a single variable that acts as a summary of the covariates (13).

Full matching.

Full matching (64, 65) combines the features of stratification and pair matching. As with stratification, all units are retained and assigned into strata and, as with pair matching, units are assigned to strata on the basis of the distances between units. Stratum size and membership are automatically selected to minimize the total within-stratum distance between exposed and unexposed units such that each stratum contains exactly 1 exposed or exactly 1 unexposed unit. A full-matching specification can be customized by adding restrictions on the closeness of matches (as with pair matching) or by changing the allowed number of units within each stratum (which controls the variability of the resulting matching weights) (34, 65, 66).

Stratification outputs.

The primary output of stratification and full matching is a vector of stratum membership for each retained unit. In some cases, these can be used to estimate exposure effects directly (e.g., by estimating stratum-specific effects and optionally combining them to form a single average marginal effect). This is often equivalently accomplished by using stratum membership to generate matching weights, which, just like inverse probability weights, can then be applied to the sample to estimate the marginal exposure effect. This method is known alternately as marginal mean weighting through stratification (67) or fine stratification weighting (68). The weights are computed by first assigning a new propensity score to each unit, equal to the proportion of exposed units in its stratum, and then using the standard formulas for computing weights from propensity scores corresponding to the desired estimand. In this way, stratification and full matching can be seen as nonparametric alternatives to propensity score weighting that are less sensitive to model misspecification (67, 69). Although subset selection methods are typically only able to be used to estimate the exposure affect among the exposed, stratification and full matching can be used to estimate that or the exposure effect in the population, depending on the formula used to compute the matching weights (4).

EVALUATING MATCHES

After arriving at a matched sample, the matching specification must be evaluated to ensure it is effective at reducing the bias due to confounding. The key qualities of a matched sample to be evaluated are the resulting covariate balance and the remaining (effective) sample size.

Covariate balance

Because the goal of matching is to achieve covariate balance, assessing balance is critical not only to find the best matching specification but also to demonstrate to readers that they can trust the results of the matching analysis (i.e., that the matching has successfully reduced the bias due to the observed confounders). Balance can be assessed numerically and graphically (5, 70), and is often assessed both before and after matching, with the postmatching balance measures computed incorporating the matching weights. Commonly used balance statistics include those that compare the similarity of distributions on a scale-free metric, such as standardized mean differences and Kolmogorov–Smirnov statistics (71). Ideally these should be as small as possible. Although statistical tests, such as t tests and χ² tests for independence, may seem appropriate for assessing balance, current methodological recommendations suggest against using them because they conflate sample size and balance (71, 72). In addition to numeric statistics, graphical displays of balance can be used to enable visual comparison of the distributions of a covariate in the 2 groups, such as kernel density or empirical cumulative density function plots (70).

Remaining (effective) sample size

Subset selection methods involve discarding units from the sample; if too many units are discarded, the resulting exposure effect estimates will lack precision. For this reason, it is important to ensure sample sizes are adequate in the matched sample. This is especially important when imposing restrictions on the closeness of matches, because doing so can involve discarding exposed as well as unexposed units. When using methods that produce variable matching weights, including stratification methods, matching with replacement, and full matching, a measure known as the effective sample size can be used, computed within each exposure group a as 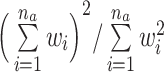, where w_i denotes the matching weight for unit i and n_a is the size of group a. The effective sample size represents the size of a hypothetical unweighted sample that carries the same amount of information as the weighted sample; it is used to measure the loss in precision due to the matching weights (73, 74). Even though some matching methods retain all units, the resulting effective sample size may be quite small, in fact; this same problem can arise when using inverse probability weighting (75), though it is often less pronounced with matching methods (66, 69).

ESTIMATION AND INFERENCE AFTER MATCHING

If an adequate matching solution (i.e., with good covariate balance and a reasonable effective sample size) is not found after repeated specification and assessment of the quality of the resulting matched samples, it may be that the exposure groups are so fundamentally different that no effect can be robustly estimated without using models to extrapolate. In these cases, causal inference may not be possible without strict assumptions (5, 33). Otherwise, if a satisfactory matching solution is found, it comes time to estimate the exposure effect and its uncertainty (i.e., its standard error, confidence interval, and P value).

Several approaches exist to estimate exposure effects, including randomization-based inference (34, 76), imputation-based approaches (77, 78), and model-based methods (5, 79). We focus on the latter because they are the most applicable to epidemiologic research in that they are appropriate to use with various outcome types and population-based inference, whereas the other approaches are more restricted.

Estimating effects

The most straightforward way to estimate exposure effects after matching is to fit a regression model of the outcome on the exposure, including the matching weights in the estimation, and using the coefficient on exposure as the exposure effect estimate (5); this is equivalent to computing a (weighted) difference in means (80). The specific outcome model can be tailored to the effect measure of interest; for example, with a binary outcome, a binary regression model with a log link can be used to estimate the risk ratio. It is often beneficial to adjust for covariates used in matching in the outcome model, because doing so can improve precision and reduce any slight remaining imbalance (81–84); this is conceptually similar to using doubly robust estimators that involve both an exposure model and a covariate-adjusted outcome model (85, 86). Methods recommended for estimating covariate-adjusted effects in randomized trials, including g-computation and targeted minimum loss-based estimation, can be used after matching to achieve the same benefits (87, 88). These methods ensure the resulting effect estimate is interpretable as marginal rather than conditional when the effect measure is noncollapsible. Note that the coefficient on exposure in stratified, conditional, and covariate-adjusted models for odds or hazard ratios corresponds to a conditional effect; thus, these models should be avoided after matching, which is best suited for estimating marginal effects (89).

Estimating uncertainty of estimated effects

Though the statistics of uncertainty estimation after matching are not straightforward (77, 79, 90), a wealth of simulation evidence and theoretical guidance exists to provide recommendations that are straightforward to implement. The most well-studied and best performing methods involve using robust standard errors, including cluster-robust standard errors, and bootstrapping.

Robust and cluster-robust standard errors.

Robust standard errors are an adjustment to the usual model-based standard errors resulting from ordinary least squares or maximum likelihood estimation of the exposure effect model (91–93) and should be used with matching methods that involve few or no strata, such as propensity score stratification or methods of subset selection without pairing. Despite early disagreement about the importance of accounting for pair membership after pair matching (94, 95), simulation evidence and analytic derivations indicate that accounting for pair membership (e.g., by using cluster-robust standard errors that adjust for the correlation between outcomes for units within the same pair or stratum (96)) is necessary for valid inference (79, 95, 97). After pair matching with replacement, in which some units are assigned to multiple pairs, special adjustments may be required to account for pair membership (e.g., see Austin and Cafri (39)), though additional research in this area is needed.

Bootstrapping.

Another possibility is to use bootstrapping to estimate standard errors and confidence intervals (98). Bootstrapping typically involves randomly drawing units from the original sample with replacement and performing the analysis—the propensity score estimation, matching, and effect estimation—within each bootstrap sample (38, 97). The distribution of the resulting effect estimates across the replications can then be used to compute standard errors and confidence intervals. Bootstrapping can be particularly useful when the assumptions required for analytic standard errors are not met due, for example, to small sample sizes. The cluster bootstrap (96), which involves resampling pairs after matching, can also be effective with pairing methods and avoids the computational burden of the standard bootstrap (79, 97). Though there has been doubt about the theoretical validity of bootstrap methods after pair matching with replacement (99), some studies have provided support for its use (38, 100).

DISCUSSION

Comparing matching and weighting

Many epidemiologists will be more familiar with weighting approaches than matching, so we end with a discussion of some of the differences and similarities between them. Matching and weighting methods serve the same purpose: to reduce the bias due to confounding in an observational study by balancing the distribution of covariates between the exposed and unexposed groups (4). They operate under the same causal assumptions—conditional exchangeability, positivity, and the stable unit treatment value assumption—and involve adjusting the sample in a way that does not involve reference to the outcome, akin to the design process of a randomized trial. However, they differ in a few important ways; in particular, matching can offer advantages over weighting with respect to robustness to assumptions about the exposure and outcome models and increased opportunities for customization. We also discuss how to choose between matching and weighting when conducting an analysis of observational data.

Robustness to assumptions about the exposure model.

Weighting methods that rely on the propensity score can be sensitive to its correct specification. Because the weights are a direct function of the propensity score, extreme propensity scores can yield extreme weights, which can fail to balance the covariates and cause the effect estimate to have high variance and be dependent on a few units with high weights (101). Matching methods offer a potential solution to this problem because they are less sensitive to correct specification of the propensity score (57, 102). Some matching methods do not even require a propensity score, including coarsened exact matching (59), cardinality matching (52), Mahalanobis distance matching (35), and genetic matching (50). Even with methods that do use a propensity score, the actual value of the propensity score is not used directly to compute the matching weights; rather, the order of scores and the order of the differences between scores are used, which are often similar across small perturbations of the propensity score model (102).

Robustness to assumptions about the outcome model.

Although one of the benefits of design-based methods like matching and weighting is that the form of the true outcome model does not need to be known or specified, in choosing the terms on which to assess balance, one makes implicit assumptions about the outcome model (103). For example, not checking balance on a 3-way interaction of covariates implicitly assumes that such an interaction is not relevant to the outcome (104). When assessing balance after weighting, one generally cannot check balance on all possible transformations of and interactions between covariates, and thus cannot guarantee that the specified weighting method balances those terms. Unless it can be guaranteed a priori that the theoretical balancing properties of the propensity score are in effect, the full joint distribution of covariates may not be adequately balanced. In contrast, exact matching on the covariates guarantees adequate balance regardless of the outcome model (46). Though exact matching on all covariates is often impossible, some methods, such as coarsened exact matching or matching with restrictions on the closeness of paired units, retain some of the balancing properties exact matching affords that are otherwise inaccessible with weighting methods (61).

Opportunities for customization.

Matching methods involve many ways to customize a matching specification to adapt it to the specific properties of the data set and research problem. For example, the tradeoff between bias and precision can be carefully managed by adjusting the number of unexposed units matched to each exposed unit and choosing whether matching is done with or without replacement (37, 43). Similarly, with stratification methods, the number and size of the strata can be constrained to prioritize balance or effective sample size. Although all these options can make finding the optimal matching specification more burdensome, they allow for manipulation of the sample to yield the optimal matched sample in ways that do not depend directly on the exposure or outcome models. There are fewer ways to customize a weighting specification to have such control over the properties of the weighted sample.

Choosing between matching and weighting

Some researchers may be hesitant to use matching methods (especially subset selection methods) because dropping unmatched units can seem like wasting data. We are sympathetic to this hesitance, especially when data may have been expensive and time-consuming to collect, but we wish to assuage this perception of matching methods for several reasons, described in more detail by Ho et al. (5). First, though dropping units through matching may increase the variance of an effect estimate, it can dramatically reduce bias, which is paramount in the absence of randomization, because there is little use in a precise estimate of a biased quantity. Second, dropping unmatched units can actually decrease the variance of an effect estimate by reducing variability in the outcome, especially when paired units are close to each other on covariates prognostic of the outcome (13). Third, some matching methods, such as full matching and propensity score stratification, preserve all units and may provide better bias reduction than weighting while retaining precision (69).

In any given data set, however, there is no guarantee that any 1 method will always dominate. Researchers should try several methods to find the 1 that works best in their data set (i.e., provides the best covariate balance while maintaining a large effective sample size). In some scenarios, the substantive considerations of the research problem may favor 1 method over another; for example, if the exposure process is well understood, it may be worth it to rely on the direct use of the propensity score involved in weighting. We describe in Table 3 some circumstances that might preferentially motivate matching or weighting.

Table 3.

Situations in Which One Might Prefer Weighting or Matching

Weighting	Matching
The form of the exposure model is (approximately) known	The form of the exposure model is not known.
No units have extreme covariate values or propensity scores	Exact matching is possible on several important covariates.
	There are few covariates to adjust for.
	Outcome analysis is complex and challenging to incorporate variable weights.
	Simplicity of explanation to a broad audience is desired.

Software

Matching methods are available in several software packages, including R (R Foundation for Statistical Computing, Vienna, Austria), SAS (SAS Institute Inc., Cary, North Carolina), and Stata (StataCorp LP, College Station, Texas). We recommend the R package MatchIt (105), which can perform all of the stratification and pair matching methods and their customizations discussed in this review and contains extensive documentation for estimating effects and standard errors after matching. In SAS, the PSMATCH procedure offers similar functionality. In Stata, the teffects procedure implements some matching methods, but it relies on the imputation-based estimation framework that may be less suitable for epidemiologic research.

Conclusion

Matching methods provide an alternative to weighting methods for the estimation of exposure effects in the presence of confounding by observed variables. They offer many options for customization to enhance their robustness properties and allow them to be fine tuned to optimize their performance. Substantive information about the research problem at hand can be easily incorporated through the prioritization of certain covariates and careful management of bias-variance tradeoffs. We hope epidemiologists will feel empowered to consider matching as an option in their analyses to enhance the robustness of their conclusions.