Abstract
The exact mechanism behind general anesthesia remains an open question in neuroscience. It has been proposed that anesthetics selectively prevent consciousness and memory via acting on microtubules (MTs). It is known that the magnetic field modulates MT organization. A recent study shows that a radical pair model can explain the isotope effect in xenon-induced anesthesia and predicts magnetic field effects on anesthetic potency. Further, reactive oxygen species are also implicated in MT stability and anesthesia. Based on a simple radical pair mechanism model and a simple mathematical model of MT organization, we show that magnetic fields can modulate spin dynamics of naturally occurring radical pairs in MT. We propose that the spin dynamics influence a rate in the reaction cycle, which translates into a change in the MT density. We can reproduce magnetic field effects on the MT concentration that have been observed. Our model also predicts additional effects at slightly higher fields. Our model further predicts that the effect of zinc on the MT density exhibits isotopic dependence. The findings of this work make a connection between microtubule-based and radical pair-based quantum theories of consciousness.
Subject terms: Biological physics, Chemical physics, Quantum physics, Biophysics, Neuroscience, Molecular medicine
Introduction
The question of how we perceive and experience the world we live in is a fascinating, long-standing open question in neuroscience, philosophy and psychology. This conscious experience vanishes during dreamless sleep or under general anesthesia1,2. Every day millions of surgeries all over the world would not be possible without anesthetics. However, despite a century of research, the mechanisms by which anesthetics cause a reversible loss of consciousness remain obscure3. During anesthesia, old memories are preserved, but no new memory is formed. Furthermore, anesthetics act relatively selectively on consciousness, as many non-conscious brain activities, including sensory-evoked potentials, persist during anesthesia. Understanding anesthesia, apart from its benefits in designing and developing novel anesthetics, could help explain the mystery of consciousness.
The connections between theories of anesthesia, related to neural correlates of consciousness, and the Meyer Overton correlation–solubility of anesthetics in a non-polar, ‘hydrophobic’ medium—has not been completely understood, and direct anesthetic effects on synaptic receptors are variable and inconsistent. Further, single-cell organisms perform cognitive activities predominantly by cytoskeletal microtubules (MTs) and are inhibited by anesthetic gases even without synapses or networks4. Moreover, Linganna et al. reported that alteration of MT stability is one of a number of mechanisms of inhaled anesthetics related to the function5. Bernard showed that anesthetics act directly on cytoplasm, depending on cytoskeletal proteins’ dynamics comprising actin filaments and MTs6. Franks and Lieb found that anesthetics act directly within proteins in non-polar hydrophobic regions7. This led some anesthetic researchers to search for new target protein/molecule for anesthetics. Moreover, Eckenhoff et al. found that anesthetics bind to 23 membrane proteins and 34 cytoplasmic proteins , including actin and tubulin8,9. Studies suggest anesthetics exert their effects via acting on protein reaction networks involved in neuronal growth, proliferation, division, and communication, which depend on MTs10. Although the affinity of anesthetics binding to tubulin is a thousand times weaker than to membrane protein, the abundance of tubulin is a thousand to ten thousand times more than membrane protein sites.
It has also been proposed that anesthetics act on quantum electronic activity in neuronal hydrophobic regions rather than binding to specific receptors. Consistently, Turin et al. showed that specific electron spin resonance (ESR) signals, consistent with free electrons, can be observed during anesthesia11. The same authors proposed that the anesthetic action may involve some form of electron transfer. Moreover, Li et al. showed experimentally that isotopes of xenon with non-zero nuclear spin had reduced anesthetic potency in mice compared with isotopes with no nuclear spin12. These findings are consistent with the idea that different nuclear spins of anesthetics can modulate the electron transfer process differently. Motivated by this line of thought, a recent study shows that radical pairs may explain the mechanism behind xenon-induced anesthesia13.
Quantum physics has been proposed to be part of the solution for the mystery of consciousness. In particular the holistic character of quantum entanglement might provide an answer to the binding problem14. In the 1990s, Penrose and Hameroff proposed a theory of consciousness based on quantum computations in MTs15–18. Computational modeling suggested that electron resonance transfer among aromatic amino acid tryptophan (Trp) rings in tubulin (subunits of MTs) in a quantum electronic process could play roles in consciousness19. Craddock et al. showed that anesthetic molecules might bind in the same regions and hence result in loss of consciousness20. In a recent experiment, Zhang et al. observed a connection between electronic states and vibrational states in tubulin and MTs21. However, quantum electronic coherence beyond ultrafast timescales demands more supporting evidence and has been recently challenged experimentally22. In contrast, quantum spin coherence could be preserved for much longer timescales23. For example, Fisher has proposed that phosphorus nuclear spins could be entangled in networks of Posner molecules, , which could form the basis of a quantum mechanism for neural processing in the brain24. However, this particular spin-based model also requires more supporting evidence and recently has faced experimental challenges25.
It is known that magnetic fields (MFs) can influence different brain functions26–32. Recently, it has been shown that shielding the geomagnetic field–exposure to hypomagnetic field (HMF)–influences adult hippocampal neurogenesis and hippocampus-dependent cognition in mice, where reactive oxygen species (ROS) are implicated33. There exists a considerable amount of evidence showing that MFs affect MTs34–39. Wang et al. show that exposure to HMF caused tubulin assembly disorder40. Moreover, Wu et al. observe that low-frequency sub-millitesla MF modulates the density of MTs in cells41. All these observations establish the magnetosensitivity of MTs for wide ranges of MF strengths.
Magnetosensitive reactions often involve radical molecules—transient molecules with an odd number of electrons42. A radical pair is a short-lived reaction intermediate comprising two radicals formed in non-equilibrium states whose unpaired electron spins may be in a superposition of singlet (S) and triplet (T) states43, depending on the parent molecule’s spin configuration44. The radical pair mechanism (RPM) is the most promising explanation for weak magnetic field effects on chemical reactivity45. Schulten was the first to propose the RPM to explain the magnetoreception of migratory birds46, and to date, the RPM is the most well-established model for this phenomenon47. Recently, it has also been proposed that RPM may explain xenon induced general anesthesia13, lithium effects on hyperactivity48 and the magnetic field effects on the circadian clock49.
MTs are made of tubulin heterodimers. The distribution and organization of MTs in cells are governed by a large number of MT-associated proteins (MAPs)50. MTs play crucial roles in cell shape, cell transport, cell motility, cell division51–57, neuronal polarity58, information processing of living systems59, synaptic activity60, regulating the precise timing of nerve spikes61, and Alzheimer’s disease (AD)62.
Evidence suggests that oxidative stress is vital for regulating actin and MT dynamics63. MTs contain specific amino acid residues, including Trp, tyrosine (Tyr), and phenylalanine (Phe), susceptible to oxidation. This, in turn, affects the ability of MT to polymerize and causes the severing of actin microfilaments in neuronal and non-neuronal cells. Contrarily, ROS inhibition causes aberrations in actin polymerization, decreases neurite outgrowth, and affects neurons’ normal development and polarization.
To be magnetically sensitive, tubulin must have (para)magnetic agents. With an unpaired electron, radicals are paramagnetic and could serve as magneto-sensing molecules. Trp and radicals are well-known radicals, particularly in animal avian magnetoreception, in the form of [] or [], wherein the latter case is the donor and acceptor while in the former case is the donor and is the acceptor45,47,64,65. It is thought that [] is formed in a photo-induced process. This case is similar to the NMDA receptor (NMDAR) in Xenon-induced anesthesia13. In both tubulin and the NMDAR, Trp is one of the key aromatic molecules66,67. It is also known that Trp can absorb environmental photons to reach an excited state, and it is considered in the excitation coherency in tubulins68. Furthermore, it is shown that Trp and superoxide can be involved in an electron transfer process69,70. For instance, in the context of the bird’s magnetic compass, a new study suggests that involvement of other radicals rather than the conventional ones is plausible71. Moreover, this model could be adapted for other RP complexes in the microtubule dynamics, e.g. involving flavin and Tyr. Such radical pairs can be formed via flavoenzymes72,73.
Various studies have proposed mathematical models for the dynamics and stability of MTs74,75. Craddock et al. show that the dynamics of MT can be framed in a simple kinetic model76. In the context of the RPM, Player et al. show that quantum effects can be introduced to a kinetic model by considering the quantum effects on the corresponding reaction rates in the chemical equations77. Taking the same approach, a new study shows that quantum effects can directly modulate the period of the circadian clock in Drosophila, where the spin dynamics of the RPs are the key elements49.
In the present work, we propose that there are naturally occurring RPs in the form of and , which is an important paramagnetic ROS, that play important roles in MT organization, as shown in Fig. 1. Oxygen is abundant, and tryptophan is an essential aromatic ring for tubulin; thus, the formation of such radical pairs can occur broadly. Our model predicts that the applied magnetic fields alter the spin dynamics of such RPs, similar to Ref.13, and hence modulate the assembly of MTs in cytoskeleton. It is also known that changes in zinc ion concentration in neurons influence the stability of polymerized MTs76. Following the work of Craddock et al.76 , our model further predicts that the effect of zinc on the MT density exhibits isotopic dependence.
Figure 1.

Schematic presentation of [the aromatic molecule] and [the red molecule] radical pair, considered in the RPM model in the present work, similar to Ref.13. The radical pair undergoes interconversion between singlet and triplet states. Image rendered using Avogadro (https://avogadro.cc).
In the following, we review the experimental results for the effects of applied magnetic field40,41 on the density of MTs. We then describe the quantum spin dynamics of our radical pair model and a simple kinetic model for the MT dynamics. Next, we introduce the quantum effect to the density of the MT, and we show that our model can reproduce the observed magnetic field effects; it further makes new predictions for experiments using low-frequency MFs. Lastly, the model predicts that the zinc effect on the MT density is isotope dependent.
Results
Prior experiment
Wang et al. report that shielding Earth’s geomagnetic field (GMF) (0.025–0.065 mT) caused disorders in tubulin self-assembly40. They show that the absorbance at 350 nm, which is for monitoring tubulin self-assembly, was altered by exposure to 30 min HMF. Average gray volume per cell was reported based on the amount of fluorescence in each cell. About 95% of tubulin were assembled in the GMF, while much less of the tubulin assembled ( 64) in the HMF. In that work, the magnitude of the residual GMF was 10–100 nT.
Radical pair model calculations
We develop an RP model to reproduce the HMF effects on the MT density observed by Wang et al.40. Among the amino acids in MTs, as mentioned above, Trp is redox active70, as shown by its involvement in RP formation in the context of cryptochrome, and could feasibly participate in the creation of RPs. We propose that the magnetic field interacts with the spins of RPs on Trp and superoxide. Note, that superoxide is thought to form RPs with flavins in other contexts78. The correlated spins of RP are assumed to be in the [] form, following Ref.13, where the unpaired electron on each molecule couples to the nuclear spins in the corresponding molecule. Oxygen has zero nuclear spin and thus zero coupling with its nucleus.
We consider a simplified system in which the unpaired electron on is coupled to the Trp’s -proton with the largest isotropic HF coupling constant (HFCC) of 1.6046 mT79 among all the nuclei in Trp. We consider only Zeeman and HF interactions45,80. For the RPs, we assume the g-values of a free electron (which is an excellent approximation in the low-field regime that we are considering here). The Hamiltonian for the RP system reads:
| 1 |
where and are the spin operators of radical electron on and , respectively, is the nuclear spin operator of ’s -proton, is HFCC, and is the Larmor precession frequency of the electrons due to the Zeeman effect. In the model presented here, for zinc effects, corresponds to the nuclear spin of zinc. We assumed the initial state of RPs to be singlet states (see the “Discussion” section).
The spin density matrix of RPs can be calculated using the Haberkorn master equation, where the kinetic reaction rates for singlet and triplet products are assumed to be equal43,81,82. For simplicity, the kinetic reaction rates were assigned equal first-order rate constants, k. Introducing spin relaxation phenomenologically83,84, the fractional triplet yield can be calculated as:
| 2 |
where M is the nuclear spin multiplicity, is the singlet projection operator, |m and |n are eigenstates of with corresponding eigenenergies of and , respectively, k is the RP reaction rate, and r is the RP spin-coherence rate (relaxation rate). In this model, we assumed the reaction rates for singlet and triplet have the same values. Of note, the singlet and triplet product of the RP system in [] are H2O2 and 78, respectively, which are the major ROS in redox regulation of biological activities and signaling85.
Here we look at the dependence of the triplet yield on changes in the strength of the external static magnetic field for the [] radical complex, as shown in Fig. 2, for s, and s with mT. One can notice a fairly strong HMF effect (the triplet yield goes from around 60% to around 40%). Our choices for the rate constants are discussed below and in the “Discussion” section.
Figure 2.

The dependence of the triplet yield of the [] complex on applied static magnetic field for s, s, mT. The triplet yield goes from around 60% to around 40% by changing the magnetic field strength from GMF to HMF. The strong HMF effect is further emphasized by the inset.
Chemical kinetics model for MT dynamics
We use a simple mathematical model for the dynamics of MT, following the work of Craddock et al.76. This model is based on the interconversion of the free tubulins, Tu, and the MT in cytoskeleton:
| 3 |
where and are the polymerization rate and the depolymerization rate, respectively. The chemical equation reads as follows:
| 4 |
which yields .
Craddock et al. suggest that changes in the concentration of zinc can be incorporated by modulating the polymerization rate76. In the present work, it is assumed that the total tubulin protein concentration [P] is 400 M, such that [MT]+[Tu]=[P], = 90 s and = 150 s. These values are chosen such that we could be able to reproduce the experimental findings, which are comparable to those in Ref.76.
Quantum effects on microtubule density
Here we explain how quantum effects can play an essential role in tubulin polymerization.
Spin is a magnetic moment and hence obeys the spin conservation. This leads to spin selectivity of chemical reactions. In other words, depending on whether radical pairs are in a singlet or triplet state, the chemical reaction will take different paths. It thus results in modulating the reaction rates. The work of Wang et al.40 shows that the absence of the GMF decreased the tubulin polymerization. Thus, it is natural to assume that effects of applied magnetic fields and hyperfine interactions can be incorporated into the classical model Eq. (4) by influencing the polymerization rate, , similar to other studies for introducing zinc effect into the stability of polymerized MTs76. The key assumption in our model is that this rate is influenced by a RP reaction. The effect of the triplet yield change on reads:
| 5 |
where , , and are the modified rate constant , the triplet yield under natural quantum effects (only GMF and no isotope effects), and the triplet yield resulting from quantum effects due to the external MF effects and hyperfine interactions from isotope effects, respectively.
Magnetic field effects on microtubule density
Here, we look at the explicit effects of an applied magnetic field on the density of microtubules. Using Eq. (4), we explore the parameter space of relaxation rate r and recombination rate k in order to investigate the effects of shielding geomagnetic field on MT’s density. Wang et al. report that the ratio MT density of geomagnetic field over hypomagnetic field is about 1.4840. Figure 3 show that the ratio of the MT density of GMF over HMF can reach above 1.3, which has the right trend compared to the experimental findings. However the uncertainty of the experiment was not reported. Our model predicts a magnetic dependence of the MT density. Figure 4 show the dependence of the MT density ratio of in GMF compared to applied static magnetic field, for mT based the RP complex of [], s, and s. Figure 4 indicates that exposure to static magnetic fields stronger than the geomagnetic field could decrease the the microtubule density ratio. The maximum MT density occurs around 0.05 mT, which is in the range of the GMF.
Figure 3.

The RPM model prediction of the microtubule density ratio in geomagnetic field compared to hypomagnetic field based on the RP complex of []. The geomagnetic field and hypomagnetic field are 0.05 mT and 10 nT, respectively. The magnetic field modulates rate for mT. The maximum HMF effect is obtained for s and s.
Figure 4.

The dependence of the microtubule density ratio in geomagnetic field compared to applied static magnetic field based on the RP complex of []. The geomagnetic field is 0.05 mT. The magnetic field modulates rate for mT, s, and s. HMF causes strong decrease on the microtubule density. The maximum microtubule density occurs around GMF.
Zinc isotope effect on microtubule density
The RPM typically leads to isotope effects13,48, and thus an isotope effect would be a good test of our proposal. It is known that alterations in zinc ion concentration in neurons influence the stability of polymerized MTs76. Zn is a positively charged ion. Thus it is natural to assume that couples with a molecule with a negative charge. Among all stable isotopes of zinc, only has a nuclear spin of , with a natural abundance of 4. Here we explore the isotope effect of zinc on the density of MTs. In this model nuclear spin of zinc modulates the spin dynamics of the RPs via hyperfine interactions. The Hamiltonian for the RP system here reads:
| 6 |
where is the nuclear spin operator of , and mT is the HFCC of .
We look at the effect of on the MT density. We assume that interacts with the superoxide radical. Our model predicts that administration of increases the density of MTs compared to Zn with zero nuclear spin, as shown in Fig. 5. We explored the parameter space of relaxation rate r and recombination rate k in order to investigate the effects of the treatment on MT’s density, for mT and mT, as shown in Fig. 5. Figure 6 shows the dependence of the MT density ratio of the administration of Zn over on the strength of applied magnetic field based on the RP complex of []. The geomagnetic field is 0.05 mT. The magnetic field modulates rates and for s and s. Our model predicts that administering increases the MT density compared to Zn without nuclear spin.
Figure 5.

The RPM model prediction of the MT density ratio of the administration of Zn (with zero nuclear spin) over (with nuclear spin of ) based on the RP complex of []. The geomagnetic field has a strength of 0.05 mT. ’s nuclear spin modulates rate for mT and mT.
Figure 6.

The dependence of the MT density of the administration of Zn (with zero nuclear spin) [Red] and (with nuclear spin of ) [Blue] on the strength of applied magnetic field based on the RP complex of []. The geomagnetic field is 0.05 mT. The magnetic field modulates rate for mT, mT, s, and s.
DFT analysis
The ORCA package86 was used for our - DFT calculations, and the molecular structure was optimized using PBE0/def2-TZVP. The orbitals obtained from the optimization calculations were used to calculate orbital energies as well as the hyperfine coupling constant . Using RI-B2GP-PLYP/def2-QZVPP87, we obtained mT. In these calculations, relativistic effects were treated by a scalar relativistic Hamiltonian using the zeroth-order regular approximation (ZORA)88. Solvent effects were considered by using the conductor-like polarizable continuum model (CPCM)89 , with a dielectric constant of 2. The resulting Mulliken charge and spin population of the [-] complex indicates that the unpaired electron resides primarily on the O2 molecule but is extended slightly onto the zinc atom, see Table 1. The highest occupied molecular orbital (HOMO) of [-] is shown in Fig. 7.
Table 1.
Mulliken charge and spin population of [].
| Atom | Charge population | Spin population |
|---|---|---|
| O | –0.203235 | 0.554431 |
| O | –0.203243 | 0.554413 |
| Zn | 1.406478 | –0.108844 |
| Sum | 1 | 1 |
Figure 7.
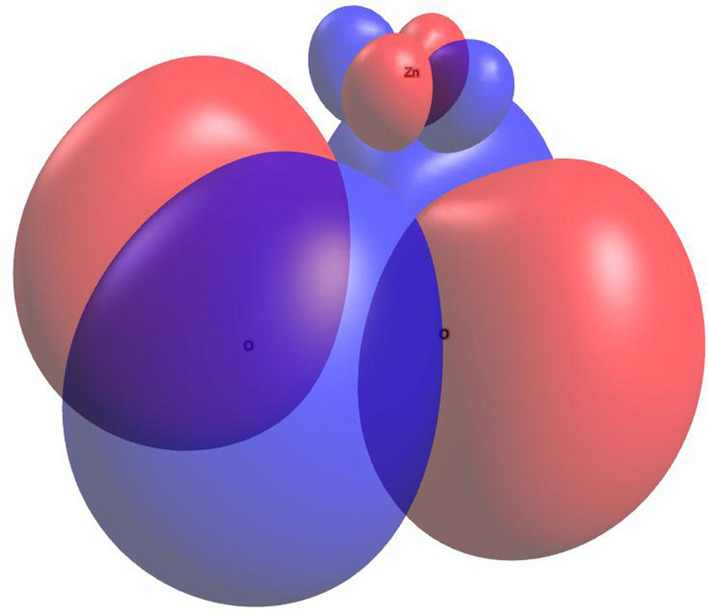
The highest occupied molecular orbital of -]. Imaged rendered using Avogadro (https://avogadro.cc).
Discussion
In the present work, our main goal was to explore whether an RP model can help explain the magnetic field effects on the MT density. We showed that the quantum effects influence the rates in the chemical kinetics of the MT dynamics, and then this results in a change in the density of MT in cytoskeleton. Our model reproduces the experimental findings of Ref.40 fairly well, as shown in Fig. 3. Our model further predicts that exposure to static magnetic fields stronger than the geomagnetic field could decrease the microtubule density ratio, with the maximum microtubule density occurs at a magnetic field strength in the range of the geomagnetic field, which might have evolutionary roots.
The radical is thought to have a fast spin relaxation rate. However, it has also been proposed that this fast spin relaxation can be decreased by reducing the molecular symmetry in the biological environment64,90–92, i.e. an asymmetric environment. In this case the degeneracy of the HOMOs () of will be removed and hence its fast reorientation molecular will be prevented. It is shown experimentally that in frozen solutions93 and alkali halide crystals94 such the fast spin relaxation of can be hindered. Additionally, Kattnig and Hore show that scavenger species around the superoxide radical can also reduce its fast spin relaxation95,96.
The present work predicts that the zinc effects on the MT density exhibits an isotope dependent manner. Isotope effects are generally a good indication for radical pairs. In addition, magnesium (Mg) is required for MT stability and function97–99. Furthermore, Buchachenko et al. showed that adenosine triphosphate (ATP) production was more than two folds in the presence of compared to in purified pig skeletal muscle PGK100. Hence, it would be interesting to perform an experiment to probe Mg isotope effects in MT stability.
The ground state of the oxygen molecule is a triplet state. For this reason, oxygen-based radical pairs are often assumed to start from triplet states. However, if the dioxygen molecule goes to its singlet state, the initial state of the radical pairs will be a singlet state. Singlet oxygen is generated naturally101,104–106 and therefore there is also the possibility of the pair being created from singlet oxygen. In this case, the initial state of the radical pairs will be singlet states. Furthermore, spin-orbit interactions lead to the non-radiative transition between two electronic states with different spin multiplicity ( e.g. singlet and triplet)– intersystem crossing (ISC), which is ubiquitous and important in fields ranging from chemical physics to chemical biology, including chiral molecules70,107–111.
A well-known indication of the pathogenesis of tauopathy–loss-of-function effects on the microtubules and the gain-of-function effects of the toxic tau species-is oxidative stress, which contributes to tau phosphorylation and the formation of neurofibrillary tangles112. However, the mechanisms behind the connection between reactive oxygen species (ROS) generated by oxidative stress and tau hyperphosphorylation are elusive68. Further, redox signaling and oxidative stress regulate cytoskeletal dynamics63. Proper balances between chemical reduction and oxidation (known as redox balance) are crucial for normal cellular physiology. Imbalances in the production of oxidative species lead to DNA damage, lipid peroxidation, and aberrant post-translational modification of proteins, which could induce injury, cell death, and disease85. These findings further emphasize the role of radicals and likely the need for a RPM in the context of the brain. Our proposed RPM model for magnetic field effects and Zn isotope effects on the microtubule organization includes superoxide radical.
It is also worth mentioning that any changes in the natural system could lead to various effects and complexify the entire system. Nonetheless, changes in superoxide concentration would likely affect the polymerization rate. This is in line with other observations in the work of Zhang and colleagues, where they reported that exposure to hypomagnetic fields caused hippocampal neurogenesis in mice to hypomagnetic fields caused hippocampal neurogenesis in mice33; however, this adverse effect was reversible by elevating ROS levels through pharmacological inhibition of ROS removal. Thus, it would be interesting to test whether modulating ROS levels pharmacologically can influence the HMF effects on tubulin polymerization.
Microtubules not only play crucial roles in cell shape, cell transport, cell motility, and cell division, but also are important targets for curing devastating diseases, such as Alzheimer’s disease113–115, Parkinson’s diseases116,117, and cancer118–120. The dynamics of MAPs signaling proteins play critical roles in the MT network, hence in the process of synaptic plasticity and brain function. Studies suggest that memory is encoded in MT of neuronal dendrites and cell bodies. Anesthetic causes loss of consciousness and memory formation via acting on MTs121–123. Disintegration and separation of the MT-associated protein tau have been observed in memory neurodegenerative diseases and disorders, e.g., in AD124; MT-stabilizers are currently the target for curing such diseases62,125,126. However, the underlying mechanism for such diseases is mostly unknown. Thus this project also paves a potential path to study other functionalities of the body and the brain connected to MTs in the light of the RPM.
In conclusion, our results suggest that quantum effects may underlie the magnetic field effects on the microtubule dynamics. This is likely a similar mechanism to those behind magnetoreception in animals47, xenon-induced general anesthesia13, lithium treatment for mania48, the magnetic field effects on the circadian clock49. Our work is thus another piece of evidence that quantum entanglement14,24,127–134 may play essential roles in the brain’s functions, anesthesia, and consciousness15,135. Particularly, the photo-emission of singlet oxygen could serve as quantum messengers to establish long-distance connections136 that might be essential for consciousness. Our work also provides a potential connection between microtubule-based and spin-based quantum approaches to consciousness.
Acknowledgements
The authors would like to thank Jack Tuszyński for valuable discussions. This work was supported by the Natural Sciences and Engineering Research Council of Canada.
Author contributions
H.Z.H. and C.S. conceived the project; H.Z.H. performed the calculations; H.Z.H. and C.S. wrote the paper; C.S. supervised the project.
Data availability
The generated datasets and computational analysis are available from the corresponding author on reasonable request.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Hadi Zadeh-Haghighi, Email: hadi.zadehhaghighi@ucalgary.ca.
Christoph Simon, Email: csimo@ucalgary.ca.
References
- 1.Koch C, Massimini M, Boly M, Tononi G. Neural correlates of consciousness: Progress and problems. Nat. Rev. Neurosci. 2016;17:307–321. doi: 10.1038/nrn.2016.22. [DOI] [PubMed] [Google Scholar]
- 2.Mashour GA. Integrating the science of consciousness and anesthesia. Anesth. Analges. 2006;103:975–982. doi: 10.1213/01.ane.0000232442.69757.4a. [DOI] [PubMed] [Google Scholar]
- 3.Brown EN, Purdon PL, Van Dort CJ. General anesthesia and altered states of arousal: A systems neuroscience analysis. Annu. Rev. Neurosci. 2011;34:601–628. doi: 10.1146/annurev-neuro-060909-153200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Craddock TJA, Hameroff SR, Ayoub AT, Klobukowski M, Tuszynski JA. Anesthetics act in quantum channels in brain microtubules to prevent consciousness. Curr. Top. Med. Chem. 2015;15:523–533. doi: 10.2174/1568026615666150225104543. [DOI] [PubMed] [Google Scholar]
- 5.Linganna RE, Levy WJ, Dmochowski IJ, Eckenhoff RG, Speck RM. Taxane modulation of anesthetic sensitivity in surgery for nonmetastatic breast cancer. J. Clin. Anesth. 2015;27:481–485. doi: 10.1016/j.jclinane.2015.05.001. [DOI] [PubMed] [Google Scholar]
- 6.Perouansky M. The quest for a unified model of anesthetic action: A century in claude bernard’s shadow. J. Am. Soc. Anesthesiol. 2012;117:465–474. doi: 10.1097/ALN.0b013e318264492e. [DOI] [PubMed] [Google Scholar]
- 7.Franks N, Lieb W. Do general anaesthetics act by competitive binding to specific receptors? Nature. 1984;310:599–601. doi: 10.1038/310599a0. [DOI] [PubMed] [Google Scholar]
- 8.Xi J, Liu R, Asbury GR, Eckenhoff MF, Eckenhoff RG. Inhalational anesthetic-binding proteins in rat neuronal membranes. J. Biol. Chem. 2004;279:19628–19633. doi: 10.1074/jbc.M313864200. [DOI] [PubMed] [Google Scholar]
- 9.Pan JZ, Xi J, Tobias JW, Eckenhoff MF, Eckenhoff RG. Halothane binding proteome in human brain cortex. J. Proteome Res. 2007;6:582–592. doi: 10.1021/pr060311u. [DOI] [PubMed] [Google Scholar]
- 10.Pan JZ, Xi J, Eckenhoff MF, Eckenhoff RG. Inhaled anesthetics elicit region-specific changes in protein expression in mammalian brain. Proteomics. 2008;8:2983–2992. doi: 10.1002/pmic.200800057. [DOI] [PubMed] [Google Scholar]
- 11.Turin L, Skoulakis EM, Horsfield AP. Electron spin changes during general anesthesia in drosophila. Proc. Natl. Acad. Sci. 2014;111:E3524–E3533. doi: 10.1073/pnas.1404387111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li N, et al. Nuclear spin attenuates the anesthetic potency of xenon isotopes in mice: Implications for the mechanisms of anesthesia and consciousness. Anesthesiology. 2018;129:271–277. doi: 10.1097/ALN.0000000000002226. [DOI] [PubMed] [Google Scholar]
- 13.Smith J, Zadeh-Haghighi H, Salahub D, Simon C. Radical pairs may play a role in xenon-induced general anesthesia. Sci. Rep. 2021;11:6287. doi: 10.1038/s41598-021-85673-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Simon C. Can quantum physics help solve the hard problem of consciousness? J. Conscious. Stud. 2019;26:204–218. [Google Scholar]
- 15.Hameroff S, Penrose R. Consciousness in the universe: A review of the ‘orch or’theory. Phys. Life Rev. 2014;11:39–78. doi: 10.1016/j.plrev.2013.08.002. [DOI] [PubMed] [Google Scholar]
- 16.Stuart, H.: Quantum computation in brain microtubules? the penrose–hameroff ‘orch or ‘model of consciousness. Philos. Trans. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci.356, 1869–1896 (1998).
- 17.Matsuno K. The internalist enterprise on constructing cell motility in a bottom-up manner. Biosystems. 2001;61:115–124. doi: 10.1016/S0303-2647(01)00165-4. [DOI] [PubMed] [Google Scholar]
- 18.Hagan, S., Hameroff, S. R. & Tuszyński, J. A. Quantum computation in brain microtubules: Decoherence and biological feasibility. Phys. Rev. E65, 061901 (2002). [DOI] [PubMed]
- 19.Hameroff S, Nip A, Porter M, Tuszynski J. Conduction pathways in microtubules, biological quantum computation, and consciousness. Biosystems. 2002;64:149–168. doi: 10.1016/S0303-2647(01)00183-6. [DOI] [PubMed] [Google Scholar]
- 20.Craddock, T. J. et al. Computational predictions of volatile anesthetic interactions with the microtubule cytoskeleton: Implications for side effects of general anesthesia. PLoS ONE7, e37251 (2012). [DOI] [PMC free article] [PubMed]
- 21.Zhang, W. et al. Fano resonance line shapes in the raman spectra of tubulin and microtubules reveal quantum effects. Biophys. Rep.2, 100043 (2022). [DOI] [PMC free article] [PubMed]
- 22.Cao, J. et al. Quantum biology revisited. Sci. Adv.6, eaaz4888 (2020). [DOI] [PMC free article] [PubMed]
- 23.Hu H, Wu M. Spin-mediated consciousness theory: Possible roles of neural membrane nuclear spin ensembles and paramagnetic oxygen. Med. Hypotheses. 2004;63:633–646. doi: 10.1016/j.mehy.2004.04.002. [DOI] [PubMed] [Google Scholar]
- 24.Fisher MP. Quantum cognition: The possibility of processing with nuclear spins in the brain. Ann. Phys. 2015;362:593–602. doi: 10.1016/j.aop.2015.08.020. [DOI] [Google Scholar]
- 25.Chen R, Li N, Qian H, Zhao R-H, Zhang S-H. Experimental evidence refuting the assumption of phosphorus-31 nuclear-spin entanglement-mediated consciousness. J. Integr. Neurosci. 2020;19:595–600. doi: 10.31083/j.jin.2020.04.250. [DOI] [PubMed] [Google Scholar]
- 26.Romero MC, Davare M, Armendariz M, Janssen P. Neural effects of transcranial magnetic stimulation at the single-cell level. Nat. Commun. 2019;10:1–11. doi: 10.1038/s41467-018-07882-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang R, Fan Y, Wu Y. Spontaneous electromagnetic induction promotes the formation of economical neuronal network structure via self-organization process. Sci. Rep. 2019;9:1–13. doi: 10.1038/s41598-019-46104-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lenz M, et al. Repetitive magnetic stimulation induces plasticity of inhibitory synapses. Nat. Commun. 2016;7:1–13. doi: 10.1038/ncomms10020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rauš Balind, S., Selaković, V., Radenović, L., Prolić, Z. & Janać, B. Extremely low frequency magnetic field (50 hz, 0.5 mt) reduces oxidative stress in the brain of gerbils submitted to global cerebral ischemia. PLoS One9, e88921 (2014). [DOI] [PMC free article] [PubMed]
- 30.Pacini, S. et al. Effect of 0.2 t static magnetic field on human neurons: Remodeling and inhibition of signal transduction without genome instability. Neurosci. Lett.267, 185–188 (1999). [DOI] [PubMed]
- 31.Grehl S, et al. Cellular and molecular changes to cortical neurons following low intensity repetitive magnetic stimulation at different frequencies. Brain Stimul. 2015;8:114–123. doi: 10.1016/j.brs.2014.09.012. [DOI] [PubMed] [Google Scholar]
- 32.Manikonda PK, et al. Influence of extremely low frequency magnetic fields on ca2+ signaling and nmda receptor functions in rat hippocampus. Neurosci. Lett. 2007;413:145–149. doi: 10.1016/j.neulet.2006.11.048. [DOI] [PubMed] [Google Scholar]
- 33.Zhang B, et al. Long-term exposure to a hypomagnetic field attenuates adult hippocampal neurogenesis and cognition. Nat. Commun. 2021;12:1–17. doi: 10.1038/s41467-020-20314-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vassilev PM, Dronzine RT, Vassileva MP, Georgiev GA. Parallel arrays of microtubles formed in electric and magnetic fields. Biosci. Rep. 1982;2:1025–1029. doi: 10.1007/BF01122171. [DOI] [PubMed] [Google Scholar]
- 35.Glade N, Tabony J. Brief exposure to high magnetic fields determines microtubule self-organisation by reaction-diffusion processes. Biophys. Chem. 2005;115:29–35. doi: 10.1016/j.bpc.2004.12.048. [DOI] [PubMed] [Google Scholar]
- 36.Bras W, et al. The susceptibility of pure tubulin to high magnetic fields: A magnetic birefringence and x-ray fiber diffraction study. Biophys. J. 1998;74:1509–1521. doi: 10.1016/S0006-3495(98)77863-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang, L. et al. 27 t ultra-high static magnetic field changes orientation and morphology of mitotic spindles in human cells. Elife6, e22911 (2017). [DOI] [PMC free article] [PubMed]
- 38.Qian, A.-R. et al. Large gradient high magnetic field affects the association of macf1 with actin and microtubule cytoskeleton. Bioelectromagn.: J. Bioelectromagn. Soc. Soc. Phys. Regul. Biol. Med. Eur. Bioelectromagn. Assoc.30, 545–555(2009). [DOI] [PubMed]
- 39.Luo Y, et al. Moderate intensity static magnetic fields affect mitotic spindles and increase the antitumor efficacy of 5-fu and taxol. Bioelectrochemistry. 2016;109:31–40. doi: 10.1016/j.bioelechem.2016.01.001. [DOI] [PubMed] [Google Scholar]
- 40.Wang DL, Wang XS, Xiao R, Liu Y, He RQ. Tubulin assembly is disordered in a hypogeomagnetic field. Biochem. Biophys. Res. Commun. 2008;376:363–368. doi: 10.1016/j.bbrc.2008.08.156. [DOI] [PubMed] [Google Scholar]
- 41.Wu, X. et al. Weak power frequency magnetic fields induce microtubule cytoskeleton reorganization depending on the epidermal growth factor receptor and the calcium related signaling. PLoS ONE13, e0205569 (2018). [DOI] [PMC free article] [PubMed]
- 42.Rodgers CT, Hore PJ. Chemical magnetoreception in birds: the radical pair mechanism. Proc. Natl. Acad. Sci. 2009;106:353–360. doi: 10.1073/pnas.0711968106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Steiner UE, Ulrich T. Magnetic field effects in chemical kinetics and related phenomena. Chem. Rev. 1989;89:51–147. doi: 10.1021/cr00091a003. [DOI] [Google Scholar]
- 44.Timmel CR, Till U, Brocklehurst B, Mclauchlan KA, Hore PJ. Effects of weak magnetic fields on free radical recombination reactions. Mol. Phys. 1998;95:71–89. doi: 10.1080/00268979809483134. [DOI] [PubMed] [Google Scholar]
- 45.Hore PJ, Mouritsen H. The radical-pair mechanism of magnetoreception. Annu. Rev. Biophys. 2016;45:299–344. doi: 10.1146/annurev-biophys-032116-094545. [DOI] [PubMed] [Google Scholar]
- 46.Schulten K, Swenberg CE, Weller A. A biomagnetic sensory mechanism based on magnetic field modulated coherent electron spin motion. Z. Phys. Chem. 1978;111:1–5. doi: 10.1524/zpch.1978.111.1.001. [DOI] [Google Scholar]
- 47.Xu J, et al. Magnetic sensitivity of cryptochrome 4 from a migratory songbird. Nature. 2021;594:535–540. doi: 10.1038/s41586-021-03618-9. [DOI] [PubMed] [Google Scholar]
- 48.Zadeh-Haghighi H, Simon C. Entangled radicals may explain lithium effects on hyperactivity. Sci. Rep. 2021;11:12121. doi: 10.1038/s41598-021-91388-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zadeh-Haghighi H, Simon C. Radical pairs can explain magnetic field and lithium effects on the circadian clock. Sci. Rep. 2022;12:269. doi: 10.1038/s41598-021-04334-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Brouhard GJ, Rice LM. Microtubule dynamics: An interplay of biochemistry and mechanics. Nat. Rev. Mol. Cell Biol. 2018;19:451–463. doi: 10.1038/s41580-018-0009-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nogales E. Structural insights into microtubule function. Annu. Rev. Biophys. Biomol. Struct. 2001;30:397–420. doi: 10.1146/annurev.biophys.30.1.397. [DOI] [PubMed] [Google Scholar]
- 52.Wu J, Akhmanova A. Microtubule-organizing centers. Annu. Rev. Cell Dev. Biol. 2017;33:51–75. doi: 10.1146/annurev-cellbio-100616-060615. [DOI] [PubMed] [Google Scholar]
- 53.Akhmanova A, Steinmetz MO. Tracking the ends: A dynamic protein network controls the fate of microtubule tips. Nat. Rev. Mol. Cell Biol. 2008;9:309–322. doi: 10.1038/nrm2369. [DOI] [PubMed] [Google Scholar]
- 54.Akhmanova A, Steinmetz MO. Control of microtubule organization and dynamics: Two ends in the limelight. Nat. Rev. Mol. Cell Biol. 2015;16:711–726. doi: 10.1038/nrm4084. [DOI] [PubMed] [Google Scholar]
- 55.Redwine WB, et al. Structural basis for microtubule binding and release by dynein. Science. 2012;337:1532–1536. doi: 10.1126/science.1224151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Monroy BY, et al. A combinatorial map code dictates polarized microtubule transport. Dev. Cell. 2020;53:60–72. doi: 10.1016/j.devcel.2020.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Monroy BY, et al. Competition between microtubule-associated proteins directs motor transport. Nat. Commun. 2018;9:1–12. doi: 10.1038/s41467-018-03909-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Burute, M., Jansen, K. I., Mihajlovic, M., Vermonden, T. & Kapitein, L. Matrix elasticity gradients guide neuronal polarity by controlling microtubule network mobility. bioRxiv (2021).
- 59.Sanchez-Castro N, et al. Microtubules as one-dimensional crystals: Is crystal-like structure the key to the information processing of living systems? Curr. Comput.-Aided Drug Des. 2021;11:318. [Google Scholar]
- 60.Dixit R, Ross JL, Goldman YE, Holzbaur EL. Differential regulation of dynein and kinesin motor proteins by tau. Science. 2008;319:1086–1089. doi: 10.1126/science.1152993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Singh P, et al. Cytoskeletal filaments deep inside a neuron are not silent: They regulate the precise timing of nerve spikes using a pair of vortices. Symmetry. 2021;13:821. doi: 10.3390/sym13050821. [DOI] [Google Scholar]
- 62.Congdon EE, Sigurdsson EM. Tau-targeting therapies for alzheimer disease. Nat. Rev. Neurol. 2018;14:399–415. doi: 10.1038/s41582-018-0013-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wilson C, González-Billault C. Regulation of cytoskeletal dynamics by redox signaling and oxidative stress: implications for neuronal development and trafficking. Front. Cell. Neurosci. 2015;9:381. doi: 10.3389/fncel.2015.00381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Player, T. C. & Hore, P. Viability of superoxide-containing radical pairs as magnetoreceptors. J. Chem. Phys.151, 225101 (2019). [DOI] [PubMed]
- 65.Mondal P, Huix-Rotllant M. Theoretical insights into the formation and stability of radical oxygen species in cryptochromes. Phys. Chem. Chem. Phys. 2019;21:8874–8882. doi: 10.1039/C9CP00782B. [DOI] [PubMed] [Google Scholar]
- 66.Furukawa H, Singh SK, Mancusso R, Gouaux E. Subunit arrangement and function in NMDA receptors. Nature. 2005;438:185–192. doi: 10.1038/nature04089. [DOI] [PubMed] [Google Scholar]
- 67.Sardar PS, Maity SS, Das L, Ghosh S. Luminescence studies of perturbation of tryptophan residues of tubulin in the complexes of tubulin with colchicine and colchicine analogues. Biochemistry. 2007;46:14544–14556. doi: 10.1021/bi701412k. [DOI] [PubMed] [Google Scholar]
- 68.Kurian P, Obisesan T, Craddock TJ. Oxidative species-induced excitonic transport in tubulin aromatic networks: Potential implications for neurodegenerative disease. J. Photochem. Photobiol. B. 2017;175:109–124. doi: 10.1016/j.jphotobiol.2017.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.McCormick, J. P. & Thomason, T. Near-ultraviolet photooxidation of tryptophan. proof of formation of superoxide ion. J. Am. Chem. Soc.100, 312–313 (1978).
- 70.Saito, I., Matsuura, T. & Inoue, K. Formation of superoxide ion from singlet oxygen. use of a water-soluble singlet oxygen source. J. Am. Chem. Soc.103, 188–190 (1981).
- 71.Bradlaugh, A. A. et al. Essential elements of radical pair magnetosensitivity in drosophila. bioRxiv (2021). [DOI] [PMC free article] [PubMed]
- 72.Liu Q, et al. Mical3 flavoprotein monooxygenase forms a complex with centralspindlin and regulates cytokinesis. J. Biol. Chem. 2016;291:20617–20629. doi: 10.1074/jbc.M116.748186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yamauchi T, Fujisawa H. Disassembly of microtubules by the action of calmodulin-dependent protein kinase (kinase ii) which occurs only in the brain tissues. Biochem. Biophys. Res. Commun. 1983;110:287–291. doi: 10.1016/0006-291X(83)91293-7. [DOI] [PubMed] [Google Scholar]
- 74.White D, de Vries G, Martin J, Dawes A. Microtubule patterning in the presence of moving motor proteins. J. Theor. Biol. 2015;382:81–90. doi: 10.1016/j.jtbi.2015.06.040. [DOI] [PubMed] [Google Scholar]
- 75.Bowne-Anderson H, Zanic M, Kauer M, Howard J. Microtubule dynamic instability: A new model with coupled gtp hydrolysis and multistep catastrophe. BioEssays. 2013;35:452–461. doi: 10.1002/bies.201200131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Craddock, T. J. et al. The zinc dyshomeostasis hypothesis of alzheimer’s disease. PLoS ONE7, e33552 (2012). [DOI] [PMC free article] [PubMed]
- 77.Player TC, Baxter ED, Allatt S, Hore P. Amplification of weak magnetic field effects on oscillating reactions. Sci. Rep. 2021;11:1–9. doi: 10.1038/s41598-021-88871-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Usselman RJ, et al. The quantum biology of reactive oxygen species partitioning impacts cellular bioenergetics. Sci. Rep. 2016;6:1–6. doi: 10.1038/srep38543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lee AA, et al. Alternative radical pairs for cryptochrome-based magnetoreception. J. R. Soc. Interface. 2014;11:20131063. doi: 10.1098/rsif.2013.1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Efimova O, Hore P. Role of exchange and dipolar interactions in the radical pair model of the avian magnetic compass. Biophys. J. 2008;94:1565–1574. doi: 10.1529/biophysj.107.119362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Haberkorn R. Density matrix description of spin-selective radical pair reactions. Mol. Phys. 1976;32:1491–1493. doi: 10.1080/00268977600102851. [DOI] [Google Scholar]
- 82.Ivanov KL, Petrova MV, Lukzen NN, Maeda K. Consistent treatment of spin-selective recombination of a radical pair confirms the haberkorn approach. J. Phys. Chem. A. 2010;114:9447–9455. doi: 10.1021/jp1048265. [DOI] [PubMed] [Google Scholar]
- 83.Bagryansky VA, Borovkov VI, Molin YN. Quantum beats in radical pairs. Russ. Chem. Rev. 2007;76:493–506. doi: 10.1070/RC2007v076n06ABEH003715. [DOI] [Google Scholar]
- 84.Hore, P. J. Upper bound on the biological effects of 50/60 hz magnetic fields mediated by radical pairs. Elife8, e44179 (2019). [DOI] [PMC free article] [PubMed]
- 85.Sies H, Jones DP. Reactive oxygen species (ros) as pleiotropic physiological signalling agents. Nat. Rev. Mol. Cell Biol. 2020;21:363–383. doi: 10.1038/s41580-020-0230-3. [DOI] [PubMed] [Google Scholar]
- 86.Neese F. The orca program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:73–78. [Google Scholar]
- 87.Goerigk L, Grimme S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011;13:6670–6688. doi: 10.1039/c0cp02984j. [DOI] [PubMed] [Google Scholar]
- 88.Van Lenthe, E. v. Snijders, J. & Baerends, E. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys.105, 6505–6516 (1996).
- 89.Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B. 2009;113:6378–6396. doi: 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- 90.Hogben HJ, Efimova O, Wagner-Rundell N, Timmel CR, Hore P. Possible involvement of superoxide and dioxygen with cryptochrome in avian magnetoreception: Origin of zeeman resonances observed by in vivo epr spectroscopy. Chem. Phys. Lett. 2009;480:118–122. doi: 10.1016/j.cplett.2009.08.051. [DOI] [Google Scholar]
- 91.Karogodina, T. Y. Dranov, I. G. Sergeeva, S. V. Stass, D. V. & Steiner, U. E. Kinetic magnetic-field effect involving the small biologically relevant inorganic radicals NO and o2.-. ChemPhysChem12, 1714–1728 (2011). [DOI] [PubMed]
- 92.Karogodina TY, Sergeeva SV, Stass DV. Magnetic field effect in the reaction of recombination of nitric oxide and superoxide anion. Appl. Magn. Reson. 2009;36:195–208. doi: 10.1007/s00723-009-0018-2. [DOI] [Google Scholar]
- 93.Symons, M. C. R., Eastland, G. W. & Denny, L. R. Effect of solvation on the electron spin resonance spectrum of the superoxide ion. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases76, 1868 (1980).
- 94.Känzig W, Cohen MH. Paramagnetic resonance of oxygen in alkali halides. Phys. Rev. Lett. 1959;3:509–510. doi: 10.1103/PhysRevLett.3.509. [DOI] [Google Scholar]
- 95.Kattnig DR. Radical-pair-based magnetoreception amplified by radical scavenging: Resilience to spin relaxation. J. Phys. Chem. B. 2017;121:10215–10227. doi: 10.1021/acs.jpcb.7b07672. [DOI] [PubMed] [Google Scholar]
- 96.Kattnig DR, Hore P. The sensitivity of a radical pair compass magnetoreceptor can be significantly amplified by radical scavengers. Sci. Rep. 2017;7:1–12. doi: 10.1038/s41598-017-09914-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Martin, S. R. Butler, F. M. Clark, D. C. Zhou, J.-M. & Bayley, P. M. Magnesium ion effects on microtubule nucleation in vitro. Biochimica et Biophysica Acta (BBA) - Prot. Struct. Mol. Enzymol.914, 96–100 (1987). [DOI] [PubMed]
- 98.O’Brien ET, Salmon ED, Walker RA, Erickson HP. Effects of magnesium on the dynamic instability of individual microtubules. Biochemistry. 1990;29:6648–6656. doi: 10.1021/bi00480a014. [DOI] [PubMed] [Google Scholar]
- 99.Menéndez M, Rivas G, Diaz JF, Andreu JM. Control of the structural stability of the tubulin dimer by one high affinity bound magnesium ion at nucleotide n-site. J. Biol. Chem. 1998;273:167–176. doi: 10.1074/jbc.273.1.167. [DOI] [PubMed] [Google Scholar]
- 100.Buchachenko AL, Kouznetsov DA, Orlova MA, Markarian AA. Magnetic isotope effect of magnesium in phosphoglycerate kinase phosphorylation. Proc. Natl. Acad. Sci. 2005;102:10793–10796. doi: 10.1073/pnas.0504876102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Kerver ED, et al. In situ detection of spontaneous superoxide anion and singlet oxygen production by mitochondria in rat liver and small intestine. Histochem. J. 1997;29:229–237. doi: 10.1023/A:1026453926517. [DOI] [PubMed] [Google Scholar]
- 102.Miyamoto S, Martinez GR, Medeiros MH, Di Mascio P. Singlet molecular oxygen generated by biological hydroperoxides. J. Photochem. Photobiol. B. 2014;139:24–33. doi: 10.1016/j.jphotobiol.2014.03.028. [DOI] [PubMed] [Google Scholar]
- 103.Kanofsky JR. Singlet oxygen production by biological systems. Chem. Biol. Interact. 1989;70:1–28. doi: 10.1016/0009-2797(89)90059-8. [DOI] [PubMed] [Google Scholar]
- 104.Hayyan M, Hashim MA, AlNashef IM. Superoxide ion: Generation and chemical implications. Chem. Rev. 2016;116:3029–3085. doi: 10.1021/acs.chemrev.5b00407. [DOI] [PubMed] [Google Scholar]
- 105.Mano CM, et al. Excited singlet molecular o 2 (1 g) is generated enzymatically from excited carbonyls in the dark. Sci. Rep. 2014;4:1–10. doi: 10.1038/srep05938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Pospíšil P, Prasad A, Rác M. Role of reactive oxygen species in ultra-weak photon emission in biological systems. J. Photochem. Photobiol. B. 2014;139:11–23. doi: 10.1016/j.jphotobiol.2014.02.008. [DOI] [PubMed] [Google Scholar]
- 107.Goushi K, Yoshida K, Sato K, Adachi C. Organic light-emitting diodes employing efficient reverse intersystem crossing for triplet-to-singlet state conversion. Nat. Photon. 2012;6:253–258. doi: 10.1038/nphoton.2012.31. [DOI] [Google Scholar]
- 108.Fay, T. P. & Manolopoulos, D. E. Radical pair intersystem crossing: Quantum dynamics or incoherent kinetics?. J. Chem. Phys.150, 151102 (2019). [DOI] [PubMed]
- 109.Khudyakov IV, Serebrennikov YA, Turro NJ. Spin-orbit coupling in free-radical reactions: On the way to heavy elements. Chem. Rev. 1993;93:537–570. doi: 10.1021/cr00017a023. [DOI] [Google Scholar]
- 110.Li H, Kamasah A, Matsika S, Suits AG. Intersystem crossing in the exit channel. Nat. Chem. 2019;11:123–128. doi: 10.1038/s41557-018-0186-5. [DOI] [PubMed] [Google Scholar]
- 111.Marian CM. Understanding and controlling intersystem crossing in molecules. Annu. Rev. Phys. Chem. 2021;72:617–640. doi: 10.1146/annurev-physchem-061020-053433. [DOI] [PubMed] [Google Scholar]
- 112.Ballatore C, Lee VM-Y, Trojanowski JQ. Tau-mediated neurodegeneration in Alzheimer’s disease and related disorders. Nat. Rev. Neurosci. 2007;8:663–672. doi: 10.1038/nrn2194. [DOI] [PubMed] [Google Scholar]
- 113.Gong C-X, Iqbal K. Hyperphosphorylation of microtubule-associated protein tau: a promising therapeutic target for alzheimer disease. Curr. Med. Chem. 2008;15:2321–2328. doi: 10.2174/092986708785909111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Alonso, A. d. C., Grundke-Iqbal, I. & Iqbal, K. Alzheimer’s disease hyperphosphorylated tau sequesters normal tau into tangles of filaments and disassembles microtubules. Nat. Med.2, 783–787 (1996). [DOI] [PubMed]
- 115.Iqbal K, Liu F, Gong C-X, Grundke-Iqbal I. Tau in alzheimer disease and related tauopathies. Curr. Alzheimer Res. 2010;7:656–664. doi: 10.2174/156720510793611592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Feng J. Microtubule: A common target for parkin and parkinson’s disease toxins. Neuroscientist. 2006;12:469–476. doi: 10.1177/1073858406293853. [DOI] [PubMed] [Google Scholar]
- 117.Kett LR, et al. Lrrk2 parkinson disease mutations enhance its microtubule association. Hum. Mol. Genet. 2012;21:890–899. doi: 10.1093/hmg/ddr526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Parker AL, Kavallaris M, McCarroll JA. Microtubules and their role in cellular stress in cancer. Front. Oncol. 2014;4:153. doi: 10.3389/fonc.2014.00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Mukhtar E, Adhami VM, Mukhtar H. Targeting microtubules by natural agents for cancer therapy. Mol. Cancer Ther. 2014;13:275–284. doi: 10.1158/1535-7163.MCT-13-0791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Jordan MA, Wilson L. Microtubules as a target for anticancer drugs. Nat. Rev. Cancer. 2004;4:253–265. doi: 10.1038/nrc1317. [DOI] [PubMed] [Google Scholar]
- 121.Craddock, T. J., Tuszynski, J. A. & Hameroff, S. Cytoskeletal signaling: is memory encoded in microtubule lattices by camkii phosphorylation?. PLoS Comput. Biol.8, e1002421 (2012). [DOI] [PMC free article] [PubMed]
- 122.Janke C, Kneussel M. Tubulin post-translational modifications: Encoding functions on the neuronal microtubule cytoskeleton. Trends Neurosci. 2010;33:362–372. doi: 10.1016/j.tins.2010.05.001. [DOI] [PubMed] [Google Scholar]
- 123.Janke C, Bulinski JC. Post-translational regulation of the microtubule cytoskeleton: Mechanisms and functions. Nat. Rev. Mol. Cell Biol. 2011;12:773–786. doi: 10.1038/nrm3227. [DOI] [PubMed] [Google Scholar]
- 124.Goldstein, L. E. et al. Chronic traumatic encephalopathy in blast-exposed military veterans and a blast neurotrauma mouse model. Sci. Transl. Med.4, 134ra60–134ra60 (2012). [DOI] [PMC free article] [PubMed]
- 125.Brunden KR, et al. Epothilone d improves microtubule density, axonal integrity, and cognition in a transgenic mouse model of tauopathy. J. Neurosci. 2010;30:13861–13866. doi: 10.1523/JNEUROSCI.3059-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Li C, Götz J. Tau-based therapies in neurodegeneration: Opportunities and challenges. Nat. Rev. Drug Discov. 2017;16:863–883. doi: 10.1038/nrd.2017.155. [DOI] [PubMed] [Google Scholar]
- 127.Adams, B. & Petruccione, F. Quantum effects in the brain: A review. AVS Quant. Sci.2, 022901 (2020).
- 128.Gauger, E. M., Rieper, E., Morton, J. J., Benjamin, S. C. & Vedral, V. Sustained quantum coherence and entanglement in the avian compass. Phys. Rev. Lett.106, 040503 (2011). [DOI] [PubMed]
- 129.Bandyopadhyay, J. N., Paterek, T. & Kaszlikowski, D. Quantum coherence and sensitivity of avian magnetoreception. Phys. Rev. Lett.109, 110502 (2012). [DOI] [PubMed]
- 130.Cai, J., Guerreschi, G. G. & Briegel, H. J. Quantum control and entanglement in a chemical compass. Phys. Rev. Lett.104, 220502 (2010). [DOI] [PubMed]
- 131.Kominis I. Magnetic sensitivity and entanglement dynamics of the chemical compass. Chem. Phys. Lett. 2012;542:143–146. doi: 10.1016/j.cplett.2012.06.014. [DOI] [Google Scholar]
- 132.Pauls, J. A., Zhang, Y., Berman, G. P. & Kais, S. Quantum coherence and entanglement in the avian compass. Phys. Rev. E87, 062704 (2013). [DOI] [PubMed]
- 133.Tiersch M, Guerreschi G, Clausen J, Briegel H. Approaches to measuring entanglement in chemical magnetometers. J. Phys. Chem. A. 2014;118:13–20. doi: 10.1021/jp408569d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Zhang, Y., Berman, G. P. & Kais, S. Sensitivity and entanglement in the avian chemical compass. Phys. Rev. E90, 042707 (2014). [DOI] [PubMed]
- 135.Hameroff SR, Craddock TJ, Tuszynski JA. Quantum effects in the understanding of consciousness. J. Integr. Neurosci. 2014;13:229–252. doi: 10.1142/S0219635214400093. [DOI] [PubMed] [Google Scholar]
- 136.Kumar S, Boone K, Tuszyński J, Barclay P, Simon C. Possible existence of optical communication channels in the brain. Sci. Rep. 2016;6:36508. doi: 10.1038/srep36508. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The generated datasets and computational analysis are available from the corresponding author on reasonable request.


