Risk Stratification in Cost-Effectiveness Analyses of Cancer Screening: Intervention Eligibility, Strategy Choice, and Optimality

Abstract

Introduction

There is increasing interest in risk-stratified approaches to cancer screening in cost-effectiveness analysis (CEA). Current CEA practice regarding risk stratification is heterogeneous and guidance on the best approach is lacking. This article suggests how stratification in CEA can be improved.

Methods

I use a simple example of a hypothetical screening intervention with 3 potential recipient risk strata. The screening intervention has 6 alternative intensities, each with different costs and effects, all of which vary between strata. I consider a series of alternative stratification approaches, demonstrating the consequences for estimated costs, effects, and the choice of optimal strategy. I supplement this analysis with applied examples from the literature.

Results

Adopting the same screening policy for all strata yields the least efficient strategies, where efficiency is understood as the volume of net health benefit generated across a range of cost-effectiveness threshold values. Basic stratification that withholds screening from lower-risk strata while adopting a common strategy for those screened increases efficiency. Greatest efficiency is achieved when different strata receive separate strategies. While complete optimization can be achieved within a single analysis by considering all possible policy combinations, the resulting number of strategy combinations may be inconveniently large. Optimization with separate strata-specific analyses is simpler and more transparent. Despite this, there can be good reasons to simulate all strata together in a single analysis.

Conclusions

If the benefits of risk stratification are to be fully realized, policy makers need to consider the extent to which stratification is feasible, and modelers need to simulate those choices adequately. It is hoped this analysis will clarify those policy and modeling choices and therefore lead to improved population health outcomes.

Introduction

Screening for cancer can typically be applied at varying intensities, with alternative screening start ages, stop ages, and screening intervals. The capacity to benefit from screening can vary with many factors, including disease risk. It is well recognized that there can be benefits to stratifying screening intensity,^1,2 typically by offering higher-intensity screening to those at greater risk of disease. Current interest in screening stratification will continue to grow as our knowledge of the many determinants of disease risk expands.

Cost-effectiveness analysis (CEA) offers one way to assess the benefits of stratification. Indeed, CEA can usefully guide policy makers to the most beneficial tailoring of screening by risk. Some of the existing methods literature has examined the modeling implications of heterogeneous risk groups.^3,4 O’Mahony et al. concluded that where differences in patient subgroups result in different cost-effectiveness, then, in as far as is practicable, such subgroups should be assessed separately to identify optimal policies. ⁴

There are numerous examples of stratified CEAs that follow the approach of assessing screening strategies separately for separate risk strata. These include analyses that differentiate by risk factors including sex, ethnicity, family history of disease, smoking status, genetic factors, tissue density, and previous screening history.^5–10 There are also examples of CEAs that consider multiple risk strata together in a single analysis, meaning the variation of eligibility between risk strata is combined with variation of screening intensity when specifying alternative screening strategies.^11–19

The problem addressed by this study is the notable variation of methods used within the risk-stratified cancer-screening CEA literature and the attendant likelihood that present analyses might not necessarily provide policy makers with optimal policies. This problem primarily relates to analyses within the latter group of studies identified above—those that use variation in the eligibility criteria as part of the definition of alternative screening strategies. Specifically, some studies assume all eligible screenees receive a common screening strategy, and it is unclear if the consequences of this assumption are appreciated. More generally, it is also unclear if relevant combinations of risk eligibility and screening intensity are being considered.

Part of the following analysis concerns the issue of mutual exclusivity and its implication for the interpretation of incremental cost-effectiveness ratios (ICERs) [20]. The ICER is the ratio of incremental costs to incremental health effects of an intervention of interest relative to the next-best comparator within the efficient set of interventions. It is recognized that ICERs should be calculated only between mutually exclusive policy options. ²⁰ For example, to estimate the ICER of biennial mammography for the prevention of breast cancer in women, its costs and effects should be compared with those of triennial mammography ²¹ ; they should not be compared with the costs and effects of annual prostate examination in men. The choices of alternative mammography screening intensities are either-or choices between mutually exclusive alternatives; therefore, the relevant ICER comparisons are between such strategies. Conversely, there is no either-or choice between mammography and prostate screening; therefore, making comparisons between non–mutually exclusive strategies will not yield the appropriately estimated ICERs required for health maximization from finite health care resources.

This objective of this article is to typify the current approaches used in risk-stratified cancer-screening CEAs, examine the implications of alternative approaches, and provide suggestions on which methods would provide clearer policy guidance to better health outcomes. While the existing methods literature addresses some of these issues at a high level, this study is the first to specifically examine the issues regarding analyses that consider multiple risk strata simultaneously. It is hoped that this guide will lead to better understanding of appropriate CEA methods among analysts, peer reviewers, journal editors, and policy makers. Ultimately, the goal is to achieve better screening policies that are appropriately tailored to disease risk.

Methods

I use an example of a hypothetical screening intervention that has various intensities with varying costs and effects. I assume 3 discrete risk strata, between which the costs and effects of all strategies vary. I do not use a simulation model but simply assume values of costs and effects that are qualitatively representative of the variation of costs and health effects between strategies and across strata.

The 3 strata have low, medium, and high risk of disease, respectively. There are 6 policy alternatives for each strata: no screening and 5 alternative screening intensities. The assumed costs and health effects for the 5 alternative screening intensities disaggregated across each of the 3 subgroups are shown in the lower portion of Table 1. Effectiveness is generally assumed to increase as costs increase but less than proportionately, as is typically observed in CEAs of cancer screening. One exception is the low-risk strata, in which screening effectiveness eventually diminishes for the most expensive strategy, corresponding to examples in which screening-related harm can arise. All strategies are assumed more effective and less costly as disease risk increases. This reflects a greater capacity to benefit from screening and greater associated late-stage treatment savings in higher-incidence groups.

Table 1 .

Costs, Effects, ICERs, and Optimal Policy Choices under Approaches 1 and 2

Analysis Approach	Risk Strata	Strategy	Effects, QALYs	Costs, €	ACER, €/QALY	ICER, €/QALY	Policy Choice
	Aggregated	1	0.00	0	—	—
		2	1.92	38,750	20,217	20,217
		3	3.25	100,500	30,923	46,313	Optimal
1		4	4.00	161,250	40,313	81,000
		5	4.37	220,000	50,382	160,227
		6	4.45	278,750	62,640	705,000
	Low	1	0.00	0	—	—
	Low	2	0.50	25,000	50,000	50,000	Optimal
	Low	3	0.80	58,000	72,500	110,000
	Low	4	0.90	90,000	100,000	320,000
	Low	5	0.90	120,000	133,333	SD
	Low	6	0.80	150,000	187,500	SD
	Medium	1	0.00	0	—	—
	Medium	2	0.67	18,750	28,125	28,125
2	Medium	3	1.10	37,500	34,091	43,269	Optimal
	Medium	4	1.30	56,250	43,269	93,750
	Medium	5	1.37	75,000	54,878	281,250
	Medium	6	1.40	93,750	66,964	562,501
	High	1	0.00	0	—	—
	High	2	0.75	–5,000	—	SD
	High	3	1.35	5,000	3,704	16,667
	High	4	1.80	15,000	8,333	22,222
	High	5	2.10	25,000	11,905	33,333	Optimal
	High	6	2.25	35,000	15,556	66,667

ICER, incremental cost-effectiveness ratio; QALY, quality-adjusted life-year.

I examine 5 alternative approaches to identifying optimal policies given subgroup differences and compare the results graphically. In each case, the initial objective is to identify the efficient frontier within the available set of possible screening interventions, that is, the set of strategies that maximize net health benefit for a range of cost-effectiveness thresholds.^22,23 Then, the optimal intervention is found as the most effective within the efficient set that has an ICER not exceeding the cost-effectiveness threshold. An illustrative cost-effectiveness threshold of €50,000/quality-adjusted life-year (QALY) is assumed.

The 5 alternative approaches are as following:

1. Approach 1 corresponds with no stratification. It assumes a common strategy across all strata and that no strata can be excluded from screening. It simply makes aggregated estimates of costs and effects for each screening strategy across all 3 strata combined. The efficient frontier and optimal strategy from this case serve as a benchmark for subsequent analyses.

2. Approach 2 assesses each risk strata separately and finds the optimally cost-effective strategy independently in each case. Unlike approach 1, this permits different screening intensities for different strata.

3. Approach 3 considers just 1 screening intensity while cumulatively expanding the eligibility threshold from the highest risk subgroup to the lowest. Like approach 1, this assumes a common screening intensity for those screened, but unlike approach 1, it permits the exclusion of certain strata from screening and considers only 1 level of screening intensity. The analysis considers strategy 3 as an illustrative example under approach 3. The optimal policy is chosen as the eligibility threshold yielding the most cost-effective option.

4. Approach 4 extends approach 3 by considering the alternative screening strategies while cumulatively expanding the eligibility threshold from the highest risk subgroup to the lowest. Like approach 3, this assumes a common screening intensity for those screened and permits the exclusion of certain strata from screening, but unlike approach 3, it considers more than 1 screening intensity. The optimal policy is chosen as the combination of screening strategy and eligibility threshold yielding the most cost-effective option.

5. Approach 5 considers all possible combinations of screening strategies in all subgroups within a single analysis. Like approach 2, this permits different screening intensities for different strata, but unlike approach 2, it examines all possible combinations in a single analysis.

In each case, I examine the efficient frontier and identify the optimally cost-effective policy. I plot a selection of the efficient frontiers from the approaches described above to provide an overall comparison.

The 5 different approaches described above are, in part, informed by practice observed within the published literature to date. I have formalized the description of each approach to make the assumptions and constraints explicit. Furthermore, I have selected the sequencing of these approaches to represent alternative ways to expand stratification from an unstratified to a partially and then fully stratified analyses. The sequencing is chosen to demonstrate the consequences and limitations of alternative approaches. The Discussion section supplements this analysis with published examples of stratified analyses from the literature for comparison.

The 5 different approaches to stratification described above have implications for what strategies are considered mutually exclusive and whether the cost-effectiveness ratios along the resulting efficient frontiers can be considered ICERs or not. The following analysis deliberately uses the general term cost-effectiveness ratio (CER), as not all of the ratios presented correspond to the conventionally understood ICER and average cost effectiveness ratio (ACER) terms. This issue is discussed in detail in the Discussion section.

The funder of this research, the Health Research Board (of Ireland), had no role in this study.

Results

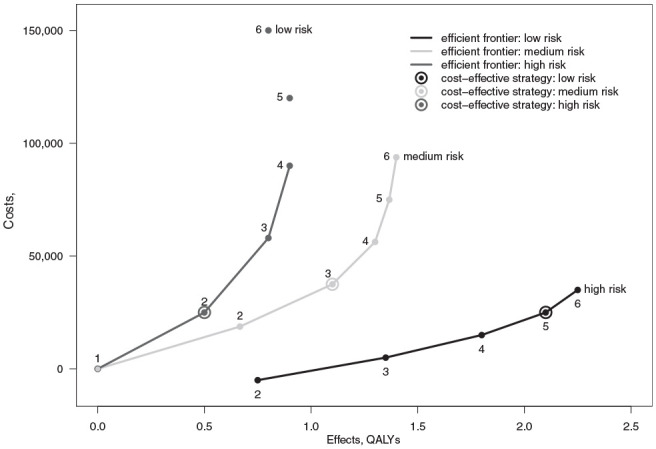
Table 1 shows the assumed costs and effects for the 3 strata separately and when aggregated together. The table shows the ACERs and ICERs in each case. The most effective strategy with an ICER not exceeding a threshold of €50,000/QALY is denoted as optimal in the final column in each case. The optimum according to the aggregated results under approach 1 is strategy 3. According to the disaggregated results under approach 2, the optimal strategies for the low-, medium-, and high-risk strata are 2, 3, and 5, respectively.

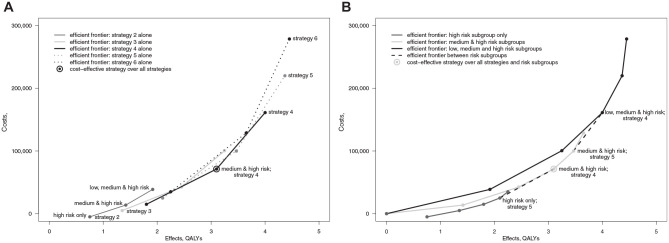
Figure 1 shows the efficient frontier for all strata aggregated together under approach 1. The strategies are numbered on the frontier. Strategy 1 represents no screening and lies at the origin. The optimal strategy is circled. Figure 2 shows the 3 efficient frontiers and optimal strategies when the analysis is stratified according to approach 2. The efficient frontier for the low-risk group does not extend to the 2 most costly strategies, as these are dominated. Similarly, the efficient frontier for the high-risk group does not start at no screening, as this strategy is dominated. The CERs along the efficient frontiers in Figures 1 and 2 correspond to the standard definition of the ICER under the assumption that the strategies compared represent mutually exclusive alternatives.

Figure 1.

Costs and effects for combined strata under approach 1.

Figure 2.

Costs and effects for separate strata under approach 2.

Comparing the policy recommendations from the aggregated and stratified analyses, we see that approach 1 recommends a higher than optimal screening intensity for the low-risk stratum. This will result in a cost-ineffective provision of an intervention with an ICER of €320,000/QALY when the stratum is assessed separately. For the medium-risk stratum, the optimal policy from the aggregated analysis happens to be the same as from the disaggregated analysis, so there is no inefficiency in provision for this group. For the high-risk stratum, the aggregate analysis results in an underintensive policy that provides only approximately 65% of the health gain of the optimal strategy.

Table 2 includes the costs, effects, and CERs using approaches 3 to 5. The inefficient strategies under approach 5 have been omitted for brevity. Note the CERs under approach 3 of expanding eligibility over a single strategy correspond with the ACERs of strategy 3 for each stratum shown in Table 1. For example, the CERs of the optimal strategy under approach 3 in Table 2 is formed by a comparison of strategy 3 provided to the high- and medium-risk strata versus strategy 3 for the high-risk stratum alone. This corresponds to the ACER of strategy 3 in the medium-risk group of €34,091/QALY. This is simply because the incremental change in this case is to extend screening to the medium-risk strata, and no other screening intensities are considered. These CERs under approach 3 could also be interpreted as ICERs under the assumptions that there is only 1 possible screening strategy available (strategy 3) and the only means of stratification is to vary the eligibility threshold.

Table 2.

Costs, Effects, CERs, and Optimal Policy Choices under Approaches 3 to 5

Analysis Approach	Risk Strata	Strategy	Effects, QALYs	Costs, €	ACER, €/QALY	CER, €/QALY	Policy Choice
	High only	3	1.35	5000	3704	3704
3	High and medium	3	2.45	42,500	17,347	34,091	Optimal
	High, medium, and low	3	3.25	100,500	30,923	72,500
	High only	2	0.75	–5000	—	—
	High and medium	2	1.42	13,750	9706
	High, medium, and low	2	1.92	38,750	20,217
	High only	3	1.35	5000	3704	16,667
	High and medium	3	2.45	42,500	17,347
	High, medium, and low	3	3.25	100,500	30,923
	High only	4	1.80	15,000	8,333	22,222
4	High and medium	4	3.10	71,250	22,984	46,250	Optimal
	High, medium, and low	4	4.00	161,250	40,313	114,844
	High only	5	2.10	25,000	11,905	33,333
	High and medium	5	3.47	100,000	28,846	78,409
	High, medium, and low	5	4.37	220,000	50,382	160,227
	High only	6	2.25	35,000	15,556
	High and medium	6	3.65	128,750	35,274
	High, medium, and low	6	4.45	278,750	62,640	705,000
	High only	2	0.75	–5000	—	—
	High only	3	1.35	5000	3704	16,667
	High only	4	1.80	15,000	8333	22,222
	High and medium	4, 2	2.47	33,750	13,682	28,125
	High and medium	5, 2	2.77	43,750	15,813	33,333
	High and medium	5, 3	3.20	62,500	19,531	43,269
5	High, medium, and low	5, 3, 2	3.70	87,500	23,649	50,000	Optimal
	High, medium, and low	6, 3, 2	3.85	97,500	25,325	66,667
	High, medium, and low	6, 4, 2	4.05	116,250	28,704	93,750
	High, medium, and low	6, 4, 3	4.35	149,250	34,310	110,000
	High, medium, and low	6, 5, 3	4.42	168,000	38,038	281,250
	High, medium, and low	6, 5, 4	4.52	200,000	44,280	320,000
	High, medium, and low	6, 6, 4	4.55	218,750	48,077	562,501

Figure 3 illustrates approach 3, with the efficient frontier under approach 1 included for reference. It shows costs and effects of strategy 3 as the indication progressively broadens from the high-risk stratum to include lower-risk strata. The upper end of this frontier converges with that from approach 1. Lower down the frontier, we see that efficiency can be gained relative to approach 1 as the efficient frontier under approach 3 lies to the southeast of that from the aggregated analysis. The optimal strategy under approach 3 is to provide strategy 3 to the high- and medium-risk strata and to withhold screening from the low-risk stratum.

Figure 3.

Costs and effects for strategy 3 under approach 3.

Approach 4 considering all available screening strategies while cumulatively expanding screening eligibility under the constraint of applying a common strategy for all recipients can be represented in 2 ways. One is to consider it as approach 3 repeated across all the screening strategies. This is as represented in Table 2 and Figure 4A. The figure shows a series of overlapping efficient frontiers for each strategy as the eligibility threshold is relaxed. Lines connecting no screening to each strategy for the high-risk strata only have been omitted for clarity. Alternatively, and probably more transparently, approach 4 can be considered as an extension of approach 1: assessing all strategies together as the eligible strata are cumulatively expanded from high to low risk, as represented in Figure 4B. The black line represents the efficient strategies for all risk strata combined across the available screening strategies assuming a common strategy is applied to all strata. This corresponds to the frontier from approach 1 shown in Figure 1. The dark gray color represents the efficient strategies for the high-risk strata alone. This corresponds to the frontier for the high-risk strata from approach 2 shown in Figure 2. The light gray line represents the efficient strategies for the high and medium strata combined assuming a common strategy is applied to both strata. Under approach 4, the optimal policy for the given threshold is strategy 4 for medium- and high-risk strata, which is circled in Figure 4A and B.

Figure 4.

(A) Costs and effects for all strategies under approach 4. (B) Costs and effects for all strategies under approach 4.

The points in Figure 4A and B are all the same. The efficient frontier over all strategies is omitted from Figure 4A for clarity but is shown in Figure 4B. Two notable portions of this frontier are plotted as the dashed lines. They connect the policies of, first, strategy 5 in the high-risk-only stratum to strategy 4 in the medium- and high-risk strata combined and, second, strategy 5 in the medium- and high-risk strata to strategy 4 in all strata. These segments of the frontier are notable because they are not comparisons between mutually exclusive alternatives as the extension of screening to one subgroup is accompanied by a reduction in screening intensity for other subgroups. Accordingly, the derived CERs depart from the conventional definition of the ICER. These ratios could be interpreted as ICERs under the assumption that the policy maker does have a choice of alternative strategies but is constrained to applying a common strategy to all recipients and can only achieve a degree of stratification by excluding certain risk strata.

Another notable feature of the efficient frontier under approach 4 is that the intensity of screening does not continuously increase along it. For example, at one point, the efficient policy is strategy 5 provided to the medium- and high-risk groups alone, yet the adjacent efficient policy with greater effects is strategy 4 provided the low-, medium-, and high-risk groups. This is despite strategy 4 being a lower-intensity strategy than 5. When the strata are assessed separately, the intensity of screening increases when moving from the southwest to northeast of the efficient frontier. Under approach 4, however, the screening intensity can drop as policies move to lower-intensity screening as eligibility expands to include lower-risk strata.

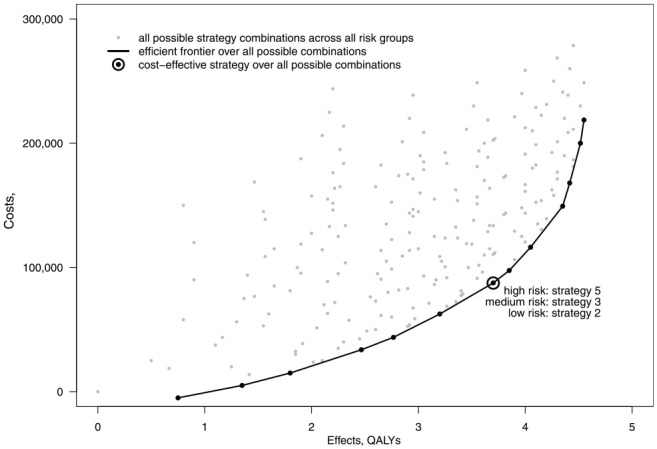
The results under approach 5 are shown in Figure 5. The large number of points represent all the many policy combinations possible when the screening intensity can vary between strata. Many policies lie far from the efficient frontier. These inefficient policies combine high-intensity screening for the low-risk stratum with low-intensity screening for the high-risk stratum. In practice, it will be computationally wasteful to simulate all such combinations. A more efficient way to find the overall efficient frontier across all risk subgroups may be to identify the efficient frontier within each strata independently then combine each segment from the separate efficient frontiers in rank order of the ICERs ranging from low to high. For instance, note how the CERs under approach 5 in Table 2 correspond to all the ICERs across all strata under approach 2 in Table 1. This is because the efficient frontier under approach 5 is a composite of the 3 efficient frontiers under approach 2. This finding, however, stems in part from some of the simplifying assumptions made within this example and will not apply generally.

Figure 5.

Costs and effects for all strategy combinations for all strata under approach 5.

Unlike Figure 4A and B, the efficient frontier in Figure 5 is solely composed of mutually exclusive strategies. Consequently, the CERs accord with the conventional definition of the ICER.

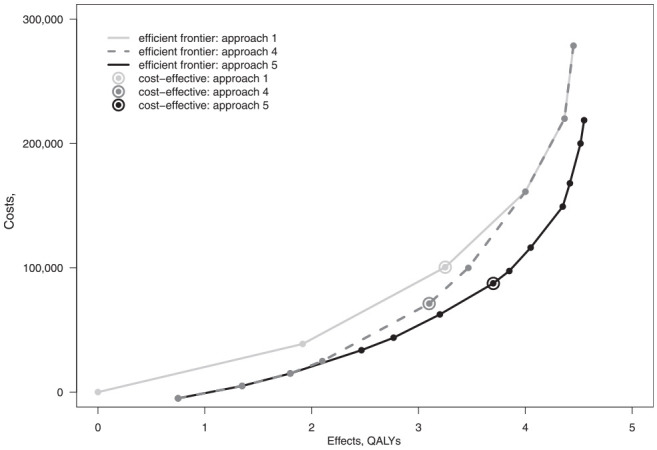
Figure 6 compares the efficient frontiers from approaches 1, 4, and 5. Approach 1 produces the least efficient policy set, whereas approach 5 yields the most efficient. The difference between approaches 1 and 5 simply reflects the benefit moving from no stratification and complete stratification. Note that, in this example, there is a gain in efficiency at both low and high screening intensities. The dotted gray line in Figure 6 represents the efficient frontier from approach 4. At lower intensities of screening, this frontier lies close to the overall optimal frontier, as much of the efficiency can be gained simply by excluding the lower risk strata from screening. At greater screening intensities, this frontier then converges with that of approach 1, and the efficiencies gained by excluding lower-risk strata diminish. This shows that simply by limiting screening eligibility to higher-risk strata and adopting a common strategy for all those screened will realize much of the gains of stratification at lower screening intensities in this example, but at higher screening intensities, this simple approach fails to capture the benefits of stratification.

Figure 6.

Comparison of efficient frontiers from approaches 1, 4, and 5.

Discussion

Examples from the Literature

Before discussing the findings presented here, I note examples from the literature that correspond to the alternative approaches identified. Analyses corresponding to approach 2 are relatively common. The benefits of stratification have been shown in analyses considering multiple screening intensities in women who have and have not been vaccinated against the human papillomavirus.^24,25 Similarly, an analysis of multiple colorectal screening strategies disaggregated by sex provides another such example. ⁹

Pashayan et al. ²⁶ provided an example of an applied CEA using the approach 3 of expanding eligibility over a single strategy. This example examined the current UK breast cancer screening policy of triennial mammography between ages 50 and 69 y in a risk stratified approach based on polygenic risk scores. It considered the efficiency gained by excluding low-risk women from screening. Similarly, McLeod et al. ²⁷ presented an analysis of a single colorectal cancer screening strategy when stratified by ethnicity and other factors in New Zealand.

There are a number of applied examples that resemble approach 4, mostly from the recent lung cancer screening literature.^14–17 Toumazsis et al. ¹⁷ demonstrates an efficient frontier that is partially composed of a comparison between policies that are not mutually exclusive comparisons of alternative intensities but rather different screening intensities between different eligible risk groups. ¹⁷

Two examples of applied studies that have considered a wide variety of screening strategies are Vilaprinyo et al.’s analysis of breast screening strategies for 4 risk strata combined in 1 analysis and Cenin et al.’s analysis of alternative colorectal cancer screening intensity based on polygenic and familial risk.^11,18 Although not documented within the studies, it appears both have identified the overall optimal frontier by determining the within-strata frontiers and then combined them. These 2 examples could be interpreted as resembling approach 5.

Relative Advantages of the Alternative Approaches

We can consider the advantages and disadvantages of the alternative approaches illustrated in this analysis. An obvious conclusion is that it matters if strata-specific policies are feasible. If they are, then more efficient policies are possible. If strata-specific policies are not feasible, then decision makers are restricted to a more limited form of risk tailoring by varying the eligibility threshold to exclude lower-risk individuals from screening as demonstrated under approaches 3 and 4. An advantage of approaches 3 and 4 is that at least some benefit of targeting can be achieved by excluding those at too low a disease risk to benefit. This already happens implicitly with analyses of average-risk groups when we consider the age to start screening. When we expand our analyses to consider identifiers of risk other than age, such as smoking history in the lung cancer screening context, then we must further consider the implications of varying eligibility thresholds.

Approach 4 offers greater health gain than approach 3 in our example, and it is expected that this result will apply generally as the former offers the choice over alternative strategies rather than limiting policy to one strategy alone. While we find examples of approach 3 in the literature, it seems unlikely that decision makers will actually only have the choice of varying screening eligibility over one screening strategy alone, and we will not consider it further.

Although approach 4 can improve efficiency by varying the eligibility threshold to access a common screening intensity, it is a rather blunt tool, as it permits risk tailoring only by exclusion. If we wish to intensify screening for the benefit of higher-risk groups, the constraint of deploying a common policy means this may have to be traded off against reduced coverage for those of lower risk. Consequently, constraint of a common screening policy for all eligible screenees under approach 4 has the disadvantage that it leads to vertical equity concerns, whereby services are not adjusted to account for differences between groups. For example, a common screening policy for all eligible screenees could result in the exclusion of low-risk groups that could benefit from low-intensity screening, and those of high risk might not be offered screening of insufficient intensity.

The limitations of simple stratification by exclusion under approach 4 seem particularly relevant to the growing CEA literature on low-dose computed-tomography (LDCT) lung screening in which risk is related to smoking history. Several recent analyses apply basic risk tailoring by exclusion akin to approach 4 in that they employ various risk threshold for screening eligibility and consider alternative screening strategies, but all eligible screenees receive a common screening strategy.^14–17 As such, I perceive a danger that these studies could overlook the benefits of low-intensity screening for lower-risk candidates. For example, Tomonaga et al. ¹⁶ considers the cost per life year gained (LYG) of annual, biennial, and triennial LDCT strategies and assume an indicative €50,000/LYG threshold. That analysis finds annual screening for those with a 40-y pack-year history and a maximum smoking cessation date of 10 y ago would be optimally cost-effective. Accordingly, the analysis indicates it is not cost-effective to offer screening to individuals with less than a 40 pack-year history. What that analysis does not assess separately is the cost-effectiveness of lower-intensity strategies of biennial and triennial screening for those with a less than 40 pack-year history. Accordingly, it may overlook strategies that are potentially cost-effective for larger populations with more moderate smoking histories.

Analyses applying simple stratification by exclusion may do so deliberately on the understanding that the decision maker is constrained from applying more than 1 strategy to eligible strata. Despite this, I have not read any assumption of such constraints or the possible consequences in the lung screening literature. Accordingly, it seems possible that the implications of a constraint of a common policy for all are not yet widely appreciated.

The analysis presented here shows that equivalent results can be achieved by applying strata-specific analyses under approach 2 or a combined analysis under approach 5. Given the equivalence of the results in this example, it is important to consider the generality of this equivalence and the relative benefits of the 2 approaches. Approach 5 has disadvantages relating to the need to simulate all strategies and related issues of transparency. Finding all optimal policy choices in a combined assessment under approach 5 requires the analyst to have included all relevant combinations at the outset when specifying the analysis. If the analyst exhaustively simulates all possible combinations, they will find all efficient policies but will likely incur substantial simulation runtimes. If they choose to reduce the simulation burden by simulating only a selection of combinations, they risk omitting efficient strategies. Unless analysts publish complete results for all combinations they considered, it can be difficult for readers to determine what strategies were considered and if any relevant combinations were omitted. For example, recent LDCT lung screening studies that considered a large number of combinations of strategies and eligibility thresholds report only costs and effects for efficient strategies.^15–17 The lack of reported results for all strategies obscures whether any relevant combinations have been omitted.

Compared with approach 5, approach 2 seems easier, both conceptually and practically. Conducting separate analyses for each strata enhances transparency and reduces the number of unique strategies required to simulate and report. Despite this, there are 2 important counter arguments in favor of approach 5. One relates to fixed program costs. A recent simulation of lung screening in the United Kingdom appears to contain substantial economies of scale, ¹⁴ likely owing to large fixed program costs. Indeed, the costs of the initial risk stratification itself using risk prediction tools is one such source of fixed costs that is especially relevant to stratified screening. A combined analysis may be necessary in such cases, as it is unclear how such fixed costs should be apportioned over different strata in an analysis that considers strata separately. The second reason to use approach 5 is that the risk groups may not be independent. Some risk prediction scores may be a function of age or some other progressive risk factor ²⁸ ; therefore, an individual may transition between strata over time. This potential for individuals to migrate between strata, combined with the fact that the cost-effectiveness of screening is in part contingent on prior screening history, indicates that a combined analysis across all strata might be necessary to capture such interstrata dependencies. The equivalence of approaches 2 and 5 shown here is on the basis of a simple example with no fixed costs and independent strata and therefore is not a general result.

Implications for Decision Makers

The findings presented here are intuitive and largely unsurprising. Nevertheless, I believe they are still relevant as the prevalence of apparently suboptimal forms of stratification in the literature indicates analysts may be giving the issue of strategy choice under stratification insufficient consideration and could benefit from clearer methods guidance.

The hypothetical model presented here assumed just 3 risk strata and 6 possible screening intensities for the sake of simplicity. In principle, greater efficiency can be achieved by greater stratification and the provision of more risk-tailored strategies. In practice, this requires more data to support both the stratification and the estimation of outcomes in each group. Data limitations will therefore limit the scope for stratification. Thus, policy makers need to be aware of the need to enhance evidence regarding specific population subgroups to realize the benefits of tailored screening. Furthermore, implementing many different strategies will bring obvious challenges because of the impact of additional complexity on screening adherence and administration costs. What is the optimal tradeoff between program simplicity and tailored efficiency does not have an obvious answer and will depend on the judgment of the decision makers. These practical considerations are separate concerns from the theoretical issues addressed in this analysis. Indeed, it remains important that the degree of risk tailoring permitted by the data and practical program implementation constraints are informed by a sound interpretation of the CEA evidence.

The analysis shows that some of the CERs on the efficient frontier under approach 4 differ from the conventional interpretation of the ICER. How these CERs should be interpreted depends on what we consider truly mutually exclusive. If it is assumed that strata-specific policies are not possible in practice, then it seems reasonable to consider such constrained policy choices as being those between mutually exclusive options and the resulting CERs as ICERs.

This analysis focused on finding the optimal screening strategies for different risk thresholds. The hypothetical example presented in this analysis and most applied CEAs take the risk strata as given and attempt to find optimal policies for them. In principle, screening could be better optimized by reversing this approach, that is, to determine the risk thresholds for stratification with respect to available screening intensities. Indeed, an excellent applied example of this approach has already been published by Wilson et al. ²⁹ in their appraisal of a stratified melanoma surveillance program. Their work highlights the importance of not simply accepting the given risk stratification but rather considering the potential benefit of stratifying screenees in an informed way. Work applying the method adopted by Wilson et al. promises to be a useful direction for further research.

This study presents a highly abstracted and stylized example for convenience of exposition. A limitation of this approach is that it is not as representative of actual decision modeling had it examined an applied example. Another limitation of this study is that it has not examined intermediate degrees of stratification between basic stratification by exclusion and complete stratification. It is hoped, however, that the simple analysis presented here is sufficient to convey the relevant principles.

Recommendations

The primary recommendation from this study is to be explicit about constraints on applying strata-specific strategies. If a common strategy is required for all screenees, then analysts should carefully consider the implications of over- and underscreening those of low and high risk, respectively. If strata-specific strategies are feasible, then analysts may wish to conduct strata-specific analyses for the sake of simplicity and transparency. If there are good reasons to adopt a single analysis for all strata, then analysts are urged to check whether they have simulated all relevant strategy combinations across the strata assessed. While detailed stratification for multiple subgroups might be impractical, analysts may wish to consider the potential gains of partial stratification by splitting the screened population into a limited number of risk strata. Finally, consider the possibility of tailoring the risk thresholds to the available screening intensities.

Conclusions

Risk stratification is already having a considerable impact on the cancer screening CEA literature, and this is likely to continue. In principle, the optimization of screening to disease risk is not conceptually complicated. In practice, modeling multiple strategies for multiple strata within a single simulation can present a range of analytical problems. Modelers considering all strata within a single analysis need to carefully consider how to combine alternative screening strategies with eligibility thresholds. Failing to do so can result in both inefficiency and inequity in the provision of cancer prevention. The optimal degree of stratification and risk tailoring of screening will remain context specific and will require dialogue between decision makers and modelers. The analysis presented here intends to elucidate the issues involved and support a more structured and explicitly articulated approach toward stratification. In turn, it is hoped this will lead to improved population health outcomes.