Abstract
Species ranges are shifting in response to climate change, but most predictions disregard food–web interactions and, in particular, if and how such interactions change through time. Predator–prey interactions could speed up species range shifts through enemy release or create lags through biotic resistance. Here, we developed a spatially explicit model of interacting species, each with a thermal niche and embedded in a size-structured food–web across a temperature gradient that was then exposed to warming. We also created counterfactual single species models to contrast and highlight the effect of trophic interactions on range shifts. We found that dynamic trophic interactions hampered species range shifts across 450 simulated food–webs with up to 200 species each over 200 years of warming. All species experiencing dynamic trophic interactions shifted more slowly than single-species models would predict. In addition, the trailing edges of larger bodied species ranges shifted especially slowly because of ecological subsidies from small shifting prey. Trophic interactions also reduced the numbers of locally novel species, novel interactions and productive species, thus maintaining historical community compositions for longer. Current forecasts ignoring dynamic food–web interactions and allometry may overestimate species' tendency to track climate change.
Keywords: range shift, marine food–web, climate change, metabolic theory, body size, extinction debt
1. Introduction
Species ranges are shifting in response to climate change and variability [1–3]. These spatial shifts in species ranges are having an impact on ecosystem functions [4,5] and the provision of ecosystem services with subsequent impacts on local economies [6]. Most efforts to project how and why species ranges are shifting have focused on the direct impacts of climate change on individual species [7–9]. These ‘one at a time’ species projections reveal substantial potential for reorganized and novel community compositions [10,11]. However, food–web interactions among species can also affect the rate and direction of species range shifts [12–14]. A key lesson so far is that competition can keep species from shifting with warming [12], a prediction recently corroborated experimentally [15]. However, much less is known about how the combination of trophic interactions and warming simultaneously affect geographical shifts in species ranges, despite their anticipated importance [16]. To date, most spatially explicit studies of species range shifts have not accounted for changes in trophic interations in a warming world [17–19].
Several food–web characteristics are likely to be important for species range shift under warming. Empirical evidence suggests that many food–webs are strongly organized by body size as well as by temperature, particularly those in marine environments [20,21]. Body size and temperature both mediate organismal metabolic rates and trophic interactions [22]. In these communities, mortality imposed by predators [23] and competition for prey may prevent novel species from invading, processes that fall under the term biotic resistance [24–26]. Alternatively, small prey that escape traditional predators—either because predators are specialists or are the first to decline [27]—may accelerate prey leading edge shifts more than larger predators, which has been termed enemy or predator release [28]. Large-scale comparative studies show ambiguous patterns regarding size or trophic differences in species range shifts, potentially because hypotheses have been vague and challenging to test [2,29]. Developing clear expectations for the influence of food–web interactions on species range shifts will help with the specification of more precise and testable hypotheses.
Here, we have developed a dynamic and spatially explicit food–web model that is based on allometric and metabolic relationships. We use this model to develop new theory and insight into how trophic interactions, and their re-organization through time and space, affect species range shifts under warming. Multi-species food–webs (not just food chains [30]) of multiple trophic levels can emerge in this model from dispersal and the differences among species in body sizes and thermal preferences (see [10]). To complement this model, we also created a set of single-species counterfactual models to clarify expectations in the absence of dynamic trophic interactions. Our results reveal that trophic interactions slow down the rate of species range shifts, suggesting that most studies of future range shifts overestimate how well species will track changing climates.
2. Methods
To explore the influence of species interactions on species range shifts, we developed a discrete-time and discrete-space food–web model (equation (2.1)). This food–web model was initialized with a basal resource with body size 10−2 g and N = 200 heterotroph species distributed across 21 spatial patches x. Temperature across patches at time t = 0 spanned 4 to 24°C (1°C per patch) to roughly represent a transect from pole to equator (figure 1a). Each patch was a square with sides measuring 471 km. Each species was assigned a body size si (log10-uniformly random between 100 and 106 g) and optimal temperature for searching prey Ti,opt (uniformly random between 0 and 34°C). Heterotrophs from species i in patch x of biomass Bix consumed the basal resource (which is described in more detail below) and other species with efficiency λ and at rate fijx that depended on relative predator (i) – prey (j) body sizes [31], while also experiencing a body size- and temperature-dependent metabolic cost Dix [32] and while dispersing to each adjacent patch at a rate κ d−1 (or fraction of biomass dispersed per day). The cross-patch dispersal rate κ was related to the diffusion coefficient m (table 1: T3), which was varied at the same levels across all species for the simulation experiments (table 2). Empirical observation support no or even negative relationships between body size and dispersal or correlates of dispersal [45,46], including no correlation between offspring size and pelagic larval duration [47]. Even though swim speed increases with size [35], it remains unclear how linear speed translates into dispersal because species have different tendencies to return home. Nevertheless, we also relaxed the assumption of size-independent dispersal in a sensitivity test (see eqn A2 in the electronic supplementary material, appendix A). For the main results, we used κ values of 0, 4.5 × 10−12, 4.5 × 10−9, 4.5 × 10−6, 4.5 × 10−5 and 4.5 × 10−4 d−1. Dispersal rates above these generated unrealistic results. For simplicity, we labelled dispersal rates in figures only by magnitudes (omitting the 4.5 multiplier). κ was set to zero at both ends of the patch array.
| 2.1 |
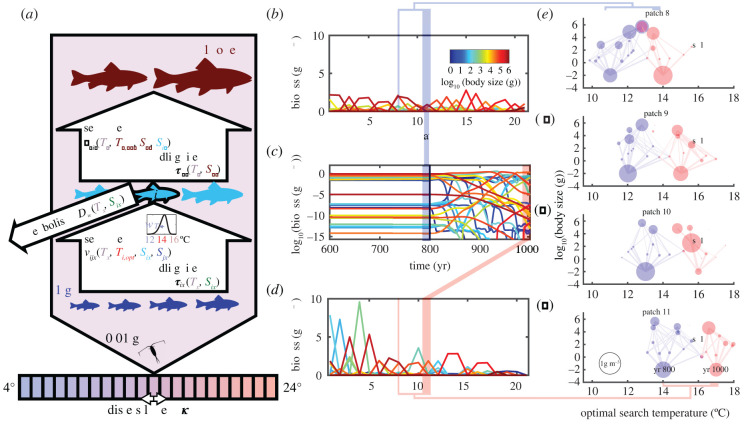
Figure 1.
Spatial food–web model. (a) The heterotrophic consumer i feeds on other heterotrophs of smaller sizes and, for some consumers, on the basal resource (0.01 g). The rate of biomass flow from one species (j) to another (i) is determined by search rate (vijx) and handling time (τix), which are functions of local temperature Tx, species-specific optimal search temperature Ti,opt (see example curve), and predator and prey body sizes (si, sj). Metabolic cost (Dix) is dependent on temperature and body size. The food–web is spatially coupled across 21 patches with an initial temperature gradient of 4 to 24°C. (b) A snapshot of individual species biomass distributions across patches before warming (dispersal rate κ = 4.5 × 10−9 d−1). (c) Time series of species biomass at patch 11, which is at 14°C until year 800 (vertical black line) and warms to 17°C by year 1000. (d) A snapshot of individual species biomass distributions across patches after warming. (e–h) Food–webs in four patches (patches 8 to 11) from colder to warmer temperatures along the gradient. Within-patch species are plotted by optimal search temperature (x) and body size (y) traits, with circle area representing biomass (see legend in (h)) and lines representing consumptions above 10−5 gm−3 d−1 (line width scaled to log of consumption). Species before warming are shown in blue, and species after warming are shown in red. The blue species in (h) are expected to shift and become the red species in (e) if they keep up with the thermal shift. Overlapping blue and red species with identical centres within patch are those that remain in the original patch after warming. One species (sp.1) is labelled for reference across patches and temperature change.
Table 1.
Food–web model equations. (Bold symbols are parameters that we vary in this study. Table 2 for additional definitions. References for each equation are shown in the first column. Indices i, j and k refer to species identity, and x refers to patch location. The electronic supplementary material, appendix A provides further explanations to the model specifications and choices.)
| definition | equation | units |
|---|---|---|
| (T1) change in basal resource [33] | ||
| (T2) functional response [34] | ||
| (T3) dispersal rate to adjacent patches | ||
| (T4) active metabolic cost [32,35] | ||
| (T5) conversion from watts to d−1 | ||
| (T6) search rate of species i for species j [12] | ||
| (T7) handling time (species i) [36] | ||
| (T8) metabolic cost factor from swimming [35] | ||
| (T9) maximum search rate at reference prey density [35] | ||
| (T10) feeding kernel [37] | ||
| (T11) maximum production rate [36] | ||
| (T12) swim speed [35] | ||
| (T13) body length [38] | ||
| (T14) log10 mean predator–prey mass ratio [31] | ||
| (T15) skew normal function [12] |
Table 2.
Parameter definitions. (Bold symbols are parameters that we vary in our analyses. Values in parentheses are the alternative parameter values, with † to indicate the value used in the electronic supplementary material, figure S4 (other alternative values are shown in the electronic supplementary material, figures S5–S7). See in the electronic supplementary material, appendix A.)
| symbol | definition | value |
|---|---|---|
| A | patch area (m2) | 471, 4292 |
| αD | body size to metabolic rate power-law constant | 18.47 [32] |
| αl | body length-mass power-law constant | 0.012 [38] |
| αP | body size to biomass production power-law constant | 10.85 [36] |
| αR | body size to predator–prey mass ratio power-law constant | 2.66 (2.08†, 2.37, 2.95, 3.24) [31] |
| βD | body size to metabolic rate scaling exponent | 0.71 [32] |
| βγ | body size-swim speed scaling exponent | 0.13 [35] |
| βl | body length-mass scaling exponent | 3 [38] |
| βP | body size to biomass production scaling exponent | 0.761 [36] |
| βR | body size-predator–prey mass ratio scaling exponent | 0.24 [31] |
| B0max | maximum basal biomass (g m−3) | 5 [39] |
| Br | reference prey biomass (g m−3) | 1 |
| Cd → s | conversion factor from days to seconds (s d−1) | 86 400 |
| Ea | activation energy (eV) | 0.63 (0.57, 0.6, 0.66, 0.69†) [32] |
| Ec | energetic content of organisms (Jg−1) | 7000 [40] |
| F | basal chemostatic dilution rate (d−1) | 0.0075 [41] |
| Fh | fraction of time hunting | 0.26 (0.13†) [42] |
| k | Boltzmann's constant (eV°C−1) | 8.62 × 10−5 |
| λ | consumption efficiency | 0.4 (0.2†) [43] |
| m | diffusion coefficient (m2 d−1) | 0, 1, 103, 106, 107, 108 |
| N | number of heterotroph species | 200 |
| σ | width of feeding kernel | 0.569 [37] |
| PN | per cent of prey inedible | 0 (10, 20†, 30, 40, 50) |
| Res | coefficient for swimming cost (day/m) | 3.47 × 10−5 [35] |
| s | body mass (g) | 0.01, 101–106 |
| Tx | local temperature (°C) | 4–24 (+3) |
| Ti,opt | optimal search temperature (°C) for species i | 0–34 |
| Toset | optimal search temperature offset to align the skew normal mode with Ti,opt (°C) | 0.435 |
| wT | search performance standard deviation (°C) | 0.884 [44] |
| θ | search rate scaling factor so that skew normal function is 1 at Ti,opt | 0.622 |
| thermal performance skew | −2.7 [12] |
The basal resource grew chemostatically without temperature dependence (table 1: T1) and an initial biomass equal to the maximum biomass of 5 gm−3, which is around the upper bound of global mesozooplankton estimates (after wet weight conversion) [39]. It may be reasonable to assume that basal growth and maximum biomass are relatively temperature independent compared to individual heterotrophs (fishes), since organisms of around 10−2 g in size have similar biomass across latitude [39]. We do not address complexity at or below the basal level; instead we aim for a stable representation of this food–web component. Heterotroph species consumed according to a Type III functional response (fijx) (table 1: T2) with search rate vijx and handling time τix [34] (table 1: T6 and T7). We chose a Type III because of its stabilizing properties that generate realistic food–web complexity and species richness [48]. The search rate vijx of predator i on prey j was a skew normal function of temperature Tx (table 1: T15) such that consumers could not feed if they were far from their optimal temperature. Production of a species was defined as consumption minus predation across all patches, which equalled the rate of biomass loss to predation (see eqn A3 in the electronic supplementary material, appendix A). Table 1 contains the detailed equations and table 2 provides definitions, values and references for parameters corresponding to a typical ectotherm marine food–web. A detailed explanation of the equations in table 1 is provided in the electronic supplementary material, appendix A. In summary, metabolic cost rises with size and temperature, handling time decreases with predator size and temperature, and search rate decreases with predator size and is maximized at preferred prey size and temperature (figure 1a).
The model was run forward at daily timesteps for 1600 to 2400 years (varied randomly to avoid phase effects of any potential cycles) with stationary temperatures. This ‘spin-up’ phase was used so that population dynamics settled into a quasi-equilibrium, similarly to how Earth System Models are initialized [49]. The daily timesteps are comparable to other large marine ecosystem models [50], which not only accounts for the short generation time of smaller organisms, but also describes feeding and metabolism dynamics. After this spin-up period, which was observed to maintain stable biomass trajectories across a reasonably high species diversity of three trophic levels, gradual warming was imposed as a 3°C warming over 200 years at all patches (figure 1b,c). The warming scenario was in line with current ocean warming projections [51]. We replicated these simulations 40 times with independent log-uniformly random initial biomass for each species and patch between 2.2 × 10−15 and 2.2 × 10−10 gm−3.
During the simulations, we recorded shifts in the centroid of each species' range (a species’ average location weighted by biomass), leading range edge (2.5th quantile of biomass starting from the coldest patch), trailing range edge (97.5th quantile biomass) and range size (patches from leading to trailing edge). Given the spatial gradient in temperatures, isotherms shifted three patches towards the cold region, so a 100% range shift corresponded to a three-patch shift. We also recorded the percentage of the local species and species pairs that were novel or that were extirpated after warming, with the presence meaning a local biomass above the floating-point error (2.2 × 10−16 gm−3 in Matlab). The percentage of novel species pairs was 100 times the global number of species pairs that were found together in any patch after but not before warming, divided by the sum of coexisting pairs after warming. The percentage of extirpated species pairs was 100 times the global number of species pairs that were found together in any patch before warming but lost after warming, divided by the sum of coexisting pairs before warming. For size-specific analyses, we divided the results into small species (102 to 103 g body-weight) and large species (105 to 106 g body-weight). Species with leading edges in the coldest three patches before warming were omitted from the analyses to avoid edge effects, since these species would run out of room to track a 3°C warming.
For comparison, we fit counterfactual single-species models to species biomass outcomes during the no-warming spin-up period in the food–web models, except that dynamic trophic interactions were removed (equation (2.2)). These models capture the single-species equivalent of dynamics in food–webs, which can then be used to project what is expected if only species characteristics and not food–web interactions respond dynamically to warming. Each species experienced metabolic costs and relative intrinsic growth just as specified in the food–web models. However, temporally constant maximum (intrinsic) growth rates (ri) and self-competition (ai) rates were specified instead of dynamic consumption and predation terms, consistent with a single-species model:
| 2.2 |
Biomass was labelled with tilde to distinguish the counterfactual projections from the food–web outcomes. We included a skew normal function of temperature Tx (table 1: T15) so that realized growth rate declined to zero if species were far from their optimal temperature. To estimate the two parameters ri and ai that best matched the species in the food–web models, we needed to match long-run production in addition to biomass (two equations to solve for two parameters). We defined production in the model as growth minus metabolic cost and a portion (1/c) of intraspecific competition. We partitioned intraspecific competition this way because, by definition, competition can come from either suppressed birth and growth or increased mortality, the latter being interpreted here as production through a loss effect attributed to conspecifics.
| 2.3 |
In this formulation, c controls whether competition results in production owing to increased mortality (c = ∞), no production owing to suppressed birth (c = 1, which also implies no net production in equation (3.3)), or somewhere in between. For each species i from the food–web simulations, we recorded the average biomass and average production (consumption minus metabolism) from the transient no-warming period of the food–web simulation. We then fit the model's equilibrium biomass (from solving equation (2.2)) and production (equation (3.3)) against these modelled data after fixing c for all species. We repeated this across a range of c to find the value that produced the closest match between the aggregate community biomass and production and the food–web's total biomass and production (minimum sum of squares divided by each variable's magnitude) (electronic supplementary material, table S1). This phenomenological single-species model resembles what a scientist might do with historical data if trying to project single-species shifts during the warming period. This model can also be understood as a counterfactual to the food–web model, one with similar species biomasses and productions but with dynamic trophic interactions taken out (electronic supplementary material, figure S2). The sensitivity of the single-species projections to parameterization was tested using two alternative values of c that underestimated and overestimated production (electronic supplementary material, table S1), which should, respectively, underestimate and overestimate intrinsic growth rate, a key parameter that could influence shifting rates.
We explored the sensitivity of our food–web results by also using alternative values for the reference predator–prey mass ratio αR, the activation energy Ea, the fraction of time hunting Fh, the consumption efficiency λ (table 2) and the size dependence of dispersal rate κ. These alternative values included, respectively, the lower end of αR [31], the Ea corresponding to all organisms rather than ectotherms only [32], half of the original Fh [42], half of the original λ [43] and a κ that increased with size based on swim speed [35] (electronic supplementary material, appendix A). We also explored randomly defining PN= 10 to 50% of all prey as inedible independently for each predator, which increased specialization and the potential for enemy release of prey (table 2). Higher specialization led to food–web collapse. Finally, we conducted fine-resolution sensitivity analyses on αR, Ea and κ (table 2). For each alternative parameter value, 10 replicates were run at the mean dispersal rate of 10−12 d−1. In summary, 21 × 10 food–webs were simulated for sensitivity tests, bringing the total simulations including those in the main analysis to 450 food–webs.
3. Results
Under warming, the food–web model revealed aggregate biomass shifting towards the colder regions, as expected (figure 1b,d). Snapshots of food–web structure (mapped by the two traits of body size and optimal search temperature) over space and time revealed that some part of the original local communities (blue in figure 1h) shifted together (shown as red in figure 1e), while other species shifted less or even stayed in their original patches to rewire incoming communities (overlapping blue and red species in figure 1e). There is also evidence of enemy release, as one species moved from low biomass in its original patch (sp. 1 in figure 1h) to high biomass (figure 1f,g). Even though larger predators of sp. 1 were present in its new thermally optimal patch (figure 1e), they were saturated by the availability of other prey that were at a more optimal size for foraging.
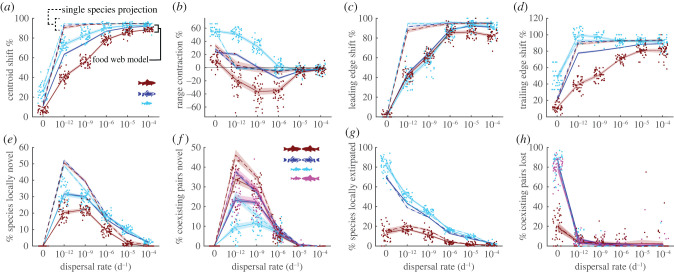
Range sizes before warming averaged from 1.4 to 5.2 patches as dispersal rate increased from 0 to 10−4 (with a larger increase for larger species; electronic supplementary material, figure S1), corresponding to distances of 1000 to 4000 km that are typical for marine species [52]. On average, species' centroids, leading edges and trailing edges tracked thermal shifts more closely at higher dispersal rates (figure 2a,c,d, solid blue curves). Species range sizes, on the other hand, on average contracted for slow dispersal rates and expanded for rapid dispersal rates (figure 2b, solid blue curve).
Figure 2.
Range shifts and assemblage changes. Solid lines indicate averages across 40 replicates from the food–web model after warming, while dashed lines indicate corresponding counterfactual single-species projections. Shades are 95% confidence bounds assuming normal error. Dots show individual simulations and are jittered on the x-axis to improve readability. Red indicates species of size 105 to 106 g, cyan indicates species of size 102 to 103 g, and blue indicates all sizes. For coexisting pairs, magenta indicates pairs that contain one small (102 to 103 g) and one large (105 to 106 g) species. (a) Centroid shift measured as the percentage of the distance that isotherms shifted. (b) Range contraction. (c) Leading edge range shift measured relative to isotherm shifts. (d) Trailing edge range shift measured relative to isotherm shifts. (e) Percentage of species locally novel, with 100% corresponding to all species after warming being absent in each patch initially. (f) Percentage of coexisting pairs novel, with 100% corresponding to all species pairs after warming being unpaired initially. (g) Percentage of species locally extirpated, with 100% corresponding to all species initially in each patch being absent after warming. (h) Percentage of coexisting pairs lost, with 100% corresponding to all initial species pairs being absent after warming.
Across body sizes, all species exhibited similar leading edge shifts (figure 2c solid curves), but centroids and trailing edges shifted much more for small (102 to 103 g body-weight) than large (105 to 106 g body-weight) sized species (figure 2a,d solid cyan versus red curves). These differences in trailing edge dynamics for large and small species meant that ranges among small species contracted at slow dispersal rates, while large species ranges expanded at all but zero dispersal rates.
In the food–web model, locally novel species and novel species pairs (pairs that coexist in any patch) were more common at intermediate dispersal rates (figure 2e,f solid blue curves). By contrast, the highest percentage of species experienced local extirpation and the highest percentage of historical species pairs were lost at low dispersal rates (figure 2g,h solid blue curves). Large species were more likely to begin coexisting with novel species than were small species (figure 2f solid cyan versus red curves), consistent with the lag in trailing edge range shifts among large species. Small species were more likely to be locally extirpated than were large species, also consistent with lags in large species’ trailing edges (figure 2g solid cyan versus red curves). Similarly, historical pairs of coexisting small species were more likely to be lost than pairs of large species at low dispersal rates (figure 2h solid cyan versus red curves).
The single-species counterfactual models suggested that, in the absence of dynamic predator–prey interactions, all species would closely match the thermal shift even at the lowest non-zero dispersal rate (figure 2a,c,d dashed curves). In addition, single-species models only predicted substantial range contractions for a zero dispersal rate (figure 2b dashed curves). Compared to the food–web model, single-species models over-predicted the distance that species shifted (figure 2e,g,h) and under-predicted changes in range size (figure 2f). Single-species models also over-predicted the percentage of locally novel species and of novel species pairs as compared to the full food–web dynamics (figure 2e,g). Finally, single-species models failed to resolve the large differences among body sizes in distance shifted, unlike for the food–web models in which larger species tended to shift their trailing edge less and expand range size more (figure 2). The lack of body size differences in range shifts appeared even though the single-species model assumed that intrinsic growth rate ri was a decreasing function of size across all simulations (equation (2.2)), consistent with metabolic theory that was also embedded in the food–web model.
Community aggregate statistics showed differences in overall stock, flow and diversity metrics between food–web and single-species projections under warming. Community biomass and production increased in the food–web model after warming at dispersal rates higher than 10−12 d−1 (electronic supplementary material, figure S3A and B). By contrast, the single-species model projected on average little to no changes to biomass and production after warming, along with large differences in production changes across replicates. However, these food–web changes were accompanied by a greater number of species that became unproductive (production < 0) after warming, whereas the single-species model showed no increase in unproductive species at all non-zero dispersal rates (electronic supplementary material, figure S3C). Since production is consumption minus metabolic cost, and all other terms (not counting migration since production here is computed globally) contributed negatively to net growth in equation (2.1), any existing unproductive species were on extinction trajectories—although they may have had non-extinction equilibria, especially if temperatures stabilized again during the protracted transient periods [53]. In any case, the modelled food–webs had a longer transient approach to equilibrium than single-species projections. Community composition was also impacted by food–webs, which showed a decline in mean body size not predicted by single-species projections (electronic supplementary material, figure S3D). In terms of biodiversity metrics, both food–web and single-species projections agreed only a few global extinctions would occur at non-zero dispersal rates (electronic supplementary material, figure S3E). Average alpha diversity, or local richness, showed an increase at intermediate dispersal rates and a decrease otherwise (electronic supplementary material, figure S3F).
Metrics of trophic level in conjunction with diversity suggest that the model generated qualitatively realistic food–webs. At all non-zero dispersal rates, local richness was much higher than mean and maximum trophic levels of 2.6 and 3 with 1 being the basal level, which remained similar before and after warming (electronic supplementary material, figure S3G and H). This result meant that multiple species shared similar trophic levels and formed food–webs rather than food chains. With no dispersal, simple food–webs of about five species spanning two heterotrophic levels still emerged initially, but after warming they approached food chains (two species). These results gave confidence that our model effectively captured known features of natural food–webs.
The single-species shift projections were insensitive to alternative values of the parameter c that controlled production (see the electronic supplementary material, table S1; results indistinguishible from figure 1). Sensitivity analyses that changed the portion of potential prey being inedible PN for each species (i.e. more specialists when PN> 0), the activation energy Ea, the reference predator–prey mass ratio αR, the fraction of time hunting Fh, the consumption efficiency λ (table 2) and size-dependent dispersal rate κ (electronic supplementary material, appendix A) affected the magnitude of shifts and assemblage changes, but they had little to no impact on the ordering of the changes by body size or food–web versus single-species models (electronic supplementary material, figures S4–S8). The notable exceptions were in leading edge shifts, for which low activation energy, low or high predator–prey mass ratios, and high levels of inedible prey reversed the trends from being slightly lower to slightly higher for smaller species relative to larger species (electronic supplementary material, figures S5C, S6C and S7C). In terms of magnitude of shifts, the results were most sensitive to activation energy, with values lower than expected for marine ecosystems creating species shifts that were quite similar to single-species projections (electronic supplementary material, figure S4F). The sensitivity tests suggested that food–web interactions generally impede species range shifts under warming, and more so for large predatory species, across plausible assumptions about food–web structure and dispersal rates.
4. Discussion
We developed a spatially explicit food–web model and a set of single-species counterfactual models to explore the role of species interactions in either facilitating or hindering species range shifts in a warming world. The results of the food–web model revealed that dynamic trophic interactions overall hamper species' abilities to shift their spatial distributions in response to warming temperatures at both leading and trailing range edges. In addition, trophic interactions created differences among species of different trophic levels, with larger bodied top predators persisting longer than smaller prey in historical habitats. These delayed extirpations created a lag in the trailing edge shift and an overall range expansion for these large species. By contrast, smaller bodied species experienced a contraction in their spatial distributions. Diversity, range size, trophic level outcomes and snapshots of species relationships all resembled qualitative features of real food–webs. These results highlight the importance of accounting for both spatial dispersal and trophic interactions when considering the impact of climate change on species ranges and assemblages.
Dynamic trophic interactions slowed species’ range shifts compared to expectations from single-species models. This result complements previous theoretical studies showing that competition can limit range shifts [12,23] and suggests that biotic resistance processes [25,26] are likely to be stronger than enemy release effects on range shifts [28]. We found this pattern even when a high portion of potential prey were inedible, a scenario that allowed for more opportunities to escape enemies. High levels of inedible prey did lead to greater leading edge shifts among smaller as compared to larger species, as expected from enemy release, but this did not alter the overall shift lags imposed by food–webs. Our results also complement models suggesting that competition among predators for prey will slow down range shifts [54]. In nature, it is difficult to isolate food–web effects, but one approach is to compare communities in protected areas with those not in such areas, with protection generally preserving stronger predation processes. In temperate reef communities protected from fishing, for example, high-trophic-level species are more abundant than in unprotected communities [25]. Despite warming water, these protected communities had fewer biodiversity changes and fewer colonizations by novel species, as compared to unprotected communities [25]. The example appears to support the theoretical prediction that natural food–web interactions would slow range shifts.
Smaller species shifted more than larger species in terms of centroids and trailing edges, resulting in range contraction across a wide range of dispersal rates that contrasted with range expansion for larger species. This difference could occur because smaller species have higher metabolic rates, faster generation times, and therefore faster extirpation from patches that are no longer suitable owing to warming. However, our counterfactual single-species model that also incorporated higher metabolic rate in smaller species did not show a large difference in shift patterns across size, suggesting that a size-metabolism explanation is not sufficient.
Instead, food–web interactions are a stronger explanation for the lag among larger bodied species. Smaller species preyed to a greater extent upon a basal resource that was not temperature sensitive. Consequently, the primary limit on small heterotrophs' growth was their own temperature-sensitive search rate. In nature, small marine organisms that heterotrophs depend on may indeed be relatively temperature insensitive owing to high species diversity [55] and genetic diversity [56] that assist in adaptation to changing conditions. However, nutrient and ecosystem dynamics also modulate small organisms in nature, which we did not examine in our model [57]. By contrast, larger species near their trailing range edge were subsidized by novel prey that expanded into new habitat (despite also facing the same temperature-dependent feeding limitations that smaller species experienced). The increase that we observed in community biomass and production in food–webs after warming probably reflects the same process. Since large species had no production (they were not consumed), the increase in community production can be attributed to smaller species. This influx of smaller species as prey at the trailing edges of large species would have helped prevent predator extirpation. This phenomenon may be further amplified if prey defence evolution is also considered, since prey are likely to be naïve to novel predators [58].
The ecological subsidy from colonizing species that benefits top predators would not appear in closed food–webs without the possibility of colonization. Closed food–webs generally suggest that top predators are the most vulnerable to changing climate [27]. The persistence of large predators in their historically occupied patches, in turn, imposed a top-down control that slowed the rate of colonization by small prey relative to models without food–web interactions. This effect is consistent with previous findings that predators have larger effects near species range edges [59]. These predicted differences among species also align with empirical studies that find faster shifts in species centroids among small species [2,60].
Although warming led to novel local assemblages (coexisting species pairs) in both the trophic and single-species models, the presence of dynamic trophic interactions led to fewer ecologically novel species assemblages. This finding is contrary to effects from competitive interactions, which predicted more novel assemblages [12]. Changes in local and global richness were generally small and similar between food–web and single-species projections. The extinction pattern differs from previous theoretical works, which found extinction to be exacerbated by competitive species interactions [61]. These results highlight important differences in the ecological consequences of competitive versus trophic interactions for range shifts and future communities.
Even though lags in range shifts persisted over 200 years of warming in our simulations, the increase in non-productive species among warming food–webs suggested that some species, particularly large species, may eventually have experienced more rapid extirpation at their trailing edges. Compared to the single-species model, the food–web model suggested longer transient dynamics [53] and extinction debt [62], making non-equilibrium phenomena more important than in hypothetical non-trophic communities.
We modelled food–webs across a size range that corresponds to heterotrophic, size-structured food–webs characteristic of marine fish communities, which have been a common focus in ecological modelling [40]. However, size- and temperature-depedent metabolic theory can be extended to smaller sizes, including the basal planktonic class [63]. Future research incorporating a larger size range in food–web models would introduce both computational and theoretical challenges because of different generation times and error propagation from low- to high-trophic levels. However, the proper inclusion of smaller organisms would also clarify the role of bottom-up contributions to geographical shifts [64]. While we saw that size dependence of dispersal across species did not appreciably affect range shift patterns, differences across life stages may mediate trophic interactions, which can be addressed through individual based or age-structured modelling. Moving forward, range shift projections will be more informative when human action [65] and genetic evolution [61] are coupled with ecological dynamics.
Our results show that projecting species range shifts based on single-species distribution models [9] will probably overestimate any given species’ tendency to keep track with climate change. Thus, dynamic trophic interactions and body size are important factors for ecological projections under changing environments.
Supplementary Material
Acknowledgements
We thank Charles A. Stock, Anieke van Leeuwen, Ken H. Andersen, Emily Moberg, Rebecca L. Selden and Matthieu Barbier for discussions. The authors acknowledge the Office of Advanced Research Computing (OARC) at Rutgers for providing access to the Amarel computing cluster.
Data accessibility
All Matlab codes are available on GitHub/Zenodo at https://doi.org/10.5281/zenodo.6374072 [66].
The data are provided in the electronic supplementary material [67].
Authors' contributions
E.W.T.: formal analysis, methodology, writing—original draft and writing—review and editing; J.R.W.: conceptualization, methodology and writing—review and editing; M.L.P.: conceptualization, methodology and writing—review and editing.
All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Competing interests
The authors declare no competing interests.
Funding
This work was funded by the Gordon and Betty Moore Foundation (grant no. GBMF5502), a Hakai Postdoctoral Fellowship and NSF awards OCE-1426891, DEB-1616821 and OISE-1743711.
References
- 1.Parmesan C. 2006. Ecological and evolutionary responses to recent climate change. Annu. Rev. Ecol. Evol. Syst. 37, 637-669. ( 10.1146/annurev.ecolsys.37.091305.110100) [DOI] [Google Scholar]
- 2.Pinsky ML, Worm B, Fogarty MJ, Sarmiento JL, Levin SA. 2013. Marine taxa track local climate velocities. Science 341, 1239-1242. ( 10.1126/science.1239352) [DOI] [PubMed] [Google Scholar]
- 3.Poloczanska ES, et al. 2013. Global imprint of climate change on marine life. Nat. Clim. Change 3, 919-925. ( 10.1038/nclimate1958) [DOI] [Google Scholar]
- 4.Doney SC, et al. 2012. Climate change impacts on marine ecosystems. Annu. Rev. Mar. Sci. 4, 11-37. ( 10.1146/annurev-marine-041911-111611) [DOI] [PubMed] [Google Scholar]
- 5.Moore JK, et al. 2018. Sustained climate warming drives declining marine biological productivity. Science 359, 1139-1143. ( 10.1126/science.aao6379) [DOI] [PubMed] [Google Scholar]
- 6.Fenichel EP, Levin SA, Mccay B, St. Martin K, Abbott JK, Pinsky ML. 2016. Wealth reallocation and sustainability under climate change. Nat. Clim. Change 6, 237-244. ( 10.1038/nclimate2871) [DOI] [Google Scholar]
- 7.Guisan A, Thuiller W. 2005. Predicting species distribution: offering more than simple habitat models. Ecol. Lett. 8, 993-1009. ( 10.1111/j.1461-0248.2005.00792.x) [DOI] [PubMed] [Google Scholar]
- 8.Buckley LB, Urban MC, Angilletta MJ, Crozier LG, Rissler LJ, Sears MW. 2010. Can mechanism inform species' distribution models?: correlative and mechanistic range models. Ecol. Lett. 13, 1041-1054. ( 10.1111/j.1461-0248.2010.01479.x) [DOI] [PubMed] [Google Scholar]
- 9.Morley JW, Selden RL, Latour RJ, Frölicher TL, Seagraves RJ, Pinsky ML. 2018. Projecting shifts in thermal habitat for 686 species on the North American continental shelf. PLoS ONE 13, e0196127. ( 10.1371/journal.pone.0196127) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang L, Takahashi D, Hartvig M, Andersen KH. 2017. Food-web dynamics under climate change. Proc. R. Soc. B 284, 20171772. ( 10.1098/rspb.2017.1772) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Selden RL, Batt RD, Saba VS, Pinsky ML. 2018. Diversity in thermal affinity among key piscivores buffers impacts of ocean warming on predator-prey interactions. Glob. Change Biol. 24, 117-131. ( 10.1111/gcb.13838) [DOI] [PubMed] [Google Scholar]
- 12.Urban MC, Tewksbury JJ, Sheldon KS. 2012. On a collision course: competition and dispersal differences create no-analogue communities and cause extinctions during climate change. Proc. R. Soc. B 279, 2072-2080. ( 10.1098/rspb.2011.2367) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alexander JM, Diez JM, Levine JM. 2015. Novel competitors shape species’ responses to climate change. Nature 525, 515-518. ( 10.1038/nature14952) [DOI] [PubMed] [Google Scholar]
- 14.Thompson PL, Gonzalez A. 2017. Dispersal governs the reorganization of ecological networks under environmental change. Nat. Ecol. Evol. 1, 0162. ( 10.1038/s41559-017-0162) [DOI] [PubMed] [Google Scholar]
- 15.Legault G, Bitters ME, Hastings A, Melbourne BA. 2020. Interspecific competition slows range expansion and shapes range boundaries. Proc. Natl Acad. Sci. USA 117, 26 854-26 860. ( 10.1073/pnas.2009701117) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gilman SE, Urban MC, Tewksbury J, Gilchrist GW, Holt RD. 2010. A framework for community interactions under climate change. Trends Ecol. Evol. 25, 325-331. ( 10.1016/j.tree.2010.03.002) [DOI] [PubMed] [Google Scholar]
- 17.Brose U, Dunne JA, Montoya JM, Petchey OL, Schneider FD, Jacob U. 2012. Climate change in size-structured ecosystems. Phil. Trans. R. Soc. B 367, 2903-2912. ( 10.1098/rstb.2012.0232) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fussmann KE, Schwarzmüller F, Brose U, Jousset A, Rall BC. 2014. Ecological stability in response to warming. Nat. Clim. Change 4, 206-210. ( 10.1038/nclimate2134) [DOI] [Google Scholar]
- 19.Schwarz B, et al. 2017. Warming alters energetic structure and function but not resilience of soil food webs. Nat. Clim. Change 7, 895-900. ( 10.1038/s41558-017-0002-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Riede JO, Binzer A, Brose U, De Castro F, Curtsdotter A, Rall BC, Eklöf A. 2011. Size-based food web characteristics govern the response to species extinctions. Basic Appl. Ecol. 12, 581-589. ( 10.1016/j.baae.2011.09.006) [DOI] [Google Scholar]
- 21.Brose U, et al. 2019. Predator traits determine food-web architecture across ecosystems. Nat. Ecol. Evol. 3, 919-927. ( 10.1038/s41559-019-0899-x) [DOI] [PubMed] [Google Scholar]
- 22.Gilbert B, et al. 2014. A bioenergetic framework for the temperature dependence of trophic interactions. Ecol. Lett. 17, 902-914. ( 10.1111/ele.12307) [DOI] [PubMed] [Google Scholar]
- 23.Holt RD, Barfield M. 2009. Trophic interactions and range limits: the diverse roles of predation. Proc. R. Soc. B 276, 1435-1442. ( 10.1098/rspb.2008.1536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Levine JM, Adler PB, Yelenik SG. 2004. A meta-analysis of biotic resistance to exotic plant invasions: biotic resistance to plant invasion. Ecol. Lett. 7, 975-989. ( 10.1111/j.1461-0248.2004.00657.x) [DOI] [Google Scholar]
- 25.Bates AE, Barrett NS, Stuart-Smith RD, Holbrook NJ, Thompson PA, Edgar GJ. 2014. Resilience and signatures of tropicalization in protected reef fish communities. Nat. Clim. Change 4, 62-67. ( 10.1038/nclimate2062) [DOI] [Google Scholar]
- 26.Bates AE, Stuart-Smith RD, Barrett NS, Edgar GJ. 2017. Biological interactions both facilitate and resist climate-related functional change in temperate reef communities. Proc. R. Soc. B 284, 20170484. ( 10.1098/rspb.2017.0484) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Petchey OL, Mcphearson PT, Casey TM, Morin PJ. 1999. Environmental warming alters food-web structure and ecosystem function. Nature 402, 69-72. ( 10.1038/47023) [DOI] [Google Scholar]
- 28.Sorte CJB, Williams SL, Carlton JT. 2010. Marine range shifts and species introductions: comparative spread rates and community impacts: range shifts and non-native species introductions. Glob. Ecol. Biogeogr. 19, 303-316. ( 10.1111/j.1466-8238.2009.00519.x) [DOI] [Google Scholar]
- 29.Angert AL, Crozier LG, Rissler LJ, Gilman SE, Tewksbury JJ, Chunco AJ. 2011. Do species' traits predict recent shifts at expanding range edges?: traits and range shifts. Ecol. Lett. 14, 677-689. ( 10.1111/j.1461-0248.2011.01620.x) [DOI] [PubMed] [Google Scholar]
- 30.Barbier M, Loreau M. 2019. Pyramids and cascades: a synthesis of food chain functioning and stability. Ecol. Lett. 22, 405-419. ( 10.1111/ele.13196) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Barnes C, Maxwell D, Reuman DC, Jennings S. 2010. Global patterns in predator–prey size relationships reveal size dependency of trophic transfer efficiency. Ecology 91, 222-232. ( 10.1890/08-2061.1) [DOI] [PubMed] [Google Scholar]
- 32.Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. 2004. Toward a metabolic theory of ecology. Ecology 85, 1771-1789. ( 10.1890/03-9000) [DOI] [Google Scholar]
- 33.Loreau M, Holt RD. 2004. Spatial flows and the regulation of ecosystems. Am. Nat. 163, 606-615. ( 10.1086/382600) [DOI] [PubMed] [Google Scholar]
- 34.Holling CS. 1959. Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385-398. ( 10.4039/Ent91385-7) [DOI] [Google Scholar]
- 35.Megrey BA, Rose KA, Klumb RA, Hay DE, Werner FE, Eslinger DL, Smith SL. 2007. A bioenergetics-based population dynamics model of Pacific herring (Clupea harengus pallasi) coupled to a lower trophic level nutrient–phytoplankton–zooplankton model: description, calibration, and sensitivity analysis. Ecol. Model. 202, 144-164. ( 10.1016/j.ecolmodel.2006.08.020) [DOI] [Google Scholar]
- 36.Ernest SKM, et al. 2003. Thermodynamic and metabolic effects on the scaling of production and population energy use: thermodynamic and metabloic effects. Ecol. Lett. 6, 990-995. ( 10.1046/j.1461-0248.2003.00526.x) [DOI] [Google Scholar]
- 37.Colloca F, Carpentieri P, Balestri E, Ardizzone G. 2010. Food resource partitioning in a Mediterranean demersal fish assemblage: the effect of body size and niche width. Mar. Biol. 157, 565-574. ( 10.1007/s00227-009-1342-7) [DOI] [Google Scholar]
- 38.Froese R. 2006. Cube law, condition factor and weight-length relationships: history, meta-analysis and recommendations. J. Appl. Ichthyol. 22, 241-253. ( 10.1111/j.1439-0426.2006.00805.x) [DOI] [Google Scholar]
- 39.Moriarty R, O'brien TD. 2013. Distribution of mesozooplankton biomass in the global ocean. Earth Syst. Sci. Data 5, 45-55. ( 10.5194/essd-5-45-2013) [DOI] [Google Scholar]
- 40.Watson JR, Stock CA, Sarmiento JL. 2015. Exploring the role of movement in determining the global distribution of marine biomass using a coupled hydrodynamic–size-based ecosystem model. Prog. Oceanogr. 138, 521-532. ( 10.1016/j.pocean.2014.09.001) [DOI] [Google Scholar]
- 41.Hernandez-Leon S. 2005. A global assessment of mesozooplankton respiration in the ocean. J. Plankton Res. 27, 153-158. ( 10.1093/plankt/fbh166) [DOI] [Google Scholar]
- 42.Brownscombe J, Gutowsky L, Danylchuk A, Cooke S. 2014. Foraging behaviour and activity of a marine benthivorous fish estimated using tri-axial accelerometer biologgers. Mar. Ecol. Prog. Ser. 505, 241-251. ( 10.3354/meps10786) [DOI] [Google Scholar]
- 43.Andersen KH, Beyer JE, Lundberg P. 2009. Trophic and individual efficiencies of size-structured communities. Proc. R. Soc. B 276, 109-114. ( 10.1098/rspb.2008.0951) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stuart-Smith RD, Edgar GJ, Bates AE. 2017. Thermal limits to the geographic distributions of shallow-water marine species. Nat. Ecol. Evol. 1, 1846-1852. ( 10.1038/s41559-017-0353-x) [DOI] [PubMed] [Google Scholar]
- 45.Stevens VM, et al. 2014. A comparative analysis of dispersal syndromes in terrestrial and semi-terrestrial animals. Ecol. Lett. 17, 1039-1052. ( 10.1111/ele.12303) [DOI] [PubMed] [Google Scholar]
- 46.Fenchel T, Finlay BJ. 2004. The ubiquity of small species: patterns of local and global diversity. BioScience 54, 777. ( 10.1641/0006-3568(2004)054[0777:TUOSSP]2.0.CO;2) [DOI] [Google Scholar]
- 47.Bradbury IR, Laurel B, Snelgrove PVR, Bentzen P, Campana SE. 2008. Global patterns in marine dispersal estimates: the influence of geography, taxonomic category and life history. Proc. R. Soc. B 275, 1803-1809. ( 10.1098/rspb.2008.0216) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rall BC, Guill C, Brose U. 2008. Food-web connectance and predator interference dampen the paradox of enrichment. Oikos 117, 202-213. ( 10.1111/j.2007.0030-1299.15491.x) [DOI] [Google Scholar]
- 49.Yool A, et al. 2020. Spin-up of UK Earth System Model 1 (UKESM1) for CMIP6. J. Adv. Model. Earth Syst. 12, e2019MS001933. ( 10.1029/2019MS001933) [DOI] [Google Scholar]
- 50.Pethybridge HR, et al. 2019. Calibrating process-based marine ecosystem models: an example case using Atlantis. Ecol. Model. 412, 108822. ( 10.1016/j.ecolmodel.2019.108822) [DOI] [Google Scholar]
- 51.Cheng L, Abraham J, Hausfather Z, Trenberth KE. 2019. How fast are the oceans warming? Science 363, 128-129. ( 10.1126/science.aav7619) [DOI] [PubMed] [Google Scholar]
- 52.Lester SE, Ruttenberg BI, Gaines SD, Kinlan BP. 2007. The relationship between dispersal ability and geographic range size. Ecol. Lett. 10, 745-758. ( 10.1111/j.1461-0248.2007.01070.x) [DOI] [PubMed] [Google Scholar]
- 53.Hastings A, et al. 2018. Transient phenomena in ecology. Science 361, eaat6412. ( 10.1126/science.aat6412) [DOI] [PubMed] [Google Scholar]
- 54.Fernandes JA, Cheung WWL, Jennings S, Butenschön M, De Mora L, Frölicher TL, Barange M, Grant A. 2013. Modelling the effects of climate change on the distribution and production of marine fishes: accounting for trophic interactions in a dynamic bioclimate envelope model. Glob. Change Biol. 19, 2596-2607. ( 10.1111/gcb.12231) [DOI] [PubMed] [Google Scholar]
- 55.Reuman DC, Gislason H, Barnes C, Mélin F, Jennings S. 2014. The marine diversity spectrum. J. Anim. Ecol. 83, 963-979. ( 10.1111/1365-2656.12194) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Thomas MK, Kremer CT, Klausmeier CA, Litchman E. 2012. A global pattern of thermal adaptation in marine phytoplankton. Science 338, 1085-1088. ( 10.1126/science.1224836) [DOI] [PubMed] [Google Scholar]
- 57.Sarmiento JL, et al. 2004. Response of ocean ecosystems to climate warming. Glob. Biogeochem. Cycles 18, GB3003. ( 10.1029/2003GB002134) [DOI] [Google Scholar]
- 58.Urban MC, Scarpa A, Travis JMJ, Bocedi G. 2019. Maladapted prey subsidize predators and facilitate range expansion. Am. Nat. 194, 590-612. ( 10.1086/704780) [DOI] [PubMed] [Google Scholar]
- 59.Boudreau SA, Anderson SC, Worm B. 2015. Top-down and bottom-up forces interact at thermal range extremes on American lobster. J. Anim. Ecol. 84, 840-850. ( 10.1111/1365-2656.12322) [DOI] [PubMed] [Google Scholar]
- 60.Perry AL, Low PJ, Ellis JR, Reynolds JD. 2005. Climate change and distribution shifts in marine fishes. Science 308, 1912-1915. ( 10.1126/science.1111322) [DOI] [PubMed] [Google Scholar]
- 61.Norberg J, Urban MC, Vellend M, Klausmeier CA, Loeuille N. 2012. Eco-evolutionary responses of biodiversity to climate change. Nat. Clim. Change 2, 747-751. ( 10.1038/nclimate1588) [DOI] [Google Scholar]
- 62.Tilman D, May RM, Lehman CL, Nowak MA. 1994. Habitat destruction and the extinction debt. Nature 371, 65-66. ( 10.1038/371065a0) [DOI] [Google Scholar]
- 63.Andersen KH, et al. 2016. Characteristic sizes of life in the oceans, from bacteria to whales. Annu. Rev. Mar. Sci. 8, 217-241. ( 10.1146/annurev-marine-122414-034144) [DOI] [PubMed] [Google Scholar]
- 64.Stock CA, et al. 2017. Reconciling fisheries catch and ocean productivity. Proc. Natl Acad. Sci. USA 114, E1441-E1449. ( 10.1073/pnas.1610238114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Pinsky ML, Fogarty M. 2012. Lagged social-ecological responses to climate and range shifts in fisheries. Clim. Change 115, 883-891. ( 10.1007/s10584-012-0599-x) [DOI] [Google Scholar]
- 66.Tekwa E. 2022. Code for: body-size and food-web interactions mediate species range shifts under warming. Zenodo. ( 10.5281/ZENODO.6374072) [DOI] [PMC free article] [PubMed]
- 67.Tekwa EW, Watson JR, Pinsky ML. 2022. Data from: Body size and food–web interactions mediate species range shifts under warming. Figshare. ( 10.6084/m9.figshare.c.5933153) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Tekwa E. 2022. Code for: body-size and food-web interactions mediate species range shifts under warming. Zenodo. ( 10.5281/ZENODO.6374072) [DOI] [PMC free article] [PubMed]
- Tekwa EW, Watson JR, Pinsky ML. 2022. Data from: Body size and food–web interactions mediate species range shifts under warming. Figshare. ( 10.6084/m9.figshare.c.5933153) [DOI] [PMC free article] [PubMed]
Supplementary Materials
Data Availability Statement
All Matlab codes are available on GitHub/Zenodo at https://doi.org/10.5281/zenodo.6374072 [66].
The data are provided in the electronic supplementary material [67].