Whole-brain 3D mapping of oxygen metabolism using constrained quantitative BOLD

Abstract

Quantitative BOLD (qBOLD) MRI permits noninvasive evaluation of hemodynamic and metabolic states of the brain by quantifying parametric maps of deoxygenated blood volume (DBV) and hemoglobin oxygen saturation level of venous blood (Y_v), and along with a measurement of cerebral blood flow (CBF), the cerebral metabolic rate of oxygen (CMRO₂). The method, thus should have potential to provide important information on many neurological disorders as well as normal cerebral physiology. One major challenge in qBOLD is to separate de-oxyhemoglobin’s contribution to R₂′ from other sources modulating the voxel signal, for instance, R₂, R₂′ from non-heme iron (R′_2,nh), and macroscopic magnetic field variations. Further, even with successful separation of the several confounders, it is still challenging to extract DBV and Y_v from the heme-originated R₂′ because of limited sensitivity of the qBOLD model. These issues, which have not been fully addressed in currently practiced qBOLD methods, have so far precluded 3D whole-brain implementation of qBOLD. Thus, the purpose of this work was to develop a new 3D MRI oximetry technique that enables robust qBOLD parameter mapping across the entire brain. To achieve this goal, we employed a rapid, R₂′-sensitive, steady-state 3D pulse sequence (termed ‘AUSFIDE’) for data acquisition, and implemented a prior-constrained qBOLD processing pipeline that exploits a plurality of preliminary parameters obtained via AUSFIDE, along with additionally measured cerebral venous blood volume. Numerical simulations and in vivo studies at 3 T were performed to evaluate the performance of the proposed, constrained qBOLD mapping in comparison to the parent qBOLD method. Measured parameters (Y_v, DBV, R′_2,nh, nonblood magnetic susceptibility) in ten healthy subjects demonstrate the expected contrast across brain territories, while yielding group-averages of 64.0 ± 2.3 % and 62.2 ± 3.1 % for Y_v and 2.8 ± 0.5 % and 1.8 ± 0.4 % for DBV in cortical gray and white matter, respectively. Given the Y_v measurements, additionally quantified CBF in seven of the ten study subjects enabled whole-brain 3D CMRO₂ mapping, yielding group averages of 134.2 ± 21.1 and 79.4 ± 12.6 µmol/100 g/min for cortical gray and white matter, in good agreement with literature values. The results suggest feasibility of the proposed method as a practical and reliable means for measuring neurometabolic parameters over an extended brain coverage.

1. Introduction

The cerebrovascular system adaptively regulates itself in close interaction with neuronal cells. Thus, changes in oxygen metabolism reflect alterations in cerebral hemodynamics or perturbations of brain function, for example, during aging (Yamaguchi et al., 1986) and in disease states such as ischemic stroke (Girouard and Iadecola, 2006). Further, the brain’s oxygen demand decreases during states of reduced consciousness, including sleep (Caporale, 2021; Madsen et al., 1991) and anesthesia (Renou et al., 1978). Hence, cerebral metabolic rate of oxygen (CMRO₂) representing brain oxygen utilization and consumption is an important parameter that provides valuable information about cerebral physiology in health and disease. As cerebral metabolism is tightly coupled to oxygen supply from arterial blood and oxygen extraction in the capillary bed, CMRO₂ is typically expressed by the following equation (known as Fick’s principle):

$$C\hspace{0.17em}M\hspace{0.17em}R{O}_2=C_a\cdot C\hspace{0.17em}BF\cdot \left(Y_a-Y_{\upsilon }\right)$$ (1)

Here, C_a is the oxygen carrying capacity of arterial blood in µmol O₂ per ml blood, CBF is the cerebral blood flow in units of ml blood per minute per 100 g tissue, and Y_a and Y_v are the percent hemoglobin oxygen saturation levels of arterial and venous blood, respectively. Eq. [1] indicates that both CBF and oxygen extraction fraction (OEF = (Y_a−Y_v)/Y_a) must be ascertained to derive CMRO₂.

Positron emission tomography is generally regarded as the gold standard for regional CMRO₂ mapping (Frackowiak et al., 1980; Mintun et al., 1984), in which radioactive tracers in the form of ¹⁵O₂ and H₂¹⁵ O are separately administered to the subject for measurements of OEF and CBF, respectively. However, the method’s clinical utility has been limited largely by high radiation exposure, long imaging time, and the cost and complexity of the experimental setting. As a potentially more practical and noninvasive alternative, MRI-based methods have emerged, such as arterial-spin-labeling (ASL) (Alsop et al., 2015) in conjunction with quantitative BOLD (qBOLD) (An and Lin, 2000; He and Yablonskiy, 2007) yielding CBF and OEF, respectively, on a pixel-by-pixel basis. Additionally, methods generally referred to as calibrated BOLD (cBOLD) (Blockley et al., 2013) permit voxel-wise estimation of relative changes of CMRO₂ in response to neural stimulation by calibrating BOLD signal in two presumed isometabolic states of the brain (Davis et al., 1998). Recent dual-gas calibration approaches further enable measurements of resting-state CMRO₂ in absolute physiologic units (Gauthier and Hoge, 2013; Wise et al., 2013). Nevertheless, in cBOLD experimental preparation for gas administration and subject discomfort from the procedure are limiting factors. Furthermore, some of the assumptions made in the calibration model remain arguable (e.g., Grubb’s constant (Chen and Pike, 2010) and isometabolicity of gas challenges (Englund et al., 2020; Peng et al., 2017)).

qBOLD is a calibration-free technique and instead directly quantifies the two critical determinants of the BOLD signal, i.e., deoxygenated hemoglobin (dHb) concentration in venous blood ([dHb]_v = C_a(1-Y_v)) and deoxygenated blood volume (DBV). Under the static dephasing regime (Yablonskiy and Haacke, 1994), the qBOLD model characterizes the MR signal evolution at short and long time scales, and particularly for the latter the RF-reversible portion of the transverse relaxation rate (R₂′) is linearly proportional to the two parameters (Y_v and DBV). Thus, the qBOLD method typically acquires R₂′-weighted time-series data and then attempts to separate measured R₂′ into Y_v and DBV. However, conventional qBOLD presents two major problems. First, on the data acquisition side, currently practiced R₂′ mapping methods (Ni et al., 2015), generally referred to as GESSE (gradient-echo sampling of spin-echo) (Yablonskiy, 1998), GESFIDE (gradient-echo sampling of free-induction-decay and echo) (Ma and Wehrli, 1996), or ASE (asymmetric spin-echo) (An and Lin, 2003), commonly rely on the spin-echo mechanism applying a 180° RF pulse. Thus, the utility of these methods has been largely limited to 2D quantifications, and their extension to 3D qBOLD would entail impractically long scan times for 3D encoding. Second, from the parameter estimation perspective, the qBOLD model presents limited parameter sensitivity (Lee et al., 2018; Sedlacik and Reichenbach, 2010). Specifically, mutual coupling between Y_v and DBV in the signal model renders the quantification error-prone and unstable, resulting in relatively low reproducibility of the method. Furthermore, in the original qBOLD model, contribution of non-heme iron to R₂′ is not accounted for (i.e., the relative magnetic susceptibility of extravascular tissue is approximated to that of fully oxygenated blood ∼ −0.1 ppm (Yablonskiy et al., 2013a)), which may result in erroneous estimates, particularly in deep brain structures presenting susceptibility values higher on the positive side (up to +0.2 ppm (Lim et al., 2013)) due to high non-heme iron content in the basal ganglia.

More recently, an approach combining qBOLD and quantitative susceptibility mapping (QSM) has been suggested (referred to as qBOLD+QSM (Cho et al., 2018)). The method employs a 3D multi-echo spoiled gradient-echo (GRE) pulse sequence, a typical choice in QSM for local field estimation by means of phase analysis (Wang and Liu, 2015), and utilizes R₂∗-weighted magnitude images for qBOLD processing. Compared to the original qBOLD method, the parameter estimation model was modified such that non-blood tissue susceptibility (χ_nb) was explicitly included in the temporal signal decay while four-pool decomposition of voxel susceptibility (Δχ ) (i.e., deoxygenated arterial and venous blood, fully oxygenated blood, and non-blood tissue (Zhang et al., 2015)) was added as a constraint. It was shown that qBOLD+QSM with 3D multi-echo spoiled GRE achieves rapid 3D qBOLD scanning while reducing noise sensitivity in the parameter estimation (Cho et al., 2018). However, a more recent analysis (Hubertus et al., 2019) has revealed that qBOLD+QSM yields overall higher measurement accuracy in gray matter regions with GESSE than that obtainable with multi-echo spoiled GRE. This would have resulted from the fact that, unlike GRE, GESSE is able to extract R₂′ directly from signal decay curves.

In this work, we aimed to address the above noted challenges in 3D qBOLD parameter mapping, i.e., high-speed scanning and robust quantification. To this end, in the data acquisition, a recently developed, scan-time efficient 3D R₂′ mapping pulse sequence (Lee and Wehrli, 2021), termed ‘Alternating Unbalanced Steady-state-free-precession Free-Induction-Decay and Echo (AUSFIDE)’, was employed, while in the qBOLD processing pipeline, parametric information obtained from AUSFIDE (R₂, R₂′, Δχ , macroscopic magnetic field inhomogeneity) was fully integrated into a prior-constrained non-linear inverse problem. Additionally, venous cerebral blood volume (CBV_v) was separately measured using an in-house developed method (Lee and Wehrli, 2020), termed ‘velocity-selective venous-spin-labeling (VS-VSL), serving as prior information for DBV. The obtained Y_v maps along with separate CBF measurements enabled 3D CMRO₂ mapping across the entire brain. Numerical simulations and in-vivo experiments were performed to evaluate the performance of the proposed qBOLD method in comparison to the existing techniques.

2. Methods

2.1. AUSFIDE-based 3D qBOLD

One key challenge that currently practiced qBOLD techniques face is separation of the four competing mechanisms that affect temporal signal decays across echoes collected: R₂ (microscopic), R₂′ from heme (R₂′_,h) and non-heme (R₂′_,nh) iron contributions (mesoscopic), and background magnetic field inhomogeneity (ΔB₀; macroscopic). Further, extracting Y_v and DBV from the measured R₂′_,h is generally nontrivial as noted in Introduction. The following subsections along with Fig. 1 detail the proposed approach in terms of data acquisition and parameter estimation so as to disentangle the above confounders and thereby achieving reliable measurements of the qBOLD parameters. Symbols used to represent parameters and their corresponding descriptions are listed in Table 1.

Fig. 1.

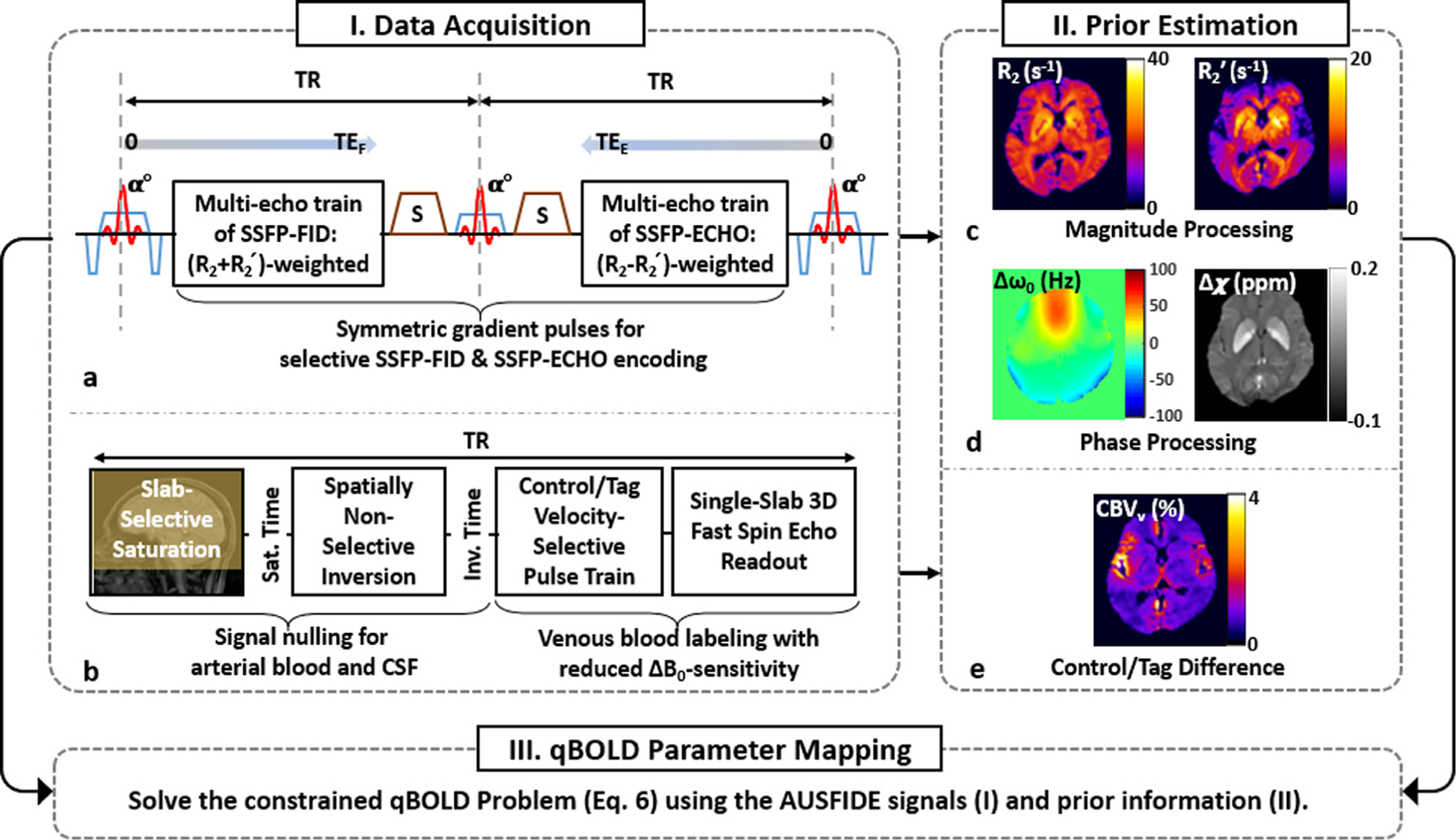
Schematic of the proposed, three-step quantification of qBOLD parameters. Step I. Data acquisition: Imaging data are collected in two separate scans using ‘Alternating Unbalanced Steady-state-free-precession (SSFP) Free-Induction-Decay and Echo (AUSFIDE)’ (a) and ‘Velocity-Selective Venous-Spin-Labeling (VS-VSL)’ (b) pulse sequences. In AUSFIDE, the SSFP-FID and SSFP-ECHO modules alternate with each other across the entire pulse train while sampling multiple echoes decaying with rate constants R₂+R₂′ and R₂-R₂′, respectively. The VS-VSL method achieves ΔB₀-resistant, selective labeling of venous blood by applying saturation, inversion, and VS modules sequentially before 3D fast spin-echo readout. Step II. Prior estimation: The AUSIFDE data are processed in magnitude and phase, leading to maps of R₂ and R₂′ (c) and Δω₀ (=γΔB₀) and Δχ (d), respectively, while the difference between control and tag VS-VSL images approximates CBV_v (e). Step III. qBOLD parameter mapping: Given acquired time-series AUSFIDE images and preliminary parametric maps derived therefrom, along with CBV_v prior information, the constrained nonlinear inverse problem in Eq. [6] is solved, yielding solutions for qBOLD parameters (DBV and Y_v) and nonblood contributions to R₂′ and Δχ (see main text for details).

Table 1.

A list of symbols used in this paper and their definitions. Values for the known or assumed parameters are provided in corresponding parentheses.

	Symbols (units)	Descriptions
Measured/ Derived	Ca (µmol/ml)	Oxygen carrying capacity of arterial blood
	CBF (ml/100 g/min)	Cerebral blood flow
	Yv (%)	Hemoglobin oxygen saturation level of venous blood
	CMRO2 (µmol/100 g/min)	Cerebral metabolic rate of oxygen
	CBVv (%)	Venous cerebral blood volume
	ζ(%)	Deoxygenated blood volume (DBV)
	R2 (s−1)	RF-irreversible transverse relaxation rate
	R2′ (s−1)	RF-reversible transverse relaxation rate
	$R_{2,h}^{\prime }$(s−1 )	Heme-originated portion of R2′
	$R_{2,nh}^{\prime }$(s−1 )	Non-heme-originated portion of R2′
	Δχ (ppm)	Voxel-averaged magnetic susceptibility
	χnb (ppm)	Magnetic susceptibility of non-blood tissue
	ΔB0 (T)	Macroscopic magnetic field inhomogeneity
	S0	Baseline steady-state signal level of SSFP-FID
	η	Signal ratio of SSFP-ECHO to SSFP-FID at TE = 0
	δω (Hz)	Characteristic frequency due to magnetic susceptibility of deoxygenated blood relative to surrounding tissue
	Hct	Blood hematocrit level
Known/Assumed	Ya (∼ 98 %)	Hemoglobin oxygen saturation level of arterial blood
	Δχ0 (∼ 3.393 ppm)	Difference in magnetic susceptibility between fully oxygenated and fully deoxygenated red blood cells
	χoHb (∼ −0.813 ppm)	Magnetic susceptibility of oxygenated hemoglobin
	χp (∼ −0.038 ppm)	Magnetic susceptibility of blood plasma
	γ(2.675ⅹ108 radian/s/T)	Gyromagnetic ratio for water proton
	B0 (2.89 T)	Static magnetic field strength
	α (∼ 0.77)	Volume fraction of venous blood relative to total blood
	λ (∼ 0.9 ml/g)	Blood-brain partition coefficient
	T1,b (∼ 1.65 s)	T1 of arterial blood at 3 T
	β (∼ 0.72)	Efficiency of pseudo-continuous arterial spin labeling
	τ (1.8 s)	Duration of pseudo-continuous arterial spin labeling

2.1.1. Estimation of preliminary parameters

The proposed 3D qBOLD protocol consists of two pulse sequences: AUSFIDE (Fig. 1a) yielding a set of volumetric maps (R₂, R₂′, Δχ , ΔB₀; Fig. 1c), and additionally VS-VSL (Fig. 1b) leading to voxel-wise CBV_v estimates (Fig. 1d) across the entire brain.

Based on the unbalanced steady-state-free-precession (SSFP) mechanism (Scheffler, 1999) generating steady-state signals in a number of spin configurations, AUSFIDE deploys SSFP-FID and SSFP-ECHO modules in an alternating and time-symmetric fashion along the entire pulse train (Fig. 1a) for selective acquisition of SSFP signals in the 0th and - 1st spin pathways, respectively, with a plurality of gradient-recalled signals within each time-of-repetition (TR). The decay rate of SSFP-FID and SSFP-ECHO signals along time is then expressed by R₂+R₂′ (= R₂∗) and R₂-R₂′, respectively, while temporal evolution of signal phase therein is governed by magnetic fields both at voxel and larger scales. Thus, AUS-FIDE enables quantification of R₂ and R₂′ from magnitude data processing (Fig. 1c), and Δχ and ΔB₀ from phase analysis (Fig. 1d) (see Eq. [2] below for signal modeling). This is a key advantage over the currently practiced qBOLD pulse sequences. On one hand, compared to the 2D-limited R₂′ measurement techniques, AUSIFDE achieves rapid 3D volumetric scanning, thus allowing for additional estimation of Δχ via QSM. On the other hand, compared to multi-echo 3D spoiled GRE, AUSIFDE is able to separate R₂∗ into R₂ and R₂′ contributions directly. Additional components in the AUSFIDE sequence include 3D z-shimming gradients along the multi-echo train (Han et al., 2015) and the radial stack-of-stars k-space sampling scheme (Block et al., 2014) so as to make the R₂′ mapping relatively immune to large-scale magnetic field inhomogeneity and physiologic bulk fluid motion, respectively (Lee and Wehrli, 2021).

In the VS-VSL pulse sequence (Fig. 1b), two magnetization preparation modules are sequentially applied to respective spatial positions to null signals for both upstream arterial blood and cerebrospinal-fluid, followed by a control/tag VS pulse train to sensitize moving spins, thereby ensuring labeling of venous blood only. Subsequently, single-slab 3D fast SE with variable refocusing flip angles and center-out k-space view ordering schemes is employed to achieve rapid and ΔB₀-insensitive signal readout with a minimal loss of the labeled venous blood population. In the quantification, a simplified VS-VSL signal model yields CBV_v directly from control/tag difference ( Lee and Wehrli, 2020 ).

2.1.2. Prior-constrained qBOLD model

In the absence of blood vessel network, the signal evolution of SSFP-FID (S_F) and SSFP-ECHO (S_E) modules in AUSFIDE can be written as:

$$\left\{\begin{array}{l}\begin{array}{l}{S}_F\left(T\hspace{0.17em}{E}_F\right)=S_0{s}^{-\left(R_2+R_2^{\prime }\right)T\hspace{0.17em}{E}_F}{F}_{V\hspace{0.17em}S\hspace{0.17em}F}\left(\mathrm{\Delta }{B}_0,T\hspace{0.17em}{E}_F\right)e^{-j\mathrm{\Phi }}\hfill \\ S_E\left(T\hspace{0.17em}{E}_E\right)=\eta S_0{e}^{\left(R_2-R_2^{\prime }\right)T\hspace{0.17em}{E}_E}{F}_{V\hspace{0.17em}S\hspace{0.17em}F}\left(-\mathrm{\Delta }{B}_0,T\hspace{0.17em}{E}_E\right)e^{j\mathrm{\Phi }}\hfill \end{array}\hfill \end{array}\right.$$ (2)

where the subscripts F and E represent SSFP-FID and SSFP-ECHO, TE is the echo time, S₀ is the baseline steady-state signal level of SSFP-FID, η is the ratio of S_E to S_F at TE = 0, F_VSF is the voxel-spread-function representing ΔB₀-induced voxel signal modulations (Yablonskiy et al., 2013b), and Φ is the signal phase as a function of total magnetic field (i.e., ΔB₀ + Δχ -induced local field). Given the estimates of ΔB₀ and the resultant F_VSF, the unknown parameters in Eq. [2], S₀, η, R₂, and R₂′, can be jointly estimated (Lee and Wehrli, 2021).

In the presence of a blood vessel network, heme iron and non-heme iron both perturb local magnetic field, altering the transverse relaxation rate R₂′ made up of R′_2,h+R′_2,nh. In the qBOLD framework aiming to resolve the dHb-related R₂′ (R′_2,h) into Y_v and DBV, the two sources of R₂′ modulation thus needs to be separately taken into account. Accordingly, Eq. [2] is modified to:

$$\left\{\begin{array}{l}\begin{array}{l}{S}_F\left(T\hspace{0.17em}{E}_F\right)=S_0{e}^{-\left(R_2+R_{2,nh}^{\prime }\right)T\hspace{0.17em}{E}_F}{e}^{-\zeta \cdot f\left(T\hspace{0.17em}{E}_F{\delta }_{\omega }\right)}{F}_{V\hspace{0.17em}S\hspace{0.17em}F}\left(\mathrm{\Delta }{B}_0,T\hspace{0.17em}{E}_F\right)e^{-j\mathrm{\Phi }}\hfill \\ S_E\left(T\hspace{0.17em}{E}_E\right)=\eta S_0{e}^{\left(R_2-R_{2,nh}^{\prime }\right)T\hspace{0.17em}{E}_E}{e}^{-\zeta \cdot f\left(T\hspace{0.17em}{E}_E{\delta }_{\omega }\right)}{F}_{V\hspace{0.17em}S\hspace{0.17em}F}\left(-\mathrm{\Delta }{B}_0,T\hspace{0.17em}{E}_E\right)e^{j\mathrm{\Phi }}\hfill \end{array}\hfill \end{array}\right.$$ (3)

Here, the term $e^{-\zeta \cdot f\left(\cdot \right)}$ is the qBOLD model representing the effect of dHb on the extravascular tissue signal, $\zeta$ is DBV, and f(•) characterizes the rate of signal decay as quadratic and linear functions of its argument asymptotically at short and long TEs, respectively (Yablonskiy and Haacke, 1994). δ_ω is the characteristic frequency due to the susceptibility of deoxygenated blood relative to the surrounding tissue, expressed by (Cho et al., 2018; Yablonskiy et al., 2013a):

$${\delta }_{\omega }\left(Y_{\upsilon },{\chi }_{nb}\right)=\frac{1}{3}\gamma B_0\left(\mathrm{\Delta }{\chi }_{0}Hct\left(1-Y_{\upsilon }\right)+{\chi }_{ba}-{\chi }_{nb}\right)$$ (4)

where γ is the gyromagnetic ratio, B₀ is the static field strength, Δχ ₀ is the susceptibility difference between fully oxygenated and fully deoxygenated red blood cells (∼ 4π × 0.27 ppm (Spees et al., 2001)), and Hct is the blood hematocrit level. χ_ba is the susceptibility of fully oxygenated blood, which can be calculated by volume-weighted combination of susceptibilities of oxygenated hemoglobin (χ_oHb ∼ −0.813 ppm) and blood plasma (χ_p ∼ −0.038 ppm) (Zhang et al., 2015; Zhang et al., 2017).

To estimate the qBOLD parameters (Y_v and DBV), AUSFIDE images along the multi-echo train may be fitted directly to the signal model in Eq. [3], which, however, makes the problem computationally intensive and potentially unstable because of many unknowns (S₀, η, R₂, $R_{2,nh}^{\prime }$, χ_nb, Y_v, ζ) being solved jointly. Instead, the solutions can be found in two steps: 1) estimating S₀, η, R₂, and R₂′ using Eq. [2], and based on this information, 2) seeking the remaining parameters by solving the following nonlinear least-squares problem:

$$\underset{\mathbf{\Theta }}{\arg \min }{\sum _{T\hspace{0.17em}E}\left|\mathbf{y}\left(T\hspace{0.17em}E\right)-\Xi \left(\mathbf{\Theta },T\hspace{0.17em}E\right)\right|}^2$$ (5)

where y is the acquired AUSFIDE signals at the sampling time TE for each voxel, $\Xi =\left\{\left|S_F\right|,\left|S_E\right|\right\}$ is the corresponding model (Eq. [3]), and $\theta =\left\{Y_{\upsilon },\zeta ,{\text{R}}_{2,nh}^{\prime },{\chi }_{nb}\right\}$ is the set of unknown parameters to be solved. Furthermore,to enhance solution accuracy while reducing noise amplifications in the parameter estimation, R₂′ and Δχ obtainable from magnitude and phase processing of the AUSFIDE data are utilized as prior information, leading to the following optimization problem:

$$\underset{\mathbf{\Theta }}{\arg \min }\sum _{T\hspace{0.17em}E}{\left|\mathbf{y}\left(T\hspace{0.17em}E\right)-\mathbf{\Xi }\left(\mathbf{\Theta },T\hspace{0.17em}E\right)\right|}^2+w{\left|\mathrm{\Delta }\chi -\mathrm{\Psi }\left(\mathbf{\Theta }\right)\right|}^2+p{\left|{\text{R}}_2^{\prime }-\text{Y}\left(\mathbf{\Theta }\right)\right|}^2$$ (6)

Here, Ψ decomposes Δχ into susceptibility contributions of the four compartments in a voxel, i.e., deoxygenated arterial and venous blood, fully oxygenated blood, and non-blood tissue, given by (Zhang et al., 2015; Zhang et al., 2017):

$$\mathrm{\Psi }=\frac{\zeta }{\alpha }\left[\mathrm{\Delta }{\chi }_{0}H\hspace{0.17em}ct\left\{\left(1-\alpha \right)\left(1-Y_a\right)+\alpha \left(1-Y_{\upsilon }\right)\right\}+{\chi }_{ba}\right]+\left(1-\frac{\zeta }{\alpha }\right){\chi }_{nb}$$ (7)

where α is the volume fraction of venous blood relative to total blood, assumed to be 0.77 (An and Lin, 2002). In Eq. [6], Y disentangles R₂′ contributions from the non-heme iron $\left({\text{R}}_{2,nh}^{\prime }\right)$ and dHb $\left({\text{R}}_{2,h}^{\prime }\right)$, written by:

$$\text{Y=}{\text{R}}_{2,nh}^{\prime }+{\text{R}}_{2,h}^{\prime }={\text{R}}_{2,nh}^{\prime }+\zeta \cdot {\delta }_{\omega }\left(Y_{\upsilon },{\chi }_{nb}\right)$$ (8)

and w and p are the regularization parameters that enforce prior knowledge of Δχ and R₂′, respectively. Thus, with w = p = 0 Eq. [6] represents the original qBOLD problem, while with w > 0 but p = 0 it is equivalent to the qBOLD+QSM approach.

Additionally, based on the recent analysis (Lee et al., 2018) suggesting substantially improved stability of the qBOLD mapping with prior information for DBV, in this work VS-VSL-derived CBV_v was employed to initialize and constrain the solution of DBV. Nevertheless, since the VS-VSL method may result in measurement errors in some voxels in which its assumptions are not valid (Lee and Wehrli, 2020), here DBV was refined during the iterative process of solving Eq. [6], rather than being fixed to CBV_v. Details in solving Eq. [6] are provided in Section 2.4.1 below.

2.2. Numerical simulations

The performance of the proposed AUSFIDE-based qBOLD in comparison to the spoiled GRE-based approach was investigated numerically in Matlab (MathWorks, Natick, MA). To this end, simulations were performed involving the following steps: 1) baseline steady-state signals (i.e., S₀ and ηS₀ in Eq. [2]) were calculated using summation of isochromats (Shkarin and Spencer, 1997), 2) given a set of nominal parameters chosen, a time series of AUSFIDE signals was computed using Eq. [3], 3) Gaussian noise was added to each of the multi-echo signals in Step 2, and 4) Eq. [5] was solved to yield a solution for R₂, R₂′, Y_v, and DBV. Steps 1–4 were repeated 10,000 times independently, leading to the mean absolute error (MAE) of the estimated parameters relative to corresponding nominal values. In each of the 10,000 simulations, nominal values for R₂, Y_v, and DBV were varied randomly in the ranges: 10 s⁻¹ < R₂ < 20 s⁻¹ , 40 % < Y_v < 80 %, and 1% < DBV < 5 %, while the following parameters were set to zero for simplicity:$R_{2,nh}^{\prime }$, χ_ba, χ_nb, and ΔB₀ . The entire procedure above was repeated seven times by changing standard deviations (SD) of the Gaussian noise from −7 to −4 (increment: 0.5) in the natural log scale (corresponding signal-to-noise ratio (SNR) levels of approximately 1100, 670, 400, 240, 150, 90, and 50). Furthermore, the effectiveness of using prior knowledge of CBV_v was also evaluated by initializing the solution for DBV to its nominal value at each time of parameter estimation. Simulation parameters pertinent to the AUSFIDE pulse sequence were: TR = 30 ms, first TE_F = 1.6 ms, first TE_E = 2.2 ms, echo spacing = 3 ms, number of echoes = 9, and flip angle = 25°. The SSFP-FID portion of the AUSFIDE signals was used to simulate the spoiled GRE signal because the steady-state signal of spoiled GRE with TR = 30 ms and flip angle ∼ 15° (Ernst angle for brain tissues) is at a level comparable to S_FID resulting from the parameters stated above.

To examine the effect of potential bias in CBV_v prior on the qBOLD parameter estimation, simulations were performed by varying errors in CBV_v with respect to a nominal value for DBV from −40 % to 40 % (increment: 10 %). Here, in addition to varying nominal values for R₂, Y_v, and DBV as above, a reference for χ_nb was also chosen randomly in the range 0.01 ppm < χ_nb < 0.1 ppm over the simulations, while a linear relationship between χ_nb and $R_{2,nh}^{\prime }$ was assumed, leading to a nominal value for $R_{2,nh}^{\prime }$ given the reference χ_nb. It is noted that χ_nb also resides on the negative side for some regions of the brain (particularly white matter) where the assumed slope defining $R_{2,nh}^{\prime }$ against χ_nb may differ (Chen et al., 2021; Emmerich et al., 2020). However, since the primary focus of this work was to separate R₂′ contributions from heme- and non-heme iron, in the simulations χ_nb values only within the positive range were examined, typical of non-heme iron. In experimental data processing (see Section 2.4.1 below), the solution for χ_nb was sought for both positive and negative sides. χ_ba was computed assuming Hct of 0.357. Given the resultant AUSFIDE signals computed, Gaussian noise yielding a SNR of ∼140 for the first echo of SSFP-FID was added. The value of 140 was based on the SNR measurement on actual brain images obtained using the AUSFIDE pulse sequence. Subsequently, Eq. [6] was solved with a biased CBV_v prior in three different manners: 1) w = p = 0; 2) w > 0, p = 0; 3) w > 0, p > 0. MAE of the solutions (Y_v, DBV, $R_{2,nh}^{\prime }$_, χ_nb) estimated over 10,000 simulations was calculated for the three scenarios.

2.3. Experiments

All experimental studies were approved by the Institutional Review Board of the University of Pennsylvania. Informed written consent was obtained from all study subjects (N = 10; five males; age mean ± SD = 31 ± 7 years) individually prior to scanning at 3 T (Siemens Prisma, Erlangen, Germany) with a 32-channel head-coil for signal reception. Following MRI data collections, hemoglobin concentration in each subject was measured via a finger stick test. The resultant value was then scaled up by 2.5 to yield Hct in a microvascular system (Eichling et al., 1975).

Data were acquired in all study participants using the AUSIFDE and VS-VSL pulse sequences, implemented in SequenceTree (Magland et al., 2016). Imaging parameters used in AUSFIDE were: field-of-view (FOV) = 240 × 240 × 120 mm³ , reconstruction matrix = 160 × 160 × 40, number of radial views = 144, echo spacing = 1.5 ms, number of echoes = 17 (nine regularly encoded + eight z-shimmed), yielding a scan time of 8 minutes. The remaining parameters were identical to those specified in the section of Numerical Simulations. Imaging parameters specific to VS-VSL were: FOV = 220 × 220 × 180 mm³ (sagittal orientation), reconstruction matrix = 72 × 72 × 60, TR = 3 seconds, saturation time = 1.6 seconds, inversion time = 1.14 seconds, cut-off velocity = 7.5 mm/s in the VS pulse train, echo train length = 40 and echo spacing = 2.5 ms in the fast SE readout, and k-space subsampling factor = 3.3, yielding a scan time of 3.3 minutes. A high-resolution T₁- weighted MP-RAGE scan (Mugler III and Brookeman, 1990) was also performed (1 mm isotropic resolution, scan duration = 5 minutes) for brain segmentation.

Additional data were collected in seven of the 10 study subjects using 3D pseudo-continuous ASL (pCASL) with stack-of-spirals readout (Vidorreta et al., 2017) and T₂-relaxation under spin tagging (TRUST) (Lu and Ge, 2008) for measuring CBF and whole-brain averaged Y_v, respectively. Imaging parameters in the pCASL pulse sequence were: FOV = 240 × 240 × 120 mm³ , reconstruction matrix = 64 × 64 × 32, slice partial Fourier factor = 6/8, labeling duration = 1.8 seconds, post labeling delay = 1.5 seconds, background suppression with four RF pulses, variable-density spiral-out trajectory with a readout duration of 340 ms, TR = 4 seconds, and measurements = 15 control/tag pairs, acquired in a scan time of 4.5 minutes. Based on a time-of-flight angiogram, the labeling plane was selected individually at a position superior to the carotid bifurcation. Acquisition parameters for TRUST were: FOV = 230 × 230 mm² , reconstruction matrix = 64 × 64, phase partial Fourier factor = 5/8, TR = 3 seconds, T₂ preparation times = 0, 40, 80, and 160 ms, and measurements = 3 control/tag pairs, with a scan time of 1.2 minutes.

2.4. Data processing and analysis

Unless otherwise stated, all data processing and analysis involving image reconstruction, parameter quantifications, and statistical comparisons were carried out in Matlab custom scripts.

2.4.1. qBOLD processing

VS-VSL data were subjected to sparsity-constrained image reconstruction (Lee et al., 2017a), and subsequently to the control/tag image difference divided by the control image, yielding CBV_v maps. Multi-echo AUSFIDE images, reconstructed by applying a Tukey window and Fourier transform along the k_z-direction and subsequent in-plane grid-ding, were processed in three steps: 1) estimating ΔB₀ and corresponding VSF (Yablonskiy et al., 2013b), 2) solving Eq. [2] on magnitude images, and 3) QSM reconstruction using the MEDI toolbox (Liu et al., 2012), leading to the maps of F_VSF, S₀, η, R₂, R₂′, Δχ as prior information for the qBOLD processing described below. Refer to (Lee and Wehrli, 2020; Lee and Wehrli, 2021) for details in the above process.

Based on the time-course of AUSFIDE images along with the derived preliminary parametric maps, qBOLD parameters were estimated by solving Eq. [6] on a voxel-by-voxel basis using the curve fitting tool-box in Matlab. In the optimization procedure, initial values (indicated by subscript 0) for the unknown parameter set, $\theta =\left\{Y_{\upsilon },\zeta ,{\chi }_{nb},R_{2,nh}^{\prime }\right\}$, was determined as follows: Y_v,0 was set equal to Y_v in large draining veins (Y_v,s; superior sagittal sinus and straight sinus), derived from measured Δχ in the respective regions. To this end, Eq. [7] was solved with α= ζ = 1 and Hct scaled up by 1.18 (inverse of 0.85 representing the Hct ratio of microvasculature relative to large vessels). ζ₀ and χ_{nb ,0} were initialized to CBV_v and Δχ , respectively. Finally, $R_{2,nh,0}^{\prime }$ was computed by subtracting ζ₀ δ_ω from measured R₂^′ lower and upper bounds of the solutions were restricted to: 10 % ≤ Y_υ ≤ 90 %, 0.5ζ₀ ≤ ζ ≤ 2ζ₀, $0.5R_{2,nh,0}^{\prime }\le R_{2,nh}^{\prime }\le 2R_{2,nh,0}^{\prime }$, and −0.1 ppm ≤ χ_nb ≤ 0.2 ppm. Y_a was assumed 98%. The regularization parameters w and p were empirically determined to 10 and 0.1, respectively. The validity of the selected values for w and p is evaluated via L-curve analysis in Supplementary Material.

To investigate the effectiveness of prior information in solving the qBOLD problem, AUSFIDE images acquired in a subject were processed in four different manners such that Eq. [6] was solved with: 1) w = p = 0 and 2) w > 0 and p = 0, 3) w > 0 and p > 0, and 4) w > 0 and p > 0 with CBV_v prior. Thus, processing 1, 2, and 4 represent conventional qBOLD, qBOLD+QSM, and the proposed method, respectively, in terms of utilizing preliminary parameters (i.e., Δχ , R₂′, and CBV_v). In processing 1 – 3, all parameter initialization and solution bounds were identical to those stated above, but ζ₀ = 3 %. Resulting maps of Y_v, DBV, and χ_nb were qualitatively compared across the four processing scenarios.

2.4.2. 3D whole-brain CMRO₂ mapping

Control and tag pCASL images were realigned to the proton-density image (M₀) acquired prior to the actual pCASL data collection using SPM12 (Penny et al., 2011), and their pair-wise difference was averaged over multiple measurements, yielding ΔSI. Subsequently, CBF was computed on a voxel-by-voxel basis using the following equation (Alsop et al., 2015):

$$\text{CBF}\left(\text{ml}/100\mathrm{g}/\min \right)=\frac{3000\hspace{0.17em}\cdot \hspace{0.17em}\lambda \hspace{0.17em}\cdot \hspace{0.17em}\mathrm{\Delta }\text{SI}\hspace{0.17em}\cdot \hspace{0.17em}{e}^{\frac{PLD}{T_{1,b}}}}{\beta \hspace{0.17em}\cdot \hspace{0.17em}{T}_{1,b}\hspace{0.17em}\cdot \hspace{0.17em}{M}_0\hspace{0.17em}\cdot \hspace{0.17em}\left(1-e^{\frac{\tau }{T_{1,b}}}\right)}$$ (9)

where λ is the blood-brain partition coefficient (0.9 ml/g (Herscovitch and Raichle, 1985)), T_1,b is the T₁ of arterial blood at 3 T (1.65 seconds (Lu et al., 2004)), PLD is the post labeling delay, τ is the labeling duration, and β is the labeling efficiency (0.72 (Vidorreta et al., 2013)). Finally, given the CBF measurements along with qBOLD-derived Y_v across the entire brain, 3D CMRO₂ maps were constructed using Eq. [1] in units of µmol O₂ per 100 g tissue per minute.

2.4.3. Data analysis

Brain tissue segmentation was performed based on the T₁-weighted MP-RAGE images using the FreeSurfer software package (Fischl, 2012), yielding the following six regions-of-interests (ROIs): cerebral cortex (cortical gray matter (GM)), cerebral white matter (WM), thalamus, pallidum, putamen, and caudate. Then, the MP-RAGE images along with the segmentation maps were coregistered to the first echo of SSFP-FID images, leading to ROI analysis of the parameters quantified in the preliminary (CBV_v, R₂, R₂′, Δχ ) and qBOLD processing (DBV, Y_v, $R_{2,nh}^{\prime }$, χ_nb) steps computing regional averages (mean ± SD) across the 10 study subjects. Furthermore, correlation between the two parameter estimates, $R_{2,nh}^{\prime }$ and χ_nb , in the six ROIs was evaluated using linear regression.

Measured Y_v, CBF, and CMRO₂ were averaged over cortical GM and WM voxels in the seven study subjects and tabulated. Additionally, TRUST data in each subject were processed via the following steps: 1) taking difference between control and tag images at the four T₂ preparation times, 2) fitting the difference signals in the superior sagittal sinus with respect to T₂, and 3) converting T₂ to Y_v using the calibration curve provided in (Lu et al., 2012). The resulting global Y_v value was compared with whole-brain averaged Y_v obtained in the proposed qBOLD method using two-tailed, paired t-test.

3. Results

3.1. Numerical simulations

Fig. 2 shows MAE of R₂ (Fig. 2a), R₂′ (Fig. 2b), Y_v (Fig. 2c), and DBV (Fig. 2d) estimates with increasing noise SD from −7 to −4 (natural log scale), obtained using SSFP-FID signals only, and using entire AUS-FIDE signals without and with CBV_v prior information. Over the entire range of noise levels, the R₂∗-based parameter estimation with SSFP-FID yielded substantially greater measurement errors than the R₂′-based approaches using AUSFIDE. Furthermore, in the presence of CBV_v prior the estimation errors of Y_v, and DBV in the AUSFIDE qBOLD method were substantially reduced, thus suggesting the need of prior knowledge of CBV_v in qBOLD parameter mapping.

Fig. 2.

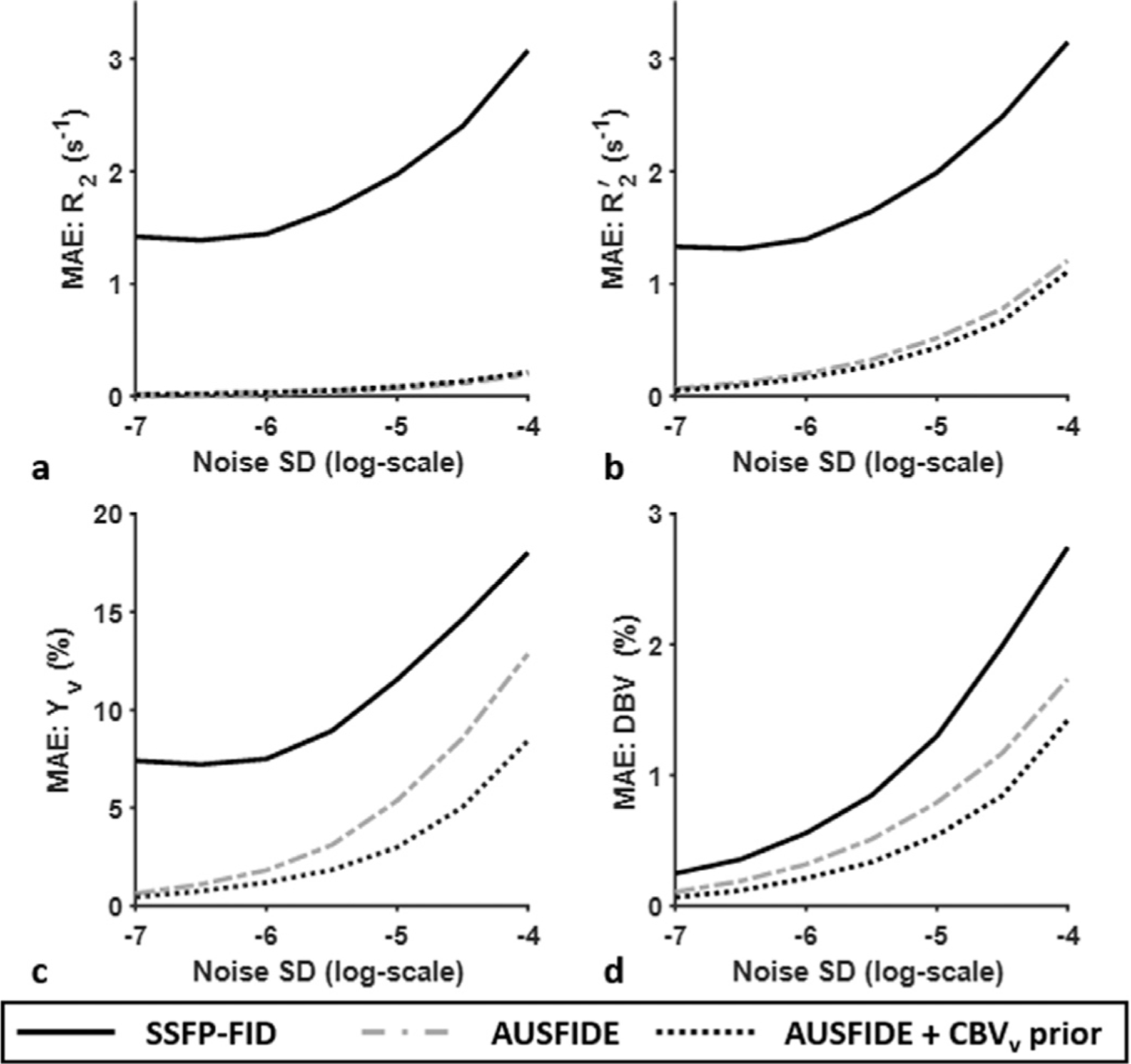
Simulated maximum absolute error (MAE) of R₂ (a), R₂′ (b), Y_v (c), and DBV (d) estimation with increasing noise levels from −7 to −4 (natural log scale), obtained by solving Eq. [5] 10,000 times independently using the SSFP-FID portion of AUSFIDE signals (mimicking R₂∗-based qBOLD) and the entire AUSFIDE dataset without and with prior information for DBV (i.e., CBV_v prior), respectively. See main text for detailed simulation setting. Compared with the R₂∗-based qBOLD approach with SSFP-FID, the R₂′-based method with AUSFIDE yields superior performance for all parameter quantifications (solid versus dash-dotted lines). Note further enhancement of measurement accuracy in Y_v and DBV with prior knowledge of CBV_v (dotted lines).

Fig. 3 plots MAE of Y_v (Fig. 3a), DBV (Fig. 3b), χ_nb (Fig. 3c), and R′_2,nh (Fig. 3d), obtained via the AUSFIDE-based qBOLD parameter estimation with respect to a bias in the CBV_v prior ranging from −40 % to 40 %, comparing three different approaches to solving Eq. [6]: 1) w = p = 0, 2) w > 0, p = 0, and 3) w > 0, p > 0. In all parameters but DBV, estimation errors in case 1 across the given error range of CBV_v are considerably larger than those predicted with the other two methods applying either constraints (i.e., Δχ or R₂′). The proposed approach (case 3), when compared with case 2, further reduces estimation errors of Y_v and $R_{2,nh}^{\prime }$, implying the effectiveness of constraining R₂′ additionally to Δχ in solving the qBOLD problem.

Fig. 3.

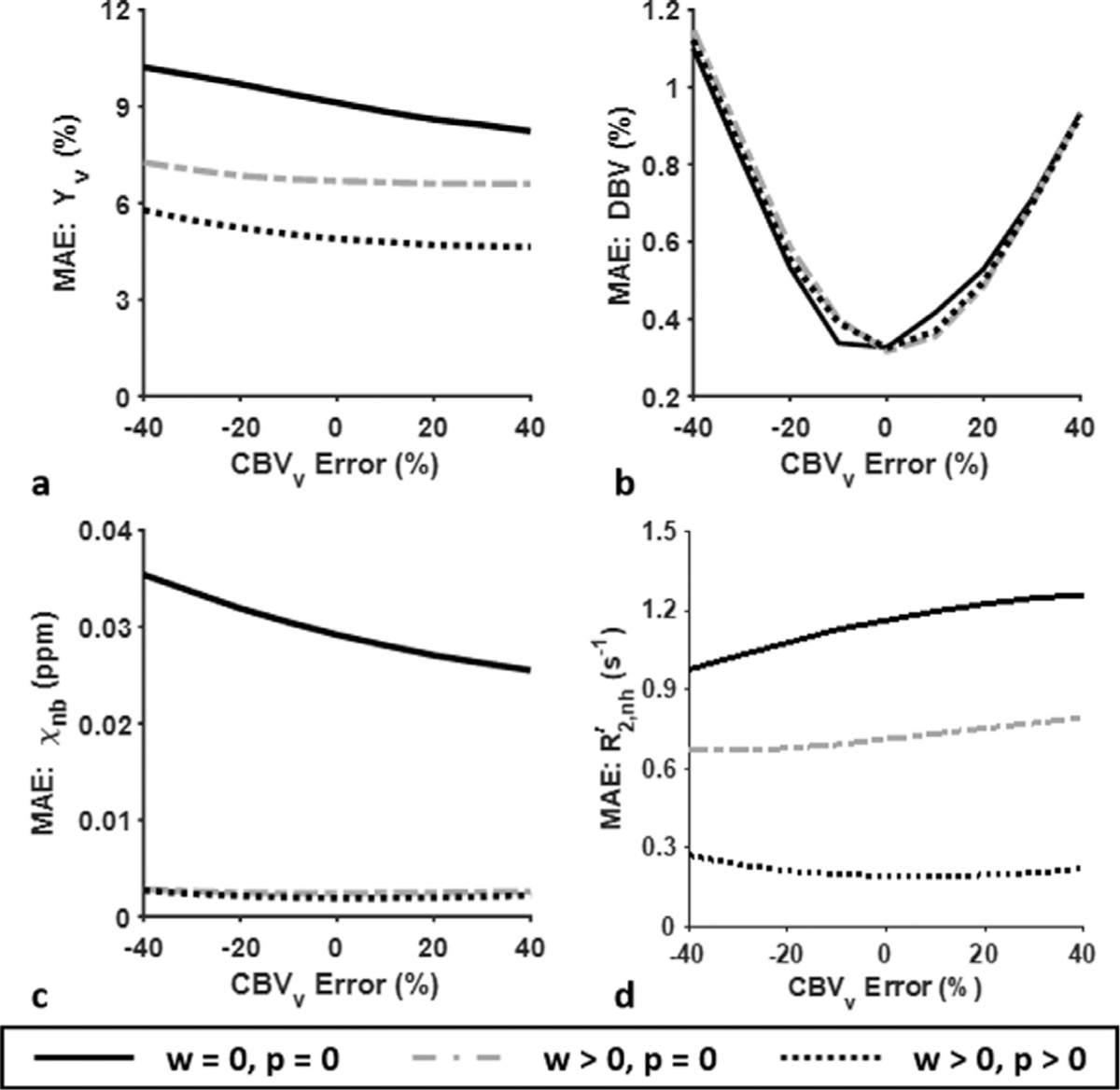
MAE of the estimated Y_v (a), DBV (b), χ_nb (c), and $R_{2,nh}^{\prime }$ (d) in AUSFIDE-based qBOLD with varying CBV_v errors ranging from −40% to 40%, obtained by solving Eq. [6] with three different combinations of the regularization parameters: 1) w = p = 0, 2) w > 0 but p = 0, and 3) w > 0 and p > 0, simulating conventional qBOLD, qBOLD+QSM, and the proposed qBOLD processing, respectively. Measurement SNR of 140 was assumed. See main text for further details in the simulations. All three cases yield comparable level of DBV estimation error (b). However, when compared to conventional qBOLD (solid lines), measurement accuracy of the remaining three parameters (a, c, d) is substantially increased with qBOLD+QSM (dash-dotted lines). Note also that MAE of Y_v and $R_{2,nh}^{\prime }$ is further reduced with the proposed method (dotted lines).

3.2. Experiments and analysis

Fig. 4 compares four sets of Y_v, DBV, and Δ χ_nb maps for which preliminary estimates are utilized in four different ways in solving Eq. [6]: no constraints (w = p = 0; Figs. 4a, 4e, 4i), Δχ -constrained only (w > 0, p = 0; Figs. 4b, 4f, 4j), both Δχ and R₂′ constrained (w > 0, p 0; Figs. 4c, 4g, 4k), and both Δχ and R₂′ constrained and inclusion of a CBV_v prior (Figs. 4d, 4h, 4l). Quantification without constraining any prior information (i.e., conventional qBOLD) results in physiologically implausible values in many voxels of all three parameter maps (Figs. 4a, 4e, 4i). Compared to conventional qBOLD, employing Δχ information (i.e., qBOLD+QSM) leads to the expected Δ χ_nb contrast (e.g., basal ganglia versus cortex; Fig. 4j), but no noticeable improvements in Y_v and DBV maps (Figs. 4b, 4f). With an additional application of R₂′ constraint, Y_v estimation is substantially stabilized yielding relatively uniform spatial distribution (Fig. 4c), but at the expense of physiologically unrealistic, nearly homogeneous DBV map (Fig. 4g). However, the proposed method, which makes full use of available prior knowledge (Δχ , R₂′, CBV_v), appears to improve DBV estimation (Fig. 4h) depicting some level of contrast between GM and WM as is the case in physiology (Leenders et al., 1990).

Fig. 4.

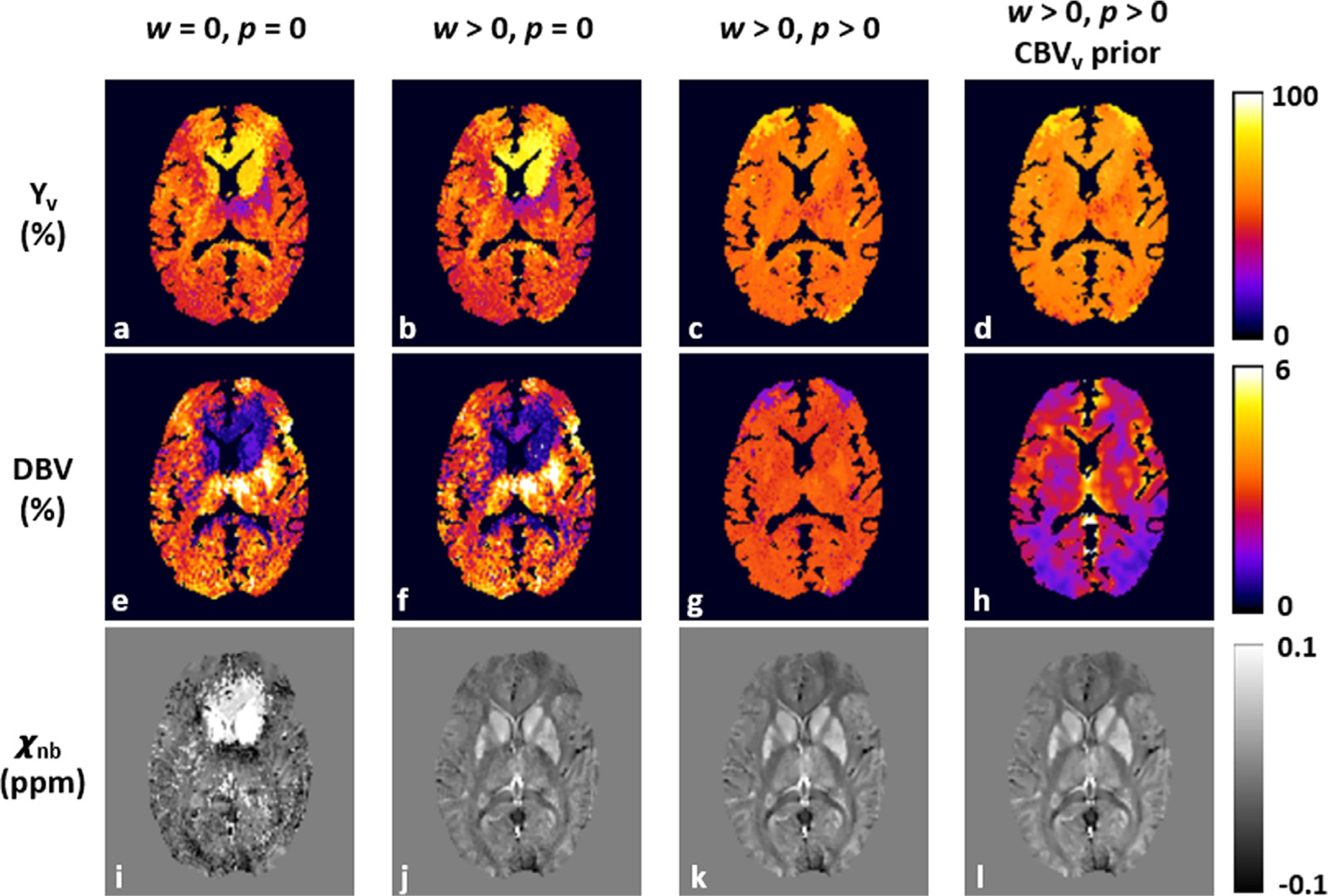
Parametric maps of Y_v (a-d), DBV (e-h), and χ_nb (i-l) in an axial plane of a representative study subject, obtained by solving Eq. [6] in four different ways of using prior information: no constraints applied (w = p = 0; first column), Δχ -only constrained (w > 0, p = 0; second column), both Δχ - and R₂′-constrained (w 0, p >0; third column), and both constraints applied with CBV_v prior (fourth column), representing conventional qBOLD, qBOLD+QSM, and the proposed qBOLD processing without and with prior knowledge of CBV_v, respectively. In the absence of any priors, all resultant maps exhibit artifactual values in many voxels (first column). The addition of Δχ and R₂′ constraints significantly stabilizes the qBOLD problem, leading to physiologically plausible contrast of χ_nb (i versus j) and Y_v (b versus c) maps, respectively, results consistent with the simulations in Fig. 3c and Fig. 3a. Nonetheless, the DBV map is nearly flat (g), which contradicts physiology. However, by using CBV_v prior information in addition to both constraints, the proposed method yields expected contrast in all parameter maps (last column).

Fig. 5 shows whole-brain 3D maps of Y_v (Fig. 5b), DBV (Fig. 5c), $R_{2,nh}^{\prime }$(Fig. 5d), and χ_nb (Fig. 5e) in the sagittal, coronal, and axial planes in two representative subjects, obtained using the proposed qBOLD method, along with the corresponding sectional images of T₁-weighted MP-RAGE on which six color-coded ROIs are overlaid (Fig. 5a). All parametric maps exhibit the physiologically expected contrast, i.e., nearly uniform Y_v, higher DBV in cortical GM relative to WM, and distinction of $R_{2,nh}^{\prime }$ in the basal ganglia, including caudate, putamen, and pallidum, versus cortical regions, in parallel with χ_nb estimates. Table 2 lists group averages (N = 10; mean ± SD) of the eight parameters pertinent to the proposed qBOLD processing: four preliminaries (CBV_v, R₂, R₂′, Δχ ) and four resultants (DBV, Y_v, $R_{2,nh}^{\prime }$, χ_nb). In all ROIs, qBOLD yielded elevated DBV and decreased R′_2,nh and χ_nb compared to their corresponding priors, CBV_v , R₂′, and Δχ. Fig. 6 displays a scatter plot of regional averages $R_{2,nh}^{\prime }$ against χ_nb across the six ROIs in the ten study subjects (r = 0.7, p<0.001), suggesting the expected relationship between the two parameters.

Fig. 5.

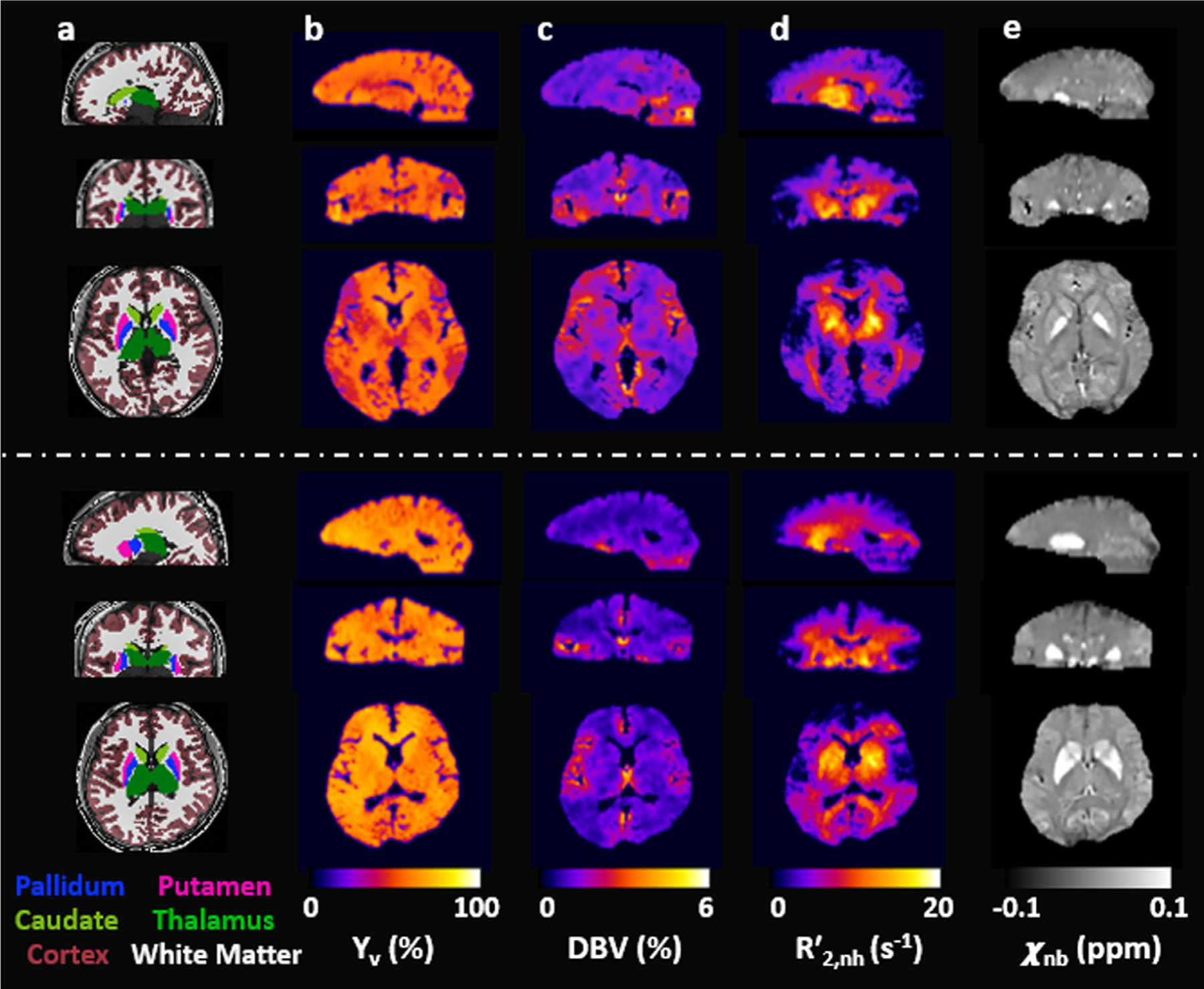
Five columns of whole-brain 3D images in the three orthogonal planes in two representative study subjects. a: color-coded six regions-of-interests (ROIs) overlaid onto T₁-weighted MP-RAGE images. b-e: Quantitative maps of Y_v, DBV, $R_{2,nh}^{\prime }$ and χ_nb, obtained using the proposed qBOLD method. Note that all parameter maps depict expected contrast across brain territories, i.e., near-uniform distribuction of Y_v (b), distinction between cortical gray and white matter in DBV (c), and highlighted deep brain structures in both $R_{2,nh}^{\prime }$ (d) and χ_nb (e).

Table 2.

Group averages (mean ± SD; N = 10) of the four preliminary parameters (CBV_v, R₂, R₂′, and Δχ ) and the four qBOLD-processed parameters (DBV, Y_v, ${\text{R}}_{2,\text{nh}}^{\prime }$, and χ_nb), quantified using the proposed method in the six ROIs (cortical GM, WM, pallidum, putamen, caudate, and thalamus).

ROI	Preliminary Parameters				qBOLD-Processed Parameters
	CBVv (%)	R2 (s−1)	R2′ (s−1)	Δχ (ppm)	DBV (%)	Yv (%)	$R_{2,nh}^{\prime }$ (s−1)	χnb (ppm)
Cortical GM	2.1 ±0.4	13.8 ±0.4	5.8 ±0.6	0.002 ±0.003	2.8 ±0.5	64.0 ±2.3	4.1 ±0.5	−0.012 ±0.017
WM	1.3 ±0.3	17.6 ±0.9	7.5 ±0.4	−0.006 ±0.003	1.8 ±0.4	62.1 ±2.8	6.0 ±0.6	−0.018 ±0.015
Pallidum	1.5 ±0.4	21.0 ±3.2	11.1 ±2.0	0.070 ±0.025	2.2 ±0.5	58.7 ±2.9	9.4 ±2.3	0.057 ±0.034
Putamen	1.7 ±0.4	18.7 ±2.2	8.4 ±1.9	0.029 ±0.014	2.4 ±0.5	60.2 ±2.8	6.4 ±2.1	0.018 ±0.022
Caudate	1.7 ±0.5	18.6 ±2.1	9.9 ±0.9	0.031 ±0.009	2.6 ±0.7	61.7 ±3.1	7.6 ±1.3	0.017 ±0.017
Thalamus	1.7 ±0.3	17.0 ±1.1	9.3 ±1.0	0.003 ±0.004	2.4 ±0.4	62.0 ±2.3	7.2 ±1.2	−0.010 ±0.016

Fig. 6.

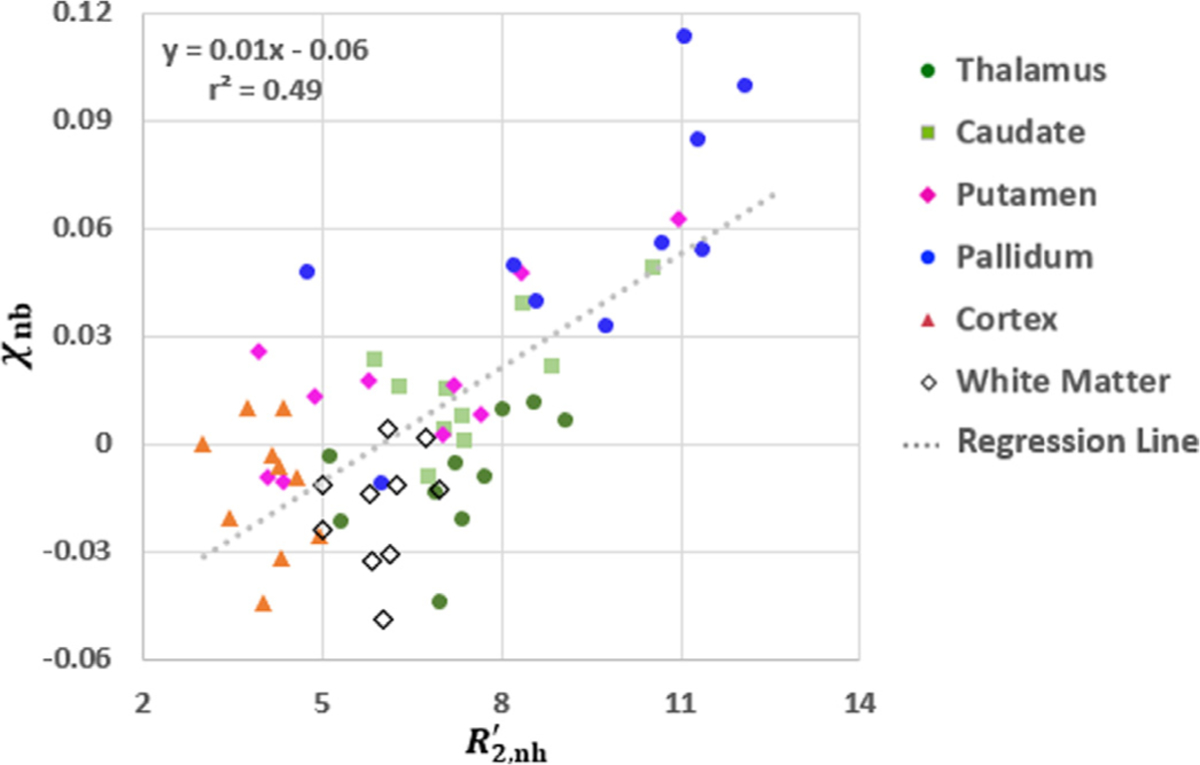
Correlation between $R_{2,nh}^{\prime }$, and χ_nb , quantified in the six ROIs (Fig. 5a) across 10 study participants. Each symbol represents a regional average in each subject. The linear regression (dotted line) is statistically significant (p<0.001), and the resultant equation along with r² value is provided at the top-left corner. Parameter estimates in deep brain structures (caudate, putamen, pallidum) present overall high values extending over a wide range of values across subjects.

Fig. 7 displays whole-brain 3D images in the three orthogonal planes in two study subjects: T₁-weighted magnitude (Fig. 7a), and CBF (Fig. 7b), Y_v (Fig. 7c), and CMRO₂ (Fig. 7d) maps. Consistent with the results in Fig. 5, Y_v obtained using the proposed qBOLD method is largely invariable across the entire brain. In contrast, CBF maps high-light GM/WM differences, thereby contributing predominantly to the contrast of the derived CMRO₂ maps. Table 3 compares TRUST’s global Y_v against the proposed method’s Y_v averaged across the entire brain voxels in the seven study volunteers, and summarizes individual averages of both CBF and CMRO₂ estimates in cortical GM and WM regions, respectively. Two-tailed, paired t-test suggests that the difference of whole-brain average Y_v values in TRUST and the proposed method is not statistically significant (p = 0.98).

Fig. 7.

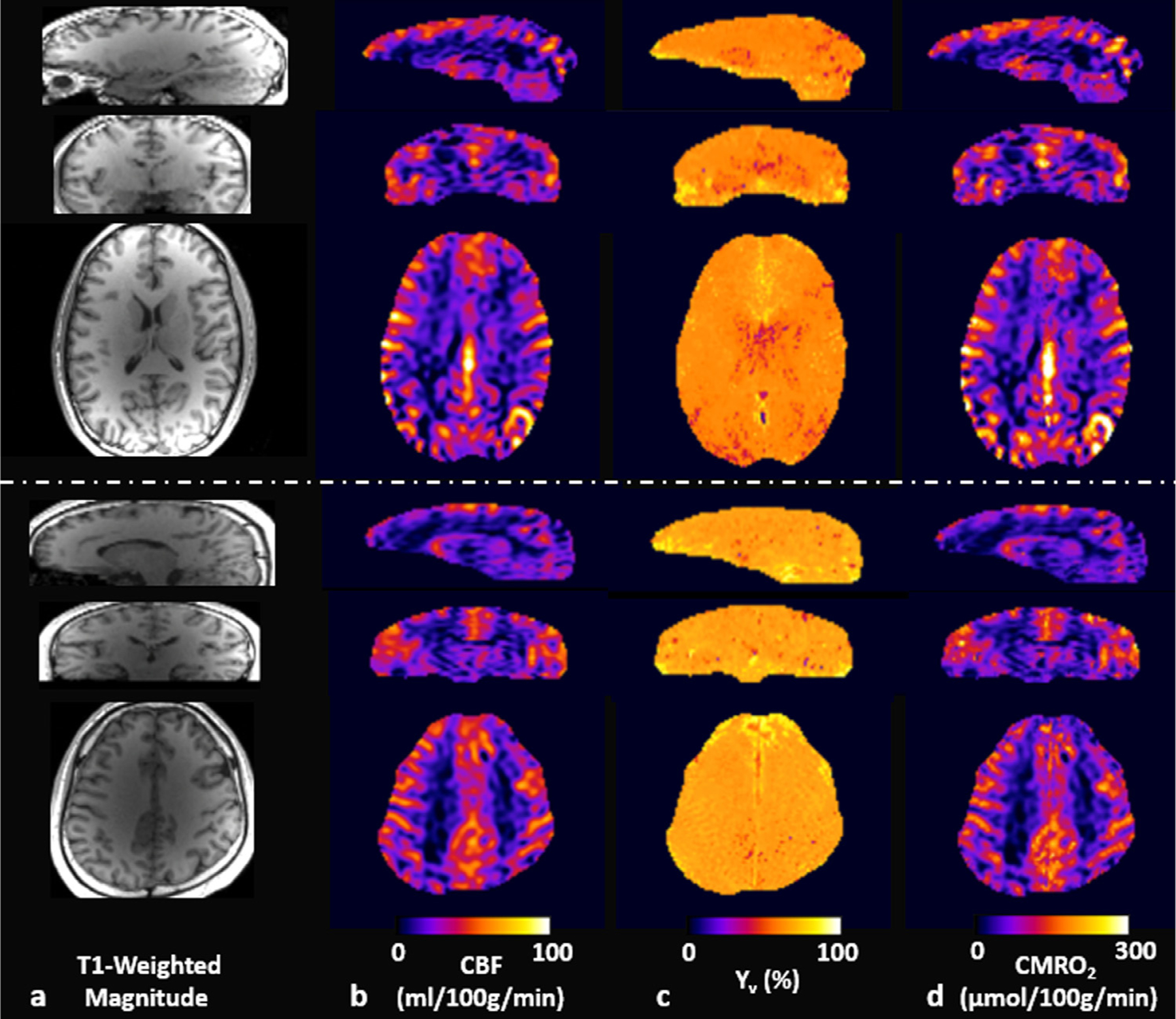
Whole-brain 3D images of two representative subjects in sagittal (top row), coronal (middle row), and axial (bottom row) planes. a: T₁-weighted magnitude images, b: pCASL-derived CBF maps, c: Y_v maps obtained via the proposed qBOLD method, and d: CMRO₂ maps computed by using the maps in b and c. Note that the CMRO₂ contrast, being physiologically plausible between gray and white matter regions, is largely determined by CBF measurements because of the relatively homogenous Y_v across the brain.

Table 3.

Regional means of Y_v, CBF, and CMRO₂ measurements in seven study subjects.

	Yv (%)		CBF		CMRO2
Subject #	TRUSTa	Proposed qBOLDb	Cortical GM	WM	Cortical GM	WM
1	56.0	61.7	34.7	25.7	111.3	82.1
2	67.4	68.6	37.6	18.5	105.7	52.7
3	61.7	60.7	44.0	26.7	131.0	87.4
4	66.2	62.9	42.8	23.3	134.9	80.5
5	62.2	57.5	52.1	26.3	174.3	91.9
6	56.7	61.7	46.1	27.2	135.7	79.9
7	64.6	62.0	49.9	27.7	146.5	81.6
Mean±SD	62.1±4.1	62.2±3.1	43.9±5.8	25.1±3.2	134.2±21.1	79.4±12.6

^aThe values were measured on the superior sagittal sinus, representing whole-brain global Y_v.

^bThe values were obtained by averaging voxel Y_v across the entire brain.

^a,bp-value from two-tailed, paired t-test: 0.98.

4. Discussion and conclusion

This work introduces a new, MRI-based, regional oximetry technique by means of 3D qBOLD parameter mapping. At the core of the present qBOLD method is the AUSFIDE pulse sequence that enables rapid, high-resolution 3D scanning for the full brain while providing prior information of voxel-averaged magnetic susceptibility (Δχ ) and associated parameters at different scales (R₂, R₂′, ΔB₀), which is difficult to achieve with the currently practiced 2D R₂′-based qBOLD (Stone and Blockley, 2017) as well as 3D R₂∗-based approaches (Cho et al., 2018; Ulrich and Yablonskiy, 2016). Furthermore, the proposed qBOLD model (Eq. [6]) decomposes both Δχ and R₂′ into dHb and non-dHb contributions, and constrains their respective estimates for stabilizing the solution process. In combination, along with additional, rapid CBV_v mapping, the proposed method achieves separation of several sources that complicate a voxel signal decay, i.e., 1) R₂∗ being resolved into R₂ and R₂′ , 2) R₂′ being separated into heme iron ($R_{2,h}^{\prime }$) and non-heme iron ($R_{2,nh}^{\prime }$∝ χ_nb ) contributions, and 3) $R_{2,h}^{\prime }$ being solved into DBV and Y_v, with all being relatively insensitive to macroscopic-scale magnetic field variations.

The group-averaged DBV values obtained using the proposed method (Table 2), while physiologically plausible (e.g., 2.8 % and 1.8 % for cortical GM and WM), differ from some of those in the literature. Indeed, different qBOLD methods, including the conventional approach (He and Yablonskiy, 2007), qBOLD+QSM (Cho et al., 2018), and Bayesian qBOLD (Cherukara et al., 2019), have so far reported disparate DBV estimates, ranging from 1.8 %, 4.5 %, up to 7.0 % for GM, which indicates that qBOLD parameter mapping is generally prone to error. Nonethe-less, the DBV values found in this work agree well with those (3.1 % and 2.0 % for GM and WM) obtained via an interleaved qBOLD method (Lee et al., 2018), which also employs prior knowledge of unknown parameters, albeit being limited to 2D single-slice quantification. Hence, in the framework of prior-guided qBOLD, the proposed technique is expected to be reproducible to some extent, warranting further validation studies.

In this study, the DBV estimates are higher than their CBV_v counterparts consistently across all six ROIs by approximately 30 – 50 % (Table 2). Ideally, higher DBV values relative to CBV_v are expected, because DBV should represent the portion of deoxygenated blood across the entire blood vessels in a voxel while CBV_v only captures post-capillary venules and downstream blood thereafter. Additionally, CBV_v itself may also have been underestimated due to the following two limitations inherent to VS-VSL: 1) post-capillary venular blood (which flows more slowly than the set cutoff velocity of the VS block), may not have been fully captured, and 2) the simplified CBV_v estimation model, which assumes equal T₁/T₂ relaxation times between brain tissues and venous blood, can lead to errors by up to 45 % according to the authors’ prior analysis (Lee and Wehrli, 2020). Despite the above sources of systematic underestimation, the CBV_v estimates obtained here clearly distinguish GM from WM regions, and serve as an effective initializer for DBV quantification (Fig. 4g vs. Fig. 4h), thus suggesting the need for providing CBV_v as prior information and updating it to DBV in the qBOLD processing. Alternatively, quantifying Y_v from separate measurements and providing the values to the qBOLD problem might be considered. However, methods based on venous blood T₂ mapping (Bolar et al., 2011; Guo and Wong, 2012), the only feasible alternative to qBOLD for voxelwise measurements of baseline Y_v in the microvasculature, would require impractically long scan times. In fact, the need for repeated scans with a range of T₂ preparation times is one possible reason that has limited their extension to 3D Y_v quantifications. Additionally, it has been numerically and experimentally shown that preliminary estimation of Y_v, when compared to the DBV prior (CBV_v), is less efficient in stabilizing the qBOLD problem (Lee et al., 2018).

The regional averages of AUSFIDE-derived preliminary parameters (R₂, R₂′, and Δχ ; Table 2) are consistent with those reported in our previous study (Lee and Wehrli, 2021). Furthermore, the χ _nb values obtained in this study agree well with those reported in the qBOLD+QSM paper (−0.02 ± 0.004 ppm and −0.019 ± 0.004 ppm for cortical GM and WM) (Cho et al., 2018). However, to the best of the authors’ knowledge, no $R_{2,nh}^{\prime }$ have been published elsewhere. Nevertheless, the measured $R_{2,nh}^{\prime }$ shows clear distinction across different brain territories (Fig. 5d and Table 2) while presenting the expected, strong correlation with χ_nb (Fig. 6), with the elevated values in the iron-rich, deep brain structures relative to cortical GM and WM areas. Furthermore, both $R_{2,nh}^{\prime }$ and χ _nb estimates in Table 2 are smaller than their corresponding priors, R₂′ and Δχ, across all six ROIs. The respective mean differences ranging from 1.5 to 2.3 s⁻¹ and from 0.011 to 0.014 ppm are plausible according to Eq. [8] and Eq. [7], thus suggesting that dHb-induced modulations of RF-reversible transverse relaxation rate and magnetic susceptibility have been correctly extracted from the qBOLD processing.

The group-averaged whole-brain Y_v obtained via the proposed qBOLD method (62.2 %; Table 3) is in good agreement with values obtained by TRUST (62.1 %; Table 3). When assuming Y_a ∼ 98 %, one obtains a mean OEF of 36.5 %, which is consistent with values reported for a range of imaging modalities: Dual-calibrated fMRI: 35 % (Gauthier and Hoge, 2012) and 38 % (Bulte et al., 2012), other qBOLD MRI techniques: 38.3 % (He and Yablonskiy, 2007) and 39.3 % (Cho et al., 2018), as well as PET-based measurements: 35.7 % (Perlmutter et al., 1987) and 30 – 40 % (Raichle et al., 2001). Given the nearly uniform spatial distribution of Y_v, CMRO₂ contrast in the normal brain is largely driven by CBF (Fig. 7). The group average of the CMRO₂ estimates in cortical GM (134.2 ± 21.1 µmol/100 g/min; Table 3) also agrees well with the values measured by means of dual-calibrated fMRI: 145 ± 30 (Gauthier and Hoge, 2012) and 155 ± 39 (Bulte et al., 2012), and ¹⁵O PET: 133 ± 20 (Ito et al., 2004) and 128 – 144 (Leenders et al., 1990), all in units of µmol/100 g/min. In WM, on the other hand, the mean CMRO₂ of 79.4 ± 12.6 µmol/100 g/min (Table 3) is somewhat higher than the values obtained via ¹⁵ O PET: 57 ± 10 µmol/100 g/min (Leenders et al., 1990) and 62 ± 11 µmol/100 g/min (Hatazawa et al., 1995). The discrepancy has likely resulted from CBF measurement errors because with current ASL techniques it is challenging to achieve accurate CBF mapping for WM region (Alsop et al., 2015). In fact, some of WM voxels presented negative CBF values, and thus were excluded in the statistical analysis of this study.

A close look at Fig. 4 suggests that the R₂′ constraint acts as a strong smoothing operator for both Y_v (Fig. 4b versus Fig. 4c) and DBV (Fig. 4f versus Fig. 4g) maps. The results may also imply that constraining measured R₂′ has compromised the sensitivity of the original qBOLD model to DBV. Nonetheless, additionally measured CBV_v serves as an initializer for DBV (Fig. 4h), suggesting that it has complemented the model’s limited sensitivity. However, it is uncertain whether that is the case for Y_v as Y_v is well-known to be rather homogeneous in healthy brains. Therefore, further investigation would be needed to ascertain the effect of regularization on Y_v estimation, particularly in the brain where Y_v is regionally altered, for example, due to ischemic lesions. A validation study that can be performed before testing on patients would be experiments with gas-breathing challenges, in which relative to baseline, Y_v alteration is expected in response to gas mixtures (e.g., hyperoxia and hypercapnia).

Several studies (Dickson et al., 2010; Dickson et al., 2011; Stone et al., 2019) have shown that the static dephasing regime is not valid for small vessels (approximately < 30 µm) where the effect of water diffusion becomes significant. Furthermore, the diffusion-induced signal modulation is dependent on data sampling time, being relatively higher for echoes collected after the refocusing RF pulse compared to FID samples (Dickson et al., 2010; Dickson et al., 2011). As a result, the GESFIDE/GESSE methods under the static dephasing regime are potentially prone to systematic errors in qBOLD parameter estimation. The AUSFIDE pulse sequence acts similar to the GESFIDE data acquisition in that it samples time-courses of FID (SSFP-FID) and RF-refocused signal (SSFP-ECHO) until before a SE point. Hence, one could expect that the proposed qBOLD method, which does not take the diffusion effect into account in the signal model, would cause systematic errors comparable to those in GESFIDE in the very small vessel regime. Nevertheless, since in AUSFIDE steady-state signals following a number of spin pathways contribute to SSFP-FID and SSFP-ECHO, the effect of water diffusion is complicated by spin history, making it difficult to predict to what extent the present qBOLD mapping is affected. This is an issue that would need further scrutiny, possibly via simulations accounting for water diffusion in the AUSFIDE signal model.

It has been shown that R₂ also presents a dependence on blood oxygenation levels, manifesting itself as a significant BOLD contributor (Kida et al., 2000). In fact, blood oximetry relies on the measurement of R₂ (Wright et al., 1991), and some techniques for the quantification of brain iron make use of the modulation of R₂ via diffusion in microscopic induced fields from brain iron stores (Vymazal et al., 1996). Given these prior studies, our quantification model can be expanded such that an additional constraint is added to enforce measured R₂ to the sum of heme and non-heme contributions. Here, a calibration model relating blood R₂ (heme-originated R₂) to Y_v could be employed. The additional R₂ constraint may help the present method further enhance sensitivity to the qBOLD parameters. On the other hand, this approach adds one more parameter (non-heme-related R₂) to the solution set as well as one more regularization parameter to be determined, and thus would result in increased computational complexity. Additionally, quantification errors may be propagated from the employed R₂-Y_v calibration model. Given the above considerations, the impact of additional R₂ constraint on the qBOLD parameter estimation would need to be investigated in future studies.

The qBOLD model in this study does not account for signal contributions from extracellular fluid or intravascular compartments. Compared to the extravascular tissues, intravascular venous blood contribution to baseline AUSFIDE signals remains close to noise levels, because of its relatively low T₂/T₁ ratio and small DBV. By contrast, signal contribution from the extracellular space would not be insignificant, considering the fact that interstitial fluid and cerebrospinal fluid present a high T₂/T₁ ratio. Additionally, an offset frequency of the extracellular fluid may result in modulation of the signal decay. Given the above considerations, it appears desirable to account for the extracellular compartment in the AUSFIDE-based qBOLD analysis. Nevertheless, it would need further scrutiny whether the qBOLD mapping benefits from the inclusion of additional signal sources relative to increased complexity and potential errors resulting from an accordingly increased number of fitting parameters.

The present 3D qBOLD method may find further improvements in data acquisition, modeling, and data processing. First, data collection for AUSFIDE and VS-VSL, currently separated, may be integrated into one single pulse sequence by inserting the AUSFIDE component into the long dead time in VS-VSL (∼1.65 seconds; Fig. 1b) in a segmented manner. Doing so would break down the steady-state nature of the AUSFIDE data, which, however, should not alter the signal time-course along echoes within each TR, and thus would not penalize qBOLD analysis. Second, the current qBOLD model may be expanded to account for multiple compartments in WM (e.g., myelin water) and local frequency shift (and thus R₂′) depending on the fiber orientation relative to B₀ (Lee et al., 2017b). Since the multi-echo AUSFIDE data can also be utilized for myelin water fraction mapping (Alonso‐Ortiz et al., 2015), the information from the procedure may serve as additional prior information to address such confounders in WM qBOLD mapping. Finally, while the stack-of-stars trajectory in the current implementation of AUSFIDE makes it relatively insensitive to physiologic bulk fluid motion (Lee and Wehrli, 2021), it is still sensitive to subject’s involuntary head movements. Full 3D radial encoding can be considered as an alternative, which enables data-driven detection and correction of large-scale head motion (Lee et al., 2020) as well as isotropic spatial resolution of quantified parameter maps, albeit at the cost of increased scan times.

In conclusion, we introduced a new, noninvasive, MRI-based approach to mapping resting-state brain oxygen metabolism by means of prior information guided 3D qBOLD. The AUSFIDE data acquisition strategy permits rapid 3D qBOLD scanning and preliminary parameter estimation (R₂, R₂′, Δχ , ΔB₀), and constraining prior information (R₂′, Δχ , CBV_v) to the parent qBOLD model is effective in stabilizing the qBOLD problem, leading to expected contrast of all measured parameters across brain territories. Although results suggest feasibility of the AUSFIDE-based qBOLD technique as a practical means to measuring brain oxygen utility, the method would benefit from further validation in terms of modeling (i.e., assumption of static dephasing regime and inclusion of extracellular compartment as discussed above) and its sensitivity to focal abnormalities in which tissue oxygen metabolism is regionally altered, for example, due to arterial stenosis/occlusion.