Optimizing the surgical instrument tray to immediately increase efficiency and lower costs in the operating room

Abstract

Background:

Surgical trays are often poorly configured and can be ongoing sources of frustration and excess costs. We conducted an observational study to determine if the use of a customized mathematical inventory optimization model would result in a greater reduction in the number of instruments on a surgical tray than a clinician review of the tray.

Methods:

Utilization of instruments on the major orthopedic tray at a large academic hospital was documented over 80 procedures. Processes in the medical device reprocessing department and operating room were observed to comprehensively quantify all associated costs. Results of the observations were applied to a customized mathematical model to determine the ideal tray configuration. For comparison, a clinician review was also performed.

Results:

The mathematical model alone produced an ideal tray size of 47 instruments, a reduction of 41 instruments from the original size of 88 instruments (47% reduction). This represented $34 440 in annual savings. In contrast, the clinician review alone suggested an ideal tray size of 67 instruments (23% reduction), representing $17 640 in annual savings. When clinicians were provided with the additional information from the model, they reduced the tray size to 51 instruments (42% reduction), producing $31 870 in savings. The mathematical model yielded an additional 22% instrument reduction and $14 230 in savings compared with clinician review alone.

Conclusion:

Our mathematical model is generalizable and can be applied to all specialties and hospitals to determine optimal tray configuration. As such, the financial implications are broad; at our institution, application to all surgical trays would result in $205 000 of savings annually. Surgeons and managers looking to streamline surgical trays should consider this evidence-based approach.

Many hospitals are placing increased emphasis on cost reduction initiatives. Perioperative services are often examined, as they typically comprise a substantial proportion of a hospital’s budget.^1,2 Furthermore, surgical instruments comprise a large portion of perioperative budgets.³ In general, instruments frequently used together are aggregated into a “tray,” while items less frequently used are wrapped individually as peel-packs.⁴ Historically, items have been added to a surgical tray on an ad hoc basis according to surgeon requests, which can result in excessively large and inefficient trays. This method is not economically sustainable.⁵

Hospitals can minimize inefficiency and reduce costs by addressing poorly configured surgical trays.⁶ The challenge in determining the ideal contents of a surgical tray lies in finding the right balance between having the necessary instruments available to perform a procedure and having infrequently used instruments batched unnecessarily on a tray. A solution must take into account the conflicting issues of clinical need, costs, ease of batching, prevention of adverse clinical events and minimization of wear and tear on instruments.⁷

Clinician review and cost analysis are 2 methods that have been used historically to optimize surgical trays.^5,6,8–10 Clinical review typically involves using a systematic method such as Lean methodology to facilitate a group of surgeons auditing their surgical trays.⁶ However, this method relies on self-reporting rather than direct observation and is plagued by recency bias.¹¹ Several cost-based approaches have also been described, although they do not make use of mathematical optimization formulae that account for major cost drivers such as instrument depreciation.^4,8 The aim of this study was to determine the impact of a customized single-period inventory model (the newsvendor model) in optimizing the major orthopedic (MO) tray at our institution.¹² We hypothesized that application of the customized mathematical model would result in a greater reduction in the number of instruments on the MO tray than clinician review only.

Methods

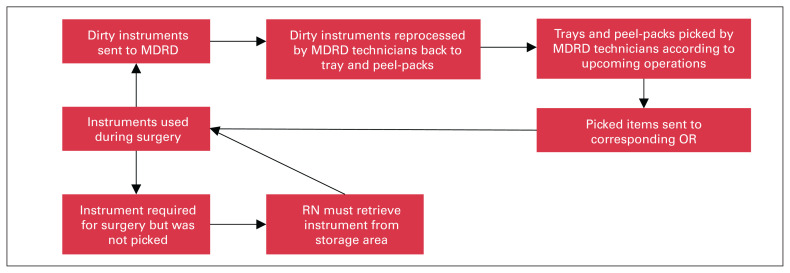
This was a single-site observational study conducted at a large academic hospital in a major metropolitan city, which performs more than 3000 procedures requiring the MO tray annually. The MO tray was used by 8 surgeons, each of whom had been in practice for a minimum of 2 years and a maximum of 25 years, for all orthopedic procedures including hip and knee arthroplasty, trauma and orthopedic oncology. This study was performed with the assistance of the managers of the operating room (OR) and the medical device reprocessing department (MDRD). At our institution, surgical instruments are used in the OR and subsequently reprocessed in the MDRD after the case. A synopsis of the instrument cycle between the OR and MDRD is shown in Figure 1.

Fig. 1.

Simplified process map illustrating instrument flow between the OR and MDRD. MDRD = medical device reprocessing unit; OR = operating room; RN = registered nurse.

Data collection

A trained observer was present in the OR during 80 procedures requiring an MO tray. To reflect our institution’s annual case mix, 20 procedures were randomly selected from each subspeciality of hip arthroplasty, knee arthroplasty, trauma and orthopedic oncology. The observer documented the following variables: procedure type, surgeon name, instruments used, pick list contents, pick list–related adverse supply events (instrument required but not picked for case or instrument picked for case but not required), tray-related adverse supply events (contamination, missing instrument, broken instrument) and intraoperative item retrieval time. An instrument was defined as used if it touched the surgeon’s hand. In addition, a trained observer was present in the MDRD over a 3-week period during standard workload times and observed 550 instances of tray reprocessing. The variables collected were as follows: instrument name, time to decontaminate, time to assemble, total tray assembly time and list assembly time.

Mathematical optimization model

A single-period order inventory optimization model was applied to determine optimal surgical tray configuration for the MO tray, with a customized formula to account for all related costs of overage and underage.¹³ The optimal inventory quantity of each instrument on a surgical tray was calculated with the following equation: Q = m + z × σ; where m is the mean utilization of that instrument over the surgeries observed, z is the service level (number of standard deviations from the mean) and σ is the standard deviation of utilization. A normal distribution was used to represent the probabilities of a surgical instrument being used. The formula used to calculate service level is z = F⁻¹ (C_overage ÷ [C_overage + C_underage]); where F⁻¹ (x) is the inverse normal distribution function and C is cost. All costs are reported in Canadian dollars.

Cost of overage

The cost of overage is the cost associated with having an instrument on the tray when it is not needed. A formula was created to capture the main determinants of instrument overage cost: C_coverage = C_reprocessing + C_{contamination} + C_depreciation. A deconstruction of the formula into subformulae and an explanation of the variables follows.

Reprocessing cost

We performed a time study of 550 observations of instrument reprocessing events across 4 randomly selected MDRD technicians. Time was measured using a stopwatch with the time beginning when the technician touched an instrument and ending when the instrument was clean and left the technician’s hand. This was multiplied by the MDRD technician wage to determine the reprocessing cost. This can be represented by the following equation: C_reprocessing = t_reprocess × W_{MDRD technician}; where t_reproces is the reprocessing time in minutes and W_{MDRD technician} is the wage of the technician per minute.

Contamination cost

If a tray is found to be contaminated, the entire tray needs to be removed from the OR and replaced with a new tray. This has 2 consequences from a cost perspective. First, there are costs associated with reprocessing an additional tray. Second, there are costs associated with an OR delay while the new set arrives. The equation for contamination cost is C_{contamination} = P_{tray contaminated} (C_reprocessing + C_{OR time} × t_delay) ÷ N_instruments; where P_{tray contaminated} is the probability that a tray is contaminated, C_{OR time} is the cost of OR time per minute, t_delay is the OR delay in minutes and N_instruments is the number of instruments on the tray. During observation of the 80 procedures, all incidents of contamination were documented and the subsequent OR delay was timed; the delay period started the moment the contamination was noted and ended when a replacement tray was brought into the OR, opened and ready for use. The cost of OR time was requested from the accounting office, which collects case costing data and calculates cost using a standard top–down costing technique.¹³

Depreciation cost

The cost of overage must take into account depreciation expense, as wear and tear occurs every time an instrument is used and reprocessed. The formula to represent this is C_depreciation = C_{instrument purchase} ÷ N_{designated uses}. The device procurement office provided the researchers with the instrument purchase cost (C_{instrument purchase}) as well as the maximum number of uses recommended by the manufacturer (N_{designated uses}), which was used as a proxy for the lifespan of the instrument.

Cost of underage

The cost of underage is the cost associated with the instrument not being on the tray when it was needed and is represented by C_underage = C_peel-packing + C_picking + C_retrieval. This custom subformula is explained in the following sections.

Peel-packing cost

Peel-packing is the alternative to having an item stored on the surgical tray. It involves manually placing the individual reprocessed instrument in a disposable sterile package. The cost is a sum of the disposable wrapper procurement price (C_{peel-pack consumabl}) and the cost of reprocessing as described in the cost of overage section: C_peel-packing = C_{pee-pack consumable} + C_reprocessing.

Picking cost

The cost of picking a peel-packed instrument was calculated with the following equation: C_picking = t_pick × W_{MDRD technician} ÷ N_{items on pick list}; where t_pick is the time required to pick the instrument in minutes, W_{MDRD technician} is the wage of the technician per minute and N_{items on pick list} is the number of individual peel-packed items on the pick list. The time required for the MDRD technician to pick a surgical instrument that was peel packed was determined using a time study of 20 randomly selected surgery picks performed by 4 technicians.

Retrieval cost

When an instrument was not immediately available from a tray and not present among the picked instruments but was required for the operation, the circulating nurse retrieved it from where it was stored. The retrieval cost was defined as C_retrieval = P_{not picked} × t_retrieve × W_RN; where P_{not picked} is the probability that an instrument was needed but not picked, t_retrieve is the time required to retrieve an instrument in minutes and W_RN is the wage of the circulating nurse per minute. The t_retrieve variable was determined using a time study of 20 randomly selected retrieval events and P_{not picked} was measured during the observation of 80 surgeries.

Clinician review

Four orthopedic surgeons and 3 OR nurses volunteered to independently assess the surgical tray configurations and provide their opinion on the ideal tray configuration. This was done in 2 parts. First, each participant was provided the current configuration and asked to determine the ideal quantity of each instrument using only their qualitative experience. Following this, the participant was provided the results of the mathematical analysis and asked to complete the same task again. For an instrument to be removed from the tray, all 7 clinicians had to be in full agreement.

Results

Three different tray configurations were created on the basis of the optimization method: mathematical model alone, clinician review alone and combined approach. The mathematical model alone produced an ideal tray size of 47 instruments, a reduction of 41 instruments from the original size of 88 (47% reduction). In contrast, the clinician review alone suggested an ideal tray size of 67 instruments (23% reduction). When the clinicians were provided with the additional information from the mathematical model (combined approach), they reduced their tray size to 51 instruments (42% reduction).

Mathematical model

Overage and underage costs were used to determine a unique service level for each instrument, which ranged between 75.1% and 62.6%. This was in turn used to calculate the service level (z) and subsequent ideal quantity for each instrument, which produced a mathematically optimal tray containing 47 instruments.

A detailed summary of the results of the overage and underage cost calculations underlying the service level determination is provided in Table 1. The overage costs to reprocess each instrument varied between $0.48 and $1.02; the variation was due to variations in the type of instrument (simple or complex) and the purchase cost of that instrument. The underage costs varied between $1.47 and $1.71, with the variation similarly due to variations in the type of instrument (simple or complex).

Table 1.

Summary of variables used in overage and underage cost calculations

Variable	Value
Overage costs, $	0.48–1.02
Reprocessing cost, $
Simple instruments*	0.19
Complex instruments†	0.43
Time to reprocess, s
Simple instruments*	38
Complex instruments†	86
MDRD technician hourly wage, $‡	30.00
Contamination, $	0.26
Probability of contamination, %	5
Duration of time delay, min	15.35
OR time cost per minute, $	34.00
Cost to reprocess tray, $§	50
Depreciation, $	0.03–0.33
Cost of purchase, $‡	30–330
Designated no. of uses	1000
Underage costs, $	1.47–1.71
Peel-packing cost, $
Simple instruments*	0.99
Complex instruments†	1.24
Disposable packaging cost, $‡	0.80
Picking cost, $	0.11
Time to pick single item, min	5.5
No. of pick list items, mean	15
Retrieval time cost, $	0.33
Probability of occurrence, %	11
RN time to retrieve, min	4
RN hourly wage, $‡	45

MDRD = medical device reprocessing department; OR = operating room; RN = registered nurse.

^*Nonhinge, single-hinge and nonluminal instruments.

^†Multiple-hinge, luminal or sharpness-tested instruments.

^‡These data were provided by the accounting department.

^§Includes substantial fixed overhead costs that are difficult to allocate to a single tray. As such, the value used was based on the literature.⁷

Comparison of tray configurations

Table 2 compares the tray contents by listing the quantity of each instrument, and Figure 2 compares the current MO tray with the 3 different optimized tray configurations. Table 3 compares the reprocessing costs of the 3 tray configuration options with the costs of the original tray. The proposed annual savings using the mathematically ideal MO tray would be $34 440 whereas with clinician review it would be $17 640. The combined approach would yield savings of $31 870.

Table 2.

Ideal quantities of each surgical instrument on the major orthopedic tray

Instrument	Current quantity	Ideal quantity; optimization approach
		Mathematical model alone	Clinician review alone	Combined
Straight Mayo scissors	1	1	1	1
Curved Mayo scissors	1	1	1	1
Metz scissors	1	0	0	0
Needle drivers	3	3	3	3
Bulldog forceps	1	0	1	0
Sponge sticks	4	2	2	2
Lauer forceps	2	1	2	1
Kelly forceps, short	6	2	4	2
Kocher forceps	2	2	2	2
Long	2	2	2	2
Short	4	2	4	2
Curved Crile hemostatic forceps	6	2	4	2
Sharp towel clips	4	2	4	2
Dull Edna towel clips	2	1	2	2
Jackson retractors
Small	2	1	2	2
Medium	1	1	1	1
Large	1	1	1	1
Right-angle (Langenbeck) retractors	2	1	2	2
Right-angle retractors, long	2	1	2	2
Israel rake retractors	2	1	2	0
Bone cutter, large	1	0	0	0
Leksell rongeur	1	1	1	1
Double-action rongeur, small	1	0	1	0
Pointer hohman retractors, small	4	3	4	4
Ruler	1	1	1	1
Cobb elevator
3/4”	2	0	1	1
1/2”	1	0	1	0
3/8”	1	0	1	1
Bone curette
No. 1	1	0	1	1
No. 2	1	1	0	0
No. 3	1	1	0	0
No. 3 blade handles	3	1	1	1
No. 3 long blade handles	1	1	1	1
Bayonet forceps	1	1	0	1
Bonnie forceps	2	1	2	2
McKenzie forceps
Nontoothed	1	2	0	0
Toothed	1	1	1	1
Forceps
Short nontoothed	1	1	0	0
Short toothed	2	0	1	0
Long toothed	1	0	1	1
Adson forceps
Nontoothed	1	0	0	0
Toothed	2	2	2	2
No. 9 suction tip	1	0	0	0
No. 11 short suction tip	2	1	1	1
Six-prong rake retractors	2	2	2	2
Four-prong rake retractors	2	0	2	0
Howarth elevators	2	2	2	2
Total	88	47	67	51

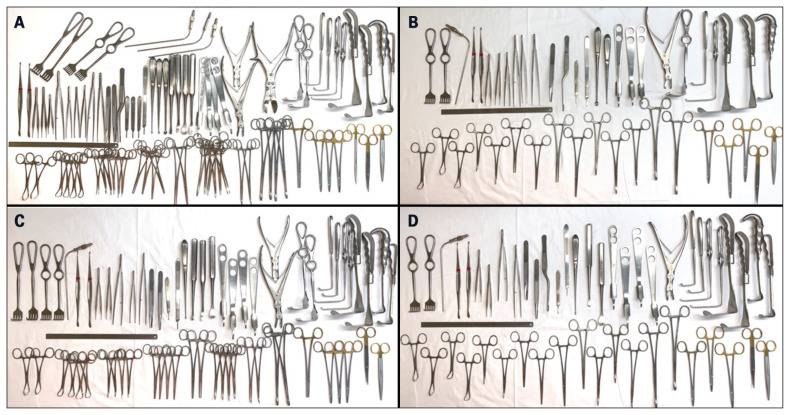
Fig. 2.

(A) Current MO tray. (B) Ideal MO tray determined via the mathematical model. (C) Ideal MO tray determined by clinician review. (D) Ideal MO tray as determined by clinician review with additional information from the mathematical model (combined approach). MO = major orthopedic.

Table 3.

Comparison of trays configurations by instrument quantity and cost savings

Measure	Current	Optimization approach
		Mathematical model alone	Clinician review alone	Combined
Quantity of instruments on tray	88	47	67	51
Reduction in quantity, %	NA	47	24	42
Reprocessing cost per year, $	150 000	115 560	132 360	118 920
Savings per year, $	NA	34 440	17 640	31 870

NA = not applicable.

Discussion

The aim of this study was to determine the impact of a customized single-period inventory model (newsvendor model) in optimizing the MO tray at our institution. We correctly predicted that application of the customized mathematical model, with or without a concomitant clinician review, would result in a greater reduction in the number of instruments on the MO tray than clinician review alone. Previous studies have attempted to optimize surgical tray configuration, either through a cost analysis or a clinician review alone approach. Our study shows the results of both methods, as well as the results of a combined approach.

With the mathematical model we attempted to capture the true underage and overage costs to determine an accurate service level to calculate instrument inclusion on or exclusion from a tray. There are multiple cost drivers associated with a surgical tray, and each can be difficult to measure.^4,8,14 By customizing calculations of overage and underage costs to the major processes involved in surgical tray assembly, processing and utilization in the OR, our model incorporates major relevant costs and creates a novel, comprehensively optimized surgical tray. We expand on the work of previous studies that attempted to assess instruments while taking into account variation such as complexity of reprocessing.¹⁴ Our model builds upon this principle by assessing each instrument on an individual basis, including purchase cost, which can account for 45% of underage cost variation. For example, a simple retractor costs $30 while a cannulated wire passer is $330, according to our institution’s procurement data. It would be ideal to avoid wear and tear on the more expensive instrument, as depreciation on a more expensive instrument leads to a relatively high underage cost. This individualized cost and labour analysis accounts for our model’s range of service levels on the basis of each instrument.

Clinician review entails sorting instruments according to clinical judgment or a utilization cut-off number, usually between 20% and 25%.^6,10,15 When combined with a systematic approach such as Lean, it can result in successfully reducing the number of unnecessary surgical instruments.^6,10 This methodology also ensures that no essential instruments are removed from the surgical tray, which is an important safety consideration. However, 1 of the shortcomings of this methodology is the potential for surgeon availability bias and substantial variability between surgeon users. Furthermore, this method typically does not maximize potential cost savings as the reduction is fairly modest. In our study, clinician review alone resulted in a 24% reduction in the number of instruments. When evidence in the form of the ideal tray configuration via the mathematical model was provided to those same clinicians, there was an additional reduction of 18%. Notably, combining clinician review with our mathematical model helps ensure that essential instruments that are critical, but rarely used, are not incorrectly removed.

Limitations

Our study is not without limitations. First, a normal distribution was used to approximate the probability distribution of surgical instrument utilization in any given surgery. Although the Poisson distribution may be more precise, our sample size was large enough to use the normal distribution.¹² Second, only labour costs were considered relevant by the model as consumable costs (i.e., water, electricity and detergent) are related to the number of trays reprocessed, irrespective of the number of instruments per tray; any optimization would not reduce these costs. Third, with respect to the reprocessing time measurement, we only took into account time to decontaminate and assemble. We excluded management time, quality checks and other miscellaneous tasks such as set-up time as these are fixed and independent of the number of instruments per tray. However, in a larger scale application of tray optimization, these factors may become variable rather than fixed and require consideration. Fourth, although actual instrument lifespan would be preferable in our depreciation calculations, we employed recommended maximum uses as a proxy for instrument lifespan because the instrument-level tracking required for actual lifespan calculation is not available at our institution. Fifth, in our cost modelling we excluded certain events that occurred at low frequency. For example, a contaminated instrument can result in a surgery cancellation or OR delay, which has downstream financial and workflow impacts. To determine the actual relationships between surgical tray size and such low-frequency events, a study would require a considerably larger series of observations, which is not practical. Furthermore, the impact on the optimization calculation would be minimal as the events occur at such low frequencies. Lastly, any institution using this approach would need to do their own data collection, as the variables would differ among institutions.

Conclusion

As the trend toward promoting efficiency in health care accelerates, the OR continues to have many opportunities for positive change. Surgical tray inefficiency is a major issue in most perioperative service departments. As such, the results of our study have broad financial implications as our mathematical approach can be applied to any surgical tray at any hospital. For example, if this model was applied to all surgical trays at our institution, conservative projections estimate cost savings of $205 000 annually. Surgeons, nurses and managers looking to streamline surgical trays should consider this combined mathematical and clinician review approach. We have planned a follow-up study as we apply this methodology to all surgical trays at our institution.