Bayesian analysis of longitudinal and multidimensional functional data

Summary

Multi-dimensional functional data arises in numerous modern scientific experimental and observational studies. In this article, we focus on longitudinal functional data, a structured form of multidimensional functional data. Operating within a longitudinal functional framework we aim to capture low dimensional interpretable features. We propose a computationally efficient nonparametric Bayesian method to simultaneously smooth observed data, estimate conditional functional means and functional covariance surfaces. Statistical inference is based on Monte Carlo samples from the posterior measure through adaptive blocked Gibbs sampling. Several operative characteristics associated with the proposed modeling framework are assessed comparatively in a simulated environment. We illustrate the application of our work in two case studies. The first case study involves age-specific fertility collected over time for various countries. The second case study is an implicit learning experiment in children with autism spectrum disorder.

1. Introduction

We investigate Bayesian modeling and inference for longitudinal functional data, conceptualized as functional data observed repeatedly over a dense set of longitudinal time points. A typical dataset would contain 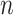patients observed over the course of multiple visit times, with each visit contributing a functional datum. Thus, for patient 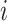we would record the outcome 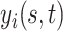, where 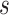is the visit time and 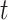is the functional argument. In this setting, it is reasonable to expect non-trivial correlations between functions from one visit time to another. Therefore, appropriate modeling of this dependence pattern would be critical for the validity of statistical inference. This manuscript outlines a flexible Bayesian framework for the estimation of the functional mean structure, possibly dependent on a set of time-stable covariates, as well as an adaptive regularization framework for the estimation of the covariance operator of 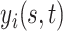and its eigenstructure.

The frequentist analysis of longitudinal functional data is a mature field. In particular, semiparametric modeling strategies, depending on the mixed effects modeling framework, have been proposed by Di and others (2009) in the context of hierarchical functional data, and Greven and others (2010) for longitudinal functional data. Important generalizations have been introduced by Chen and Müller (2012), through structured functional principal components analysis (FPCA), with more parsimonious representations introduced by Park and Staicu (2015), and Chen and others (2017) in the more general context of function-valued stochastic processes. The appealing nature and flexibility of structured FPCA modeling strategies has seen the application and extension of these methods to challenging scientific problems ranging from functional brain imaging (Hasenstab and others, 2017; Scheffler and others, 2020), to the exploration of complex data from wearable devices (Goldsmith and others, 2016). The vast majority of approaches based on FPCA, generally focus on point estimation from a frequentist perspective, and do not provide reliable uncertainty quantification without bootstrapping. The very application of the bootstrap methodology to structured functional data has not been the subject of rigorous investigation. The literature, in fact, is ambiguous on the handling of the many tuning parameters, typical of structured FPCA models. Although there are some consistency results regarding the bootstrap for functional data (Cuevas and others, 2006; Ferraty and others, 2010), the procedure is relatively underdeveloped for hierarchical data (Ren and others, 2010). Bayesian methods in functional data analysis define a straightforward mechanism for uncertainty quantification. This appealing inferential structure comes, however, at the cost of having to specify a full probability model, and priors with broad support on high-dimensional spaces (Shi and Choi, 2011; Yang and others, 2016; Yang and others, 2017). In hierarchical and multi-dimensional functional data settings, starting from the seminal work of Morris and others (2003), and recent extensions in Lee and others (2019), the prevalent strategy has been to work within the framework of basis function transforms, defining flexible mixed effect models at the level of the basis coefficients (Morris and others, 2003; Baladandayuthapani and others, 2008; Zhang and others, 2016). The resulting functional mixed effects models, like their finite dimensional counterpart, require a certain degree of subject matter expertise in the definition of random effects and their covariance structure (Morris and others, 2011; Morris and Carroll, 2006).

This manuscript aims to merge the appealing characterization of longitudinal functional data through FPCA decompositions (Chen and Müller, 2012; Park and Staicu, 2015; Chen and others, 2017), with flexible probabilistic representations of the classical Karhunen–Loéve expansion of square integrable random functions. Our work builds on the ideas of Suarez and Ghosal (2017) and Montagna and others (2012), who adapted the regularized product Gamma prior for infinite factor models of Bhattacharya and Dunson (2011), to the analysis of random functions. Extensions of this framework to the longitudinal functional setting are discussed in Section 2. In Section 3, we discuss prior distributions and ensuing implications for the covariance operator. A comprehensive framework for posterior inference is discussed in Section 4. Section 5 contains a comparative simulation study. Finally, in Section 6 we discuss the application of our proposed methodology to two case studies. The first case study explores age-specific fertility dynamics in the global demographic study conducted by the Max Plank Institute and the Vienna Institute of Demography (HFD, 2019). While purely illustrative, these data allow for a direct comparison with the original analysis of Chen and others (2017). The second case study, involves the analysis of electroencephalogram (EEG) data from an investigation of implicit learning in children with autism spectrum disorder (ASD) (Jeste and others, 2015). The main interest in both case studies is modeling and interpreting the longitudinal component.

2. A probability model for longitudinal functional data

Let 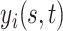denote the response for subject 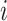, (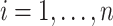), at longitudinal time 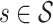and functional time 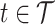, where 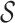and 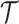are compact subspaces of 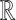. Furthermore, for each subject, assume we observe a time-stable 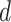-dimensional covariate 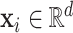. In practice, we only obtain observations 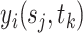at discrete sampling locations 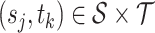, , 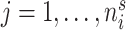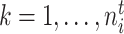. However, in subsequent developments, we maintain the lighter notation 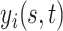without loss of generality.

Let 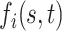be a Gaussian Process with mean 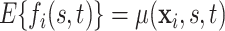and covariance kernel 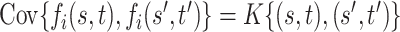. A familiar sampling model for 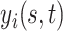assumes:

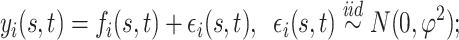(2.1)

where 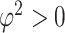is the overall residual variance. Given a set of suitable basis functions 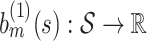, , 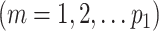and 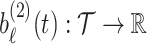, , 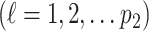and a set of random coefficients 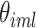, the prior for the underlying signal 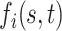is constructed through a random tensor product expansion, so that

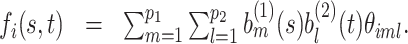(2.2)

Since the truncation values 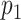and 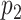may be large to ensure small bias in the estimation of the true 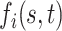, we follow Bhattacharya and Dunson (2011) and project the basis coefficients on a lower-dimensional space.

Let 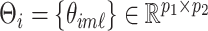be the matrix of basis coefficients for subject 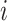. After defining loading matrices 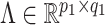, , 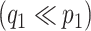and 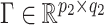, (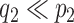), and a latent matrix of random scores 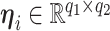, we assume

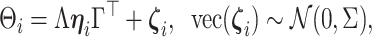(2.3)

where 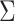is taken to be diagonal. The foregoing construction has connections with factor analysis. In fact, vectorizing 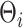we obtain

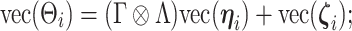which resembles the familiar (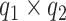) latent factor model, with loading matrix 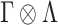and latent factors 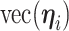. Differently from standard latent factor models, our use of a Kronecker product representation for the loading matrix introduces additional structural assumptions about 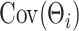, and the ensuing form of the covariance kernel .

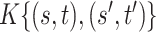More precisely, assuming 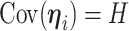, the marginal covariance of 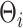takes the form

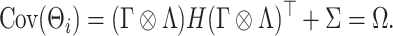(2.4)

Furthermore, defining 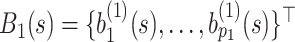and 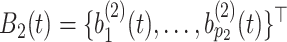, the model in (2.3) induces the following representation for the covariance kernel 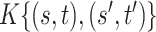, s.t.

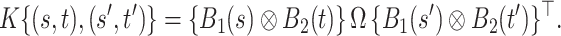(2.5)

The low-rank structure of 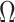in (2.4), depends on the number of latent factors 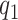and 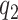in the quadratic form 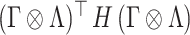. Rather than selecting the number of factors a priori, in Section 3, we introduce prior distributions encoding rank restrictions through continuous stochastic regularization of the loading coefficient’s magnitude. Additional structural restrictions may ensue from specific assumptions about the latent factors’ covariance 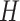. Specifically, setting 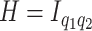leads to strong covariance separability of the longitudinal and functional dimensions. A more flexible covariance model hinges on the notion of weak-separability (Lynch and Chen, 2018). This is achieved by assuming .

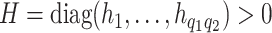Finally, let 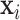be a 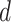-dimensional time-stable covariate for subject 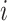. Dependence of the longitudinal functional outcome 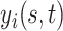on this set of predictors is conveniently introduced through the prior expectation of 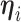. More precisely, let 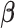be a 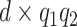matrix of regression coefficients, we assume

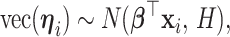which implies the following marginal mean structure for ,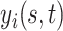

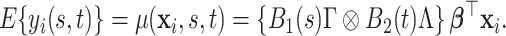(2.6)

The model in (2.1), together with the sandwich factor construction in (2.3) defines a probabilistic representation of the product FPCA decomposition in Chen and others (2017). An intuitive parallel is introduced in Section 3, and a technical discussion is provided in the accompanying web-based supplementary document (Appendix A of the supplementary material available at Biostatistics online). Differently from Chen and others (2017), we propose model-based inference through regularized estimation based on the posterior measure.

3. Rank regularization and prior distributions

The selection of prior distributions for all parameters introduced in Section 2 is guided by the following considerations. Let 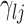and 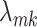be specific entries in the loading matrices 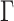and 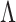in (2.3), respectively. Defining 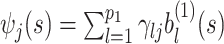and 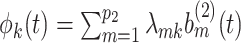, we may expand 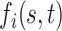as follows:

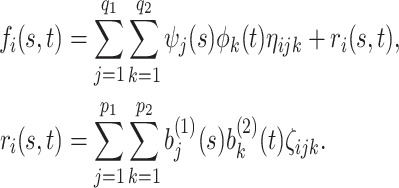The first component in the expression for 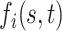describes a mechanism of random functional variability which depends on the tensor combination of 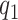and 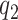data-adaptive basis functions 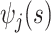and 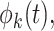respectively, and 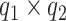basis coefficients 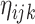. Given 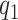and , any residual variability is represented in the random function 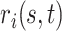. When 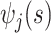and 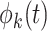are chosen to be eigenfunctions of the marginal covariance kernels in 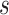and 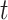, this representation is essentially equivalent to the product FPCA construction of Chen and others (2017).

Statistical inference for FPCA constructions, commonly selects a small number of eigenfunctions on the basis of empirical considerations. Here, we take an adaptive regularization approach, choose 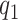and 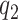relatively large, and assume the variance components in the priors for 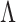and 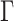to follow a modified multiplicative gamma process prior (MGPP) Bhattacharya and Dunson (2011),Montagna and others (2012).

Let 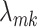denote the 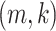entry of 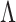. The modified MGPP is defined by setting

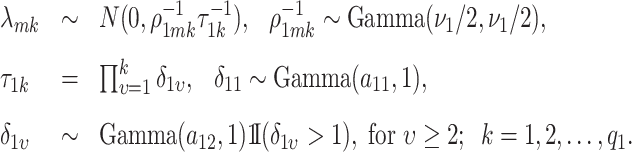(3.7)

Using the “rate” parametrization for Gamma distributions (i.e., if 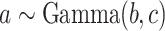, then 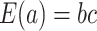), this prior is designed to encourage small loadings in 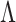as the column index increases. In the original formulation of Bhattacharya and Dunson (2011) and Montagna and others (2012), choosing 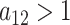, insures stochastic ordering of the prior precision, in the sense that 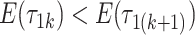, for any 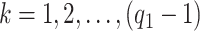. In our setting, we require the more stringent probabilistic ordering 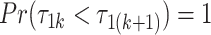, by assuming 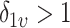, which results in a more stable and efficient Gibbs sampling scheme. Analogous regularization over the columns of 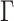is achieved by setting:

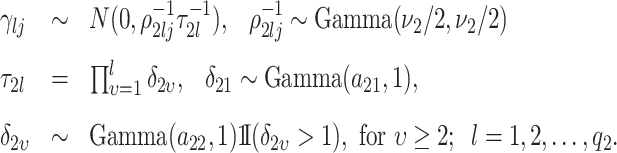(3.8)

Adaptive shrinkage is induced by placing hyper-priors on 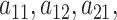and 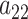, such that

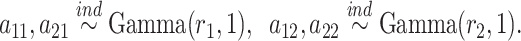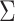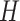The model is completed with priors on residual variance components and regression coefficients. Specifically, conditionally conjugate priors are placed on the diagonal elements of and , respectively, as well as the residual variance 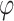, such that:

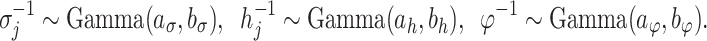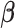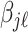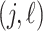Finally, we induce a Cauchy prior for the regression coefficients matrix as in Montagna and others (2012). Denoting with the entry of 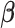, we assume

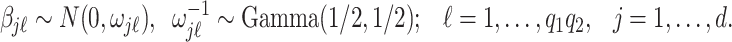In summary, our approach starts with the projection of the observed data onto a set of known basis functions in (2.2). This initial projection is similar to the interpolation or smoothing step commonly used in functional data analysis (Chen and others, 2017; Morris and Carroll, 2006). The basis coefficients are assumed to arise from the latent factor model in (2.3), resulting in the weakly separable covariance model in (2.4) and (2.5). Finally, the MGPP priors in (3.7) and (3.8), allow for adaptive regularization of the covariance operator. The mean structure is made dependent on a set of time stable covariates through a varying coefficient model in (2.6).

4. Posterior inference

Posterior simulation through Markov chain Monte Carlo is relatively straightforward, after selection of an appropriate basis transform and truncation of 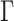and 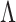to include 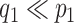and 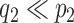columns respectively. The use of conditionally conjugate priors allows for simple Gibbs transitions for all parameters, with the exception of the shrinkage parameters 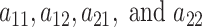, which are updated via a Metropolis–Hastings step. A detailed description of the proposed algorithm is reported in the web-based supplement (Appendix B of the supplementary material available at Biostatistics online).

We note that the decomposition of 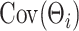in (2.4) may not be unique. However, from a Bayesian perspective, one does not require identifiability of the loading elements for the purpose of covariance estimation. Direct inference for and its functionals may be achieved by post-processing Monte Carlo draws from the posterior 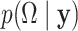and evaluating the covariance function over arbitrarily dense points 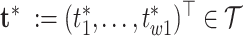and 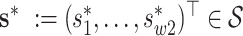using (2.5). 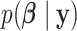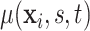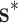Analogously, given samples from , inference about the mean structure is achieved by evaluating over and 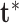using the expansion in (2.6).

Some useful posterior summaries may be obtained through marginalization. We define marginal covariance functions 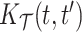and 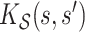as follows:

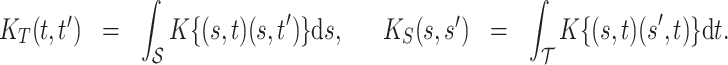(4.9)

Intuitively, 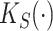and 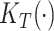summarize patterns of functional co-variation along a specific coordinate, and their lower-dimensional posterior summaries may be obtained through functional eigenanalysis as in Chen and others (2017). We outline details on extracting lower-dimensional summaries of the marginal covariance functions without computing 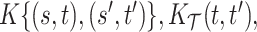or 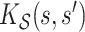in Appendix F of the of the supplementary material available at Biostatistics online. Simultaneous credible intervals for all functions of interest are easily obtained from Monte Carlo samples, by applying the methodology discussed in Crainiceanu and others (2007) and Baladandayuthapani and others (2005).

Specifically, 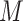Monte Carlo draws from a posterior function of interest, say , are used to estimate the posterior mean 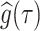, and standard deviation 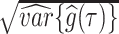. Assuming approximate normality of the posterior distribution, we derive the 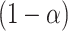quantile 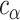of the pivotal quantity

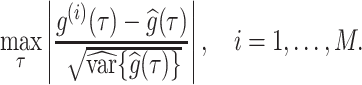An approximate simultaneous 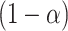posterior band can then be constructed as a hyperrectangular region over 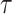: 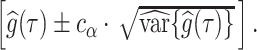More general simultaneous bands have been proposed by Krivobokova and others (2010), but are not implemented in this manuscript.

The proposed modeling framework relies on a specific basis transform strategy. While the literature has suggested the use of zero-loss transforms as a default option (Morris and others, 2003; Lee and others, 2019), we find that it is not uncommon to observe some sensitivity to the number of basis functions used in the initial projection. Furthermore, the choice of more parsimonious designs, when warranted by the application, may lead to important gains in computational and estimation efficiency.

Model flexibility is governed by choice of 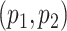, as the number of smoothing basis functions, and 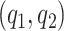as the number of latent factors. Due to the adaptive rank regularizing prior, 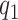and 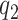should be chosen as large as possible. In practice 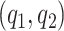are chosen as fraction of .

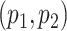Our simulation studies (Appendix C of the supplementary material available at Biostatistics online) demonstrate that point estimates and uncertainty of mean and covariance functions are generally insensitive to choice of 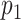and 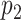, provide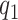d and 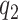are large. Some sensitivity is, however, observed in the posterior estimate of the residual error 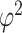. An alternative method is to simply rely on the minimization of information criteria. In this article, we consider simple versions of the deviance information criterion (DIC), and two versions of the Bayesian information criteria (BIC and 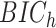Delattre and others (2014)). Our simulations studies (Appendix C of the supplementary material available at Biostatistics online) indicate that the proposed information criteria perform well in selecting an adequate number of basis functions.

From a computational perspective, the most time consuming steps in the Gibbs sampling algorithm are the Cholesky decompositions used in updating 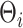and 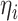, requiring 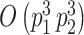and 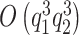floating point operations, respectively. Therefore, scalability of naïve Gibbs sampling is a potential issue for very large samples and/or very long longitudinal or functional evaluation domains. In these cases, adapting the estimation approach of Morris and Carroll (2006), is easily implemented, by treating the estimation of 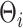as a pre-processing step, and considering 2.3 as the sampling model. For big data applications, other analytical approximations to the posterior measure are also accessible, e.g., Integrated Nested Laplace Approximations (INLA) (Rue and others, 2009).

5. A Monte Carlo study of operating characteristics

We performed a series of numerical experiments aimed at evaluating the estimation performance for both the functional mean and covariance. We study three simulation scenarios, including two weakly separable kernels (Cases 1 and 2) and one non-separable covariance function (Case 3). Specifically, for 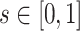and 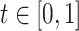, we take:

• (1) 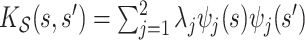, with eigenvalues 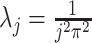and eigenfunctions 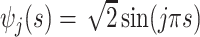, , 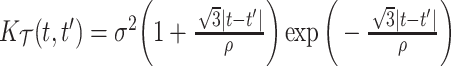in the Matèrn class, and mean .

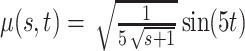• (2) 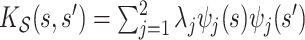, with eigenvalues 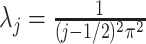and eigenfunctions 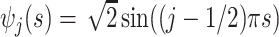, , 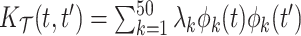with 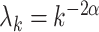and 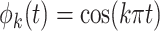, and mean .

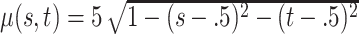• (3) 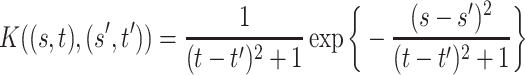, stationary non-separable (Gneiting, 2002), and mean .

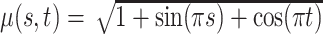Scenario 1 combines a simple Matèrn class pattern on the time-domain with a more complex oscillatory dependence pattern for the functional domain . Covariance 2 includes an oscillatory pattern in both 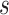and 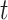. Finally, Covariance 3, while defining simple parametric dependence in both longitudinal and functional times, is not weakly separable, allowing for comparisons on misspecified models.

We consider estimation of the mean, covariance, marginal covariance functions, and the associated two principal eigenfunctions. Each simulation includes 1000 Monte Carlo experiments. For each experiment, posterior estimates are based on 10 000 iterations of four independent Markov chains, after discarding 2500 draws for burn-in. We compare estimation of covariance, marginal covariance functions, and associated two principal eigenfunctions to the respective estimates provided by the product FPCA (Chen and others, 2017), as well as finite-dimensional empirical estimates of the mean and covariance defined as by their vectorized sample counterparts. Estimates obtained with the product FPCA have data type set to sparse and fraction of variance explained threshold set to 0.9999.

All comparisons are based on the relative mean integrated squared error. For a function with domain 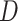and estimator 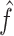, we define 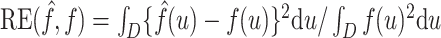. Note that 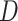can be multi-dimensional and in practice the integral is replaced with a sum. Table 1 compares mean 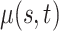and covariance 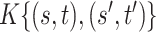estimation under the three settings listed above. We find that estimates from each method improve in accuracy with increasing sample size (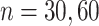), with the posterior and product FPCA showing greater accuracy than empirical approach in terms of covariance estimation. Similar findings characterize the estimation performance of all marginal covariance functions (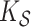, 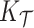), and the associated two principal eigenfunctions (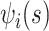, 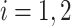), and (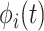, 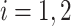). Detailed numerical results and extended simulations are reported in the web-based supplement (Appendix C of the supplementary material available at Biostatistics online).

Table 1.

Mean and covariance relative errors under the three simulation cases described in section 5. Bayes refers to the proposed method in this paper, product refers to the product decomposition Chen and others (2017), and empirical refers to point-wise empirical estimation. Each case is repeated 1000 times for sample sizes of 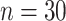and 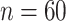. We report the 50th percentile of the relative error, with the numbers in the parentheses denoting the 10th and 90th percentiles of the relative error.

Case 1		Bayes	Product	Empirical
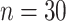
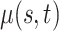
		0.014 (0.005, 0.038)	0.019 (0.010, 0.044)	0.019 (0.010, 0.044)
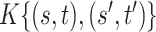
		0.062 (0.023, 0.224)	0.085 (0.047, 0.200)	0.151 (0.097, 0.297)
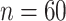
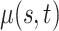
		0.007 (0.003, 0.019)	0.010 (0.005, 0.021)	0.010 (0.005, 0.021)
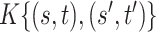
		0.030 (0.010, 0.097)	0.057 (0.038, 0.128)	0.076 (0.050, 0.151)
Case 2
		0.024 (0.007, 0.101)	0.031 (0.013, 0.118)	0.031 (0.013, 0.118)
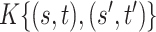
		0.039 (0.011, 0.184)	0.050 (0.012, 0.202)	0.067 (0.030, 0.228)
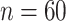
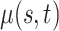
		0.014 (0.004, 0.054)	0.017 (0.007, 0.062)	0.017 (0.007, 0.062)
		0.019 (0.005, 0.091)	0.024 (0.007, 0.093)	0.032 (0.014, 0.106)
Case 3
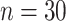
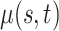
		0.155 (0.046, 0.389)	0.160 (0.051, 0.393)	0.160 (0.051, 0.393)
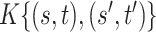
		0.051 (0.016, 0.187)	0.051 (0.014, 0.183)	0.067 (0.023, 0.200)
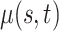
		0.073 (0.019, 0.216)	0.076 (0.021, 0.219)	0.076 (0.021, 0.219)
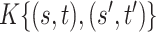
		0.028 (0.008, 0.091)	0.027 (0.007, 0.089)	0.034 (0.011, 0.099)

In summary, we observe that posterior estimates are associated with similar, and potentially improved accuracy in the estimation of the mean and covariance functions, when compared with product FPCA. This similarity in estimation performance, provides some empirical assurances that the chosen probabilistic representation of structured covariance functions, and estimation based on adaptive shrinkage, maintains a data-adaptive behavior with good operating characteristics.

6. Case studies

We illustrate the application of the proposed modeling frameworks in two case studies. The first dataset concerns fertility rate and age of mothers by country. The second case study focuses on functional brain imaging through EEG in the context of implicit learning in children with ASD.

6.1. Fertility rates

The Human Fertility Database (HFD, 2019) compiles vital statistics to facilitate research on fertility in the past twentieth century and in the modern era. Age-specific fertility rates are available for 32 countries over different time periods. The age-specific fertility rate 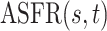is defined as

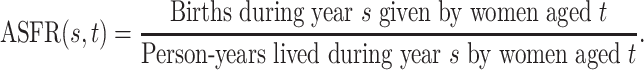The dataset was previously analyzed and interpreted in a longitudinal functional framework using the product FPCA (Chen and others, 2017). This section focuses on a comparative analysis of product FPCA and the proposed probability model.

We follow Chen and others (2017), and consider 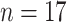countries, with complete data for the time period 1951 to 2006, 44 functional time points (ages 12–55), and 56 longitudinal time points (years 1951 to 2006). Since these rates are population measurements, we expect the data to contain very little noise.

We use cubic b-splines as our basis functions since the data look smooth with no sharp changes in fertility rate over year or age of mother (Figure S1 of the supplementary material available at Biostatistics online) and consider splines and 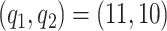latent factors, selected by minimizing the DIC.

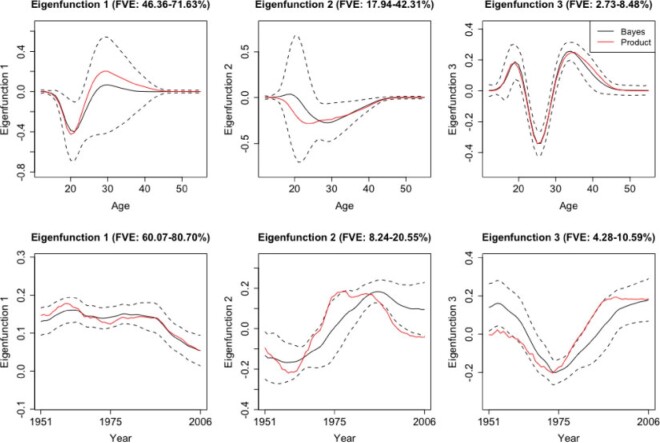
Longitudinal and aging dynamics are largely determined by their associated marginal covariance functions 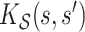and 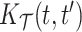. Figure 1 displays the first three marginal eigenfunctions for age and calendar year. We include the 95% simultaneous credible bands (Crainiceanu and others, 2007) as well as estimates obtained via product FPCA. We note that Bayesian posterior mean eigenfunctions are qualitatively similar to the inferred product FPCA estimates, therefore warranting similar interpretations to the one originally offered by Chen and others (2017).

Fig. 1.

Age and calendar year marginal eigenfunctions. The above plots include the Bayesian posterior means, 95% credible bands, and the product FPCA marginal eigenfunctions.

In particular, the first marginal eigenfunction for age (Figure 1, left panel) can be interpreted as the indexing variability in young fertility before the age of 25, with the second marginal eigenfunction for age (Figure 1, central panel) indexing variability in fertility for mature age, between the ages of 20 and 40. As our modeling framework allows for rigorous uncertainty quantification in these posterior summaries, we note that the credible bands for the first and second eigenfunction are relatively wide, indicating that specific patterns should be interpreted with care. Examining directions of variance in fertility through the years, we note that the first marginal eigenfunction for year (Figure 1, left panel) is relatively constant and can be interpreted as representing an overall “size-component” of fertility from 1951 to 2006. The second eigenfunction (Figure 1, central panel) defines a contrast of fertility in countries before and after 1975. For both the year and age coordinates, the third marginal eigenfunctions capture a smaller fraction of the total variance and index higher patterns of dispersion at and around age 25 and at or around the year 1975.

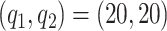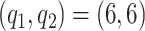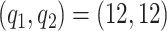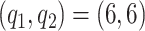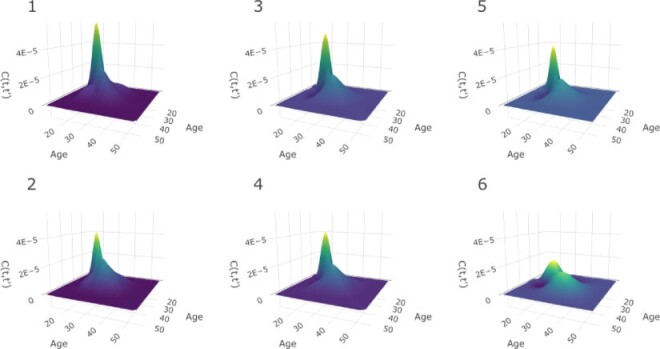
We investigate sensitivity to the number of basis and latent factors considering four different models: model 1: , ; model 2 , ; model 3: , ; and model 4: , . We also estimate the marginal covariance function with product FPCA using both the dense and sparse settings. Point estimate for 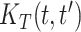are reported in Figure 2. Comparing estimates within column (left and center panels), we assess sensitivity to a drastic reduction in the number of latent factors. Comparing estimates within row (left and center panels), we instead assess sensitivity to a drastic reduction in the number of basis functions. We note that the marginal age covariance function is relatively stable in all four settings. We contrast this relative robustness with estimates based on the product FPCA. In particular, sparse estimation using 10-fold cross-validation results in meaningfully diminished local features. A possible reason for the instability is due to the small sample size (n = 17). In this example, Bayesian estimation is perhaps preferable, as adaptive penalization allows for stable estimates within a broad class of model specifications.

Fig. 2.

Sensitivity analysis for the marginal covariance function 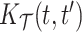(HFD study). Panels (1,2,3,4) refer to posterior mean estimates obtained under different projections and numbers of latent factors (Specific details are provided in Section 6.1). Panels (5, 6) refer to product FPCA estimates obtained under dense (5) or sparse (6) settings.

6.2. An EEG study on implicit learning in children with ASD

This analysis is motivated by a functional brain imaging study of implicit learning in young children with autism spectrum disorder (ASD), a developmental condition that affects an individual’s communication and social interactions (Lord and others, 2000). Implicit learning is defined as learning without the intention to learn or without the conscious awareness of the knowledge that has been acquired. We consider functional brain imaging through EEG, an important and highly prevalent imaging paradigm aimed at studying macroscopic neural oscillations projected onto the scalp in the form of electrophysiological signals.

This study, carried out by our collaborators in the Jeste laboratory at UCLA, targets the neural correlates of implicit learning in the setting of an event-related shape learning paradigm (Jeste and others, 2015). Children aged 2–6 years old with ASD were recruited through the UCLA Early Childhood Partial Hospitalization Program (ECPHP). Each participant had an official diagnosis of ASD prior to enrollment. Age-matched typically developing (TD) children from the greater Los Angeles area were recruited as controls.

Six colored shapes (turquoise diamond, blue cross, yellow circle, pink square, green triangle, and red octagon) were presented one at a time in a continuous “stream” in the center of a computer monitor. There were three shape pairings randomized to each child. For instance, a pink square may always be followed by a blue cross. After the blue cross would come a new shape pair. Within a shape pair would constitute an “expected” transition and between shape pairs would constitute an “unexpected” transition. Each child would wear a 128-electrode Geodesic Sensor Net and observe the stream of shapes on the computer monitor. Each stimulus, or presentation of a single shape, is referred to as a trial, and can result in frequency-specific changes to ongoing EEG oscillations, which are measured as event related potentials (ERPs).

Each waveform contains a phasic component called the P300 peak which represents attention to salient information. This phasic component is typically studied in EEG experiments and is thought to be related to cognitive processes and early category recognition (Jeste and others, 2015). We use the same post-processed data as in Hasenstab and others (2017). Namely, we consider 37 ASD patients and 34 TD patients using data from trials 5 through 60 and averaging ERPs in a 30 trial sliding window (Hasenstab and others, 2015). The sliding window enhances the signal to noise ratio at which the P300 peak locations can be identified for each waveform. Each waveform is sampled at 250 Hz resulting in 250 within-trial time points over 1000 ms. Following Hasenstab and others (2017), we reduce each waveform to a 140 ms window around each P300 peak. This 140 ms window results in 37 within-trial time points. We do not apply warping techniques because each within-trial curve is centered about the P300 peak. Our analysis focuses on condition differentiation, formally defined as the difference between the expected and subsequent unexpected condition. Modeling condition differentiation for waveforms within a narrow window about the P300 peak over trials may give insights into learning rates for the ASD and TD groups. Thus, the main interest in this study is changes in condition differentiation over trials, and a longitudinal functional framework is required for statistical inference in this setting. Our analysis is based on the condition differentiation, averaged within subject over the four electrodes in the right frontal region of the brain. In summary, for each subject we consider 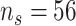observations within trial, and 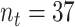total trials.

We model the ASD and TD data cohorts separately, in order to estimate ERP time and trial covariance functions within group. All inference is based on a model with 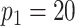, , 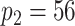, , 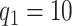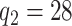selected minimizing DIC. A comprehensive analysis is reported in the web-based supplementary material available at Biostatistics online. Statistical inference is based on 50K MCMC posterior draws, after 20K burn-in. We considered relatively diffuse priors: 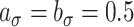, , 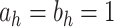, , 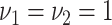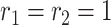and 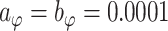. Results are relatively insensitive to these hyperparameter settings.

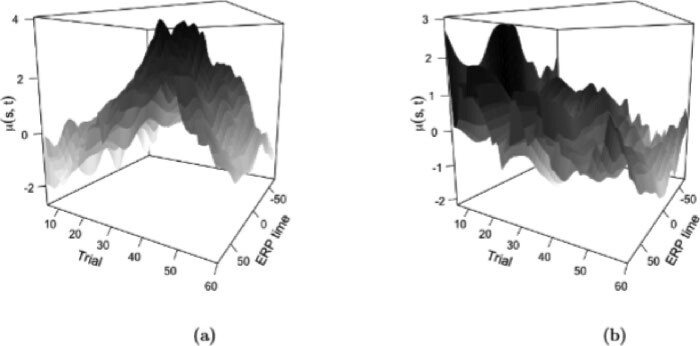
The estimated mean surfaces for the two groups are plotted in Figure 3. The ASD group tends to have positive condition differentiation between trials 30 and 55, whereas the TD group tends to have positive condition differentiation in earlier trials. Positive condition differentiation is thought to be indicative of learning, so these results suggest that the TD group is learning at a faster rate than the ASD group. However, even though qualitatively the surfaces look very different, there is a substantial amount of heterogeneity in the subject-level data, resulting in broad confidence bands around the mean, and perhaps suggesting that differential patterns of condition differentiation between ASD and TD groups are best explored considering both the mean and the covariance structure.

Fig. 3.

Posterior expected mean condition differentiation along trial and ERP time for the ASD (a) and the TD (b) cohorts.

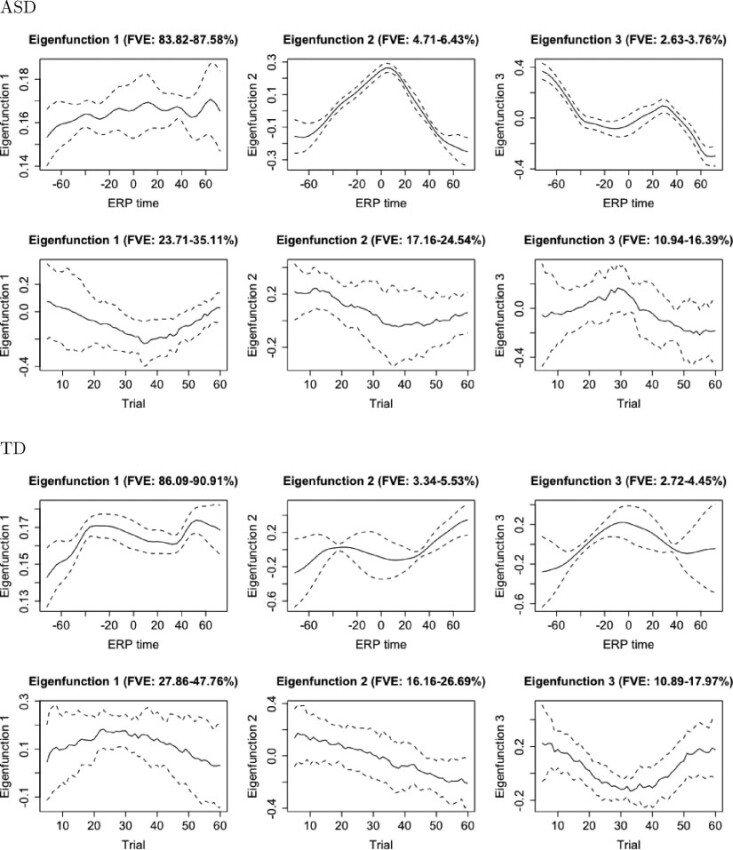
Next we conduct an eigen-analysis of the covariance structure for both cohorts separately. Figure 4 plots eigenfunctions of the marginal covariances over ERP time and trials. Credible intervals are calculated following Crainiceanu and others (2007). We start by analyzing summaries indexing variability in ERP time. For both the TD and ASD cohorts, the first eigenfunction explains the vast majority of the marginal covariance (84–88% in ASD, and 86–90% in TD). In both groups, this first eigenfunction is relatively flat and can be interpreted as representing variability in the overall level of condition differentiation within a trial. The magnitude and shape of variation is comparable between TD and ASD children. Finer differences may be detected in the second and third eigenfunction, which further characterize variability in the shape of the ERP waveforms about the P300 peak. For both cohorts, however, these summaries represent only a small percentage of the variance in ERP waveform within trial.

Fig. 4.

Marginal eigenfunctions with associated uncertainty for the ASD and TD groups. Solid black lines represent posterior means and dotted lines represent 95% simultaneous credible bands.

Perhaps more interesting is an analysis of the marginal covariance across trial, as probabilistic learning patterns are likely to unfold with prolonged exposure to expected vs. unexpected shape pairings. For the ASD group, the first eigenfunction dips in an approximately quadratic fashion, suggesting enhanced variability in condition differentiation at around trial 35. Similarly, for the TD group, the first trial eigenfunction has a slight peak around trial 25. A possible interpretation of these covariance components relates to implicit learning, with higher variance in differentiation occurring earlier for TD than for ASD children. For both TD and ASD, the second eigenfunction across trials is interpreted as a contrast between high condition differentiation at early trials and low condition differentiation at later trials. Finally for the ASD cohort, the third eigenfunction exhibits a peak around trial 30. A possible interpretation would identify heterogeneity in the timing of learning, with some of the trajectories inducing variation in condition differentiation around trial 30, as opposed to the first eigenfunction identifying increased variance at around trial 35. Similarly for the TD group, the third trial eigenfunction has a dip around trial 35, indexing delayed increased variability in condition differentiation around trial 35.

7. Discussion

In this article, we provide a probabilistic characterization of longitudinal functional data. As part of our work, we propose a joint framework for the estimation of the mean or the regression function, and a flexible prior for covariance operators. Regularized estimation relies crucially on the projection of a set of basis coefficients onto a latent subspace, with adaptive shrinkage achieved via a broadly supported class of product Gamma priors. While we have not established theoretical results on posterior consistency, we have shown that the proposed framework exhibits competitive operating characteristics, when compared with alternative modeling strategies.

Importantly, uncertainty quantification, is achieved without having to rely on the asymptotic performance of bootstrap methods. From an applied perspective, analysts are charged with choosing the appropriate projection space. However, we see this as a feature rather than a problem, as different data scenarios may require and motivate the use of alternative basis systems. Because regularization is achieved jointly with estimation, inference is straightforward and does not need to account separately for the estimation of nuisance parameters or the choice of a finite number of eigenfunctions to use in a truncated version of the model, as is the case for FPCA-based methods.

Crucially, the level of flexibility afforded by the proposed method is most important when inference centers on both the mean and covariance structure. Simpler modeling strategies, e.g., the Integrated Nested Laplace Approximations (LFPCA) approach of Greven and others (2010), are likely to be more appropriate when the number of longitudinal observations is small, or if inference centers mostly on the mean structure. In a small simulation study (Appendix C of the supplementary material available at Biostatistics online), we found that the proposed approach performs similarly to LFPCA, even when data are generated from the latter scheme.

We have shown that posterior inference using MCMC is implemented in a relatively straightforward fashion and need not rely on complicated posterior sampling strategies. When dealing with large data-sets, this naïve inferential strategy may not be appropriate. For example, in updating the basis coefficients 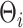, the number of floating point operations grow at a cubic rate with respect to the dimensions of the spline bases. When naïve Gibbs is not scalable (e.g., for very large samples or long evaluation domains), potentially promising acceleration strategies include the zero-loss projection approach of Morris and Carroll (2006), and adaptations of the INLA framework for approximate inference (Rue and others, 2009).

From a modeling perspective, our probabilistic characterization of the longitudinal functional covariance function is essentially equivalent to the weakly separable model of Chen and others (2017). While more general than a strictly separable model, this strategy makes strong assumptions about the structure of a high-dimensional covariance operator. Testing strategies have been developed in the literature (Lynch and Chen, 2018). However, we find that a more natural approach to the problem is one of regularized estimation. In this setting, a possible extension of our modeling framework could include an embedding strategy for the regularization of a nonseparable covariance operator towards a weakly separable one.

8. Software

Software in the form of an R package including complete documentation and a sample data set is available from https://github.com/jshamsho/LFBayes.

Supplementary material

Supplementary material is available online at http://biostatistics.oxfordjournals.org.

Funding

The National Institute of Mental Health (R01 MH122428-01 to D.S., D.T.).