Mechanisms of inbreeding avoidance in a wild primate

Summary

Inbreeding often imposes net fitness costs^1–5, leading to the expectation that animals will engage in inbreeding avoidance when the costs of doing so are not prohibitive^4–9. However, one recent meta-analysis indicates that animals of many species do not avoid mating with kin in experimental settings⁶, and another reports that behavioral inbreeding avoidance generally evolves only when kin regularly encounter each other and inbreeding costs are high⁹. These results raise questions about the processes that separate kin, how these processes depend on kin class and context, and whether kin classes differ in how effectively they avoid inbreeding via mate choice—in turn demanding detailed demographic and behavioral data within individual populations. Here we address these questions in a wild mammal population, the baboons of the Amboseli ecosystem in Kenya. We find that death and dispersal are very effective at separating opposite-sex pairs of close adult kin. Nonetheless, adult kin pairs do sometimes co-reside, and we find strong evidence for inbreeding avoidance via mate choice in kin classes with relatedness ≥0.25. Notably, maternal kin avoid inbreeding more effectively than paternal kin despite having identical coefficients of relatedness, pointing to kin discrimination as a potential constraint on effective inbreeding avoidance. Overall, demographic and behavioral processes ensure that inbred offspring are rare in undisturbed social groups (1% of offspring). However, in an anthropogenically disturbed social group with reduced male dispersal, we find inbreeding rates 10x higher. Our study reinforces the importance of demographic and behavioral contexts for understanding the evolution of inbreeding avoidance⁹.

eTOC Blurb

Galezo et al. examine processes that prevent kin from mating in a wild primate population. They find that dispersal and mate choice play important roles, and that maternal kin are more avoidant than paternal kin (“asymmetrical inbreeding avoidance”). Anthropogenic disturbance can disrupt these processes, increasing the risk of inbreeding.

Results and Discussion

We characterized inbreeding avoidance in wild baboons in the Amboseli ecosystem of Kenya. This population consists of primarily yellow baboons (Papio cynocephalus) with some admixture from the congeneric anubis baboon (P. anubis)^10–13. These baboons live in discrete multi-male, multi-female social groups characterized by female philopatry and male dispersal; males undergo natal dispersal at 7–8 years of age^14–16 and often engage in secondary dispersal as adults. As in many mammals^15,17, male baboons often do not reproduce before dispersing from their natal group, and female baboons prefer to mate with immigrant males¹⁴. In Amboseli, mating between maternal kin is rare¹⁶ and is more likely to occur between genetically distant partners¹⁸. Mating between paternal kin in Amboseli has previously been examined only in an anthropogenically-disturbed social group with limited male dispersal: there, paternal siblings regularly engage in mate-guarding episodes, but engage in fewer mounts than non-kin¹⁹. Inbreeding depression is substantial among captive baboons²⁰, with relatively limited evidence in the wild^14,16.

We examined inbreeding avoidance across multiple classes of kin: mother-son and father-daughter (both with coefficient of relatedness r=0.5; n=132 and n=239 pairs respectively) maternal half-siblings and paternal half-siblings (expected r=0.25, n=67 and n=130 pairs respectively), half-aunt-nephew and half-uncle-niece (expected r=0.125, n=148 and n=164 pairs respectively), and half-first cousins (expected r=0.0625, n=202 pairs; see STAR Methods for definitions of all kin classes). Full-sibling pairs were excluded from the analysis because of small sample size. Previous studies of behavioral inbreeding in the wild have typically either focused only on maternal kin, or have used pairwise relatedness estimates that do not differentiate between maternal and paternal kin^21–27. Here, we compared maternal versus paternal kin by combining demographic and behavioral data collected between 1971 and 2019 with an in-depth population pedigree (1624 individuals with known mothers and 652 individuals with known fathers). Despite our large data set, some kin pairs may have gone undetected in our sample. However, we only considered pairs to be unrelated when we knew all ancestors going back at least two generations. Further, undetected kin will produce conservative estimates of the extent of inbreeding avoidance (see STAR Methods).

Demographic barriers to inbreeding

In baboons, mating occurs between males and females that reside in the same social group. Therefore, to assess the opportunity for inbreeding, we measured the extent of co-residence (residence in the same social group) between adult maternal and paternal kin. We found that most opposite-sex kin pairs never co-resided in the same social group as adults, including 90% of mother-son pairs, 81% of father-daughter pairs, 86% of maternal siblings, 86% of paternal siblings, 95% of half-aunt-nephew pairs, 96% of half-uncle-niece pairs, and 94% of half-first cousins.

Death was the dominant demographic force preventing kin pairs with overlapping lifespans from living together as adults. Between 56% and 61% of all opposite-sex kin pairs (between 773 and 816 of 1,319 pairs) were prevented from co-residing as adults by the death of one (or both) members of the pair before adulthood; the difference in the minimum and maximum numbers is attributable to males who disappeared from the study population with unknown fate, i.e., they may have died or dispersed. This high frequency of separation by death reflects the naturally high mortality rates in a wild primate population, particularly for infants and juveniles (see²⁸ for comparative data).

Mother-son pairs experienced the highest frequency of separation by death: between 74%−79% of mother-son pairs (336 to 359 of 454 pairs) failed to co-reside as adults because the mother or son died before the son reached adulthood (Figure 1). In contrast, only 31%−45% of father daughter pairs (57 to 83 of 182 pairs) were separated by death. Mother-son pairs were separated by death more often than father-daughter pairs because sons reach adulthood at a later age (~7.5 years²⁹) than daughters (~4.5 years²⁹), increasing the likelihood that one member of the parent-offspring pair will die before the son reaches adulthood. Maternal and paternal half-siblings were intermediate between parent-offspring pairs in the percentages of pairs separated by death: 45%−51% of maternal half-siblings (112 to127 of 248 pairs) and 52%−56% of paternal half-siblings (228 to 247 of 435 pairs; Figure 1).

Figure 1. Demographic barriers to adult co-residency in opposite-sex kin whose lifespans overlapped: (A) mother-son pairs, (B) father-daughter pairs, (C) maternal half-siblings, (D) paternal half-siblings.

Each light gray branch of the Sankey diagram represents a reason that an opposite-sex pair did not live together for any length of time as adults. We included all opposite sex pairs with overlapping lifespans and uncensored co-residency length data (i.e. one or both individuals were dead at the time of analysis). “Pre-birth demographic events” include dispersals and group fissions that separate the individuals before the birth of the younger individual. See also Figures S1 and S2.

Male dispersal was also an important force preventing kin pairs from co-residing as adults (Figure 1). Considering only those kin pairs in which both members were known or likely to have survived to adulthood (586 of the 1,319 pairs with overlapping lifespans), dispersal prevented co-residency for 40%−54% of adult pairs (236 to 319 pairs). These values varied among kin classes, from a high of 47%−68% for father-daughter pairs (59 to 85 pairs in which the father dispersed, of 125 pairs total), to a low of 36%−45% for paternal half-sibling pairs (75 to 94 pairs in which the brother dispersed, of 207 total; Figure 1). Social group fissions, which occur once every ~10–20 years in any given social group, played a relatively small role in preventing the co-residency of adult kin compared to death and dispersal (Figure 1).

When adult co-residency did occur, these periods were typically short: of the 282 male-female kin pairs that lived together as adults, 76% co-resided for less than one year (including 82% of mother-son pairs, 56% of father-daughter pairs, 89% of maternal siblings, 92% of paternal siblings, 72% of half-aunt-nephew pairs, 71% of half-uncle-niece pairs, and 44% of half-first cousins; Figure S1). Nonetheless, a full 24% of kin pairs co-resided for more than one year, and 4% (12 of 282 pairs) co-resided for between 5 and 10 years of their adult life (Figure S1).

We also measured co-residency in a semi-provisioned, anthropogenically-disturbed social group with reduced male dispersal: the Lodge group. Lodge group males exhibited reduced dispersal (Figure S2) and no males immigrated into the group during the period of near-daily monitoring, 1984–1997, perhaps because of the close proximity of the Lodge group to a human settlement³⁰. This created a natural experiment for examining the relationship between co-residence and dispersal. As predicted, the proportion of opposite-sex related pairs that lived together as adults in the semi-provisioned Lodge group (13%, 24 of 185) was substantially greater than the proportion of wild-feeding opposite-sex related pairs that did so (8%, 282 of 3447) (Figure S2). In addition, semi-provisioned kin pairs tended to live together for longer periods (median: 648 days) than wild-feeding kin pairs (median: 97 days) (Figure S2).

Behavioral inbreeding avoidance via mate choice

Given that kin do sometimes co-reside, we assessed the effectiveness and stringency of behavioral inbreeding avoidance. In baboons, the large majority of copulations occur in the context of mate-guarding episodes, or “consortships,” that occur during the follicular phase of the sexual cycle^31–33. Therefore, we assessed the absence versus presence of consortships in different relatedness categories during the 5-day window of highest fertility (the “fertile window”) in each female’s sexual cycles, in three different statistical models described below.

The main model: Inbreeding avoidance in multiple kin classes.

In our main model, we analyzed inbreeding avoidance in adult pairs that included only wild-feeding, fully adult females (i.e., those past adolescence, see next section, ‘The adolescent model’); we excluded the semi-provisioned Lodge group from the main model. For 1700 fertile windows in the sexual cycles of 178 adult females between 1979 and 2019, we identified all adult males (see STAR Methods) in the group during that 5-day fertile window and recorded, as a binary variable (0/1), whether or not each of those males attained a consortship during the same fertile window. The data set included 208 unique adult males. We constructed a Bayesian logistic regression model using the R package rstanarm³⁴ with this binary variable as the response variable. We included pedigree relatedness for each male-female pair as a predictor variable, as well as the male’s natal status (whether he was a “natal male” born in that social group or an immigrant), because research on another baboon population indicates that natal males are less likely to obtain consortships than immigrants, a presumed mechanism of inbreeding avoidance¹⁴. We also included other known sources of variance in consortship occurrence¹⁸ (Table 1 and STAR Methods).

Table 1. Main model:

Results of a Bayesian logistic regression predicting the probability of a sexual consortship for different classes of kin pairs, controlling for known sources of variance in male consortship success (N = 1700 unique fertile windows for 178 adult females). See also Figure S3.

90% credible interval
	log odds2	Sd	Lower	Upper	odds ratio3	Interpretation
Intercept	−1.793	0.671	−2.654	−0.947	0.166
kinship classes1
mother-son*	−3.791	1.345	−5.574	−2.191	0.023	↓ Pr(consort)
father-daughter*	−1.818	0.562	−2.546	−1.128	0.162	↓ Pr(consort)
maternal siblings*	−3.274	1.422	−5.166	−1.586	0.038	↓ Pr(consort)
paternal siblings*	−1.315	0.470	−1.933	−0.733	0.268	↓ Pr(consort)
half-aunt-nephew	−0.259	0.355	−0.712	0.191	0.772	No effect
half-uncle-niece	−0.210	0.293	−0.584	0.160	0.811	No effect
half-first cousins*	0.388	0.252	0.061	0.709	1.474	Pr(consort) slightly ↑ for these pairs
male dominance rank*	−0.377	0.051	−0.443	−0.311	0.686	↑ male rank = ↑ Pr(consort)
natal male*	−0.685	0.393	−1.203	−0.189	0.504	natal males = ↓ Pr(consort)
# adult males in group*	−0.072	0.024	−0.103	−0.041	0.931	↑ # males = ↓ Pr(consort) per male
male rank:# adult males in group*	0.009	0.004	0.005	0.014		↑ # males = ↓ benefit to high-ranking males
female age	0.003	0.014	−0.015	0.021	1.003	No effect of female age
female dominance rank*	−0.041	0.017	−0.063	−0.020	0.960	↑ female rank = ↑ Pr(consort)
female rank:male rank*	0.005	0.003	0.002	0.009		↑ male and female ranks = ↑ Pr(consort)4
# co-resident days*	0.423	0.120	0.272	0.579	1.527	↑ time co-resident = ↑ Pr(consort)

¹Reference category is unrelated pairs.

²Log odds represent the posterior median estimate.

³Odds ratios for interactions are not reported because calculating an odds ratio involves exponentiation, which does not yield an easily interpretable number for an interaction.

⁴See Figure S3(B) for a visualization of this interaction

^*Bold text and asterisks designate kin classes for which behavioral inbreeding avoidance is demonstrated by the credible intervals of the log odds ratio, which do not overlap zero. Asterisks without bold text indicate other variables for which the credible intervals do not overlap zero.

We predicted that kin would be less likely to consort than non-kin, i.e., that they would exhibit behavioral inbreeding avoidance via mate choice, avoid consorting with each other, and that the most closely related pairs would show the strongest consortship avoidance. We also predicted that this form of behavioral inbreeding avoidance would be stronger between maternal than paternal kin. Baboons generally have strong, persistent, multi-year relationships with their mothers and other maternal relatives^35,36. In contrast, relationships between male baboons and their offspring are more variable, and paternal kin may therefore identify each other with greater uncertainty^37–42.

Both predictions were supported. First, the probabilities of mother-son, father-daughter, maternal half-sibling, and paternal half-sibling consortships were extremely low compared to unrelated pairs (Table 1, Figure 2; the figure depicts consortship probability as a function of male dominance rank because rank is a primary determinant of male mating success). Half-aunt-nephew and half-uncle-niece pairs were somewhat less likely to consort than unrelated pairs, but the credible intervals for these estimates overlapped with zero. In contrast, half-first cousins appeared slightly more likely to consort than unrelated pairs. However, we do not consider this strong evidence for mating attraction between half-first cousins because of the presence of undetected kin in our pedigree. Because undetected kin are inevitably included with non-kin in our analysis, their presence is likely to obscure relatively weak kin avoidance effects, for instance between half-first cousins. Additionally, natal males were only half as likely to engage in consortships as immigrant males (Table 1), and this effect by itself will prevent many first cousin matings.

Figure 2. Predicted probabilities, calculated from Bayesian logistic regression models, of a consortship occurring for different categories of female-male pairs, as a function of the male’s dominance rank and controlling for other predictors.

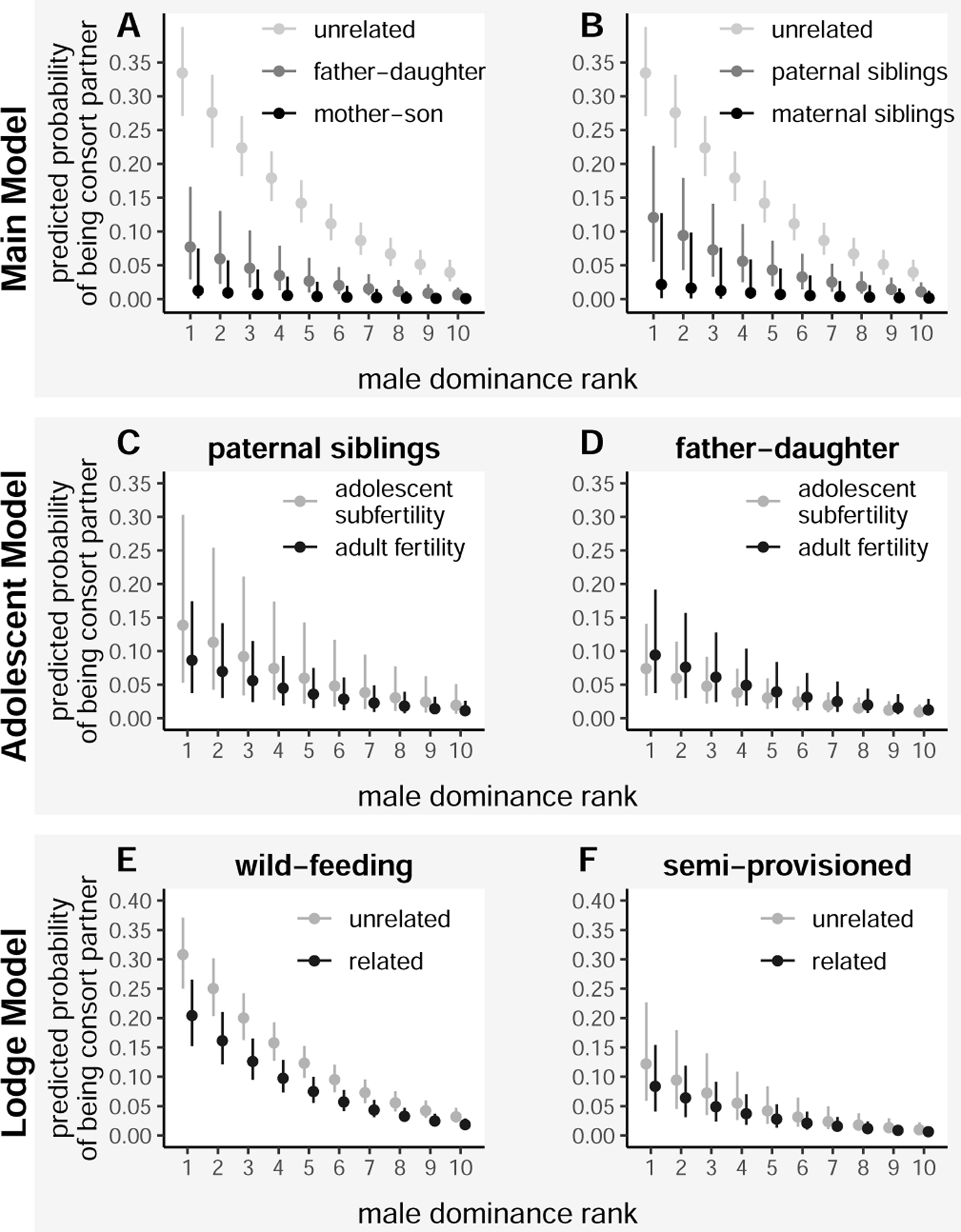
(A) and (B) Results of the main model: Black, gray, and light gray points (± 90% credible intervals) represent the posterior distributions of the probabilities of consortships between different kin classes, involving only fully adult, post-adolescent females in wild-feeding groups. (A) Mother-son pairs and father-daughter pairs had substantially lower probabilities of consorting than unrelated pairs, and mother-son probabilities were lower than father-daughter probabilities. For visualization, the other predictors were set to female rank=1, number of males in the group=10, female age =10 years, and male status=not natal. (B) Maternal half-siblings and paternal half-siblings had substantially lower probabilities of consorting than unrelated pairs, and maternal sibling probabilities were lower than paternal sibling probabilities. Other predictors as in panel A. (C) and (D) Results of the adolescent model: Points and credible intervals represent the posterior distributions of the probabilities of consortship for females experiencing adolescent subfertility (i.e., their first nine sexual cycles after adolescence) versus adult fertility; the analysis was restricted to wild-feeding groups. Other predictors as in panel A. (C) Subfertile adolescent females were more likely to consort with their paternal siblings than adult females were. Note that this pattern is the reverse of the overall effect of adolescent subfertility: subfertile females were in general much less likely to engage in a consortship with any given male (Table 2). (D) Subfertile adolescent females were less likely than adult females to consort with their fathers, consistent with the overall pattern of lower consortship probabilities for subadolescent females. (E) and (F) Results of the Lodge group model: Points and credible intervals represent the posterior distributions of the probabilities of consortship for related versus unrelated female-male pairs in (E) wild-feeding groups and (F) the semi-provisioned Lodge group. All kin categories with r ≥ 0.0625 are collapsed into the ‘related’ category. Other predictors as in panel A. In both wild-feeding groups and the Lodge group, related pairs were less likely to engage in consortships than unrelated pairs. See also Figure S3 and Table S2.

Second, maternal kin showed stronger avoidance than paternal kin. A male’s odds of securing a consortship with his mother were 97.7% lower than with an unrelated female (controlling for the effect of being a natal male and other predictors in the model). In contrast, his odds of securing a consortship with his daughter were only 83.8% lower than with an unrelated female (Table 1, Figure 2a). Similarly, a male’s odds of securing a consortship with his maternal sister were 96.2% lower than with an unrelated female, but his odds of securing a consortship with his paternal sister were only 73.2% lower (Table 1, Figure 2b).

We also re-ran the main model to include admixture-related variables: as noted above, the Amboseli baboon population includes yellow-anubis baboon hybrids (Papio cynocephalus x P. anubis), and genetic ancestry is known to affect consortship formation in this population¹⁸ (STAR Methods). The results were qualitatively similar to the main model, even with the reduced sample size resulting from including only animals with genome-wide admixture scores⁴³ (Table S1).

The adolescent model: Inbreeding avoidance when females were subfertile.

Evidence from several mammals suggests that females may be most likely to mate with kin when they are least likely to conceive^44,45. Many primate females experience reduced fertility and low interest from adult males during the period immediately following menarche^46–49. In Amboseli, this period encompasses roughly a female’s first nine sexual cycles, inclusive: nine is the median number of cycles to first conception in this population (Figure S3). Therefore, we built the adolescent model to test whether father-daughter avoidance and paternal sibling avoidance was less stringent when females were in their period of adolescent subfertility. We followed the same procedure as in the main model, except that (i) our fixed effects included the female’s fertility status (adolescent subfertility or adult fertility), (ii) we restricted the analysis to three kin classes (father-daughter, paternal siblings, and unrelated pairs), and (iii) we included an interaction between female fertility status and kin class. Other predictors were similar to the main model (Table 2). We did not consider maternal kin in this analysis because mating between them was so rare, and we did not consider more distant relatives because of the relatively weak inbreeding avoidance they exhibited in the main model.

Table 2. Adolescent model:

Results of a Bayesian logistic regression predicting the probability of a sexual consortship for different classes of paternal kin pairs, during adolescent female subfertility, controlling for known sources of variance in male consortship success (N = 2500 unique fertile windows for 204 females). See also Figure S3.

90% credible interval
	log odds3	sd	lower	upper	odds ratio4	Interpretation
intercept	−2.029	0.639	−2.856	−1.227	0.131
adolescent subfertility1*	−1.253	0.117	−1.404	−1.103	0.286	Pr(consort) ↓ during adolescence
kinship classes2
father-daughter*	−1.415	0.531	−2.119	−0.759	0.243	Pr(consort) ↓
paternal siblings*	−1.495	0.491	−2.128	−0.884	0.224	Pr(consort) ↓
father-daughter:adolescent subfertility*	0.999	0.638	0.206	1.817		Pr(consort) ↓ during adolescence
paternal siblings:adolescent subfertility*	1.789	0.677	0.914	2.650		Pr(consort) ↑ during adolescence
male dominance rank*	−0.339	0.047	−0.400	−0.279	0.712	↑ male rank = ↑ Pr(consort)
natal male	−0.090	0.405	−0.606	0.430	0.914	No effect
# of adult males in group*	−0.066	0.022	−0.095	−0.038	0.936	↑ # males = ↓ Pr(consort) per male
male rank:# of adult males in group*	0.010	0.003	0.006	0.015		↑ # males= ↓ benefit to high-ranking males
female age	−0.003	0.015	−0.021	0.016	0.997	No effect of female age
female dominance rank*	−0.042	0.016	−0.062	−0.022	0.959	↑ female rank = ↑ Pr(consort)
female rank:male rank*	0.004	0.002	0.002	0.007		↑ male and female ranks = ↑ Pr(consort)
# co-resident days*	0.423	0.114	0.281	0.573	1.527	↑ time co-resident = ↑ Pr(consort)

¹Reference category: adult fertility

²Reference category: unrelated

³Log odds represent the posterior median estimate.

⁴Odds ratios for interactions are not reported because calculating an odds ratio involves exponentiation, which does not yield an easily interpretable number for an interaction.

^*Bold text and asterisks designate kin classes for which behavioral inbreeding avoidance is demonstrated by the credible intervals of the log odds ratio, which do not overlap zero, or cases in which kin classes have significant interactions with female fertility status, demonstrated by the credible intervals of the log odds ratio, which do not overlap zero. Asterisks without bold text indicate other variables for which the credible intervals do not overlap zero.

As predicted, sub-fertile adolescent females were ~70% less likely to experience a consortship than fully adult females (Table 2). Inbreeding avoidance via mate choice was relaxed for paternal siblings during female adolescent subfertility, but not for father-daughter pairs. Specifically, paternal siblings were roughly twice as likely to consort during adolescent subfertility than during the adult fertile period. In contrast, father-daughter pairs – like unrelated pairs – were slightly more likely to consort during adult fertility than adolescent subfertility (Table 2, Figure 2c, 2d).

The Lodge group model: Inbreeding avoidance under reduced dispersal.

We predicted that behavioral inbreeding avoidance would be less stringent in the Lodge group because the greatly reduced emigration and immigration in that group meant that members of that group had fewer unrelated mates available, increasing the costs of avoiding kin. Our Bayesian logistic regression model measured the probability of a sexual consortship between kin pairs in the Lodge group versus kin pairs in wild-feeding groups. Because of the small sample of each type of kin pair in the Lodge group, we collapsed our relatedness categories into a simple binary variable: related (r ≥ 0.0625) or unrelated. As with the main model, we considered only fully adult (post-adolescent) females, and we controlled for other known sources of variance in male consortship success (Table S2).

Contrary to our prediction, the tendency to consort with unrelated groupmates in favor of related groupmates did not differ between the Lodge group and wild-feeding groups: the interaction between kinship status (related vs. unrelated) and group type (semi-provisioned vs. wild-feeding) was small in magnitude and the credible intervals greatly overlapped zero (Table S2). Interestingly, all types of pairs in the Lodge group were overall 69% less likely to engage in consortships during any given fertile window than pairs in wild-feeding groups, perhaps reflecting a reduced tendency to mate in a context in which a large proportion of potential mates are kin.

Serial isolating barriers vs. occurrence of inbreeding

Finally, we examined the production of inbred offspring, predicting that the serial barriers to inbreeding avoidance—death, dispersal, and mating behavior—would be very effective in preventing the production of inbred offspring in wild-feeding groups, but less so in the Lodge group. Our analyses were limited to offspring with paternity assignments: therefore, our counts of inbred offspring represent minimum estimates, because many offspring die before samples can be collected for paternity assignment.

As predicted, inbred offspring were rare in wild-feeding groups: six of 607 offspring of wild-feeding animals (1%) were born to known relatives. In contrast, four of 45 offspring in the Lodge group (9%) were born to known relatives, a value nearly 10 times higher than in wild-feeding groups (Pearson’s Chi-squared test, Chi-squared = 17.3, p = 0.003).

The four inbred Lodge group animals were all the offspring of a male that mated with four different paternal sisters. The six inbred wild-feeding animals included five offspring of half-first cousins (three of them born to the same male-female pair), and one offspring of a pair of paternal siblings who were born in different natal groups and co-resided as adults after the brother dispersed into his paternal sister’s social group.

Conclusions

Using demographic, life-history, behavioral, and pedigree data to assess how behavioral inbreeding avoidance varies between maternal and paternal kin classes in a wild mammal, we present four key findings. First, death and dispersal are strikingly effective at limiting opportunities for inbreeding (Figure 1). However, when these barriers failed, we found robust evidence for behavioral inbreeding avoidance via mate choice among kin classes with r ≥ 0.25 (Figure 2, Table 1). These results point to strong selection for inbreeding avoidance via mate choice, even in the presence of sex-biased dispersal. Second, maternal kin are more avoidant than paternal kin. This pattern of “asymmetrical inbreeding avoidance”⁵⁰ suggests the existence of constraints on differentiating paternal kin in this complex polygynandrous society; it also implicates early-life social exposure as critical to the development of kin-biased behaviors in adults. Furthermore, the near-total avoidance of mating between maternal kin indicates that the benefit-to-cost ratio of avoiding inbreeding is likely to be high^4,5; thus, the inbreeding depression documented in this species may select, over time, for behavioral inbreeding avoidance between paternal kin equivalent to that between maternal kin^9,20. Third, the evidence for relaxed inbreeding avoidance during female adolescence is mixed, providing partial support for the idea that the selection pressure to avoid mating with relatives varies across the lifespan (see also^51,45,44). Finally, when demographic processes fail to separate kin, as in the semi-provisioned Lodge group, baboons are potentially at greater risk of producing inbred offspring than those in undisturbed groups. This result, although based on the small sample of inbred individuals in Lodge group, reinforces the importance of sex-biased dispersal—even if it does not fully prevent inbreeding—as a crucial component of evolved inbreeding avoidance strategies in mammals. This result also emphasizes the breadth of potential adverse anthropogenic influences on wild populations.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Susan C. Alberts (alberts@duke.edu).

Materials Availability

This study did not generate new unique reagents.

Data and code availability

• The data underlying these analyses have been deposited at The Duke Digital Repository and are publicly available as of the date of publication. DOI: 10.7924/r4kd20t7c

• The R code underlying these analyses are deposited at Github: https://github.com/aligalezo/InbreedingAvoidance

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Study population

The Amboseli Baboon Research Project is a longitudinal study of a population of wild baboons in and around Amboseli National Park, Kenya. Behavioral, environmental, and demographic data have been collected from individually recognized baboons on a near-daily basis since 1971. Baboons in Amboseli live in stable social groups containing multiple adults and juveniles of both sexes, ranging in size from approximately 20 to 100 animals. The Amboseli Baboon Research Project monitors multiple such groups (‘study groups’) in the Amboseli ecosystem⁵². All subjects are individually recognized based on unique morphological and facial features. All behavioral, demographic and life-history events (births, maturation events, immigrations, deaths, and emigrations) are recorded on a routine basis as part of the near-daily monitoring of the study groups. Genetic ancestry in the population is largely from the yellow baboon (P. cynocephalus), but admixture over time with anubis baboons (P. anubis; also known as the olive baboon) means that nearly all animals in the population are hybrids^11,12,43,53. The study system has been described in-depth elsewhere^13,52.

METHOD DETAILS

The large majority of data collected in this population come from social groups that fed completely on wild foods (referred to hereafter as “wild-feeding groups”). However, from 1984 to 1997 data were collected on a semi-provisioned social group that fed part-time at a refuse pit associated with a tourist lodge (the “Lodge group”). Foraging at the refuse pit accounted for at least one-third of the nutritional intake of these semi-provisioned baboons, who spent only one-third as much time foraging as wild-feeding animals, and were 50% larger in body mass, primarily because of increased body fat percentage^54,55. Male dispersal into and out of the semi-provisioned group was limited during the time it was monitored, possibly due to the effects of provisioning and human contact¹⁹. Because of the atypical patterns of dispersal in this group, we analyzed the semi-provisioned group separately from the population’s wild-feeding groups to assess how disrupted male dispersal affected the co-residency and inbreeding rates of relatives.

Identification of kin

A multi-generational population pedigree exists for the study population, containing 1624 individuals with known mothers and 652 individuals with known fathers. The pedigree includes up to 9 generations for the deepest maternal lineage, but most maternal lineages are of shorter depth, and paternal lineages are 1–5 generations deep. Maternity was assigned based on reliable behavioral cues (e.g., nursing and a continuous extended relationship between the dependent infant and the mother from birth) and in many cases was confirmed using genetic data extracted from fecal, blood, or tissue tissue samples^39,56. We used at least 6 microsatellite loci for exclusion analysis of locus matches between mothers and offspring using Cervus versions 2.0 and 2.0^39,56. Paternity was assigned via microsatellite exclusion analysis, again using Cervus versions 2.0 and 3.0^39,56–58. Paternity was evaluated by first including all potential fathers that were residing in the mother’s social group at the time of conception, and second by including all potential fathers in the population at the time; paternity was assigned only when these two methods produced the same consensus father. In all cases, the assigned father was residing in the mother’s social group at the time of conception; no cases of extra-group paternity have ever been identified in this population⁵⁶.

We first identified all pairs of relatives that were detectable with our existing pedigree, creating a class of “related” pairs and a class of “unrelated” pairs. For animals in wild-feeding social groups, opposite-sex pairs were considered “unrelated” if they 1) had no unknown parents or grandparents and 2) did not fall into any relative-class with a coefficient of relatedness ≥ 0.0625. Based on the pedigree, we assigned related pairs to kin categories as follows. Mother-son and father-daughter pairs were identified as described in the previous paragraph. Maternal half-sibling and paternal half-sibling were siblings that shared either their mother or their father but not both (expected r=0.25); the 62 pairs of full siblings in our data set were omitted from the analysis because they were relatively few in number. In a half-aunt-nephew pair (expected r=0.125), the aunt is the half-sister of her nephew’s mother or of his father, and in a half-uncle-niece pair (expected r=0.125), the uncle is the half-brother of his niece’s mother or of her father. In a half-first cousin pair (expected r=0.0625), the mother or father of one member of the pair was the half-sibling of the mother or father of the other individual. Note that coefficients of relatedness in non-parent-offspring kin classes are ‘expected’ because allele-sharing between these types of kin is probabilistic rather than deterministic. Allele sharing between half-siblings, for instance, is expected on average to be 0.25, but this and other non-parent-offspring kin classes exhibit variance in the actual extent to which they share alleles^59,60.

Pedigree depth in the semi-provisioned Lodge group was generally lower than in wild-feeding groups due to their limited observation period, so in the semi-provisioned Lodge group, a pair was considered unrelated if they 1) had no unknown parents and 2) did not fall into any relative-class with a coefficient of relatedness ≥ 0.0625. Kin categories were assigned as above. The lower pedigree depth in the Lodge group increases the likelihood that true relatives would go undetected in this group compared to the wild feeding groups. We are therefore more likely to underestimate the degree of inbreeding in the Lodge group than in wild-feeding groups. Despite this potential bias towards underestimating inbreeding in the Lodge group, we still found a higher level of inbreeding in the Lodge group than in wild-feeding groups. Thus, for this aspect of the study, the difference in pedigree depth for wild-feeding vs. Lodge group animals makes our results conservative rather than anti-conservative.

We note that our pedigree depth varied not only between the Lodge group and the wild-feeding groups, but also across individuals within the wild-feeding groups, with some individuals having deeper pedigree information than others. Variation in pedigree depth could potentially bias our results if we failed to classify male-female pairs as “related” due to incomplete pedigree data. However, the resulting bias would be small and conservative (i.e., it would result in our underestimating the degree of inbreeding avoidance). Specifically, in our main mate choice model, individuals that did not have four known grandparents were entirely excluded from the analysis - thus, when pedigree data were missing, pairs were not assumed to be unrelated, but were excluded from analysis completely. Therefore, even if some related pairs were erroneously classified as unrelated due to pedigree incompleteness (for instance, in the case of pairs whose grandparents were kin), this would result in our “unrelated” pool of male-female pairs containing some related pairs. This would make us less likely to find a difference in mate choice behavior between related vs. non-related male-female pairs. In other words, a more incomplete pedigree would give us a more conservative result rather than an anti-conservative one.

QUANTIFICATION AND STATISTICAL ANALYSIS

Demographic barriers to co-residency

We first sought to identify the demographic events that separated opposite-sex pairs of kin and, for pairs that did not become separated, to measure the lengths of their co-residencies. To achieve this goal, we identified all opposite-sex related pairs that had 1) overlapping lifespans and 2) uncensored co-residency data (i.e., one or both individuals were dead at the time of analysis). This data set included 454 mother-son pairs, 182 father-daughter pairs, 248 pairs of opposite-sex maternal half-siblings, 435 pairs of opposite-sex paternal half-siblings, 1117 half-aunt-nephew pairs, 690 half-uncle-niece pairs, and 321 half-first cousins. The 62 pairs of full siblings in our data set were omitted from the analysis because of small sample size. For each pair included in the analysis, we determined the cumulative number of days that they resided in the same group after both individuals had reached adulthood, using near-daily census data collected from July 1971 to June 2019. In females, the onset of adulthood was defined as the date of menarche (i.e., first sexual cycle). In males, the onset of adulthood was defined as the attainment of adult rank (i.e., the first date on which a male consistently outranked another adult male in his group) rather than the attainment of puberty, because males rarely mate with fertile females prior to adult rank attainment⁶¹. Male dominance ranks, and the attainment of adult dominance rank for males, were assessed based on the outcomes of dyadic agonistic interactions⁶².

We used the monitoring data from the Amboseli Baboon Research Project’s long-term records to determine the reasons that kin-pairs in wild-feeding groups failed to co-reside as adults: separation by group fission, death of one or both individuals before both reached adulthood, or male dispersal to a different social group. We did not conduct an analysis at the same level of detail for the semi-provisioned Lodge group because sample sizes of uncensored co-residencies were small.

For all related pairs that did co-reside for at least one day as adults (n=282 wild-feeding pairs, n=24 semi-provisioned pairs), we examined the distribution of their co-residency lengths to gain insight into how long animals were generally exposed to the risk of inbreeding.

Behavioral inbreeding avoidance via mate choice

Female baboons experience a sexual cycle that is approximately 39 days long, which is characterized by highly visible sexual skin swellings that increase in size during the follicular phase of the sexual cycle and decrease during the luteal phase⁴⁹. Females mate only during the follicular phase of the cycle⁴⁹, and the large majority of mating occurs in the context of mate-guarding episodes, often called ‘consortships’ in primates^31–33. Further, conception is most likely to occur when sexual swellings reach maximum size, which typically occurs during the 5-day window before the end of the follicular phase, hereafter the ‘5-day fertile window’^49,63. Previous work in this population has shown that a male’s success at attaining consortships during the fertile window is a good predictor of paternity^56,64.

We constructed three different Bayesian logistic regression models using the R package rstanarm³⁴ to assess the probability of consortships occurring between female-male pairs of different relatedness categories. We refer to these models as the ‘main model,’ the ‘adolescent model,’ and the ‘Lodge group model.’ For all three models, we specified weakly informative prior distributions: normal distributions with mean 0 and standard deviation 2.5. We ran 6000 iterations of each model and evaluated model fit by examining traceplots for convergence, evaluating the Gelman-Rubin potential scale reduction statistic Rhat, and quantifying autocorrelation between samples. Each of the three models is described below.

The main model.

To quantify the occurrence of inbreeding avoidance via mate choice, we examined the probability of a consortship occurring for each adult male-female pair during the 5-day fertile window of each female sexual cycle. Specifically, for each sexual cycle, we identified all adult males that were co-resident in the group with the female during the 5-day fertile window and recorded, as the binary response variable (0/1), whether or not each of those males attained a consortship during that 5-day fertile window. We then assigned a kin category to each pair; the 62 pairs of full siblings were omitted from the analysis. In addition to kin category, we included the following predictors: the female’s age, the number of adult males in the group on the date of the consortship, the number of days that each pair co-resided in the same group (“number co-resident days” in Table 1), whether or not the male was born in that social group (i.e., was a natal male), and the male’s and female’s ordinal dominance rank. In an ordinal dominance rank system, the highest-ranking individual of each sex is assigned rank number 1, with successive numbers representing lower ranks. For male baboons in particular, mating success is higher for males with higher dominance rank^{31–33,62,65}; we have previously reported a similar, but weaker, effect for females¹⁸. We included two interaction terms, one between male dominance rank and the number of adult males in the group (because highly-ranked males have higher mating success in groups with fewer competing males³³) and one between male and female dominance rank, which is known to influence consortship formation¹⁸. Finally, we also included random effects for 1) male identity and 2) female identity to account for multiple observations of the same individuals. Further details of the main model are given in the Results and Discussion section.

The adolescent model.

Given evidence in other mammals suggesting that females may be more likely to avoid kin when they are most likely to conceive^44,45, we differentiated between “adult fertility” and “adolescent subfertility” in the adolescent model of inbreeding avoidance. Female adolescent subfertility is the period immediately following menarche, during which females are unlikely to conceive^46,47,49. For our study, we defined female adolescent subfertility as encompassing a female’s first 9 sexual cycles, inclusive: this represents the median number of cycles to first conception in this population (Figure S1). For this model, we only included consortships from wild-feeding social groups, and only included male-female pairs among the relatedness classes for which we anticipated having the most power to detect an effect: father-daughter pairs and paternal siblings. The binary response variable (0/1) was whether or not each of the candidate males attained a consortship during the female’s 5-day fertile window. Fixed effects included the female’s fertility status (adolescent subfertility or adult fertility) and kin class (unrelated, father-daughter, or paternal siblings), as well as the other fixed effects in the main model (Table 2). We also included an interaction between female fertility status and male-female kin class. We included male and female identities as random effects. Note that the coefficients from this model are not directly comparable to those from the main model, a problem particular to comparisons of logistic regressions that include different, even if overlapping, sets of predictor variables. The problem arises from the fact that, in the case of logistic regressions, unobserved heterogeneity affects the scale of the dependent variable in a manner that does not occur with a continuous dependent variable; see Ref. ⁶⁶ for a more detailed discussion. Further details of the adolescent model are given in the Results and Discussion sections.

The Lodge group model.

This model allowed us to test whether the degree of inbreeding avoidance via mate choice differed for animals in wild-feeding social groups versus the semi-provisioned Lodge group. As with the adolescent model (see above), we note that the coefficients from this model are not directly comparable to those from the main model⁶⁶. For this model, we only analyzed females who had reached adult fertility, and collapsed our relatedness categories into a simple binary variable: related or unrelated. Our fixed effects included relatedness category (related or unrelated), group identity (wild-feeding or semi-provisioned), male ordinal dominance rank, the number of adult males in the group on the date of the consortship, female age and female ordinal dominance rank, and the number of days that each pair co-resided in the same group. Once again, we included interactions between male dominance rank and the number of adult males in the group, and between male and female dominance rank. A key added interaction term was that between relatedness and foraging mode (semi-provisioned versus wild-feeding) to assess whether inbreeding avoidance via mate choice was relaxed in the semi-provisioned Lodge group. We included male and female identities as random effects. Further details of the Lodge group model are given in the Results and Discussion section.

Measuring age at natal dispersal

We quantified the difference in age at natal dispersal in the semi-provisioned Lodge group vs. wild-feeding groups by fitting Kaplan-Meier survival curves for semi-provisioned (n = 93) and wild-feeding (n = 633) males using the R package survival⁶⁷. Males were considered to be censored if they died before natal dispersal, if their study group was dropped before natal dispersal, or if they were still alive and under observation but had failed to disperse from their natal group as of the last time they were observed. We used the R package survminer to run a log-rank test to determine if the survival curves of wild-feeding vs. semi-provisioned males differed⁶⁸ (Fig. S2).

Quantifying admixture

Animals in the Amboseli baboon population harbor primarily yellow baboon ancestry, but as a result of recent and historical waves of admixture, all are admixed with anubis baboons⁴³. Because genetic ancestry has previously been shown to predict consortship formation in this population¹⁸, we re-ran the main model with the addition of fixed effects for male ancestry, female ancestry, and an assortative admixture index based on both male and female ancestry values (following Ref. ¹⁸). We did not incorporate these estimates in the primary model because ancestry estimates were available for only a subset of individuals in the inbreeding data set (182 of 386). Further, our analyses indicated that inclusion of ancestry-related effects do not qualitatively alter our conclusions about inbreeding avoidance.

In brief, estimates of individual ancestry were derived from composite likelihood estimation of local ancestry across the genome using the software LCLAE and reference allele frequencies for yellow and anubis baboons¹⁰. Local ancestry estimates were obtained from low coverage resequencing data (mean ~1x coverage), and overall ancestry estimates were derived from local ancestry calls across all autosomal regions of the genome (see ⁴³). These estimates range from 0 to 1, where 0 corresponds to unadmixed yellow ancestry and 1 corresponds to unadmixed anubis ancestry. Because the assortative admixture index is correlated with genome-wide estimates of admixture (Pearson’s r = −0.76, p = 2.2⁻¹⁶ for males), we used the residuals of the assortative admixture index, controlling for male genetic ancestry, as the assortative admixture index in the model.

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Bacterial and virus strains
Biological samples
Chemicals, peptides, and recombinant proteins
Critical commercial assays
Deposited data
Data underlying analyses	This paper	Duke Data Repository DOI: 10.7924/r4kd20t7c
R Code underlying these analyses	This paper	https://github.com/aligalezo/InbreedingAvoidance
Experimental models: Cell lines
Experimental models: Organisms/strains
Oligonucleotides
Recombinant DNA
Software and algorithms
Other

Highlights.

• In wild baboons, death and dispersal effectively separate most pairs of adult kin.

• Nonetheless, close kin (r ≥ 0.25) avoid mating when they live together as adults.

• Maternal kin are more avoidant than paternal kin, revealing ‘asymmetrical avoidance.’

• Anthropogenic disturbance appears to greatly increase the risk of inbreeding.