Summary
During motor learning1, as well as during neuroprosthetic learning2–4, animals learn to control motor cortex activity in order to generate behavior. Two different population of motor cortex neurons, intra-telencephalic (IT) and pyramidal tract (PT) neurons, convey the resulting cortical signals within and outside the telencephalon. Although a large amount of evidence demonstrates contrasting functional organization among both populations5,6, it is unclear whether the brain can equally learn to control the activity of either class of motor cortex neurons. To answer this question, we used a Calcium imaging based brain-machine interface (CaBMI)2 and trained different groups of mice to modulate the activity of either IT or PT neurons in order to receive a reward. We found that animals learn to control PT neuron activity faster and better than IT neuron activity. Moreover, our findings show that the advantage of PT neurons is the result of characteristics inherent to this population as well as their local circuitry and cortical depth location. Taken together, our results suggest that motor cortex is more efficient at controlling the activity of pyramidal tract neurons, embedded deep in cortex, and relaying motor commands outside of the telencephalon.
Keywords: Motor cortex, Pyramidal tract neurons, Neuroprosthetics, Brain-machine interfaces, Operant control, Neural circuits, Operant learning
eToc
The brain may exert better control over some subpopulation of neurons. Vendrell-Llopis et al. show how animals learn to control PT neurons faster and better than IT neurons and that this is the result of inherent characteristics of PT neurons, their local circuitry, and their cortical depth location.
Results & Discussion
To execute a complex natural or neuroprosthetic behavior, animals learn to control the activity of neuronal circuits in motor cortex and the commands are sent downstream. Motor cortex output is mainly dominated by two cell-classes: intra-telencephalic neurons (IT) which project to the contralateral cortex and bilaterally to the striatum; and extra-telencephalic or pyramidal-tract neurons (PT) which project ipsilaterally to the striatum, to the brainstem and to the spinal cord. PT neurons are exceptionally well positioned to generate a cortical output to downstream areas7,8. On the contrary, IT neurons are more adaptable9,10, which should be advantageous for efficient learning in neuronal circuits. It is also possible that other neuronal characteristics such as location, activity or circuit dynamics of neighboring neurons are more relevant to neural control and manipulation than cell-class. Understanding what drives the adaptive mechanisms of control over cortical neurons is not only relevant for clarifying the role of IT and PT neurons during learning, but it can also enlighten the different roles of cortical cell-classes in disease10 and motor function11,12.
To distinguish IT neurons from PT neurons, we obtained cell-class specific expression with a red fluorescence marker in two groups of tetO-GCaMP6s/-Camk2a-tTA transgenic mice. One group (n=9) was injected with AAVrg-CAG-tdTomato in the contralateral motor cortex to label IT neurons and the other group (n=8) in the ipsilateral pons to label PT neurons (Figure 1.A–E). We trained both groups of mice to control a CaBMI (see methods) while simultaneously recording in four different planes the activity of both red-labeled and unlabeled neurons (Figure S1.A–C). Because the recordings span a large part of the cortical column (400µm, Figure S1.D), unlabeled neurons may contain excitatory neurons from both cell-classes and possibly inhibitory neurons13,14. Each session, a different pair of red-labeled neurons were arbitrarily selected and assigned to neural ensembles. By using only PT or only IT neurons as the neurons directly controlling the CaBMI (direct neurons), we studied the differences in learning between these genetically different subpopulations of cortical neurons as well as the neural dynamics that surrounded them.
Figure 1: Cell-class specific CaBMI shows differences on learn.
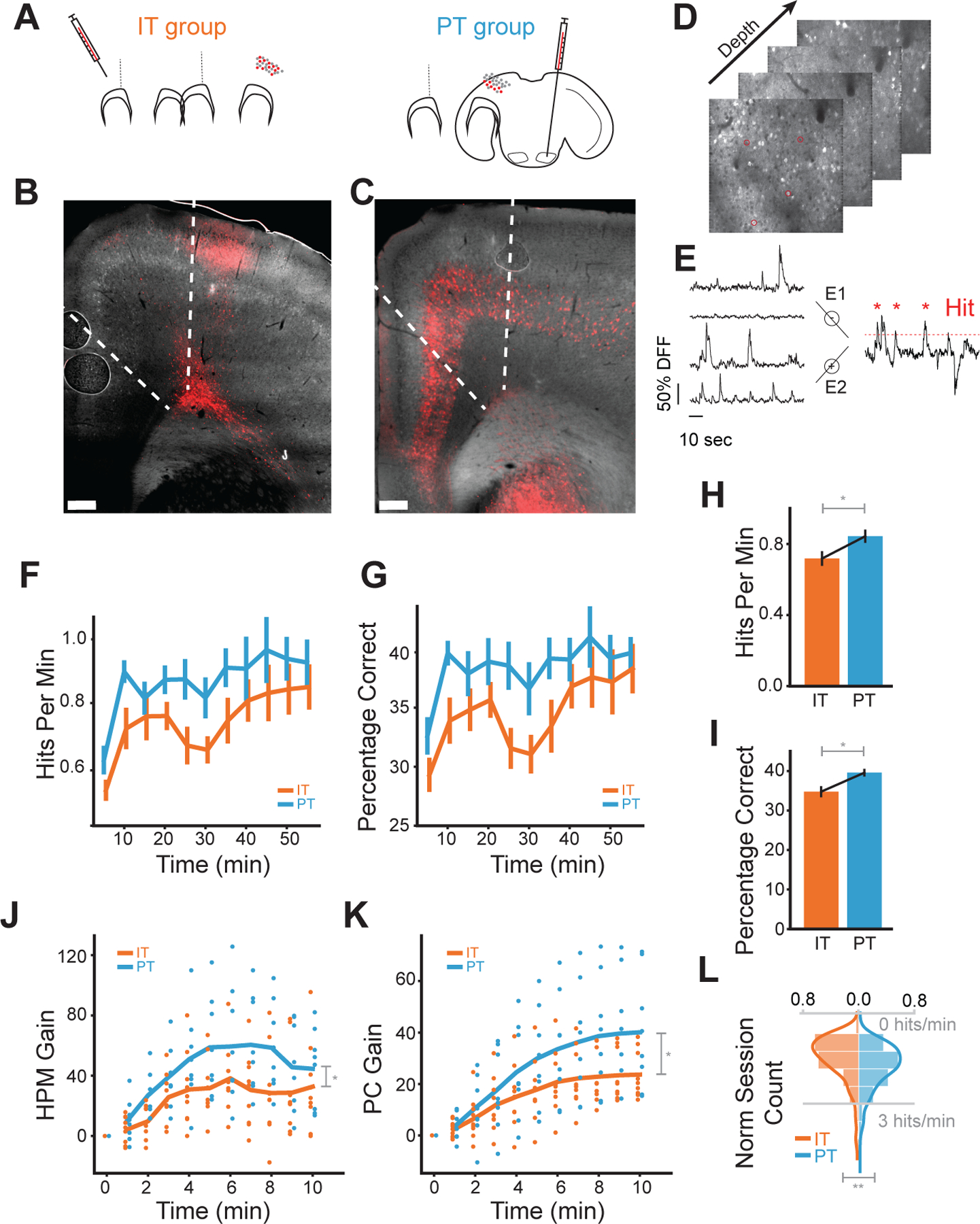
A) AAVrg-CAG-tdTomato retroviruses injection regions for IT (left), contralateral motor cortex, and PT (right), ipsilateral pons. (B-C) Coronal sections for the IT (B) and PT (C) animals. Neurons with viral expressions were located in L2/3 and L5–6 of motor cortex (M1-M2) for IT group and in L5–6 across cortex for PT. D) Typical depth planes for calcium recordings. Marked neurons were randomly picked as direct neurons. See also Figure S1.A–D. E) Schematics for the calcium decoding algorithm. Neural cursor is calculated as the difference between sum dF/Fs of two groups. Red dashed line denotes one instantiation of the reward threshold simulated from baseline. F) HPM, the number of hits within a one-minute window, calculated for each session across IT experiments (orange) and PT experiments (blue). Values are binned in five-minute windows. G) As in (F), but for PC, the percentage of correct trials within the same one-minute window. Because trial lengths can be variable, PC represents the reward rate normalized by the number of trials in each time window. See also Figure S1.E. H) HPM values across all time windows of a session (*: p < 0.05 with Mann-Whitney U test). HPM chance level = 0.46 ±0.04. I) As in (H), but for PC. PC chance level 0.25±0.02 J) The relative gain in HPM during the first 10 minutes of a session from the beginning of the session. Specifically, we calculated the difference in HPM from the first minute of the experiment, then normalized this measure for each session by dividing by the mean HPM. This normalization allowed us to compare performance increases across sessions with different starting reward rates. K) As in (J), but for PC. L) Distribution of maximum HPM obtained per session. All sessions (IT group:163 sessions, 9 animals, PT group: 125 sessions, 8 animals) were used for these plots. Values were averaged first across sessions of each animal and then across animals (**: p < 0.005 with one-way Anova) (**: p < 0.005 with one-way Anova).
Our task differs from previous studies in a few ways. Each session we chose new direct neurons to test the learning capabilities of as many neurons as possible. Although we studied different stages of this learning process within a session (initial vs final performance), it should all be considered early learning with respect to previous work that spanned multiple sessions with the same direct neurons. For that reason, our results can only be compared to initial sessions of other CaBMI experiments2,4,15–17 (see Figure S1.E). By using naive neurons, we investigated the role of IT and PT neurons during the acquisition of a learned behavior which may entail different processes and circuits than the refinement of that behavior18. The role of different cortical neurons in late learning including consolidation and refinement should be addressed in further experiments. Furthermore, in this study animals learned to control a one-dimensional CaBMI. Our aim was to simplify the task and minimize the relevant circuit to study. However, more complex BMI experiments, for instance BMIs with multiple degrees of freedom in the effector19, might take advantage of a more complex circuit encompassing multiple diverse cell types.
Animals learn to control pyramidal tract neurons better and faster than intra-telencephalic neurons during CaBMI learning
We first investigated whether our choice of IT or PT neurons as direct neurons affected the animal’s learning ability. We quantified learning through two measures: hits-per-minute (HPM) and percentage-correct (PC). Hits-per-minute quantifies reward rate over time while percentage-correct is the reward rate normalized by the number of trials. Both groups showed an increase from chance level (HPM: 0.46±0.04, PC: 0.25±0.02) in both hits-per-minute and percentage-correct throughout the experiment (Figure 1.F–G). However, the PT group (n=125 sessions) achieved greater reward rates than the IT group (n=163 sessions) across equivalent time windows of a session (Figure 1.F–G) and across the whole session (Figure 1. H–I).
To address if differences in starting reward rate explained the learning differences between the IT and PT group, we obtained the gain of each learning measure over the first 10 minutes. We found that the PT group reached a higher performance than the IT group and did so faster (Figure 1.J–K). Similarly, we compared the best performance of each group to address any other effects on the behavior (motivation loss, satiety, etc.). We observed that the PT group tended to have significantly higher maximum performance (p<0.005, Figure 1.L).
Taken together, our results demonstrate that, although both groups can learn the task, the PT group consistently outperforms the IT group across a variety of learning measures. Strikingly, the PT group achieves a higher reward rate than the IT group in less time. Much of this performance difference occurs in the first few minutes of an experiment (Figure 1.J–K). A possible explanation is that the network involved in this task learns to modulate the activity of PT neurons and/or re-enter the neuronal patterns that granted reward, more effectively and quickly. If so, known characteristic differences between IT and PT neurons, such as connectivity or cortical depth11, may be relevant. However, other factors besides neuron properties can also contribute to these observed differences. Experimental confounds, such as imaging quality, may explain these differences. In the rest of the paper, we tackle the extent to which a diverse range of factors could explain the higher learning performance of the PT group.
Evaluating experimental and neural features that influence learning
To control for possible experimental confounds and understand the impact of cell-class and other neural features on learning, we implemented a feature attribution framework. We used a gradient-boosted decision tree, XGBoost20, as a model to predict the percentage of correct trials (henceforth percentage-correct), our measure of learning. Then, we used SHapley Additive exPlanations (SHAP)21,22 to explain how each feature contributed to the model’s prediction each session (Figure S2). Thus, positive SHAP values represent that a feature pushed the predicted value of percentage-correct higher, suggesting a positive influence on learning. On the contrary, negative SHAP values represent that a feature reduced the predicted value of percentage-correct, suggesting a negative influence on learning (Figure 2.A).
Figure 2: Dissecting the influence of features on learning outcome.
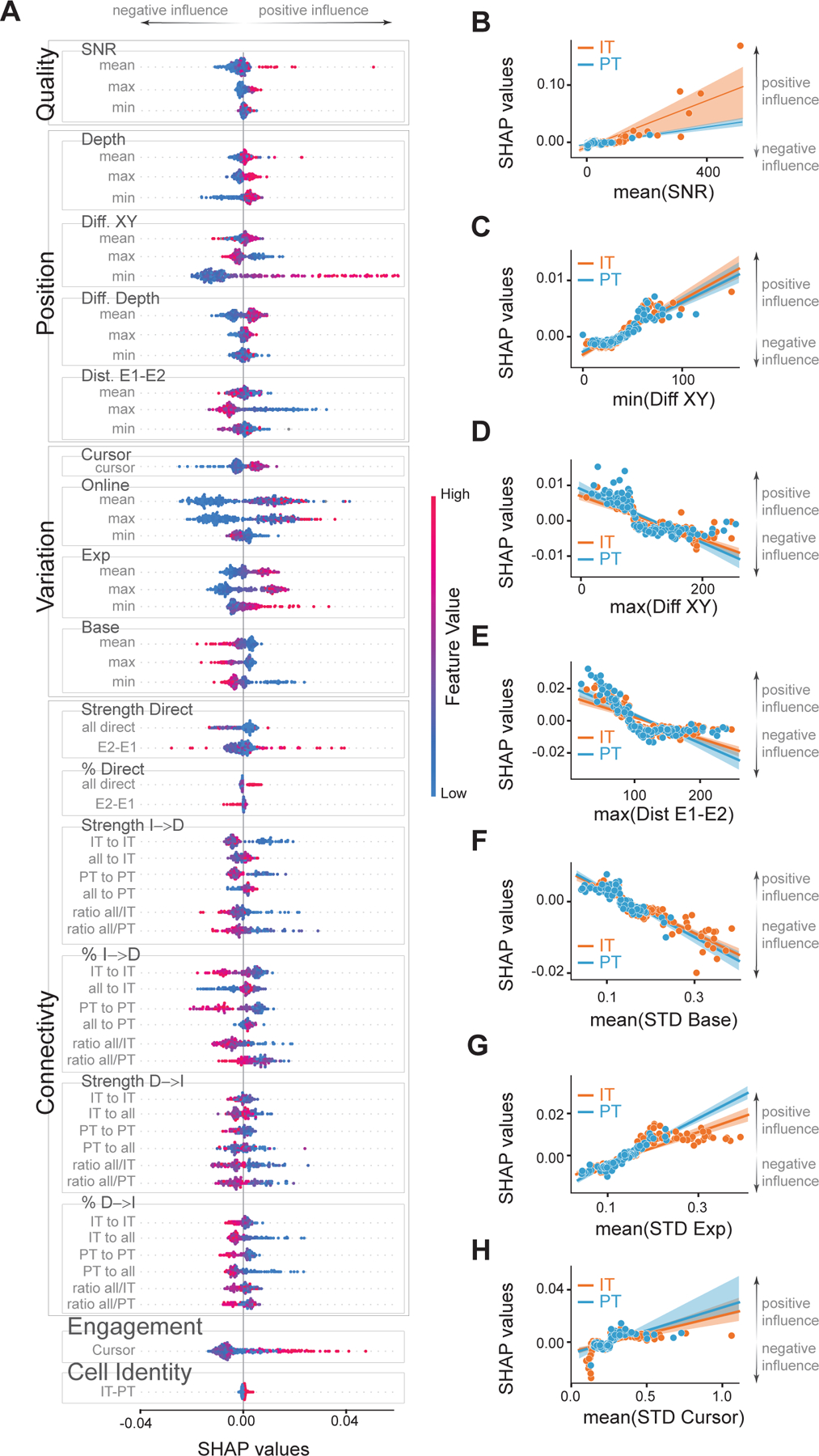
A) SHAP values for all the features used in the XGBoost models (see Figure S2 for description). Positive SHAP values indicate a positive effect on the PC measure and a better learning outcome. Negative SHAP values indicate a negative effect on learning. Features are divided into 6 groups: Quality, Position, Variation, Connectivity, Engagement and Cell Identity for clarity. Quality features are comprised of the signal-to-noise ratio. Position features include depth (Depth) of direct neurons, the distance between direct neurons on a plane (Diff. XY), their difference in depth (Diff. Depth), and the distance between neurons of the ensemble E1 and the ensemble E2 (Dist. E1-E2). Variation features include STD of the cursor (Cursor) based on neuronal activity E2-E1, STD of the online calcium signals that operated the CaBMI (Online), and also the post-processed calcium signals of direct neurons during baseline (Base) or during the whole experiment (Exp). Measures that were calculated for each direct neuron were included as features with their minimum (min), mean, or maximum (max) value. Color (red-to-blue) represent the value of the feature. Sessions from IT and PT groups were included. B-H) Linear regression between SHAP values and the value of mean SNR (B); minimum distance (C) and maximum distance (D) in the XY plane between 2 direct neurons; maximum distance between neurons belonging to different ensembles (E). Activity of direct neurons during baseline (F) or whole experiment (G). H) Mean of the STD of the neural cursor. Each dot represents 1 session. Shaded area is the confidence interval. Orange dots are sessions from the IT group whereas blue dots are sessions of the PT group. See also Figure S3.A–F for IT-PT differences of these features.
We applied XGBoost/SHAP to a) the percentage-correct at 10 min, to study which features could explain the faster learning of the PC group, and to b) the final percentage-correct value, to study which features could explain the differences on learning performance. We focused this study on the latter, thus, unless indicated otherwise, results at 10 min were no different from final performance or no relevant.
Untangling the true effect each feature had on the animal’s learning each session is a complicated endeavor. For example, depth, signal quality and cell identity are highly correlated but may have opposite effects on learning. By using a highly accurate model and a reliable explainer we offer a reasonable approximation to the immeasurable independent contributions of each feature to learning.
Experimental-dependent features and cell-class activity variability do not explain learning differences
We first investigated if experimental-dependent features (features that were solely affected by experimental limitations or experimenter bias) affected learning. These features captured signal quality and distance between direct neurons (excluding cortical depth which is dependent on cell-class). SHAP values were highly correlated with signal-to-noise ratio (SNR), indicating that cleaner signals resulted in better animal performance (Figure 2.B). Thus, the generally lower signal-to-noise ratio of PT neurons (due to brain-scatter imaging limitations in deep tissue) hindered the predicted percentage-correct (Figure S3.A,D). Additionally, the distances between direct IT or PT neurons (Figure 2.C–E) affected the value of the predicted percentage-correct similarly in both groups. These results indicate that none of the experimental features that were independent of cell-class were responsible for the improved performance of the PT group.
Distinct activity characteristics have been identified in IT and PT neurons23. To investigate if these differences could influence learning, we added features based on the standard deviation (STD) of neuronal activity to the model. Highly active direct neurons during baseline negatively affected the value of predicted percentage-correct (Figure 2.F). Contrarily, highly active direct neurons during the experiment increased the predicted percentage-correct (Figure 2.G). These apparently contradicting results are consistent with CaBMI benefiting from silent neurons during baseline becoming more active during the task. The generally tonic firing characteristics of PT neurons23 resulted in reduced changes of fluorescence in calcium imaging and therefore low variability (Figure S3.B–C). These had contradicting effects on the predicted percentage-correct (Figure S3.E–F). In addition, there was no cell-class difference due to the variability of the CaBMI cursor (Figure 2.H). These findings indicate inconclusive effects of the different activity characteristics of PT and IT neurons over learning.
Local connectivity and position of PT neurons account for the differences in learning
Learning modulates the activity of indirect neurons24,25, neurons of the local circuitry recorded during the experiments but not in direct control of the CaBMI. However, the influence that local circuitry may pose on learning has not yet been investigated. To address this, we studied how two different measures, connectivity to/from direct neurons and task engagement of indirect neurons, would influence learning.
To begin, we used Granger causality as a measure of effective connectivity. We determined the percentage of neurons that were connected as well as the strength of those connections, during the baseline period (see methods). It is important to note that this method cannot capture the effects of neurons not recorded and/or fast recurrent networks due to our recording framerate (10Hz).
Interestingly, the impact of connectivity (not its value) varied depending on the different stages within one session learning (Figure 2.A, Figure S3.G–H). Higher effective connectivity from direct neurons to indirect neurons, regardless of cell-class, impacted the value of percentage-correct positively only during the first 10 minutes of learning (Figure 2.A, Figure S3.G–H). On the contrary, higher effective connectivity from unlabeled indirect neurons to IT direct neurons increased the predicted percentage-correct (Figure 2.A, Figure S3.I–J) in all stages of learning, suggesting general better performance for neurons receiving higher, in both number of connections and strength of those connections, indirect input.
Lastly, to evaluate how engaged were the indirect neurons with the task, we calculated how well these indirect neurons could predict the neural cursor controlling the CaBMI (see methods). Besides some fluctuations, better cursor prediction by indirect neurons was tightly linked with higher predicted percentage-correct (Figure 2.A), indicating a positive influence in learning.
These findings suggest that generally, a strong support from local circuitry positively impacts learning. However, our results are limited to the acquisition of a learned behavior over the span of a session. Previous research have shown that during late learning across multiple sessions (see also Figure S1.E), task modulation of indirect neurons decreases24,25 and there is less functional connectivity from indirect neurons to direct neurons than vice versa26. It is possible that local circuitry may be more relevant during early learning facilitating the re-entrance of the neuronal patterns that grant reward. On the contrary, the effects of refinement over days may entail different neural processes, including the pruning of indirect neurons deemed impractical.
Interestingly, both measures quantifying the involvement of indirect neurons (effective connectivity and task engagement) increased the predicted percentage-correct for the PT group but decreased it for the IT group (Figure 3.A–B, Figure S3.K–M). This may imply that deep local circuitry surrounding PT neurons more effectively supports learning than circuitry in the upper cortical layers. Is this also true for IT neurons? To investigate this, we examined if choosing IT direct neurons from deeper planes affected learning outcomes. We found that sessions with IT direct neurons in deeper cortical layers increased the predicted percentage-correct (Figure 3.C). Additionally, depth was highly correlated with indirect-to-direct connectivity (Figure 3.D, Figure S3.N) which our results indicate facilitates learning. Taken together, these findings suggest that direct IT neurons located in the vicinity of PT neurons learned more effectively than their counterparts in upper layers. However, it is possible that this learning difference arises not from a supportive deep local circuitry but from the postsynaptic circuit. IT neurons projecting into striatum are oftentimes found in deeper layers than IT neurons that only project into other cortical regions10. Thus, the behavioral outcome may be largely influenced by synaptic proximity to the next stop of the cortico-basal-thalamo-cortical loop that governs learning.
Figure 3: Inherent characteristics, connectivity and location of PT neurons lead to better performance.
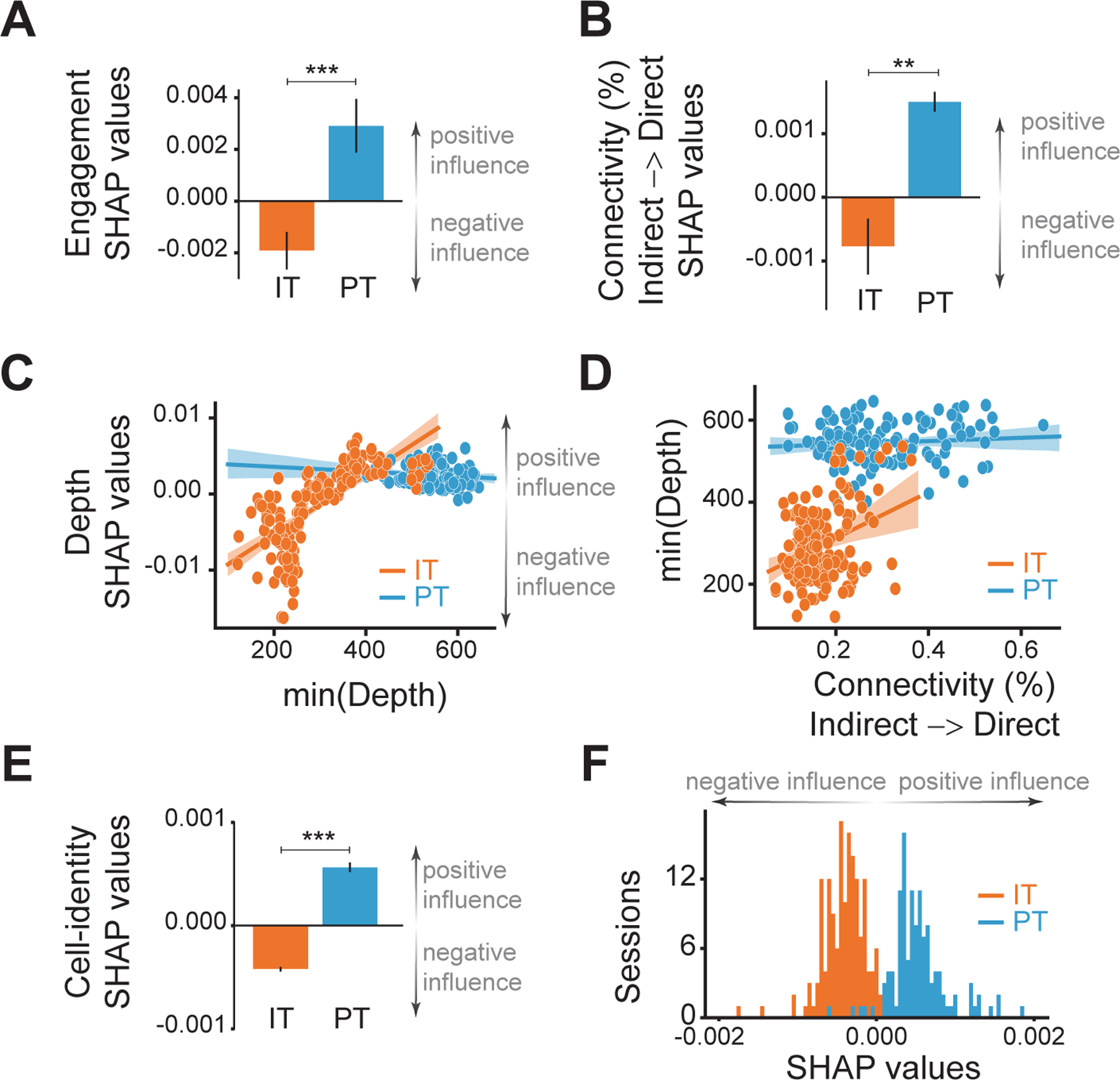
SHAP values for circuit-related features: (A) engagement of indirect neurons and (B) effective connectivity from indirect to direct neurons in sessions of the IT (orange) or PT (blue) groups. C) SHAP values depending on the minimum depth of all direct neurons. See also Figure S3.G–N. D) Linear regression between the minimum depth of all direct neurons and the effective connectivity from indirect to direct neurons. Each dot is a session of the IT (orange) or the PT (blue) groups. The line is the linear regression and the shaded area its confidence interval. E) SHAP values for the cell-identity feature and their distribution (F) with IT group sessions in orange and PT group sessions in blue. Black lines in bar graphs represent SEM. (**: p<0.005, ***: p<0.0005 with independent t-Test).
We aimed to investigate if location is the only relevant feature to determine learning. However, we could not measure all possible different characteristics of IT and PT neurons (such as input from other cortical areas, thalamic input, spike burstiness, etc.). Instead, we added one more feature that encoded the identity of the neurons chosen for CaBMI, i.e., a feature that specified if the direct neurons had been IT or PT, hence accounting for the remainder of other inherent cell-class characteristics. Strikingly, the difference in SHAP values was very consistent. Sessions that used PT neurons as direct neurons for CaBMI had generally positive SHAP values. Therefore, selecting PT neurons generally increased the predicted percentage-correct, indicating a positive influence on task performance. On the contrary, sessions that used IT neurons as direct neurons for CaBMI had entirely negative SHAP values, namely a negative impact on the predicted percentage-correct (Figure 3.E–F). This feature represents solely the cell-class of the direct neurons and does not infer the cell-class of every cortical neuron participating in the circuit responsible for learning. Although our approach did not allow us to identify multiple cell-classes on the same animal, it is highly likely that IT neurons participated as indirect neurons in sessions of the PT group and vice versa. The above effect shows that using PT neurons as direct neurons was consistently advantageous for successful learning, and that this effect is the result of inherent characteristics of PT neurons different from the features under study.
In summary, by using a method that measures the impact of different cell-type features on the learning of an operant CaBMI task, our work provides insights into the understanding of the factors that contributed to operant control of cortical activity. Our results demonstrate that animals learned to control PT neurons faster and more effectively than IT neurons and that this effect cannot be attributed to any experimental confounds. Instead, our results suggest that the brain is more effective at manipulating and controlling output neurons that project from cortex to regions outside the telencephalon, and that this results from connectivity and position in the cortex.
STAR Methods:
Resource Availability
Lead contact:
Further information and requests should be directed to and will be fulfilled by the lead contact Nuria Vendrell-Llopis (nvl@berkeley.edu)
Material availability
This study did not generate new unique materials.
Data and code availability:
CaImAn27 and other processed data has been deposited in Dryad and is publicly available. Raw data (Ca Imaging) will be shared by the lead contact upon request. All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and virus strains | ||
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Critical commercial assays | ||
| Deposited data | ||
| Post-processed data for “Diverse operant control of different motor cortex populations during learning” | Dryad | doi:10.6078/D1ZB0D |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Mouse: tetO-GCaMP6s/Camk2a-tTA mice | ||
| Original strains: | ||
| tetO-GCaMP6s | The Jackson Laboratory | jax-024742 |
| Camk2a-tTA mice | The Jackson Laboratory | jax-007004 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| AAVrg-CAG-tdTomato | Addgene | viral prep # 59462-AAVrg |
| Software and algorithms | ||
| Analysis code | Zenodo | DOI: 10.5281/zenodo.5810405 |
| Acquisition code | Zenodo | DOI: 10.5281/zenodo.5776954 |
| XGBoost | 20 | https://xgboost.readthedocs.io/en/latest/python/ |
| Shap/ TreeShap | 21, 22 | https://shap.readthedocs.io/en/latest/index.html |
| Scanimage 2019 | Vidriotech | http://scanimage.vidriotechnologies.com/ |
| Python version 3.6 | Python Software Foundation | https://www.python.org |
| Matlab 2017b | Mathworks | https://www.mathworks.com/products/matlab.html |
| Other | ||
Experimental model and subject details:
Animals & Surgery:
All experiments were performed in compliance with the regulations of the Animal Care and Use Committees at the University of California, Berkeley and according to NIH guidelines. Adult mice (male/female) were housed with a 12-h dark, 12-h light cycle. Two groups of tetO-GCaMP6s/-Camk2a-tTA mice (original strains from The Jackson Laboratory, Bar Harbor, Maine: jax-024742, jax-007004) were injected with a retrograde virus in the contralateral motor cortex (n=9) or in the ipsilateral pons (n=8) in order to label intratelencephalic (IT) neurons and pyramidal tract (PT) neurons, respectively. Although cortico-thalamic neurons would also be relevant to this study, their location deep in the brain, made them impossible to study under the current state of the art of two-photon microscopy.
Prior to surgery, tools and materials were sterilized by autoclaving or gas sterilization. Mice were initially anesthetized by placing them briefly (2–3 mins) in a box containing 3 – 4% isoflurane and were then kept at 1–2% isoflurane in a nose cone respirator connected to a precision vaporizer. The animal was secured into a stereotaxic frame (Kopf instruments, Tujunga, CA) and kept warm (37.5 ± 1 °C). A single incision was made along the midline of the skull in the rostro-caudal direction and the skull was cleaned. Using a rotary micromotor drill (Foredom, Bethel, CT) equipped with a 0.5mm carbon burr (Fine Science Tools, Foster City, CA), a small burr hole was made over the contralateral motor cortex (1.4 mm rostral, 1.3 mm lateral to Bregma) or the ipsilateral pons (4.26 mm posterior, −0.6 mm lateral to Bregma), and 400nl of AAVrg-CAG-tdTomato (Addgene Watertown, MA, viral prep # 59462-AAVrg) was injected 300um (for IT) or 4.6mm (for PT) below the pia. The tracer was delivered using a pulled glass pipette (tip diameter = 40–60μm) at a rate of 50nl min with a Nanojet 3 (Drummond Scientific Company, Broomall, PA). The pipette was left in the brain for 15 min after completion of the injection to prevent backflow. After removal of the pipette, the burr hole was covered with Metabond dental cement (Parkell Edgewood, NY, S396-S398-S371). A 3mmØ craniotomy was opened over motor cortex (coordinates of the center relative to Bregma ML-1.5, AP 1.3). Two sterile glass coverslips (3–5mm, #1 thickness) were glued concentrically to each other (Norland Optical Adhesive, Cranbury, NJ, NOA71) and positioned over the skull so the 3mm coverslip would fit in the craniotomy. Metabond was applied to create a thin seal between the skull and the sides of the cranial window, and a steel headplate was affixed posterior to the coverslips. We allowed 3–4 weeks for recovery and for the expression of tdTomato, before starting the behavioral experiments. Animals with injections in the contralateral motor cortex had IT neurons labeled with tdTomato (IT group), whereas animals injected in the pons had PT neurons labeled with tdTomato (PT group).
Method details
Two-photon imaging:
Recordings of calcium imaging were performed with a Bruker Ultima Investigator (Bruker, Millerica, MA) using a Chameleon Ultra II Ti:Sapphire mode-locked laser (Coherent, Santa Clara, CA) tuned to 920 nm. Photons were collected with two GaAsP PMTs for different channels using an Olympus objective (XLUMPLFLN 20XW). Animals were head-fixed over a styrofoam ball (JetBall, PhenoSys, Berlin, Germany) that allowed them to run freely under the two-photon microscope. A piezo controller (400um travel, nPoint, Middleton, WI) allowed the sawtooth recording of 4 different planes with 100um separation for a full sweep of the cortical column. The power of the laser was set so that high quality images of the planes with direct neurons could be achieved without damaging shallow planes. Different imaging fields were used every day. In a given session, the imaged planes spanned 400 microns in depth. These planes were centered ~350–550 microns below pia depending on the session. Frames of 256 × 256 pixels (∼290 × 290μm) were collected at 9.7 Hz using ScanImage software (Vidriotech, Ashburn, VA) running on Matlab 2017b (Mathworks, Natick, MA). Motion drifts (if any) were corrected online by the software and/or manual control. Motion artifacts resulted in poor task performance (since both ensembles moved accordingly) and the mice seemed to remain more still during late learning sessions. Additionally, we added the quality of the recorded calcium signals of the direct neurons (measured as SNR) as features of the XGBoost-SHAP models. SNR was positively correlated with SHAP values, indicating that animals performed better in sessions with higher signal quality.
Behavioral task and online processing:
This behavioral task has been described previously in electrophysiology 3,28,29 and calcium imaging2 studies. Activities of two pairs of M1 neurons were summed within ensemble (∑E1 – ∑E2) and entered into a decoder that mapped neuronal activity to an auditory signal (range 2–18kHz). Head-fixed mice could increase the frequency of the auditory cursor by increasing the activity in the first ensemble (E1) and decreasing the activity in the other ensemble (E2). Mice could instead decrease the frequency of the auditory cursor by decreasing the activity of E1 and increasing the activity of E2. Mice received reward (20% sucrose) if they decreased the cursor frequency under a predefined target. To set the target cursor frequency, neuronal activity was recorded during a baseline period of 15 minutes. Each day the target was set such that mice would have received reward in 30% of trials in a hypothetical simulation with the recording from the baseline period. The auditory signal was provided to the animals as feedback of their performance.
In each group of animals (IT or PT), only tdTomato labeled neurons were used to control the auditory cursor. To study within-session learning, different IT or PT neurons (respectively) were selected each day. The animals had 30 seconds to reach the target and achieve a “hit”. Otherwise, the trial was considered a “miss”. With a successful trial, sucrose reward was given to the animal. After a 3 second pause, the auditory cursor was required to return to a baseline value in order to start the next trial. If the animal did not hit the target in the allowed time, white noise was indicative of fail, and the mice were given a 10 second timeout before a new trial started.
Neuron segmentation for online processing was obtained by a template matching function30. Fluorescence change of each of the identified neurons, defined as (Ft-F0)/F0 or dF/F was obtained online as a measure of neuronal activity. F0 was calculated dynamically to avoid bleaching effects without compromising processing time as F0 = (n-1) * F0 /n + Ft-1 where n was the number of frames acquired. For online processing, the Ft value of each M1 neuron was averaged over the last second before calculating dF/F, to provide robustness against motion artifacts.
Image preprocessing:
Each of the 4 imaging planes was separated into a block and independently analyzed with CaImAn27 to obtain the activity of each neuron during the recording. Direct neurons selected during the online experiment were matched with CaImAn-identified neurons by activity and space correlation. If a direct neuron could not be matched to a CaImAn-identified neuron (i.e., the activity or position was too different from online ensemble), the neuron was assumed to have had a low SNR and was removed from the ensemble, reducing the post-hoc ensemble to one neuron. If both neurons were discarded from an experimental session, the session was not used for analysis. Because the positions given by CaImAn are dependent on the whole spatial filter of the neuron and not the soma, new positions were obtained by filtering the image to locate the center of each neuron soma. To identify which CaImAn-identified neurons corresponded with tdTomato labeled neurons, the positions obtained by the template matching function30 (over the red channel image) were matched to the positions of CaImAn-identified neurons if the Euclidean distance between both centers was less than 4 pixels.
Data analysis:
Analysis programs were custom-written in Python using a variety of packages. The analysis pipeline was consistent across all animals.
Signal to noise ratio analysis:
Online recordings of direct neurons saved by ScanImage during experiments were used to calculate the online signal to noise ratio (SNR), where Since ScanImage may drop frames of data during online collection to achieve the desired image rate, we filled the missing frames using linear interpolation and nearest neighbor extrapolation for post-processing. To disentangle noise power from signal power, we averaged over the high frequency ranges (f/4, f/2 with f as frame rate) of the raw trace’s power spectral density31. To validate the method’s efficacy, we simulated noisy calcium traces with different noise and bleaching conditions and found that this method, compared to other SNR estimations, better minimizes the L2 norm of the error from predicting ground-truth SNRs.
Cursor engagement analysis:
The cursor engagement value for an experiment is a measure of how well the activity of indirect neurons can predict the auditory cursor. We used L1-regularized linear regression to predict the cursor with the fluorescence of indirect neurons at each frame. Specifically, for each experiment, we collect the ∆F/F values of the N indirect neurons over the T frames of the experiment into a matrix X(N × T). The auditory cursor over the T frames is collected into a T-length vector . Thus, for each experiment we obtained T samples of data with N features. For some frame tϵ{1, …, T}, the goal was then to predict with X∙{1:t−1}. We first split the T samples 80/20 into a training set and a testing set. The training set was used to train the model and select hyperparameters with 5-fold cross validation.
The model’s performance was then evaluated on the testing set. The quality of the testing set prediction was quantified by the R2 coefficient of determination value. The best possible R2 value is 1. A constant model that always predicts the expected value of the cursor would have R2 = 0. A model that does worse than this constant model would have R2 < 0. Since the R2 value can become arbitrarily negative and since models with R2 ≤ 0 were ineffective in predicting the cursor, the cursor engagement for an experiment was calculated as max{0, R2}. This allowed the cursor engagement value to lie in a predefined range.
Granger Causality analysis:
We used Granger causality to estimate the effective directional connectivity among all pairs of tdTomato-labeled neurons and between each direct neuron and indirect neuron pair. Granger causality models time series as autoregressive series. Consider two neural traces x and y, if y activity is dependent on x, we have the following formulations:
| (1) |
| (2) |
In (2), activities of x and y at time point t − τ, (xt−τ, yt−τ) contribute to yt with coefficient and βτ respectively. However, if we ignore x contribution to y, we get formulation in (1) instead, where yt−τ contributes to yt with coefficient . The variables are error residuals for formulation (1) and (2) respectively, with being the corresponding standard deviations. Intuitively, variance of residual term would be greatly reduced with the inclusion of x as regressor if y is dependent on x. A trace x is said to be “Granger causal” to y if the Granger causality value is significantly above 0. We compared Bayesian information criterions (BIC) in autoregressive models of different order ρ for each session and selected ρ = 2 since it minimizes BIC on average case.
For each directed pair, we used chi-squared tests on sum of squared residuals (SSR) to determine the statistical significance of the directed influence. Only estimated effective connectivity values for neuron pairs with p-value less than 0.05 were kept as raw features.
To determine the effectiveness of Granger causality inference algorithm in reconstructing effective connectivity for calcium data, we performed validations with both simulated data and shuffled experimental data. First, we simulated a series of excitatory neural networks with Integrate-And-Fire neurons with connectivity determined by an Erdos-Renyi graph with different n, p parameters. We converted the simulated spike data into calcium data with the Leogang model 32. We then performed granger causality tests on the simulated data and obtained the Area-Under-Curve for the Receiver Operating Characteristics (AUC-ROC) graph significantly over chance level. Second, we compared the connectivity values among neuron pairs to values among shuffled pairs in experimental calcium data. To generate realistic random activities with comparable statistics, we shuffled the calcium data by re-convolving shuffled deconvolved spikes. As a control for artifacts introduced by deconvolution, we also re-convolved all unshuffled spike data and calculated their inferred connectivity to compare against the shuffled version
XGboost/SHAP:
SHAP values21, were obtained for XGBoost (eXtreme Gradient Boosting) models20 with a TreeSHAP22 explainer for each of the features and experimental sessions. XGBoost models regressing percentage-correct values (average mean square error = 0.026, representing less than 7% of the average percentage-correct) outperformed XGBoost models regressing hits-per-minute values (average mean square error =0.27 ~ 35%). Thus, we selected percentage-correct as the learning measure to regress, and all following analysis was done only for percentage-correct models.
The number of sessions recorded was a total 288 and there were 43 features we wanted to study. With such a small dataset, we opted to use ensemble learning methods to aggregate multiple different XGBoost-models + SHAP-explainers and therefore obtain a more accurate final interpreter of the features (Figure S2.A). A total of 10000 combinations of XGBoost-model + SHAP-explainer, within specs, were used. Each model was trained on 80% of the experimental sessions and tested on the remaining 20% with XGBoost using independent random sampling, i.e., each model used a different randomized subset of the data for training/testing. If a model did not reach a minimum error calculated with the .632 estimator33 of 7% or the mean squared error regression loss34,35 of 7%, it was discarded. Parameters for the XGBoost models were chosen to maximize the accuracy of the model although varying them only affected accuracy slightly (learning _rate=0.1, repetitions=100).
SHAP values were obtained with TreeSHAP22 explainers for the test data only. We used “tree_path_dependent” as feature perturbation to remain true to data36. After a XGBoost model was trained, we obtained a SHAP-explainer (with the test data) for that model and then evaluated its stability. To check if the SHAP values were stable, we retrained the XGBoost model with bootstrap resamples (n=1000) of the training dataset. We then correlate the SHAP values resulting of using the original model with the original training dataset with the SHAP values resulting of the bootstrapping model with the bootstrapping training data. Only explainers that had a minimum correlation of r>0.5 were used for analysis. If a combination of model+explainer resulted in high error or lower stability, it was discarded and a new model+explainer was obtained.
Because we obtained 10000 different combinations of models+explainers within specifications (errors < 7%, stability > 0.5), each experimental session was part of the test data more than once, resulting in multiple SHAP values for each experimental session and feature. Each session was used in a model an average of 2010 times. However, 3 sessions with high performance (PC = 0.9151, 0.9202 and 0.8519) had way less occurrences than average (25% less than average). All the distributions of SHAP values (for each session and feature) were normal (Kolmogorov-Smirnov test with pval<1e-8) (Figure S2.B). As a result, SHAP values of the same experimental session resulting from evaluating different models+explainers combinations were averaged to obtain a single value per experimental session and feature (Figure S2.A).
To measure the validity of our full XGBoost/SHAP pipeline described above, we generated two synthetic datasets [X, y]. In the first dataset (independent) we forced the features (X) to be completely independent from each other, with covariance=0 and mean=0 (X values [−0.5|0.5]). The second dataset (dependent) had random features (X values [0:1]) and the variable to be regressed had added noise. The number of occurrences was selected to resemble the proportion of occurrences and features of the real dataset (N=288sessions/43features*5synthetic features=32synthetic sessions). In both datasets, the value of the variable (y) to be predicted was a linear representation of the 5 features under study as follows:
The result of the SHAP explainers (Figure S2.C–D) shows how features that added value to the predicted variable y (F_pos_high, F_pos_low) have positive SHAP values, features that subtract value to the predicted variable (F_neg_high, F_neg_low)) had negative SHAP values and features that had no contribution (F_zero) to the predicted value had no impact on SHAP values.
For features representing a measure of various direct neurons, we calculated the mean (mean), maximum (max) and minimum (min) of those measures and they were introduced in the model as different features. For features representing many neurons (as in connectivity) we only obtained the mean of those measures. 43 features were used on the models. Those features were grouped in categories (in order from Figure 2.A): for quality SNR (mean, max, min); for position: depth (mean, max, min), the Euclidean distance (without depth) between neurons (mean, max, min), the difference on depth (mean, max, min) and the distance between neurons of the ensemble E1 and E2 (mean, max, min); for variation: STD of the neuronal cursor, STD of the direct neurons recoded online (mean, max, min), STD of the direct neurons calculated offline after applying CaImAn during the whole experiment (mean, max, min) or the baseline (mean, max, min); for connectivity: the average result of Granger causality between direct neurons, same for ensemble E2 to/from ensemble E1, the percentage of those pairs that Granger causality considered possible connections (also for all direct and for ensemble E1 to/from ensemble E2), the average result of granger causality from indirect neurons to direct neurons, the percentage of those pairs that were connections and the same from direct to indirect neurons. Two other features were introduced in the model that did not belong to any category: engagement of indirect neurons to the neuronal cursor and finally a feature labelling if the session was from the IT group or the PT group. Figure 2 shows 55 features (instead of 43) after separating connectivity results for different cell-classes (IT-PT). Features were not separated by cell-class when introduced in the model, they were separated during analysis in measures of connectivity.
Determining which feature is the most relevant through the magnitude of the SHAP values is not recommended as some features may be dependent on or correlated with others, e.g., all the features representing the mean, max or min of a measure (mean SNR, max SNR, min SNR). As a result, their SHAP values might get arbitrarily distributed amongst them. Although the ensemble of multiple models+explainers (10000) should mitigate this effect we should still take it into consideration. Since SHAP values are additive, similar features (e.g., all SNR) can be grouped in order to obtain an approximation of the total impact of each group on predicting percentage correct (Figure S2.E). However, there may still be features in a group correlated with features of other groups (such as depth, connectivity, and SNR) and since the value is additive this representation may change if we added/removed features to a particular group.
This limitation of the SHAP explainer does not affect our analysis as we only compare within feature. Our goal is not to determine the best feature for learning (a final numerical value), but to discover positive or negative contributions to learning and differences for IT and PT groups.
Final note on selection of neurons for CaBMI control
The XGBoost/SHAP approach helped us understand how to better select neurons for successful CaBMI experiments. Signal quality (SNR) was highly correlated with SHAP values (Figure 2.A). In addition, SHAP values were higher, the higher the distance among all direct neurons plateauing at 100um (Figure 2.C). However, if any 2 direct neurons were too far apart with a distance higher than 50–75um (Figure 2.D), even for neurons belonging to different ensembles (Figure 2.E), SHAP values were negative. This would indicate an optimal distance between direct neurons: not too far apart that they may involve change on further neuronal circuits, not too close to decrease the probability of neurons of different ensembles receiving input from the same pre-synaptic neuron. In terms of neuronal activity, positive SHAP values arose when selecting direct neurons that were silent during the baseline acquisition but highly active during CaBMI (Figure 2.F–H). We suggest experimenters attempting CaBMI to choose direct neurons that are 50 to 100um apart from each other with high SNR and the capacity of increasing their baseline activity greatly.
Quantification and statistical analysis
Statistical analysis was performed using Python with Scipy35 or Statsmodel37 packages. Group IT: n=9 mice with a total of n=163 sessions, group PT: n=8 mice with a total of n=125 sessions. Statistical details of each analysis can be seen in each figure legend and/or in the correspondent methods section. Wherever significance is used in a figure, it is defined in the correspondent figure legend.
Supplementary Material
Highlights.
Mice learn to control PT neurons faster and better than IT neurons.
The differences on learning cannot be attributed to experimental confounds.
Location in cortex and local circuitry are responsible for PT neurons advantage.
Inherent characteristics of PT neurons also contribute to differences on learning.
Acknowledgments
This work was supported by the NIH U19 grant to RMC and JMC, and the Army Research Office Award W911NF-16–1-0453 to JMC.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Inclusion and diversity
We worked to ensure sex balance in the selection of non-human subjects. One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in science.
Declaration of interests
The authors declare no competing interests.
References
- 1.Peters AJ, Liu H & Komiyama T Learning in the Rodent Motor Cortex 10.1146/annurev-neuro-072116-031407 40, 77–97 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Clancy KB, Koralek AC, Costa RM, Feldman DE & Carmena JM Volitional modulation of optically recorded calcium signals during neuroprosthetic learning. Nat. Neurosci 17, 807–809 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Koralek AC, Jin X, Long JD, Costa RM & Carmena JM Corticostriatal plasticity is necessary for learning intentional neuroprosthetic skills. Nature 483, 331–335 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Athalye VR, Santos FJ, Carmena JM & Costa RM Evidence for a neural law of effect. Science 359, 1024–1029 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Beloozerova IN, Sirota MG & Swadlow HA Activity of different classes of neurons of the motor cortex during locomotion. J. Neurosci 23, 1087–1097 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cowan RL & Wilson CJ Spontaneous firing patterns and axonal projections of single corticostriatal neurons in the rat medial agranular cortex. J. Neurophysiol 71, 17–32 (1994). [DOI] [PubMed] [Google Scholar]
- 7.Egger R et al. Cortical Output Is Gated by Horizontally Projecting Neurons in the Deep Layers. Neuron 105, 122–137.e8 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Takahashi N et al. Active dendritic currents gate descending cortical outputs in perception. Nat. Neurosci 23, 1277–1285 (2020). [DOI] [PubMed] [Google Scholar]
- 9.Harris KD & Shepherd GMG The neocortical circuit: Themes and variations. Nature Neuroscience vol. 18 170–181 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shepherd GMG Corticostriatal connectivity and its role in disease. Nat. Rev. Neurosci 14, 278–291 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reiner A Organization of Corticostriatal Projection Neuron Types. Handb. Behav. Neurosci 20, 323–339 (2010). [Google Scholar]
- 12.Li N, Chen TW, Guo ZV, Gerfen CR & Svoboda K A motor cortex circuit for motor planning and movement. Nature 519, 51–56 (2015). [DOI] [PubMed] [Google Scholar]
- 13.Nathanson JL, Yanagawa Y, Obata K & Callaway EM Preferential labeling of inhibitory and excitatory cortical neurons by endogenous tropism of adeno-associated virus and lentivirus vectors. Neuroscience 161, 441–450 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Watakabe A et al. Comparative analyses of adeno-associated viral vector serotypes 1, 2, 5, 8 and in marmoset, mouse and macaque cerebral cortex. Neurosci. Res 93, 144–157 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Hira R et al. Reward-timing-dependent bidirectional modulation of cortical microcircuits during optical single-neuron operant conditioning. Nat. Commun 5, 5551 (2014). [DOI] [PubMed] [Google Scholar]
- 16.Prsa M, Galiñanes GL & Huber D Rapid Integration of Artificial Sensory Feedback during Operant Conditioning of Motor Cortex Neurons. Neuron 93, 929–939.e6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mitani A, Dong M & Komiyama T Brain-Computer Interface with Inhibitory Neurons Reveals Subtype-Specific Strategies. Curr. Biol 28, 77–83.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Athalye VR, Carmena JM & Costa RM Neural reinforcement: re-entering and refining neural dynamics leading to desirable outcomes. Curr. Opin. Neurobiol 60, 145–154 (2020). [DOI] [PubMed] [Google Scholar]
- 19.Moorman HG, Gowda S & Carmena JM Control of Redundant Kinematic Degrees of Freedom in a Closed-Loop Brain-Machine Interface. IEEE Trans. Neural Syst. Rehabil. Eng 25, 750–760 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Chen T & Guestrin C XGBoost. in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining - KDD 16 785–794 (ACM Press, 2016). doi: 10.1145/2939672.2939785. [DOI] [Google Scholar]
- 21.Lundberg SM, Allen PG & Lee S-I A Unified Approach to Interpreting Model Predictions In Proceedings of the 31st international conference on neural information processing systems 4765–4774 (2017). [Google Scholar]
- 22.Lundberg SM et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell 2, 56–67 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dembrow NC, Chitwood RA & Johnston D Projection-specific neuromodulation of medial prefrontal cortex neurons. J. Neurosci 30, 16922–16937 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ganguly K, Dimitrov DF, Wallis JD & Carmena JM Reversible large-scale modification of cortical networks during neuroprosthetic control. Nat. Neurosci 14, 662–669 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zippi EL, You AK, Ganguly K & Carmena JM Selective modulation of population dynamics during neuroprosthetic skill learning 1 2. bioRxiv 2021.01.08.425917 (2021) doi: 10.1101/2021.01.08.425917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.So K, Koralek AC, Ganguly K, Gastpar MC & Carmena JM Assessing functional connectivity of neural ensembles using directed information. J. Neural Eng 9, (2012). [DOI] [PubMed] [Google Scholar]
- 27.Giovannucci A et al. CaImAn an open source tool for scalable calcium imaging data analysis. Elife 8, (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koralek AC, Costa RM & Carmena JM Temporally Precise Cell-Specific Coherence Develops in Corticostriatal Networks during Learning. Neuron 79, 865–872 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Neely RM, Koralek AC, Athalye VR, Costa RM & Carmena JM Volitional Modulation of Primary Visual Cortex Activity Requires the Basal Ganglia. Neuron 97, 1356–1368.e4 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Ohki K, Chung S, Ch’ng YH, Kara P & Reid RC Functional imaging with cellular resolution reveals precise microarchitecture in visual cortex. Nature vol. 433 597–603 (2005). [DOI] [PubMed] [Google Scholar]
- 31.Pnevmatikakis EA et al. Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron 89, 285 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stetter O, Battaglia D, Soriano J & Geisel T Model-Free Reconstruction of Excitatory Neuronal Connectivity from Calcium Imaging Signals. PLoS Comput. Biol 8, e1002653 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Efron B & Tibshirani R Improvements on cross-validation: The .632+ bootstrap method. J. Am. Stat. Assoc 92, 548–560 (1997). [Google Scholar]
- 34.Pedregosa F et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res 12, 2825–2830 (2011). [Google Scholar]
- 35.Virtanen P et al. SciPy 1.0: fundamental algorithms for scientific computing in Python 17, 261–272 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen H, Janizek JD, Lundberg S & Lee S-I True to the Model or True to the Data? (2020).
- 37.Seabold S & Perktold J Statsmodels: Econometric and Statistical Modeling with Python Proc. 9th Python Sci. Conf. 92–96 (2010) doi: 10.25080/majora-92bf1922-011. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
CaImAn27 and other processed data has been deposited in Dryad and is publicly available. Raw data (Ca Imaging) will be shared by the lead contact upon request. All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and virus strains | ||
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Critical commercial assays | ||
| Deposited data | ||
| Post-processed data for “Diverse operant control of different motor cortex populations during learning” | Dryad | doi:10.6078/D1ZB0D |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Mouse: tetO-GCaMP6s/Camk2a-tTA mice | ||
| Original strains: | ||
| tetO-GCaMP6s | The Jackson Laboratory | jax-024742 |
| Camk2a-tTA mice | The Jackson Laboratory | jax-007004 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| AAVrg-CAG-tdTomato | Addgene | viral prep # 59462-AAVrg |
| Software and algorithms | ||
| Analysis code | Zenodo | DOI: 10.5281/zenodo.5810405 |
| Acquisition code | Zenodo | DOI: 10.5281/zenodo.5776954 |
| XGBoost | 20 | https://xgboost.readthedocs.io/en/latest/python/ |
| Shap/ TreeShap | 21, 22 | https://shap.readthedocs.io/en/latest/index.html |
| Scanimage 2019 | Vidriotech | http://scanimage.vidriotechnologies.com/ |
| Python version 3.6 | Python Software Foundation | https://www.python.org |
| Matlab 2017b | Mathworks | https://www.mathworks.com/products/matlab.html |
| Other | ||


