Abstract
Polygenic risk scores (PRS) suffer reduced accuracy in non-European populations, exacerbating health disparities. We propose PolyPred, a method that improves cross-population PRS by combining two predictors: a new predictor that leverages functionally informed fine-mapping to estimate causal effects (instead of tagging effects), addressing LD differences; and BOLT-LMM, a published predictor. When a large training sample is available in the non-European target population, we propose PolyPred+, which further incorporates the non-European training data. We applied PolyPred to 49 diseases/traits in 4 UK Biobank populations using UK Biobank British training data, and observed relative improvements vs. BOLT-LMM ranging from +7% in South Asians to +32% in Africans, consistent with simulations. We applied PolyPred+ to 23 diseases/traits in UK Biobank East Asians using both UK Biobank British and Biobank Japan training data, and observed improvements of +24% vs. BOLT-LMM and +12% vs. PolyPred. Summary statistic-based analogues of PolyPred and PolyPred+ attained similar improvements.
Polygenic risk scores (PRS) can identify individuals at elevated risk of complex diseases, providing opportunities for preventative action1–6. However, many studies have shown that PRS based on European training data attain lower accuracy when applied to populations of non-European ancestry7–26. This loss of accuracy is primarily driven by LD differences12–15, allele frequency differences (including population-specific SNPs)13,14,27, and causal effect size differences12–14,28–31, though differences in heritability also play a minor role13,14,32. PRS based on non-European training data do not suffer from these limitations, but are currently limited by much smaller training sample sizes1,12–15,21,33. The development of new methods to reduce this gap in cross-population PRS accuracy has the potential to ameliorate health disparities13.
Here, we propose PolyPred, which linearly combines two complementary predictors derived from European training data: (1) PolyFun-pred, a new predictor that circumvents LD differences by applying genome-wide functionally informed fine-mapping34,35 to precisely estimate causal effects (instead of tagging effects); and (2) BOLT-LMM36,37, a published predictor that analyzes all loci jointly and can capture all signals in extremely polygenic loci. BOLT-LMM requires individual-level training data. If individual-level training data is not available, we propose two analogous methods: (i) PolyPred-S, which linearly combines PolyFun-pred with SBayesR38, and (ii) PolyPred-P, which linearly combines PolyFun-pred with PRS-CS39. Recommendations for when to use PolyPred, PolyPred-S, or PolyPred-P are provided below.
In the special case where there exists a large (e.g., N≥50K) non-European training sample from the target population (or a closely related population), we propose PolyPred+, a polygenic prediction method that leverages both European and non-European training data. PolyPred+ linearly combines (1) PolyFun-pred; (2) BOLT-LMM; and (3) BOLT-LMM-pop, which is obtained by applying BOLT-LMM to the non-European training data, addressing MAF differences and causal effect size differences. If individual-level training data is not available, we propose the alternative methods PolyPred-S+ and PolyPred-P+, which replace BOLT-LMM with either SBayesR or PRS-CS, respectively. Recommendations for when to use PolyPred+, PolyPred-S+, or PolyPred-P+ are provided below.
We compared PolyPred and PolyPred+ (and their summary statistic-based analogues) to state-of-the-art polygenic prediction methods via simulations and analyses of 49 diseases and complex traits in 4 populations from the UK Biobank40, in Biobank Japan41, and in Uganda-APCDR42,43. We conclude that PolyPred and its summary statistic-based analogues substantially increase cross-population polygenic prediction accuracy, and that PolyPred+ and its summary statistic-based analogues further increases cross-population prediction accuracy in the special case where non-European training data is available in large sample size.
Results
Overview of Methods
PolyPred combines two complementary predictors: PolyFun-pred and BOLT-LMM (Table 1 and Figure 1a). PolyFun-pred is a new predictor that leverages genome-wide functionally informed fine-mapping34,35 to estimate posterior mean causal effects (instead of tagging effects; see Supplementary Note) for all SNPs with European MAF≥0.1% (18 million SNPs in this study) by applying PolyFun + SuSiE35 to European training data across 2,763 overlapping 3Mb loci. Leveraging fine-mapped posterior mean causal effects for cross-population polygenic prediction aims to address LD differences between populations. BOLT-LMM36,37 is a published predictor that estimates posterior mean tagging effects of common SNPs (1.2 million HapMap 3 SNPs44 in this study) using European individual-level training data. Combining PolyFun-pred with BOLT-LMM is advantageous because they have complementary advantages: PolyFun-pred estimates causal effects rather than tagging effects. BOLT-LMM estimates tagging effects, but it analyzes all loci jointly and it can potentially capture all signals in extremely polygenic loci (Methods).
Table 1:
Summary of main methods evaluated.
| Method | Constituent methods | SNP set | Training data | Fine-mapped effect sizes | Summary statistics | Ref. |
|---|---|---|---|---|---|---|
| P+T | - | All (18 million) | Eur | No | Yes | 45,46 |
| BOLT-LMM | - | HapMap 3 (1.2 million) | Eur | No | No | 36,37 |
| SBayesR | - | HapMap 3 (1.2 million) | Eur | No | Yes | 38 |
| PRS-CS | - | HapMap 3 (1.2 million) | Eur | No | Yes | 39 |
| PolyPred | PolyFun-pred, BOLT-LMM | All (18 million) | Eur | Yes | No | This work |
| PolyPred-S | PolyFun-pred, SBayesR | All (18 million) | Eur | Yes | Yes | This work |
| PolyPred-P | PolyFun-pred, PRS-CS | All (18 million) | Eur | Yes | Yes | This work |
| PolyPred+ | PolyFun-pred, BOLT-LMM, BOLT-LMM-pop | All (18 million) | Eur + target pop | Yes | No | This work |
| PolyPred-S+ | PolyFun-pred, SBayesR, SBayesR-pop | All (18 million) | Eur + target pop | Yes | Yes | This work |
| PolyPred-P+ | PolyFun-pred, PRS-CS, PRS-CS-pop | All (18 million) | Eur + target pop | Yes | Yes | This work |
For each method we report its constituent methods (or “-” for individual methods), the set of SNPs analyzed in model training using UK Biobank training data (and its size when restricted to imputed UK Biobank SNPs with European MAF≥0.1% and INFO score≥0.6), the training data analyzed, whether it incorporates fine-mapped effect sizes (as opposed to tagging effect sizes), whether it can work with summary statistics, and the corresponding reference. Eur: European; target pop: non-European target population; Method-pop: Method applied to training data from non-European target population.
Figure 1: Overview of PolyPred and PolyPred+.
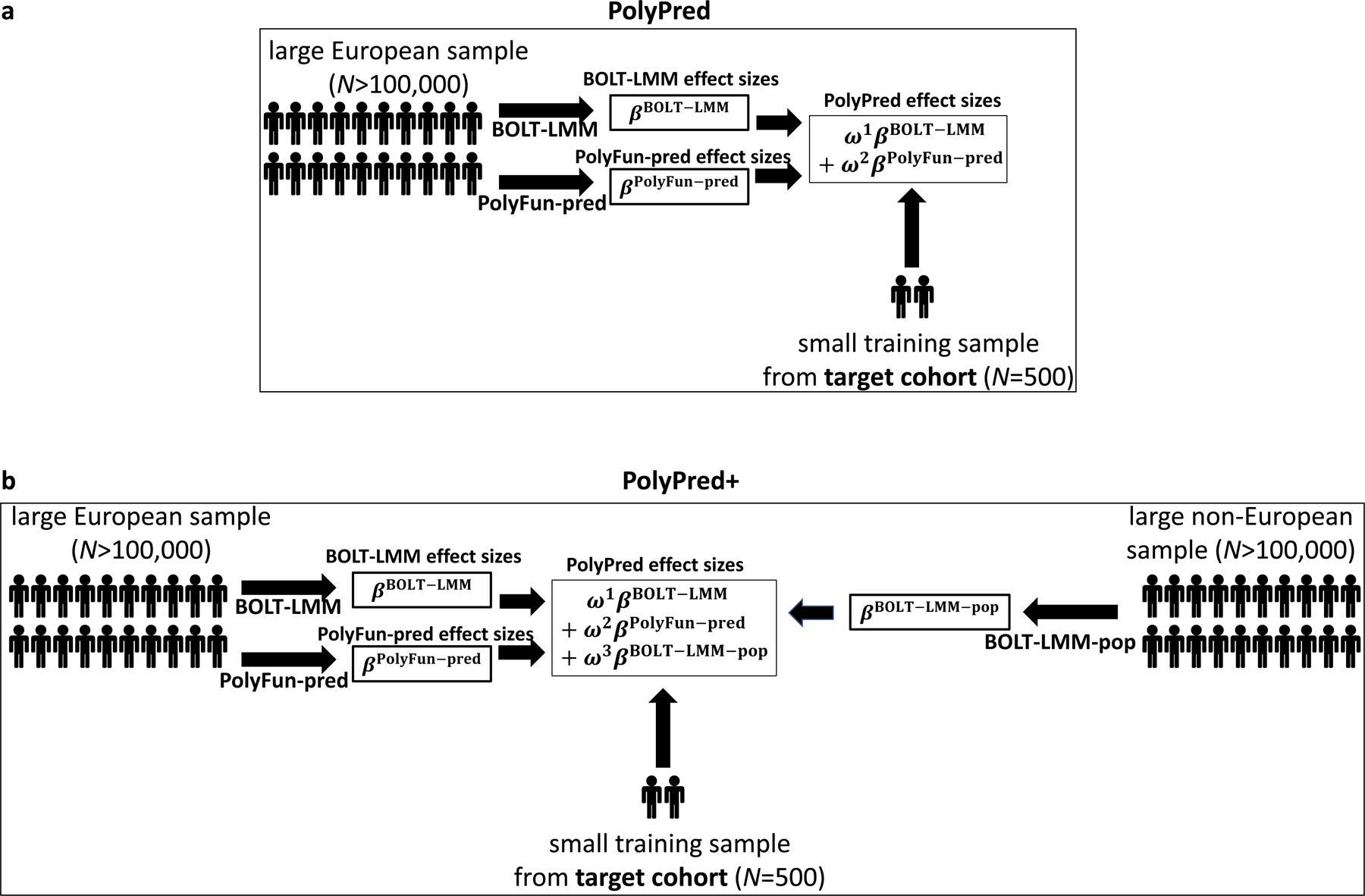
(a) Overview of PolyPred. PolyPred linearly combines the effect sizes of BOLT-LMM (βBOLT–LMM) and PolyFun-pred (βPolyFun–pred), (trained using European training data). It uses a small training sample from the target population to estimate mixing weights (ω1, ω2) for the constituent methods. (b) Overview of PolyPred+. PolyPred+ linearly combines the effect sizes of BOLT-LMM (βBOLT–LMM), PolyFun-pred (βPolyFun–pred) (trained using European training data), and BOLT-LMM-pop (βBOLT–LMM–pop) (trained using non-European training data from the target population). It uses a small training sample from the target population to estimate mixing weights (ω1, ω2, ω3) for the constituent methods. PolyPred-S and PolyPred-P (resp. Poly-Pred-S+ and PolyPred-P+) replace all instances of BOLT-LMM with SBayesR or PRS-CS, respectively.
In the special case where a large training sample is available in the target population (or a closely related population), we propose PolyPred+, which combines three complementary predictors: PolyFun-pred, BOLT-LMM, and BOLT-LMM-pop (Table 1 and Figure 1b); BOLT-LMM-pop refers to application of BOLT-LMM to common SNPs (1.2 million HapMap 3 SNPs in this study) using training data from the non-European target population, addressing MAF differences and causal effect size differences.
PolyPred computes linear combinations of the estimated effect sizes of their constituent predictors:
| (1) |
where i indexes SNPs, j indexes the constituent predictors (PolyFun-pred and BOLT-LMM for PolyPred; PolyFun-pred, BOLT-LMM and BOLT-LMM-pop for PolyPred+), is the PolyPred (+) per-allele effect size of SNP i, wj are method-specific weights, and is the per-allele effect size of SNP i for method j (or 0 if SNP i was not considered by method j). Predicted phenotypes are computed by applying effect sizes to target genotypes:
| (2) |
where is the predicted phenotype of an individual from the target population and xi is the number of minor alleles of SNP i carried by the individual. The mixing weights wj in Equation 1 are estimated via non-negative least squares regression using a small number of training individuals from the target population (500 in this study), regressing true phenotypes on a linear combination of the constituent predictors (which are computed as in Equation 2).
PolyPred requires individual-level training data for its BOLT-LMM component. If only summary statistics (and summary LD information) are available, we propose two analogous methods (Table 1): (i) PolyPred-S, which linearly combines PolyFun-pred and SBayesR38; and (ii) PolyPred-P, which linearly combines PolyFun-pred and PRS-CS39. We also propose the analogous methods PolyPred-P+ and PolyPred-S+ (Table 1). Further details of PolyPred and PolyPred+ (and their summary statistic-based analogues) are provided in the Methods section; we have publicly released open-source software implementing these methods (see Code Availability).
We evaluate prediction accuracy for each method and target population using relative-R2, defined as the R2 obtained in the target non-European population (after correcting for covariates and potential confounders; see Methods) divided by the R2 obtained by BOLT-LMM in UK Biobank non-British Europeans (employing the same correction), using the same training data for the numerator and the denominator. This quotient transforms the prediction accuracies from an absolute scale to a scale of relative improvement (vs. the BOLT-LMM predictor in the UK Biobank non-British European target population), which is invariant to factors such as training sample size and trait heritability. For disease traits, we additionally evaluated the area under the receiving operating characteristic. We provide further details in the Methods section. We compare PolyPred and PolyPred+ (and their summary statistic-based analogues) to 4 published methods: LD-pruning + P-value thresholding (P+T)45,46, BOLT-LMM36,37, SBayesR38, and PRS-CS39 (Table 1).
Our recommendation for which version of PolyPred to use (see Table 1) depends on three factors: (i) whether individual-level training data is available; (ii) the size and consistency of matched ancestry of the LD reference panel (if individual-level training data is not available); and (iii) whether non-European training data is available. Our results for the underlying constituent methods are summarized in Table 2 (detailed below), and our recommendations are summarized in Figure 2.
Table 2:
Summary of the relative performance of constituent PRS methods.
| LD | BOLT-LMM | SBayesR | PRS-CS | Figure(s)/Table(s) |
|---|---|---|---|---|
| Individual-level data (UKB, N=337K) | ✔✔ | ✔ | ✔ | Figures 3,4,6 |
| In-sample LD (UKB, N=337K) | --- | ✔✔ | ✔ | Figures 3,4,6 |
| Very large unmatched LD (UKB, N=337K) | --- | ✔ | ✔✔ | Extended Data Figure 1 |
| Small unmatched LD (1000G, N=489) | --- | ✘ | ✔✔* | Tables S4–S6 |
For each of three constituent PRS methods (BOLT-LMM, SBayesR, PRS-CS) we report its relative performance in prediction in UK Biobank non-British Europeans under various settings; we also provide links to the corresponding Figure(s)/Table(s). ✔✔: the method is significantly more accurate than the second best method in the same row, and combining this method with PolyFun-pred increases prediction accuracy; ✔✔*: the method is significantly more accurate than the second best method in the same row, and combining this method with PolyFun-pred does not increase prediction accuracy; ✔: the method is significantly less accurate than the best method in the same row, but is significantly more accurate than P+T; ✘: the method is not significantly more accurate than P+T; ---: the method is not applicable, because it requires individual-level data. For individual-level data, the difference between BOLT-LMM and the second-best method was significant in simulations but non-significant in real trait analyses. For In-sample LD, the difference between SBayesR and PRS-CS was significant in simulations but non-significant in real traits analyses. For Very large unmatched LD (a likely scenario when analyzing summary statistics from a meta-analysis of many cohorts), we performed real trait analyses only, as simulations would have required another very large individual-level data set in addition to UK Biobank (see Supplementary Note). For small unmatched LD, we performed both simulations and real trait analyses but report results of real trait analyses, which we believe to be most reflective of real-life settings (in simulations, SBayesR was significantly more accurate than PRS-CS; see Supplementary Note). Results for non-European target populations from UK Biobank were similar, though some of the differences were not statistically significant due to smaller prediction accuracies and sample sizes. We have facilitated the use of very large LD reference panels for European training data by publicly releasing summary LD information for N=337K British-ancestry UK Biobank samples across 18 million SNPs (see Data availability).
Figure 2: Recommendations for the application of PolyPred, PolyPred+ and related methods.
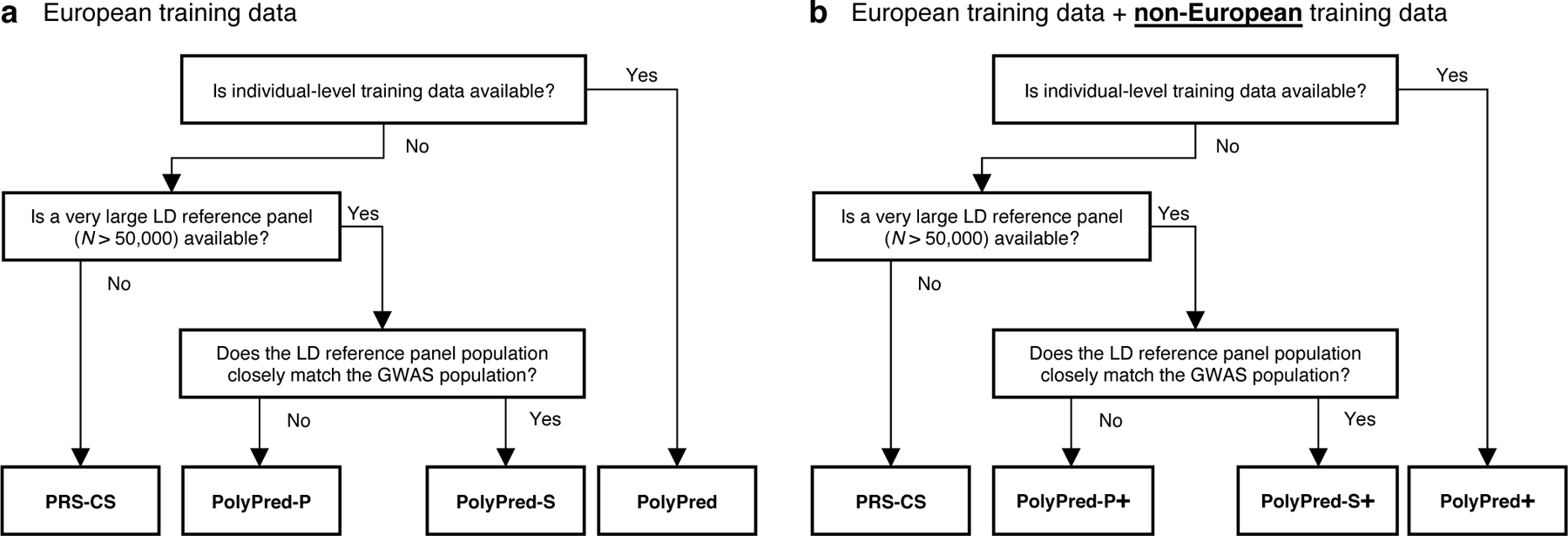
(a) Flowchart of recommendations when only European training data is available. (b) Flowchart of recommendations when both European and non-European training data are available. We note that when working with summary statistics from a meta-analysis of many cohorts, there is typically no LD reference panel that closely matches the GWAS population. Also, it is possible that the answers to the flowchart questions are different for European vs. non-European training data, in which case the recommendation would be to use a hybrid method based on the answers to each flowchart in turn (e.g. PolyFun-pred + BOLT-LMM + PRS-CS-pop; not listed in Table 1). For both (a) and (b), we recommend training PolyFun-pred using a very large LD reference panel (e.g. N=337K UK Biobank British) with a dense SNP set (e.g. 8 million SNPs). We have facilitated this by publicly releasing summary LD information for N=337K British-ancestry UK Biobank samples across 18 million SNPs (see Data availability).
Simulations with in-sample LD
We compared PolyPred, PolyPred-S and PolyPred-P to P+T, BOLT-LMM, SBayesR, and PRS-CS via simulations, using real genotypes or in-sample LD from the UK Biobank40. We trained each method using 337,491 unrelated British-ancestry individuals40, and computed predictions in four target populations: non-British Europeans, South Asians, East Asians, and Africans. We estimated mixing weights for PolyPred, PolyPred-S and PolyPred-P using 500 individuals from the target population. We evaluated prediction accuracy using held-out individuals from each target population that were not included in the training sets: 42K non-British Europeans, 7.7K South Asians, 0.9K East Asians, and 6.2K Africans. We computed PRS using 250,963 MAF≥0.1% SNPs with INFO score≥0.6 on chromosome 22.
Generative trait architectures were specified as follows. We simulated traits with polygenicity (genome-wide proportion of causal SNPs) equal to either 0.1% (less polygenic) or 0.3% (more polygenic) and heritability equal to 5%. We specified prior causal probabilities for each SNP in proportion to per-SNP heritabilities, which we generated for each SNP based on its British LD, MAF, and functional annotations, using the baseline-LF model47. For each causal SNP, we sampled ancestry-specific causal effect sizes from a multivariate normal distribution assuming cross-population genetic correlations of 0.813,30. Other parameter settings were explored in secondary analyses (see below).
We computed relative-R2 for each method, target population, and trait architecture, averaged across 100 simulations. In addition to the simulations with in-sample LD described below, we also performed simulations with reference panel LD (Supplementary Note; also see Table 2). Further details of the simulation framework are provided in the Methods section.
The simulation results are reported in Figure 3 and Supplementary Table 1 (also see Table 2). PolyPred was the most accurate method in each target population, with relative improvements vs. BOLT-LMM (resp. P-values for improvement) ranging from +13% in non-British Europeans (P<10−16) to +65% in Africans (P<10−16) for the less polygenic architecture, and from +2% in non-British Europeans (P=0.0001) to +17% in Africans (P=10−8) for the more polygenic architecture. PolyPred-S and PolyPred-P performed slightly worse than PolyPred, but were substantially and significantly more accurate than their corresponding constituent methods. Among the remaining methods, BOLT-LMM was consistently the most accurate and P+T was consistently the least accurate method, far underperforming the other methods (despite its widespread recent use11,13–18,23,31,48–52). We note that the higher accuracy of BOLT-LMM vs. SBayesR and PRS-CS does not imply that BOLT-LMM is a superior method, as BOLT-LMM analyzes individual-level training data whereas SBayesR and PRS-CS analyze summary statistics.
Figure 3: Cross-population PRS results for simulated UK Biobank traits using in-sample LD.
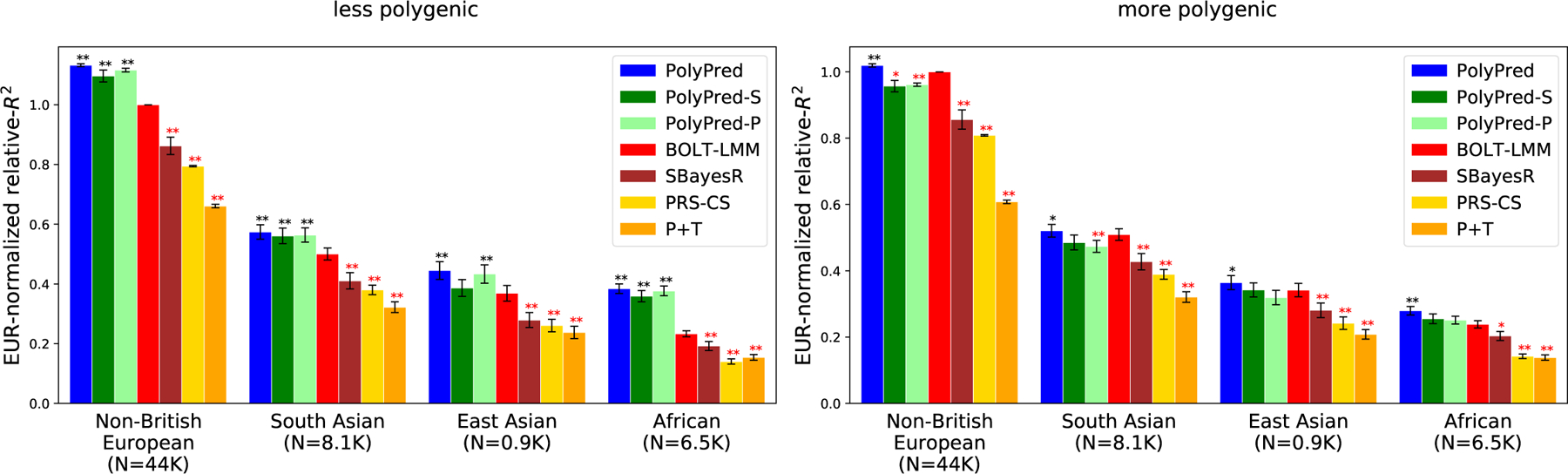
We report average prediction accuracy (relative-R2; see main text) for PRS trained in UK Biobank British samples (N=337K) and applied to 4 UK Biobank target populations across 100 simulated traits with less polygenic (0.1% of SNPs causal; left panel) or more polygenic (0.3% of SNPs causal; right panel) architectures. Target population sample sizes are indicated in parentheses; PolyPred and its summary statistic-based analogues used 500 additional training samples from each target population to estimate mixing weights. Asterisks above each bar denote statistical significance of the difference vs. BOLT-LMM, with black asterisks denoting an advantage and red asterisks denoting a disadvantage (*P<0.05; **P<0.001). P-values were computed using a two-sided Wald test and were not adjusted for multiple comparisons. Errors bars denote standard errors. Numerical results, absolute prediction accuracies (R2), and P-values of relative improvements vs. BOLT-LMM are reported in Supplementary Table 1.
We additionally performed many secondary analyses to investigate the sensitivity of the results to the simulation parameters, the SNP set and the functional annotations, and to evaluate the computational cost and memory cost of each method (Supplementary Note, Supplementary Tables 1–2).
We conclude that PolyPred and its summary statistic-based analogues are more accurate than BOLT-LMM, SBayesR, PRS-CS, and P+T, with small but significant improvements vs. BOLT-LMM in Europeans and substantial improvements in Africans.
PRS in 4 UK Biobank populations using British training data
We applied PolyPred and its summary statistic-based analogues to 49 diseases and complex traits from the UK Biobank, analyzing 4 target populations (Methods, Supplementary Table 3). As in our simulations, we used UK Biobank British training data (average N=325K) to estimate SNP effect sizes; used 500 additional individuals from the target population to estimate mixing weights; evaluated prediction accuracy using individuals from each of the 4 target populations that were not included in the training data: 42K non-British Europeans, 7.7K South Asians, 0.9K East Asians, and 6.2K Africans; and compared PolyPred and its summary statistic-based analogues to P+T, BOLT-LMM, SBayesR, and PRS-CS. We meta-analyzed relative-R2 across traits by restricting to 7 well-powered, independent complex traits from the UK Biobank40 (|rg|<0.3; see Methods and Supplementary Table 3) that were also available in Biobank Japan and in Uganda-APCDR (see below). We have publicly released SNP effect sizes used for prediction for each of the 4 methods (see Data Availability).
We computed relative-R2 for each method and target population. The results are summarized in Figure 4 and provided in Supplementary Tables 4–6 (also see Table 2). Among the published methods, BOLT-LMM attained the highest prediction accuracy in all target populations (differences between BOLT-LMM and SBayesR were small and not statistically significant). P+T was much less accurate than the other methods (despite its widespread recent use11,13–18,23,31,48–52), suffering relative losses of 37–50% vs. BOLT-LMM. We thus used BOLT-LMM as a benchmark.
Figure 4: Cross-population PRS results for real UK Biobank traits.
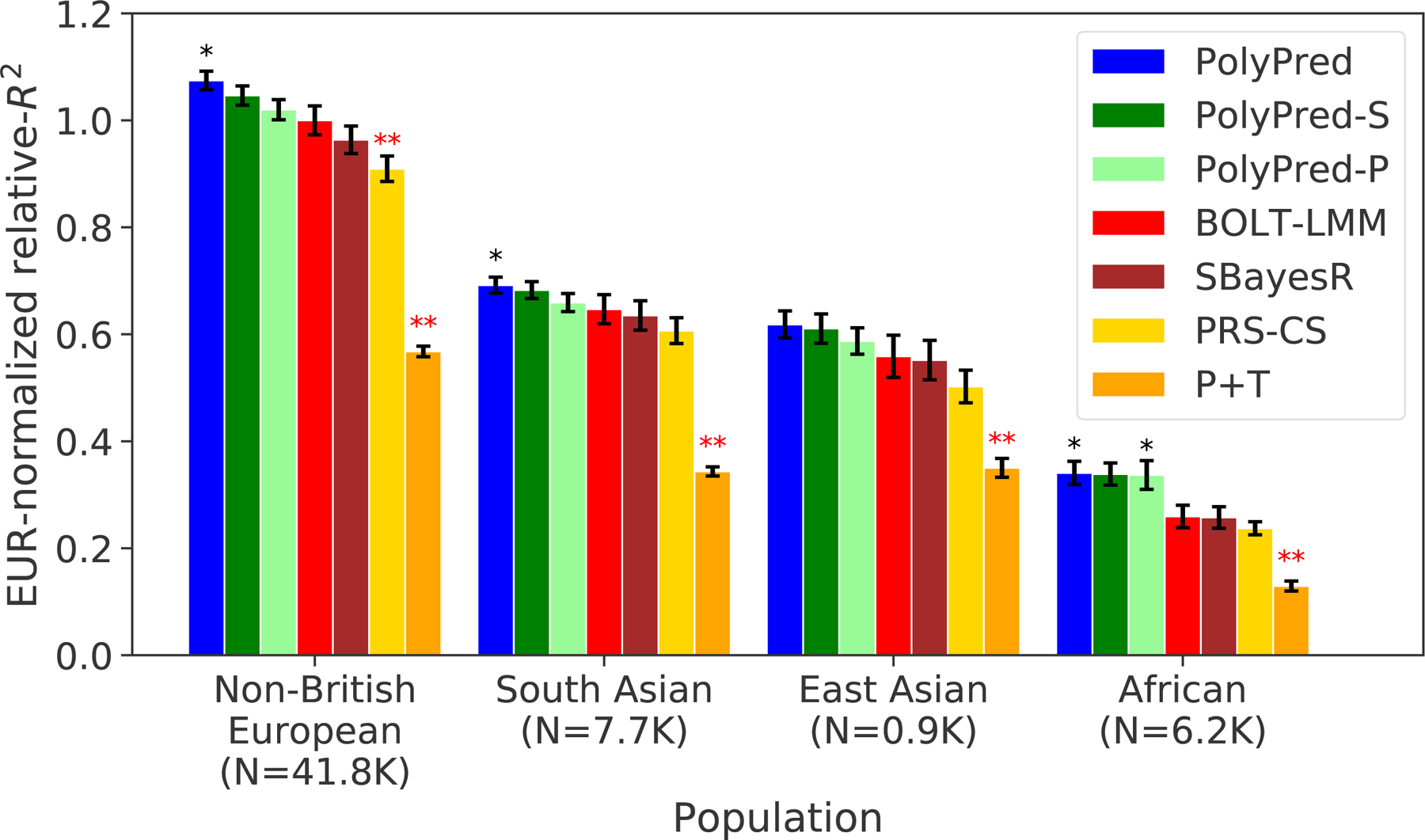
We report average prediction accuracy (relative-R2; see main text), meta-analyzed across 7 well-powered, independent traits, for PRS trained in UK Biobank British samples (average N=325K) and applied to 4 UK Biobank target populations. Target population sample sizes are indicated in parentheses; PolyPred and its summary statistic-based analogues used 500 additional training samples from each target population to estimate mixing weights. Asterisks above each bar denote statistical significance of the difference vs. BOLT-LMM, with black asterisks denoting an advantage and red asterisks denoting a disadvantage (*P<0.05; **P<0.001). P-values were computed using a two-sided Wald test and were not adjusted for multiple comparisons. Errors bars denote standard errors. Numerical results, results for all 49 traits analyzed, absolute prediction accuracies (R2), and P-values of relative improvements vs. BOLT-LMM are reported in Supplementary Tables 4–6.
Among all 7 methods, PolyPred attained the highest prediction accuracy in each target population. Improvements in average relative-R2 of PolyPred vs. BOLT-LMM were equal to +7.5% in non-British Europeans (P=0.05), +6.8% in South Asians (P=0.02), +11% in East Asians (P=0.12) and +32% in Africans (P=0.02). The larger improvement in Africans reflects the larger LD differences vs. British training data, due to earlier divergence times13,14,53. The lack of statistical significance in East Asians reflects the low power to detect significant differences in very small target samples. PolyPred-S and PolyPred-P were consistently the second and third most accurate methods, respectively, with statistically significant improvements vs. their constituent methods. We additionally verified that PolyPred was well-calibrated (i.e., regressing the true phenotype on the predicted phenotype yields a slope of 1) in all target populations, whereas the alternative methods were not always well-calibrated (Supplementary Tables 4–6, Supplementary Note). Despite the improvements attained by PolyPred, the reductions in prediction accuracy in non-European populations remained significant (P<0.002), with meta-analyzed absolute R2 equal to 0.17 in non-British Europeans, 0.11 in South Asians, 0.093 in East Asians, and 0.053 in Africans (Methods, Supplementary Tables 4–5).
As a secondary analysis, we meta-analyzed the results of each method across three independent diseases: type 2 diabetes, asthma, and all autoimmune disease (Methods); these diseases were not included in our primary meta-analyses due to low heritabilities. PolyPred attained the highest prediction accuracy for each target population and each disease, except for East Asians (where standard errors were large due to the small sample size) and for type 2 diabetes in non-British Europeans (where BOLT-LMM performed slightly but non-significantly better) (Supplementary Table 4). We performed additional secondary analyses to evaluate the impact of the LD reference panel and the SNP set on prediction accuracy, to evaluate additional methods, and to evaluate the results when modifying the parameters of PolyPred and the other evaluated methods (Supplementary Note, Supplementary Tables 4–7).
We conclude that PolyPred and its summary statistic-based analogues substantially increase cross-population polygenic prediction accuracy vs. published methods (with a particularly large improvement in Africans), consistent with simulations. However, there remains a large gap in cross-population polygenic prediction accuracy as compared to Europeans.
PRS using ENGAGE meta-analysis training data
We sought to analyze training data consisting of summary statistics for real traits from a meta-analysis of many European cohorts, for which in-sample LD is generally not available. We analyzed 8.1 million meta-analyzed summary statistics from the European Network for Genetic and Genomic Epidemiology (ENGAGE) consortium54–56 for four traits (BMI, waist-hip-ratio (adjusted for BMI), total cholesterol, and triglycerides; average N=61,365), and evaluated the prediction accuracy using the same four UK Biobank populations analyzed previously. For each method, we used an LD reference panel based on UK Biobank British individuals; we emphasize that unlike the other primary analyses, the LD reference panel was mis-specified, because it was not based on in-sample LD. We excluded methods that require individual-level training data (BOLT-LMM and PolyPred) from this analysis.
The results are summarized in Extended Data Figure 1 and reported in Supplementary Tables 5 and 8 (also see Table 2). Briefly, PolyPred-P was generally the most accurate method, and PRS-CS outperformed SBayesR (with a significant improvement for non-British Europeans and Africans), consistent with a previous study57 (unlike our analysis of UK Biobank training data, where SBayesR outperformed PRS-CS; Figure 4). However, differences between similarly performing methods were generally not statistically significant (due to moderately large standard errors), and thus caution should be exercised in their interpretation; for this reason, we did not perform secondary analyses to further assess differences between methods.
We conclude that PolyPred-P can increase cross-population polygenic prediction accuracy vs. published methods when analyzing summary statistics from a meta-analysis of many cohorts.
PRS in Biobank Japan and Uganda-APCDR cohorts
We applied PolyPred and its summary statistic-based analogues to predict 23 diseases and complex traits in Biobank Japan41 and 7 complex traits in Uganda-APCDR, an African-ancestry cohort42,43 (Methods, Supplementary Table 3). We performed these experiments to avoid training effect sizes and testing predictions in the same cohort, which may produce inflated prediction accuracies33,58–60. We again used UK Biobank British training data (average N=325K) to estimate SNP effect sizes, and used 500 individuals from the target population to estimate mixing weights. We evaluated prediction accuracy using individuals from each of the 2 target cohorts that were not included in the training data: 5K Biobank Japan individuals and 1.3K Uganda-APCDR individuals. We again compared PolyPred and its summary statistic-based analogues to P+T, BOLT-LMM, SBayesR, and PRS-CS. We meta-analyzed relative-R2 across the same 7 well-powered, independent complex traits used in the UK Biobank analyses (Supplementary Table 3).
The results are summarized in Figure 5 and reported in Supplementary Tables 5 and 9. Among the published methods, we again observed that BOLT-LMM attained the highest prediction accuracy in each target population, and that P+T was substantially less accurate than the other methods. Among all 7 methods, PolyPred attained the highest prediction accuracy in Biobank Japan, and PolyPred-P attained the highest prediction accuracy in Uganda-APCDR (although the difference between PolyPred and PolyPred-P in Uganda-APCDR was not statistically significant). Improvements of PolyPred vs. BOLT-LMM in average relative-R2 were equal to +13% in Biobank Japan (P=2×10−6) and +22% in Uganda-APCDR (P=0.26), similar to our UK Biobank results above. We observed similar improvements for PolyPred-S vs. SBayesR and PolyPred-P vs. PRS-CS (both of which were statistically significant in Biobank Japan). Prediction accuracy for each method was much smaller in Biobank Japan and Uganda-APCDR (e.g. 0.32 and 0.11 for PolyPred; Figure 5) than in UK Biobank East Asians and UK Biobank Africans (0.62 and 0.34; Figure 4), likely due to higher SNP-heritabilities in the UK Biobank (see below). We also applied PolyPred+ and its summary statistic-based analogues to Biobank Japan, incorporating additional Biobank Japan training data (average N=124K), with the caveat that this analysis involved training and testing in the same cohort (Methods). PolyPred+ attained increased prediction accuracy, with a further +23% improvement vs. PolyPred (P=0.0004), with similar results for PolyPred-S+ and PolyPred-P+ (Supplementary Tables 5, 9).
Figure 5: Cross-population PRS results for Biobank Japan and Uganda-APCDR traits.
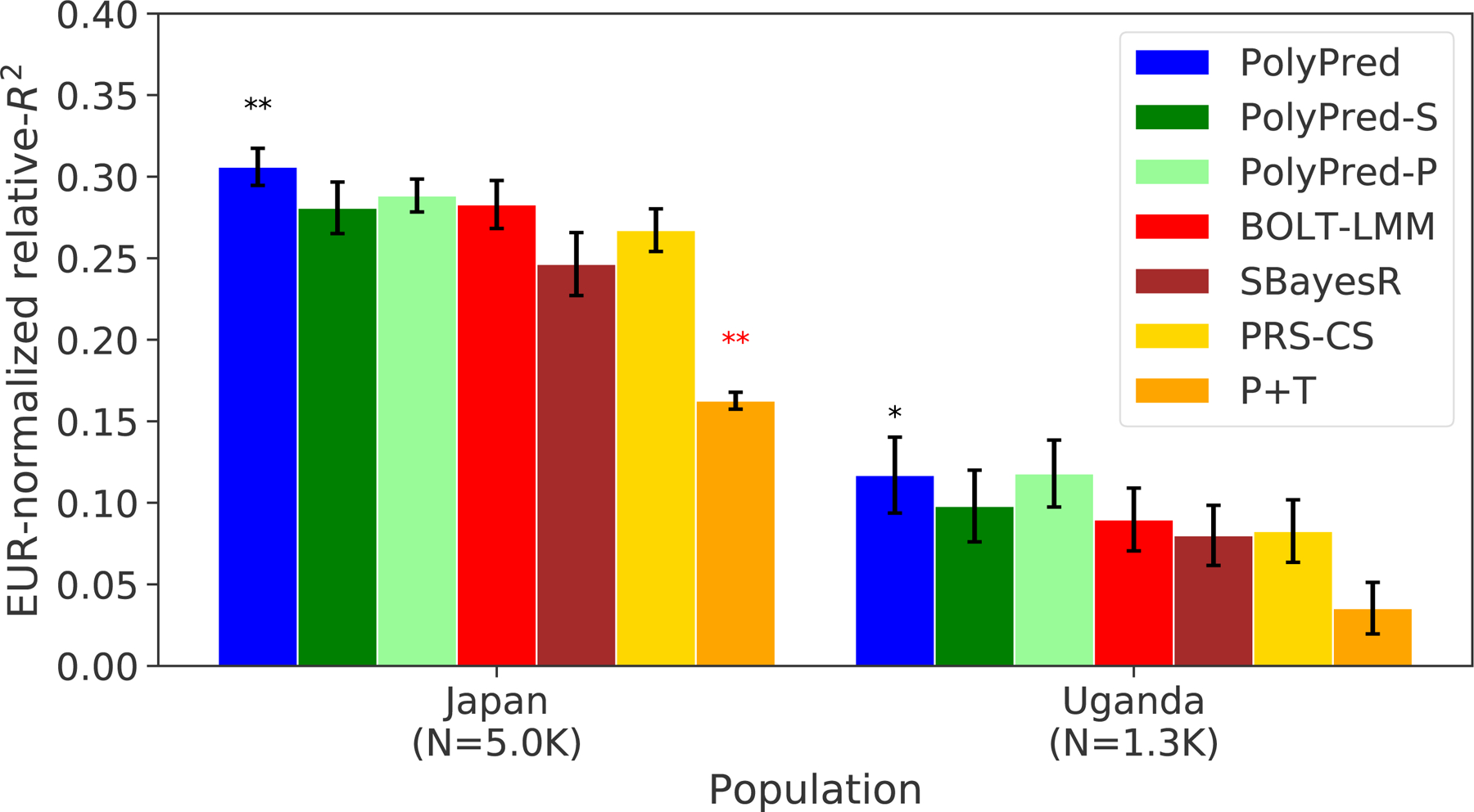
We report average prediction accuracy (relative-R2; see main text), meta-analyzed across 7 well-powered, independent traits, for PRS trained in UK Biobank British samples (average N=325K) and applied to Biobank Japan and Uganda-APCDR target populations. Target population sample sizes are indicated in parentheses; PolyPred and its summary statistic-based analogues used 500 additional training samples from each target population to estimate mixing weights. Asterisks above each bar denote statistical significance of the difference vs. BOLT-LMM, with black asterisks denoting an advantage and red asterisks denoting a disadvantage (*P<0.05; **P<0.001). P-values were computed using a two-sided Wald test and were not adjusted for multiple comparisons. Errors bars denote standard errors. Numerical results, results for all 23 traits analyzed, absolute prediction accuracies (R2), and P-values of relative improvements vs. BOLT-LMM are reported in Supplementary Table 9.
We performed additional experiments to investigate the above result of decreased prediction accuracy in Biobank Japan vs. UK Biobank East Asians. We matched the BOLT-LMM British training sample size to the Biobank Japan training sample size, and obtained a relative-R2 in UK Biobank non-British Europeans (using UK Biobank British training samples) +108% larger than in Biobank Japan (using Biobank Japan training samples), consistent with the +104% increase expected from theory61,62 based on the +67% higher SNP-heritabilities in UK Biobank (Supplementary Table 10, Supplementary Note). This suggests that differences in SNP-heritability due to ancestry or cohort differences may explain most of the differences in prediction accuracies observed between the UK Biobank and Biobank Japan. Further experiments and interpretation are provided in the Supplementary Note. We performed 6 additional secondary analyses to evaluate the sensitivity of the results to various factors (Supplementary Note, Supplementary Tables 5, 9).
We conclude that PolyPred and its summary statistic-based analogues substantially increase cross-population polygenic prediction accuracy vs. published methods when applied to target cohorts different from the training cohort.
PRS in East Asians using British and Japanese training data
We applied PolyPred+ and its summary statistic-based analogues to predict 23 diseases and complex traits in UK Biobank East Asians using UK Biobank British and Biobank Japan training data (Supplementary Table 3). We performed this experiment to explore the special case where non-European training data is available in large sample size from a population that is genetically similar to the target population, in a cohort that is distinct from the target cohort (previous studies considered only European training data or analyzed non-European training data from the target cohort11,13–17). We note that this experiment is still imperfect in that the European training data and non-European target data are from the same cohort (UK Biobank); however, we believe that cohort effects would deflate rather than inflate the relative improvement of PolyPred+ vs. other methods, since they would confer an advantage to the European training data but not the non-European training data. We used UK Biobank British training data (average N=325K) and Biobank Japan training data (average N=124K) to estimate SNP effect sizes. We again used 500 individuals from the target population to estimate mixing weights, and evaluated prediction accuracy using 900 UK Biobank East Asians that were not included in the training data. We compared PolyPred, PolyPred+, and their summary statistic-based analogues to P+T, BOLT-LMM, SBayesR, and PRS-CS (Methods). We meta-analyzed relative-R2 across the same 7 well-powered, independent complex traits used in the previous analyses (Supplementary Table 3).
The results are summarized in Figure 6 and reported in Supplementary Tables 4–6. PolyPred+ attained the highest prediction accuracy, with a +24% improvement vs. BOLT-LMM (P=0.0009) and a +12% improvement vs. PolyPred (P=0.0014). This implies that incorporating non-European training data can provide a substantial advantage, if it is available in large sample size. Results for PolyPred-S+ (vs. SBayesR and PolyPred-S) and PolyPred-P+ (vs. PRS-CS and PolyPred-P) were similar. We emphasize that the +12% improvement for PolyPred+ vs. PolyPred should be viewed as a lower bound on the improvement that would be obtained in settings without cohort effects that may confer an advantage to the European training data. We performed additional secondary analyses to evaluate the sensitivity of the results to various factors (Supplementary Note, Supplementary Tables 4–6).
Figure 6: Cross-population PRS results for UK Biobank East Asians when incorporating both European and non-European training data.

We report average prediction accuracy (relative-R2; see main text), meta-analyzed across 7 well-powered, independent traits, for PRS trained in UK Biobank British (average N=325K) and Biobank Japan samples (average N=124K; used by PolyPred+ and its summary statistic-based analogues only) and applied to UK Biobank East Asians. The target population sample size is indicated in parentheses; PolyPred, PolyPred+, and their summary statistic-based analogues used 500 additional training samples from the target population to estimate mixing weights. Asterisks above each bar denote statistical significance of the difference vs. BOLT-LMM, with black asterisks denoting an advantage and red asterisks denoting a disadvantage (*P<0.05; **P<0.001). P-values were computed using a two-sided Wald test and were not adjusted for multiple comparisons. Errors bars denote standard errors. Numerical results, results for all 23 traits analyzed, absolute prediction accuracies (R2), and P-values of relative improvements vs. BOLT-LMM are reported in Supplementary Tables 4–6.
We conclude that PolyPred+ and its summary statistic-based analogues further increase cross-population prediction accuracy in the special case where non-European training data from the target population (or a closely related population) is available in large sample size. We emphasize that efforts to assess the benefit of incorporating non-European training data should analyze non-European training data from a cohort that is distinct from the target cohort, otherwise results may be inflated due to cohort effects.
Discussion
We have introduced PolyPred, which improves cross-population polygenic risk prediction by incorporating causal effects in addition to tagging effects, addressing cross-population LD differences. Across seven well-powered independent traits, PolyPred significantly increased prediction accuracy over BOLT-LMM by 32% in UK Biobank Africans and by 13% in Biobank Japan (with similar results vs. SBayesR and PRS-CS). In the special case where a large training sample is available in the non-European target population (or a closely related population), we have introduced PolyPred+, which further incorporates the non-European training data, addressing MAF differences and causal effect size differences. PolyPred+ significantly increased prediction accuracy in UK Biobank East Asians over BOLT-LMM by 24% (and over PolyPred by 12%). PolyPred and PolyPred+ require individual-level training data (for their BOLT-LMM component), but we have also introduced summary statistic-based analogues of PolyPred and PolyPred+ in cases where individual-level training data is not available; specific recommendations are provided in Figure 2 (also see Table 2). In conclusion, PolyPred and its summary statistic-based analogues substantially improve cross-population polygenic prediction accuracy, ameliorating health disparities13. We have publicly released the PRS coefficients for all SNPs and traits analyzed under all evaluated methods (see Data Availability).
Although we substantially improved cross-population PRS accuracy over the state of the art, prediction accuracy in non-Europeans is still substantially lower compared to Europeans, even within the UK Biobank. There are two reasons for the remaining accuracy gap. First, European sample sizes are still limited, which limits the ability of PolyFun-pred to estimate causal rather than tagging effects. Second, non-European sample sizes are limited, which limits the ability of BOLT-LMM applied to non-European samples to estimate tagging effects. Even with an infinite European training sample, which allows estimating causal effects perfectly (thus addressing LD differences), prediction accuracy could still be higher for Europeans vs. non-Europeans due to cross-population genetic correlations less than 113,30,63,64 and different allele frequencies (including population-specific SNPs) (Supplementary Note). Hence our theory and results confirm that larger non-European GWAS are the best way to further improve PRS accuracy in non-European populations9,10,12,13,21.
Our work has several limitations, providing opportunities for future work. First, we did not evaluate a setting where the British training data, the non-British training data, and the target population are sampled from three different cohorts. Second, PolyPred requires a large number of imputed SNPs (e.g. 8.1 million SNPs in the ENGAGE analysis) to perform fine-mapping, motivating the need for large cross-population imputation panels. Third, it may be possible to improve PRS accuracy for admixed individuals by using European effect sizes for European alleles and non-European effect sizes for non-European alleles16,17. Fourth, PolyPred and its summary statistic-based analogues are slower than alternative PRS methods (Supplementary Note). Fifth, PolyPred cannot use data from a fixed-effects meta-analysis of GWAS data of different populations (Supplementary Note). Sixth, PolyPred requires a small training sample from the target cohort to maintain calibrated predictions (Supplementary Note). Seventh, PolyPred prediction accuracy could in principle be improved if it were possible to decompose its constituent predictors into shared and non-shared components (Supplementary Note). Despite all these limitations, PolyPred and PolyPred+ and their summary statistic-based analogues provide a clear improvement for cross-population polygenic risk prediction.
Methods
PolyPred and its summary statistic-based analogues
All methods in this paper use a linear PRS, i.e., , where is the PRS of an individual, xi is the number of minor alleles of SNP i carried by that individual, and is the estimated per-allele causal effect size of SNP i. The methods differ in the way they estimate .
PolyPred and PolyPred+ both combine the methods PolyFun-pred and BOLT-LMM; PolyPred-S and PolyPred-S+ both combine the methods PolyFun-pred and SBayesR; and PolyPred-P and PolyPred-P+ both combine the methods PolyFun-pred and PRS-CS. PolyFun-pred estimates as the (approximate) posterior mean causal effect size of SNP i, as estimated by PolyFun + SuSiE35 based on European training data, using 187 functional annotations to specify prior causal probabilities (see below). BOLT-LMM (resp. SBayesR and PRS-CS) estimates tagging effects (Supplementary Note) of HapMap 3 SNPs by applying BOLT-LMM36,37 (resp. SBayesR38 and PRS-CS39) to European training data. BOLT-LMM (resp. SBayesR) treats the effect of each SNP i as a random effect sampled from a mixture of two (resp. four) zero-mean normal distributions, whose variances and mixture weights are determined in a data-driven manner. PRS-CS treats the effect of each SNP i as a random effect sampled from a continuous shrinkage prior distribution.
PolyPred and its summary statistic-based analogues compute the effect size of each SNP i that is either in HapMap 3 or has a European MAF≥0.1% and INFO score ≥0.6 as a weighted combination of (1) its PolyFun-pred effect size based on European training data; and (2) its BOLT-LMM (resp. SBayesR and PRS-CS) effect size based on European training data:
| (1) |
where is the PolyFun-pred approximate posterior mean causal effect size of SNP i based on European training data, is the approximate posterior mean tagging effect size of SNP i based on European training data using the indicated method (setting the effects of SNPs not in HapMap 3 to zero), and wPolyFun–pred, wBOLT–LMM/SBayesR/PRS–CS are mixing weights. PolyPred estimates the mixing weights via non-negative least squares estimation (i.e., least squares estimation constrained to produce to non-negative estimates) based on training individuals from the target cohort. Specifically, PolyPred (resp. PolyPred-S and PolyPred-P) estimates the mixing weights by computing the PRS corresponding to the PolyFun-pred effect sizes (given by ) and the PRS corresponding to the BOLT-LMM (resp. SBayesR and PRS-CS) effect sizes (given by ), and then fitting the mixing weights by regressing the true phenotypes yi of the training individuals in the target cohort on the PolyFun-pred and the BOLT-LMM (resp. SBayesR and PRS-CS) PRSs. The use of non-negative least squares estimation guarantees that the correlation of the predicted phenotype with the true phenotype is at least as large as the smallest of the correlations between each constituent predicted phenotype and the true phenotype.
PolyPred+ and its summary statistic-based analogues compute the effect size of each SNP i that is either in HapMap 3 or has a European MAF≥0.1% and INFO score ≥0.6 as a weighted combination of (1) its PolyFun-pred effect size based on European training data; (2) its BOLT-LMM (resp. SBayesR and PRS-CS) effect size based on European training data; and (3) its effect size as estimated by applying BOLT-LMM (resp. SBayesR and PRS-CS) to training data from the target population (or a closely related population):
| (2) |
where is the BOLT-LMM (resp. SBayesR or PRS-CS) approximate posterior mean tagging effect of SNP i based on training data from the non-European population (and set to zero for SNPs that are not in HapMap 3), and wBOLT–LMM/SBayesR/PRS–CS–nonEur is the mixing weight of . The mixing weights are estimated as in PolyPred.
In practice, we apply PolyPred and its summary statistic-based analogues by linearly combining the PolyFun-pred PRS and the BOLT-LMM (or SBayesR or PRS-CS) PRS (rather than linearly combining the SNP effect sizes). The two procedures are almost mathematically identical, with the only difference being that a linear combination of PRSs can also accommodate an intercept, which explicitly bias-corrects the PRS to the target population.
We applied PolyFun-pred in the same way that we applied PolyFun + SuSiE in our previous work35. Briefly, we applied PolyFun-pred across 2,763 overlapping 3Mb loci (equally spaced starting at chromosome 1, position 0) spanning 18,212,157 European MAF>0.1% imputed SNPs with INFO score>0.6 (excluding the HLA and two other long-range LD regions)35, assuming 10 causal SNPs per locus. We used summary statistics computed by BOLT-LMM, based on up to N=337,491 unrelated British-ancestry UK Biobank individuals, and using summary LD information estimated directly from the target samples. Full details are provided in ref.35. We note that the use of BOLT-LMM summary statistics is mathematically equivalent to regressing the target phenotypes on BOLT-LMM off-chromosome PRS prior to applying PolyFun + SuSiE37. We also note that the use of 3Mb loci guarantees that for each SNP, the estimation of its causal effect size takes into account virtually all relevant SNPs that may be in LD with that SNP (because LD in European populations rarely ranges beyond 1Mb65), allowing to disentangle its causal effect size from its tagging effect size.
PRS methods that include non-common SNPs (MAF<5%) may be sensitive to MAF-dependent and LD-dependent architectures66,47,67. Previous PRS methods have largely alleviated this concern by discarding non-common SNPs instead of explicitly modeling their lower per-SNP heritability33,38,39,68–70,58,59,71–73. In contrast, PolyFun-pred accounts for MAF-dependent and LD-dependent architectures by specifying SNP-specific prior causal probabilities based on the baseline-LF model47 (Supplementary Table 11). In detail, PolyFun-pred uses 187 overlapping functional annotations from the baseline-LF model (previously described in ref.35), including 10 common MAF bins (MAF≥0.05); 10 low-frequency MAF bins (0.05>MAF≥0.001); 6 LD-related annotations for common SNPs; 5 LD-related annotations for low-frequency SNPs; 40 binary functional annotations for common SNPs; 7 continuous functional annotations for common SNPs; 40 binary functional annotations for low-frequency SNPs; 3 continuous functional annotations for low-frequency SNPs; and 66 annotations constructed via windows around other annotations74 (Supplementary Table 11).
Estimating relative-R2 and its standard error
We measured prediction accuracy for each trait via a measure that we call relative-R2, defined via the following computations:
Compute R2-PRS: the R2 obtained via a linear predictor that includes PRS, age, sex, age*sex (if the correlation with age was <0.95), UK Biobank assessment center (defined via dummy binary variables), genotyping array, 10 principal components (computed separately for each ancestry; see below), and dilution factor (for biochemical traits only).
Compute R2-noPRS, defined like R2-PRS but omitting the PRS
Compute R2-PRS-BOLT-EUR, computed by applying BOLT-LMM to UK Biobank non-British Europeans as in step 1
Compute R2-noPRS-BOLT-EUR, computed by applying BOLT-LMM but omitting the PRS to non-British Europeans.
Compute relative-R2 as (R2-PRS - R2-noPRS) / (R2-PRS-BOLT-EUR - R2 - noPRS-BOLT-EUR).
We note that fold improvement in relative-R2 is the same as fold improvement in absolute difference in R2, (i.e., in R2-PRS - R2-noPRS), because the denominator (R2-PRS-BOLT-EUR - R2-noPRS- BOLT-EUR) is a trait-specific scaling factor.
We computed standard errors of relative-R2, of differences in relative-R2 (e.g., vs. BOLT-LMM), of ancestry-specific regression slopes, and of the area under the receiver operating curve (for disease traits) via genomic block-jackknife, partitioning the genome into 200 equally-sized consecutive loci and omitting each one in turn. In secondary analyses, we computed standard errors by applying jackknife over individuals from the target population. These analyses yielded much smaller standard errors in the UK Biobank, suggesting that genomic block-jackknife standard errors may be conservative, whereas individual-based jackknife estimates maty be anti-conservative. We emphasize that individual-based jackknife explicitly assumes a fixed training set.
We estimated statistics (e.g., relative-R2) for meta-analyzed traits via an inverse-variance weighted average, using weights inversely proportional to the standard error of the R2 of BOLT-LMM in the target population (as estimated via genomic block-jackknife). We estimated the standard error of the meta-analyzed statistics as the square root of the weighted average of the trait-specific sampling variances (obtained via genomic block-jackknife), divided by the square root of the number of traits. We computed p-values of differences in relative-R2 vs. BOLT-LMM via a Wald test.
We computed the statistical significance of the decrease in R2 in non-European vs. European target samples via a Wald test for the difference in R2, conservatively estimating the sampling variance of this difference as the sum of the sampling variances of the European R2 and the non-European R2 (this is a conservative estimate as long as the R2 estimates in Europeans and non-Europeans are not negatively correlated, which is extremely unlikely).
Cohorts Analyzed
UK Biobank
The UK Biobank is a UK-based population cohort40. We used version 3 of the imputed genotypes, as described in our previous work35. We computed ancestry-specific PCs for UK Biobank Africans, UK Biobank East Asians, and UK Biobank South Asians via plink 1.975, restricting to SNPs that have ancestry-specific MAF>5%, missingness<10%, HWE p-value>10−10, and that were LD-pruned using the command --indep-pairwise 1000 50 0.05, and restricted to unrelated individuals (kinship coefficient <0.05) from the target ancestry with missingness <10%. We used the UK Biobank provided PCs for UK Biobank Europeans.
We defined the ‘autoimmune disease’ trait in the UK Biobank as a union of the following UK Biobank codes: 1154 (irritable bowel syndrome); 1222 (type 1 diabetes); 1224 (thyroid problem); 1225 (hyperthyroidism/thyrotoxicosis); 1226 (hypothyroidism/myxoedema); 1256 (acute infective polyneuritis/guillain-barre syndrome); 1260 (myasthenia gravis); 1261 (multiple sclerosis); 1313 (ankylosing spondylitis); 1372 (vasculitis); 1377 (polymyalgia); 1378 (wegners granulmatosis); 1381 (systemic lupus erythematosis/sle); 1382 (sjogren’s syndrome/sicca syndrome); 1384 (scleroderma/systemic sclerosis); 1437 (myasthenia gravis); 1453 (psoriasis); 1456 (malabsorption/coeliac disease); 1461 (inflammatory bowel disease); 1462 (Crohns disease); 1463 (ulcerative colitis); 1464 (rheumatoid arthritis); 1477 (psoriatic arthropathy); 1522 (grave’s disease); 1661 (vitiligo); 1667 (alopecia / hair loss).
European Network for Genetic and Genomic Epidemiology
European Network for Genetic and Genomic Epidemiology (ENGAGE) is a consortium comprised of 24 cohorts to study the impact of genetic variations on medical phenotypes through GWAS54. The consortium has performed over 80,000 GWASs using genetic and phenotype samples from over 600,000 individuals, and made the GWAS summary statistics publicly available54.
We obtained ENGAGE GWAS summary statistics, representing fixed-effect meta-analyses from 22 studies of European ancestry, for 2 lipid phenotypes55 (triglyceride (N=56,267) and total cholesterol (N=58,327)), and 2 obesity-related phenotypes56 (BMI (N=80,938) and BMI-adjusted waist hip ratio (N=49,877)). In each ENGAGE study, up to 37.4 million autosomal variants were imputed using the 1000 Genomes Project (we used 8.1 million variants which were also imputed in the UK Biobank); phenotypes were adjusted for age, age squared, genotype principal components, and other study-/trait-specific covariates, and were inverse rank normalized; GWASs were performed for each sex separately and combined using fixed-effect meta-analysis; a single genomic control correction was performed for each study prior to a cross-study meta-analysis55,56.
Biobank Japan
Biobank Japan (BBJ) is a multi-institutional hospital-based biobank with DNA and serum samples from approximately 200,000 participants from 12 medical institutions in Japan41. The participants are mainly of Japanese ancestry and had been diagnosed with at least one of 47 diseases by physicians at the cooperating hospitals. Written informed consent was obtained from all the participants, as approved by the ethics committees of RIKEN Center for Integrative Medical Sciences and the Institute of Medical Sciences at the University of Tokyo.
We genotyped samples with either (i) the Illumina HumanOmniExpressExome BeadChip or (ii) a combination of the Illumina HumanOmniExpress and HumanExome BeadChips. We applied standard quality control criteria for both samples and variants as detailed elsewhere76. We then pre-phased genotypes with Eagle277 and imputed dosages with Minimac378 using 1000 Genomes project phase 3 (version 5) data (N=2,504) and Japanese whole-genome sequencing (WGS) data (N=1,037) as a reference76. We computed PCs using EIGENSOFT’s smartpca79.
For phenotypes, we retrieved clinical medical records from the participating hospitals through interviews and a standardized questionnaire. We used 23 diseases and complex traits in Biobank Japan which are also analyzed in UK Biobank (Supplementary Table 3). We normalized quantitative phenotypes via inverse-rank normal transformation as described elsewhere80. We defined the ‘autoimmune disease’ trait in Biobank Japan as a union of Graves’ disease and rheumatoid arthritis.
Uganda-APCDR
Uganda-APCDR is a population-based cohort from the General Population Cohort (GPC), Uganda. We retrieved genotype and phenotype data through the African Partnership for Chronic Disease Research (APCDR) initiative via the European Genome-Phenome Archive (EGA), using EGAD00010000965 to access genotype data. Phenotype data were accessed via sftp from EGA (reference: DD_PK_050716 gwas_phenotypes_28Oct14.txt). The participants are from nine ethno-linguistic groups in sub-Saharan Africa and had been recruited from the study area located in southwestern Uganda in Kyamulibwa subcounty of Kalungu district, approximately 120 km from Entebbe town. These ethno-linguistic groups have diverse population structure with varying degrees of admixture between Eurasian and East African Nilo-Saharan ancestries, which has been extensively characterized elsewhere81. The detailed cohort demographics, sample collection, and processing were described previously42,43.
Briefly, the samples were genotyped using the Illumina HumanOmni 2.5M BeadChip at the Wellcome Trust Sanger Institute. We used the Ricopili pipeline to conduct pre-imputation QC and perform phasing and imputation82. Briefly, we phased the data using Eagle 2.3.577 and imputed variants using minimac378 in chunks ≥3Mb. The 1000 Genomes project phase 3 haplotypes65 were used as the reference panel for phasing and imputation.
As described previously, phenotypes were collected using a standard individual questionnaire, blood samples (laboratory tests), and biophysical measurements (height, weight, waist and hip circumferences and blood pressure)42. We normalized quantitative phenotypes via inverse-rank normal transformation.
UK Biobank Simulations
We simulated data based on real genotypes of UK Biobank individuals, using 250,963 MAF≥0.1% SNPs with INFO score≥0.6 on chromosome 22 (including short indels) (Supplementary Note). We trained all methods using 337,491 unrelated British-ancestry individuals40, and we estimated the mixing weights of PolyPred and its summary statistic-based analogues using up to 1000 additional individuals from each of the four non-British ancestries. We computed summary statistics by applying linear regression via Plink 2.0. We did not evaluate PolyPred+ in the simulations because of the relatively small sample sizes of the UK Biobank non-European populations. We evaluated prediction accuracy via R2, using held-out individuals that were not included in the training sets and were unrelated to the training set individuals and to each other, using 42K non-British Europeans, 7.7K South Asians, 0.9K East Asians, and 6.2K Africans. We computed PRSs by applying plink 2.0 with the --score command, using imputed dosage data (rather than hard-called SNP values). We computed standard errors via a jackknife over simulations.
We trained BOLT-LMM by applying BOLT-LMM v2.3.4 to plink files of HapMap 3 SNPs (hard-coded from imputed dosages), using the same covariates specified in the “Estimating relative-R2 and its standard error” Methods subsection, and specifying the flag –predBetasFile to report PRS coefficients.
We trained SBayesR using summary statistics from the infinitesimal version of BOLT-LMM (BOLT-LMM-inf36), which yielded far superior accuracy vs. using summary statistics from the non-infinitesimal version of BOLT-LMM. We ran SBayesR using 10,000 iterations, 4,000 burn-in iterations, using values from 10% of the iterations to compute posterior means, using the HapMap 3 LD files published the SBayesR authors83. We attempted to run SBayesR using a mixture of four distributions (using π = [0.95,0.02,0.02,0.01] and γ = [0,0.01,0.1,1]). In case SBayesR failed with these parameters, we iteratively shrank the last entry in the vector γ by 50% until it was smaller than 10−6, at which point we removed the last mixture component and redefined π such that the first entry was equal to 0.95 and all other entries had the same value such that all values sum to 1.0.
We trained PRS-CS using summary statistics from BOLT-LMM-inf (as in SBayesR) with the parameters a=1, b=0.5, thin=5, n_iter=10000, n_burnin=500, and without specifying the value of phi (corresponding to PRS-CS-auto). We used the UK Biobank LD reference panels made publicly available by the authors of PRS-CS (see Data Availability).
We trained P+T by applying plink with the command –clump-r2 0.5 –clump-kb 250 with various values of –clump-p1 (following ref.13), and using 10,000 randomly selected unrelated UK Biobank British individuals to compute LD. We estimated LD using 10,000 individuals to balance between runtime and accuracy (noting that P+T is relatively insensitive to the LD reference panel size compared to the other methods evaluated in this manuscript). We used summary statistics based on BOLT-LMM, using marginal effect sizes derived from reported χ2 values (i.e., the square root of χ2 divided by the square root of the BOLT-LMM effective sample size35, and multiplied by the sign of the effect size estimated by the infinitesimal version of BOLT-LMM). We used the best value of –clump-p1 (out of the evaluated values 10−2, 10−3, 10−4, 10−6, 5×10−8) based on the target sample phenotypes, which leads to anti-conservative prediction accuracy estimates for P+T.
We used slightly different LD reference panels for PolyFun-pred, SBayesR, and PRS-CS, because (i) they use different algorithms to impose sparsity on LD matrices, and different file formats to store them; and (ii) we assume that naively running SBayesR or PRS-CS using summary LD from the 18 million SNPs used by PolyFun-pred would be computationally infeasible, based on information provided in the manuscripts describing these methods38,39. When modifying the training sample size, we kept the LD reference panel sample size fixed to alleviate computational costs.
Analysis of real data
We performed four sets of analyses: (i) Analysis of 4 UK Biobank populations using UK Biobank British training data; (ii) Analysis of 4 UK Biobank populations using ENGAGE meta-analysis training data; (iii) Analysis of Biobank Japan and Uganda-APCDR cohorts; and (iv) Analysis of UK Biobank East Asians using UK Biobank British and Biobank Japan training data. In analysis sets (i), (iii) and (iv), we evaluated PRSs generated by training all methods using unrelated UK Biobank British-ancestry individuals. In analysis set (ii), we evaluated PRSs generated by training all methods using summary statistics from 8.1 million meta-analyzed summary statistics from the ENGAGE consortium54–56. In a subset of analysis set (iii) and in analysis set (iv) we additionally evaluated PRSs generated by training BOLT-LMM-BBJ (BOLT-LMM trained on Biobank Japan individuals). In all analysis sets, the individuals in the target populations were unrelated to each other and to the individuals in the training set (when available).
In analysis sets (i), (iii) and (iv), we selected the 7 traits to meta-analyze by first restricting the set of 49 traits analyzed in ref.35 to traits that are available in Biobank Japan and Uganda-APCDR and are well-powered across multiple ancestries, having h2>0.05 in UK Biobank non-British Europeans, in UK Biobank South Asians, and in UK Biobank Africans (see below for details on ancestry-specific heritability estimation). We then iteratively greedily selected ranked traits according to their heritability in UK Biobank non-British Europeans (estimated as in ref. 35), such that no selected trait had |rg|<0.3 with a previously selected trait.
We computed ancestry-specific SNP heritabilities in each UK Biobank ancestry by applying GCTA84 to unrelated sets of individuals using hard-called HapMap 3 SNPs (using a random set of 10,000 individuals for non-British Europeans to facilitate the computations). We did not use more advanced methods85 because of the relatively small sample sizes. We meta-analyzed ancestry-specific SNP heritabilities by averaging the estimated heritabilities, and we estimated the meta-analyzed standard error via the square root of the average sampling variance, divided by the square root of the number of traits.
In analysis sets (i), (iii) and (iv), We trained all PRS methods on UK Biobank unrelated British-ancestry individuals (average N=325) as described in the Methods subsection “UK Biobank simulations”, but using summary statistics generated by BOLT-LMM when applied to UK Biobank British-ancestry individuals, as described in our previous work35. We trained P+T separately for each non-UK Biobank cohort by restricting the set of SNPs considered to the set of SNPs available in both the UK Biobank and in the target cohort. We computed the contribution of PolyFun-pred (resp. BOLT-LMM) towards PolyPred via the ratio of the mixing weight of PolyFun-pred (resp. BOLT-LMM) to the sum of the mixing weights of PolyPred and of BOLT-LMM.
In analysis sets (i), (ii) and (iv), we computed a PRS for each UK Biobank individual using imputed dosage data as described in the “UK Biobank Simulations”. In analysis set (iii), we computed a PRS for each individual in Biobank Japan and in Uganda-APCDR using imputed dosage data using Plink 2.086,87.
In secondary analyses of analysis set (i) we also evaluated LDpred33. We trained LDpred using HapMap 3 SNPs and using two different LD reference panels: 1000 Genomes project65 and UK10K88. We used summary statistics from the infinitesimal version of BOLT-LMM (as in SBayesR) and with default parameters, using the parameter --ldr 400. We used the value of “--F” (corresponding to the assumed proportion of causal SNPs, using all the default evaluated values) that yielded the best prediction accuracy in the target sample, yielding anti-conservative accuracy estimates as in P+T.
In analysis sets (iii) and (iv), we trained BOLT-LMM-BBJ, SBayesR-BBJ, and PRS-CS-BBJ (BOLT-LMM, SBayesR, and PRS-CS, respectively, trained using Biobank Japan training data) (average N=124K). We selected individuals for training these methods as described in our previous work13, but excluding a random subset of 5,000 individuals that were used for evaluating prediction accuracy. For SBayesR-BBJ, we used a subset of individuals (N=50K) from Biobank Japan to compute in-sample LD, following the recommendations of the authors of SBayesR38. For PRS-CS-BBJ, we used the East Asian LD reference panels made publicly available by the authors of PRS-CS (see Data Availability).
Data availability
Access to the UK Biobank resource is available via application (http://www.ukbiobank.ac.uk). PRS coefficients generated in this study are available for public download at http://data.broadinstitute.org/alkesgroup/polypred_results. Summary LD information of N=337K British-ancestry UK Biobank individuals for 2,763 overlapping 3Mb loci is available at: https://data.broadinstitute.org/alkesgroup/UKBB_LD. Summary LD information of N=50K UK Biobank individuals for SBayesR is available at: https://zenodo.org/record/3350914. Summary LD information used by PRS-CS is available at: https://github.com/getian107/PRScs. Baseline-LF v2.2.UKB annotations and LD-scores for UK Biobank SNPs are available at: https://data.broadinstitute.org/alkesgroup/LDSCORE/baselineLF_v2.2.UKB.tar.gz Source data are provided with this paper.
Code availability
PolyPred and PolyPred+ are provided as part of the open-source software package PolyFun, which is freely available at https://doi.org/10.5281/zenodo.613967989 and https://github.com/omerwe/polyfun. BOLT-LMM is available at https://data.broadinstitute.org/alkesgroup/BOLT-LMM. SBayesR is available at https://cnsgenomics.com/software/gctb. PRS-CS is available at https://github.com/getian107/PRScs.
Extended Data
Extended Data Fig. 1. Cross-population PRS results for real UK Biobank traits, using summary statistics from a meta-analysis of many cohorts.
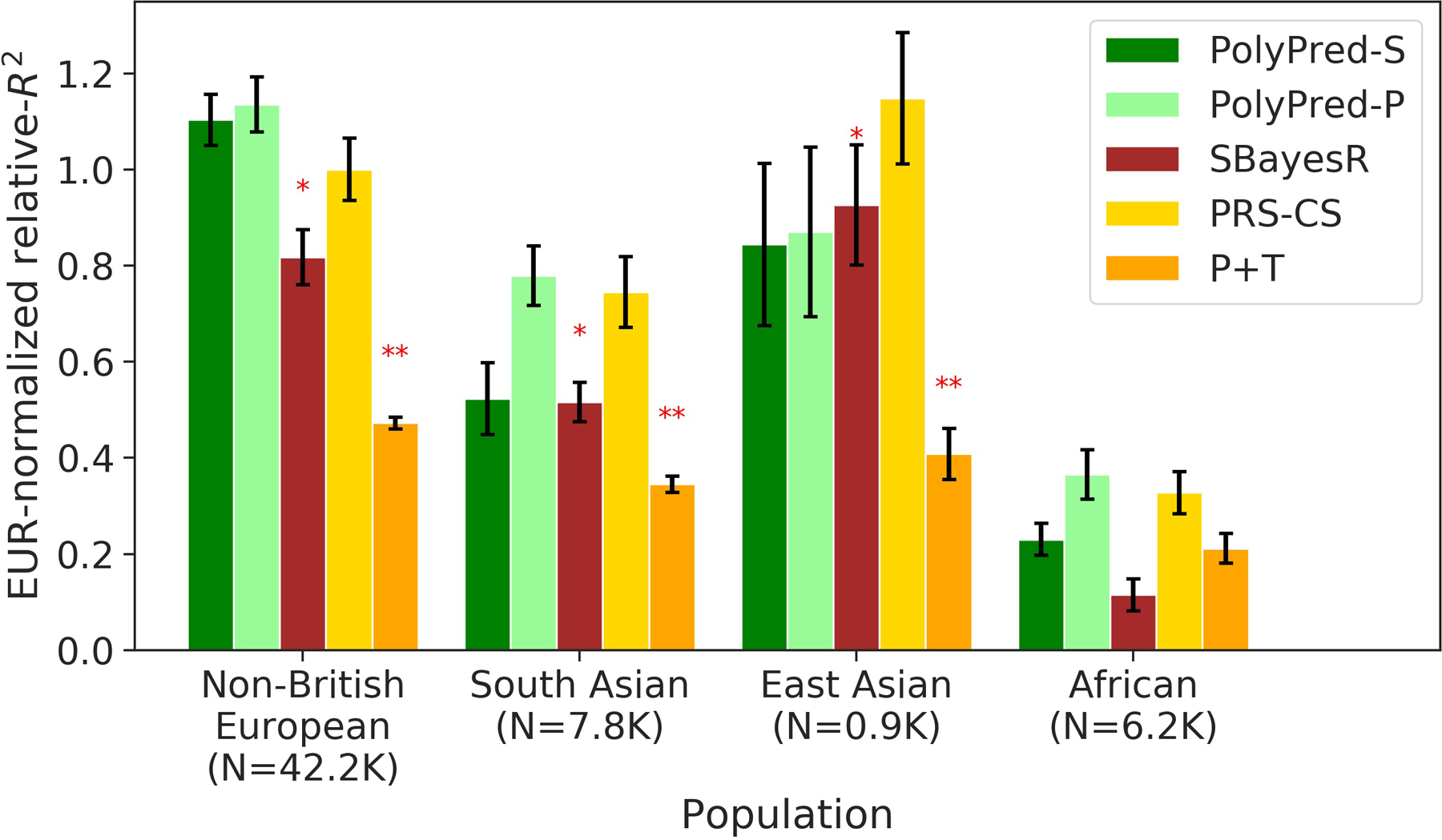
We report average prediction accuracy (relative-R2, but computed with respect to PRS-CS instead of BOLT-LMM; see main text), meta-analyzed across 4 well-powered, approximately independent traits, for PRS trained in European Network for Genetic and Genomic Epidemiology (ENGAGE) samples (average N=61,365) and applied to 4 UK Biobank populations. Target population sample sizes are indicated in parentheses; PolyPred and its summary statistic-based analogues used 500 additional training samples from each target population to estimate mixing weights. Asterisks above each bar denote statistical significance of the difference vs. PRS-CS, with red asterisks denoting a disadvantage (*P<0.05; **P<0.001). P-values were computed using a two-sided Wald test and were not adjusted for multiple comparisons. Errors bars denote standard errors. Numerical results, results for all 4 traits analyzed, absolute prediction accuracies (R2), and P-values of relative improvements vs. PRS-CS are reported in Supplementary Table 5 and Supplementary Table 8.
Supplementary Material
Acknowledgements
We thank Armin Schoech and Carla Márquez-Luna for helpful discussions. This research was conducted using the UK Biobank Resource under Application #16549 and was funded by NIH grants U01 HG009379, U01 HG012009, R37 MH107649, R01 MH101244 and R01 HG006399. MK is supported by a Nakajima Foundation Fellowship and the Masason Foundation. WJP is supported by an NWO Veni grant (91619152). ARM is supported by NIMH K99/R00MH117229. HKF is supported by Eric and Wendy Schmidt. AVK is supported by grants 1K08HG010155 and 1U01HG011719 from the National Human Genome Research Institute and a sponsored research agreement from IBM Research. YO is supported by JSPS KAKENHI (19H01021, 20K21834), and AMED (JP21km0405211, JP21ek0109413, JP21ek0410075, JP21gm4010006, JP21km0405217), JST Moonshot R&D (JPMJMS2021, JPMJMS2024). Computational analyses were performed on the O2 High-Performance Compute Cluster at Harvard Medical School.
Footnotes
Competing interests
O.W. is an employee and holds equity in Eleven Therapeutics. H.S. is an employee of Genentech and holds stock in Roche. A.V.K. is an employee and holds equity in Verve Therapeutics, has served as a scientific advisor to Sanofi, Amgen, Maze Therapeutics, Navitor Pharmaceuticals, Sarepta Therapeutics, Novartis, Silence Therapeutics, Korro Bio, Veritas International, Color Health, Third Rock Ventures, Foresite Labs, and Columbia University (NIH); received speaking fees from Illumina, MedGenome, Amgen, and the Novartis Institute for Biomedical Research; and received a sponsored research agreement from IBM Research. All other authors declare no competing interests.
BioBank Japan Project – members and affiliations
Koichi Matsuda.
Laboratory of Genome Technology, Human Genome Center, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Laboratory of Clinical Genome Sequencing, Graduate School of Frontier Sciences, The University of Tokyo, Tokyo, Japan.
Yuji Yamanashi.
Division of Genetics, The Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Yoichi Furukawa.
Division of Clinical Genome Research, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Takayuki Morisaki.
Division of Molecular Pathology, IMSUT Hospital Department of Internal Medicine, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Yoshinori Murakami.
Department of Cancer Biology, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Yoichiro Kamatani.
Laboratory of Complex Trait Genomics, Graduate School of Frontier Sciences, The University of Tokyo, Tokyo, Japan.
Laboratory of Clinical Genome Sequencing, Graduate School of Frontier Sciences, The University of Tokyo, Tokyo, Japan.
Kaori Muto.
Department of Public Policy, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Akiko Nagai.
Department of Public Policy, Institute of Medical Science, The University of Tokyo, Tokyo, Japan.
Wataru Obara.
Department of Urology, Iwate Medical University, Iwate, Japan.
Ken Yamaji.
Department of Internal Medicine and Rheumatology, Juntendo University Graduate School of Medicine, Tokyo, Japan.
Kazuhisa Takahashi.
Department of Respiratory Medicine, Juntendo University Graduate School of Medicine, Tokyo, Japan.
Satoshi Asai.
Division of Pharmacology, Department of Biomedical Science, Nihon University School of Medicine, Tokyo, Japan.
Division of Genomic Epidemiology and Clinical Trials, Clinical Trials Research Center, Nihon University. School of Medicine, Tokyo, Japan.
Yasuo Takahashi.
Division of Genomic Epidemiology and Clinical Trials, Clinical Trials Research Center, Nihon University School of Medicine, Tokyo, Japan.
Takao Suzuki.
Tokushukai Group, Tokyo, Japan.
Nobuaki Sinozaki.
Tokushukai Group, Tokyo, Japan.
Hiroki Yamaguchi.
Department of Hematology, Nippon Medical School, Tokyo, Japan.
Shiro Minami.
Department of Bioregulation, Nippon Medical School, Kawasaki, Japan.
Shigeo Murayama.
Tokyo Metropolitan Geriatric Hospital and Institute of Gerontology, Tokyo, Japan.
Kozo Yoshimori.
Fukujuji Hospital, Japan Anti-Tuberculosis Association, Tokyo, Japan.
Satoshi Nagayama.
The Cancer Institute Hospital of the Japanese Foundation for Cancer Research, Tokyo, Japan.
Daisuke Obata.
Center for Clinical Research and Advanced Medicine, Shiga University of Medical Science, Shiga, Japan.
Masahiko Higashiyama.
Department of General Thoracic Surgery, Osaka International Cancer Institute, Osaka, Japan.
Akihide Masumoto.
IIZUKA HOSPITAL, Fukuoka, Japan.
Yukihiro Koretsune.
National Hospital Organization Osaka National Hospital, Osaka, Japan.
References
- 1.Chatterjee N, Shi J & García-Closas M Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 17, 392–406 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Khera AV et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 50, 1219–1224 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Torkamani A, Wineinger NE & Topol EJ The personal and clinical utility of polygenic risk scores. Nat. Rev. Genet. 19, 581–590 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Khera AV et al. Polygenic prediction of weight and obesity trajectories from birth to adulthood. Cell 177, 587–596 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mavaddat N et al. Polygenic risk scores for prediction of breast cancer and breast cancer subtypes. Am. J. Hum. Genet. 104, 21–34 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li R, Chen Y, Ritchie MD & Moore JH Electronic health records and polygenic risk scores for predicting disease risk. Nat. Rev. Genet. 1–10 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Márquez-Luna C, Loh P-R, Consortium, S. A. T. 2 D. (SAT2D), Consortium, S. T. 2 D. & Price AL Multiethnic polygenic risk scores improve risk prediction in diverse populations. Genet. Epidemiol. 41, 811–823 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Grinde KE et al. Generalizing polygenic risk scores from Europeans to Hispanics/Latinos. Genet. Epidemiol. 43, 50–62 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Peterson RE et al. Genome-wide association studies in ancestrally diverse populations: opportunities, methods, pitfalls, and recommendations. Cell 179, 589–603 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sirugo G, Williams SM & Tishkoff SA The missing diversity in human genetic studies. Cell 177, 26–31 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Duncan L et al. Analysis of polygenic risk score usage and performance in diverse human populations. Nat. Commun. 10, 1–9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gurdasani D, Barroso I, Zeggini E & Sandhu MS Genomics of disease risk in globally diverse populations. Nat. Rev. Genet. 20, 520–535 (2019). [DOI] [PubMed] [Google Scholar]
- 13.Martin AR et al. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 51, 584 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang Y et al. Theoretical and empirical quantification of the accuracy of polygenic scores in ancestry divergent populations. Nat. Commun. 11, 3865 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Amariuta T et al. Improving the trans-ancestry portability of polygenic risk scores by prioritizing variants in predicted cell-type-specific regulatory elements. Nat. Genet. 52, 1346–1354 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marnetto D et al. Ancestry deconvolution and partial polygenic score can improve susceptibility predictions in recently admixed individuals. Nat. Commun. 11, 1–9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bitarello BD & Mathieson I Polygenic Scores for Height in Admixed Populations. G3 g3.401658.2020 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen M-H et al. Trans-ethnic and ancestry-specific blood-cell genetics in 746,667 individuals from 5 global populations. Cell 182, 1198–1213 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mahajan A et al. Trans-ancestry genetic study of type 2 diabetes highlights the power of diverse populations for discovery and translation. medRxiv (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cavazos TB & Witte JS Inclusion of variants discovered from diverse populations improves polygenic risk score transferability. Hum. Genet. Genomics Adv. 2, 100017 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mills MC & Rahal C The GWAS Diversity Monitor tracks diversity by disease in real time. Nat. Genet. 52, 242–243 (2020). [DOI] [PubMed] [Google Scholar]
- 22.Lehmann BC, Mackintosh M, McVean G & Holmes CC High trait variability in optimal polygenic prediction strategy within multiple-ancestry cohorts. bioRxiv (2021). [Google Scholar]
- 23.Ji Y et al. Incorporating European GWAS findings improve polygenic risk prediction accuracy of breast cancer among East Asians. Genet. Epidemiol. (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ruan Y et al. Improving Polygenic Prediction in Ancestrally Diverse Populations. medRxiv 2020. –12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cai M et al. A unified framework for cross-population trait prediction by leveraging the genetic correlation of polygenic traits. Am. J. Hum. Genet. (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Huang QQ et al. Transferability of genetic loci and polygenic scores for cardiometabolic traits in British Pakistanis and Bangladeshis. medRxiv (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Durvasula A & Lohmueller KE Negative selection on complex traits limits phenotype prediction accuracy between populations. Am. J. Hum. Genet. 108, 620–631 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Coram MA, Fang H, Candille SI, Assimes TL & Tang H Leveraging Multi-ethnic Evidence for Risk Assessment of Quantitative Traits in Minority Populations. Am. J. Hum. Genet. 101, 218–226 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wojcik GL et al. Genetic analyses of diverse populations improves discovery for complex traits. Nature 570, 514–518 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shi H et al. Population-specific causal disease effect sizes in functionally important regions impacted by selection. Nat. Commun. 12, 1–15 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kuchenbaecker K et al. The transferability of lipid loci across African, Asian and European cohorts. Nat. Commun. 10, (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mostafavi H et al. Variable prediction accuracy of polygenic scores within an ancestry group. Elife 9, e48376 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vilhjálmsson BJ et al. Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. Am. J. Hum. Genet. 97, 576–592 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schaid DJ, Chen W & Larson NB From genome-wide associations to candidate causal variants by statistical fine-mapping. Nat Rev Genet 19, 491–504 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Weissbrod O et al. Functionally informed fine-mapping and polygenic localization of complex trait heritability. Nat. Genet. 1–9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Loh P-R et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Loh P-R, Kichaev G, Gazal S, Schoech AP & Price AL Mixed-model association for biobank-scale datasets. Nat. Genet. 50, 906–908 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lloyd-Jones LR et al. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 10, 1–11 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ge T, Chen C-Y, Ni Y, Feng Y-CA & Smoller JW Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun. 10, 1–10 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bycroft C et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nagai A et al. Overview of the BioBank Japan Project: study design and profile. J. Epidemiol. 27, S2–S8 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Asiki G et al. The general population cohort in rural south-western Uganda: a platform for communicable and non-communicable disease studies. Int. J. Epidemiol. 42, 129–141 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Heckerman D et al. Linear mixed model for heritability estimation that explicitly addresses environmental variation. Proc. Natl. Acad. Sci. 113, 7377–7382 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Duan S, Zhang W, Cox NJ & Dolan ME FstSNP-HapMap3: a database of SNPs with high population differentiation for HapMap3. Bioinformation 3, 139 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Purcell SM et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460, 748–752 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Stahl EA et al. Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet. 44, 483–489 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gazal S et al. Functional architecture of low-frequency variants highlights strength of negative selection across coding and non-coding annotations. Nat. Genet. 50, 1600–1607 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lam M et al. Comparative genetic architectures of schizophrenia in East Asian and European populations. Nat. Genet. 51, 1670–1678 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nievergelt CM et al. International meta-analysis of PTSD genome-wide association studies identifies sex- and ancestry-specific genetic risk loci. Nat. Commun. 10, 4558 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sakaue S et al. Trans-biobank analysis with 676,000 individuals elucidates the association of polygenic risk scores of complex traits with human lifespan. Nat. Med. 26, 542–548 (2020). [DOI] [PubMed] [Google Scholar]
- 51.Vuckovic D et al. The Polygenic and Monogenic Basis of Blood Traits and Diseases. Cell 182, 1214–1231.e11 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Guo J et al. Global genetic differentiation of complex traits shaped by natural selection in humans. Nat. Commun. 9, 1–9 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sved JA, McRae AF & Visscher PM Divergence between human populations estimated from linkage disequilibrium. Am. J. Hum. Genet. 83, 737–743 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Budin-Ljøsne I et al. Data sharing in large research consortia: experiences and recommendations from ENGAGE. Eur. J. Hum. Genet. 22, 317–321 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Surakka I et al. The impact of low-frequency and rare variants on lipid levels. Nat. Genet. 47, 589–597 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Horikoshi M et al. Discovery and fine-mapping of glycaemic and obesity-related trait loci using high-density imputation. PLoS Genet. 11, e1005230 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pain O et al. Evaluation of polygenic prediction methodology within a reference-standardized framework. PLoS Genet. 17, e1009021 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chung W et al. Efficient cross-trait penalized regression increases prediction accuracy in large cohorts using secondary phenotypes. Nat. Commun. 10, 1–11 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chun S et al. Non-parametric Polygenic Risk Prediction via Partitioned GWAS Summary Statistics. Am. J. Hum. Genet. (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Im C et al. Generalizability of “GWAS Hits” in Clinical Populations: Lessons from Childhood Cancer Survivors. Am. J. Hum. Genet. 107, 636–653 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Daetwyler HD, Villanueva B & Woolliams JA Accuracy of predicting the genetic risk of disease using a genome-wide approach. PloS One 3, e3395 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Visscher PM & Hill WG The limits of individual identification from sample allele frequencies: theory and statistical analysis. PLoS Genet 5, e1000628 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Galinsky KJ et al. Estimating cross-population genetic correlations of causal effect sizes. Genet. Epidemiol. 43, 180–188 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Brown BC, Ye CJ, Price AL & Zaitlen N Transethnic Genetic-Correlation Estimates from Summary Statistics. Am. J. Hum. Genet. 99, 76–88 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Methods-only References
- 65.1000 Genomes Project Consortium. A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zeng J et al. Signatures of negative selection in the genetic architecture of human complex traits. Nat. Genet. 50, 746 (2018). [DOI] [PubMed] [Google Scholar]
- 67.Schoech AP et al. Quantification of frequency-dependent genetic architectures in 25 UK Biobank traits reveals action of negative selection. Nat. Commun. 10, 790 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zhang Q, Privé F, Vilhjálmsson B & Speed D Improved genetic prediction of complex traits from individual-level data or summary statistics. Nat. Commun. 12, 4192 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hu Y et al. Leveraging functional annotations in genetic risk prediction for human complex diseases. PLoS Comput. Biol. 13, e1005589 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Marquez-Luna C et al. LDpred-funct: incorporating functional priors improves polygenic prediction accuracy in UK Biobank and 23andMe data sets. bioRxiv 375337 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Mak TSH, Porsch RM, Choi SW, Zhou X & Sham PC Polygenic scores via penalized regression on summary statistics. Genet. Epidemiol. 41, 469–480 (2017). [DOI] [PubMed] [Google Scholar]
- 72.Yang S & Zhou X Accurate and Scalable Construction of Polygenic Scores in Large Biobank Data Sets. Am. J. Hum. Genet. (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Qian J et al. A fast and scalable framework for large-scale and ultrahigh-dimensional sparse regression with application to the UK Biobank. PLoS Genet. 16, e1009141 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Finucane HK et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet. 47, 1228–1235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Purcell S et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81, 559–75 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Akiyama M et al. Characterizing rare and low-frequency height-associated variants in the Japanese population. Nat. Commun. 10, 1–11 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Loh P-R et al. Reference-based phasing using the Haplotype Reference Consortium panel. Nat. Genet. 48, 1443–1448 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Das S et al. Next-generation genotype imputation service and methods. Nat. Genet. 48, 1284–1287 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Price AL et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38, 904–909 (2006). [DOI] [PubMed] [Google Scholar]
- 80.Sakaue S et al. A global atlas of genetic associations of 220 deep phenotypes. medRxiv (2020). [Google Scholar]
- 81.Gurdasani D et al. Uganda genome resource enables insights into population history and genomic discovery in Africa. Cell 179, 984–1002 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lam M et al. RICOPILI: Rapid Imputation for COnsortias PIpeLIne. Bioinformatics 36, 930–933 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Lloyd-Jones L GCTB SBayesR shrunk sparse linkage disequilibrium matrices for HM3 variants, summary statistics and predictors generated from ‘Improved polygenic prediction by Bayesian multiple regression on summary statistics’ by Lloyd-Jones, Zeng et al. 2019. (2019) doi: 10.5281/ZENODO.3350914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Yang J, Lee SH, Goddard ME & Visscher PM GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88, 76–82 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gazal S, Marquez-Luna C, Finucane HK & Price AL Reconciling S-LDSC and LDAK functional enrichment estimates. Nat. Genet. 51, 1202–1204 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Chang CC et al. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience 4, 7 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Purcell S & Chang C PLINK v2.00a3LM.
- 88.The UK10K Consortium et al. The UK10K project identifies rare variants in health and disease. Nature 526, 82 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Weissbrod Omer. Source code for PolyFun. (Zenodo, 2022). doi: 10.5281/ZENODO.6139679. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Access to the UK Biobank resource is available via application (http://www.ukbiobank.ac.uk). PRS coefficients generated in this study are available for public download at http://data.broadinstitute.org/alkesgroup/polypred_results. Summary LD information of N=337K British-ancestry UK Biobank individuals for 2,763 overlapping 3Mb loci is available at: https://data.broadinstitute.org/alkesgroup/UKBB_LD. Summary LD information of N=50K UK Biobank individuals for SBayesR is available at: https://zenodo.org/record/3350914. Summary LD information used by PRS-CS is available at: https://github.com/getian107/PRScs. Baseline-LF v2.2.UKB annotations and LD-scores for UK Biobank SNPs are available at: https://data.broadinstitute.org/alkesgroup/LDSCORE/baselineLF_v2.2.UKB.tar.gz Source data are provided with this paper.


