Abstract
Understanding the dynamics of airflow in alveoli and its effect on the behavior of particle transport and deposition is important for understanding lung functions and the cause of many lung diseases. The studies on these areas have drawn substantial attention over the last few decades. This Review discusses the recent progress in the investigation of behavior of airflow in alveoli. The information obtained from studies on the structure of the lung airway tree and alveolar topology is provided first. The current research progress on the modeling of alveoli is then reviewed. The alveolar cell parameters at different generation of branches, issues to model real alveolar flow, and the current numerical and experimental approaches are discussed. The findings on flow behavior, in particular, flow patterns and the mechanism of chaotic flow generation in the alveoli are reviewed next. The different flow patterns under different geometrical and flow conditions are discussed. Finally, developments on microfluidic devices such as lung-on-a-chip devices are reviewed. The issues of current devices are discussed.
I. INTRODUCTION
Human lung is the main organ that is directly connected to the environment and interacts with harmful particles, mists, vapors, or gases.1 The lungs' main function is to exchange gases between the human body and the atmosphere by inhaling oxygen from the atmosphere and exhausting carbon dioxide metabolized by the human body. Adult humans can inhale more than 10 000 l of air per day, which contains about 100 × 109–10 × 1012 particles.2 A large number of these particles will be inhaled into the lung. The inhalation may cause lung diseases, such as chronic obstructive pulmonary diseases, asthma, and lung cancer.3–5 Millions of people worldwide die from these diseases every year.6–8 Therefore, it is very important to understand how the particles carried by air flow in the lung penetrate deeply and affect the health of the lungs.
Over the last few decades, there has been a great deal of research effort devoted to this area. The studies include pulmonary structure,9–11 alveolar flow,12–15 and particle transport.16–19 A number of review articles have been published recently to report the research progress.20–26 For example, Kleinstreuer et al.20 reviewed theoretic models that govern particle transport in lungs and commonly used techniques for delivering aerosol drugs. Tsuda et al.21 reviewed the studies on the phenomena of gas transport and theoretic models on gas transport in alveoli. The chaotic mixing of aerosol particles in alveoli was also covered in the review. Hofmann22 reviewed whole-lung models for predicting aerosol deposition. Sznitman23 reviewed the fluid mechanics of acinar airflows and its effect on the transport of inhaled aerosols in the distal regions of the lungs. Phalen and Raabe24 summarized inhaled aerosol dose models. Tenenbaum-Katan et al.25 gave their perspective views on understanding airflow in the pulmonary environment using microfluidic in vitro models. The most recent article from Sznitman26 gave an in-depth review of acinar flow and aerosol transport in microfluidics.
While these reviews are very comprehensive, this paper will discuss the very recent progress on the understanding of alveolar flows, with a view to decipher the mechanism of particle transport and deposition in the alveolar cells. First, we give a brief introduction to the pulmonary structures and the morphology of alveoli. We then review the research methods and key findings on alveolar flows. Next, the development of three-dimensional lung-on-a-chip models is reviewed. Finally, some future prospects in this field are discussed.
II. PULMONARY AIRWAYS AND ALVEOLAR MORPHOLOGY
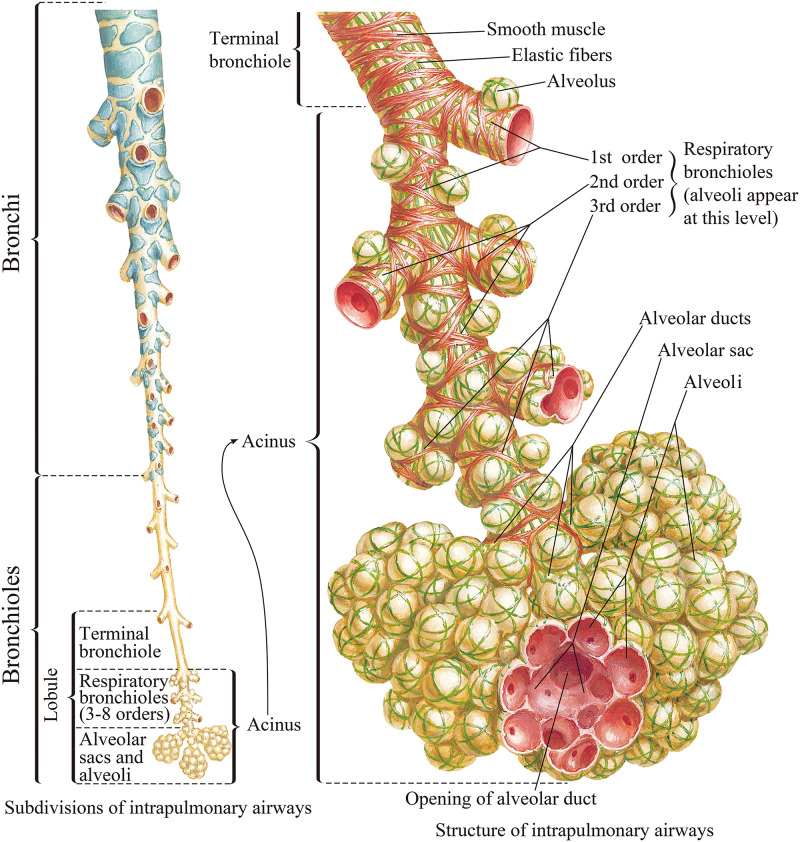
The lung is a large, gas-filled organ located within the body's chest cavity.3,27,28 It has a complex structure with a highly branched tree-like airway as shown in Fig. 1. Lung tissue is spongy with a large number of tiny cavities, i.e., alveoli, where gas exchanges take place. The lungs can inhale and exhale air by expansion and contraction. Inhaled air passes through the nose, pharynx, and larynx into the trachea of the lower respiratory tract. The end of the trachea is divided into two branches to form the left and right main bronchi, which are divided into smaller bronchi and finally into bronchioles. The bronchioles also are divided into sub-branches and the alveoli appear first in the transitional bronchioles, which are branches of terminal bronchioles.10,29 The airway tree from the transitional bronchioles to the alveolar sacs is referred to as the pulmonary acinus. Based on the average acinar volume, it is estimated that there are approximately 30 000 acini in the adult lung. It is estimated that the lung of an adult has a total of 274–790 × 106 alveoli.3,29,30
FIG. 1.
Model of a human airway system. From Netter, Atlas of Human Anatomy, 6th Edition. Copyright 2014 Elsevier Inc. Adapted with permission from Elsevier Inc.
The acinar airway is a space-filling tree with ends that are evenly distributed and fill every space.10,29 From the first to the last generation of the acinus, the diameter of alveoli decreases while the density of alveoli increases. The morphology of alveoli in the lung is polyhedron rather than spherical due to the space-filling structure of the acini,21 which are supported by numerous studies, e.g., the scanning electron micrograph of acinus cast by perfusion with formaldehyde [Figs. 2(a)–2(c)],10,29 alveoli of rat lung documented by light microscopy,31 and images of alveoli observed through confocal microscopy [Fig. 2(d)].11,32–34
FIG. 2.
Anatomy of the pulmonary acini and alveoli. (a) Scanning electron micrograph (SEM) of acinus from lung cast by perfusion with formaldehyde.10 Part of the alveolar ducts (ad) and alveolar sacs (as) were removed to expose the transitional bronchiole (tb) and the respiratory bronchioles (rb); scale bar 1 mm. (b) SEM of portions of sub-acinus.10 One alveolar duct (ad') is stretched to show the arrangement of single (a) or clustered (ac) alveoli. Dense alveolar accumulation in unstretched alveolar ducts (ad). (c) SEM of the cross section of alveolar duct D surrounded by densely packed alveoli in human lung.29 (d) Observation of alveoli on a slice of reconstructed three-dimensional rat lung by confocal microscopy technique.11 Images (a) and (b) are reproduced with permission from Haefeli-Bleuer and Weibel, Anat. Rec. 220(4), 401–414 (1988). Copyright 1988 John Wiley & Sons, Inc. Image (c) is reproduced with permission from Weibel et al., Respir. Physiol. Neurobiol. 148(1–2), 3–21 (2005). Copyright 2005 Elsevier. Image (d) is reproduced with permission from Yang et al., ACS Nano 13(2), 1029–1041 (2019). Copyright 2019 American Chemical Society.
III. CURRENT PROGRESS ON ALVEOLAR MODELING
A. Pulmonary tree and alveolar structure
The human pulmonary airway is usually modeled as a dichotomous tree and with an average of 24 generations according to the studies from Weibel et al.29 The trachea is the first generation and is labeled as the 0th generation. The diameters of the branches in the pulmonary airway tree vary from 18 mm (trachea) to 290 μm with the increase of airway generations under the condition of total lung capacity. The last nine generations (from 15th to 23rd generations) are the lung acinus. Dong et al.35 proposed a method to calculate the alveolar and ductal sizes in the acini based on the anatomical data of lungs from Weibel’s group.10,29 Table I lists the size of the alveoli and ducts in the dichotomous acinar airways. The alveolar diameters are between 111 and 225 μm under the condition of functional residual capacity (i.e., at the beginning of inspiration or end of expiration). The ductal diameters decrease from 409 to 238 μm along with the acinar generations under the functional residual capacity condition.
TABLE I.
Acinar data of a typical human adult.35
| ith Gen. | Dd-TLC,i a(μm) | Dd,i b(μm) | Da-TLC,i c(μm) | Da,i d(μm) | |
|---|---|---|---|---|---|
| Respiratory bronchioles | 15 | 498 | 409 | 134.7 | 111 |
| 16 | 497 | 409 | 135.3 | 111 | |
| 17 | 492 | 404 | 138.7 | 114 | |
| 18 | 397 | 326 | 202.0 | 166 | |
| Alveolar ducts | 19 | 382 | 314 | 212.0 | 174 |
| 20 | 356 | 293 | 229.3 | 189 | |
| 21 | 335 | 275 | 243.3 | 200 | |
| 22 | 311 | 256 | 259.3 | 213 | |
| Alveolar sacs | 23 | 289 | 238 | 274.0 | 225 |
Ductal diameter at the ith generation under total lung capacity (TLC) condition.
Ductal diameter at the ith generation under functional residual capacity (FRC) condition.
Alveolar diameter at the ith generation under TLC condition.
Alveolar diameter at the ith generation under FRC condition.
B. Issues to model real alveolar flow
To model alveolar flows, it is necessary to achieve geometric similarity and dynamic similarity between real alveolar flow and alveolar flows in numerical simulations or experiments.15,23,35,36 Geometric similarity indicates that two models should be exactly alike except for the different sizes. The dynamic similarity of fluid flow is achieved by matching the dimensionless parameters, which are the Reynolds number (Re) and the Womersley number (Wo) between the model and real alveoli,
| (1) |
| (2) |
where Dd is the diameter of the alveolar duct, ud is the flow velocity in the duct, ν is the kinematic viscosity of air, and ω = 2π/T, T refers to the respiratory period.
To study the particle transport and deposition by the air flow in the lung, particles are usually simplified as uniform spheres without deformation and rotation. The particle concentration in the respiratory tract is assumed to be too small to affect the airflow. The particle density is mostly considered to be 1 g/cm3, which is about 1000 times the density of air.19,37–40 Based on these assumptions, the electrostatic force and buoyant force of particles in the airflow are usually ignored.23 As a result, the motion of particles in airflow is mainly affected by gravity (FG), viscous drag force (FD), and random force [F(t)].2,16,19,23 Random force describes the diffusion process due to Brownian collisions. Three dimensionless numbers need to be considered to model the particle dynamics, namely, the Stokes number (Stk), the Peclet number (Pep), and the gravity number (H), respectively,
| (3) |
| (4) |
| (5) |
where ω = 2π/T is the breathing frequency, ρp is the density of the particles, g is the gravitational acceleration, dp is the particle diameter, μ is the dynamic viscosity of the fluid, Dmol is the diffusion constant of spherical particles, kB is the Boltzmann constant, Tem is the temperature in Kelvin, and Cc is the Cunningham slip correction factor.41
C. Numerical simulations
1. Numerical methods
There are two strategies to realize the expansion and contraction of alveolar walls in numerical simulations. In the first strategy, the alveolar geometry maintains self-similarity throughout a breathing period, and the length scale L(t) was given by a displacement function L(t) = L0 ⋅ F(t)12,42–47 during expansion and contraction. The second strategy is considering force exerted by the muscles of respiration on the lungs. This is a process of interaction between fluid and solid. The fluid–solid interaction (FSI) method is used to achieve the expansion and contraction of alveoli. Dailey and Ghadiali48 were the first to use the FSI method to simulate the expansion and contraction of the alveoli. Dong et al.35 developed a method to calculate alveolar flow parameters and the alveolar expansion ratios. The alveolar flows were also modeled using the FSI method by Chen and Zhao49 and Lv et al.15
The numerical simulations of alveolar flow and particle transport can be classified into two categories according to the different alveolar modeling methods, namely the regular alveolar model50 and the irregular alveolar models generated by the anatomically inspired algorithm51 or by computed tomography (CT) images.52,53 Studies using these two models are discussed below.
2. Regular alveoli
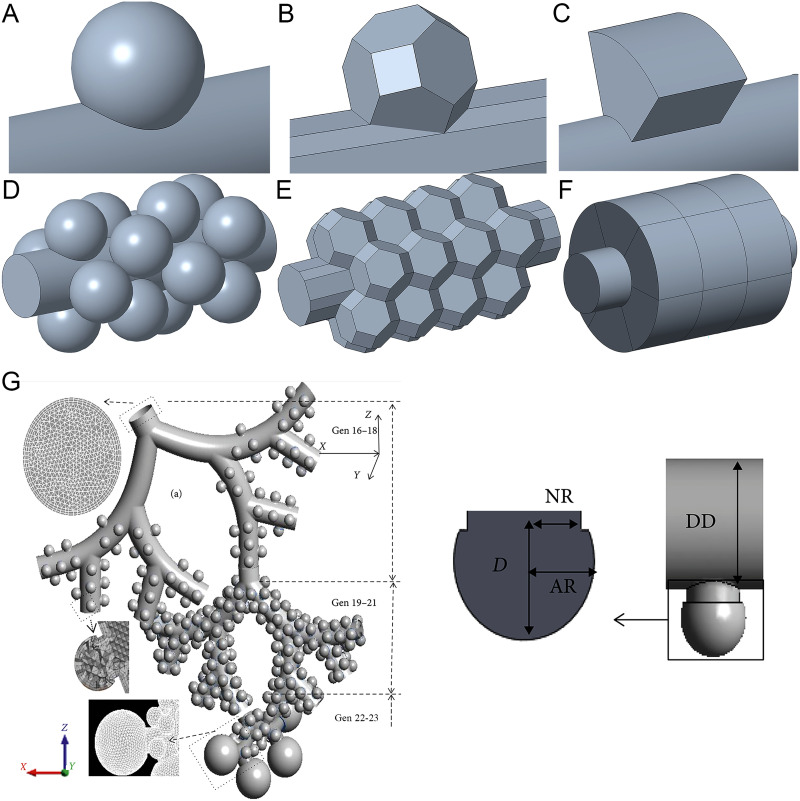
The first commonly used method is to build alveolar models with a regular geometry as shown in Figs. 3(a)–3(f). The geometry is similar to that of real alveoli. These three types of alveoli are spherical, polyhedral (i.e., truncated octahedron), and toroidal alveolar models, respectively. They represent the average morphological characteristics of the alveolar structure.51
FIG. 3.
(a) and (d) spherical alveolus. (b) and (e) Polyhedral (i.e., truncated octahedron) alveolus. (c) and (f) Toroidal alveolus. Images (a)–(c) are single alveolar models. Images (d)–(f) are multi-alveolar models. (g) Alveoli with long necks in whole-lung airway model.61 From Kolanjiyil and Kleinstreuer, Comput. Math. Method Med. 2019, 5952941 (2019). Copyright 2019 Author(s), licensed under a Creative Commons Attribution (CC BY) license.
Spherical alveoli models are widely used to study alveolar flows. Haber and Tsuda54 and Haber et al.13 used a spherical cap to model an alveolus, which was placed on a flat surface. The alveolus can expand and contract in a self-similar manner. Based on quasi-steady conditions, the flow field, the motion of massless particles, and the deposition of actual particles by convection and gravity within the alveolus were computed. A similar computational model was reported by Haber and Tsuda,55 in which they used two eccentrically nested cylinders of different diameters to study hydrodynamic phenomena within an alveolus. The two eccentric cylinders can expand and contract with self-similarly. The fluid fills the cavity between the two cylinders. The inner tube can be rotated periodically. Lee and Lee56 used a model with a spherical alveolus on a cylinder to study the differences in particle motion in alveoli with both expanding–contracting and fixed wall conditions. Sznitman et al.43,44 and Henry et al.14 modeled alveolar flows in the single spherical alveolus with rhythmically expanding alveolar walls. They presented the streamlines in the alveoli to visualize the three-dimensional flow patterns. Harding and Robinson57 studied alveolar flows in the last generation using a multi-alveolar model of spherical alveoli. In their study, only the alveoli could expand and contract. Semmler-Behnke et al.45 showed the changes in alveolar flow patterns during alveolus development. With the development of alveoli, the depth of the alveolar cavity increases. The age-dependent changes in acinar fluid mechanics and particle depositions were studied. Ma and Darquenne40,58 used multi-generation multi-alveolar models to study alveolar flows and particle deposition. A whole-lung airway model for studying alveolar flows was developed by Kolanjiyil and Kleinstreuer59–61 as shown in Fig. 3(g). In their model, the alveolus was connected with the duct by a cylindrical neck. The geometry of the alveolus is a spherical cap, which is different from Fig. 3(a). Only alveoli can expand. The effect of the neck on alveolar flow was not evaluated. To save computation time, their whole-lung airway was divided into three parts (i.e., Gen 16–18, Gen 19–21, and Gen 22–23) for numerical simulations.
From the previous studies, it can be found that the alveoli in the spherical alveolar model were not arranged in the space-filling manner. There were spaces between alveoli and, therefore, the effect of the expansion and contraction movements of alveolar walls during breathing was not taken into account. These models should not be used for locations where alveolar cells are tightly packed. In the latter case, the space-filling models should be used, in which case the adjacent alveoli would share the same wall and thus interactions between neighboring alveoli are considered.
Fung62 and Denny and Schroter63 designed a truncated octahedron to describe the space-filling alveoli. The truncated octahedron was constructed from a regular octahedron by removing six right square pyramids from each vertex of the octahedron. The length of each side of the truncated octahedron was the same. Figure 3(e) shows the assembly of multiple truncated octahedrons.62 Any two adjacent alveoli share the same alveolar septum. This alveolus structure was adopted in many studies of alveolar flows using space-filling models that resemble real alveoli. Sznitman et al.44,64 used asymmetric space-filling acinar trees (from 18th to 23rd generation), a sub-region of the pulmonary acinus to study alveolar flows and particle trajectories. Similar asymmetric space-filling acinar trees of the last five generations were modeled by Khajeh-Hosseini-Dalasm and Longest,65 Ostrovski et al.,66 Hofemeier and Sznitman,46 and Oakes et al.67 These studies focused on particle transport and deposition. Among these studies, Oakes et al.67 showed flow patterns in healthy and emphysema sub-acini. No inter-septal walls were present in the diseased regions. A more detailed study on alveolar flow patterns in a truncated octahedron was carried out by Kumar et al.68 based on a single duct surrounding multiple alveoli, which is similar to Fig. 3(e). The model of the alveolar sac was designed by adding an alveolus on one end of the duct. Kumar et al.69 used an alveolar duct with multiple alveoli to study the mixing patterns by tracking grids of massless particles.
The toroidal alveolar model can be also space-filling. However, unlike the truncated octahedron, alveoli on this model can only be space-filling on the same alveolar duct. There are two types of toroidal alveolar models. One is similar to the model in the study of Tsuda et al.12 that a torus with a circular section is an alveolus. They first discovered the chaotic fluid flow in the alveoli under rhythmically expanding alveolar walls. Henry et al.42 studied chaotic mixing using an alveolar model with multiple tori of circular sections on a cylinder. However, adjacent alveoli in this model are separated by a distance and are not space-filling. Subsequently, Henry et al.70 studied chaotic mixing patterns in multiple toroidal alveoli with quadrilateral cross sections. The arrangement of these alveoli is space-filling. In a subsequent paper, Henry and Tsuda71 used a similar model of the toroidal alveoli to study flow patterns and radial particle transport along the human acinar tree. In a separate study, Henry and Tsuda47 used the same model to study alveolar flows in alveoli at different stages of development by changing the depth of the alveolar cavities. Another model is that a torus is cut into multiple alveoli, or referred to as segmented toroidal alveoli as shown in Figs. 3(c) and 3(f), respectively. Adjacent alveoli share the same alveolar septum. Darquenne and Paiva,72 Darquenne et al.,73 and Ciloglu et al.74,75 used a single alveolated duct with multiple segmented toroidal alveoli to carry out the studies on particle deposition and alveolar flow. Harrington et al.76 designed a fully alveolated bifurcation of two generations based on the segmented toroidal alveoli. These studies mainly investigated particle transport behavior.
3. Irregular alveoli
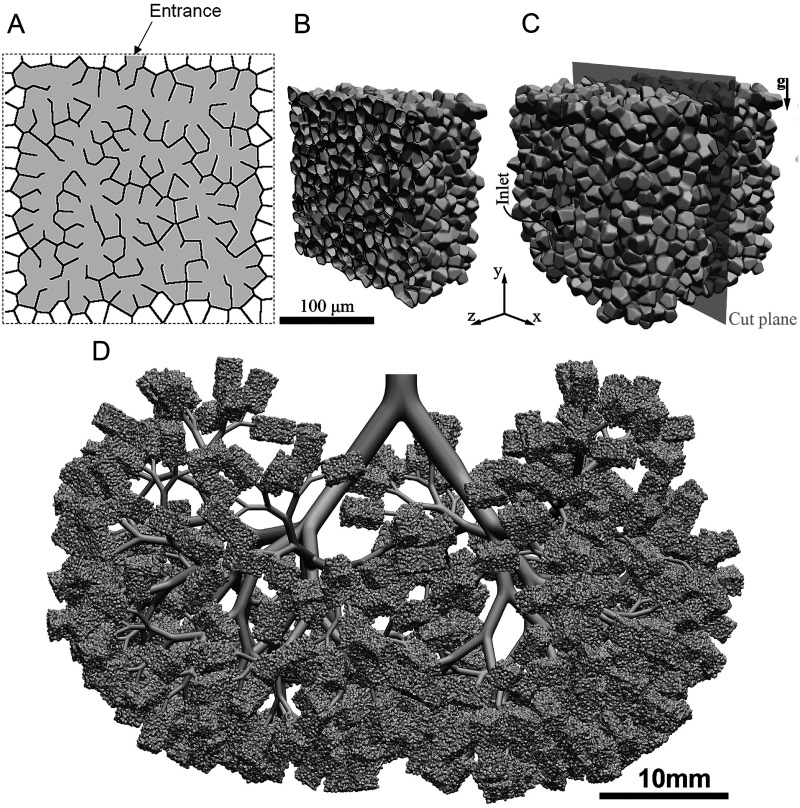
One of the approaches to recreate alveolar models of irregular alveoli is based on anatomically inspired algorithms. It can generate space-filling acinar geometries of variable shapes that reflect statistical morphometric measurements in humans. This method was proposed by Koshiyama and Wada,51 in which they used the combination of Voronoi tessellation and Delaunay tessellation to model a heterogeneous acinus structure with irregular sizes, shapes, and locations, as shown in Fig. 4(a). Hofemeier et al.77 and Shachar-Berman et al.78 used the heterogeneous acinus structure, as shown in Figs. 4(b) and 4(c), to numerically simulate the transport and deposition of aerosol particles. Such a structure was also used in Refs. 79–81 on aerosol transport and deposition in whole-lung models. An example of the model is shown in Fig. 4(d).80 While this method can reflect the heterogeneity of acinar architecture, it does not take into account of the variations of sizes of ducts and alveoli across different acinar generations.35
FIG. 4.
Heterogeneous acinus structure. (a) Two-dimensional schematic diagram of the acinus structure model.51 (b) Cross-sectional cut through the acinar model.77 (c) Whole view of the acinar model.77 (d) Whole-lung model (simplified deep lung model).80 Image (a) is reproduced with permission from Koshiyama and Wada, Comput. Biol. Med. 62, 25–32 (2015). Copyright 2015 Elsevier Ltd. Images (b) and (c) are reproduced with permission from Hofemeier et al., Eur. J. Pharm. Sci. 113, 53–63 (2018). Copyright 2017 Elsevier B.V. Image (d) is reproduced with permission from Koullapis et al., J. Aerosol. Sci. 144, 105541 (2020). Copyright 2020 Elsevier Ltd.
The last approach for constructing acinar models of irregular alveoli is based on computed tomography (CT) images of an intact acinus.52,53 Acinar morphometric metrics such as diameters, lengths, and branching angles of the alveolar ducts, acinar volume, alveolar surface area, surface area/volume ratios, and total path lengths from the acinar entrance to the alveolar sacs can be assessed using high-resolution CT images. For example, Williams et al.82 studied the drug deposition in the upper airway structure using a model generated from a CT scan image.
D. Experimental studies
1. Experimental methods
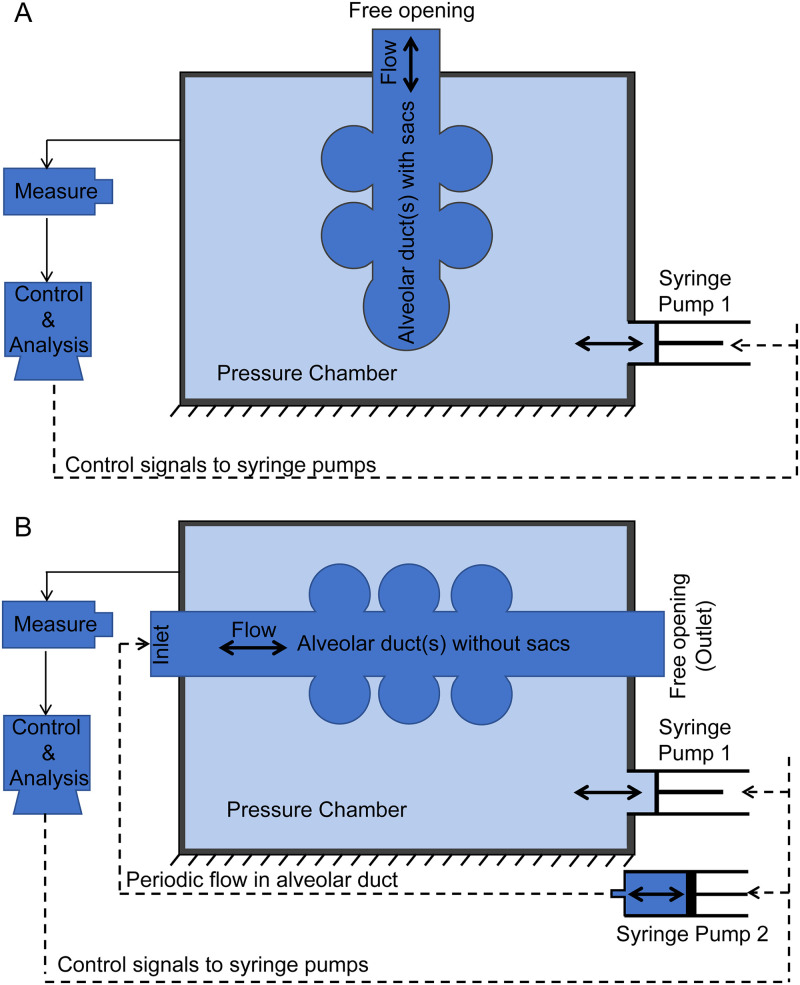
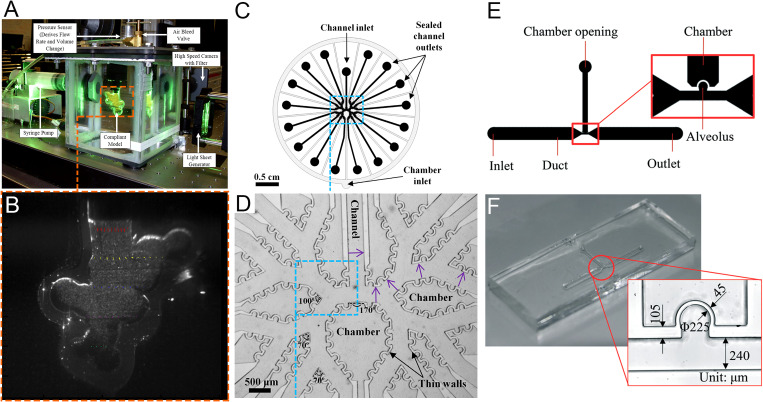
In experimental studies, there are two methods to realize the expansion and contraction of alveoli. The schematic illustrations are shown in Figs. 5(a) and 5(b). The alveolar model is contained in a pressure chamber that is filled with liquid. A syringe pump is used to control the pressure in the chamber. When the liquid in the chamber is pumped out, the pressure in the chamber decreases, resulting in the expansion of alveoli due to the negative pressure (relative to atmospheric pressure) in the chamber. When the fluid is injected into the chamber, the pressure in the chamber increases and results in the contraction of alveoli. If the alveolar model ends with alveolar sacs, the alveolar model only has one entrance that is connected to the outside atmosphere as shown in Fig. 5(a). This method was used in several studies, e.g., Berg et al.83 and Fishler et al.84 In the second method [Fig. 5(b)], the system is set up without sacs. This alveolar model has both an inlet and an outlet. The inlet is connected to a second syringe pump that controls the transient fluid flow in the alveolar duct.15,38
FIG. 5.
Schematic illustrations of control systems for expansion and contraction of alveoli. (a) Alveolar model with alveolar sac. (b) Alveolar model without alveolar sac.
Flow field measurements and particle tracking measurements are mostly required in experimental studies. Two types of alveoli are usually used, i.e., the scale-up models and real-size models. The measurement of the flow field includes two methods. The first method is flow visualization, i.e., qualitative observation of the flow field in the alveoli. In this method, the position of seeding particles at different time points is recorded by taking pictures for a short period of time and then superimposing these pictures to obtain a flow field map.85,86 In order to obtain an accurate flow field in the alveoli, the commonly used measurement method is particle image velocimetry (PIV). Macroscopic PIV was used in the scaled-up alveolar experiments, which requires a light sheet.83,87–90 Microscopic PIV was used in the alveolar chip experiments.15,84
Particle tracking is to measure the movement of particles in alveoli. It is carried out for the detection and tracking of particle trajectories as recorded by video imaging. The time interval for time sequences in the video imaging should be small enough for particle identification. After data acquisition, the positions of the tracked particles are determined using image processing algorithms. The corresponding particle trajectories can be obtained by connecting the positions of the same particle at different time sequences.17,86,91 However, both the flow field measurement and the particle tracking are usually two-dimensional snapshots of the three-dimensional flow phenomenon. Measurements using 3D techniques are still missing.
The experimental studies involve two types of models, i.e., the scale-up and real-size models. In the scale-up models, the kinematic viscosity (ν) or the fluid velocity (ud) can be adjusted to match Re, and ν or T can be adjusted to match Wo. On the contrary, the real-size model has the same dimension with the real alveoli. Studies using these two models are discussed below.
2. Scaled-up alveolar models
van Ertbruggen et al.87 designed an alveolar bend and Ma et al.92 designed a three-generation alveolar bifurcation. They both used toroidal alveoli. The cross section of the alveolus was rectangular and a torus represented an alveolus. Both models were made of silicone by casting. The model sizes of the two studies were about 50 and 75 times of that of a real alveolus, respectively. However, the alveolar walls were rigid without deformation.
An example of a scaled-up model that can achieve rhythmical alveolar expansion is shown in Figs. 6(a) and 6(b). The first scaled-up model of the spherical alveoli that could imitate the expansion and contraction of alveoli was designed by Cinkotai.93 The alveolus size in the model is about 100 times that of the real lung. The author used this model to visualize the mixing of the tidal and residential air. Tippe and Tsuda85 reproduced alveolar flows in a circular toroidal alveolus by experimental work. The dimensions of this alveolus were enlarged by a factor of about 20. The alveolar model was obtained by casting of silicone rubber. The flow patterns were visualized by tracer trajectories, which were obtained by superposition of some images from one series. The three similarities were matched in the latter two studies except that they did not consider Wo and the dynamic similarity of particle motion. Chhabra and Prasad38,94,95 designed a single-alveolus model with a scale-up ratio of ∼100. Only the alveolus could expand and contract while the duct remained rigid. The Reynolds number and the Womersley number were matched around the 18th and 19th acinar generations. Results for velocity maps at different stages of breathing cycles were presented. The alveolar model of Li et al.96 was made of a rubber balloon with a scale-up ratio of 75, and the method as that in Fig. 5(a) was used to achieve contraction and expansion. In the study by Oakes et al.,88 two models of alveolar sacs were made to mimic healthy and emphysemic alveolar sacs, respectively. The scale-up ratio was 75 and the Re and Wo numbers were matched. Other studies of flow field in alveolar sacs using scale-up models include those reported by Berg et al.,83 Berg and Robinson,89 and Sera et al.90 in which the models were made either using SEM images of real lung cast or the synchrotron computed tomography (CT) of the real lung.
FIG. 6.
Models of scaled-up alveoli and alveolar chips. (a) Experimental PIV setup of scaled-up model.83 (b) Cross section of scaled-up model (magnified 22 times).83 (c) CAD drawing of multi-generation alveoli chip.84 (d) Multi-generation alveoli chip.84 (e) CAD drawing of alveolar chip of single alveolus.15 (f) Alveolar chip of single alveolus.15 Images (a) and (b) are reproduced with permission from Berg et al., J. Biomech. 43(6), 1039–1047 (2010). Copyright 2009 Elsevier. Images (c) and (d) are reproduced with permission from Fishler et al., J. Biomech. 46(16), 2817–2823 (2013). Copyright 2013 Elsevier. Images (e) and (f) are reproduced with permission from Lv et al., Lab Chip 20(13), 2394–2402 (2020). Copyright 2020 The Royal Society of Chemistry.
The scaled-up model has several advantages. The geometric scaled-up model is easy to be fabricated. We can easily fabricate the alveolar model of the real alveolar shape, such as the regular alveoli of sphere and polyhedron and the irregular alveoli obtained by CT scanning. It is easier to measure the flow field in the scaled-up model, and even a three-dimensional flow field can be easily measured. However, the scaled-up model has a great defect, that is, it cannot simultaneously match the dimensionless number that makes the dynamics between the scaled-up model and the real alveoli similar. When particle transport is not considered, Re and Wo numbers need to be matched. We can match these two dimensionless numbers with high viscosity fluids and extended breathing cycles. According to the formula of two dimensionless numbers, not only the viscosity will increase but also the breathing cycle will be significantly prolonged. When studying particle transport and deposition, Stk, Pep, and H numbers are additionally matched, but the high viscosity coefficient of the fluid and the excessively prolonged period make it impossible for the dimensionless numbers to be matched at the same time.
3. Real-size alveolar model
The real-size models for studying alveolar flows are mostly alveolar microfluidic chips that are fabricated using microfabrication technologies. The methods for achieving contraction and expansion are the same as those used in the scale-up models, as shown in Figs. 5(a) and 5(b). While in real-size models all the non-dimensional numbers can be matched, the main drawback is that the shape of alveoli in the alveolar chip is different from the real shape, i.e., neither spherical nor polyhedral due to limitations of the currently available fabrication techniques. The cross section of the alveolar duct is a rectangle and the alveoli are partial cylinders. The sidewalls and top walls in the alveolar chip can expand and contract. The multi-generation and single-generation alveolar chips are similar to Figs. 6(d) and 6(f), respectively. The application of microfluidics for studying alveolar flows was first introduced by Fishler et al.84 They fabricated a five-generation polydimethylsiloxane-based alveolar chip using a standard soft-lithography microfabrication technique. The working fluid is a 64/36 (v/v) glycerol/water mixture, which has approximately the same kinematic viscosity as air at ∼24 °C. They measured the fluid flow field in the alveoli using micro-particle image velocimetry (μPIV). Their detailed fabrication and measurement can be found in the work of Fishler and Sznitman.97 Fishler et al.17 designed another five-generation alveolar chip with gas as the working fluid. They tracked the trajectories of aerosol particles in the alveoli. Tenenbaum-Katan et al.25 adapted the latter design and presented the corresponding flow patterns. Fishler et al.91 used a similar design to track the particle trajectories in alveoli and duct for multiple periods. Lv et al.15,98 designed an alveolar chip of a single alveolus. The model is shown in Figs. 6(e) and 6(f). Then, Dong et al.16 designed a platform based on the latter alveolar chip to track the particles for a long term in alveoli with a 36:64 (v/v) glycerol/water mixture as the working fluid under the effect of gravity and gravity directions. Subsequently, Zhang et al.86 of the same research group conducted extended research based on this particle tracking platform. They studied the transport and deposition of particles of different sizes and greatly extended the particle tracking time.
Although alveolar chips have great advantages in studying alveolar fluid flow and particle transport in real-size models and have gained increasing attention in recent years, they cannot fully reproduce the real three-dimensional structure of the alveoli and the duct. Furthermore, the expansion and contraction of the duct walls cannot be well modeled. These drawbacks need to be overcome for improving the understanding of alveolar flows. This awaits the advancement of current micro- and nano-fabrication technologies including high precision 3D printing technologies.
IV. FLUID FLOW IN ALVEOLI
A. Flow patterns in alveoli
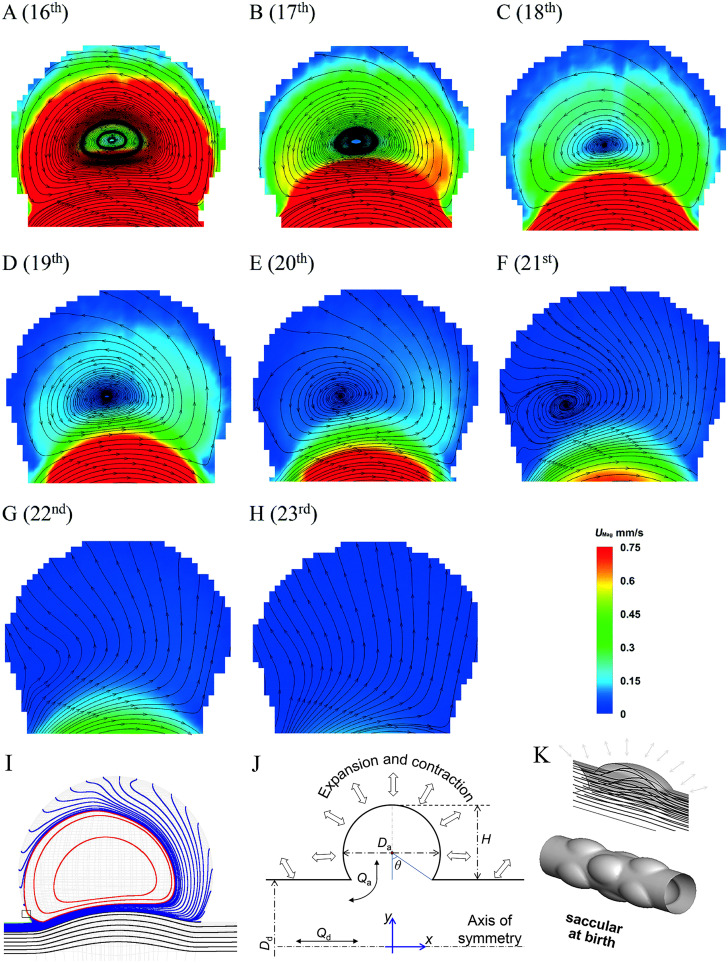
The fluid flow in pulmonary alveoli has been extensively studied over the last few decades using both numerical and experimental methods. The early studies on alveolar flow using numerical modeling were mainly based on models with rigid alveolar walls and steady fluid flow conditions.12,99,100 For example, Tsuda et al.12 simulated flows in an alveolus with a rigid alveolar wall. The model consisted of a central duct surrounded by a torus. The torus represented an alveolus. The modeling revealed a vortex with closed streamlines formed inside the alveolus. The recirculating flow inside the alveolus and the duct flow are separated by a streamline at the mouth of the alveolus and fluid elements in the duct do not enter the alveolus. The streamlines in the ductal flow slightly bulges toward the alveolar region, and as the Reynolds number increases, the depth and asymmetry become greater.56,100 Since the rigid alveolar flow with the steady flow cannot represent the transient alveolar flow, Tsuda et al.12 extended the earlier work and used the same toroidal alveolus to study the fluid flow in the alveolus with rhythmically expansible alveolar walls. The fluid flow in this alveolus differs from that in the alveolus with a rigid wall. Both recirculation flow patterns and radial flow patterns could be found, as shown in Figs. 7(a)–7(f) and Figs. 7(g) and 7(h), respectively.
FIG. 7.
Images (a)–(h) Flow patterns and velocity fields on the midplane of alveolar cavities at the 16th to 23rd generations.15 Reproduced with permission from Lv et al., Lab Chip 20(13), 2394–2402 (2020). Copyright 2020 The Royal Society of Chemistry. (i) Recirculation flow pattern with closed streamlines in vortex region (red lines).14 Reproduced with permission from Henry et al., J. Biomech. Eng. 134(12), 121001 (2012). Copyright 2012 ASME. (j) Schematic diagram of alveoli. θ is the opening half angle, H is the height of alveolar cavity, Qa is alveolar flow rate, Qd is ductal flow rate, Dd is the ductal diameter, and Da is the alveolar diameter (k) Streamlines in an alveolus at birth.45 Reproduced with permission from Semmler-Behnke et al., Proc. Natl. Acad. Sci. U.S.A. 109(13), 5092–5097 (2012). Copyright 2012 National Academy of Science.
Several studies have also confirmed both flow fields by experiments and simulations, respectively. Due to the difficulties in fabricating alveolar models, there are only limited number of experimental studies, which include the scaled-up models38,83 and alveolar chips.15,17,84 On the contrary, numerical investigations have been extensively carried out. These include studies using single alveolus,14,43,56 multiple alveoli,42,47,68,69,73 and multi-generation alveoli,44,60,61,64 respectively.
Although the existence of the two flow patterns has been extensively verified, there is still disagreement on the structure of the flow fields, that is, whether the streamlines in the vortex region of the recirculation flow pattern are closed. Haber et al.13 used an alveolus of spherical cap to directly derive the flow patterns based on the stream function. Tsuda et al.,12 Lee and Lee,56 Sznitman et al.,43 and Henry et al.14 revealed alveolar flow patterns in the single alveolus by solving unsteady Navier–Stokes equations in numerical simulations. Several simulation studies on multi-alveolar flow fields42,47,69 also revealed the flow patterns similar to single-alveolus studies. In the vortex region of the recirculation flow patterns of these studies, the streamlines are closed, indicating that there is a center point in the vortex. The vortex region with closed streamlines in the recirculation flow pattern is shown in Fig. 7(i). Henry et al.14 also presented the three-dimensional recirculation streamlines of the Russian-nesting-doll structure and three-dimensional radial streamlines in the alveoli with rhythmic expansion and contraction. In the vortex region of the recirculation flow, streamlines are spirally connected to the alveolar wall. However, in the other studies, the streamlines in the vortex region are unclosed, which formed the spiral sink/source,15,44,50,84,101 as shown in Figs. 7(a)–7(f). The difference was argued to be due to that the previous simulations by Tsuda et al.12 were based on the assumption of self-similar expansion of alveolar walls. This assumption was found be questionable. Lv et al.98 pointed out that the expansion and contraction of the alveoli did not follow self-similarity and could cause non-uniform radial perturbation to alveolar flows. As a consequence, the unstable closed streamline could become a spiral form.
The flow patterns in alveoli are mostly determined by three parameters, i.e., the alveolar to ductal flow rate β = Qa/Qd, the opening half angle θ, and the geometry of the alveoli.12,90 Figure 7(j) shows the definition of the parameters. As the β value or the θ value increases, the vortex region in the recirculation flow pattern will become smaller, and eventually, the recirculation flow pattern becomes a radial flow pattern.12,15,50,84 Currently, there are two ways to calculate the value of β. The first is that all alveoli expand and contract according to the same expansion coefficient. All length scales are proportional to a time-dependent scale, as in Tsuda et al.,12 Henry et al.,42 Sznitman et al.,43,44 Kumar et al.,69 and Henry and Tsuda.47 Dong et al.35 devised another calculation method based on the mechanism by which the alveoli expand and contract under the action of respiratory muscles. They determined the expansion coefficient and the value of β assuming that all alveoli are uniformly stressed and that the volume of inhaled air is limited. The β values obtained by the two methods are quite different, and the β values used in different literature studies are also different. However, the changes in β values within the alveoli are similar. In the lung acini, the magnitude of the β value is related to the generations in which the alveoli are located. The value of β increases from the first to the last generation of the acini.
The θ value of the alveolar cavity can vary at different ages. As the lung develops, the θ value becomes smaller. Tsuda et al.12 and Henry ad Tusda47 found that the recirculation flow pattern changes to a radial flow pattern with the increase of θ. The study by Semmler-Behnke et al.45 showed that at an earlier age the alveolar ducts are shallow saccular airways with large θ. The flow field in the alveoli is neither radial nor eddy, but a simple bulge as shown in Fig. 7(k). The study by Lv et al.15 showed that the θ value also changed with time during a respiratory cycle.
The geometry of the alveoli also dictates the flow patterns in alveoli. Hofemeier and Sznitman50 studied the flow field within three regular alveoli, i.e., spherical, polyhedral, and toroidal. Their research showed that the different shapes of alveoli had a significant effect on the velocity profile and the magnitude within the alveoli. However, it was not sufficient to change the qualitative flow patterns significantly. Sera et al.90 visualized the flow patterns measured by particle image velocimetry (PIV) in alveolated ducts based on CT images. The alveolated duct was scaled-up by 100 times from the actual alveolar sizes. The alveoli in the duct were irregular. The measured flow patterns in the alveoli were different from those in the regular alveoli. Radial flow patterns and single, double, and triple flow patterns of spiral vortex in an alveolus could be found.
B. Chaotic mixing in alveoli
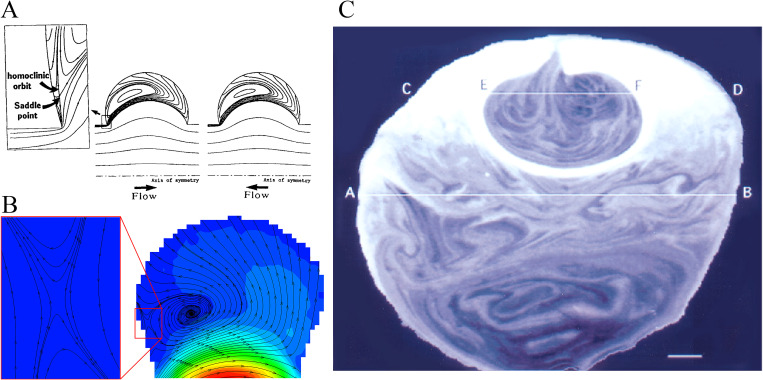
Flow mixing in the lung attracted a great deal of research attention in the last few decades due to the importance in the understanding particles/aerosols transport and deposition. The study on flow mixing in the lung dates back to 1960s, and the earlier studies were mostly on the respiratory tract.102–104 The earliest study on flow mixing in alveoli is perhaps that of Cinkotai’s.93 In this study, Cinkotai used a latex balloon model with rhythmical movement of expansion and contraction to experimentally visualize the flow patterns inside an alveolus. The fluid flow was directly injected into the alveolus, i.e., the flow direction aligned with the axis of the alveolus. He found that the flow was reversible due to the homogeneous movement of the alveolar walls and postulated that fluid mixing could occur for inhomogeneous movement in real alveoli. This area of study has been quite for nearly 20 years until the early work by Tsuda et al.12 Tsuda et al.12 found that the low Reynolds flow in alveoli with geometrically similar movement of expansion and contraction could be kinematically irreversible. This study was carried out on the basis of a numerical simulations, and, most critically, the flow was induced by a duct flow with the axis perpendicular to the axis of the alveolus (different from the setup of Cinkotai).93 The simulation revealed a stagnation saddle point near the alveolar opening [Figs. 8(a) and 8(b)], leading to a flow with chaotic characteristics, which was demonstrated by the trajectories of massless particles. In a follow-up study using rat lungs, Butler and Tsuda111 observed the mixing patterns due to the stretching and folding of convective flow patterns as shown in Fig. 8(c). The chaotic mixing was confirmed in a later study105 from flow visualization of rhythmically ventilated rat lungs and a number of investigations using numerical modelings.12–14,55,69,70
FIG. 8.
Chaotic mixing in alveoli. (a) Instantaneous flow patterns with closed streamlines.12 Reproduced with permission from Tsuda et al., J. Appl. Physiol. 79(3), 1055–1063 (1995). Copyright 1995 American Physiological Society. (b) Instantaneous flow patterns with unclosed streamlines.15 Reproduced with permission from Lv et al., Lab Chip 20(13), 2394–2402 (2020). Copyright 2020 The Royal Society of Chemistry. (c) Stretched and folded mixing pattern.111 Reproduced with permission from Butler and Tsuda, J. Appl. Physiol. 83(3), 800–809 (1997). Copyright 1997 American Physiological Society.
It should be noted that while the existence of stagnation saddle points in the alveoli was initially revealed in the numerical studies of Tsuda et al.,12 the first experimental verification was achieved by Lv et al.15 The stagnation saddle point of a homoclinic orbit near the entrance corner in the recirculation flow pattern, shown in Figs. 8(a) and 8(b),12–15 has been recognized as a sign of flow chaos since material lines could bifurcate from the saddle points.12,69 However, in addition to the stagnation saddle point caused by the special geometric expansion of the alveolar walls, kinematic irreversibility is also related to the flow asynchrony.69,106 A small flow asynchrony, i.e., phase lags between wall motion and ductal flow, could cause highly irreversible particle trajectories.101,107 It was confirmed using studies of flow visualization of tracer patterns in a T-shaped junction108 and a number of investigations using numerical modelings.69,101,107 Moreover, the radial flow in the alveoli of the distal generation could still achieve effective mixing as a result of flow asynchrony.107 The kinematic irreversibility due to saddle points and flow asynchrony is the fundamental mechanisms of chaos. The existence of flow chaos can enhance mixing and deposition in alveoli.12,13,19,109
The observed chaotic mixing phenomena can be described by stretched and folded fractal patterns, which are associated with the kinematic irreversibility.13,105,108,110 The structure is recognized as a hallmark of chaotic flow. Many studies have been published to reveal these patterns based on numerical and experimental methods.42,105,106,108,111 The rhythmically ventilated rat lungs105,106 and a T-shaped junction108 showed similar folded tracer filaments. Henry et al. also found this structure in their simulation.42 The role of this stretch-and-fold structure in chaotic mixing in the alveoli can be briefly summarized in the following way. In alveolar flows with stretch-and-fold patterns, a tracer is stretched and folded cycle by cycle. Due to the irreversibility, the trace cannot return to its initial position. The area over which diffusion can take place grows as the cycle number increases. The number of the folded tracer stripes also increases, indicating that the transverse distance between two adjacent folded tracer stripes decreases. As a result, the diffusion length can be increased, which is fast than a system without the stretch-and-fold patterns. Therefore, chaotic acinar flow with stretch-and-fold patterns is the essence of the chaotic mixing in the acini.
V. LUNG-ON-A-CHIP
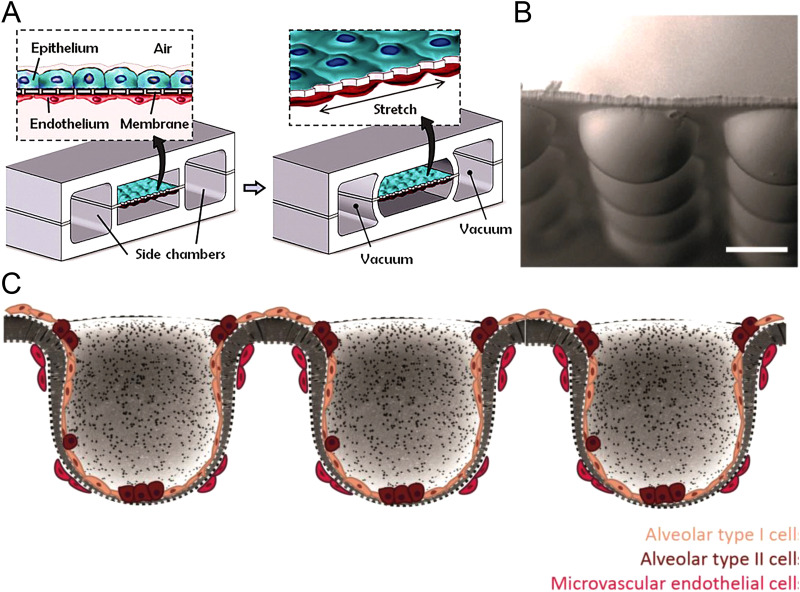
The advent of microfluidics motivated the development of lung-on-a-chip devices for studying the physiological response of tissues of alveolar cells to drugs or particles, an important step to replace animal models for drug studies. Huh et al.112 designed a lung-on-a-chip model that consisted of two channels separated by a thin porous membrane and two side pressure chambers as shown in Fig. 9(a). The membrane with alveolar epithelium and microvascular endothelium is the air–liquid interface or alveolar–capillary barrier. The air–liquid interface can be stretched to imitate alveolar expansion. This study revealed that cyclic mechanical strain accentuates toxic and inflammatory responses of the lung to silica nanoparticles. Many studies have used this design to investigate drug discovery113–116 and pathophysiology.117–119 However, the air–liquid interface in this design only represents a partial alveolar–capillary barrier. The current lung-on-chip platforms with the air–liquid interface still mostly use 2D membranes for cell growth,120 which differ significantly from the curved surfaces of 3D alveolar walls for epithelial and endothelial cells10,29,120 and thus different cell development processes.121
FIG. 9.
Two- and three-dimensional lung-on-a-chip. (a) The microfabricated lung-on-a-chip device with a two-dimensional alveolar–capillary barrier.112 Reproduced with permission from Huh et al., Science 328(5986), 1662–1668 (2010). Copyright 2010 American Association for the Advancement of Science. (b) SEM image of spherical microwells (side views; scale bars: 100 μm).120 Baptista et al., Biomaterials 266, 120436 (2021). Copyright 2021 Author(s), licensed under a Creative Commons Attribution (CC BY) license. (c) Cross-sectional view of three-dimensional alveolar–capillary interface with alveolar epithelial–endothelial/capillary barrier.120 Baptista et al., Biomaterials 266, 120436 (2021). Copyright 2021, licensed under a Creative Commons Attribution (CC BY) license.
To improve the model, Baptista et al.120 created a three-dimensional membrane using a combination of the three-dimensional micro-film (thermo)forming and ion track technology as shown in Figs. 9(b) and 9(c). The authors fabricated an array of hemispherical microwells on a planar membrane. The alveolar epithelial cell layer and microvascular endothelial cell layer successfully grew in the hemispherical alveolar surface. A similar three-dimensional membrane was fabricated by Zamprogno et al.122 by pipetting a drop of collagen-elastin solution on a scaffold that consisted of an array of hexagonal pores. This membrane could be stretched by applying negative pressure and could form the air–liquid interface. Huang et al.123 developed a lung-on-a-chip platform with a three-dimensional porous hydrogel, which was similar to the alveolar sacs and formed the air–liquid interface. Even though these models can form 3D air–liquid interfaces to mimic alveolar walls, they are still far from ideal since the dynamics of airflow and its interaction with cell walls have not been incorporated to represent the inhalation process of air and particles. As mentioned earlier, the flow fields, particle properties, and breathing patterns can all affect the deposition amount and deposition region of particles in the alveoli. The development of advanced lung-on-a-chip platform incorporating these functions still needs a breakthrough.
VI. SUMMARY AND FUTURE PROSPECTS
Understanding the dynamics of airflow in alveoli is important for understanding lung functions and the cause of many lung diseases. This paper has reviewed the current progress in the modeling of alveolar cells and methods of fluid flow simulation and the application of lung-on-a-chip devices. As discussed in this Review, great progress has been made in the understanding of alveolar flow and chaotic mixing in the alveoli. Both recirculation and radial flow patterns exist in the alveoli. The flow patterns are dictated mainly by three factors, i.e., the ratio of alveolar to ductal flow rates, the opening half angle, and the geometry of the alveoli. For alveoli with large alveolar to ductal flow rate ratios, i.e., in the last two generations of alveoli (22th and 23th), the flow is mostly of radial format. For alveoli at other generations with smaller alveolar to ductal flow rate ratios, recirculation flow patterns (i.e., vortex) dominate. The size of the vortex gradually decreases as the ratio decreases. For recirculation flow patterns, the streamlines are of the spiral format due to the non-self-similar expansion and contraction of alveolar cells during breathing. This differs from the closed format reported for cases where self-similar movements of alveolar cells are considered. There is a stagnation saddle point in the recirculation flows in alveoli from 15th to 21th generations. Saddle point and phase lags are considered to be two important factors that cause chaotic mixing in the alveoli. The underlining stretched and folded flow patterns are the key enablers of chaotic mixing in the alveoli. In addition to the fundamental studies of alveolar flows, there have been recent developments in lung-on-a-chip devices to mimic the key function of alveoli for studying the effect of nanoparticles and drugs on alveolar cells.
Although studies on alveolar flow have made impressive progress, there are still challenges to be addressed. First, current numerical and experimental studies use highly simplified and regular alveolar models and, therefore, cannot reflect the interactions between alveoli. Lungs are fully filled by alveoli and ducts in the acinar region. The expansion and contraction of alveoli are affected by the surrounding alveoli, and the deformations at the local pulmonary acinar scale are intrinsically anisotropic. These factors should be taken into account for future studies. Second, computation of fluid flows in alveoli needs to be further improved to fully reveal the chaotic flow structures. There is a lack of understanding of the three-dimensional chaotic mixing in the alveoli, such as Lagrangian coherent structures, Poincaré maps, and Lyapunov exponents. Third, current numerical modeling needs more rigorous validation using experimental data. However, the measurements of 3D alveolar flows are still limited by 2D techniques. Only the 2D snapshot of the flow patterns is currently available experimentally. The 2D alveolar flow and particle motion (e.g.., on the symmetry plane of alveoli) cannot fully present the three-dimensional phenomena. The application of 3D microflow measurement techniques (e.g., 3D microPIV, stereoscopic PIV) is imperative. Finally, better lung-on-a-chip devices are needed for biological application, e.g., the effect of flow patterns on the gas exchange in the alveoli and the effect of flow and particle on the cells on the alveolar walls. It is highly desirable to design a lung-on-a-chip device that can simulate alveolar breathing, fluid flow, and particle transport in the biological microenvironment within the three-dimensional alveoli.
ACKNOWLEDGMENTS
This research was supported by the National Natural Science Foundation of China under Grant No. 11772112 and the Science, Technology and Innovation Commission of Shenzhen Municipality under Grant No. KQJSCX20170329111827540. Y.Z. also acknowledges the financial support from HIT and Shenzhen Government via the special talent start-up programs.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
DATA AVAILABILITY
The data that support the findings of this study are available within the article.
REFERENCES
- 1.Chuang H.-C., in Oxidative Stress in Lung Diseases, edited by Chakraborti S., Chakraborti T., Das S. K., and Chattopadhyay D. (Springer, Singapore, 2019), Vol. 1, pp. 293–307. [Google Scholar]
- 2.Tsuda A., Henry F. S., and Butler J. P., Compr. Physiol. 3(4), 1437–1471 (2013). 10.1002/cphy.c100085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hogan B. and Tata P. R., “Cellular organization and biology of the respiratory system,” Nat. Cell Biol. (published online) (2019). 10.1038/s41556-019-0357-7 [DOI] [PubMed] [Google Scholar]
- 4.Kim K. H., Kabir E., and Kabir S., Environ. Int. 74, 136–143 (2015). 10.1016/j.envint.2014.10.005 [DOI] [PubMed] [Google Scholar]
- 5.Chen R., Hu B., Liu Y., Xu J. X., Yang G. S., Xu D. D., and Chen C. Y., Biochim. Biophys. Acta Gen. Subj. 1860(12), 2844–2855 (2016). 10.1016/j.bbagen.2016.03.019 [DOI] [PubMed] [Google Scholar]
- 6.WHO, see https://www.who.int/en/news-room/fact-sheets/detail/chronic-obstructive-pulmonary-disease-(copd) for WHO, Vol. 2021 (2017).
- 7.WHO, see https://www.who.int/news-room/fact-sheets/detail/asthma for WHO, Vol. 2021 (2020).
- 8.WHO, see https://www.who.int/news-room/fact-sheets/detail/cancer for WHO, Vol. 2021 (2021).
- 9.Weibel E. R., Morphometry of the Human Lung, 1st ed. (Springer-Verlag, Berlin, 1963). [Google Scholar]
- 10.Haefeli-Bleuer B. and Weibel E. R., Anat. Rec. 220(4), 401–414 (1988). 10.1002/ar.1092200410 [DOI] [PubMed] [Google Scholar]
- 11.Yang L., Feuchtinger A., Moller W., Ding Y. B., Kutschke D., Moller G., Schittny J. C., Burgstaller G., Hofmann W., Stoeger T., Razansky D., Walch A., and Schmid O., ACS Nano 13(2), 1029–1041 (2019). 10.1021/acsnano.8b07524 [DOI] [PubMed] [Google Scholar]
- 12.Tsuda A., Henry F. S., and Butler J. P., J. Appl. Physiol. 79(3), 1055–1063 (1995). 10.1152/jappl.1995.79.3.1055 [DOI] [PubMed] [Google Scholar]
- 13.Haber S., Butler J. P., Brenner H., Emanuel I., and Tsuda A., J. Fluid Mech. 405, 243–268 (2000). 10.1017/S0022112099007375 [DOI] [Google Scholar]
- 14.Henry F. S., Haber S., Haberthur D., Filipovic N., Milasinovic D., Schittny J. C., and Tsuda A., J. Biomech. Eng. 134(12), 121001 (2012). 10.1115/1.4007949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lv H., Dong J., Qiu Y., Yang Y., and Zhu Y., Lab Chip 20(13), 2394–2402 (2020). 10.1039/C9LC01273G [DOI] [PubMed] [Google Scholar]
- 16.Dong J., Qiu Y., Lv H., Yang Y., and Zhu Y., Micromachines 12(2), 184 (2021). 10.3390/mi12020184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fishler R., Hofemeier P., Etzion Y., Dubowski Y., and Sznitman J., Sci. Rep. 5, 14071 (2015). 10.1038/srep14071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Heyder J., Gebhart J., Rudolf G., Schiller C. F., and Stahlhofen W., J. Aerosol Sci. 17(5), 811–825 (1986). 10.1016/0021-8502(86)90035-2 [DOI] [Google Scholar]
- 19.Haber S., Yitzhak D., and Tsuda A., J. Appl. Physiol. 95(2), 657–671 (2003). 10.1152/japplphysiol.00770.2002 [DOI] [PubMed] [Google Scholar]
- 20.Kleinstreuer C., Zhang Z., and Donohue J. F., Annu. Rev. Biomed. Eng. 10, 195–220 (2008). 10.1146/annurev.bioeng.10.061807.160544 [DOI] [PubMed] [Google Scholar]
- 21.Tsuda A., Henry F. S., and Butler J. P., Respir. Physiol. Neurobiol. 163(1–3), 139–149 (2008). 10.1016/j.resp.2008.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hofmann W., J. Aerosol Sci. 42(10), 693–724 (2011). 10.1016/j.jaerosci.2011.05.007 [DOI] [Google Scholar]
- 23.Sznitman J., J. Biomech. 46(2), 284–298 (2013). 10.1016/j.jbiomech.2012.10.028 [DOI] [PubMed] [Google Scholar]
- 24.Phalen R. F. and Raabe O. G., J. Aerosol Sci. 99, 7–13 (2016). 10.1016/j.jaerosci.2015.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tenenbaum-Katan J., Artzy-Schnirman A., Fishler R., Korin N., and Sznitman J., Biomicrofluidics 12(4), 042209 (2018). 10.1063/1.5023034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sznitman J., “Revisiting airflow and aerosol transport phenomena in the deep lungs with microfluidics,” Chem. Rev. (published online) (2021). 10.1021/acs.chemrev.1c00621 [DOI] [PubMed] [Google Scholar]
- 27.Bajaj P., Harris J. F., Huang J. H., Nath P., and Iyer R., ACS Biomater. Sci. Eng. 2(4), 473–488 (2016). 10.1021/acsbiomaterials.5b00480 [DOI] [PubMed] [Google Scholar]
- 28.Netter F., Atlas of Human Anatomy, 6th ed. (Elsevier, Philadelphia, 2008). [Google Scholar]
- 29.Weibel E. R., Sapoval B., and Filoche M., Respir. Physiol. Neurobiol. 148(1–2), 3–21 (2005). 10.1016/j.resp.2005.03.005 [DOI] [PubMed] [Google Scholar]
- 30.Ochs M., Nyengaard L. R., Jung A., Knudsen L., Voigt M., Wahlers T., Richter J., and Gundersen H. J. G., Am. J. Respir. Crit. Care Med. 169(1), 120–124 (2004). 10.1164/rccm.200308-1107OC [DOI] [PubMed] [Google Scholar]
- 31.Burri P. H., Biol. Neonate 89(4), 313–322 (2006). 10.1159/000092868 [DOI] [PubMed] [Google Scholar]
- 32.Perlman C. E. and Bhattacharya J., J. Appl. Physiol. 103(3), 1037–1044 (2007). 10.1152/japplphysiol.00160.2007 [DOI] [PubMed] [Google Scholar]
- 33.Perlman C. E., Lederer D. J., and Bhattacharya J., Am. J. Respir. Cell Mol. Biol. 44(1), 34–39 (2011). 10.1165/rcmb.2009-0005OC [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Westphalen K., Gusarova G. A., Islam M. N., Subramanian M., Cohen T. S., Prince A. S., and Bhattacharya J., Nature 506(7489), 503 (2014). 10.1038/nature12902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dong J., Yang Y., and Zhu Y. G., Microfluid. Nanofluid. 24(9), 1 (2020). 10.1007/s10404-020-02377-9 [DOI] [Google Scholar]
- 36.Chanson H., in Hydraulics of Open Channel Flow, 2nd ed., edited by Chanson H. (Butterworth-Heinemann, Oxford, 2004), pp. 253–274. [Google Scholar]
- 37.Anjilvel S. and Asgharian B., Fundam. Appl. Toxicol. 28(1), 41–50 (1995). 10.1006/faat.1995.1144 [DOI] [PubMed] [Google Scholar]
- 38.Chhabra S. and Prasad A. K., J. Fluids Eng. 133(7), 071001 (2011). 10.1115/1.4004362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Imai Y., Miki T., Ishikawa T., Aoki T., and Yamaguchi T., J. Biomech. 45(10), 1809–1815 (2012). 10.1016/j.jbiomech.2012.04.017 [DOI] [PubMed] [Google Scholar]
- 40.Ma B. S. and Darquenne C., J. Appl. Physiol. 113(3), 442–450 (2012). 10.1152/japplphysiol.01549.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Finlay W. H., The Mechanics of Inhaled Pharmaceutical Aerosols (Academic Press, London, 2001). [Google Scholar]
- 42.Henry F. S., Butler J. P., and Tsuda A., J. Appl. Physiol. 92(2), 835–845 (2002). 10.1152/japplphysiol.00385.2001 [DOI] [PubMed] [Google Scholar]
- 43.Sznitman J., Heimsch F., Heimsch T., Rusch D., and Rosgen T., J. Biomech. Eng. 129(5), 658–665 (2007). 10.1115/1.2768109 [DOI] [PubMed] [Google Scholar]
- 44.Sznitman J., Heimsch T., Wildhaber J. H., Tsuda A., and Rosgen T., J. Biomech. Eng. 131(3), 031010 (2009). 10.1115/1.3049481 [DOI] [PubMed] [Google Scholar]
- 45.Semmler-Behnke M., Kreyling W. G., Schulz H., Takenaka S., Butler J. P., Henry F. S., and Tsuda A., Proc. Natl. Acad. Sci. U.S.A. 109(13), 5092–5097 (2012). 10.1073/pnas.1119339109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hofemeier P. and Sznitman J., J. Appl. Physiol. 118(11), 1375–1385 (2015). 10.1152/japplphysiol.01117.2014 [DOI] [PubMed] [Google Scholar]
- 47.Henry F. S. and Tsuda A., J. Appl. Physiol. 120(1), 38–54 (2016). 10.1152/japplphysiol.01161.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dailey H. L. and Ghadiali S. N., J. Aerosol Sci. 38(3), 269–288 (2007). 10.1016/j.jaerosci.2007.01.001 [DOI] [Google Scholar]
- 49.Chen L. and Zhao X., PLoS ONE 14(3), e0214441 (2019). 10.1371/journal.pone.0214441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hofemeier P. and Sznitman J., J. Biomech. Eng. 136(6), 061007 (2014). 10.1115/1.4027328 [DOI] [PubMed] [Google Scholar]
- 51.Koshiyama K. and Wada S., Comput. Biol. Med. 62, 25–32 (2015). 10.1016/j.compbiomed.2015.03.032 [DOI] [PubMed] [Google Scholar]
- 52.Kizhakke Puliyakote A. S., Vasilescu D. M., Newell J. D., Wang G., Weibel E. R., and Hoffman E. A., J. Appl. Physiol. 121(1), 115–122 (2016). 10.1152/japplphysiol.00317.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Koshiyama K., Nishimoto K., Ii S., Sera T., and Wada S., Clin. Biomech. 66, 32–39 (2019). 10.1016/j.clinbiomech.2018.01.001 [DOI] [PubMed] [Google Scholar]
- 54.Haber S. and Tsuda A., J. Aerosol. Sci. 29(3), 309–322 (1998). 10.1016/S0021-8502(97)00451-5 [DOI] [Google Scholar]
- 55.Haber S. and Tsuda A., J. Fluid Mech. 567, 157–184 (2006). 10.1017/S0022112006002345 [DOI] [Google Scholar]
- 56.Lee D. Y. and Lee J. W., J. Aerosol Sci. 34(9), 1193–1215 (2003). 10.1016/S0021-8502(03)00097-1 [DOI] [Google Scholar]
- 57.Harding E. M. and Robinson R. J., Inhalation Toxicol. 22(8), 669–678 (2010). 10.3109/08958371003749939 [DOI] [PubMed] [Google Scholar]
- 58.Ma B. S. and Darquenne C., J. Appl. Physiol. 110(5), 1271–1282 (2011). 10.1152/japplphysiol.00735.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kolanjiyil A. V. and Kleinstreuer C., J. Biomech. Eng. 135(12), 121003 (2013). 10.1115/1.4025332 [DOI] [PubMed] [Google Scholar]
- 60.Kolanjiyil A. V. and Kleinstreuer C., J. Aerosol Sci. 114, 301–316 (2017). 10.1016/j.jaerosci.2017.10.001 [DOI] [Google Scholar]
- 61.Kolanjiyil A. V. and Kleinstreuer C., Comput. Math. Method Med. 2019, 1–13 (2019). 10.1155/2019/5952941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Fung Y. C., J. Appl. Physiol. 64(5), 2132–2141 (1988). 10.1152/jappl.1988.64.5.2132 [DOI] [PubMed] [Google Scholar]
- 63.Denny E. and Schroter R. C., J. Biomech. Eng. 118(2), 210–215 (1996). 10.1115/1.2795961 [DOI] [PubMed] [Google Scholar]
- 64.Sznitman J., Schmuki S., Sutter R., Tsuda A., and Rosgen T., WIT Tr. Biomed. Health 12, 147 (2007). 10.2495/BIO070151 [DOI] [Google Scholar]
- 65.Khajeh-Hosseini-Dalasm N. and Longest P. W., J. Aerosol Sci. 79, 15–30 (2015). 10.1016/j.jaerosci.2014.09.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ostrovski Y., Hofemeier P., and Sznitman J., Int. J. Nanomed. 11, 3385–3395 (2016). 10.2147/IJN.S102138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Oakes J. M., Hofemeier P., Vignon-Clementel I. E., and Sznitman J., J. Biomech. 49(11), 2213–2220 (2016). 10.1016/j.jbiomech.2015.11.026 [DOI] [PubMed] [Google Scholar]
- 68.Kumar H., Tawhai M. H., Hoffman E. A., and Lin C.-L., J. Biomech. 42(11), 1635–1642 (2009). 10.1016/j.jbiomech.2009.04.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kumar H., Tawhai M. H., Hoffman E. A., and Lin C.-L., Phys. Fluids 23(4), 041902 (2011). 10.1063/1.3567066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Henry F. S., Laine-Pearson F. E., and Tsuda A., J. Biomech. Eng. 131(1), 011006 (2009). 10.1115/1.2953559 [DOI] [PubMed] [Google Scholar]
- 71.Henry F. S. and Tsuda A., J. Biomech. Eng. 132(10), 101001 (2010). 10.1115/1.4002371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Darquenne C. and Paiva N., J. Appl. Physiol. 80(4), 1401–1414 (1996). 10.1152/jappl.1996.80.4.1401 [DOI] [PubMed] [Google Scholar]
- 73.Darquenne C., Harrington L., and Prisk G. K., Philos. Trans. R. Soc. London A 367(1896), 2333–2346 (2009). 10.1098/rsta.2008.0295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Ciloglu D., Athari H., Bolukbasi A., and Rosen M. A., Appl. Sci. 7(2), 113 (2017). 10.3390/app7020113 [DOI] [Google Scholar]
- 75.Ciloglu D., Sadhana Acad. Proc. Eng. Sci. 46(4), 186 (2021). 10.1007/s12046-021-01704-2 [DOI] [Google Scholar]
- 76.Harrington L., Kim Prisk G., and Darquenne C., J. Aerosol. Sci. 37(1), 37–62 (2006). 10.1016/j.jaerosci.2005.03.005 [DOI] [Google Scholar]
- 77.Hofemeier P., Koshiyama K., Wada S., and Sznitman J., Eur. J. Pharm. Sci. 113, 53–63 (2018). 10.1016/j.ejps.2017.09.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Shachar-Berman L., Ostrovski Y., Koshiyama K., Wada S., Kassinos S. C., and Sznitman J., Eur. J. Pharm. Sci. 137, 105003 (2019). 10.1016/j.ejps.2019.105003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Koullapis P., Ollson B., Kassinos S. C., and Sznitman J., Curr. Opin. Biomed. Eng. 11, 130–136 (2019). 10.1016/j.cobme.2019.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Koullapis P. G., Stylianou F. S., Sznitman J., Olsson B., and Kassinos S. C., J. Aerosol Sci. 144, 105541 (2020). 10.1016/j.jaerosci.2020.105541 [DOI] [Google Scholar]
- 81.Zhao J. A., Feng Y., Koshiyama K., and Wu H. M., Phys. Fluids 33(10), 101906 (2021). 10.1063/5.0065309 [DOI] [Google Scholar]
- 82.Williams J., Kolehmainen J., Cunningham S., Ozel A., and Wolfram U., Int. J. Pharm. 612, 121321 (2022). 10.1016/j.ijpharm.2021.121321 [DOI] [PubMed] [Google Scholar]
- 83.Berg E. J., Weisman J. L., Oldham M. J., and Robinson R. J., J. Biomech. 43(6), 1039–1047 (2010). 10.1016/j.jbiomech.2009.12.019 [DOI] [PubMed] [Google Scholar]
- 84.Fishler R., Mulligan M. K., and Sznitman J., J. Biomech. 46(16), 2817–2823 (2013). 10.1016/j.jbiomech.2013.08.020 [DOI] [PubMed] [Google Scholar]
- 85.Tippe A. and Tsuda A., J. Aerosol Sci. 31(8), 979–986 (2000). 10.1016/S0021-8502(99)00572-8 [DOI] [Google Scholar]
- 86.Zhang W., Dong J., Lv H., Bai W., Lu H., Noack B. R., Zhu Y., and Yang Y., Micromachines 13(3), 485 (2022). 10.3390/mi13030485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.van Ertbruggen C., Corieri P., Theunissen R., Riethmuller M. L., and Darquenne C., J. Biomech. 41(2), 399–405 (2008). 10.1016/j.jbiomech.2007.08.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Oakes J. M., Day S., Weinstein S. J., and Robinson R. J., J. Biomech. Eng. 132(2), 021008 (2010). 10.1115/1.4000870 [DOI] [PubMed] [Google Scholar]
- 89.Berg E. J. and Robinson R. J., J. Biomech. Eng. 133(6), 061004 (2011). 10.1115/1.4004251 [DOI] [PubMed] [Google Scholar]
- 90.Sera T., Kamiya N., Fukushima T., and Tanaka G., J. Biomech. Eng. 143(7), 074501 (2021). 10.1115/1.4050285 [DOI] [PubMed] [Google Scholar]
- 91.Fishler R., Ostrovski Y., Lu C. Y., and Sznitman J., J. Biomech. 50, 222–227 (2017). 10.1016/j.jbiomech.2016.11.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Ma B. S., Ruwet V., Corieri P., Theunissen R., Riethmuller M., and Darquenne C., J. Aerosol Sci. 40(5), 403–414 (2009). 10.1016/j.jaerosci.2009.01.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Cinkotai F. F., J. Appl. Physiol. 37(2), 249–251 (1974). 10.1152/jappl.1974.37.2.249 [DOI] [PubMed] [Google Scholar]
- 94.Chhabra S. and Prasad A. K., J. Biomech. Eng. 132, 051009 (2010). 10.1115/1.4001112 [DOI] [PubMed] [Google Scholar]
- 95.Chhabra S. and Prasad A. K., J. Biomech. Eng. 132(5), 051010 (2010). 10.1115/1.4001113 [DOI] [PubMed] [Google Scholar]
- 96.Li R., Xu X.-X., Qiao Y., and Zhao X.-G., J. Med. Biol. Eng. 39(4), 470–479 (2019). 10.1007/s40846-018-0419-5 [DOI] [Google Scholar]
- 97.Fishler R. and Sznitman J., J. Visualized Exp. 111, e53588 (2016). 10.3791/53588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Lv H. M., Dong J., Yang Y., and Zhu Y. G., Lab Chip 21(8), 1431–1432 (2021). 10.1039/D0LC01271H [DOI] [PubMed] [Google Scholar]
- 99.Federspiel W. J. and Fredberg J. J., J. Appl. Physiol. 64(6), 2614–2621 (1988). 10.1152/jappl.1988.64.6.2614 [DOI] [PubMed] [Google Scholar]
- 100.Tsuda A., Butler J. P., and Fredberg J. J., J. Appl. Physiol. 76(6), 2497–2509 (1994). 10.1152/jappl.1994.76.6.2497 [DOI] [PubMed] [Google Scholar]
- 101.Hofemeier P., Fishler R., and Sznitman J., Fluid Dyn. Res. 46(4), 041407 (2014). 10.1088/0169-5983/46/4/041407 [DOI] [Google Scholar]
- 102.Schroter R. C. and Sudlow M. F., Respir. Physiol. 7(3), 341–355 (1969). 10.1016/0034-5687(69)90018-8 [DOI] [PubMed] [Google Scholar]
- 103.Heyder J., Blanchard J. D., Feldman H. A., and Brain J. D., J. Appl. Physiol. 64(3), 1273–1278 (1988). 10.1152/jappl.1988.64.3.1273 [DOI] [PubMed] [Google Scholar]
- 104.Balashazy I., Heistracher T., and Hofmann W., J. Aerosol Med. 9(3), 287–301 (1996). 10.1089/jam.1996.9.287 [DOI] [Google Scholar]
- 105.Tsuda A., Rogers R. A., Hydon P. E., and Butler J. P., Proc. Natl. Acad. Sci. U.S.A. 99(15), 10173–10178 (2002). 10.1073/pnas.102318299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Butler J. P. and Tsuda A., Respir. Physiol. Neurobiol. 148(1–2), 195–206 (2005). 10.1016/j.resp.2005.06.001 [DOI] [PubMed] [Google Scholar]
- 107.Laine-Pearson F. E. and Hydon P. E., Eur. J. Mech. B Fluids 29(4), 278–284 (2010). 10.1016/j.euromechflu.2010.03.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Tsuda A., Otani Y., and Butler J. P., J. Appl. Physiol. 86(3), 977–984 (1999). 10.1152/jappl.1999.86.3.977 [DOI] [PubMed] [Google Scholar]
- 109.Haber S., Yitzhak D., and Tsuda A., J. Aerosol Med. Pulm. Drug Deliv. 23(6), 405–413 (2010). 10.1089/jamp.2009.0774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Metcalfe G., “World scientific lecture notes in complex systems,” in Complex Physical Biophysical and Econophysical Systems: Proceedings 22nd Canberra International Physics Summer School, edited by Dewar R. L. and Detering F. (World Scientific Publishing Co. Pte. Ltd., 2008), pp. 187–239. [Google Scholar]
- 111.Butler J. P. and Tsuda A., J. Appl. Physiol. 83(3), 800–809 (1997). 10.1152/jappl.1997.83.3.800 [DOI] [PubMed] [Google Scholar]
- 112.Huh D., Matthews B. D., Mammoto A., Montoya-Zavala M., Hsin H. Y., and Ingber D. E., Science 328(5986), 1662–1668 (2010). 10.1126/science.1188302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Service R. F., Science 338(6108), 731 (2012). 10.1126/science.338.6108.731 [DOI] [PubMed] [Google Scholar]
- 114.Barros A. S., Costa A., and Sarmento B., Adv. Drug Delivery Rev. 170, 386–395 (2021). 10.1016/j.addr.2020.09.008 [DOI] [PubMed] [Google Scholar]
- 115.Yang X. Y., Li K. Y., Zhang X., Liu C., Guo B. K., Wen W. J., and Gao X. H., Lab Chip 18(3), 486–495 (2018). 10.1039/C7LC01224A [DOI] [PubMed] [Google Scholar]
- 116.Esch E. W., Bahinski A., and Huh D., Nat. Rev. Drug Discovery 14(4), 248–260 (2015). 10.1038/nrd4539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Jain A., Barrile R., van der Meer A. D., Mammoto A., Mammoto T., De Ceunynck K., Aisiku O., Otieno M. A., Louden C. S., Hamilton G. A., Flaumenhaft R., and Ingber D., Clin. Pharmacol. Ther. 103(2), 332–340 (2018). 10.1002/cpt.742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Humayun M., Chow C.-W., and Young E. W. K., Lab Chip 18(9), 1298–1309 (2018). 10.1039/c7lc01357d [DOI] [PubMed] [Google Scholar]
- 119.Ingber D. E., Cell 164(6), 1105–1109 (2016). 10.1016/j.cell.2016.02.049 [DOI] [PubMed] [Google Scholar]
- 120.Baptista D., Teixeira L. M., Birgani Z. T., van Riet S., Pasman T., Poot A., Stamatialis D., Rottier R. J., Hiemstra P. S., Habibovic P., van Blitterswijk C., Giselbrecht S., and Truckenmuller R., Biomaterials 266, 120436 (2021). 10.1016/j.biomaterials.2020.120436 [DOI] [PubMed] [Google Scholar]
- 121.Duval K., Grover H., Han L. H., Mou Y., Pegoraro A. F., Fredberg J., and Chen Z., Physiology 32(4), 266–277 (2017). 10.1152/physiol.00036.2016 [DOI] [PMC free article] [PubMed] [Google Scholar] [Research Misconduct Found]
- 122.Zamprogno P., Wuthrich S., Achenbach S., Thoma G., Stucki J. D., Hobi N., Schneider-Daum N., Lehr C. M., Huwer H., Geiser T., Schmid R. A., and Guenat O. T., Commun. Biol. 4(1), 1 (2021). 10.1038/s42003-021-01695-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Huang D., Liu T., Liao J., Maharjan S., Xie X., Pérez M., Anaya I., Wang S., Tirado Mayer A., Kang Z., Kong W., Mainardi V. L., Garciamendez-Mijares C. E., García Martínez G., Moretti M., Zhang W., Gu Z., Ghaemmaghami A. M., and Zhang Y. S., Proc. Natl. Acad. Sci. U.S.A. 118(19), e2016146118 (2021). 10.1073/pnas.2016146118 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available within the article.