A novel method for carbon emission forecasting based on EKC hypothesis and nonlinear multivariate grey model: evidence from transportation sector

Abstract

Greenhouse gas emissions have brought a serious challenge to the global environment and climate. Efficient and accurate prediction of carbon emissions is essential for the decision-making sectors to control growth and formulate policies. Firstly, considering the economic, demographic, and energy factors, a novel nonlinear multivariate grey model (ENGM(1,4)) based on environmental Kuznets curve (EKC) is proposed with respect to the data characteristics of the incomplete information of carbon emission of transportation sector. The model integrates the IPAT (“Influence = Population, Affluence, Technology”) equation and the extended atochastic impacts by regression on population, affluence, and technology model (STIRPAT). Secondly, the derivation method is used to solve the time response equation of the model and the quantum particle swarm optimization algorithm (QPSO) is designed to optimize the model parameters. Then, 18 years of carbon emission data from China, the USA, and Japan are selected as the validation set. Comparative analysis indicates that the prediction accuracy of the statistical models and the intelligent models depends on sufficient samples and complex variables, and has certain limitations in limited sample prediction. The calculation results show that the new model outperforms other models in various evaluation indicators, indicating that its prediction accuracy is higher. Finally, the projections show that in 2019–2025, the average increase in carbon emissions from the transport sector in China and the USA was 2.837% and 2.394%, respectively, while Japan shows a downward trend with an average decline rate of 1.2231%. The analyzed prediction results are consistent with current situation of the three countries and the transport sectors, demonstrating the high accuracy and reliability of the new model.

Introduction

This section is divided into two parts: the “Background and significance of the study” section explains the background and importance of this study in the light of the current international environmental situation and carbon emissions data. The “Motivation” section analyzes the current approaches to carbon emissions research and summarizes the advantages and disadvantages of each type of approach, explaining the motivation for this paper.

Background and significance of the study

Carbon dioxide emissions are a major contributor to the global greenhouse effect. There are studies showing that two-thirds of greenhouse gases come from the combustion of fossil fuels (Wu et al. 2015). Excessive carbon emissions will have a huge negative impact on the global ecological environment, economic development, and human life (Zhou et al. 2021; Rao and Yan 2020). The need to reduce energy production and carbon emissions in various industries has attracted growing attention from an increasing number of countries around the world (Saidi and Omri 2020). With the continuous acceleration of industrialization and urbanization, the demand for convenient transportation and freight transportation in modern society continues to increase. Therefore, the energy consumption of the transportation sector is also increasing, becoming one of the industries with high carbon emissions (Li et al. 2021; Wang et al. 2022). Carbon emissions from the transportation sector are one of the major contributors to greenhouse gases. Data from the International Energy Agency (IEA) indicate that carbon emissions from the transportation sector have accounted for nearly 30% of the total carbon emissions (IEA 2021), and this proportion will gradually increase. In recent years, carbon emissions from the transportation has become a major concern for countries and related sectors in recent years (Tian et al. 2018), and energy conservation and emission reduction in the transportation sector will become the top priority of low-carbon city construction (Agbulut 2022). Therefore, it is crucial to analyze the factors influencing carbon emissions and adopt a scientific method to predict future carbon emissions efficiently and accurately. It can provide an important reference for the formulation of government energy saving and emission reduction measures, and the accuracy of the prediction results is of great significance to the concretization and refinement of government environmental protection policies (Sevgül and Agbulut 2021). Based on the forecast results, the government and relevant decision-making departments can anticipate and grasp the development trend of carbon emissions in advance, so as to reasonably optimize the transport structure to reduce energy consumption and formulate targeted carbon emission strategies to achieve sustainable development, which plays a key role in achieving the goal of “carbon neutrality” and “carbon peaking” as early as possible.

Motivation

Current carbon emission research methods can be roughly divided into three categories: statistical analysis models, intelligent prediction models, and grey prediction models, which mostly forecast carbon emissions according to time series. The prediction effect and accuracy of the first two types of models usually depend on sufficient samples and complex variables, and they have the disadvantage of low robustness. Firstly, the current international energy structure is changing rapidly, the reliability of short-term carbon emission forecasting with long data spans is low, and the phased carbon emission data are mostly limited samples with dispersion and uncertainty. The grey model is proven to have high accuracy and validity in such data forecasting. Secondly, in view of the characteristic that carbon emissions are also influenced by economic, demographic, and energy use, the EKC hypothesis is widely used in studying the influencing factors of carbon emissions (Bilgili et al. 2016; Bibi and Jamil 2021; Bilgili et al. 2022a). In summary, considering the characteristics of carbon emission data and many influencing factors, statistical analysis models usually cannot adapt to the complex and changeable research background due to their simple structure, and the prediction accuracy is not stable enough due to the influence of the sample size. Although nonlinear intelligent prediction models have high prediction performance, they often have defects such as over-fitting, falling into local optima, and poor generalization ability, and show certain limitations in limited sample prediction based on the research background of this paper (Xiao et al. 2021; Gao et al. 2022). Therefore, apart from the characteristics of carbon emission data, various influencing factors must be considered. A short-term prediction model based on the EKC hypothesis, which is consistent with the intrinsic mechanism of carbon emission change, should be established. The model parameters should be optimized by using intelligent algorithms so as to improve the accuracy of the model, which is also the focus of this study.

Next, this paper reviews the common methods of carbon emission prediction and related research status.

Literature review

In recent years, due to the pressure of global energy conservation, emission reduction, and environmental protection, countries have strengthened their research on carbon emissions. In this section, by reviewing relevant literature and combining the research background of this paper, the main research methods are determined: Based on the EKC assumption, a multivariate grey model is established to study the relationship between carbon emissions and other influencing factors and to predict carbon emissions. This section is divided into four parts: the “Research progress on carbon emission forecasting” section introduces the relevant methods and research progress of carbon emission prediction in recent years. The “Grey prediction model” section mainly introduces the application of grey prediction model in carbon emission. The “Theories related to the factors in fluencing carbon emissions” section introduces the theoretical research progress of carbon emission influencing factors. The “Contribution and organization” section introduces the research contribution of this paper and the organization of the whole text.

Research progress on carbon emission forecasting

The three types of methods commonly used for carbon emission prediction are summarized in Table 1, namely statistical analysis models, intelligent forecasting models, and grey forecasting models. In aspects of statistical analysis models, Yin et al. (2017) first calculated the carbon dioxide content in flue gas using fuel characteristic coefficients and then predicted carbon emissions in Guangdong Province using a multiple linear regression model. Fang et al. (2018) proposed an improved Gaussian regression method based on the hyper parameters of covariance function in the Gaussian processes regression for predicting carbon emissions in China, the USA, and Japan. Sutthichaimethee and Ariyasajjakorn (2018) developed the integrated moving average with explanatory variables (ARIMAX) model for carbon emission projections in the industrial sector in Thailand. Hosseini et al. (2019) used time series-based multiple linear regression (MLR) and polynomial regression (MPR) to predict Iran’s carbon emissions from 2017 to 2030. The biggest shortcoming of the statistical model is that it requires sufficient sample input to accurately estimate the model parameters and requires a high level of raw data (Pao et al. 2012). In aspects of intelligent predictive models, Sun et al. (2017) used the particle swarm optimization (PSO) algorithm to optimize the extreme learning machine and used it to predict the carbon emissions of Hebei Province, China. Wen and Cao (2020) optimized the parameters in a support vector machine model through an improved chicken swarm optimization (ICSO) algorithm and used this improved model in a study of residential energy-related carbon emission prediction in China. Qiao et al. (2020) first optimized the traditional least squares support vector machine model using the lion swarm optimization algorithm and genetic algorithm, and then applied the improved model to the carbon emissions of China, Japan, and South Africa for the period 2018–2025. Leerbeck et al. (2020) adopted a novel machine learning algorithm to predict the CO₂ emission intensities of the European grid. Wen and Yuan (2020) combined random forest, particle swarm optimization algorithm and BP neural network to establish a hybrid forecasting model to predict the carbon emissions of China’s commercial sector. Ren and Long (2021) combined fast learning network (FLN) and chicken swarm optimization algorithm (CSO) to predict the carbon emissions of Guangdong Province in the next 40 years based on energy, cement, technology, and forest carbon emissions data. The above two types of models selected appropriate single or hybrid models from different perspectives to effectively study and predict carbon emissions, which have achieved better results and provided new ideas for carbon emission prediction. The disadvantage is that these two types of models require large sample input in practical applications. Moreover, the prediction results depend on complex parameters and variables, and the robustness is insufficient. The next section will focus on the characteristics and applications of grey prediction models in carbon emissions.

Table 1.

Summary of the literature on forecasting models

Author	Model type	Model	Application
Yin et al. (2017)	Statistical analysis model	Multiple linear regression analysis	China’s CO2 emissions
Fang et al. (2018)	Statistical analysis model	Improved Gaussian processes regression method	China, the USA, and Japan’s CO2 emissions
Sutthichaimethee and Ariyasajjakorn (2018)	Statistical analysis model	ARIMAX model	Industrial CO2 emissions in Thailand
Hosseini et al.(2019)	Statistical analysis model	Time series model based on MLP and MPR	Iran’s CO2 emissions
Sun et al. (2017)	Nonlinear intelligent model	PSO-ELM model	CO2 emissions in Hubei, China
Wen and Cao (2020)	Nonlinear intelligent model	SVM based on ICSO algorithm	Residential energy related CO2 emissions
Qiao et al. (2020)	Nonlinear intelligent model	Improved lion swarm optimizer	CO2 emissions from 14 countries
Leerbeck et al. (2020)	Nonlinear intelligent model	A novel machine learning	CO2 emission intensity in power grids
Wen and Yuan (2020)	Nonlinear intelligent model	Neural network based on random forest and PSO	CO2 emissions in Chinas commercial department
Ren and Long (2021)	Nonlinear intelligent model	FLN and CSO algorithm	CO2 emissions of Guangdong, China
Ding et al. (2020)	Grey forecasting method	A novel DGPM(1, N) model	Chinese energy-related CO2 emissions
Zhou et al. (2021)	Grey forecasting method	A novel grey rolling GRPM(1,1) model	China’s CO2 emissions
Gao et al. (2021)	Grey forecasting method	FAGGM(1,1) model	American industrial sector’s CO2 emissions
Guo et al. (2021)	Grey forecasting method	Exponential cumulative grey model	BRICS countries’ CO2 emissions
Ofosu-Adarkwa et al. (2020)	Grey forecasting method	Hybrid Verhulst-GM(1,N) model	CO2 emissions of China’s cement industry
Xie et al. (2021)	Grey forecasting method	RWGM(1,N) model based on LASSO regression	CO2 emissions in European
Duan et al. (2020)	Grey forecasting method	GMC(1,N) model	CO2 emissions of Chongqing, China
Ye et al. (2021)	Grey forecasting method	A time-delay multivariate ATGM (1, N) model	CO2 emissions from China’s transportation sectors
Cao et al. (2021)	Grey forecasting method	TIGM(1, N) model	CO2 emissions from Chinese marine fleets

Grey prediction model

At present, the international ecological environment is changing rapidly. The significant changes that have occurred and are occurring in the global energy structure, which make carbon emissions show distinct development trends at different stages. On the one hand, this characteristic makes the prediction based on historical data spanning too long a time less reliable (Wang et al. 2020). On the other hand, in practical applications, carbon emission data series are usually in years, possessing discreteness and uncertainty. Therefore, a grey model that shows high accuracy and effectiveness for incomplete information and sparse sample prediction is considered (Deng 1982; Xie and Liu 2009). A dataset with few samples is chosen to train the model and then perform short-term prediction. In terms of univariate grey prediction models, Ding et al. (2020) designed a new discrete grey prediction model (DGPM(1,N)) to predict China’s carbon emissions from 2016 to 2020. Zhou et al. (2021) proposed a novel rolling grey prediction model (GRPM(1,1)) to dynamically predict carbon emissions in China. Gao et al. (2021) developed a new fractional order cumulative grey model (FAGGM(1,1)) based on the Gompertz differential equation for the study of carbon emissions in the USA. Guo et al. (2021) constructed an exponential-order cumulative grey model (ECGM(1,1)) to predict the carbon emissions of BRICS (Brazil, Russia, India, China, South Africa) countries, and adjusted the weight of information by adjusting the size of the parameters. In terms of multivariate grey prediction models, Ofosu-Adarkwa et al. (2020) used a hybrid Verhulst-GM(1,N) model to predict carbon emissions in China’s cement industry. Xie et al. (2021) used a novel robust reweighted multivariate grey model (RWGM(1,N)) to study the European carbon emissions forecast. Duan et al. (2020) developed a new multi-kernel nonlinear multivariate grey model with convolution integral (GMC(1,N)) based on a Gaussian vector basis kernel function and a global polynomial kernel function to predict Chongqing’s carbon emissions from 2016 to 2020. Ye et al. (2021) developed an accumulative time-delay multivariate grey model (ATGM(1,N)) for predicting carbon emissions in the transportation sector in China and demonstrated that the model predicts better than other comparative models. Cao et al. (2021) developed a multivariate trend interaction grey model (TIGM(1,N)) for carbon emission prediction, taking into account the inherent trends of carbon emissions in the context of the marine fleet and the interaction between its influencing factors. The above grey model optimizes and improves the traditional grey model from different perspectives, which is well adapted to the carbon emission data characteristics. In addition to the choice of an appropriate prediction model, adequate consideration of the factors influencing carbon emissions also occupies an important place in carbon emissions research. Next, the theoretical research progress on the influencing factors of carbon emissions will be introduced.

Theories related to the factors influencing carbon emissions

With the global energy restructuring in recent years, factors such as economic development, population migration, and energy use have influenced carbon emissions. In practical applications, apart from considering characteristics of carbon emission data, the influence of various complex factors should be integrated. A prediction model that conforms to the inherent development law of carbon emissions should be established. In the study of the factors influencing carbon emissions, economist Kuznets proposed the environmental Kuznets curve (EKC) in 1955 that can be used to reflect the relationship between environmental and economic variables (Kuznets 1995). Grossman and Krueger proposed the EKC theory in 1991 (Grossman and Krueger 1991), which specifically explores the relationship between carbon emissions and GDP. They validated this theory in 1995 through different environmental indicators (Grossman and Krueger 1995). The EKC curve reflects the impact of GDP on carbon emissions to a certain extent by revealing the inverted “U”-shaped relationship between economic development and environmental change (Bilgili et al. 2021b, a, 2022a, b). The EKC-related theory is then widely used in carbon emission studies. Dong et al. (2018) used the EKC theory to explore the dynamic causal relationship between per capita carbon emissions, per capita GDP, and per capita fossil fuel consumption in China. Brown et al. (2020) studied the relationship between carbon emissions and investor remittances in Jamaica using a modified asymmetric EKC. Bilgili et al. (2021b) established the EKC model through quantile simulation, and studied the relationship between environmental pollution and energy research and development in 13 developed countries. There are many other studies of this type (Aslam et al. 2021; Kharbach and Chfadi 2017; Altıntaş and Kassouri 2020; Ali et al. 2017). Based on the related research on the EKC, American ecologists Ehrlich and Holden proposed the IPAT equation in the 1970s (Ehrlich and Holdren 1970), which is widely used to study the relationship between the environment (carbon emissions) and the economy, population, and technology (Chontanawat 2018; Wang et al. 2011). However, the single-factor variation characteristic of IPAT cannot adapt to the complex social environment (Lin et al. 2017). To overcome this shortcoming, York et al. (2003) improved it to obtain the extended STIRPAT model, which converted the original IPAT equation into exponential form and enhanced the flexibility of the model. Subsequently, many scholars used the STIRPAT model in carbon emission studies (Wang et al. 2017; Liu and Xiao 2018; Zhang and Zhao 2019). The above model studies the influence of economic, energy, and population factors on carbon emissions. The above models analyze the implications of factors such as economy, energy, and population on carbon emissions, and explain the internal mechanism of carbon emissions changes. These models can make predictions under the premise of comprehensively considering various influencing factors, with high reliability and prediction accuracy.

In this study, starting from the characteristics of carbon emission data and internal development law and considering that carbon emission is influenced by various factors such as economy, population, and energy use, the population factor in the IPAT equation and the extended STIRPAT model is introduced. A new nonlinear multivariate grey model (ENGM(1,N)) based on the assumption of EKC hypothesis is constructed. The new model is a coupling of multiple methods with multiple features that can predict carbon emissions with high accuracy and flexibility. It considers complex influencing factors, which provides new ideas and methods for short-term prediction of carbon emissions. Definitions of abbreviations appearing in the text are listed in Table 2.

Table 2.

Definition of abbreviations

Abbreviation
EKC	Environmental Kuznets curve
IPAT	Influence = population, affluence, technology
STIRPAT	Atochastic impacts by regression on population, affluence, and technology model
IEA	International Energy Agency
IBRD	The World Bank
BRICS	Brazil, Russia, India, China, South Africa
R&D	Research and development
ENGM(1,N)	Nonlinear multivariate grey model based on EKC
DGPM(1,N)	Multivariate discrete grey prediction model
GRPM(1,1)	Rolling grey prediction model
FAGGM(1,1)	Fractional order cumulative grey model
ECGM(1,1)	Exponential-order cumulative grey model
GM(1,1)	Grey model
GMC(1,N)	Multivariate grey model with convolution integral
RWGM(1,N)	Robust reweighted multivariate grey model
ATGM(1,N)	Accumulative time-delay multivariate grey model
TIGM(1,N)	Multivariate trend interaction grey model
ARIMAX	Integrated moving average with explanatory variables
ARIMA	Autoregressive integrated moving average model
MLR	Multiple linear regression
MPR	Multiple polynomial regression
PSO	Particle swarm optimization
QPSO	Quantum particle swarm optimization
CSO	Chicken swarm optimization
ICSO	Improved chicken swarm optimization
FLN	Fast learning network
SVR	Support vector regression
ANN	Artificial neural network

Contribution and organization

The main contributions of this study are outlined below.

1. A new type of multivariate grey prediction model is established on the basis of the EKC theory, combined with the IPAT equation and the extended STIRPAT model. The model considers the impact of economic development, population, and energy use on carbon emissions.

2. The time response equation of the new model is obtained by the derivation method. The parameter values are obtained by the least squares method. The quantum particle swarm algorithm is designed to optimize the model parameters to improve the accuracy of the model.

3. Data on carbon emissions from the transportation sector in China, the USA, and Japan are selected for model validation. The data from these three countries have increasing, fluctuating, and decreasing characteristics, so the adaptability of the new model to different types of data is depicted. The new model is applied to the prediction of carbon emissions in these three countries for the next 7 years.

The remainder of this paper is organized as follows. The structure diagram of the full text is shown in Fig. 1. The “Model building” section introduces the process of model building. The “Model solving” section describes the model solving process, which mainly includes estimating parameters using least squares method, solving the whitenization differential equation using the derivative method, and optimizing the model parameters using the quantum particle swarm algorithm. The “Model verification” section selects carbon emission data from the transportation sector in three countries, China, the USA, and Japan, as a validation set to verify the validity of the model. The “Application” section predicts the carbon emissions of the transportation sector in the three countries of China, the USA, and Japan from 2019 to 2025, and analyzes the prediction results. The main conclusions of this study are summarized in the “Conclusion” section.

Fig. 1.

Full text structure

Model building

This section is divided into two parts: the “Carbon emission prediction model for transportation sector” section introduces the process of establishing the differential equation for carbon emission prediction based on the EKC assumption. The “Theoretical modeling of the ENG(1,N)” section derives the ENGM(1,4) model through the differential information principle.

Carbon emission prediction model for transportation sector

The EKC proposed by economist Kuznets in 1955 revealed an “inverted U-shaped” relationship between economic development and environmental damage (Ali et al. 2017). The EKC hypothesis proposed by Grossman and Krueger (1991) states that there is a certain degree of linear and non-linear correlation between carbon emissions and economic factors in carbon emission studies; the expression of which can be found in Eq. (1):

$${\mathit{CO}}_{2,t}=f\left(Y,,,Y^2,,,R,E,,,F,O\right)$$ 1

where $Y^2$ and $Y$ denote economic development; $\mathit{RE}$ and $\mathit{FO}$ denote renewable energy and fossil fuel, respectively, representing primary energy and secondary energy, which can be replaced by total energy consumption ($\mathit{EC}$) (Le and Van 2020). Thus, Eq. (2) is obtained. The EKC hypothesis indicates that there is a relationship between carbon emissions, the economy, and energy sources.

$${\mathit{CO}}_{2,t}=f\left(Y^2,,,Y,,,E,C\right)$$ 2

Based on related research on the EKC, Kharbach and Chfadi (2017) tested the significant differences between $\mathit{GDP}$, ${\mathit{GDP}}^2$, and road diesel consumption ($\mathit{RSD}$) and road traffic carbon emissions (${\mathit{RCO}}_{2,t}$). They verified the differences to get Eq. (3):

$${\mathit{RCO}}_{2,t}={\alpha }_0{{+\alpha }_1{\mathit{GDP}}_t^2+\alpha }_2{\mathit{GDP}}_t+{\alpha }_3{\mathit{RSD}}_t+{\mu }_t$$ 3

Further extending Eq. (3) to the carbon emissions of the transportation sector (${\mathit{TCO}}_{2,t}$), the Eq. (4) can be obtained:

$${\mathit{TCO}}_{2,t}={\alpha }_0^{{}^{\prime }}+{\alpha }_1^{{}^{\prime }}{\mathit{GDP}}_t^2+{\alpha }_2^{{}^{\prime }}{\mathit{GDP}}_t+{\alpha }_3^{{}^{\prime }}{\mathit{EC}}_t+{\mu }_t^{{}^{\prime }}$$ 4

In Eq. (4), ${\mathit{TCO}}_{2,t}$ represents the carbon emissions of the transportation sector, ${\mathit{EC}}_t$ represents energy consumption, and the constant term ${\mu }_t^{{}^{\prime }}$ is used to reduce the error caused by random disturbance factors.

On the basis of the EKC and in addition to considering economic and energy factors, Ehrlich and Holdren (1970) further introduced demographic factors to establish a constant expression for the IPAT equation, as shown in Eq. (5) (Dogan and Inglesi-Lotz 2020):

$$I=P\times A\times T$$ 5

To enhance the flexibility of the model based on the IPAT equation, York et al. (2003) introduced exponents to establish an extended STIRPAT model, as shown in Eq. (6):

$$I_i=a{P}_i^b{A}_i^c{T}_i^d{e}_i$$ 6

where $I$ can be interpreted as the rate of environmental change (in carbon emission studies as the level of carbon emissions), $P$ is the population size, $A$ is regarded as the degree of affluence, and $T$ is the environmental damage caused by production or technology (usually expressed in carbon emission studies as the consumption of nuclear energy representing the technology) (Liu and Xiao 2018).

The IPAT equation and the extended STIRPAT model consider the effect of demographic factors on carbon emissions. The significant effect of demographic factors on carbon emissions has been tested in recent years in carbon emission-related studies (Chontanawat 2018). Therefore, the population factor $P_t$ is introduced on the basis of Eq. (4) to obtain the relationship between transportation sector carbon emissions and economy, energy, and population, as given in Eq. (7):

$${\mathit{TCO}}_{2,t}={\alpha }_0^{{}^{\prime }}+{{\alpha }_1^{{}^{\prime }}{\mathit{GDP}}_t^2+\alpha }_2^{{}^{\prime }}{\mathit{GDP}}_t+{\alpha }_3^{{}^{\prime }}{\mathit{EC}}_t+{\alpha }_4^{{}^{\prime }}{P}_t+{\mu }_t^{{}^{\prime }}$$ 7

Assuming that the carbon emissions of the transportation sector at time $t$ is $X_1^{\left(0\right)}\left(t\right)$, then the total carbon emissions in the time period $\left[1,,,t\right]$ can be expressed as follows:

$$X_1^{\left(1\right)}\left(t\right)={\int }_0^t{X}_1^{\left(0\right)}\left(u\right)du\mathrm{or}{X}_1^{\left(0\right)}\left(u\right)=\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}$$ 8

Combining Eq. (7) and Eq. (8), we can obtain:

$$\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}=X_1^{\left(0\right)}\left(u\right)={\mathit{TCO}}_{2,t}={\alpha }_0^{{}^{\prime }}+{{\alpha }_1^{{}^{\prime }}{\mathit{GDP}}_t^2+\alpha }_2^{{}^{\prime }}{\mathit{GDP}}_t+{\alpha }_3^{{}^{\prime }}{\mathit{EC}}_t+{\alpha }_4^{{}^{\prime }}{P}_t+{\mu }_t^{{}^{\prime }}$$ 9

When the research stage is short, the national energy structure changes are ignored. The increment of carbon emissions $\mathrm{\Delta }{X}_1^{\left(1\right)}$ and the total energy consumption ${\mathit{TEC}}_t$ can be considered as an approximate linear relationship:

$$\mathrm{\Delta }{X}_1^{\left(1\right)}\left(t\right)=X_1^{\left(1\right)}\left(t\right)-X_1^{\left(1\right)}\left(1\right)=\gamma {\mathit{EC}}_t$$ 10

then:

$${\mathit{EC}}_t=\frac{1}{\gamma }{X}_1^{\left(1\right)}\left(t\right)-\frac{1}{\gamma }{X}_1^{\left(1\right)}\left(1\right)$$ 11

Data from IEA shows that the total energy consumption in the transport sector accounts for approximately 29% of the total overall energy consumption (IEA 2021). According to Eqs. (10) and (11), the total energy consumption of the transportation sector ($\mathit{TEC}$) can be used to represent the total energy consumption ($\mathit{EC}$):

$${\mathit{EC}}_t=\left(1,-,p\right){\mathit{EC}}_t+{\mathit{TEC}}_t=\left(1,-,p\right)\ast \left(\frac{1}{\gamma },X_1^{\left(1\right)},\left(t\right),-,\frac{1}{\gamma },X_1^{\left(1\right)},\left(1\right)\right)+{\mathit{TEC}}_t={\gamma }_0+{\gamma }_1{X}_1^{\left(1\right)}\left(t\right)+{\mathit{TEC}}_t$$ 12

where $p$ is the proportion of total energy consumption in the transportation sector to total energy consumption, ${\gamma }_0=\left(p,-,1\right)\frac{1}{\gamma }{X}_1^{\left(1\right)}\left(1\right)$, ${\gamma }_1=\frac{1-p}{\gamma }$. Bringing Eq. (12) into Eq. (9), we get:

$$\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}={\alpha }_0^{{}^{\prime }}+{\alpha }_1^{{}^{\prime }}{\mathit{GDP}}_t^2+{\alpha }_2^{{}^{\prime }}{\mathit{GDP}}_t+{\alpha }_3^{{}^{\prime }}\left({\gamma }_0,+,{\gamma }_1,X_1^{\left(1\right)},\left(t\right),+,{\mathit{TEC}}_t\right)+{\alpha }_4^{{}^{\prime }}{P}_t+{\mu }_t^{{}^{\prime }}$$ 13

Equation (13) reveals the relationship between the growth rate of carbon emissions in the transportation sector and GDP, energy consumption in the transportation sector, and population. $X_2$, $X_3$, and $X_4$ are used to denote GDP, transportation sector energy consumption, and population values over a period of time. Considering that economic development is influenced by various internal and external factors and has the characteristics of instability, the index of ${\mathit{GDP}}^2$ variable is extended from 2 to $r$ to enhance the model flexibility. The optimal $r$ value can be obtained by an optimization algorithm to improve the prediction accuracy of the model. Let $a=-{\alpha }_3^{{}^{\prime }}{\gamma }_1$, $b={\alpha }_1^{{}^{\prime }}$, $c_i={\alpha }_i^{{}^{\prime }}\left(i,=,2,3,,,4\right)$, $d={\alpha }_0^{{}^{\prime }}+{\mu }_t^{{}^{\prime }}$, and simplify Eq. (13) to obtain:

$$\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}+a{X}_1^{\left(1\right)}\left(t\right)=b{\left[X_2^{\left(1\right)},\left(t\right)\right]}^r+{\sum }_{i=2}^N{c}_i{X}_i^{\left(1\right)}\left(t\right)+d,N=4$$ 14

That is, Eq. (14) is a predictive differential equation about the cumulative carbon emissions $X_1^{\left(1\right)}\left(t\right)$ of the transportation sector within $\left[1,,,t\right]$.

Theoretical modeling of the$ENGM\left(1,,,N\right)$

Equation (14) is a first-order nonlinear differential equation containing multiple variables, whereas $X_1^{\left(1\right)}\left(t\right)$ is a first-order continuous derivable and contains the infinite information. In carbon emissions research, carbon emissions are usually measured in years, which is a discrete time series with limited uncertain information or so-called grey information. According to the differential information principle (Deng 1982), Eq. (14) is discretized and transformed to obtain a new nonlinear multivariate grey model based on the EKC assumption.

Suppose that the data series of annual carbon emissions from transportation sector is $X_1^{\left(0\right)}=\left(X_1^{\left(0\right)},\left(1\right),,,X_1^{\left(0\right)},\left(2\right),,,\cdots ,,,X_1^{\left(0\right)},\left(t\right)\right)$. Then, according to Eq. (8), $X_1^{\left(1\right)}\left(t\right)$ is the total carbon emission during the period of $\left[1,,,t\right]$, which can be expressed as follows:

$$X_1^{\left(1\right)}\left(t\right)=\sum _{k=1}^t{X}_1^{\left(0\right)}\left(t\right),t=1,2,\cdots ,n$$ 15

As for the cumulative carbon emissions $X_1^{\left(1\right)}\left(t\right)$, the rate of its changing during the time period $\left[k,-,1,,,k\right]$ can be approximated as follows (Deng 1982):

$$\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}{|}_{t=k}\approx \frac{\mathrm{\Delta }{X}_1^{\left(1\right)}\left(t\right)}{\mathrm{\Delta }t}{|}_{t=k}=\frac{X_1^{\left(1\right)}\left(k\right)-X_1^{\left(1\right)}\left(k,-,1\right)}{k-\left(k,-,1\right)}=X_1^{\left(1\right)}\left(k\right)-X_1^{\left(1\right)}\left(k,-,1\right)=X_1^{\left(0\right)}\left(k\right)$$ 16

It was worth noticing that $X_1^{\left(0\right)}\left(k\right)$ is usually be regarded as the grey derivative and can provide the necessary information on time-dependent function $X_1^{\left(1\right)}\left(k\right)$. Namely, $X_1^{\left(0\right)}\left(k\right)$ can be regarded as the grey derivative sequence of $X_1^{\left(1\right)}\left(k\right)$ and take the place of $\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}$ during $\left[k,-,1,,,k\right]$. Besides, the background value of the grey derivative $z_1^{\left(1\right)}\left(k\right)$ can be formalized as follows:

$$X_1^{\left(1\right)}\left(t\right){|}_{\left[k,-,1,,,k\right]}\approx p{X}_1^{\left(1\right)}\left(k\right)+\left(1,-,p\right)X_1^{\left(1\right)}\left(k\right)=z_1^{\left(1\right)}\left(k\right)$$ 17

where $p\in \left[0,1\right]$. To simplify $z^{\left(1\right)}\left(k\right)$, $p$ is equal to 0.5 in general. In grey modeling, the background value $z_i^{\left(1\right)}\left(k\right)$ can usually take the place of the value of $X_i^{\left(1\right)}\left(k\right)$ during the period $\left[k,-,1,,,k\right]$, $i=1,2,\cdots ,n$. Hence, the following grey model can be defined.

Definition 1.

Equation (18) is named as the ENGM(1,4) model. The whitenization differential equation of the ENGM(1,4) model can be expressed as Eq. (19):

$$X_1^{\left(0\right)}\left(k\right)+a{z}_1^{\left(1\right)}\left(k\right)=b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)+d,N=4$$ 18

$$\frac{d{X}_1^{\left(1\right)}\left(t\right)}{\mathit{dt}}+a{X}_1^{\left(1\right)}\left(t\right)=b{\left[X_2^{\left(1\right)},\left(t\right)\right]}^r+{\sum }_{i=2}^N{c}_i{X}_i^{\left(1\right)}\left(t\right)+d,N=4$$ 19

In Eq. (18), $a$ is the development coefficient that can reflect the development trend of $X_1^{\left(0\right)}$ and $X_1^{\left(1\right)}$, $b$ and $c_i$ are the control coefficients, $i=2,3,4$, $d$ is a constant term, and $r$ is the power exponent.

Model solving

This section is divided into three parts: The “Parameter estimation based on least squares method” section introduces the process of parameter estimation using the least squares method. The solution of the whitenization differential equation by the derivative method is discussed in the “Derivative method for solving whitenization differential equation” section. The quantum particle swarm algorithm is designed in the “Parameter optimization” section to optimize the exponent $r$ thus improving the model accuracy.

Parameter estimation based on least squares method

The parameters $a$, $b$, $c_2$, $c_3$, $c_4$, …, $c_N$, $d$ and the power exponent $r$ in the model affect the prediction effect and accuracy of the model. To facilitate the calculation, the power exponent is first considered as a known parameter and the expression containing the parameter $r$ for $a$, $b$, $c_2$, $c_3$, $c_4$, …, $c_N$, $d$ is derived using the least squares method.

Theorem 1

Let $P={\left(a,,,b,,,c_2,,,c_3,,,\cdots ,,,c_N,,,d\right)}^T$ be the sequence of parameters in the equation, $Y=\left(\begin{array}{c}{X}_1^{\left(0\right)}\left(2\right)\\ X_1^{\left(0\right)}\left(3\right)\\ ⋮\\ X_1^{\left(0\right)}\left(n\right)\end{array}\right),B=\left[\begin{array}{c}\begin{array}{ccc}-z_1^{\left(1\right)}\left(2\right)& {\left(z_2^{\left(1\right)},\left(2\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(2\right)& \cdots & z_N^{\left(1\right)}\left(2\right)\end{array}& 1\end{array}\end{array}\\ \begin{array}{ccc}-z_1^{\left(1\right)}\left(3\right)& {\left(z_2^{\left(1\right)},\left(3\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(3\right)& \cdots & z_N^{\left(1\right)}\left(3\right)\end{array}& 1\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{ccc}⋮& ⋮& ⋮\end{array}& \begin{array}{ccc}⋮& ⋮& ⋮\end{array}\end{array}\\ \begin{array}{ccc}-z_1^{\left(1\right)}\left(n\right)& {\left(z_1^{\left(1\right)},\left(n\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(n\right)& \cdots & z_N^{\left(1\right)}\left(n\right)\end{array}& 1\end{array}\end{array}\end{array}\right]$. Then, the least squares estimate of this sequence satisfies $\widehat{P}={\left(a,,,b,,,c_2,,,c_3,,,\cdots ,,,c_N,,,d\right)}^T={\left(B^T,B\right)}^{-1}{B}^{T}Y$.

Proof

The original grey model can be written as follows:

$$X_1^{\left(0\right)}\left(k\right)=-a{z}_1^{\left(1\right)}\left(k\right)+b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+{\sum }_{i=2}^N{\mathrm{c}}_i{z}_i^{\left(1\right)}\left(k\right)+d$$

Perform 1-AGO processing on the original sequence $X_1^{\left(0\right)}$ to get:

$$\left\{\begin{array}{c}{X}_1^{\left(0\right)}\left(2\right)=-a{z}_1^{\left(1\right)}\left(2\right)+b{\left(z_2^{\left(1\right)},\left(2\right)\right)}^r+{\sum }_{i=2}^N{\mathrm{c}}_i{z}_i^{\left(1\right)}\left(2\right)+d\\ X_1^{\left(0\right)}\left(3\right)=-a{z}_1^{\left(1\right)}\left(3\right)+b{\left(z_2^{\left(1\right)},\left(3\right)\right)}^r+{\sum }_{i=2}^N{\mathrm{c}}_i{z}_i^{\left(1\right)}\left(3\right)+d\\ ⋮\\ X_1^{\left(0\right)}\left(n\right)=-a{z}_1^{\left(1\right)}\left(n\right)+b{\left(z_2^{\left(1\right)},\left(n\right)\right)}^r+{\sum }_{i=2}^N{\mathrm{c}}_i{z}_i^{\left(1\right)}\left(n\right)+d\end{array}\right)$$ 20

The matrix form of Eq. (20) can be written as $Y=BP$, where $Y$ is the original sequence, $B$ is the mixed matrix processed by 1-AGO on the original sequence, and $P$ is the parameter sequence. The error sequence can be written as $\epsilon =Y-BP$.

$$s={\epsilon }^T\epsilon ={\left(Y,-,B,P\right)}^T\left(Y,-,B,P\right)$$ 21

To make $min{\Vert Y-BP\Vert }^2=\min s=min{\left(Y,-,B,P\right)}^T\left(Y,-,B,P\right)=min{\sum }_{k=2}^n{\left(X_1^{\left(0\right)},\left(k\right),+,a,z_1^{\left(1\right)},\left(k\right),-,b,{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r,-,{\sum }_{i=2}^N,{\mathrm{c}}_i,z_i^{\left(1\right)},\left(k\right),-,d\right)}^2$:

Taking the partial derivatives of $a$, $b$, $c_2$, $c_3$, $c_4$, …, $c_N$ and $d$ in the above equation and making the right-hand side of the Eq. 0, we get:

$$B^T\epsilon =0\Rightarrow B^T\left(Y,-,B,P\right)=0\Rightarrow B^{T}Y-B^{T}BP=0\Rightarrow {P=\left(B^T,B\right)}^{-1}{B}^{T}Y$$

where:

$$\left\{\begin{array}{c}\frac{\partial s}{\partial a}=2X_1^{\left(0\right)}\left(k\right)z_1^{\left(1\right)}\left(k\right)+2a{\left(z_1^{\left(1\right)},\left(k\right)\right)}^2-2b{z_1^{\left(1\right)}\left(k\right)\left(z_2^{\left(1\right)},\left(k\right)\right)}^r-2z_1^{\left(1\right)}\left(k\right){\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)-2d{z}_1^{\left(1\right)}\left(k\right)\\ \frac{\partial s}{\partial b}=-2X_1^{\left(0\right)}\left(k\right){\left(z_2^{\left(1\right)},\left(k\right)\right)}^r-2a{z_1^{\left(1\right)}\left(k\right)\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+2b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^{2r}+2{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)+2d{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r\\ \frac{\partial s}{\partial c_i}=-2X_1^{\left(0\right)}\left(k\right)z_i^{\left(1\right)}\left(k\right)-2a{z}_1^{\left(1\right)}\left(k\right)z_i^{\left(1\right)}\left(k\right)+2b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r{z}_i^{\left(1\right)}\left(k\right)+2{\sum }_{i=2}^N{c}_i{\left(z_i^{\left(1\right)},\left(k\right)\right)}^2+2d{z}_i^{\left(1\right)}\left(k\right)\\ \frac{\partial s}{\partial d}=-2X_1^{\left(0\right)}\left(k\right)-2a{z}_1^{\left(1\right)}\left(k\right)+2b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+2{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)+2d\end{array}\right)$$

From this, the expression of the parameter is obtained as follows:

$$\left\{\begin{array}{c}\begin{array}{c}a=\frac{b{z_1^{\left(1\right)}\left(k\right)\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+z_1^{\left(1\right)}\left(k\right){\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)+d{z}_1^{\left(1\right)}\left(k\right)-X_1^{\left(0\right)}\left(k\right)z_1^{\left(1\right)}\left(k\right)}{{\left(z_1^{\left(1\right)},\left(k\right)\right)}^2}\\ b=\frac{X_1^{\left(0\right)}\left(k\right){\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+a{z_1^{\left(1\right)}\left(k\right)\left(z_2^{\left(1\right)},\left(k\right)\right)}^r-{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)-d{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r}{{\left(z_2^{\left(1\right)},\left(k\right)\right)}^{2r}}\\ c_i=\frac{X_1^{\left(0\right)}\left(k\right)z_i^{\left(1\right)}\left(k\right)+a{z}_1^{\left(1\right)}\left(k\right)z_i^{\left(1\right)}\left(k\right)-b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r{z}_i^{\left(1\right)}\left(k\right)-d{z}_i^{\left(1\right)}\left(k\right)}{{\left(z_i^{\left(1\right)},\left(k\right)\right)}^2}\\ d=X_1^{\left(0\right)}\left(k\right)+a{z}_1^{\left(1\right)}\left(k\right)-b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r-{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)\end{array}\end{array}\right)$$ 22

According to Eq. (22), if the original sequence $X_1^{\left(0\right)}$ is known, then the estimated value of the parameter sequence $P={\left(a,,,b,,,c_2,,,c_3,,,\cdots ,,,c_N,,,d\right)}^T$ can be obtained by the least squares method. The prediction in the validation and application is mainly based on the time response equation corresponding to the whitenization differential equation, and there is an unknown index $r$ in it. The model corresponding to the whitenization differential equation is a multivariate grey model, which brings some difficulties to the solution of the equation. Hence, the derivation method applicable to the multivariate grey model is considered to solve the equation.

Derivative method for solving whitenization differential equation

The grey model is $X_1^{\left(0\right)}\left(k\right)+a{z}_1^{\left(1\right)}\left(k\right)=b{\left(z_2^{\left(1\right)},\left(k\right)\right)}^r+{\sum }_{i=2}^N{c}_i{z}_i^{\left(1\right)}\left(k\right)+d$.

$X_i^{\left(0\right)}\left(k\right)$ is the original sequence and $X_i^{\left(1\right)}\left(k\right)$ is the first-order cumulative sequence. According to Eq. (16) the approximate representation of $\frac{d{X}_1^{\left(1\right)}\left(k\right)}{\mathit{dk}}$ can be written as follows:

$$\frac{d{X}_1^{\left(1\right)}\left(k\right)}{\mathit{dk}}=X_1^{\left(0\right)}\left(k\right)$$

From the above equation, we get $X_i^{\left(1\right)}\left(k\right)-X_i^{\left(1\right)}\left(k,-,1\right)=X_i^{\left(0\right)}\left(k\right),i=1,2,\cdots ,n$, that is $X_i^{\left(1\right)}\left(k\right)=X_i^{\left(1\right)}\left(k,-,1\right)+X_i^{\left(0\right)}\left(k\right),i=1,2,\cdots ,n$.

Then, $z_i^{\left(1\right)}\left(k\right)=0.5\left(X_i^{\left(1\right)},\left(k\right),+,X_i^{\left(1\right)},\left(k,-,1\right)\right)=0.5\left(X_i^{\left(0\right)},\left(k\right),+,X_i^{\left(1\right)},\left(k,-,1\right),+,X_i^{\left(1\right)},\left(k,-,1\right)\right)=0.5X_i^{\left(0\right)}\left(k\right)+X_i^{\left(1\right)}\left(k,-,1\right)$

Substituting the above formula into Eq. (18) can obtain:

$$X_1^{\left(0\right)}\left(k\right)+a\left[0.5,X_1^{\left(0\right)},\left(k\right),+,X_1^{\left(1\right)},\left(k,-,1\right)\right]=b{\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]}^r+{\sum }_{i=2}^N{c}_i\left[0.5,X_i^{\left(0\right)},\left(k\right),+,X_i^{\left(1\right)},\left(k,-,1\right)\right]+d$$

that is:

$${\left(1,+,0.5,a\right)X}_1^{\left(0\right)}\left(k\right)+a{X}_1^{\left(1\right)}\left(k,-,1\right)=b{\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]}^r+0.5{\sum }_{i=2}^N{c}_i{X}_i^{\left(0\right)}\left(k\right)+{\sum }_{i=2}^N{c}_i{X}_i^{\left(1\right)}\left(k,-,1\right)+d,N=4$$

If $1+0.5a\ne 0$, then:

$$X_1^{\left(0\right)}\left(k\right)=-\frac{a}{1+0.5a}{X}_1^{\left(1\right)}\left(k,-,1\right)+\frac{b}{1+0.5a}{\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]}^r+0.5\frac{{\sum }_{i=2}^N{c}_i}{1+0.5a}{X}_i^{\left(0\right)}\left(k\right)+\frac{{\sum }_{i=2}^N{c}_i}{1+0.5a}{X}_i^{\left(1\right)}\left(k,-,1\right)+\frac{1}{1+0.5a}d$$ 23

Equation (23) is the time response equation of the whitenization differential equation corresponding to the grey model $ENGM\left(1,,,N\right)$. The time response equation of the whitenization differential equation corresponding to the $ENGM\left(1,4\right)$ model can then be written as Eq. (24):

$$X_1^{\left(0\right)}\left(k\right)=-\frac{a}{1+0.5a}{X}_1^{\left(1\right)}\left(k,-,1\right)+\frac{b}{1+0.5a}{\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]}^r+\frac{c_2}{1+0.5a}\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]+\frac{c_3}{1+0.5a}\left[0.5,X_3^{\left(0\right)},\left(k\right),+,X_3^{\left(1\right)},\left(k,-,1\right)\right]+\frac{c_4}{1+0.5a}\left[0.5,X_4^{\left(0\right)},\left(k\right),+,X_4^{\left(1\right)},\left(k,-,1\right)\right]+\frac{1}{1+0.5a}d$$ 24

Parameter optimization

The particle swarm algorithm is a global random search algorithm based on swarm intelligence proposed by Kennedy and Eberhart, inspired by the results of artificial life research, by simulating the migration and swarming behavior of birds in the foraging process (Kennedy and Eberhart 1995). The traditional particle swarm algorithm is easy to lead to the local optimum, so the quantum particle swarm algorithm has achieved optimization and improvement in the search mechanism. To overcome the uncertainty of quantum mechanics, the wave function is used to represent the particle shape, and the Schrodinger equation is employed to obtain the probability density function of each individual at any position. The Monte-Carlo stochastic simulation is introduced to obtain the position equations of particle in the problem space (Xia et al. 2019), which can improve the global search capability of the population and the accuracy of the algorithm. Quantum particle swarm algorithm is widely used in various fields (Feng et al. 2017; Li et al. 2019; Song et al. 2020; Turgut 2016).

According to the least squares estimation, all other parameters of the model can be represented by the power exponent $r$. The value of $r$ largely affects the prediction results and accuracy of the model. To obtain the optimal parameter combination, the average absolute percentage error ($\mathit{MAPE}$) of the model is selected to measure the estimation accuracy of the model. The smaller the $\mathit{MAPE}$, the smaller the unexplainable error of the model and the higher the accuracy of the model. The power index $r$ is the optimal object, $MAPE(r)$ is the optimal function (Eq. (25)), and the nonlinear optimization model is constructed as shown in Eq. (26) by combining the parameter constraints in the above time response equation (Fig. 2).

$$MAPE\left(r\right)=\frac{1}{n-1}\sum _{k=2}^n\frac{\left|{\widehat{X}}_1^{\left(0\right)},\left(k\right),-,X_1^{\left(0\right)},\left(k\right)\right|}{X_1^{\left(0\right)}\left(k\right)}\times 100\%$$ 25

$$\left\{\begin{array}{c}{X}_1^{\left(0\right)}\left(k\right)=-\frac{a}{1+0.5a}{X}_1^{\left(1\right)}\left(k,-,1\right)+\frac{b}{1+0.5a}{\left[0.5,X_2^{\left(0\right)},\left(k\right),+,X_2^{\left(1\right)},\left(k,-,1\right)\right]}^r+\\ {\sum }_{i=2}^4\frac{b_i}{1+0.5a}\left[0.5,X_i^{\left(0\right)},\left(k\right),+,X_i^{\left(1\right)},\left(k,-,1\right)\right]+\frac{1}{1+0.5a}d\\ \widehat{P}={\left(a,,,b,,,c_2,,,c_3,,,\cdots ,,,c_N,,,d\right)}^T={\left(B^T,B\right)}^{-1}{B}^{T}Y\\ Y=\left(\begin{array}{c}{X}_1^{\left(0\right)}\left(2\right)\\ X_1^{\left(0\right)}\left(3\right)\\ ⋮\\ X_1^{\left(0\right)}\left(n\right)\end{array}\right)\\ B=\left[\begin{array}{c}\begin{array}{ccc}-z_1^{\left(1\right)}\left(2\right)& {\left(z_2^{\left(1\right)},\left(2\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(2\right)& \cdots & z_N^{\left(1\right)}\left(2\right)\end{array}& 1\end{array}\end{array}\\ \begin{array}{ccc}-z_1^{\left(1\right)}\left(3\right)& {\left(z_2^{\left(1\right)},\left(3\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(3\right)& \cdots & z_N^{\left(1\right)}\left(3\right)\end{array}& 1\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{ccc}⋮& ⋮& ⋮\end{array}& \begin{array}{ccc}⋮& ⋮& ⋮\end{array}\end{array}\\ \begin{array}{ccc}-z_1^{\left(1\right)}\left(n\right)& {\left(z_1^{\left(1\right)},\left(n\right)\right)}^r& \begin{array}{cc}\begin{array}{ccc}{z}_2^{\left(1\right)}\left(n\right)& \cdots & z_N^{\left(1\right)}\left(n\right)\end{array}& 1\end{array}\end{array}\end{array}\right]\\ z_i^{\left(1\right)}=0.5\left(X_i^{\left(1\right)},\left(k\right),+,X_i^{\left(1\right)},\left(k,-,1\right)\right),k=2,3,\cdots ,N\\ X_1^{\left(0\right)}=\left(X_1^{\left(0\right)},\left(1\right),,,X_1^{\left(0\right)},\left(2\right),,,\cdots ,,,X_1^{\left(0\right)},\left(n\right)\right)\\ X_1^{\left(1\right)}=AGO\left(X_1^{\left(0\right)}\right)\end{array}\right)$$ 26

Fig. 2.

Pseudo code of QPSO

Model verification

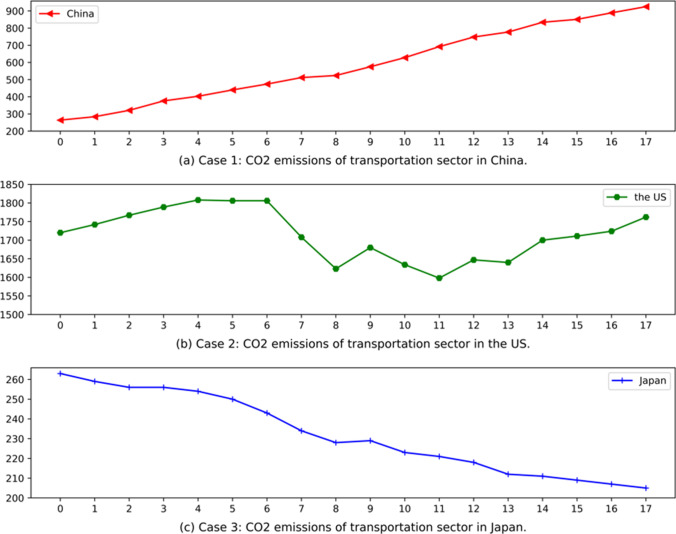
China, the USA, and Japan are the top three countries in the world in terms of GDP as well as among the top five countries in terms of carbon emissions. This section validates the accuracy and validity of the ENGM(1,4) model using the transportation sector carbon emissions dataset for these three countries for the 18-year period of 2001–2018. The transportation sector carbon emissions and transportation sector energy consumption data are from the IEA (International Energy Agency) (IEA 2021), and the GDP and population data from the World Bank (IBRD 2021). The 13 years of data from 2001 to 2013 are used to fit to build the model, and the 5 years of data from 2014 to 2018 are used to forecast to verify the accuracy of the model. The different transportation status, economic development, and energy use of these three countries constitute three carbon emission trends with different characteristics, as shown in Fig. 3. The transportation sectors of these three countries show increasing, fluctuating, and decreasing carbon emissions during the 18 years from 2001 to 2018, respectively. The validation of the model with these three datasets with different characteristics shows that the model can adapt to different types of data series with high accuracy and flexibility.

Fig. 3.

Comparison of carbon emissions data from China, the USA, and Japan

We compare the results with GM(1,4), GMC(1,4), SVR (support vector regression), ANN (artificial neural network), and ARIMA (autoregressive integrated moving average model). The indicators for evaluating the predictive effect are shown in Table 3. In the calculation result table, the numbers in bold are the optimal values.

Table 3.

Metrics for evaluating effectiveness of the models

Name	Abbreviation	Formulation
The mean absolute simulation percentage error	MAPESIM	$\frac{1}{n-1}\left({\sum }_{i=2}^n,\left|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right|\right)\times 100\%$
The mean absolute prediction percentage error	MAPEPRE	$\frac{1}{v}\left({\sum }_{i=1}^v,\left|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right|\right)\times 100\%$
The total mean absolute percentage error	MAPETOT	$\frac{1}{n-1}\left({\sum }_{i=2}^n,\left|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right|\right)\times 100\%$
Mean absolute percentage error	MAE	$\frac{1}{n-1}{\sum }_{i=2}^n\left|X^{\left(0\right)},\left(i\right),-,{\widehat{X}}^{\left(0\right)},\left(i\right)\right|$
Root mean square error	RMSE	$\sqrt{\frac{1}{n-1}{\sum }_{i=2}^n{\left(x^{\left(0\right)},\left(i\right),-,{\widehat{x}}^{\left(0\right)},\left(i\right)\right)}^2}$
Standard deviation	STD	$\sqrt{\frac{1}{n-1}{\sum }_{i=2}^n{\left(\left|\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right|,-,M,A,P,E\right)}^2}$
The absolute percentage error	APE	$\left(\frac{x^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{x^{\left(0\right)}\left(i\right)}\right)\times 100\%$

Validation case 1: China

The dataset of the first verification case includes China’s transportation sector carbon emissions, GDP, energy consumption, and population data from 2001 to 2018. Carbon emissions show an increasing trend. The parameter value $r=3$ of the ENGM(1,4) model is obtained by the quantum particle swarm algorithm. The fitted and predicted values of each model and the MAPE values are shown in Table 4. Other comparison indices are shown in Table 7. Table 4 shows that the new models MAPE_SIM and MAPE_TOT are the lowest among all models with 0.4465% and 1.8963%, respectively. MAPE_PRE is 5.3759%, which is the second lowest among all models, indicating that the overall fit and prediction of the model is relatively good. The three types of MAPE values of the GM(1,4) model are also small, all within 3%, indicating that the GM(1,4) model is also suitable for the background of this research. The three types of MAPE values of the GMC(1,4) model all exceed 10%, indicating that the fitting and prediction effects are not ideal. The MAPE_SIM of both ANN and SVR are less than 5%, which is a good fit. However, the MAPE_PRE is more than 10%, which is a large prediction error due to the phenomenon of “overfitting.” The fitting error of the ARIMA model is as high as 20%, indicating that the model is not suitable for the background of this research.

Table 4.

Validation case 1: fitted and predicted values of each model for carbon emissions in China’s transportation sector

Year	Actual values	ENGM(1,4)	GM(1,4)	GMC(1,4)	SVR	ANN	ARIMA
		Simulated data	Simulated data	Simulated data	Simulated data	Simulated data	Simulated data
Fitting
2001	264	264	264	264	285	251	921
2002	284	286	243	264	296	283	279
2003	321	322	342	318	326	315	319
2004	376	376	381	360	367	352	322
2005	403	404	403	389	407	389	378
2006	440	442	439	411	443	426	406
2007	474	475	472	426	474	463	446
2008	512	512	511	437	505	499	481
2009	524	525	523	449	545	529	521
2010	575	577	575	455	594	625	533
2011	628	630	626	446	649	660	586
2012	692	695	689	470	698	679	639
2013	748	754	744	527	727	697	705
MAPESIM(%)		0.4465	2.0313	14.4541	2.6038	3.7326	24.5755
Prediction
2014	777	796	773	688	728	713	730
2015	834	843	835	737	701	729	765
2016	851	894	856	796	657	745	804
2017	889	925	895	932	608	760	843
2018	925	1055	990	1244	566	776	882
MAPEpre(%)		5.3759	1.7726	13.7749	23.0955	12.7786	5.9273
MAPETOT(%)		1.8963	1.9552	14.2544	8.2959	6.2454	19.3955

Table 7.

Comparison of other index values for each model in the three validation cases

Country	Index	ENGM(1,4)	GM(1,4)	GMC(1,4)	SVR	ANN	ARIMA
China	MAE	15.6352	9.4103	95.9102	64.7824	44.4606	70.5802
	RMSE	34.9310	19.5100	129.5526	121.9970	63.6885	159.6783
	STD	0.0335	0.0375	0.1058	0.1110	0.0474	0.5571
The USA	MAE	17.9124	31.3363	660.0481	69.3164	45.6668	75.1263
	RMSE	29.4537	73.7406	841.3790	121.4052	68.9790	98.1774
	STD	0.0136	0.0381	0.2914	0.0577	0.0297	0.0364
Japan	MAE	3.2985	4.6182	56.9676	5.3140	4.1557	6.5597
	RMSE	5.5335	10.8091	61.2977	9.0988	5.6492	15.6659
	STD	0.0218	0.0377	0.0800	0.0361	0.0188	0.0539

To further demonstrate the approximation effect of fitting and prediction, the fitted and predicted values of each model are transformed into curve trend plots and APE comparison plots, as shown in Fig. 4. In the trend plot (Fig. 4a), the ENGM(1,4) and GM(1,4) models fit the original series more closely. The ENGM(1,4) model is slightly higher than the original value in the prediction part, and the GM(1,4) model shows a slight fluctuation at the beginning of the initial few time points. Overall, these two models seem to have a higher degree of approximation to the original value. The GMC(1,4) model fits the original values better at the initial time point, and then shows large fluctuations and deviates from the original values. SVR and ANN models are closer to the original sequence in the fitting part. The predicted value is significantly lower than the original value though, and the prediction error is large. The ARIMA model shows a large fluctuation at the first time point. Then, the fitted and predicted values are slightly lower than the original series overall. Figure 4b shows the APE value of each model. Of note, the APE of the ARIMA model at the first point in time is as high as 200%, which is excluded for the esthetics and readability of the image. The ENGM(1,4) model has an APE value of less than 5% at most of the remaining time points, excluding the APE value of more than 10% at time point in 2018. The overall fitting and forecasting errors are small.

Fig. 4.

Fitted and predicted trends and APE values for each model in case 1

In summary, although there are individual indicators that are non-optimal, the ENGM(1,4) model can fit and predict the carbon emissions of China’s transportation sector most effectively in terms of fitting and predicting the overall situation.

Validation case 2: the USA

The dataset of the second verification case includes the transportation sector carbon emissions, GDP, energy consumption, and population data of the USA from 2001 to 2018. Carbon emissions show a fluctuating trend. The parameter value $r=0.1840$ of the ENGM(1,4) model is obtained by the quantum particle swarm algorithm. The fitted and predicted values of each model and the MAPE values are shown in Table 5. Other comparison indices are shown in Table 7. Table 5 shows that the MAPE_SIM and MAPE_TOT of the new model are the lowest among all models, with 0.2367% and 1.0495%, respectively, which are less than 2%. This outcome implies that the fitting and overall accuracy are higher. The MAPE_PRE of the GM(1,4) model is 0.2275%, which is the lowest among all models and nearly 3% lower than the 3.0004% of the new model. The new model is inferior to the GM(1,4) model in terms of predictive ability. From the other comparison indices in Table 7, the MAE, RMSE, and STD of the new model are the lowest, so the ENGM(1,4) model seems to be the overall best. In addition, the fitting accuracy of the SVR and ANN models is high, but the prediction results are not ideal. The phenomenon of “overfitting” occurs. The MAPE_SIM of the GMC(1,4) model is as high as 50.4846%, and the performance of other indicators is not ideal, indicating that the GMC(1,4) model is not suitable for the research background.

Table 5.

Validation case 2: fitted and predicted values of each model for carbon emissions in the US transportation sector

Year	Actual values	ENGM(1,4)	GM(1,4)	GMC(1,4)	SVR	ANN	ARIMA
		Simulated data	Simulated data	Simulated data	Simulated data	Simulated data	Simulated data
Fitting
2001	1720	1720	1720	1720	1727	1743	1538
2002	1742	1741	1508	186	1743	1754	1741
2003	1767	1764	1951	304	1760	1765	1720
2004	1789	1789	1848	424	1788	1776	1772
2005	1808	1809	1819	545	1815	1786	1795
2006	1806	1806	1806	667	1813	1796	1814
2007	1806	1811	1806	788	1772	1783	1809
2008	1708	1713	1707	906	1715	1721	1809
2009	1623	1621	1620	1018	1671	1658	1694
2010	1680	1684	1683	1129	1647	1647	1600
2011	1634	1635	1627	1240	1627	1637	1697
2012	1598	1595	1598	1349	1615	1628	1624
2013	1647	1669	1659	1458	1640	1619	1592
MAPESIM(%)		0.2367	2.4387	50.4846	0.8184	1.1198	3.0395
Prediction
2014	1640	1687	1640	1569	1727	1610	1590
2015	1700	1668	1700	1681	1857	1601	1583
2016	1711	1776	1717	1796	1974	1592	1572
2017	1724	1681	1721	1912	2031	1584	1560
2018	1762	1832	1751	2028	2016	1575	1549
MAPEpre(%)		3.0004	0.2275	7.2767	12.4258	6.6670	7.9452
MAPETOT(%)		1.0495	1.7884	37.7764	4.0427	2.6607	4.4022

Table 6.

Validation case 3: fitted and predicted values of each model for carbon emissions in Japan’s transportation sector

Year	Actual values	ENGM(1,4)	GM(1,4)	GMC(1,4)	SVR	ANN	ARIMA
		Simulated data	Simulated data	Simulated data	Simulated data	Simulated data	Simulated data
Fitting
2001	263	263	263	263	261	265	199
2002	259	260	224	113	260	261	263
2003	256	256	282	192	258	258	255
2004	256	257	264	198	256	254	256
2005	254	256	255	198	253	251	256
2006	250	252	250	195	248	247	254
2007	243	245	243	190	241	242	250
2008	234	235	234	184	235	234	243
2009	228	228	228	178	230	227	233
2010	229	230	229	177	227	223	227
2011	223	224	223	176	225	222	228
2012	221	222	221	173	222	221	222
2013	218	220	219	170	220	221	220
MAPESIM(%)		0.4967	2.3464	25.0597	0.6216	0.8156	3.2016
Prediction
2014	212	217	213	165	219	220	218
2015	211	209	213	161	220	219	214
2016	209	218	210	160	223	219	210
2017	207	198	208	159	227	218	206
2018	205	223	206	157	232	217	202
MAPEpre(%)		4.0454	0.6025	23.1431	7.3684	4.7280	1.2414
MAPETOT(%)		1.5404	1.8335	24.4960	2.4957	1.9024	2.6571

To further demonstrate the approximation effect of fitting and prediction, the fitted and predicted values of each model are transformed into curve trend plots and APE comparison plots, as shown in Fig. 5. From the trend plot (Fig. 5a), except for the GMC(1,4) model, which deviates from the original values to a large extent, the other five models are able to stick to the original series to different degrees. The GM(1,4) model shows significant fluctuations at the first few time points, deviating from the original values, and then performs better in the subsequent fitting and prediction. SVR, ANN, and ARIMA are all closer to the original series in the fitting part, but SVR is much higher than the original value in the prediction part. ANN and ARIMA are lower than the original value. Compared with the other models, the ENGM(1,4) model has the highest approximation to the original series, with only slight fluctuations in the prediction part. The APE comparison chart (Fig. 5b) illustrates that the APE value performance is consistent with the trend plot. The APE value of the new model is less than 10% at most time points, especially in the fitting part, which is around 1%. The overall performance is optimal compared with other models.

Fig. 5.

Fitted and predicted trends and APE values for each model in case 2

In summary, even if there are individual indicators that are non-optimal, from the perspective of fitting and predicting the overall situation, the ENGM(1,4) model can most effectively fit and predict the carbon emissions of the US transportation sector.

Validation case 3: Japan

The dataset of the third verification case includes Japan’s transportation sector carbon emissions, GDP, energy consumption, and population data from 2001 to 2018. Carbon emissions show a decreasing trend. The parameter value $r=0.9630$ of the ENGM(1,4) model is obtained by the quantum particle swarm algorithm. The fitted and predicted values of each model and the MAPE values are shown in Table 6. Other comparison indices are shown in Table 7. Table 6 shows that the MAPE_SIM and MAPE_TOT of the new model are the lowest among all models, with 0.4967% and 1.5404%, respectively, which are less than 2%. This outcome indicates that the overall accuracy is higher. The MAPE_PRE of the GM(1,4) model is 0.6025%, which is the lowest among all the models and nearly 4% lower than the 4.0454% of the new model. The predictive ability of the new model is not as good as that of the GM(1,4) model. From the other comparison indices in Table 7, it seems that the new model has the lowest MAE and RMSE among all the models except for the STD, which is lower than that of the ANN. Overall, the ENGM (1,4) model is the best. The MAPE_SIM of the SVR and ANN models are 0.6216% and 0.8156%, respectively, both of which are less than 1%, indicating that these two models fit better, and their MAPE_PRE are 7.3684% and 4.7280%, respectively, both of which are less than 10%, indicating that these two models are also better adapted to the context of this study, but their prediction effects and overall accuracy are not as good as the new model. All three MAPE values of the GMC(1,4) model are around 25% and the rest of the indicators performed poorly, indicating that GMC(1,4) has poor accuracy in this study context.

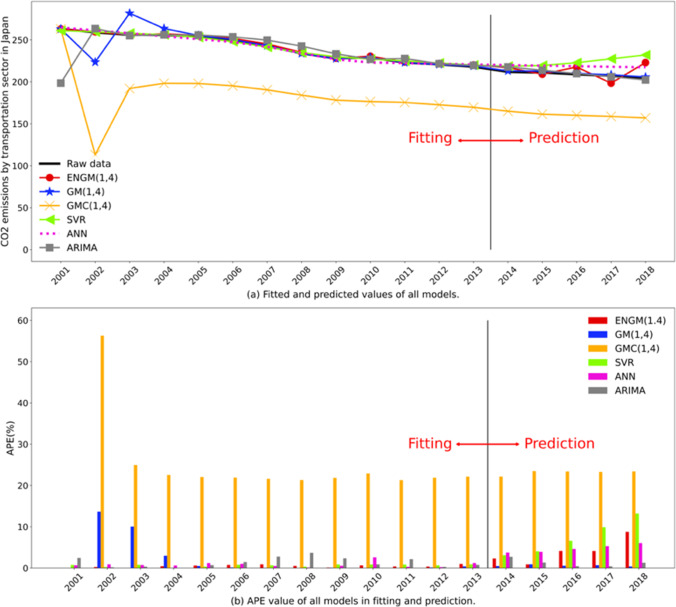
To further demonstrate the approximation effect of fitting and prediction, the fitted and predicted values of each model are transformed into curve trend plots and APE comparison plots, as shown in Fig. 6. As can be seen from the Fig. 6a trend plot, the prediction and fitting trends of GMC(1,4) are significantly lower than the original series with larger errors, and the remaining five models are able to fit the original series to varying degrees. The GM(1,4) and ARIMA models generally coincide with the original sequence, except for the large fluctuations at the previous several time points that deviate from the original value, indicating that the errors of these two models are relatively small. The SVR and ANN models are very close to the original series in the fitting part, but both are significantly higher than the true values in the prediction part, indicating that these two models are not good enough for prediction. Compared to the other models, ENGM(1,4) approximates the original series the most, with only slight fluctuations in the prediction part, which is the closest to the original value as a whole. From the comparison of APE values in Fig. 6b, the APE values of ENGM(1,4) are the lowest among all models in the fitting part, and the APE values in the prediction part are also within 10%, so the APE performance of ENGM(1,4) seems to be the best overall.

Fig. 6.

Fitted and predicted trends and APE values for each model in case 3

In summary, even if individual indicators are non-optimal, from the perspective of fitting and predicting the overall situation, the ENGM(1,4) model can most effectively fit and predict the carbon emissions of Japan’s transportation sector.

Analysis of results

The three validation cases mentioned above are analyzed. By comparing the fitting and prediction results and the values of each statistical indicator and parameter, the following conclusions are drawn.

1. The parameter values of the ENGM(1,4) model for the three validation cases are shown in Table 8.

Table 8.

Parameter values of the ENGM(1,4) model in the three validation cases

Parameters	r	a	b	c2	c3	c4	d
China	3	42.8068	5.84e-15	− 0.0203	0.1296	2.13e-05	323.2469
The USA	0.1840	− 31.7518	290.4235	0.0293	− 0.1106	0.2562	− 606.5978
Japan	0.9629	− 9.0313	0.0086	− 0.0041	− 0.0271	0.0006	237.9455

$r$ and $c2$ are the indices and coefficients of multiple variables of GDP, where $r$ can reflect the impact of GDP on changes in carbon emissions. The value of $r$ in the case of China is as high as 3, and the value of $r$ in the cases of the USA and Japan is less than 1. Based on the data characteristics and economic development of the three countries, China’s GDP has increased by approximately 4.6 times since its accession to the World Trade Organization in 2001 to 2011. The implementation of the “12th Five-Year” and “13th Five-Year” plans, which were implemented from 2011 to 2018, resulted in great efforts to develop economic policies that have allowed GDP to continue to maintain rapid growth. The economic development has brought the transportation industry to take off. Therefore, the index $r$ in China’s case is the largest; that is, GDP changes have a high degree of impact on carbon emissions. Compared with China, the USA and Japan, which have already entered the ranks of developed countries, have shown steady economic growth in the past 20 years, so they have relatively small $r$.

The coefficient $a$ can reflect the characteristics of the original series data to some extent. $a$ is 42.8068, − 31.7518, and − 9.0313 in the three cases of China, the USA, and Japan, respectively, which show increasing, fluctuating, and decreasing characteristics of carbon emissions in the transportation sector in the last 20 years. The increase in China from 2001 to 2018 was as high as 250.3788%, while the USA showed a decreasing trend from 2005 to 2014, with a decrease of 9.2920%; and Japan decreased by 28.2926% from 2001 to 2018. These indicate that the positive and negative values of $a$ can represent the increase or decrease of the original series and that the size of $a$ can reflect the increase or decrease.

The coefficients $b$, $c3$, and $c4$ can reflect the impact of GDP, energy consumption in the transportation sector, and population on the carbon emissions of various countries to a certain extent. If the coefficient is positive, it is positively correlated, and if the coefficient is negative, it is negatively correlated.

The constant term $d$ represents the degree of influence of random disturbance factors on the model, which can somewhat balance the error and improve the accuracy of the model.

• (2)Comparing the ENGM(1,4) model with the other five models, it can be seen by the three types of MAPE indicators that in these three national transportation sector carbon emission forecasts show that there are cases in which the comparison indicators of other models are better than the new model. Overall though, the new model has the best fitting and forecasting effect. The APE values at each time point are lower, implying that the new model has less error and higher validity. The three categories of MAE, RMSE, and STD of each model are compared in Table 7. The indicators of the new model are optimal or suboptimal compared with those of other models. The ENGM(1,4) model thus has high robustness in carbon emission prediction. The GM(1,4) model also achieves ideal results in fitting and prediction, indicating that it is also suitable for the background of this research. SVR and ANN models have high accuracy in fitting, but the phenomenon of “overfitting” makes their prediction errors large. The GMC(1,4) model has poor indicators and calculation results in the verification case, so the model is not suitable for the background of this research.
• (3)The three application cases of China, the USA, and Japan in the “Validation case 1: China” to “Validation case 3: Japan” sections respectively apply the ENGM(1,4) model to three types of data series with different characteristics: increasing, fluctuating, and decreasing. The model is built with data from 2001 to 2013 to predict carbon emissions from the transportation sector in each country for the next 5 years from 2014 to 2019. The trend plots of the fitted and predicted values and each statistical indicator can illustrate the flexibility and validity of the new model with high accuracy. The new model can be adapted to the research context of short-term carbon emission prediction with data characterized by incomplete information.

Application

Further prediction

In the fifth part, by comparing it with six other five models, it is proved that the ENGM(1,4) model can better fit and predict the carbon emissions of the transportation sectors of China, the USA, and Japan. In this section, the new model is used to predict the carbon emissions of the transportation sector in these three countries for the next 7 years. The corresponding analysis and recommendations are given based on the prediction results. (It should be noted that carbon emissions are energy data, and there is usually a time delay in the statistical process. The latest carbon emissions data for these three countries from the International Energy Agency (IEA) are currently available as of 2018).

The multivariate grey model relies on the values of other influencing factors in the forecast. As such, the values of the three influencing factors of GDP (X₂), total energy consumption in the transportation sector (X₃), and population (X₄) for the three countries are predicted for the next 7 years using the GM(1,1) model based on the data of the last 10 years from 2009 to 2018 before the prediction. The results are shown in Table 9. Based on the data of the three countries for the 18 years (2001–2018), the ENGM(1,4) model is used to predict the value of carbon emissions in the transportation sector for the 7 years (2019–2025) for each country. The predicted values and the rate of change are obtained as shown in Table 10. The values of the model parameters are provided in Table 11, and the trend graphs of the fitted and predicted values compared with the real values are depicted in Fig. 7. The results of the projections for the three countries according to Table 10 and Fig. 7 are analyzed as follows.

1. China’s carbon emissions from the transportation sector show a steady upward trend from 2019 to 2025, with an average growth rate of 5.3692%. The slope of the change curve in 2019–2020 is significantly lower than in 2021–2025, due to the impact of the COVID-19 and a significant decrease in the transportation travel rate as a result of the government’s closure management measures. In the “14th Five-Year Plan,” China specifies the goal of peaking carbon in 2030, in which transportation carbon emissions account for 10% of the country’s total carbon emissions. At present, China’s new energy industry is in a stage of vigorous development, and the transportation sector’s energy conservation and emission reduction policies are gradually being implemented. Owing to the wide coverage of the policy and the long period of time, related technical research is still in its infancy. According to the “Report on China’s Car Ownership Data,” the number of private and public travel vehicles continues to increase, so low-carbon travel-related measures are effective yet slow. CICC research data points out that China’s overall carbon emission growth rate in the past 20 years is 5.6%, which is higher than the average growth rate predicted in this study. By comparing the slope of the graph, it can be seen that the future growth rate of carbon emissions in the transportation sector will slow down to a certain extent. This partly explains the effectiveness of transportation reform and the reliability of the conclusions of this paper.

2. The overall carbon emissions of the US transportation sector show a fluctuating upward trend, with an average rate of change of 0.9392%. The characteristics of changes from 2019 to 2021 are related to the COVID-19. The US epidemic monitoring and control policies lagged behind those of China, and related measures were gradually adopted in the second half of 2020. Therefore, the carbon emissions of its transportation sector were on the rise in 2019–2020, declined in 2020–2021, and then will rise in volatility. The slow growth rate and low overall rate of change in carbon emissions from the US transportation sector are consistent with the state of the country’s transportation development and national energy policy. The USA is the first country to implement carbon emission standards. It has implemented the optimization of energy structure and transportation structure very early, and it has the world’s most complete integrated transportation system. Figure 7 shows that carbon emissions from the US transportation sector are in a relatively stable state. The growth of automobiles and population has brought fluctuations within a reasonable range, which shows that the prediction results of this article are in line with the actual situation.

3. The overall carbon emission of Japan’s transportation sector shows a steady downward trend, with an average decline rate of 1.2231%. The slope of the curve shows a slow decline from 2019 to 2020 and a faster decline after 2020, which can be partly explained by the impact of the COVID-19. The COVID-19 in Japan was gradually revealed by 2020, and the policy of staying at home and reducing travel made the decline of transportation carbon emissions faster in 2020–2021. The characteristics of Japan’s carbon emissions are related to its national conditions and transportation energy policies. On the one hand, Japan is the most aging country in the world, with a decreasing trend in population changes. The number of transportation vehicles also grows slowly, so the level of carbon emissions from the transportation sector is low and on a decreasing trend. On the other hand, according to the statistics and reports of the National Energy Agency, Japan is short of energy resources, has a low self-sufficiency rate, and mostly relies on imports. Therefore, the Japanese government began to implement new energy policies and low-carbon reforms in the transportation industry in the twentieth century, and achieved better results as early as around 2000. Japan’s national conditions, energy, and transportation conditions provide support for the predicted results of this paper.

Table 9.

Predicted values of factors influencing carbon emissions in the transportation sector by country and predicted MAPE

Country	Year	X2	X3	X4
		GDP ($100 million)	Energy consumption (k toe)	Population (10 thousand)
China	2019	150,710	365,820	139,990
	2020	164,090	389,420	140,700
	2021	178,650	414,530	141,420
	2022	194,500	441,270	142,140
	2023	211,760	469,740	142,860
	2024	230,550	500,040	143,590
	2025	251,010	532,290	144,330
	MAPESIM	4.5466%	2.2507%	0.0227%
US	2019	212,160	639,580	32,944
	2020	220,550	646,890	33,174
	2021	229,280	654,290	33,405
	2022	238,350	661,770	33,637
	2023	247,780	669,340	33,872
	2024	257,580	676,990	34,108
	2025	267,780	684,730	34,345
	MAPESIM	0.3924%	1.1056%	0.0501%
Japan	2019	44,248	69,258	12,640
	2020	42,803	68,353	12,622
	2021	41,405	67,459	12,604
	2022	40,053	66,577	12,586
	2023	38,744	65,706	12,568
	2024	37,479	64,847	12,550
	2025	36,255	63,999	12,532
	MAPESIM	6.6367%	0.4341%	0.0258%

Table 10.

Parameters and future CO₂ emission forecasting of the ENGM(1,4) model

Predictive value	2019	2020	2021	2022	2023	2024	2025
China	1062.1564	1070.9672	1142.0436	1211.1907	1286.1209	1366.3890	1452.0233
US	1723.7837	1772.4361	1762.9033	1791.2436	1794.5603	1813.9879	1822.5725
Japan	198.8973	198.6185	194.6241	192.6855	189.7079	187.3499	184.7219
Rate of change	2019–2020	2020–2021	2021–2022	2022–2023	2023–2024	2024–2025	average value
China	0.8287%	6.6367%	6.0547%	6.1865%	6.2411%	6.2672%	5.3692%
US	2.8240%	− 0.5374%	1.6076%	0.1852%	1.0826%	0.4732%	0.9392%
Japan	− 0.1402%	− 2.0111%	− 0.9961%	− 1.5453%	− 1.2430%	− 1.4027%	− 1.2231%

Table 11.

Parameter values of the ENGM(1,4) model in three prediction cases

Parameter	r	a	b	c2	c3	c4	d
China	0.0002	2.4938	− 1,447,563.33	0.0045	0.0039	0.0037	1,450,337.77
US	1.2647	9.5767	− 5.6874e-06	− 0.0108	0.0321	− 0.0442	1715.0059
Japan	2.3764	6.6212	− 7.6142e-13	3.8825e-05	0.0194	− 0.0006	270.9546

Fig. 7.

Fitting and predicted trends of carbon emissions in various countries predicted by the ENGM(1,4) model

Analysis and expansion

In the “Further prediction” section, the ENGM(1,4) model is used to forecast and analyze the carbon emissions of the transportation sector in three countries, China, the USA, and Japan, respectively, for the 7 years from 2019 to 2025. Based on the projection results, the following conclusions and insights are drawn.

1. The different economic developments, energy policies, and transportation reforms of these three countries have resulted in three carbon emission data profiles for the transport sector. As developed countries, the USA and Japan have implemented energy structure optimization and low-carbon travel policies in the twentieth century, and the related technology development has been at the world’s leading level, so the overall change trend of carbon emissions is not significant. Among them, the impact of Japan’s serious population aging on transportation travel has led to a decreasing trend of carbon emissions. China’s rapid economic development in recent years has led to major changes in the transportation industry. China’s implementation of related environmental protection policies is lagging behind the USA and Japan. Therefore, the carbon emissions of China’s transportation sector will continue to grow for a period of time in the future, but the growth rate will slow down.

2. Drawing on the energy policies of the USA and Japan, we focus on providing some suggestions for the future development of carbon emissions from the transportation sector in China. First of all, the government and relevant units can learn from the US transportation structure reform measures, and accelerate the progress of transportation energy-saving and emission reduction-related technology research, so as to improve the level of transportation intelligence thus enhance the intelligent transportation system, and establish a more scientific and environmentally friendly travel system from a macro perspective. Second, complete fuel economy standards and low-carbon fuel standards must be formulated. On the one hand, advanced technologies can be used to improve engine equipment and in turn fuel economy efficiency. On the other hand, the government should strengthen the management of transportation tools and strictly control the emissions carbon in the transportation sector through policies and methods. Finally, the research and development (R&D) of new automotive technologies and popularization of new energy vehicles should be strengthened by relying on China’s well-known auto companies. Energy-saving and environmentally friendly vehicles should be vigorously developed, and automotive innovation and industry alliances must be promoted. A public R&D led by the government should be established, with the joint participation of enterprises and research institution platforms.

Conclusion

In this study, a new nonlinear multivariate grey model based on the EKC is proposed for use in the analysis of carbon emissions from the transportation sector in China, the USA, and Japan. According to the verification cases and predictions of the three countries, the following conclusions are drawn:

1. Considering the change of energy structure and the data characteristics of carbon emissions with incomplete information in short-term forecasting and basing on the theory related to EKC, this study combines the characteristics of IPAT equation and extended STIRPAT model, and identifies the factors affecting carbon emissions in transportation sector as GDP, energy consumption in transportation sector, and population. The index of GDP in the EKC assumption is extended from 2 to $r$ to further enhance the flexibility of the model. A new type of ENGM(1,N) model is established on the basis of the differential information principle. The least squares estimation is used to obtain the model parameters, and the quantum particle swarm optimization algorithm is designed to optimize the unknown index and improve the model accuracy. The new model is a coupling of multiple models and methods, with multiple characteristics, and it provides a new idea for carbon emission prediction.

2. The economic development, energy policy, and transportation conditions of China, the USA, and Japan differ greatly, with carbon emissions in the transportation sector showing increasing, fluctuating, and decreasing characteristics in the past 20 years, respectively. The ENGM(1,4) model is compared with five models, namely, GM(1,4), GMC(1,4), SVR, ANN, and ARIMA, through three validation case sets. The new model is used in the prediction of carbon emission data from the transportation sector for these three countries for the 7 years (2019–2025). The results show that the ENGM(1,4) model has the best fitting and prediction effect than other models, and can better adapt to the data characteristics of carbon emissions.

Although the new model has strong theoretical and practical significance, the model needs to be further improved and perfected:

1. The degree of influence of different factors on carbon emissions should be further explored. A data-based structure selection algorithm can be considered to determine the coefficient values in a more intuitive and scientific way, so as to clarify the laws of parameters’ values and analyze the correlation degree of influencing factors and the development trend of prediction results, and fully explore the value of the model.

2. Through the research in this paper, it can be seen that the prediction and early warning of carbon emissions are of great significance for planning the low-carbon development of specific industries. In the future, from a sectoral perspective, the model can be further extended to carbon emissions research in other industries, such as the industrial sector and the power sector, which account for a large proportion of carbon emissions. The new model can also be used to study carbon emissions from different fossil energy sources (e.g., coal, oil, natural gas) from an energy perspective. In addition, from the model perspective, the new model of this paper is proposed based on the EKC hypothesis to explore the relationship between the environment and the economy, so that it can also be considered for application to study the association between energy consumption and economic and other influencing factors in different types and sectors.

Author contribution

Siyuan Huang: methodology, data curation, writing—original draft, visualization, formal analysis. Xinping Xiao: conceptualization, methodology, supervision, writing—review and editing. Huan Guo: writing—review and editing, supervision.

Funding

This work is supported by the National Natural Science Foundation of China (Nos. 71871174) and the Fundamental Research Funds for the Central Universities (WUT: 2019IA005).

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

Declarations

Ethics approval and consent to participate

There is no ethical approval and patient consent to participate is required for this study.

Consent for publication

The authors confirm that the final version of the manuscript has been reviewed, approved, and consented for publication by all authors.

Competing interests

The authors declare no competing interests.