Identifying phenotype-associated subpopulations by integrating bulk and single-cell sequencing data

Abstract

Single-cell RNA sequencing distinguishes cell types, states, and lineages within the context of heterogeneous tissues. However current single-cell data cannot directly link cell clusters with specific phenotypes. Here we present Scissor, a method that identifies cell subpopulations from single-cell data that are associated with a given phenotype. Scissor integrates phenotype-associated bulk expression data and single-cell data by first quantifying the similarity between each single cell and each bulk sample. It then optimizes a regression model on the correlation matrix with the sample phenotype to identify relevant subpopulations. Applied to a lung cancer single-cell RNA-seq dataset, Scissor identified subsets of cells associated with worse survival and with TP53 mutations. In melanoma, Scissor discerned a T cell subpopulation with low PDCD1/CTLA4 and high TCF7 expression associated with an immunotherapy response. Beyond cancer, Scissor was effective in interpreting Facioscapulohumeral muscular dystrophy (FSHD) and Alzheimer’s disease datasets. Scissor identifies biologically and clinically relevant cell subpopulations from single-cell assays by leveraging phenotype and bulk-omics datasets.

Single-cell sequencing technologies are revolutionizing biomedical research and clinical practice by enabling the comprehensive characterization of cells from complex tissues^{1, 2}. In contrast to bulk data that measures the averaged properties of whole tissue, single-cell RNA sequencing (scRNA-seq) allows identifying cell types, states, and lineages of different cell subpopulations in a heterogeneous tissue ecosystem^3–5. To recognize critical subpopulations from single-cell data, the standard approach is to perform unsupervised clustering to define cell clusters, inspect marker genes of each cluster, and assess the enrichment of the marker genes in known cell types and pathways to evaluate the importance for each cell cluster^{6, 7}. However, identifying cell subpopulations that drive phenotypes, such as disease stage, tumor metastasis, treatment response, and survival outcome, is of indispensable importance since it will facilitate cell-type targeted therapies as well as prognostic biomarker discovery^{3, 8}. Unfortunately, single-cell technology is not practical in large cohorts, and most single-cell experiments involve less than twenty patient samples^9–11, which lacks the statistical power to identify the cell subpopulations driving the phenotype of interest.

Meanwhile, valuable clinical phenotype information is widely available from big data consortia like The Cancer Genome Atlas (TCGA)¹² through a decade-long collection of clinicopathologic annotations. Clinical phenotype information is primarily collected on bulk tissue samples, especially in the form of formalin-fixed-paraffin-embedded samples, which are not feasible for single-cell profiling. Therefore, there is an unmet need to leverage such widely accessible and valuable phenotype information to guide cell subpopulation identification from single-cell data.

To the best of our knowledge, there is no bioinformatics tool that uses external bulk phenotypes to guide the identification of key cell subpopulations in a unified framework for single-cell data analysis. Therefore, in this study, we introduce Single-Cell Identification of Subpopulations with bulk Sample phenOtype coRrelation (Scissor). By leveraging bulk data and phenotype information, this algorithm automatically selects cell subpopulations from single-cell data that are most responsible for the differences of phenotypes. The novelty of Scissor is that it utilizes phenotype information from bulk data to identify the most highly disease-relevant cell subsets. Our studies suggest that Scissor is a promising tool to explore and interpret single-cell data from a new perspective, which can shed fresh light on disease mechanisms and improve the diagnosis and treatment of diseases.

Results

Overview of Scissor.

To utilize bulk data and phenotype information for assisting single-cell data analysis, we developed an algorithm, Scissor, to identify cell subpopulations from single-cell data that are most highly associated with the given phenotypes. Briefly, the three data sources for Scissor are a single-cell expression matrix, a bulk expression matrix, and a phenotype of interest (Fig. 1a). The phenotype annotation of each bulk sample can be a continuous dependent variable, binary group indicator vector, or clinical survival data. The key step of Scissor is to quantify the similarity between the single-cell data and bulk data through a measurement like Pearson correlations for each pair of cells and bulk samples. After this, Scissor optimizes a regression model on the correlation matrix with the sample phenotype (Fig. 1b). The selection of the regression model depends on the type of the input phenotype, i.e., linear regression for continuous variables, logistic regression for dichotomous variables, and Cox regression for clinical survival data. Since a small subset of cells could drive the phenotype of interest¹³, a sparse penalty and a graph regularization are imposed on the regression model to select similar cells that are important for the given phenotype with high confidence (Fig. 1b). Based on the signs of the estimated regression coefficients, the cells with non-zero coefficients can be indicated as Scissor positive (Scissor+) cells and Scissor negative (Scissor-) cells, which are positively and negatively associated with the phenotype of interest, respectively (Fig. 1c). The cells with coefficients of zero are indicated as background cells. Furthermore, to control the false associations between single-cell and bulk data, we designed a reliability significance test to determine whether the chosen data is suitable for our phenotype-to-cell associations (Fig. 1d). Finally, the Scissor selected cells will be further characterized in downstream analyses, such as exploration of signature genes and functionally enriched pathways (Fig. 1e).

Fig. 1. The workflow of Scissor and its performance in applications with known phenotype-associated cell subpopulations.

a, The inputs for Scissor are a single-cell expression matrix, a bulk expression matrix, and a corresponding phenotype of interest such as drug response or clinical information. b, Scissor calculates a correlation matrix and a cell-cell similarity network based on input sources, which are further integrated with the phenotype into a network regularized sparse regression model to select the most relevant cell subpopulations. c, The selected cells by Scissor with red and blue dots indicating the cells positively or negatively associated with the phenotype of interest. d, The Scissor results are evaluated by a reliability significance test to control the false associations between single-cell and bulk data. MSE, mean squared error; AUC, area under the ROC curve; c-index, concordance index. e, The selected cells by Scissor can be further investigated by downstream analyses. f, The UMAP visualization of the simulated cells. The orange and green dots are the ground truth cell subpopulations specific to phenotype I and II, respectively. g, The visualization of the Scissor selected cells on the same UMAP as in a. The red and blue dots are the Scissor selected cells associated with phenotype I and II. h, The Venn diagrams show overlaps between the Scissor selected cells and the ground truth phenotype-specific cells. i, The UMAP visualization of 29,888 LUAD cells. The color encoding the cell types defined in the original paper. j, The UMAP visualization of the Scissor selected cells. The red and blue dots are cells associated with the tumor and normal phenotypes. k. The pie chart of the Scissor selected cells with the corresponding bar plots showing the detailed constitutions in each type defined in i.

Capturing phenotype-associated subpopulations in simulations.

We first assessed the performances of Scissor on a series of simulated datasets to test whether Scissor can recover the known phenotype-associated cell subpopulations. To achieve this, we employed Splatter¹⁴ to simulate two phenotype-specific cell subpopulations as the ground truth and one common cell type shared by the two phenotypes as well as the corresponding bulk expression data (Fig. 1f; Methods). In one simulation, the two ground-truth phenotype-specific cell subpopulations were characterized by 21 true differentially expressed genes (DEGs) between them but cannot be distinguished by standard single-cell analysis pipelines since they were in the same cluster (Supplementary Fig. 1a, b). Utilizing bulk gene expressions to guide the cell subpopulation identification, we found that Scissor recovered 90.5% and 91.8% of the ground truth cells unique to each phenotype, with low false positive rates of 2.1% and 0.9%, respectively (Fig. 1g, h). There were 22 DEGs between the two cell subpopulations identified by Scissor, including all 21 true DEGs between the two ground-truth phenotype-associated cell subpopulations (Supplementary Fig. 1b). In contrast, the fold change signals of these 21 true DEGs at the bulk level were weak with values less than 1.1 (Supplementary Fig. 1c). Such improved phenotype-specific gene signal detection will facilitate the reliable downstream interrogation of different cell types and states within a heterogeneous cell population. When performing this simulation 100 times, Scissor had an average recall of 0.88 and precision of 0.93 in identifying phenotype-associated subpopulations.

Furthermore, to check whether the performance of Scissor depends on the true DEG signals at the bulk level, we reset the expression levels of these true DEGs as the least differentially expressed genes (Methods). We found that Scissor can still identify 87.6% and 87.3% of the ground truth cells for each phenotype, with slightly higher false positive rates of 4.2% and 5.9% (Supplementary Fig. 1d, e). In this setting, Scissor detected all 21 true DEGs with only two false positive DEGs (Supplementary Fig. 1b). Finally, we demonstrated the robustness of Scissor on the batch-effects corrected scRNA-seq data (Supplementary Fig. 1 f–i). Overall, the results from these simulations were largely consistent with each other, indicating Scissor’s capacity to identify the phenotype-associated cell subpopulations from single-cell data.

Identifying subpopulations of tumors and normal phenotypes.

We then applied Scissor to a lung cancer scRNA-seq data that included tumor cells and cells from the tumor microenvironment with known cell types¹⁰ (Fig. 1i). In order to demonstrate the efficacy of our algorithm, we utilized the tumor and normal phenotypes from 577 TCGA lung adenocarcinoma (LUAD) bulk samples¹⁵ to guide Scissor analysis. We expected that, by using these data, Scissor would infer cells that were most highly associated with cancer or normal phenotype in this heterogeneous single-cell dataset. Because of the binary phenotype settings of this application, where samples with a phenotype indicator value 1 correspond to tumor samples, Scissor+ cells should be associated with the cancer cells, and Scissor- cells should be associated with the normal phenotype. Among 29,888 cells from different cell types (Fig. 1i), 361 Scissor+ cells and 534 Scissor- cells were selected by Scissor, which were associated with the tumor and normal phenotypes with high confidence (Fig. 1j). As anticipated, over 98% of Scissor+ cells were verified to be malignant cells (Fig. 1k). Such a high proportion of cancer cells in Scissor+ cells cannot be selected by chance (Supplementary Fig. 1j, hypergeometric test p<2e-16), which confirmed that Scissor can identify the cells associated with the phenotypes of interest. As for Scissor- cells, the cell types were relatively more balanced than Scissor+ cells since it was designed to associate with more diverse non-malignant cell types (Fig. 1k). Myeloid cells and alveolar cells were the two main selected cell types, accounting for 42.3% and 36.9% of total Scissor- cells, respectively. All cell types in Scissor- cells, especially the alveolar cells, are important cell types in normal lung tissues. Thus, we demonstrated that Scissor can precisely identify the most phenotype-associated cells from single-cell data with the guidance of phenotype information from bulk data.

Detecting a hypoxic subpopulation related to worse survival.

Cancer cells are heterogeneous and include subpopulations such as cancer stem cells, which are known to drive tumor progression and poor prognosis^{16, 17}. Therefore, we applied Scissor, guided by 471 TCGA-LUAD bulk samples with survival information¹⁵, to identify aggressive cancer cell subpopulations within 4,102 cancer cells from the same lung cancer scRNA-seq dataset¹⁰. These cells were separated into 12 clusters (Fig. 2a), which demonstrated the heterogeneous nature of the cancer cells. Out of 205 Scissor selected cells, 201 Scissor+ cells were associated with Worse Survival (defined as Scissor_WS cells thereafter), and only 4 Scissor- cells were associated with good survival (Fig. 2b). The Scissor_WS cells were mainly from clusters 1 and 3 (Fig. 2c). To understand the underlying transcriptional patterns of Scissor_WS cells, we compared the gene expressions of those cells with all other cells. As a result, 23 up-regulated genes and 205 down-regulated genes were differentially expressed in Scissor_WS cells over all other cells, respectively (Fig. 2d and Supplementary Table 1). Notably, we found that multiple important hypoxia-related genes were among the above 23 overexpressed genes (Fig. 2e). Functional enrichment analysis also confirmed that the hypoxia-related pathways, such as glycolysis and glucose metabolism processes, were activated in Scissor_WS cells (Fig. 2f and Supplementary Table 1). Consistently, motif analysis revealed that the HIF1A binding motif was the most enriched motif in the 23 up-regulated genes (Supplementary Table 1), which is a key mediator of cellular response to lowered oxygen levels ¹⁸. We also observed higher hypoxia pathway activities in an identified cell subpopulation related to higher tumor stages (Supplementary Fig. 2).

Fig. 2. Scissor identification results on lung cancer cells guided by TCGA-LUAD survival outcomes.

a, The UMAP visualization of 4,102 LUAD cancer cells. b, The UMAP visualization of the Scissor selected cells. The red and blue dots are Scissor+ (worse survival) and Scissor- (good survival) cells. c, The bar plot shows the constitution of Scissor+ cells in different clusters. d, The volcano plot of differential gene expressions in Scissor+ cells versus all other cells. The two vertical dashed lines represent ± ln(1.25) fold-changes in gene expression, and the horizontal dashed line denotes FDR cutoff 0.05. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. e, The violin plots of expression levels of selected up-regulated genes in Scissor+ cells. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. f, The enrichment bar plot of selected hypoxia-related Reactome and Hallmark pathways. g, The Kaplan-Meier survival curves show the clinical relevance of the lung cancer signature on four independent datasets. Tick marks indicate censoring events. The statistical p-values were determined by the two-tailed log-rank sum test. h, The forest plots show the hazard ratios and 95% confidence intervals for the lung cancer signature and three additional clinical features according to the univariate Cox model. i, The forest plots show the hazard ratios and 95% confidence intervals for the lung cancer signature and stage information according to the multivariable Cox model. Squares represent the hazard ratios and the horizontal bars extend from the lower limits to the upper limits of the 95% confidence intervals of the estimates of the hazard ratios. These statistics are calculated on GSE11969 (n = 149 biologically independent samples) and GSE13213 (n = 117 biologically independent samples), respectively. The statistical p-values were determined by the two-tailed Wald test.

To further examine the clinical relevance of the above 23 overexpressed genes (defined as lung cancer signature; Supplementary Table 1), we chose six independent lung cancer datasets collected in PRECOG¹⁹ (Supplementary Table 1). We found that in 5 out of 6 datasets, the patients with higher signature scores had significantly worse survival time than the patients with lower signature scores (Fig. 2g and Supplementary Fig. 3). This observation indicated that the lung cancer signature derived from Scissor_WS cells was associated with worse survival and could provide potential drug targets for further investigation²⁰. Among the six chosen datasets, two of them have additional clinical features. We thereby investigated whether our lung cancer signature had predictive power for patient survival beyond clinical features. To achieve this, we examined pathological stage, sex, age at diagnosis, and our lung cancer signature in these two datasets. We found that only the pathological stage and our signature were significantly associated with patient survival in univariate Cox survival analyses (Fig. 2h). Furthermore, our signature remained statistically significant in both datasets after adjusting for tumor stage in multivariable Cox survival analyses (Fig. 2i).

In summary, Scissor identified an aggressive cancer cell subpopulation from the LUAD scRNA-seq data that was associated with worse survival outcomes and can be characterized by the overexpression of hypoxia-related genes. The high hypoxia activity might drive LUAD progression and thereby conferred poor outcomes to patients whose tumors contained significant numbers of such cells.

Profiling a cell subpopulation associated with TP53 mutation.

To further demonstrate the high flexibility of Scissor in exploring a variety of hypotheses of cell states in single-cell data, we used other phenotypical features provided by TCGA-LUAD to guide the identification of cell subpopulations within the same 4,102 lung cancer cells. Here we focused on TP53, a commonly mutated tumor suppressor genes found in human malignancies.

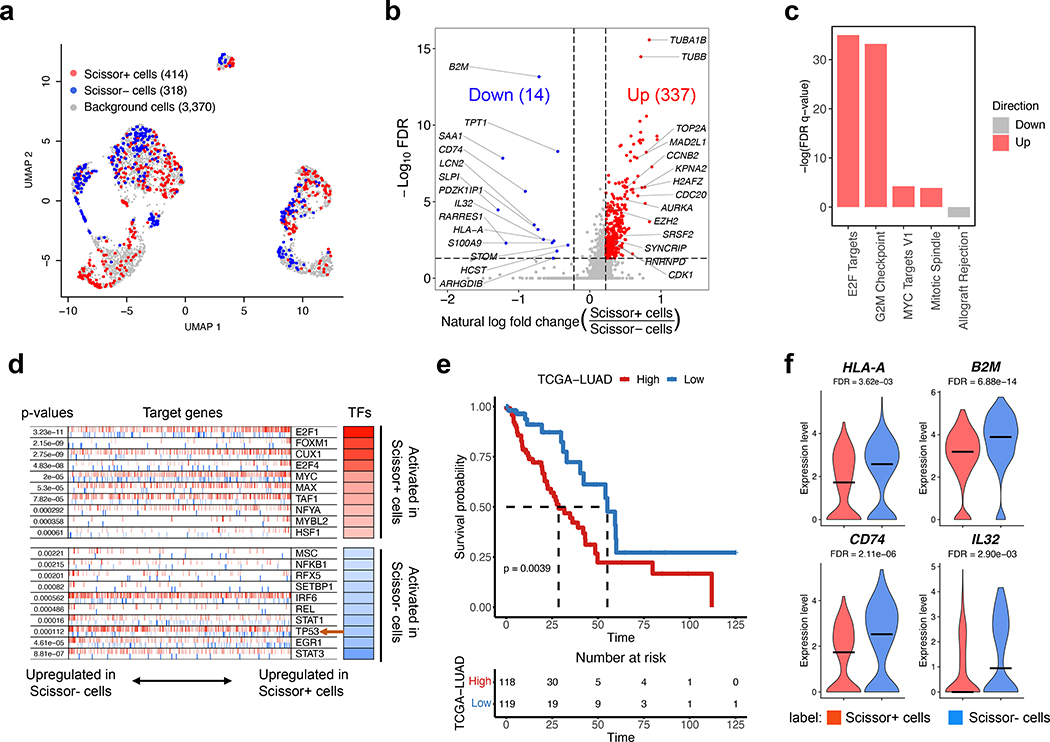
We collected TP53 mutation status (mutant or wild-type) from TCGA-LUAD as the phenotypes of 498 bulk samples. Scissor identified a total of 414 Scissor+ cells associated with the TP53 mutant and 318 Scissor- cells associated with the wild-type (Fig. 3a). To uncover the transcriptional differences between these cells, we compared the gene expressions of Scissor+ cells with that of Scissor- cells. As a result, 337 up-regulated genes and 14 down-regulated genes were differentially expressed in Scissor+ cells over Scissor- cells (Fig. 3b and Supplementary Table 2). The 337 up-regulated genes include multiple E2F target genes and cell cycle progression-related genes, e.g., AURKA, CDK1, CCNB2, and TOP2A (Fig. 3b). Functional enrichment analysis also confirmed that cell cycle-related pathways, such as hallmark E2F targets, were activated in Scissor+ cells (Fig. 3c and Supplementary Table 2). Consistently, master regulator analysis revealed that the activities of E2F transcription factors (TFs) family members E2F1 and E2F4 were both highly elevated in Scissor+ cells (Fig. 3d). In this analysis, we also found that TFs FOXM1 and MYC, which are known to be repressed by wild-type TP53^{21, 22}, were activated in the cell subpopulation associated with the TP53 mutant (Fig. 3d). FOXM1 is reported as a major predictor of unfavorable outcomes in human cancers²². These observations are in line with the literature that TP53 mutation leads to tumorigenesis by involving its impaired capability to arrest cell cycle and maintain DNA repair in response to oncogenic stimuli²³. Indeed, master regulator analysis confirmed that TP53 is inactivated in Scissor+ cells (Fig. 3d), which further demonstrates the capability of Scissor in identifying phenotype-associated cell subpopulations.

Fig. 3. Scissor identification results on lung cancer cells guided by TP53 mutation status.

a, The UMAP visualization of the Scissor selected cells. The red and blue dots are cells associated with the TP53 mutant and wild-type phenotypes. b, The volcano plot of differential gene expressions in Scissor+ cells versus Scissor- cells. Red and blue points mark the genes with significantly increased or decreased expressions in Scissor+ cells (FDR <0.05 and absolute fold-change > 1.25). The two vertical dashed lines represent ± ln(1.25) fold-changes in gene expression, and the horizontal dashed line denotes FDR cutoff 0.05. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. c, The enrichment bar plot of selected cell cycle-related pathways in the Hallmark domain. d, The master regulator analysis reveals the top 10 most activated TFs in Scissor+ cells and Scissor- cells, respectively. The targets of each TF are shown as tick marks with red vertical lines representing positive targets and blue vertical lines for negative targets. Each row also illustrates the statistical p-value and the inferred differential activity for each transcription factor. e, The Kaplan-Meier survival curve shows the clinical relevance of the TP53 mutation signature. Tick marks indicate censoring events. A table is attached below to display the number of alive patients at given time points. The statistical p-value was determined by the two-tailed log-rank sum test. f, The violin plots of expression levels of selected down-regulated genes in Scissor+ cells. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test.

Furthermore, by linking those 337 up-regulated genes (defined as TP53 mutation signature; Supplementary Table 2) with clinical outcomes, we demonstrated that the patients with higher TP53 mutation signature scores had significantly worse survival time than the patients with lower scores (Fig. 3e). For the down-regulated genes, we found that major histocompatibility complex (MHC) class-related genes HLA-A, B2M, and CD74 are down-regulated in Scissor+ cells, and only one of them can be directly identified from the bulk level gene expression (Fig. 3f, Supplementary Fig. 4). Notably, B2M is a critical component of MHC class I antigen presentation and loss-of-function mutations in B2M have been reported in cancer patients resistant to immunotherapy²⁴. Thus, our phenotype-guided scRNA-seq analysis implied that TP53 mutation is likely a mechanism of resistance to checkpoint inhibitor treatment. In summary, this application demonstrated the versatile abilities of Scissor in integrating a variety of phenotypes for single-cell subpopulation annotations.

Identifying a T-cell subpopulation related to immunotherapy.

Immune checkpoint blockade (ICB) has achieved exciting results in a wide variety of cancers^{25, 26}. To understanding the mechanism underlying ICB response, we performed Scissor on a melanoma scRNA-seq dataset to identify a T cell subpopulation related to ICB response.

We focused our analysis on 1,894 T cells from the metastatic melanoma tumor microenvironment²⁷ and collected 70 melanoma bulk patients with known immunotherapy response information from two studies^{28, 29}. In the standard scRNA-seq data analysis, these T cells were clustered into six clusters (Fig. 4a). By performing Scissor, we identified 105 T cells as Scissor+ cells, which were associated with a Favorable immunotherapy Response (defined as Scissor_FR cells thereafter), and did not report any cells that are associated with the unfavorable immunotherapy responses (Fig. 4b). These 105 Scissor_FR cells mainly resided in clusters 2 and 3 (Fig. 4c), indicating clusters 2 and 3 were more associated with the effective responses than other clusters. To characterize the transcriptional identities of the Scissor_FR cells, we compared the gene expression of these cells with all other cells. In total, 17 up-regulated and 120 down-regulated differential expression genes were identified in Scissor_FR cells (Fig. 4d and Supplementary Table 3). The Scissor_FR cells that were associated with an effective ICB response had increased expressions of genes linked to T cell memory (CCR7 and SELL) and survival (IL7R) as well as lower expressions of inhibitory genes (HAVCR2, LAG3, PDCD1, CTLA4) and MHC II class genes (HLA-DRB5, HLA-DRB1, HLA-DPA1, HLA-DQB2, and HLA-DRB6) (Fig. 4d, e and Supplementary Table 3). The Scissor_FR cells also exhibited enhanced expression of transcript factor TCF7 that is associated with a favorable outcome in ICB treatment^{30, 31} (Fig. 4e). In addition, pathway enrichment analysis showed the Scissor_FR cells had higher TNF-α signaling and lower activity of CTLA4, PD1 signaling, and LCMV/tumor exhaustion pathways (Fig. 4f).

Fig. 4. Scissor identification results on melanoma T cells.

a, The UMAP visualization of 1,894 melanoma T cells in six clusters. b, The UMAP visualization of the Scissor selected cells. c, The bar plot shows the distribution of Scissor+ cells across the six T cell populations. d, The volcano plot of differential gene expressions in Scissor+ cells versus all other cells. The two vertical dashed lines represent ± ln(1.25) fold-changes, and the horizontal dashed line denotes FDR cutoff 0.05. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. e, The violin plots show the expression levels of important immune genes in Scissor+ cells. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. f, The enrichment bar plot shows the significantly enriched pathways in Scissor+ cells compared with all other cells (FDR <0.05). g, The boxplot shows the enrichment scores of the immunotherapy responsive signature in the non-responders and responders from Sade-Feldman’s cohort. h, The GSEA enrichment plot of the up and down signature genes in the responder vs. non-responder comparison from Sade-Feldman’s cohort. i, The boxplot shows the enrichment scores of the immunotherapy responsive signature in five types of CD8 T cells from a mouse liver tumor model (n = 3 biologically independent replicates per group from left to right). j, The boxplot shows the enrichment scores of the immunotherapy responsive signature in the memory precursor CD8 T cells and short-lived effector CD8 T cells (n = 3 biologically independent replicates in each condition). Box plot center line and box limits represent median value, upper, and lower quartiles, respectively. Box whiskers indicate the largest and smallest values no more than 1.5 times the interquartile range from the limits. The statistical p-value was determined by the two-tailed Student’s t-test, unless otherwise indicated.

The above 137 differential expression genes related to effective immunotherapy response (defined as immunotherapy responsive signature; Supplementary Table 3) could be informative in predicting treatment success. We found that our signature scores were significantly higher in ICB responders than in non-responders in an independent ICB dataset (Fig. 4g, Student’s t-test p=5.0e-4). Additionally, the up-regulated and down-regulated genes in our immunotherapy responsive signature were also significantly enriched in responders and non-responders (Fig. 4h, Kolmogorov-Smirnov test FDR=0.002 and 0.0085, respectively). We further evaluated our immunotherapy responsive signature in five types of tumor-infiltrating lymphocytes (TILs) with distinctive differentiation states. We found that LAG3-low/PD1-low effector CD8 T cells had the highest signature scores, followed by Naïve CD8, Bystander TIL, LAG3-high/PD1-high effector CD8, and exhausted CD8 T cells (Fig. 4i). Notably, our signature can significantly distinguish between PD1-low effector CD8, PD1-high effector CD8, and exhausted CD8 T cells (Fig. 4i and Supplementary Fig. 5a, b). Furthermore, the pseudotime analysis based on our immunotherapy responsive signature revealed the relative orders of the six clusters as cluster 2->3->4->5->6->1 (Supplementary Fig. 5c). Moreover, we found that our signature was more enriched in the memory precursor CD8 T cells than the short-lived effector T cells (Fig. 4j, Student’s t-test p=0.02). This observation indicated that Scissor_FR cells were more like PD1-low memory-precursor cells, which have higher TCF7 expression and are associated with a good immunotherapy response.

Collectively, our Scissor analysis of a scRNA-seq melanoma dataset independently revealed a PDCD1/CTLA4 low and TCF7 high T cell subpopulation whose distinct transcriptome was essential to favorable response to immunotherapy. These results demonstrated that Scissor analysis of single-cell data is capable of identifying subpopulations associated with the specific phenotype even though the single-cell data itself has no such phenotype information.

Identifying cell subpopulations associated with FSHD.

We further applied Scissor on an Facioscapulohumeral muscular dystrophy (FSHD) single-cell dataset to explore the applicability of our method on non-cancer studies. In total, 6,899 cells derived from FSHD and control samples³² were analyzed by Scissor with the guidance of 35 bulk muscle biopsies (27 FSHD patients and 8 controls). These cells were initially grouped into 14 clusters in scRNA-seq data analysis (Fig. 5a). After integrating these cells and bulk data by Scissor, 579 cells were identified as Scissor+ cells, which were associated with the FSHD; and 74 cells marked as Scissor- cells were linked with the normal phenotype (Fig. 5b). Consistent with the encoded phenotype information for Scissor in this application, 559 out of 579 Scissor+ cells (97.5%) originated from FSHD patients, and nearly 80% of Scissor- cells were from normal samples (Fig. 5c), indicating that Scissor can identify phenotype-associated subpopulations with high specificity in non-cancer cases.

Fig. 5. Scissor identification results on Facioscapulohumeral muscular dystrophy (FSHD) cells.

a, The UMAP visualization of 6,899 cells derived from FSHD and control samples. b, The UMAP visualization of the Scissor selected cells. The red and blue dots are representing Scissor+ and Scissor- cells, associated with FSHD and control phenotypes, respectively. c, The bar plot shows the detailed phenotypic constitutions of the Scissor selected cells. d, The volcano plot of differential gene expressions in Scissor+ cells versus Scissor- cells. Red and blue points mark the genes with significantly increased or decreased expressions in Scissor+ cells compared to Scissor- cells (FDR <0.05 and absolute fold-change > 1.25). The two vertical dashed lines represent ± ln(1.25) fold-changes in gene expression, and the horizontal dashed line denotes FDR cutoff 0.05. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. e, The violin plots show the expression levels of selected dysregulated genes in Scissor+ cells. The FDR was the adjusted p-value calculated by the two-tailed Wilcoxon rank-sum test. f, The enrichment bar plot of selected muscle-related pathways in the Hallmark, GO’s biological process, and cellular component domains. g, The boxplots show the enrichment scores of the FSHD molecular signature in the FSHD and normal controls from three independent validation datasets. The statistical p-values were determined by the two-tailed Student’s t-test. Box plot center line and box limits represent median value, upper, and lower quartiles, respectively. Box whiskers indicate the largest and smallest values no more than 1.5 times the interquartile range from the limits.

Given the adequate number of the Scissor selected cells, we could directly compare the gene expression of Scissor+ cells with Scissor- cells to uncover the underlying transcriptional patterns of the identified cells with distinct phenotypes. As a result, 299 up-regulated genes and 83 down-regulated genes were differentially expressed in Scissor+ cells over Scissor- cells, respectively (Fig. 5d and Supplementary Table 4). Among these genes, we found that many down-regulated genes in Scissor+ cells are involved in normal muscle functions (Fig. 5e), like myogenesis (LSP1, MEF2C, MYL1), muscle contraction (IGFBP5, MYBPC1, MYOM1), and actin filament or myosin-based functions (PDLIM3, TTN, SGCD). As for the up-regulated genes in Scissor+ cells, we found a proportion of these genes may be dysregulated due to fibrotic infiltration³³, which includes extracellular matrix proteins as collagen types III and IV (COL3A1, COL4A1) and fibronectin (FN1). FSHD region gene 1 (FRG1) was also over-expressed in Scissor+ cells (Fig. 5e), which is crucial for angiogenesis and epithelial to mesenchymal transition³⁴. The functional enrichment analysis also confirmed that Scissor+ cells were characterized by the reduction of muscle fibers as well as loss of myogenesis and muscle contraction functions (Fig. 5f and Supplementary Table 4), which is consistent with the molecular hallmarks of FSHD^{35, 36}. To further demonstrate the characteristics of the phenotype-associated cells identified by Scissor, we built an FSHD molecular signature using the 382 differentially expressed genes between the two cell subpopulations (Supplementary Table 4) and examined the signature’s ability in distinguishing FSHD patients from normal controls. We found that on all three independent datasets, the enrichment scores of the FSHD molecular signature were significantly higher in FSHD patients than in normal controls (Fig. 5g, Student’s t-test p=5.44e-3, 3.46e-2, and 4.99e-2, respectively).

Therefore, our Scissor analysis of FSHD scRNA-seq data identified disease-associated subpopulations characterized by the dysfunction of fibrinolysis, myogenesis, as well as muscle contractions, which substantiates the utility of Scissor on non-cancer studies.

Discerning subpopulations related to Alzheimer’s disease.

Single-cell technology presents immense opportunities to disentangle cellular diversity and alterations in neurological disorders. Here, we applied Scissor on three brain cell types from an Alzheimer’s disease (AD) scRNA-seq study³⁷ to explore the cell subpopulations that are most highly associated with the disease status and progression. Collectively, 7,432 oligodendrocytes, 1,078 oligodendrocyte progenitor cells (OPCs), and 2,171 astrocytes (Supplementary Fig. 6a) were analyzed separately by Scissor with the guidance of 14 bulk samples (7 AD patients and 7 healthy controls). For oligodendrocytes, Scissor identified 206 Scissor+ cells associated with the AD patients and 194 Scissor- cells associated with the healthy controls (Fig. 6a). When compared with the cell sources, 203 out of 206 Scissor+ cells (99%) were from AD patients, and 86% of Scissor- cells were from normal samples (Fig. 6b). For OPCs, 20 Scissor+ cells and 201 Scissor- cells were identified (Fig. 6c), with 90% Scissor+ cells from AD patients and 95% Scissor- cells from normal samples (Fig. 6d). As for astrocytes, the identified cell subpopulations consisted of 179 Scissor+ and 14 Scissor- cells (Fig. 6e), with 83% Scissor+ cells from AD patients and 93% Scissor- cells from normal samples, respectively (Fig. 6f). Therefore, Scissor successfully associated cell subpopulations with the desired phenotype in all three brain cell types.

Fig. 6. Scissor identification results on Alzheimer’s disease.

a-f. The UMAP visualizations of the Scissor selected cells on oligodendrocytes (a), OPCs (c), and astrocytes (e) with corresponding bar plots showing the phenotypic constitutions of the Scissor selected cells on oligodendrocytes (b), OPCs (d), and astrocytes (f). g, The heatmap of differential gene fold-changes in Scissor+ cells versus Scissor- cells across all three brain cell types. Red and blue elements mark the genes with significantly increased or decreased expressions in Scissor+ cells (FDR <0.05 and absolute fold change > 1.25). h, The heatmap of enriched Reactome pathways. The red and blue elements represent the activated and repressed pathways in corresponding cell types. i, The boxplot shows the enrichment scores of the oligodendrocytes molecular signature in AD patients and normal controls from GSE109887. j, The boxplot shows enrichment scores of the OPCs molecular signature in AD patients and normal controls from GSE109887. k, The boxplot shows the enrichment scores of the astrocytes molecular signature in AD patients and normal controls from GSE109887. l, The boxplot shows the enrichment scores of the astrocytes molecular signature in control, incipient, moderate, and severe stage AD patients from GSE28146 (n = 8, n = 7, n=8, and n = 7 biologically independent patients per group from left to right). The statistical p-value was determined by the Kruskal-Wallis test. The linear regression line represents the relationship between median enrichment scores and AD stages. Box plot center line and box limits represent median value, upper, and lower quartiles, respectively. Box whiskers indicate the largest and smallest values no more than 1.5 times the interquartile range from the limits. The statistical p-value was determined by the two-tailed Student’s t-test, unless otherwise indicated.

We then investigated DEGs between Scissor+ cells and Scissor- cells within each cell type (Fig. 6g; Supplementary Fig. 6b and Supplementary Table 5). In oligodendrocytes and OPCs, multiple heat shock and chaperone genes involving proper protein folding (e.g., HSPA1A, HSPB1, DNAJB1) were up-regulated in Scissor+ cells, consistent with the previous observation³⁸. Pathway enrichment analysis confirmed that the HSF1 pathway, a master activator of chaperone gene expression³⁹, is highly activated in Scissor+ cells to protect cells against protein misfolding (Fig. 6h and Supplementary Table 5). In astrocytes, most DEGs were down-regulated in Scissor+ cells, including GRIA2, which increases NMDA receptor activity⁴⁰. Pathway enrichment results also suggested the impaired NMDA-dependent long-term potentiation in Scissor+ astrocytes (Fig. 6h and Supplementary Table 5), which has been observed in AD⁴¹. Additionally, glial fibrillary acidic protein (GFAP) was coordinately up-regulated in Scissor+ cells across all three cell types (Fig. 6g). It has been reported that GFAP expressions correlate with amyloid-β plaque density in AD brain tissue⁴², and elevated GFAP levels in the blood positively correlate with cognitive impairment⁴³. All these results showed that Scissor indeed identified cell subpopulations with characteristics consistent with the corresponding bulk phenotype.

To further demonstrate the phenotypic associations of the cell subpopulations identified by Scissor, we constructed molecular signatures based on the DEGs in Scissor-identified cell subpopulations (Supplementary Table 5) and used independent AD datasets to evaluate the functions of these signatures. As a result, the enrichment scores of the corresponding molecular signatures in each cell type were significantly higher in AD patients than in normal controls (Fig. 6i–k, Student’s t-test p=2.66e-4 for oligodendrocytes, 5.43e-5 for OPCs, and 5.45e-7 for astrocytes). Notably, we also found that our astrocytes molecular signature is positively associated with the progression of AD from incipient, moderate, to severe conditions (Fig. 6l, Kruskal-Wallis test p=1.44e-2). Thus, this Scissor+ cell subpopulation of astrocytes could play a vital role in the early stages of AD.

Taken together, our Scissor analysis identified cell subpopulations that are most highly associated with AD in three brain cell types, which could contribute to comprehending the underlying pathogenesis of Alzheimer’s disease and might facilitate disease diagnosis and therapy.

Discussion

Identifying the phenotype-specific cell subpopulations from single-cell data can give rise to breakthroughs in understanding disease mechanisms. Multiple efforts have been made to discern disease-relevant cells from single-cell data⁴⁴. For example, HoneyBadger⁴⁵ and inferCNV⁴⁶ can identify cancerous cells by predicting copy number variations from scRNA-seq data. However, there are a variety of external phenotypes beyond tumor-vs-normal in cancer and non-cancer diseases, such as treatment resistance, disease stages, survival outcomes and aging, which are widely available in bulk data. Therefore, there is a great need for further methodological progress to utilize these abundant phenotypes in single-cell data analysis. To this end, we introduce Scissor as a new computational tool to leverage the phenotype information from bulk data to identify the most highly phenotype-associated cell subpopulations.

We demonstrated the broad utilities of Scissor in a total of ten applications across different diseases, ranging from engineered simulations, cancer cells, immune cells, and FSHD cells to multiple types of brain cells in AD (Supplementary Table 6). One of the advantages is that Scissor does not require any unsupervised clustering on single-cell data, which avoids subjective decisions of cell cluster numbers or clustering resolution⁴⁷. Most importantly, Scissor provides a flexible framework to integrate various external phenotypes in bulk data to guide single-cell data analysis, enabling hypothesis-free identification of clinically and biologically relevant cell subpopulations.

The signs of the regression coefficients were used to infer the relation of the Scissor selected cells with the phenotypes. We designed generalized criterion for proper interpretation of Scissor results (Supplementary Table 7 and Methods) since we observed little proportions of negative correlations between single-cell and bulk samples in real applications (Supplementary Table 8). Based on our criterion, those little proportions of negative correlations did not affect our current results and interpretations. Furthermore, we also performed correlation evaluations for the Scissor selected cells in each application, which could help check the validity of the Scissor result (Supplementary Table 9–11). Besides, we tested Scissor’s performance in various perturbed bulk samples and demonstrated that the Scissor identification results were robust to noise (Supplementary Fig. 7 and 8, Supplementary Table 12) and had no model-driven preferences to experimental noise or bias (Supplementary Fig. 9). For computational efficiency, the running time and memory usages of Scissor in real applications are acceptable, with cell numbers ranging from ~1,000 to ~30,000 (Supplementary Table 13).

The construction of the correlation matrix is a key step in Scissor to quantify the dependence or similarity between the single-cell data and bulk data. Except for the Pearson correlation applied in Scissor, we will explore other similarity measurements like entropy-based mutual information and hypothesis testing-based methods. Furthermore, although we only conducted the integration of bulk gene expressions with scRNA-seq data, Scissor can also be applied to other single-cell measurements like chromatin accessibility⁴⁸ and DNA methylation⁴⁹.

Overall, Scissor demonstrates promise for integrating single-cell data with phenotype information to dissect clinically significant subsets from heterogeneous cell populations. This strategy will boost biological discoveries and interpretation. We anticipate that Scissor will enable a broad application of widely available phenotype information on single-cell data analysis and help unravel the most disease-relevant subpopulations for cell-targeted therapies.

Methods

Phenotype-guided single-cell subpopulation identification by Scissor

The workflow of Scissor is shown in Fig. 1. Denote m and n as the cell number and the bulk sample number, respectively. The three data sources for Scissor inputs are a single-cell expression matrix with m cells, a bulk profiling data with n samples, and a sample phenotype Y of interest (Fig. 1a). Y annotates each bulk sample and can be a continuous dependent variable, binary group indicator vector, or clinical survival data. Scissor first uses quantile normalization on the single-cell and bulk expression data to remove the underlying batch effect. After this, a Pearson correlation matrix $S={\left(s_{ij}\right)}_{n\times m}$ is calculated for each pair of cells and bulk samples to quantify the similarity between the single-cell data and bulk data, where S_ij is the correlation of sample i and cell j across common genes in normalized single-cell and bulk data.

Scissor optimizes a regression model on the correlation matrix S with the sample phenotype Y (Fig. 1b). Let β denote a vector of coefficients on cells, and l(β) denote an appropriately chosen log-likelihood function. The formula of l(β) depends on the input phenotype Y, i.e., linear regression for continuous dependent variables, logistic regression (classification) for dichotomous variables, and Cox regression for clinical survival data (see more details in next section). Since a cell subpopulation alone could drive the phenotype of interest, we impose a sparse penalty (l₁-norm) on the model to select the high confidence cells that are important for the given phenotype. Furthermore, the network-based penalty enforces the tightly connected nodes (cells) in the network to have more similar coefficients⁵⁰, making the phenotype-to-cell association results more consistent and interpretable. Inspired by this, we use the shared nearest neighbor graph calculated in Seurat⁵¹ to serve as a cell-cell similarity network G and impose a corresponding graph regularization on the regression model.

Overall, Scissor is formulated as the following network regularized sparse regression model (Fig. 1b):

$$\underset{\beta }{\min }-\frac{1}{n}l\left(\beta \right)+\lambda \left\{\alpha {‖\beta ‖}_1+\frac{1-\alpha }{2}{\beta }^{T}L\beta \right\},$$

where L is a symmetric normalized Laplacian matrix, which is defined as

$$L=D^{-\frac{1}{2}}\left(D-A\right)D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}},$$

where $A={\left(a_{ij}\right)}_{m\times m}$ is a binary or weighted adjacency matrix of G. a_ij equals one or a value ranging from 0 to 1 if cell i and j are connected in G, and a_ij=0, otherwise. $D={\left(d_{ij}\right)}_{m\times m}$ is the degree matrix of G, where $d_{ii}=\sum _{j=1}^m{a}_{ij}$, and d_i,j=0 for i≠j. The tuning parameter λ controls the overall strength of the penalty and λ balances the amount of regularization for smoothness and sparsity.

The non-zero coefficients of β solved by the above optimization model are used to select the cell subpopulations associated with the phenotype of interest (Fig. 1c). According to the sign of β, we denote the selected cells by Scissor+ cells and Scissor- cells, which are positively and negatively associated with the phenotype of interest, respectively. The cells with coefficients of zero are denoted as background cells. Furthermore, to control false associations between the single-cell and bulk data, we designed a reliability significance test to determine whether the chosen data is suitable for our phenotype-to-cell associations (Fig. 1d). Finally, the Scissor selected cells will further be investigated by several downstream analyses, such as the differential expression gene analysis, functional enrichment analysis, and motif analysis, to reveal the underlying biological mechanisms of the selected cell subpopulations (Fig. 1e).

Log-likelihood functions

The formula of log-likelihood function l(β) depends on the type of the phenotype Y. Scissor can do: (1) linear regression for continuous dependent variables; (2) classification for dichotomous variables; (3) Cox regression for clinical survival data.

In detail, denote $S_i={\left(s_{i1},s_{i2},\cdots ,s_{im}\right)}^T$ as the correlation coefficients for sample i across all m cells. If $Y={\left(y_1,y_2,\cdots ,y_n\right)}^T$ is a continuous variable, the linear regression log-likelihood function is used:

$$l\left(\beta \right)=-\sum _{i=1}^n{\left(y_i-{\beta }^T{S}_i\right)}^2$$

If Y is a binary group indicator vector, e.g., y_i ∈{0,1}, the logistic regression log-likelihood function is used:

$$l\left(\beta \right)=\sum _{i=1}^n\left[y_i{\beta }^T{S}_i-\mathrm{l}\mathrm{o}\mathrm{g}(1+\mathrm{e}\mathrm{x}\mathrm{p}({\beta }^T{S}_i)\right]$$

For time-to-event outcomes subject to independent censoring, the Cox regression is considered. Let T_i be the non-negative event time, and C_i be the censoring time. Denote ${\widehat{T}}_i=\mathrm{m}\mathrm{i}\mathrm{n}(T_i,C_i)$ as the observed event time or censoring time, and ${\delta }_i=I\left(T_i\le C_i\right)$ as the event indicator, where I(·) is an indicator function. The following log-likelihood function is used:

$$l\left(\beta \right)=\sum _{i=1}^n{\delta }_i\left[{\beta }^T{S}_i-log\left(\sum _{k\in R_i}\mathrm{e}\mathrm{x}\mathrm{p}\left({\beta }^T{S}_k\right)\right)\right]$$

where $R_i=\{k:{\widehat{T}}_k\ge {\widehat{T}}_i\}$ denotes the risk set at time ${\widehat{T}}_i$.

Parameter tunings and implementations

The algorithm proposed by Li et al.⁵² is used to solve the above network regularized sparse regression. In Scissor, two model parameters need to be determined. First, parameter λ controls the overall strength of the whole penalty term. For a fixed λ, we set 100 possible λ and applied 10-fold cross-validation to select the optimal λ with the minimum averaged error. Second, parameter α∈[0,1] balances the effect of the l₁-norm and the network-based penalties. A larger λ inclines to emphasize l₁-norm to encourage sparsity. And a smaller λ gives more weight to the network term to encourage selecting similar cells. In real applications, a fixed value of λ cannot work for all kinds of datasets since different datasets could have different sensitivities to the changes of λ. In order to select similar cells as many as possible, thus they can be drawn from similar cell types, we will start to search λ from a small value, and the default searching list for λ in Scissor is {0.005, 0.01, 0.05, 0.1, 0.2,0.3, ⋯, 0.9}. For each fixed α,λ is determined by grid search based on the cross-validation. The goal of Scissor is to identify a small group of cells that are most highly correlated with the specific phenotypes with high confidence. Based on this motivation as a priori, we determined λ using the following criteria: the number of Scissor selected cells should not exceed a certain percentage of total cells (default 20%) in the single-cell data. In each experiment, a search on the above searching list is performed from the smallest to the largest until a value of λ meets the above criteria.

Reliability significance test

We designed a reliability significance test to exclude the false association between the identified cell subpopulations and bulk phenotypes (Fig. 1d). This statistical test can determine whether the inferred phenotype-to-cell associations are reliable (statistical p-value less than 0.05) or are false positives. Our motivation for the test is: if the chosen single-cell and bulk data are not suitable for the phenotype-to-cell associations, the correlations would be less informative and not well associated with the phenotype labels. Thus, the corresponding prediction performance would be poor and not be significantly distinguishable from the randomly permutated labels. Inspired by this, we used the following procedures to perform the reliability significance test:

First, we performed k-fold cross-validation (CV) on correlation matrix S and used the training sets only to estimate the coefficients of cells in Scissor. The prediction performances of the trained Scissor models were evaluated on testing sets, and an averaged evaluation measurement was obtained to serve as an actual test statistic. Second, we randomly permutated the bulk sample labels multiple times to break up the original bulk phenotype-genotype relationships. By performing the same Scissor analysis and CV evaluation using each permutated bulk data, we obtained a background distribution of the corresponding evaluation measurement quantifying the prediction performances at the random level. Finally, the actual test statistic calculated in the original data was compared to the background distribution values. The reliability significance test p-value was the number of the permutation-based test statistics above (or below) the actual test statistic, divided by the permutation times. In this study, the evaluation measurements used in the reliability significance test are the mean squared error (MSE) for linear regression (smaller is better), the area under the ROC curve (AUC) for classification (higher is better), and the concordance index (c-index) for Cox regression (higher is better).

Then, we explored whether the reliability significance test can effectively detect the ‘false positive’ associations between the single-cell and bulk data by reporting non-significant p-values. We performed two kinds of randomizations on bulk data to generate false positive examples. After Scissor analysis of those randomized bulk data, our reliability significance test reported that the p-values for these counterexamples were all greater than 0.05 (Supplementary Table 14), indicating that these randomized bulk data were not suitable to use in Scissor to identify the corresponding phenotype-associated cells. We also performed the reliability significance test on the main applications used in this study and found that the test p-values were all less than 0.05 (Supplementary Fig. 10), indicating that the inferred phenotype-to-cell associations are reliable.

Scissor selected cells interpretations

Both Scissor+ cells and Scissor- cells are the Scissor selected cells that are most highly associated with the specified phenotypes, corresponding to the cells with the estimated coefficients greater than and less than zero, respectively. The associations between the Scissor selected cells and phenotypes depend on the model in use and should be interpreted in a context-specific manner. For both linear regression and classification models, the initial values in Y will affect the interpretations. The Scissor+ cells will be associated with the phenotypes encoded as a higher value in Y, and Scissor- cells will correspond to the phenotypes encoded as a lower value. For example, in Scissor’s application on the FSHD single-cell dataset, if the FSHD patients are encoded as one, and the normal controls are encoded as zero in Y, Scissor+ cells will be associated with the FSHD, and Scissor- cells will be associated with the normal phenotype. If the encoding for the two phenotypes is reversed in Y, the interpretations of Scissor+ cells and Scissor- cells are reversed accordingly. For Cox regression, Scissor+ cells are always associated with worse survival, and Scissor- cells are associated with good survival.

Scissor can associate cells with phenotypes, and this kind of association is a relative concept between phenotypes. Namely, Scissor assigns which phenotype a cell is more likely associated with than the other phenotype. Considering the possible negative correlations between the single-cell and bulk samples, we can further interpret a cell by assigning it to the following three categories: if the average of a cell’s correlations with all bulk samples is greater than 0 and the number of positive correlations is larger than the number of the negative correlations, this cell is more similar to the associated phenotype; if the average of a cell’s correlations is less than 0 and the number of negative correlations is larger than the number of positive correlations, this cell should be interpreted as more dissimilar to the other phenotype; otherwise, this cell’s association with the phenotype is undeterminable (Supplementary Table 7). In most cases, the negative correlation values are very few and the identified cells fall into the “more similar” category.

In total, there are ten applications of Scissor in this study. The corresponding phenotype encoding and the interpretations of the Scissor selected cells were summarized in Supplementary Table 6. We showed that Scissor was capable of detecting both Scissor+ and Scissor- cells through a variety of applications. In some datasets, Scissor+ cells and Scissor- cells can be largely unbalanced. Scissor can detect more cells of one phenotype than the other phenotype depending on how strong the cells in a dataset are associated with the specific phenotypes.

Simulation setup

We used Splatter¹⁴ to simulate a single-cell dataset with 1,000 cells and 5,000 expression genes. These cells were from three simulated cell types with group probabilities of 0.8, 0.1, and 0.1, respectively, leading to one large and two small cell subpopulations. The probabilities of a gene being differentially expressed in each of the three groups were set as 0.1, 0.01, and 0.01. Then, we assigned these cells to two different phenotypes (named phenotype I and phenotype II) to simulate the known relationships between cells and phenotypes as the ground truth. To achieve this, we set the large cell subpopulation as common cells shared by the two phenotypes and assigned the other two small cell subpopulations to each phenotype, respectively. These two small subset cells are unique to each phenotype and thus can be viewed as the ground truth phenotype-specific cell subpopulations. To simulate the expression profiles of bulk samples for each phenotype, we randomly selected 1000 cells with replacement from the cell subpopulations contained by each phenotype and then averaged the expressions. In this way, we generated bulk gene expressions of 50 samples for each phenotype.

The differential expression genes between the two cell subpopulations were called by Seurat⁵¹ using the default two-tailed Wilcoxon rank-sum test. To explore how the performance of Scissor was affected by the true DEG signals at the bulk level, we simulated another bulk data that the true DEGs are not differentially expressed. In detail, we first selected the least differentially expressed gene from bulk data and then used its expression profiles to replace the expressions of all the true DEGs. This true DEG signal-removed bulk expression data would make Scissor more challenging to capture the real phenotype-to-cell associations.

We used precision and recall measurements in supervised learning to evaluate the performance of Scissor. The precision is defined as the proportion of the Scissor-identified ground truth cells among all Scissor selected cells, and recall is the proportion of the Scissor-identified ground truth cells among all ground truth cells.

Single-cell RNA-seq data preprocessing

We applied Seurat R package (version 3.2.1)⁵¹ functions to preprocess the scRNA-seq data used in Scissor. Similar to the standard quality control step in single-cell data analysis, we first filtered out the genes with low expressions in cells. After this, we normalized the filtered expression matrix using the NormalizeData function with the default parameters. Furthermore, we focused on the genes that exhibited high cell-to-cell variation and identified the variable genes using the FindVariableFeatures function with the default ‘vst’ method. We then performed the principal components analysis on the scaled variable gene expressions. Using the first ten principal components, we constructed a shared nearest neighbor graph for cells and identified cell clusters using the FindClusters function. Finally, we applied the Uniform Manifold Approximation and Projection (UMAP)⁵³ technique using the RunUMAP function to visualize cells in low dimensions.

Differential expression gene analysis

The differentially expressed genes in Scissor+ cells versus Scissor- cells (or all other cells in some applications) were identified using the FindMarkers function in Seurat⁵¹ with the default Wilcoxon rank-sum test. We required the following criteria to obtain the differential expression genes: First, the gene expression between the two groups is statistically significant with a false discovery rate (FDR) less than 0.05. Second, the absolute value of expression fold change between the two groups is greater than 1.25. We used the VlnPlot function to exhibit the relative expression levels of the selected differential expression genes.

We built several Scissor-derived signatures based on the differential expression genes in each experiment. The complete lists of signature genes can be found in Supplementary Tables.

Pathway enrichment analysis

The pre-ranked version of CAMERA⁵⁴ (function name: cameraPR) in the limma R package (version 3.42.2) was used to evaluate the enriched pathways. cameraPR needs a pre-ranked gene list according to a user-defined statistic score. This study used the differential expression genes output of the FindMarkers function to obtain the pre-ranked gene list. In detail, the statistic ranking score for each gene was calculated using the following formula:

$$\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{F}\mathrm{C}\mathrm{\ast }{log}_{10}\frac{1}{\mathrm{F}\mathrm{D}\mathrm{R}+{10}^{-100}}$$

where logFC stands for the log-transformed fold change between the two groups, and FDR is the adjusted Wilcoxon rank-sum test p-value. The pathways used in CAMERA were downloaded from the Molecular Signatures Database (MSigDB, version 7.3)⁵⁵. The Mognol_LCMV_Tumor_Exhaustion gene set contains the up-regulated genes in exhausted T cells from both OT-I mouse model and lymphocytic choriomeningitis virus (LCMV) infected mice⁵⁶.

Survival analysis

We performed some survival analyses to examine the clinical relevance of the Scissor-derived signatures (lung cancer signature and TP53 mutation signature). The gene set variation analysis (GSVA) algorithm⁵⁷ with the default settings, as implemented in the GSVA R package (version 1.34.0), was applied to calculate our signature score for each sample. Next, the samples were stratified into two groups based on the quantile values of the signature scores (upper quartile versus lower quartile). Survival curves of these two groups of patients were estimated by the Kaplan-Meier method with statistical significance calculated using the log-rank test.

We used the univariate Cox proportional hazard (Cox PH) model to examine the association between survival time and clinical features (Pathological Stage: Stage I=1, Stage II=2, Stage III=3; Sex: ‘Male’=1, ‘Female’=2; Age at diagnosis). The significant prognostic factors (p < 0.05) in the univariate Cox PH model were included in the subsequent multivariable Cox PH model. The Kaplan-Meier estimator, log-rank test, Wald test and Cox PH models were calculated in the survival R package (version 3.2–3).

Motif analysis

The oPOSSUM software⁵⁸ (version 3.0) was used to detect the motifs of the transcription factor binding sites for the lung cancer signature genes. We used the transcription factor binding site annotations provided by the tool (JASPAR CORE Profiles). For the parameter settings, we set 2000 base pairs in upstream and downstream sequences and kept other parameters as default values. Only motifs with a Z-score larger than ten and a Fisher score larger than seven were reported in the final motif list.

Master regulator analysis

Transcription factor activity was inferred using the master regulator inference algorithm (MARINa)⁵⁹ in the viper R package (version 1.20.0). A pre-ranked gene list with scores and a regulatory network are the two data sources required as the inputs. In this work, we used the same pre-ranked gene list calculated in the pathway enrichment analysis. The transcription factor regulome was curated from several databases as previously described⁶⁰.

Signature enrichment score calculation

A pseudo-regulon was built based on the significantly up-regulated and down-regulated genes between the cell subpopulations identified by Scissor. These genes were served as the positive and negative target genes of the constructed pseudo-regulon, respectively. The single-sample extension of MARINa⁶¹ (function name: viper) in the viper R package (version 1.20.0) was employed to infer the activity of the constructed pseudo-regulon, which was used as the signature enrichment score for each sample.

Data availability

All datasets analyzed in this study were published previously. The corresponding descriptions and preprocessing steps are described in Supplementary Materials.

Software availability

The open-source Scissor R package and tutorial are available at GitHub: https://github.com/sunduanchen/Scissor.