Estimating subglottal pressure and vocal fold adduction from the produced voice in a single-subject study (L)

Abstract

We previously reported a simulation-based neural network for estimating vocal fold properties and subglottal pressure from the produced voice. This study aims to validate this neural network in a single–human subject study. The results showed reasonable accuracy of the neural network in estimating the subglottal pressure in this particular human subject. The neural network was also able to qualitatively differentiate soft and loud speech conditions regarding differences in the subglottal pressure and degree of vocal fold adduction. This simulation-based neural network has potential applications in identifying unhealthy vocal behavior and monitoring progress of voice therapy or vocal training.

I. INTRODUCTION

This study concerns the inverse problem in voice production, i.e., estimating vocal fold properties (geometry, stiffness, and position) and subglottal pressure from the produced voice outcome. Solving the voice production inversion problem has many important applications. In the clinic, such a voice production inversion system would allow clinicians to directly evaluate changes in vocal fold properties due to pathology or misuse of vocal mechanisms (e.g., vocal hyperfunction), thus improving diagnosis of voice disorders. It would also allow the clinician or the speaker to monitor progress of voice therapy or vocal training, and possibly the emotional state of the speaker.

In our previous studies (Zhang, 2020, 2021), we reported a simulation-based neural network for voice production inversion. Using voice features extracted from the produced voice as inputs, the neural network maps these voice features to the underlying vocal fold properties and subglottal pressures that produce the corresponding voice. The mapping was trained using data from parametric simulations using a three-dimensional vocal fold model, which establish the cause-effect relationship between vocal fold properties and the produced voice features. The use of a three-dimensional continuum vocal fold model makes it possible to estimate realistic, directly measurable vocal fold properties, which is important to clinical applications. Our previous study showed reasonable agreement between estimations from this neural network and excised human larynx experiments (Zhang, 2020).

The goal of this study is to further validate this simulation-based neural network for voice production inversion in live humans, an important step toward clinical and speech technology applications. Due to difficulties in reliably measuring the physiological control parameters in live humans, validation of such voice inversion systems in humans is challenging and is often limited to the subglottal pressure. In this study, we attempt to validate our neural network against data collected from a single human subject producing repetitions of /pa/ at different loudness levels. During the experiment, the output sound, glottal flow rate at the lips, and intraoral pressure behind the lips were recorded. This protocol was chosen for two reasons: First, the intraoral pressure measured during the /p/ segment is often used as an indirect measure of the subglottal pressure and its trend of variation during the following vowel production. This allows us to quantitatively evaluate the accuracy of the neutral network in estimating the subglottal pressure. Second, the production of consecutive /pa/s requires alternating adduction (from /p/ to /a/) and abduction (from /a/ to /p/) of the vocal folds. In particular, louder /pa/ production is expected to have a higher subglottal pressure and thus requires a larger maximum abduction angle of the vocal folds in order to suppress vocal fold vibration during the /p/ segment, and tighter adduction during the vowel in order to maintain sufficient glottal closure. Thus, compared to soft speech, loud speech production would exhibit large modulation in the initial glottal angle (a measure of prephonatory vocal fold adduction), which will allow us to qualitatively validate our neural network in predicting changes in the initial glottal angle.

The focus on the subglottal pressure and the initial glottal angle in our validation is clinically motivated. High subglottal pressure and tight vocal fold adduction are two important factors contributing to high vocal fold contact pressure and risk of vocal fold injury. Although phonotraumatic vocal hyperfunction is among the most frequently occurring voice disorders, patients often seek medical assistance only after such hyperfunctional behavior has led to vocal difficulties or noticeable voice changes. The neural network developed in this study would have the potential for the speaker to monitor the voice and facilitate early diagnosis and intervention.

II. NEUTRAL NETWORK AND TRAINING

Details of the neutral network and training can be found in our previous work (Zhang, 2020, 2021). In this study, the inputs to the neural network are voice features extracted from the output acoustics and glottal flow waveform. These include the fundamental frequency (F0), sound pressure level (SPL), cepstral peak prominence (CPP), harmonic-to-noise ratio (HNR), subharmonic-to-harmonic ratio (SHR), the differences between the first harmonic and the second harmonic (H1-H2), the fourth harmonic (H1-H4), the harmonic nearest 2 kHz (H1-H2k), and the harmonic nearest 5 kHz (H1-H5k) in the spectrum of the time derivative of the glottal flow waveform, mean (Qmean) and peak-to-peak amplitude (Qamp) of the glottal flow waveform, closed quotient (CQ) of the glottal flow waveform, maximum flow declination rate (MFDR), and maximum flow acceleration rate (MFAR). We intentionally did not include any features characterizing vocal fold vibration so that application of the trained network does not require specialized equipment that may not be readily available outside the clinic.

The output of the neural network is the estimated control parameters of a three-dimensional, body-cover, continuum model of voice production (Zhang, 2020), including the subglottal pressure P_s, initial glottal angle α quantifying the degree of vocal fold adduction, vocal fold geometry (length, depth, and vertical thickness), and vocal fold stiffness. In this study, we focused on the subglottal pressure and the initial glottal angle, two important parameters determining the risk of vocal fold injury.

Data used for neural network training were from numerical simulations using the three-dimensional body-cover voice production model, with parametric variations in nine geometric and stiffness control parameters, as described in detail in Zhang (2020). A total of 221 400 vocal fold conditions were simulated, and 116 902 conditions resulted in sustained phonation and thus were used in neural network training. The 116 902 conditions were first z-score normalized and then randomly divided into three sets, each for training (70%), validation (15%), and testing (15%), respectively. The neural network was trained to minimize the mean squared error with regularization between the truth and network prediction, using the scaled conjugate gradient method in the matlab Deep Learning Toolbox. Training stops when the mean squared error in the validation set has increased more than a specified number of iterations since the last iteration it decreased. The training process generally takes about 15 000 iterations, depending on the number of input/output and network configuration.

III. HUMAN DATA COLLECTION AND ANALYSIS

For validation of the neural network, acoustic and aerodynamic data were collected in a single male human subject producing utterances of five repetitions of the syllable /pa/ at different loudness levels. The produced speech sound was measured using a 1/2-inch microphone. The oral volume flow rate was measured using a pneumotachograph attached to a circumferentially vented facemask (Glottal Enterprises, Syracuse, NY) attached to the speaker's face. The intraoral air pressure behind the lips was measured using a pressure transducer connected to a catheter, which passed through a fitting in the facemask and was held between the lips into the oral cavity. The speaker was instructed to think of the string of repetition of /pa/ as a five-syllable word spoken slowly, in order to obtain steady-state intraoral pressure during the plosives and oral volume velocity during the vowels. The speaker produced the utterance at varying loudness levels, ranging from soft, comfortable, to loud, without prescribed pitch/loudness levels.

The peak intraoral pressure during the plosives was identified for each /p/ segment. Linear interpolation between the peak intraoral pressures of two consecutive /p/s was used to approximate the subglottal pressure during the vowel /a/ in between the two /p/s. From the recorded sound pressure data, the F0, CPP, HNR, SHR, H1-H2, H1-H4, H1-H2k, H1-H5k, and SPL were extracted using the software VoiceSauce (Shue et al., 2011). Note that the measures of H1-H2, H1-H4, H1-H2k, and H1-H5k were corrected for the effect of formant frequencies, as described by Iseli et al. (2007). Because the neural network was trained using simulation data produced without a vocal tract, the measured SPL was subtracted by 15 dB to correct for the effect of vocal tract resonance. This 15-dB correction was determined using simulation data generated with an /ɑ/ vocal tract and without a vocal tract. The SPL data from these simulations showed on average a 15-dB difference at medium and high subglottal pressures, and this SPL difference decreased to about 5–10 dB at very low subglottal pressures. Since the subglottal pressure was unknown a priori, a constant 15-dB SPL correction was applied to all conditions. The oral volume flow rate was inverse filtered to obtain the glottal flow waveform using the INVF software developed at UCLA (Kreiman et al., 2016), from which the glottal flow-related measures (Qmean, Qamp, CQ, MFDR, and MADR) were extracted.

IV. RESULTS

Figure 1 compares the neural network–predicted subglottal pressure and the approximations from the intraoral air pressure measurement. The estimated subglottal pressure in general followed the experimentally measured values. Linear regression showed a slope of 1.47, indicating that the neural network tended to overestimate the subglottal pressure at high pressures and underestimate at low pressures, and an R² (coefficient of determination) value of 0.83. The mean absolute error was 290 Pa, which is higher than the error (115 Pa) in our previous study using an excised human larynx experiment (Zhang, 2020). The mean absolute percentage error was 24.5%, which is comparable to other studies (Gomez et al., 2019; Ibarra et al., 2021).

FIG. 1.

(Color online) Comparison between experimentally estimated subglottal pressure and estimates from the neural network. The solid line is a line through the origin with a slope of 1. The equation shows linear regression and the corresponding R² value.

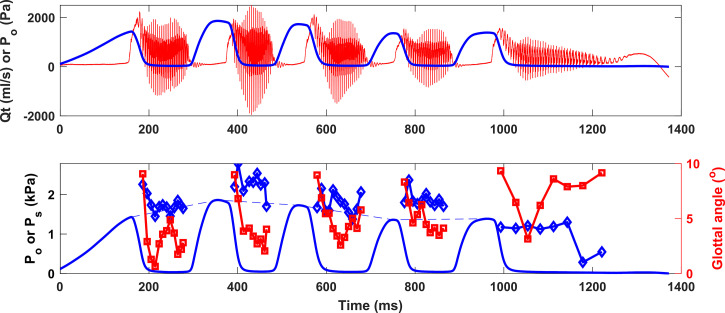
The top panel of Fig. 2 shows the oral volume flow and intraoral air pressure data collected during a loud production condition. For each repetition of the syllable /pa/, the oral flow was zero during the plosive, increased rapidly as the oral closure was released, and then decreased slightly as phonation was initiated. The peak oral flow increased again as the peak-to-peak flow amplitude started to increase, before eventually decreasing again toward the transition to the next plosive. Note that the oral flow had a negative minimum value during all five vowel productions, indicating that the vocal folds were sufficiently adducted during the vowels. The peak intraoral air pressure increased from the first /p/ to the second /p/ and then slowly decreased toward the end of the utterance. The peak intraoral air pressure in general was high, ranging between 1.3 and 1.8 kPa.

FIG. 2.

(Color online) Loud /pa/ production. Top: measured oral volume flow rate Qt (ml/s) and intraoral air pressure (Po) during the production of five repetitions of the syllable /pa/. Bottom: the measured intraoral air pressure (solid lines) and neural network–estimated subglottal pressure Ps (diamonds) and initial glottal angle (squares). The dashed line is linear interpolation of the peak intraoral pressures between two consecutive /p/s, an approximation of the subglottal pressure during the vowel production.

The bottom panel of Fig. 2 shows the subglottal pressure (diamonds) and initial glottal angle (squares; a measure of vocal fold adduction) estimated from the neural network. The estimated subglottal pressure was generally higher than the linear interpolation (dashed line) from the measured intraoral pressure, although it did follow the general trend. It first increased from the first vowel to the second vowel before it gradually decreased toward the end of the utterance. For each vowel, the initial glottal angle had a very large value (around 9°) during the early part of the /p/-/a/ transition (as indicated by the rapid decline of the intraoral pressure and rise of the oral flow), decreased rapidly to a much smaller value (as small as 0.6° in the first vowel), and slowly increased again toward the transition to the next plosive. The minimum initial glottal angle within each vowel production was the smallest in the first vowel and slowly increased toward the end of the utterance.

The general trends of the estimated initial glottal angle shown in Fig. 2 is consistent with observations in previous studies of plosive-vowel transitions. For high subglottal pressures as in the case of Fig. 2, the maximum vocal fold abduction angle is expected to be large in order to suppress vocal fold vibration during the plosives. On the other hand, loud vowel production is often accompanied by increased vocal fold adduction. Thus, the transition from /p/ to /a/ during loud speech is expected to involve a large change in the initial glottal angle. In Fig. 2, vocal fold vibration started early in the transition period as the vocal folds were still being adducted, probably due to the high subglottal pressure and likely high speed of adduction. This allowed us to capture the late part of the vocal fold adduction process during the transition from /p/ to /a/. The maximum vocal fold abduction angle during the plosives was expected to be even larger than 9° as estimated in the transition period in Fig. 2.

Figure 3 shows similar data and estimations for a soft loudness condition. In this case, the oral flow never decreased to zero, indicating that the glottis was likely never fully closed during the vowel production. The intraoral pressure increased first during the first /pa/ and then decreased toward the end of the utterance, similar to the loud production condition in Fig. 2. During vowel production, oscillations in the oral flow waveform started relatively late in the transition compared to that in the loud production condition in Fig. 2. The peak-to-peak flow amplitude was also smaller, and the maximum oral flow occurred at the beginning of the transition period instead in the middle of the vowel as in the loud production condition in Fig. 2.

FIG. 3.

(Color online) Soft /pa/ production. Top: measured oral volume flow rate Qt (ml/s) and intraoral air pressure (Po) during the production of five repetitions of the syllable /pa/. Bottom: the measured intraoral air pressure (solid lines) and neural network-estimated subglottal pressure Ps (diamonds) and initial glottal angle (squares). The dashed line is linear interpolation of the peak intraoral pressures between two consecutive /p/s, an approximation of the subglottal pressure during the vowel production.

The bottom panel of Fig. 3 shows the subglottal pressure and initial glottal angle estimated from the neural network. The estimate subglottal pressure was lower than the intraoral pressure but showed a similar trend of variation. The estimated subglottal pressure was much lower than that in the loud speech condition in Fig. 2. The initial glottal angle hovered around 8° and was much larger than that in the loud production condition, indicating a low degree of vocal fold adduction. These differences are expected in soft versus loud productions.

In contrast to the loud speech condition, which showed a large modulation in the initial glottal angle during each repetition of /pa/, in the soft speech condition the estimated initial glottal angle remained relatively constant. However, a similar modulation trend (an initial adduction followed by abduction) can still be observed during the second and third vowels, although the degree of modulation was small. This small variation in the initial glottal angle likely resulted from a weak vocal fold adduction during the vowels and a reduced maximum vocal fold abduction angle during the plosives (with reduced subglottal pressure, large abduction was no longer required to suppress vibration during the /p/). Due to the delayed voice onset in the soft speech condition, no voice data were available during the early part of the /p/-/a/ transition when the initial glottal angle rapidly decreased, which may have further reduced the range of modulation in the estimated initial glottal angle in Fig. 3.

V. DISCUSSION AND CONCLUSION

Our results showed reasonable accuracy of the neural network in estimating the subglottal pressure. The neural network was also able to qualitatively differentiate soft and loud speech conditions in terms of the subglottal pressure and the degree of vocal fold adduction. While further improvement in accuracy is desired, this qualitative evaluation would allow us to qualitatively identify vocal behaviors that are of high risk of vocal fold injury, such as the use of high subglottal pressure or vocal fold hyperadduction. This has potential clinical applications in facilitating diagnosis of vocal hyperfunction as well as monitoring progress of voice therapy or other interventions. This approach does not require specialized equipment and thus allows speakers to monitor their own voice production without a visit to the clinic.

Due to difficulties in reliably measuring vocal fold properties in humans, the neural network was trained using data generated from computational simulations of voice production. An important goal of this study was to evaluate whether such simulation-based neural networks can be applied to human speech and still produce reasonable accuracy. The reasonable agreement in this study is encouraging considering that the model geometry (Zhang, 2020), although three-dimensional in nature, is still quite different from the realistic geometry in humans (Wu and Zhang, 2019). More importantly, the neural network was trained using simulation data generated without a vocal tract, and inverse filtering was used to recover the source information from human data. In other words, the estimation process implicitly assumes no source–tract interaction, whereas source–tract interaction is known to exist in human phonation. Despite these simplifications, the reasonable agreement in this study suggests that the computational model and the simulation data it generated do capture the major cause–effect relationships between vocal fold physiology and voice production in humans, and the simulation-based machine learning approach has the potential to be applied to human speech production for clinical and speech technology applications.