A divisive hierarchical clustering methodology for enhancing the ensemble prediction power in large scale population studies: the ATHLOS project

Abstract

The ATHLOS cohort is composed of several harmonized datasets of international groups related to health and aging. As a result, the Healthy Aging index has been constructed based on a selection of variables from 16 individual studies. In this paper, we consider additional variables found in ATHLOS and investigate their utilization for predicting the Healthy Aging index. For this purpose, motivated by the volume and diversity of the dataset, we focus our attention upon data clustering, where unsupervised learning is utilized to enhance prediction power. Thus we show the predictive utility of exploiting hidden data structures. In addition, we demonstrate that imposed computation bottlenecks can be surpassed when using appropriate hierarchical clustering, within a clustering for ensemble classification scheme, while retaining prediction benefits. We propose a complete methodology that is evaluated against baseline methods and the original concept. The results are very encouraging suggesting further developments in this direction along with applications in tasks with similar characteristics. A straightforward open source implementation for the R project is also provided (https://github.com/Petros-Barmpas/HCEP).

Supplementary Information

The online version contains supplementary material available at 10.1007/s13755-022-00171-1.

Introduction

Health Informatics has received much attention in the past years, since it permits Big Data collection and analysis, as well as the extraction of patterns that are free of the strict methodological assumptions of statistical modeling [1, 2]. Recent advances in the biomedical domain that contribute in the early and accurate disease detection, patient care and community services, generate data at an increasing rate. These complex datasets belong to the Big Data field, containing various variable types with different scales or experimental setups, in many cases incomplete [3]. The large data volume on each biomedical research field offers the opportunity to open new avenues for exploring the various biomedical phenomena. Machine Learning (ML) methods are considered as the first choice for the analysis of this data, as they can tackle their volume and complexity. In recent years, both unsupervised and supervised ML methods have been applied to biomedical challenges with reliable results.

A large category on this perspective is the population studies for aging and health analysis, where they offer a plurality of large scale data with high diversity and complexity. Aging and health indicators are an important part of such research as the population aging observed in most developed countries leads to an increasing interest in studying health and aging, since the elderly are nowadays the fastest-growing segment in large regions, such as Europe, Asia and the USA [4–8]. As such, discovering health-related factors in an attempt to understand how to maintain a healthy life is of crucial importance. Meanwhile, it has long been reported that Sociodemographic factors are significant determinants of various health outcomes, such as healthy aging [9, 10], while evidently aging involves interactions between biological and molecular mechanisms with the environment, and as a result, it is a multifactorial phenomenon that everyone experiences differently [11].

The EU-funded ATHLOS (Ageing Trajectories of Health: Longitudinal Opportunities and Synergies (EU HORIZON2020-PHC-635316, http://athlosproject.eu/)) Project produces a large scale dataset in an attempt to achieve a better understanding of aging. The produced harmonized dataset includes European and international longitudinal studies of aging to identify health trajectories and determinants in aging populations. Under the context of ATHLOS, a metric of health (the Healthy Aging index) has been created using an Item Response Theory (IRT) approach [12] delivering a common metric of health across several longitudinal studies considered in ATHLOS. Interestingly, there is a plethora of available variables within the harmonized dataset that have not been considered when generating the aforementioned metric of health, encouraging the further exploration of associated factors through the utilization of Pattern Recognition and ML approaches. Nevertheless, the imposed data volume and complexity generate challenges for ML related to Big Data management and analytics.

There exist many recently published studies based on the ATHLOS dataset with promising results in several scientific fields, such as cardiovascular disease evaluation [13–17], demographic studies about sociodemographic indicators of Healthy Aging index [18] and the impact of socioeconomic status [19–21], nutrition science studies such as nutrition effects on health [22–24], alcohol drinking patterns effects on health [25, 26] and even psychology studies assessing the impact of depression and other psychological disorders related to aging and health [27–29]. Nevertheless, the ATHLOS data specifications require analysis through state of the art ML methods to uncover hidden patterns, tackle the data complexity and help to better interpret the characteristics that affect the state of human health. Predicting the Healthy Aging index can be considered one of the greatest challenges of ATHLOS projects in the health informatics domain. Previously, members of the ATHLOS consortium published studies [30, 31] by applying various supervised ML algorithms on part of ATHLOS data (ATTICA and ELSA study respectively). While these studies have shown remarkable results, a study of the Healthy Aging index prediction in the unified and harmonized ATHLOS data utilizing all additional information has not yet been done.

In this study, we proposed a hybrid framework that includes the integration of unsupervised and supervised ML algorithms to enhance prediction performance on large-scale complex data. More precisely, we developed a divisive hierarchical clustering framework for ensemble learning to enhance the prediction power on ATHLOS large-scale data regarding its Healthy Aging index. We focus our attention upon the clustering for the prediction scheme. Evidently, unsupervised learning enhances the prediction power, exploiting the structure of the data. We show that imposed computation bottlenecks can be surpassed, when using appropriate hierarchical clustering within a clustering for ensemble classification scheme, while retaining prediction benefits. We propose a complete methodology that is evaluated against other baseline methods. The results are very encouraging, suggesting further developments in this direction along with applications in tasks with similar characteristics.

Related work

In the last decade, several studies have been published regarding the integration of unsupervised and supervised learning strategies, most of which concern the incorporation of clustering models to classification algorithms for the improvement of the prediction performance. Although there has been a remarkable progress in this area, there is a need for more robust and reliable frameworks under this perspective given the ever-increasing data generation in various domains. Clustering can be considered as a preprocessing step in a classification task, since in complex data with non-separable classes the direct application of a classifier can be ineffective. In [32] the authors provided evidence that the training step in separated data clusters can enhance the predictability of a given classifier. In their approach the k-means and a hierarchical clustering algorithm were utilized to separate the data, while neural networks were applied for the classification process.

The utilization of clustering in an attempt to gain more information regarding the data and subsequently reducing errors in various prediction tasks has been previously explored. The clustering outcome can be considered as a compressed representation of the dataset and has the potential to exploit information about its structure. In [33], the authors examine the extent to which analysis of clustered samples can match predictions made by analyzing the entire dataset at once. For this purpose, they compare prediction results using regression analysis on original and clustered datasets. It turned out that clustering improved regression prediction accuracy for all examined tasks. Additionally, the authors in [34] also investigated whether clustering can improve prediction accuracy by providing the appropriate explanations. They proposed the coordination of multiple predictors through a unified ensemble scheme. Furthermore, in [35], the authors integrated the semi-supervised fuzzy c-means (SSFCM) algorithm into the Support Vector Machine (SVM) classifier offering promising results regarding the improvement of SVM’s prediction power. Their hypothesis lies on the fact that unlabeled data include an inner structure, which can be efficiently uncovered by data clustering tools. This has been shown to be a crucial preprocessing step to enhance the training phase of a given classifier.

Following a similar perspective, the SuperRLSC algorithm utilizes a supervised clustering method to improve classification performance of the Laplacian Regularized Least Squares Classification (LapRLSC) algorithm [36]. Their motivation is based on the intuition that the clustering process contributes to the identification of the actual data structure by constructing graphs that can reflect more refined structures. A step further is to incorporate ensemble clustering before the classification stage, since an ensemble approach can elucidate the data structure in a more realistic manner [37]. The authors applied this framework to identify breast cancer profiles and provide reliable results, since ensemble clustering algorithms capable to deal with the biological diversity are essential for clinical experts. Other approaches such as the work in [38] utilize a clustering process to reduce the number of instances used by the imputation on incomplete datasets. The unsupervised learning part in this method offered better results not only in the classification accuracy, but also in terms of computational execution time. Given that the most population-based studies include a plethora of missing values, this framework has a great potential to export reliable results in cases.

Although several hybrid approaches, including supervised and unsupervised ML techniques, have been recently proposed, the rise of Big Data challenges along with the diversity issues on population studies, necessitates further research in this direction. Since the ATHLOS dataset has a strong inherent complexity and diversity with a plethora of missing values, developments in clustering-assisted classification should be beneficial. Next, we will show that an incorporated clustering methodology enhances the prediction power of various classification and regression tools.

Background material

Data description

The ATHLOS harmonized dataset [39] includes European and international longitudinal studies of aging. It contains more than 355,000 individuals who participated in 17 general population longitudinal studies in 38 countries. We specifically used 15 of these studies, which are the 10/66 Dementia Research Group Population-Based Cohort Study [40], the Australian Longitudinal Study of Aging (ALSA) [41], the Collaborative Research on Ageing in Europe (COURAGE) [42], the ELSA [43], the Study on Cardiovascular Health, Nutrition and Frailty in Older Adults in Spain (ENRICA) [44], the Health, Alcohol and Psychosocial factors in Eastern Europe Study (HAPIEE) [45], the Health 2000/2011 Survey [46], the HRS [47], the JSTAR [48], the KLOSA [49], the MHAS ([50]), the SAGE [51], the SHARE [52], the Irish Longitudinal Study of Ageing (TILDA) [53] and the Longitudinal Aging Study in India (LASI) [54].

Ensemble learning

Ensemble methods have seen rapid growth in the past decade within the ML community [55]. An ensemble is a group of predictors, each of which gives an estimate of a response variable. Ensemble learning is a way to combine these predictions with the goal that the generalization error of the combination is smaller than each of the individual predictors. The success of ensembles lies in the ability to exploit the predictors’ diversity. Thus, if a predictor exhibits enhanced generalization performance regarding a class or subspace of the dataset, then the aggregated strength of all the predictors can form a global, more reliable one.

A significant portion of research outcomes in ensemble learning aims towards finding methods that encourage diversity in the predictors. Mainly, there are three reasons for which ensembles perform better than the individual predictors [56]. The first reason is statistical. A learning algorithm can be considered a way to search the hypotheses space to identify the best one. The statistical problem is caused due to insufficient data. Thus, the learning algorithm would give a set of different hypotheses with similar accuracy on the training data. With ensembling, the risk of choosing the wrong hypothesis would be averaged out to an extend. The second reason is of computational nature. Often, while looking for the best hypothesis, the algorithm might be stuck in a local optimum, thus giving the inferior results. By considering multiple such hypotheses, we can obtain a much better approximation of the true function. The third reason is representational. Sometimes the underlining function might not be any hypothesis in the hypotheses space. With the ensemble method, the representational space might be expanded to give a better approximation of the unknown function.

Ensemble learning also coincides with the task of clustering, since the performance of most clustering techniques is highly data-dependent. Generally, there is no clustering algorithm, or algorithm with distinct parameter settings, which performs well for every set of data [57]. To overcome the difficulty of identifying a proper alternative, the methodology of cluster ensemble has been continuously developed in the past decade.

Projection based hierarchical divisive clustering

Hierarchical clustering algorithms create clusters either in a divisive (top-down) or an agglomerative (bottom-up) approach. In the former, the whole dataset is considered a single cluster in the first step. According to predefined split criteria, a succession of splits produces subsets down to the final clustering scheme. On the other hand, the agglomerative approach starts by considering each data point as its own unique pre-cluster. In contrast, according to some similarity measures, successive joints of pre-clusters produce hyper-sets of points that finally lead up to the clustering structure. Despite the promising performance of hierarchical clustering algorithms in uncovering the data structure [58, 59], the computational overhead opposed impedes their usage in Big Data scenarios. However, more recent advancements in both agglomerative [60, 61] and divisive strategies [62, 63] have exposed their broad applicability and robustness. In particular, it has been shown that, when divisive clustering is combined with integrated dimensionality reduction [59, 64, 65], we can still get methods capable of indexing extensive data collections. In contrast to agglomerative methodologies, such indexes allow fast new sample allocation to clusters.

In more detail, several projection-based hierarchical divisive algorithms try to identify hyper-planes that best separate the clusters. This can be achieved with various strategies, more notably by calculating the probability distribution of the projected space and avoid separating regions with high-density [66–68]. The latter presents computational challenges in the calculation of the density of each neighborhood. Motivated by the work of [69], instead of finding the regions with high density, the authors in [59, 64] try to identify regions with low density to create the separating hyper-planes.

The dePDDP [64] algorithm builds upon the Principal Direction Divisive Partitioning (PDDP) [70], a divisive hierarchical clustering algorithm defined by the compilation of three criteria, for cluster splitting, cluster selection, and algorithm termination, respectively. These algorithms incorporate information from the projections $p_i$: $p_i=u_1\left(d_i,-,b\right),i=1,2,\dots ,n$ onto the first principal component $u_1$ to produce the two subsequent partitions at each step. In more detail, dePDDP splits the selected partition ${\mathcal{P}}^{\mathcal{l}}$ by calculating the kernel density estimation ${\widehat{f}}^{\prime }\left(x,;,h^{\prime }\right)$ of the projections $p_i^l$ and the corresponding global minimizer $x^{\ast }$ defined as the best local minimum of the kernel density estimation function. Then constructs $P_1^l=\left\{d_i,\in ,\mathcal{D},:,p_i^l,\le ,x^{\ast }\right\}$ and $P_2=\left\{d_i,\in ,\mathcal{D},:,p_i^l,>,x^{\ast }\right\}$. Now, let $\mathcal{P}$ a partition of the dataset D into k sets. Let F be the set of the density estimates $f_i=\widehat{f}\left(x_i^{\ast },;,h\right)$ of the minimizers $X_i^{\ast }$ for each $C_i\in \mathcal{P}$. The next set to split is $C_j$, with $j=arg{max}_i\left\{f_i,:,f_i,\in ,\mathcal{F}\right\}$. Finally, the algorithm allows the automatic determination of clusters by terminating the splitting procedure as long as there are no minimizer for any of the clusters $C_i\in \mathcal{P}$.

By using techniques like the fast Gauss transform, linear running time for the kernel density estimation is achieved, especially for the one-dimensional case. To find the minimizer, only the density at n positions (between the projected data points) needed to be evaluated, since those are the only places with valid splitting points. Thus, the total complexity of the algorithm remains $\mathrm{O}\left(k_{max},\left(2,+,k_{\mathit{SVD}}\right),\left(s_{\mathit{nz}},n,a\right)\right)$.

The Minimum Density Hyper-planes (MDH) algorithm [59] follows a similar clustering procedure. However, instead of using the First Principal Component for the calculation of the splitting hyper-plane that minimizes the density, MDH follows a projection pursuit formulation of the associated optimization problem to find minimum density hyper-planes. Projection pursuit methods optimize a measure of interest of a linear projection of a data sample, known as the projection index, in this case the minimum value of the projected density. Although this is a theoretically justified approach, it is more computationally intensive, mainly due to the optimization procedure. Thus, when the clustering efficiency is not of crucial importance (data indexing) or the computational resources are limited or real-time performance is required, the dePDDP approach can be considered as a satisfactory approximation of MDH.

The proposed ensemble methodology

The concept proposed in [34] showed that an ensemble learning predictor based on different clustering outcomes can improve the prediction accuracy of regression techniques. The performance gains are associated with the change in locality features when training prediction models for individual clusters, rather than the whole dataset. Different clustering outputs $\mathcal{P}$ are retrieved by providing various k values to the k-means clustering algorithm, increasing the diversity of the outcomes. For $k=1,2,\cdots ,L$, we retrieve L ${\mathcal{P}}_k$ individual partitionings. Then, for each cluster $C_k^i\in {\mathcal{P}}_k$, with $i=1,2,\cdots ,k$ and $k=1,2,\cdots ,L$, a model is trained. The final predictions for each data point are calculated by averaging among the predicted values retrieved by the models that correspond to the clusters $C_k^i$ that falls within. Selecting a cutoff L for k (how many individual partitionings ${\mathcal{P}}_k$ should be calculated) is not straightforward, but data dependent heuristics can be estimated.

There is a crucial trade-off, however, for this methodological framework with respect to the computational complexity, imposed by the number of predictors that need to be trained. Even though each model is trained upon a subset of the original dataset, we still need to train $\frac{L\times (L+1)}{2}$ predictors. As a result, the computational complexity increases exponentially. Large scale prediction tasks similar to the one studied here can prohibit the extensive utilization of this concept, in particular when combined with computationally demanding predictors, such as Neural Networks and Support Vector Machines.

In this work, motivated by recent advantages in projection-based divisive hierarchical algorithms, we proposed an ensemble algorithmic scheme able to surpass the aforementioned computational burden, while retaining prediction benefits. The key idea is to generate the L partitionings by iteratively expanding a binary tree structure. Divisive clustering algorithms allow us to stop the clustering procedure, when the predefined number of clusters k has been retrieved. Then, to retrieve the partitioning for $k=k+1$, we only need to split one of the leaf nodes. In practice, L partitionings can be retrieved by a single execution of the algorithm, where k is set to the threshold value L. By monitoring the order of binary splits, we retrieve $\mathcal{P}$ constituted by the individual partitionings that correspond to the $k=1\cdots L$ values.

Arguably, we sacrifice some of the diversity between the individual partitionings ${\mathcal{P}}_k$, since each two consecutive partitionings only differ with respect to the portion of the dataset that constitutes the selected for splitting leaf node, but simultaneously benefit greatly by only having to train $2L+1$ models. Again, to provide the final prediction for each data point, we need to average the predicted values retrieved by the models that correspond to the clusters $C_k^i$. This means that we need to combine information retrieved by the nodes (clusters) appearing along the path each sample followed from the root node (containing the full dataset) the the leaf node that lies within. Note that this divisive structure not only allow us to interpret the ensemble procedure, but is also straightforward to efficiently assign new observations to the tree structure providing the corresponding predictions for new arriving samples.

In Algorithm 1, we present the complete proposed algorithmic procedure entitled Hierarchical Clustering for Ensemble Prediction (HCEP). In summary, the first step is to execute the projection based divisive clustering algorithm of choice and retrieve the complete resulting binary clustering tree. Keep in mind that the response variable is not taken into account for this step, as such, this is an unsupervised procedure. Then for each node of the tree, we train the selected prediction algorithm based only on samples belonging to the particular training set. For every sample belonging to the test set, we can now provide final predictions by averaging across the individual predictions of this particular sample retrieved by the corresponding nodes of the tree that lies within. For each new arriving sample, we initially pass it through the tree structure until reaching the appropriate leaf node. This is done by projecting the new sample onto the one dimensional vector retrieved for each node of the tree and deciding whether it should be assigned at the right or the left child. Then the prediction mechanism is applied as before.

Naive clustering for prediction

We are also interested in investigating the effectiveness of clustering in prediction, when used as a single preprocessing step [33]. We expect that the characteristics of the ATHLOS dataset employed in this work, such as its large scale and the imposed complexity by the appearance of both continuous and categorical variables, present a unique opportunity to expose the benefits, if any, in training individual models for sub-populations of samples belonging to the same cluster.

In practice, this procedure can be achieved utilizing any clustering algorithm. Here, we employ both the k-means and projection based divisive clustering as representatives of partitioning and hierarchical clustering, respectively. The algorithmic procedure is presented in Algorithm 2. The clustering takes place initially for a given number of clusters, which is subject to further investigation. Then, a prediction model is trained for each cluster utilizing the respective train samples, while for each sample in the train set, the final prediction is provided by the model that corresponds to the cluster it lies within. The new arriving sample is initially allocated to a cluster and then a similar procedure is followed to provide predictions. Notice that this procedure should be significantly more computationally efficient than the ensemble methodology, since we only need to train L models. In addition, for particular prediction algorithms with close to exponential complexity with respect to the number of samples, we also expect a significant computational boost against their application on the full dataset $\mathcal{D}$.

Data preprocessing

The aforementioned studies’ dataset described in Sect. 3.1 consist of 990,000 samples from more than 355,000 individuals, who participated in 17 general population longitudinal studies in 38 countries. The dataset contains 184 variables; two response and 182 independent variables. Response variables are the raw and the scaled Healthy Aging index of each patient. Regarding the independent variables (see supplementary material sheet S1), nine variables were removed including various indexes (sheet S2), 13 variables were removed including obviously depended variables that cannot be taken into account (sheet S3), and six variables were removed including information that cannot be considered within the prediction scheme (sheet S4). Furthermore, the 47 variables (sheet S5), which used to originally calculate the Healthy Aging index [12] are also excluded. Not only these features create a statistical bias regarding the Healthy Aging index, which is the response variable in our analysis, but in this work we aim to uncover new insights for external variables that have previously been considered not significantly relevant. Removing any samples for which the Healthy Aging index is not available, the resulting data matrix is constituted by 770,764 samples and 107 variables.

To this end, we have to deal with the critical step of missing value imputation. For this purpose, we utilized the Vtreat [71] methodology, a cutting-edge imputation tool with reliable results. Vtreat is characterized by a unique strategy for the creation of the dummy variables, which resulted in the construction of 458 dummy variables. Next, a significance pruning process step took place, where each variable was evaluated based on its correlation with the Healthy Aging index (response variable).

Experimental analysis

In the first part of our experimental analysis, we compare the proposed ensemble scheme based on Projection Based Hierarchical Clustering (HCEP) against the original one (based on the k-means partitioning clustering). We also examine if there are any benefits when compared against the naive clustering for prediction scheme presented in Sect. 4.1, utilizing both aforementioned clustering approaches. For this set of experiments, the divisive algorithm of choice is dePDDP, while the maximum number of clusters L is set to 40, which is a value greater than the average optimal number of clusters retrieved by dePDDP to effectively examine the behavior of the proposed methodology. For every run of k-means and dePDDP, the number of clusters k is given as input. k-means is allowed to choose the most appropriate convergence among 10 random initializations [72, 73], while for the dePDDP algorithm, the bandwidth multiplier parameter is set to 0.05, a relative small value to guarantee enough binary splits that will lead to the required number of leafs (clusters). Finally, to avoid highly unbalanced tree structures, we set a threshold so that clusters with less than N/k points are not allowed to be split [74], where N is the total number of points in the dataset. All methodologies are implemented using the R-project open source environment for statistical computing, while specifically for dePDDP we utilize a native efficient implementation and for k-means we employed the implementation provided by the “biganalytics” package, called BigKmeans [75], which benefit from the lack of memory overhead by not duplicating the data. The choice for the employed clustering algorithms is based not only on their satisfying performance, but also on their simplicity and the structural ability to create an index that can be used to allocate future observations. For dePDDP algorithm, new instances are pushed into the tree until it reaches the respective leaf node. For the k-means algorithm, we allocate every instance of the testing set to the closest cluster by calculating the minimum distance to the cluster centroids.

For the prediction task, we employ the traditional Linear Regression (LR) and Random Forests (RF) algorithms. Again, the default parameter values are those provided by the corresponding implementations found in [76]. For the RF, we used 50 trees to guarantee its low computational complexity, due to hardware imposed restrictions, and the $M_{\mathit{try}}$ variable was defined as p/3, where p are the number of variables. The regression performance is evaluated with respect to the Root Mean Square Error and the R-squared (RSQ). The mean squared error (MSE) is a measure of an estimator’s quality, with values closer to zero indicating better performance. The MSE is the second moment of the error. Thus, it incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the truth). MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error RMSE [77]. R-squared (R²) is a statistical measure that represents the proportion of the variance for a dependent variable that’s explained by an independent variable or variables in a regression model.

$$\begin{array}{c}\hfill {\mathrm{R}}^2=1-\frac{\mathit{UnexplainedVariation}}{\mathit{TotalVariation}}\end{array}$$ 1

R-squared indicates to what extent the variance of one variable explains the variance of the second variable. So, if the R² of a model is 0.50, then approximately half of the observed variation can be explained by the model’s inputs.

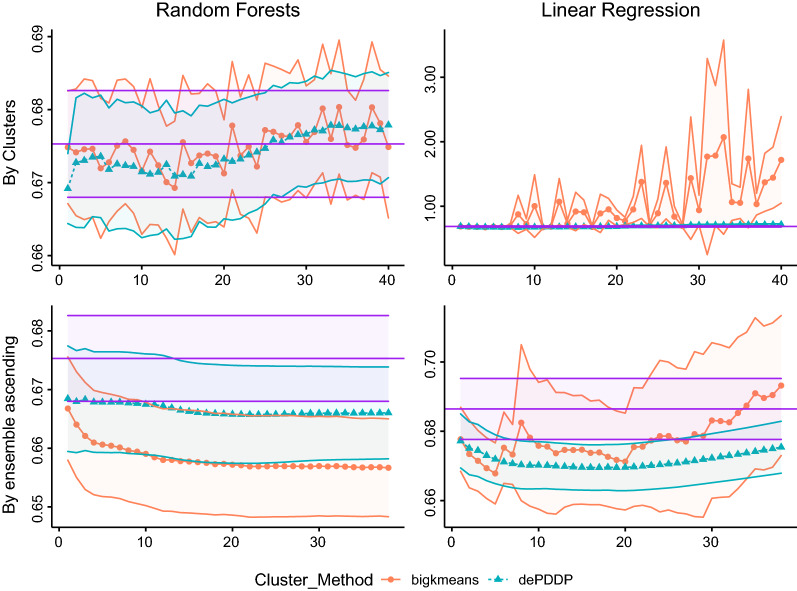
The results with respect to the RMSE metric regarding the prediction of Healthy Aging index are reported in Fig. 1. To achieve robust validation of the results, while maintaining reasonable execution times, we utilize a bootstrapping technique by randomly sampling (with replacement) 50,000 samples for training and 1000 samples for testing [78]. The procedure is repeated 10 times, with different subsets for training and testing, respectively. Then, we estimate the performance of each model by computing the average score and the corresponding standard deviation. These are reported using line plots for mean values and shaded ares for standard deviation respectively. The top row of figures corresponds to the naive methodology, while the bottom row corresponds to the ensemble approaches, respectively. For both cases we report the performance of the catholic models indicated by the straight purple shaded area, parallel to axes X. Orange and green shaded areas indicate the performance of the k-means and the dePDDP algorithms, when combined with either Random Forests (left column) or Linear regression (right column), respectively. Notice that performance is reported with respect to the number of clusters (X axes). For the naive methodology, each number of clusters L corresponds to the RMSE value retrieved for this particular value of L, while for the ensemble models for each L value we observe the RMSE resulting by aggregating predictions for $k=1,2,\cdots ,L$,.

Fig. 1.

RMSE metric results with respect to the Healthy Aging index prediction for Random Forests (first column) and Linear Regression (second column). Circular points with continuous red lines represent the results (vertical axes) when bigKmeans algorithm is utilized, while triangular points with blue dashed lines represent the results for the dePDDP algorithm, respectively. Each row of the plots depicts the clustering for different prediction strategies; naive methodology (first row) and Ensemble on ascending range of clusters (second row). The horizontal purple shaded area represents the corresponding values for the catholic models (training a single predictor in the entire dataset). Mean values are reported according to the utilized bootstrapping, while colored ribbons present the standard deviation between the experiments

In Fig. 1, we observe a performance boost compared to the catholic regression models that is more evident and robust for the ensemble methodologies (Algorithm 1). For up to 20 clusters, the naive models also appear to improve prediction performance, at least when utilizing RF, but when k-means is selected there is no consistency. For the ensemble models best performance is achieved by k-means combined to RF.

Finally, for the Ensemble Linear Regression we observe that the utilization of dePDDP leads to a more robust behavior where the prediction performance is not significantly affected for minor variations in the number of clusters.

This is most likely due to over-fitting, since for a high enough number of retrieved clusters, we expect to end up with clusters characterized by low sample size compared to the number of variables.

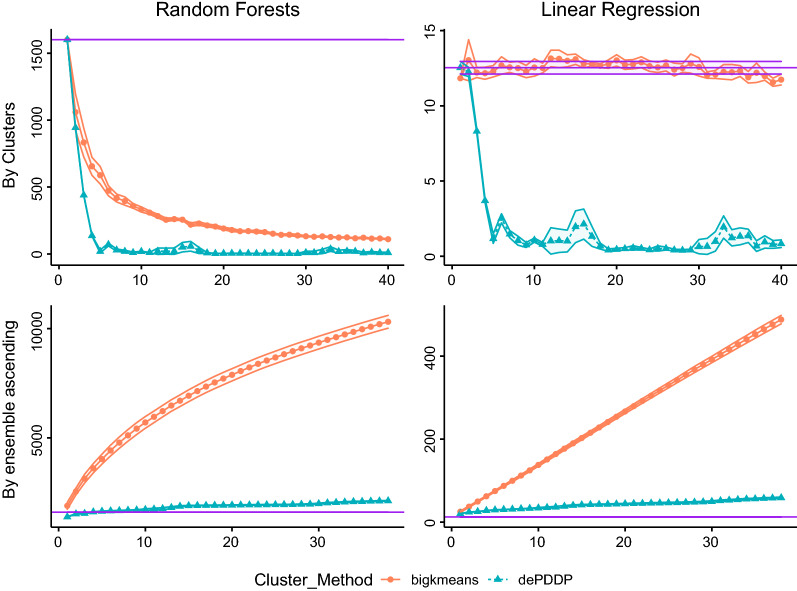
Having concluded that the HCEP framework is able to enhance prediction performance compared to the catholic models and the naive approach, its computational overhead is studied, as well. Figure 2 is devoted to the computational time comparisons. As expected, the naive approach can reduce computational time, at least for complex method such as the RF that are greatly affected by samples size. More importantly, the computational complexity comparison between the ensemble approaches indicates that the utilization of the proposed method is justified. It is evident that consistent prediction power benefits can be achieved with minimal computational overhead. Notice here that the aforementioned computational times for RF have been achieved by implementing a parallel execution strategy accommodated by the “foreach” R package [79]. Experiments took place on a PC with Intel i9 7920x processor and 32 GB of RAM running the Ubuntu Linux operating system.

Fig. 2.

Computational cost in seconds utilizing Random Forest (first column) and Linear Regression (second column) prediction models, respectively. Circular points with continuous red lines represent the results (vertical axes) when bigKmeans algorithm is utilized, while triangular points with blue dashed lines represent the results for the dePDDP, respectively. Each row of the plots depicts the clustering for different prediction strategies. Naive methodology (first row) and Ensemble on ascending range of clusters (second row). The horizontal purple shaded area represents the corresponding values for the catholic models (training a single predictor in the entire dataset). Mean values are reported according to the utilized bootstrapping, while colored ribbons present the standard deviation between the experiments

Extended comparisons

The performance of the proposed HCEP methodology is further evaluated by comparing it against state-of-the-art regression models in predicting the Healthy Aging index using the same bootstrapping technique. In detail, six regression models have been applied, namely the Linear Regression (LR) model, the Random Forests (RF), the k nearest neighbors (kNN), the XGboost [80], and two Deep Neural Network architectures ($DN{N}_1$ and $DN{N}_2$).

Briefly, in kNN regression, the average of the Healthy Aging index values of the five Nearest Neighbors of a given test point is calculated. The RF regression performs the RF process by calculating the average output of all trees in the final prediction for each test sample. We applied 100 trees and the $M_{\mathit{try}}$ variable was defined as $\sqrt{p}$, where p are the number of variables. Extreme Gradient Boosting (XGBoost) is a cutting-edge classifier, based on an ensemble of classification and regression trees [80]. Given the output of a tree $f(x)=wq(x_i)$, where x is the input vector and wq is the score of the corresponding leaf q, the output of an ensemble of K trees will be: $y_i={\sum }_{k=1}^K{f}_k(x_i)$. The first DNN ($DN{N}_1$) is constructed with two hidden layers of 100 neurons and one output layer of one neuron, while the second ($DN{N}_2$) with one hidden layer with 100 neurons. The ReLU activation function is utilized in hidden layers to control the gradient vanishing problem. The Backpropagation (BP) training algorithm is applied with the learning rate set to 0.001. We selected these two DNN architectures to deal with both the over- and under-fitting challenges of ATHLOS dataset after an extensive parameter optimization search was conducted utilizing the Adam algorithm [81].

The results are summarized in Table 1. For both ensemble methods we chose to present the values when the maximum number of clusters is set to $L=30$, which is the average estimated value provided by dePDDP algorithm, when utilized for cluster number determination with its default parameters. Notice that, computational limitations do not allow the extensive use of traditional approaches for this purpose [82, 83], while minor variations to this number do not significantly alter the comparison outcome. As shown, the ensemble methodologies outperform any other confirming the prediction enhancement assumption. More precisely, the k-means based method combined with RF achieve the best score with respect to both metrics. However, the proposed HCEP performs better when LR is utilized for prediction. In general, HCEP comes second to the original k-means based scheme, something to be expected due to the loss of clustering diversity, as previously discussed in Sect. 4. However, the added value of HCEP arises when considering the minimal computational overhead.

Table 1.

Mean RMSE and $R^2$ for different regression models

	RMSE (std)	R${}^2$(std)
LR	0.6851586(0.01815245)	0.5420653(0.02738484)
RF	0.6753074(0.01462793)	0.5551348(0.02472105)
XGboost	0.6937884(0.0138055)	0.5494156(0.02426911)
KNN	0.7858604(0.01970342)	0.4205703(0.02504982)
DNN1	0.6891531(0.01597495)	0.5364436(0.03170498)
DNN2	0.6923526(0.016212242)	0.5105284(0.03162947)
ENS-LR-dePDDP	0.6774225(0.04522381)	0.5505334(0.06650373)
ENS-LR-Kmeans	0.6783292(0.02592916)	0.5516001(0.02380914)
ENS-RF-dePDDP	0.6671423(0.01575666)	0.5659424(0.02244701)
ENS-RF-Kmeans	0.6583103(0.01672183)	0.577264(0.02440015)

The models presented are: Linear Regression (LR), Random Forrests (RF), XGboost, Deep Neural Network with 1 (DNN1) and 2 (DNN2) hidden layers, Hierarchical Ensemble method (HCEP) using Linear Regression or RF based on dePDDP (ENS-LR-dePDDP and ENS-RF-dPDDP, respectively) and ensemble method using LR or RF based on k-means (ENS-LR-Kmeans and ENS-RF-Kmeans, respectively). In parentheses are the Standard Deviation of the metrics across their 10 individual executions and the best performing method for every metric is denoted in bold font

Tree visualization and variable importance

In Fig. 3, we visually investigate the clusterability of the dataset at hand through projection based hierarchical clustering. to this end, we used the MDH implementation [84] provided for the R package. For this experiment, we utilized HCEP, where the maximum number of cluster is conveniently set to $L=4$. Through the iterative 2D visualization for each node of the tree, we visually identify clear patters indicating visually separable clusters. Apparently, the algorithms performs well in identifying clusters, confirming the prediction performance boost we observed previously, even for the naive clustering approach. Note that, sample coloring across the tree structure is following the categorization of the four clusters retrieved at the leaf nodes. For example, for train samples that fall in cluster 5, the predicted Healthy Aging index is retrieved by averaging the corresponding predictions of the models fitted for clusters 1, 3 and 5.

Fig. 3.

Tree structure example of the hierarchical MDH experiment. In this instance, each step of the algorithm is presented in a top-down order, with every level indicating the corresponding cut for a total of 4 clusters. The data points are colored according to the final clustering and each subset is indicated with numbering from 1 (original dataset) to 6 and 7 (last split producing two of the final clusters)

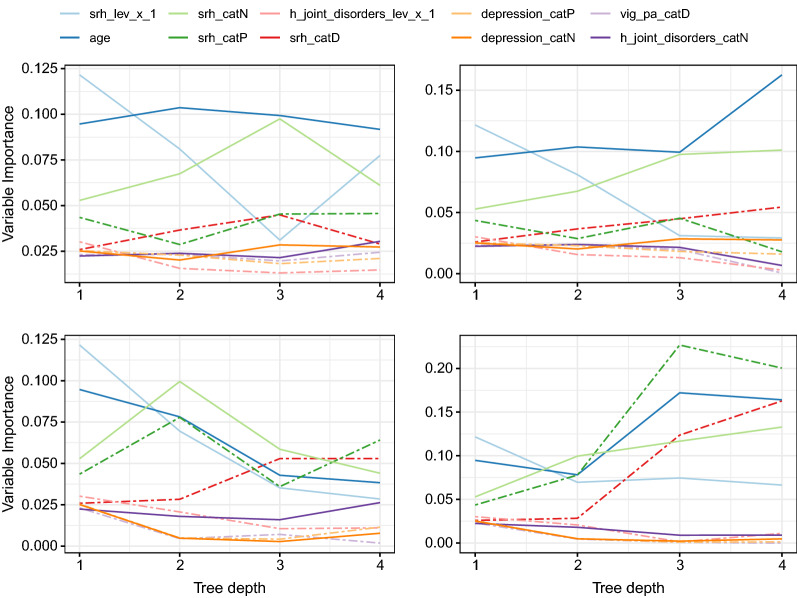
The straightforward interpretability of the HCEP approach motivated us to further investigate the potential of utilizing it in describing an innovating variable importance analysis. Notice here, that this is an uncommon task for most ensemble prediction approaches or even impossible in many cases. For this purpose we utilized the Percentage Increase in MSE (PiMSE) metric [76] through the Random Forests model for very node of the tree. Then for every path from the root node to each one of the leaf nodes, we investigate the PiMSE metric of the nodes within the path, since every point in the test set will be eventually predicted based on one of these paths. For the example at hand (Fig. 3), we consider the 10 most important variables, calculated by averaging PiMSE across all aforementioned paths. Figure 4 illustrates how these variables differentiate for each one of the four paths (1-3-4, 1-3-4, 1-2-7 and 1-2-6), according to the changes in PiMSE from the root to the leaf nodes. In more detail, each subplot depicts one of the four different paths. The PiMSE score is presented in the vertical axes, with the horizontal axes indicating the corresponding node in each path. Larger values in a variable indicate greater PiMSE score, thus expressing a more significant influence of that variable in that particular node. More specifically, the most important variables depicted here were the “srh” (Respondent’s self-rated/self-reported health, with $``cat{P}^{\prime \prime }$, $``cat{N}^{\prime \prime }$, etc. being their transformation after the statistical prepossessing), the “h-joint-disorders” (History of arthritis, rheumatism or osteoarthritis), “depression” (Current depressive status) and “age” (Age at time of measure). Another observation we can make through this visualization is that for 2 paths, “age” significance drops as tree depth is increasing, in contrast to the other two paths for which it grows. This finding may lead to the conclusion that there exist sub-populations for which a particular variable is relevant in predicting the response variable.

Fig. 4.

Variable importance propagation of the prediction model’s ten most influencing variables across each node in the different paths of the tree structure

Concluding remarks

Population studies for aging and health analysis offer a plurality of large scale data with high diversity and complexity. Aging and health indicators are an important part of such research, while predicting the Healthy Aging index can be considered one of the greatest challenges. Motivated by the volume and diversity of the ATHLOS dataset, we focus our attention upon the clustering for prediction scheme, where unsupervised learning is utilized to enhance the prediction power. We show that imposed computation bottlenecks can be surpassed, when using appropriate hierarchical clustering within a clustering for ensemble classification scheme, while retaining prediction benefits. In addition, we investigated in depth the interpretability of the proposed architecture exposing additional advantages, such as a novel variable importance analysis. The proposed methodology is evaluated against several regression methods and the original concept exhibits very encouraging results, suggesting further developments in this direction are possible. Additionally, a straightforward open source implementation for the R project is provided. The direct expansion of the proposed methodology in classification could suggest a promising future direction, while the utilization of random space transformations to increase diversity of ensemble schemes [85, 86] seems also feasible.

Supplementary Information

Below is the link to the electronic supplementary material.