Estimation and Validation of Cardiac Conduction Velocity and Wavefront Reconstruction Using Epicardial and Volumetric Data

Abstract

Objective:

In this study, we have used whole heart simulations parameterized with large animal experiments to validate three techniques (two from the literature and one novel) for estimating epicardial and volumetric conduction velocity (CV).

Methods:

We used an eikonal-based simulation model to generate ground truth activation sequences with prescribed CVs. Using the sampling density achieved experimentally we examined the accuracy with which we could reconstruct the wavefront, and then examined the robustness of three CV estimation techniques to reconstruction related error. We examined a triangulation-based, inverse-gradient-based, and streamline-based techniques for estimating CV cross the surface and within the volume of the heart.

Results:

The reconstructed activation times agreed closely with simulated values, with 50–70% of the volumetric nodes and 97–99% of the epicardial nodes were within 1 ms of the ground truth. We found close agreement between the CVs calculated using reconstructed versus ground truth activation times, with differences in the median estimated CV on the order of 3–5% volumetrically and 1–2% superficially, regardless of what technique was used.

Conclusion:

Our results indicate that the wavefront reconstruction and CV estimation techniques are accurate, allowing us to examine changes in propagation induced by experimental interventions such as acute ischemia, ectopic pacing, or drugs.

Significance:

We implemented, validated, and compared the performance of a number of CV estimation techniques. The CV estimation techniques implemented in this study produce accurate, high-resolution CV fields that can be used to study propagation in the heart experimentally and clinically.

1. Introduction

Cardiac conduction velocity (CV) is an important electrophysiological property that describes the speed and direction of electrical propagation through the heart. Pathologies such as myocardial ischemia and infarction, atrial fibrillation, or a wide range of ventricular arrhythmias can introduce changes to the normal, highly coordinated heart conduction and activation. Accurate CV measurements provide a valuable quantitative description of electrical propagation that can help identify arrhythmias, localize diseased tissue, and stratify patient risk for a major adverse cardiac events [1]. However, while two-dimensional (surface based) approaches exist, until now, there has been no documented, well-validated, and tractable means of obtaining high-resolution three-dimensional (volumetric) CV measurements.

Conduction velocity is a difficult physiological parameter to measure because of sampling limitations and algorithmic challenges to approximating or reconstructing the wavefront, especially volumetrically. Acquiring a dense enough sampling on a surface of the heart to estimate epicardial or endocardial activation is already challenging. Achieving sufficient sampling for three-dimensional or volumetric measurements in animals is even more daunting, due to the invasive nature of such recordings and the specialized instrumentation required.

Once measurements are available, further processing is necessary to reconstruct a high-density map of conduction velocity. Accurately reconstructing conduction velocity across a curved surface or within a volume at sufficient spatial density is fundamentally challenging because the underlying mechanisms of myocardial activation are so complex, nonlinear, and heterogeneous [2], [3]. All reconstruction approaches are based on simplifying assumptions, whose accuracy is difficult to evaluate. Even with surface reconstructions, inaccuracies arise because the measurements across a curved surface are fitted to planes between co-localized points. The resulting errors increase as the surface curvature increases. For this study, we attempted to compensate for high curvature by using a fitted mesh rather than a plane to project measured values and then reconstruct the values over the entire surface.

The measurement of CV is increasingly used clinically and during experiments, however, little is known how various approaches compare against one another, particularly in cases of limited sampling. Several CV estimation techniques have been reported in the literature [4], [5], including triangulation [6]–[8] and inverse-gradient techniques [3], [9]–[11]; however, these techniques suffer from assumptions that have not been thoroughly tested or validated using a shared interpolation-based wavefront reconstruction approach. Reconstructing the wavefront using an interpolation-based approach allows CV to be estimated at a high-resolution, but estimating CV on these interpolated maps lacks robust validation. Both triangulation and the inverse-gradient techniques are vulnerable to interpolation-related artifacts because they are local operators applied to single elements and hence spatially independent of the surrounding geometry. Therefore, one might reasonably expect a regional or even global integrative technique to improve the accuracy of CV reconstruction. In this study, we compared several techniques, including the spatial integrative streamline technique against one another in the epicardial and volumetric domains.

We have implemented a novel streamline-based technique for estimating CV that is robust to interpolation-related artefacts and compared a number of techniques for estimating CV over the epicardial surface and within the volume of the left ventricle. The novel technique starts with element-wise estimation of the gradient of local activation times; however, it then leverages the propagation directionality and neighborhood-level information to maintain CV estimation accuracy in the presence of interpolation-based artifacts. We demonstrate that this technique is capable of operating both over the epicardial surface and within the myocardial volume. To assess the accuracy of the streamline-based technique we simulated spread of activation in image-based models of the hearts from our large-animal experiments using the eikonal simulation framework in the Cardiac Arrhythmia Research Package (CARPentry) [12]. We then compared our approach against several others reported in the literature and documented improved performance.

2. Methods

A. Simulation of activation times

To validate the techniques for conduction velocity reconstruction required high resolution volumetric activation times, which are only available through simulation. In order to link the reconstructions to measurements, we created the necessary geometric models from images of hearts from experiments and then used the electrode locations from those experiments as the sampled values for reconstruction. The activation times came from the Cardiac Arrhythmia Research Package (CARPentry) simulation platform [12], a well verified and validated set of tools used extensively in the field of cardiac simulation. These particular CARPentry simulations used an eikonal-based depolarization sequence from an initial pacing site with assigned orthotropic CV tensors based on a rule-based fiber orientation. [12] CV ratios of 1, 2/3, and 1/3 for the eikonal-activation were prescribed along the longitudinal fiber direction (CV_l), transverse to the fiber (CV_t), and across sheets (CV_s), respectively. [12] Conduction velocities were chosen and assigned manually based on a priori knowledge of the pacing site location (different assignment based on stimulation in endo-,mid-, and epicardium) so as to match the measured total activation time (TAT) from animal experiments (see Sec.2.1.1).

We created the geometric models from high-resolution, post mortem MR imaging of hearts explanted after five large-animal (canine) experiments, using a pipeline similar to that described previously [13], [14]. In short, MR images of the excised heart were semi-automatically segmented to identify myocardium and blood pools using Seg3D (http://www.sci.utah.edu/cibc-software/seg3d.html). The segmentations were meshed with an approximate edge length of 650 μm using Cleaver (https://www.sci.utah.edu/cibc-software/cleaver.html), and pacing sites were labeled using the open-source package meshtool [15]. Myocardial fibers were generated with a rule-based approach that prescribed orientations ranging from 60° on the endocardium to −60° on the epicardium. [16] We also adopted the Universal Ventricular Coordinates (UVCs) [17], consisting of apico-basal (z), transmural (ρ), ventricular (ν), and rotational (ϕ) coordinates, to allow for pacing-site definitions in a consistent reference frame that applied across all hearts.

All five experiments followed our standard protocols [7], [14], [18], [19] and were approved by the Institutional Animal Care and Use Committee of the University of Utah and adhered to the Guide for the Care and Use of Laboratory Animals (Protocol 17–04016, Approved 05-02-2017). Intramyocardial electrograms were measured using 20–40 intramural plunge needles that recorded signals from 10 unipolar electrodes each. Epicardial electrograms were measured using a 247-electrode sock array [20]. Electrograms and activation times from one of the five experiments was used to parameterize the CARPentry simulation (see Sec. 2.1.1), while all five were used to provide subject specific anatomy and electrode placement.

1). Stimulation Site and CV Parameterization:

Our simulations included 11 pacing sites per heart to assess the variability associated with the activation sequence. Pacing sites #1–5 were distributed throughout the volume sampled by the needle electrodes while sites #6–11 followed a single needle across the left ventricular wall. Sites #1–5 were fixed using UVCs to ensure anatomically consistent positions across all five hearts, with 2 endo-, 1 mid-, and 2 epicardial sites. Sites 6–11 were specific to each experiment as they followed an intramural needle roughly in the center of the sampled region with 2 subendocardial, 2 midwall, and 2 subepicardial locations. The simulated activation patterns were visually analyzed to ensure they agreed qualitatively to those generated experimentally.

The CARPentry simulations were parameterized using data captured during a large animal experiment (Exp. ID-E). The simulations in CARPentry were assigned CVs in order to replicate the total activation times (TATs) observed during Exp. ID-E where the ventricles were electrically stimulated from a number of sites and depths. Exp. ID-E was a torso tank experiment in which an isolated heart was paced from 45 sites throughout the ventricular myocardium using neighboring pairs of needle electrodes (9 beats along each of 5 needles) which allowed us to associate transmural pacing depth (i.e., endo-,mid-,and epicardium) with a resultant TAT. Experimentally, we observed the average TATs from the subendocardium was 82 ± 6 ms, midmyocardium was 86 ± 5 ms, and finally the subepicardium was 96 ± 5 ms. We then adjusted the CVs in the CARPentry model of Exp. ID-E to achieve TATs that agreed with those we measured, varying the prescribed CV_l, 99 ± 3 cm/s, based on whether the simulated pacing site was subendocardial(CV_l= 96 cm/s), midmyocardial (CV_l= 101 cm/s), or subepicardial(CV_l= 97 cm/s). We then applied these prescribed CVs to the four additional subject specific geometric models achieving average simulated TATs of 96 ± 8 ms subendocardially, 90 ± 9 ms midmyocardially, and 96 ± 11 ms subepicardially.

B. Estimating conduction velocity using the streamline-based technique

In this study, we implemented and validated a novel streamline-based technique for estimating conduction velocity both across the epicardial surface and within the myocardial volume. The first step in this approach is to reconstruct the activation sequence as a traveling wavefront from electrograms recorded at a limited set of locations. From the activation sequence, the second step was to apply gradient estimation and streamline generation to estimate the direction and speed of the wavefront. We performed all these steps using either the open-source SCIRun problem-solving environment (www.sci.utah.edu/cibc-software/scirun.html) or custom programs written in MATLAB [21].

1). Step 1: Reconstruction of the Activation Sequence:

In order to reconstruct the activation sequence over the surface and within the volume from the sparsely sampled measurement sites, activation times have to be interpolated to a higher resolution mesh (the mesh of the geometric model), for which we used thin-plate spline radial basis functions (RBFs). [22] To mimic the sparse epicardial sampling of the experiments, we sub-sampled activation times from the simulations at locations corresponding to the epicardial sock electrodes, which were spaced 6.6 ± 2 mm apart. We then interpolated these values to all epicardial nodes in the geometric model. We carried out similar sub-sampling of the intramyocardial activation times from locations corresponding to the 20–40 needles used in the experiments, each with 10 closely spaced (1.5–1.8 mm) electrodes. Spacing between needles was much larger, 1–2 cm depending on the experimental preparation. The region outlined by the needles, the ‘needle envelope’, defined the region over which sampled activation times were then interpolated to the original geometric model. The needle envelope was constructed by taking the convex hull of the intramural needles and then removing the blood pools from the resulting volume.

To evaluate the accuracy of activation sequence reconstruction, we used two quality metrics to compare the simulated ground truth values and those interpolated from the equivalent measurement locations: (1) the root-mean-square error (RMSE) and (2) the percentage of activation times below 1 ms of error. A threshold of 1 ms was chosen because the sampling frequency used during our experiments was 1 kHz.

2). Step 2: Estimation of Conduction Velocity using Streamlines:

Our novel technique to estimate streamlines for conduction velocity begins with an estimate of the gradient of activation times and then smooths and parses the resulting field with a streamline-generation algorithm. [23] The gradient field is defined according to the standard operator

$$\nabla A_t(x,y,z)=\frac{\partial A_t}{\partial x}\partial x+\frac{\partial A_t}{\partial y}\partial y+\frac{\partial A_t}{\partial z}\partial z.$$ (1)

where A_t represents the activation times associated with sites either on the epicardium or within the needle envelope.

From the resulting values of ∇A_t, we uniformly distributed 5000 seed points throughout the domain (either the epicardium or needle envelope) from which streamlines emanated and ascended the local gradient using an adaptive Runge-Kutta-Fehlberg integration in 0.0001 mm steps [23]. The techniques followed the equation

$${\overrightarrow{V}}_{\mathit{\text{Streams}}}=\left[\frac{d_{N1,N2}}{\left(A_{t2}-A_{t1}\right)}\right]\cdot \widehat{{\overrightarrow{d}}_{N1,N2}},$$ (2)

where d_N1,N2 represents the geodesic distance between the two nodes (N1 and N2) and A_t1 and A_t2 are the activation times at the same nodes. ${\overrightarrow{d}}_{N1,N2}$ represents the euclidean unit vector between the points (N1 and N2). Note, activation times are used to compute the gradient field for the streamlines and then again for the estimation of CV.

To smooth the estimation of CV we sampled values at empirically selected intervals along the streamline of 1 mm in the volume and 2 mm on the epicardial surface. The larger intervals on the epicardium provided adequate sampling of the relatively discontinuous wavefronts and put the estimated distribution in line with the other techniques. The estimated CVs $\left({\overrightarrow{V}}_{\mathit{\text{Streams}}}\right)$ along the streamlines were then filtered using a three-element box filter over each streamline.

Streamline computations deliver smoother results and follow the gradient more precisely when applied in three dimensions than in two. In order to apply this method to the epicardial surface, we dilated it by 2 mm to create a thin volume. To restrict the resulting streamlines to the surface, we used true epicardial locations as seed points and interpolated only from nearest epicardial neighbors.

C. Alternative Techniques to Estimate Conduction Velocity

In order to asses the performance of the streamline-based technique, we also implemented the inverse-gradient- and triangulation-based methods described previously. [3], [6], [8]–[10] We implemented both techniques on both the ground truth and reconstructed wavefronts.

A goal of this study was to evaluate activation time reconstruction using radial basis function interpolation and then compare the accuracy of a set of methods to estimate conduction speed. The simulated, high resolution activation times formed the ground truth against which we could evaluate reconstruction accuracy, starting from a sparse set of values located at measurement sites. We lacked such ground truth for the evaluation of conduction speed estimates but could compare the novel streamline-based technique against the inverse-gradient and triangulation approaches based on the distribution medians. We also compared differences in CVs estimated from the ground-truth activation times and from the reconstructed values for all three CV estimation techniques. We estimated each CV estimation technique’s vulnerability to interpolation-related by computing the ‘error,’ which we define to be the percent difference between the CV estimated using ground-truth versus reconstructed activation times.

1). Inverse-Gradient Technique:

The inverse gradient method in both the epicardial surface and volumetric approaches is estimated using Eq.(1) with ∇A_t(x, y, z) used to directly estimate CV (x,y,z) using the following equation proposed by Bayly et al. [3], [9], [10]:

$$\begin{gathered} {\overrightarrow{V}}_x=\frac{\partial x}{\partial A_t}=\frac{t_x}{{t_x}^2+{t_y}^2+{t_z}^2} \\ {\overrightarrow{V}}_y=\frac{\partial y}{\partial A_t}=\frac{t_y}{{t_x}^2+{t_y}^2+{t_z}^2} \\ {\overrightarrow{V}}_z=\frac{\partial z}{\partial A_t}=\frac{t_z}{{t_x}^2+{t_y}^2+{t_z}^2} \\ {\overrightarrow{V}}_{\mathit{\text{Inv.Grad.}}}={\overrightarrow{V}}_x+{\overrightarrow{V}}_y+{\overrightarrow{V}}_x \end{gathered}$$ (3)

In this formulation t_x is equivalent to $\frac{\partial A_t}{\partial x}$ and the same for t_y and t_z. Whereas Bayly et al. evaluated the method with polynomial surfaces to estimate wavefronts, we applied it to the RBF interpolation of activation times in order to compare with our streamline approach.

2). Triangulation:

The surface triangulation technique reported by Cantwell et al. [6], [8] calculates the CV magnitude and direction for every triangular face, using edge lengths, the recorded activation times, and the angles between face edges. See the supplemental material for the full triangulation-based formulation and estimation used here.

In order to extend the original approach to volumes, we transformed the vectors calculated on each face ${\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}}$, which are traditionally anchored to a node in the triangle, to the face center. V_Mag. is the resulting conduction speed and to determine conduction direction, we first determined $\widehat{{\overrightarrow{d}}_{pq}}$ as the unit vector from the first (p) and second (q) activated nodes. From this basis, ‘α’ is then the angle between the wavefront and this edge. The resulting equation for these steps is:

$${\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}}=\left(\left(V_{\mathit{\text{Mag.}}}\cdot \widehat{{\overrightarrow{d}}_{pq}}\right)\circ \left[\begin{array}{cc}\text{cos}\alpha & -\text{sin}\alpha \\ \text{sin}\alpha & \text{cos}\alpha \end{array}\right]\right)+{\overrightarrow{d}}_{pc},$$ (4)

where $\widehat{{\overrightarrow{d}}_{pq}}$ is the edge unit vector, which is scaled by V_Mag. and then rotated by ‘α’ and translated to the triangle centroid by ${\overrightarrow{d}}_{pc}$, the vector connecting p to the centroid c.

After using Eq. (4) to estimate the CV on each face of a given tetrahedral, the tetrahedral CV was estimated by summing the face vectors as

$${\overrightarrow{V}}_{\mathit{\text{Vol.Tet.}}}={\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}1}+{\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}2}+{\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}3}+{\overrightarrow{V}}_{\mathit{\text{Face.Tri.}}4},$$ (5)

where ${\overrightarrow{V}}_{\mathit{\text{Vol.Tet.}}}$ is the volumetric CV vector for a given tetrahedron. To prevent discontinuities and non-physiological CV calculations, we imposed the ad hoc constraints that each triangle required at least 0.2 ms difference in activation time across each edge and for each edge to be longer than 0.2 mm.

3. Results

A. Activation Time Reconstruction Accuracy

The first objective of the study was to examine the radial basis reconstruction of activation times from the sparse sampling in experiments with both an epicardial sock and intramural plunge needles. Table I shows the epicardial and volumetric sampling densities achieved during the five experiments. While the epicardial sampling density was relatively consistent across the experiments, there was more variability in the volumetric sampling. Needle placement was unique for each experiment of which four used in situ, open/re-closed chest preparations and one (Exp. ID-E) made use of an isolated heart suspended in a torso-shaped electrolytic tank. Needles in in situ experiments were densely spaced but with coverage limited by access to the chest cavity, whereas in torso-tank case, they were placed throughout the myocardium, resulting in a much larger sampled region but decreased density. Figure 1 shows an example of electrode placement and reconstruction accuracy from Exp. ID-A.

TABLE I.

Summary of measurement geometry from ventricular sock array and the intramural needle envelope for all five experiments.

Experiment ID	Surface Area per Electrode (mm2)	Avg. Edge Length on Sock (mm)	Needle Envelope Volume (mm3)	# of Needle Electrodes	Volume per Electrode (mm3)
A	37	6.8 ± 2.1	15500	250	62
B	34	6.7 ± 2.1	16900	250	68
C	37	6.7 ± 2.0	13300	200	67
D	33	6.4 ± 2.2	16900	190	89
E	39	6.7 ± 1.6	72200	310	233

Fig. 1.

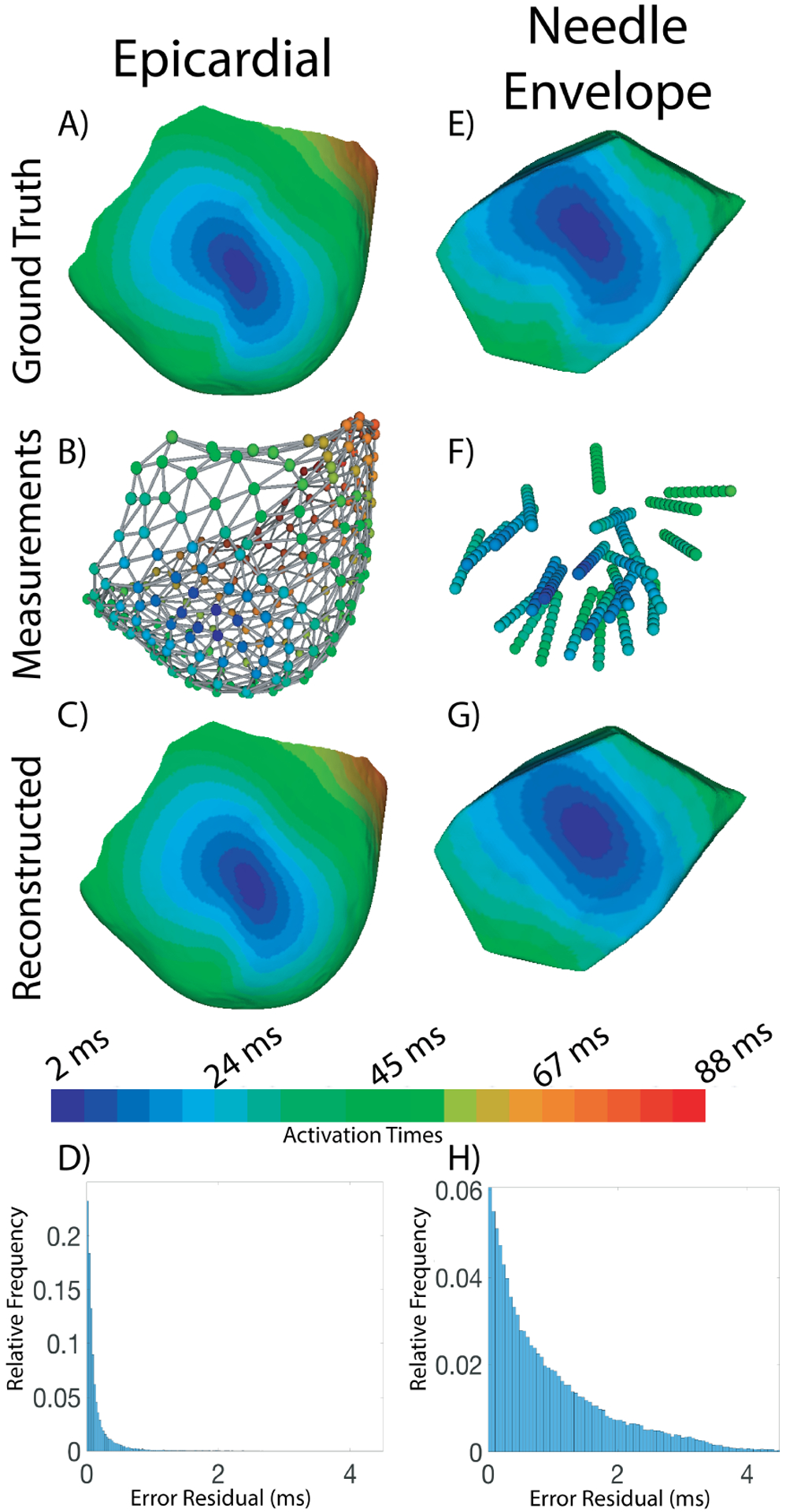
Sample Activation sequence reconstructed from limited sampling of both the epicardial surface and ventricular volume. The colorbar shows the mapping between color and activation time for images A, B, C, E, F, and G. A) The epicardial surface of Exp. ID-A with the activation map from pacing site #11. B) The ventricular sock with nodes showing electrode positions and measured activation times represented in color. C) The reconstructed epicardial activation map. D) Histogram showing the errors in activation times across the epicardial surface. E) The portion of the ventricular myocardium sampled by the intramural needles, referred to as the ‘needle envelope’. F) The intramural needles with nodes showing electrode locations and measured activation times represented in color. G) The reconstructed activation times within the needle envelope. H) Histogram showing the errors in activation times within the needle envelope.

Table II shows the average reconstruction accuracy across all 11 pacing sites for each experiment. For the epicardial sock reconstructions, root mean squared errors between ground truth and reconstructed activation times ranged from only 0.16 to 0.41 ms across all experiments (avg. 0.26 ms) and greater than 96% of all nodes had an activation times within 1 ms (avg. 0.99) of the ground truth. For the volume reconstructions, errors were larger overall but still very acceptable, with RMSE ranging from 0.61–2.1 ms (avg. 1.3 ms) and 50–89% of the nodes under 1 ms (avg. 67%) for Exp. ID- A–D. In Exp. ID-E, the reconstruction accuracy showed larger errors; RMSE ranged from 1.9–2.4 ms (avg. 2.1 ms) and 46–58% of the needle envelope nodes under 1 ms of error(avg. 52%), the expected result of the lower sampling density in this experiment.

TABLE II.

Accuracy of wavefront reconstruction across the epicardial surface and within the needle envelope. RMSE=root mean squared error and the Percent Under 1 ms measures the relative number of nodes with errors less then 1 ms.

Experiment ID	Epicardial RMSE (ms)	Epicardial Percent Under 1 ms	Volumetric RMSE (ms)	Volumetric Percent Under 1 ms
A	0.24 ± 0.06	99% ± 0.06%	1.2 ± 0.26	69% ± 10 %
B	0.30 ± 0.03	98% ± 0.06%	1.5 ± 0.25	59% ± 5 %
C	0.25 ± 0.05	99% ± 0.08%	1.3 ± 0.18	73% ± 5 %
D	0.27 ± 0.06	99% ± 0.09%	1.4 ± 0.26	66% ± 8 %
E	0.27 ± 0.04	99% ± 0.07%	2.1 ± 0.22	52% ± 3 %

Fig. 2 shows an example of spatial maps of the errors between the ground truth and reconstructed activation time across the epicardium and within the volume for pacing site 5 (LV apical epicardium) in Exp. ID- A. The volumetric results show a consistent finding that errors were largest in the volume directly adjacent to the stimulation site. The worst accuracy generally arose under similar conditions, e.g., Exp. ID-B stimulation site 1 (RV endocardium) in which the RMSE was 2.1 ms and only 50% of the nodes were within 1 ms of the ground truth. The best volumetric reconstruction occurred in Exp. ID- A stimulation site 4 (Epicardial Anterior Ventricular Junction) in which the RMSE was 0.61 ms and 89% of the nodes were within 1 ms of the ground truth. Epicardial error is generally low but as Fig. 2 suggests can be as high as 1 ms near the ventricular junction.

Fig. 2.

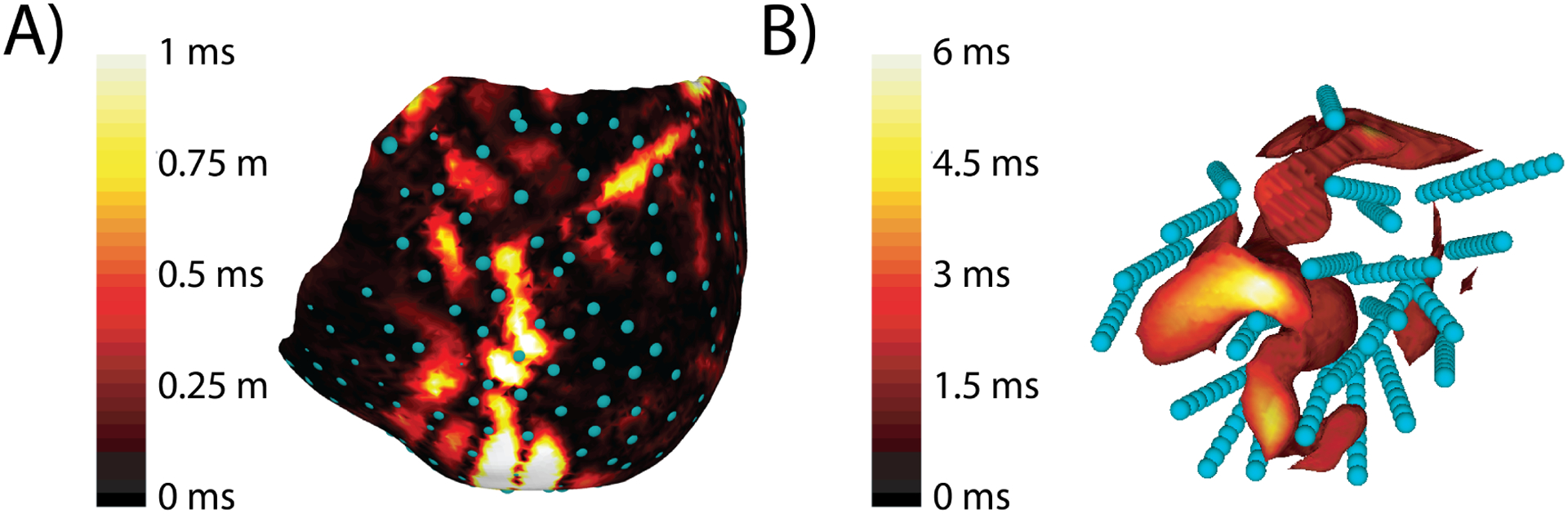
Error in reconstructing the activation sequence shown on the epicardium and within the needle envelope. This pacing site and Exp. ID- was the same as used in Figure 1. A) Epicardial error in activation sequence reconstruction. Blue spheres represent the location of the epicardial sock electrodes. B) Volumetric error in milliseconds displayed within the needle envelope. The volume is thresholded to highlight regions with errors higher than 2 ms. Blue spheres represent the location of the intramural needle electrodes. Note a separate colorbar from A.

Not surprisingly because of the low sampling density, Exp. ID-E had the lowest reconstruction accuracy, with pacing site 9 reaching an RMSE of 2.4 ms with only 50% of the nodes within 1 ms of the ground truth.

B. Comparison of Estimates of Epicardial Conduction Velocity

We first computed epicardial CVs using all three CV estimation techniques using the ground truth activation times from the simulations. The streamline-based technique generated the largest median conduction speeds, followed by the inverse-gradient technique, and then the triangulation-based method. Fig. 3 shows an example in which the peak conduction speed values of the distributions from the stream-line, inverse-gradient, and triangulation techniques occurred at 97, 81, and 81 cm/s, respectively. The inverse-gradient and triangulation techniques consistently had similar distribution peaks, however, the inverse-gradient technique had a larger proportion of what we named ‘extremely fast CS’ (> 150 cm/s) than the triangulation technique. In Fig. 3, the regions of early activity and the secondary breakthrough sites on the anterior portion and the posterior generally showed extremely fast CS. The inverse-gradient and streamline-based techniques also estimated fast CSs in this region, indicating that this speed may be realistic. Therefore it is unclear if the rightward shift in the peak of the streamline-based results was artefactual or realistic.

Fig. 3.

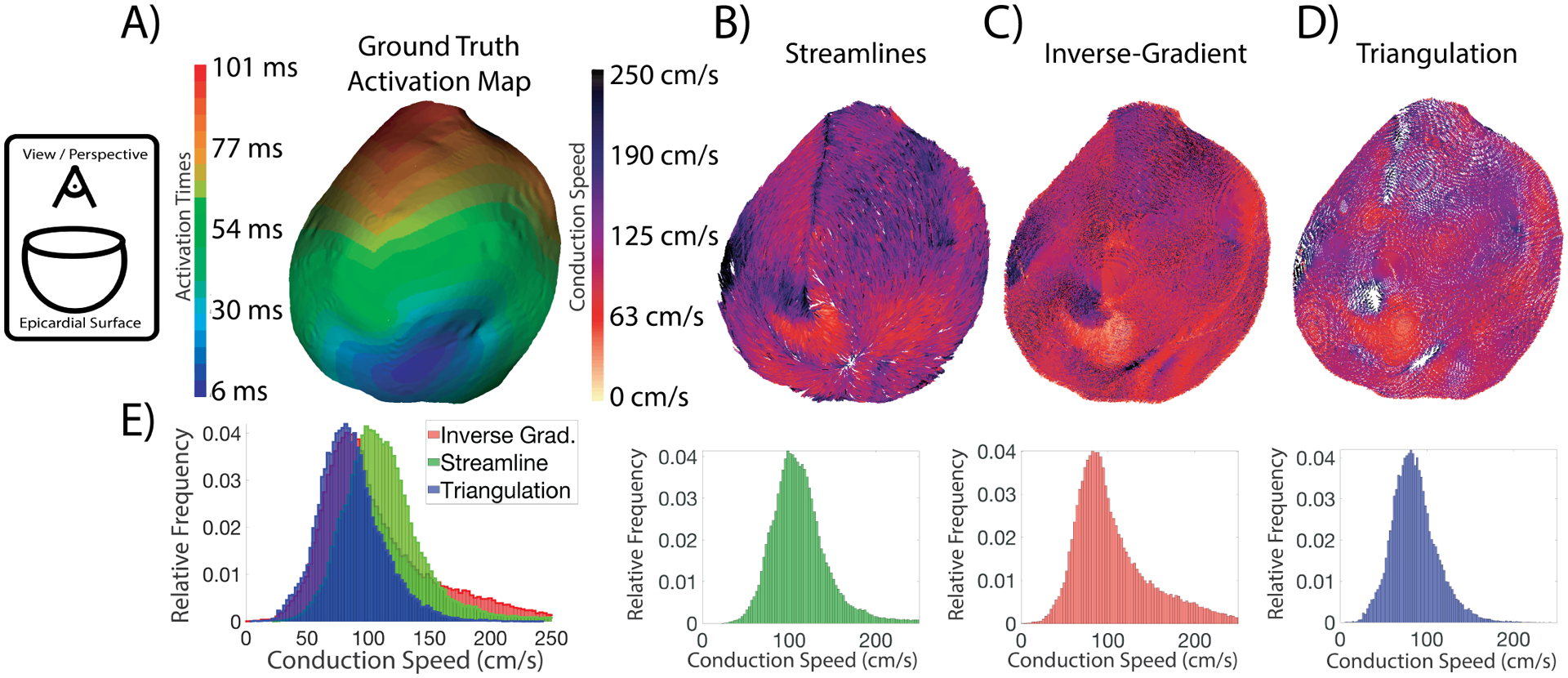
Epicardial surface CV fields and speed distribution generated from an epicardial pacing site (Pacing site #11) using the three techniques. The view/perspective of the fields is from a point above the base of the heart toward the apex, as indicated by the schematic on the far left. The rainbow colormap relates activation time to color for the ground truth epicardial maps in Panel A; the white-to-black colormap applies to the amplitude of the CV fields in Panels B–D, A) The map of activation times displayed across the epicardial surface. B) The CV field created by the streamline-based technique. C) The CV field created by the inverse-gradient technique. D) The CV field created by the triangulation-based technique. E) The speed distributions for the three techniques. The leftmost distribution is an overlay of all the histograms.

The CVs estimated on the reconstructed activation times were compared to the values estimated using the ground-truth times to understand the vulnerability of each CV estimation technique to errors that come from interpolation. The median conduction speeds differed by 2.3–2.6% when averaging on an experiment basis. The largest error seen across the 55 pacing sites and three estimation techniques was 12.5% on pacing site #6 in Exp. ID- D, estimated using the inverse-gradient method. In comparison, results of the streamline-based technique differed by 6.8% from the ground truth, and the difference for triangulation was 5.3%. The smallest error seen across the 55 sites and three estimation techniques was 0.04% on pacing site #10 in Exp. ID-A, estimated using the streamline technique. On the same case, the error of the inverse-gradient technique was 1.5% and for triangulation was 0.9%. Generally, for Exp. ID-D, the epicardial stimulations resulted in lower errors than those from the endocardium; however, this trend was not observed in the other experiments.

C. Comparison of Estimates of Volumetric Conduction Velocity

We computed volumetric CVs using all three estimation technqiues using the ground truth activation times from the simulations and compared them to the CVs prescribed in the model. Additional comparison opportunities with the simulations exist because the conduction velocities relative to the local fibers are an explicit part of their specification. Fig. 4 shows the estimated CV fields (and associated speed distributions) using the three estimations techniques for one epicardial and one endocardial stimulation site. All three CV estimation techniques across the two pacing sites showed similar patterns in the estimated velocity fields. The two peaks seen in the inverse-gradient speed distribution (for both pacing sites) correspond to the prescribed transverse(CV_t) and sheet CV(CV_s). The peak corresponding to the transverse CS is also seen with the distribution from the streamline-based technique, however, the sheet-related peak is much less prominent and more of a shoulder of the main distribution. The associated peaks are present in the distribution from the triangulation technique, but are shifted to the right, by 5–20% relative to the other two methods. This trend in the peaks of the distributions appeared for the majority of pacing sites across all five experiments. This shift in CS peak for the triangulation technique applied to volumes differed from the trend observed with epicardial estimation. Another consistent difference between results for the surfaces and volumes was that the median speeds observed volumetrically for all three techniques were lower than the speeds observed on the surface across all pacing sites and experiments. Note the anisotropic CS measured at the earliest sites of activation, for which we saw faster conduction along the long axis of these breakthrough sites and the relatively slower CS across the short axis of the breakthrough site.

Fig. 4.

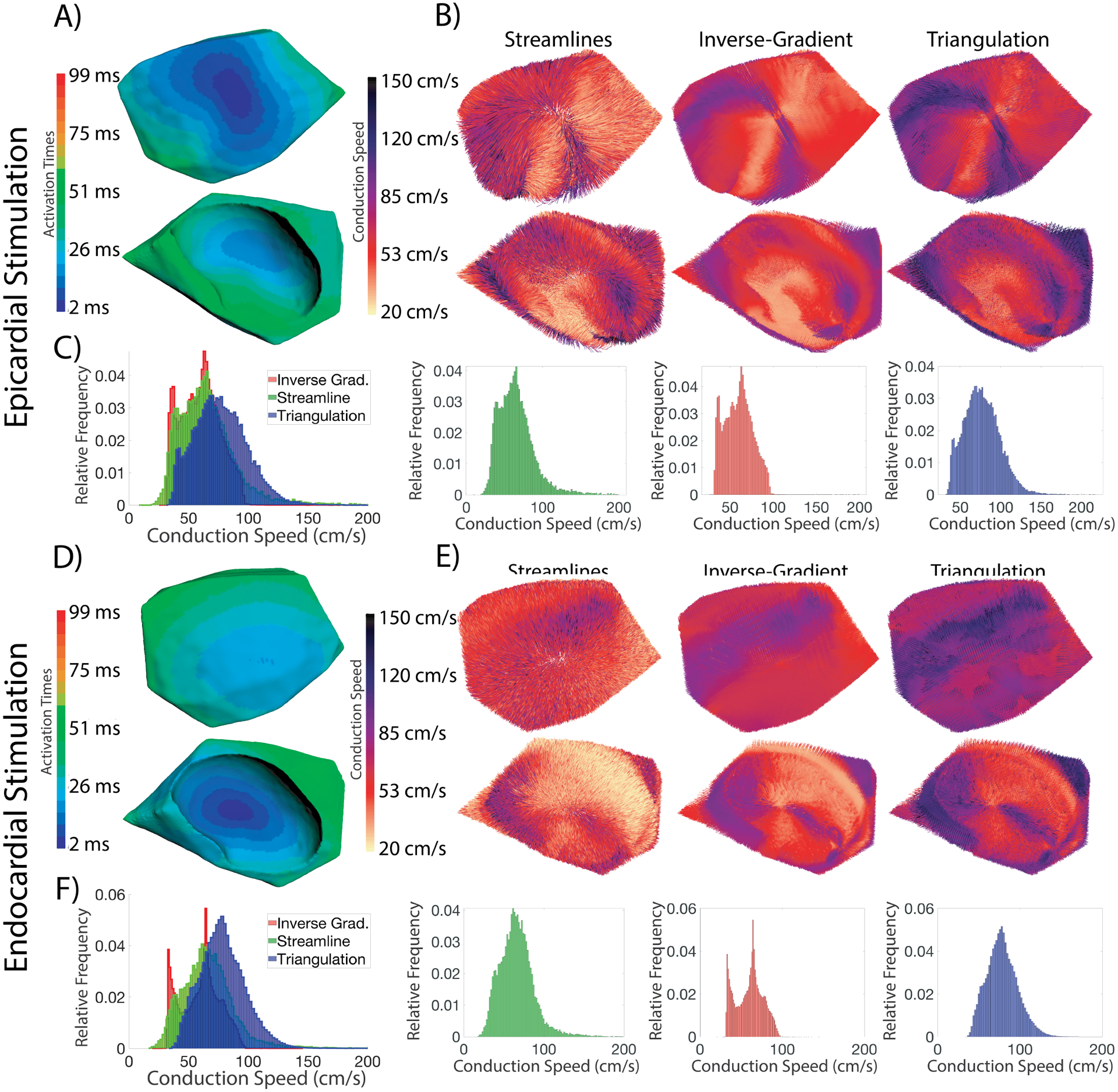
Volumetric CV fields and speed distributions for two pacing sites for the three CV estimation techniques. Both stimulations shown are Exp. ID-A. A) The activation map for from an epicardial pacing site(top image) and an endocardial site(bottom image) perspectives. All images in B), D), and E) share these views. B) The conduction velocity fields created using the three techniques for an epicardial pacing site. C) The conduction speed distributions for stimulation #11. The leftmost image is an overlay of all three speed distributions, and each subsequent image corresponds to a velocity field in B). D)The activation map for an endocardial pacing site from two perspectives. E)The conduction velocity fields created using the three techniques. F)The associated conduction speed distributions. The leftmost image is an overlay of all three speed distributions, and each subsequent image corresponds to a velocity field in E).

We again applied all techniques on the volumetric activation times reconstructed using interpolation. Fig. 5 contains a comparison of results from the ground truth and reconstructed activation times following epicardial pacing. While the CVs generated from reconstructed volumetric activation times were not as accurate as those from epicardial reconstructions, the errors were acceptable at 0.1%–19.9% (Avg. 4–5%) across all pacing sites and the four similarly sampled experiments (Exp. ID–A,B,C,D). All three estimation techniques showed similar performance. One consistent result was that distributions of CS values became broader and shifted slightly to larger values when they were estimated from reconstructed activation times (see the left-hand column of Fig. 5). The CV maps were also more similar across activation times (rows of Fig. 5) than across estimate techniques (columns of Fig. 5). The elementwise estimation techniques (inverse-gradient and triangulation) producing some artifacts close to the pacing site not visible for the streamline technique. In the experiment with the lowest sampling density, Exp. ID- E, the median CV estimated using all techniques had errors between 0.3%–15.5% (Avg. 9–10%) across all pacing sites.

Fig. 5.

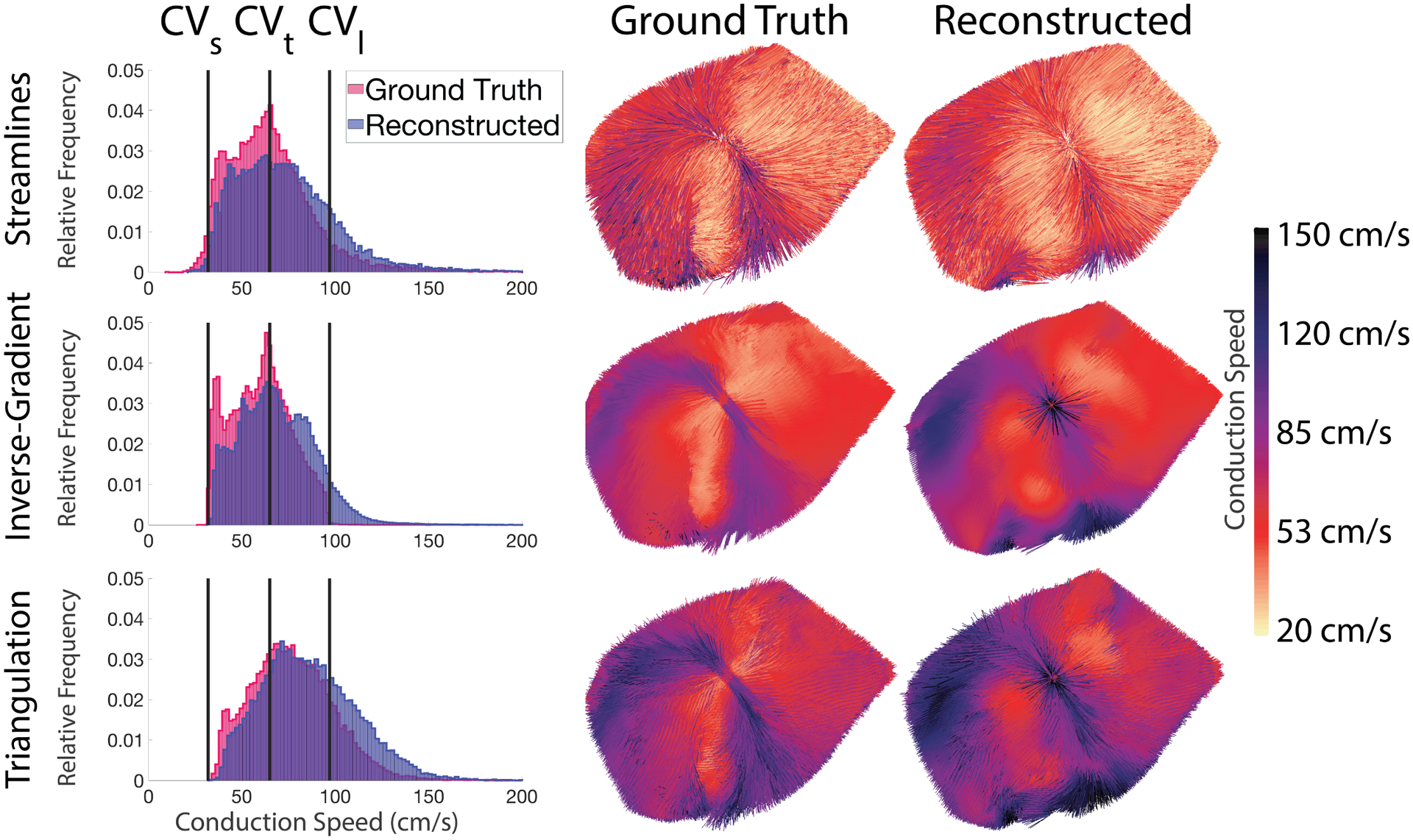
CV fields generated using the ground truth and reconstructed activation times and the associated speed distributions. (Top row: Results using the streamline technique; Middle row: Inverse Gradient technique; Bottom row: Triangulation technique). The three vertical lines on each histogram correspond to the prescribed CVs (CV_l,CV_t, and CV_s) for pacing site #11, the same case as in Figures 1, 2, and 4.

4. Discussion

The objectives of this study were to validate and compare the performance of both a realistic application of interpolation to reconstruct activation times from measurements along with a novel streamline-based technique to estimate cardiac conduction velocity (CV). We applied these methods both over the epicardial surface and within the myocardial volume and compared the CV estimates to previously described methods. [3], [6], [7], [9]–[11]

The basis for the study was a merging of measured values from a set of experiments using instrumented large animal hearts and computer simulations of activation using a well validated cardiac modeling system (CARPentry [12]). In this way, the simulations were guided by the subject-specific anatomy, electrode locations, pacing sites, and physiologically tuned CVs. To evaluate the radial basis function (RBF) based reconstruction approach, we sampled the results of the high resolution simulations at sparse locations corresponding to electrode locations, reconstructed the complete set of activation times, and then compared the results to those from the original simulation. To determine the practical utility of the approach, we applied it to both epicardial (surface) and intramyocardial (volume) sampling, corresponding to the modes of measurement from the experiments.

The novel conduction velocity estimation technique we have described and evaluated derives from an approach used in scientific visualization, generating streamlines of vector values in space. Our implementation is based on calculations derived from activation times, hence it depends on accurate reconstructions of these values at much higher resolutions than are possible with measurements. For conduction velocity, there is no complete ground truth available, which challenges the evaluation of the accuracy of estimation. Instead, we compared results from the streamlines technique to those from two other published methods. To provide at least partial ground-truth evaluation, we also compared specific components of the distributions of estimated conduction speeds to the values used in the simulations. Simulations of cardiac propagation require input parameters that include the conduction speeds relative to the local orientation of myocardial fibers. We could extract these values from the complete set of CV estimates by analyzing histograms of conduction speed. In addition to these quantitative evaluations, qualitative comparisons of the results of the three estimation techniques suggest how useful each would be in practice. Finally, we compared the results of the estimation approaches using both the ground truth activation times from the simulations and those reconstructed using the RBF interpolation technique, to further predict the utility and robustness of each in practice.

Reconstruction of activation times:

This is the first study to our knowledge to validate the accuracy of reconstruction of activation times from sparse samples across the epicardial surface and within the myocardial volume. We showed that using an electrode sock that achieves resolution of 30–40 mm² per electrode across the ventricles is sufficient to reconstruct activation times with a high degree of fidelity from ventricularly paced beats. The reconstructed activation times typically had RMSEs on the order of 0.15–0.30 ms with 97–99% of the nodes within 1 ms of the ground truth value. Generally, beats from endocardial pacing sites were reconstructed with greater fidelity than from epicardial pacing sites; epicardially paced beats had RMSEs of approximately 0.35 ms while endocardial sites produced errors of only 0.23 ms. This difference can be explained by the observation that endocardial paced beats break through the epicardium with more circular shape than beats paced from near the epicardium, resulting in better reconstruction using radial basis functions.

Electrode densities for intramyocardial measurements are generally lower than epicardial so it was not surprising that reconstruction of myocardial activation times was also less accurate. Our experiments achieved spatial resolutions of 62–89 mm³ associated with each electrode during the in situ preparation, in which coverage was sacrificed for needle electrode density. However, even with much lower density than on the surface, average RMSE values of reconstruction within the volume ranged from only 1.2–1.5 ms, very close to the accuracy dictated by the 1 kHz sampling rate used to capture electrograms. Similarly to the results on the endocardium, intramural reconstruction performed better with remotely paced beats or in regions remote from the pacing site. Figure 1B shows local errors in the range of 4–6 ms near the pacing site but much lower errors <1.5 ms in remote regions. In both epicardial and volumetric approaches, the reconstructed activation sequences maintained the macroscopic, qualitative features of the activation sequences, such as the earliest site of activation, and anisotropic propagation.

Subject-specific simulations driven by experiments:

A unique feature and strength of this study is the use of well validated computational models that recreated propagation using parameters and geometry derived from our experiments. This combination allowed us to simulate activation times and then subsample and reconstruct in a way that mimics experimental practice. Using a simulation also allowed us to set anisotropic conduction velocities beforehand and then determine if these values could be recovered from the estimated CV fields. Our choice of the eikonal propagation model versus the more realistic bidomain [24] was both pragmatic and justified. Eikonal simulations run at a fraction of the computational cost of those with the bidomain and have been shown to perform with high precision when the goal is to compute activation times rather than extracellular potentials. [12] Such simulations also require conduction velocities to be set a priori, which means that conduction velocities extracted from the activation times must reflect these settings, providing another means of validation.

Estimation of Conduction Velocity:

Previous studies have estimated CV across surfaces [3], [6], [9], [11] and within volumes [7], [10], but few have applied multiple CV estimation techniques across the same hearts and activation times and none, to our knowledge have explored the streamline based technique described here. We compared how the three CV estimation techniques contrasted by comparing the statistical distributions from each technique when estimated using the ground truth activation times. We also evaluated the robustness of each technique to interpolation-related artifacts by comparing the CV estimated using both the ground-truth and reconstructed activation times.

We successfully estimated CV on the epicardial surface using three techniques and observed reproducible and consistent differences between the approaches. Triangulation consistently produced lower estimated median CVs than the gradient-based methods (streamlines and inverse-gradient). The ad hoc constraints placed on the triangulation technique may explain the lower median CV, ignoring elements when there is less than 0.2 ms of activation time difference across a given triangular edge, meaning it is unable to compute extremely high CVs (some 300 cm/s) seen at breakthrough sites and when wavefronts collide. The inverse-gradient technique can compute CVs even in these regions, but they result in, at times, a rightwards skew in the CV distribution that is likely artefactual due to the very small gradients. The streamline-based technique, since it too uses the underlying gradient field to construct the streamlines, is similarly capable of computing CVs in these regions. Because of the built-in integrations and smoothing provided by the streamline technique, the resultant field minimizes these extremely high CVs relative to the inverse-gradient technique. However, while we expected the streamline technique to be robust to these extremely fast CVs, the peak of the distribution was shifted rightwards and may over-predict bulk CVs. However, the more substantial proportion and emphasis of the fast CV (~150 cm/s) in the posterior regions of the heart, upon closer inspection, also seems realistic, which could explain the rightward shift of the bulk of the distributions.

We then estimated CV within the needle envelope using the three techniques and observed reproducible and consistent differences between the approaches. We also compared the estimated CVs against the CV prescribed in the model. The inverse-gradient and streamline-based techniques both typically produced distributions with two peaks corresponding to the CV_t and CV_s values with most of the distribution falling between these bounds. The inverse-gradient technique produced distributions that fell entirely (99.83% of nodes for the stimulation shown in Fig.5) within the prescribed bounds for CV. The peaks occurring at the CVs prescribed along the secondary and tertiary directions was a surprising result, with the tertiary peak occurring at CV_l. In the eikonal model, depending on the propagation direction through an element, the resultant speed will be a function of the three prescribed CVs, meaning the largest volumetric CVs (CV_l) would be in the longitudinal fiber direction and the smallest tertiary CV when propagating across sheets (CV_s). The two peaks observed with the distribution estimated by triangulation likely also correspond to these values but are skewed to the right. However, this overestimation is minimal—on the order of 5–20% greater than the two gradient-based techniques. The triangulation-based technique had a similar magnitude range as both gradient-based techniques and the prescribed CVs, albeit shifted 5–20% to the right, supporting the theory that the triangulation technique systematically overestimates volumetric CV. The overestimation is likely due to projection-related artefacts introduced in the extension to the volumetric implementation. Both gradient-based techniques appear to agree with one another, and comparisons with the prescribed CV values suggest their estimation of CV throughout the volume is accurate. Depending on the requirements of the analysis, either gradient-based approach will produce accurate volumetric estimations of CV. For visual analyses, streamlines may be preferable, wherein studies that evaluate other metrics elementwise should use the inverse gradient approach.

When comparing the performance of the three estimation techniques across the two domains (epicardial or intramyocardial) we observed vital differences and some similarities in performance. One stark difference was that all three estimation techniques produced faster CV distributions on the epicardium than those seen within the tissue volume. Electrical propagation through the ventricular myocardium is a volumetric phenomenon with the wavefront interacting and collapsing against the epicardial surface and colliding with other wavefronts, creating the systematic overestimation that we observed. Fig. 3 (site #6 - endocardium) shows a relatively rapid epicardial CV where the wavefront collides with the epicardial surface of the needle envelope.

The interaction with the epicardium creates many epicardial discontinuities that are not present within the myocardium. Our volumetric sampling density was lower than used on the surface; however, the relatively high reconstruction accuracy achieved volumetrically may be due to far fewer discontinuities in propagation. Both epicardial and volumetric CV fields were smoother (independent of technique) when using reconstructed activation times, which, combined with the lower degree of discontinuity, may explain the low error in computing CV within the myocardium (regardless of technique). The volumetric and surface implementations of the streamline-based technique appeared to be more robust to interpolation related artefacts then the other techniques. This robustness suggests an advantage of the streamline-based technique when using limited sampling. The artefacts introduced via interpolation lead to overestimations of CV in certain regions, as shown in Fig. 5, to which the streamline technique seems robust.

Fundamental Assumptions of the Techniques:

The improved performance and robustness of the streamline-based technique can be explained by the fundamental assumptions that underpin the method. The assumptions behind the streamline-based technique are aligned with physiology, as propagation is piece-wise contiguous across space, resulting in preservation of the topology of the CV field post-reconstruction. The streamline technique produces CV fields that are more contiguous, collinear, and coherent than the elementwise inverse-gradient and triangulation techniques. This smoothing performed by the streamline-based method makes it robust to sampling irregularities introduced by the underlying geometry, sacrificing spatial sensitivity to achieve this artefact robustness. This robustness to interpolation-related artifacts is illustrated in Fig. 5, where the CV field created using the reconstructed wavefront did not have as many regions of extremely high (> 150 cm/s) values of CV and was qualitatively more similar to the ground truth vector field. This reduction in the extremely high CV estimation was likely due to smoothing, which with streamlines results in the vectors being averaged in the direction of propagation rather than from its transverse neighborhood. This robustness to artefacts suggests the streamline-based technique may have an advantage over elementwise operators when using a reconstructed wavefront. However, if the goal of the analysis is to identify areas of conduction block or small critical isthmuses, it is possible the streamline-based technique may smooth away these features, and therefore this approach is best suited to a mostly homogeneous substrate. In such cases, the inverse-gradient and triangulation techniques could perform better as they evaluate CV one element at time, at the cost of possible vulnerability to interpolation related artefacts. Unfortunately, in regions of high curvature and critical points (pacing sites and epicardial breakthrough sites), elementwise operators may report artefactually high values. A final assumption of both elementwise approaches is that propagation is planar through the element being evaluated, a reasonable assumption based on our recovering the wavefront on the high-resolution underlying computational mesh.

Personalized geometric model assumptions:

The goal of this study was to assess the accuracy and performance of conduction velocity measurement techniques as they would be applied in realistic experimental recording conditions. To replicate the achievable experimental recording density, and validate the estimates based on those measurements, we created simulations using experimentally derived, image-based models and electrode sampling locations. The simulations, which generated the gold-standard values were based on high-resolution models derived from those created from the experiments. Then we subsampled these gold-standard values to the resolution of the measurements, estimated CV values, and compared those to the values simulated at high resolution. This study is the first to evaluate and compare the current CV measurement techniques, including triangulation, inverse gradient, and our novel streamline-based [8], [10]. Future studies could include a detailed analysis of each individual technique within a less realistic, but highly controllable, slab model that would also allow control of substrate parameters such as anisotropy of conduction and insertion of scar regions.

1). Data Sharing:

The geometric models and simulations will be hosted on EDGAR, [25] a database hosted by the Consortium for Electrocardiographic Imaging (www.ecg-imaging.org/) and can be found at: https:\edgar.sci.utah.edu/.

5. Conclusion

This study performed a comparative analysis on three different techniques for estimating CV on both the ventricular epicardium and within the myocardial volume. By employing the simulations, we were able to compare the performance of the novel streamline-based technique with those of two techniques from the literature (inverse-gradient and triangulation). We introduced a novel technique for estimating CV, the streamline-based technique, that can operate epicardially and volumetrically and was shown to be robust to interpolation-related artefacts. Furthermore, the streamline technique enhances visual interrogation of the CV fields due to the coherence and collinear vectors produced by the streamline technique. We showed that RBF-based interpolation using the sampling we achieve during our large animal experiments are sufficient to adequately reconstruct epicardial and volumetric wavefronts with high-fidelity and perform accurate CV estimations in these domains. The inverse-gradient technique appears to be best suited for spatial analyses in the volume and epicardium when estimations of CV when element-wise vectors are necessary, say with fibrosis overlap or during acute myocardial ischemia. Conversely, the streamline-based technique produces visually interrogative CV fields that emphasize propagation and may be particularly useful in the examination of reentrant phenomena and lines of block.