Abstract

Ionic liquids offer unique bulk and interfacial characteristics as battery electrolytes. Our continuum approach naturally describes the electrolyte on a macroscale. An integral formulation for the molecular repulsion, which can be quantitatively determined by both experimental and theoretical methods, models the electrolyte on the nanoscale. In this article, we perform a systematic series expansion of this integral formulation, derive a description of chemical potentials in terms of higher-order concentration gradients, and rationalize the appearance of fourth-order derivative operators in modified Poisson equations, as recently proposed in this context. In this way, we formulate a rigorous multiscale methodology from atomistic quantum chemistry calculations to phenomenological continuum models. We apply our generalized framework to ionic liquids near electrified interfaces and perform analytical asymptotic analysis. Three energy scales describing electrostatic forces between ions, molecular repulsion, and thermal motion determine the shape and width of the long-ranging charged double layer. We classify the charge screening mechanisms dependent on the system parameters as dielectricity, ion size, interaction strength, and temperature. We find that the charge density of electrochemical double layers in ionic liquids either decays exponentially, for negligible molecular repulsion, or oscillates continuously. Charge ordering across several ion diameters occurs if the repulsion between molecules is comparable with thermal energy and Coulomb interactions. Eventually, phase separation of the bulk electrolyte into ionic layers emerges once the molecular repulsion becomes dominant. Our framework predicts the exact phase boundaries among these three phases as a function of temperature, dielectricity, and ion size.
1. Introduction
Strong electrostatic correlations in crowded environments play an important role in biology, chemistry, and physics.1−3 For example, in molecular biology, they account for DNA packing,4 which is crucial for the compaction of genetic material in viruses,5 impact the cytoskeleton organization,6 and influence transport in ion channels.7 Furthermore, such correlations explain the thermodynamic stability of plasmas8,9 and charged colloidal suspensions.10,11
Surprisingly, the complexity of these phenomena can be understood to a large degree by models derived initially for electrolyte solutions.12 Starting from the fundamental Debye–Hückel theory for dilute solutions,13 increasingly accurate models for concentrated electrolytes were developed,14 taking more complex Coulomb correlations into account.
Because ionic liquids (ILs) consist only of positive and negative ions without a neutral solvent, they constitute the extreme limit for the examination of electrostatic correlations in electrolytic solutions. Indeed, ILs possess characteristic properties in the bulk regime,15,16 but also near electrified interfaces.17 This makes them highly attractive from both fundamental and applied perspectives.18−24 The study of interfacial electrochemistry is of wide-ranging interest. For example, the behavior of ILs near electrified interfaces has paramount importance for their performance as battery electrolytes.25,26
Theoretical studies of ILs near electrified interfaces discuss the structure of charged electrochemical double layers (EDL) on atomistic/molecular scales. These include classical density functional theory (cDFT) simulations and molecular dynamics (MD) simulations. cDFT gives detailed insights into the arrangement of molecules in the EDL.27−29 MD resolves the molecular motion and can elucidate the EDL structure.30−32
However, cDFT/MD simulations are limited by their computational costs. Simulations at length scales above the nanometer scale are hardly accessible to the atomistic/molecular approach. Thus, continuum theories and mean-field theories (MFT) provide a complementary methodology for the simulation of larger systems, where the microscopic details can be neglected or are used as averaged parameters (e.g., constant dielectric parameters).
Usually, MFTs for electrolytes are based on lattice gas models of ions, as first proposed by Bikermann.33 Recently, these MFTs have attracted great interest for the study for ILs. As proposed by Santangelo for aqueous systems,34 the extension of MFTs by higher-order electrostatic correlations is useful for the description of long-range structures emerging in electrolytes. Bazant, Storey, and Kornyshev (BSK) applied this approach to ILs near electrified interfaces.35 By using a phenomenological model, which is based on a generalized Ginzburg–Landau functional, BSK describes charge oscillations known as overscreening and charge saturation known as crowding. Yochelis et al. rationalized this approach and extended it to bulk properties.36−38,40 However, MFT models are usually restricted to equilibrium effects of binary ILs with structureless bulk, although rare MFT models, complemented by continuum methods39,41 and extended to the ternary case,42 exist.
This highlights the advantage of continuum frameworks which describe dynamic transport processes. In addition, continuum models based on rigorous physical assumptions43 identify coupled phenomena arising from the interplay of mechanics, thermodynamics, and electromagnetic theory.44 Furthermore, this approach allows us to develop a unified, thermodynamically consistent framework that provides the common theoretical basis for the description of different electrochemical systems.45−49 Continuum models are not restricted to binary or ternary systems because they can be formulated for arbitrary many species, charged and uncharged. Thus, they apply to more realistic electrolytes.
Recently, we proposed such a novel continuum transport theory.45 In this theory, we account for steric effects via the mean volume, which is due to finite molar volumes of the ion species. For this purpose, we impose a volume constraint on the electrolyte. This mechanism stabilizes the bulk structure against Coulomb collapse50 and leads to charge saturation near electrified interfaces. Thus, our theory resolves the deficiencies of the classical Poisson–Boltzmann (PB) theory, which predicts unrealistically high interface concentrations.14 Furthermore, the existence of finite molar volumes of the electrolyte species leads to a pressure dependence of the chemical potentials (in accordance with thermodynamic arguments).51
However, this bulk framework cannot describe the emergence of long-range structures in ILs near electrified interfaces. Therefore, in a joint experimental/theoretical work, we extended our framework with nonlocal interactions and validated it with results obtained from atomic force microscopy.52 Thus, we extended the mean volume effect of the bulk theory with molecular volume exclusion due to hardcore repulsion. Our holistic framework allows us to couple dynamic transport processes occurring in the bulk electrolyte with interfacial electrochemical processes. Thus, we provide a continuum model which bridges the length scales from nanometers, e.g., EDL, to millimeters, e.g., battery cells. Moreover, our framework allows us to connect the continuum description with correlation functions generated by MD.
However, the dependence of EDL structures on molecular repulsion, molecular size, temperature, and dielectricity is still unknown. In this article, we derive such an understanding with asymptotic analysis. To this aim, we present our thermodynamically consistent transport theory with an integral formulation of nonlocal interactions in section 2.1. These correlations represent atomistic volume exclusion and lead to modified constitutive equations (eqs S-10 to S-13). Moreover, the interactions impose contributions on the stress tensor and thus modify the mechanical coupling to the transport equation (eq S-14). In section 2.2, we approximate the interaction functional with a gradient expansion, which facilitates the analytical asymptotic analysis of the EDL structure. In section 2.3, we apply our extended framework to study the EDL structure for neat ILs. When we nondimensionalize our dynamic description in section 2.4, three competing energy scales describing electrostatic forces among ions, molecular repulsion, and thermal motion appear in the theory. Because our focus lies on the formation of equilibrium structures, we discuss the stationary state in section 2.5. In section 2.6, we discuss limiting cases of our stationary theory.
We perform numerical simulations and analytical asymptotic analysis to study the interplay and the effect of the competing energy scales on EDL structures. First, in section 3, we discuss the EDL structure for the mean volume constraint. Second, in section 4, we incorporate molecular repulsion into our analysis and classify the EDL structure dependence on the relation between competing energy scales.
2. Theory
2.1. Generalized Transport Theory
Recently, we proposed a free-energy functional Fb = ∫ dV ρφH for the dynamical description of ionic liquids in the bulk phase.45 In this bulk model, the Helmholtz free energy density φH(Υ) = φH(T, c1,..., cN, D, B, κ) is a function of the variables temperature T, concentration cα, dielectric displacement D, magnetic field B, and strain-rate tensor κ. This variable set Υ constitutes material-specific properties of multicomponent, viscous, and polarizable media in the liquid state.
In contrast, models describing nonlocal interactions rely on functionals Fint[Υ], such that the free energy takes the form
| 1 |
This functional approach constitutes a more general description for electrolyte materials and allows the incorporation of nonlocal correlations between field quantities. Such correlations typically arise from microscopic effects occurring on the nanometer scale, e.g., in the vicinity of electrified interfaces. Despite the conceptual difference between the functional approach (eq 1) and the canonical bulk approach, the derivation of the resulting transport theory is rather similar to the rationale outlined in great detail in ref (45) for the free energy Fb = ∫ dVρφH. We present a detailed derivation for the functional approach in the Supporting Information (section S-1).
The extension of the free energy according to eq 1 leads to modified constitutive
equations
for entropy density s, electric field strength 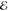 , magnetic
field
, magnetic
field 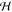 , chemical
potentials μα, and stress tensor σ in the form of functional
derivatives (eqs (S-10) to (S-14) in section S-1.1). We evaluate this framework for the bulk energy of a linear dielectric
medium discussed in ref (45) (eq S-17). The resulting forces
are supplemented by contributions stemming from the nonlocal correlations
(eq S-21).
, chemical
potentials μα, and stress tensor σ in the form of functional
derivatives (eqs (S-10) to (S-14) in section S-1.1). We evaluate this framework for the bulk energy of a linear dielectric
medium discussed in ref (45) (eq S-17). The resulting forces
are supplemented by contributions stemming from the nonlocal correlations
(eq S-21).
For the remaining part
of this work, we neglect thermal driving
forces by setting the temperature equal to constant values and assume
the electrostatic limit, B = 0 and 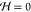 . This determines the electric field
. This determines the electric field 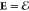 by the electrostatic potential E = –∇Φ.
by the electrostatic potential E = –∇Φ.
2.2. Gradient Expansion of Molecular Interactions
We proposed a model for hardcore-interactions based on a convolution functional for the interaction free energy in ref (52)
| 2 |
leading to transport contributions in the form of (section S-1.4)
| 3 |
The symmetric potentials 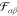 determine
the correlation length
determine
the correlation length  and the magnitude of the interaction.
The number of additional parameters describing this interaction depends
upon the model for
and the magnitude of the interaction.
The number of additional parameters describing this interaction depends
upon the model for 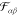 . In a previous publication, we used a Lennard-Jones-type
force field for
. In a previous publication, we used a Lennard-Jones-type
force field for 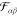 .52 Such potentials
are often used in the literature.53−57 Furthermore, because
.52 Such potentials
are often used in the literature.53−57 Furthermore, because
| 4 |
the potentials  determine the direct pair correlation functions
used in liquid-state theory.50
determine the direct pair correlation functions
used in liquid-state theory.50
Experimental
results suggest that such interactions typically decay after some
ionic diameters.52 Thus, we focus on potentials  ranging
over the size of one molecule.
Their extent
ranging
over the size of one molecule.
Their extent 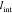 is large
compared to the exponential decay
of the electric field, i.e., the Debye length,58,59 yet small compared to the battery cell.
is large
compared to the exponential decay
of the electric field, i.e., the Debye length,58,59 yet small compared to the battery cell.
In the SI (section S-1.3), we show that
such convolution functionals Fint can
be approximated in a power series of concentration gradients when  are short-ranged,
are short-ranged,
| 5 |
where
| 6 |
Here, Γαβn are symmetric perturbation coefficients of dimension [Γαβ] = J m3+2n mol–2. We state the complete free-energy functional for IL electrolytes in the SI (eq S-17).
The excess chemical potentials are determined via functional derivatives (eq S-13). In section S-1.4, we show that this ansatz leads to force contributions
| 7 |
The corresponding electrochemical potentials for ionic liquid electrolytes are
| 8 |
We specify our electrolyte model and assume a one-dimensional Gaussian interaction potential for symmetric ions,
| 9 |
Here,  denotes the characteristic interaction
energy, and a is the extension of ion pairs. This
material parameter determines the correlation length
denotes the characteristic interaction
energy, and a is the extension of ion pairs. This
material parameter determines the correlation length 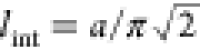 of the interaction. We assume that a emerges naturally
from the common molar volume ν
= ν+ + ν– via ν = NAa3, which is justified
below (section 4.1.2 and eq 48). Thus,
only
of the interaction. We assume that a emerges naturally
from the common molar volume ν
= ν+ + ν– via ν = NAa3, which is justified
below (section 4.1.2 and eq 48). Thus,
only 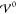 is introduced
as a novel independent material
parameter. In contrast, potentials of the Lennard-Jones type need
at least one more parameter for the well depth. In the case of a binary
system, the lowest-order expansion coefficients (eq 6) of the interspecies correlations for the
Gaussian model in eq 9 are (section S-3.4.1)
is introduced
as a novel independent material
parameter. In contrast, potentials of the Lennard-Jones type need
at least one more parameter for the well depth. In the case of a binary
system, the lowest-order expansion coefficients (eq 6) of the interspecies correlations for the
Gaussian model in eq 9 are (section S-3.4.1)
| 10 |
| 11 |
2.3. Binary IL
In this section, we apply our formalism to binary ILs at electrified interfaces. Thus, we use the extended electrochemical forces (eq 8) in our multicomponent framework derived in ref (45).
Scheme 1. Scheme of the As-Modeled Setup.

The binary IL-electrolyte PYR[1,4]TFSI is subject to the negatively charged interface at the left, which causes the formation of an electrochemical double layer (EDL). Charge ordering diminishes with increasing distance from the interface (towards the right side), and the electrolyte is electroneutral in the bulk.
As discussed in section 2.1, binary electrolytes are described with the variables electric potential Φ, charge density ϱ, and center-of-mass convection velocity v. Furthermore, the electrical conductivity κ is the only independent transport parameter in this case.45 The dynamical transport equations are
| 12 |
| 13 |
| 14 |
Here, M± are the molar masses of the ionic species,
which
sum
to MIL, and 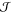 is the electric
current relative to the
center-of-mass motion,
is the electric
current relative to the
center-of-mass motion,  .
.
Solutions to eqs 12 to 14 determine the ionic concentrations via ϱ = Fz+(c+ – c–) (charge conservation) and via the Euler equation for the volume (eq S-20).
We restrict our setup to one spatial dimension and assume that the inert electrified interface is located at x = 0. The electroneutral boundary condition ϱ(x → ∞) = 0 implies that the bulk concentration cb = c±(x → ∞) is completely determined by the total partial molar volume ν = ν+ + ν– via cbν = 1. Because binary ILs are electrically neutral, z– = −z+, and we choose z+ > 0.
We neglect viscous forces in our discussion
of the EDL (∇τ = 0). Therefore, the Gibbs–Duhem
relation (eq S-22) becomes c+∇μ+el + c–∇μ– = 0, and
the expression for the electric flux simplifies to 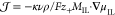 , where we use the chemical potential of
the anion species to determine the IL electrolyte (∇μIL = ∇μ–el),
, where we use the chemical potential of
the anion species to determine the IL electrolyte (∇μIL = ∇μ–el),
| 15 |
Here, we introduced the relative magnitude of the molar volumes γ± = ν±/ν. Thus, the forces given by eq 15 depend upon the model for Fint. Furthermore, by using the Gauss model (eq 9), we can either close the forces via the “complete” integral equation (eq 3) or we can use the gradient expansion (eq 7).
We want to apply the half-cell potential Δϕ. Because the electric potential Φ is continuous across the electrode–electrolyte interface, Φ(0) in the electrolyte is subject to the boundary condition
| 16 |
Without a loss of generality, we set the electrolyte potential in the bulk to zero, limx→∞Φ = 0. Hence, Δϕ = Φ(0) is the potential applied to the electrode.
We perform one-dimensional numerical simulations of this system of eqs 12 and 13 in the completely dissociated state, subject to an inert electrified interface (details in section S-4.1). This electrolyte is part of the IL family composed of TFSI anions and PYR cations. Because of their excellent electrochemical properties, these ILs are widely studied and used for applications in lithium ion batteries.60 We state the electrolyte parameters in the SI (section S-4.2).
2.4. Energy Scales and Dimensions
In this section, we clarify the notation and state the nondimensional form of principal quantities appearing in our theory. For a complete discussion, we refer to the SI (section S-2), where we share the motivation for our choices.
We introduce dimensionless variables for electric potential Φ̃ = ΦFz+/RT, charge density ϱ̃ = ϱνc̃b/Fz+, and concentration c̃α = cανc̃b. As a consequence, the Euler equation for the volume becomes c̃b = γ+c̃+ + γ–c̃–, with the dimensionless molar volumes γ± = ν±/ν and the dimensionless bulk concentration c̃b. The Poisson equation suggests defining the generalized Debye length
| 17 |
Here, we used F = eNA for the Faraday constant, where e is the elementary charge and NA is Avogadro’s constant, and the model ν = NAa3 for the partial molar volumes introduced above. This Debye length differs from the canonical definition by the asymmetry factors γ±.61 However, it reproduces the textbook definition for symmetric ions (γ± = 0.5). LD becomes minimal for γ± = 0.5 because the mixing entropy of a binary electrolyte is extreme for equal ion size. Thus, asymmetry increases the Debye screening length.
With this length scale, we nondimensionalize our grid, viz, x̃ = x/LD and ∇̃ = LD·∇ and obtain the dimenionless Poisson equation:
| 18 |
In the SI (section S-2), we nondimensionalize the transport equations (eqs 12 and 14) for binary symmetric ILs. Because we neglect convective effects in our EDL discussion, the complete set of equations consists of the Poisson equation and one transport equation for the charges. By substituting eq 3 into eq 15, we find for the integral description
| 19 |
where χ = (γ–M+/MIL – γ+M–/MIL)/c̃b measures the “asymmetry” of the ion species and ∂t̃ = (ε0εR/κ)∂t.
The interaction potential is nondimensionalized (see eq S-40) by two energy scales for thermal energy Eth and electrostatic energy Eel,
| 20 |
| 21 |
such that 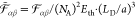 . In the case of symmetric ions γ± = 0.5, these energy scales take the textbook form for
thermal energy and Coulomb energy of charges at distance a. Apparently, both energy scales are coupled by the generalized Debye
length LD,
. In the case of symmetric ions γ± = 0.5, these energy scales take the textbook form for
thermal energy and Coulomb energy of charges at distance a. Apparently, both energy scales are coupled by the generalized Debye
length LD,
| 22 |
The integral form (eq 19) for the transport equation allows us to relate our continuum framework to MD simulations as discussed in section 5.1.
In this article, we restrict the
gradient expansion of the interaction
to the trivial and first nontrivial modes [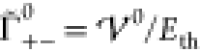 and
and 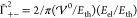 , see eq S-41] and obtain
, see eq S-41] and obtain
| 23 |
2.5. Stationary State
Because our focus is the formation of equilibrium structures, we discuss the system of equations in the stationary limit. This allows us to integrate the differential equations using electroneutral boundary conditions, which results in a simplified description susceptible to analytical techniques.
Stationarity (∂tϱ = 0) implies that all fluxes are constant. Here, we have
no flux conditions  , which implies that both species are in
equilibrium, ∇μ+el = ∇μ–, i.e.,
, which implies that both species are in
equilibrium, ∇μ+el = ∇μ–, i.e.,
| 24 |
Thus, the stationary state for the binary electrolyte is described by the Poisson equation and eq 24. Here, we evaluate the equilibrium condition using the gradient description (eq 15) in the nondimensionalized form (eq S-41 and eq 23) and integrate the result using electroneutral boundary conditions in the bulk,
| 25 |
Apparently, in contrast to
the dynamical case where electrolyte
momentum is important, the molar masses appearing as parameters in
fluxes v and  become irrelevant
in the stationary limit.
Instead, the relative magnitude of the molar volumes γ± enters the system of equations. This highlights the principal role
of molar volumes as parameters in the stationary state and is a consequence
of the Euler equation for the volume (eq S-20).
become irrelevant
in the stationary limit.
Instead, the relative magnitude of the molar volumes γ± enters the system of equations. This highlights the principal role
of molar volumes as parameters in the stationary state and is a consequence
of the Euler equation for the volume (eq S-20).
For completeness, we state the integral transport equation (eq 19) in the stationary limit (section S-3.1)
| 26 |
2.6. Small and Large Potentials
Equations 18 and 25 (or eq 26) constitute the complete set of equations necessary to describe a binary IL electrolyte in a stationary state. In sections 3.1 and 4.3, we solve these equations using numerical methods. Our goal is to supplement these numerical methods by an analytical examination of the gradient description. However, the analytical solution of the gradient description is hindered by the higher-order gradients appearing in eq 25 and by the different prefactors of the logarithmic terms (in general, γ+ ≠ γ–). Therefore, we distinguish different limiting cases in our analysis in sections 3.2 and 4.1. In the SI, we describe the special case of symmetric ion species (sections S-3.2 and S-3.3.3).
In section 3.2, we show that the limiting case of small charge densities, ϱ̃ ≪ 1, is useful. In this case, we can expand the logarithmic terms in eqs 25 and 26 around the electroneutral state,
| 27 |
such that eqs 18 and 25 become
| 28 |
| 29 |
where ε̂R is defined as the dielectric operator
| 30 |
In the absence of molecular repulsion,  , the
dielectric operator reduces to the
canonical, scalar-valued dielectric parameter ε̂R → 1.
, the
dielectric operator reduces to the
canonical, scalar-valued dielectric parameter ε̂R → 1.
Furthermore, quantities similar to ε̂R also arise in the liquid-state theory of classical statistical mechanics. This expansion corresponds to a small wave vector expansion of the dielectric function expressed as a correlation function of the molecular dipole densities, e.g., ref (50).
In the following sections, we show that the gradient
expansion, eqs 28 and 29, allows significant insight into the competing
effects of
interactions 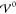 , Eel, and Eth and
predicts the EDL structure as a function
of the temperature, dielectricity, ion size, and interaction strength.
, Eel, and Eth and
predicts the EDL structure as a function
of the temperature, dielectricity, ion size, and interaction strength.
3. Mean Steric Effect: Charge Saturation
In
this section, we neglect nonlocal interactions,  , and
discuss the EDL structure of the electrolyte
due to bulk effects alone based on Fb (eq 1). In this way, we reveal
the competition between Coulombic ordering and entropic disordering,
i.e., diffusion.
, and
discuss the EDL structure of the electrolyte
due to bulk effects alone based on Fb (eq 1). In this way, we reveal
the competition between Coulombic ordering and entropic disordering,
i.e., diffusion.
Toward this aim, we consider the system of
equations constituted
by the Poisson equation (eqs 18) and eq 25 subject
to  ,
,
| 31 |
First, in section 3.1, we solve this system of equations numerically. We supplement this investigation with an analytical analysis and focus on the two limiting regimes of large and small electric potentials. In section 3.2.1, we discuss the case of Φ̃ ≪ 1, and in section 3.2.2, we discuss the case of Φ̃ ≫ 1. For the special case of symmetric ion species (γ± = 0.5), we derive analytical solutions for the electric field Ẽ(Φ̃) and for the charge density ϱ̃(Φ̃) as functions of the electrolyte electric potential in the SI (section S-3.3.3).
3.1. Simulations
Figure 1 shows numerical results for the system of eqs 18 and 25. Figure 1a,b illustrates screening profiles of the electric potential, the charge density, and the ion concentrations for varying electrode potentials Δϕ.
Figure 1.
Simulation results of the EDL structure perpendicular to the electrode–electrolyte interface for a binary IL (eqs 18 and 23). If not mentioned otherwise, T = 300 K, εR = 15, and Δϕ = −0.1 V. (a) Profiles of the electric potential and charge density (inset) for different electrode potentials Δϕ. (b) Concentration profiles of the anions and cations for different electrode potentials Δϕ. (c) Concentration profiles for different volume ratios γ+. The inset shows the corresponding electrical potential. (d) Concentration profiles for varying dielectric constants (dashed lines) and temperatures (solid lines).
Apparently, the application of a negative electrode potential (Δϕ < 0) polarizes the electrolyte. The electric potential (Figure 1a) is continuous across the interface and decays smoothly toward the electroneutral bulk region. The inset of Figure 1a shows that, for low electrode potentials, the charge density decays exponentially. Similar behavior can be observed in Figure 1b for the concentrations. The concentration of positive counterions increases toward the interface, whereas negative ions get depleted. Apparently, the electrolyte screens the electrode potential by the accumulation of counterions. However, above Δϕ ≈ −0.05 V, the counterion concentration saturates near the interface. A further increase of Δϕ broadens the EDL.
This behavior can be explained by the mean volume effect. The application of a negative potential Δϕ implies that positive ions accumulate near the interface and negative ions are depleted. However, the Euler equation for the volume, eq S-20, implies the saturation concentration c+sat = 1/ν+. Once the accumulated species reaches this saturation, the screening mechanism transitions from increasing the concentration at the interface to broadening the width of the EDL. The simulated EDL approaches a thickness of 0.6 nm at Δϕ ≈ −0.05 V, which is significantly wider than predicted by the canonical Debye–Hückel theory with the Debye length LD ≈ 0.7 Å (eq 17). This phenomenon is typically denoted as “crowding”.35
Because the saturation concentration depends upon the molar volume, cαsat = 1/να, the partial molar volumes directly affect the screening behavior. Figure 1c shows numerical results for the ionic concentrations at different volume ratios γ± = ν±/ν (in which v is kept fixed). The EDL is thinner for smaller γ+ because this allows for a tighter packing of cations.
The effects of temperature T and dielectricity εR on the EDL structure are illustrated in Figure 1d. The screening is more effective for smaller values of εR, and the EDL width increases with increasing magnitude of εR. This is in qualitative agreement with the screening behavior for dilute solutions as predicted by the Debye–Hückel theory. Likewise, the EDL becomes more diffuse with increasing temperature because of the disordering effect of thermal motion. The observed effects of T and εR highlight the competing interplay between the electrostatic effect of charge ordering and the disordering effect of entropy.
To summarize, the simulations show two distinct regimes of EDL structure. First, for large electrode potentials, where Δϕ̃ ≫ 1, the charge is saturated near the interface. Second, near the electroneutral bulk region, where Δϕ̃ ≪ 1, the charge density decays exponentially. These two distinct EDL structures, charge saturation and exponential decrease, correspond to two disjointed electrolyte regimes, |Φ̃| ≫ 1 and |Φ̃| ≪ 1, respectively.
3.2. Asymptotic Analysis
The simulation results in section 3.1 motivate our procedure for analyzing the EDL structure. First, we study the EDL far away from the electrode close to the electroneutral bulk (large x̃). For this purpose, we expand the stationary equations around the electroneutral bulk for small charge densities ϱ̃ ≪ 1. According to eq 31, this regime corresponds to small dimensionless potentials |Φ̃| ≪ 1. Note that this coincides with the high-temperature regime because Φ̃ = Φ(Fz+/RT) (section 3.2.1).
Second, we analyze the behavior close to the electrode (small x̃) at large electrode potentials |Δϕ̃| ≫ 1, where the electrolyte potential satisfies |Φ̃| ≫ 1. This corresponds to low temperatures (section 3.2.2).
3.2.1. Asymptotic Analysis: Small Potentials |Φ̃| ≪ 1
As outlined above, we begin our analytical examination of the EDL in the limit of small dimensionless potentials |Φ̃| ≪ 1. Our idea is to approach the EDL from the electroneutral bulk region along the direction of decreasing x̃. Thus, we use the expansion of ionic concentrations around the bulk electrolyte in eq 27, c̃± = c̃b ± ϱ̃γ∓ ≈ c̃b.
For this aim, we insert ϱ̃ from eq 28 into eq 29 for ε̂R = 1, yielding
| 32 |
With the boundary conditions discussed above, Φ̃(0) = Δϕ̃ = Fz+Δϕ/RT and Φ̃(x̃ → ∞) = 0, we obtain the solution
| 33 |
| 34 |
The corresponding dimensionalized electrolyte potential,
| 35 |
decays exponentially with damping parameter 1/LD. Thus, the decay length in the limit |Φ̃| ≪ 1 is the Debye length LD (eq 17).
In Figure 2, we compare the analytical predictions for this limit (dashed green lines) with the numerical results (blue lines) for different electrode potentials. Apparently, the analytical and numerical results for the electric potential and the charge density are in excellent agreement for small electrode potentials Δϕ̃ ≈ – 0.4 when the condition |Φ̃| ≪ 1 is fulfilled everywhere.
Figure 2.

Comparison of the asymptotic analysis of the EDL structure with the numerical results obtained from eqs 18 and 23 (T = 300 K and εR = 15). We consider two different values of the interface potential corresponding to the regimes of small and large potentials at Δϕ = −0.01 V (Δϕ̃ = −0.4) and Δϕ = −0.35 V (Δϕ̃ = −13.5). (a) Profiles of the electrical potentials as predicted by the analytical approximation (eqs 33 and 36). The inset highlights the region close to the interface for the case Δϕ = −0.01 V. (b) Profiles of the charge density as predicted by the asymptotic analysis in eqs 34 and 38. The inset compares numerical and analytical values for the total charge in the EDL (section S-3.3.2 in the SI).
In the SI, we derive the expressions for the total EDL surface charge density and the differential capacitance (section S-3.3.1).
3.2.2. Asymptotic Analysis: Large Potentials |Φ̃| ≫ 1
Next, we discuss the EDL in the limit of large potentials |ϕ̃| ≫ 1. This regime can be found for large electrode potentials ΔΦ̃ ≫ 1 close to the electrode/electrolyte interface. Because Φ̃ = Fz+Δϕ/RT, this analysis is exact in the limit of zero temperature, T = 0.
In this case, the logarithmic terms in eq 31 must compensate for the diverging potential term Φ̃. Because of the mean volume constraint (eq S-20), one of the logarithmic terms is diverging if one species is depleted and the other species saturates, ϱ(x = 0) = Fzα*/να*. Here, we denote the saturating species by the index α*. Because electrical potentials are continuous across interfaces, the saturation species α* is uniquely determined by the sign of the electrode potential, sign(zα*) = −sign(Δϕ̃).
Therefore, ϱ̃sat = −sign(Δϕ̃)c̃sat solves eq 31, where c̃sat = c̃b/γα*. Upon integration of the Poisson equation (eq 28), we find
| 36 |
where the width
of the EDL depends on the
electrode potential 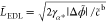 . Thus, the dimensionalized EDL length is
. Thus, the dimensionalized EDL length is
| 37 |
Apparently, the
decay length increases with
ion size because of the mean-volume effect. Also, it scales with the
asymmetry 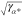 ; i.e., it is small for
small screening
species. Comparison with the Debye screening length shows that LEDL > LD in the
limit of small temperatures T or large potentials
|Δϕ̃| ≫ 1.
; i.e., it is small for
small screening
species. Comparison with the Debye screening length shows that LEDL > LD in the
limit of small temperatures T or large potentials
|Δϕ̃| ≫ 1.
In the limit of vanishing temperature T = 0, the charge profile is box-shaped and is determined by the screening length LEDL,
| 38 |
where θ is the Heaviside function. In the SI, we calculate the analytical expressions for the total charge in the EDL and for the differential capacitance in this limit (section S-3.3.2).
In Figure 2, we compare the analytical predictions for this limit (dashed yellow lines) with the numerical results (solid red lines) for Δϕ̃ = −13.5. The box-shaped charge profile is in good qualitative agreement with the numerical results because it almost predicts the correct width of the EDL. However, the transition from saturation to the bulk state is more diffuse in the numerical profile. This is due to the entropic, thermal influence, which “washes out” the box. Nevertheless, the inset shows that the charge in the EDL, as predicted by the analytical approximation, is quantitatively in good agreement with the numerical results. We note that this profile and its temperature dependence are reminiscent of the Fermi distribution.
4. Nonlocal Interactions: Charge Oscillations
In this section, we discuss the influence of nonlocal interactions
( ) on the structure of the EDL. As in section 3, we discuss the
two limiting cases of small and large potentials separately.
) on the structure of the EDL. As in section 3, we discuss the
two limiting cases of small and large potentials separately.
4.1. Static Asymptotic Analysis
4.1.1. Asymptotic Analysis: Large Potentials |Φ̃| ≫ 1
Let us first discuss the regime of diverging electrolyte
potentials |Φ̃| → ∞. In this limit, the
interaction contribution cannot compensate for the diverging electrolyte
potential in eq 25.
The logarithmic terms are diverging if one species is depleted, and
we recover the same results as described in section 3.2.2 for the case of vanishing interaction
contributions 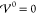 .
.
4.1.2. Asymptotic Analysis: Small Potentials |Φ̃| ≪ 1
In this section, we consider the full theory with molecular repulsion in the regime of small potentials |Φ̃| ≪ 1. As outlined above, we expand the interaction free energy in gradients of the charge density and restrict our analysis to the first two perturbation modes n = 0 and n = 1. With the assumption of small charge densities ϱ̃ ≪ 1, we derived the linear equations above (eqs 28 and 29), which we rephrase in matrix form as
| 39 |
where
 |
40 |
We solve eq 39 via the eigenvalue decomposition
with the eigenvalues α̃1,2 of the matrix in eq 40. These are determined
by the relative magnitudes of the three competing energy scales, Eth, Eel, and  ,
,
| 41 |
Each eigenvalue α̃i gives rise to a dimensionless wave vector,
| 42 |
These determine the general solution of eq 39 together with the eigenvectors ãα̃i = (ã1α̃i, ã2)T = (−α̃i, 1)T,
 |
43 |
The expansion coefficients Ai are determined by boundary
conditions and physical arguments. Apparently, the corresponding wave
vectors are functions 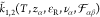 , which
determine the structure of the EDL,
, which
determine the structure of the EDL,
 |
Thus, the EDL structure depends upon the relative
magnitudes of the energies Eth, Eel, and 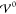 via eq 41. In particular, the classification of k̃± depends upon the sign of the root
via eq 41. In particular, the classification of k̃± depends upon the sign of the root
| 44 |
appearing in eq 41.
Thus, the critical
values  , defined by the condition
, defined by the condition  determine the thresholds for the transition
between the phases of the EDL structure,
determine the thresholds for the transition
between the phases of the EDL structure,
| 45 |
Thus, with eq 45 we can draw the phase diagram for the EDL structures.
Because  , there are three phases. In the SI, we discuss each case in great detail (section S-3.4.2). Next, we give a short description
of each phase.
, there are three phases. In the SI, we discuss each case in great detail (section S-3.4.2). Next, we give a short description
of each phase.
Phase 1: . In this regime, α̃1,2 ≥ 0, which implies a real-valued wave vector. Thus,
this
phase corresponds to exponentially damped profiles
. In this regime, α̃1,2 ≥ 0, which implies a real-valued wave vector. Thus,
this
phase corresponds to exponentially damped profiles  . A harmonic analysis
of the root
. A harmonic analysis
of the root  reveals that (section S-3.4.3)
reveals that (section S-3.4.3)
| 46 |
Thus, solutions with the damping parameter k̃1 vanish quickly and are rendered as unphysical, whereas the limit of vanishing interactions for k̃2 reproduces the bulk expansion for Φ̃ ≪ 1 from section 3.2.1 (eq 33).
Phase 2: . In this regime,
. In this regime,  , and thus the root (eq 44) becomes complex. Therefore, the wave vector
has nonvanishing real and imaginary parts,
, and thus the root (eq 44) becomes complex. Therefore, the wave vector
has nonvanishing real and imaginary parts, 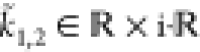 . This
corresponds to charge profiles of
exponentially damped oscillations,
. This
corresponds to charge profiles of
exponentially damped oscillations,
| 47 |
Phase 3: . In this
regime, both eigenvalues are real
but negative, α̃1,2 ≤ 0. Therefore,
. In this
regime, both eigenvalues are real
but negative, α̃1,2 ≤ 0. Therefore, 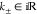 , which
corresponds to undamped oscillatory
profiles. The limiting case for indefinitely strong interactions yields
, which
corresponds to undamped oscillatory
profiles. The limiting case for indefinitely strong interactions yields
| 48 |
Thus, the result
for 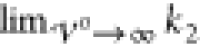 reproduces the experimental findings obtained
by AFM measurements that the wavelengths λ ≈ a/2π of the observed oscillations scale with the size
of molecules a.52,62 Apparently,
the incompressibility of ions in our model prevents a further decrease
of the wavelength.
reproduces the experimental findings obtained
by AFM measurements that the wavelengths λ ≈ a/2π of the observed oscillations scale with the size
of molecules a.52,62 Apparently,
the incompressibility of ions in our model prevents a further decrease
of the wavelength.
Thus, the critical values 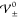 constitute exactly the boundaries between
the different EDL phases.
constitute exactly the boundaries between
the different EDL phases.
In Figure 3, we
illustrate the phase space of EDL structures as functions of temperature
and dielectricity. (In section S-6.1, we
also show the phase space as a function of ion size, ion asymmetry,
and valency.) Apparently, three distinct phases of EDL structures
are present. The exponentially damped EDL phase corresponds to the
regions below  (red line), whereas the damped-oscillatory
EDL phase corresponds to the regions between the blue and red lines.
Finally, the undamped oscillatory EDL phase corresponds to the regions
above
(red line), whereas the damped-oscillatory
EDL phase corresponds to the regions between the blue and red lines.
Finally, the undamped oscillatory EDL phase corresponds to the regions
above  (blue line). Figure 3a illustrates that temperature T and hardcore interactions
(blue line). Figure 3a illustrates that temperature T and hardcore interactions  are in competition and that the
critical
interaction strengths
are in competition and that the
critical
interaction strengths  increase with increasing temperature T, i.e., thermal
energy Eth.
increase with increasing temperature T, i.e., thermal
energy Eth.
Figure 3.
Phase spaces for EDL
structure as functions of T and εR for equally sized ions (γ± = 0.5); see eq 45.
(a) Critical interaction energies  as a function of temperature (here, εR = 15 and a = 1.3 nm). (b) Critical interaction
energies
as a function of temperature (here, εR = 15 and a = 1.3 nm). (b) Critical interaction
energies 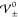 as a function of dielectricity (here, T = 300 K and a = 1.3 nm). Three phases
are present: exponentially damped charge density (shaded red), decaying
oscillatory charge density (shaded gray), and quasi-crystallinity
(shaded blue).
as a function of dielectricity (here, T = 300 K and a = 1.3 nm). Three phases
are present: exponentially damped charge density (shaded red), decaying
oscillatory charge density (shaded gray), and quasi-crystallinity
(shaded blue).
Figure 3b reveals the influence of dielectricity, i.e., electrostatic forces, on the EDL phases. Apparently, the damped oscillatory phase becomes narrower for ILs with larger dielectricity εR, i.e., smaller electric energy Eel.
We note that the exponentially damped regime for small interaction strengths (small compared to electrostatic and thermal energy) corresponds to the EDL structure found in section 3.2.1 in the absence of hardcore interactions. However, as can be inferred from Figure 3a, this phase is hardly present for reasonable temperatures.
Figure 4 shows the
nondimensionalized wave vector as a function of the relative energy
scale 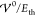 (where T = 300 K, εR = 15, and a = 1.3 nm). For small interaction
energies
(where T = 300 K, εR = 15, and a = 1.3 nm). For small interaction
energies 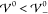 the wave vector is real,
the wave vector is real, 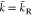 , which corresponds to exponentially damped
profiles. In particular, the static profile at
, which corresponds to exponentially damped
profiles. In particular, the static profile at  reproduces the case described in section 3.2 where the exponential
profile is determined by the scales Eth and Eel alone, i.e., k̃ = 1. Apparently,
reproduces the case described in section 3.2 where the exponential
profile is determined by the scales Eth and Eel alone, i.e., k̃ = 1. Apparently,  increases with
increases with 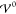 up to the
threshold
up to the
threshold  , beyond which it starts to
decrease. Thus,
the EDL has minimal extension at
, beyond which it starts to
decrease. Thus,
the EDL has minimal extension at 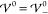 . This suggests
that the increasing strength
of the repulsive ion correlations compresses the screening layer.
Once the hardcore potential exceeds
. This suggests
that the increasing strength
of the repulsive ion correlations compresses the screening layer.
Once the hardcore potential exceeds 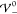 , the system overscreens, i.e., the ion
layers begin to oscillate. The damping parameter Re(k̃) vanishes exactly when
, the system overscreens, i.e., the ion
layers begin to oscillate. The damping parameter Re(k̃) vanishes exactly when  , i.e., when the system
transitions into
nanosegregation of the ion species. Interestingly, the frequency
of the oscillations Im(k̃)
exhibits a local maximum and minimum in the regime of damped oscillations.
Furthermore, Im(k̃) attains
its maximal value in the limit of prevailing interaction strength
, i.e., when the system
transitions into
nanosegregation of the ion species. Interestingly, the frequency
of the oscillations Im(k̃)
exhibits a local maximum and minimum in the regime of damped oscillations.
Furthermore, Im(k̃) attains
its maximal value in the limit of prevailing interaction strength 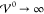 .
.
Figure 4.

Real and imaginary parts of the nondimensionalized wave vector k̃ = kLD as a function of the relative magnitude of the energy scales 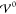 and Eth (eqs 41 and 42). Here, T = 300 K, εR =
15, and a = 1.3 nm.
and Eth (eqs 41 and 42). Here, T = 300 K, εR =
15, and a = 1.3 nm.
In the SI (sections S-3.4.4 and S-3.4.5), we investigate the influence of individual perturbation modes Γ120 and Γ12 on the phase diagram. As it turns out, neglecting all but the zeroth-order correction Γ120 results in a binary phase diagram comprising only exponentially damped profiles and undamped oscillatory profiles. In contrast, neglecting the zeroth-order correction and taking only the first nontrivial order Γ12 into account results in a binary phase diagram comprising only exponentially damped profiles and damped oscillatory profiles. This is the case for MFTs based on the BSK framework. Thus, for the “complete” set of the three different phases, both perturbation modes Γ120 and Γ12 are necessary.
Interestingly, for the pathologic case of negative interaction
strengths  , the phase space reduces to the two screening
phases of exponentially damped profiles and undamped oscillatory profiles.
This follows straightforwardly from eq 41 (and also from the discussions in sections S-3.4.4 and S-3.4.5).
, the phase space reduces to the two screening
phases of exponentially damped profiles and undamped oscillatory profiles.
This follows straightforwardly from eq 41 (and also from the discussions in sections S-3.4.4 and S-3.4.5).
4.2. Dynamic Asymptotic Analysis: Linear Stability Analysis
In this section, we complement the static analysis of section 4.1 by an analytical analysis of the dynamic transport equation in the gradient description (eq 23).
For this purpose, we perform a linear stability analysis and consider the limit of small potentials, |Φ̃| ≪ 1. Thus, the logarithmic terms can approximated as in eq 27, and eq 23 becomes
| 49 |
We expand the electric potential around a uniform bulk state Φ̃b,
| 50 |
Here, the equilibrium state is determined by the electroneutral bulk condition Φ̃b = 0 and ϱ̃b = 0. Thus, the first order perturbation takes the form
| 51 |
Here, the wavenumber k̃ determines the spatial distribution of the dimensionless perturbation ϵ̃1 ≪ 1, and the parameter s̃ measures the temporal growth rate of this perturbation.
We restrict our analysis to probing the linear stability and substitute eq 50 and the Poisson equation into eq 49. Next, we collect terms up to the first order in perturbation mode ϵ̃1, which yields a dispersion relation for the growth rate of the perturbation,
| 52 |
The uniform state is stable under perturbation if and only if s̃ < 0. This defines an instability onset k̃c for the wavenumbers
| 53 |
The corresponding stability criterion s̃(k̃1,2c) < 0 determines the phase boundary at which the bulk of the IL electrolyte becomes unstable. This stability threshold exactly equals the phase boundary between the damped oscillatory phase and the nanosegregated phase (eq 45),
| 54 |
Thus,
for interaction energies  the bulk state of
the system becomes unstable
and phase separation emerges. The initial cause of the structure formation
can be driven by external agents or boundary conditions, e.g., by
the application of an electrical potential to an IL/electrode interface.
the bulk state of
the system becomes unstable
and phase separation emerges. The initial cause of the structure formation
can be driven by external agents or boundary conditions, e.g., by
the application of an electrical potential to an IL/electrode interface.
This stability analysis complements the static analysis and rationalizes
the emergence of phase separation into ionic layers occurring at interaction
energies above  .
.
4.3. Validation with Simulation
Our goal in this section is to compare the results of our asymptotic analysis (eqs 41 to 43 in section 4.1.2), with numerical simulations of the completely coupled system subject to the two theoretical descriptions (integral description, eqs 18 and 19; gradient description, eqs 18 and 23).
We start our
numerical investigations with an overview of the screening profiles
for the charge density at different values 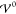 , as obtained from the integral
description
in eqs 18 and 19 (Figure 5). Next, we compare our different EDL descriptions in detail
for two different energies
, as obtained from the integral
description
in eqs 18 and 19 (Figure 5). Next, we compare our different EDL descriptions in detail
for two different energies  (Figures 6 and 7). Finally,
we generalize
these exemplary findings via a systematic study over the complete
phase space of interaction energies (Figure 8). This provides a clear illustration of
the complete set of phase transitions which the system undergoes and
highlights the consistency among the three descriptions.
(Figures 6 and 7). Finally,
we generalize
these exemplary findings via a systematic study over the complete
phase space of interaction energies (Figure 8). This provides a clear illustration of
the complete set of phase transitions which the system undergoes and
highlights the consistency among the three descriptions.
Figure 5.

Screening profiles
of the charge density ϱ̃ as obtained
from numerical simulations of the integral description (eqs 18 and 19)
for different values  . The y axis is scaled
from −1 to 1, where |ϱ̃| = 1 corresponds to charge
saturation.
. The y axis is scaled
from −1 to 1, where |ϱ̃| = 1 corresponds to charge
saturation.
Figure 6.

Results for the electric potential and charge
density as obtained
from numerical simulations of the integral description (eqs 18 and 19)
and of the gradient description (eqs 18 and 23) and as predicted by
the analytical predictions (eqs 41 to 43) at 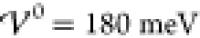 .
.
Figure 7.

Screening profile for
the charge density ϱ̃ obtained
from numerical simulations with respect to the gradient description
(eqs 18 and 23) and according to the analytical description (eqs 41 to 43) at 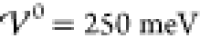 .
.
Figure 8.

Meta analysis
of the interfacial profiles for four thousand simulations.
The dashed vertical yellow lines show the phase boundaries  (eq 45). The dashed
and solid red/blue lines show the peak variance
of the complete set of simulations as defined by eq 55 with respect to the integral description
(eqs 18 and 19) and with respect to the gradient description (eqs 18 and 23). The left inset shows the onset of the oscillations at small
interaction energies. The right inset shows the variance in a nonlogarithmic
setting, which highlights the occurrence of phase transitions.
(eq 45). The dashed
and solid red/blue lines show the peak variance
of the complete set of simulations as defined by eq 55 with respect to the integral description
(eqs 18 and 19) and with respect to the gradient description (eqs 18 and 23). The left inset shows the onset of the oscillations at small
interaction energies. The right inset shows the variance in a nonlogarithmic
setting, which highlights the occurrence of phase transitions.
All simulations were performed for a symmetric
cell setup, where
the IL electrolyte is located within two oppositely charged, blocking
interfaces separated by a distance of Lcell = 60 nm. The electrode on the left side is negatively charged with Δϕ = −100 mV, whereas, on the right side
the electrode is positively charged with Δϕ = 100 mV. Because charge saturation begins roughly at Δϕ = 70 mV (Figures 1 and 2), the charge distribution can safely
be assumed to be saturated adjacent to the interfaces, i.e., |ϱ̃|
= 1. The electrolyte is considered to consist of symmetric ions (γ± = 0.5) of size a = 1.3 nm. Hence, the
cell geometry allows a “maximal” number of roughly 90
ions. In addition, we assume room temperature, T =
300 K, and εR = 15. The phase boundaries corresponding
to these parameters as predicted by our analytical description are 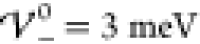 and
and  (eq 45).
(eq 45).
Figure 5 shows the
numerical results of the charge density for the integral description
(eqs 18 and 19), where 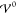 takes values across two orders
of magnitude.
First, at
takes values across two orders
of magnitude.
First, at 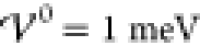 the profile shows charge saturation
near
the two electrified electrodes, ϱ̃(x =
0) = 1 and ϱ̃(x = Lcell) = −1. Near both electrodes, the profile decays
exponentially toward the electroneutral bulk (ϱ̃ = 0).
This corresponds to the profiles which we discussed in great detail
in section 3.1. Because
the profile shows charge saturation
near
the two electrified electrodes, ϱ̃(x =
0) = 1 and ϱ̃(x = Lcell) = −1. Near both electrodes, the profile decays
exponentially toward the electroneutral bulk (ϱ̃ = 0).
This corresponds to the profiles which we discussed in great detail
in section 3.1. Because 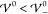 , this is
in accordance with the analytical
prediction. The next two profiles show results for interaction energies
within the intermediate phase,
, this is
in accordance with the analytical
prediction. The next two profiles show results for interaction energies
within the intermediate phase, 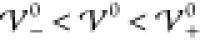 . Both simulations show damped oscillatory
profiles, where the long-ranged oscillatory profiles span many nanometers.
Apparently, the oscillations in the profile for
. Both simulations show damped oscillatory
profiles, where the long-ranged oscillatory profiles span many nanometers.
Apparently, the oscillations in the profile for  extend across almost the entire cell. A
slight increase of 2 meV to
extend across almost the entire cell. A
slight increase of 2 meV to  causes the profile to transition to a crystalline
phase with undamped oscillatory shape. Note that the amplitudes between
the electrodes are smaller than unity, i.e., the bulk region consists
of mixed ion layers with one dominant ion species. An increase to
causes the profile to transition to a crystalline
phase with undamped oscillatory shape. Note that the amplitudes between
the electrodes are smaller than unity, i.e., the bulk region consists
of mixed ion layers with one dominant ion species. An increase to  enhances the amplitudes of the oscillations
further, i.e., enhances the segregation of ion species. The last plot
shows the corresponding profile for a significantly enhanced interaction
energy (
enhances the amplitudes of the oscillations
further, i.e., enhances the segregation of ion species. The last plot
shows the corresponding profile for a significantly enhanced interaction
energy (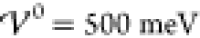 ). Here, the amplitudes of the
oscillations
have reached saturation (|ϱ̃| = 1), and the electrolyte
has transitioned into a crystalline phase consisting of alternating
pure ion layers. In Figure S-2 (section S-6.2), we highlight that the ionic layers
coincide exactly with the ion size a/2. Thus, with
increasing energy
). Here, the amplitudes of the
oscillations
have reached saturation (|ϱ̃| = 1), and the electrolyte
has transitioned into a crystalline phase consisting of alternating
pure ion layers. In Figure S-2 (section S-6.2), we highlight that the ionic layers
coincide exactly with the ion size a/2. Thus, with
increasing energy 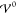 , the interfacial
structure increases into
the bulk electrolyte until the bulk itself gets nanostrucured by the
layering of the ion species. This phase transition occurs rapidly
within a few meV.
, the interfacial
structure increases into
the bulk electrolyte until the bulk itself gets nanostrucured by the
layering of the ion species. This phase transition occurs rapidly
within a few meV.
Apparently, the numerical results for the
integral description
confirm the existence of three different screening phases. However,
quantitative deviations between our descriptions is present. As we
show in the SI (Figure S-4) the phase transitions
from exponential decay to damped oscillations occurs roughly at  . In addition, as can be inferred from Figure 5, the transition
from damped oscillations to undamped oscillations appears at
. In addition, as can be inferred from Figure 5, the transition
from damped oscillations to undamped oscillations appears at  . Hence, both phase boundaries are slightly
shifted to smaller values compared to analytical predictions
. Hence, both phase boundaries are slightly
shifted to smaller values compared to analytical predictions 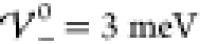 and
and  (eq 45). Thus, the analytical
prediction, which is based on the
gradient description, slightly underestimates the influence of
(eq 45). Thus, the analytical
prediction, which is based on the
gradient description, slightly underestimates the influence of  when compared with Eth and Eel. This can be attributed
to the fact that the gradient description is an approximation based
on only the first two perturbation modes, whereas the integral description
comprises all modes.
when compared with Eth and Eel. This can be attributed
to the fact that the gradient description is an approximation based
on only the first two perturbation modes, whereas the integral description
comprises all modes.
Next, we give a quantitative comparison
between the numerical results
of the two theoretical descriptions and the analytical predictions.
Here, we restrict our discussion to the interaction energy 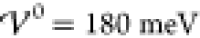 , i.e., the intermediate phase of damped
oscillations. Figure 6 shows the profiles for the charge density and electrolyte electric
potential as obtained from the numerical simulations and as predicted
by the analytical description for the first few nanometers of the
left half-cell. Figure 6a illustrates the charge distribution adjacent to the negatively
charged electrode. The dashed blue line shows the screening profile
obtained from the gradient description, which exhibits a damped oscillatory
shape. This confirms the analytical prediction for this interaction
energy. The dashed yellow line shows the resulting analytical profile.
Note that the analytical prediction in section 4 does not capture charge saturation but determines
only the damping parameter and the oscillation frequency of the screening
profile. However, in section 3.2.2, we derived an analytical prediction for the saturation
width LEDL, which is valid close to the
interface (eq 37). Hence,
to reconstruct the “complete” profile, we supplement
the contribution emerging from the bulk (eq 43), which is valid far away from the interface,
by constant charge saturation ϱ̃ = 1 spanning over the
width LEDL. Apparently, the analytical
and numerical results of the gradient description are quantitatively
in very good agreement. Finally, the solid red line in Figure 6a shows the numerical results
for the integral description. In accordance with the results shown
in Figure 5, these
results reproduce the analytically predicted screening phase, but
the oscillations are more pronounced. Hence, the influence of the
interaction energy
, i.e., the intermediate phase of damped
oscillations. Figure 6 shows the profiles for the charge density and electrolyte electric
potential as obtained from the numerical simulations and as predicted
by the analytical description for the first few nanometers of the
left half-cell. Figure 6a illustrates the charge distribution adjacent to the negatively
charged electrode. The dashed blue line shows the screening profile
obtained from the gradient description, which exhibits a damped oscillatory
shape. This confirms the analytical prediction for this interaction
energy. The dashed yellow line shows the resulting analytical profile.
Note that the analytical prediction in section 4 does not capture charge saturation but determines
only the damping parameter and the oscillation frequency of the screening
profile. However, in section 3.2.2, we derived an analytical prediction for the saturation
width LEDL, which is valid close to the
interface (eq 37). Hence,
to reconstruct the “complete” profile, we supplement
the contribution emerging from the bulk (eq 43), which is valid far away from the interface,
by constant charge saturation ϱ̃ = 1 spanning over the
width LEDL. Apparently, the analytical
and numerical results of the gradient description are quantitatively
in very good agreement. Finally, the solid red line in Figure 6a shows the numerical results
for the integral description. In accordance with the results shown
in Figure 5, these
results reproduce the analytically predicted screening phase, but
the oscillations are more pronounced. Hence, the influence of the
interaction energy 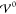 is more
dominant in the integral description
than in the gradient description. Next, in Figure 6b we show the profiles for the normalized
electrolyte electric potential. The dashed blue line shows the profile
due to the gradient description. It is in accordance with the charge
profile shown in Figure 6a. Again, we reconstruct the analytical profile by supplementing
the profile (eq 36),
which is valid close to the interface, by the profile (eq 43), which is valid toward the electroneutral
bulk. Apparently, the analytical results are quantitatively in very
good agreement with the results stemming from the gradient description.
The red line shows the profile as obtained from the integral description.
As in Figure 6a for
the charge density, the oscillations are slightly enhanced when compared
with the gradient description. In addition, the brown solid lines
show the analytical envelopes for the screening. Apparently, it captures
both numerical results qualitatively very well. Interestingly, the
differences in electrolyte potential among the three descriptions
depend on the electrode potential near the electrode as shown in Figure S-3 (section S-6.3). However, the qualitative agreement is independent of the boundary
conditions.
is more
dominant in the integral description
than in the gradient description. Next, in Figure 6b we show the profiles for the normalized
electrolyte electric potential. The dashed blue line shows the profile
due to the gradient description. It is in accordance with the charge
profile shown in Figure 6a. Again, we reconstruct the analytical profile by supplementing
the profile (eq 36),
which is valid close to the interface, by the profile (eq 43), which is valid toward the electroneutral
bulk. Apparently, the analytical results are quantitatively in very
good agreement with the results stemming from the gradient description.
The red line shows the profile as obtained from the integral description.
As in Figure 6a for
the charge density, the oscillations are slightly enhanced when compared
with the gradient description. In addition, the brown solid lines
show the analytical envelopes for the screening. Apparently, it captures
both numerical results qualitatively very well. Interestingly, the
differences in electrolyte potential among the three descriptions
depend on the electrode potential near the electrode as shown in Figure S-3 (section S-6.3). However, the qualitative agreement is independent of the boundary
conditions.
In Figure 7, we
show results for the charge distribution at enhanced interaction energy 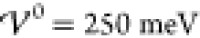 , i.e., close to the phase boundary
, i.e., close to the phase boundary 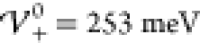 . As can
be inferred from Figure 5, the integral description
has already transitioned to the phase of undamped oscillations for
this interaction energy. Hence, we show only the screening profile
as obtained from the numerical simulation of the gradient description
(solid blue line) and compare it with the analytical prediction (yellow
line). Apparently, in accordance with the analytical prediction, the
numerical profile has a damped oscillatory shape, where the oscillations
extend over roughly 40 ion sizes. This highlights the influence of
the enhanced interaction energy (see also Figure 6). Overall, the analytical profile shown
here is in nice agreement with the numerical results.
. As can
be inferred from Figure 5, the integral description
has already transitioned to the phase of undamped oscillations for
this interaction energy. Hence, we show only the screening profile
as obtained from the numerical simulation of the gradient description
(solid blue line) and compare it with the analytical prediction (yellow
line). Apparently, in accordance with the analytical prediction, the
numerical profile has a damped oscillatory shape, where the oscillations
extend over roughly 40 ion sizes. This highlights the influence of
the enhanced interaction energy (see also Figure 6). Overall, the analytical profile shown
here is in nice agreement with the numerical results.
Finally,
we conduct a quantitative comparison between the two EDL
discriptions and the analytical description across multiple orders
of magnitude of 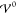 . To address
this goal, we examine the simulation
results of roughly 4000 EDL simulations across the parameter range
from 0.1 meV up to 500 meV. As above, we apply Δϕ = ± 100 meV at the electrodes such that we can safely assume
charge saturation near the interfaces.
. To address
this goal, we examine the simulation
results of roughly 4000 EDL simulations across the parameter range
from 0.1 meV up to 500 meV. As above, we apply Δϕ = ± 100 meV at the electrodes such that we can safely assume
charge saturation near the interfaces.
We evaluate the simulation
results by extracting two characteristic
properties. First, we count the number of peaks 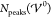 appearing in each screening profile. Because
of charge saturation, a minimal number of two peaks always occur.
At most, roughly 90 ion layers fit into the cell geometry of length Lcell = 60 nm. We present the number of peaks
occurring in the full cell as a function of the interaction strengths
in the SI (Figure S-4 in section S-6).
appearing in each screening profile. Because
of charge saturation, a minimal number of two peaks always occur.
At most, roughly 90 ion layers fit into the cell geometry of length Lcell = 60 nm. We present the number of peaks
occurring in the full cell as a function of the interaction strengths
in the SI (Figure S-4 in section S-6).
However, beyond the number of peaks, we also want to evaluate the
peak amplitudes. For this purpose, we investigate the peak variance  of the left half-cell, defined by
of the left half-cell, defined by
| 55 |
Here, xi is the discrete
location of the ith peak
ϱ̃i = |ϱ̃(xi)| (such that 0 ≤ ϱ̃i ≤ 1, where ϱ̃i = 1 corresponds to a saturated peak, i.e., a pure
ion layer) appearing in the profile of the charge density. In the SI (section S-6.4), we show analytically that
σ converges to Lcell/√3 if
the set of simulation energies comprises energies 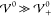 . For such interaction energies, the bulk
electrolyte has transitioned to a crystalline phase composed of nanosegregated
ion layers (Figure 5).
. For such interaction energies, the bulk
electrolyte has transitioned to a crystalline phase composed of nanosegregated
ion layers (Figure 5).
Figure 8 shows
the
results for variance σ normalized to its maximum Lcell/√3 on a logarithmic scale. In this figure,
the vertical dashed yellow lines indicate the phase boundaries 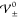 , as predicted by the analytical description
(eq 45). The left inset
shows the simulation results for small values
, as predicted by the analytical description
(eq 45). The left inset
shows the simulation results for small values  , and the right inset comprises
the overall
results in a nonlogarithmic representation highlighting the transition.
The blue dashed line shows the results for σ according to the
gradient description (eqs 18 and 23). At small interaction energies
, and the right inset comprises
the overall
results in a nonlogarithmic representation highlighting the transition.
The blue dashed line shows the results for σ according to the
gradient description (eqs 18 and 23). At small interaction energies 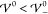 , the variance
is zero. This corresponds
to an exponentially damped, nonoscillatory screening profile. (Note
that the only peak, due to charge saturation, is located at x̃i = 0). The variance
starts increasing exactly at
, the variance
is zero. This corresponds
to an exponentially damped, nonoscillatory screening profile. (Note
that the only peak, due to charge saturation, is located at x̃i = 0). The variance
starts increasing exactly at 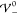 (left inset). This corresponds to an increasing
number of damped oscillations, where the amplitudes of the peaks also
increase with
(left inset). This corresponds to an increasing
number of damped oscillations, where the amplitudes of the peaks also
increase with  . Finally,
at
. Finally,
at  , the variance converges to it is constant
limiting value Lcell/√3 (right
inset). In this energy regime, the bulk electrolyte consists completely
of ion layers. Altogether, these results reproduce the phases exactly
as predicted by the analytical description.
, the variance converges to it is constant
limiting value Lcell/√3 (right
inset). In this energy regime, the bulk electrolyte consists completely
of ion layers. Altogether, these results reproduce the phases exactly
as predicted by the analytical description.
The red curve shows
the results for σ according to the integral
description (eqs 18 and 19). In contrast to the gradient description, the
variance starts increasing from zero at roughly 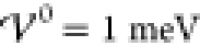 , i.e., before the analytically predicted
phase boundary
, i.e., before the analytically predicted
phase boundary  (left inset). Hence, the phase
transition
from exponentially damped screening profiles to damped oscillatory
screening profiles is slightly shifted to smaller energies. Next,
the variance increases exponentially up to roughly
(left inset). Hence, the phase
transition
from exponentially damped screening profiles to damped oscillatory
screening profiles is slightly shifted to smaller energies. Next,
the variance increases exponentially up to roughly  , above which it transitions to the constant
limiting value Lcell/√3. Altogether,
the phase boundaries of the integral description still exhibit qualitatively
good agreement with the analytical predictions, although being slightly
shifted to smaller values. Apparently, this behavior is due to the
cumulative effect of the integral term in eq 19, which comprises all interaction modes.
In contrast, we consider only the first two modes (n = 0 and n = 1) of the gradient expansion in eq 23.
, above which it transitions to the constant
limiting value Lcell/√3. Altogether,
the phase boundaries of the integral description still exhibit qualitatively
good agreement with the analytical predictions, although being slightly
shifted to smaller values. Apparently, this behavior is due to the
cumulative effect of the integral term in eq 19, which comprises all interaction modes.
In contrast, we consider only the first two modes (n = 0 and n = 1) of the gradient expansion in eq 23.
5. Multiscale Methodology
In this section, we highlight the relation of our model to theories on smaller and larger length scales. We discuss in section 5.1, on the basis of basic concepts from liquid-state theory, how atomistic simulations can directly parametrize our theory. Next, in section 5.2 we sketch the phenomenologic BSK continuum approach for the description of ILs near electrified interfaces and illustrate its relation to our work. In addition, we state the relation of our framework to AFM experiments in section S-5 (ref (52)).
5.1. From Molecular Dynamics to Nonequilibrium Thermodynamics
Here, we explain how the parameters of our continuum theory can be rigorously calculated with quantum chemistry, i.e., DFT and MD.
Ab initio DFT calculations predict the forces between ions and molecules by calculating their electronic structure. The DFT-generated force fields are the focal quantity for MD simulations,63 which calculate the classical trajectories of ions and molecules. Results from MD simulations are often interpreted via profiles of the radial distribution function g(r).
Liquid-state theory50 connects this atomistic description to thermodynamic concepts and scattering experiments.64 On the one hand, the radial distribution function allow a straightforward comparison with the structure factor S from scattering experiments.65,66 On the other hand, the density distribution function g(r) can be used to calculate different correlation functions. Subtracting its asymptotic value follows the so-called total correlation function used in integral equation theories (IETs), h(r) = g(r) – 1.3 In IETs, the pairwise total correlation function h relates to the direct correlation function c(2), used in classical density functional theory (cDFT), via the Ornstein–Zernike relation,67
| 56 |
In cDFT, the direct pair correlation
functions cαβ(2) account for pairwise interactions
between two ions of species α and β, i.e., the excess
free energy due to pairwise ion interactions.68 Thus, they can be obtained via the 2-fold functional derivative
of Fint,64 i.e.,
via our interaction potential  (eq 4),
(eq 4),
| 57 |
To summarize, DFT determines force fields for MD, MD determines g(r) for liquid-state theory, g(r) determines c(2) via the Ornstein–Zernike relation, and c(2) determines Fint and generates our nonequilibrium thermodynamic theory.
The dynamic properties of our theory can also be determined from atomistic simulations. These dynamic properties are encoded in the Onsager coefficients,45 which can be measured experimentally.69 The Onsager coefficients can be determined by MD simulations (“Green Kubo relations”).70−72
5.2. From Nonequilibrium Thermodynamics to Phenomenologic BSK Theory
Now we compare our thermodynamically consistent
continuum approach with the phenomenologic theory proposed by Bazant,
Storey, and Kornyshev (BSK), a seminal MFT approach for ILs near electrified
interfaces.35 In their continuum model
of the EDL, BSK incorporates ion correlations using a modified linear
dielectric relation 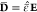 between electrostatic fields D̅ and E, where
between electrostatic fields D̅ and E, where  is their
dielectric operator. The second-order
gradient term in ϱ̅ accounts for nonlocal ion interactions,
being effectively short-ranged with correlation length
is their
dielectric operator. The second-order
gradient term in ϱ̅ accounts for nonlocal ion interactions,
being effectively short-ranged with correlation length  . This Ansatz
yields a modified Poisson
equation,
. This Ansatz
yields a modified Poisson
equation, 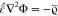 . The chemical potential connects the electric
potential and charge density. Finally,
. The chemical potential connects the electric
potential and charge density. Finally,
| 58 |
holds in the limit of small potentials Φ̃.
Our model conceptually differs from BSK theory. Because we incorporate electrostatic correlations in the free energy, nonlocal ion interactions enter the set of equations via the chemical potentials. This implies that the MFT quantities appearing in the BSK description, D̅ and ϱ̅ = ∇D̅, differ from the corresponding quantities ϱ and D appearing in our formalism. In contrast to the “mean field charge density” ϱ̅, the charge density ϱ relates to the bulk quantity D, which does not incorporate ion correlations.
Despite these differences, the resulting model equations are very similar. This can be seen as follows. Equations 28 and 29 for the limit of small potentials can be cast into one equation for the electric potential alone,
| 59 |
where the dielectric operator ε̂R is defined
in eq 30. Noting the
conceptual similarity between the dielectric
operators ε̂R and 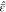 , the
similarity between our model and BSK
theory becomes apparent. In this way, we give physical meaning to
the correlation length
, the
similarity between our model and BSK
theory becomes apparent. In this way, we give physical meaning to
the correlation length  in BSK theory
and outline its calculation.
in BSK theory
and outline its calculation.
Finally, we emphasize that the higher-order gradient terms, which are phenomenologically incorporated in the BSK approach, emerge naturally within our rigorous continuum model. In particular, they merely constitute the limiting case for small potentials of the more fundamental integral formulation (eq 26). Furthermore, in contrast to the phenomenological BSK model, our order expansion also comprises a zero-order correction in the dielectric operator (eq 30). This mode is mandatory in realizing the complete phase space of interfacial profiles (sections S-3.4.4 and S-3.4.5 in the SI).
5.3. Outlook
In this section, we discuss how our framework can be extended to account for additional microscopic IL effects.
In this work, we have supplemented our bulk description for ILs and highly correlated electrolytes, as recently presented in ref (45), with nonlocal interactions. Furthermore, we applied the resulting framework for the case of short-ranged hardcore interactions. However, the generality of our framework based on the modeling of the free energy offers the possibility to incorporate a wide range of nonlocal effects into our framework.
This includes properties such as ion asymmetry, ion geometry, polarization, and charge delocalization, which have a significant influence on the structure of ILs near electrified interfaces.62,73−76 These effects partially result from the relative orientation between the ions, which makes a one-dimensional approach challenging. Nevertheless, assuming a highly symmetric setup, the one-dimensional description might still capture some basic consequences of these effects.
Similar to the force fields used in atomistic simulations, the short-ranged repulsive interaction can be supplemented by a longer-ranged attractive tail, taking account of higher-order electrostatic effects of the van der Waals type, or larger ions with complex geometry, i.e., long alkyl chains.53,54,63 Also, by refining the short-ranged repulsive interaction potential, more detailed models for the ion geometry and ion asymmetry can be incorporated into our model. However, the strong influence of these microscopic properties on the EDL structure may lead to some novel features within our framework. For example, the three energy scales which determine the screening profile might transition to field quantities which exhibit spatial variation. Also, the phase space of screening profiles might become higher-dimensional, which can lead to a more complex set of phase boundaries allowing for “mixed” screening types.
Nontrivial polarization effects could be incorporated into our linear constitutive model for the coupling between the electric field and the dielectric displacement. This would result in a spatially varying dielectric function εR(x) appearing on the electrostatic energy scale Eel (eq 21) and a direct coupling of the chemical potentials with the ion polarization. For small dielectric perturbations, we hypothesis that the electrostatic energy scale becomes more diffuse, which has the effect that the phase boundaries between the screening profiles wash out. Only in the case of large dielectric variations do we expect the phase space of screening profiles to be altered significantly.
Our dynamical theory offers the possibility to investigate transport processes occurring in electrochemical devices, e.g., the influence of EDL charging on the electrolyte performance, or the influence of the EDL structure on the electrode-transfer kinetics. However, electrochemical devices have some characteristic properties which must be carefully taken into account when they are modeled. For example, overlapping double layers in nanoporous electrodes could be taken into account.77
In our description, we assumed an ideally flat surface, which can be a bad approximation for many electrochemical systems.78 The influence of interface roughness on the EDL structure can be modeled by modifying the entropic contributions in the free-energy functional.79 In our analysis, this would alter the thermal energy scale Eth (eq 20). Depending upon the surface morphology, this would enhance the disordering effect of the thermal energy on the EDL structure. As a result, the formation of crystalline phases might become suppressed at rougher surfaces, similar to increasing the temperature.
6. Conclusions
In this work, we complement our thermodynamically consistent continuum framework for IL electrolytes by nonlocal molecular repulsion. Our integral formulation can be determined by ab initio MD simulations. Assuming short-ranged interactions, we expand the interaction free energy in concentration gradients and adjust the dynamic equations for transport. The resulting equations connect to the phenomenologic approach of BSK theory. We validate our approach by simulations and find remarkable agreement between the different variants of our theory.
In this way, we develop a predictive multiscale approach to the theory of ILs at electrified interfaces. Atomistic density functional theory calculations parametrize MD simulations, MD simulations yield an integral formulation for molecular repulsion in our thermodynamically consistent transport theory, and our theory can be expanded to give the phenomenological BSK theory.
The expanded continuum approach allows us to perform analytical asymptotic analysis which creates deeper insights into the parameter dependence of the EDL structure as we demonstrate for the example of binary ILs. First, we have neglected molecular repulsion. We can analytically describe both limits: the dilute Debye limit, where charge density is exponentially decaying, and the concentrated crowding limit, where charge is saturated due to steric effects. Second, we have taken into account molecular repulsion. We discuss the structure of the EDL dependence on energy scales for thermal motion, molecular repulsion, and electric Coulomb forces and find three different phases. For small interactions, we recover the dilute Debye limit. For intermediate interactions, a multilayer structure of ions emerges which is washed out over several atom layers. For very large interactions, the analysis predicts the long-ranged, nondecaying crystalline order of the EDL. In simulations of our full theory, we eventually observe charge ordering of quasi-crystalline multilayers in this case.
In summary, we have proposed a thermodynamically consistent description of ILs at electrified interfaces that closes the gap in their multiscale understanding. This makes possible a predictive theoretical approach for tailoring ILs. We prove that the intermolecular forces determine the EDL structure of binary ILs. Future work should be extended to ternary mixtures of ILs and should incorporate the shapes of molecules into the theory.
Acknowledgments
This work was supported by the European Union’s Horizon 2020 research and innovation program via the “Si-DRIVE” project (grant agreement no. 814464). The authors acknowledge support by the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 cluster) and the state of Baden-Württemberg through bwHPC.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c00215.
Transport theory of interacting electrolytes (including gradient expansion and functional derivatives); nondimensional formulation; a binary ionic liquid (including chemical forces, symmetric ion species, charge saturation, and charge oscillations); simulations (including computational details and binary ionic liquids); the relation to experimental methods; and simulation results (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Eisenberg B. Interacting ions in biophysics: real is not ideal. Biophysical journal 2013, 104, 1849–1866. 10.1016/j.bpj.2013.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosberg A. Y.; Nguyen T.; Shklovskii B. Colloquium: the physics of charge inversion in chemical and biological systems. Reviews of modern physics 2002, 74, 329. 10.1103/RevModPhys.74.329. [DOI] [Google Scholar]
- Henderson D. Attractive energy and entropy or particle size: the yin and yang of physical and biological science. Interdisciplinary sciences: computational life sciences 2009, 1, 1–11. 10.1007/s12539-008-0001-3. [DOI] [PubMed] [Google Scholar]
- Chen Y.-G.; Weeks J. D. Local molecular field theory for effective attractions between like charged objects in systems with strong Coulomb interactions. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 7560–7565. 10.1073/pnas.0600282103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield V. A. Condensation of DNA by multivalent cations: considerations on mechanism. Biopolymers: Original Research on Biomolecules 1991, 31, 1471–1481. 10.1002/bip.360311305. [DOI] [PubMed] [Google Scholar]
- Wong G. C.; Pollack L. Electrostatics of strongly charged biological polymers: ion-mediated interactions and self-organization in nucleic acids and proteins. Annu. Rev. Phys. Chem. 2010, 61, 171–189. 10.1146/annurev.physchem.58.032806.104436. [DOI] [PubMed] [Google Scholar]
- Eisenberg B.; Hyon Y.; Liu C. Energy variational analysis of ions in water and channels: Field theory for primitive models of complex ionic fluids. J. Chem. Phys. 2010, 133, 104104. 10.1063/1.3476262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher M. E.; Levin Y. Criticality in ionic fluids: Debye-Hückel theory, Bjerrum, and beyond. Physical review letters 1993, 71, 3826. 10.1103/PhysRevLett.71.3826. [DOI] [PubMed] [Google Scholar]
- Levin Y.; Fisher M. E. Criticality in the hard-sphere ionic fluid. Physica A: Statistical Mechanics and its Applications 1996, 225, 164–220. 10.1016/0378-4371(95)00336-3. [DOI] [Google Scholar]
- van Roij R.; Hansen J.-P. Van der Waals–like instability in suspensions of mutually repelling charged colloids. Physical review letters 1997, 79, 3082. 10.1103/PhysRevLett.79.3082. [DOI] [Google Scholar]
- Hansen J.-P.; Löwen H. Effective interactions between electric double layers. Annu. Rev. Phys. Chem. 2000, 51, 209–242. 10.1146/annurev.physchem.51.1.209. [DOI] [PubMed] [Google Scholar]
- Levin Y. Electrostatic correlations: from plasma to biology. Rep. Prog. Phys. 2002, 65, 1577. 10.1088/0034-4885/65/11/201. [DOI] [Google Scholar]
- Hückel E.Ergebnisse der Exakten Naturwissenschaften; Springer: 1924; pp 199–276. [Google Scholar]
- Kilic M. S.; Bazant M. Z.; Ajdari A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. 10.1103/PhysRevE.75.021502. [DOI] [PubMed] [Google Scholar]
- Hayes R.; Warr G. G.; Atkin R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. 10.1021/cr500411q. [DOI] [PubMed] [Google Scholar]
- Bruce D. W.; Cabry C. P.; Canongia Lopes J. N.; Costen M. L.; D’Andrea L.; Grillo I.; Marshall B. C.; McKendrick K. G.; Minton T. K.; Purcell S. M.; et al. Nanosegregation and Structuring in the Bulk and at the Surface of Ionic-Liquid Mixtures. J. Phys. Chem. B 2017, 121, 6002–6020. 10.1021/acs.jpcb.7b01654. [DOI] [PubMed] [Google Scholar]
- Fedorov M. V.; Kornyshev A. A. Ionic liquids at electrified interfaces. Chem. Rev. 2014, 114, 2978–3036. 10.1021/cr400374x. [DOI] [PubMed] [Google Scholar]
- Plechkova N. V.; Seddon K. R. Applications of ionic liquids in the chemical industry. Chem. Soc. Rev. 2008, 37, 123–150. 10.1039/B006677J. [DOI] [PubMed] [Google Scholar]
- Wishart J. F. Energy applications of ionic liquids. Energy Environ. Sci. 2009, 2, 956–961. 10.1039/b906273d. [DOI] [Google Scholar]
- Torimoto T.; Tsuda T.; Okazaki K.-i.; Kuwabata S. New frontiers in materials science opened by ionic liquids. Adv. Mater. 2010, 22, 1196–1221. 10.1002/adma.200902184. [DOI] [PubMed] [Google Scholar]
- Werner S.; Haumann M.; Wasserscheid P. Ionic liquids in chemical engineering. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 203–230. 10.1146/annurev-chembioeng-073009-100915. [DOI] [PubMed] [Google Scholar]
- Welton T. Room-temperature ionic liquids. Solvents for synthesis and catalysis. Chem. Rev. 1999, 99, 2071–2084. 10.1021/cr980032t. [DOI] [PubMed] [Google Scholar]
- Endres F. Ionic liquids: Promising solvents for electrochemistry. Zeitschrift für Physikalische Chemie 2004, 218, 255–284. 10.1524/zpch.218.2.255.25920. [DOI] [Google Scholar]
- Armand M.; Endres F.; MacFarlane D. R.; Ohno H.; Scrosati B.. Materials for Sustainable Energy; World Scientific: 2011; pp 129–137. [Google Scholar]
- Endres F.; Höfft O.; Borisenko N.; Gasparotto L. H.; Prowald A.; Al-Salman R.; Carstens T.; Atkin R.; Bund A.; El Abedin S. Z. Do solvation layers of ionic liquids influence electrochemical reactions?. Phys. Chem. Chem. Phys. 2010, 12, 1724–1732. 10.1039/b923527m. [DOI] [PubMed] [Google Scholar]
- MacFarlane D. R.; Pringle J. M.; Howlett P. C.; Forsyth M. Ionic liquids and reactions at the electrochemical interface. Phys. Chem. Chem. Phys. 2010, 12, 1659–1669. 10.1039/b923053j. [DOI] [PubMed] [Google Scholar]
- Wu J.; Jiang T.; Jiang D.-e.; Jin Z.; Henderson D. A classical density functional theory for interfacial layering of ionic liquids. Soft Matter 2011, 7, 11222–11231. 10.1039/c1sm06089a. [DOI] [Google Scholar]
- Henderson D.; Wu J. Electrochemical properties of the double layer of an ionic liquid using a dimer model electrolyte and density functional theory. J. Phys. Chem. B 2012, 116, 2520–2525. 10.1021/jp212082k. [DOI] [PubMed] [Google Scholar]
- Jiang J.; Cao D.; Jiang D.-e.; Wu J. Time-dependent density functional theory for ion diffusion in electrochemical systems. J. Phys.: Condens. Matter 2014, 26, 284102. 10.1088/0953-8984/26/28/284102. [DOI] [PubMed] [Google Scholar]
- Sharma S.; Gupta A.; Kashyap H. K. How the structure of pyrrolidinium ionic liquids is susceptible to high pressure. J. Phys. Chem. B 2016, 120, 3206–3214. 10.1021/acs.jpcb.6b01133. [DOI] [PubMed] [Google Scholar]
- Sharma S.; Kashyap H. K. Structure of quaternary ammonium ionic liquids at interfaces: effects of cation tail modification with isoelectronic groups. J. Phys. Chem. C 2015, 119, 23955–23967. 10.1021/acs.jpcc.5b06460. [DOI] [Google Scholar]
- Hu Z.; Vatamanu J.; Borodin O.; Bedrov D. A molecular dynamics simulation study of the electric double layer and capacitance of [BMIM][PF 6] and [BMIM][BF 4] room temperature ionic liquids near charged surfaces. Phys. Chem. Chem. Phys. 2013, 15, 14234–14247. 10.1039/c3cp51218e. [DOI] [PubMed] [Google Scholar]
- Bikerman J. XXXIX. Structure and capacity of electrical double layer. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1942, 33, 384–397. 10.1080/14786444208520813. [DOI] [Google Scholar]
- Santangelo C. D. Computing counterion densities at intermediate coupling. Phys. Rev. E 2006, 73, 041512. 10.1103/PhysRevE.73.041512. [DOI] [PubMed] [Google Scholar]
- Bazant M. Z.; Storey B. D.; Kornyshev A. A. Double Layer in Ionic Liquids: Overscreening versus Crowding. Phys. Rev. Lett. 2011, 106, 046102. 10.1103/PhysRevLett.106.046102. [DOI] [PubMed] [Google Scholar]
- Yochelis A. Transition from non-monotonic to monotonic electrical diffuse layers: impact of confinement on ionic liquids. Phys. Chem. Chem. Phys. 2014, 16, 2836–2841. 10.1039/c3cp55002h. [DOI] [PubMed] [Google Scholar]
- Yochelis A. Spatial structure of electrical diffuse layers in highly concentrated electrolytes: a modified Poisson–Nernst–Planck approach. J. Phys. Chem. C 2014, 118, 5716–5724. 10.1021/jp412616f. [DOI] [Google Scholar]
- Yochelis A.; Singh M. B.; Visoly-Fisher I. Coupling Bulk and Near-Electrode Interfacial Nanostructuring in Ionic Liquids. Chem. Mater. 2015, 27, 4169–4179. 10.1021/acs.chemmater.5b00780. [DOI] [Google Scholar]
- Gavish N.; Yochelis A. Theory of Phase Separation and Polarization for Pure Ionic Liquids. J. Phys. Chem. Lett. 2016, 7, 1121–1126. 10.1021/acs.jpclett.6b00370. [DOI] [PubMed] [Google Scholar]
- Bier S.; Gavish N.; Uecker H.; Yochelis A. From bulk self-assembly to electrical diffuse layer in a continuum approach for ionic liquids: The impact of anion and cation size asymmetry. Phys. Rev. E 2017, 95, 060201. 10.1103/PhysRevE.95.060201. [DOI] [PubMed] [Google Scholar]
- Lee A. A.; Kondrat S.; Vella D.; Goriely A. Dynamics of Ion Transport in Ionic Liquids. Phys. Rev. Lett. 2015, 115, 106101. 10.1103/PhysRevLett.115.106101. [DOI] [PubMed] [Google Scholar]
- Gavish N.; Elad D.; Yochelis A. From Solvent-Free to Dilute Electrolytes: Essential Components for a Continuum Theory. J. Phys. Chem. Lett. 2018, 9, 36–42. 10.1021/acs.jpclett.7b03048. [DOI] [PubMed] [Google Scholar]
- Bothe D.; Dreyer W. Continuum thermodynamics of chemically reacting fluid mixtures. Acta Mechanica 2015, 226, 1757–1805. 10.1007/s00707-014-1275-1. [DOI] [Google Scholar]
- Kovetz A.Electromagnetic Theory; Oxford University Press: Oxford: 2000; Vol. 975. [Google Scholar]
- Schammer M.; Horstmann B.; Latz A. Theory of Transport in Highly Concentrated Electrolytes. J. Electrochem. Soc. 2021, 168, 026511. 10.1149/1945-7111/abdddf. [DOI] [Google Scholar]
- Latz A.; Zausch J. Multiscale modeling of lithium ion batteries: thermal aspects. Beilstein journal of nanotechnology 2015, 6, 987–1007. 10.3762/bjnano.6.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt T.; Arlt T.; Manke I.; Latz A.; Horstmann B. Zinc electrode shape-change in secondary air batteries: A 2D modeling approach. J. Power Sources 2019, 432, 119–132. 10.1016/j.jpowsour.2019.126649. [DOI] [Google Scholar]
- Becker-Steinberger K.; Schardt S.; Horstmann B.; Latz A.. Statics and Dynamics of Space-Charge-Layers in Polarized Inorganic Solid Electrolytes. arXiv 2020, 2101.10294. [Google Scholar]
- Single F.; Horstmann B.; Latz A. Theory of impedance spectroscopy for lithium batteries. J. Phys. Chem. C 2019, 123, 27327–27343. 10.1021/acs.jpcc.9b07389. [DOI] [Google Scholar]
- Hansen J.; McDonald I.. Theory of Simple Liquids; Elsevier Science: 2006. [Google Scholar]
- Landstorfer M.; Guhlke C.; Dreyer W. Theory and structure of the metal-electrolyte interface incorporating adsorption and solvation effects. Electrochim. Acta 2016, 201, 187–219. 10.1016/j.electacta.2016.03.013. [DOI] [Google Scholar]
- Hoffmann V.; Pulletikurthi G.; Carstens T.; Lahiri A.; Borodin A.; Schammer M.; Horstmann B.; Latz A.; Endres F. Influence of a silver salt on the nanostructure of a Au(111)/ionic liquid interface: an atomic force microscopy study and theoretical concepts. Phys. Chem. Chem. Phys. 2018, 20, 4760–4771. 10.1039/C7CP08243F. [DOI] [PubMed] [Google Scholar]
- Bedrov D.; Piquemal J.-P.; Borodin O.; MacKerell A. D.; Roux B.; Schröder C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. 10.1021/acs.chemrev.8b00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz H.; Lin T.-J.; Kishore Mishra R.; Emami F. S. Thermodynamically consistent force fields for the assembly of inorganic, organic, and biological nanostructures: the INTERFACE force field. Langmuir 2013, 29, 1754–1765. 10.1021/la3038846. [DOI] [PubMed] [Google Scholar]
- Eisenberg B.; Hyon Y.; Liu C. A mathematical model for the hard sphere repulsion in ionic solutions. Communications in Mathematical Sciences 2011, 9, 459–475. 10.4310/CMS.2011.v9.n2.a5. [DOI] [Google Scholar]
- Lin T.-C.; Eisenberg B. A new approach to the Lennard-Jones potential and a new model: PNP-steric equations. Communications in Mathematical Sciences 2014, 12, 149–173. 10.4310/CMS.2014.v12.n1.a7. [DOI] [Google Scholar]
- Lin T.-C.; Eisenberg B. Multiple solutions of steady-state Poisson–Nernst–Planck equations with steric effects. Nonlinearity 2015, 28, 2053. 10.1088/0951-7715/28/7/2053. [DOI] [Google Scholar]
- Lee A. A.; Perez-Martinez C.; Smith A. M.; Perkin S. Underscreening in concentrated electrolytes. Faraday Discuss. 2017, 199, 239–259. 10.1039/C6FD00250A. [DOI] [PubMed] [Google Scholar]
- Rotenberg B.; Bernard O.; Hansen J.-P. Underscreening in ionic liquids: a first principles analysis. J. Phys.: Condens. Matter 2018, 30, 054005. 10.1088/1361-648X/aaa3ac. [DOI] [PubMed] [Google Scholar]
- Karuppasamy K.; Theerthagiri J.; Vikraman D.; Yim C.-J.; Hussain S.; Sharma R.; Maiyalagan T.; Qin J.; Kim H.-S. Ionic Liquid-Based Electrolytes for Energy Storage Devices: A Brief Review on Their Limits and Applications. Polymers 2020, 12, 918. 10.3390/polym12040918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmickler W.; Santos E.. Interfacial Electrochemistry; Springer Science & Business Media, 2010. [Google Scholar]
- Li H.; Endres F.; Atkin R. Effect of alkyl chain length and anion species on the interfacial nanostructure of ionic liquids at the Au (111)–ionic liquid interface as a function of potential. Phys. Chem. Chem. Phys. 2013, 15, 14624–14633. 10.1039/c3cp52421c. [DOI] [PubMed] [Google Scholar]
- González M. A. Force fields and molecular dynamics simulations. JDN 2011, 12, 169–200. 10.1051/sfn/201112009. [DOI] [Google Scholar]
- Van Beijeren H.; Felderhof B.U. Thermodynamics and correlation functions of plasmas and electrolyte solutions. Mol. Phys. 1979, 38, 1179–1199. 10.1080/00268977900102331. [DOI] [Google Scholar]
- Billinge S. J. L. The rise of the X-ray atomic pair distribution function method: a series of fortunate events. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2019, 377, 20180413. 10.1098/rsta.2018.0413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kats E. I.; Muratov A. R. Simple analysis of scattering data with the Ornstein-Zernike equation. Phys. Rev. E 2018, 97, 012610. 10.1103/PhysRevE.97.012610. [DOI] [PubMed] [Google Scholar]
- Archer A. J.; Chacko B.; Evans R. The standard mean-field treatment of inter-particle attraction in classical DFT is better than one might expect. J. Chem. Phys. 2017, 147, 034501. 10.1063/1.4993175. [DOI] [PubMed] [Google Scholar]
- Cao S.; Konovalov K. A.; Unarta I. C.; Huang X. Recent Developments in Integral Equation Theory for Solvation to Treat Density Inhomogeneity at Solute–Solvent Interface. Advanced Theory and Simulations 2019, 2, 1900049. 10.1002/adts.201900049. [DOI] [Google Scholar]
- Fong K. D.; Self J.; McCloskey B. D.; Persson K. A. Ion Correlations and Their Impact on Transport in Polymer-Based Electrolytes. Macromolecules 2021, 54, 2575–2591. 10.1021/acs.macromol.0c02545. [DOI] [Google Scholar]
- Fong K. D.; Bergstrom H. K.; McCloskey B. D.; Mandadapu K. K. Transport phenomena in electrolyte solutions: Nonequilibrium thermodynamics and statistical mechanics. AIChE J. 2020, 66, e17091. 10.1002/aic.17091. [DOI] [Google Scholar]
- Götze W.; Latz A. Generalised constitutive equations for glassy systems. J. Phys.: Condens. Matter 1989, 1, 4169–4182. 10.1088/0953-8984/1/26/013. [DOI] [Google Scholar]
- Latz A.Verallgemeinerte konstituierende Gleichungen und Formfaktoren fijr einfache Glasbildner. Ph.D. Dissertation, TU; München, 1991. [Google Scholar]
- de Souza J. P.; Pivnic K.; Bazant M. Z.; Urbakh M.; Kornyshev A. A. Structural Forces in Ionic Liquids: The Role of Ionic Size Asymmetry. J. Phys. Chem. B 2022, 126, 1242. 10.1021/acs.jpcb.1c09441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei C.; Jiang K.; Fang T.; Liu X. Effects of anions and alkyl chain length of imidazolium-based ionic liquids at the Au (111) surface on interfacial structure: a first-principles study. Green Chemical Engineering 2021, 2, 402–411. 10.1016/j.gce.2021.07.006. [DOI] [Google Scholar]
- Izgorodina E. I.; Forsyth M.; MacFarlane D. R. On the components of the dielectric constants of ionic liquids: ionic polarization?. Physical chemistry chemical physics 2009, 11, 2452–2458. 10.1039/b815835e. [DOI] [PubMed] [Google Scholar]
- Paek E.; Pak A. J.; Hwang G. S. On the influence of polarization effects in predicting the interfacial structure and capacitance of graphene-like electrodes in ionic liquids. J. Chem. Phys. 2015, 142, 024701. 10.1063/1.4905328. [DOI] [PubMed] [Google Scholar]
- Lian Z.; Chao H.; Wang Z.-G. Effects of confinement and ion adsorption in ionic liquid supercapacitors with nanoporous electrodes. ACS Nano 2021, 15, 11724–11733. 10.1021/acsnano.1c02506. [DOI] [PubMed] [Google Scholar]
- Jänsch T.; Wallauer J.; Roling B. Influence of electrode roughness on double layer formation in ionic liquids. J. Phys. Chem. C 2015, 119, 4620–4626. 10.1021/jp512617j. [DOI] [Google Scholar]
- Aslyamov T.; Sinkov K.; Akhatov I. Electrolyte structure near electrodes with molecular-size roughness. Phys. Rev. E 2021, 103, L060102. 10.1103/PhysRevE.103.L060102. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




