Randomization-based inference for a marginal treatment effect in stepped wedge cluster randomized trials

Abstract

In a cross-sectional stepped wedge cluster randomized trial (SWT), clusters are randomized to crossover from control to intervention at different time periods and outcomes are assessed for a different set of individuals in each cluster-period. Randomization-based inference is an attractive analysis strategy for SWTs because it does not require full parametric specification of the outcome distribution or correlation structure and its validity does not rely on having a large number of clusters. Existing randomization-based approaches for SWTs, however, either focus on hypothesis testing and omit technical details on confidence interval (CI) calculation with noncontinuous outcomes, or employ weighted cluster-period summary statistics for p-value and CI calculation, which can result in suboptimal efficiency if weights do not incorporate information on varying cluster-period sizes. In this article, we propose a framework for calculating randomization-based p-values and CIs for a marginal treatment effect in SWTs by using test statistics derived from individual-level generalized linear models. We also investigate how study design features, such as stratified randomization, subsequently impact various SWT analysis methods including the proposed approach. Data from the XpertMTB/RIF tuberculosis trial are reanalyzed to illustrate our method and compare it to alternatives.

1 |. INTRODUCTION

In a stepped wedge cluster randomized trial (SWT), clusters are randomized to crossover from control to intervention at different time periods.¹ At the start of a SWT, all clusters begin under the control condition; at each subsequent period, one or more clusters initiate the intervention until, eventually, all clusters are receiving it. SWTs have become popular recently due to their ethical and practical advantages, especially for evaluating large-scale public health interventions.^2,3 In this article, we focus on cross-sectional SWTs in which different sets of participants within a cluster contribute data to each period, rather than a cohort SWT involving repeated measures over time on the same set of individuals (though our method can be used for either, see Section 5).

Individual-level outcomes from a SWT can be analyzed using generalized linear mixed models (GLMMs) fit via maximum likelihood or using marginal models fit via solving a generalized estimating equation (GEE).^4,5 The standard GLMM introduced by Hussey and Hughes includes a fixed treatment effect, fixed categorical period effects, and random cluster effects.⁶ Correspondingly, the standard marginal model fit via a GEE includes fixed effects for treatment and period and often employs an exchangeable working correlation structure. Various modifications and extensions of these standard models have been made by specifying more complex correlation structures, allowing the treatment effect to vary over time, by cluster, or by time since treatment was introduced, or by specifying varying period effects across clusters.^7–13 In general, GEEs require a large number of clusters and GLMMs additionally require distributional assumptions to be met (eg, normally distributed random effects, correct specification of the correlation structure) to maintain nominal type I error and confidence interval (CI) coverage. Several small-sample adjustments have been proposed and evaluated for SWTs, all of which significantly improve upon the validity of GLMMs and GEEs in settings with a small number of clusters, though their relative performance can vary depending on the particular trial scenario (eg, whether or not and by how much cluster sizes vary).^14–17 Furthermore, including additional covariates in a GLMM or GEE to account for design features, such as stratified randomization, alters the target estimand from a nonstratified treatment effect to one that is conditional on the stratification covariate(s) and, as demonstrated in our simulations and others,¹⁸ can result in even worse type I error and CI coverage of GEEs in finite samples.

Randomization-based inference is an attractive alternative method for analyzing SWTs because it does not require full parametric specification of the outcome distribution or correlation structure and its validity does not rely on having a large number of clusters.^19–22 In addition, randomization-based methods can account for design features in a straightforward and intuitive fashion that does not require changing the target of inference. Aside from using a similar inferential framework, existing randomization-based approaches for SWTs differ in their choice of test statistic—a choice that can have a substantial impact on the power of the randomization test and the precision of the corresponding CI. Ji et al²³ described randomization tests for SWTs using regression parameter estimates from individual-level mixed models, but did not detail how corresponding CIs would be calculated for noncontinuous outcomes. Wang and De Gruttola²⁴ proposed a similar approach using mixed effects models and discussed how permutation tests can be inverted to obtain CI estimates for continuous outcomes and survival outcomes when the parameter of interest is one in an accelerated failure time model. Thompson et al²⁵ developed a nonparametric within-period (NPWP) approach to calculate randomization-based p-values and CIs using inverse-variance weighted cluster-period summaries. The NPWP method focuses solely on vertical differences (ie, within-period contrasts between clusters on and off treatment) and combines these period-specific estimates into an overall effect estimate for the trial. The weights proposed by Thompson et al²⁵ were calculated based on the number of clusters on treatment and control, and the corresponding empirical variances of the cluster-period summaries under each treatment condition; as mentioned in their discussion, these weights may not be optimal if cluster-period sizes vary. Kennedy-Shaffer et al²⁶ proposed a crossover approach also based on cluster-period summaries, but one that incorporated horizontal comparisons (ie, within-cluster contrasts between subsequent periods) into their estimator; their weights did not incorporate information on variable cluster-period sizes. Different weights could be used for the NPWP or crossover approaches, but as described in Kennedy-Shaffer et al, changing the weights generally changes the treatment effect parameter targeted.²⁶ Hughes et al²⁷ derived closed-form randomization-based point and variance estimators for a vertical treatment effect similar to that targeted by the NPWP method. To derive their variance estimators, Hughes et al assumed all cluster-period sizes were the same but found their method to be only slightly sensitive to this assumption in their simulation studies.

In this article, we extend previous work on randomization-based CIs in parallel cluster randomized trials to the SWT setting.²⁸ This entails modifying the way in which treatment assignments are permuted for the test and CI procedure, changing the specification of the offset-adjusted regression model used for CIs, and carefully determining the underlying population model under which randomization-based inference is guaranteed to be valid. Our approach naturally incorporates efficient weights into the inferential procedure and targets a marginal treatment effect by using test statistics derived from individual-level generalized linear models. In Section 2, we provide a detailed overview of the method and demonstrate how to account for design features in a randomization-based analysis and why it is important to do so. Extensive simulations in Section 3 illustrate how our randomization-based method compares in terms of validity and efficiency to various commonly used alternatives including GLMMs, GEEs, and existing randomization-based approaches for SWTs based on cluster-period summary statistics. In Section 4, we apply our method to the XpertMTB/RIF trial, a SWT that compared the impact of two diagnostic tests of tuberculosis (TB) on reducing unfavorable outcomes;²⁹ this trial was previously reanalyzed in Thompson et al and Kennedy-Shaffer et al.^25,26 We close with a discussion in Section 5 and provide a link to our R package in Section 6.

2 |. METHODS

2.1 |. Setting and notation

Suppose we have i = 1, … , N clusters, j = 1, … , J periods, k = 1, … , m_ij individual-level outcomes sampled from cluster i at time period j (referred to together as cluster-period ij), and $M={\sum }_{i=1}^N{\sum }_{j=1}^J{m}_{ij}$ total individual-level outcomes in the study. Let X_ij = 1 indicate cluster i receiving intervention (treatment) at period j, X_ij = 0 for no intervention (control), X_i = (X_i1, … , X_iJ)^T denote the entire random treatment vector for cluster i, and X denote the entire N × J matrix whose ijth element is X_ij. According to the SWT design, clusters are randomized to crossover from control to treatment at a particular time period. Let x_ij, x_i, and x denote the resulting observed treatment value, vector, and matrix, respectively, after randomization has occurred. For example, a SWT with N = 3 clusters and J = 4 periods would correspond to

$$\mathbf{x}=\left(\begin{array}{l}{\mathbf{x}}_1^T\hfill \\ {\mathbf{x}}_2^T\hfill \\ {\mathbf{x}}_3^T\hfill \end{array}\right)=\left(\begin{array}{llll}{x}_{11}\hfill & x_{12}\hfill & x_{13}\hfill & x_{14}\hfill \\ x_{21}\hfill & x_{22}\hfill & x_{23}\hfill & x_{24}\hfill \\ x_{31}\hfill & x_{32}\hfill & x_{33}\hfill & x_{34}\hfill \end{array}\right)=\left(\begin{array}{llll}0\hfill & 1\hfill & 1\hfill & 1\hfill \\ 0\hfill & 0\hfill & 1\hfill & 1\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right),$$

if the first cluster were randomized to crossover at period 2, the second at period 3, and the third at period 4. Let Y_ijk denote the outcome random variable for individual k in cluster-period ij. In this article, we focus on exponential family outcome types (eg, binary, count, continuous). Collect all cluster-period outcomes in the vector ${\mathbf{Y}}_{ij}={\left(Y_{ij1},\dots ,Y_{ij{m}_{ij}}\right)}^T$, all cluster-specific outcomes in the vector ${\mathbf{Y}}_i={\left({\mathbf{Y}}_{i1}^T,\dots ,{\mathbf{Y}}_{iJ}^T\right)}^T$, and all study outcomes in the vector $\mathbf{Y}={\left({\mathbf{Y}}_1^T,\dots ,{\mathbf{Y}}_N^T\right)}^T$.

2.2 |. Randomization test and CI

Consider the population model

$$\left({\mathbf{Y}}_i\mid {\mathbf{X}}_i={\mathbf{X}}_{*}\right)~F\left({\mathbf{\eta }}_{{\mathbf{x}}_{*}},\mathbf{\varphi }\right),{\mathbf{\eta }}_{{\mathbf{x}}_{*}}={\left({\eta }_{1x_1},\dots ,{\eta }_{J{x}_J}\right)}^T,{\eta }_{jx}=g\left\{E\left(Y_{ijk}\mid X_{ij}=x\right)\right\}=\mu +{\beta }_j+\theta x,$$ (1)

for i = 1, … , N, j = 1, … , J, k = 1, … , m_ij, and where x_* = (x₁, … , x_J)^T denotes an arbitrary cluster-level observed treatment vector and g denotes the link function. Here, F is a common (but unspecified) distribution parameterized by ${\mathbf{\eta }}_{{\mathbf{x}}_{*}}$, a vector whose jth element corresponds to the g-transformed mean individual-level outcome for a particular randomized treatment value x_j = x ∈ {0, 1} at period j, and ϕ, a vector of nuisance parameters explicitly assumed not to be affected by treatment assignment. Model specification (1) imposes a constant marginal treatment effect θ across time and clusters and permits the underlying g-transformed mean outcome to vary in a piecewise fashion over time via categorical β_j (with β₁ = 0 for identifiability). By leaving both the distribution F and correlation structure unspecified, (1) is quite general and encompasses many SWT models commonly used in practice. For example, if continuous outcomes were generated from the linear mixed model $Y_{ijk}=\mu \ast +{\beta }_j^{*}+a_i+\theta \ast X_{ij}+{ϵ}_{ijk}$ with random cluster effects $a_i~N\left(0,{\sigma }_a^2\right)$ and independent errors ${ϵ}_{ijk}~N\left(0,{\sigma }_{ϵ}^2\right)$,⁶ these data would coincide with model (1) where F is the multivariate normal distribution with mean vector elements ${\eta }_{jx}=\mu \ast +{\beta }_j^{*}+\theta \ast x$ and an exchangeable covariance matrix parameterized by $\mathbf{\varphi }=\left({\sigma }_a^2,{\sigma }_{ϵ}^2\right)$. More complex correlation structures, such as nested exchangeable,^7,8 which incorporates additional random cluster-period effects to allow the correlation of two outcomes within the same cluster and period (ie, the within-period correlation, or WPC) to be larger than the correlation of two outcomes within the same cluster but from different periods (ie, the interperiod correlation, or IPC), or exponential decay,¹⁰ which allows the IPC to decrease between periods that are further apart, also correspond to this model because (1) imposes no structure on the correlation apart from it not being impacted by treatment assignment. An example that does not comply with (1) is the treatment heterogeneous correlation structure,⁹ since it presumes the within-cluster correlation changes with intervention, violating the condition that no components of ϕ are impacted by treatment. Similarly, any model allowing for treatment effect heterogeneity across clusters or time, such as model extensions C-E described in Hemming et al,⁷ would also not comply with (1).

Invariance can be used to justify the validity of a randomization test.²¹ Under population model (1) and the null hypothesis of no treatment effect (ie, H₀ ∶ θ = 0), it follows that η_j0 = η_j1 = μ + β_j for j = 1, … , J. This implies that the distribution of (Y|X = x) is invariant under row permutations of x and therefore, by theorem 15.2.1 of Lehmann and Romano,²¹ a randomization test based on these data will achieve level α, the prespecified type I error rate. Note that by permuting rows of x, we are mimicking the actual randomization performed in the SWT; that is, randomly permuting rows of x (each row corresponding to a particular cluster-specific treatment pattern) is equivalent to randomly assigning clusters to initiate treatment at different time periods (fixing the number of clusters assigned to each unique treatment pattern across randomizations), the latter having been operationalized in Wang and De Gruttola.²⁴ Also note the distinction between this procedure for SWTs (permuting rows of a matrix x) and its analog for parallel cluster randomized trials (permuting elements of a vector x).²⁸

For the randomization test, we first fit the generalized linear model

$$g\{E(Y_{ijk}\mid X_{ij}^{(p)})\}=\mu +{\beta }_j+\theta X_{ij}^{(p)},$$ (2)

via maximum likelihood (eg, with the glm function in R or Stata or PROC GENMOD in SAS) using values from the observed treatment matrix X⁽¹⁾ = x to obtain the observed marginal treatment effect estimate ${\widehat{\theta }}^{(1)}=\widehat{\theta }$. Then for p = 2, … , P, we randomly permute rows of x in accordance with the SWT randomization scheme and refit the generalized linear model (2), but now using values from the permuted treatment matrix X^(p) to obtain a new estimate ${\widehat{\theta }}^{(p)}$. The p-value is calculated as the proportion of ${\{{\widehat{\theta }}^{(p)}\}}_{p=1}^P$ as or more extreme than $\widehat{\theta }$ and we reject H₀ if this p-value is less than α.³⁰ An appropriate number of permutations P for this test can be based on the standard error of this Monte Carlo approximation to the exact p-value, that is, by ensuring $\sqrt{q(1-q)/P}$ is adequately small for a particular p-value = q, or most conservatively for q = 0.5.

A randomization-based confidence set for θ is obtained by inverting this test, that is, testing null hypotheses of the form H₀ ∶ θ = θ₀ ∈ Θ and collecting the set of values not rejected by these tests. As described in prior work, this can be done by introducing a fixed offset term into the regression model.²⁸ In particular, we can test an equivalent null hypothesis H₀ ∶ τ = (θ − θ₀) = 0 by fitting the generalized linear model

$$g\{E(Y_{ijk}\mid X_{ij}^{(p)})\}=\mu +{\beta }_j+{\theta }_0{x}_{ij}+\tau X_{ij}^{(p)},$$ (3)

with values from the observed treatment matrix x for the fixed offset term θ₀x_ij and values from the permuted treatment matrix X^(p) for the offset-adjusted treatment effect term $\tau X_{ij}^{(p)}$. Under population model (1) and H₀ ∶ τ = 0, the only functional relationship preventing (Y|X = x) from being invariant is a g-transformed mean shift of θ₀ between cluster-periods under treatment and control. By including the fixed offset term θ₀x_ij in model (3) across all P permutations, we eliminate this shift, resulting in invariance and, thus, a level α randomization test for any θ₀ ∈ Θ. Collecting the set of values not rejected by this offset-adjusted randomization test provides a (1 − α) randomization-based confidence set for θ, the bounds of which form a (1 − α) × 100% CI.

In practice, one could employ a standard grid or binary search by performing many randomization tests at different θ₀ ∈ Θ to identify bounds of the confidence set; however, such procedures can be computationally intensive (or even infeasible) for large datasets, such as those assembled in SWTs with individual-level outcomes. As an alternative, we recommend using a computationally efficient CI search procedure that adapts well to our offset-adjusted method.³¹ At each step of the search, the upper or lower bound estimate is updated based on only a single permutation of the treatment matrix (thus, a single model fit). For example, suppose we carry out a P-step search for U, the correct upper confidence limit of θ (note, this P could be different from that we used for the randomization test). At the pth step of the search, we fit model (3) with the current value of the upper limit θ₀ = U^(p) and permuted treatment matrix X^(p) to obtain the permuted offset-adjusted estimate ${\widehat{\tau }}^{(p)}\left({\mathbf{X}}^{(p)}\right)$. We also directly calculate the observed offset-adjusted estimate ${\widehat{\tau }}^{(p)}(\mathbf{x})=\widehat{\theta }-U^{(p)}$ based on the initial fit of model (2). We update the upper limit based on whether the permuted estimate is larger than the observed estimate via U^(p+1) in

$$\begin{gathered} U^{(p+1)}=\{\begin{array}{ll}{U}^{(p)}-\frac{s(\alpha /2)}{p},\hfill & \text{if}{\widehat{\tau }}^{(p)}({\mathbf{X}}^{(p)})>{\widehat{\tau }}^{(p)}(\mathbf{x})\hfill \\ U^{(p)}+\frac{s(1-\alpha /2)}{p},\hfill & \text{if}{\widehat{\tau }}^{(p)}({\mathbf{X}}^{(p)})\le {\widehat{\tau }}^{(p)}(\mathbf{x}),\hfill \end{array} \\ {L}^{(p+1)}=\{\begin{array}{ll}{L}^{(p)}+\frac{s(\alpha /2)}{p},\hfill & \text{if}{\widehat{\tau }}^{(p)}({\mathbf{X}}^{(p)})<{\widehat{\tau }}^{(p)}(\mathbf{x})\hfill \\ L^{(p)}-\frac{s(1-\alpha /2)}{p},\hfill & \text{if}{\widehat{\tau }}^{(p)}({\mathbf{X}}^{(p)})\ge {\widehat{\tau }}^{(p)}(\mathbf{x}),\hfill \end{array} \end{gathered}$$ (4)

where s > 0 is a chosen step length constant. An independent search is carried out for the correct lower limit L in the same fashion using L^(p+1) in (4). To avoid early steps changing dramatically in size, the P-step search should begin with p = m with m = min{⌈0.3(4 − α)/α⌉, 50}.³¹ Thus, [L^(m), U^(m)] represent the chosen starting values and the final updated values [L^{(m+P )}, U^{(m+P )}] are adopted as the CI. As the number of steps increase, estimates converge in probability to the correct randomization-based CI bounds.³¹ Longer searches (eg, P ≥ 200 000) are improved by modifying the step size during later phases of the search and averaging rather than using only the final values for CI estimation,³² the details of which are included in Section B of the Supporting Information. Additional guidance about fine-tuning this algorithm, such as choosing an appropriate number of steps, starting values, or step length, can be found in prior work.^28,31,32 This fast CI search procedure has been implemented in our R package (see Section 6).

2.3 |. Accounting for study design features

Stratification or other forms of restricted randomization can be employed in the design of a SWT to ensure balance of important characteristics between control and intervention conditions.^33,34 This is especially pertinent in SWTs with a small number of clusters, which occur often in practice. To ensure nominal type I error and CI coverage, such design features should be accounted for in the analysis;^35,36 if ignored, the result is often conservative inference and a loss of statistical efficiency, that is, p-values that are too large and CIs that are too wide.^37–39 In a typical regression analysis, stratified randomization is accounted for by including additional terms for the stratifying variables in the model. Although this technique properly accounts for the design, it can change the numerical value and interpretation of the targeted treatment effect parameter when a nonlinear link function (eg, g = logit) is used. Moreover, numerical issues can also arise when adding covariates into the regression model. For example, as we will discover in our simulations in Section 3.2, even the inclusion of a single additional binary covariate can worsen GEE performance in settings with a small number of clusters. If there are more than a few stratification groups, requiring too many additional terms to be introduced into the model relative to the size of the dataset, model fitting algorithms could be unstable or even fail to converge altogether.

Stratification can be addressed differently in a randomization-based analysis. Rather than adding terms into the model, we can retain the parsimonious nonstratified model and simply restrict the set of permutations considered in the test and CI procedure. For example, if the randomization of 10 clusters across six periods was stratified on a single binary cluster-level covariate Z with five clusters within each level, we would still target θ from the nonstratified marginal model (2) (ie, the model that does not include an additional term for Z), but would now sample X^(p) from among the (5!)² = 14, 400 possible permuted treatment matrices under a stratified design rather than all ${\mathbf{\prod }}_{i=1}^5\left(\begin{array}{c}2i\\ 2\end{array}\right)=113,400$ possible under a nonstratified design. The same approach would apply for other restricted SWT randomization schemes. For example, if we followed the restricted procedure employed by Moulton et al,⁴⁰ which boils down to choosing one randomization from a list of 1000 potential randomization sequences (all of which attain a certain level of covariate balance), we would sample X^(p) from among those 1000 in the analysis.

Of course, the further we restrict randomization in the design, the further we do so in the analysis. In some cases, this might allow us to fully enumerate all possible randomizations rather than sampling from them (though with a large enough number of randomly sampled permutations, the results would be similar). Highly restricted randomization could also result in more noticeably conservative inference due to the discreteness of the randomization distribution of $\widehat{\theta }$. For example, with only 50 potential randomization sequences, a randomization test could achieve p-values of 2/50 = 0.04 or 3/50 = 0.06, but not 0.05. In this case, an exact α = .05 test would theoretically require a randomized testing procedure, that is, flipping a biased coin for values on the boundary of the rejection region. Li et al³⁴ also considered such implications of a restricted design on a randomization-based analysis in the parallel cluster randomized trial setting.

Finally, let us gain some intuition about why ignoring such design features in a randomization-based analysis generally leads to conservative inference and a reduction in power and precision. Suppose randomization were stratified, and we properly carried out the randomization test and CI procedure in a stratified fashion. In this case, the empirical randomization distribution of $\widehat{\theta }$ would be an accurate representation of the sampling variability of $\widehat{\theta }$ given the underlying data generation procedure and stratified design. If instead we improperly carried out a nonstratified test and CI procedure, many values sampled from the nonstratified randomization distribution would be far too extreme given that the study design controlled some of this variability via stratified randomization. In other words, with the nonstratified procedure, we would be comparing the single observed value of the test statistic—which was generated under a stratified design—to its randomization distribution under a nonstratified design, the latter of which inherently has more variability associated with it. Given that the nonstratified randomization distribution would have more extreme values than its stratified counterpart, it would be more difficult to reject the null hypothesis than it should be (ie, power of the randomization test—and precision of the corresponding CI—would be reduced). We include a simple illustration of this point via simulation in Figure S1 in the Supporting Information. More extensive simulations in Section 3.2 demonstrate that conservative inference is generally the result of ignoring design features in a randomization-based analysis, and that power and precision are improved by restricting the permutation procedure in accordance with the design, as described above.

3 |. SIMULATIONS

We carried out simulations to evaluate the performance of our randomization-based approach and how it compared with existing analysis methods for SWTs. Alternative methods (detailed below) included three different GLMMs, a standard and small-sample adjusted GEE, and three randomization-based approaches that use cluster-period summary statistics. To evaluate the validity of each method, we calculated empirical type I error and CI coverage; to evaluate efficiency, we calculated empirical power and average CI width. In Section 3.1, we consider a nonstratified SWT with a binary outcome and in Section 3.2 we consider a SWT in which randomization is stratified on a single binary cluster-level covariate, again with a binary outcome. Simulations were run in R 3.4.1 or higher. Results for each scenario were based on 2000 independently generated datasets.

3.1 |. Nonstratified randomization

3.1.1 |. Data generation and analysis methods

First, we considered a nonstratified SWT with a binary outcome. Data were generated from the logistic GLMM

$$\mathrm{logit}\left\{E\left(Y_{ijk}\mid X_{ij},a_i,b_{ij}\right)\right\}={\mu }^{*}+{\beta }_j^{*}+a_i+b_{ij}+{\theta }^{*}{X}_{ij},$$ (5)

where μ∗ denotes the cluster-period-conditional baseline log odds of the outcome under the control condition, ${\beta }_j^{*}$ denotes a fixed categorical period effect, a_i is a random cluster effect, b_ij is a random cluster-period effect, and θ∗ denotes the cluster-period-conditional log odds ratio (OR) associated with intervention. Note, the cluster-period-conditional interpretations of μ∗ and θ∗ are due to inclusion of random cluster-period effects b_ij in (5). We set the population-level prevalence of the outcome under the control condition during the first period at 25%, that is, μ∗ = logit(0.25), and set ${\beta }_j^{*}=(j-1)/\{5(J-1)\}$ so that the underlying prevalence increased to about 29% by the end of the trial. We considered θ∗ ∈ {0, 0.25, 0.5}, which correspond with ORs ∈{1, 1.28, 1.65}. We drew the random effects independently from normal distributions centered at zero, that is, a_i ~ N(0, σ²) and b_ij ~ N(0, υ²) with (σ, υ) = (0.1, 0.01); for settings with θ∗ = 0, we ran additional simulations with (σ, υ) ∈ {(0.1, 0.1), (0.5, 0.01), (0.5, 0.1)}. With σ > 0 and υ > 0, the WPC is larger than the IPC. For example, with (σ, υ) = (0.1, 0.1), the induced WPC and IPC values on the log-odds scale were 0.006 and 0.003, respectively. Since binary outcomes were generated from a logistic GLMM, induced WPC and IPC values can be calculated on either the log-odds or proportion scale.^41,42 All WPCs and IPCs induced by the various simulation settings are presented in Tables S17 and S18 in the Supporting Information. We examined different numbers of clusters and periods (N : J ∈ {6: 4,8: 5, 10: 6, 12: 7, 14: 8}) with two clusters crossing over at a time, and different cluster-period sizes (m_ij drawn from discrete uniform distributions U{20, 30} and U{20, 80}).

We analyzed each dataset with our proposed randomization-based method. We targeted θ, the marginal log OR associated with intervention, by using $\widehat{\theta }$ from model (2) for the randomization test of no treatment effect and $\widehat{\tau }$ from offset-adjusted model (3) for the randomization-based CI, both with g = logit. Note the distinction between the marginal log OR θ we target for inference here and the cluster-conditional log OR θ∗ in model (5) used to generate the data (we discuss this distinction in more detail in the final paragraph of this Section 3.1.1). The p-value and each bound of the 95% CI were based on P = 5, 000, which provided sufficiently accurate p-value estimates (eg, standard error of 0.003 for p-value = .05) and acceptable coverage precision of the CI search.^28,31

Each dataset was also analyzed using various alternative approaches. First, we considered two GLMMs commonly used in analyzing SWTs: GLMM-CP corresponded exactly with data generation model (5); GLMM-C corresponded with model (5) without the b_ij terms, that is, random cluster effects only. Next, we fit a marginal model via GEE but used two different variance estimators: the first was the standard GEE sandwich variance estimator;⁵ the second employed the δ₅ adjustment proposed by Fay and Graubard,⁴³ which has been shown to perform well in SWTs with a small number of clusters.^14,17 For both GEEs, we specified an exchangeable working correlation structure, which—although misspecified given the random cluster-period effects in model (5)—is straightforward to implement in most statistical software packages, is often chosen in the analysis of SWTs, and has been shown to perform adequately in SWTs even when the true underlying correlation structure is more complex, especially when the WPC and IPC values are relatively small.^12,44 For all GLMMs and GEEs, we used Wald tests and corresponding 95% CIs. Next, we applied three randomization-based approaches that use cluster-period summary statistics: the NPWP method,²⁵ the crossover method,²⁶ and the closed-form permutation-based estimator (CF-Perm).²⁷ The NPWP and crossover methods directly employ randomization-based inference via weighted summaries; the former compares cluster-period means between treatment conditions within each period, and the latter compares cluster-period mean differences between clusters that crossover to those that do not at each crossover point. To conduct the nonzero null hypothesis tests necessary to calculate a CI with the NPWP and crossover methods, we applied the usual transformation approach by subtracting off a fixed value from summary statistics of cluster-periods under the intervention condition (eg, the approach described in Section 4.1 of Ernst);²⁰ the fast CI search procedure described at the end of Section 2.2 was adapted here as well. Weights for the NPWP and crossover estimators were chosen according to those provided by Thompson et al and Kennedy-Shaffer et al.^25,26 The CF-Perm approach proposed by Hughes et al is also based on cluster-period summary statistics, but circumvents the actual permutation procedure by employing a closed-form (though still randomization-based) variance expression.²⁷ For these three alternative randomization-based approaches, we used the empirical log odds of the outcome within each cluster-period as the summary statistic; if a cluster-period sample proportion was zero or one, we added 0.5 to both the number of individuals with and without the outcome of interest, as suggested by Thompson et al.²⁵ Further details about these cluster-period summary approaches can be found in Section A in the Supporting Information.

To assess how deviations from population model (1) impacted the performance of these methods, we ran additional simulations generating data from

$$\mathrm{logit}\left\{E\left(Y_{ijk}\mid X_{ij},a_i,b_{ij},c_i\right)\right\}={\mu }^{*}+{\beta }_j^{*}+a_i+b_{ij}+{\theta }^{*}{X}_{ij}+c_i{X}_{ij},$$ (6)

where the only modification from (5) is the addition of random cluster-intervention effects c_iX_ij with c_i ~ N(0, λ²) and λ ∈ {0.1, 0.5, 1}. Under (6) with λ > 0, WPC and IPC both increase once the intervention is introduced (see Tables S17–S18 in the Supporting Information), thus, violating the condition in population model (1) that the correlation structure is unaffected by treatment. For this setting, we considered one additional analysis model, GLMM-CPI, in which we specified the additional random cluster-intervention effects to coincide with (6).

Given the nonlinear function (ie, logit) used to generate data, fit the regression models, and calculate cluster-period summaries, each analysis method generally targets a different parameter when θ∗ ≠ 0. Therefore, for a given analysis method, we calculated empirical CI coverage with respect to the induced true parameter value targeted by that particular method. For the underspecified GLMMs and for the marginal model fit via GEE and via our offset-adjusted method, we approximated these values using Gauss-Hermite quadrature; given the relatively small values (σ, υ) = (0.1, 0.01) used to generate data in settings with θ∗ > 0, these values were numerically close to θ∗, though slightly attenuated (eg, for θ∗ = 0.5, the true marginal parameter was θ = 0.499). For the cluster-period summary approaches, this relationship was more complex and depended on the underlying proportion of the outcome expit(μ∗), the cluster sizes m_ij, and the heuristic adjustment value (here, 0.5) used for cluster-period sample proportions of zero or one. Given this complexity, we calculated induced values via simulation; these values were further away from θ∗ and slightly larger (eg, for θ∗ = 0.5 and m_ij ~ U{20, 30}, the value targeted by each cluster-period summary approach was about 0.53).

3.1.2 |. Results

Let us first focus on results from data generation model (5) with (σ, υ) = (0.1, 0.01). Power, coverage, and average CI widths are shown in Figure 1. The unadjusted GEE had poor performance across the board, with inflated type I error (9%-25%) and undercoverage (75%-91%) (hence its exclusion from Figure 1 for clarity). The small-sample adjusted GEE performed much better, but was sometimes overly conservative (eg, 3% type I error and 97% coverage with N = 6 clusters). With a smaller number of clusters, the CF-Perm estimator had inflated type I error (eg, 9% with N = 6 and m_ij ~ U{20, 80}) and undercoverage (eg, 91%), though both became nominal as N increased. Aside from CF-Perm, all other approaches using randomization-based inference and both GLMMs led to nominal type I error and coverage across these scenarios. In terms of efficiency, GLMM-C generally performed the best (highest power and narrowest CIs) followed closely by the correctly specified GLMM-CP; however, the latter failed to converge up to 10% of the time with larger N, J, and m_ij. The CF-Perm approach and our proposed randomization-based method had the next best efficiency, though in settings where type I error and coverage were nominal, our individual-level approach resulted in narrower CIs. Next in line were the NPWP method and small-sample GEE, which had similar performance and were worst overall with N = 6. Finally, except for N = 6 (and as we will see later, settings with larger σ), the crossover approach had the lowest power and widest CIs. Additional simulations with fixed cluster-period sizes demonstrated that, in terms of efficiency, the cluster-period summary methods were more negatively impacted by varying cluster sizes than were the individual-level regression approaches (see Table S4 in the Supporting Information). As the number of clusters increased, average width of the randomization-based CIs using our offset-adjusted method approached the average CI widths of the best performing fully parametric GLMMs.

FIGURE 1.

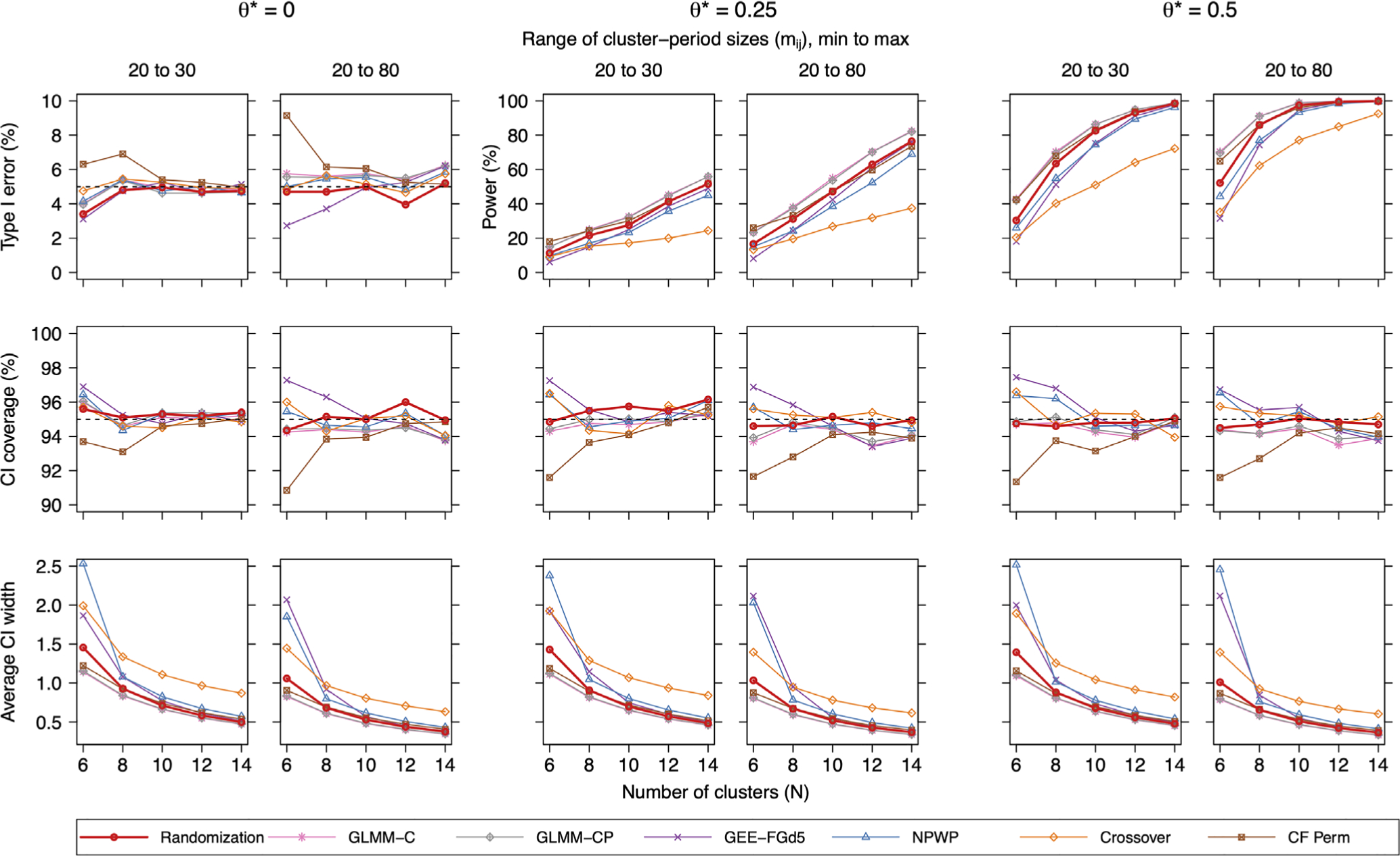
Simulation results of a nonstratified SWT across 2000 datasets simulated via model (5) as described in Section 3.1.1 with (σ, υ) = (0.1, 0.01). Methods considered included our proposed individual-level randomization-based approach (Randomization), a logistic mixed model with random cluster effects (GLMM-C), a logistic mixed model with random cluster and cluster-period effects (GLMM-CP), a marginal model fit via a small-sample adjusted generalized estimating equation (GEE-FGd5), a nonparametric within-period approach (NPWP), a crossover method (Crossover), and a closed-form permutation-based estimator (CF-Perm). This figure appears in color in the electronic version of this article. SWT, stepped wedge cluster randomized trial

In settings with larger σ = 0.5 (ie, larger WPC and IPC), the small-sample GEE was not as conservative with small N, the CF-Perm method was even more liberal, the crossover approach now produced the narrowest CIs among all randomization-based methods, and the relative efficiency of our randomization-based method compared with the best performing GLMMs got considerably worse—at least when N ≤ 14. With larger υ = 0.1 (ie, larger WPC relative to IPC), the only apparent difference in relative performance was that both GLMMs had a slight inflation of type I error and undercoverage.

In settings with data generated from model (6), which has the addition of random cluster-intervention effects, our randomization-based method (and similarly the other randomization-based cluster-period summary approaches) did not always result in nominal type I error or CI coverage. For example, in the most extreme setting with λ = 1, our randomization-based method resulted in type I error up to 14% and CI coverage as low as 87%. These findings make sense because conditions in population model (1) are no longer met; they are also consistent with results demonstrated and briefly discussed in Ren et al.⁴⁴ Across the settings we examined, though, our method was least sensitive to such deviations from population model (1) among all randomization-based approaches and performed better than GLMM-C and GLMM-CP. In terms of type I error and coverage, the two best performers under data generation model (6) were the small-sample adjusted GEE and the correctly specified GLMM-CPI, though notably the latter failed to converge up to 40% of the time in settings with larger N and J.

Complete simulation results for all nonstratified settings are reported in Tables S1 to S10 in the Supporting Information.

3.2 |. Stratified randomization

3.2.1 |. Data generation and analysis methods

Next, we considered a SWT in which randomization was stratified on a single baseline binary cluster-level covariate Z. Similar to our first set of simulations, data were generated from a logistic GLMM, but now Z was also related to the outcome via

$$\mathrm{logit}\left\{E\left(Y_{ijk}\mid X_{ij},Z_i,a_i,b_{ij}\right)\right\}={\mu }^{*}+{\beta }_j^{*}+a_i+b_{ij}+{\gamma }^{*}{Z}_i+{\theta }^{*}{X}_{ij},$$ (7)

where γ∗ represents the cluster-period-conditional log OR associated with Z. We assumed that by design N/2 clusters with Z = 0 and N/2 with Z = 1 were enrolled in the study. For each dataset, we randomized clusters according to the SWT design, but now within each level of Z, resulting in balance of Z between control and intervention conditions. We varied γ∗ ∈ {0, 0.2, 0.7, 1.5} to examine how different strengths of association between Z and Y impacted the performance of each method; all other data generation parameters (μ∗, ${\beta }_j^{*}$, σ = 0.1, υ = 0.01) were set to the same values as in Section 3.1.1. For these stratified simulations, we considered the same set of cluster and period numbers (N : J ∈ {6 : 4, … , 14 : 8}) and cluster sizes (m_ij ~ U{20, 30} and m_ij ~ U{20, 80}) as before, but considered only θ∗ = 0 for convenience.

We analyzed each dataset with our proposed randomization-based method. We again targeted θ, the nonstratified marginal log OR associated with the intervention, by using $\widehat{\theta }$ from (2) for the randomization test and $\widehat{\tau }$ from (3) for the corresponding CI. We carried out randomization-based inference in both a nonstratified and stratified fashion, as described in Sections 2.2 and 2.3, respectively. The p-value and each bound of the 95% CI were based on P = 5, 000. Each dataset was also analyzed via nonstratified and stratified versions of the individual-level regression methods considered previously: GLMM-CP, GLMM-C, and both GEEs. Keep in mind, since these alternative methods address stratification by including an additional term for Z in the model, the targeted intervention effect corresponds to the Z-conditional log OR, which in general is numerically different from the nonstratified marginal log OR targeted by our randomization-based method (though they are identical with θ∗ = 0).

3.2.2 |. Results

Condensed results for the smaller and less variable cluster sizes (ie, m_ij ~ U{20, 30}) are presented in Table 1; complete results are presented in Tables S11 to S16 in the Supporting Information. The unadjusted GEE performed poorly whether or not Z was included in the model; interestingly, the unadjusted GEE had more severe inflation of type I error and undercoverage when appropriately stratified by Z. The small-sample adjusted GEE performed well in most settings, but was conservative for datasets with the fewest (N = 6) clusters. Regardless of whether Z was included, the GLMM-C and GLMM-CP models again performed well and similarly to each other. Accounting for stratification in the randomization-based analysis resulted in closer to nominal type I error and coverage rates. For example, when a strong Y-Z association was not accounted for in the analysis, randomization-based CIs were widest and coverage was much higher than 95% (eg, 100% coverage when γ∗ = 1.5); however, the stratified permutation procedure completely resolved this conservativeness and resulted in close to 95% coverage across all simulation settings. Accounting for stratification also more markedly improved precision of the randomization-based CIs, sometimes even leading to narrower CIs than the fully parametric GLMMs. For example, with smaller and less variable cluster sizes (ie, m_ij ~ U{20, 30}), comparing no Y-Z association (γ∗ = 0) to the strongest (γ∗ = 1.5), the reduction in average CI width was more pronounced for the randomization-based method (eg, 15% reduction with N = 10) than it was for GLMM-C and the small-sample adjusted GEE (eg, 3% and 4%, respectively). By contrast, the reduction in average CI width was less pronounced for the randomization-based method with larger and more variable cluster sizes (ie, m_ij ~ U{20, 80}), sometimes even resulting in slightly wider CIs with larger γ∗ (see Supplementary Table S16). Finally, we point out that the conservative type I error (3%) of the stratified randomization test with N = 6 is expected due to the discreteness of only (3!)² = 36 unique randomization sequences from which to sample (ie, the largest achievable p-value smaller than α = .05 is 1/36 ≈ 0.03); interestingly though, the corresponding CI coverage rates in this setting were closer to the nominal level, demonstrating that some of this discreteness is “smoothed over” by using the stochastic CI search procedure outlined at the end of Section 2.2.

TABLE 1.

Simulation results of a stratified SWT across 2000 datasets simulated via model (7) as described in Section 3.2.1 with cluster sizes m_ij ∼ U{20, 30}

		Type I error (%)			CI coverage (%)			Average CI width
		N
Method	γ*	6	10	14	6	10	14	6	10	14
Randomization	0-ns	5	6	4	94	95	95	1.42	0.71	0.50
	0	3	5	4	94	95	96	1.67	0.72	0.50
	0.2	3	5	5	96	95	95	1.69	0.71	0.49
	0.7	3	5	5	95	95	94	1.58	0.67	0.46
	1.5	3	5	4	95	95	96	1.46	0.61	0.43
	1.5-ns	0	0	0	100	100	100	4.73	2.10	1.58
GLMM-C	0-ns	6	7	5	94	93	95	1.14	0.66	0.47
	0	6	7	5	94	93	95	1.12	0.65	0.47
	0.2	5	6	6	95	94	94	1.11	0.64	0.46
	0.7	6	6	6	94	94	94	1.06	0.62	0.44
	1.5	5	5	6	95	95	94	1.08	0.63	0.45
	1.5-ns	4	5	5	96	95	95	1.29	0.77	0.56
GEE-FGd5	0-ns	3	5	5	97	95	95	1.97	0.77	0.52
	0	2	6	5	98	94	95	2.11	0.77	0.51
	0.2	2	5	6	98	95	94	2.02	0.75	0.50
	0.7	2	5	6	98	95	94	2.20	0.73	0.48
	1.5	2	5	5	98	95	95	2.13	0.74	0.49
	1.5-ns	4	5	4	96	95	96	1.49	0.76	0.52

Note: Methods considered included our proposed individual-level randomization-based approach (Randomization), a logistic mixed model with random cluster effects (GLMM-C), and a marginal model fit via a small-sample adjusted generalized estimating equation (GEE-FGd5). Increasing values of γ* correspond to increasing strengths of Y-Z association. Rows designated with “-ns” correspond to a nonstratified analysis; all other rows correspond to a stratified analysis. For complete stratified SWT simulation results, see Tables S11 to S16 in the Supporting Information.

Abbreviations: CI, confidence interval; SWT, stepped wedge cluster randomized trial.

4 |. EXAMPLE

The XpertMTB/RIF trial was a SWT carried out in 2012 to assess the impact of replacing smear microscopy with XpertMTB/RIF, a rapid diagnostic test of TB and rifampicin resistance.⁴⁵ The study randomized 14 primary care laboratories in Brazil to crossover from control (smear microscopy) to intervention (XpertMTB/RIF) at one of seven different time points (thus, eight periods including the first where all clusters were under the control condition). Although the primary aims of the trial were to increase the notification rate of lab-confirmed TB to the Brazilian national notification system and to reduce the time to treatment initiation, Trajman et al carried out a follow-up analysis of individuals diagnosed with TB in the trial to determine whether the rapid test had any impact on reducing unfavorable outcomes (a composite binary outcome indicating death from any cause, loss to follow-up, transfer out due to first-line drug failure, or suspicion of drug resistance).²⁹ Among the 3926 individuals included in their final analysis, 31% (556/1777) under control and 29% (625/2149) under intervention had unfavorable outcomes. The authors used a logistic mixed effects model with random cluster (lab) effects and a fixed effect for intervention (note, no adjustment for any possible period effects) to quantify the treatment effect, which led to an estimated crude OR of 0.92 (95% CI: 0.79–1.06). On average, there were 35 individuals within each cluster-period, though sizes were quite variable across cluster-periods (minimum 6, maximum 96, empirical coefficient of variation 0.52, see Figure 2).

FIGURE 2.

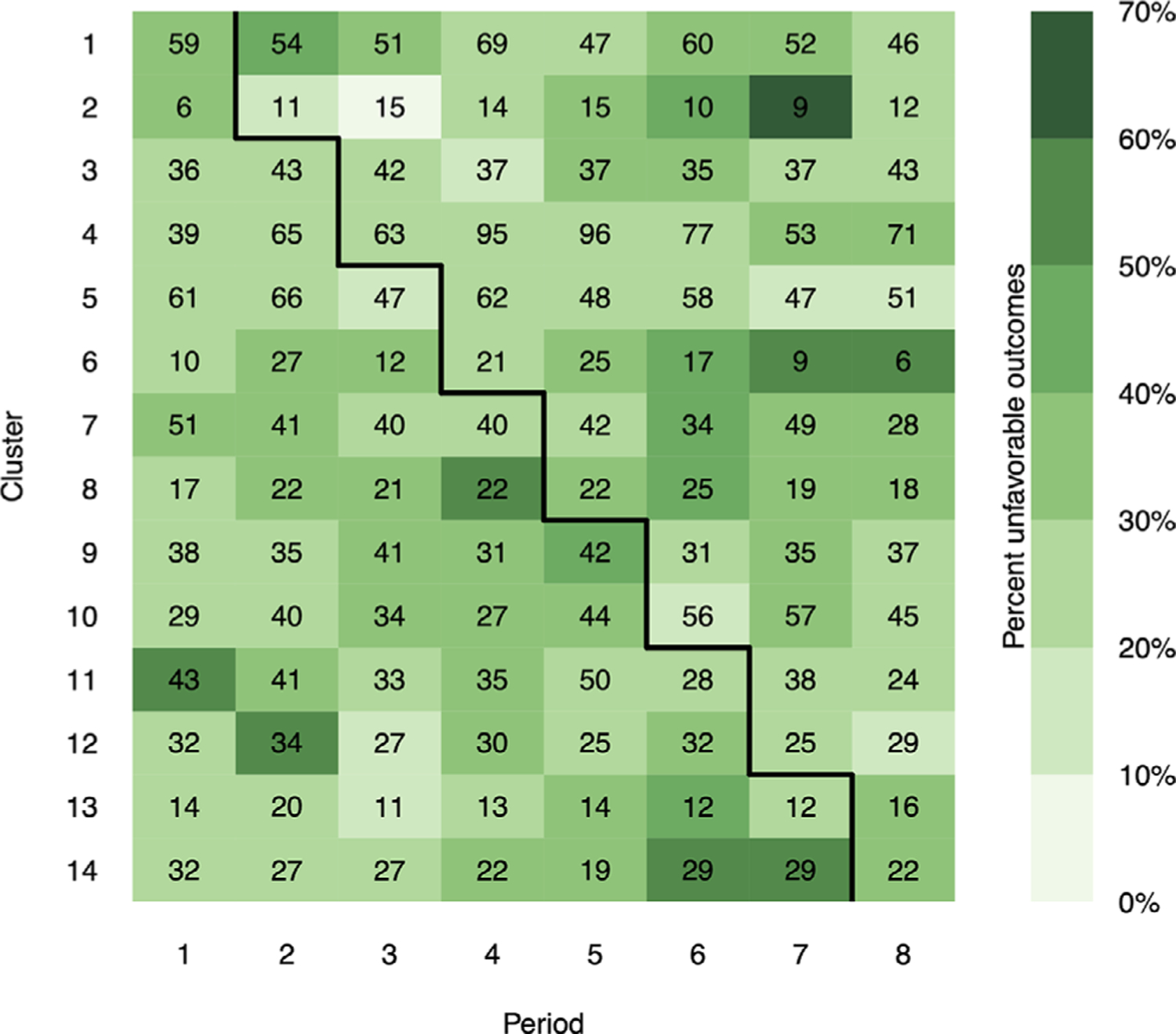
Cluster-periods in the XpertMTB/RIF SWT. Cell numbers correspond to cluster-period sizes; darker cell colors indicate higher percentage of unfavorable (ie, worse) outcomes within each cluster-period. Cells below/above solid black line correspond to control/intervention condition

We reanalyzed data from this trial using our individual-level randomization-based method for SWTs and the alternative approaches outlined in Section 3.1.1. We removed two individuals from the dataset whose recorded treatment allocation did not match the SWT design, resulting in 3924 individual-level binary outcomes. Restricted randomization was employed in the design of this trial to ensure a balance of low/intermediate/high monthly case load and low/high HIV prevalence between labs that crossed over early (periods 2–5) and late (periods 5–8).⁴⁵ We carried out analyses both ignoring and accounting for this design feature. The unrestricted analysis was done to align with previous analyses of these data.^25,26,29 The restricted analysis was carried out with the intention of improving power and precision. The restricted randomization-based analyses were carried out by restricting the permutations considered in the test and CI procedure, as described in Section 2.3; we did not carry out a restricted analysis using the CF-Perm method, as it was not immediately clear how this could be done. For the restricted GLMMs and GEEs, we simply included additional categorical terms in the regression model for monthly case load and HIV prevalence. Though we deemed 5000 permutations reasonable for each randomization test and CI search procedure, it was computationally feasible to increase to 20 000 for these data to further refine the CI estimates. These 20 000 permutations were sampled from among all 681 080 400 potential unrestricted randomizations (for the unrestricted analysis) or among all 100 018 800 potential restricted randomizations (for the restricted analysis).

Results are presented in Table 2. All methods using individual-level regression models resulted in similar OR estimates between 0.83 and 0.85. As expected, accounting for restricted randomization resulted in slightly smaller randomization-based p-values and narrower CIs. In particular, our randomization-based approach accounting for the restricted design led to an estimated OR of 0.84 with 95% CI [0.65, 1.05] (p-value = .11). Results were generally similar for the alternative individual-level methods, though the GLMMs gave somewhat narrower CIs and smaller p-values, while the GEEs gave wider CIs and larger p-values. The more complex mixed models GLMM-CP and GLMM-CPI had estimated variance components near or at the boundary of the parameter space, which can lead to invalid p-values and CIs (though here, results generally align with GLMM-C, which did not have this issue). Notably, all three approaches using cluster-period summaries led to moderately stronger treatment effect estimates ranging from 0.72 (crossover method) to 0.78 (NPWP and CF-Perm) and the smallest p-values (.01-.06).

TABLE 2.

Estimated odds ratio (OR) of the intervention effect in the XpertMTB/RIF SWT

		Unrestricted			Restricted
Analysis type	Method	OR	95% CI	p-value	OR	95% CI	p-value
Individual-level model	Randomization	0.84	[0.64, 1.07]	.13	0.84	[0.65, 1.05]	.11
	GLMM-C	0.84	[0.68, 1.03]	.09	0.85	[0.69, 1.04]	.12
	GLMM-CP*	0.84	[0.68, 1.03]	.09	0.85	[0.69, 1.04]	.12
	GLMM-CPI*	0.84	[0.68, 1.03]	.09	0.84	[0.67, 1.05]	.12
	GEE	0.83	[0.61, 1.14]	.25	0.84	[0.62, 1.15]	.28
	GEE-FGd5	0.83	[0.57, 1.21]	.31	0.84	[0.58, 1.22]	.33
Cluster-period summaries	NPWP	0.78	[0.61, 0.97]	.02	0.78	[0.60, 0.95]	.01
	Crossover	0.72	[0.52, 1.01]	.05	0.72	[0.52, 1.00]	.05
	CF-Perm	0.78	[0.61, 1.01]	.06	·	·	·

Note: Methods considered included our proposed individual-level randomization-based approach (Randomization), a logistic mixed model with random cluster effects (GLMM-C), a logistic mixed model with random cluster and cluster-period effects (GLMM-CP), a logistic mixed model with random cluster and cluster-period and cluster-intervention effects (GLMM-CPI), a marginal model fit via a generalized estimating equation (GEE), a small-sample adjusted GEE (GEE-FGd5), a nonparametricwithin-period approach (NPWP), a crossover method (Crossover), and a closed-form permutation-based estimator (CF-Perm). Analyses were carried out ignoring (Unrestricted) and accounting for (Restricted) the restricted randomization procedure used in the trial design; we did not carry out a restricted analysis using the CF-Perm method, as it was not immediately clear how this could be done. Asterisk (*) denotes model resulting in (near) singularity, due to random effect variance estimates of (close to) zero.

Abbreviations: CI, confidence interval; SWT, stepped wedge cluster randomized trial; OR, odds ratio.

To provide more insight into these differences, we provide a visualization of cluster-period sizes and outcomes from the XpertMTB/RIF trial in Figure 2. Consider, for example, the contribution to the crossover estimator of Kennedy-Shaffer et al from the first crossover point (period 1–2) and from clusters where the intervention was introduced (clusters 1 and 2). In cluster 1, outcomes got worse after the intervention was introduced (37%-46% unfavorable outcomes), whereas in cluster 2, outcomes got better (33%-18%). Even though the latter contrast favoring treatment was inherently much less stable than the former (based on only 17 individuals compared with 113), each was weighted equally by the crossover estimator. A similar observation can be made for clusters 5 and 6 at their crossover point in the study. Similar weighing schemes that did not directly account for varying cluster-period sizes were embedded in the NPWP and CF-Perm estimators. On the other hand, the individual-level approaches—including our randomization-based method—accounted for varying cluster-period sizes via regression-based test statistics. These different ways in which cluster-period sizes were (or were not) incorporated into the analysis could explain why the cluster-period summary approaches led to stronger effect estimates in the XpertMTB/RIF trial. Of course, there is a lot more complexity involved in each inferential procedure that could have driven these numerical differences as well. For example, cluster-period summary methods generally target different parameter values, as mentioned in Section 3.1.1. These differences could also have been simply the result of sampling variability, as we demonstrated in Figure S3 in the Supporting Information by simulating datasets similar to the XpertMTB/RIF trial and comparing the concordance of coefficient estimates across methods.

5 |. DISCUSSION

In this article, we investigated the use of randomization-based inference for analyzing cross-sectional SWTs. Randomization-based methods do not require assuming the data come from a known family of distributions, specifying a particular correlation structure for the outcomes, or having a large number of clusters, periods, or individuals to guarantee nominal type I error and CI coverage. Extending previous work in the parallel setting,²⁸ we developed a framework for calculating randomization-based p-values and CIs for a marginal treatment effect in SWTs using test statistics derived from individual-level generalized linear models. We also demonstrated that a randomization-based analysis can maintain a nonstratified marginal target of inference while accounting for design features.

Let us now step back and consider how this proposed randomization-based approach fits in with other existing SWT analysis methods. On one end of the spectrum, randomization-based methods using cluster-period summary statistics, such as those proposed by Thompson et al and Kennedy-Shaffer et al,^25,26 are the most robust: their statistical validity does not require specifying a mean model for individual-level outcomes nor does it rely on having a large number of clusters. On the other end, fully parametric approaches like fitting a GLMM via maximum likelihood could result in optimally powerful tests and precise CIs, especially if cluster-period sizes vary substantially; however, maintaining nominal type I error and CI coverage would hinge upon these structural and distributional assumptions being met as well as a large enough number of clusters to ensure adequate accuracy of the asymptotic approximations relied upon for inference. Our randomization-based method offers a compromise between these two extremes. By using test statistics derived from individual-level generalized linear models, which additionally requires correct specification of the mean model for individual-level outcomes, we gain some efficiency; by leaving other components unspecified (eg, outcome distribution, correlation structure), we retain some robustness; and by using randomization as the basis for inference, we do not require a large number of clusters to guarantee nominal type I error and CI coverage rates. Similar to our randomization-based method, semiparametric marginal models fit via GEE also offer a compromise between these two extremes; thus, it is important to weigh the advantages and disadvantages of each. For example, GEEs may be advantageous in settings where the underlying correlation structure is impacted by treatment assignment, since our randomization-based method relies on such features being unaffected by the intervention, whereas GEEs do not. However, valid GEE-based inference requires either a large number of clusters or an appropriate small-sample adjustment, the latter of which is complicated by the fact that the performance of different adjustment methods can vary depending on attributes of the trial, such as cluster size variability.^14–17 As we presented in Section 2.3, randomization-based inference may have the advantage over GEE in terms of it naturally accounting for design features in the analysis without requiring additional covariates being introduced into the regression model, thus, maintaining a nonstratified marginal target of inference.

For illustration and comparison in our simulations and example, we examined only a single GEE small-sample adjustment method based on Fay and Graubard.⁴³ Other finite-sample adjustment methods have been proposed, for example, Kauermann and Carroll or Mancl and DeRouen.^46,47 Ford and Westgate demonstrated that a method averaging these two adjustments works especially well in SWTs with at least six clusters and when a given cluster’s size does not vary across periods; they also provided general guidance on when certain GEE adjustments should or should not be used in the SWT setting.¹⁶ Another recent paper by Thompson et al examined the comparative performance of various small-sample adjustments in SWTs with a binary outcome.¹⁷ Further examination of how the validity and efficiency of these alternative small-sample GEEs compare to randomization-based methods for SWTs would be useful.

Although we focused on cross-sectional SWTs in this article (ie, where each participant contributes to only a single cluster-period), our method could also be used for cohort SWTs, in which each participant provides repeated outcome measurements across the study periods. Since we do not impose any particular within-cluster correlation structure in model (1)—other than it not depending on treatment—any additional within-individual dependence induced by repeated measures will not impact the validity of our randomization-based approach. We also focused on randomization-based inference for a marginal treatment effect from a generalized linear model rather than a conditional treatment effect from a GLMM.^23,24 It would be useful to investigate theoretical and practical implications of using our offset adjustment method to calculate randomization-based CIs for such conditional treatment effects in SWTs. For example, given the computational fitting procedure for GLMMs is more complex than fitting a generalized linear model, this could mean longer computation times for obtaining a randomization-based p-value and CI, or could even cause the entire procedure to fail if some permutations of the data result in model convergence issues.

Some structure imposed by population model (1) might be insufficient in certain settings. For example, the assumption of a common θ across time means that the only impact of treatment occurs immediately at the crossover point (before outcomes are assessed) and treatment has no additional effect during subsequent periods. Depending on the intervention and outcome, this could be unreasonable. One could extend (1) to allow for treatment effect heterogeneity, but this would require modification of the randomization test and CI procedure. Model (1) also assumes any distributional components aside from the g-transformed mean are not impacted by treatment. Again, this assumption could be violated if, for example, correlation or variance components change once the intervention is introduced, as we demonstrated in some of our simulations in Section 3.1. More work on such extensions of our randomization-based method would be useful.

DATA AVAIALABILITY STATEMENT

An R package for our method is available online at https://github.com/djrabideau/permuter. The data for the example in Section 4 were provided to us by Trajman et al.²⁹