Assessing Measurement Invariance Across Multiple Groups: When Is Fit Good Enough?

Abstract

Complex research questions often need large samples to obtain accurate estimates of parameters and adequate power. Combining extant data sets into a large, pooled data set is one way this can be accomplished without expending resources. Measurement invariance (MI) modeling is an established approach to ensure participant scores are on the same scale. There are two major problems when combining independent data sets through MI. First, sample sizes will often be large leading to small differences becoming noninvariant. Second, not all data sets may include the same combination of measures. In this article, we present a method that can deal with both these problems and is user friendly. It is a combination of generating random normal deviates for variables missing completely in combination with assessing model fit using the root mean square error of approximation good enough principle, based on the hypothesis that the difference between groups is not zero but small. We demonstrate the method by examining MI across eight independent data sets and compare the MI decisions of the traditional and good enough approach. Our results show the approach has potential in combining educational data.

Complex research questions about educational achievement often require complex analytical methods. Historically, two issues may have deterred researchers from attempting to examine complex questions. The first issue relates to the limited computational power of software and hardware. For example, many complex analytical methods that were thought up early in the 20th century were not possible until a couple of decades ago when computational power allowed for maximum likelihood solutions. With the increase in computational power of software and hardware, it is now technically feasible for researchers to examine these complex questions. However, a second issue that arises in using more complex methods is the increased sample size that is necessary to obtain accurate estimates of parameters and adequate power. Unlike computational power, it has always been theoretically possible to obtain large sample sizes, but in practice, the resources (e.g., time, money) needed have often stood in the way.

One way to mitigate the challenges of collecting large samples, is to combine smaller, extant samples into one large data set, commonly referred to as data fusion (Marcoulides & Grimm, 2017). Currently, many data fusion statistical methods that combine independent data samples have taken an integrative data analysis approach using moderated nonlinear factor analysis (MNLFA; Curran & Hussong, 2009; Curran et al., 2014; Hussong et al., 2013). In this approach, researchers find similar items among data sets and then use various latent modeling techniques to put the participants on the same scale by estimating a factor score on a latent variable underlying all items. By allowing covariates to influence the factor loadings and item intercepts, for example, MNLFA can account for systematic differences between data sets. The subsequent factor scores can then be thought of as providing a common, unbiased scaling across the data sets being combined. Other researchers have approached data fusion from an item response theory standpoint, scaling participants by estimating their latent ability using items from multiple tests or different versions of the same test (Marcoulides & Grimm, 2017). Both these techniques to combining data sets are dependent on having access to item level data on participants. However, education researchers do not always store the participant outcomes of assessments and measures at the item level but rather enter the raw or converted scores into their data management system. Raw scores are typically computed on the protocols used to assess the participants and might be converted into scaled or standard scores. In many cases, it is unlikely openly available data will be provided at the item level. It is therefore important to find ways to combine data from multiple different data sets by putting participants on the same scale at the test level instead of at the item level.

One way that total scores from participants obtained from different data sets can be put on a similar scale is using measurement invariance testing. In most approaches, measurement invariance (MI) testing uses a multiple group confirmatory factor analysis (MCFA) to indicate if groups are the same or different on (a) the underlying factor structure, (b) factor loadings, (c) intercepts, and (d) factor variance (Sörbom, 1974). Invariance is tested on each of the set of parameters by posing equality constraints. To be able to put participants on the same scale and subsequently make comparisons of factor means, the MI testing should establish scalar invariance, meaning that the factor structure, factor loadings, and measurement intercepts are equal among the groups (Kline, 2014).

While MI is an appropriate way to combine total scores across samples, there are additional issues that need to be considered. First, researchers interested in combining data sets to answer questions about a particular behavior or particular participant group are likely interested in creating a large total sample. However, MI is usually established by comparing nested models using the likelihood ratio test, and decisions about invariance are most commonly based on p values, which in turn are dependent on sample size. The larger the number of participants in a total sample, the more likely a CFA model will be deemed noninvariant across the groups, even in the presence of trivial differences. Second, researchers may have access to multiple data sets (i.e., more than two) that may not have scores on the same combination of measures for given constructs (e.g., timed or untimed word reading performance). In other words, Set A may have five measures of interest, Set B may have three of those, and Set C may have four, and Sets B and C overlap in only two measures. While each of these problems has been the focus of previous research, the combination of these problems in light of combining three or more data sets has (to our knowledge) not been addressed.

The objective of this article is to present one possible solution to the conundrum of using a MI framework to combine more than three independent data sets at the test level when the number of measures across groups are not equal. Our substantive example uses data from eight intervention studies in reading with the goal of placing the scores from participants of all data sets on a common reading scale using five reading measures. In order to be successful, our solution should be able to handle the differences in the number of measures across groups, be insensitive to sample size, and provide inferential tests of measurement invariance to formally test expected group differences. Finally, our solution optimally needs to be applicable across a range of statistical platforms and doable for many applied researchers. In the following section, we will discuss recent approaches of dealing with missing measures, quantifying invariance regardless of sample size, and inferential testing of measurement invariance for large samples.

Manifest Variables Missing Completely

Researchers hoping to combine multiple data sets have to deal with missing data at two different levels. First, there might be missing data at the participant level. In the case of MCFA, this can be handled by using a full information maximum likelihood estimator (FIML), provided the data are missing at random (MAR) or missing completely at random (MCAR) (Enders & Bandalos, 2001). Second, each data set may not consist of the same combinations of measures, or manifest variables. Of the total set of manifest variables across groups, each group has a set of manifest variables present (MVP) and a set of manifest variables missing completely (MVMC). MVMC prohibit the inversion of a variance-covariance matrix, and subsequently no statistical analysis using FIML can be conducted (Widaman et al., 2013). Widaman et al. (2013) noted three possible solutions to deal with MVMC: (a) using pattern mixture procedures with known groups (b) using a program that can handle MVMC automatically; and (c) generating random normal deviates for all observations in a data set for all MVMC manually.

These three possible solutions are all based on previous suggestions of how to deal with missing data patterns in structural equation models by creating subgroups based on these patterns. Pattern mixture models allow for several missing data patterns and parameters estimates of a model are averaged across the groups (Hedeker & Gibbons, 1997). Often, pattern mixture models are used to discover subgroups in data (i.e., latent classes), but models can also be estimated using known groups. This requires fixing parameter estimates of MVMC to 0. A drawback of this approach is that fitting pattern mixture models with known groups can only be done in Mplus. Moreover, the pattern mixture procedure does not provide indices of absolute and global fit. Thus, comparisons between models in the MI framework would be based on values of various information criteria (Kim et al., 2017). This does not fit our requirement of having the ability to formally test expected group differences nor is it widely available.

The second option is based on a suggestion of creating subgroups of missing data patterns within a single large data set and using these in MCFA (e.g., Duncan et al., 1998; Graham et al., 1995). The factor score based on these subgroups are estimated with all parameters of MVP constrained to be equal across groups. For the missing variables (which for each subgroup can be considered MVMC), most parameters are constrained to 0, with exception of the residual variance, which is constrained to 1. This is an elegant solution limited in applicability by the fact that the only program that is capable of handling MVMC in MI modeling automatically is EQS.

This leaves the final option of manually computing random normal deviates for MVMC as the most accessible option for applied researchers. Generating random normal deviates circumvents the missing data problem, because, after the procedure, all participants will have a value for each MVMC. This approach has two steps (see Widaman et al., 2013 for more details). First, for all participants in a group with MVMC, random normal deviates are sampled from a normally distributed population (i.e., M = 0 and SD = 1). The addition of the random normal deviates has the assumption of not adding information to the parameter estimates of the MCFA beyond the information provided by the MVP. This is because in the population the mean of a random variable would be 0, its variance would approach unity (i.e., 1), and it would not be correlated to any other variable (i.e., r = 0). These expectations form the basis of Step 2. This step involves respecifying the MCFA model according to the the population characteristics of these random normal deviates. This includes fixing all factor loadings for MVMC to zero, and freely estimate intercepts, factor variances, and covariances of the residual variances of MVMC with those of all MVP with no group constraints. These additional model respecifications lead to a model with equal degrees of freedom to a model that only includes MVP. This is because the number of sample statistics (i.e., means, covariances, and variances) of the MVMC is equal to the number of parameter estimates associated with MVMC. Therefore, adding MVMC to a MCFA model provides no additional information or changes in degrees of freedom to a MCFA. In their demonstration article, Widaman et al. (2013) showed the outcomes from this option were identical to those generated by the MCFA in EQS and pattern mixture models with known groups. Additionally, they showed outcomes of models with generated random normal deviates had little to no bias in their results, even if MVP had incidental missing data. This final option has several potential benefits for researchers wanting to combine data sets. First, both steps, generating random values and respecifying model parameters, can be done in a variety of software programs making this an accessible option. Second, using MVMC enables researchers to include all available data and get results with minimal to no bias. This is important especially when some data sets have limited overlap in MVP.

Quantifying Magnitude of Invariance

Traditional MI methods are highly influenced by sample size. In a large sample, the power to detect statistically significant difference on parameters of interest between two or more groups can result in rejecting models even if the difference between them is very small. Researchers have come up with various ways to quantify the magnitude of these differences in order to help understand the impact of the noninvariance. These strategies include (a) providing effect sizes as well as significance values, so that the size of the difference can be evaluated for practical significance besides statistical significance; (b) bootstrapping confidence intervals for the difference parameters; and (c) estimating the number of individuals meaningfully affected in scores by the invariance.

In the past decade, several effect sizes to evaluate MI differences have been proposed (e.g., d_MACS, d_MACS-Signed, UDI₂, SDI₂, WSDI, and WUDI; Gunn et al., 2020; Meade, 2010; Nye & Drasgow, 2011; Nye et al., 2019). These effect sizes are all indications of a standardized difference between two groups for one specific indicator in a MCFA model. Each of the indices incorporates both factor loadings and intercepts to estimate the difference between the reference and focal group, and standardize the metric using a pooled standard deviation. Within the set of six effect sizes, there are three main differences. The first is a difference in the choice of standard deviations used for pooling (i.e., d_MACS and d_MACS-Signed use the standard deviation for both groups, and UDI₂ and SDI₂ use the standard deviation of the focal group only). A second difference lies in the ability of the index to capture the direction of the effect and possible cancellations (i.e., d_MACS, UDI₂, and WUDI are squared effect sizes incapable of showing which group is higher or lower, and affected by opposite effects that cancel out. Conversely, d_MACS-Signed, UDI₂, and WUDI are not squared). The last difference is that these effect size differ in their choice of reference group (i.e., WSDI and WUDI compare the focal group to a single-group model, whereas the other effect sizes compare two groups from the MCFA). All effect sizes can, in theory, be calculated between multiple groups by changing the reference group and making separate estimates for each comparison. In situations with a large number of groups, this approach would lead to a high number of individual calculations, and a considerable burden on the researcher.

A second approach to indicate the magnitude of difference between groups separates out effects for factor loadings and intercepts. For example, Cheung and Lau (2012) propose a bias-corrected bootstrap method to obtain confidence intervals around each parameter difference that will aid in determining which differences are statistically significant. Finally, in their approach to quantify the impact of the difference, Millsap and Olivera-Aguilar (2012) use this difference between the reference and focal group to estimate the effect of noninvariance on factor scores. Unlike effect sizes, however, they do not estimate one score to indicate this difference. Instead, they identify those cases within the sample for which the difference score would fall outside a predetermined meaningful range. If the expected number of cases falling outside of this range is low, the factor loading difference can be considered negligible and ignorable, because it affects only a small subset of the total sample. For intercept differences, the proportion of variance in mean differences across groups due to the intercept differences can be calculated. Again, if the proportion is deemed relatively small, the intercept differences may be ignored. A downside to this approach to determine the impact of invariance is the freedom of the researcher to indicate what is acceptable. Additionally, Millsap and Olivera-Aguilar demonstrated these approaches for two group situations only.

Assessing Small Differences

Besides effect size methods, researchers have a second option to deal with problems due to an excess of power in large samples. This option is to change the specification of the null hypothesis. Traditional hypothesis testing in MCFA assumes there is no difference between two models. The idea that two models, or two populations, are never exactly the same and that increased precision in parameter estimates due to sample size hinders the interpretation of null hypothesis testing had been first posed by Meehl (1967). As a solution to this problem, Serlin and Lapsley (1985) proposed the good-enough principle. Within this approach, researchers specify a range within which the true value of a parameter should lie. This combats the problem of large sample sizes. Three current approaches for MI are based on this approximation of invariance, with two focusing on small differences in specific parameters (i.e., Bayesian approximate MI testing [BAMI] and the alignment method [AM]), and the third focusing on small differences in global model fit (hereafter called the root mean square error of approximation [RMSEA] good-enough principle).

The first approach, BAMI (Van De Schoot et al., 2013), uses Bayesian structural equation modeling as its basis. The main difference between “traditional” MI testing and BAMI is that BAMI allows for constraints on parameters to be approximately zero, instead of exactly zero (Van De Schoot et al., 2013). By specifying the prior distribution on the difference between parameters to have a small variance around zero, models with small differences on those parameters will still fit adequately. BAMI reduces the trade-off between model fit and equality of parameters (Van De Schoot et al., 2013). BAMI has several downsides that make it less suitable for our purposes. First, BAMI seems ideal for small noninvariance across a large number of items, but less suited for partial invariance models. Furthermore, while the approximation method circumvents the null-hypothesis dilemma, priors also have decreasing impact on parameter estimation as sample sizes increase. Finally, Bayesian models can be computationally intensive, and execution time increases with larger samples and models (Kim et al., 2017).

A second approach that is less sensitive to sample size and explicitly suitable to accommodate multiple groups is the AM (Asparouhov & Muthén, 2014). The AM can be used both with Bayesian and maximum likelihood estimation and works similarly to the rotation option of exploratory factor analysis (EFA). First, a configural model is estimated, with free factor loadings and intercepts. Then the alignment occurs to minimize the amount of noninvariance. Like in EFA, this method does not compromise on the fit of the model. As a final step, researchers can estimate which (sub)groups in their sample are invariant from each other on a specific parameter. The AM can be used both as a way to analyze measurement invariance and as an exploratory step to determine which items in a data set are invariant to simplify later MCFA models (Asparouhov & Muthén, 2014). Recent research has extended the AM (Asparouhov & Muthén, 2014) to be able to include different sets of items and item response options across data sets (Mansolf et al., 2020). While this extension has opened up the AM to researchers dealing with disparate items across data sets, it has not yet been shown to work for test level data. It is still unclear if the AM is suitable for researchers dealing with MVMC. In addition, the creators of the extension made custom changes to the AM in R, and the method may not be feasible to implement for educational researchers without heavy coding and statistical backgrounds.

The final approach focusing on assessing small differences works from the alternative hypothesis for MCFA based on the good-enough principle and states that the difference between two models is very small (MacCallum et al., 2006). Each researcher will need to explicitly state the range of difference between the two models that they consider good enough. Testing if the difference between two models lies within this range diverges from typical procedures in only one way: the critical value of the obtained chi-square statistic is based on a noncentral distribution instead of a central chi-square distribution. This noncentral distribution is characterized by the difference in degrees of freedom of the two models and a noncentrality parameter. The noncentrality parameter, in turn, is a product of the sample size and the prespecified difference the researcher considers to be good enough. MacCallum et al. (2006) propose to base the difference on values of the RMSEA index of goodness of fit, an index Browne and Cudeck (1993) had previously proposed to represent close (or good enough) fit of an observed model to the population. We believe the RMSEA good enough principle approach provides a better solution than the effect size methods, since it allows for the use of inferential tests of measurement invariance and not negatively influenced by large sample sizes. Moreover, in contrast to the AM the RMSEA good enough principle approach can be easily combined with computing random normal deviates to overcome MVMC, making it a more feasible option for applied researchers using test level data. Additionally, the RMSEA good enough principle approach uses maximum likelihood estimation, making it computationally faster than BAMI. It can also be used for models with higher levels of partial invariance as opposed to BAMI which is more suited to detect small invariance across many items (Kim et al., 2017).

Specifically, with the RMSEA good enough principle researchers test the null hypothesis that the difference in model fit is equal or smaller to a predetermined acceptable difference: ${\mathit{H}}_0:({\mathit{F}}_{\mathit{A}}^{*}-F_{\mathit{B}}^{*})\le {\mathit{\delta }}^{*}$ , where F is the sample value of a model’s discrepancy function. The acceptable difference is usually defined as ${\mathit{\delta }}^{*}=({\mathit{d}}_{\mathit{A}}{\mathit{\epsilon }}_{\mathit{A}}^2-{\mathit{d}}_{\mathit{B}}{\mathit{\epsilon }}_{\mathit{B}}^2)$ , where d is the degrees of freedom of a model, and $\mathit{\epsilon }$ a prespecified RMSEA value. Then, the critical value for model comparison is determined based on a noncentral ${\mathit{\chi }}^2$ distribution with degrees of freedom ${\mathit{d}}_{\mathit{A}}-{\mathit{d}}_{\mathit{B}}$ , a noncentrality parameter of $\mathit{\lambda }=(\mathit{N}-1){\mathit{\delta }}^{*}$ , and $\mathit{\alpha }=0.05$ . Finally, the sample value of the sample’s central ${\mathit{\chi }}^2$ distribution is compared with this adjusted critical value. If the sample value of a model comparison exceeds the adjusted critical value, the hypothesis of a small difference in model fit is rejected. Of considerable importance to note is that the choice of values for ${\mathit{\epsilon }}_{\mathit{A}}$ and ${\mathit{\epsilon }}_{\mathit{B}}$ is up to the researcher. To date, no set of agreed-on recommendations exist; however, MacCallum et al. (2006) use values of 0.6 and 0.5 to represent a small difference in fit between models. Equally of note is that, within a MI study, the actual values of ${\mathit{\delta }}^{*}$ and consequently $\mathit{\lambda }$ will change for each model comparison, because the degrees of freedom for at least one of the models changes. These values will need to be calculated separately for each comparison in order to make valid inferences.

Purpose

Our aim is to provide applied researchers with a feasible and efficient procedure to combine multiple data sets (i.e., more than two) containing total scores from achievement measures into one integrated set with a large sample. In this article, we will demonstrate our preferred approach, the RMSEA good enough approach, to estimate MI in a MCFA framework, that provides a solution to all three challenges mentioned above (i.e., be able to handle the differences in the number of measures across groups, be able to deal with excess of power due to sample size, and be able to formally test expected group differences with three or more data samples). To deal with differing patterns of measures used across samples, we first use Widaman et al.’ s (2013) recommendation to generate random normal deviates to deal with MVMC. Then, to ensure models are not rejected due to an excess of power from large samples while still using inference testing, we estimate MCFA models and compare models using the RMSEA good enough principle following MacCallum et al.’ s (2006) guidelines specified above. Finally, to free model parameters across groups, we use traditional methods of inspecting modification indices. After demonstrating the method, we will show the factor scores obtained with this approach correlate highly with those obtained with a traditional no difference model comparison approach.

Method

Our current demonstration uses eight different data sets. We begin by describing the reading measures available to use in our latent reading model and provide a short description of each of the study samples. We go on to describe the EFA procedure used and how we handled the problem of having different sets of measures across groups. Finally, we describe the RMSEA good enough principle approach we employed to investigate measurement invariance across the eight groups. All data analyses were conducted in R (R Core Team, 2020) version 4.0.2, using the lavaan (Rosseel, 2012), semTools (Jorgensen et al., 2020), and psych (Revelle, 2020) packages. Code for all analyses are openly available at https://osf.io/gps35/.

Measures

Each of the eight projects used a different set of standardized reading assessments to examine the initial status and progress of participants. From the wide set available, we choose a subset of five assessments used across most of the projects that represent several aspects of reading skills to estimate a latent reading score. These include four subtests of the Woodcock–Johnson Tests of Achievement (i.e., Letter word Identification subtest [LWID], Word Attack subtest [WA], Picture Vocabulary subtest [PV], and Passage Comprehension subtest [PC]; Woodcock et al., 2001) and the Print Knowledge subtest of the Test of Preschool Early Literacy (TOPEL; Lonigan et al., 2007). Participants in the projects were assessed at multiple timepoint in a year, but for this demonstration we used total scores at the beginning of the year only. Table 1 indicates which of these five measures were included in each project.

Table 1.

Overview of Manifest Variables Across Projects.

Project	N	WJ-LWID	WJ-WA	WJ-PV	WJ-PC	TOPEL-PK
Project 1	481	X	X	X	X	X
Project 2	386	X	–	X	–	X
Project 3	248	X	X	X	X	–
Project 4	603	X	X	X	X	–
Project 5	296	X	X	X	X	–
Project 6	360	X	X	X	X	–
Project 7	269	X	X	X	X	–
Project 8	283	X	–	X	X	–

Note. WJ = Woodcock–Johnson-III Test of Achievement; LWID = Letter word Identification subtest; WA = Word Attack subtest; PV = Picture Vocabulary subtest; PC = Passage Comprehension subtest; TOPEL = Test of Preschool Early Literacy; PK = Print Knowledge subtest. X = manifest variable present; — = manifest variable missing completely

WJ-LWID

The LWID subtest of the WJ-III (Woodcock et al., 2007) consists of 78 letters and sight words. This subtest taps into students’ ability to recognize words and is untimed. Test–retest reliability estimates range between .90 and .96 and split half reliability estimates range between .88 and .99 (McGrew et al., 2007).

WJ-WA

The WA subtest of the WJ-III (Woodcock et al., 2007) consists of 45 nonsense words of increasing difficulty. This subtest taps into participants’ ability to apply phonics rules and structural analysis and is untimed. One-year test–retest reliability estimates range from .63 to .81 and split half reliability estimates range from .78 to .94 (McGrew et al., 2007).

WJ-PV

The PV subtest of the WJ-III (Woodcock et al., 2007) consists of pictured objects and measures oral language development and expressive vocabulary. Split half reliability ranges from .70 to .93 (McGrew et al., 2007).

WJ-PC

The PC subtest of the WJ-III (Woodcock et al., 2007) consists of several passages ranging from one sentence to short paragraphs. One word in these passages is replaced with a blank. Participants are asked to read the passage and provide a word that would fit in the blank. To be able to supply the correct words, participants need to read and comprehend most of each passage, and no word bank is provided. Alternate form reliability estimates range between .84 to .96 and split-half reliability estimates range from .73 to .96 (McGrew et al., 2007).

TOPEL-PK

The PK subtest of the TOPEL (Lonigan et al., 2007) consists of 36 items related to alphabet knowledge and knowledge about written language conventions. Items increase in difficulty and range from identifying which picture has a word in it, to naming the sound of a specific letter. The internal consistency of the TOPEL-PK is reported at $\alpha =.96$ (Lonigan et al., 2007).

Description of Data Sample

All data sets came from reading intervention projects conducted between 2005 and 2013 in schools in a southeastern state. All original data protocols were made available through Project KIDS (Daucourt et al., 2018) to the authors and reentered at the item level. During reentry, adjustments were made to the original samples to ensure none of the participants were present in more than one data set, as the participants were mostly drawn from the same local schools. Thus, the sample sizes from the originally published studies will vary. First, we provide brief descriptions of the interventions and the samples, based on the adjusted numbers.

Project 1

Data Set 1 came from an iteration of the individualizing student instruction (ISI; Connor et al., 2007; Connor et al., 2009) intervention. The ISI intervention project had two main features, (a) a software program through which recommended amounts of instruction for each student was calculated based on student language and reading data, and (b) extensive professional development for teachers to learn how to use the software and adapt instruction accordingly (Al Otaiba et al., 2011). In this iteration, ISI was extended down from first grade to kindergarten students and their teachers. The sample consists of 481 students in 44 classrooms, 209 students received regular instruction and 272 students received ISI. To assess students’ reading abilities, researchers administered the TOPEL, the Test of Silent Reading Efficiency and Comprehension (TOSREC), and the Test of Language Development (TOLD) at the beginning of the year; the Comprehensive Test of Phonological Processes (CTOPP) blending and elision subtasks at the beginning and end of the year; and the WJ-III Academic Knowledge (AK), LWID, PC, PV, and WA subtests at 3 time points per year.

Project 2

Similar to Project 1, Data Set 2 also came from a Kindergarten iteration of the ISI intervention study. This sample consists of 386 students in 34 classrooms, 187 in the control condition and 199 in the treatment condition. Details about this study are specified in Al Otaiba et al. (2016). To assess students’ reading abilities, researchers administered the TOPEL and the TOLD at the beginning of the year; the CTOPP blending and elision subtasks at the beginning and end of the year; and the WJ-III AK, LWID, PC, and PV, subtests at 3 time points per year. Additionally, students finished the WA in winter and spring.

Project 3

Data Set 3 was taken from another study that used the first grade ISI intervention, and in which two types of response to intervention (RTI) models were compared. In the traditional model, students complete a cycle of classroom instruction only before being assessed and receiving supplemental intervention. In the dynamic model, students were immediately placed into intervention, if pretest scores indicated at-risk status. See for more details Al Otaiba et al. (2014). In this study, 248 students in 34 classrooms participated. Ninety-seven students were enrolled in the typical RTI condition and 151 in the dynamic RTI condition. Students were administered the CTOPP and WJ-III AK in fall, the TOLD and WJ-III WA in fall and spring, the TOSREC in spring, and the WJ-III LWID, PC, and PV in fall, winter, and spring.

Project 4

Data Set 4 came from the first iteration of the ISI. Details about this study are detailed in Connor et al. (2007). The project consisted of 603 first-grade students from 53 classrooms of which 303 were in the ISI condition and 300 in the no intervention control condition. All participants were assessed in the fall, winter, and spring on their reading skills with the WJ-III LW-ID, PV, WA, WF, SA, AK, and PC subtests.

Project 5

Set 5 also included data from the ISI intervention. This was the second iteration of this project (see for details Connor, Morrison, Schatschneider, et al., 2011), and included 296 first-grade participants from 26 teachers, 192 treatment, and 104 control. As in the previous iteration, participants were assessed on their reading abilities at three timepoints throughout the school year using the WJ-III LW-ID, PV, and PC subtests. The WA, WF, SA, and AK subtests were only administered at the beginning and end of the school year.

Project 6

Data Set 6 was taken from an ISI intervention study where this intervention was compared with a vocabulary intervention condition. This study included 360 second grade participants from 40 classrooms; 143 students received the vocabulary instruction and 217 the ISI intervention. Data from this study have not been published in peer-review journal articles previously. All students were administered the WJ-II LWID, AK, PC, PV, SA, and WA subtests at in fall, winter, and spring.

Project 7

Data Set 7 included data from an extension project using the ISI intervention and the vocabulary intervention conducted in third grade (see Connor, Morrison, Fishman, et al., 2011 for details). Data from this project included 269 third-grade students in 31 classrooms; 126 students received the vocabulary intervention and 143 students received the ISI intervention. As in the aforementioned iteration of ISI, participants were assessed on their reading abilities at three timepoints throughout the school year using the WJ-III LW-ID, PV, and PC subtests. The WA, WF, SR, and AK subtests were only administered at the beginning and end of the school year.

Project 8

Data Set 8 included data from a 3-year longitudinal study of the ISI intervention. Students in this sample were followed in first through third grade, and each year received either the ISI intervention or a math intervention (see Connor et al., 2013 for details). For the current study, we only used data from first grade. This included data on 283 students, 211 of which received the reading intervention and 172 received math intervention. Students attended 29 classrooms. Similar to the above-mentioned studies on ISI, students were assessed on their reading abilities at 3 time points per year using the WJ-III LWID, AK, PV, and PC subtests.

Establishing Factor Structure

Before checking for measurement invariance, we established the factor structure of the five measures using EFA. We first used stratified random sampling to select 25% from the original sample to use for the EFA, with each project considered a stratum. With this hold out sample, we estimated the number of factors to extract using the parallel analysis (Horn, 1965). In parallel analysis, the eigenvalues of principal components based on data are compared against eigen values based on random data matrices. Components are counted if the eigen values of the original data are greater than those of the simulated values. We used the fa.parallel function in the psych package in R to perform the parallel analysis, with maximum likelihood as the factoring method. After establishing the factor structure, we estimated the unrotated EFA using the semTools package, using robust maximum likelihood. To determine the fitness of each indicator for the latent factor, we examined if the standardized factor loading exceeded the threshold of 0.3. Note that the EFA was conducted with the sample as one, so MVMC did not pose a problem here. Also, since we expected unidimensionality, rotation was not needed.

Creating Random Normal Deviates

Our next step was to create random normal deviates for all MVMC, separately for each project. We considered variables with more than 95% missing values to be MVMC. Table 1 shows the distribution of MVP and MVMC across all projects. As laid out in Widaman et al. (2013), random normal deviates are sampled from a normally distributed population with M = 0 and SD = 1. We examined the mean and standard deviation of the generated values, as well as their correlation with other variables, which is expected to be r = 0.

Establishing Measurement Invariance

To establish invariance, we employed the free-baseline approach (Stark et al., 2006), increasingly posing constraints on models to examine (a) configural invariance, (b) weak or metric invariance, and (c) strong or scalar invariance. Configural invariance indicates that the same number of factors are representative for each group and that the same variables define these factors (Millsap & Olivera-Aguilar, 2012). Weak or metric invariance holds when factor loadings are invariant across groups, and strong or scalar invariance is confirmed when intercepts are invariant across groups (Millsap & Olivera-Aguilar, 2012; Widaman et al., 2013). In case invariance was rejected, we established partial invariance models. We used the modification indices to determine which parameter constraints to set free. Because our MCFA model included eight projects, we released constraints within indicators two projects at a time. For example, when releasing the equality constraint for WJ-PV Projects 1 and 2, the remaining projects (i.e., 3-8) were still estimated as having the same parameter value. Finally, following the methods detailed by Widaman et al. (2013), we made the following general adaptations to the MCFA models. First, all factor loading for MVMC were constrained to zero. Second, intercepts for MVMC were always freely estimated. Third, the residual variances of MVMC were allowed to covary with those of all MVP.

We only considered goodness of fit for the configural models. Due to our large sample, we disregarded the test statistic based on the ${\chi }^2$ distribution. Additionally, because both RMSEA and Tucker–Lewis index (TLI) fit statistics are penalized for MCFA, we considered model fit to be adequate with comparative fit index (CFI) at or greater than 0.95 and standardized root mean square residual (SRMR) at or less than 0.08 (Hu & Bentler, 1999). To compare models, we employed the RMSEA good enough principle as explained above and demonstrated by MacCallum et al. (2006). In this demonstration, we choose ${\mathit{\epsilon }}_{\mathit{A}}$ and ${\mathit{\epsilon }}_{\mathit{B}}$ values of 0.6 and 0.5 to represent a small difference in fit between models as per MacCallum et al. (2006).

Results

Factor Structure

To establish the factor structure of latent reading ability, we first determined the number of factors using the parallel test in the psych (Revelle, 2020) package in R (R Core Team, 2020) with the hold-out sample of 25%. Results indicated a single factor underlying latent reading ability. We then estimated an EFA using the semTools (Jorgensen et al., 2020) package. The results clearly supported the one-factor solution. The model fit the data well: ${\chi }^2\left(5\right)=13.413$ , $p=.02$ , RMSEA = 0.10, CFI = 0.99, TLI = 0.96, SRMR = 0.04. Additionally, the factor loadings indicated that all assessments had statistically significant factor loadings with slight differences in the relation to the underlying reading factor (see Table 2 for all estimates of the EFA).

Table 2.

Results of One-Factor Exploratory Factor Analysis for Five Reading Assessments.

Indicator	b	SE	p	B
WJ-LWID	4.89	0.41	<.001 ***	0.96
WJ-WA	1.24	0.12	<.001 ***	0.79
WJ-PV	1.72	0.29	<.001 ***	0.51
WJ-PC	1.22	0.31	<.001 ***	0.57
TOPEL-PK	6.45	0.73	<.001 ***	0.77

Note. b = unstandardized factor loading. B = standardized factor loading. WJ = Woodcock–Johnson-III Test of Achievement; LWID = Letter word Identification subtest; WA = Word Attack subtest; PV = Picture Vocabulary subtest; PC = Passage Comprehension subtest; TOPEL = Test of Preschool Early Literacy; PK = Print Knowledge subtest.

^***p < .001.

Random Normal Deviates

To handle the MVMC, we generated random normal deviates per group. In order for the MVMC to not affect model-based estimates, means of MVMC must approach 0, variances of MVMC must approach unity (i.e., 1), and correlations with MVP should be zero. Descriptive statistics of all manifest variables and their correlations are presented in Table 3 and show the generated MVMC performed as expected.

Table 3.

Correlations of Variables.

Data set	Indicator	n	M	SD	WJ-LWID	WJ-WA	WJ-PV	WJ-PC	TOPEL-PK
Data set 1	WJ-LWID	470	12.37	5.60	1.00
	WJ-WA	456	2.87	2.41	0.74	1.00
	WJ-PV	470	16.30	3.13	0.42	0.29	1.00
	WJ-PC	453	5.54	2.67	0.59	0.64	0.22	1.00
	TOPEL-PK	446	30.74	6.74	0.58	0.40	0.42	0.21	1.00
Data set 2	WJ-LWID	381	11.98	5.85	1.00
	WJ-WA	386	0.09	1.00	0.06	1.00
	WJ-PV	382	16.02	3.22	0.49	0.07	1.00
	WJ-PC	386	0.01	1.00	0.06	0.03	0.02	1.00
	TOPEL-PK	351	29.32	8.31	0.62	0.08	0.40	0.02	1.00
Data set 3	WJ-LWID	246	26.47	9.22	1.00
	WJ-WA	245	9.48	6.16	0.85	1.00
	WJ-PV	244	19.20	3.34	0.47	0.50	1.00
	WJ-PC	247	12.11	6.15	0.89	0.81	0.50	1.00
	TOPEL-PK	248	0.01	1.03	−0.09	−0.04	−0.02	−0.07	1.00
Data set 4	WJ-LWID	551	24.00	7.63	1.00
	WJ-WA	298	9.40	4.69	0.73	1.00
	WJ-PV	567	18.49	3.06	0.42	0.37	1.00
	WJ-PC	450	14.42	5.15	0.79	0.65	0.40	1.00
	TOPEL-PK	603	−0.02	1.03	−0.08	0.04	−0.06	−0.06	1.00
Data set 5	WJ-LWID	292	26.17	8.10	1.00
	WJ-WA	173	10.96	5.10	0.74	1.00
	WJ-PV	292	19.10	2.67	0.34	0.26	1.00
	WJ-PC	195	13.99	5.75	0.86	0.66	0.39	1.00
	TOPEL-PK	296	−0.01	1.06	−0.07	−0.01	−0.06	−0.04	1.00
Data set 6	WJ-LWID	347	40.50	8.03	1.00
	WJ-WA	188	18.39	6.02	0.78	1.00
	WJ-PV	345	20.64	3.32	0.46	0.37	1.00
	WJ-PC	332	22.53	4.32	0.76	0.68	0.57	1.00
	TOPEL-PK	360	−0.07	0.99	0.03	0.02	−0.03	−0.09	1.00
Data set 7	WJ-LWID	252	46.15	6.87	1.00
	WJ-WA	234	20.77	5.70	0.73	1.00
	WJ-PV	253	21.92	3.22	0.50	0.23	1.00
	WJ-PC	253	23.76	4.05	0.67	0.49	0.60	1.00
	TOPEL-PK	269	−0.16	1.01	0.04	0.03	0.08	0.04	1.00
Data set 8	WJ-LWID	366	27.24	7.45	1.00
	WJ-WA	384	−0.06	1.01	−0.06	1.00
	WJ-PV	368	19.25	19.00	0.30	−0.03	1.00
	WJ-PC	384	12.63	12.00	0.84	−0.03	0.32	1.00
	TOPEL-PK	346	0.08	0.06	−0.02	0.01	0.03	0.01	1.00

Note. Correlations with manifest variables missing completely (MVMC) are in boldface. WJ = Woodcock–Johnson-III Test of Achievement; LWID = Letter Word Identification subtest; WA= Word Attack subtest; PV = Picture Vocabulary subtest; PC = Passage Comprehension subtest; TOPEL = Test of Preschool Early Literacy; PK = Print Knowledge subtest.

Measurement Invariance

In the next step, we followed the free baseline approach to check for measurement invariance across all groups, using the RMSEA good enough approach for model comparisons. We first fit the configural model, which showed adequate fit: ${\chi }^2\left(15\right)=185.902$ , $p<.001$ , RMSEA = 0.17, CFI = 0.96, TLI = 0.81, SRMR = 0.02. ¹ We then constrained the factor loadings of all MVP to be equal, while leaving the loadings of MVMC constrained to zero. Model fit decreased slightly: ${\chi }^2\left(35\right)=410.697$ , $p<.001$ , RMSEA = 0.17, CFI = 0.92, TLI = 0.82, SRMR = 0.08. Using the traditional null hypothesis test, this model would have been rejected, $\mathrm{\Delta }{\chi }^2\left(20\right)=224.794$ , $p<.001$ . We proceeded by comparing this sample value of the test statistic to the critical value based on the noncentrality parameter. We first calculated the small difference between the models with ${\delta }^{*}=(d_A{\epsilon }_A^2-d_B{\epsilon }_B^2)$ = (35 * 0.06²) − (15 * 0.05²) = 0.089. Our adjusted null hypothesis can be expressed as $H_0:(F_A^{*}-F_B^{*})\le 0.089$ . The reference distribution is the noncentral ${\chi }^2$ distribution with 35-15 = 20 degrees of freedom and the noncentrality parameter $\lambda =(N-1){\delta }^{*}$ = (3027-1)*0.089 = 267.80. Using $\alpha =0.05$ , the corresponding critical value for the discrepancy statistic is 344.269. Since the sample value of the test statistic was below the critical value of the noncentral distribution, the weak invariance model was retained.

We then proceeded to test for strong invariance by constraining the intercepts of the MVP to be equal to each other, while freely estimating the intercepts of the MVMC. This model did not fit the data at all: ${\chi }^2\left(61\right)=3766.49,$ $p<.001$ , RMSEA = 0.40, CFI = 0.21, TLI = − 0.03, SRMR = 1.5. Unsurprisingly, this model could not be considered equal to the weak invariance model: $\mathrm{\Delta }{\chi }^2\left(26\right)=3355.793$ , $p<.001$ , using the traditional null hypothesis of no difference. We proceeded to test the hypothesis of small difference between the models: $H_0:(F_A^{*}-F_B^{*})\le d^{*}$ , with ${\delta }^{*}=(d_A{\epsilon }_A^2-d_B{\epsilon }_B^2)$ = (61 * 0.06²) − (35 * 0.05²) = 0.132. The critical value of the reference distribution of a noncentral ${\chi }^2$ distribution with 26 degrees of freedom, noncentrality parameter $\lambda =(N-1){\delta }^{*}$ = (3027-1) * 0.132 = 399.735, and $\alpha =0.05$ was 494.216. The sample statistic exceeded this adjusted critical value, indicating the hypothesis of a small difference between the two models was rejected.

We then proceeded to attempt to establish partial strong variance, by fitting a series of increasingly relaxed models. The choice of releasing specific equality constraints were made by inspecting the modification indices established by the Lagrange multiplier test. For each of the subsequent models, we released the equality constraint for two groups that would yield the largest decrease in sample test statistic. The final partial strong model included only two sets of constraints on two of the indicators, Projects 4 and 5 on LWID, and Projects 3, 4, 5, and 7 on PC. While the fit of the model was not ideal ${\chi }^2\left(40\right)=610.11,$ $p<.001$ , RMSEA = 0.19, CFI = 0.88, TLI = 0.76, SRMR = 0.10, it passed the test of small difference. $H_0:(F_A^{*}-F_B^{*})\le d^{*}$ , with ${\delta }^{*}=(d_A{\epsilon }_A^2-d_B{\epsilon }_B^2)$ = (40 * 0.06²) − (35 * 0.05²) = 0.057. The critical value of the reference distribution of a noncentral ${\chi }^2$ distribution with 5 degrees of freedom, noncentrality parameter $\lambda =(N-1){\delta }^{*}$ = (3027-1) * 0.057 = 170.97, and $\alpha =0.05$ was 220.934. The sample statistic $\mathrm{\Delta }{\chi }^2\left(5\right)=199.409$ , $p<.001$ was lower than this adjusted critical value, indicating the hypothesis of a small difference between the two models should not be rejected. The composite reliability estimates for the factor scores based on partial strong invariance ranged from .74 to .95, providing additional evidence of unidimensionality of the construct across groups (see Table 4).

Table 4.

Composite Reliability Estimates of the Factor Scores for the Final Partial Strong Model.

Project	Composite reliability
Project 1	.75
Project 2	.74
Project 3	.95
Project 4	.91
Project 5	.93
Project 6	.86
Project 7	.85
Project 8	.91

Finally, we correlated the factor scores obtained with the strong partial invariance model based on the RMSEA good enough principle to factor scores of a weak partial invariance model estimated with traditional null hypothesis testing based on no difference. The Pearson correlation coefficient between the scores were high: $r=0.98$ , indicating factor scores generated after our RMSEA good enough principle are near equivalent to the factor scores from the traditional method. Using the RMSEA good enough principle, however, would be preferable, since scores of the participants can be considered to be on the same scale. Figure 1 shows a scatterplot of the factor scores.

Figure 1.

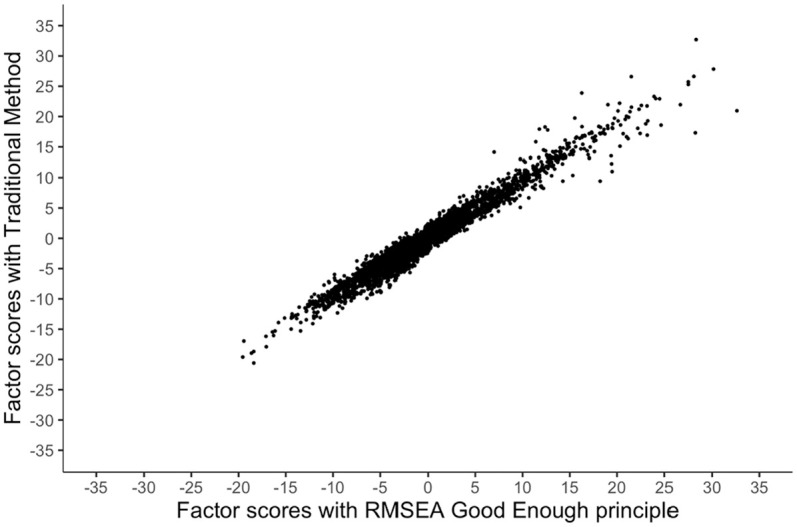
Scatterplot of factor scores.

Discussion

Data fusion is an emerging field with high utility for the educational sciences. Previous methods have demonstrated the success of integrating data sets at the item level, using MNLFA (Curran et al., 2008; Curran & Hussong, 2009) or IRT-based approaches (e.g., Marcoulides & Grimm, 2017). In this article, we demonstrated a combination of strategies to pool data sets from independent studies together at the test score level that deals with likely issues educational researchers will encounter in real life: differing patterns of measures missing completely across data sets and rejection of invariance based on large sample sizes. Our approach involved three phases: (a) establishing the factor structure with a hold-out sample, (b) generating random normal deviate values for MVMC, and (c) testing for measurement invariance using the RMSEA good enough principle based on the hypothesis that two models will differ slightly in fit. The methods can be applied in a variety of commercially available statistical software and are relatively straightforward to implement. Additionally, the approach can be extended to include different patterns of MVMC and an unlimited range of data sets. As such, it presents a workable and flexible way for researchers to generate large samples without having to expend additional precious resources.

The outcome of our demonstration underscores the point made by MacCallum et al. (2006) that the discrepancy in decisions on model equivalency based on tests of no difference and tests of small differences emphasizes the value of using the alternative approach. In our case, the initial rejection of no difference was not convincing, since the RMSEA good enough principle approach provided evidence of only small difference. Had both approaches led to rejection of their respective null-hypothesis, evidence of difference would be clear. It is possible that other data sets might even show only a small difference for strong invariance, while the test for no difference in weak invariance is rejected.

This article highlights the utility of our approach in two ways. First, the correlation between factor scores of the partial weak invariance model based on the traditional method and the factor scores of the partial strong invariance model based on the RMSEA good enough principle was r = 0.98. However, anchoring participants’ scores to a common metric by establishing strong invariance is essential if researchers plan to use these scores in subsequent analyses. Our approach allows for these types of analyses without losing integrity of the factor scores.

Second, our approach is considerably less intensive than other current methods. For example, while our approach does not allow for modeling the influence of other covariates on sources of invariance beyond the projects themselves, possible for example with the MNLFA approach, we believe this not to be problematic when using highly standardized norm-referenced assessments. All the assessments in our demonstration had undergone extensive psychometric testing to reduce bias. Daucourt et al. (2018) previously showed the correlation between the total scores of the WJ-III LWID subtest and scaled scores based on MNLFA exceeded r = 0.97. Other approaches to data fusion have also regarded standardized norm-referenced assessments unbiased across groups (e.g., Marcoulides & Grimm, 2017). Researchers can save valuable time with our approach using the total scores instead of generating test-level factor scores using the individual items based on the MNLFA approach.

Previous researchers have indicated the need to make subjective decisions in most integrative data analysis applications (e.g., Curran et al., 2008). In that respect, our approach is no different. First, we followed the RMSEA values used by MacCallum et al. (2006) (i.e., RSMEA of 0.05 and 0.06) to establish the maximum acceptable difference between models. Currently, there are no guidelines for determining which RMSEA values researchers should use in measurement invariance models, but outcomes will likely differ when more liberal RMSEA values are chosen. Second, as with the traditional null hypothesis test of no-difference, it is unclear how to establish and interpret partial variance models. We used modification indices to release constraints for two groups at a time moving through the indicators guided by the data. Other approaches might include releasing one group at a time or establishing partial invariance one indicator at a time. Given the number of groups in our sample, there are many possible sources of variance; using the modification indices to specify the series of less constrained models may have led to misspecification of the final model (Asparouhov & Muthén, 2014) and was cumbersome. In our final model, only two variables were invariant across a small subset of groups (i.e., 2 and 4 groups), but applying other decision-making criteria may lead to a different final model.

Several questions still remain. First, it is unclear what the minimum proportion of MVP and MVMC within and across samples should be and how this influences factor scores. While Widaman et al. (2013) demonstrated the use of random normal deviates did not influence fit of the models, and our EFA on the hold-out sample confirmed uni-dimensionality, it is unclear if the factor scores are influenced by the MVMC. One possible influence lies in the reliability of the factor scores. For example, only two data sets in our demonstration included TOPEL scores, and we generated random normal deviates for the remaining six data sets. The composite reliability estimates for data sets without the TOPEL scores were much higher than those including TOPEL. It is possible this a result of having a large number of MVMC. It is also possible the TOPEL scores themselves influenced the reliability, suggesting TOPEL may not be a strong indicator of the latent reading construct. Reliability did not seem to be related to the number of MVMC within a data set.

Second, recent research has presented extensions to both the AM (Asparouhov & Muthén, 2014) and the MNLFA (Curran et al., 2014) for data fusion. Mansolf et al. (2020) demonstrated the AM could be modified to include disparate items across data sets. It is possible this method might be extended even further to test level models that include MVMC. McGrath et al. (2020) extended the MNLFA to include Likert-type responses, effectively using a moderated linear factor analysis. Broadening the use of a moderated linear factor analysis to test level data seems a second plausible avenue for educational researchers. Future research should determine if outcomes using our current approach or these plausible further extensions to both the AM and MNLFA approaches are meaningfully different, and if so, which approach (a) would yield the most reliable and valid integrated scores and (b) be feasible to conduct by applied educational researchers.

Conclusion

Many of the item-based methods for integrative data analysis may not be an option for researchers using data sets containing total scores from highly standardized assessments. On the other hand, traditional ML-CFAs may unnecessarily reject more constrained models when sample sizes are large. With this approach to pooling data sets from independent studies at the assessment score level, including estimating random normal deviates for MVMC and establishing invariance based on the good enough principle, we hope to broaden the use of integrative data analysis methods. Many high-quality data sets exist within the educational sphere that contributed to a relatively small portion of science. Pooling these data sets together will permit researchers to answer more complex research questions while optimizing the use of these (often costly) data. Additionally, pooling data sets allows researchers to replicate effects of an analysis directly across studies, increasing the generalizability of their findings.