Objective Detection of Eloquent Axonal Pathways to Minimize Postoperative Deficits in Pediatric Epilepsy Surgery using Diffusion Tractography and Convolutional Neural Networks

Abstract

Convolutional neural networks (CNNs) have recently been used in biomedical imaging applications with great success. In this paper, we investigated the classification performance of CNN models on diffusion weighted imaging (DWI) streamlines defined by functional MRI (fMRI) and electrical stimulation mapping (ESM). To learn a set of discriminative and interpretable features from the extremely unbalanced dataset, we evaluated different CNN architectures with multiple loss functions (e.g., focal loss and center loss) and a soft attention mechanism, and compared our models with current state-of-the-art methods. Through extensive experiments on streamlines collected from 70 healthy children and 70 children with focal epilepsy, we demonstrated that our deep CNN model with focal and central losses and soft attention outperforms all existing models in the literature and provides clinically acceptable accuracy (73−100%) for the objective detection of functionally-important white matter pathways including ESM determined eloquent areas such as primary motor, aphasia, speech arrest, auditory, and visual functions. The findings of this study encourage further investigations to determine if DWI-CNN analysis can serve as a noninvasive diagnostic tool during pediatric presurgical planning by estimating not only the location of essential cortices at the gyral level, but also the underlying fibers connecting these cortical areas, to minimize or predict postsurgical functional deficits. This study translates an advanced CNN model to clinical practice in the pediatric population where currently available approaches (e.g., ESM, fMRI) are suboptimal. The implementation will be released at https://github.com/HaotianMXu/Brain-fiber-classification-using-CNNs.

I. Introduction

THE principle of presurgical evaluation in epilepsy is to determine the relationships between the epileptogenic zone and the surrounding functionally important cortex, such as primary motor, language, auditory, and visual areas (“eloquent cortex”) [1]. Without accurate localization of such brain regions, one cannot achieve the ultimate goal of epilepsy surgery, which is to eliminate epileptic seizures without creating new functional deficits. The current gold standard method to identify eloquent cortex is direct electrical stimulation mapping (ESM) of brain function [2]. However, ESM is not an ideal method, since it requires implantation of invasive intracranial electrodes, carries the inherent risk of electrically-induced seizures, and sometimes fails to identify eloquent cortex, especially in children. For instance, our previous study [3] reported that a contralateral hand movement was not elicited by electrical stimulation in 15 of 65 children. The average age of children in this “no motor response group” was 3.4 years old, suggesting that younger patients are at risk for ESM failure when identifying motor functions. Also, of the 50 children with a contralateral hand movement elicited by electrical stimulation, 24 showed the motor hand area in the postcentral gyrus, and 17 children showed the hand area in both pre- and postcentral gyri, indicating that a substantial proportion of young patients with focal epilepsy had a prominent variation in the hand motor area between these two regions. Such variations are more prominent in lesional cases.

An alternative approach to ESM is functional MRI (fMRI) [4], [5], which is non-invasive but highly susceptible to movement artifacts and demands cooperative behavior during scanning. Thus, it is challenging to perform fMRI studies in young patients with epilepsy (success rate < 60% at age 4–6 years [6]). Furthermore, the epileptogenic zone frequently involves the bottom of a deep sulcus [5], [7], which is in close proximity to adjacent axonal pathways. Both ESM via subdural electrodes and fMRI are inherently unable to localize crucial subcortical white matter structures, which may therefore be at risk for damage during surgery. Thus, there is an urgent need in presurgical planning to accurately identify eloquent regions of interest including both cortical areas and white matter pathways to prevent postoperative deficits in children with intractable epilepsy.

The present study proposes a critical translational application of a diffusion weighted imaging (DWI) tractography method that may serve as an efficient noninvasive localizing tool supplementing, and in some cases replacing, fMRI and ESM in children with intractable epilepsy. In the last decade, DWI tractography has been a powerful technique to visualize whole brain white matter tracts with minimal patient cooperation [8], [9]. Many investigators have attempted to dissect the complicated tract patterns of DWI whole brain tractography by objectively recognizing their shape, length, and anatomical features within multiple frameworks, including virtual dissection based on expert knowledge [10], [11], clustering using fiber similarity measures [12], [13], [14], [15], atlas-based labeling and annotation [16], [17], [18], [19], and machine learning methods [20], [21]. These approaches apply a set of target models, including white matter atlases, exemplar streamlines, or other pre-defined anatomical information, to extract known pathways from whole brain tractography with two common objectives: to remove superficial or spurious tracts and to save effort in white matter dissection. All of the reported approaches differ methodologically and mixed outcomes have been reported depending on the employed tractography model, features, similarity measures, and data acquisition.

In contrast to previous studies, we focus on clinical validation of automatic white matter dissection by performing systemic comparisons of DWI tractography to detect electrophysiologically-confirmed eloquent white matter pathways in children. Such pathways are functionally relevant but challenging to label (or annotate) in the context of currently available large-scale white matter atlases. Herein, it should be noted that our fiber targets of interest (i.e., classes) are not the entire white matter fasciculi but functionally specific-white matter pathways, including (i) primary motor areas supporting movement of different body parts: face/finger/hand/leg, (ii) language areas at which stimulation elicited different types of symptoms: expressive aphasia/receptive aphasia/speech arrest, (iii) primary auditory area associated with stimulation-induced auditory hallucination, and (iv) visual areas associated with phosphene or perception of visual distortion. These individual pathways share similar tract shapes but have different locations of cortical terminals. For instance, fiber trajectories associated with each category of primary motor, language, and visual functions are very similar in pattern and geometry, making classification by current clustering methods difficult (e.g., see similar patterns of streamline exemplars (or centroids) presented in Fig. 1).

Fig. 1.

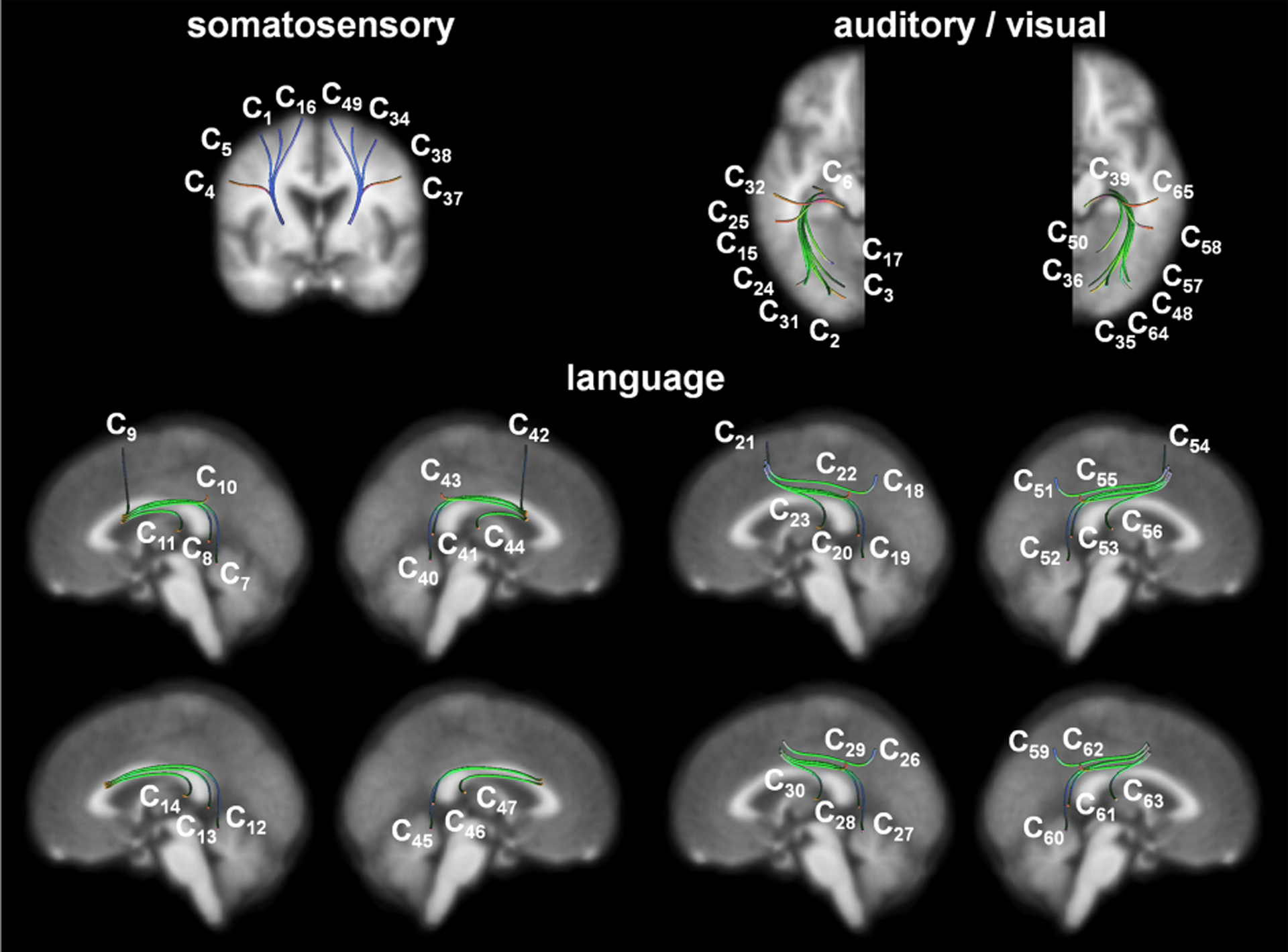
QuickBundles centroid streamlines of 64 functionally important white matter pathways of interest, C_i, are obtained from the healthy children group. QuickBundles distance threshold [13], [15] was set at 20 mm for each of 64 group-streamline clusters, C_i (n = 70).

Motivated by this limitation, our previous studies (DWI-MAP) [22], [23] proposed a Bayesian inference-based tract detection paradigm which can effectively discriminate subtle differences in tract location with minimal effort towards feature design. A major advantage of DWI-MAP is the simultaneous localization of functionally-important white matter and grey matter without using any supplementary acquisitions like fMRI and ESM. In addition, it does not require the patient to cooperate with a task, and can ultimately be extended to localize other important pathways of infants and young patients, in whom functional localization cannot be done using either fMRI or ESM (about 30% of surgical cases). However, DWI-MAP was designed to classify a given streamline into one of a limited number of target classes (i.e., six primary motor pathways including face, finger, and leg fibers in both hemispheres and five language pathways in left hemisphere), by computing the maximum posteriori probability of individual fiber streamlines with fMRI-derived white matter probability maps and equal class priori assumptions. In this paper, we investigate whether an end-to-end deep learning framework of DWI tractography without any priori information can effectively classify functionally-important white matter pathways for successful epilepsy surgery.

As one of the most powerful deep learning frameworks, convolutional neural networks (CNNs) have been widely used in biomedical imaging tasks with unknown priori distribution [20], [24], [21]. In this work, an off-line, retrospective IRB-approved study was conducted to investigate the detection capability of CNNs for 64 functionally-important white matter pathways that should be preserved in epilepsy surgery, including primary motor, language, auditory, and visual pathways. Compared to previous approaches, our key insight is that rather than first building a tract atlas based on priori information and then feeding the input into a statistical model, we can instead utilize CNNs to provide an end-to-end learning which integrates white matter pathway classification with direct representation learning without any priori distribution information [25]. From a computing perspective, the novelty of present work is as follows:

• Two CNN architectures with different depths were investigated in this study. The first is a shallow CNN model with 3 layers from our previous work [26]. Inspired by the success of very deep CNNs [27], we also adapted the shallow CNN into a deep model with 21 layers. The proposed CNN models generate different feature maps of the input data (i.e., 3D spatial coordinates of individual fiber streamlines) by using a sequence of convolutional and pooling layers before classifying input data using fully connected layers.

• Multiple CNN loss functions [28], [29] were employed for white matter pathway classification. First, since our dataset is highly unbalanced and cannot be handled well by CNNs with conventional cross-entropy loss, we applied focal loss [29] to train the proposed CNN models. Focal loss applies a modulating term to the cross-entropy loss to help focus on hard examples and down-weight the numerous easy ones. Second, to further improve the classification performance and generalization of the proposed CNN models, center loss [28] was employed, which adds a cluster-based loss term to the cross-entropy loss ensuring that the learned representations have both compact intra-class variations and large inter-class margins. That is, the learned fiber representation is not only separable but also discriminative.

• Although CNNs have led to breakthroughs in many applications, the end-to-end learning strategy makes the entire CNN model a “black box.” This weakness is particularly prominent in biomedical imaging: if we do not know how the trained CNNs classify each fiber, we cannot fully trust the classification results provided by the CNN models. In this study, we applied a soft attention mechanism [30] in the proposed CNNs, which highlights the most useful segments of a fiber for its classification. We demonstrated that the attention provides perspectives on how our CNNs classify white matter pathways.

A goal of the present study is to identify and evaluate a novel deep learning approach that achieves the highest accuracy and best interpretability in detecting eloquent white matter pathways of interest. This is a critical step toward minimizing postoperative deficits in pediatric epilepsy surgery. By intensive in vivo comparisons with current gold standard ESM, this study demonstrates that CNNs have high translational value, and that the concepts derived from them might increase localization accuracy of functionally important brain tissue and minimize risk of postoperative deficit.

The rest of the paper is organized as follows: Section II describes the details of our CNN models: the architecture, the loss functions for training, and the soft attention mechanism. Section III describes the setup and results of our CNN-based fiber classification experiments. Lastly, Section IV presents discussion, conclusion, and future applications of our models.

II. Methodology

A. Subjects

To construct training and test datasets of the proposed CNN-based fiber classification, 70 healthy children (age: 12.01 ± 4.80, 36 boys) were recruited for the present study. Also, 70 children with drug-resistant epilepsy who underwent presurgical workup for epilepsy between 2009 and 2017 were retrospectively selected for the validation dataset (age: 11.60±4.80 years, 36 males). Inclusion criteria were 1) drug-resistant epilepsy requiring two-stage epilepsy surgery with chronic subdural ESM mapping at the Children’s Hospital of Michigan or Harper University Hospital, 2) no motor and/or language impairment, and 3) MRI abnormalities, except massive brain malformation and other extensive lesions that likely destroyed the ipsilateral tracts and led to reorganization. Exclusion criteria were 1) history of prematurity or perinatal hypoxic-ischemic event, 2) hemiplegia on preoperative examination by pediatric neurologists, and 3) dysmorphic features suggestive of a clinical syndrome.

B. Data acquisition

All participants underwent DWI using a GE Signa 3T scanner with eight channel head coil at TR = 12500 ms, TE = 88.7 ms, FOV = 24 cm, 128 × 128 acquisition matrix (nominal resolution = 1.89 mm), contiguous 3 mm thickness in order to cover entire axial slices of whole brain using 55 isotropic gradient directions with b = 1000 s/mm², number of excitations = 1, and single b = 0 image. For anatomical reference, a three-dimensional fast spoiled gradient echo sequence (FSPGR) was applied to acquire T1-weighted image at TR/TE/TI of 9.12/3.66/400 ms, slice thickness of 1.2 mm, and planar resolution of 0.94 × 0.94 mm².

Healthy children underwent two fMRI studies at TR = 2000 ms, TE = 30 ms, FOV = 24 cm, 64 × 64 acquisition matrix, 4 mm thickness in order to localize 4 primary motor areas (face, fingers, arm, leg), 10 language regions: inferior frontal operculum (ifop), inferior frontal triangularis (iftr), middle frontal gyrus (mdfg), inferior precentral gyrus (prec), superior temporal gyrus (stg), middle temporal gyrus (mtg), inferior temporal gyrus (itg), supplementary motor area (sma), angular gyrus (ang), supramarginal gyrus (spm), 2 auditory regions: stg, mtg, and 7 visual regions: inferior occipital gyrus (iocc), middle occipital gyrus (mocc), superior occipital gyrus (socc), calcarine (calc), lingual (ling), fusiform (fusi), cuneous (cune). Briefly, for mapping primary motor areas, event-related tasks triggering a single movement of the face, fingers, arm, and leg to each side (left/right) were presented every five seconds in a 15-second block. The block was repeated 10 times for each side, resulting in total 20 sequential movements of face, fingers, arm and leg in a 5-minute session. BOLD activation was recorded for each primary motor area of each hemisphere and utilized as a binary mask to distinguish relative primary motor tracts to posterior limb of internal capsule (PLIC). To map semantic language, auditory, and visual areas, three different patterns (square, triangle, and circle) were randomly displayed every five seconds in a 30-second block. Subjects were instructed to press one of two buttons (yes, no) in response to an audio question (ON 30-second block) or visual pattern comparison (OFF 30-second block). These ON-OFF blocks were repeated four times, resulting in a 4-minute session. BOLD activation was recorded for each functional area and utilized as a binary mask to distinguish relative pathways from the inferior colliculus geniculate (icg, hearing) and lateral geniculate nucleus (lgn, vision). SPM 12 software package (https://www.fil.ion.ucl.ac.uk/spm/) was used to process all fMRI data, including motion correction, general linear modeling, and statistical analysis, to identify the locations of brain activation in response to functional tasks at uncorrected p-value < 0.05 [31].

Epilepsy patients underwent subdural electrode placement as a part of their clinical management for medically-uncontrolled seizures. ESM, using the method previously established [32], [33], was performed as part of clinical care during extraoperative electrocorticography recordings. Briefly, subdural electrode pairs were stimulated by an electrical pulse-train of 5-second maximum duration using pulses of 300 μsec duration and 50 Hz frequency. Initially, stimulus intensity was set to 3 mA. Stimulus intensity was increased from 3 to 9 mA in a stepwise manner by 3 mA increments until a clinical response or an after-discharge on electrocorticography was observed. When after-discharge without an observed clinical response occurred, or when neither clinical response nor after-discharge was induced by the maximally-intense stimuli, the site was declared “not proven eloquent.” When both clinical response and after-discharges occur, another pulse-train of the same or 1 mA smaller intensity was used until either clinical response or after-discharge failed to develop. Finally, a site with a contralateral movement induced by stimulation, without after-discharges, was defined as the “primary motor area” for the associated body part. Likewise, a site with speech arrest, expressive aphasia, receptive aphasia, auditory hallucination, or visual perception was classified as an essential eloquent area for comparison with the proposed CNN-based fiber classification (Table I). Using the landmark based registration procedure [34], those electrodes were spatially registered to native brain space (i.e. T1-weighted and DWI b = 0 image) and used as the ground truth of the CNN-based fiber classification.

TABLE I.

22 eloquent ESM electrode classes, D_j, are the present targets for detection using the proposed CNN methods.

Eloquent function	Class index	Description
primary motor processing of the contralateral body	D 1,2	left,right arm
	D 3,4	left,right face
	D 5,6	left,right hand
	D 7,8	left,right foot
specific types of language function	D 9,10	left,right speech arrest
	D 11,12	left,right receptive aphasia
	D 13,14	left,right expressive aphasia during naming impairment
	D 15,16	left, right expressive aphasia during visual naming
hearing ability	D 17,18	left,right hallucination
visual ability	D 19,20	left,right phosphene
	D 21,22	left,right distortion

C. DWI tractography analysis

NIH TORTOISE [35] and FSL eddy package [36] were used to correct motion, noise, physiological artifacts, susceptibility-induced distortion, and eddy current-induced distortion in the DWI data. Whole brain streamline tractography was reconstructed using probabilistic tractography with second-order integration over fiber orientation distributions (iFOD2) to sample the FOD at three equi-distant sample points along each candidate path segment for the next step [37]. Spherical-deconvolution informed filtering of tractograms (SIFT) [38] was applied to the resulting whole brain tractography in order to make streamline densities proportional to the fiber densities as estimated by spherical deconvolution throughout the white matter. At every voxel of grey/white matter boundary identified by the FSL FAST package [39], 100 dynamically randomized seeding points were applied in the framework of anatomically constrained tractography [40] to reconstruct biologically realistic streamlines. Then, the binary masks from fMRI activation were applied as an inclusion mask to sort out class relative streamline pathways from whole brain tractography (Table II). The resulting streamline pathways were spatially normalized to FreeSurfer average template space with Advanced Normalization Tools [41], sampled into 100 equal-distance segmentation points (s_k=1–100), and finally 3D coordinates of these 100 segmentation points were used to represent each fiber for subsequent CNN classification. Fig. 1 presents 64 centroid streamlines of C_i obtained by applying the QuickBundles algorithm [13] to C_i of the 70 healthy children, which illustrates the most representative streamline trajectories of C_i in the FreeSurfer average template.

TABLE II.

64 functionally important white matter pathways of interest, C_i (left,right hemisphere), are the present targets for detection using the proposed CNN methods.

Function	Fiber Class Index	From	To
primary motor	C 1,34	arm area	PLIC
	C 4,37	face area	PLIC
	C 5,38	finger area	PLIC
	C 16,49	leg area	PLIC
language	C 7,40	ifop	itg
	C 8,41	ifop	mtg
	C 9,42	ifop	sma
	C 10,43	ifop	spm
	C 11,44	ifop	stg
	C 12,45	iftr	itg
	C 13,46	iftr	mtg
	C 14,47	iftr	stg
	C 18,51	mdfg	ang
	C 19,52	mdfg	itg
	C 20,53	mdfg	mtg
	C 21,54	mdfg	sma
	C 22,55	mdfg	spm
	C 23,56	mdfg	stg
	C 26,59	prec	ang
	C 27,60	prec	itg
	C 28,61	prec	mtg
	C 29,62	prec	spm
	C 30,63	prec	stg
auditory	C 25,58	mtg	icg
	C 32,65	stg	icg
visual	C 2,35	calc	lgn
	C 3,36	cune	lgn
	C 6,39	fusi	lgn
	C 15,48	iocc	lgn
	C 17,50	ling	lgn
	C 24,57	mocc	lgn
	C 31,64	socc	lgn
other	C 33	-	-

D. Shallow CNN model for DWI streamline classification

Fig. 2 presents our shallow CNN model which has one input layer, one convolution layer, one sub-sampling layer and one fully connected layer with the softmax function. The details of each layer are described as follows.

Fig. 2.

Shallow CNN (SCNN) architecture for DWI streamline classification.

1. Input layer: Formally, we denote $x_l\in {ℝ}^k$ as the k-dimensional point representation for the lth point in a fiber. A fiber of length L is denoted as

   $$X_{1:L}=x_1\oplus x_2\oplus \cdots \oplus x_L,$$ (1)

   where ⊕ is the concatenation operator. By this, each input fiber is represented as a L × k matrix. In practice, we sample 100 points for each fiber and utilize coordinates of each point as its representation. Thus, each matrix has the same size, 100 × 3.
2. Convolution layer: A convolution filter $w\in {ℝ}^{h\times k}$ is applied to a window of h points of k-dimensional embedding in the convolution layer to produce a feature map. For instance, given a window of points X_l:l+h−1 and a bias term $b\in ℝ$, a feature g_i is generated by

   $$g_i=f\left(w\cdot X_{l:l+h-1}+b\right),$$ (2)

   where f is a non-linear function. In our case, we apply ReLU to the input matrices which sets negative elements in g_i as 0. A feature map g = [g₁, g₂, ⋯, g_L−h+1] is obtained from all the possible windows of a fiber of length L. In our system, multiple filters of various sizes are applied in the convolution layer to produce multi-scale feature maps.
3. Sub-sampling layer: In the sub-sampling layer, we apply max pooling over each feature map produced in the convolution layer and output the maximum element $\widehat{g}=max\left\{g\right\}$. We denote features generated by the max pooling layer as

   $$\widehat{G}={\widehat{g}}_1\oplus {\widehat{g}}_2\oplus \cdots \oplus {\widehat{g}}_M,$$ (3)

   where M is the number of feature maps.
4. Dropout: Dropout is a technique to reduce the chance of overfitting for neural networks [42]. Given feature map $\widehat{G}$, we generate a dropout mask vector $r\in {ℝ}^m$ of Bernoulli variables with probability p_d of being set as 0 and 1 − p_d of being set as 1. The output of dropout is

   $${\widehat{G}}_d=\widehat{G}\circ r,$$ (4)

   where ∘ denotes the element-wise multiplication operator. Empirically, we chose p_d = 0.5 in this study.
5. Fully connected layer: Given ${\widehat{G}}_d$ as the input, fully connected layers generate output

   $${\widehat{G}}_{fc}=\text{ReLU}\left(w\cdot {\widehat{G}}_d+b\right).$$ (5)
6. Output layer: On the output layer, we apply softmax function instead of ReLU to get the final classification probabilities

   $$p^i=\text{sofmax}\left({\widehat{G}}_{fc}\right),$$ (6)

   where pⁱ denotes prediction probabilities of the ith fiber belonging to each class. The class with highest probability is chosen as the final classification result for the corresponding fiber.
7. Optimization: Cross-entropy loss is selected as the training objective to minimize. The cross-entropy loss for the ith fiber is defined as

   $$L_{CE}^i=-\text{log}{p}_c^i,$$ (7)

   Where $p_c^i$ is the prediction probability of the ith fiber in the dataset belonging to the ground truth class c.

E. Deep CNN model for DWI streamline classification

Fig. 3 shows the proposed deep network consisting of a series of stages. The first stage is composed of two types of layers: convolution layers and pooling layers. The input fibers are passed through a set of filters followed by non-linear transformations. Then, the maximum of local patches are extracted. Second, four blocks of convolution, pooling, and concatenation layers are applied to learn high-level fine features from the brain fibers. For each residual unit, its input is added to the output before the ReLU layer. The basic idea is that, rather than expecting blocks to approximate the fiber classification function, we explicitly let these layers approximate a residual function, which is easier to be optimized. Third, fully connected and softmax layers are induced to get the final prediction which contains the probabilities of the input fiber belonging to each class. The class with the highest probability is taken as the final prediction. The dropout units are also applied to help prevent overfitting.

Fig. 3.

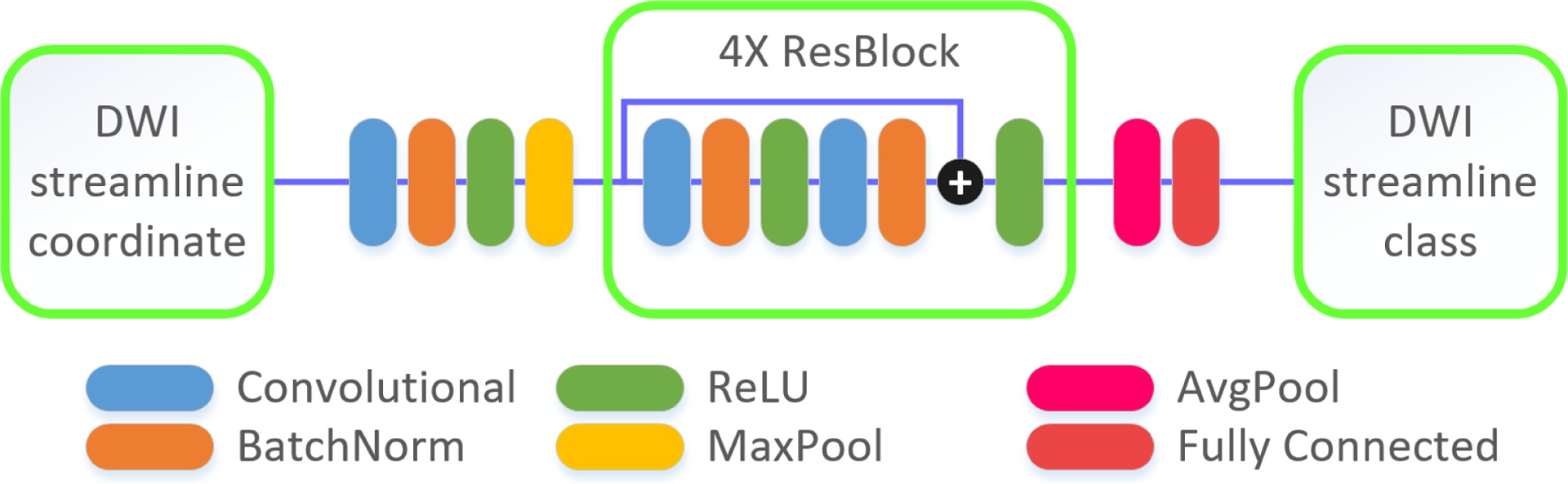
Deep CNN (DCNN) architecture for DWI streamline classification.

For optimization, the cross-entropy loss is applied to compare the shallow and deep CNN models. To further improve the classification performance, we also applied and evaluated two novel loss functions:

1. Focal loss: In general, the large class unbalance encountered during training overwhelms the cross-entropy loss. Easily classified fibers comprise most of the loss and dominate the gradient. In this work, we replace the conventional cross-entropy loss in CNN with focal loss [29] in order to reduce the loss for well-classified fibers and focus on harder, misclassified ones. We define the focal loss for the ith fiber as

   $$L_F^i=-{\left(1-p_c^i\right)}^{\gamma }\text{log}{p}_c^i,$$ (8)

   where γ is the focusing parameter. Empirically, we choose γ = 2. The modulating factor ${\left(1-p_c^i\right)}^{\gamma }$ reduces the loss contribution from easy examples: a fiber classified with $p_c^i\ge 0.9$ contributes at least 100× lower focal loss compared to cross-entropy loss; while hard examples with $p_c^i\le 0.5$ would only be scaled down at most 4×.
2. Center loss: The conventional cross-entropy loss only encourages the separability of features. To further improve the performance and generalization ability of the proposed CNN classifier, the learned fiber representation needs to be not only separable but also discriminative. We added an item, i.e., center loss [28], to the classification loss, which simultaneously learns a center for deep features of each class and penalizes the distances between the deep features and their corresponding class centers. Formally, we denote the center loss of the ith fiber as

   $$L_C^i=\parallel f_c^i-e_c{\parallel }_2,$$ (9)

   where $f_c^i\in R^d$ denotes the deep feature vector of the ith fiber in class c, and e_c ∈ R^d denotes the current centroid of class c. Note that the centroid updates itself during the mini batch training of our model [28]. Thus, the overall loss to be optimized is

   $$L^i=L_{\mathit{\text{class}}}^i+\lambda L_C^i,$$ (10)

   where $L_{\mathit{\text{class}}}^i$ denotes the classification loss, and $L_C^i$ is the center loss. Empirically, we choose λ = 1 in this study. As defined in Eq. (6), the class with highest probability, $p_c^i$ is taken as the final prediction of the ith fiber.

F. Learning interpretable fiber representation

CNNs have achieved great success in many tasks. However, the end-to-end learning strategy makes the CNN model a “black box.” This weakness is particularly prominent in biomedical imaging: if we do not know how the trained CNN classifies each fiber, we cannot fully trust the classification results provided by this model. By incorporating an attention mechanism [30] into our CNN fiber classifiers, we are able to highlight the attention of our CNN model and understand how it makes predictions.

As shown in Fig. 4, each soft attention unit returns a continuous, weighted average over different locations on all the feature channels. We denote the location variable as s where the model decides to focus, the attention weight as α, and the feature of the ith fiber as fⁱ. The expectation of the attention-weighted output feature map zⁱ is then given as follows,

$${\mathbb{E}}_{p(s)}\left[z^i\right]=\alpha f^i.$$ (11)

In practice, we insert one attention unit to the end of each residual block as shown in Fig. 5. Since the soft attention is smooth and differentiable, it is straightforward to update the attention weights by using standard backpropagation during the training of CNNs.

Fig. 4.

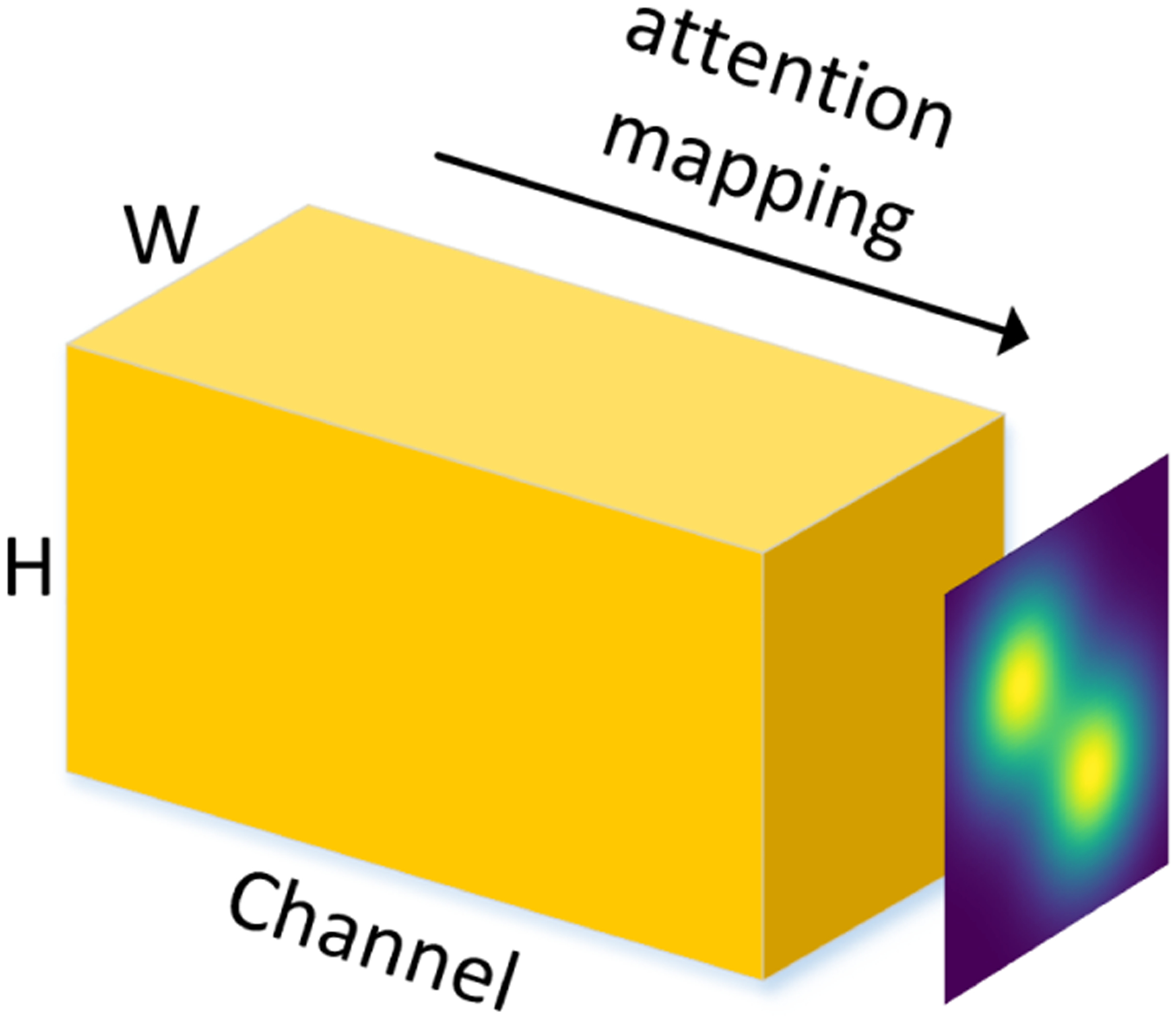
An example of the attention map of feature maps (with width W and height H) in different channels.

Fig. 5.

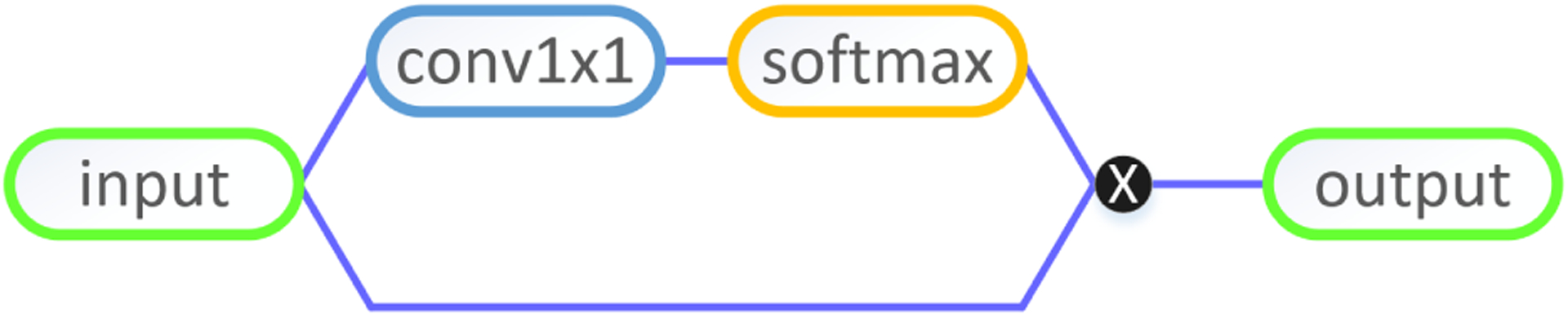
Soft attention unit in CNN models.

III. Experimental Results

A. Experiment setup

We performed thorough ablation study of our CNN models and compared ours with the current state-of-the-art models in brain fiber classification. Specifically, based on the same training and testing splits, we evaluated and compared the following models:

• Baseline: linear SVM (LSVM) and Logistic Regression (LR). Since our dataset is large, the implementation was approximated using PyTorch 0.2 [43].

• State-of-the-art models: RecoBundles [15], a clustering method based on fiber similarity, and FiberNet [20], which has an architecture similar to our shallow CNN model.

• CNN models with different loss functions including shallow CNN with cross-entropy loss (SCNN-CE), deep CNN with cross-entropy loss (DCNN-CE), deep CNN with focal loss (DCNN-FL), and deep CNN with both focal loss and center loss (DCNN-CL).

• Deep CNN models with attention mechanism combined with DCNN-CL (DCNN-CL-ATT).

• Fiber shapes, i.e., curvature and torsion, were also computed using an open resource code provided by [21] and then concatenated with spatial coordinates of a fiber as the input to our DCNN-CL-ATT (DCNN-CL-ATT-TC).

All the proposed CNN models were implemented using PyTorch 0.2. Adam [44], an adaptive learning rate approach for Stochastic Gradient Descent, was utilized to minimize the selected loss functions. The learning rate was empirically set at 0.0001 for all CNNs.

In our study, we first evaluated the impact of training sample size on network convergence. Fig. 6 shows training and testing losses of DCNN-CL-ATT obtained by varying sample size of training subject (i.e., 14, 28, 42, and 56). Red curves represent the training and testing losses with 14 training subjects. Clearly, this convergence is the slowest, and stability is lower when compared to the training losses with a larger number of subjects. Also, it is notable that the training and testing losses of 56 training subjects were slightly reduced compared with ones of 42 subjects. Thus, we decided to utilize streamline fibers from 56 randomly chosen healthy subjects as our training C_i set. Streamline fibers from the remaining 14 healthy subjects were used as the testing C_i set in our experiments.

Fig. 6.

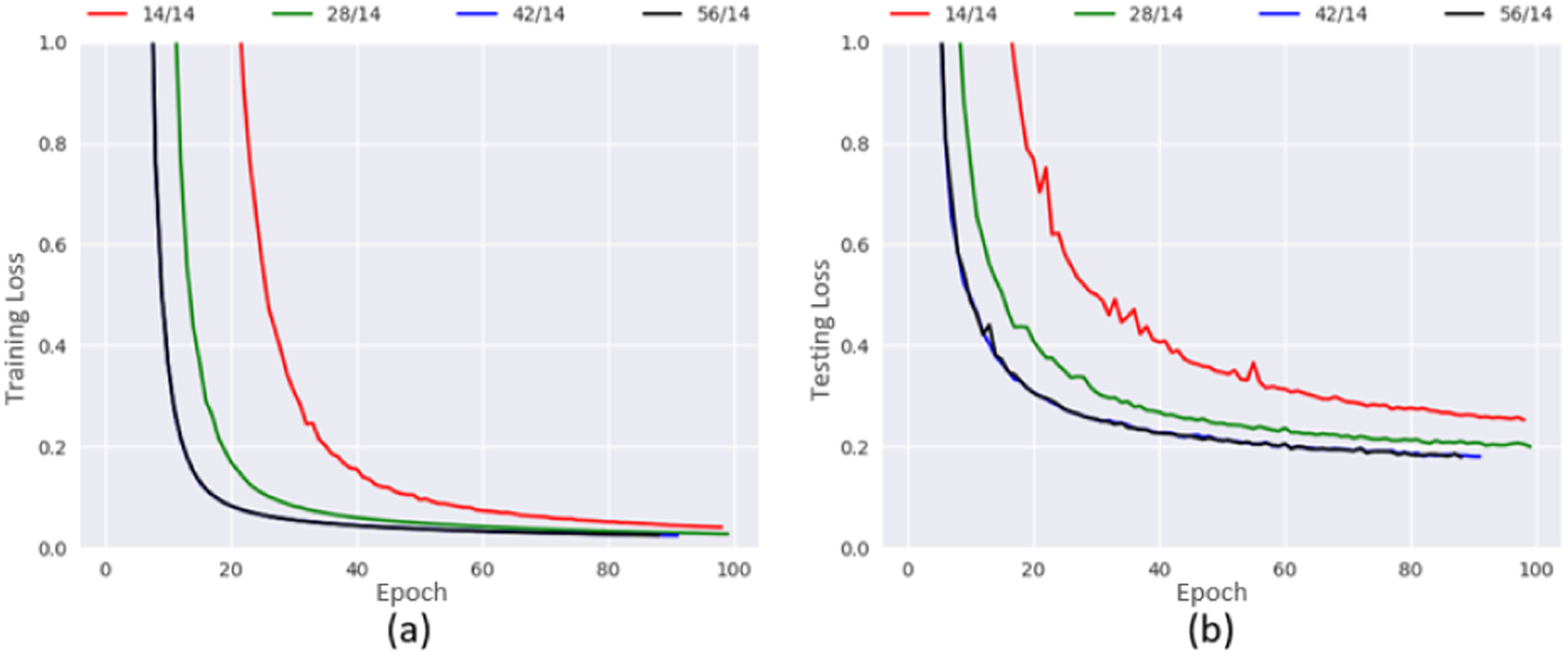
Convergence of training (a) and testing (b) losses in DCNN-CL-ATT obtained from different sample sizes of (training/testing) subjects.

The number of fiber streamlines for each class C_i in the training set is presented in Fig. 7. Clearly, the distribution is highly unbalanced: the most frequent classes have 40× to 220× more fibers than the least frequent classes. To evaluate the performance of each model over the highly unbalanced dataset we assessed F₁ score, which is calculated as follows:

$$F_1=2\cdot \frac{\text{precision}\cdot \text{recall}}{\text{precision}+\text{recall}}.$$ (12)

The corresponding macro-averaged F₁ scores with different numbers of training subjects are reported in Table III for DCNN-CL-ATT, which confirms that 56 subjects are sufficient for training a deep CNN.

Fig. 7.

Histogram of fiber streamlines in training set, C_i.

TABLE III.

Mean and standard deviation of the DCNN-CL-ATT macro-averaged F₁ scores over all classes at different training set size.

Number of Training Subjects	Macro-averaged Score
14	0.8689 ± 0.0045
28	0.8970 ± 0.0173
42	0.9437 ± 0.0021
56	0.9525 ± 0.0053

B. Fiber classification results

Average classification performance over all classes is listed in Table IV for each of the aforementioned methods. For the baselines, LR performed better than LSVM, demonstrating the advantage of non-linear models over linear models in brain fiber classification. Also, RecoBundles outperformed LR (12.30%) when thresholding to a 15 mm pruning distance from the 64 QuickBundles centroids presented in Fig. 1. 15 mm pruning distance threshold was selected because it provided the best macro-averaged F₁ score in our training set (i.e., 0.368 ± 0.182 and 0.327 ± 0.182 for 10 mm and 20 mm threshold, respectively).

TABLE IV.

Mean and standard deviation of the macro-averaged F₁ scores across all classes for each method. Best scores in bold.

Method	Macro-averaged Score
LSVM	0.2986±0.0021
LR	0.3381±0.0131
RecoBundles	0.3797±0.1818
FiberNet	0.8831±0.0075
SCNN-CE	0.8632±0.0020
DCNN-CE	0.9211±0.0098
DCNN-FL	0.9362±0.0026
DCNN-CL	0.9494±0.0066
DCNN-CL-ATT	0.9525±0.0053
DCNN-CL-ATT-CT	0.9337±0.0015

The CNN models significantly outperformed RecoBundles by 127.34% or more, which indicates the strong classification ability of deep learning models. Since the architecture of FiberNet is similar to our shallow CNN but with one more convolution layer and one more fully-connected layer, it was found that FiberNet performed better than the proposed shallow CNN but worse than the other deep CNN models. In addition, DCNN-CE outperformed SCNN-CE by 6.71%, which shows the advantage of deep learning in CNN architecture. It is worth pointing out that introducing focal loss to deep CNN improved the performance by 1.64% comparing to deep CNN with conventional cross-entropy loss. This demonstrates that the focal loss function is better suited for the classification of our highly unbalanced dataset. Moreover, DCNN-CL achieved better performance than DCNN-FL by 1.41%, indicating the advantage of discriminative representation learning using the center loss.

Our experiments showed that the best results could be obtained by DCNN-CL-ATT, with a macro-averaged score of 0.9525. It also showed that adding curvature and torsion to the spatial coordinates (DCNN-CL-ATT-CT) would negatively impact the classification performance (0.9337). This is likely because fibers from different classes often share highly similar shapes (i.e., curvature and torsion values), causing the learned features to be less discriminative. Thus, we used DCNN-CL-ATT-derived white matter pathways in the validation and visualization studies subsequently presented.

To demonstrate high sensitivity and specificity of DCNN based fiber classification, Fig. 8 presents confusion matrices of the top four DCNN models (i.e., DCNN-CE, DCNN-FL, DCNN-CL and DCNN-CL-ATT), which show actual F₁ scores obtained from training C_i set. The detailed F₁ scores of all models reported in Table IV are also available in the supplementary material.

Fig. 8.

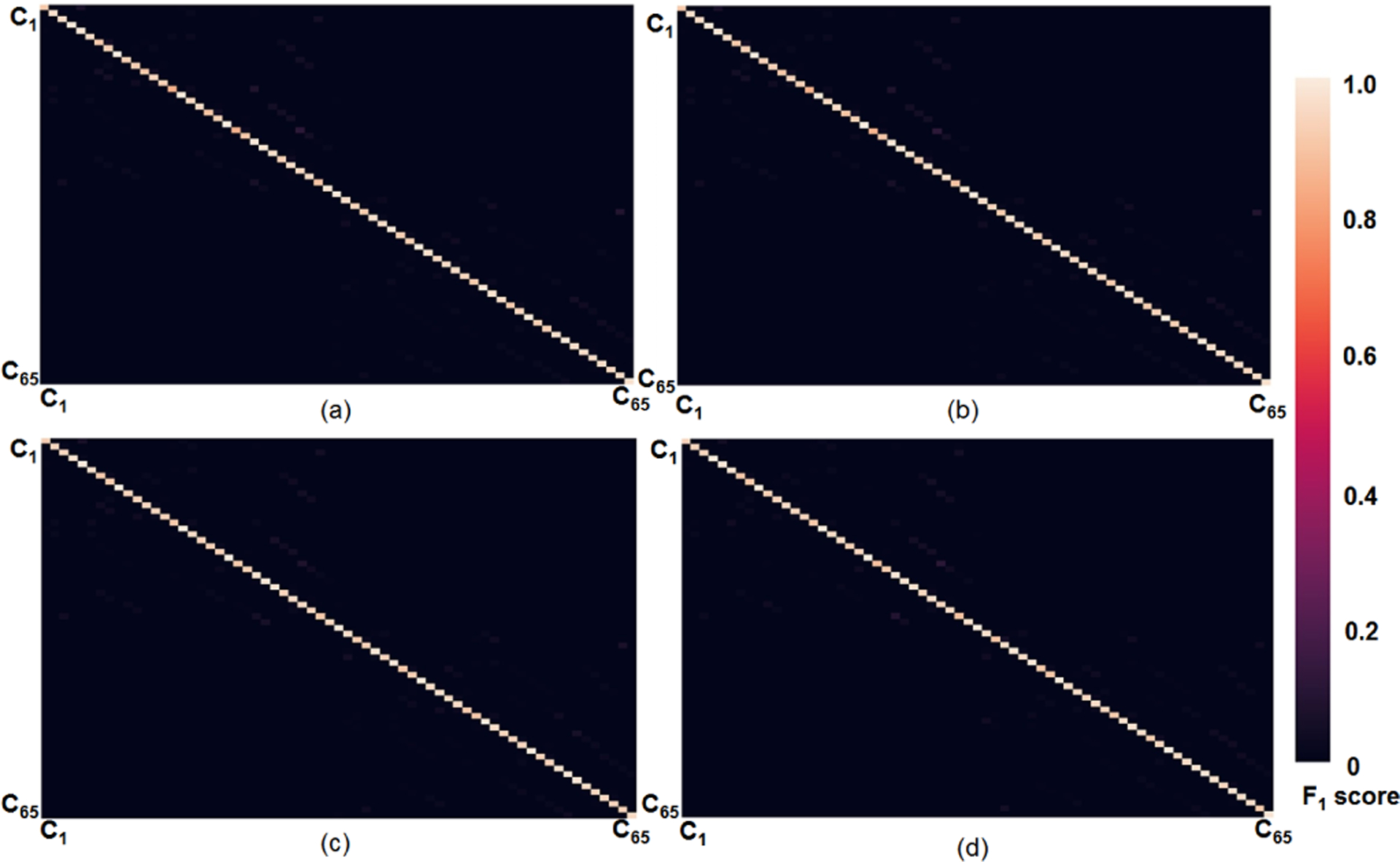
Confusion matrices of the top four DCNNs which present actual F₁ scores in training data. (a) DCNN-CE (b) DCNN-FL (c) DCNN-CL (d) DCNN-CL-ATT.

C. Validation results

An illustrative example of white matter tracts associated with finger movement, C₅, detected by DCNN-CL-ATT, is presented in Fig. 9. This example shows the clinical case where right hand finger movement was successfully induced during the ESM procedure of an 8 year old patient. DCNN-CL-ATT successfully localized the individual streamlines that have high prediction probability of $p_c^i$ for class C₅ (Eq. (6), greater than specific threshold β) and also terminate in ESM-defined finger areas of the precentral gyrus (two black-colored boxes). Our experiments show that false detections localized outside the electrodes were significantly reduced at β = 0.95 without reducing true positives, suggesting high specificity of the proposed DCNN-CL-ATT method to delineate functionally eloquent areas and pathways from individual patients. Thus, in the following validation study, we decided β = 0.95 as the threshold value to distinguish true positive fibers belong to each class C_i.

Fig. 9.

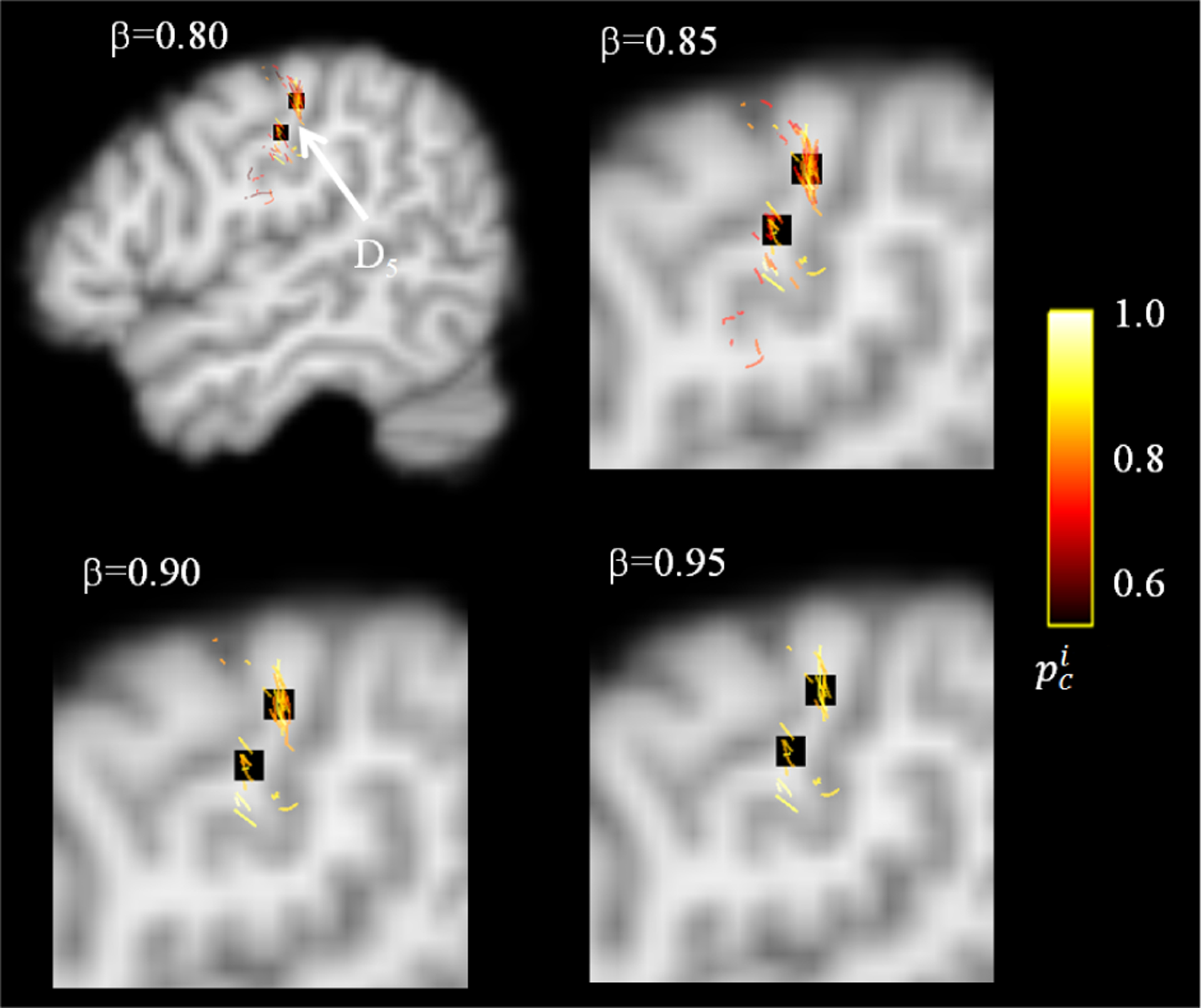
An example of DCNN-CL-ATT derived-white matter pathway, C₅, for cortical area associated with finger movement of right hand, D₅. Black colored boxes indicate ESM electrodes of D₅ which are spatially well-matched to cortical terminals of C₅ obtained at β = 0.95

To assess the ability of DCNN-CL-ATT to detect eloquent areas of interest determined by ESM, we performed receiver operating characteristic (ROC) curve analysis at the group level (n = 70 children with a diagnosis of focal epilepsy, Fig. 10 and 11). For each of four functional categories (primary motor, language, auditory, and visual function), voxel-wise overlap count of the ESM electrodes (D_j) was measured in FreeSurfer average template surfaces (i.e., lh.inflated, rh.inflated) by spatially transforming individual electrodes from native T1 space to FreeSurfer average T1 space (Fig.10, left column). The resulting count was scaled by its maximum value in the template space in order to estimate overlap probability across subjects. Moreover, the voxel-wise overlap count of DCNN-CL-ATT classifications corresponding to the same function was measured in the template and scaled by its maximum value to estimate overlap probability across subjects (Fig.10, right column). Since both probability measurements were obtained from different numbers of observations (651 electrodes vs. >10⁶ streamlines at β = 0.95), we applied Gaussian surface smoothing to both measurements at full width at half maximum (FWHM) = 5 mm (i.e. half of ESM resolution). Finally, to assess area under curve (AUC), sensitivity, and specificity of the classification, we first thresholded the overlap probability map of ESM at 0.01 to define the “target area” and then sequentially thresholded the overlap probability map of DCNN-CL-ATT to define the “classification area” as a function of overlap probability(streamline). Fig. 11 presents the results of the ROC curve analysis. At group level, it was found that DCNN-CL-ATT classification provides excellent prediction for primary motor/language/auditory/visual function, AUC=0.972/0.954/0.904/0.965 yielding outstanding sensitivity, 0.930/0.909/0.842/0.906 and specificity, 0.929/0.910/0.841/0.906 at the threshold of overlap probability(streamline) = 0.147/0.126/0.011/0.011.

Fig. 10.

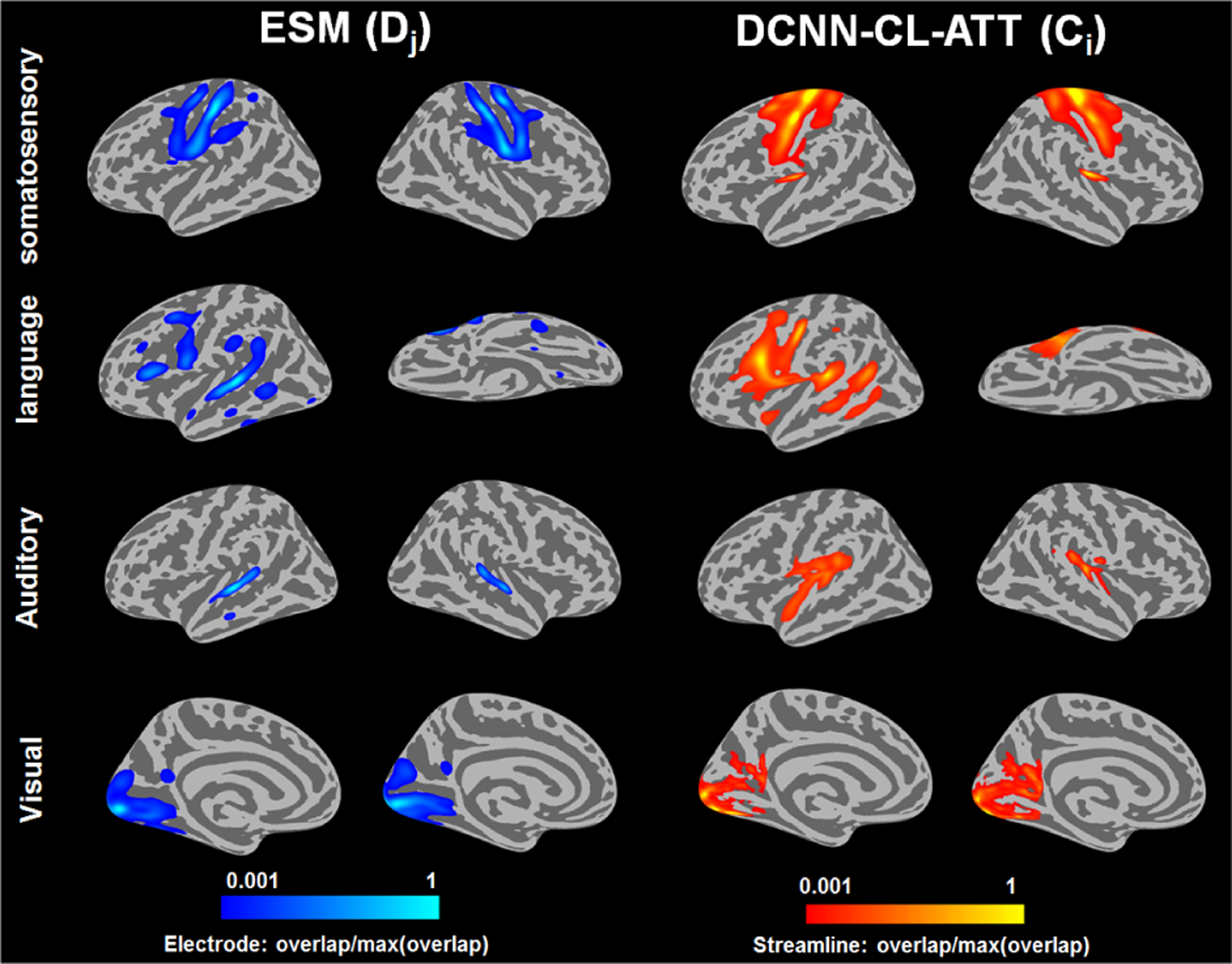
Comparison of DCNN-CL-ATT derived-white matter pathways C_i with ESM electrode classes D_j. For each functional category of 70 children with a diagnosis of focal epilepsy, voxel-wise overlap count of the ESM electrodes (D_j) was measured in FreeSurfer average template and scaled by its maximum value to estimate overlap probability across subjects in whole bran (left). Similarly, voxel-wise overlap count of corresponding DCNN-CL-ATT classification (C_j) was measured in FreeSurfer average template and scaled by its maximum value to estimate overlap probability across subjects (right).

Fig. 11.

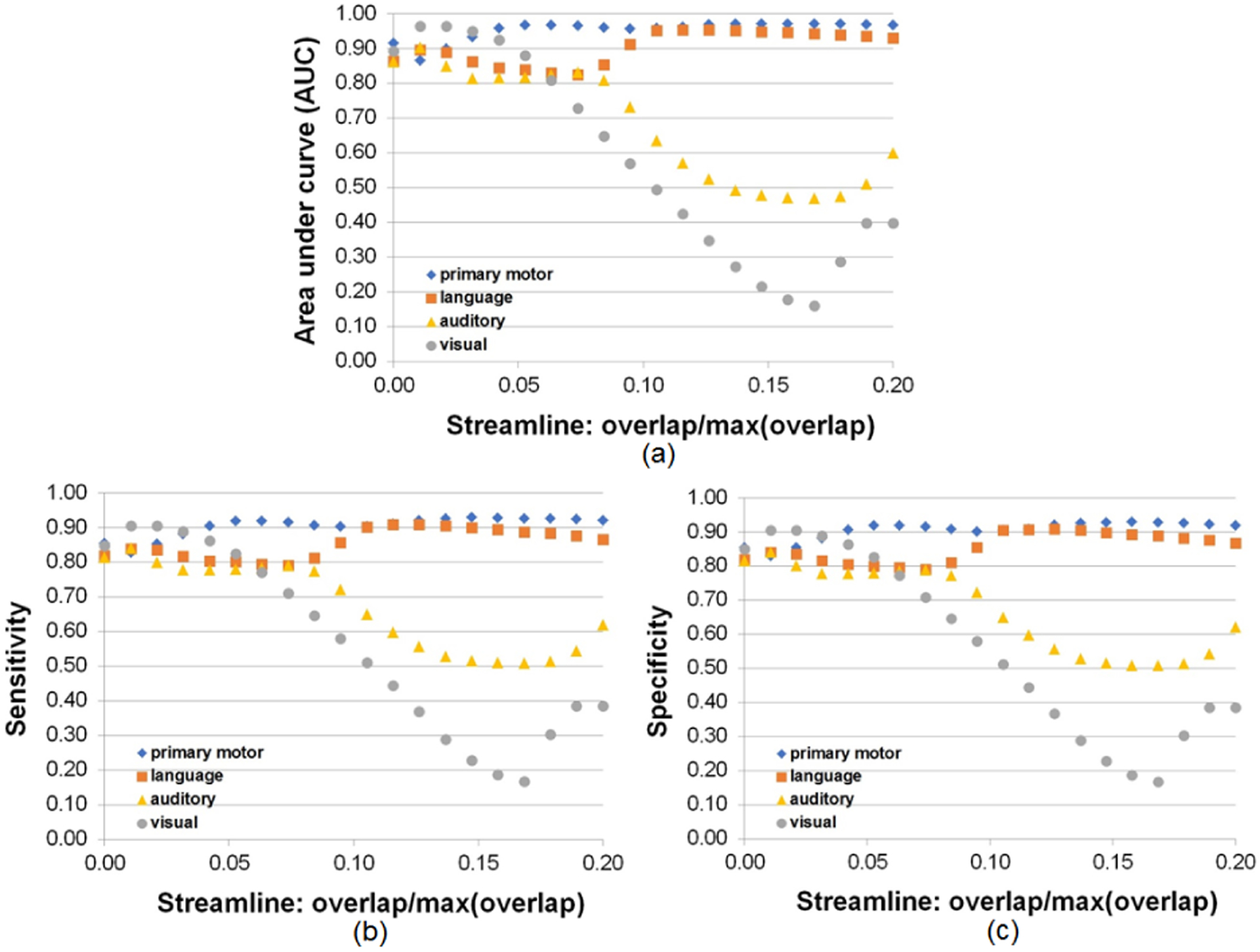
Performance of DCNN-CL-ATT derived-white matter pathways, C_i, to detect ESM electrode classes, D_j, at the group level (n=70). ROC curve analysis was performed as a function of overlap probability (streamline) in C_i in order to evaluate (a) area under curve, (b) sensitivity, and (c) specificity overlapping between all surface vertices of C_i and D_j.

Finally, fiber streamlines classified by DCNN-CL-ATT, C_i, were compared with the gold standard ESM, D_j, for validation (Table. V). Cortical terminals of the selected C_i were spatially matched with their gold standard ESM electrode locations D_j, where a match was considered to occur if the DCNN area contacted and overlapped the area of the gold standard. The percentage of matching was assessed as a function of Euclidean distance between the center point of each ESM electrode and the cortical terminal point of an individual DCNN-driven fiber streamline. For this validation, cortical terminals of class fibers C_i whose $p_c^i$ values were thresholded at β = 0.95 were spatially matched with the locations of ESM results, D_j, in 70 children with focal epilepsy. The overlap match was counted if any of the fiber terminals included the measured ESM electrode within each of four Euclidean distances, contact (<1 cm, within a diameter of individual electrode), 1 cm, 1.5 cm, and 2 cm. The detection probability gradually increased according to this distance. For instance, the average values of detection probability were 0.72/0.83/0.90/0.90 (contact/1 cm/1.5 cm/2 cm) for primary motor areas, 0.74/0.81/0.87/0.93 (contact/1 cm/1.5 cm/2 cm) for language areas, 0.4/0.8/0.8/0.9 (contact/1 cm/1.5 cm/2 cm) for auditory areas, and 0.57/0.85/0.87/0.88 (contact/1 cm/1.5 cm/2 cm) for visual areas, respectively. We found that compared with our previous DWI-MAP analysis of primary motor and language function [22], [23], the proposed DCNN-CL-ATT method improved about 9–14% of the detection probability by classifying more true positive streamlines (e.g., association fibers) into the correct ESM localizations.

TABLE V.

Probability of an individual DWI class C_i to match an individual ESM class C_i using DCNN-CL-ATT. Four distance thresholds were applied at β = 0.95.

ESM	DWI	contact	1.0cm	1.5cm	2.0cm
D 1	C 1	0.7857	0.8571	1.0000	1.0000
D 2	C 34	0.6000	0.8000	0.9333	0.9333
D 3	C 4	0.6071	0.8571	0.9286	0.9286
D 4	C 37	0.7879	0.8182	0.8788	0.8788
D 5	C 5	0.7241	0.7931	0.8966	0.9310
D 6	C 38	0.6364	0.7879	0.8182	0.8182
D 7	C 16	0.8574	0.8574	0.8574	0.8574
D 8	C 49	0.7333	0.8667	0.8667	0.8667
D 9	C 29,30	0.7368	0.8947	0.8947	0.8947
D 10	C 62,63	0.9091	0.9091	0.9091	0.9091
D 11	C 8,11,14	0.6923	0.8462	0.8462	0.8462
D 12	N.A	N.A	N.A	N.A	N.A
D 13	C 8,13,14	0.6667	0.7222	1.000	1.000
D 14	N.A	N.A	N.A	N.A	N.A
D 15	C 7,12,19	0.6667	0.6667	0.6667	1.000
D 16	N.A	N.A	N.A	N.A	N.A
D 17	C 25,32	0.2000	0.8000	0.8000	0.8000
D 18	C 58,65	0.6000	0.8000	0.8000	1.0000
D 19	C 2,17,24	0.6333	0.8000	0.8333	0.8333
D 20	C 35,50,57	0.5625	0.7500	0.8125	0.8438
D 21	C 6,7,15	0.7500	1.0000	1.0000	1.0000
D 22	C 39,48	0.3333	0.8333	0.8333	0.8333

N.A indicates no ESM acquired.

Representative examples of DCNN-CL-ATT-derived white matter fibers C_i at β = 0.95 are presented in Fig. 12 and compared with eloquent areas determined by ESM. These areas were obtained from four different test subjects: D_2,8 from an 8 year old boy, D_3,5 from a 12 year old girl, D_9,11 from another 8 year old boy, and D_13,15,17,19 from a 14 year old girl. It is notable that all predictions given by DCNN-CL-ATT (i.e., RGB-colored fibers) are spatially well matched to the gold standard ESM electrodes, which highlights the translational value of this approach: if an imaging tool can suggest likely eloquent areas, clinical ESM may more accurately place electrodes there for useful mapping. In contrast, Fig. 13 shows two cases where DCNN-CL-ATT-derived white matter fibers, C₂₅ and C₃₉ at β = 0.95, did not match with their corresponding ESM classes, D₁₇ and D₂₂, representing left auditory and right visual pathways, respectively. This is reflected by the poor contact probability (0.2 and 0.33) reported in Table V.

Fig. 12.

Representative examples of DCNN-CL-ATT derived-white matter pathways C_i of which cortical terminals completely overlap D_j. Light green colored clusters indicate ESM class electrodes D_j, spatially well-matched to cortical terminals of the obtained C_i.

Fig. 13.

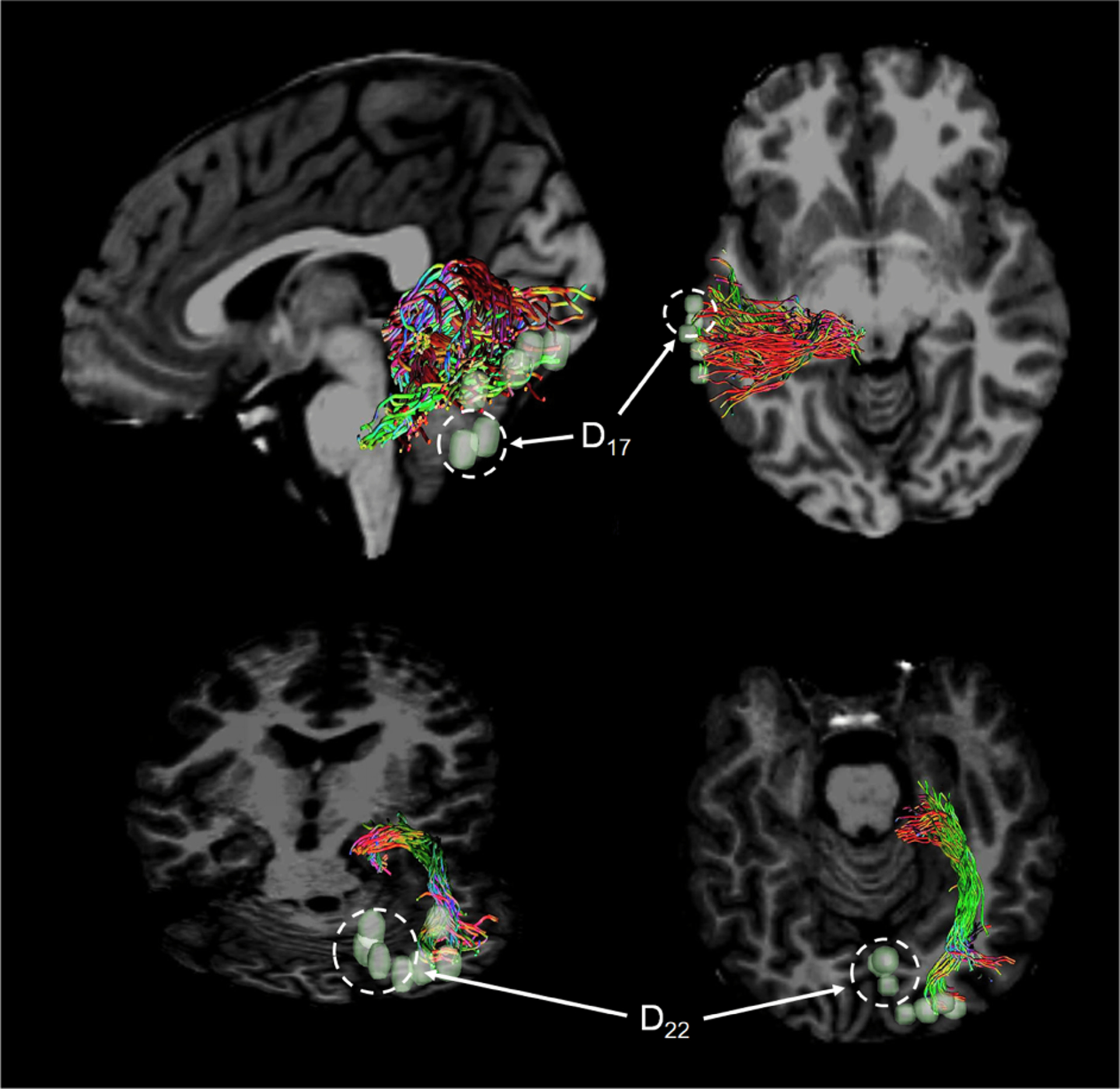
Representative examples of DCNN-CL-ATT derived-white matter pathways C_i of which cortical terminals incompletely overlap D_j. White dotted circles indicate ESM class electrodes, D₁₇ and D₂₂, spatially illmatched to cortical terminals of the obtained C₂₅ and C₃₉, yielding their low contact probability reported in Table V.

With regard to the computation time, the proposed CNN framework is implemented with PyTorch 0.2 and trained on a NVidia GeForce GTX 1080 Ti graphic card. It takes about 6 hours to train DCNN-CL-ATT. Given whole brain tractography consisted of about 1 million streamlines, DCNN-CL-ATT took about 15 minutes to classify them into 64 classes. As a comparison, our prior work (DWI-MAP) took about 20 minutes to classify 11 classes of primary motor and language related fiber streamlines.

D. Discriminative fiber representation

Center loss helps us learn a discriminative fiber representation. We extracted the output from the penultimate layer in DCNN-FL and DCNN-CL models as the representations of corresponding brain fibers. Then, we performed a quantitative analysis by computing the intra- and inter-class distances of representation vectors learned by DCNN-FL and DCNN-CL. To make the distances comparable, the average intra-class distances were normalized to 1. The normalized average distances over all fiber classes are reported in Table VI. The inter/intra distance ratio of fiber representations learned with DCNN-CL is 32.55 times greater than that of the representations learned with DCNN-FL, indicating that center loss results in more discriminative fiber representation, better intra-class compactness, and higher inter-class variations.

TABLE VI.

Normalized mean and standard deviation of intra- and inter-class distances of the representations learned by DCNN-FL and DCNN-CL.

Method	Intra-class Distance	Inter-class Distance
DCNN-FL	1 ± 0.5826	30.9720 ± 1.2217
DCNN-CL	1 ± 0.4958	1007.9916 ± 245.2773

E. Visualization of interpretable fiber representation

To illustrate how our DCNN models classify streamlines, we visualized the attention maps for brain fibers in several representative classes. First, we selected fibers with high classification confidence $(p_c^i>0.85)$. Next, the corresponding attention maps over 100 points of the selected fibers were extracted from the trained DCNN-CL-ATT model. Finally, we computed the average attention weights for fibers belonging to the same class and took that as the attention map of the class.

Fig. 14 provides a clue on how the DCNN model makes predictions for brain fiber streamlines. Primary motor streamlines C_1,4,5,16 showed noticeable changes in attention weight only at both s₁(prec) and s₁₀₀(PLIC). These changes directly support the traditional homunculus representation of the human brain’s precentral gyrus and posterior limb of internal capsule [45], [46]: specific cortico-spinal tracts connect unique segments of prec and PLIC, resulting in multiple classes of prec and PLIC associated with the unique motor functions of C_1,4,5,16. Meanwhile, other language and auditory tracts of C_11,21,24,32, whose anatomical trajectories terminate at different cortices (s₁, s₁₀₀), show different patterns of attention weights widely spread through the entire range of spatial coordinates s_1–100. This example demonstrates the potential of this attention map to identify the most important segments of a streamline, providing a supplementary marker which can be used to identify incorrectly tracked outliers (i.e. false positives).

Fig. 14.

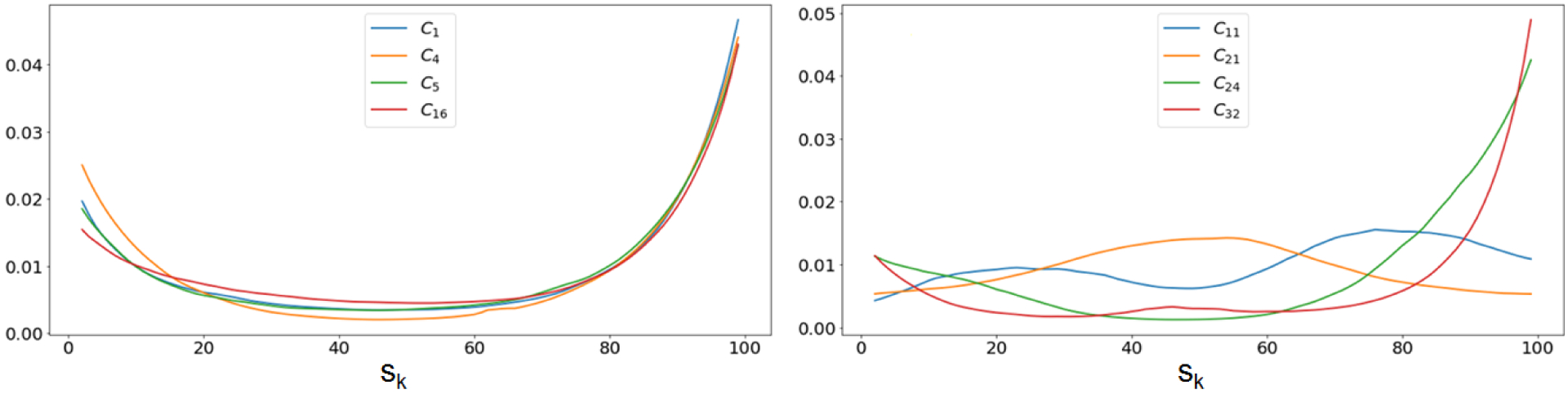
Attention maps of representative classes related to primary motor, language, auditory, and visual functions. Higher values are more important for classification. Left: Attention maps for C₁, C₄, C₅, and C₁₆. Right: Attention maps of C₁₁, C₂₁, C₂₄ and C₃₂.

IV. Discussion

The present study demonstrated that our deep CNN model with focal and center losses and soft attention mechanism can effectively learn discriminative and interpretable feature representations of in-vivo DWI streamline trajectories, and accurately detect eloquent functional areas determined by gold standard ESM data. Actual streamline coordinates outperformed shape features such as curvature and torsion in training the DCNN-CL-ATT model, providing better anatomical characteristics of individual fiber classes in most white matter trajectories. The higher reliability of streamline coordinates might be partially explained by taking into consideration that malformation of cortical development (MCD) is by far the most common epileptogenic pathology in pediatric epilepsy surgery cohorts, accounting for up to 50% of the cases (or even higher in some reports) [47], [48]. A diagnosis of MCD includes a variety of pathologies, most commonly focal cortical dysplasia type I/II, in which MRI can detect cortical thinning/thickening, hypointense/hyperintense signals, abnormal gyrification, and enlargement of the lateral ventricles [49], [50]. Thus, the proposed DCNN method utilizing spatial coordinates of entire white matter trajectories may better minimize the effect of cortical malformations on tract classification, where cortical-atlas-based tract clustering would likely be limited by malformed gyrification, especially near the cortical mantle. In contrast to parametric Gaussian approaches, the proposed DCNN method makes no assumption regarding a priori probabilistic distribution of individual streamlines.

In vivo visualization of white matter connections using DWI tractography is a promising but challenging task in clinical applications, which relies on a complex model characterizing diffusion signals of water displacement on either multi shells or Cartesian grids in the diffusion-encoding q-space [51], [52], [53], [54]. The present study aimed to generalize the application of a state-of-the-art DCNN classification to clinical DWI data, which is typically limited by low angular resolution and diffusion weighting [55], [56]. Importantly, the accuracy of this DCNN model is highly dependent on DWI model and the reconstruction algorithm used to generate training data for the DWI streamlines. Given these dependencies and the controversial limitations of DWI reconstruction (i.e. crossing fiber problem), we elected to use an open source pipeline (MRtrix3: www.mrtix.org) based on the principle of spherical deconvolution reconstruction, which provides promising reproducibility [37]. Although this reconstruction provided clinically acceptable accuracy of 73–100% to detect eloquent functions within the spatial resolution of ESM (1cm), future implementation of advanced methods that overcome the previously mentioned limitations may create a significantly better training set, which is essential to improve the accuracy of this and alternative methods.

In this study, we mainly attempted to detect white matter pathways with sufficient size and high coherence, since smaller tracts like the association fibers or less coherent connections are not reliably assessable in our current DWI data. Higher resolution imaging that employs greater field strength, stronger diffusion gradients, and high angular resolution DWI (i.e., human connectome data available at http://www.humanconnectomeproject.org) could enable the delineation of such structures in the proposed DCNN-CL-ATT model. Our target classes were also constructed using fMRI, inevitably limited by ill-posed neurovascular coupling [57]. More importantly, fundamental ambiguities in current DWI tractography models have been reported, limiting continuous tracking of valid long-range fiber bundles in-vivo and generating a large amount of false-positive bundles near the cortical mantle [58], [59]. Thus, the detection of eloquent areas using the proposed DCNN-CL-ATT model may only be naturally effective and valid on the gyral level and within relatively short range, rather than at the nominal voxel resolution.

From a technical point of view, the proposed DCNN-CL-ATT model requires a large amount of training data. In the future, we plan to investigate how transfer learning techniques [60] can help alleviate this limitation. Moreover, we will further investigate the proposed attention map to see if it can be used to detect malformed or incorrectly tracked white matter trajectories (e.g., “wiggly tracked” fibers [61]) by systematically labeling a specific range of a given input tract with significantly altered attention weights. It would also be interesting to investigate whether the total number of individual streamline coordinates in s_k may affect overall performance in relatively longer (or shorter) pathways by disturbing the proposed DCNN-CL-ATT model at the prefixed learning parameters.

In conclusion, the benefits of the proposed DCNN-CL-ATT method in presurgical planning for epileptic resection candidates include: 1) no added risk or cost to identify functionally important areas, including both cortex and subcortical pathways, 2) no need for patient task cooperation, which is particularly important in young children, and 3) easy applicability to other types of neurosurgical procedures (e.g., brain tumor resection). This study translates advanced deep learning techniques to clinical practice in the pediatric population, where currently available approaches are suboptimal; ESM often provides low sensitivity to localize eloquent areas in young children, and fMRI suffers from motion artifact and poor cooperation to map eloquent areas in children with cognitive deficits. Systematic investigation of the proposed DCNN-CL-ATT method will further improve presurgical planning and provide a unique opportunity to minimize or predict postsurgical functional deficits in the future.