Novel Torque and Drag Model for Drilling Two-Dimensional High-Angle Wells

Abstract

Planning high-angle wells involves diverse areas; one of the most important of these areas is torque and drag (T&D) management. Not only could uncontrolled T&D cause various drilling problems like drill string (D/S) failures, casing wear, stuck pipes, and slow rates of penetration but it could also entirely stop the drilling progress, if torque and/or drag exceed rig or string capabilities. Modeling T&D in advance would alleviate these problems by prediction of friction forces to be encountered and urging the drilling team to take the required measures to mitigate these forces or upgrade the drilling hardware (rig equipment and/or D/S). Modeling T&D is still a complex and time-consuming job to be carried out at the rig site while drilling, so that an accurate and rig-friendly model would be very useful to industry. In this work, a novel and simple model had been developed to predict T&D values while drilling both curve and tangent sections of high-angle wells based on a soft-string concept, in which the D/S is assumed to be a chain lying on the lower side of the well that can transmit torsional forces. Despite the simplicity of the calculations, the model accounts for components of drilling torque that are overlooked in most complex packages. Friction within the top drive system had been considered to predict the torque acting on the D/S only. In addition, the torque applied on the D/S by the viscous drilling fluid was accounted for by reversing the concept of viscometers. The model proved to be practical and reliable for the two-dimensional wellbore and thus is superior in terms of quick field application. The developed model was tested using data from the Western Desert, Egypt. Statistical analysis had been used to assure the accuracy of the proposed model and to assess the effect of different drilling parameters and practices on both T&D. The reliability of the model had been proven with a negligible error for drag calculations and 10% error on average for torque calculations. Also, the effect of distance between successive survey stations on T&D modeling had been proven mathematically. This research narrows the gap between theory and practice by studying the dominant factors and determining the extent of the effect of each of them on wellbore friction forces. In addition, the work sheds light on the best practices concluded from the application of the developed model on field data.

1. Introduction

The petroleum industry is facing the necessity of drilling more and more high-angle, horizontal, and extended-reach wells (ERWs).¹ Excessive torque and drag (T&D) problem is one of the major limitations of horizontal and extended-reach drilling. Therefore, it is necessary to determine the best practices to reduce T&D and avoid their catastrophic consequences. Torque is the rotational force required to overcome resistance to rotation from several sources within the wellbore such as geometric, bit, drive system frictional, and viscous torque. On the other hand, drag is the axial force generated only when the pipe is moved in an axial direction as a result of frictional contact with the wellbore.² It always has an opposite direction to that in which the pipe is moved. During tripping in and out operations, when the drill string (D/S) is not rotated, the drag forces are higher, while, when the drill string is rotated, the drag forces are significantly reduced.³

Besides T&D, buckling of tubular is also a major problem while drilling. However, for high-angle wells, buckling occurrence is less likely to happen compared to severe T&D problems. This is mainly due to the fact that critical buckling load increases with both the hole angle and hole curvature.⁴ Moreover, a well-managed T&D will also reduce the potential occurrence of buckling. If T&D are not managed efficiently, the following hazards could exist;⁵⁻⁷

• Parting of the D/S and/or bottom hole assembly (BHA).

• Reduction in true weight on bit (WOB) and rates of penetration.

• Sinusoidal or (the more damaging) helical buckling in D/S.

• Steering and orienting down hole tools may be difficult and time consuming.

• Wear of drilling equipment, tubular, and casing.

• Difficulty to run lower completion of horizontal wells.

• Makes fishing more difficult: friction between the drill string and hole acts to dissipate the impact energy of jar.

Modeling of T&D is an extremely important step in the planning phase of high-angle wells. Drilling the well efficiently and avoiding risks accompanying non-managed torque or drag are highly targeted. Torque modeling has a paramount importance as it causes most of the drilling problems related to friction forces.^6,8,9

Two broad categories of T&D modeling exist in the industry, which are soft-string and stiff-string models. The soft-string model assumes continuous contact between the D/S and wellbore and a smooth path between survey stations.¹⁰ On the other hand, the stiff-string model assumes the contact between the D/S and wellbore to be at certain points, which complicates the required mathematical treatment.¹¹ Historically, the first mathematical modeling of T&D was performed by Johancsik et al.,¹² where he adopted the soft-string model by considering only the friction due to contact of the D/S with the wellbore. Later, Sheppard et al.¹³ also adopted the soft-string model in their work, which became the backbone of industry models nowadays. Stiff-string models suffer many practical shortcomings; that is why there is no one industry-standard stiff-string model yet despite abundance of publications.⁷ To be accurate, stiff-string models require closely spaced survey stations to know the exact path of wellbores between survey stations.^10,11 On the other hand, soft-string models although preferred due to their simple mathematical treatment suffer less accuracy in situations with high dog-leg severity (DLS) and very stiff D/S components or narrow clearance with the wellbore.^7,11 The turning point from which stiff string should be used is not clearly defined; some authors proposed a DLS of 30°/100 ft to be the threshold between soft-string and stiff-sting adoption, and they even proposed a combination between them where the stiff-string model is used for stiff BHA components and the soft-string model is used for the remaining D/S.¹⁰

Unfortunately, not all sources of torque are accounted for in current torque modeling packages. For example, torque caused by viscosity of drilling fluid and torque lost in drive system friction are overlooked. Moreover, the mathematical formulas used in these packages are too complex to be implemented at the rig site level. The main objective of this paper is to develop a novel and simplified model, which accounts for different components of the drilling torque. Besides being quick, the model is a great candidate for rig implementation due its simplicity and accuracy.

1.1. Geometric Component of T&D

Geometric torque is a part of the drilling torque that depends on the shape of the wellbore, properties of D/S components, formation type, and the lubrication of drilling mud.^5,14 It is a function of the normal force, friction factor, and pipe diameter. Normal force is the component of the D/S weight that is normal to the wall of the wellbore. Regarding drag, it is a function of the normal force, friction factor, and even direction of movement.¹⁵ The friction factor is rather a combined parameter that implies several aspects (Figure 1) such as;¹⁶

• Hole cleaning.

• Wellbore stability.

• Drilling fluid properties.

• Deflection technology.

• Formation type.

Figure 1.

Friction factor is rather a combined parameter that implies several aspects.

1.1.1. Hole Cleaning

During the drilling of high-angle wells, gravitational forces cause deposits of the drill cuttings along the lower side of the wellbore and result in the formation of a “cutting bed”. If left unattended, this accumulation of drill cuttings becomes severe enough to lead to high T&D on the drill string, hole pack-offs, stuck pipes, wear and tear of equipment, and other unwanted incidents of lost or nonproductive time. Removal of these cuttings, particularly from wells drilled at high angles, has been proven to be problematic.^17,18

1.1.2. Wellbore Stability

Wellbore instability is, in fact, the most significant technical problem area in drilling and one of the largest sources of lost time and trouble cost.^19,20 Operational problems that occur as a result of such instabilities may range from high solid loading of the mud requiring dilution to hole cleaning problems due to reduced annular velocities in enlarged-hole sections to full-scale stuck pipes as a result of well caving and collapse.²¹

Wellbore instability is more prominent in ERWs. One problem in ERW drilling is the variable water depth along the wellbore and thus different pore and fracture gradient.²² Therefore, an extra casing string may be required. Most ERWs may cross faults due to long reach, and thus, loss of circulation is expected.⁹

Loss of circulation may occur at mud weights less than those required to stabilize adjacent formations. To maintain a conventional hole size (e.g., 8.5 in.), the hole will be exposed for longer time than required in vertical or conventional deviated wells. A number of time-dependent effects may occur, such as more cycles of pressure variations and D/S contact with borehole walls that reduces the strength of formations as a consequence of fatigue-type mechanisms.^22,23

1.1.3. Drilling Fluid Properties

Many types of drilling fluids exist and can be selected based on severity of T&D. Generally, water-based mud is not the best candidate for horizontal drilling. Although, polymer muds have good inhibition properties as they encapsulate drill solids to prevent dispersion, coat shales for inhibition, increase viscosity, and reduce fluid loss. Oil-based mud (OBM) is still superior due to better inhibition and lubrication properties. When using OBM, the salinity of water portion must be checked. Although OBM would be the best candidate on paper in most situations, this must be justified in terms of environmental considerations, the required degree of inhibition, lubricity, cost, and logistics.²⁴ Synthetic fluids are designed to mirror performance of OBM, without their environmental hazards.

1.1.4. Deflection Technology

The most commonly used technologies for directional drilling nowadays are²⁵ positive displacement mud motors (PDMs) and rotary steerable systems (RSSs). Mud motors are generally less expensive, but the borehole quality of RSSs is better than that of mud motors. This is due to constant rotation of the D/S, which reduces tortuosity and DLS. When motors are in use, the hole is drilled in two modes: rotary and sliding. The tendency of stuck pipes is great in the sliding mode. Different concerns arise for different directional tools. Mud motors usually induce high tortuosity and rugosity. On the other hand, RSSs (both point-the-bit and push-the-bit variations) induce less tortuosity and rugosity.²⁶ Tortuosity causes erratic torque, which in turn may lead to a situation where there is no axial weight to be applied on bit. More on selection of optimum deflection technology can be found in the study by Nour et al.²⁷

1.1.5. Formation Type

The lithology of overburden rocks that must be drilled in order to reach a target zone will also affect T&D. Coal, salt, and shale tend to collapse,²⁸ and thus cause high T&D values. This is more likely to happen in wells that take longer to drill, such that the downhole formations are exposed to the drilling mud and D/S longer. This is the case in ERWs. One of the most common causes of hole collapse is the chemical difference (specifically salinity) between the formation saltwater and the drilling mud.²⁴

1.2. Other Components of T&D

The simplified model accounts for three other friction components that are usually ignored or even not introduced in the first place in current T&D models. Friction due to drilling fluid viscosity and inside top drive system (TDS) bearings besides torque on bit (TOB) is considered in the simple model. The first and last components would be explained in next section, where an elaboration will be introduced here for the second one due to its novelty to the author’s knowledge.

In rigs with old, inefficient, or non-maintained TDS, the internal friction losses may account for as high as 50% of total torque noticed on gauges. This reveals not only the importance of maintaining TDS but also vitality of predicting torque at different points from the bit to TDS. To further manifest this point, a drilling rig is assumed with a TDS capable of handling up to 40 klb-ft torque and a D/S with 20 klb-ft make-up torque. If the torque while drilling reached 25 klb-ft, for example, the team would stop drilling directly. However, if we know that 7 klb-ft out of these 25 klb-ft is merely friction within TDS, then we consequently know that the effective torque on the top joint of string is only 18 klb-ft and on TDS is 25 klb-ft. Thus, neither has reached the limit, so we can resume drilling operations. A step-by-step method of calculating friction within TDS is presented in this research for the sake of both safe and efficient drilling operations.

2. Mathematical Modeling

The prediction and follow-up of T&D is one of the most important tools in the planning and execution of high-angle wells. A novel and simplified model was developed to predict hook loads (HLs) and torque for a certain wellbore trajectory, D/S configuration, drilling fluid properties, and drilling parameters.

HLs include pickup weight while pulling the string out of the hole, slack-off weight while running the string in the hole, and rotating weight. In the meanwhile, torque may be on-bottom torque (drilling torque, when a weight is applied to the bit) and off-bottom torque (when no weight is applied to the bit).

This model works by dividing the D/S into small sections along the wellbore, and then, the normal force for every section is calculated based on a single inclination angle equivalent to the average of the inclination angles at the start and end of the section.

Based on normal force, the drag and geometric component of torque can be calculated by using a suitable friction factor. Generally, the friction factor can be arbitrarily selected in earlier wells and then refined based on actual data and assigned for a certain formation.

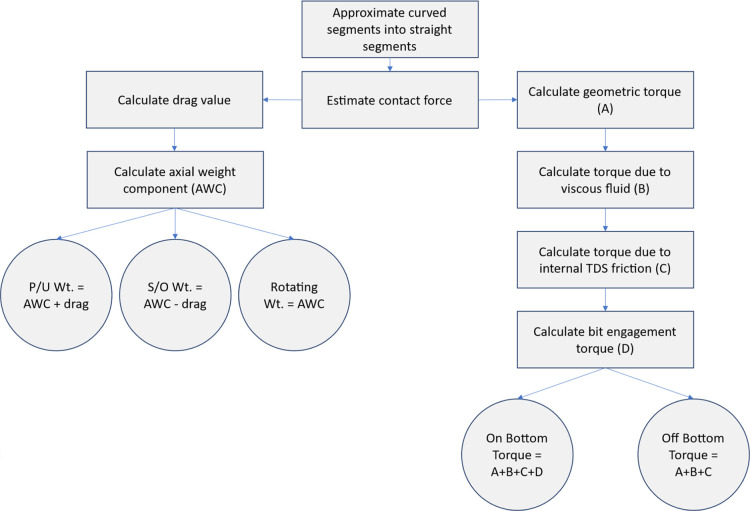
The viscous component of torque can be calculated for every segment, depending on rheological properties of drilling fluids. This is carried out by analogy to rheology measurements, where the dial readings which represent that the torque is read, and then the rheological parameters are concluded. In the model, we use the rheological parameters and simulate the torque values. A novel formula was introduced for torque loss in the TDS that accounts for the friction loss within gears and internal parts. Bit torque is also calculated based on bit aggressiveness and WOB. Figure 2 shows a flow chart representation of the mathematical modeling calculations.

Figure 2.

Flow chart representation of the mathematical modeling process.

2.1. Simplified Model Assumptions and Limitations

The developed model had been formulated based on different assumptions:

• The model is based on Coulomb friction theory, which assumes friction force to be proportional to normal load and independent of the contact area.

• The model supposes no significant change in borehole azimuth while drilling.

• The model approximates the curved intervals to straight intervals to facilitate the calculations of normal force.

• Lengths of selected intervals should not exceed 100 ft to improve the model accuracy.

• Normal force is calculated for every segment of the wellbore.

• HLs are calculated depending on the normal force and friction factor, based on Coulomb friction theory.

• Resulting torque is calculated for each segment, and torque values are summed from the bit up to TDS.

• The model is suitable for wells with a maximum DLS of 8–11°/100 ft to avoid significant bending forces that will deteriorate model accuracy.

Figure 3 shows a schematic illustration that simplifies the different D/S segments within a wellbore into straight segments to facilitate mathematical treatment even at the rig site.

Figure 3.

Schematic illustration simplifies the curved D/S segment into a straight one.

2.2. Geometrical Torque and Weight Components

The model replaces each actual D/S segment with a straight one. For simplicity, the inclination angle of this segment is assumed to be equal to the average inclination at the start and end of it. Normal force is calculated as follows

1

where w = air weight of pipe (lb/ft), Δl = segment length (ft), β = buoyancy factor (dimensionless), and θ = average inclination angle of segment (degrees).

To calculate tension, one starts from bit, where tension is almost zero and calculates upwards to the TDS using the following equation

2

where T₁ and T₂ are the tensions at the start (bottom) and end (top) of the segment, respectively.

or

3

Then, the corresponding geometrical torque component is calculated for each segment as follows

or

4

where D is the diameter of the segment (inch).

2.3. Viscous Torque Component

The drilling fluid viscosity acts to increase the resulting torque while drilling. A step-by-step procedure is presented here to calculate the viscous component of the drilling torque. According to the yield-power law (Herschel–Bulkley) model, the shear stress (τ) of drilling fluid subjected to a shear rate of (γ) due to the rotation of a D/S with a diameter D in the hole with diameter D_h was presented by Kenny et al.;²⁹

5

where τ_y = yield point (lb/100 in.²), K = fluid consistency (cp), and n = fluid behavior index (dimensionless).

The shear rate can be calculated as follows

6

where RPM = rotary speed of the D/S (revolution per minute).

From

7

and

8

Then

9

Thus, the viscous torque component can be calculated from the following equation

10

2.4. TDS Torque Loss

An ideal TDS will yield zero torque at any RPM as long as there is no load, but this is not the truth. Friction loss always occurs in internal gears and bearings, so torque will be required to rotate the TDS with no load attached to it. Attaching the D/S to TDS will induce more load on it and will require more and more torque to rotate the string even in the vertical section of the hole.

TDS torque response was investigated by the authors, and a new empirical equation was introduced to estimate this torque loss at any rotary speed and HL combination based on TDS field data.

11

where a, b, and c are empirical constants depending on the TDS type and efficiency and α_f is the rotary speed-dependent torque factor (or free torque factor) and α_l is the load-dependent torque factor.

The first term is relevant to the torque loss where there is no load attached to the TDS whereas the second computes this torque loss under loading conditions.

To find (α_f) and (a), rotating TDS (with no load attached) at two different rotary speeds (at minimum) and recording torque loss at each RPM are required.

12

13

14

15

Finding α_l, b, and c is a bit more complex, and at least three sets of torque measurements are required. Every set includes recording-free torque (i.e., without load attached to the TDS) and loaded TDS torque with a certain load at the same rotary speed at which free torque was recorded.

TDS was assumed to be rotating at certain rotary speed with no load attached, and this gave certain torque loss (M_free). Now, a certain length of the D/S with a weight of HL₁ (lb) is attached and the TDS is rotated with the same rotary speed. The resulting torque is recorded as M₁, so we have

16

17

The same procedure is repeated with HL₂ and HL₃ attached to the TDS but with a different RPM for HL₃. Therefore, we have three equations with three unknowns as follows

18

19

20

Solving the three equations yields the following

21

22

23

Here are the conditions that must be fulfilled for an accurate determination of TDS torque loss response;

• The loaded TDS measurements must be performed while the entire D/S is still in a vertical-cased section of the well, so that the only sources of friction are TDS friction and viscous drag in case if there is a fluid in this section.

• These measurements should be corrected for viscous torque by subtracting the estimated viscous torque along the drill string length from the surface torque reading.

• The surface torque, rotary speed, and HL gauges should be calibrated and in a good working condition.

• Testing the TDS under many HLs and rotary speeds will be much more accurate although it will need simple computer programs like MS-EXCEL to yield the TDS constants (in a timely manner) using regression.

• Generating a reactive torque chart for every TDS by applying a wide range of loading (rotary speed and thrust load) is highly recommended and it should be regularly updated.

2.5. Bit Torque

Bit-induced torque depends greatly on the type of bit and its characteristics. The mostly used formula in calculating bit induced torque is;³⁰

24

where μ_B is the bit aggressiveness or bit friction factor (dimensionless), WOB = weight on bit (lb), and D_B = bit diameter (inch).

2.6. Equations of the Model

The formulas deduced from previous sections to estimate T&D are summarized here. It is apparent that HL here is assumed to be only affected by the geometric component, where torque has—at least—three different factors.

25

26

27

28

29

3. Actual Case Studies

Four actual wells were studied as follows:

• 1.Horizontal well (A) with 4890′/2025′ MD/TVD, (ER = 2.41)
• 2.Horizontal well (B) with 4950′/2181′ MD/TVD, (ER = 2.27)
• 3.Horizontal well (C) with 8645′/5897′ MD/TVD, (ER = 1.47)
• 4.Horizontal well (D) with 11 092′/7930′ MD/TVD, (ER = 1.4)

The directional plots of the four wells are shown in Figures 4 and 5.

Figure 4.

Directional plots of wells A and B with the direction of horizontal stress.

Figure 5.

Directional plots of wells C and D with the direction of horizontal stress.

4. Work Strategy

In the following sections, the strategy will be as follows;

• 1.The validity of the simplified model will be checked for predicting T&D values by comparing its results with the actual values experienced during drilling of the mentioned wells.
• 2.Four statistical parameters will be used to verify the validity of the model, namely, average percent relative deviation (APRD), average absolute percent relative deviation (AAPRD), standard deviation (SD), and correlation coefficient (CC) (as shown in eq 30 through 34)
• 3.After verifying the model validity, it will be used in new spaces by studying how sensitive the model is toward certain inputs.

Statistical parameters are

30

where

31

32

33

34

5. Results and Discussion

The simplified model had been applied to four wells that obey the assumptions. Two of these wells are shallow, while the other two are deeper wells. Figure 6 through 13 demonstrates torque and HL versus depth for the wells from actual data and simplified-model outputs.

Figure 6.

Modeled vs actual torque and HL values in the 8 1/2″ section of well-A.

Figure 13.

Modeled vs actual torque and HL values in the 6″ section of well-D.

5.1. Well-A, 8 1/2″ Section

Actual on-bottom torque is erratic, which is attributed to the casing window, use of PDM (and subsequent micro-tortuosity), and high DLS in this section (up to 10.02°/100 ft). Despite this erratic torque, the simplified model gives reliable averaged torque prediction with a CC of 0.86. The model also gives excellent matching for pickup weight with CC = 0.93. Actual data for off-bottom torque, slack-off weight, and rotating weight suffer sampling frequency problems, but the model still gives reliable prediction for them (Figure 6).

5.2. Well-A, 6″ Section

The model predicted on-bottom torque with reasonable accuracy till 3200 ft, after which the combined effects of bit dull and extensive use of lost circulation material (LCM) pills caused the torque to drop. The pickup prediction for this section is still reliable with a CC of 0.82. Actual data for off-bottom torque and rotating weight also have sampling frequency problems, but the model still has small deviation and dependable output (Figure 7).

Figure 7.

Modeled vs actual torque and HL values in the 6″ section of well-A.

5.3. Well-B, 8 1/2″ Section

The erratic on-bottom torque in this section is similar to that of well-A, the model is representative of the average values of torque with only 6.5% APRD. The actual recorded off-bottom torque is not reliable at all; hence, the model cannot be verified for this parameter. The model accurately predicts pickup, slack-off, and rotating weights with a maximum of 6.6% APRD (Figure 8).

Figure 8.

Modeled vs actual torque and HL values in the 8 1/2″ section of well-B.

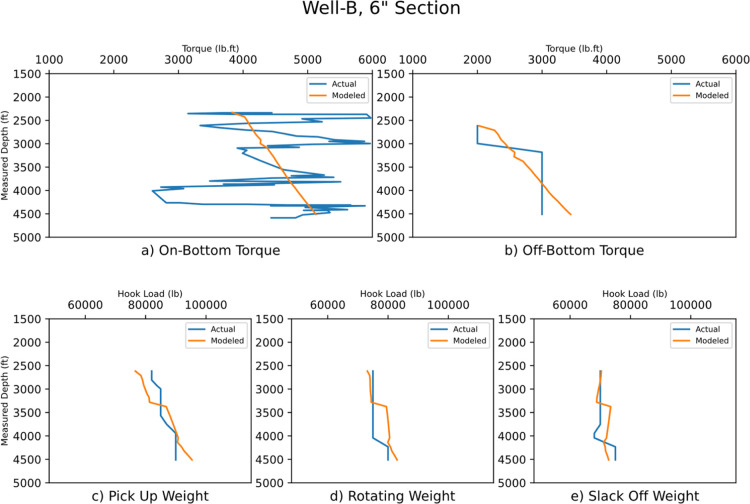
5.4. Well-B, 6″ Section

Despite the apparent sampling frequency problems of actual off-bottom torque and rotating weight, the simplified model has negligible errors in all modeled parameters (Figure 9).

Figure 9.

Modeled vs actual torque and HL values in the 6″ section of well-B.

5.5. Well-C, 12 1/4″ Section

Again, actual off-bottom torque and rotating weight in this section are not reliable; apart from these two parameters, the simplified model accurately predicts friction forces, especially pickup weight with only 0.14% APRD (Figure 10).

Figure 10.

Modeled vs actual torque and HL values in the 12 1/4″ section of well-C.

5.6. Well-C, 8 1/2″ Section

The simplified model accuracy was verified in this section, where we have very minor deviation which proves that the model performs best as DLS decreases and depth increases (Figure 11).

Figure 11.

Modeled vs actual torque and HL values in the 8 1/2″ section of well-C.

5.7. Well-D, 12 1/4″ Section

The simplified model seems to be very sensitive to the bit type, BHA, and drilling parameters as it is apparent from sharp change in torque charts at 6600 ft, where a trip was performed and mentioned factors were changed. These factors, off-course, do not affect HLs (Figure 12). An important point here is that all of the actual friction forces are less than modeled ones; this may be attributed to the fact that the well was drilled in the direction of minimum horizontal stress, which in the opinion of the authors is a recommended direction as it promotes wellbore stability. The enhancement to wellbore stability is primarily due to the effect of almost equivalent stresses on the wellbore (e.g., overburden and maximum horizontal stresses), compared to non-equivalent stresses in the case of drilling in the direction of maximum horizontal stress. The same note applies also to the next section of this well.

Figure 12.

Modeled vs actual torque and HL values in the 12 1/4″ section of well-D.

5.8. Well-D, 6″ Section

In this section, apart from off-bottom torque, the simplified model showed reliable outputs with APRD ranging from 0.16 to 7%. For off-bottom torque, the sampling frequency greatly affects the resolution of actual data, but the simplified model still represents the actual situation with CC = 0.97. The on-bottom torque in this section was not as erratic as previous sections; this was due to the higher wiper trip frequency in this section (1.54 per 1000 ft) compared to other sections (Figure 13).

5.9. Model Reliability

Cross-plots of actual versus modeled values are demonstrated for all values of both torque and HL for the eight sections of the four wells. As it is shown in Figure 14, the accuracy of the developed model is great for HL prediction with only—0.72% APRD and minimal dispersion around the diagonal line. The model is also reliable for torque prediction with a uniform distribution around the diagonal line, 0.93 CC and −10.3% APRD. Table 1 shows a summary of the model errors for all the studied wells, where one can link the model accuracy to the drilling conditions.

Figure 14.

Cross-plots for modeled vs actual torque and HL.

Table 1. Summary of the Model Errors for All of the Studied Wells.

well	section	value	APRD	AAPRD	SD	CC
A	8 1/2″	on bottom torque	1.89	14.31	18.22	0.857
A	8 1/2″	off bottom torque	0.86	14.34	16.808	0.9027
A	8 1/2″	pick up weight	4.979	7.007	9.988	0.932
A	8 1/2″	slack off weight	8.04	8.04	10.183	–0.193
A	8 1/2″	rotating weight	5.683	5.733	7.417	0.914
A	6″	on bottom torque	–41.19	52.701	70.537	–0.342
A	6″	off bottom torque	–31.429	31.429	35.403	0.995
A	6″	pick up weight	–0.851	3.81	4.178	0.816
A	6″	slack off weight	2.82	5.663	7.047	0.495
A	6″	rotating weight	0.387	4.055	4.865	–0.403
B	8 1/2″	on bottom torque	6.489	18.337	20.197	0.421
B	8 1/2″	off bottom torque	3.203	40.899	44.665	–0.995
B	8 1/2″	pick up weight	4.912	5.062	7.413	0.975
B	8 1/2″	slack off weight	6.684	6.684	7.281	0.7926
B	8 1/2″	rotating weight	6.211	6.401	9.074	–0.192
B	6″	on bottom torque	–9.99	22.645	32.963	–0.259
B	6″	off bottom torque	–3.265	8.865	10.527	0.7899
B	6″	pick up weight	0.328	3.488	3.829	0.905
B	6″	slack off weight	–0.895	2.933	3.473	0.158
B	6″	rotating weight	–2.66	3.631	4.328	0.584
C	12 1/4″	on bottom torque	19.039	19.039	19.83	0.863
C	12 1/4″	off bottom torque	6.861	23.951	27.649	0.723
C	12 1/4″	pick up weight	0.142	1.239	1.34	0.827
C	12 1/4″	slack off weight	–2.57	3.053	3.679	–0.337
C	12 1/4″	rotating weight	–1.386	1.693	1.885	0.178
C	8 1/2″	on bottom torque	–0.116	7.146	9.561	0.907
C	8 1/2″	off bottom torque	–15.177	17.998	23.022	0.728
C	8 1/2″	pick up weight	–2.073	2.386	2.651	0.907
C	8 1/2″	slack off weight	–5.913	6.044	6.686	0.301
C	8 1/2″	rotating weight	–7.834	7.834	7.948	–0.367
D	12 1/4″	on bottom torque	1.393	16.267	18.943	0.732
D	12 1/4″	off bottom torque	–31.678	31.678	33.146	0.894
D	12 1/4″	pick up weight	–2.427	3.142	3.392	0.857
D	12 1/4″	slack off weight	–3.989	4.247	4.65	–0.587
D	12 1/4″	rotating weight	–3.594	3.75	3.816	0.502
D	6″	on bottom torque	–6.941	10.359	16.329	0.959
D	6″	off bottom torque	–25.815	28.465	35.094	0.972
D	6″	pick up weight	–0.164	3.676	4.184	0.98
D	6″	slack off weight	–7.145	7.145	8.116	0.768
D	6″	rotating weight	–3.045	3.045	3.235	0.928

From these findings, the novel/simplified model reliability was verified within the model limitations, and it could be used for further calculations like sensitivity analysis.

5.10. Sensitivity Analysis

In order to study the factors that greatly affect the T&D model, sensitivity analysis was performed as shown in Figure 15 and the results are as follows;

• friction factor set was the parameter with the greatest impact on T&D values. That is why selection of the correct set of friction factors is vital for the success of T&D modeling. Besides T&D modeling, the friction factor was also very important in prediction of potential D/S buckling problems.³¹ Trend charts are very important tools in monitoring the hole conditions. In the 6 in. hole of well-D, the drilling was stopped at 11 092 ft due to high torque values although it was planned to drill the well deeper than that depth. The trend chart shows that the friction factor set shifted from 0.15/0.20 toward 0.20/0.25 at 10 200 ft and further toward 0.25/0.30 near TD.

• BHA placement played a crucial role in determining the torque acting on the D/S components. Although a BHA in the horizontal section may yield a lower read-out torque on surface gauges, due to lower rotating weight in most cases which generates lower torque loss in TDS, this placement strategy will induce more torque on the topmost joint of the D/S.

• Survey stations spacing was studied with three different modes (90, 180, and 360 ft). It was concluded that for the simplified model, 90 and 180 ft spacing yielded close values but increasing to 360 ft yielded totally erroneous outputs. This is inherent in the model assumptions, which treat every D/S segment as a straight one, while it will introduce tolerable errors at lower spacings; the error will be higher at greater spacing, especially in curved sections. Although 90 ft distance between stations is the standard oilfield practice, some circumstances dictate taking as much check shot surveys as possible like when the target is too tight or when many close targets are to be hit.³²

Figure 15.

Model sensitivity analysis for the friction factor, BHA placement, and spacing of survey stations.

5.11. Comments on Drilling Operations

From the eight studied cases using the simplified model, there appear some good practices during the drilling operations, like the fact that there was no D/S washout or twist-off occurred despite high torque values, this may be due to the strict inspection program which rejected many drill pipes before being used. The strict inspection program proved to be of a big value, especially in case of drilling abrasive formations.³³⁻³⁶

The practice of periodic wiper trips in some wells also appears to have a good effect on the friction profile. This is a proven practice to improve hole cleaning, especially if deviation from the normal drag trend is observed.³⁷ The degree of deviation from normal drag is used as an indicator for required wiper trip frequency.³⁸

In addition, LCM pumping to cure losses had a good side effect on T&D by causing a reduction in the friction factor. This is aligned with the findings from the Wytch Farm ERD project.³⁹ Also, the rigs used for drilling these wells were not over-engineered, and only fit-for-purpose rigs were used that caused a cost-effective drilling operation. On the other hand, recording (sampling) frequency of torque and HLs was not appropriate in many cases, which should be improved to enhance hole condition monitoring. A final comment is about use of RSSs; although it proved to reduce tortuosity, the authors see that using more expensive technologies should be justified on a case-by-case basis with respect to economics and operational needs. The results of this work suggested that drilling a well in the direction of minimum horizontal stress is better in terms of friction forces. This can be justified by the hole ovality that occurs due to greater stress anisotropy than that of a well drilled in the direction of maximum horizontal stress. Another practice that can reduce torque acting on the D/S is the split-BHA strategy. This strategy suggests placing heavier D/S members in the vertical or low-angle part of the well to provide necessary weight to overcome drag and to reduce torque by reducing contact force between the D/S and hole. In addition, bit aggressiveness should be quantified and standardized as an important drill bit characteristic, so that it can be used in T&D models directly.

6. Conclusions

A rig site-friendly T&D model was introduced with the advantage of simplicity and reliability. The model was built based on a soft-string concept with two-dimensional wells in mind, where DLS is not severe. Validity and practicality of the model had been proved by accounting for torque components that are always looked over in current models (like friction within TDS and friction due to mud viscosity) and replacing complex equations with much more simple equations. The model determines HLs with negligible errors and estimates drilling torque with about 10% APRD. Based on the obtained results, the following conclusions can be drawn from this research:

• 1.friction factor is not a unique value for a wellbore. Not only does it changes with the hole condition but also with the well trajectory, type of movement (axial or rotation), and even direction of movement.
• 2.Viscous torque can be neglected for predicting T&D values of high-angle wells as it is usually in the range of 2% of the total torque.
• 3.TDS-reactive torque charts should be continuously built and updated for each well. This is performed for a better monitoring of the actual torque to which D/S components are subjected.
• 4.Current standard survey station spacing of 91 ft is adequate for good T&D modeling in two-dimensional wells; even in cases where operations dictate less survey frequency, doubling the spacing has an acceptable effect on T&D modeling.

The model is very useful for the drilling team in office and on rig as it is quick and requires only a well-crafted spreadsheet to perform all the calculations. All commercial T&D packages require considerable time, cost, computational resources, and input data, which may be mandatory in three-dimensional designer wells. Simpler directional wells with no major azimuthal turns or excessive DLS are still the majority of wells drilled today and can be handled efficiently using the presented model.

7. Research Limitations

The findings of this study have to be seen in light of some limitations that could be addressed in future research. The first of them is the DLS range that this model was developed for. Wells with DLS above 11°/100 ft were not included in this paper. In this range of DLS, the effect of bending stress and tension would be too prominent to be ignored, and hence, further research would be required to assess the exact effect of too high DLS.

The second limitation is application of this model to three-dimensional wells with considerable azimuthal change (designer wells). Both types of wells have not been studied on this paper due to lack of reliable and complete data, and further research would be required.

Glossary

Acronyms

BHA

bottom-hole assembly

D/S

drill string

ERW

extended-reach well

LCM

lost circulation materials

OBM

oil-based mud

PDM

positive displacement motor

ROP

rate of penetration

RSS

rotary steerable system

T&D

torque and drag

TDS

top drive system

TOB

torque on bit

WBM

water-based mud

Glossary

Nomenclature

A

surface area (in.²)

AAPRD

average absolute percent relative deviation (%)

APRD

average percent relative deviation (%)

a, b, c

top-drive reactive torque constants

α_f

rotary speed-dependent torque factor, lb ft min^a

α_l

load-dependent torque factor, lb^(1–c) ft min^b

β

buoyancy factor (dimensionless)

CC

correlation coefficient (dimensionless)

CHFF

cased-hole friction factor

D

outside diameter of the pipe (inch)

D_B

diameter of bit (inch)

D_h

inside diameter of the hole section (inch)

DLS

dog-leg severity (°/100 ft)

ER

extended-reach ratio (dimensionless)

F

force (lb)

HL

hook load (lb)

K

fluid consistency (cp)

L

length of pipe (ft)

M

torque (lb-ft)

MD

measured depth (ft)

μ

friction factor (dimensionless)

μ_B

bit aggressiveness (dimensionless)

n

fluid flow index (dimensionless)

OHFF

open-hole friction factor

P/U wt

pick-up weight (lb)

RPM

rotary speed (rpm)

S/O wt

slack-off weight (lb)

SD

standard deviation

TD

total depth (ft)

TVD

true vertical depth (ft)

T

tension (lb)

τ

hydraulic shear stress (lb/100 in.²)

τ_y

yield point (lb/100 in.²)

WOB

weight on bit (lb)

w

nominal weight of the pipe (lb/ft)

γ

hydraulic shear rate (s^–1)

θ

inclination angle (deg)

The authors declare no competing financial interest.