Abstract
How do slums shape the economic and health dynamics of pandemics? A difference-in-differences analysis using millions of mobile phones in Brazil shows that residents of overcrowded slums engaged in less social distancing after the outbreak of Covid-19. We develop and calibrate a choice-theoretic equilibrium model in which individuals are heterogeneous in income and some people live in high-density slums. Slum residents account for a disproportionately high number of infections and deaths and, without slums, deaths increase in non-slum neighborhoods. Policy analysis of reallocation of medical resources, lockdowns and cash transfers produce heterogeneous effects across groups. Policy simulations indicate that: reallocating medical resources cuts deaths and raises output and the welfare of both groups; mild lockdowns favor slum individuals by mitigating the demand for hospital beds, whereas strict confinements mostly delay the evolution of the pandemic; and cash transfers benefit slum residents to the detriment of others, highlighting important distributional effects.
Keywords: Covid-19, Slums, Health, Social distancing, Public policies
“The issue is that everything is so close together here. One house next to the other; one on top of the other. What looks like only a small one is actually five or six in the same space. A lot of people here work outside of Paraisopolis. If the virus spreads here, it will spread all over Sao Paulo”. Hebert Douglas, resident of Paraisopolis, one of the largest slums in Brazil (Folha de São Paulo, 2020)
1. Introduction
Disease outbreaks can affect vulnerable people disproportionately, contributing to the increase in health and economic disparities. Since its onset, the Covid-19 pandemic has affected places where most social interactions occur, as the new coronavirus spreads mainly through close contact among people. Consequently, health authorities advise people to avoid crowded areas and to practice social distancing. Such measures can be challenging to put in practice in densely populated areas, such as overcrowded slums in developing countries. Residents of these neighborhoods are also poorer individuals whose incomes are likely to be more adversely affected by lockdowns. Slums are prevalent in the majority of cities in developing countries and more than 1 billion people in the world live in them (United Nations, 2020). Despite their importance, to the best of our knowledge, no paper in the growing literature on the economics of epidemics has addressed the role of slums in shaping the economic and health dynamics of pandemics. This paper fills this gap and makes three contributions.
Our first contribution is empirical. We use daily geo-localized data from millions of mobile phones in Sao Paulo and Rio de Janeiro, the two largest cities in Brazil, one of the countries most affected by the Covid-19 pandemic.1 Through a difference-in-differences analysis, we show that social distancing increased significantly less in areas with slums after the adoption of non-pharmaceutical interventions (NPIs) – such as the closure of schools, restaurants and retail stores – in both of these cities. Moreover, areas with slums are associated with more fatalities.
The second contribution is theoretical. We build a model with heterogeneous housing location and behavioral choices to address how the prevalence of slums contributes to the spread of infectious diseases. Individuals live in two localities: poorer agents live in high-density places (slums), while richer agents do not. Slum residents are also less likely to have access to intensive care units (ICUs) in hospitals, but they are on average younger (as in the data). People leave their houses to work or enjoy leisure outside and this can lead to infections. Individuals from different locations interact when they leave their homes. The model allows for both negative and positive externalities regarding social distancing. The risks that one group takes might spill over onto others through increased transmission (negative externality), but the point of herd immunity may be reached more quickly (positive externality).
The paper’s third contribution is quantitative. We parameterize the model to be consistent with Covid-19 transmission and with key empirical moments of the city of Rio de Janeiro. The model reproduces our empirical finding that, after the outbreak of the pandemic, low-income slum residents engage in less social distancing relative to individuals who live in other neighborhoods. As they are poorer, slum residents work relatively more hours even though this means spending more time in crowded areas. This leads to worse health outcomes for this group. Although slum dwellers correspond to 22% of Rio de Janeiro’s population, they account for around 30% of the Covid-19 deaths in the city. This group thus contributes more towards reaching herd immunity in society.2 In a counterfactual world without slums, residents in other neighborhoods end up catching the virus more and die in higher numbers.
The emergence of several epidemics (such as Ebola and three lethal coronaviruses) in less than 20 years highlights the importance of adequate policy responses to disease outbreaks. We then use the model to simulate a variety of policy experiments: the reallocation of existing medical resources, shelter-at-home policies, and cash-transfer schemes. In developing countries, most poor individuals do not have private health insurance and must rely on publicly provided health care that is often at capacity. We investigate the pooling of all intensive care units in Rio de Janeiro into one group that is offered to anyone who needs it, regardless of insurance. This alleviates the capacity constraints and decreases the death burden of the disease among both groups of the population. The total death rate is reduced by 28% relative to an environment with no policies. In our simulations, this redistributive policy positively impacts aggregate welfare and output.
Shelter-at-home policies act to delay the dynamics of the disease substantially. These policies buy time but, if vaccines or new treatments are not introduced quickly, they hardly change overall death rates. Lighter lockdowns can be more effective as they lead to an equilibrium in which the rate of growth in the number of infected individuals is slower than in the benchmark. This smooths the burden on hospital resources and saves lives. On the other hand, very strict lockdowns contain the disease so much that, when lifted, the health dynamics is quite similar to a no-policy scenario, only delayed. In addition, strict lockdowns promote a deep economic downturn in the short run. Confinement policies that shelter one particular group lead to a redistribution of deaths from the sheltered group to the other. This actually leads to the welfare of both groups to fall: one faces more deaths and the other a restriction on their movement.
Cash transfers are particularly important for the poorer individuals who live in slums. When we implement a policy that hands over cash to the population, slum dwellers can afford to become relatively more cautious. This decreases the number of infections among this group and consequently increases this statistic among those living in other neighborhoods.
We also explore extensions in our framework in which we relax some assumptions of the baseline environment. One such extension is the possibility of a vaccine. The economy will have essentially reached herd immunity if the pandemic develops unchecked and a vaccine only arrives 18 months after the outbreak. Another extension analyzes the case in which individuals do not necessarily become immune after recovering from Covid-19. In this scenario with partial immunity, the epidemic lasts longer and death tolls are substantially higher than in the baseline case (in which recovered individuals enjoy full immunity against the virus). We also introduce the possibility of telework among non-slums residents, increasing the contribution of slum residents for society to achieve herd immunity and heightening the disparities across the two groups.
This paper relates to the economics literature that adds behavioral choices to epidemiological models in the tradition of Kermack and McKendrick (1927). This effort has been mostly theoretical, e.g. Kremer (1996), Quercioli and Smith (2006), and Toxvaerd (2019). There exists some quantitative articles in the context of HIV/AIDS, such as Greenwood et al., 2017, Greenwood et al., 2019 and Chan et al. (2016). Our paper shares the principle of modeling infectious diseases with a special attention to behavioral choices. We contribute to this literature by studying individual choices in slums, which are an important feature in cities in the majority of developing countries.3
There has recently been a great incursion of the economics literature into the study of the Covid-19 pandemic.4 Some papers have looked at optimal confinement policies that force stricter levels of social distancing beyond what individuals endogenously choose, e.g., Alvarez et al. (2021), Farboodi et al. (2021), Giannitsarou et al. (2021) and Eichenbaum et al. (2021). A few papers have added choices made by heterogeneous groups, like different sectors (Kaplan et al., 2020) or age groups (Brotherhood et al., 2020) and (Favero et al., 2020). We also connect with the strand using spatial economic models to understand the diffusion of the Covid-19 pandemic (e.g., Argente et al. (2020), Bognanni et al. (2020), Cunat and Zymek (2020) and Fajgelbaum et al. (2020)). Our work is mostly related to Brotherhood et al. (2020) and Alon et al. (2020). We expand the framework developed by Brotherhood et al. (2020) by adding different locations (slums and other neighborhoods), poorer and richer agents, and differential access to health care. Few quantitative papers focus on studying the Covid-19 pandemic in developing countries.5 One exception is Alon et al. (2020), but they do not model slums and the impact of high-density environments as we do.
Our work also relates to two strands of the urban economics literature. First, we connect to the papers on agglomeration economies aiming to understand the advantages and disadvantages of density in cities (Duranton and Puga, 2004, Ahlfeldt et al., 2015, Henderson and Turner, 2020). Most of the papers in this field focus on the advantages of density and increased physical proximity, such as sharing ideas, fostering innovation, and faster technology adoption (Duranton and Puga, 2020). We add to some recent papers studying the costs of agglomeration (e.g., Combes et al. (2019)) by explicitly taking into account externalities of physical proximity in the context of a pandemic. Second, we add to the strand modeling the causes and consequences of slums (e.g., Alves, 2021, Brueckner and Selod, 2009, Monge-Naranjo et al., 2018, Cavalcanti et al., 2019 and Henderson et al. (2021)) by taking into account the externalities of slums during disease outbreaks.
This paper is organized as follows. The next section presents an empirical analysis regarding how the Covid-19 pandemic evolved differently in slums and other areas in Brazil. Section 3 describes the model environment and Section 4 discusses its calibration. Section 5 presents our baseline results and Section 6 provides results for policy experiments. Section 7 discusses some extensions to the baseline model. Section 8 concludes.
2. Empirical motivation
Slums are densely populated areas with narrow alleys and small houses.6 Most informal settlements lack adequate sanitation and piped water supply. Poverty is widespread. According to the 2010 Brazilian Population Census, the population density in slums in the cities of Rio de Janeiro and Sao Paulo is approximately five times larger than in other neighborhoods. In addition, per capita income of households living in slums in these two cities is roughly one-third of the income of those living in other areas. These features of slums imply that movement restrictions are in general more costly for individuals living in slums compared with those living in other neighborhoods. The impact of the pandemic on the adherence to social distancing practices in slums is, however, conceptually ambivalent: some factors may induce greater mobility (e.g., the need to work more hours because income losses are more severe for low-income families) or lower mobility (e.g., slum residents are more exposed to precarious employment conditions and more likely to lose their jobs) compared to non-slum areas.
To investigate how social distancing changed during the pandemic in areas with and without slums, we use a social distancing index created and developed by Inloco (www.inloco.com.br), a Brazilian technology company. The company collects anonymized location data from millions of mobile phones in Brazil, tracking (with a 3-meter precision) the devices’ location and movements to different places, but ensuring user privacy.7 The company divides cities into non-overlapping “hexagons” and measures the percentage of devices in a given hexagon that remained within a radius of 450 m of the location identified as home. The index is computed daily and ranges from zero to one, where the index corresponds to the fraction of devices that stay at home in a given day. We obtained the social distancing index for each hexagon from February 1 to May 30, 2020 (120 days) for two cities: Rio de Janeiro and Sao Paulo. Rio de Janeiro has 841 hexagons, Sao Paulo 1301 (see Figures A1 and A2 in Appendix A for more details on the non-overlapping hexagons).
We define slums as housing units in “subnormal agglomerations”. According to the population census, a subnormal agglomeration satisfies three conditions: (i) it consists of a group of at least 50 housing units, (ii) where land is occupied illegally and (iii) is urbanized in a disordered pattern and/or lacks basic public services such as sewage or electricity. Notice that there is a connection between housing units in subnormal agglomeration and the notion of a “slum”. See online Appendix A for more detail on data sources and definitions.8
Fact 1: Social distancing increased after non-pharmaceutical interventions (NPIs)
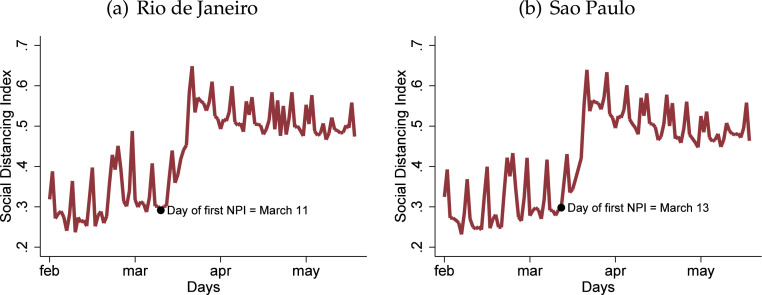
Fig. 1 contains the daily average social distancing index for the cities of Rio de Janeiro (Fig. 1(a)) and Sao Paulo (Fig. 1(b)). It shows that social distancing increased in both cities after NPIs were implemented. The first NPI affecting the city of Rio de Janeiro was announced on March 11. One can observe a sharp increase in the social distancing index just a few days after this measure was implemented. A similar pattern is observed for Sao Paulo, where the first NPI was announced on March 13.9
Fig. 1.
Social distancing index. Notes. The figure shows the evolution of the social distancing index for the cities of Rio de Janeiro and Sao Paulo between February 1 and May 18. The first non-pharmaceutical intervention in Rio de Janeiro was put in place on March 11 and in Sao Paulo on March 13.
Fact 2: In slums, social distancing increased less after the adoption of NPIs
We now present reduced-form evidence showing an association between social distancing and slums. The unit of investigation is the hexagon provided by Inloco. We build a dataset of socioeconomic characteristics for each hexagon based on the census tracts of the 2010 Brazilian Population Census conducted by the country’s statistical office (Instituto Brasileiro de Geografia e Estatística, IBGE) – see Appendix A for more details – and combine this dataset with our social distancing index. We then calculate the number of slum housing units in each hexagon. We create a dummy variable that equals one if the hexagon has any slum within its boundaries and zero otherwise. Rio de Janeiro has 510 hexagons with slums; Sao Paulo has 598 (see Figure A3 in online Appendix A for the location of those hexagons). The “treated group” is composed of hexagons with slums, while the comparison group is composed of hexagons without slums.
To investigate how social distancing evolved in slums compared to other areas after the implementation of NPIs, we use the following dynamic difference-in-differences specification:
| (1) |
where is the social distancing index for hexagon on day . The hexagon fixed effect accounts for unobserved time-invariant determinants of social distancing, while the inclusion of time fixed effects adjusts for aggregate shocks that are common to all hexagons. The indicator variable takes the value of one for hexagons with slums when days away from the day of the first NPI (), and zero otherwise. The parameter is the dynamic treatment effect. We set the coefficient on equal to zero to use the day before the first NPI as the base date—March 10 in Rio de Janeiro and March 12 in Sao Paulo. As the social distancing index is bounded between 0 and 1, each coefficient should be interpreted as a change in percentage points relative to the day before the first NPI. We cluster standard errors at the hexagon level and weight the observations by the hexagon population in 2010.10 The identifying assumption is that in the period of analysis, hexagons with slums would have had similar trends in social distancing (compared to hexagons without slums) in the absence of NPIs.
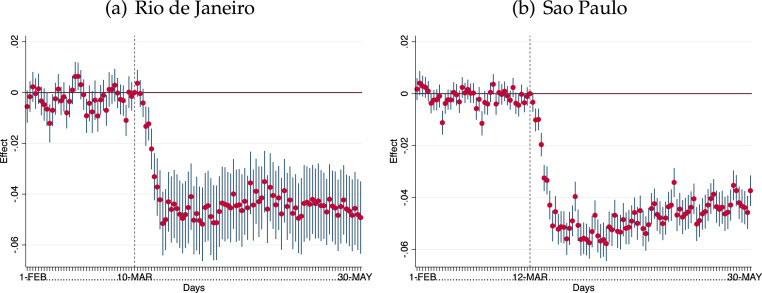
Fig. 2 shows the results of the dynamic difference-in-differences analysis. Hexagons with and without slums evolved similarly before the NPIs in both cities. This suggests the absence of different pre-trends in social distancing and therefore yields support for the main identifying assumption. Furthermore, this result suggests that prior to the NPIs there was no differential effect of the pandemic on social distancing. This is consistent with (i) the small change in mobility before the NPIs we observed in Fact 1 and (ii) the fact that at that time, the pandemic was in its early stages—the first COVID-19 case (on Feb 26, 2020 in Sao Paulo and Mar 05, 2020 in Rio de Janeiro) happened a few days before the NPIs.11
Fig. 2.
Dynamic difference-in-differences analysis: Effect of NPIs on social distancing in areas with slums relative to those without slums. Notes. The figure shows the results for coefficients estimated from Eq. (1). Coefficients should be interpreted as a change in percentage points relative to the base period, which corresponds to the day before each NPI. Vertical dotted lines indicate the day of the NPI in each city. The “treated group” is composed of hexagons with at least one housing unit in a slum. We use 841 hexagons in Rio de Janeiro and 1,301 hexagons in Sao Paulo. Data are provided at the hexagon-day level. The dependent variable is the social distancing index for hexagon on day . Standard errors clustered at the hexagon level. Confidence intervals: 95%.
After the first NPI, a sharp decline in social distancing (of about 4–5 percentage points) follows in hexagons with slums, relative to those without slums. Indeed, the results of a standard difference-in-difference strategy in Table B1 in online Appendix B show a (statistically significant) average reduction of the social distancing index of 3.9 and 4.3 percentage points in slum areas in Rio de Janeiro and Sao Paulo, respectively. This decline is relative to pre-Covid social distancing index of about 0.30 in both cities.12
The adherence of individuals to social distancing measures is different in areas with and without slums. The magnitude of the treatment effect is similar in both Rio de Janeiro and Sao Paulo, but the coefficients are more precisely estimated for the latter. Given the spatial distribution of slums in Rio de Janeiro, several hexagons in Appendix Figure A3(a) have a small part of slums within their boundaries. Standard errors may increase when we code hexagons using the slum dummy because part of the population lives outside a slum and thus may have a different mobility pattern. In Sao Paulo, slums are located in more remote areas, and the several hexagons in Appendix Figure A3(b) have a large share of slums within their boundaries. Appendix Figure B6 shows that the qualitative implications are similar when we change the treatment dummy for the slum share in each hexagon. Besides, standard errors reduce for Rio de Janeiro and remain precisely estimated for Sao Paulo.
Appendix Figure B7 depicts that lower-income workers are more likely to be working in-person. This is consistent with the observed relative drops in social distancing. Behavioral choices regarding social distancing can also be driven by leisure decisions. Our model in Section 3 rationalizes how labor and leisure decisions explain social distancing outcomes.13
Fact 3: More Covid-19 deaths occurred in areas with slums than in areas without slums.
The risk of Covid-19 transmission is higher in overcrowded areas, such as urban slums. In addition, one might expect that health facilities would be more congested in areas near slums. People in slums usually have less access to private health providers.14 Therefore, we would expect more Covid-related deaths in areas with slums than in other neighborhoods.
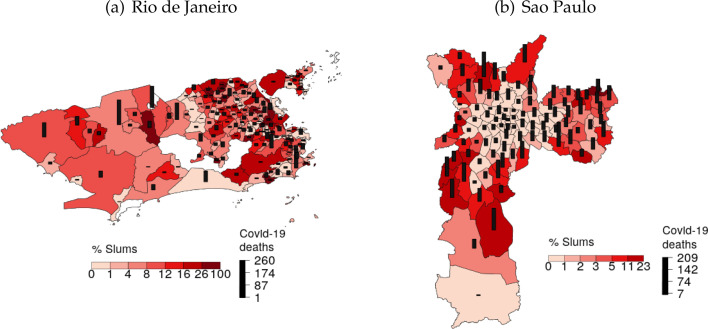
Fig. 3 provides descriptive evidence suggesting that places in Rio de Janeiro and in Sao Paulo with more slums experienced more Covid-19 deaths. This figure uses Covid-19 death data at the neighborhood level (which is a group of hexagons), as this is the most disaggregated level officially reported by both cities.
Fig. 3.
Slums and Covid-19 deaths. Notes. The figure shows Covid-19 deaths for the cities of Rio de Janeiro on June 14 and Sao Paulo on May 25. The percentage of slums in each area is from the 2010 census.
We now conduct the difference-in-differences analysis to check how (Covid and non-Covid related) deaths evolved in slums and non-slums areas using neighborhood-by-month data due to constraints on data availability (see Appendix A). We use the same specification as in Eq. (1) with deaths as the dependent variable, but now we use neighborhood fixed effects and month fixed effects. The dynamic treatment effect measures the differential impact of the pandemic on the number of deaths comparing neighborhoods with and without slums. Again, given the nature of our specification, we estimate the effect of the pandemic on the difference between neighborhoods with and without slums. The analysis period is from January 2018 until June 2021. The base period is January 2020—the month before the first case in Sao Paulo and Rio de Janeiro. Standard errors are clustered at the neighborhood level.
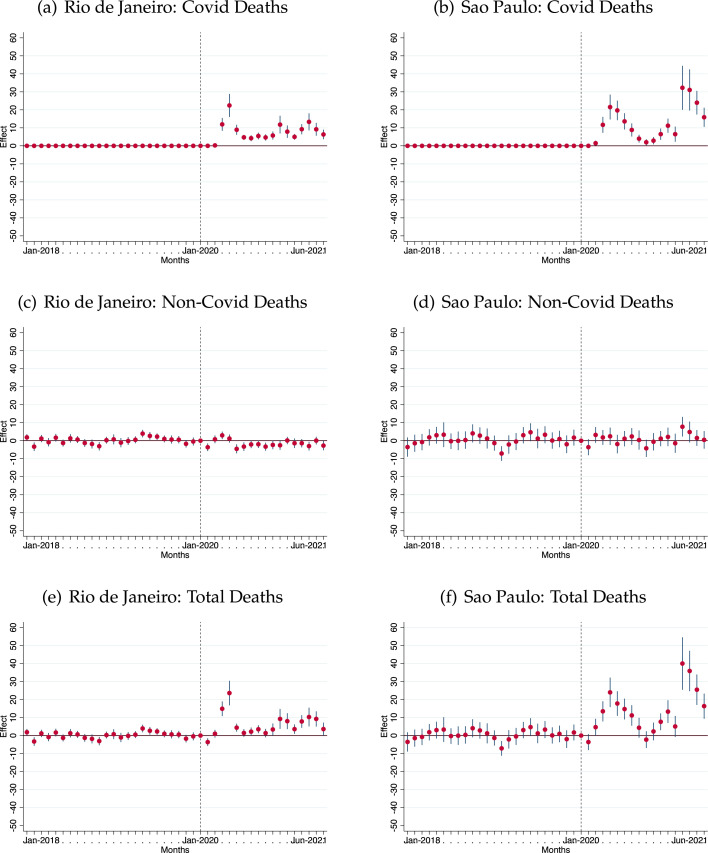
The results of Fig. 4 reveal statistically significant effects: neighborhoods with slums have more deaths by Covid-19 than those without slums in Rio de Janeiro and Sao Paulo (see panels (a) and (b)). The point estimate of every period after January 2020 is positive, and most of them are significantly different from zero. We observe that the effects present two peaks: in May-2020 and Apr-2021, consistent with the shape of the Covid-19 waves in Brazil—notice that the shape of the waves is more pronounced in Sao Paulo. In panels (c) and (d), we find no effects on non-Covid deaths, which suggests that the pandemic had no differential effects on other deaths. Finally, in panels (e) and (f), we analyze the impacts on total deaths. Our findings show that all the pre-treatment effects are indistinguishable from zero, i.e., there are no effects on total deaths before the pandemic. In addition, after January 2020, deaths are higher in neighborhoods with slums compared to those without slums, which is consistent with the rise in Covid deaths we observed.15
Fig. 4.
Dynamic difference-in-differences analysis: Effect on deaths in areas with slums relative to those without slums. Notes. The figure shows the results for coefficients estimated from Eq. (1) with neighborhood and month fixed effects. Coefficients should be interpreted as a change in number of deaths relative to the base period, which corresponds to January 2020. The “treated group” is composed of neighborhoods in Rio de Janeiro or Sao Paulo with at least one housing unit in a slum. There are 156 neighborhoods in Rio de Janeiro and 96 neighborhoods in Sao Paulo. Data are provided at the neighborhood-month level. Vertical dotted lines indicate the month before the first Covid case in Brazil (January 2020). Panels (a), (c), and (e) are for Rio de Janeiro, while Panels (b), (d), and (f) are for Sao Paulo. Panels (a) and (b): the dependent variable is the number of Covid-related deaths—the number of deaths between Jan-2018 and Feb-2020 is equal to zero. Panels (c) e (d): the dependent variable is the number of non-Covid-related deaths. Panels (e) and (f): the dependent variable is the total number of deaths. Standard errors clustered at the neighborhood level. Confidence intervals: 95%.
3. Model
In this section, we present a choice-theoretic SIR model in which individuals are heterogeneous on their income, location and access to ICUs. Individuals leave their house to work or enjoy leisure outside. Leaving home increases the risk of Covid-19 infection. We use the model to study the role of slums in shaping the economic and health dynamics of the Covid-19 pandemic.
Time is discrete. Suppose there are two groups of agents in this economy: those who live in slums (or favelas), , and others who do not, .16 Agents work, enjoy leisure outside their home, and home hours. Home hours can also be seen as a proxy for home production. In the presence of the new coronavirus, denote the agent’s health status by . A susceptible agent is denoted by . By spending time outside the house, the agent may catch Covid-19. An infected agent is denoted by . Conditional on being infected, the agent may either recover (with probability ) or develop more serious symptoms that require hospitalization in an ICU (with probability ). Denote a hospitalized agent by . Someone in the hospital may either recover (with probability ) or die (with probability ). The death probability is time varying as it may depend on the usage of scarce hospital resources. Such resources may also be different across the two groups. Moreover, we assume that the average slum resident is younger. This reflects different recovery and death probabilities across groups.17 A recovered individual () is assumed to be immune to the disease forever. Agents discount the future with factor .
An individual is endowed with one unit of time per period that may be used for work , leisure outside the house , and hours at home (“domestic” hours). The time constraint thus reads:
| (2) |
An individual derives utility from consumption , a composite leisure good consumed outside the home , and domestic hours . The good is produced using hours and buying “intermediate” goods according to the function . We normalize the utility after death to zero and capture the bliss from being alive through the parameter . The utility function is given by:
The term expresses an additional preference for staying at home when infected and is supposed to capture some partial altruism. This variable can take two levels: and , so that individuals who can transmit the virus are partially altruistic and the others have no need for that; has a similar role, but from the point of view of the government.18 This captures simple policies that confine all groups to staying at home ( but can also capture group-specific confinements ( and even condition on infection status.
An individual’s income consists of two terms. The first is labor income . Note that the wage per unit of time can vary by group. The second term corresponds to government transfers and can be time dependent. Denote it by . The budget constraint of the agent is given by:
| (3) |
A susceptible individual () may become infected when away from home. The longer one spends outside, the more likely it is that an infection takes place. For each unit of time spent outside the house, the transmission risk is given by . Note that this is time varying as it depends on two aggregate variables: (i) the fraction of infected people in the economy and (ii) the time infected people spend outside their houses. It can also be group specific as individuals from different groups may be more exposed to one group versus the other, due to differences in the density in their neighborhoods, for instance. This will be elaborated on later. The probability of catching the virus in a given period is given by
| (4) |
We turn now to decision making. The problem of a susceptible individual is described by the following maximization problem:
| (5) |
The first line in this problem corresponds to the instantaneous utility from consumption and leisure. The second line spells out the continuation value. The first term in curly brackets represents the situation in which the individual does not get infected this period and continues life as a susceptible person in the next period. The second term denotes the case in which the agent gets infected today and continues life as an infected individual in the next period.
The value function for an infected person who does not require hospitalization is given by
| (6) |
The first line captures the instantaneous utility from consumption and leisure and the situation in which the agent recovers from the disease. The second line is the continuation value in which the agent either requires hospitalization (first term in square brackets) or continues life as an infected person (second term).
Set the flow utility for a hospitalized individual at an ICU () to the same as death (i.e., zero). These individuals may still recover and enjoy utility from consumption, leisure, and bliss of life later. These agents do not work, but we assume they interact with people in the hospital and may thus infect others. Set an exogenous amount of time they interact with their carers to . Their value function thus reads as follows:
| (7) |
This value function consists of two scenarios: the first term corresponds to the patient recovering and leaving the ICU and the second term represents the case in which life continues in the hospital. With the remaining probability, the agent dies and the utility is normalized to zero.
Finally, an agent who has already recovered and is resistant to the virus enjoys utility:
| (8) |
It is important to keep track of the number of agents who find themselves in each of the situations described earlier. Denote the measure of agents of each type of group in period by . Let be the set of these for all s and s. Moreover, let and denote the policy function for hours worked and outside leisure, respectively, for each agent. Let the equilibrium time allocations in period across all and be summarized in . The law of motion from one period to the next is represented by the mapping :
| (9) |
The law of motion for susceptible people of a group reads as follows:
| (10) |
That is, the measure of susceptible people next period consists of those who are susceptible today and did not catch the virus. The right-hand side of (10) thus describes the mapping for susceptible individuals. The corresponding equations for the other groups are provided in Appendix C. The aggregate mapping in (9) is given by the collection of all .
Aggregate output in this economy is given by all the work supplied by agents of the different groups and infection statuses multiplied by their wages:
| (11) |
Turn now to the calculation of the probability of getting infected per unit of time spent outside. First, let represent an exogenous transmission rate from infected to susceptible. Now, assume that, when outside their homes, both groups (those who live or do not live in favelas) spend a fraction of their time in a common space shared by everyone. The remaining fraction of their time is spent only among members of their own group ( or ). These group-specific activities are undertaken within separate areas for each group. Denote by the fraction of the space that is assigned to group . This is supposed to represent the fact that slums have a much higher density than the rest of a city. Slum dwellers thus have to interact in much more confined spaces, and this contributes to a faster spread of the virus. We then have the following:
| (12) |
When , this expression reduces to a pure random-mixing situation.
The parameter is usually calibrated to match a basic reproduction number () at the outbreak of the epidemic. This number can be high enough such that it drives Eq. (12) to more than 1 because we do not control for the possibility of multiple infections in a given period. To avoid this, we take a continuous-time approximation that yields:
| (13) |
If is small, then .
We now define the probability that an agent that requires hospitalization () dies, . This is time varying, as it depends on the supply of scarce hospital resources (e.g., ICU beds) and the demand by sick patients. Suppose there are two networks of medical services: a public one to which everyone has access and a private one. Only individuals with health insurance can access the private network. Let and be the number of beds in the public and private hospitals, respectively. Assume also that no slum dweller () has access to health insurance and therefore to private hospitals. For the others (), a fraction has health insurance.
Let and be the number of users in the public and private networks, respectively. These are given by
| (14) |
where is the number of type- agents who need hospitalization.
Assume that an individual who needs hospital care and has access to an ICU bed dies with probability . Those without access to a hospital bed die with probability .19 The death probability for individuals living or not living in slums is given by the following two equations:
| (15) |
The first line spells out the probability of death for a slum dweller that requires hospitalization. This only depends on the excess demand for hospital beds in the public network. The second and third lines show the same for other agents. Now, with probability , they have access to the private network through their health insurance. With complementary probability, they use the public hospital network.
A rational-expectations equilibrium in this economy with initial number of agents consists of a sequence of infection and death rates and equilibrium time allocations such that these time allocations are part of the solutions to the individual optimization problems (5) to (8), and the resulting law of motion (9), and their aggregation in (13), (15) indeed gives rise to the sequence .
4. Fitting the model to the data
To analyze the role of slums in the Covid-19 pandemic, we must assign values to the model parameters. There are 28 parameters to be set. Some (22 parameters) are externally calibrated and others (6 parameters) are chosen such that certain model moments match their empirical counterparts. We focus our analysis on the city of Rio de Janeiro. Given that this is a framework to understand social behavior during a pandemic, we set the model period to one week.
City parameters: According to the 2010 Brazilian census, 22% of Rio de Janeiro’s population live in slums. We normalize the area of the model city to one. Then, given the share of the population living in slums (22%) and the population density in areas with slums relative to those without slums (4.05), we have the fraction of space assigned to slums as .20
The proportion of time individuals spend with members of their same group is given by . We set . This corresponds to the fraction of time spent outside that is not work related. The implicit assumption is that work-related activities take place across all groups whereas leisure outside is separate for each group.21
We normalize the wage rate of individuals who do not live in slums to one, that is, . We then set the wage rate of agents who live in slums to . Therefore, the relative hourly wage per capita of individuals who live in slums to those who do not is 27.7%, which is the number observed in the 2010 census data for Rio de Janeiro.
Panel A of Table 1 reports the values of the parameters related to Rio de Janeiro.
Table 1.
Calibration and estimation of model parameters: Rio de Janeiro.
| Parameter | Value | Interpretation | Source |
|---|---|---|---|
| Panel A: City parameters (6 parameters) | |||
| 0.222 | Fraction of people living in slums | Census | |
| 1 | Wage rate of non-slum agents | Normalization | |
| 0.277 | Wage rate of slum agents | Census | |
| 0.065 | Frac. of space assigned to slums | Census | |
| 0.934 | Frac. of space assigned to areas wo slums | Census | |
| 0.334 | Prop. of time spent within group | Work/all time outside | |
| Panel B: Disease parameters (15 parameters) | |||
| 11.43 | Infectiousness of Covid-19 | Internally estimated | |
| , | 1 | Prob. (serious sympt. no recovery from mild) | 1 week w/mild symptoms |
| 0.971 | Prob. of recovery from mild Covid-19, other | CDC & Verity et al. (2020) | |
| 0.979 | Prob. of recovery from mild Covid-19, slum | CDC & Verity et al. (2020) | |
| , | 0.284 | Prob. of recovery from serious Covid-19 | CDC & Verity et al. (2020) |
| 0.118 | Wkly death rate, other; critically ill with ICU | CDC & Verity et al. (2020) | |
| 0.073 | Wkly death rate, slum; critically ill with ICU | CDC & Verity et al. (2020) | |
| , | 1.0 | Wkly death rate; critically ill wo ICU | Assumption |
| 0.158 | Infections through the health care system | Butler et al. (2018) | |
| 0.152 | Prop. non-slum agents with priv. insurance | ANS | |
| 8.12e−5 | ICU beds (per capita) in public system | Covid Radar | |
| 4.9e−4 | ICU beds (per capita) in private system | Covid Radar | |
| Panel C: Preference parameters (7 parameters) | |||
| −1.72 | Elast. of subst. bw leisure time and goods | Kopecky (2011) | |
| 0.108 | Production of leisure goods | Internally estimated | |
| 1.089 | Rel. utility weight—leisure goods | Internally estimated | |
| 2.453 | Rel. utility weight—leisure at home | Internally estimated | |
| 1.995 | Rel. utility weight—leisure at home; infected | Internally estimated | |
| Discount factor | Standard | ||
| 8.575 | Value of being alive | Internally estimated | |
Disease transmission and development: We now turn to parameters that control the transmission and disease development of Covid-19. To discipline how infectious the disease is, we target the basic reproduction number, . Appendix D.1 describes how we can compute this statistic in the model. The parameter determines the per-period transmission rate in the model and is intimately related to . We thus pick to target a value of 2.5 for the basic reproduction number. This lies within the range used by Atkeson (2020). Ferguson et al. (2020) use while Zhang et al. (2020) estimate it to be 2.28. Remuzzi and Remuzzi (2020) report values between 2.76 and 3.25. This yields .
We set for both groups. This implies that an individual who is infected with Covid-19 spends one week with mild symptoms and then either recovers or becomes critically ill. To determine the probabilities of recovery, we turn to medical data. CDC (2020) reports age-specific transition rates between infection and ICU care, and from ICU to death. We aggregate these using Rio de Janeiro’s population pyramids for both slums and other areas, which come from the 2010 Brazilian census. This yields a 2.1% chance that someone in a slum who is infected ends up needing ICU care; the counterpart for other areas is 2.9%. Moreover, the probability of death conditional on being critically ill is 15.5% for slum residents and 22.9% for other individuals. The lower probabilities for hospitalization and death for slum residents is a consequence of a younger population living in these neighborhoods. We turn these probabilities into weekly rates to conform with our chosen model period.22 Moreover, Verity et al. (2020) report that a critically ill patient is discharged from the ICU after around 24.7 days, or 3.52 weeks. We assume the same length of treatment for both groups. This yields weekly probabilities of recovery from mild symptoms of and , weekly probabilities of recovering from the ICU of for all , and weekly death probabilities conditional on being in the ICU of and . We assume the death probability of a hospitalized patient who does not have access to an ICU bed to be for all .
Note that we assumed that a patient who is being treated in the ICU does not work or enjoy leisure but still interacts with others and may infect them. The amount of time in the model during which this interaction takes place is given by . Butler et al. (2018) estimate ICU patients interact with doctors, nurses, and other people around 7.6 h a day. Since this is a controlled environment, we use half this number to determine infections. This yields .
Panel B of Table 1 summarizes the calibrated values of the parameters related to the Covid-19 pandemic.
Preference parameters: We assume that the composite leisure good is produced according to the following function: . Following Kopecky (2011), we set . This yields an elasticity of substitution between leisure and goods of 0.368, which means they are complements.
We set the preference parameters , , and to target three data moments related to time use and expenditures in Brazil. First, we target the fraction of income spent on goods consumed outside the home.23 According to the Brazilian expenditure survey (POF), individuals in Rio de Janeiro spend on average 27.82% of their income on goods outside the home.24 Second, we target the average weekly hours at work. According to the Brazilian household survey (PNAD-C), Rio de Janeiro residents spend 34.2 h per week at work.25 Assuming an endowment of 112 non-sleeping weekly hours, this yields the fraction 0.306 for their time spent at work. Third, we target the leisure time outside. In Brazil, the average person spends around 17.2 h a week outside, which corresponds to the fraction 0.154 of their endowment of non-sleeping hours.26
The parameter denotes the increase in the marginal utility of staying at home for agents who are infected with Covid. This parameter is related to the extra amount of time an individual spends at home without any influence from the government. To identify this parameter, we turn to how agents behave when they contract influenza. Akazawa et al. (2003) report that the average American worker takes 1.3 days of sick leave when infected with influenza. Given a 40-h workweek, this implies an average of 10.4 h. We assume that the same would happen with Covid. As the disease lasts an average of one week (absent the need for ICU care), this implies a 26% decline in work time. We assume the same number for Brazilian workers. Suppose that leisure outside declines by the same amount. We then choose to match an increase in time spent at home by 26% compared with a world without Covid.
For the preference discount factor, we assume that agents discount the future at roughly 4% per year and set . The average real interest rate in Brazil was approximately 4.9% from 2005.1 to 2020.5 and 3.5% from 2009.1 to 2020.5.27
Finally, we must set a value for , the per-period value of being alive. Note that a higher value for this parameter implies that an individual will engage in more cautious behavior to avoid death. We thus pick to generate an increase in time at home as the one observed at the outbreak of the Covid-19 pandemic. The issue is that most countries adopted lockdowns at the same time. We thus look at Sweden, a country that did not implement severe restrictions. Google Mobility Data reports an increase of 15.7% in time at home in Sweden in April 2020. We take this to represent week 8 of the epidemic. As slums are not an important factor in Sweden, we use this 15.7% hike as the target of a version of our model without slums. This yields a value of .
Panel C of Table 1 contains the calibrated preference parameters. Table 2 summarizes some targeted moments of the model and their data counterpart. The model matches the moments of Rio de Janeiro quite well.28 Throughout the results of the following sections, we show that the model also fits some non-targeted moments. In particular, the model quantitatively replicates the differential behavioral response of individuals in slums and other neighborhoods as well as the decline in output during the pandemic.
Table 2.
Targeted moments—model vs. data.
| Moment | Model | Data (ranges) |
|---|---|---|
| Share of individuals living in slums | 22% | 22% |
| Pop. density in slums/Pop. density in non-slum areas | 4.5 | 4.5 |
| Relative hourly labor income of individuals in slums | 27.7% | 27.7% |
| , Covid-19 | 2.5 | 1.6–4 |
| % of infected in critical care | 3.6 | 3.6 |
| Weeks in critical care | 3.5 | 3–6 |
| % in critical care who die | 20.24 | 10.6–31.8 |
| Hours/day interacting while in ICU | 3.8 | 7.6 (controlled) |
| Hours of work per week | 34.2 | 34.2 |
| Hours of outside activities per week | 17.2 | 17.2 |
| % of income on goods outside | 27.28 | 27.28 |
| % in time @ home – mild symptoms | 26 | 26 (Influenza) |
| % in time @ home — outset of Covid-19 | 15.7 | 15.7 |
| % of non-slum agents with priv. insurance | 15.21 | 15.21 |
5. Baseline results
This section presents our baseline results. Our main focus is to understand the role of slums in the pandemic. We first describe the path of our baseline economy when there is an outbreak of Covid-19 and no policy intervention. Different policies are investigated in the next section.
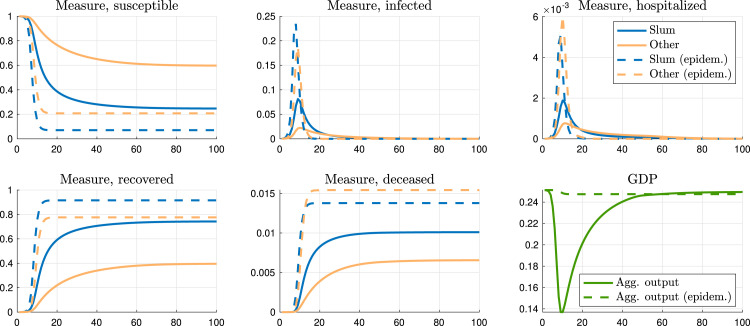
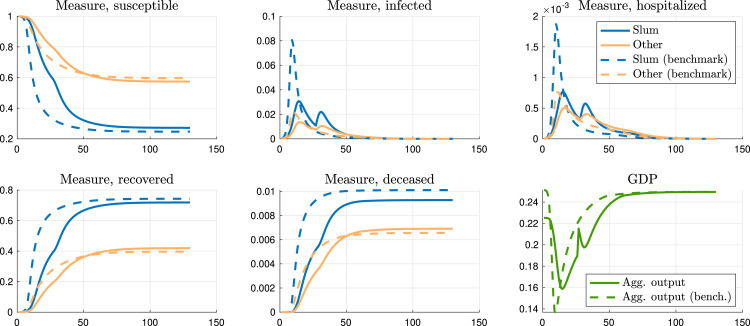
Fig. 5 shows the masses of individuals in different health states: susceptible, infected, hospitalized, recovered, and deceased. The blue lines describe the dynamics of individuals who live in slums, while the orange lines represent those who are not slum dwellers.29 The solid lines display our economic model with equilibrium social distancing, and the dashed lines show, for comparison, the counterfactual epidemiological model, in which behavior is unchanged relative to a world without the pandemic.30 The last graph in this figure displays aggregate output. Along with this figure, Table 3 summarizes key moments of the pandemic in our baseline model (first column) and in a typical epidemiological model (second column), where behavior is kept constant by assumption.
Fig. 5.
Aggregate variables, baseline.
Table 3.
Baseline results.
| Benchmark | Epidem. | No slum | Homog. | Homog. | Homog. | |
|---|---|---|---|---|---|---|
| densities | wage rates | age struct. | ||||
| Wks to peak srsly ill (slum) | 10.00 | 9.00 | – | 15.00 | 10.00 | 10.00 |
| Wks to peak srsly ill (other) | 11.00 | 10.00 | 14.00 | 14.00 | 11.00 | 11.00 |
| Srsly ill p/1000 @ peak (slum) | 1.88 | 5.09 | – | 0.66 | 1.19 | 2.18 |
| Srsly ill p/1000 @ peak (other) | 0.77 | 6.02 | 0.65 | 0.68 | 0.74 | 0.75 |
| Dead p/1000 1year (slum) | 10.04 | 13.78 | – | 6.32 | 8.87 | 13.49 |
| Dead p/1000 1year (other) | 6.35 | 15.43 | 6.87 | 6.86 | 6.78 | 6.57 |
| Dead p/1000 1year (all) | 7.16 | 15.06 | 6.87 | 6.74 | 7.25 | 8.11 |
| Dead p/1000 LR (slum) | 10.11 | 13.78 | – | 6.53 | 9.07 | 13.68 |
| Dead p/1000 LR (other) | 6.57 | 15.43 | 7.47 | 7.30 | 7.13 | 6.83 |
| Dead p/1000 LR (all) | 7.35 | 15.06 | 7.47 | 7.13 | 7.56 | 8.34 |
| Immune in LR (slum), % | 74.33 | 91.60 | – | 51.78 | 70.11 | 72.37 |
| Immune in LR (other), % | 39.69 | 77.66 | 46.01 | 44.72 | 43.03 | 40.76 |
| Immune in LR (all), % | 47.36 | 80.75 | 46.01 | 46.28 | 49.03 | 47.76 |
| GDP at peak - rel to BM | 1.00 | 1.82 | 1.48 | 1.23 | 1.29 | 1.03 |
| GDP 1year - rel to BM | 1.00 | 1.14 | 1.17 | 1.00 | 1.17 | 0.99 |
| Hrs @ home (slum) - peak | 80.95 | 60.48 | – | 69.19 | 86.38 | 83.22 |
| Hrs @ home (other) - peak | 86.28 | 60.48 | 78.00 | 80.00 | 82.26 | 84.90 |
| Hrs @ home (slum) - 6 m | 66.03 | 60.48 | – | 65.35 | 74.38 | 68.93 |
| Hrs @ home (other) - 6 m | 69.40 | 60.48 | 72.42 | 72.82 | 70.79 | 70.12 |
| Value - susceptible (slum) | 1968.10 | 1962.10 | – | 1976.60 | 4305.90 | 1960.20 |
| Value - susceptible (other) | 4317.40 | 4283.10 | 4315.00 | 4315.30 | 4315.60 | 4316.50 |
| Value - susceptible (all) | 3797.00 | 3769.00 | 4315.00 | 3797.20 | 4313.50 | 3794.50 |
The total duration of the unchecked epidemic is about a year (when herd immunity becomes strong enough to essentially prevent further contagion), and the peak in terms of seriously ill individuals is reached in about 11 weeks. As the virus spreads, social distancing endogenously rises as evidenced by the hike in hours at home by both groups. The number of infected people is thus reduced relative to the typical epidemiological model. This also translates into a lower death toll in the benchmark. GDP at the peak is substantially higher in the epidemiological model relative to the baseline. With the rising risk of getting infected and possibly dying, agents cut time spent outside their home and sharply reduce their working hours.
Turning now to the role of slums in shaping health and economic dynamics, Table 3 shows that the benchmark economy features a much higher death toll in slums relative to other areas. The total death rate is 7.35 per 1000 individuals, but in slums it is roughly 10 per 1000 residents. Though slum dwellers represent only 22% of the city’s population, they account for 30% of the overall deaths. This can be explained by the higher population density in slums and therefore more contagion, as well as more congestion of intensive care units – more on these issues later – but also by differences in the individual choices of slum and non-slum residents.
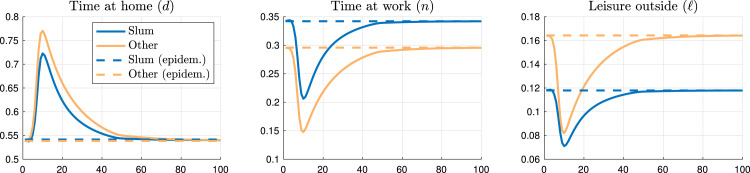
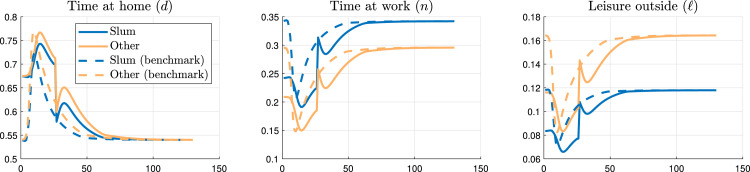
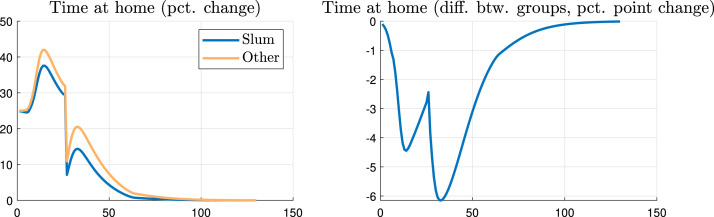
Fig. 6 displays the time spent at home, at work, and with leisure outside. Social distancing (the increase in time at home relative to an epidemiological model with no behavioral change) is lower for slum dwellers than for other individuals. Since they are poorer, slum residents decrease the number of hours worked by less than non-slum individuals even though they have a higher chance of catching the virus. Fig. 7 shows the difference in social distancing between the two groups at the outbreak of the pandemic. At the peak of the disease, social distancing is about 10 percentage points lower for slum residents compared with others. This is qualitatively consistent with our difference-in-differences analysis using mobile phones in Rio de Janeiro, displayed in Fig. 2. Quantitatively, the unchecked epidemic generates a larger effect on the difference in social distancing between slum and non-slum individuals.31 Recall that in our model this is an unchecked epidemic, while the data includes NPIs. We will discuss the effects of NPIs in our model in the next section.
Fig. 6.
Choices of susceptible agents.
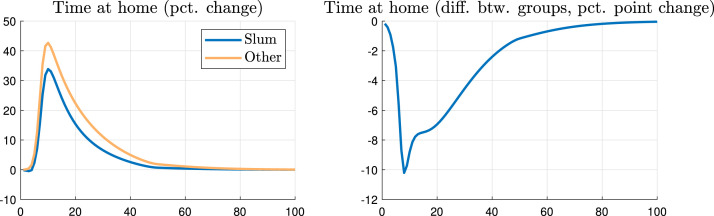
Fig. 7.
Difference in protection behavior between slum and non-slum agents.
To further assess the role of slums in the pandemic, we run a counterfactual in which we set the measure of slum individuals to zero and keep all other parameters at their baseline values. See the third column of Table 3. For the non-slum residents (the only ones in this hypothetical world), the death rate is now higher than the baseline: 7.47 per 1000 in the counterfactual versus 6.57 in the benchmark. There are two reasons for this. First, in the baseline, close to 75% of slum residents are immune in the long run. That is, they contribute a lot to reach herd immunity. In the benchmark, only 40% of non-slum individuals are infected throughout the pandemic. Without slums, this number rises to 46%. The second reason is that with a safer environment in the non-slum world, other individuals are less cautious. For instance, at the peak, they spend about eight fewer hours at home.32 In the end, residents from other areas end up with a lower welfare in this scenario without slums.
In our model environment, slum dwellers are different in four important characteristics: they live in denser areas, their wage rate is lower, they are on average younger, and it is harder for them to be admitted to an ICU. We now investigate the role of the first three factors in shaping the dynamics of the pandemic. Easier access to ICU beds will be assessed in our policy section.
The fourth column of Table 3 contains statistics for a counterfactual in which , which implies that the population density in slums is the same as that observed in other areas. All other parameters are kept at their baseline values. The pandemic lasts longer now since the spread of the virus is reduced, and it takes more time to reach herd immunity. Relative to the baseline, the death rate of slum dwellers is reduced from 10.11 to 6.53 per 1000 individuals—a 35% reduction. The death rate of other individuals rises from 6.57 to 7.30—a rise of about 11%. That is, living in a neighborhood with higher density is crucial to generating more deaths among slum residents. With less contagion due to a lower population density in slums, individuals expose themselves more by spending less time at home, offsetting in part the direct effect of a lower population density in slums.
In the fifth column of Table 3, we increase the wage of slum dwellers and equate it to the wage of other agents; that is, . All other parameters remain at their baseline values. Relative to the benchmark, since they are now richer, individuals who live in slums spend more time at home. As these agents are now more cautious, their death rate is reduced from 10.11 to 9.07, a reduction of 10%. Given that a lower number of slum dwellers are infected now, the economy can only reach herd immunity with a higher fraction of non-slum residents being infected. This also translates into a higher death toll among the latter group, an increase from 6.57 to 7.13 per 1000. As non-slum residents account for a larger fraction of the population, the overall death rate slightly increases.
Slum dwellers are on average younger, and this translates into lower hospitalization and death probabilities for members of this group. The last column in Table 3 reports the results of a counterfactual in which we equate these probabilities across the two groups. In this thought experiment, slum residents face the same (worse) recovery and death probabilities as individuals from other areas. Even though the infection rates are similar to the benchmark, death numbers are about 13% higher in this scenario. Therefore, ignoring the fact that individuals living in slums are younger can lead to misleading conclusions about the number of fatalities in these communities. As life is now riskier in slums, this group becomes more cautious and spends more time at home. With a lower supply of labor, GDP goes down even further compared to the baseline.
In sum, in our unchecked pandemic calibrated to Rio de Janeiro, slums have a nontrivial role in shaping the effects of Covid-19. First of all, the death rate in slums is higher than in other areas. Slum dwellers’ share in total deaths is much higher than their fraction in the overall population of the city. In addition, the high population density in slums compared with other parts of the city is a key feature in explaining the high death rate observed in slums. The presence of slums decreases significantly the time to reach herd immunity and protects individuals who live in other neighborhoods. Policies that aim to curb the Covid-19 pandemic in societies with a high fraction of their population living in slums must then take this fact into account. The next section explores the effects of a variety of such policies.
6. Policy experiments
In this section, we assess the impact of NPIs to control the health and economic impact of the pandemic in our model economy. We evaluate three policies: the government requisition of private hospital intensive care units to increase capacity to meet the demand for Covid-19-related treatment, lockdown interventions to increase social distancing (shelter-at-home orders), and financial aid policies to help people stay at home.
6.1. Public hospital beds
In Rio de Janeiro, approximately 15% of individuals have private health insurance and therefore access to private hospital beds. Intensive care units in public and private hospitals have 510 and 3079 beds, respectively (in a city of about 6.3 million people).
In our calibration, we assume that slum dwellers have no health insurance and approximately 19% of the individuals who do not live in slums have private insurance. We should expect that congestion of health services is therefore greater in slum areas.33 In this policy intervention, we investigate the impact of a counterfactual experiment in which the ICUs in private hospitals could be used to treat all individuals in need of critical care.
Table 4 shows that the total death rate is reduced by approximately 28% with this policy. Although slum dwellers are the ones who benefit the most from this policy, individuals who live in non-slum areas are also positively affected since only a small fraction of them have private health insurance. Observe that most of the agents decrease social distancing with this intervention as time at home decreases. But the difference is not quantitatively so different from the unchecked epidemic. The decrease in the death rate is mainly explained by the direct effect of reducing congestion in access to public hospital care units rather than by indirect effects of changing behavior. In the long run, more individuals of both groups survive and become immune to the disease. This policy increases GDP and the welfare of both groups.
Table 4.
All hospital beds used by the public system.
| Benchmark | All beds | |
|---|---|---|
| public | ||
| Wks to peak srsly ill (slum) | 10.00 | 10.00 |
| Wks to peak srsly ill (other) | 11.00 | 11.00 |
| Srsly ill p/1000 @ peak (slum) | 1.88 | 2.84 |
| Srsly ill p/1000 @ peak (other) | 0.77 | 1.07 |
| Dead p/1000 1year (slum) | 10.04 | 6.84 |
| Dead p/1000 1year (other) | 6.35 | 4.82 |
| Dead p/1000 1year (all) | 7.16 | 5.27 |
| Dead p/1000 LR (slum) | 10.11 | 6.85 |
| Dead p/1000 LR (other) | 6.57 | 4.86 |
| Dead p/1000 LR (all) | 7.35 | 5.30 |
| Immune in LR (slum), % | 74.33 | 77.03 |
| Immune in LR (other), % | 39.69 | 42.89 |
| Immune in LR (all), % | 47.36 | 50.46 |
| GDP at peak - rel to BM | 1.00 | 1.02 |
| GDP 1year - rel to BM | 1.00 | 1.04 |
| Hrs @ home (slum) - peak | 80.95 | 80.26 |
| Hrs @ home (other) - peak | 86.28 | 85.01 |
| Hrs @ home (slum) - 6 m | 66.03 | 62.61 |
| Hrs @ home (other) - 6 m | 69.40 | 65.91 |
| Value - susceptible (slum) | 1968.10 | 1974.90 |
| Value - susceptible (other) | 4317.40 | 4325.80 |
| Value - susceptible (all) | 3797.00 | 3805.10 |
6.2. Shelter-at-home policies
We now investigate stay-at-home orders that can be implemented with the closing of nonessential businesses and schools, among other interventions. Table 5 displays results for different lockdown restrictions.
Table 5.
Shelter-at-home policies.
| Benchmark | 6-week late | ||||||
|---|---|---|---|---|---|---|---|
| Immediate lockdown |
lockdown | ||||||
| 25%, all | 25%, slums | 25%, non-slum | 75%, all | 25%, all | |||
| 26 weeks | 26 weeks | 26 weeks | 35 weeks | 26 weeks | |||
| Wks to peak srsly ill (slum) | 10.00 | 14.00 | 13.00 | 11.00 | 66.00 | 11.00 | |
| Wks to peak srsly ill (other) | 11.00 | 16.00 | 14.00 | 12.00 | 67.00 | 12.00 | |
| Srsly ill p/1000 @ peak (slum) | 1.88 | 1.07 | 1.11 | 1.86 | 1.88 | 1.10 | |
| Srsly ill p/1000 @ peak (other) | 0.77 | 0.48 | 0.71 | 0.57 | 0.77 | 0.48 | |
| Dead p/1000 1year (slum) | 10.04 | 9.21 | 9.13 | 10.00 | 0.00 | 8.68 | |
| Dead p/1000 1year (other) | 6.35 | 5.84 | 6.92 | 5.28 | 0.00 | 5.26 | |
| Dead p/1000 1year (all) | 7.16 | 6.58 | 7.41 | 6.33 | 0.00 | 6.02 | |
| Dead p/1000 LR (slum) | 10.11 | 9.51 | 9.29 | 10.19 | 10.10 | 9.29 | |
| Dead p/1000 LR (other) | 6.57 | 6.48 | 7.22 | 5.91 | 6.56 | 6.34 | |
| Dead p/1000 LR (all) | 7.35 | 7.15 | 7.68 | 6.86 | 7.35 | 7.00 | |
| Immune in LR (slum), % | 74.33 | 73.58 | 70.96 | 76.68 | 74.36 | 73.29 | |
| Immune in LR (other), % | 39.69 | 40.32 | 42.96 | 38.18 | 39.67 | 40.57 | |
| Immune in LR (all), % | 47.36 | 47.69 | 49.16 | 46.71 | 47.35 | 47.82 | |
| GDP at peak - rel to BM | 1.00 | 0.96 | 1.12 | 0.86 | 0.99 | 0.95 | |
| GDP 1year - rel to BM | 1.00 | 0.87 | 0.98 | 0.89 | 0.47 | 0.87 | |
| Hrs @ home (slum) - peak | 80.95 | 83.18 | 84.40 | 79.79 | 80.19 | 83.76 | |
| Hrs @ home (other) - peak | 86.28 | 85.87 | 81.83 | 89.56 | 85.95 | 86.16 | |
| Hrs @ home (slum) - 6 m | 66.03 | 78.32 | 79.22 | 63.80 | 105.84 | 77.22 | |
| Hrs @ home (other) - 6 m | 69.40 | 79.79 | 70.83 | 78.39 | 105.84 | 78.36 | |
| Value - susceptible (slum) | 1968.10 | 1964.40 | 1964.20 | 1968.20 | 1863.20 | 1964.40 | |
| Value - susceptible (other) | 4317.40 | 4312.90 | 4315.30 | 4314.80 | 4213.00 | 4313.30 | |
| Value - susceptible (all) | 3797.00 | 3792.70 | 3794.50 | 3795.00 | 3692.50 | 3793.10 | |
The first column in Table 5 reports moments related to the baseline unchecked pandemic for comparison. The second column shows the same statistics for a scenario in which a shelter-at-home policy covers 26 weeks from the start of the health crisis. During the duration of this policy, individuals are required to increase their time at home by 25% relative to an environment without the pandemic.34 As we can also see in Fig. 8, the lockdown (solid lines) flattens out the infected and critically ill curves relative to the unchecked pandemic (dashed lines). The total death rate decreases, mainly among slum dwellers. There is less congestion of public beds with the lockdown, which is a more binding issue for individuals living in slums. The total death rate among slum dwellers decreases by approximately 6% while the overall death rate is reduced by 3%.
Fig. 8.
Aggregate variables (lockdown, 25% increase in time at home, all groups, 26 weeks).
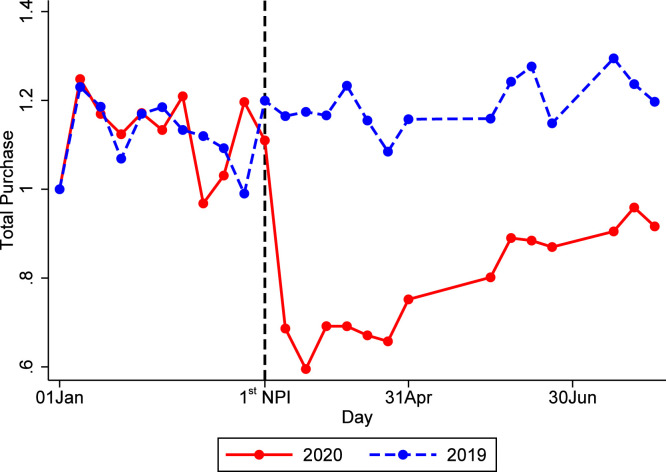
GDP during the first year of the pandemic decreases by 13% relative to the no-policy baseline. In the first few weeks of the epidemic, however, the drop in output is more pronounced, reaching a trough around 45% lower than the no-disease scenario. As the disease wanes, GDP starts to recover. To provide a (non-targeted) comparison with the data, Fig. 9 shows a quantitatively similar evolution in credit card transactions in Rio de Janeiro.35 Fig. 9 displays a sharp decrease in transactions of about 40% a few weeks after the first NPI.
Fig. 9.
Card transactions in Rio de Janeiro: 2019 and 2020. Notes. The figure shows the evolution of the weekly value of credit card transactions in the municipality of Rio de Janeiro. The figure plots two periods for comparison: January 01 and 31 July 2019, and January 01 and 31 July 2020. The value is normalized to 1 in the first week of January of each year. Credit card transaction data stem from one of Brazil’s largest banks, which has a large market share in many indicators, including assets and the number of credit card customers (more than one-third of the market share). The transaction data is aggregated to the municipality-week level. The first non-pharmaceutical intervention (NPI) in Rio de Janeiro was on March 11, 2020.
The strong impact on the economy comes from a reduction in the time spent at work. Fig. 10 reports the choice of the agents with a 26-week shelter-at-home policy (solid lines), as well as the benchmark (dashed lines). Individuals stay longer at home with this lockdown policy than in the baseline, reducing the peak of infection but increasing the duration of the health crisis.
Fig. 10.
Choices of susceptible agents (lockdown, 25% increase in time at home, all groups, 26 weeks).
The time spent at home increases by about 20 percentage points relative to the baseline before the outset of the disease (left panel of Fig. 10). This is approximately the average percentage point change in the social distancing index observed in the city of Rio de Janeiro (see Fig. 1 in Section 2). In addition, the model implies a difference in social distancing between slum and non-slum dwellers of around five percentage points (Fig. 11). This is similar to those reported in our difference-in-differences analysis in Fig. 2 of Section 2.
Fig. 11.
Difference in protection behavior between slum and non-slum agents (lockdown, 25% increase in time at home, all groups, 26 weeks).
To understand the role of slums in shaping the dynamics of the pandemic under a lockdown, we also investigate the effects of targeted shelter-at-home orders: a policy of increased social distancing applied only to individuals living in slums (third column of Table 5) and one applied only to those who live in other areas (fourth column of Table 5). The shelter-at-home policy in slums only increases the long-run death rate for non-slum individuals because the fraction of non-slum dwellers necessary to reach herd immunity would need to rise to compensate for the lower transmission in slums. As the non-slum group is larger, this translates into a higher overall death rate. This policy ends up lowering the welfare of both groups: slum residents are worse off because they are sheltered (even though deaths among this group decrease) and the others suffer a worse health shock.
We also implement a more extreme lockdown policy (fifth column of Table 5) in which we target a rise in 75% in the time spent at home relative to the baseline. This policy lasts for 35 weeks or approximately 8 months. Almost no deaths occur in the first year of the pandemic, which now lasts much longer. Therefore, a stricter lockdown is an effective strategy to delay the peak and to control temporarily the number of infected individuals and deaths. This might be an important policy while waiting to build public infrastructure (e.g., hospital beds) and/or define a future plan of action to control the virus, including waiting for a possible treatment or vaccine. Without improvements in infrastructure, treatment, or a vaccine, however, the total number of deaths with or without an extreme lockdown is roughly the same: when the extreme lockdown is relaxed, the numbers of infections and seriously ill patients rise sharply leading to similar deaths compared with the case without the policy. The extreme shelter-at-home policy clearly causes a deep economic downturn.
Our shelter-at-home policies so far were implemented in the beginning of the pandemic, when congestion of public ICUs is not necessarily binding. In the last column of Table 5, we implement a lockdown policy similar to the one in the second column, but that is imposed in week 6 of the pandemic, instead of week 1. This later lockdown is more effective in saving lives. The total death rate is reduced by 5% instead of 3%, as in the lockdown that is implemented in week 1. The economic effects of both shelter-at-home policies are similar.
6.3. Financial aid
We now turn to study the effects of an emergency measure designed to compensate individuals for income losses due to a rise in social distancing. Table 6 contains such counterfactual experiments. Again for comparison, the first column of this table contains the moments of the unchecked pandemic. The second column displays the same statistics for the case in which the government transfers 300 Brazilian Reais (R$) per month for all individuals in the first 26 weeks of the pandemic.36 This corresponds to 44% and 12% of the monthly income of slum and non-slum dwellers, respectively.
Table 6.
Financial aid policies.
| Benchmark | Only financial aid |
Aid and 25% lockdown for all |
||||||
|---|---|---|---|---|---|---|---|---|
| 300R$, all | 300R$, slums | 600R$, slums | 300R$, all | 300R$, slums | 600R$, slums | |||
| 26 weeks | 26 weeks | 26 weeks | 26 weeks | 26 weeks | 26 weeks | |||
| Wks to peak srsly ill (slum) | 10.00 | 15.00 | 14.00 | 32.00 | 32.00 | 32.00 | 32.00 | |
| Wks to peak srsly ill (other) | 11.00 | 16.00 | 15.00 | 19.00 | 33.00 | 33.00 | 33.00 | |
| Srsly ill p/1000 @ peak (slum) | 1.88 | 0.77 | 0.80 | 1.16 | 1.51 | 1.23 | 1.61 | |
| Srsly ill p/1000 @ peak (other) | 0.77 | 0.50 | 0.63 | 0.52 | 0.67 | 0.58 | 0.63 | |
| Dead p/1000 1year (slum) | 10.04 | 8.99 | 8.94 | 8.81 | 9.01 | 8.96 | 9.07 | |
| Dead p/1000 1year (other) | 6.35 | 6.40 | 6.94 | 6.89 | 5.49 | 5.98 | 5.88 | |
| Dead p/1000 1year (all) | 7.16 | 6.97 | 7.39 | 7.31 | 6.27 | 6.64 | 6.59 | |
| Dead p/1000 LR (slum) | 10.11 | 9.28 | 9.16 | 9.15 | 9.54 | 9.40 | 9.58 | |
| Dead p/1000 LR (other) | 6.57 | 6.91 | 7.30 | 7.36 | 6.48 | 6.72 | 6.70 | |
| Dead p/1000 LR (all) | 7.35 | 7.43 | 7.71 | 7.76 | 7.15 | 7.32 | 7.34 | |
| Immune in LR (slum), % | 74.33 | 71.90 | 70.69 | 70.33 | 73.58 | 72.44 | 72.27 | |
| Immune in LR (other), % | 39.69 | 41.95 | 43.41 | 43.96 | 40.35 | 41.39 | 41.55 | |
| Immune in LR (all), % | 47.36 | 48.58 | 49.45 | 49.80 | 47.71 | 48.27 | 48.36 | |
| GDP at peak - rel to BM | 1.00 | 1.16 | 1.24 | 1.30 | 1.10 | 1.20 | 1.12 | |
| GDP 1year - rel to BM | 1.00 | 0.94 | 0.99 | 0.98 | 0.84 | 0.89 | 0.91 | |
| Hrs @ home (slum) - peak | 80.95 | 78.61 | 80.46 | 77.55 | 78.85 | 77.99 | 80.36 | |
| Hrs @ home (other) - peak | 86.28 | 77.74 | 77.99 | 80.32 | 83.88 | 82.00 | 84.49 | |
| Hrs @ home (slum) - 6 m | 66.03 | 73.96 | 74.77 | 80.16 | 82.24 | 83.64 | 87.05 | |
| Hrs @ home (other) - 6 m | 69.40 | 71.91 | 70.83 | 70.03 | 77.57 | 77.49 | 72.87 | |
| Value - susceptible (slum) | 1968.10 | 1985.60 | 1985.70 | 1998.80 | 1982.40 | 1982.60 | 1996.70 | |
| Value - susceptible (other) | 4317.40 | 4322.20 | 4315.70 | 4315.60 | 4320.70 | 4315.10 | 4316.70 | |
| Value - susceptible (all) | 3797.00 | 3804.60 | 3799.60 | 3802.40 | 3802.80 | 3798.50 | 3802.80 | |
Fig. 12 shows that this policy flattens out the infection curves. This effect is more pronounced in slums. The income effect is stronger for slum dwellers than for those individuals who live in other areas (time at home at the peak is essentially the same across the two groups). This implies that individuals living in slums increase social distancing much more than in the benchmark. The total death rate among individuals living in slums is reduced by 8% relative to the baseline. Given that the threshold for herd immunity rises for non-slum dwellers, their total death rate ends up increasing by 5% during the pandemic. The overall death rate rises since the measure of individuals not living in slums is large. This composition effect on death rates becomes more pronounced when only slum dwellers receive the financial aid – third column of Table 6 – or when the financial aid is more generous (600 R$ for 26 weeks instead of 300 R$)—fourth column of Table 6.
Fig. 12.
Aggregate variables (300R$ financial aid for 26 weeks, all groups).
We now combine cash transfers lasting 26 weeks with stay-at-home orders that cover the same period (we target a rise in 25% in the time spent at home relative to the baseline by rising , see Appendix D.3). Such a combination of policies was implemented in several countries including Brazil.37 Start with a transfer of 300 R$. The combined policy extends the duration of the pandemic, much longer than when each of the policies is implemented separately. When the policy is relaxed, infections rise rapidly and the overall death rate is only 3% below the baseline. However, the death rate among slum dwellers is higher than in the case of only cash transfers or only the lockdown. Welfare with transfers and lockdown is of course higher than in the case with only lockdown. Targeting the transfer to slum dwellers exacerbates the differences across groups, as it decreases infections and deaths in slums and increases these statistics in other areas.
7. Extensions
In our baseline framework, the pandemic ends when the virus cannot infect enough people to sustain the spread of the disease. This occurs when a large measure of individuals becomes immune after recovering from the disease. When Covid-19 emerged, there were some expectations that recovery from the disease could confer permanent immunity. However, there is evidence showing that there is only temporary immunity and vaccines against the virus have been developed. Concerning these observations, this section provides two important extensions of the baseline environment: we introduce a vaccine in the middle of the pandemic such that individuals can acquire immunity through vaccination (Section 7.1); and we analyze the case in which individuals who overcome the disease can either become immune or susceptible again (Section 7.2).
Moreover, Section 7.3 discusses the results of an extension of the model in which richer non-slum individuals can partially telework and hence decrease their exposure to the virus. Finally, Section 7.4 provides an alternative calibration based on data for the city of Sao Paulo, the largest city in Brazil.
7.1. A world with a vaccine
Dozens of Covid-19 vaccines have been authorized or approved around the globe. Getting everyone vaccinated, however, takes time. We relax our baseline environment by assuming that a vaccine arrives after 78 weeks, or approximately 18 months. Suppose there is no uncertainty about this time frame and individuals in the model have perfect foresight.
Table F4 in the Appendix provides the results for the benchmark under the assumption of vaccine arrival. Time to peak, death rates, and behavior are virtually the same as under the baseline calibration. When we simulate the world without slums, residents in other neighborhoods face higher infection rates and deaths. They also have ex-ante higher utility in a world with slum individuals than when we set the measure of these agents to zero. By the time the vaccine arrives 18 months after the outbreak, most of the dynamics of an unchecked epidemic will have already come to pass.
7.2. Partial immunity
In our baseline framework, individuals who recover from the disease acquire immunity to the virus. Since the degree of acquired immunity is somewhat uncertain, we relax the assumption of permanent immunity and consider the case in which agents can become susceptible again after recovering from infection. More specifically, suppose that, after recovering from the disease, individuals can transit to the recovered state , where they are immune forever, with probability . With complementary probability , individuals become susceptible again (state ). Given the lack of evidence in the medical literature, we set . Table F5 in the Appendix provides the results. Since more individuals are susceptible to the disease, death rates rise substantially and approximately 1.4% of the population dies during the pandemic. Although its peak still happens around three months after the outbreak, an unchecked epidemic lasts longer now. Unlike the baseline scenario, a substantial fraction of total deaths happens in the second year of the epidemic.
The role of slums in shaping the composition of deaths during the pandemic is robust when we relax the assumption of permanent immunity. There is still a lower number of deaths among non-slum individuals in the presence of slums than when we run the counterfactual model without slums. In addition, non-slum agents still prefer to live in an environment when there are slum dwellers than when we set the measure of those agents to zero.
7.3. A scenario in which richer individuals can telework
In our benchmark model, individuals can only work by venturing outside their home, a risky proposition in the presence of Covid-19. During the pandemic, however, some individuals were able to telework. In this section, we allow for this possibility for the richer non-slum residents.38
Besides spending time in outside work , outside leisure and domestic leisure , assume now that non-slum residents can also choose some fraction of time to telework, such that . For these individuals, their budget constraint is now given by . The function is decreasing in and represents the fact that, as more work is moved from in-person to the home, the productivity of workers may fall (the details of the calibration are provided in Appendix F).
Our main insights carry over to this scenario with teleworking for the richer non-slum population. The health disparities across groups are now more pronounced. The infection and death rates among the non-slum group decreases since they can now protect themselves better via teleworking without incurring a complete loss in income. Consequently, this extra protection among the non-slum group generates an externality for the slum population that now has to contribute more towards herd immunity.
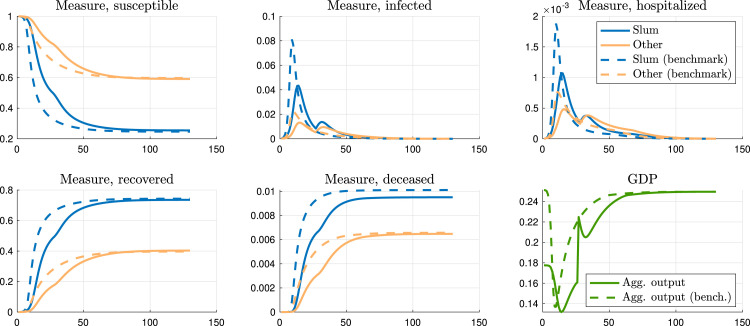
7.4. An alternative calibration for Sao Paulo
Our baseline calibration used data for the city of Rio de Janeiro. In this section, we briefly discuss an alternative calibration that targets statistics for the city of Sao Paulo (see Appendix F for more detailed results). In Sao Paulo, around 11% of the population live in slums, which is about half the share in Rio de Janeiro. Moreover, there are slightly more ICU beds per capita in the public hospital network in Sao Paulo than in Rio de Janeiro and slum residents are a little richer relative to non-slum dwellers.
The main difference in the benchmark scenario between Rio de Janeiro and Sao Paulo is that the non-slum residents in Sao Paulo are more impacted by Covid-19. Non-slum residents in Sao Paulo contract the virus in higher numbers and, consequently, the death rates among this group are higher compared with Rio de Janeiro. The main reason for this result is that the slum population in Sao Paulo corresponds to a smaller fraction of the overall population. Hence, slum residents contribute less towards achieving herd immunity and the burden falls relatively more heavily among the non-slum dwellers.
8. Conclusions
More than one billion people in the world live in slums. These are usually crowded neighborhoods where social distancing is hard to implement, and access to improved water and sanitation are limited. Infectious diseases can thus spread rapidly in such areas. This paper studies the role of slums in shaping the health and economic dynamics of pandemics. Using data gathered from millions of mobile phones in Brazil, we show that social distancing increased less in slums at the outset of the Covid-19 pandemic. Moreover, there were more deaths in areas with slums.
We build a model with endogenous social distancing where poor agents live in high-density slums and richer individuals live in other areas. Slum residents have a harder time accessing health care due to capacity constraints in public hospitals, but they are on average younger. We fit our model such that it is consistent with epidemiological parameters of the Covid-19 pandemic and to match key moments of Rio de Janeiro, where 22% of individuals live in slums. In the outbreak of the Covid-19 pandemic, our model produces relatively lower social distancing among slum residents. In equilibrium, individuals living in slums spend more time outside working because they are poorer and their marginal utility of consumption is higher—this difference is reinforced when we introduce the possibility of working from home for the richer non-slum individuals. Our simulations show that a disproportionately high number of deaths occur in slums. In a counterfactual scenario without slums, the pandemic lasts longer and a higher fraction of residents from other areas catches the disease and die, as the burden to achieve herd immunity falls only onto this group.
Using the model to explore a variety of policy experiments highlights the importance of taking this heterogeneity into account. Reallocating private ICUs into a single pool helps all groups, decreasing the death toll significantly. Very stringent shelter-at-home orders buy time but only delay deaths if no other policy, vaccine or new treatments are introduced. If lockdowns shelter a particular group, the other group suffers worse health outcomes, and the welfare of both groups declines. Cash transfers have a disproportional impact on slum residents and, as they can now afford to cut their labor supply, infections fall more heavily on the other group.
Though our framework has considerable heterogeneity that allows for an array of policy experiments, we have abstracted from potentially important margins. For instance, individuals in our model are assigned a place of residence and cannot move. Perhaps long-lasting pandemics may lead them to relocate, and health considerations may then affect the very structure of the city. Additionally, temporary cuts in labor supply may have enduring effects on job prospects. Being more likely to have informal jobs, slum dwellers may suffer more from such displacements. Finally, optimal policies may depend on the existence of heterogeneous groups living in the same geographical location. These and other issues are left for future research.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Financial support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001, Faperj and the Keynes Fund is gratefully acknowledged. This research received institutional support from the Spanish Science, Technology and Innovation System (project reference PID2020-114040RB-I00). Caio Castro, Bruna Mirelle, Pedro Sant’Anna and Pedro Ogeda provided excellent research assistance. The views expressed in this article are those of the authors and do not necessarily represent those of Banco de Portugal or the Eurosystem.
Inloco (www.inloco.com.br), a Brazilian technology company, shared the data on social distancing. See Section 2 for details on these data.
We also consider an extension in which there is a possibility of working from home among the non-slum dwellers, which reinforces these results.
From a historical perspective, the association between slums and pandemics goes well beyond the Covid-19 pandemic, including the cholera outbreak in the 1850s in London’s slums (Smith, 1964, Ambrus et al., 2020) and the Spanish Flu outbreak in slums in Philadelphia (Crosby, 2003).
See Boissay and Rungcharoenkitkul (2020), Brodeur et al. (2021) and Stantcheva (2022) for recent reviews of this growing literature.
There are some articles investigating empirically the health and economic effects of the Covid-19 pandemic in developing countries. See, for instance, Egger et al. (2021) and the World Development articles on “Pandemics, COVID19, and Sustainability and Development”, including the paper by Ray (2020). See also Bottan et al., 2020, Palamim and Marson, 2020 and Rocha et al. (2021).
The definition of slums varies depending on the country, but slums are always associated with low standards of urban services, overcrowding and illegal occupation of land (Cavalcanti et al., 2019).
See Peixoto et al. (2020) for more details on the Inloco data. Ajzenman et al. (2022) compare Inloco’s and Google’s social distancing indexes for Brazil and show a high correlation between the two measures.
Before the pandemic, there were no large differences in cellphone penetration between slum and non-slum areas. Using the 2019 National Health Survey data and Pitcairn et al. (2021)’s methodology to classify households into slum and non-slum residents, we find that 95.80% and 92.58% of households in non-slum and slum areas have cellphones, respectively. However, individuals in slums might use their phones differently during the pandemic (e.g., the possibility of remote working is different between the two groups of residents).
In Sao Paulo, Decree 64,862, on March 13, suspended public events with more than 500 people and public school classes (and recommended the same for private schools). In Rio de Janeiro, Decree 45,966, on March 11, stipulated the measures that would be adopted: isolation, quarantine, and specific medical treatments.
Figure B4 in Appendix B shows that results are qualitatively similar when we do not use population weights, but the point regression coefficients are less precisely estimated. Results remain significant when we cluster standard errors at the neighborhood level—see Appendix Figure B5.
This is different from other settings where there was a differential effect of the pandemic itself between rich and poor areas, followed by an additional differential effect after NPIs.
Column (III) of Table B1 in Appendix B shows that the reduction in the social distancing index was 0.43 percentage points lower in Rio de Janeiro compared to Sao Paulo (but statistically not significant).
The day-by-day analysis of Fig. 2 suggests that the relative decrease in social distancing is similar during weekend days (leisure days) and weekdays (work days). Appendix Figure B8 splits the sample and finds comparable magnitudes of relative social distancing drops on weekdays (Monday to Friday) and weekend days (Saturday and Sunday). This fact can be rationalized by (i) ethnography studies suggesting that slum dwellers work relatively more during weekend days (e.g., Nisbett (2017)); and (ii) a mechanism in our model regarding labor and leisure times changing in the same proportion due to the equalization of marginal benefits and costs—See Section 3.
Approximately 15% and 22% of the overall population have access to private health insurance in Rio de Janeiro and Sao Paulo, respectively.
Serological tests in Brazilian slums point out that Covid-19 infections are higher in slums and exceed official data (Prefeitura Rio de Janeiro, 2020). Due to data restrictions, excess mortality data cannot be analyzed at the intra-city level in Brazil. Bruce et al. (2020) show that the Covid-19 health impacts in a given slum in Rio de Janeiro depend on the type of criminal organization that operates in its territory.
We abstract from endogenous housing choice and other characteristics of slums such as weak property rights; see Cavalcanti et al. (2019). Due to the swift timeline of a pandemic, we take housing choice and the spatial housing distribution of a city as given.
Slum residents are on average younger than individuals in other areas both in our Brazilian data and in data from other countries; see United Nations (2006). Despite their younger age, slum residents may not necessarily be healthier. We explore the impact of the different death and recovery probabilities in Section 5.
The subscript denotes that is a policy instrument.
We assume the death probabilities to be group specific to reflect different age structures across the two neighborhoods. See Section 4 for details.
The population density in areas with and without slums in the city of Rio de Janeiro is from the 2010 census data. Although informal settlements are changing the geography of Rio de Janeiro, we consider only the current habitable areas of city. Population density in Rio de Janeiro’s slums is about 25,701.18 individuals per square kilometer and in areas without slums it is 6,344.46. The difference is a factor of four.
Table E3 in Appendix E provides robustness exercises in which . The main insights are qualitatively similar to our baseline calibration.
See Appendix D.2.
As do (Brotherhood et al., 2020), we classify the following items of the consumption basket as goods consumed outside: food away from home, public transportation, medical services, and entertainment.
The expenditure survey POF is the Pesquisa de Orçamento Familiar for 2008–09.
The national household survey PNAD-C is the Pesquisa Nacional por Amostra de Domicílios Contínua. For the year 2019, we get the average hours worked per week and multiply by the share of people who have a job or are self-employed.
The total hours of leisure outside are computed adding time spent commuting (Pereira and Schwanen, 2013) and activities related to socializing and cultural and sport activities. These data come from the 2009 PNAD and the test pilot time-use survey.
This is the monthly Over/Selic interest rate (Brazilian Central Bank rate) minus the inflation rate measured by the IGP-DI (general price index from Vargas Foundation). We annualized the monthly average real interest rate and inflation. These two variables can be downloaded from www.ipeadata.gov.br.
Appendix E provides sensitivity analysis with respect to the model parameters. The baseline results are similar to the ones obtained with the benchmark calibration.
In our calibration, 22% of individuals live in slums. Thus, any change in the figure is relative to this initial mass.
In a world without Covid-19, individuals’ health status are unchanged. They choose consumption and their allocation of time to maximize their static utility function subject to the time and budget constraints.
We should interpret with caution the comparison of our theoretical social distancing measure with the empirical index based on mobile phones. The theoretical measure is an intensive margin proxy for social distancing, while the index constructed by Inloco is an extensive margin measure. If we interpret in the model the home time as the fraction of households that stay at home, then the model and the empirical counterpart would be equivalent.
Slum dwellers live in high-density areas and, in equilibrium, spend more time outside working than non-slum individuals because they are poorer and their marginal utility of consumption is higher. This increases the rate of infection among them and the risk of contagion among any other agent who goes outside their home. So, in equilibrium, non-slum individuals are more cautious in a world with slums compared with a scenario without them. In addition, without slums, the duration for the unchecked pandemic to peak is about 40% longer than when there are slums. Hence, non-slum individuals have more time to contract the virus.
Rocha et al. (2021) show that in Brazil the correlation of Covid-19 death rates and ICU beds in the public sector is −0.5 with a -value of 0.02; while the correlation of death rates and ICU beds in the private sector is not statistically different from zero.
We implement this by increasing to the necessary value to induce agents to follow the lockdown policy. Appendix D.3 reports the calibrated values for all counterfactuals in this section.
Credit card transaction data stem from one of Brazil’s largest banks, which has more than one-third of the credit card market share. Ajzenman et al. (2022) compares these transaction data with the Brazilian Central Bank’s administrative credit registry on the universe of transactions and find a strikingly high correlation between both measures.
This amount is approximately 60 US dollars in July 2020.
In 2020, Brazilian informal workers received 600 R$ per month for three months during the pandemic (“Emergency Assistance”) as a compensation for their confinement. There were several issues related to the timing of the policy and to the bureaucracy involved in receiving this cash transfer.
According to PNAD-Covid, a nationally representative household survey conducted by IBGE between May and October 2020, more than 60% of lower-income individuals were working in person; for higher-income individuals only 20% of them were working in person—see Appendix Figure B7.
Online appendix
An online appendix to this article can be found online at https://doi.org/10.1016/j.jdeveco.2022.102882.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Data availability
Data will be made available on request.
References
- Ahlfeldt Gabriel M., Redding Stephen J., Sturm Daniel M., Wolf Nikolaus. The economics of density: Evidence from the Berlin wall. Econometrica. 2015;83(6):2127–2189. [Google Scholar]
- Ajzenman Nicolás, Cavalcanti Tiago, Da Mata Daniel. More than words: Leaders’ speech and risky behavior during a pandemic. Amer. Econ. J.: Econ. Policy. 2022;forthcoming [Google Scholar]
- Akazawa Manabu, Sindelar Jody L., Paltiel A. David. Economic costs of influenza-related work absenteeism. Value in Health. 2003;6(2):107–115. doi: 10.1046/j.1524-4733.2003.00209.x. [DOI] [PubMed] [Google Scholar]
- Alon Titan, Kim Minki, Lagakos David, VanVuren Mitchell. Lockdown in developing and developed countries. Covid Econ. 2020;22:1–46. [Google Scholar]
- Alvarez Fernando, Argente David, Lippi Francesco. A simple planning problem for COVID-19 lock-down, testing, and tracing. Amer. Econ. Rev.: Insights. 2021;3(3):367–382. [Google Scholar]
- Alves Guillermo. Slum growth in Brazilian cities. J. Urban Econ. 2021;122(C) [Google Scholar]
- Ambrus Attila, Field Erica, Gonzalez Robert. Loss in the time of cholera: Long-run impact of a disease epidemic on the urban landscape. Amer. Econ. Rev. 2020;110(2):475–525. [Google Scholar]
- Argente David O., Hsieh Chang-Tai, Lee Munseob. National Bureau of Economic Research; 2020. The Cost of Privacy: Welfare Effects of the Disclosure of COVID-19 Cases: Working Paper 27220. [Google Scholar]
- Atkeson Andrew. National Bureau of Economic Research; 2020. What Will Be the Economic Impact of COVID-19 in the US? Rough Estimates of Disease Scenarios: Working Paper 26867. [Google Scholar]
- Bognanni Mark, Hanley Doug, Kolliner Daniel, Mittman Kurt. IIES; 2020. Economic and Epidemics: Evidence from an Estimated Spatial Econ-SIR Model: IIES Working Paper. [Google Scholar]
- Boissay Frederic, Rungcharoenkitkul Phurichai. BIS Bulletin, Vol. 7. Bank for International Settlements; 2020. Macroeconomic effects of Covid-19: an early review. [Google Scholar]
- Bottan Nicolas, Hoffmann Bridget, Vera-Cossio Diego. The unequal impact of the coronavirus pandemic: Evidence from seventeen developing countries. PLoS One. 2020;15(10) doi: 10.1371/journal.pone.0239797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodeur Abel, Gray David, Islam Anik, Bhuiyan Suraiya. A literature review of the economics of COVID-19. J. Econ. Surv. 2021;35(4):1007–1044. doi: 10.1111/joes.12423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brotherhood Luiz, Kircher Philipp, Santos Cezar, Tertilt Michèle. CEPR; 2020. An Economic Model of the Covid-19 Epidemic: The Importance of Testing and Age-Specific Policies: Technical Report DP14695. [Google Scholar]
- Bruce, Raphael, Cavgias, Alexsandros, Meloni, Luis, 2020. Filling the Void? Organized Crime and COVID-19 in Rio De Janeiro. Working Paper.
- Brueckner Jan K., Selod Harris. A theory of urban squatting and land-tenure formalization in developing countries. Amer. Econ. J.: Econ. Policy. 2009;1(1):28–51. [Google Scholar]
- Butler Rachel, Monsalve Mauricio, Thomas Geb W., Herman Ted, Segre Alberto M., Polgreen Philip M., Suneja Manish. Estimating time physicians and other health care workers spend with patients in an intensive care unit using a sensor network. Amer. J. Med.The American Journal of Medicine. 2018;131(8):972.e9–972.e15. doi: 10.1016/j.amjmed.2018.03.015. [DOI] [PubMed] [Google Scholar]
- Cavalcanti Tiago, Da Mata Daniel, Santos Marcelo. On the determinants of slum formation. Econ. J. 2019;129(621):1971–1991. [Google Scholar]
- CDC Severe outcomes among patients with coronavirus disease 2019 (COVID-19) — United States, february 12–march 16, 2020. MMWR Morb Mortal Wkly Rep 2020. 2020;69(12):343–346. doi: 10.15585/mmwr.mm6912e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan Tat, Hamilton Barton, Papageorge Nicholas. Health, risky behavior and the value of medical innovation for infectious disease. Rev. Econom. Stud. 2016;83(3):1737–1755. [Google Scholar]
- Combes Pierre-Philippe, Duranton Gilles, Gobillon Laurent. The costs of agglomeration: House and land prices in french cities. Rev. Econom. Stud. 2019;86(4):1556–1589. [Google Scholar]
- Crosby Alfred W. second ed. Cambridge University Press; 2003. America’s Forgotten Pandemic: The Influenza of 1918. [Google Scholar]
- Cunat Alejandro, Zymek Robert. CESifo; 2020. The (Structural) Gravity of Epidemics: Cesifo Working Paper Series 8295. [Google Scholar]
- Duranton Gilles, Puga Diego. In: Cities and Geography. Henderson J. Vernon, Thisse Jacques-François., editors. vol. 4. Elsevier; 2004. Chapter 48 - micro-foundations of urban agglomeration economies; pp. 2063–2117. (Handbook of Regional and Urban Economics). [Google Scholar]
- Duranton Gilles, Puga Diego. The economics of urban density. J. Econ. Perspect. 2020;34(3):3–26. [Google Scholar]
- Egger Dennis, Miguel Edward, Warren Shana S., Shenoy Ashish, Collins Elliott, Karlan Dean, Parkerson Doug, Mobarak A. Mushfiq, Fink Gunther, Udry Christopher, Walker Michael, Haushofer Johannes, Larreboure Magdalena, Athey Susan, Lopez-Pena Paula, Benhachmi Salim, Humphreys Macartan, Lowe Layna, Meriggi Niccolo F., Wabwire Andrew, Davis C. Austin, Pape Utz Johann, Graff Tilman, Voors Maarten, Nekesa Carolyn, Vernot Corey. Falling living standards during the COVID-19 crisis: Quantitative evidence from nine developing countries. Sci. Adv. 2021;7(6):1–12. doi: 10.1126/sciadv.abe0997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum Martin S., Rebelo Sergio, Trabandt Mathias. The macroeconomics of epidemics. Rev. Financ. Stud. 2021;34(11):5149–5187. [Google Scholar]
- Fajgelbaum Pablo, Khandelwal Amit, Kim Wookun, Mantovani Cristiano, Schaal Edouard. National Bureau of Economic Research; 2020. Optimal Lockdown in a Commuting Network: Working Paper 27441. [Google Scholar]
- Farboodi Maryam, Jarosch Gregor, Shimer Robert. Internal and external effects of social distancing in a pandemic. J. Econom. Theory. 2021;196 [Google Scholar]
- Favero Carlo, Ichino Andrea, Rustichini Aldo. SSRN; 2020. Restarting the economy while saving lives under Covid-19: Technical Report 3580606. [Google Scholar]
- Ferguson Neil M., Laydon Daniel, Nedjati-Gilani Gemma, Imai Natsuko, Ainslie Kylie, Baguelin Marc, Bhatia Sangeeta, Boonyasiri Adhiratha, Cucunubá Zulma, Cuomo-Dannenburg Gina, Dighe Amy, Dorigatti Ilaria, Fu Han, Gaythorpe Katy, Green Will, Hamlet Arran, Hinsley Wes, Okell Lucy C, van Elsland Sabine, Thompson Hayley, Verity Robert, Volz Erik, Wang Haowei, Wang Yuanrong, Walker Patrick G T, Walter Caroline, Winskill Peter, Whittaker Charles, Donnelly Christl A, Riley Steven, Ghani Azra C. Imperial College Covid-19 response team; 2020. Restarting the Economy While Saving Lives under Covid-19: Technical Report. [Google Scholar]
- Folha de São Paulo . Diário da privação: Apesar do coronavírus, quase tudo tá funcionando em paraisópolis. Folha São Paulo. 2020 https://www1.folha.uol.com.br/equilibrioesaude/2020/04/diario-da-privacao-apesar-do-coronavirus-quase-tudo-ta-funcionando-em-paraisopolis.shtml April 02, 2020. [Google Scholar]
- Giannitsarou Chryssi, Kissler Stephen, Toxvaerd Flavio. Waning immunity and the second wave: Some projections for SARS-CoV-2. Amer. Econ. Rev.: Insights. 2021;3(3):321–338. [Google Scholar]
- Greenwood Jeremy, Kircher Philipp, Santos Cezar, Tertilt Michèle. The role of marriage in fighting HIV: A quantitative evaluation for malawi. Amer. Econ. Rev. 2017;117(5):158–162. doi: 10.1257/aer.p20171056. [DOI] [PubMed] [Google Scholar]
- Greenwood Jeremy, Kircher Philipp, Santos Cezar, Tertilt Michèle. An equilibrium model of the african HIV/AIDS epidemic. Econometrica. 2019;87(4):1081–1113. [Google Scholar]
- Henderson J. Vernon, Regan Tanner, Venables Anthony J. Building the city: urban transition and institutional frictions. Rev. Econom. Stud. 2021 [Google Scholar]
- Henderson J. Vernon, Turner Matthew A. Urbanization in the developing world: Too early or too slow? J. Econ. Perspect. 2020;34(3):150–173. [Google Scholar]
- Kaplan, Greg, Moll, Benjamin, Violante, Gianluca, 2020. Pandemics According to HANK. Working Paper.
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1927;114(772):700–721. [Google Scholar]
- Kopecky Karen A. The trend in retirement. Internat. Econom. Rev. 2011;52(2):287–316. [Google Scholar]
- Kremer Michael. Integrating behavioral choice into epidemiological models of AIDS. Q. J. Econ. 1996;111(2):549–573. (05) [Google Scholar]
- Monge-Naranjo Alexander, Ferreira Pedro Cavalcanti, Pereira Luciene. Human Capital and Economic Opportunity Working Group; 2018. Of Cities and Slums: Working Papers 2018–005. [Google Scholar]
- Nisbett Melissa. Empowering the empowered? Slum tourism and the depoliticization of poverty. Geoforum. 2017;85:37–45. [Google Scholar]
- Palamim Camila Vantini Capasso, Marson Fernando Augusto Lima. Covid-19–the availability of ICU beds in Brazil during the onset of pandemic. Ann. Glob. Health. 2020;86(1) doi: 10.5334/aogh.3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peixoto Pedro S, Marcondes Diego, Peixoto Cláudia, Queiroz Lucas, Gouveia Rafael, Delgado Afonso, Oliva Sérgio M. Potential dissemination of epidemics based on Brazilian mobile geolocation data. Part I: Population dynamics and future spreading of infection in the states of sao paulo and Rio de Janeiro during the pandemic of COVID-19. MedRxiv. 2020 the Preprint Server for Health Sciences. [Google Scholar]
- Pereira Rafael Henrique Moraes, Schwanen Tim. Texto Para Discussão, Vol. 1813. IPEA; 2013. Tempo de deslocamento casa-trabalho no brasil (1992–2009): Diferenças entre regiões metropolitanas, nívei de renda e sexo. [Google Scholar]
- Pitcairn Charlie F.M., Laverty Anthony A., Chan Jasper J.L., Oyebode Oyinlola, Mrejen Matías, Pescarini Julia M., Machado Daiane Borges, Hone Thomas V. Inequalities in the prevalence of major depressive disorder in Brazilian slum populations: a cross-sectional analysis. Epidemiol. Psychiatric Sci. 2021;30 doi: 10.1017/S204579602100055X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prefeitura Rio de Janeiro . 2020. Prefeitura divulga resultado da primeira etapa de pesquisa sobre covid-19 em comunidades cariocas. https://prefeitura.rio/saude/prefeitura-divulga-resultado-da-primeira-etapa-de-pesquisa-sobre-covid-19-em-comunidades-cariocas/ June 22, 2020. [Google Scholar]
- Quercioli Elena, Smith Lones. University of Michigan; 2006. Contagious Matching Games. Unpublished Manuscript. [Google Scholar]
- Ray Isha. Viewpoint–handwashing and COVID-19: Simple, right there…? World Dev. 2020;135 doi: 10.1016/j.worlddev.2020.105086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remuzzi Andrea, Remuzzi Giuseppe. Covid-19 and Italy: what next? The LancetLancet. 2020;395(10231):1225–1228. doi: 10.1016/S0140-6736(20)30627-9. (2020/04/21) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocha Rudi, Atun Rifat, Massuda Adriano, Rache Beatriz, Spinola Paula, Nunes Letícia, Lago Miguel, Castro Marcia C. Effect of socioeconomic inequalities and vulnerabilities on health-system preparedness and response to COVID-19 in Brazil: a comprehensive analysis. Lancet Glob. Health. 2021 doi: 10.1016/S2214-109X(21)00081-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith Cecil Woodham. Florence Nightingale, 1820-1910. Collins; 1964. (Fontana Books. no. 1042). [Google Scholar]
- Stantcheva Stefanie. Working Paper Series. National Bureau of Economic Research; 2022. Inequalities in the times of a pandemic. [Google Scholar]
- Toxvaerd Flavio. Rational disinhibition and externalities in prevention. Internat. Econom. Rev. 2019;60(4):1737–1755. [Google Scholar]
- United Nations . In: State of the World’s Cities 2006/2007. United Nations Human Settlements Programme (UN-Habitat) ., editor. Routledge; 2006. [Google Scholar]
- United Nations . In: UNDESA World Social Report 2020. United Nations ., editor. United Nations publication; 2020. [Google Scholar]
- Verity Robert, Okell Lucy C, Dorigatti Ilaria, Winskill Peter, Whittaker Charles, Imai Natsuko, Cuomo-Dannenburg Gina, Thompson Hayley, Walker Patrick GT, Fu Han, et al. Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Sheng, Diao MengYuan, Yu Wenbo, Pei Lei, Lin Zhaofen, Chen Dechang. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the diamond princess cruise ship: A data-driven analysis. Int. J. Infect. Dis. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.