Super-resolved live-cell imaging using random illumination microscopy

Summary

Current super-resolution microscopy (SRM) methods suffer from an intrinsic complexity that might curtail their routine use in cell biology. We describe here random illumination microscopy (RIM) for live-cell imaging at super-resolutions matching that of 3D structured illumination microscopy, in a robust fashion. Based on speckled illumination and statistical image reconstruction, easy to implement and user-friendly, RIM is unaffected by optical aberrations on the excitation side, linear to brightness, and compatible with multicolor live-cell imaging over extended periods of time. We illustrate the potential of RIM on diverse biological applications, from the mobility of proliferating cell nuclear antigen (PCNA) in U2OS cells and kinetochore dynamics in mitotic S. pombe cells to the 3D motion of myosin minifilaments deep inside Drosophila tissues. RIM's inherent simplicity and extended biological applicability, particularly for imaging at increased depths, could help make SRM accessible to biology laboratories.

Graphical abstract

Highlights

• •RIM exploits speckled illumination for 3D super-resolution microscopy of live cells
• •The spatiotemporal resolution and toxicity levels of RIM match that of 3D-SIM
• •RIM's intrinsic robustness to aberrations allows increased depth of imaging
• •RIM is low cost and easy to use, making the method accessible to many researchers

Motivation

Super-resolution optical microscopy (SRM) has been instrumental to rapid progress in cell biology. Many SRM variants are now available with different compromises between phototoxicity, spatiotemporal resolutions, and sensitivity to aberrations. Yet, established SRM techniques, even implemented as expensive turn-key systems, require expert know-how at the instrumentation or image reconstruction levels to operate at the best of their capabilities. The present challenge is to develop a simple, easy to use, and low-cost SRM technique that would combine artifact-free super-resolution, robustness to aberration, low toxicity, and good temporal resolution for routine functional imaging of live cells within normal or pathological tissues.

Mangeat et al. use speckled illumination to develop a simple, low-cost super-resolution microscopy method, called RIM, that matches traditional SIM performances in a more robust fashion. RIM's intrinsic robustness to aberrations, high spatiotemporal resolution, and low toxicity allow dynamic live-cell imaging at increased depth as a routine technique.

Introduction

Learning how cells function requires a detailed knowledge of their structural organization and of the dynamic interplay of their many constituents, often over extended periods of time. But imaging subcellular structures required improving the resolution beyond the diffraction barrier that limits the best widefield optical microscopes.

In the past two decades, several super-resolution microscopy (SRM) techniques have been developed to break the diffraction limit in fluorescence imaging, notably stimulated emission depletion (STED) (Hell and Wichmann, 1994; Klar and Hell, 1999), stochastic optical reconstruction microscopy and photoactivated localization microscopy (STORM/PALM) (Betzig et al., 2006; Hess et al., 2006; Rust et al., 2006), or structured illumination microscopy (SIM) (Gustafsson, 2000; Gustafsson et al., 2008; Heintzmann and Cremer, 1999). These techniques and their later improved versions have provided impressive details of subcellular structures (for a review see Sahl et al., 2017, and Sigal et al., 2018). But each of them present caveats that limit their general use for live-cell imaging. Saturated fluorescence (STED), pointillist methods (STORM and PALM), and intrinsic fluorescence fluctuation approaches (Dertinger et al., 2009) reach their performance at the cost of intense illumination detrimental to live cells and/or prolonged data acquisition time that restrict imaging to small volumes of observation or slow temporal dynamics (Schermelleh et al., 2019). Therefore, SRM is essentially used on fixed samples which might present artifacts induced by the chemical treatments (Richter et al., 2018).

In this context, SIM presents the best compromise between spatial and temporal resolutions with low toxicity for live imaging (Schermelleh et al., 2019). In interference-based SIM, a super-resolved image is formed numerically from several low-resolution images obtained for different positions and orientations of a two-dimensional (2D) or 3D periodic illumination pattern (Heintzmann and Cremer, 1999; Gustafsson, 2000). The success of the numerical reconstruction rests on a precise knowledge of the illumination. When aberrations or scattering, possibly induced by the sample itself, distort the illumination pattern, the reconstruction fails. Thus, the best 3D SIM resolution on live samples, about 120 nm laterally and 360 nm axially at an excitation wavelength of 488 nm, is obtained with thin, transparent cell monolayers (Shao et al., 2011). Other versions of SIM have been introduced for imaging subcellular processes in thicker samples, but at a lower xyz resolution, 220 × 220 × 370 nm for the lattice light sheet version (Chen et al., 2014), and about 160 × 160 × 400 nm for the point-scanning illumination (Airyscan) (Müller and Enderlein, 2010; Sivaguru et al., 2018) and its related multi-point scanning or non-linear versions (Winter et al., 2014; York et al., 2013). Implementing adaptive optics (AO) to correct for the aberrations on the illumination and/or collection sides was also developed to extend SIM depth imaging (Liu et al., 2018). Lateral resolutions between 140 and 200 nm were obtained a few tens of μm deep inside fixed biological tissues with AO-SIM (Thomas et al., 2015; Turcotte et al., 2019) and even deeper with non-linear AO-SIM (Zheng et al., 2017). Yet, these achievements came at the cost of a significant complication of the experimental setups.

Recently, it was demonstrated theoretically (Idier et al., 2018) and experimentally (Labouesse et al., 2017; Mudry et al., 2012) that the periodical or focused illuminations of interference-based or point-scanning SIM could be replaced by random speckles. Counter-intuitively, low-resolution images obtained under random speckled illuminations could be processed into a sample image of better lateral resolution than with classical widefield microscopy. Speckled illumination appeared ideally suited for live-cell imaging given its ease of use (no lengthy monitoring of experimental drifts, no time-consuming calibration protocols when changing the sample, objective, or wavelength), widefield configuration, low levels of energy transfer to the samples, and an extremely simple experimental setup. Yet, the resolution remained too low for imaging subcellular dynamics.

In this work, we developed an imaging technique based on speckled illumination that we call random illumination microscopy (RIM), which achieves a super-resolution level comparable with the best interference-based 3D SIM. The gain of resolution in three dimensions was obtained by using a novel data-processing method combining the statistical approach of fluctuation microscopy with the demodulation principle of SIM.

RIM performances in terms of resolution, fidelity to the ground truth, and resistance to aberrations were evaluated by imaging well-defined samples in non-aberrated and aberrated environments and by comparison with established super-resolution techniques. Then, RIM dynamic in depth imaging was illustrated on specific biological examples ranging from the mobility of proliferating cell nuclear antigen (PCNA) during DNA replication, kinetochore dynamics in mitotic S. pombe cells, to the 3D motion of myosin minifilaments deep inside Drosophila tissues. These examples illustrated the wide range of possible applications of RIM for imaging live-cell processes and related pathologies in vivo. The simplicity of the RIM experimental setup and operation mode should democratize SRM, at low cost, in cell biology laboratories.

Results

RIM exploits speckled illuminations and statistical image reconstruction

RIM consists in forming numerically a super-resolved reconstruction of the sample from multiple low-resolution images of the sample recorded by using random speckled illuminations (hereafter named speckled images) (Video S1). A speckled light pattern is formed when a coherent beam (laser) is reflected or transmitted by a random medium (Figure 1A). It exhibits many randomly scattered bright grains with a typical width of half the light wavelength. The illumination by multiple bright spots connects RIM to multi-point-scanning SIM (York et al., 2013), whereas the random excitation of the fluorescence connects RIM to super-resolution optical fluctuation microscopy (SOFI) (Dertinger et al., 2009). We developed an original reconstruction method, named algoRIM, that combines the advantages of these two techniques. First, algoRIM forms the variance of the speckled images, as in SOFI, then it uses the spatial characteristics of the illumination patterns to improve the resolution, as in SIM. A rigorous mathematical analysis (Idier et al., 2018) showed that a 2-fold increase in resolution, comparable with that of SIM, could be obtained from this approach. The key step of algoRIM consists of estimating the sample fluorescence density so that the variance model of the speckled images best matches the experimental one (Figure 1B) (STAR Methods). The variance-matching procedure requires the knowledge of the speckle autocorrelation (basically, the typical width of the bright grains) and the observation point spread function (PSF). Implemented without a priori on the sample, it significantly improves the resolution of the image variance alone (more precisely of the image standard variation, hereafter, named SOFI speckle) as seen in Figures 1B and S1. In addition, this process restores a linear response to brightness, as shown numerically in Figure S1C where algoRIM faithfully recovers the variations of the actual fluorescence density.

Figure 1.

RIM principle and performances

(A and B) RIM setup and data processing.

(A) RIM implementation. A binary phase spatial light modulator (SLM) acting as a diffuser is implemented in a classical inverted microscope. Illuminated by multicolor lasers, the SLM sends hundreds of different speckle patterns per second onto the specimen. The fluorescence light is collected onto one or two sCMOS cameras after appropriate filtering. The same setup is operational for different objectives with numerical apertures between 0.15 and 1.49, and for wavelengths in the range of 400 to 600 nm.

(B) RIM data processing, algoRIM. Multiple raw images of the sample are recorded under different speckled illuminations and filtered with a Tikhonov regularized inverse filter before forming their variance. The variance-matching process estimates the fluorescence density iteratively by minimizing the distance between the measured variance and the variance model. It significantly improves the resolution of the square root of the measured variance (standard deviation, SOFI speckle).

(C and D) RIM resolution.

(C) RIM reconstruction of a calibrated sample (ARGO-SIM slide, Argolight) with an objective of NA = 1.49 and excitation wavelength of 405 nm. The interdistances between the two center lines from left to right are 180–150–120–90–60 nm. Top panel: deconvolved widefield microscopy. Bottom panel: RIM reconstruction. RIM is able to distinguish two lines separated by 90 nm and the resolution estimated by FIRE (Nieuwenhuizen et al., 2013) is 76 nm. For comparison, RIM theoretical resolution, given by one-fourth of the emission wavelength (420 nm) divided by NA, is 70 nm. Eight hundred speckled images were used in this reconstruction but the 90 nm lines were resolved with as few as 25 speckled images. See Figure S1C for an analysis of the noise on the reconstruction as a function of the number of speckled images.

(D) Two-color RIM image of calibrated DNA nanorulers (SIM 140 YBY), where two red fluorophores (Alexa 561) attached to the DNA ends are separated by 140 nm, and are equidistant (70 nm) to a green fluorophore (Alexa 488). The green and red reconstructed fluorescence density profiles are plotted for 20 different nanorulers. The bold lines indicate the mean profiles. RIM estimated the red-to-green distance to about 70 nm using a co-location analysis. The RIM profiles are similar to those obtained using SIM, see Figure S2A and the STAR Methods.

(E and F) Robustness to aberrations.

(E) Imaging of DNA nanorulers using a defective objective (NA = 1.2) without aberration (left) at the center of the field of view and with strong aberrations (right) at the edge of the field of view. Top: speckle intensity obtained after reflection from the slide by removing the fluorescence filter. The speckle statistics are similar in the aberrated and non-aberrated configurations. Middle: observation PSF estimated from 200 nm beads at the center (left) and the edge (right) of the field of view (Debarnot et al., 2020; STAR Methods). The full width at half maximum (FWHM) of the PSF is estimated to be 375 nm in the non aberrated conditions and 1,025 nm along its longest dimension in the aberrated conditions. Bottom: RIM reconstruction of the same sample of DNA nanorulers (GATTA-confocal 270) consisting of two fluorophores separated by 270 nm translated from the center (left) to the edge (right) of the field of view. When the observation PSF is accurately estimated, the reconstructions are similar in the aberrated and non aberrated configurations.

(F) RIM imaging of the RFP-tagged myosin II motor protein at different depths inside a fixed Drosophila melanogaster pupa leg (NA = 1.35). Top left: cartoon showing the assembly of myosin II into a 300 nm long minifilament tagged at both ends (Hu et al., 2017) and the sagittal cut of the Drosophila leg. About ten isolated myosin II minifilaments, appearing as characteristic fluorescent doublets (shown in the bottom panels), are observed at 0.5, 5, 30, and 100 μm from the slide. Top right: intensity profiles along the filaments observed at each depth and their average. The colors refer to the depths indicated by the arrows. RIM estimated the doublet lengths to about 300 nm whatever the depths, with the FWHM of myosin heads varying from about 120 to 190 nm at 0.5 and 100 μm depth, respectively.

(G–I) 3D imaging.

(G) Comparison of widefield and RIM images of green-fluorescent beads (nominal diameter 100 nm), NA = 1.49. Top: transverse (left) and axial (right) views of the beads with widefield microscopy. Middle: same with RIM. Bottom: Fourier transforms of the widefield (pink) and RIM (green) transverse and axial views of the beads. In addition to the filling of the missing cone, the spatial frequencies cut-offs of RIM were about twice larger than that of widefield microscopy in all directions. The beads FWHM were estimated to 112 ± 16 nm transversally and 320 ± 16 nm axially for RIM and 208 ± 16 nm and 512 ± 64 nm, respectively, for the widefield (10 beads, 800 speckled illuminations).

(H) RIM 3D imaging of myosin II minifilaments 6 μm deep, inside a live developing Drosophila leg, NA = 1.4. The 3D image is a magnification (using a bicubic interpolation) extracted from Video S2, part 3 and Figure S1E. It shows the ability of RIM to distinguish the fluorescent doublet whatever its orientation in the (x,z) plane. The FIRE resolution in the transverse plane was 120 nm. The fluorophores FWHM in the axial direction was 300 ± 60 nm.

(I) Axial and transverse cuts of 3D RIM images of Z-rings from live S. pneumoniae containing FtsZ tagged with mEos3.2 taken at different stages of cell division; NA = 1.49. Early (left) and late (middle) FtsZ annular constrictions from two dividing cells are shown in the axial cut. Right, transverse cut at the equatorial plane of the Z-rings of two attached daughter cells (late division stage). The FIRE resolution in the transverse plane was 105 nm. The FWHM of the ring along the axial direction was estimated to be 280 ± 25 nm.

In (H) and (I) the displacement of the z-stage has been corrected by a factor of 0.8 (H) and 0.66 (I) to account for the focal shift due to the refractive index mismatch between the oil objective and the aqueous mounting medium (STAR Methods).

Video S1. RIM raw images, related to Figures 1, S1, and 2

(1) Comparison of RIM raw images and high-density direct STORM raw images of the same sample.

(2) RIM raw images recorded at different depths for 3D imaging.

(3) RIM two-color images obtained simultaneously on two cameras.2

To implement RIM, we modified a standard widefield epi-fluorescence microscope by replacing the lamp with different laser diodes and introducing a spatial light modulator (SLM), displaying random phase masks, along the illumination path (Figures 1A and S1A). This experimental setup could provide both RIM and SIM images for comparison purposes; however, there is no need for an SLM for generating the speckles, a simple optical diffuser as in (Ventalon and Mertz, 2005) could be used. Several hundreds of different speckle patterns could be generated per second by changing the SLM display. RIM can be used with different objectives and excitation wavelengths without modifying the SLM patterns or the optics or tuning. For all our imaging experiments, the excitation intensity varied from 4 to 20 W/cm², depending on the samples and the recording time per raw image between 2 and 12 ms, depending on the field of view. The number of reconstructed images could reach 1,000 for the longest movie. The above values are a convenient compromise between the signal to noise ratio and the toxicity, comparable with that of all SIM implementations (Wu and Shroff, 2018), except for the unrivalled lattice light sheet technique (Chen et al., 2014).

The potential of RIM in terms of resolution, robustness to aberrations and 3D imaging is shown in Figure 1.

Resolution

We estimated the transverse resolution of RIM by using a resolution target (Argo-SIM slide, Argolight) compared with widefield microscopy (Figure 1C). Under optimal conditions, with a 1.49 numerical aperture (NA) objective and an excitation wavelength of 405 nm, RIM achieved a sub-100-nm resolution of 76 nm, as estimated by Fourier image resolution (FIRE) (Nieuwenhuizen et al., 2013), comparable with the best 2D SIM resolution of 84 nm (Li et al., 2015). The homogeneity of the reconstruction increased with the number of raw images used for estimating the variance but the resolution gain was already visible with as few as 25 speckled images (Figure S1C). Next, we imaged calibrated two-color DNA nanorulers (SIM 140 YBY) where two Alexa 561 fluorophores are separated by 140 nm and are equidistant (70 nm) to an Alexa 488. RIM succeeded in separating the red fluorophores and accurately located the green middle one, much like interference-based SIM (compare Figures 1D and S2A). In these experiments, RIM resolution matched that of interference-based SIM with a simple experimental protocol that could be run in a few minutes without the need for calibrating the microscope system. By contrast, the calibration protocol for two-color 3D SIM imaging is rather complex and can take up to 2 h (Demmerle et al., 2017).

Robustness to aberrations

The main asset of RIM is that the speckle autocorrelation, which plays a major role in RIM super-resolution (Idier et al., 2018), is well known and is insensitive to scattering or aberrations. Indeed, the speckle patterns are not statistically affected by a strong aberration context as demonstrated theoretically by (Goodman, 2007) (STAR Methods) and shown experimentally in Figure 1E (upper panels). Thus, under degraded imaging conditions, RIM resolving power is only affected by the deterioration of the observation PSF, as opposed to SIM approaches, which are also affected by the deterioration of the illumination. We show (Figure 1E, lower panels) that, as long as the observation PSF was correctly estimated from PSF calibration measurements (STAR Methods), RIM reconstructions of DNA nanorulers were not detectably modified when strong aberrations were artificially introduced in the optical path. Note that for this experiment we used a low resolution, strongly aberrated 1.2 NA objective that imposed the use of 270 nm DNA nanorulers. The intrinsic resistance of RIM to aberrations is of critical importance for tissue imaging at increased depth and is illustrated in Figure 1F, where RIM was used to image the motor protein myosin II at different depths inside a fixed Drosophila melanogaster leg. Myosin II assembles into 300 nm long minifilaments, which, when labeled at both ends with Sqh-RFP, form characteristic fluorescent doublets that can be used as resolution targets, much like DNA nanorulers (Beach et al., 2014; Hu et al., 2017). The Drosophila leg is a topographically complex biological tissue (depicted in the cartoon of Figure 1F) in which the squamous epithelium, the numerous interstitial lipid droplets, and the cell nuclei induce substantial scattering and aberrations (see the 3D refractive index map of the fly leg in Video S2, first part). The images of the fluorescent doublets at 0.5, 5, 30, and 100 μm depth were remarkably similar, the widening of the Full Width at Half Maximum (FWHM) of the fluorescent heads with depth (from 120 to 190 nm) mirroring that of the observation PSF due to aberrations on the emission side (Figure 1F). The minifilaments were also well resolved on a live sample at depths between 6 and 25 μm, with a FIRE resolution varying from 120 to 157 nm, respectively (see Figures 1H, S1E, and S1F; Video S2, third part).

Video S2. Imaging of myosin II in fixed and live Drosophila pupa legs, related to Figures 1, S1, 2, and S2

(1) 3D map of the refractive index of the leg obtained by quantitative phase microscopy.

(2) Comparison between RIM and SIM raw images of the same sample.

(3) Time-lapse imaging of myosin II minifilaments in a live leg at 6 and 25 μm from the slide.3

3D imaging

In algoRIM, the raw speckled images are processed as if the sample was restricted to a thin slice placed at the focal plane. 3D reconstructions are obtained by simply translating the sample through the focal plane (Video S1, second part) and treating each position independently. Deconvolving each speckled image and taking the variance ensure an efficient optical sectioning that is further improved by the variance-matching process (Dertinger et al., 2009; Idier et al., 2018; Ventalon and Mertz, 2005; Ventalon et al., 2007). Simulations and experiments on calibrated beads (Figures S1D and 1G, respectively) revealed that RIM doubled the optical resolution of widefield microscopy both in the transverse and axial directions. These performances were confirmed by experiments conducted on live samples. RIM provided 3D images of differently oriented 300 nm myosin II minifilaments 6 μm deep inside a live Drosophila pupa leg (extracted from Video S2, third part; Figure S1E) with a resolution about 120 nm laterally and 300 nm axially with a 1.4 NA objective (Figure 1H). RIM also resolved the cell division ring of live bacteria Streptococcus pneumoniae (Figure 1I extracted from the 3D reconstruction displayed in Video S3). The diameter of this division ring ranges from 0.3 to 0.9 μm depending on the division stage (Fleurie et al., 2014) and is roughly perpendicular to the observation focal plane when the bacteria lies on the substrate, which makes it ideally suited to evaluate RIM axial and transverse resolution. The resolution was estimated to 105 nm laterally and 280 nm axially with a 1.49 NA objective.

Video S3. Slice by slice (3D) imaging of FtsZ rings in live bacteria, related to Figure 1

4

All the above experiments illustrated the intrinsic potential of RIM that makes the technique particularly suitable for super-resolution imaging deep inside live and aberrating biological tissues. RIM lateral and axial resolutions matched that of the best 3D SIM and was maintained deep inside biological tissues. In addition, it is worth noting that RIM improved depth of focus (about 300 nm) is achieved with only one recorded z-slice, whereas 3D SIM requires the simultaneous processing of at least seven z-slices (Gustafsson et al., 2008).

RIM versus established microscopy techniques

To thoroughly assess the performances of RIM, we investigated the fidelity of RIM reconstructions to the ground truth on complex biological samples, and compared it with that of other established SRM techniques (Figure 2).

Figure 2.

Comparison of RIM with competing super-resolution microscopy techniques

(A) We imaged the same vimentin network from fixed HUVEC cell with, successively, 2D SIM, RIM, confocal, and 2D-STED, using a fluorescent antibody dedicated to STED microscopy with excitation at 561 nm and emission at 700 nm (large Stokes shift), NA = 1.4. The RIM image was very close to the 2D-STED image (RIM resolution even matched that of 3D-STED on a 3D sample of vimentin filaments, Figures S2C and S2D) and was better than the SIM reconstruction using the data processing developed in (Wicker et al., 2013) and implemented in the Zeiss Elyra.

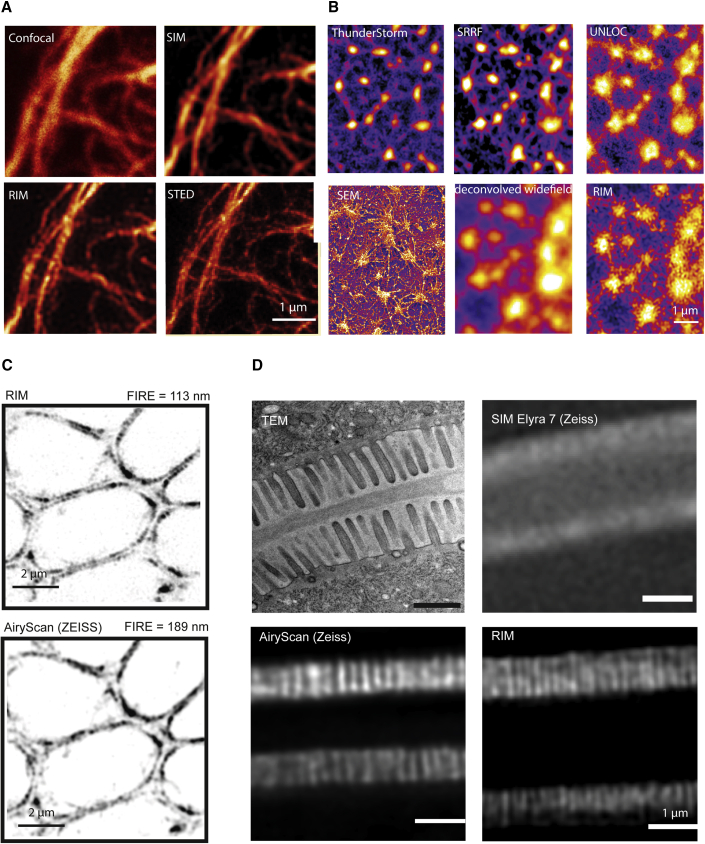
(B) Widefield, RIM, and dense emitter localization microscopy images of the same sample of a fixed F-actin network of unroofed macrophages. Ten thousand localization microscopy raw images were recorded following the direct STORM protocol with an excitation intensity of 10 kW/cm². Localization microscopy data were reconstructed by using different algorithms (top) based on the estimation of the second-order cumulant using NanoJ SRRF (Gustafsson et al., 2016), or based on multi-emitter fluorophore localization using either ThunderSTORM (Ovesný et al., 2014) or UNLOC (Mailfert et al., 2018). Eight hundred RIM speckled images were recorded with an excitation intensity of 4 W/cm². The deconvolved widefield image (bottom middle) was obtained by simply forming the average of the deconvolved speckled images. A scanning electron microscopy (SEM) image of a similar sample is provided as a reference (bottom left). RIM reconstruction is significantly better resolved than the deconvolved widefield image and is closer to the SEM image than the dense emitter localization microscopy images.

(C) RIM and point-scanning SIM (Airyscan) imaging of the same sample of tagged bipolar myosin II minifilaments at the apical plane, 6 μm deep, of a fixed Drosophila pupa leg. FIRE resolution was estimated to be 113 nm for RIM and 189 nm for Airyscan. RIM resolution permits to observe the roughly periodical pattern of the myosin II fluorescent doublets along the cell junctions.

(D) RIM, Airyscan, and 3D SIM (Lattice SIM, Zeiss Elyra 7) images, at about 13 μm depth, of the microvilli brush border intestine of live ERM-1/ezrin endogenously tagged with mNeonGreen C. elegans L4 larvae. The transmission electron microscopy image of a similar sample shows a comb-like structure with apparent inter-microvillous spacings varying from 100 to 250 nm (see also Figure S2F). Contrary to interference-based SIM, RIM and Airyscan were able to disclose the periodic organization of the microvilli at 13 μm depth. RIM could even disclose inter-microvillous spacings of 120 nm (Figure S2F)

In the experiment shown in Figure 2A, we imaged the vimentin network from fixed HUVEC cells with excitation light at 561 nm and fluorophores emitting at 700 nm, NA = 1.4. RIM image was much better resolved than that of confocal microscopy and even better than that of interference-based 2D SIM (at similar photon budget). Indeed, the standard SIM reconstruction process was affected by the large Stokes shift (Wicker et al., 2013). However, using a more sophisticated reconstruction procedure (Ayuk et al., 2013) we could recover a SIM image similar to that of RIM (Figure S2B). Comparison with the 2D STED image underscored the fidelity of RIM reconstruction. In particular, RIM was free from common artifacts, such as the disappearance or thinning of unresolved filaments. Note that, although RIM resolving power was smaller than that of STED in this 2D imaging configuration, it was similar to STED when imaging the 3D network of vimentin filaments (Figures S2C and S2D).

We imaged the F-actin network of podosomes attached to substrate with phalloidin-Alexa Fluor 647 (Figure 2B). Podosomes are actin-rich, cellular adhesion structures capable of applying protrusive forces on the extracellular environment (Bouissou et al., 2017) and are characterized by densely and sparsely tagged regions that are particularly difficult to image. A comparison between the RIM reconstruction and the deconvolved widefield image of the same sample illustrated the resolution gain brought about by RIM and its good linearity to brightness (Figure 2B, bottom). Next, RIM was compared with dense emitter localization microscopy in which the experimental protocol of direct STORM (Heilemann et al., 2008) was run with a higher density of activated fluorophores to lower the number of frames required for the reconstruction. RIM reconstruction was obtained from 800 speckled images with an injected power of 4 W/cm², whereas the localization microscopy reconstructions were obtained from 10,000 images with an injected power of 10 kW/cm² (see Video S1, first part). The dense emitter localization microscopy reconstructions were performed by using different algorithms, based on temporal correlations, SOFI (Dertinger et al., 2009), and SRRF (Gustafsson et al., 2016), or on localization (Thunderstorm [Ovesný et al., 2014] and UNLOC [Mailfert et al., 2018]) and are shown in Figure 2B (top). Remarkably, RIM reconstruction was closer to a scanning electron microscopy (SEM) image of a similar sample than the localization microscopy reconstructions. In particular, RIM showed more details than the SOFI/SRRF and Thunderstorm images, which were plagued by numerous artifacts, such as the disappearance and collapse of structures together with an artificial sharpening (Marsh et al., 2018).

Next, we evaluated the ability of RIM to hold its resolution level inside thick and aberrating biological tissues compared with SIM. We imaged the myosin II fluorescent doublets at the apical plane of epithelial cells 6 μm deep inside a fixed Drosophila leg (Figure 2C). This sample could not be imaged with interference-based SIM because of the frequent disappearance of the illumination grid (see 2D SIM raw images in Figure S2E and Video S2, second part). RIM was thus compared with the more robust point-scanning SIM known commercially as Airyscan. On the same sample and with the same injected power, RIM resolution, estimated by FIRE, was 113 nm whereas that of Airyscan was 189 nm. This difference in resolution enabled RIM to distinguish the well-documented, seemingly periodical pattern of the Myosin doublets aligned side by side at the epithelium cell junctions (Ebrahim et al., 2013; Hu et al., 2017). In addition, we found that less photobleaching occurred with RIM than with Airyscan (Figure S2E).

We imaged the fluorescent ERM-1/ezrin, a protein constitutive of microvilli, 13 μm deep inside live C. elegans (Figure 2D). Microvilli are membrane protrusions that increase the surface area of the intestine and have a roughly periodic spatial organization with a spacing varying from 100 to 250 nm as indicated by electron microscopy images (Figures 2D top left and S2F). This imaging configuration is plagued by significant aberrations due to the optical index mismatch between the specimen, the aqueous mounting medium, and the immersion oil of the objective. Three similar samples were imaged by using RIM, interference-based 3D SIM (Lattice SIM, ELYRA 7), and Airyscan. Both RIM and Airyscan revealed the periodic organization of the microvilli (Figure 2D, bottom). RIM could even disclose structures with interdistances of 120 nm (see the plot of Figure S2F). By contrast, Lattice SIM failed to detect the microvilli because the distortion of the periodic pattern due to the sample aberrations prevented the reconstruction (Figure 2D, top right).

These experiments showed the robustness of RIM under difficult imaging conditions, such as large Stokes shift, samples showing both dense and sparse fluorescence regions, strong aberrations, and scattering. RIM images were devoid of the artifacts typically encountered with dense emitter localization microscopy (Figure 2B) and better resolved than interference-based and point-scanning SIM (Figures 2A, 2C, and 2D). Furthermore, the RIM procedure was simple, the change of objective and wavelength was as accessible as in an ordinary widefield microscope, and image reconstruction required only the estimation of the observation PSF and signal to noise ratio (STAR Methods).

Broad biological applicability of RIM

In the following, we show with a few examples the potential of RIM for multicolor imaging on thick, aberrating tissues and for molecular dynamic imaging in live cells.

RIM 3D multicolor imaging of a thick sample at different scales

We illustrate RIM super-resolution, robustness to aberration and ease of use by imaging in three dimensions and two colors a 100 μm thick Drosophila pupa leg with GFP-tagged E-cadherin (green or turquoise) and RFP-tagged myosin II (magenta or red). The developing leg, partially depicted in Figure 1F, is composed of a thin squamous epithelium surrounding a cylindrical columnar epithelium. The 3D image of the entire leg is displayed in Figure 3A, and magnified views on both sides of the leg (at 5 and 87 μm from the slide), obtained with a bigger magnification, are shown in Figure 3B. These images show that RIM resolution is maintained to a high degree (from 120 to 177 nm) throughout the aberrating leg. These resolutions are comparable with those reached by interference-based SIM by using AO (lateral resolutions from 140 to 190 nm a few tens of μm deep inside fixed samples, Thomas et al., 2015; Turcotte et al., 2019). A closer look at the undulating apical plane reveals the expected alignment of myosin II filaments on either side of E-cadherin, with a constant image quality over the field of view (Figures 3C and 3D).

Figure 3.

3D two-color imaging of a fixed Drosophila melanogaster leg

(A) RIM 3D two-color imaging of a whole fixed Drosophila melanogaster pupa leg (see the cartoon in Figure 1F) with (red or magenta) RFP-tagged spaghetti squash (Sqh), the regulatory light chain of the non-muscle myosin II motor protein, and (green orturquoise) GFP-tagged E-cadherin. The 3D image, made of 200 slices with 500 nm spacing, was obtained with a 25× NA = 1.05 objective. In this inverted representation, the slide is placed at z = 0. For ease of visualization, only the fluorescence stemming from the apical plane of the columnar epithelium is presented.

(B) Images of two slices of the same sample taken at 5 and 87 μm from the slide (corresponding to the apical plane on both sides of the leg) obtained with a 100× NA = 1.35 objective. The FIRE resolution was only moderately deteriorated when imaging throughout the whole leg (120 nm at 5 μm, 177 nm at 87 μm).

(C) 3D image (the colors code for the axial position with respect to the slide) of the E-cadherin at the apical plane 7 to 12 μm from the slide, built from 25 slices with 200 nm spacing with the same objective as in (B).

(D) Zoom-ins on the E-cadherin and myosin II corresponding to the eight yellow squares in (C). At the cell junctions, the myosin II minifilaments are well aligned on either side of the E-cadherin as expected. The image quality appears similar whatever the transverse and axial position of the magnified views.

We next evaluated the potential of RIM for functional imaging at high spatiotemporal resolution. In practice, to image a dynamic process, speckled images were recorded regularly during the observation period and super-resolved reconstructions were formed from successive (sequencing approach) or overlapping (interleaving approach, Guo et al., 2018) stacks of N raw images where N was optimized to provide the best trade-off between motion blur and reconstruction noise (STAR Methods).

Imaging PCNA dynamics at high spatiotemporal resolution

Taking advantage of the optical sectioning of RIM, we studied in Video S4 and Figures 4A–4C the dynamics of the PCNA on a plane, 5 μm deep inside the nucleus of a U2OS cell, during the S phase, when PCNA is involved in DNA replication and is bound to chromatin. We recorded 10–20 s movie sequences during early, mid, and late S phase (Video S4, first part) with an acquisition time per super-resolved image down to 0.1 s (yielding 50 frames/s with the interleaving technique, Video S4, second part). During this observation time, the PCNA motion due to the DNA replication process (1.7 kb per min; Löb et al., 2016) is negligible so that the movements of PCNA reflects chromatin dynamics during replication. As previously observed (Essers et al., 2005), there were significant differences in the spatial organization and dynamics of PCNA during the early, mid, and late S phases (Figures 4B and 4C). In the early S phase, the clusters of PCNA were smaller, more numerous, and more mobile than in the late S phase. These observations were further confirmed by single-particle tracking (Chenouard et al., 2013) and optical flow (Horn and Schunck, 1981) analyses of RIM images, both measuring a higher average displacement in early S phase compared with late S phase (Figures 4B and 4C).

Figure 4.

Dynamic imaging of cell nuclei

(A) RIM image at 4 μm from the slide of the whole nucleus of a U2OS cell expressing mCherry-PCNA at early S phase.

(B) Top: trajectories of individual spots of PCNA at mid S phase, obtained by single-particle tracking on RIM movie sequences from the first part of Video S4. Bottom: zoom-ins on the trajectories obtained at two different locations in the nucleus (left) and integrated displacements of all the trajectories found in the nucleus, at early, mid, and late S phase (right). PCNA mobility (i.e., chromatin dynamics) decreases from early to late S phase. The differences between the median trajectory lengths (1.16, 0.86, and 0.49 μm for the early, mid, and late S phases, respectively) were found statistically significant (p < 0.001), see the STAR Methods.

(C) Displacement field calculated by using optical flow on the same data as (B). The optical flow displacement field agrees with the statistics obtained with single-particle tracking. The insets display RIM images of PCNA at early, mid, and late S phase.

(D) Schematic representation of the displacements of fission yeast kinetochores during mitosis.

(E) Kinetochores harboring GFP-tagged Ndc80 were resolved in pro-metaphase, metaphase, and telophase (extracted from Video S5). The colors code for the axial position with respect to the slide (S. pombe typically measures 3 to 4 μm in diameter and 8 to 16 μm in length).

(F) Comparison of prophase to anaphase A duration as observed by RIM or classical widefield microscopy with synchronized LED illumination on 32 mitotic cells in both cases. The difference between the RIM and widefield median durations was not found statistically significant (ns, p > 0.05), see the STAR Methods.

Video S4. Imaging of PCNA dynamics in live mammalian cells at high temporal resolution, related to Figure 4

(1) Imaging of PCNA motion during early, mid, and late S phase. Interleaving approach with apparent temporal resolution of 120 ms, acquisition time for one super-resolved image 0.5 s

(early)–1.2 s (mid and late). Note: the acquisition times have been optimized to provide the best trade-off between motion blur and noise.

(2) Imaging of PCNA during early S phase. Interleaving approach with apparent temporal resolution of 20 ms, acquisition time for one super-resolved image 0.1 s.

(3) Imaging of PCNA and 53BP1 during early S phase. Interleaving approach with apparent temporal resolution of 50 ms, acquisition time for one super-resolved image 0.5 s5

This experiment demonstrates the versatility of RIM, which, from the same set of data, was able to provide both super-resolved images of the whole-cell nucleus (Figure 4A) and a trajectory analysis similar to that obtained by single-particle tracking (Figures 4B and 4C). Note that simultaneous imaging of two proteins (53BP1-GFP and mCherry-PCNA) could be easily achieved with a dual-camera RIM setup (Video S4, third part).

3D dynamic imaging of yeast mitosis and cell migration at low toxicity

RIM can also be used to image dynamic processes in three dimensions by forming sequential slice-by-slice reconstructions (the temporal resolution depending on the number of z-slices). In Figures 4D–4F and Video S5, the mitosis of the fission yeast S. pombe was recorded on eight z-slices (spaced by 150 nm) with a temporal resolution of 20 s. RIM was able to distinguish the six kinetochores with a fluorescently labeled Ndc80 protein, at all stages of mitosis, either aligned at the spindle center (spindle size of about 0.5 μm [Mary et al., 2015]) in pro-metaphase, or oscillating between the spindle pole bodies in metaphase and moving to each cell pole in telophase (Figures 4D and 4E). This level of kinetochore resolution in live fission yeast has never been attained in the past. The average prophase to anaphase duration under RIM illumination (13 min) was comparable with that observed with a regular widefield microscope (14 min) by using the same yeast strain grown under the same conditions (Figure 4F), indicating that the repeated speckled illuminations of RIM were not more stressful than the LED illumination of the widefield microscope.

Video S5. Time-lapse slice-by-slice (3D) imaging of kinetochores in a fission yeast, related to Figure 4

Left: widefield imaging. Right: RIM imaging.6

The low toxicity of RIM and its ability for dynamic 3D imaging were further demonstrated in a totally different context by observing the collective border cell migration in a Drosophila ovary during 75 min (Video S6). The rate of migration, from the anterior epithelial surface to the center, 60 μm deep, of the egg chamber, about 1.3 μm per min, was in the range of published observations (Poukkula et al., 2011), showing that the migration process was not detectably affected by the 200,000 speckled illuminations.

Video S6. 3D imaging of border cell migration in Drosophila ovary during 75 min, related to Figure 4

(1) Time-lapse widefield and RIM imaging (maximum intensity projection of 3D images) of a live Drosophila ovary expressing tagged actin. The widefield images are obtained by summing the 200 speckled images used in RIM reconstructions.

(2) 3D image of the border cells at a given time.

(3) Time-lapse imaging of the actin motion at a given depth.7

3D dynamic imaging of myosin II networks in Drosophila epithelium

To exemplify the capability of RIM to achieve high spatiotemporal resolution with low phototoxicity and robustness to aberration for functional imaging of living biological tissues, we imaged the myosin II network in the pupal notum of a live Drosophila. The pupal notum is a single-layered epithelium composed of epidermal cells and sensory organ precursor cells (SOP) (Couturier et al., 2017). Figure 5A shows a 3D RIM image over a large field of view of the myosin II networks at the apical plane of the epidermal cells, 7 μm from the coverslip. RIM clearly resolved the bipolar myosin minifilaments forming irregular networks inside the cells (medial myosin II) and accumulating neatly at cell-cell contacts (junctional myosin II) in two parallel dotted lines (Ebrahim et al., 2013). In Figure 5B, the high axial resolution of RIM revealed the upper positioning of the myosin II medial network of a SOP cell compared with that of surrounding epidermal cells. Most importantly, the temporal resolution of RIM allowed the visualization of the pulses of the medial myosin II networks, which are in a constant state of spatial reorganization (Couturier et al., 2017; Martin et al., 2009) (Figure 5C, extracted from Video S7).

Figure 5.

dynamic imaging of myosin II in live Drosophila notum

(A) RIM 3D large field of view of the medial and junctional myosin II network at the apical plane of the columnar epithelium (extracted from Video S7, part 1). The bipolar myosin II minifilaments are clearly visible. The colors code for the axial position with respect to the slide.

(B) Four consecutive RIM optical sections at the level of the medial myosin network. RIM high axial resolution enables to discriminate the positioning of the medial myosin network in a sensory organ precursor cell about 300 nm basally in relation to that of its neighboring epidermal cells (Video S7, part 3).

(C) Time-lapse imaging focused on one cell (Video S7, part 2) showing the constant reorganization of medial myosin network.

Video S7. 3D imaging of myosin II dynamics at the apical plane of the columnar epithelium of live Drosophila pupa notum, related to Figure 5

(1) Time-lapse imaging of four z-slices (200 nm apart) and maximum intensity projection.

(2) Time-lapse imaging in three dimensions (the colors code for the axial position).

(3) Time-lapse imaging of four z-slices and maximum intensity projection: zoom-in on a sensory organ precursor (SOP) cell.8

Discussion

Since the breaking of the diffraction barrier by pioneer microscopists (Betzig et al., 2006; Gustafsson, 2000; Hell and Wichmann, 1994), cutting edge SRM has not spread much outside of a few laboratories at the fore-front of research. As the costs increased inevitably with the complexity of the experimental setups, the established SRM techniques commercially available were progressively concentrated into dedicated imaging facilities under the supervision of specialized experts, thus limiting their routine use (Schermelleh et al., 2019). In this context, as we discuss further below, the main advantage of RIM lies in its unique potential to bring low-cost SRM into all cell biology laboratories.

Several SRM techniques are able to provide 3D super-resolved images over large enough fields of view, with low phototoxicity and high enough speed to enable functional imaging of live tissues (Wu and Shroff, 2018; Schermelleh et al., 2019). Among them, interference-based 3D SIM (Shao et al., 2011) shows the best axial and transverse resolution, whereas point-scanning SIM (Müller and Enderlein, 2010), which reduces the out-of-focus background, is better suited to thick samples. Lattice light sheet microscopy, by illuminating the samples along the focal plane, is the least toxic method, best suited for 3D live-cell imaging with high temporal resolution and near isotropic albeit comparably low resolution (Chen et al., 2014). Other SIM variants, such as multi-point-scanning SIM (York et al., 2013) and fast interference-based 2D SIM, particular variants with total internal reflection fluorescence SIM (Li et al., 2015) or grazing incidence illumination SIM (Guo et al., 2018), are also optimized for high speed live-cell imaging. Yet, for all these approaches, the experimental implementation is far more complex than that of standard widefield microscopy (Schermelleh et al., 2019). Even confocal microscopes and their improved versions implementing point-scanning SIM, require expert know-how to operate at the best of their capabilities.

Fundamentally, what distinguishes RIM from all SRM techniques adapted to live imaging with comparable resolution is its ease of use. RIM reconstructs super-resolved images of a sample from multiple images recorded under random speckled illuminations. Any widefield microscope can be transformed into RIM by simply replacing the lamp by a laser and introducing a diffuser on the illumination path to form the incident speckled light (Figures 1A and S1A). As no knowledge of the speckle patterns is required, control of the illumination is minimal. As a result, the RIM setup procedure is similar to that of a classical widefield microscope and changing the magnification or performing multicolor imaging is simple, in contrast to all SIM implementations (as well as confocal microscopes). Furthermore, RIM data processing requires only an estimation of the observation PSF and signal to noise ratio, similar to all deconvolution techniques (STAR Methods).

We showed mathematically that RIM resolution could be twice better than that of widefield microscopy in all directions (Idier et al., 2018). In practice, RIM achieved resolutions up to 76 nm laterally on calibrated samples (Figure 1C) and 300 nm axially (Figures 1G–1I), matching that of the best 2D and 3D SIM (Gustafsson et al., 2008; Li et al., 2015; Shao et al., 2011). In addition, RIM reconstructions, such as SIM, display a linear response to the fluorescence density (STAR Methods; Figures 2A and S1B), thus avoiding artifacts typically encountered in dense emitter localization microscopy (Figure 2B) (Marsh et al., 2018). Thanks to the robustness to aberrations and scattering of the speckle statistics, RIM 3D resolution could be maintained deep inside samples where interference-based SIM failed and only point-scanning SIM worked, although at a lesser resolution (Figures 2C and 2D). RIM's super-resolution two-color imaging at increased depth is exemplified in Figure 3 where 3D images of a 100 μm thick Drosophila pupa leg with tagged myosin II and E-cadherin were obtained with a transverse resolution increasing with depth from 120 to 177 nm.

RIM temporal resolution on large fields of view (from a few seconds to 0.1 s per frame but easily more than 50 frames per s using the interleaving technique), although not to the level of several specific implementations of 2D SIM (Li et al., 2015; Guo et al., 2018) or multi-point-scanning SIM (York et al., 2013), was comparable with that of most interference-based 3D SIM (Wu and Shroff, 2018). Combined with a low toxicity and photobleaching, it appeared sufficient for many live-cell imaging applications. For instance, the spatiotemporal resolution afforded by RIM enabled the distinction of three different PCNA dynamic states during early, mid, and late S phases of DNA replication. The low toxicity of RIM did not detectably alter the highly stress-sensitive mitosis duration in S. pombe when imaging kinetochore motion from prophase to telophase (Figure 4F). The unique combination of high spatiotemporal resolution, low toxicity, and resistance to aberrations of RIM was demonstrated in an unprecedented manner by 3D in vivo imaging of the bipolar myosin II minifilament motion deep inside live Drosophila tissues (6–25 μm) (Figures 1H, S1E, S1F, and 5; Videos S2 and S7). Until now, the fluorescent doublets of the minifilaments had only been observed in cultured cells, never in thick, live tissues (Beach et al., 2014; Hu et al., 2017; Li et al., 2015).

Limitations of the study

Of course, RIM has several limitations and there is room for improvements and modifications. First, being a widefield technique, RIM is more affected by the out-of-focus haze that occurs in thick and densely marked samples compared with point-scanning SIM approaches. Reducing the field of view via diaphragming or the axial extension of the illumination by implementing light sheet, total internal (Li et al., 2015), or grazing incidence configurations (Guo et al., 2018) can be envisaged to overcome this problem. Second, RIM is affected by the deterioration of the observation PSF due to sample-induced aberrations and scattering on the emission side. This issue can be alleviated by using objectives with smaller NA, fluorophores with a large Stokes shift (so that the emitted light, at a longer wavelength, is less perturbed by the sample inhomogeneities), or by coupling RIM to AO on the emission side (at the expense of a complication of the experimental implementation). Finally, RIM slice-by-slice imaging is not optimal because, for each speckled illumination, the whole sample fluoresces but only the emitted light stemming from the focal plane is considered useful. Implementing a multifocus technique for recording several slices of the sample simultaneously (Abrahamsson et al., 2013) in conjunction with a full 3D processing of the data could improve both the axial and temporal resolutions.

To conclude, we believe that, by combining the key advantages of SIM with the unrivalled ease of use of widefield microscopy, RIM will fulfill the expectations of cell biology laboratories, in line with the growing need for simple, fast, super-resolved functional imaging of live cells within normal or pathological tissues or model organisms. In particular, the inherent simplicity of RIM makes it possible to envisage the coupling of this SRM method to other techniques, such as force measurements, photo-ablation, or high throughput cell screening. It is worth noting that the mathematical concepts of RIM apply to all imaging techniques in which the recorded data are linearly linked to the sought parameter times and excitation field. Ultrasound imaging, diffraction microscopy, microwave scanning, photo-acoustic imaging, among others, could all benefit from the philosophy of this novel approach.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Vectashield	Vector Laboratories	Cat#H-1000
20-hydroxyecdysone	Sigma-Aldrich	Cat# H5142
DMEM Glutamax + glucose 4.5 g/L, 1 mM sodium pyruvate	Invitrogen	Cat#10569010
pen/strep	Invitrogen	Cat#15140148
FCS	Eurobio	Cat#CVFSVF0601
Geneticin	Euromedex	Cat#EU0600-A
Puromycin	Invivogen	Cat#ANT-PR-5
Hygromycin	Invivogen	Cat# ANT-HG-1
EDTA	Sigma-Aldrich	E5134
RPMI 1640	Invitrogen	21875-034
Macrophage Colony-Stimulating Factor (M-CSF)	Peprotech	300-25 SIZE B
Alexa Fluor 488-phalloidin	Molecular Probes	A12379
Alexa Fluor 647-coupled phalloidin	Molecular Probes	A22287
Mouse anti-vinculin (clone hvin-1)	Sigma-Aldrich	V9131
Secondary F(ab')2 coupled to Alexa 555	Cell Signaling Technology	4409
Experimental models: organisms/strains
D. melanogaster: Myosin-RFP: w, sqh{TI}-TagRFPt [3B]	Ambrosini et al., 2019	CBI, LBCMCP
D. melanogaster: Sqh::GFPcrispr	Daniel et al., 2018	N/A
D. melanogaster: Sqh::UtrABD-GFP, Sqh::RLCmyosinII-mCherry	Qin et al., 2017	N/A
D. melanogaster: Ecad-GFP: w; shg{TI}-GFP	BDSC	RRID:BDSC_60584
Streptococcus pneumoniae: strain R3702: FtsZ-GFP	Berger et al., 2013	N/A
S. pombe: ST102: h- ndc80-GFP:kr cdc11-CFP:kr ura4-D18 leu1-32 ST1771: h+ ndc80-GFP:kr cdc11-GFP:kr	Tournier et al., 2004	CBI, LBCMCP
U2OS cells expressing AsiSI-ER-AID, 53BP1-GFP and mCherry-PCNA	Aymard et al. 2014	N/A
HUVEC cells: HUV-EC-C (HUVEC)	ATCC	CRL-1730
C. elegans: Strain wild-type N2 Caenorhabditis	Genetics Center	RRID: WB-STRAIN N2_(ancestral)
Software and algorithms
Adobe Illustrator CS5	Adobe	RRID:SCR_010279
Fiji	https://fiji.sc/	RRID: SCR_002285
ZEN Blue	ZEISS	RRID:SCR_013672
Black Zen software	ZEISS	RRID:SCR_018163
Two-colors acquisition software	Abbelight and Inscoper	N/A
One-color acquisition software	micromanager	N/A
AlgoRIM	This paper	http://cell-rep-meth.rim-microscope.fr
Other
Schneider’s insect medium	Sigma-Aldrich	Cat#S0146
Fetal calf serum (FCS)	Sigma-Aldrich	F7524
Halocarbon oil	Sigma-Aldrich	Cat#H8773
120 μm deep Secure-Seal™	Sigma-Aldrich	Cat#GBL654008
Glass coverslips (0.17 mm ±0.005mm)	Marienfeld	0117640
Magnetic microbeads coated with antibodies directed against CD14	Miltenyi Biotec	130-050-20

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact: Thomas Mangeat (thomas.mangeat@univ-tlse3.fr).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The micromanager script monitoring the recording of the speckled raw images in the single-camera RIM implementation and the reconstruction software algoRIM developed for the current study are available at:

http://cell-rep-meth.rim-microscope.fr. Speckled raw images are also accessible from the same address, allowing the readers to reproduce some results of the paper.

Experimental models and subject details

Podosomes of macrophages

Human monocytes were isolated from blood of healthy donors as described previously (Van Goethem et al., 2010). Cells were re-suspended in cold PBS supplemented with 2 mM EDTA, 0.5% heat-inactivated fetal calf serum (FCS) at pH 7.4 and magnetically sorted with magnetic microbeads coated with antibodies directed against CD14 (Miltenyi Biotec). Monocytes were then seeded on glass coverslips at 1.5x10⁶ cells/well in six-well plates in RPMI 1640 (Invitrogen) without FCS. After 2 h at 37°C in humidified 5% CO₂ atmosphere, the medium was replaced by RPMI containing 10% FCS and 20 ng/mL of Macrophage Colony-Stimulating Factor (M-CSF) (Peprotech). For experiments, cells were used after seven days of differentiation.

Macrophages plated on glass coverslips (0.17 mm ±0.005mm, Marienfeld) were unroofed and fixed as previously described (Bouissou et al., 2017) and labelled with Alexa Fluor 488-phalloidin (Molecular Probes, 1/500) and Alexa Fluor 647-coupled phalloidin (Molecular Probes, A22287, 1/100) for RIM and dSTORM, respectively. Vinculin was stained using mouse anti-vinculin (clone hvin-1, Sigma-Aldrich, 1/500) and a secondary F(ab')₂ coupled to Alexa 555 (Cell Signaling technology).

Vimentin in HUVEC cells

For immunofluorescence microscopy, HUVEC cells were seeded and grown onto 0.17 mm H coverslip. Cells were fixed with 3.7 % PFA (Sigma Aldrich) in PBS for 10 min at 4°C, and permeabilized with 0.1 % Triton X100 for 10 min at 4°C. After washing thrice with PBS, the cells were incubated for 1h with anti-vimentin rabbit antibody (Sigma Aldrich) and then after washing thrice with PBS, incubated with anti-rabbit Aberrior Star 635P conjugated secondary antibodies (NanoTag Biotechnologies) diluted to 1/10, and subsequently washed three times with PBS for 10 min each. Coverslips were mounted on microscope slides using home-made Mowiol-DABCO.

FtsZ ring of S. pneumoniae

S. pneumoniae strain containing the FtsZ-GFP fusion (R3702, Bergé et al., 2013), was grown in C+Y medium as previously described at 37°C to an OD₅₅₀ of 0.15 (Bergé et al., 2017). Samples were collected, pelleted (3 min, 3,000 g) and resuspended in cold C medium. The C medium contained per liter: 5 g casein hydrolysate, 6 mg tryptophane, 11.25 mg cysteine, 2 g sodium acetate and 8.5 g K₂HPO₄. Cells were spotted on a microscope slide containing a slab of 1.2% agarose in C medium and covered with a pre-treated coverslip before imaging.

PCNA dynamics in U2OS cells

U2OS cells stably expressing AsiSI-ER-AID, 53BP1-GFP and mCherry-PCNA (AID-DivA 53BP1-GFP mCherry-PCNA) (Caron et al., 2015) were cultured in Dulbecco’s modified Eagle’s medium (DMEM Glutamax + glucose 4.5 g/L, 1 mM sodium pyruvate, Invitrogen), antibiotics (pen/strep; Invitrogen), 10% FCS (Invitrogen), 800 μg/mL geneticin (Sigma), 1 μg/mL puromycin (Invivogen), 250 μg/mL hygromycin (Invivogen) at 37°C in a humidified atmosphere with 5% CO2.

Mitosis of S. pombe cells

Media, growth, maintenance of strains, and genetic methods were performed as previously reported (Moreno et al., 1991). Cells were grown at 25°C on yeast extract agar plates. Strain genotype used: ST102 h ndc80-GFP:: kanR cdc11-CFP::kanR ura4-D18 leu1-32. To analyze chromosomes dynamics, kinetochore protein Ndc80 was labeled with a GFP construct (Ndc80-GFP) in wild-type cells. For live-cell analysis, the cells were put on an imaging chamber (CoverWell PCI-2.5; Grace Bio-Labs, Inc.) filled with 1 mL of 1% agarose in minimal medium and sealed with a 22 × 22 mm glass coverslip. To accurately determine the prophase to anaphase A duration in fission yeast, we imaged cells expressing simultaneously Cdc11-GFP (spindle poles) and Ndc80-GFP (kinetochores) (strain ST1771; cdc11-GFP::Kan ndc80-GFP::Kan Leu1-32 Ura4-D18), with RIM or widefield microscopy using the same imaging settings and growth conditions.

C. elegans

The C. elegans strain used in this study was maintained at 20°C under standard conditions as described in (Brenner, 1974). The ERM-1-GFP strain was FL378:erm-1(bab59[erm-1::mNGˆ3xFlag])I. L4 stages larvae were mounted on a 10% agarose pad in a suspension of 100 nm polystyrene microbeads (Polysciences Inc.) to block worm movements. For transmission electron microscopy (TEM) control L4 larvae were treated as described in (Bidaud-Meynard et al., 2019).

Drosophila melanogaster

The animal model used here is Drosophila melanogaster, in a context of in vivo/ex vivo experiments. In order to respect ethic principles, animals were anesthetized with CO2 (adults) before any manipulation. To avoid any release of flies outside the laboratory, dead flies were frozen before throwing them. Stocks of living flies were conserved in incubators, either at 18 or 25 degrees to maintain the flies in optimal condition. Fly food contains water, agar (0.8%), sugar (4%), flour (7.4%), yeast (2.8%), moldex (1%) and propionic acid (0.3%). Genotypes and developmental stages are indicated below. Experiments were performed in both males and females indifferently.

Drosophila live and fixed leg samples

For live imaging, imaginal leg discs from (Sqh-TagRFPt^KI[3B]; E-cadherin-GFP) Drosophila strain were freshly dissected from prepupae (2 h after puparium formation) in Schneider medium supplemented with 15% fetal calf serum, 0.5% penicillin-streptomycin and 2 μg/mL 20-hydroxyecdysone (Sigma-Aldrich, H5142) and mounted on slides. For the comparison between Airyscan and RIM and the two-color imaging, imaginal discs were fixed for 20 min in paraformaldehyde (PFA 4%) diluted in PBS. The samples were washed in PBS, re-suspended in Schneider medium and mounted on slides.

Drosophila pupa thorax sample

Sqh-GFP (Daniel et al., 2018) homozygous or hemizygous Drosophila pupae were maintained at 25°C. Live imaging was performed on pupae aged for 15 to 17h30 APF at 25°C. Pupae were adhered on a glass slide with a double-sided tape, and the brown pupal case was removed over the head and dorsal thorax using microdissecting forceps. Pillars made of 4 and 5 glass coverslips were positioned at the anterior and posterior side of the pupae, respectively. A glass coverslip covered with a thin film of Voltalef 10S oil is then placed on top of the pillars such that a meniscus is formed between the dorsal thorax of the pupae and the glass coverslip (Gho et al., 1999)

Drosophila strain for border cells migration

Drosophila harboring F-actin labeled by UtrABD-GFP provided by Thomas Lecuit were used to analyze the dynamics of border cells migration.

Method details

RIM implementation and acquisition parameters

The RIM setup is illustrated in Figure S1A. A Fiber Laser Combiner with 3 fast diode lasers (Oxxius) with respective wavelength 405 nm (LBX-405-180-CSB,) 488 nm (LBX-488-200-CSB), and 561 nm (LMX-561L-200-COL) is used to illuminate the sample. The diode lasers have nanosecond time response for high speed triggering and an Acousto-Optic Modulator is used to modulate the intensity of the solid state 561 nm laser. An apochromatically corrected fiber collimator (RGBV Fiber Collimators 60FC Sukhamburg) produces a collimated TEM₀₀ 2.2 mm diameter output beam for all wavelengths. The incident beam is rotated with an angle of 5 degrees before hitting a X4 Beam Expander beam (GBE04-A) to be shaped into a 8.8 mm TEM₀₀ beam which illuminates, with the appropriate polarization, a fast Spatial Light binary phase Modulator (SLM : QXGA Fourth Dimensions). The latter is conjugated to the image plane and generates different speckle patterns by displaying masks with randomly independent 0 or π phases at each pixel. Note that the diffuser (here the SLM) could be placed anywhere on the excitation pathway as long as the scattered light filled entirely the pupil at the backfocal plane of the objective. This condition ensured that the frequency cut-off of the speckle pattern at the object plane was 2NA/λ. In practice, the focal lengths of the intermediate lenses were chosen so that, at the back-focal plane of the objective, the extension of the field scattered by the SLM was significantly larger than the pupil. Thus, changing of objective or wavelength did not require any modification of the SLM pattern or lens arrangement because the pupil was always entirely illuminated (at the cost of a variation in the injected power density).

The relay lens L1 is an achromatic doublet with visible reflective coating (Thorlabs AC254-500-A). In the intermediate Fourier plane of the illumination path we introduce a quarter wave plate to produce a circular polarization state for the speckled illumination. We also block the zero order of the SLM. A second relay lens system L2 (Thorlabs AC254-150-A) and L3 (Thorlabs AC254-135-A) is used to adapt the beam to all objective lenses. A Quadrichroic Beamsplitter D1 with a cut off centered at 405/488/561/633 nm (Di01-R405/488/561/635-25x36 Semrock) reflects the laser beam towards the inverted microscope (Tei Nikon).

The same setup has been used for providing 2D SIM images. In this case, the SLM displays a periodic pattern. At the intermediate Fourier plane of the illumination path, a Fourier mask is introduced to reject the undesired spots from the SLM pixelisation and a pizza laminated polarizer with 12 segments of tangential linear polarization is used to obtain the required linear polarization of the two beams for each azimutal angle (colorPol® VIS 500 BC3 CODIX).

Different objective lenses have been used in the experiments and are detailed in Table S1. Note that, contrary to the SIM mode, changing the objectives or the wavelengths for the RIM mode did not require any change in the SLM masks nor additional tuning.

The fluorescence is collected via the objective and tube lens onto one or two (for two-color imaging) SCMOS cameras after appropriate filtering. Three band pass filters (Semrock) were used: FF01-514/30-25 for GFP, FF01-609/54-25 for mCherry and FF01-676/29-25 for the fluorophore used in STED.

The 3D image is formed by translating the sample through the focal plane with a piezoelectric Z stage. To synchronize the illumination and data recording, the rolling shutter output of the SCMOS camera is used to trigger the mask change on the SLM. Then, the SLM output triggers the laser when the binary phase mask is stable. A script from micromanager software was written to select the number of speckle patterns per slice, the acquisition time for each speckled image, the number of planes along the Z-axis, the z-spacing and the number of colors used for the acquisition. This script was used for one-color imaging. For two-colors imaging, we used Abbelight and Inscoper softwares.

The excitation and emission wavelengths, the characteristics of the objectives, the excitation power density, the number of speckle patterns per slice, the axial excursion and the total acquisition time of all the experiments are given in Tables S1 and S2 of the supplemental information.

Principles of RIM statistical image reconstruction

In this part, we explain how the stack of low-resolution speckled images is processed in order to form one super-resolved reconstruction of the sample. We assume that the object of interest is the thin slice of sample that is located at the focal plane of the microscope. The fluorescence stemming from markers outside the focal plane is considered as noise. The fluorescence density of the sample slice is denoted by f(r) where r is a two-dimensional vector that indicates a transverse position at the focal plane. The 3D reconstruction is performed by imaging different slices of the sample via a translation through the focal plane. We first summarize the mathematical demonstration of the super-resolution capacity of RIM (Idier et al., 2018) and compare it to that of fluctuation microscopy. Then, we detail the data processing that has been implemented to reach a two-fold resolution gain.

Modeling RIM data

The 2D intensity I of the low-resolution speckled image at the observation point r_obs on the camera is a random variable that can be modeled as,

I(r_obs)= ∫f(r) E(r) H_λ’(r_obs-r) dr, (Equation 1)

where f(r) is the fluorescence density, H_λ’(r) is the observation point spread function (PSF) at the fluorescence wavelength λ’ and E(r) is the speckle intensity. In practice, the speckle pattern is obtained by placing a diffuser on the path of a collimated laser beam of wavelength λ and collecting the scattered light with the microscope objective. Note that in our epi-illumination microscope, the speckle and observation PSF are formed via the same objective of numerical aperture NA.

We assume that the speckle is fully developed (Goodman, 2007). In this case, it can be modeled as a sum of plane waves with transverse wave vector k and random phase ϕ(k) uniformly distributed between 0 and 2π which satisfy, <exp[iϕ(k)]>=0 and <exp[iϕ(k)-iϕ(k’)]>=δ(k-k’) where <> stands for the ensemble average. Note that optical aberrations amount to adding a deterministic phase pattern ψ(k) to these plane waves. Thus, the probability distribution of ψ(k)+ϕ(k) remains uniformly distributed between 0 and 2π. As a consequence, even though aberrations modify the intensity pattern of a given speckle realization, they do not modify the speckle statistics. The speckle intensity E(r) at position r can be modeled as,

E(r) = | ∫p_λ (k) exp[iϕ(k)] exp[ik.r] dk |², (Equation 2)

where p_λ(k)=1 if |k|<2πNA/λ and 0 elsewhere, and scalar approximation has been used. The theoretical ensemble average of E is the constant <E> and its covariance is defined as,

S(r,r’)=< [E(r)-<E>] [E(r’)-<E>] >. (Equation 3)

Using Equation (2), one shows that S(r,r’) is similar to H_λ(r-r’), the point spread function of the microscope at the illumination wavelength λ, defined as,

H_λ(r) = | ∫l_λ(k) exp[i k.r] dk |². (Equation 4)

The first and second moments of fully developed speckles are thus well known and they are insensitive to scattering distortion or aberration (Goodman, 2007).

Super-resolution capacity of RIM

To eliminate the unknown illuminations from Equation (1), we form the covariance of the image intensity (Idier et al., 2018),

C(r_obs1,r_obs2 )=< [I(r_obs1)-<I(r_obs1)>] [ I(r_obs2 )-<I(r_obs2 )>] >

= ∫f(r₁)f(r₂) S(r₁-r₂) H_λ’(r_obs1-r₁)H_λ’(r_obs2-r₂)dr₁dr₂ (Equation 5)

which depends on the known speckle covariance and observation PSF. The covariance being a non-negative definite operator, S and C admit unique non-negative definite square roots S^1/2and C^1/2 which satisfy, (Mercer, 1909)

S(r₁-r₂ )=∫S^1/2(r₁-r’) S^1/2(r’-r₂) dr’, (Equation 6)

where the translational invariance of speckle properties has been used and,

C(r_obs1,r_obs2 )=∫C^1/2(r_obs1,r’) C^1/2(r’,r_obs2 ) dr’. (Equation 7)

Then, the image covariance can be written as,

C(r_obs1,r_obs2 )=∫C^1/2(r_obs1,r’) C^1/2(r’,r_obs2 ) dr’

= ∫dr’ ∫f(r₁)S^1/2(r₁-r’) H_λ’(r_obs1-r₁) dr₁ ∫f(r₂)S^1/2(r’-r₂ ) H_λ’(r_obs2-r₂) dr₂. (Equation 8)

Now, if the Fourier support of S is equal or included in that of H_λ’, one can filter the speckled images so that the point spread function H_λ’ becomes equal to S^1/2. In this case, the operator K acting on the function q,

K(q)= ∫q(r₁) S^1/2(r₁-r’) H_λ’(r_obs1-r₁) dr₁ = ∫ q(r₁) S^1/2(r₁-r’) S^1/2(r_obs1-r₁) dr₁

is definite and positive so it can be identified to the square root of the image covariance. Then, taking the diagonal terms, one obtains,

C^1/2(r,r) =∫f(r₂)K(r-r₂)dr₂ (Equation 9)

where K(r-r₂)=S^1/2(r-r₂ )S^1/2(r-r₂).

When the speckle is generated through the same objective as the observation point spread function, the Fourier support of S^1/2 is similar to that of H_λ’ so the support of K is twice larger than that of H_λ’. Thus, from a theoretical point of view, RIM image covariance bears enough information to reconstruct the fluorescence density with a resolution twice better than that of classical fluorescence microscopy. Note that this demonstration applies identically to three dimensional (3D) imaging by replacing the 2D speckled images, PSF and speckle covariance by 3D ones (Idier et al., 2018).

RIM versus fluctuation microscopy

At this point, one can draw a link between RIM and Fluctuation Microscopy (Dertinger et al., 2009) which is also based on the processing of the second (and sometimes higher) order statistics of ‘random’ images. In fluctuation microscopy, the sample is excited with an homogeneous intensity and one takes advantage of the natural fluctuation (or blinking) of the fluorescence with respect to time to record different realizations of a random imaging process. The images can be modeled using the same Equation 1 as that used for RIM, E being now a random variable accounting for the emission fluctuation.

The fundamental difference between speckled illumination and fluctuation microscopy is that, in the first case, the random process exciting the fluorescence is spatially correlated, S=H_λ while, in the second case, it is totally uncorrelated and S is a Dirac. This has a major incidence. Trivially, in fluctuation microscopy, the Fourier support of S is not included in that of H_λ’ so there is no mathematical proof that the second order statistics of the images can provide the fluorescence density over an enlarged Fourier domain. More precisely, the variance of fluctuation microscopy data simplifiy to a simple convolution of the square of the fluorescence density with the square of the fluorescence density,

V_fluctuation(r) = C(r,r) = ∫f²(r₁)H²_λ’(r-r₁)dr₁. (Equation 10)

This relationship permits to estimate the square of the fluorescence density on the Fourier support of H²_λ’. Now, the knowledge of the Fourier transform of f², $\mathcal{F}$ (f²), over a domain W, does not imply the knowledge of $\mathcal{F}$(f) over W. Hence, except if f is binary, the super-resolved reconstruction provided by fluctuation microscopy should be taken with caution as it depends on the square of the fluorescence density. In particular, the dynamic range of the fluorophore concentration is generally lost. The weakly and strongly labeled features are often under and over estimated, respectively (Marsh et al., 2018). On the contrary, when the speckle covariance S has a bounded Fourier support, as in RIM, the fluorescence density can theoretically be estimated on an enlarged Fourier support, without loss of the staining dynamic range, as shown in Equation 9. However, estimating the square root of the speckled image covariance matrix is impossible in practice because of the huge size of the operator.

RIM reconstruction algorithm (algoRIM)

A tractable technique consists in developing a marginal inversion procedure (Idier et al., 2018) in which the fluorescence density is estimated so as to minimize the distance between the recorded image covariance and the simulated one. Yet, while efficient, this approach cannot be applied to large fields of view as it is computationally demanding, the covariance operator scaling as MxM where M is the number of pixels on the camera.

In this work, we propose a simplified approach in which the fluorescence density is estimated so as to minimize the distance between the variance model C(r,r’) and the empirical variance. Note that the covariance C(r,r’) is maximal at r’=r and tends towards 0 when r’ moves away from r with a typical decorrelation length corresponding to the width of the observation Point Spread Function (PSF). Thus, most of the information on the fluorescence density is contained about the diagonal of the covariance.

Once N different speckled images I_l=1...N of the sample have been recorded, the data processing comprises three steps:

• 1)Each speckled image is deconvolved with a Tikhonov regularised inverse filter. More precisely, we calculate i_l so that,

F (i_l) (k) = F (I_l)(k) x F (H_λ)^∗(k) / [|F (H_λ)(k) |² + e] (Equation 11)

where e is a parameter (Tikhonov regularization) which depends on the noise level of the raw speckled image, $\mathcal{F}$ (g) stands for the Fourier Transform of g and a^∗ is the conjugate of a.

The deconvolved image i_l can be written as,

i_l (r)= ∫f(r) E_l(r) h(r_obs-r)dr (Equation 12)

where we have introduced a novel point spread function, h, such as

F (h) (k) = |F (H_λ)|²(k) / [|F (H_λ)(k) |² + e]

The width of this novel PSF being smaller, the information contained by the covariance of the deconvolved speckled images is further concentrated about the diagonal, i.e. the variance.

• 2)Second, we estimate the empirical variance of i_l as

v(r) =∑_{l = 1 … N} [i_l (r) – i(r) ]² /N, where i(r) = ∑_{l = 1 … N} i_l(r)/N^. (Equation 13)

Third, we estimate f so as to minimize the cost functional,

G(f) = ∫|v(r)-V(f,r)|² dr / ∫|v(r)|²dr (Equation 14)

where V(f,r) = C(r,r) = ∫f(r₁)f(r₂) S(r₁−r₂) h(r-r₁)h(r-r₂)dr₁dr₂. (Equation 15)

To minimize G, one needs a solver able to calculate V for a given estimation of the fluorescence f. Now, the calculation of V involves a time consuming quadruple integral, Equation (15). To speed up the iterative reconstruction procedure, we developed an approximate expression of V which necessitates only a double integral. To this aim, we recall that functions of two variables can be written as a series of the product of functions of one variable only. Let us introduce the bivariate real function,

T(r₁,r₂) = S(r₁-r₂) h(-r₁)h(-r₂). (Equation 16)

Being a non-negative definite kernel, T admits an eigenvalue decomposition as,

T(r₁,r₂) = ∑_{k = 1 … ∞}U_k(r₁)U_k(r₂). (Equation 17)

In practice, T is discretized over the pixels of the camera and implemented as an Hermitian matrix. Its eigenvalue decomposition yields the eigenvectors of decreasing norm U_k. Then, the decomposition is stopped at the K^th order, (K about 10 is usually sufficient to have an accurate estimation of T). We thus obtain a limited rank approximation of T. Other limited-rank approximations are possible, but the one we choose reaches an optimal trade-off according to the Eckart–Young theorem (Eckart and Young, 1936).

The variance is then calculated using,

V(f,r) ≈ ∑_{k = 1 … K} [w_k (f,r)]² (Equation 18)

with w_k (f,r) = ∫f(r₁)U_k(r₁−r)dr₁. (Equation 19)

It is worth noting that decomposing T(r₁,r₂) is much more efficient than decomposing S(r₁−r₂). Indeed, we have found that the number of eigenvectors required for approximating T is significantly smaller than that required for approximating S with the same accuracy.

The minimization of G is performed using a standard conjugate gradient descent algorithm (Bertero, 1998). At each iteration, f(r) is modified following,

fⁿ(r) = fⁿ⁻¹(r) + αgⁿ(r)

where,

gⁿ(r) = -2 ∫ [∑_k=1...Kw_k (fⁿ⁻¹,r₁) U_k( r−r₁ ) ] b(r₁ ) dr₁ with b(r₁) = v(r₁)-V(fⁿ⁻¹,r₁) (Equation 20)

is the residue and α is the scalar that minimizes the fourth order polynom g(α)= G[ fⁿ⁻¹ + αgⁿ ] (calculated analytically). We use an early-stopping of the iterative process as a simple (but efficient) regularization technique that basically acts as a Tikhonov regularization (Bertero, 1998) to account for the variance noise.

Details on RIM reconstruction procedure

The reconstruction process algoRIM consists in a Tikhonov regularized inverse filter of the raw speckled images, involving the observation PSF, H_λ’, and an iterative estimation of the fluorescence density via the minimization of the distance between the experimental variance of the speckled images and the variance model. The variance matching process involves the speckle covariance H_λ.

Estimation of the observation PSF and accounting for the focal shift phenomenon

Ideally, the observation PSF should be estimated from the raw images to account for the possible aberrations on the emission side. This technique was applied in Figure 1E where the aberrated and non aberrated PSF were estimated from images of 200 nm fluorescent beads using an iterative method which jointly optimizes the PSF (which is assumed to be the same for all the beads) and the beads positions and amplitudes (Debarnot et al., 2020). In all the other experiments, the observation PSF was estimated theoretically. In this case, we paid a particular attention to the aberration induced by the difference between the refractive indices of the oil immersion objective and that of the mounting medium. This aberration widens the PSF and shifts the focal plane as one images deeper in the sample (Sibarita, 2005; Bratton and Shaevitz, 2015). To deal with this important issue, we used the PSF models of (Gibson and Lanni, 1992) or (Khadir et al., 2019) which take into account the possible mismatch between the refractive indices of oil, coverslip and mounting medium. First, we estimated the distance D between the coverslip and the theoretical focal plane (which is placed at the working distance specified by the objective). D is equal to 0 when the focal plane coincides with the coverslip surface and increases, as indicated by the Z-stage, when the coverslip is moved away to image deeper in the sample. Then, for a given D, we simulated images of fluorophores at different positions along the z-axis. The image obtained with the highest intensity yielded the two-dimensional PSF. It also indicated the ‘true’ axial position of the observation plane. The latter value was a key parameter when reconstructing the 3D images from successive z-slices and for indicating the depth at which the image was taken. We found the effective position of the observation plane to be 0.66 (for small D) to 0.87 (for large D) times smaller than the position indicated by the Z-stage (piezo) (Sibarita, 2005; Bratton and Shaevitz, 2015). This correcting factor was included in the 3D image reconstructions and in the depth indications.

Estimation of the speckle covariance

The speckle statistics being insensitive to aberrations, H_λ was always estimated theoretically using Equation (4) and adapting the filter I_λ to account for the slide-sample transmission coefficient.

Tuning parameters of algoRIM

All the raw data were interpolated using zero padding to provide pixel sizes at least twice smaller than the Nyquist limit. The observation Point Spread Functions (PSF), H_λ, was generated over a grid corresponding to that of the final reconstruction. The number K of eigenvectors used for estimating the variance was always taken equal to 10. The Tikhonov regularized inverse filter parameter used in the deconvolution of the raw images (from 10⁻³ to 10⁻¹) and the number of iterations of the variance matching procedure (from 10 to 50) depended on the signal to noise ratio. The computing time per reconstruction varied from 5 s to 140 s on an Intel(R) Xeon(R) CPU E5-2687W v4 at 3.00GHz with 192 RAM, depending on the number of raw speckled images and the number of pixels per image.

Artifacts in RIM reconstructions

We have shown in (Idier et al., 2018) that, in the limit of an infinite number of speckled illuminations, one could extract, from the covariance of the raw images, the Fourier transform of the true object, within a bounded domain W corresponding to the support of the square of the observation point spread function, Equation 9. More recently, we have shown in (Labouesse et al., 2020) that there is a one to one correspondence between the variance of the raw images and the Fourier transform of the object over W. Hence, asymptotically, RIM reconstructions are artifact-free within the accessible Fourier domain in the same way as SIM reconstructions when the illumination patterns are perfectly known (and the data noiseless). In practice, if there are enough speckled illuminations for RIM or if the illumination patterns are sufficiently well-known for SIM, there is no bias in the super-resolved image except for the one stemming from a standard zero order Tikhonov regularization introduced to deal with noise. This property distinguishes RIM from other reconstruction methods found in fluctuation or localization microscopy that rely on a priori information on the sample such as binarity, positivity or sparsity and yield biased reconstructions when the samples depart from these assumptions.

Yet, in practice, RIM reconstructions are subject to statistical fluctuations because of the limited number N of available raw speckled images. Figure S1C shows the reconstructions of homogeneous fluorescent lines as a function of N. This study gives an idea of the granule-like artifacts induced by a poor estimation of the speckled image variance. It is shown that for N>400, the granularity contrast is about 10 %. Unfortunately, it seems difficult to estimate a posteriori the level of this artifact as one cannot distinguish the sample spatial fluctuations from the spatial fluctuations induced by a poor estimation of the empirical variance of the raw images. Presently, the best solution for determining the optimal N for a given type of sample is to study the convergence of the reconstruction versus N on one example.

Another issue is the noise (photon noise and camera noise) which restricts the domain of spatial frequencies that is accessible for the super-resolved reconstruction. We observed that an important condition for RIM to succeed was that the standard variation of the raw images (obtained with different speckled illuminations) be two and a half times bigger than the standard variation of repeated acquisitions of one particular raw image (with a fixed speckled illumination) (see Figure S1A for an example of typical raw speckled images). This condition indicates the level of noise (Poisson noise stemming from out-of-focus fluorescence and/or camera electronic noise) that RIM can put up with to provide super-resolved reconstructions.

RIM dynamic imaging

RIM temporal resolution, phototoxicity, and photobleaching depend on the number N of raw speckled images (the stack size) necessary for the homogeneity of the reconstruction (Figure S1C), the acquisition time per raw image (limited by the camera) and the excitation intensity (monitoring the noise level, see Figure S1A). We observed that RIM required the same global photon budget as SIM for the reconstruction process to be successful (Figures 2A and 2C). Thus, the high number of 50-200 raw image acquisitions per plane in RIM (compared to 9 or 15 raw images per plane in 2D/3D SIM) could be compensated by a smaller acquisition time per raw image (2-12ms) and a low excitation intensity (4-20 W/cm²) to provide temporal resolution, phototoxicity and photobleaching levels compatible with many live-cell imaging applications.

In practice, to image a dynamic process using RIM, raw speckled images were recorded regularly with the smallest possible acquisition time allowed by the camera. The stack size N was determined a posteriori by searching the best trade-off between motion blur and reconstruction noise (using comparisons with similar fixed samples). Then, the super-resolved movie frames were formed using either successive stacks of N raw images (sequential approach) or overlapping stacks of N raw images shifted every P images with P<N (interleaving approach) (Guo et al., 2018). We have found that the interleaving technique (akin to a moving average) could ease the visualization of the protein motions by smoothing out the jerky movements of the sequential approach. All movie sequences but that of Video S5 are performed using the sequential approach.

Other microscopy methods

Dense emitter localization microscopy (podosomes)

Data acquisition

dSTORM imaging of F-actin was performed on cells stained in situ by diluting Alexa Fluor 647-coupled phalloidin (Molecular Probes, A22287, 1/100) in the dSTORM buffer (Smart-kit buffer, Abbelight, France). Images were acquired using a 100X/1.49 oil immersion objective (Olympus) mounted on an inverted IX83 microscope (Olympus) equipped with a TIRF module (Abbelight, France) and an sCMOS ORCA FLASH4.0 v3 (100 fps, cable camera link, Hamamatsu) camera. Samples were excited with a 640 nm (400 mW, ERROL Laser) laser at oblique illumination controlled via NEO Software (Abbelight, France). Images were collected once the density of fluorescent dye was sufficient (typically, under 1 molecule/μm²) using an integration time of 50 ms. 10 000 dSTORM raw images were recorded.

Reconstructions of the dense emitter localization microscopy

All the HDLM reconstructions were performed using the Fiji software with the following camera settings: Pixel size equal to 97nm, a base level defined to 105 and a pixel gain set to 20%. The lateral drift was always corrected using the cross-correlation method and a Gaussian rendering was used for visualization in the localization methods.

Thunderstorm (Ovesný et al. 2014): Raw images were pre-filtered with a wavelet filter of width 3 pixels. The threshold for detection of molecules was fixed to the standard deviation of the 1st wavelet level. The subpixel molecule localization was obtained with the maximum likelihood fitting of the PSF model. The high density parameter was set to four molecules for the multi-emitter fitting.

SRRF (Dertinger et al., 2009; Gufstasson et al., 2016): Ring radius was defined at 1.10. The interpolation was set to 3. The PSF width was estimated to be equal to 2.6 pixels. The second order statistics has been used. The optional intensity weighting has been selected.

UNLOC (Mailfert et al., 2018): We choose the high density algorithm, with low spatial frequency background model, an integrated Gaussian PSF model with initial PSF sigma of 1.25 and an “Additive Gaussian noise” model for the camera. The detected particles were connected using an off-state lifetime of 1 frame. The points detected with an insufficient localization precision (threshold 0.4px) were removed.

SIM image acquisition and reconstruction (vimentin, C. elegans, Drosophila leg)

• -The SIM two-color images of the DNA nanorulers were made on an ELYRA PS.1 Carl Zeiss, with a Plan-Apochromat 63x / 1.4 Oil DIC M27 lens and a pco.edge sCMOS camera. The 3D SIM settings using ZEN software corresponded to a periodic grid of period 23 μm for 488 nm and 28 μm for 555 nm, 3 rotations and 5 translations. The reconstruction parameters in ZEN were: SR Frequency Weighting 1, Noise Filter -6., Sectioning 100 / 83 / 83, isotropic reconstruction.

• We performed the alignment of the XYZ stage, acquired the PSF for the different emission wavelengths and formed the realignment matrix between the different channels. The reconstruction and the application of the realignment matrix were realized with the acquisition software of ELYRA PS.1 (Zen Black). A global image control on the raw data and on the reconstruction was systematically done with SIMcheck (Ball et al., 2015).

• -The SIM images of the vimentin filaments were obtained with the home-made 2D SIM that can be run on the RIM setup (see the experimental implementation). The reconstructions were obtained using the SIM reconstruction software described in (Wicker et al., 2013) and a home-made blind-SIM algorithm (Ayuk et al., 2013).
• -The SIM experiments on the Drosophila leg were run both on the ELYRA PS.1 and the home-made 2D SIM. We tested 2D and 3D light grids and different periods. In all cases, we observed a frequent disappearance of the light grids which prevented the reconstruction.
• -The SIM images of the C. elegans were obtained using the Elyra 7 Zeiss microscope with an objective Plan-Apochromat 63x/1.40 oil immersion, illumination at 488nm and emission band pass filter [495-550 nm]. We tested 2D and 3D illumination patterns with several periods and were never able to reveal the periodic organization of the microvilli. Figure 2D displays an image obtained with a 3D lattice illumination with period 360 nm at the object plane and 3 rotations and 5 translations. The reconstruction was made using the Zeiss software.

STED microscopy and reconstruction (vimentin)

STED images were acquired with a Leica SP8 STED 3X microscope (Leica Microsystems, Germany) using a 100X NA:1.4 oil immersion objective. The power of the 775 nm STED laser was set to the maximum value that avoided bleaching. Then, the images were acquired with a pulsed 635 nm laser line. The parameters of the image acquisition were: 13 nm pixel size, 6 time average per line, 400 Hz scan speed. STED images were deconvolved with Huygens Professional (SVI, USA) using the CMLE algorithm, with a signal to noise ratio of 7 and 30 iterations.

Widefield microscopy (dynamics of S. pombe kinetochores)

Time-lapse images were taken at 25°C with an exposure times were of 200 ms using LED light source (SPECTRA X light engine®) reduced to 100 μW to avoid phototoxicity and photobleaching. Images were visualized with camera sCMOS flash 4 LT fitted to a microscope (Nikon with a 100×1.49 NA objective and Semrock filters (FF01-514/30-25) for GFP. Images were recorded using the Micromanager software package (2018/03/22). Intensity and γ adjustments (threshold) were made using Image J software for better visualization.

Airyscan imaging (Drosophila leg and C. elegans)

Airyscan images of the Drosophila leg were acquired using a LSM880 confocal microscope with the Airyscan detector (Carl Zeiss) and equipped with a Plan-Apochromat 63x/NA 1.4 Oil M27 objective. The super resolution mode of the Airyscan was used with a calibration of 0.049 μm/pixel and a z-step of 0.220 μm. The solid state laser at 561 nm was used to image TagRFPt protein fused to myosin. The energy per pixel was equal to 4 μJ. Note that an automatic alignment to calibrate the Airyscan detector was done prior to the acquisition step. The reconstruction was done using the Airyscan data processing included in the ZEN software with the automatic strength (6 by default), similar to the Tikhonov parameter of the inverse filter used for RIM.

Airyscan images of the C. elegans were acquired using a Zeiss Airyscan LSM880 and a 63X/1.4 Plan Apochromat Oil DIC objective. Figure 2D shows a single focal plane from a Z-series. The super-resolution image was reconstructed using the Zeiss software.

Quantitative phase imaging (Drosophila leg)

The 3D map of refractive index in Video S2, first part, is obtained with the phase microscope and the reconstruction method described in (Bon et al., 2014). We used a 60X 1.4 NA objective, with white light illumination.

Quantification and statistical analysis

All the statistics and the data representation have been made by using the online shyni application: https://huygens.science.uva.nl/.

To assess the statistical significance of the observed differences between two experiments, we used the randomization test presented in: https://thenode.biologists.com/user-friendly-p-values/research/

Colocalization analysis for RIM and SIM images of GATTA SIM 140YBY nanorulers

Figure 1D and S2A were made using the Distance2maxProfile code which can be found in the CBI ImageProcessing website at, https://imaprocess.pythonanywhere.com/Analymage/projets/. This code plots the intensity of two channels of the image along a user's segment and yields the interdistance between the maxima.

The mean profile of the reconstructed fluorescence density of two-colors DNA nanorulers was obtained from 20 nanorulers for RIM and 20 for SIM. There was no statistical difference between RIM and SIM profiles (p>0.05).

Myosin doublets and beads

• -Figure 1F: the mean profile of the reconstructed fluorescence density of the myosin doublets was calculated using 10 doublets at each depth.
• -Figure 1E: the mean Full Width at Half Maximum and Standard Deviation of the reconstructed fluorescence density of the beads was calculated using 10 beads.

Trajectory analysis of the PCNA

PCNA center of mass cluster was estimated using the wavelet method implemented in ICY software (De Chaumont et al., 2012). See Figure 4B.

A probabilistic method was used to track individual trajectories of PCNA cluster (Chenouard et al., 2013). 577 trajectories of PCNA were analysed (from 3 different cells) at each phase, early, mid and late S. We report the median trajectory (respectively, 1.16 μm, 0.86 μm, 0.49 μm) and calculated a 95% Confidence Interval with the bootstrap approach presented in https://thenode.biologists.com/a-better-bar/education/. The 95%CI was about 15% of the median. The differences between the median trajectories of the couples late-early, late-mid and early-mid were statistically significant with p<0.001 for all cases.

Displacement fields were estimated using the Optical Flow (Horn and Schunck, 1981) in the ICY software.

Duration of mitosis

The duration of the prophase to anaphase were observed on 32 mitotic cells for RIM and 32 for widefield microscopy. The limits of the box indicate the InterQuartile Range (IQR), the horizontal segment indicate the median and the whiskers extend to 1.5 IQR. The difference between the RIM and widefield median durations was not statistically significant ( p > 0.05). See Figure 4F.

Analysis of the resolution

The resolution was estimated from the image with classical measurements of the Full Width at Half Maximum of beads or filaments. It was also estimated from the Fourier spectrum of the image using the Fourier Image REsolution (FIRE) approach developed by (Nieuwenhuizen et al., 2013). In this case, we formed two groups of raw speckled images (taking every other image) and built two super-resolved RIM reconstructions. Then the Fourier transform of these images were correlated to extract the highest meaningful spatial frequency.

Published: April 30, 2021