Simulation-derived best practices for clustering clinical data

Abstract

Introduction:

Clustering analyses in clinical contexts hold promise to improve the understanding of patient phenotype and disease course in chronic and acute clinical medicine. However, work remains to ensure that solutions are rigorous, valid, and reproducible. In this paper, we evaluate best practices for dissimilarity matrix calculation and clustering on mixed-type, clinical data.

Methods:

We simulate clinical data to represent problems in clinical trials, cohort studies, and EHR data, including single-type datasets (binary, continuous, categorical) and 4 data mixtures. We test 5 single distance metrics (Jaccard, Hamming, Gower, Manhattan, Euclidean) and 3 mixed distance metrics (DAISY, Supersom, and Mercator) with 3 clustering algorithms (hierarchical (HC), k-medoids, self-organizing maps (SOM)). We quantitatively and visually validate by Adjusted Rand Index (ARI) and silhouette width (SW). We applied our best methods to two real-world data sets: (1) 21 features collected on 247 patients with chronic lymphocytic leukemia, and (2) 40 features collected on 6000 patients admitted to an intensive care unit.

Results:

HC outperformed k-medoids and SOM by ARI across data types. DAISY produced the highest mean ARI for mixed data types for all mixtures except unbalanced mixtures dominated by continuous data. Compared to other methods, DAISY with HC uncovered superior, separable clusters in both real-world data sets.

Discussion:

Selecting an appropriate mixed-type metric allows the investigator to obtain optimal separation of patient clusters and get maximum use of their data. Superior metrics for mixed-type data handle multiple data types using multiple, type-focused distances. Better subclassification of disease opens avenues for targeted treatments, precision medicine, clinical decision support, and improved patient outcomes.

1. Introduction

Unsupervised machine learning (ML) broadly encompasses algorithms that seek to discover latent structure in data from input features alone. Clustering analyses, a subcategory of unsupervised ML, attempt to partition these input data into distinct groups based on calculated similarities between observations, generating taxonomies of subjects. Clustering has led to meaningful discoveries in bioinformatics and high-throughput omics over the past two decades[1,2] in topics including gene annotation,[3] gene expression,[4] and histone modification.[5] Clustering holds potential for important advances in clinical informatics as well, including identification of subgroups of patient as targets for intervention,[6,7] phenotyping for precision medicine,[8] and clinical decision support.[9]

Although promising, clinical data pose unique challenges to clustering. Unlike omics data, which can commonly be clustered by the uniform application of a mathematical distance metric to a matrix of data of homogeneous, binary or continuous type,[1] clinical data are characterized by a heterogeneous mixture of data types.[10] Mixed data raise new challenges in feature selection, choosing a distance metric that captures biological meaning, and visualizing clinical data.[11]

Various solutions are in common use for handling mixed-type and clinical data. One approach is to convert all mixed features to a single data type, either transforming all categorical features to continuous [12,13] or all continuous features to categorical.[7,13] However, data conversion risks information loss.[11] An alternate approach is to construct a measure of dissimilarity for variables of each data type and combine them, possibly with some method of differential weighting, into a single coefficient.[14,15] Common implementations use one measure for calculating similarity between continuous features (usually the Minkowski, Euclidean, or Manhattan distances) and a second for the handling of categorical features (usually the Hamming distance or the Gower coefficient.[16–21] Similarly, Huang’s k-Prototypes algorithm implements k-means, which calculates the Euclidean distance, for numeric data and k-modes, which calculates the Hamming distance, for categorical features.[20,21]

Researchers clustering clinical data have applied disparate approaches to integrating heterogeneous data. Some analyses transform data to solely continuous type, such as an experiment on Z-normalized continuous data in the critical care setting[22] or an approach normalizing mixed type data on frequency for data quality control in electronic health records.[23] Other single type restrictions transform mixed-type data to categorical[7] or binary.[11] However, in many studies no description of mixed data handling is reported.[24,25] Commonly, studies employ the Euclidean distance, traditionally most suited for continuous data, in mixed-data contexts,[7,25] although some studies fail to report the employed distance metric.[22–24] The variability of analyses in the clinical literature suggests that there are no consensus, best-practice methods for clustering mixed-type clinical data, and that there is room for growth in methodology and rigor.

In this paper, we evaluate best practices for dissimilarity matrix calculation and clustering on mixed-type, clinical data. As we have just described, earlier assessments of best methods in the literature have been comprised of review articles and limited assessments on small, real-world data sets without ground truth. To the best of our knowledge, we present the most extensive assessment of clustering methods on mixed-type, clinical data to date. To this end, we implement 32,400 simulations of both single-type (continuous, binary, nominal, ordinal, and mixed categorical) and mixed-type (4 varied data mixtures) data in a test comparing 18 methods in the form of “algorithm-dissimilarity pairs”. We compare 3 common clustering algorithms: hierarchical clustering, k-medoids partitional clustering, and neural network-based self-organizing maps. We pair these with 8 methods of calculating dissimilarity: 5 single distance metrics and 3 methods of calculating dissimilarity from multiple distance metrics representing multiple data types. These mixed-metric methods of calculating dissimilarity include two existing approaches: the DAISY algorithm proposed in 1990[26] and the Supersom extension of self-organizing maps proposed by Wehrens and Kruisselbrink.[27] We also test a novel method of our own devising, by extending the Mercator R-Package,[28,29] a pipeline for clustering and visualization with many distance metrics, for a mixture of multiple distances. We draw informed conclusions about the performance of our varying methods of calculating dissimilarity specific to each single and mixed data type and the performance of the three algorithms of choice. In addition, we suggest best practices for clustering binary, continuous, categorical, and mixed-type data. Finally, we apply these methods to real, mixed-type, clinical data sets to illustrate our results in practice.

2. Materials and methods

2.1. Simulations

To test clustering algorithm solutions against ground truth cluster assignments, we generate simulations to represent important problems that could be encountered in clinical data contexts. These analytical challenges include heterogeneity of data set size, individual biological variation, variable measurement error, and mixed types.[1,10] The code to generate these simulations is presented in Supplemental Material A. The tools used to generate these simulations have been made freely available in user-friendly form as part of the Umpire 2.0 R-package. [30,31] As explained in detail in the articles describing Umpire, the simulation of heterogeneity is motivated by the multi-hit theory of carcinogenesis. Populations are modeled by a collection of latent variables called “hits”. Each hit modifies the values of a specific correlated block of features. Each cluster is characterized by the subset of hits that affects those patients. Users can specify the total number of available hits, the number of hits per cluster, and the total number of clusters.

We constructed simulation parameters to represent common problems in clinical data. (Table 1) Umpire facilitated simulations with complex population heterogeneity, feature correlation representing disease processes in organs systems and biological pathways, and clinically representative additive noise. Patient population sizes (200, 800, or 3200 patients) were chosen to represent clinical data problems including Phase II clinical trials, epidemiologic cohort studies, and retrospective EHR analyses. Finding that feature spaces in the clinical literature are variable, with some clustering studies performed on fewer than 10 features,[24,32] we simulated data with 9, 27, 81, or 243 features. After a review of the literature revealed a range in the number of clusters identified,[7,25,32,33] we produced models to simulate 2, 6, or 16 clusters.

Table 1. Simulation parameters representing a scope of clustering problems in clinical research.

Parameters were chosen to represent problems from clinical trials to retrospective electronic health record studies. Single and mixed data types were simulated from all combinations of population characteristics with multiple independent replications.

Population Characteristics	Data Types	Replications
# patients	Single data types	100
200, 800, 3200	Continuous, binary, nominal, ordinal,
# features	categorical1
9, 27, 81, 243	Mixed data types	30
# clusters	Balanced2, unbalanced continuous,
2, 6, 16	unbalanced binary, unbalanced categorical3

¹A mixture of nominal and ordinal data.

²Mixed data simulated with 33% each of binary, categorical, and continuous data.

³Unbalanced mixtures are dominated by 78% of the listed data type.

We explored clustering algorithm performance across 9 data types. Single data types simulated were continuous, binary, nominal, ordinal, and a categorical mixture of nominal and ordinal data (“categorical”). Finding that mixed data sets in the literature are often dominated by one type over others,[7,32,34] we generated mixed-type data in 4 mixtures: one mixture that balanced continuous, binary, and categorical data (“balanced”) and three mixtures each containing all 3 data classes but dominated by a single type (“unbalanced continuous”, “unbalanced binary”, and “unbalanced categorical” mixtures).The balanced data contained 1/3 features of each type. The unbalanced mixtures contained 7/9 of features of the dominant type and 1/9 of features allocated to each remaining type. In mixed simulations, we simulated categorical features as an even mixture of nominal and ordinal data. From this parameter space (324 unique combinations), we generated 100 independent replications of all combinations of simulation parameters for single data types. For each mixed data type, we generated 30 independent replications of all combinations of simulation parameters. For analysis of mixed data sets, we removed data sets with parameter combinations that are “implausible” in real data contexts: data sets with 9 features and greater than 2 clusters and data sets with 16 clusters generated from 27 features and 200 or 800 patients.

2.2. Clustering algorithms

We chose 3 algorithms with common use, representativeness of methodologic trends, and historical significance within the field. First, we used agglomerative hierarchical clustering with Ward’s criterion (HC), a dominant approach for clustering clinical data.[35–39] Second, we represented partitioning algorithms, an important class of clustering algorithms in common use on clinical data sets,[22–24] with Partitioning Around Medoids (PAM), a k-medoids clustering algorithm related to k-means. PAM resolves some problems in the k-means algorithm including greater robustness to outliers[25] and ability to implement a variety of distance metrics.[26] Third, we represented neural-network based clustering algorithms with self-organizing maps (SOM). The computational methods, advantages, and disadvantages are outlined in Table 2.[1,2,25] For each clustering algorithm, we assumed the number of clusters was known, recovering the number of clusters given from the simulation parameters.

Table 2.

Features of 3 implemented clustering algorithms.

Algorithm	Class	Computational Method	Advantages	Disadvantages
Agglomerative hierarchical clustering with Ward’s method	Connectivity-based	Sequential, bottom-up merging of objects into clusters to minimize within-cluster error sum of squares	Does not require a priori designation of number of clusters. Can be implemented with a variety of distance metrics and linkage methods.	Geometric interpretation assumes objects are in Euclidean space. Tends to result in hyperspherical clusters of similar size. Not robust to outliers. High computational cost with high-dimensional data. Requires designation of a level to cut the hierarchy to obtain a final cluster solution. Every outlier observation is forced into a cluster.
Partitioning Around Mediods (PAM) (k-medoids)	Partitioning	Iteratively defines a central observation within a cluster (medoid) and assigns each object to the nearest medoid	Robust to outliers. Can be implemented with a variety of distance metrics and linkage methods. Low computational cost.	Requires a priori designation of number of clusters. Tends to result in hyperspherical clusters of similar size. Every outlier observation is forced into a cluster.
Self-organizing maps (SOM)	Neural-network based	High-dimensional data are projecting into a 1-D or 2-D lattice of neurons, preserving the proximity relationships of original data as a topological map	Low computational intensity; very fast. Can be implemented with a variety of distance metrics and linkage methods.	Classically considered a method of visualization, not a clustering approach. Every outlier observation is forced into a cluster. Requires a priori designation of number of clusters.

Compiled from the following references: [1,2,25].

2.3. Distance metrics

We implemented distance metrics for single data types to serve as controls for mixed data. For calculating dissimilarity among single data types, we tested distance metrics for 5 types of variables: continuous, nominal, ordinal, symmetric binary, and asymmetric binary. Table 3 outlines features of single distance metrics implemented in these experiments.

Table 3.

Comparison of distance metrics.

Distance	Data type	Mathematical Expression	Method
Euclidean	Continuous	$d(i,j)={\left({\left|x_{i1}-x_{j1}\right|}^2+{\left|x_{i2}-x_{j2}\right|}^2+\cdots +{\left|x_{ip}-x_{jp}\right|}^2\right)}^{1/2}$ $d_{BINARY}=\sqrt{{(b+c)}^2}$	Distance in real space
Manhattan	Continuous	$d(i,j)=\left|x_{i1}-x_{j1}\right|+\left|x_{i2}-x_{j2}\right|+\cdots +\left|x_{ip}-x_{jp}\right|$ $d_{BINARY}=b+c$	Distance in real space
Jaccard Index	Asymmetric binary	$d=\frac{a}{a+b+c}$	Negative match exclusive
Hamming	Symmetric binary	$d=b+c$	Hamming-like
Gower	Nominal, ordinal; binary, continuous1	$s(i,j)={\sum }_{k=1}^n{s}_{ijk}/{\sum }_{k=1}^n{\delta }_{ijk}$ $s_{ijk;BINARY}=\frac{a}{a+b+c}$ $s_{ijk;NOMINAL}=1if{x}_{ik}=x_{jk};s_{ijk;NOMINAL}=0if{x}_{ik}\ne x_{jk}$ $s_{ijk;QUANTITATIV{E}^2}=1-\left|x_{ik}-x_{jk}\right|/r_k$	Simple matching

¹Although the Gower coefficient can be implemented for multiple data types, in this study it is implemented for only nominal and ordinal data.

²“Quantitative” = ordinal or continuous.

Although binary data are frequently typed as a special case of nominal data and considered as a unit with the categorical data problem, dichotomous variables can be separated into two types for more focused calculation of distance. For symmetric binary variables, both possible states (i.e., 0 or 1) carry equal value and weight. Conversely, in asymmetric binary variables, the outcomes are not equally important, such that the presence of a relatively rare attribute is more valuable than its more common absence.[40,41] Choi and colleagues clustered the behavior of 76 binary similarity and distance metrics on a random binary data set into 6 groups, which we used to inform the selection of these distance metrics.[40] For asymmetric binary data, we chose the Jaccard distance (1908), a negative match exclusive distance with easy interpretability.[26,40] For symmetric binary data, we implement the Hamming distance. For binary data in SOM, the Kohonen R-package implements a Hamming-like distance as the Tanimoto distance.[27]

For categorical data, we implement the Gower coefficient of similarity,[16] a historic mixed-distance metric for mixed-type data, which is in current use for mixed-type data.[42] Gower’s coefficient provides solutions for three data types: binary, nominal (“qualitative”), and continuous (“quantitative”). Similarity between binary features can be described by simple matching[40] in a manner equivalent to the Jaccard index. Dissimilarity between nominal features is calculated from simple matching with s_ijk = 1 if x_ik = x_jk and s_ijk = 0 if x_ik = x_jk. Dissimilarity is calculated from the ratio of difference between objects to the range of values for the k^th variable, r_k. Here, we implement the Gower coefficient to calculate distance for categorical data using the cluster R-package. [43]

These 5 single measures of distance have varying availabilities based on the R-packages we implemented, generating 13 single algorithm-distance pairs (Table 4). The Jaccard and Sokal-Michener distances cannot be implemented on non-binary data. Jaccard and Sokal-Michener were tested only on binary data. For single-distance experiments, the Gower coefficient was implemented only on categorical data.

Table 4. Algorithm-distance pairs implementing single distance metrics with 3 clustering algorithms on single data-type simulations.

Each distance metric is associated with optimal suitability for certain data types. Some distance metrics can be implemented on multiple data types, while others have type-restricted implementation. Distance metrics were applied to all permitted data types.

Algorithm	Distance	Data Type Suitability	Data Type Implementation
Agglomerative hierarchical clustering with Ward’s method	Jaccard	Binary (asymmetric)	Binary
	Sokal-Michener	Binary (symmetric)	Binary
	Gower	Nominal; categorical	Categorical
	Manhattan	Ordinal; continuous; binary	Binary, categorical, continuous
	Euclidean	Continuous; binary	Binary, categorical, continuous
Partitioning Around Medoids (PAM) (k-medoids)	Jaccard	Binary (asymmetric)	Binary
	Sokal-Michener	Binary (symmetric)	Binary
	Gower	Nominal; categorical	Categorical
	Manhattan	Ordinal; continuous; binary	Binary, categorical, continuous
	Euclidean	Continuous; binary	Binary, categorical, continuous
Self-organizing maps	Tanimoto	Binary	Binary
	Manhattan	Ordinal; continuous; binary	Binary, categorical, continuous
	Euclidean	Continuous; binary	Binary, categorical, continuous

For mixed data across these 3 algorithms, we implemented 2 single distance methods and 3 methods of dissimilarity calculated from the combination of multiple distance metrics, as allowed with package restrictions. (Table 5) Because the Manhattan distance and Euclidean distance can be applied to a variety of data types, albeit with varying efficacy, we applied these two distances with all 3 algorithms as single distance controls. First among our multiple-distance methods, we implemented DAISY,[43] which implements the Gower coefficient for categorical and binary data paired with the Euclidean distance for continuous data, a published approach for mixed data.[33]

Table 5. Clustering solutions for mixed-type data with single and mixed distance metrics and 3 clustering algorithms.

Mixed distance metrics handle data mixtures by implementing multiple distance metrics targeted towards specific data types.

Dissimilarity Method	Clustering Algorithm	Distance Metric	Data Type Target
Manhattan distance	Hierarchical clustering PAM SOM	Manhattan distance (single)	Binary, categorical, continuous
Euclidean distance	Hierarchical clustering PAM SOM	Euclidean distance (single)	Binary, categorical, continuous
DAISY	Hierarchical clustering PAM	Gower coefficient Euclidean	Categorical, binary Continuous
Mercator	Hierarchical clustering PAM	Jaccard Sokal-Michener Gower coefficient Manhattan Euclidean	Binary Binary Nominal Ordinal Continuous
Supersom	SOM	Manhattan Euclidean	Categorical, binary Continuous

Finally, we developed our own method by extending the Mercator R-Package. We began with Kaufman and Rousseeuw’s suggested guidelines for mixed-data handling.[26] They describe five data types commonly found in clinical data: asymmetric binary, symmetric binary, nominal, ordinal, and continuous. In our extension of Mercator, we compute five distinct distance metrics, d₁,…, d₅, one for each data type (Table 5). We then combine these five measures as though they were Euclidean, taking the square root of an unweighted sum of squares:

$$MD=\sqrt{d_1^2+\cdots +d_5^2}$$

In DAISY and Mercator, distance cannot be calculated in the case of a data type containing only 1 feature. This feature must be excluded from analysis.

2.4. Evaluation and validation

We assessed accuracy and quality of each clustering solution by both external (Adjusted Rand Index) and internal (Silhouette Width) criteria of validity. To assess external criteria, which validate a clustering assignment against our “ground truth” of known cluster identities, [44,45] we employ the Adjusted Rand Index (ARI),[46] considered an important external validity measure for over 30 years.[47] ARI corrects the Rand Index, a score of cluster assignment concordance,[48] for chance assignment into concordant clusters. Possible values range from 0 to 1, where 1 is perfect concordance.[46] Internal criteria validate the clustering assignment based exclusively on information intrinsic to the data.[45] We assess internal criteria, and intrinsic measure of compactness, connectedness, separation, stability, predictive power, and/or correlation of clusters,[44] by the silhouette width (SW),[49] which computes a score from −1 (worst) to 1 (best) to assess both intra-cluster homogeneity or compactness and inter-cluster separation. [44,45,49] ARI assesses accuracy of a clustering solution against a gold standard, but cannot be implemented on real data with unknown truth. SW does not compare to a gold standard and represents techniques used for cluster validation in actual research practice. Here, we compare the quality of a clustering assignment by ARI or SW quantitatively, by comparison of means, and qualitatively, by comparison of the distribution of these statistics across the test set, visualized with violin and lattice plots.[50]

For mixed distance methods, we assessed the scalability of each algorithm to high-dimensional data within reasonable computational limits.[1] To reflect the computational realities of many biomedical projects, these experiments were run on a desktop personal computer. For DAISY and Mercator, we documented the CPU time charged for the execution of the calculation of the distance metric and for each clustering algorithm. SOM implements the calculation of distance and the clustering process in a single step, for which we documented CPU time. Computational time was compared by mean and standard deviation. When identified, slower runtimes within an algorithm were compared by simulation characteristics (number of patients, features, or clusters and type of data mixture) by mean and standard deviation and visualized.

2.5. Applications

The first application employs deidentified, clinical data that were previously published. These consist of 21 mixed prognostic features, of which 15 are binary, drawn from clinical and laboratory data, collected on 247 treatment-naïve patients with chronic lymphocytic leukemia (CLL).[51–56] A description of these data can be found in Supplementary Material B. As this dataset contains 71.4% binary features, we classified it as an unbalanced, binary-dominant mixture.

We applied two analytical approaches to mixed-type data handling. First, we transformed the mixed data set to solely binary data using a previously published method[11] and clustered with HC and the commonly implemented Hamming distance. Second, we applied best practices for the data set identified by the simulation experiments. The number of clusters k was chosen by maximizing silhouette width over solutions from 2 to 12 clusters using the best practice method, and this number of clusters was recovered in the binary transformed data solution.[11] For both implementations, we visualized with t-SNE[57] and assessed intrinsic cluster quality by silhouette width.

Our second application uses data from the Medical Information Mart for Intensive Care (MIMIC-III).[58] We identified 40 features that were present in the database in a large fraction of patients, and randomly selected 6000 patients for whom complete data for the 40 features were available. The final dataset included 16 continuous features (age, heart rate, respiratory rate, glucose, potassium, sodium, creatinine, BUN, chloride, WBC, hemoglobin, magnesium, phosphorus, calcium, INR, and PTT), 1 symmetric binary (gender), 1 asymmetric binary (skin integrity), 5 ordinal (Braden mobility, Braden moisture, Braden activity, Braden nutrition, activity tolerance,), and 17 nominal (ethnicity, insurance, admission location, admission type, bowel sounds, abdominal assessment, LLL lung sounds, LUL lung sounds, RLL lung sounds, RUL lung sounds, respiratory pattern, oral cavity, assistance device, position, urine appearance, pain presence, and orientation). In order to interpret clusters, we computed the standardized mean difference between each pair of clusters for each feature.[59]

3. Results

3.1. Single-distance methods

Clustering performance for each data type varied by both clustering algorithm and distance metric. (Mean ± sd for each test and type, averaged across all other parameters, is available in Supplemental Table B.1.) On noisy simulations across each data type and distance metric, HC had higher ARI than PAM. HC had higher silhouette widths than PAM on continuous, ordinal, and mixed categorical data. SOM had highest ARI and SW for all data types and distance metrics, except nominal data.

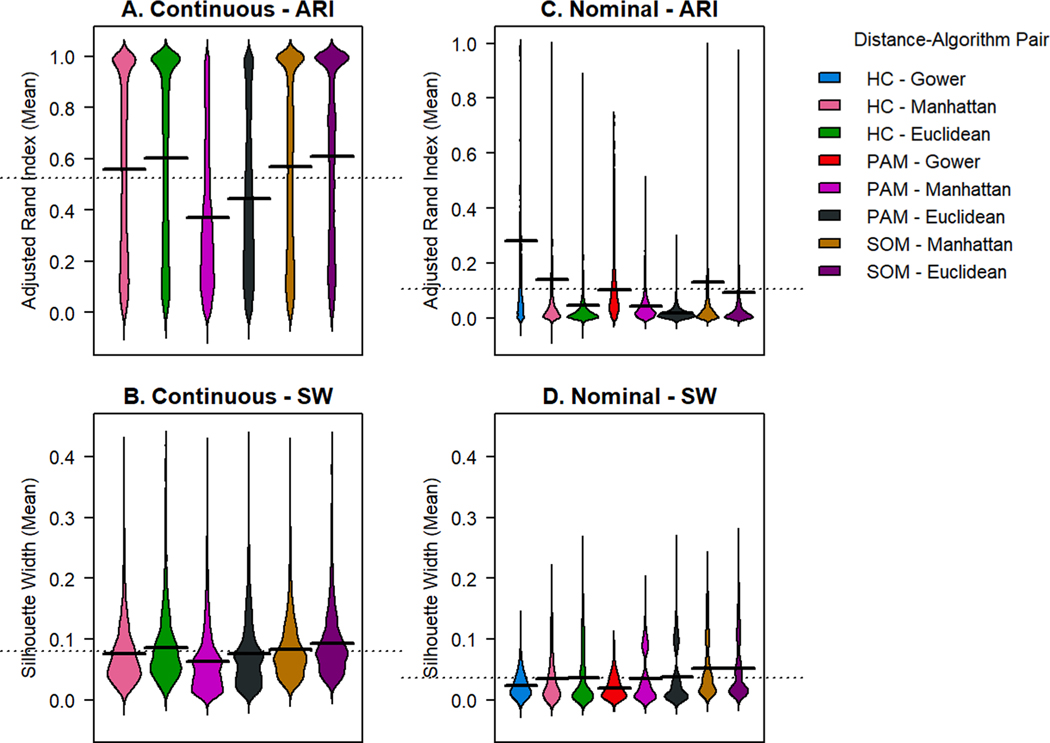
Continuous data had higher ARI and SW across distance metrics compared to other data types.(Fig. 1.A) SOM with Euclidean distance produced the highest mean ARI (0.611 ± 0.336) and highest mean SW (0.093 ± 0.051). Visualization with violin plots can show the consistency of high-quality solutions from a given method. All distance methods and algorithms produced a range of ARI from very poor (near 0) to nearly perfect (near 1). While PAM produces a bolus of clustering solutions with low ARI (0.1–0.5), HC and SOM produce a bolus of solutions with very high ARI. SW does not vary strongly across algorithms.

Fig. 1. Violin plots of adjusted rand index and silhouette width for simulated continuous and nominal data.

Simulated continuous data was clustered with 3 algorithms (hierarchical clustering “HC”, Partitioning Around Medoids “PAM”, and self-organizing maps “SOM”) with 2 distance metrics suitable for numeric data (Manhattan and Euclidean).(A,B) Simulated nominal data was clustered with 3 algorithms (HC, PAM, and SOM) with 3 dissimilarity metrics (Gower, Manhattan, and Euclidean).(C,D) For continuous data, all algorithms produced a spectrum of ARI across many simulations.(A,C) PAM produced a bolus of clustering solutions with low ARI (0.1–0.5), HC and SOM produce a bolus of solutions with very high ARI, represented as an “onion bulb” near 1. SW does not vary strongly across algorithms. (B,D) Comparatively, on nominal data, clustering solutions produced depressed ARI and SW near 0 across all algorithms and distance metrics, with PAM and SOM producing a fraction of solutions with elevated SW.

Binary data had second highest ARI and SW across distance metrics compared to other distance types, with solutions with highest ARI achieved with SOM.(Supplemental Figure B.1). Across HC or PAM, performance of all 4 distance metrics in question (Jaccard, Sokal & Michener, Manhattan, and Euclidean) produced solutions spanning a range of ARI from 0 to 1. (Figure 4.2) PAM ARI’s were heavily weighted towards inaccurate solutions (ARI between 0 and 0.4). HC and SOM produced bipolar results, with ARI clustered either near 0 or near 1. The Tanimoto distance presented with the lowest range of SW, with a tail of many values less than 0.

Nominal, ordinal, and categorical data had lowest ARI and SW across distance metrics, compared to continuous and binary data. Clustering solutions for nominal data produced the lowest ARI of any data type (Fig. 1.B). Among nominal data, the HC with Gower distance produced the solution with both highest mean ARI and largest ARI standard deviation (0.283 ± 0.298). The highest silhouette width was produced by SOM with the Manhattan distance (0.052 ± 0.046). By visualization of ARI with violin plots, all methods produced a range of values with most solutions clustered near 0 with no evidence of the bipolar distribution seen in binary and continuous data. SW also clustered near 0, with PAM and SOM producing a fraction of solutions with elevated SW. Clustering solutions of ordinal data produced intermediate ARI and SW (Supplemental Figure B.2). SOM with the Manhattan distance produced the solutions with highest mean ARI (0.405 ± 0.368) and SW (0.081 ± 0.044). The Gower distance had lower ARI and SW performance by quantitative measures and violin plot visualization than the Manhattan or Euclidean distance. Mixed categorical data resulted in low ARI and SW, like nominal data, with visualization ARI producing a range of values with a heavy distribution near 0 (Supplemental Figure B.3).

3.2. Multiple-distance methods

Clustering of mixed-type data was tested on 4 distinct data mixtures. ARI and SW (mean ± standard deviation) for simulated data mixtures clustered with 3 algorithms on 2 single distance metrics and 3 mixed-distance dissimilarity metrics are displayed in Supplemental Table B.2. Because of the poor performance of the Tanimoto distance in SOM on binary data, we supplemented the Manhattan distance for the treatment of binary data in Supersom.

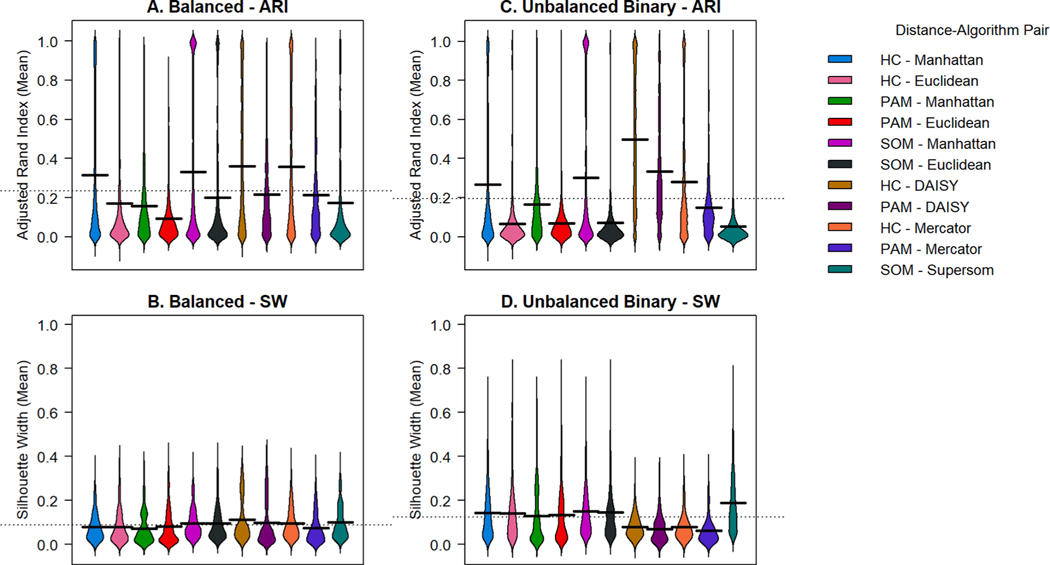
Best solutions varied by data mixture composition. For balanced, unbalanced binary, and unbalanced categorical mixtures, the DAISY algorithm with HC outperformed all tested algorithm-distance pairs by mean ARI. DAISY with HC resulted in the highest SW in balanced data, as well (0.099 ± 0.085, mean ± sd). However, for the other three data types, DAISY with PAM or HC resulted in low SW when compared with other methods. Supersom produced the highest SW for all 3 unbalanced data types and the second highest SW for balanced data (0.098 ± 0.080), but produced low mean ARI compared to other methods.

For balanced mixtures, (Fig. 2.A) the superior solution was produced by DAISY with HC (mean ARI = 0.474 ± 0.352; mean SW = 0.099 ± 0.085), closely followed by Mercator with HC (mean ARI = 0.467 ± 0.366; mean SW = 0.093 ±0.069). The performance of Mercator, an unweighted combined metric, is comparable to DAISY on balanced data, but lags in mean ARI on unbalanced data. SOM with the Manhattan distance presents elevated mean ARI with a strong bipolar distribution. ARI with PAM, regardless of distance metric, produces a distribution of solutions weighted towards 0. For unbalanced binary mixtures,(Fig. 2.B) the superior solution by mean ARI was produced by DAISY with HC (0.574 ± 0.324). Implementations of the Euclidean distance and Supersom result in solutions near 0. Higher SW are produced by single distance measures, SOM, and Supersom, with DAISY and Mercator producing SW below the overall mean. Unbalanced continuous mixtures produced distinct results,(Supplemental Figure B.4) with highest mean ARI solutions produced by SOM with the single Manhattan distance (0.564 ± 0.392).

Fig. 2. Violin plots of adjusted rand index and silhouette width for simulated balanced and unbalanced binary data mixtures.

Varying data mixtures were clustered with 3 algorithms (hierarchical clustering “HC”, Partitioning Around Medoids “PAM”, and self-organizing maps “SOM”), 2 single-distance metrics (Manhattan and Euclidean distance) and 3 mixed-distance dissimilarity metrics (DAISY, Mercator, and Supersom). For both balanced (A) and unbalanced binary (C) simulations, all algorithms tested produce solutions with a range of ARI between 0 and 1, with improved performance with DAISY and Mercator with HC and SOM with the Manhattan distance. Among balanced data, DAISY and Mercator perform similarly. Among unbalanced binary data, DAISY with HC outperforms all other metrics and algorithms. Supersom produced superior SW (D) but low mean ARI compared to other methods.

3.3. Variability of adjusted rand index across simulation parameters

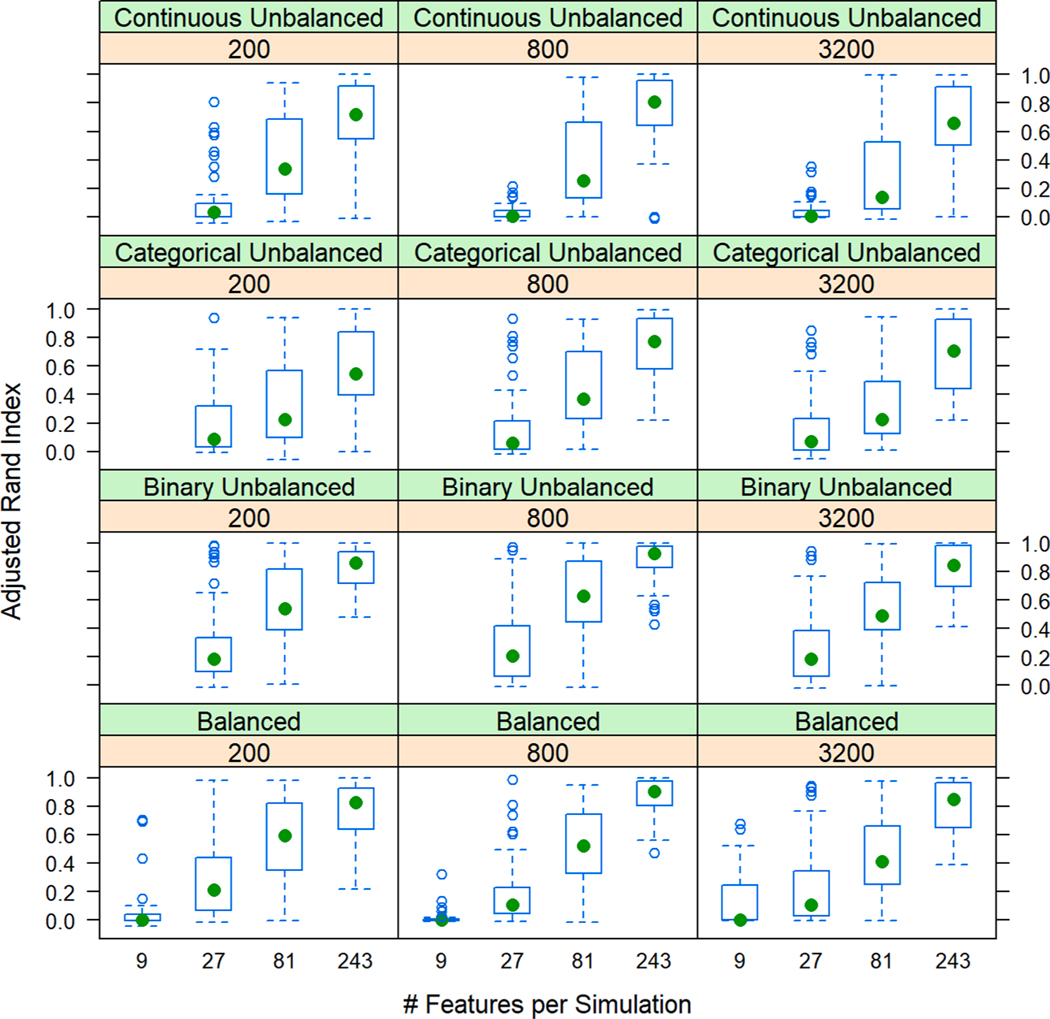
Violin plots of clustering solutions displayed variability of ARI in the form of broad spectra and bipolar distributions. We employed lattice plots to interrogate these results, stratifying performance of each algorithm-distance pair across number of simulated patients and features. (Fig. 3; Supplemental Figures B.6-B.10) A common trend emerged across single- and mixed-distance visualizations: ARI varied strongly by number of features, but not by number of patients. ARI was lowest among simulations with 9 features and highest among simulations with 243 features. Intermediate features spaces displayed higher degrees of variability, represented by broad spectra of ARI across many simulations. Categorical simulations displayed poorer performance, even at larger feature spaces. Even at simulations with 243 features, ordinal simulations presented broad, variable spectra. Nominal data, characterized by poor performance at 81 or fewer features, presented with improved, though variable, performance at 243 features. This pattern of poor performance at low feature numbers and improved performance at higher feature spaces was also present with the DAISY and Mercator algorithms across data mixtures.

Fig. 3. Lattice box plot of Adjusted Rand Index (ARI) of mixed-type simulations by number of features and patients with hierarchical clustering and the DAISY algorithm.

Four distinct mixtures of data were plotted with the DAISY dissimilarity algorithm with hierarchical clustering, an algorithm-distance pair with superior performance across data mixtures. Across data types and algorithms, ARI varied strongly by number of features, but not by number of patients: lowest in simulations with 9 features and highest in simulations with 243 features. Intermediate feature spaces displayed higher degrees of variability, represented by broad spectra of ARI across many simulations.

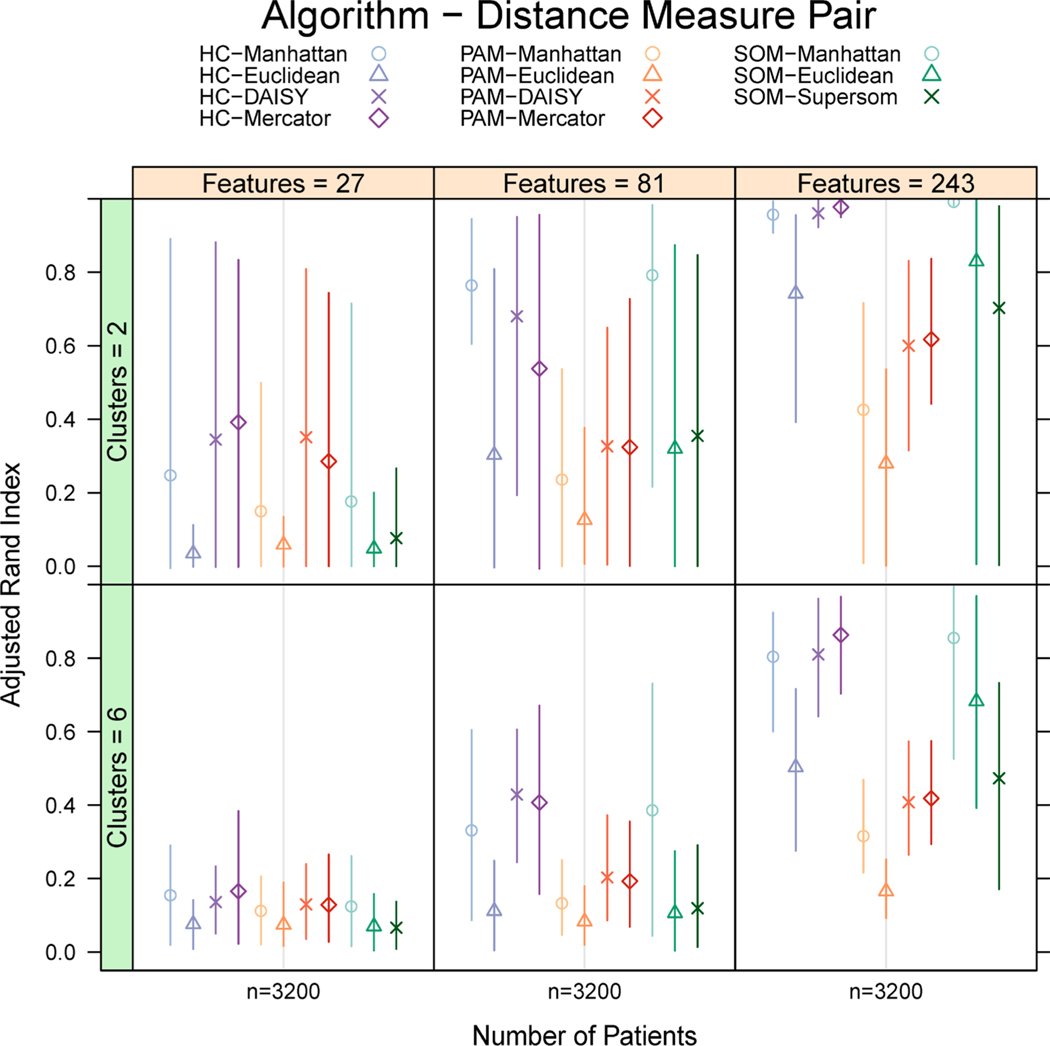
In Fig. 4, we fix the number of patients to 3200 to interrogate the performance of each algorithm-distance pair on mixed data across number of features and clusters, comparing all algorithms. On a balanced data mixture, all algorithm-distance pairs improve in performance as the number of features increases. However, algorithm performance on balanced, mixed-type data varies markedly, with superior performance from HC and decreased performance from PAM. Among feature spaces where SOM performs with high mean ARI, the range of ARI remains wide. With increased feature spaces, higher ARI present with the Manhattan, DAISY, and Mercator distances on balanced data across algorithm-distance pairs. Mean ARI is increased with a smaller number of simulated clusters, but the range of ARI is smaller with 6 clusters than 2.

Fig. 4. Lattice box plot of Adjusted Rand Index (ARI) of 11 algorithm-distance measure pairs on large (3,200 patients), balanced, mixed-type simulations by number of features and clusters.

ARI is presented as mean (symbol) with bars extending to the 10th and 90th percentile. ARI increases with increasing number of features. Simulations with 6 clusters present with decreased mean ARI but contracted ARI range. With 81 or 243 features, the Manhattan, DAISY, and Mercator distances generate higher ARI than Euclidean distance within each algorithm. PAM shows the lowest mean ARI across feature and cluster combinations. HC and SOM produce solutions with elevated ARI, though SOM presents with wide ranges in some contexts.

3.4. Computational scalability of mixed-distance methods

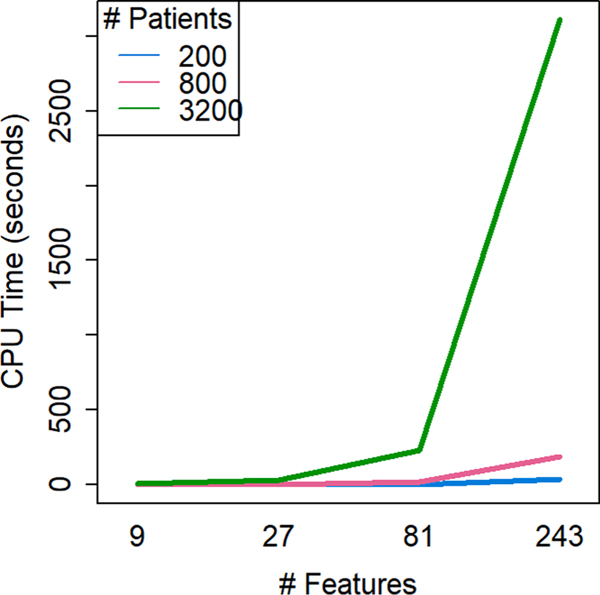
CPU time to calculate a mixed-distance dissimilarity matrix varied by algorithm. Time costs predominantly resulted from time to calculate dissimilarity, not from time to execute a clustering algorithm.(Table 6) SOM, which calculates dissimilarity and clusters within a single process, had fastest overall execution for any simulation size (mean 0.533 s), while the DAISY algorithm had the slowest CPU time averaged over all simulations sizes (mean 372 s). Time to calculate dissimilarity with DAISY varied (min = 0.3 s; max = 3869.72 s = 1hr4.5 m). By interaction, calculating the DAISY dissimilarity was slowest in simulations with both large numbers of features and large numbers of patients (Fig. 5).

Table 6.

Computational (CPU) time (s) for 3 algorithms to calculate mixed-distance dissimilarity.

Dissimilarity Algorithm	Dissimilarity Time (s)	Clustering Time (s)
		HC1	PAM2
DAISY	372.461 ± 983.599	0.105 ± 0.142	1.623 ± 3.611
Mercator	99.859 ± 139.127	0.097 ± 0.13	1.598 ± 3.46
Supersom3	0.533 ± 0.794	-	-

¹Agglomerative hierarchical clustering with Ward’s criterion.

²Partitioning Around Medoids.

³Kohonen self-organizing maps and their related mixed-distance implementation calculate dissimilarity and cluster in a single process.

Fig. 5. CPU time to calculate the DAISY dissimilarity from the interaction of number of patients and number of features in a simulation.

DAISY displayed high variability in run time (372.461 ± 983.599 s). Computational time increased with the interaction of both number of patients and number of features as dataset size increased.

3.5. Applications

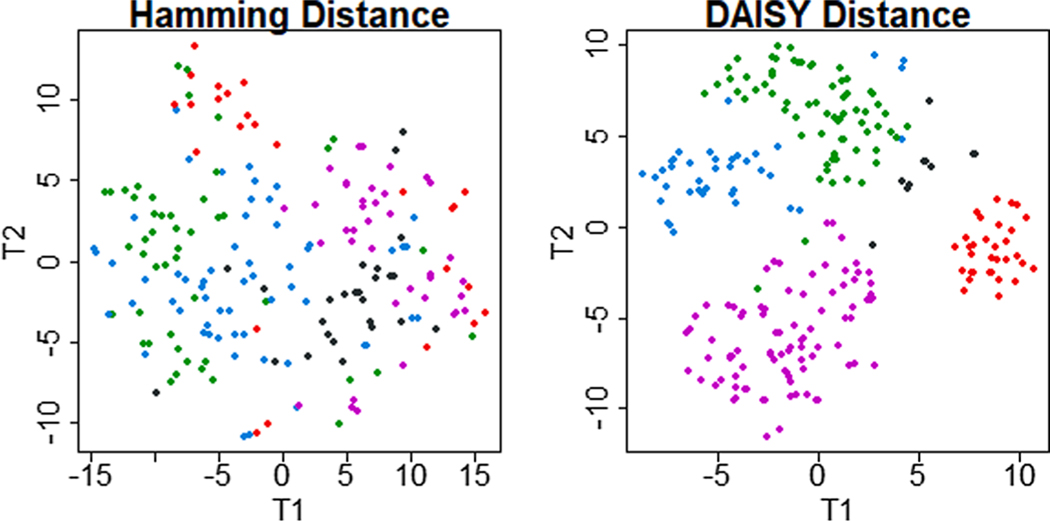
Because the first real, application data set is a small, unbalanced binary mixture, we choose DAISY with HC as a best practice solution. From local maximum silhouette width for DAISY solutions, we chose k = 5 clusters. Visualizing the Hamming distance revealed an amorphous grouping of clusters without clear boundaries or separation. Conversely, t-SNE visualization of the DAISY solution presented 4 clearly defined clusters with a small grouping of outliers (Fig. 6). SW of the DAISY solution (0.26) remained higher than SW for the Hamming solution.(0.11)

Fig. 6. Comparison of T-distributed Stochastic Neighbor Embedding visualizations of clusters obtained from the same mixed-type data set with a single-distance and a multiple-distance solution.

Clinical data from 21 mixed features on 247 patients with chronic lymphocytic leukemia was clustered with two methods. First, it was transformed to a binary matrix and clustered with the Hamming distance (left). Second, untransformed, mixed data were clustered with DAISY dissimilarity algorithm (right). The Hamming solution recover amorphous groupings without clear separation. The DAISY solution recovered 4 distinct clusters and a small grouping of outliers.

Our second application uses data for 40 features on 6000 patients with admissions to an ICU selected from the MIMIC-III database. We applied four methods to cluster the data:

1. DAISY distance with hierarchical clustering,

2. Mercator distance with hierarchical clustering,

3. Manhattan distance with self-organizing maps (SOM), and

4. Euclidean distance with partitioning around medoids (PAM).

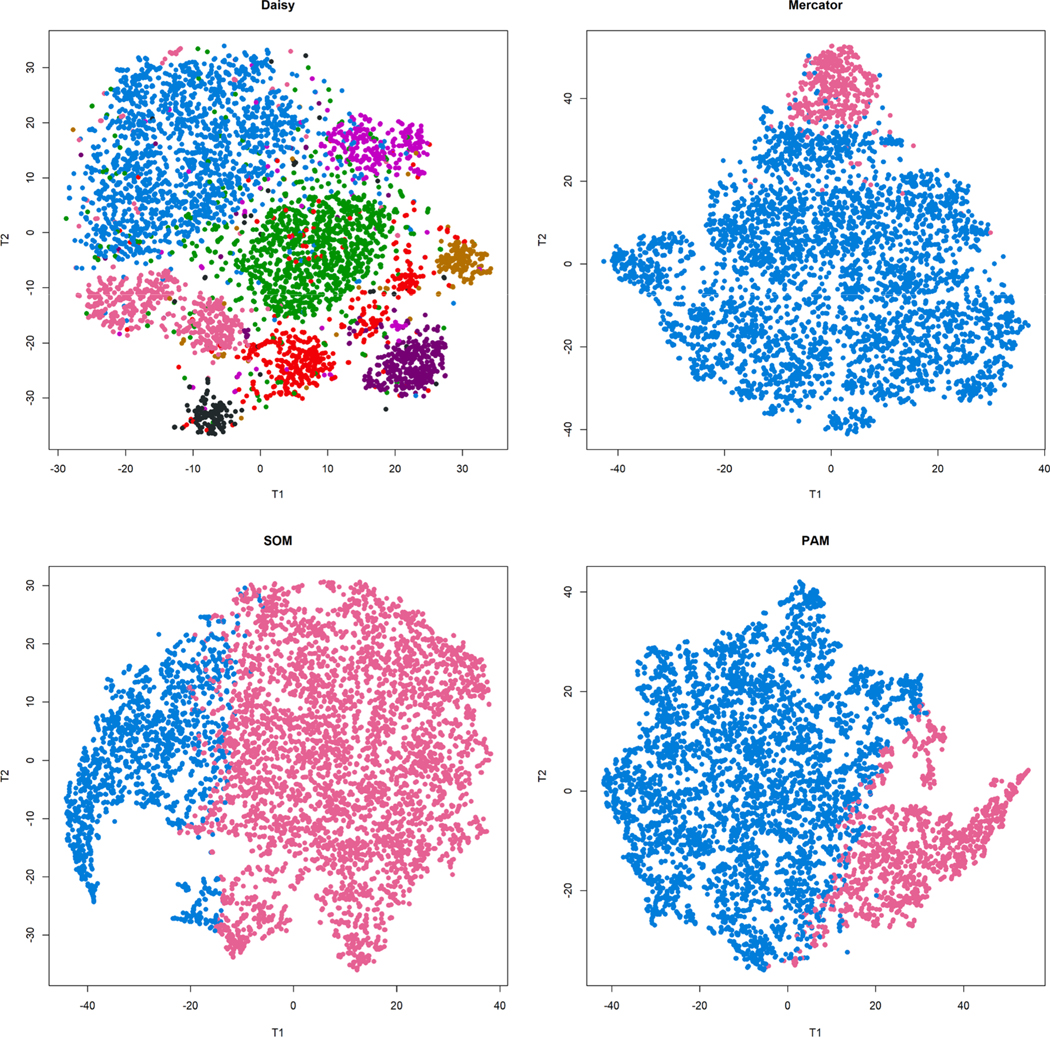
We used the maximum silhouette width across the range 2–10 to define the number of clusters (K = 8 for DAISY; K = 2 for the other three methods). Results were visualized using t-SNE (Fig. 7). The t-SNE visualization suggest that the DAISY distance leads to a clearer separation of clusters.

Fig. 7. Comparison of four methods used to cluster MIMIC-III data.

(Top left) DAISY distance with hierarchical clustering identified 8 clusters. The other three methods each identified only two clusters. (Top right) Mercator distance with hierarchical clustering. (Bottom left) Manhattan distance with self-organizing maps (SOM). (Bottom right) Euclidean distance with partitioning around medoids (PAM).

In order to interpret the 8 clusters defined by DAISY, we computed the standardized mean difference between each pair of clusters for each feature.[59] The strongest association between discrete features and clusters came from the admission type and location, lung sounds, bowel sounds, and orientation (Supplementary Table C). The strongest association of continuous variables came from respiratory rate, age, chloride and BUN. Cluster 2 (colored hot pink in the lower left of the DAISY t-SNE plot) consists almost entirely of elective admissions, either from physician referrals or for normal deliveries. Patients in Cluster 2 were more likely to have “absent” bowel sounds and “clear “lung sounds, had a higher respiratory rate, potassium, and sodium; and lower heart rate, BUN, creatinine, glucose, and hemoglobin. All other clusters consist primarily of emergency admissions, with “present” bowel sounds and a variety of different lung sound patterns and continuous clinical measurements.

Next, using chi-squared tests, we found that the clusters were associated with an outcome (death within 30 days, p < 2.2E – 16) that was not used during clustering. Cluster 2 had the best outcomes (1.5% deaths within 30 days, compared to 10–20% for other clusters). Cluster 5 (shown in medium orchid in the t-SNE plot, diagonally opposite Cluster 2) had the worst outcomes (20.24% deaths within 30 days). Cluster 5 was characterized by “crackles” in both lower lungs, had the oldest mean age (73.4 years), the highest BUN, highest WBC, and lowest chloride.

Finally, we used chi-squared test to compare the DAISY-defined clusters to the two-cluster splits produced by each of the other three methods. There was no agreement in the clustering; in particular, neither Cluster 2 nor Cluster 5 was found by any of the other three methods.

4. Discussion

In this study, we evaluated methods for clustering mixed-type data to propose best practices for clinical problems. We defined best solutions as those with superior performance by both extrinsic (ARI) and intrinsic (SW) validation criteria. We summarize our main findings with these recommendations:

• Hierarchical clustering with Ward’s criterion should be preferred to Partitioning Around Medoids, since it produces superior solutions across all data types. (Supplementary Table B.1)

• For mixed data with balanced, unbalanced binary, or unbalanced categorical composition, best results are obtained using DAISY and hierarchical clustering. (Fig. 2, Supplementary Figure B.5)

• For unbalanced continuous data mixtures, best results are obtained using SOM with the Manhattan distance. (Supplementary Table B.5) SOM also provides superior solutions for most kinds of single-type data, including binary (Euclidean distance), continuous (Euclidean distance), and ordinal (Manhattan distance) data. (Supplementary Table B.1)

• Best solutions for nominal data are generated with the Gower distance and hierarchical clustering. (Fig. 1)

A handful of previous studies have compared the performance of unsupervised algorithms on mixed-type, clinical data.[7,25,32,33] Although many have used large sample sizes from real patient cohorts, small feature space and methodological concerns, including vigorous feature reduction,[33]³² and outlier removal,[32] mixed data handling implementing inappropriate distance metrics for a given data type,[7] and scientific reporting that fails to disclose these methods in their entirety[25,32] impair generalizability of algorithm performance. This study is unique among recent clinical, mixed-type clustering comparisons in that it is undertaken on data with known, gold standard cluster assignments for algorithm comparison.

In our analysis of mixed data, we compared three measures of mixed distance. DAISY produced the highest mean ARI for mixed data types for all mixtures except unbalanced mixtures dominated by continuous data. DAISY produced broad ranges of solution accuracy DAISY also presented with an unexpected impediment to usability: mixed-type data tests were performed on only a limited number of unique simulation repeats (30 instead of 100) due to extensive computational time. Alternatively, the fastest algorithm, Supersom, was markedly outperformed not only by DAISY and Mercator but by SOM using single distance alone. Mercator performed poorly compared to DAISY on all mixed types except for balanced data. Because Mercator is, at the moment, an unweighted combination of distance metrics, good performance on balanced data and mediocre performance on unbalanced mixtures is unsurprising. Future directions for a mixed-distance extension to Mercator include weighting measures to improve application to unbalanced distance measures, pursuing comparable accuracy, greater customizability of distance metric, and reduced computational intensity.

An important limitation arises in small data sets for both DAISY and Mercator: distance cannot be calculated within a given type if only one feature of that type is present. While this scenario is unlikely in large data sets, information loss may occur in small features spaces. In the literature we saw clustering studies on as few as 6 features.[24,32] The documentation of Supersom makes no note about handling single-type features, so it is unclear if the package resolves the issue internally or if a lone feature is also lost to analysis.

Our applications illustrated the practical potential of these insights. In both cases, based on data set size and mixture of data types, we identified the DAISY algorithm with HC as best practice. Restriction to a single data type with distance calculated with a single metric, a common method of mixed data handling,[7,11–13] was unable to separate distinct clusters in the CLL data set. Three alternative methods failed to uncover clusters in the MIMIC-III data set. Bu contrast, DAISY found clear, well-defined, clinically meaningful clusters, suggesting that the results obtained in these experiments provide actionable guidelines to improve methods in practice.

Although we set out to study mixed-type data, this study revealed important conclusions about the analysis of single data types. First, an accurate solution, as measured by a high ARI, may present with a poor silhouette width. This observation should be of note and concern for researchers using silhouette widths to drive the selection of a particular algorithm or solution over another. Second, although the Hamming distance is commonly implemented for the handling of binary data in mixed-type studies, this study shows little improvement in performance over the other distances assessed, including both distances commonly used for binary (Jaccard Index) and continuous (Manhattan, Euclidean) data. Perhaps more importantly, although we implemented distance metrics in common use for all single data types tested, we noted a strong disparity in ARI and SW between data types. Specifically, performance was good for continuous and binary data, intermediate for ordinal data, and poor for nominal and mixed categorical data. While high-quality solutions for binary and continuous data exist, we were unable to identify a strong solution for categorical data in this study. Given the frequency of categorical features in mixed clinical data, the absence of quality methods for this data type is concerning for analyzing mixed data problems, and merits future work.

These studies also provided unexpected insight into the algorithms chosen. Unlike HC, k-means, k-medoids (PAM), and neural-network based (SOM) algorithms were developed to analyze larger data sets on computers. We included HC as a common standard, expecting that it would be outperformed by both techniques. However, we uncovered inconsistent performance of SOM on smaller data sets (represented by the bipolar distribution of ARI). Furthermore, we found near universal superiority of HC over PAM by mean ARI and mean SW. Although PAM presented with lower ARI, it produced more reliable solutions with narrower standard deviation. All 3 algorithms carry benefits and risks, and the selection of one over another should be undertaken with grounding in the literature and attention to the data and the researcher’s goals.

In addition to quantitative measures (mean, range, etc.) to describe ARI and SW, we also described these methods qualitatively through the inspection of violin plots. The use of violin plots allowed us to describe the distribution of these values with greater nuance than mean and range alone. Importantly, they showed that a mean ARI often reflects the presentation of a wide range of solution accuracy, either in the form of a spectrum (such as seen with DAISY) or a two-headed distribution (as seen with SOM). Further inspection revealed that the source of variability resulted from variation in feature size, with small feature spaces resulting in solutions with low accuracy and large feature spaces resulting in more reliable solutions. Conversely, the number of patients in a simulation did not have a strong effect on the ARI of a solution. These results suggest that the impact of patient populations greater than 200 may be small, but that large number of features (e.g., 200 or greater) may be required to obtain accurate and reliable clustering solutions. Conversely, distortion in small feature spaces may have arisen as a result of artifact in simulation data. Future experiments with simulations of varying and progressive size are important potential steps to define this standard.

5. Conclusion

Clustering analysis in clinical contexts holds promise to improve the understanding of patient phenotype and disease course in chronic and acute clinical medicine, but work remains to ensure that solutions are rigorous, valid, and reproducible. In this paper, we have explored best practices for clustering clinical data with simulations representing clinical trials, epidemiologic cohorts, and large-scale EHR data sets. Common approaches to mixed data handling, including transformation to a single data type with appropriate distance metric selection or applying a uniform single-type metric (such as Euclidean distance) to mixed data, result in clustering solutions with poor separation and low accuracy. Superior metrics for mixed-type data handle multiple data types through implementation of multiple, type-focused distances. Selecting an appropriate mixed-type metric, targeted to data type proportions within the mixture, allows the investigator to obtain optimal separation of patient clusters and get maximum use of their data. Better subclassification of disease opens avenues for targeted treatments, precision medicine, and improved patient outcomes. Diseases with high morbidity and mortality but subtle presentation, such as sepsis and delirium, can benefit from subclassification to identify treatment response groups, prognosis, and underlying etiology. As an extension, rigorous subclassification could be used to inform clinical decision support and improve practical treatment outcomes. We hope this work opens the door for improvements in methods for clustering analysis that can make these important advances a reality.