Uncertainty Quantification of the Effects of Segmentation Variability in ECGI

Abstract

Despite advances in many of the techniques used in Electrocardiographic Imaging (ECGI), uncertainty remains insufficiently quantified for many aspects of the pipeline. The effect of geometric uncertainty, particularly due to segmentation variability, may be the least explored to date. We use statistical shape modeling and uncertainty quantification (UQ) to compute the effect of segmentation variability on ECGI solutions. The shape model was made with Shapeworks from nine segmentations of the same patient and incorporated into an ECGI pipeline. We computed uncertainty of the pericardial potentials and local activation times (LATs) using polynomial chaos expansion (PCE) implemented in UncertainSCI. Uncertainty in pericardial potentials from segmentation variation mirrored areas of high variability in the shape model, near the base of the heart and the right ventricular outflow tract, and that ECGI was less sensitive to uncertainty in the posterior region of the heart. Subsequently LAT calculations could vary dramatically due to segmentation variability, with a standard deviation as high as 126ms, yet mainly in regions with low conduction velocity. Our shape modeling and UQ pipeline presented possible uncertainty in ECGI due to segmentation variability and can be used by researchers to reduce said uncertainty or mitigate its effects. The demonstrated use of statistical shape modeling and UQ can also be extended to other types of modeling pipelines.

1. Introduction

Electrocardiographic Imaging (ECGI) has seen continued recent interest to non-invasively diagnose and guide treatment of cardiac arrhythmias and other abnormalities. ECGI estimates cardiac electrical activity from body surface potential recordings using a numerical model of a subject’s thorax [2, 13]. However, although ECGI solutions depend heavily on model parameters and assumptions, the impact of uncertainty in those models and assumption have not yet been carefully quantified. Understanding this impact of this uncertainty is critical for confident use in clinical settings. Specifically, one important source of uncertainty in ECGI comes from the segmentations of anatomical images required to build forward models, i.e., estimates of expected surface measurements if the cardiac sources were known, that are in turn required in the “inverse procedures” of ECGI, We have previously demonstrated that segmentations can vary widely across ECGI implementations even for the same set of images, especially on the cardiac surface [11, 20], and that changes in segmentation can alter ECGI solutions [19].

However, we have not yet actually quantified this segmentation-based uncertainty. Here we introduce a method to do so and report on the results. We use a mathematical technique for quantification of parameter uncertainty called Polynomial Chaos Expansion (PCE) [21, 23, 22, 3]. Although PCE has been used previous in electrocardiographic forward models [10, 9, 18, 7, 16], employing it to quantify uncertainty due to segmentation requires parameterization of shape variability, because PCE depends on the availability of a relatively low-dimensional parameterization of the uncertain quantities. Thus we need an approach to shape models that can accurately capture geometric variability, yet can still be implemented efficiently in an uncertaintly quantification (UQ) pipeline we will refer to as ECGI-UQ. Advances in available tools for shape analysis [12] provide an opportunity to merge shape modeling with ECGI-UQ to systematically compute the effect of the segmentation variability on ECGI.

Specifically, we incorporate statistical shape modeling into UQ and use it to compute the effect of variations in segmentations on pericardial potentials obtained from ECGI as well as on the highly clinically relevant local activation times (LATs) computed from those potentials. We carried out this study in connection with colleagues in the Model Building workgroup of the Consortium for ECG Imaging (CEI,https://www.ecg-imaging.org) who generously provided a set of different segmentations of the same images from the same subject. Our pipeline was able to efficiently generate a parameterized shape model from that set of segmentations and use it with ECGI-UQ by combining the use of two open source tools: ShapeWorks[5] (https://www.sci.utah.edu/software/shapeworks.html) and a UQ tool called UncertainSCI [16] (https://www.sci.utah.edu/sci-software/simulation/uncertainsci.html). Our results showed that both the degree and location of variation in the ECGI solution corresponded to the degree and location of variation of the segmented cardiac surfaces.

2. Methods

To analyze the effect of cardiac segmentation variability on ECGI, we first computed a parameterized shape model across multiple segmented ventricular geometries and then applied it to an ECGI pipeline driven by our UQ approach (ECGI-UQ).

2.1. Shape Model

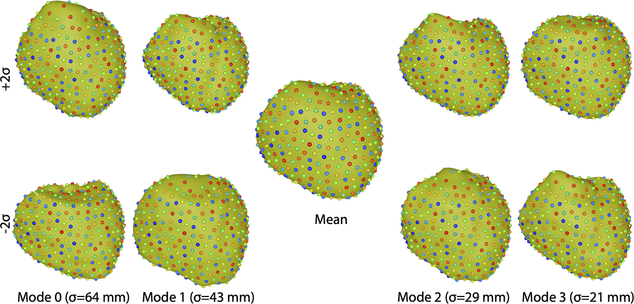
CT scans from a single subject were segmented by nine CEI research groups. The CT images, as well as the potential recordings used for ECGI, were collected as described in by Sapp et al. [17] and are freely available for use via the EDGAR database (http://edgar.sci.utah.edu) [1], a shared resource of the CEI. These nine segmentations were then analyzed in ShapeWorks to generate a pericardial shape model [20]. Specifically, shape analysis in ShapeWorks proceeds by finding corresponding locations among points (512 in this study) distributed across all of the segmentation surfaces. The points are initially placed randomly and then moved to statistically corresponding locations using a particle optimizer that minimizes the modes of variation for the cohort. Principle component analysis is then applied to these optimized point sets to find a mean shape and the modes of variation along with coefficients along each mode that approximate each segmentation. We used the first four modes of variation to form our shape model [20]. Thus the shape model that was passed to the ECGI-UQ pipeline consisted of a vector of points representing the mean shape and four vectors indicating the modes of variation. An approximation to each original segmentation can then be found by translating the points from the mean shape using a linear combination of the 4 vectors weighted by the coefficients computed for that segmentation by projecting that nine shapes onto each of mode of variation. The parameters of the shape model are then the scalar coefficients. ShapeWorks also computes statistics with respect to each of the shape modes, which we use to define parameter (coefficient) ranges in ECGI-UQ (Sec 2.3). Figure 1 shows the mean and two standard deviations of each of the four modes of variation included in the pericardial shape model.

Fig. 1.

Pericardial shape model based on nine segmentations of the same patient. The central image shows the mean shape while the other images show the shapes of the four dominant modes of variation (columns) computed at plus (top row) and minus (bottom row) two standard deviations along that mode. Point colors correspond across segmentations.

2.2. ECGI Pipeline

We used any parameterized segmentation given by the shape model (Sec 2.1) into an ECGI pipeline using the Forward/Inverse Toolkit in SCIRun [15, 14, 4] (http://scirun.org). A pericardial surface mesh was created by triangulating the points on a given shape model while maintaining local neighborhoods. Pericardial surface potentials were computed from torso surface recordings using a boundary element method (BEM) forward model and zero-order Tikhonov regularization. Local activation times (LATs) were computed from the ECGI-estimated electrograms by finding the minimum temporal derivative at each mesh node [6]. The root mean squared (RMS) potential over the pericardial surface as a function of time was also computed. The computed pericardial potentials, LATs, and RMS potentials were used as outputs of the ECGI pipeline in the UQ analysis. We computed the uncertainty of ECGI solutions for four activation profiles: sinus, LV paced, apically paced, and RV paced.

2.3. Uncertainty Quantification

We quantified the uncertainty of the ECGI solution resulting from shape variability using PCE in UncertainSCI, where the random parameters in the ECGI-UQ analysis were variations along the four principal component directions. UncertainSCI estimates uncertainty in the ECGI pipline output due to variability in these parameters using a parsimonious experimental design in parameter space. With this ensemble, a multivariate polynomial function is constructed to estimate parametric variability and can be used to map specified distributions on the parameters to distribution of the pipline outputs [3, 16]. UncertainSCI employs a Weighted Approximate Fekete Points (WAFP) strategy, a special kind of D-quasi-optimal design. This PCE emulator is used to compute statistics of the distribution of the pipeline outputs [3, 16]. We specified independent uniform distributions along each of the shape axes with bounds of ± 125, 85, 60, and 40 mm, corresponding to approximately two standard deviations the modes, cf. Figure 1. The total degree polynomial order was set to five. UncertainSCI provided statistics for the predicted distributions of pericardial potentials, LATs, and pericardial RMS potentials.

3. Results

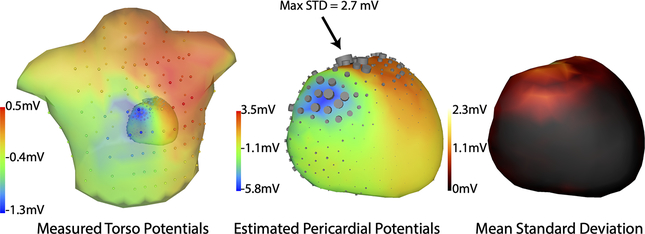
We compared the statistics of the results of our ECGI-UQ pipeline with to the statistics of the shape model itself. In general, the pericardial potential uncertainty, as shown by both standard deviation and quantile range, was correlated to amplitude of the median estimated potentials both spatially (Figure 2) and temporally (Figure 3). The uncertainty in pericardial potential was greater near the RV outflow tract and the base of the heart and was largely localized to anterior regions. The mean over time of the. The anterior areas of greater uncertainty in the pericardial potential roughly correlate to regions of high shape variability [20] (Figure 1)

Fig. 2.

Spatial distribution of uncertainty from segmentation variability. Left, center: Torso and pericardial potentials are shown near the peak of the QRS wave. Color shows potentials while the sizes of the cylinders on the surfaces represent relative standard deviation at each location, Right: Mean standard deviation over the cardiac cycle.

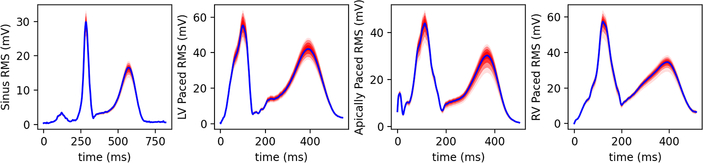
Fig. 3.

Uncertainty of reconstructed RMS potentials for four activations as indicated. Values shown are in mv as a function of time in ms. Red shading indicates quantiles.

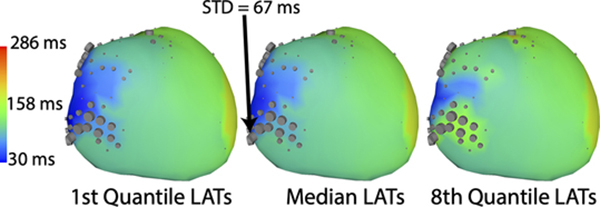
The uncertainty of the computed LATs due to segmentation variability showed broad areas of low uncertainty punctuated by smaller high uncertainty areas, as seen in the estimated quantile range (Figure 4). The ECGI-UQ pipeline predicted standard deviations resulting from segmentation uncertainty could be as high as 126 ms and an interquartile range as high as 117 ms. Regions of high variability in LATs were not geometrically consistent, but varied with activation profile. High uncertainty was often located in regions of low conduction speeds, as estimated by the gradient in the mean activation times, and was not necessarily coincident with areas of highest shape or computed potential variability. Highly variable LAT areas corresponded with the presence of computed electrograms containing QRS fractionation and other abnormal morphologies, which also make LAT determination more challenging.

Fig. 4.

Spatial distribution of LAT uncertainty illustrated by the median (center) and the minimum (left), and maximum (right) over 8 quantiles. Cylinder sizes represent relative standard deviation of the LAT at each location.

4. Discussion

Including shape modeling and UQ into an ECGI pipeline allowed us to quantify probabilisitically the possible effects of segmentation variability on computed pericardial potentials and LATs. The uncertainties predicted by our pipeline indicate that segmentation variability could dramatically alter pericardial potentials or LATs in certain regions of the heart, while the specific activation pattern could also affect which regions are most sensitive. We found that the uncertainty of pericardial potential reconstructions roughly correlate to the segmentation variability except in the posterior region of the heart. This finding is consistent with our previous results with a simpler analysis [19]. Gander et al. [8] reported similar levels of variability in the uncertainty of pericardial potentials due to changes in heart shape over the cardiac cycle.

The predicted uncertainty of the LATs demonstrated the possibility that segmentation variability could alter secondary predictions of ECGI. The predicted standard deviation of the LAT, as high as 127ms, indicate that segmentation variability could cause some early activating regions to be classified as late activating and vice versa (Figure 4). The potential adverse effect of such an error may be mitigated because high variability regions are spatially limited. Areas of high predicted variability tend to co-occur with low conduction speed, but neighboring high conduction speed areas have low variability, causing a regionally limited shift in the activation pattern in most cases. Additionally, areas of high variability did not occur near the centers of early or late activating regions, making it unlikely to adversely affect results for relatively simple activation patterns such as paced beats. However, more complex activation profiles, such as ventricular tachycardia, will likely have more areas of high gradient LATs and may thus be more impacted by segmentation error. Furthermore, since some arrhythmia substrates, such as fibrosis, have with lower conduction speeds, substrate identification could be affected by segmentation variability. Poor signal quality recordings may also be more sensitive to segmentation variability, although these effects might be mitigated with improvements in signal processing and LAT detection. Because of the many nuances involved with computing LATs, more analysis is needed to fully explore the effect of segmentation variability on LAT prediction.

In summary, our methodology of incorporating ShapeWorks and UncertainSCI to model uncertainty in ECGI resulting from shape variability could be similarly applied to other applications. This method requires availability of a dataset large enough to sufficiently characterize shape variability. ShapeWorks and SCIRun have tools to facilitate the remaining tasks. We note that UncertainSCI is designed to interfaces with most modeling software through python [16], so we anticipate adopting it to other pipelines will be relatively straightforward.