Disentangled and Proportional Representation Learning for Multi-View Brain Connectomes

Abstract

Diffusion MRI-derived brain structural connectomes or brain networks are widely used in the brain research. However, constructing brain networks is highly dependent on various tractography algorithms, which leads to difficulties in deciding the optimal view concerning the downstream analysis. In this paper, we propose to learn a unified representation from multi-view brain networks. Particularly, we expect the learned representations to convey the information from different views fairly and in a disentangled sense. We achieve the disentanglement via an approach using unsupervised variational graph auto-encoders. We achieve the view-wise fairness, i.e. proportionality, via an alternative training routine. More specifically, we construct an analogy between training the deep network and the network flow problem. Based on the analogy, the fair representations learning is attained via a network scheduling algorithm aware of proportionality. The experimental results demonstrate that the learned representations fit various downstream tasks well. They also show that the proposed approach effectively preserves the proportionality.

1. Introduction

Human brain connectomes [6] are models of complex brain networks and can be derived from diverse experimental modalities and tractography algorithms. Large-scale brains connections convey important insights for understanding the underlying yet largely unknown mechanisms of many mental disorders [11,15,26,7]. Nevertheless, the apparent characteristics of brain networks are profoundly influenced by the tractography algorithms. The designs of tractography algorithms, including tensor-based deterministic algorithms [2], probabilistic approaches [18], random forest [17] and Deep Neural Network (DNN) [20], and regularized methods guided by biologically plausible fascicle structures [3], are inspired by specific experimental questions [5], e.g., different tractography algorithms are used for predicting or classifying neurodegenerative or neurodevelopmental conditions based on various brain abnormalities. For example, the selection and accuracy of the extracted fibers are different for different tractography algorithms, and the relevance of the extracted fiber bundles depend on the different tasks and questions being addressed. Therefore, it is elusive to decide a universally optimal modality of brain networks and associated processing pipeline for distinct diagnostic tasks [5,23].

Multi-view methods can leverage the available information from diverse tractography algorithms simultaneously, and tentative studies have demonstrated that multi-modal brain networks can provide complementary viewpoints for the classification tasks, e.g., multi-view graph convolutional network [25] is found to have state-of-the-art performance in classifying Parkinson’s disease (PD) status. However, previous multi-view methods have two restrictions regarding general prediction tasks of neurodegenerative conditions. First, many methods are designed for some specific tasks. If one want to tailor these methods to other tasks, it is necessary to carefully tune the hyperparameters. Second, though some methods learn representations from multi-view brain networks, the learning is guided by some predefined prediction tasks, which may introduce bias to overemphasize a particular modality. As such, the learned embeddings cannot represent multi-modal brain networks comprehensively, and their application to the related analysis in a broader scope is potentially constrained.

To address these problem, we propose to learn unified representations from multi-modal brain networks via unsupervised learning techniques. To extend the generalization ability of the learned representations to different downstream analysis, the representations shall be of disentanglement and proportionality concerning different modalities. Here, disentanglement refers to the representations encoding salient attributes of data explicitly, which can help the analysis of the prediction tasks and the modalities. Proportionality refers to a balanced contribution to the representations of each modality, which avoids the potential bias on specific modalities. In other words, in our approach the learned representations can fairly convey the information from different modalities and can be exploited by various downstream analysis. More specifically, in this paper we propose a multi-view graph auto-encoder to learn the disentangled graph embeddings from brain networks. We formulate the proportionality-awareness in multi-view representation learning as a network scheduling problem via an analogy between training deep networks and the graph flow problems. The experimental results demonstrate the effectiveness of the proposed method.

2. Methodology

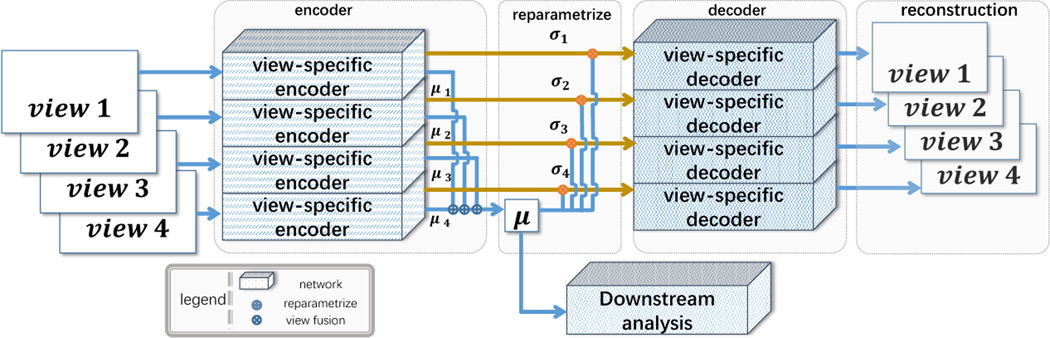
The proposed method is illustrated in Fig. 1. For each view, a Variational Graph Auto-encoder (VGAE) [10] is exploited. Let G^(v) denote the brain networks of the v^th view, f^(v) and g^(v) the corresponding encoder and decoder, [μ^(v)|σ^(v)] = f(G^(v)) is the estimated mean and variance of the encoder. The unified representations are computed by max-out the stacked μ^(v) by the position, which can be denoted as μ = maxpool1d([μ^(v)]). The reparameterization for the v^th view is then computed using μ and σ^(v). μ ∈ ℝ^k is also used as the embeddings. According to the structure of VGAE, σ^(v) ∈ ℝ^k. Besides the view-wise VGAE loss, we push μ and μ^(v) to be close so that the learned embeddings for different views are consistent. The disentanglement of the representations is acquired via introduce the β-VAE loss [8]. Disentangled representations are compact and interpretable [4]. The objective for our multi-view GVAE is:

$$\mathcal{L}=\sum _{v\in \mathcal{V}}\mathbb{B}\left(\log \left(P\left({\tilde{G}}^{(v)}\right)\right)\right)+\beta KL\left(P\left(z^{(v)}\right)\mid \mathcal{N}(0,1)\right))+\lambda {\left({\mu }^{(v)}-\mu \right)}^2$$ (1)

Fig.1:

The structure of the proposed method. Each view uses an independent VGAE to learn a unified μ, while the σ is different.

here the first term is the reconstruction loss, the second is the Kullback-Leibler divergence, and the last is the multi-view consistency.

As aforementioned, the representations shall also be fair to different views. In the above auto-encoder framework, the decoder is used for evaluating the vividness of the learned representations. However, for multi-view data, the reconstruction for different views is not necessarily equally accurate. When the imbalance occurs, some views are less included in the learned representations. To address this problem, we consider to learn fair representations regarding different views, which indicates the view-wise loss in (1) is close to each other. Such fairness, referred to as proportionality, can be achieved via an alternative training routine of the above model. We will formulate an analog between flow network problem and the training of multi-view model in the following. Based on the formulation, we design a scheduling algorithm to satisfy the proportionality requirement.

Training Multi-view Network: a Flow Network Perspective

Directed Acyclic Graph (DAG) is an important tool in graphical models [9]. It is also exploited to express network structures by many popular deep learning frameworks [19,1]. Inspired by this idea, we make an analogy between training the deep network and the flow network problems.

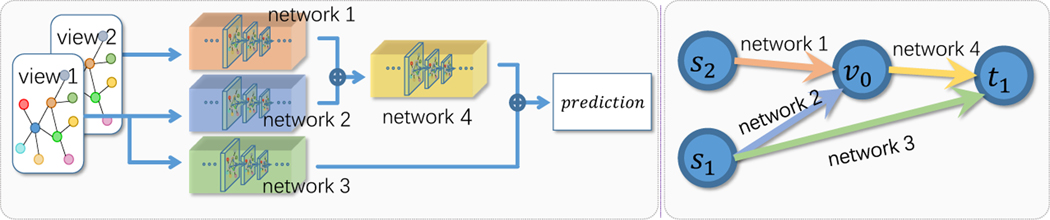
In Fig. 2, we illustrate an example for multi-view learning. To simplify the elaboration, we consider a structure taking two views s₁ and s₂, as inputs. The network consists of four sub-networks, each corresponding to one edge in the DAG. v₀ is a fused hidden representation, and t₁ is the prediction. For multiple inputs, ⊕ denotes the fusion operation for the outputs of multiple sub-networks, and it can either a weighted summation or concatenation. Consider a network trained after t steps using gradient based method. In the t + 1 step, we can define the flow d_i,j from predecessor i to successor $d_{i,j}=\Delta \mathcal{L}\left(f_j^{(t+1)}\left(h_i^{(t+1)},{\mathcal{H}}_{j\backslash i}^{(t)}\right)\right)$, here $\mathcal{L}$ is an objective defined on the targets, and $\text{Δ}\mathcal{L}$ denotes the loss difference between step t + 1 and t. Let ${\mathcal{P}}_{ij}$ represent the set of all paths from sources to targets containing $e_{i,j}\cdot f_j^{(t+1)}$ refers to the network to compute the final outputs with all paths in ${\mathcal{P}}_{ij}$ updated. ${\mathcal{P}}_{ij}$ can be defined on the node i and a set ${\mathcal{H}}_{j\backslash i}$. Here ${\mathcal{H}}_{j\backslash i}$ denotes any cut set containing node j that separate sources and targets, and ${\mathcal{H}}_{j\backslash i}$ does not include any node in ${\mathcal{P}}_{ij}$ except j.

Fig.2:

Left: a simple DNN. Right: the corresponding DAG. Each edge represents a network, and each node denote an intermediate representation.

Our definition satisfies the flow conservation, which states that if a node is neither a source or a target, its net flow shall be 0. For a node j with multiple incoming flow, the fusion operation is defined as $h_j={\sum }_{i\in {\mathcal{P}}_j}{P}_{ij}{W}_{ij}{f}_{ij}\left(h_i\right)$, here ${\mathcal{P}}_{ij}$ is the predecessor set of node j, f_ij is the sub-network between node i and j. For different fusion oeprations, P_i and W_i take different forms. For example, when both P_i and W_i are the identity matrices, the fusion is by summation; if W_i is the augmented matrix (I_i|0), fusion by concatenation is feasible by setting P_i as the corresponding permutation matrix. For a node with multiple outgoing flow, the output is equally distributed. We abuse the notation ${\mathcal{H}}_j\equiv {\mathcal{H}}_{j\backslash i}\cup \left\{i\right\}$. Consider a fixed given cut ${\mathcal{H}}_j$ for node j, we can induce two additional cuts: ${\mathcal{H}}_{{\mathcal{P}}_j}$, which excludes j and include all its predecessors; and ${\mathcal{H}}_{{\mathcal{S}}_j}$, which excludes j and include all its successors. Under the updating rule of backward propagation, the incoming flow with respect to node j is,

$$\sum _{i\in {\mathcal{P}}_j}{d}_{i,j}\approx \frac{\partial \mathcal{L}}{\partial f_j}\sum _{i\in {\mathcal{P}}_j}{P}_{ij}{W}_{ij}\frac{\partial f_j}{\partial h_i}d{h}_i=\frac{\partial \mathcal{L}}{\partial f_j}\frac{\partial f_j}{\partial h_j}d{h}_j,$$ (2)

the above equation follows because the partial differential is 0 except dh_i and dh_j term. Similarly, the outgoing flow is,

$$\sum _{k\in {\mathcal{S}}_j}{d}_{j,k}\approx \sum _{k\in {\mathcal{S}}_j}\frac{\partial \mathcal{L}}{\partial f_k}{P}_{jk}{W}_{jk}\frac{\partial f_k}{\partial h_j}d{h}_j=\frac{\partial \mathcal{L}}{\partial f_j}\frac{\partial f_j}{\partial h_j}d{h}_j,$$ (3)

(2) and (3) are bridged by the change in h_j, which ensures the net flow to be 0.

If we extend the above analogy to the accumulative case, the flow is defined to be the loss decrease with respect to the particular structure represented by i → j. Noteworthy, it is not the pure contribution of i → j. Rather, it is more of the quantification of the total loss decrease of the particular structure, as

Round-Robin			Proportionality
Input: v views, max epoch e			Input: v views, max epoch e
Output: model f			Output: model f
1 Initialize f.			1 Initialize f.
2 repeat			2 repeat
3	for i → 1 to v do		3	Compute priority w.r.t. (6)
4		Optimize (1) w.r.t. view  j.	4	Optimize (1) w.r.t. view j  with the highest priority.
5 until max epoch;			5 until max epoch;

the definition considers both the upstream and downstream computation of the entire network. The empirical loss is related to the generalization bound of the learned representations concerning downstream tasks. As such, the accumulated flow can be interpreted as the amount of information learned from each view informally. Based on this analogy, we define that the proportionality is achieved if the view-wise flow, i.e. the accumulated ${\sum }_{k\in {\mathcal{S}}_j}{d}_{j,k}$ for some view j, is balanced.

Alternative Training Routine with Proportionality Awareness

Conventionally, the proportionality concerning different views can be written as a constrained optimization problem, and a standard training routine is based on SGD. From the flow perspective, the proportional training can be interpreted as multiple views competing for the updating resources in the backward propagation, which is a network scheduling algorithm. More specifically, during the training, the accumulated flow is continuously updated, which reflexes the dynamic of loss decrease and the generalization ability. A proportional representation is then equivalent to a balanced flow avoiding the overload of some specific path.

In detail, we define the total flow as the loss decrease. When the learning rate is small enough, the summation of view-wise SGD update is equivalent to a round-robin update with respect to each view. Here, the objective associated with each view is optimized in a predefined turn. To avoid a specific view taking up too much updating resources, we can maximize the total flow of the network while allowing the minimal level of service for all views via introducing a competing mechanism for each view to occupy the update based on the estimated flow. We refer to this method as proportionality. The updating priority of each view is based on the current loss decrease and the historical cumulative loss decrease. Assume the loss decrease of view i at update t can be foreseen as r_i,t. The throughput of view i is defined as historical cumulative loss decrease at step t:

$${\theta }_{i,t}={\theta }_{i,0}+\sum _{l=1}^t\frac{r_{i,l}{I}_{i,l}}{t}=\frac{n-1}{n}{\theta }_{i,t-1}+\frac{1}{n}{r}_{i,t-1}{I}_{i,t-1},$$ (4)

where I_i,l is an indicator. I_i,l = 1 if the l^th update is conducted on view i, and 0 otherwise. Based on (4), the priority p_i,t for view i can be defined, and the t + 1 update is then applied to the view with the highest priority:

$$\underset{i\in \mathcal{V}}{\arg \max }\left\{p_{i,t}\right\},p_{i,t}=\frac{r_{i,t+1}}{ϵ+{\theta }_{i,t}}$$ (5)

where ∊ is a small positive number for computational stability. Notably, the above algorithms is not immediately applicable to our formulation, as that r_i,t is not pre-assigned as in standard proportionally fairness algorithms. Instead, the values are only known after the update is finished. Thus, we propose a compensation update method: at the beginning, we use one round robin update and compute initial r_i,0. In the following steps we use proportionally fairness algorithm, but computing the priority using the loss decrease from the last applied update:

$$\underset{i\le v}{\arg \max }\left\{\frac{r_{i,t_i}}{d_i+{\theta }_{i,t}}\right\},t_i=\max l,\text{s.t.}l\le t,I_{i,l}=1,$$ (6)

The proportionality and convergence of our scheduling algorithm are guaranteed under some weak conditions, and the analysis can be found in [13].

3. Experimental Results

In this experiments we use three datasets, including the data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) and National Alzheimer’s Coordinating Center (NACC), and the Parkinson Progression Marker Initiative (PPMI). The preprocessed ADNI brain networks [22] include 51 healthy controls (HC) (mean age=69.69 ± 10.27, 29 males), 112 people with Mild Cognitive Impairment (MCI) (mean age=71.68 ± 9.89, 41 males) and 39 individuals with AD (mean age=75.56±8.99, 14 males). The similarly preprocessed NACC brain networks [21] include 329 HCs (mean age=60.96 ± 8.96, 107 males), 57 with MCI (mean age=73.60 ± 7.93, 38 males), and 54 AD patients (mean age = 72.02 ± 10.41, 32 males). The similarly preprocessed PPMI brain networks [27,28] includes 145 HC (mean age = 66.70 ± 10.95, 96 males) and 474 subjects with PD (mean age=67.33 ± 9.33, 318 males). Nine different views are reconstructed using TFACT, T-RK2, T-TL, T-SL, O-FACT and O-RK2, Probt, Hough, and PICo (Please refer to [24] for more details on the brain network reconstruction). We use a modified network structure based on graph variational auto-encoder. The view-wise graph is the averaged brain connectome, and the node features are the corresponding row for each brain connectome. We set β = 4 recommended by β-VAE [8]. The performance is not sensitive to λ, and we set it to 0.001. In the encoder, we use three graph convolutional layers for μ and σ respectively. The first two layers are shared, both with 64 hidden units. The embedding length is 32. The encoder are limited in layers due to the potential over-smoothing for graph convolutional layers. Our model is trained 100 epochs using ADAM with batch size 32 and learning rate 0.0001.

Evaluating the Proposed Method in Down-streaming Analysis:

We compare our approach with related baselines on several classification and regression tasks. The ablation study is also included.

Table 1 summarizes the classification results. For ADNI and NACC, we predict the HC and AD. For PPMI we predict HC and PD. For multi-view predictions, we include principal component analysis (PCA), multi-view nonnegative matrix factorization (MVNMF) [14], co-regularized spectral clustering (MVSC) [12] and Deep Metric Graph Convolutional Network (DMGCN) [11]. We use the aforementioned methods to learn the representations, and then exploit two off-the-shelves methods, sparse logistic regression, and random forest to make the final prediction. We report AUC on 5-fold cross-validation. To make the comparison self-contained, single view results are also included. For the ablation study, in propose-I neither disentanglement nor proportionality is considered, and in proposed-II the disentanglement is considered. The full approach is proposed^∗. We omit more single-view ablation study in the experiments because our objective is designed for multi-view data. Of note, integrating multi-view data is also shown to be beneficial for brain network analysis [27]. From the results, we find that the prediction ability of different views with respect to different tasks are complicated, and heavily coupled with the algorithms. Multi-view methods, generally, can improve the prediction ability. However, the advantage of multi-view data is intriguing and needs careful examination. The proposed method have good performances and are robust with respect to different tasks. And at last, the ablation study demonstrates that the performance can be improved through considering disentanglement and proportionality.

Table 1:

The comparison on classification tasks.

Sparse Logistic RegressionADNI NACC | PPMI
		ADNI	NACC	PPMI
Single View	FSL	0.7786 ± 0.0976	0.7669 ± 0.0799	0.6597 ± 0.0584
	PICo	0.7615 ± 0.1408	0.7119 ± 0.1103	0.6065 ± 0.0486
	T-FACT	0.7451 ± 0.0379	0.6581 ± 0.0411	0.5850 ± 0.0433
	O-FACT	0.7278 ± 0.1066	0.7094 ± 0.0866	0.5921 ± 0.0353
	ODF-Rk2	0.7568 ± 0.0821	0.6890 ± 0.0366	0.5942 ± 0.0331
	T-RK2	0.7276 ± 0.0797	0.7281 ± 0.0674	0.5921 ± 0.0353
	T-SL	0.7402 ± 0.1371	0.6582 ± 0.0785	0.5884 ± 0.0389
	T-TL	0.6875 ± 0.0682	0.7358 ± 0.0799	0.5851 ± 0.0423
	Hough	0.7559 ± 0.0780	0.7271 ± 0.0549	0.5536 ± 0.0391
Multi View	all views	0.7966 ± 0.0904	0.7301 ± 0.1325	0.5716 ± 0.0378
	MVNMF	0.8149 ± 0.0550	0.7685 ± 0.0958	0.6104 ± 0.0332
	MVSC	0.8203 ± 0.0791	0.7595 ± 0.1013	0.6205 ± 0.0373
	DMGCN	0.8058 ± 0.1006	0.7557 ± 0.0898	0.6141 ± 0.0707
	Proposed-I	0.8074 ± 0.0493	0.7491 ± 0.0897	0.6122 ± 0.0442
	Proposed-II	0.8185 ± 0.0770	0.7549 ± 0.0790	0.6240 ± 0.0234
	proposed*	0.8278 ± 0.1537	0.8090 ± 0.1472	0.6250 ± 0.0472
Random Forest
		ADNI	NACC	PPMI
Single View	FSL	0.8124 ± 0.0455	0.3737 ± 0.7065	0.5753 ± 0.0255
	PICo	0.7838 ± 0.1067	0.1588 ± 0.9463	0.5475 ± 0.0244
	T-FACT	0.8383 ± 0.0483	0.7029 ± 0.1184	0.5654 ± 0.0331
	O-fact	0.7817 ± 0.1512	0.3789 ± 0.6903	0.5478 ± 0.0228
	O-RK2	0.7617 ± 0.1087	0.7879 ± 0.1333	0.5566 ± 0.0382
	T-RK2	0.7764 ± 0.1275	0.7029 ± 0.1333	0.5486 ± 0.0361
	T-SL	0.8148 ± 0.0587	0.7235 ± 0.1163	0.5386 ± 0.0347
	T-TL	0.7695 ± 0.0862	0.7009 ± 0.1164	0.5411 ± 0.0410
	Hough	0.8368 ± 0.0671	0.7011 ± 0.1797	0.5276 ± 0.0344
Multi View	all views	0.8560 ± 0.0574	0.7615 ± 0.1053	0.5743 ± 0.0464
	MVNMF	0.8826 ± 0.0830	0.8317 ± 0.1561	0.5659 ± 0.0528
	MVSC	0.8827 ± 0.0457	0.7997 ± 0.1435	0.5753 ± 0.0348
	DMGCN	0.8862 ± 0.0503	0.8307 ± 0.1493	0.5683 ± 0.0323
	Proposed-I	0.8578 ± 0.0516	0.7919 ± 0.0725	0.5590 ± 0.0250
	Proposed-II	0.8678 ± 0.0573	0.8327 ± 0.0988	0.5699 ± 0.0382
	Proposed*	0.8946 ± 0.0510	0.8359 ± 0.1321	0.5814 ± 0.0274

Table 2 summarizes the regression results. We use the learned representation to predict several clinical scores, including the Tremor Dominant scores (TD), the University of Pennsylvania Smell Identification Test (UPSIT), and the Montreal Cognitive Assessment Test (MoCA). Mean squared error (MSE) is used as the metric evaluating the prediction. All scores are normalized to [0,1]. The results show that the prediction is more complicated with respect to the particular medical scores and views. Similarly, we can observe the advantage of utilizing multi-view data and the robust and superior prediction abilities of our approach.

Table 2:

The comparison on regression tasks.

		TD	UPSIT	MoCA
Single View	FSL	0.0749 ± 0.0167	0.0794 ± 0.0054	0.0381 ± 0.0033
	PICo	0.0714 ± 0.0078	0.0983 ± 0.0101	0.0394 ± 0.0027
	T-FACT	0.0404 ± 0.0037	0.0545 ± 0.0043	0.0210 ± 0.0021
	O-FACT	0.0410 ± 0.0018	0.0508 ± 0.0066	0.0208 ± 0.0036
	O-RK2	0.0428 ± 0.0079	0.0503 ± 0.0015	0.0208 ± 0.0027
	T-RK2	0.0441 ± 0.0034	0.0500 ± 0.0051	0.0212 ± 0.0025
	T-SL	0.0427 ± 0.0012	0.0512 ± 0.0058	0.0212 ± 0.0017
	T-TL	0.0406 ± 0.0059	0.0517 ± 0.0019	0.0210 ± 0.0027
	Hough	0.0434 ± 0.0036	0.0495 ± 0.0058	0.0225 ± 0.0044
Multi View	all views	0.0414 ± 0.0045	0.0524 ± 0.0034	0.0227 ± 0.0074
	MVNMF	0.0378 ± 0.0122	0.0507 ± 0.0041	0.0207 ± 0.0030
	MVSC	0.0355 ± 0.0047	0.0499 ± 0.0046	0.0199±0.0013
	DMGCN	0.0365 ± 0.0071	0.0487 ± 0.0085	0.0202 ± 0.0015
	Proposed-I	0.0358 ± 0.0024	0.0501 ± 0.0022	0.0209 ± 0.0019
	Proposed-II	0.0361 ± 0.0035	0.0492 ± 0.0033	0.0200 ± 0.0022
	Proposed*	0.0351±0.0059	0.0484±0.0044	0.0199±0.0022

Evaluating the Proportionality during Training:

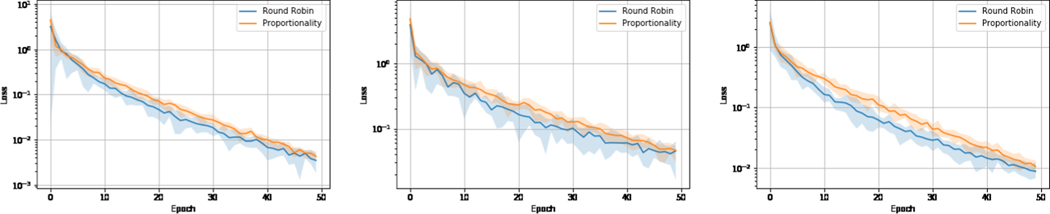
In this section, we demonstrate the proposed method can achieve proportionality using the proposed training scheduling method. Figure 4 illustrates the training loss of the proposed deep network against epochs, and the shaded area represents the variance regarding different views. From the results, we can observe that the proposed method effectively reduces the variance during training, which indicates the learned representations proportionally represent different modalities of brain networks. The results also show the training routine aware of proportionality converges slightly slower than the standard training routine. However, with moderate epochs their performance difference is negligible.

Fig.4:

Left to right: ADNI, NACC, PPMI.

Discussions:

There some works applying the fairness principle on brain analysis [16]. Our method is designed for representation learning for multi-view brain connectomes, particularly focusing on the disentangled and proportional property (which is related to algorithmic fairness) for the learned embeddings. Our experimental results demonstrate that the proposed method can be applied to various downstream works. As such, it is of potential to apply our method to broader applications, including generating a refined connectome matrix,

4. Conclusion

In this paper, we propose an unsupervised method to learn unified graph embeddings for multi-view brain networks. We design a multi-view graph variational auto-encoder to learn the representations with disentanglement and proportionality. The experimental results demonstrate that the learned representations can be effectively used by various downstream tasks.