Abstract
Deep learning has shown great potential to adaptively learn hidden patterns from high dimensional neuroimaging data, so as to extract subtle group differences. Motivated by the convolutional neural networks and prototype learning, we developed a brain-network-based convolutional prototype learning model (BNCPL), which can learn representations that simultaneously maximize inter-class separation while minimize within-class distance. When applying BNCPL to distinguish 208 depressive disorders from 210 healthy controls using resting-state functional connectivity (FC), we achieved an accuracy of 71.0% in multi-site pooling classification (3 sites), with 2.4–7.2% accuracy increase compared to 3 traditional classifiers and 2 alternative deep neural networks. Saliency map was also used to examine the most discriminative FCs learned by the model; the prefrontal-subcortical circuits were identified, which were also correlated with disease severity and cognitive ability. In summary, by integrating convolutional prototype learning and saliency map, we improved both the model interpretability and classification performance, and found that the dysregulation of the functional prefrontal-subcortical circuit may play a pivotal role in discriminating depressive disorders from healthy controls.
I. INTRODUCTION
The current diagnosis of major depressive disorder (MDD) often relies on disease history and self-reported symptoms, lacking objective and reliable imaging biomarkers, which may cause misdiagnosis and inadequate treatment [1]. As a non-invasive method to investigate brain function with high spatial resolution, functional magnetic resonance imaging (fMRI) has been widely used to characterize brain networks through functional connectivity (FC) among spatially separated brain regions, which has shown great promise in unveiling hidden pathological patterns to assist the diagnosis of brain disorders using machine learning approaches [2, 3].
On one hand, compelling evidence suggests that MDD patients exhibit abnormal FC patterns compared to healthy controls (HCs) [4]. On the other hand, it is difficult to classify MDD from HCs when using a large sample size, though appreciable accuracy (76–98%) have been achieved based on small sample size ranging from 19–58 MDD patients [2]. For example, when classifying 180 MDD from 180 HCs using FC features, Sundermann et al. achieved accuracy of 45.0%−56.1% with SVM, similar to random probability [5]. To date, most existing studies with 80% or higher classification accuracy suffered from small homogenous sample size, and mostly adopted classic classifiers including Gaussian classifiers and support vector machines (SVM) [2]. Considering that MDD shows less lesion than schizophrenia or Alzheimer’s disease on brain function and structure when compared with HCs, therefore, it is quite challenging to classify MDD from HCs with high accuracy when using multi-site, heterogeneous, and large sample size.
Recently, deep learning has shown great potential to capture subtle hidden patterns from neuroimaging big data to differentiate brain disorders from HCs, outperforming traditional machine learning methods [6, 7]. Particularly, a novel architecture of convolutional neural network was proposed to leverage the topological locality of functional brain networks (BrainNetCNN) to successfully predict cognitive performance by FC with correlation at 0.31 [8]. On the other hand, prototype learning, which can be viewed as a generative model based on Gaussian assumption, can learn a robust representation for each class, which shows remarkable advantages on clustering patterns within the same group while distinguishing patterns between different groups [9].
In this study, based on a valuable, large-scale Chinese Han resting-state fMRI dataset, we proposed a brain-network-based convolutional prototype learning (BNCPL) model for MDD classification by combining strengths from both prototype learning and BrainnetCNN. We aim to obtain compact prototypes for MDD and HCs respectively, and achieve higher classification performance by BNCPL model compared with 3 traditional classifiers and 2 alternative deep neural networks. Saliency map was also combined to identify abnormal topological FC features for MDD, which may deepen our understanding of the psychopathology of MDD.
II. MATERIALS AND METHODS
A. Data and Preprocessing
208 MDD patients (age: 31.8±10.5; gender: 85M/123F) and 210 demographically matched HCs (age: 31.3±10.3; gender: 85M/125F) were recruited from three hospitals in China. The demographic information and clinical characteristics for all subjects were summarized in Table I. The written informed consent for each subject was obtained according to the relevant ethics committees. The fMRI data were collected using 3T scanners at Xinxiang (Siemens, Verio), Huaxi (Philips, Achieva), and Anding (Siemens, Trio) hospitals. All participants underwent an 8-min fMRI scans with the following parameters: repetition time/echo time = 2000/30 ms; field of view = 220 mm (64 × 64 matrix); thickness = 4 mm (3.5 mm at Huaxi hospitals), and were instructed to lie still, and keep their eyes closed during scanning. The fMRI data were preprocessed based on SPM12 software [10]. The first 10 volumes for each subject were discarded to exclude T1 equilibration effects, and the following pipeline included slice timing, motion correction, normalization, linear detrend, band-pass filtering (0.01–0.08 Hz), and spatial smoothing with a 6-mm-FWHM Gaussian kernel. Cerebrospinal fluid signal, white matter signal, and 24 Friston head-motion parameters were also regressed out.
TABLE I.
Demographic and clinical information
| Mean ± SD | Healthy Controls | Depression | P value |
|---|---|---|---|
|
| |||
| Number | 210 | 208 | — |
| Age | 31.34 ± 10.29 | 31.80 ± 10.54 | 0.65 a |
| Gender (Male/Female) |
85/125 | 85/123 | 0.94 b |
| HDRS | — | 20.89 ± 6.62 | — |
| BDI | — | 20.82 ± 6.89 | — |
| Duration | — | 48.14 ± 65.42 | — |
| RVP | 84.2 ± 4.52 | 82.54 ± 4.79 | 0.046 b |
| Verbal Fluency | 20.06 ± 5.45 | 16.87 ± 5.10 | 8.57 × 10−4 b |
| Digit Symbol | 59.36 ± 13.59 | 47.62 ± 14.71 | 6.97 × 10−6 b |
Two-sample t test
Chi-square test; SD, standard deviation; HDRS, Hamilton Depression Rating Scale; BDI, Beck Depression Inventory; RVP, Rapid Visual Information Processing.
After data preprocessing (Fig. 1a), FC was calculated by Pearson correlation coefficient between averaged time courses for each pair of regions based on the Brainnetome atlas including cerebellum [11]. To minimize potential confounding effects, age, gender, and mean FD were set as covariates to regress out from FC features. Additionally, FC were estimated using the automated anatomical labeling (AAL) template to investigate the impact of different brain parcellation schemes.
Figure 1.
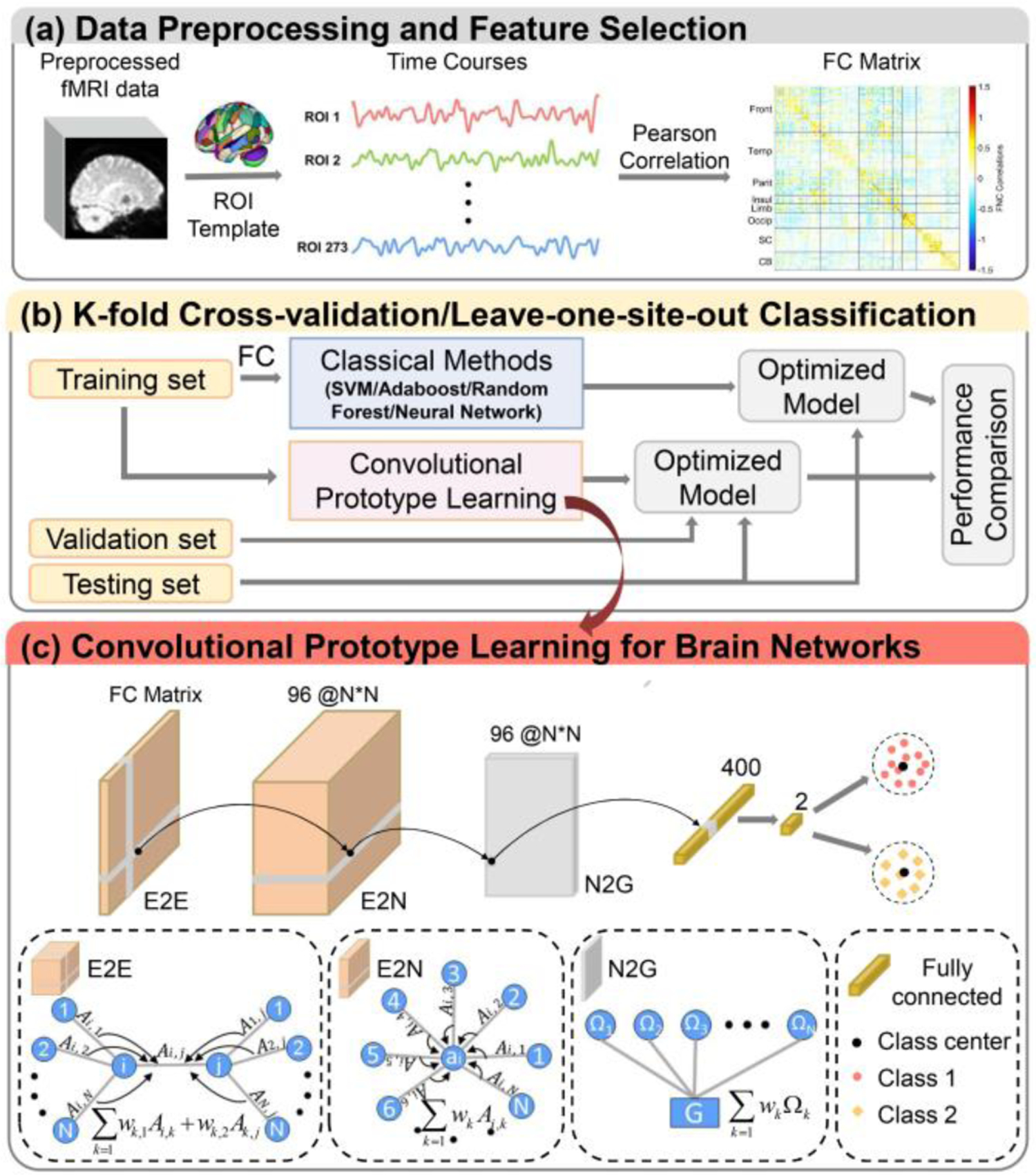
The framework of the brain-network-based convolutional prototype learning (BNCPL). (a) Data preprocessing and feature selection. (b) The performance of the BNCPL model was evaluated by 10-fold and leave-one-site-out cross validation. (c) Details of the BNCPL model. The edge-to-edge, edge-to-node, node-to-graph, and fully-connected layers were used for extracting discriminative features from FC matrix, which were further used to build intra-class compact and inter-class separable prototype for each class.
B. BNCPL
A deep BNCPL model was developed to seek site-shared biomarkers for MDD, consisting of brain-network-based CNN and prototype learning (Fig. 1c). The CNN was used to automatically extract high-level features from FC for the classification of MDD, then followed by a prototype learning to build a compact representation for each class.
1). Brain-network-based convolution neural network
Brain-network-based CNN was composed of one edge-to-edge (E2E) layer, one edge-to-node (E2N) layer, one node-to-graph (N2G) layer, and a fully-connected layer. E2E convolutional layer can learn the topological locality by combining the weight of edges that shared nodes together via a cross shape filter. Given the m-th feature map of a weighted FC matrix at the l-th layer of the network, Gl,m = (Al,m; Ω), where Al,m is the weighted FC matrix, and Ω is the set of the nodes, the E2E convolution for each edge Ai,j at l+1-th layer can be represented as (1):
| (1) |
Where Ml is the number of weighted FC matrices at the l-th layer of the network; Al+1,n is the n-th weighted FC matrix at the l+1-th layer of the network; and are the learned weight of row and column of the n-th filter corresponding to the m-th weighted FC matrix at the l-th layer of the network. E2N convolution can learn a representative value for each node by combining all weights of edges connected to the node. E2N convolution can be denoted as (2):
| (2) |
Where is the n-th weight of node i at the l+1-th layer of the network. N2G convolutional layer can learn a representative value for the input FC matrix by combining all weights of nodes in the network, which is represented as (3):
| (3) |
Where gl+1,n is the n-th representative value of the graph by combining all node weights at the l-th layer of the network. Next, a fully-connected layer was added to the end of the BNCPL to obtain a high-level representation for the input FC.
2). Prototype loss function
Followed by the brain-network-based CNN, a prototype was built for each class with the output features via prototype learning, mi for class i, which is a learned prototype center. The similarity between the prototype and the given sample was measured by the Euclidean distance between them:
| (4) |
For K categories, then given a sample (x,y), the probability of p(y|x) and the cross-entropy loss based on the Euclidean distance (DCE) to the prototype can be denoted as (5):
| (5) |
| (6) |
The distinguishing prototype mi for class i can be learned by minimizing the DCE loss between the sample and the learned prototype. To learn a compact prototype for each class, a prototype loss was added as a regularization:
| (7) |
| (8) |
Where my is the corresponding prototype with f(x), λ is a hyperparameter to control the weight of the prototype loss. For the loss function, combining the DCE and prototype loss, we can obtain inter-class separable representations and intra-class compact representation for each class.
3). BNCPL model implementation
The BNCPL network was finally constructed with an E2E layer with 96 1 × 273, and 96 273 × 1 filters producing an output of size 273 × 273 × 96, an E2N layer with 96 1 × 273 × 96 filters producing an output of size 273 × 1 × 96, an N2G layer with 400 273 × 1 × 96 filters producing an output of size 1 × 400, then followed by a fully-connected layer with two hidden layer nodes producing an output of size 2. Finally, two prototype centers were built with the output features for MDD and HCs respectively.
For the BNCPL model, the learning rate was initialized to 0.0015, then decayed after 15 epochs with a decay rate of 0.5. The training batch size was set as 20. The activation function for each hidden layer node was the leaky rectified linear unit with a leaky value of 0.2. To improve the generalization performance of the model, the model parameters were regulated by dropout (dropout = 0.5), L1, and L2-norm regularization (L1 = 0.0005, L2 = 0.0005). The model was optimized by minimizing the loss function with Adam optimizer. The training process was stopped until the training loss decreased by less than 0.001 for 5 epochs, or the training epoch reached the maximum number of the iteration (100 epochs), and the intermediate model with the highest accuracy on the validation dataset was retained for testing. The proposed model was implemented via Pytorch (https://pytorch.org/) and ScikitLearn (https://scikitlearn.org/).
Two strategies were adopted to evaluate the model, including 10-fold and leave-one-site-out cross validation, in which 10% samples of the training set were randomly selected as validation set (Fig. 1b). We then compared the performance of the proposed BNCPL model with traditional classifiers, including SVM, Adaboost, Random Forest, and deep neural network (DNN) [6]. For traditional classifiers, FC matrix was reshaped into a vector and then used as input to the model. To further examine the effectiveness of the prototype learning, the loss function followed by the brain-network-based CNN was replaced with the traditional softmax, called BrainNetCNN. The performance of the model was measured with accuracy (ACC), sensitivity (SEN), specificity (SPE), F-score (F1), and area under curve (AUC). All experiments were repeated ten times to generate the means and standards of the above metrics, and the performance of different classifiers was compared using the two-sample t-test. Additionally, to test the effect of different brain parcellation, we also test the performance of the BNCPL model by using AAL atlas.
4). Estimating the discriminative power of FC
To uncover the reliable imaging biomarkers for the classification of MDD, we used Simonyan’s method [12], which highlights the most discriminative regions by saliency map with respect to the given class. For all FC features, the absolute value of weight matrices derived from the saliency map was averaged across entire datasets for ten times. Then the top 1 ‰ FC with the largest weight were retained, indicating the most discriminative connectivity for MDD. The node weight was denoted as the sum of the weight of the relevant connectivity to represent the contribution to the classification of MDD. The brain regions were divided into nine functional networks for visualization according to Yeo’s network [13], including visual (VSN), somatomotor (SMN), ventral attention (VAN), dorsal attention (DAN), frontoparietal (FPN), limbic (Lim), and default mode networks (DMN). Additionally, subcortical (SCN) and cerebellum networks (CBN) were also included. Correlation analysis was further performed to explore the relationship between the most discriminative FC and clinical symptoms.
III. RESULTS
A. Compact representation for each class
For the BNCPL model, the prototype loss function was used to control the compactness for each class. The performance of BNCPL was compared with different λ, which was set as 0, 0.001, 0.0001, 0.00001 respectively. Results suggested that the representation of each class became more compact with bigger λ, as the dimension of the extracted feature space getting smaller (Fig. 2a). The average accuracy of the BNCPL model with λ as 0, 0.001, 0.0001, 0.00001 was 69.9 ± 1.1%, 69.6 ± 1.0%, 71.0 ± 1.3%, and 70.5 ± 1.1% respectively. In order to balance the classification performance and the compactness of the prototype, the lambda was determined as 0.0001 for further analysis.
Figure 2.
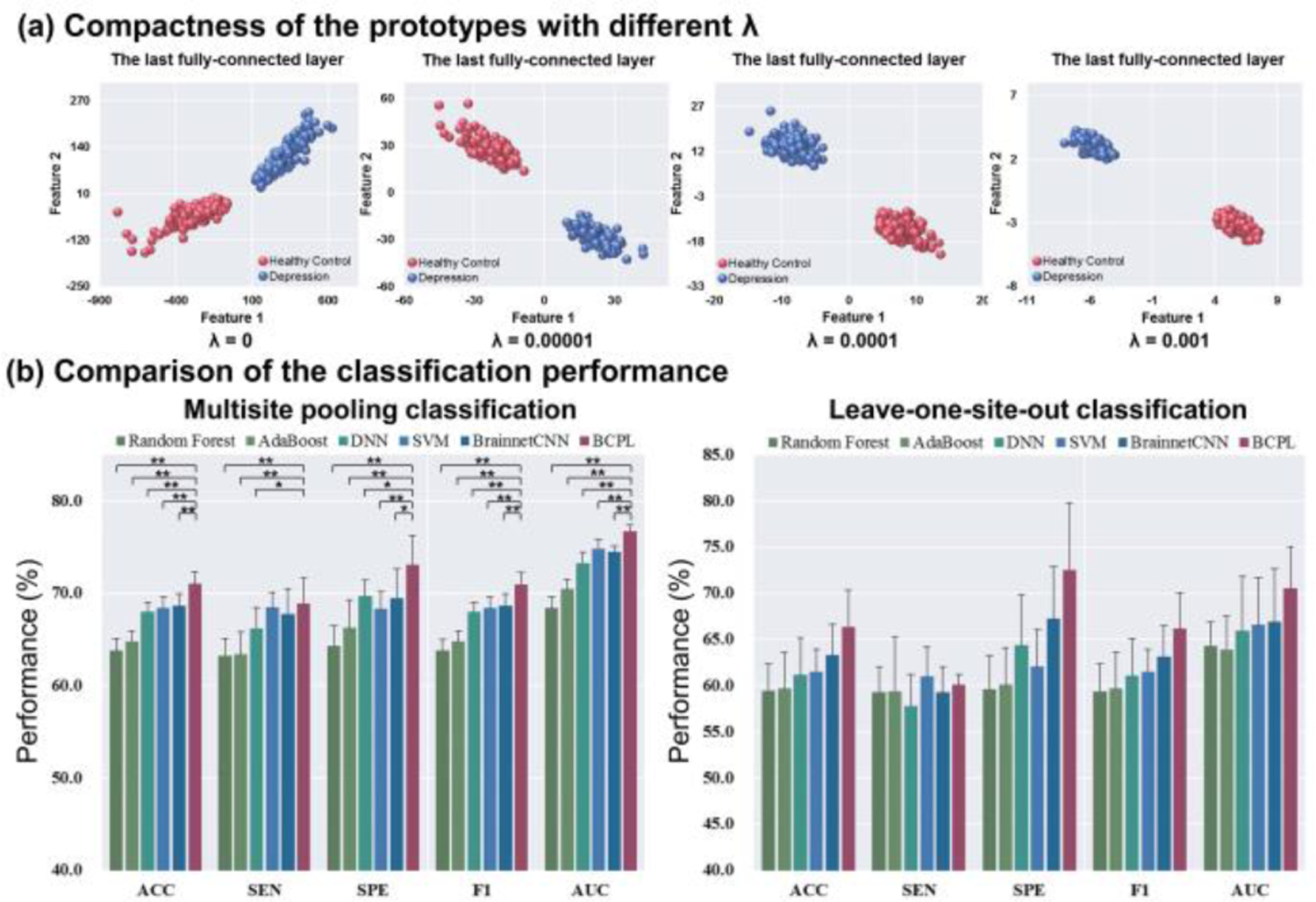
The classification performance of the BNCPL model. (a) The compactness and separability of prototypes with different λ for depression and healthy controls, in which λ is a hyper-parameter that controls the intra-class compactness. (b) The comparison of classification performance in multisite pooling and leave-one-site-out classification. * p < 0.05, ** p < 0.001.
B. Classification performance
For ten-fold cross validation, the BNCPL model achieved an average accuracy of 71.0 ± 1.3%, which was significantly higher than traditional classifiers, DNN, and BrainNetCNN (p < 0.001, two-sample t-test), whose accuracy ranged from 63.8 ± 1.3% to 68.6 ± 1.0%. The BNCPL model also outperformed in SEN, SPE, F1, and AUC metrics than other classifiers (Table II and Fig. 2b). For leave-one-site-out classification, the BNCPL model achieved an average accuracy of 66.4 ± 3.9%, which was higher than traditional classifiers, DNN, and BrainNetCNN (Table III and Fig. 2b), whose accuracy ranged from 59.4 ± 2.9% to 63.3 ± 3.4%. Additionally, the accuracy of AAL template was 66.7 ± 0.8% by the BNCPL model in ten-fold cross validation, which was lower than the Brainnetome atlas, suggesting that finer parcellation of brain regions may contribute to the classification of MDD.
TABLE II.
The performance of multi-site pooling classification
| Methods | ACC (%) | SEN (%) | SPE (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
|
| |||||
| Random Forest | 54.1 ± 1.7 | 54.0 ± 2.9 | 54.2 ± 2.2 | 54.1 ± 1.7 | 54.8 ± 2.0 |
| AdaBoost | 58.7 ± 1.5 | 58.7 ± 2.0 | 58.7 ± 2.5 | 58.7 ± 1.5 | 61.9 ± 2.1 |
| DNN | 68.0 ± 1.0 | 66.2 ± 2.3 | 69.8 ± 1.0 | 68.0 ± 1.0 | 73.3 ± 1.2 |
| SVM | 68.5 ± 1.4 | 68.2 ± 1.4 | 68.7 ± 2.1 | 68.5 ± 1.4 | 75.5 ± 1.2 |
| BrainNetCNN | 68.6 ± 1.0 | 67.8 ± 2.7 | 69.5 ± 2.3 | 68.6 ± 1.0 | 74.5 ± 0.7 |
| BNCPL | 71.0 ± 1.3 | 68.9 ± 2.8 | 73.1 ± 3.2 | 71.0 ± 1.3 | 76.7 ± 0.6 |
TABLE III.
The performance of leave-one-site-out classification
| Methods | ACC (%) | SEN (%) | SPE (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
|
| |||||
| Random Forest | 54.9 ± 3.0 | 55.8 ± 6.2 | 53.9 ± 4.2 | 54.8 ± 3.0 | 55.1 ± 5.2 |
| AdaBoost | 52.4 ± 3.4 | 55.8 ± 2.8 | 49.0 ± 4.5 | 52.3 ± 3.4 | 54.5 ± 2.0 |
| DNN | 61.1 ± 4.0 | 57.8 ± 3.4 | 64.4 ± 5.5 | 61.1 ± 4.0 | 65.9 ± 5.9 |
| SVM | 61.6 ± 2.9 | 59.6 ± 1.9 | 63.5 ± 5.5 | 61.6 ± 2.9 | 66.6 ± 5.4 |
| BrainNetCNN | 63.3 ± 3.4 | 59.3 ± 2.8 | 67.2 ± 5.6 | 63.2 ± 3.3 | 66.9 ± 5.7 |
| BNCPL | 66.4 ± 3.9 | 60.1 ± 1.1 | 72.5 ± 7.3 | 66.2 ± 3.8 | 70.5 ± 4.5 |
C. Estimating the most discriminating FC features
The most discriminating FC in the classification was analyzed based on the nine-network parcellations. Results demonstrated that the most discriminative regions primarily included right amygdala, bilateral basal ganglia, right thalamus, and right hippocampus within the SCN, left orbital gyrus (OrG), and left anterior cingulate gyrus within the DMN, bilateral dorsal lateral prefrontal gyrus (dlPFC), and right inferior parietal lobule within the FPN, parahippocampal gyrus and inferior temporal gyrus within the Lim (Fig. 3a). Among all regions, the amygdala, OrG, and dlPFC exhibited the greatest region weights. Especially for the amygdala, results showed that three FCs connected to the amygdala showed significant group difference and were also associated with symptom severity and cognitive ability (Fig. 4), including decreased FC between Amyg_212 and OrG_51 (p = 5.9×10−3, FDR corrected), and FC between Amyg_212 and OrG_43 (p = 3.4×10−2, FDR corrected), increased FC between Amyg_212 and dlPFC_16 (p = 2.8×10−4, FDR corrected) in MDD patients.
Figure 3.
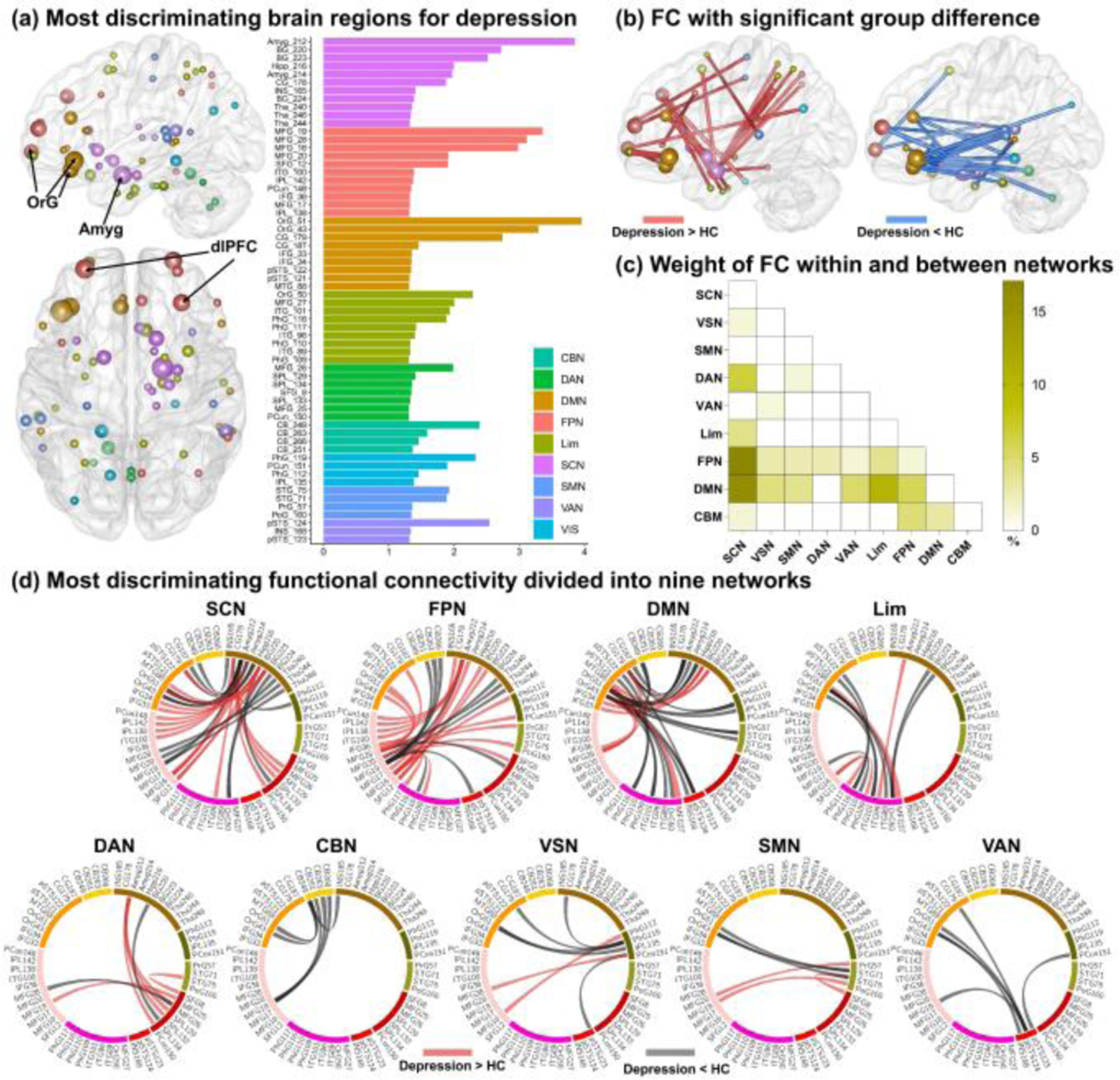
The most discriminating brain regions and functional connectivity (FC) in depression. (A) The most discriminating brain regions for depression (left) and node weights displayed in nine networks (right), in which node size denotes node weight. (B) The most discriminating FC with significant group difference. Red lines denote increased FC while blue lines denote decreased FC in depression. (C) The percentage weight distribution of intra- and inter-network FC. (D) The most discriminating FC displayed in nine networks. Red lines denote increased FC while black lines denote decreased FC in depression. OrG, orbital gyrus; Amyg, amygdala; dlPFC, dorsal lateral prefrontal cortex.
Figure 4.
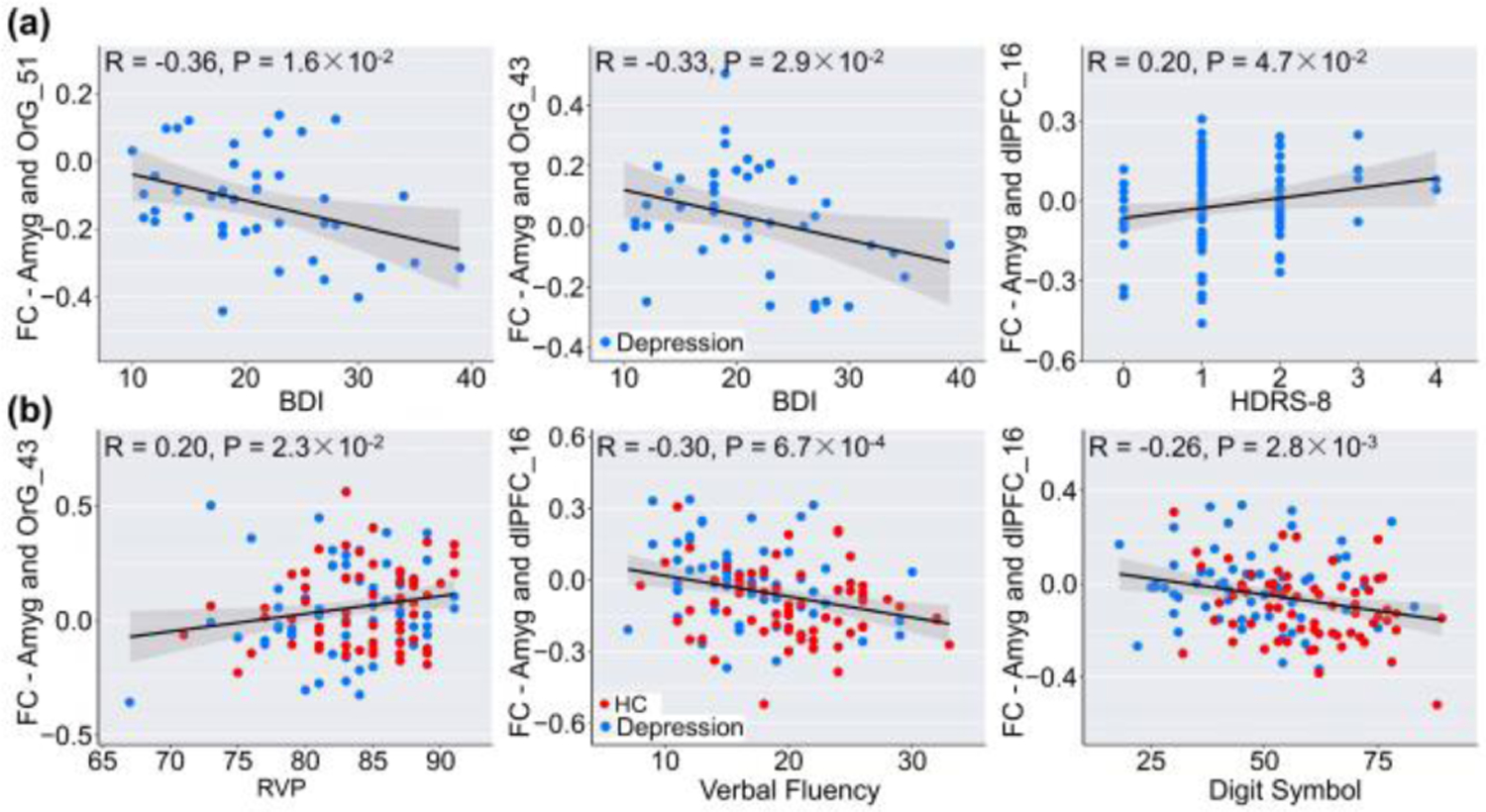
Correlations between amygdala-prefrontal connectivity and the severity of depression (A), and cognitive performance (B).
For the most discriminating FCs, nearly three quarters of the FC (55/75) showed significant group difference (p < 0.05, FDR corrected, Fig. 3b). It was obvious that most contributed FCs were mainly located in FPN, SCN, and DMN with the largest number of discriminating FC and the biggest node weights (Fig. 3a/d). The most discriminating FC was further divided into intra- and inter-network groups. Results showed that the most discriminating inter-network FCs were mainly found between SCN and FPN, and between SCN and DMN, and no significant intra-network FC were observed (Fig. 3c). A significant observation was prefrontal-subcortical circuit, as there were more than two-thirds (23/35) prefrontal-subcortical FCs of connections related to SCN. Summing up, the most discriminating regions were mainly found within SCN, DMN, and FPN, especially the prefrontal-subcortical circuit.
IV. DISCUSSION
Here we proposed a novel BNCPL model to differentiate depression from HCs, which enabled feature extraction and prototypes being learned jointly from the FC features. By integrating the topological property of brain networks and prototype learning, BNCPL can effectively learn an intra-class compact and inter-class separable representation for each class, instead of just learning a discriminative plane. MDD classification showed that the BNCPL model achieved a significantly improved classification accuracy in both multisite pooling (>2.4%−7.2%), and leave-one-site-out prediction (>3.1%−7.0%), suggesting great promise in searching potential neuroimaging biomarkers for MDD. Furthermore, based on the saliency map, we revealed that the most discriminating FCs were primarily related with FPN, DMN, and SCN. Specifically, FPN is involved in goal-directed control of attention, emotion, and self-referential thought [14], and aberrant FCs in FPN were also reported in a meta-analysis for MDD [15]. SCN is engaged in emotional stimulation and mood-congruent processing [16], especially the amygdala, which is implicated in event-related emotional experience and encoding of the emotion intensity [17]. The dysfunctional connectivity related with DMN, especially OrG and anterior cingulate gyrus, was also observed in the most discriminating FCs for MDD, consistent with previous studies [18]. To summarize (Fig. 3), FCs linking prefrontal-subcortical regions exhibited much higher weights in MDD classification, suggesting that prefrontal-subcortical pathways play a mediating role in emotion regulation [15, 18]. Coincidently, the prefrontal cortex was also reported to play a crucial role in the top-down regulation of subcortical affective circuitry [19].
V. CONCLUSION
To the best of our knowledge, this study is the first attempt to transplant convolutional prototype learning to neuroimaging classifications. The proposed BNCPL model is able to effectively learn an intra-class compact and inter-class separable representation, revealing the class-specific clustering patterns for HC and MDD. Consequently, a significantly improved performance was achieved for MDD classification, indicating the advantage of integrating the topological property of brain network and prototype learning. More importantly, the use of saliency map suggested that the most discriminative FC features were primarily located in SCN, DMN, and FPN, mostly in the prefrontal-subcortical circuit, which may shed new insight on understanding pathological mechanisms of depression, demonstrating great promise to identify potential imaging biomarkers for brain disorders with advanced deep learning techniques.
Acknowledgments
Research is supported by the National Key Research and Development Program of China (No. 2017YFB1002502, No. 2016YFC0904400), Natural Science Foundation of China (No. 82022035, 61773380, 81671300), the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB32040100), Beijing Municipal Science and Technology Commission (No. Z181100001518005), and National Institute of Health Grant (No. R01MH117107, No. P20GM103472).
Contributor Information
Dongmei Zhi, Institute of Automation, Chinese Academy of Sciences, and the School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing, China; Beijing Normal University, Beijing, China.
Vince D. Calhoun, Tri-Institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University, Georgia Institute of Technology, Emory University, Atlanta, GA, USA.
Chuanyue Wang, The National Clinical Research Center for Mental Disorders & Beijing Key Laboratory of Mental Disorders, Beijing Anding Hospital, and the Advanced Innovation Center for Human Brain Protection, Capital Medical University, Beijing, China.
Xianbin Li, The National Clinical Research Center for Mental Disorders & Beijing Key Laboratory of Mental Disorders, Beijing Anding Hospital, and the Advanced Innovation Center for Human Brain Protection, Capital Medical University, Beijing, China.
Xiaohong Ma, Psychiatric Laboratory and Mental Health Center, and the Huaxi Brain Research Center, West China Hospital of Sichuan University, Chengdu, China.
Luxian Lv, Xinxiang Medical University, Xinxiang, China; Henan Mental Hospital, The Second Affiliated Hospital of Xinxiang Medical University, Xinxiang, China.
Weizheng Yan, Institute of Automation, Chinese Academy of Sciences, and the School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing, China.
Dongren Yao, Institute of Automation, Chinese Academy of Sciences, and the School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing, China.
Shile Qi, Tri-Institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University, Georgia Institute of Technology, Emory University, Atlanta, GA, USA.
Rongtao Jiang, Institute of Automation, Chinese Academy of Sciences, and the School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing, China.
Jianlong Zhao, Beijing Normal University, Beijing, China.
Xiao Yang, Psychiatric Laboratory and Mental Health Center, and the Huaxi Brain Research Center, West China Hospital of Sichuan University, Chengdu, China.
Zheng Lin, School of Medicine, The Second Affiliated Hospital of Zhejiang University, Hangzhou, China.
Yujin Zhang, Institute of Automation, Chinese Academy of Sciences, and the School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing, China.
Young Chul Chung, Kwangwoon University, Seoul, South Korea.
Chuanjun Zhuo, Tianjin Mental Health Center, Nankai University Affiliated Anding Hospital, Tianjin, China.
Jing Sui, Tri-Institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University, Georgia Institute of Technology, Emory University, Atlanta, GA, USA; Beijing Normal University, Beijing, China.
References
- [1].Smith KM, Renshaw PF, and Bilello J, “The diagnosis of depression: current and emerging methods,” Comprehensive psychiatry, vol. 54, no. 1, pp. 1–6, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Gao S, Calhoun VD, and Sui J, “Machine learning in major depression: From classification to treatment outcome prediction,” CNS neuroscience & therapeutics, vol. 24, no. 11, pp. 1037–1052, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Calhoun VD, Sui J, Kiehl K, Turner JA, Allen EA, and Pearlson G, “Exploring the psychosis functional connectome: aberrant intrinsic networks in schizophrenia and bipolar disorder,” Frontiers in psychiatry, vol. 2, pp. 75, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zhi D, Calhoun VD, Lv L, Ma X, Ke Q, Fu Z, Du Y, Yang Y, Yang X, and Pan M, “Aberrant dynamic functional network connectivity and graph properties in major depressive disorder,” Frontiers in psychiatry, vol. 9, pp. 339, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Sundermann B, Feder S, Wersching H, Teuber A, Schwindt W, Kugel H, Heindel W, Arolt V, Berger K, and Pfleiderer B, “Diagnostic classification of unipolar depression based on resting-state functional connectivity MRI: effects of generalization to a diverse sample,” Journal of Neural Transmission, vol. 124, no. 5, pp. 589–605, 2017. [DOI] [PubMed] [Google Scholar]
- [6].Yan W, Calhoun V, Song M, Cui Y, Yan H, Liu S, Fan L, Zuo N, Yang Z, and Xu K, “Discriminating schizophrenia using recurrent neural network applied on time courses of multi-site FMRI data,” EBioMedicine, vol. 47, pp. 543–552, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Jun E, Na KS, Kang W, Lee J, Suk HI, and Ham BJ, “Identifying resting-state effective connectivity abnormalities in drug-naïve major depressive disorder diagnosis via graph convolutional networks,” Human Brain Mapping, vol. 41, no. 17, pp. 4997–5014, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Kawahara J, Brown CJ, Miller SP, Booth BG, Chau V, Grunau RE, Zwicker JG, and Hamarneh G, “BrainNetCNN: Convolutional neural networks for brain networks; towards predicting neurodevelopment,” NeuroImage, vol. 146, pp. 1038–1049, 2017. [DOI] [PubMed] [Google Scholar]
- [9].Yang H-M, Zhang X-Y, Yin F, and Liu C-L, “Robust classification with convolutional prototype learning,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3474–3482, 2018. [Google Scholar]
- [10].Xu K, Liu Y, Zhan Y, Ren J, and Jiang T, “BRANT: a versatile and extendable resting-state fMRI toolkit,” Frontiers in neuroinformatics, vol. 12, pp. 52, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Fan L, Li H, Zhuo J, Zhang Y, Wang J, Chen L, Yang Z, Chu C, Xie S, and Laird AR, “The human brainnetome atlas: a new brain atlas based on connectional architecture,” Cerebral cortex, vol. 26, no. 8, pp. 3508–3526, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Simonyan K, Vedaldi A, and Zisserman A, “Deep inside convolutional networks: Visualising image classification models and saliency maps,” arXiv preprint arXiv:1312.6034, 2013. [Google Scholar]
- [13].Thomas Yeo B, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zöllei L, and Polimeni JR, “The organization of the human cerebral cortex estimated by intrinsic functional connectivity,” Journal of neurophysiology, vol. 106, no. 3, pp. 1125–1165, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hasler G, and Northoff G, “Discovering imaging endophenotypes for major depression,” Molecular psychiatry, vol. 16, no. 6, pp. 604–619, 2011. [DOI] [PubMed] [Google Scholar]
- [15].Kaiser RH, Andrews-Hanna JR, Wager TD, and Pizzagalli DA, “Large-scale network dysfunction in major depressive disorder: a meta-analysis of resting-state functional connectivity,” JAMA psychiatry, vol. 72, no. 6, pp. 603–611, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Stuhrmann A, Suslow T, and Dannlowski U, “Facial emotion processing in major depression: a systematic review of neuroimaging findings,” Biology of mood & anxiety disorders, vol. 1, no. 1, pp. 10, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Wang S, Yu R, Tyszka JM, Zhen S, Kovach C, Sun S, Huang Y, Hurlemann R, Ross IB, and Chung JM, “The human amygdala parametrically encodes the intensity of specific facial emotions and their categorical ambiguity,” Nature communications, vol. 8, no. 1, pp. 1–13, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mulders PC, van Eijndhoven PF, Schene AH, Beckmann CF, and Tendolkar I, “Resting-state functional connectivity in major depressive disorder: a review,” Neuroscience & Biobehavioral Reviews, vol. 56, pp. 330–344, 2015. [DOI] [PubMed] [Google Scholar]
- [19].Johnstone T, van Reekum CM, Urry HL, Kalin NH, and Davidson RJ, “Failure to regulate: counterproductive recruitment of top-down prefrontal-subcortical circuitry in major depression,” Journal of Neuroscience, vol. 27, no. 33, pp. 8877–8884, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]


