Using pulmonary gas exchange to estimate shunt and deadspace in lung disease: theoretical approach and practical basis

Abstract

The common pulmonary consequence of SARS-CoV-2 infection is pneumonia, but vascular clot may also contribute to COVID pathogenesis. Imaging and hemodynamic approaches to identifying diffuse pulmonary vascular obstruction (PVO) in COVID (or acute lung injury generally) are problematic particularly when pneumonia is widespread throughout the lung and hemodynamic consequences are buffered by pulmonary vascular recruitment and distention. Although stimulated by COVID-19, we propose a generally applicable bedside gas exchange approach to identifying PVO occurring alone or in combination with pneumonia, addressing both its theoretical and practical aspects. It is based on knowing that poorly (or non) ventilated regions, as occur in pneumonia, affect O₂ more than CO₂, whereas poorly (or non) perfused regions, as seen in PVO, affect CO₂ more than O₂. Exhaled O₂ and CO₂ concentrations at the mouth are measured over several ambient-air breaths, to determine mean alveolar Po₂ and Pco₂. A single arterial blood sample is taken over several of these breaths for arterial Po₂ and Pco₂. The resulting alveolar-arterial Po₂ and Pco₂ differences (AaPo₂, aAPco₂) are converted to corresponding physiological shunt and deadspace values using the Riley and Cournand 3-compartment model. For example, a 30% shunt (from pneumonia) with no alveolar deadspace produces an AaPO₂ of almost 50 torr, but an aAPco₂ of only 3 torr. In contrast, a 30% alveolar deadspace (from PVO) without shunt leads to an AaPO₂ of only 12 torr, but an aAPco₂ of 9 torr. This approach can identify and quantify physiological shunt and deadspace when present singly or in combination.

NEW & NOTEWORTHY Identifying pulmonary vascular obstruction in the presence of pneumonia (e.g., in COVID-19) is difficult. We present here conversion of bedside measurements of arterial and alveolar Po₂ and Pco₂ into values for shunt and deadspace—when both coexist—using Riley and Cournand’s 3-compartment gas exchange model. Deadspace values higher than expected from shunt alone indicate high ventilation/perfusion ratio areas likely reflecting (micro)vascular obstruction.

INTRODUCTION

The SARS-CoV-2 virus is now known to affect multiple organ systems (1). Within the lungs, pneumonia is perhaps the primary pathological manifestation of the virus. Pneumonia results in alveolar filling with cellular debris and fluid, which in turn reduces or eliminates ventilation of the affected alveoli, thereby lowering regional ventilation/perfusion (V̇a/$\dot{\text{Q}}$) ratios and causing sometimes profound arterial hypoxemia (2). There is however evidence that the virus may also cause (micro)vascular thrombosis in the pulmonary circulation (3). Were pulmonary vascular clotting to occur, affected alveoli would become underperfused, and their V˙a/$\dot{\text{Q}}$ ratios would rise, similar to what has been found in acute pulmonary thromboembolism (4). The affected alveoli would accordingly have an elevated alveolar Po₂ (5). Thus, occurring alone, vascular obstruction should not result in arterial hypoxemia provided that the drive to breathe remains sufficient to maintain arterial Pco₂ at normal levels (6). In addition, if thrombosis were occurring diffusely in the pulmonary microvasculature, it would be hard to detect by imaging tools. Clotting in the pulmonary circulation may be even more difficult to identify when occurring in combination with COVID-19 pneumonia. Estimates of pulmonary arterial pressure in patients with COVID-19 have not consistently shown marked elevation (7–9), but it should be noted that the pulmonary circulation is characterized by recruitability and distensibility (10). That is, the pulmonary circulation has considerable ability to both recruit capillaries that may not be perfused and to distend capillaries that are open and perfused, a process that will buffer any tendency for the pulmonary arterial pressure to increase when some vessels are obstructed. In sum, detection of diffuse pulmonary microvascular thrombosis in COVID-19 is challenging.

On the basis of well-established physiological principles underlying gas exchange (5), we propose herein that simultaneously assessing O₂ and CO₂ exchange across the lungs will provide a clinically feasible approach to inferring the presence of diffuse pulmonary microvascular obstruction in spontaneously breathing patients. The key concept is that if pneumonia, giving rise to alveoli of reduced V̇a/$\dot{\text{Q}}$ ratio, is the primary consequence of COVID-19, O₂ exchange will be affected more than that of CO₂. In contrast, with microvascular obstruction creating alveoli with elevated V̇a/$\dot{\text{Q}}$ ratios, CO₂ exchange will be relatively more affected. These consequences—singly and in combination—can be identified by measuring O₂ and CO₂ levels in both arterial blood and exhaled gas and determining the alveolar-arterial gas tension differences for each gas, which can then be converted into values for physiological shunt and deadspace. Although the stimulus for developing this methodology is COVID-19, it should be generally applicable to patients with pulmonary disease of any cause.

The purpose of this article is to provide both the theoretical and practical foundations for this gas exchange approach. Although the gas exchange principles are mostly well established, their application and the proposed analyses to our knowledge are novel.

METHODS AND RESULTS

Solubility of a Gas in Blood and Its Relationship to Blood: Gas Partition Coefficient

It is known that in a lung with any degree and pattern of V̇a/$\dot{\text{Q}}$ inequality, the properties of any gas undergoing exchange determine to a large extent the magnitude of the interference to its exchange (11, 12). Comparing different gases being exchanged in a given lung, the dominant property of a gas that determines the extent of gas exchange impairment is its solubility, S, in blood (13). The purpose of this section is to develop the theoretical basis of this claim, and extrapolate it to the respiratory gases, O₂ and CO₂. The common units of S are mL of gas per 100 mL of blood per mmHg partial pressure of the gas. Solubility can also be also expressed as the blood to gas partition coefficient, commonly denoted by the Greek letter λ. In words, λ for any gas is the ratio of its concentration in blood to its concentration in gas with which it is in equilibrium. Because λ is a ratio of two concentrations, it is a dimensionless number. When S is expressed in mL/100 mL/mmHg, the numerical relationship between S and λ is as follows:

$$\mathrm{\lambda }\text{=}\mathrm{ S}\times \left(\mathrm{PB}\text{ − }\mathrm{P}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)\mathrm{/100}$$ (1)

Here PB is barometric pressure and PH₂O is saturated water vapor pressure, both in mmHg. Multiplying S by (PB − PH₂O) converts its units to mL/100 mL/atmosphere, and then dividing S by 100 further converts its units to mL/mL/atmosphere, which defines λ as the mL of gas in 1 mL of blood when in the gas phase its concentration is 1 mL/mL. Under standard conditions, i.e., PB = 760 mmHg and at body temperature of 37°C where PH₂O = 47 mmHg, the outcome is:

$$\mathrm{\lambda =7}\mathrm{.13\times S}$$ (2)

For inert gases (gases that are chemically nonreactive with blood and tissue components) and which are therefore carried in blood only in physical solution (i.e., dissolved), either S or λ is sufficient to characterize the relationship between partial pressure and concentration over any range of values.

However, for O₂ and CO₂, the relationships between partial pressure and concentration in blood are well-known to be nonlinear, and a single value of S or λ is thus insufficient to describe their partial pressure-concentration relationships quantitatively with accuracy. However, for the analysis to follow, it will be very useful in conceptual development to begin by defining the O₂ (or CO₂) dissociation curves by their average slopes between arterial and mixed venous blood, thereby assigning them average values of S and λ.

Focusing first on O₂, where breathing ambient air, normal arterial blood has a Po₂ of 100 mmHg and an O₂ concentration of 20 mL/100 mL blood and where normal mixed venous blood has a Po₂ of 40 mmHg and an O₂ concentration of 15 mL/100 mL blood, it can be seen that the average slope of the O₂ dissociation curve in the normal range becomes (20–15)/(100–40) mL O₂/100 mL blood/mmHg. This comes to 5/60 or 0.083 mL/100 mL/mmHg. In the present context, this number becomes the value of S for O₂, and multiplying by (PB − PH₂O)/100 (i.e., by 7.13 under standard conditions) yields an effective blood:gas partition coefficient for O₂ of ∼0.6.

Turning to CO₂, normal arterial blood has a Pco₂ of 40 mmHg and a CO₂ concentration of 48 mL/100 mL blood and normal mixed venous blood has a Pco₂ of 45 mmHg and a CO₂ concentration of 52 mL/100 mL blood. From these numbers, it can be seen that the average slope of the CO₂ dissociation curve in the normal range becomes (52–48)/(45–40) mL CO₂/100 mL blood/mmHg. This comes to 4/5 or 0.80 mL/100 mL/mmHg. In the present context, this number becomes the value of S for CO₂, and multiplying by 7.13 yields an effective blood:gas partition coefficient for CO₂ of ∼6.

The main point is that the average slope of the CO₂ dissociation curve is ∼10 times the average slope of the O₂ dissociation curve, and that we can go forward with the analysis considering O₂ to behave like a gas with λ = 0.6 and CO₂ to behave like a gas with λ = 6. The utility of these simplifying approximations will become apparent in the analysis that now follows.

Ventilation/Perfusion Inequality: the Simple Two-Compartment Model

Ventilation/perfusion (V̇a/$\dot{\text{Q}}$) inequality is defined as variation in the local V̇a/$\dot{\text{Q}}$ ratio across the lungs. In patients with lung disease, it is common knowledge that V̇a/$\dot{\text{Q}}$ inequality is a dominant consequence of structural and functional pulmonary abnormalities, causing interference to gas exchange manifest as arterial hypoxemia, sometimes also with hypercapnia. Research using both imaging tools and the multiple inert gas elimination technique has revealed that V̇a/$\dot{\text{Q}}$ inequality is often manifest as a distribution of lung units over a wide range of V̇a/$\dot{\text{Q}}$ ratios. However, for conceptual development here, there is major advantage to simplifying the lungs to a two-compartment structure where one compartment, or unit, has a V̇a/$\dot{\text{Q}}$ ratio in the normal range and the other is abnormal with a V̇a/$\dot{\text{Q}}$ ratio that is either lower or higher than that of the normal unit.

Gas Exchange in the Presence of V̇a/$\dot{\text{Q}}$ Inequality: the Key Role of Partition Coefficient

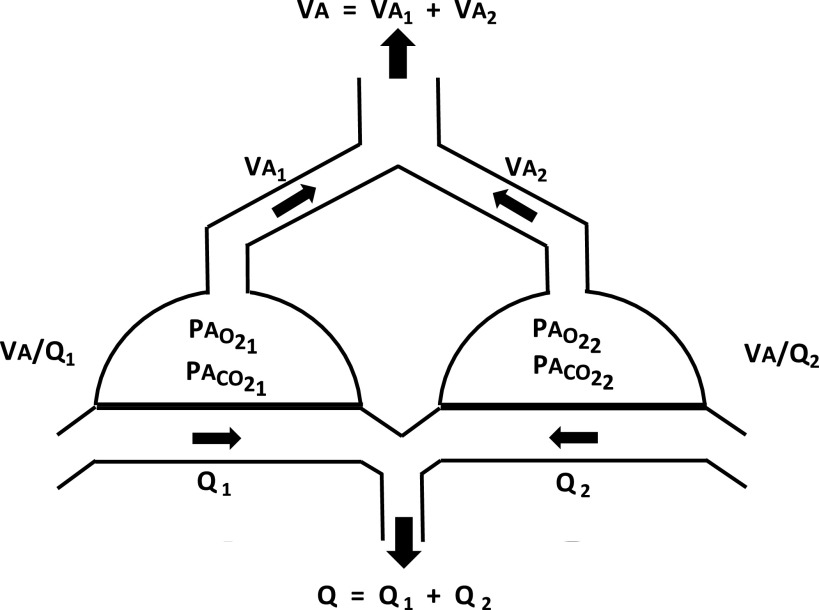
Suppose the lungs are now imagined as the simplest model of V̇a/$\dot{\text{Q}}$ inequality using a two-compartment model (Fig. 1). Here one side (left) has alveolar ventilation designated V̇a₁ and blood flow designated $\dot{\text{Q}}$₁ whereas the other side (right) has values denoted V̇a₂ and $\dot{\text{Q}}$₂. Total alveolar ventilation is V̇a = V̇a₁ + V̇a₂ whereas total blood flow $\dot{\text{Q}}$ = $\dot{\text{Q}}$₁ + $\dot{\text{Q}}$₂. Gas exchange is presumed to occur in a steady state.

Figure 1.

Two-compartment model of the lungs with total alveolar ventilation (V̇a) and blood flow ($\dot{\text{Q}}$) split between both compartments (V̇a₁ and V̇a₂; $\dot{\text{Q}}$₁ and $\dot{\text{Q}}$₂) resulting in corresponding V̇a/$\dot{\text{Q}}$ ratios (V̇a₁/$\dot{\text{Q}}$₁ and V̇a₂/$\dot{\text{Q}}$₂). The different V̇a/$\dot{\text{Q}}$ ratios then dictate corresponding values of alveolar Po₂ and Pco₂ in each compartment as shown. Arrows indicate the mixing of exhaled gas from the two compartments and mixing of compartmental blood flow from the compartments to form the mixed exhaled gas and mixed arterial blood.

Suppose further that gases are being eliminated from the blood (i.e., as for CO₂) and exhaled to the atmosphere (rather than being moved from alveolar gas into blood). Mathematically, this makes the algebra which follows simpler, because inspired levels of the gas can be set to zero and thus ignored. The direction of exchange however is immaterial to the result. Using the well-accepted principle of mass conservation in pulmonary gas exchange, the following well-known relationship can be derived relating ventilation and blood flow in an alveolus to the partial pressures of the gas in alveolar gas (PA), end-capillary blood (Pec), and mixed venous blood (Pv) and to the partition coefficient (λ) of the gas (14, 15):

$$\mathrm{P}{\mathrm{A}}_{\mathrm{1}}\mathrm{ = Pe}{\mathrm{c}}_{\mathrm{1}}\mathrm{ = Pv}\times \lambda \mathrm{/(}\lambda \mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{1}}\mathrm{)}\mathrm{ for unit 1}$$ (3)

and

$$\mathrm{P}{\mathrm{A}}_{\mathrm{2}}\mathrm{ =Pe}{\mathrm{c}}_{\mathrm{2}}\mathrm{ =Pv}\times \lambda \mathrm{/(}\lambda \mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{2}}\mathrm{)}\mathrm{ for unit 2.}$$ (4)

Here alveolar and end-capillary gas tensions are taken to be identical in each unit, although clearly different between units because v̇a₁/$\dot{\text{Q}}$₁ does not equal V̇a₂/$\dot{\text{Q}}$₂. Alveolar end-capillary equivalence implies that alveolar-capillary diffusion equilibrium does occur within the transit of each red cell through the microcirculation of the lungs.

Now defining R₁ as Pec1/Pv (the retention of unit 1) and E₁ as PA₁/Pv (the excretion of unit 1), and similarly applying this simplification to unit 2, the two equations become:

$${\mathrm{R}}_{\mathrm{1}}\mathrm{ = }{\mathrm{E}}_{\mathrm{1}}\mathrm{ = }\lambda \mathrm{/(}\lambda \mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{1}}\mathrm{) }\mathrm{ for unit 1}$$ (5)

and

$${\mathrm{R}}_{\mathrm{2}}\mathrm{ = }{\mathrm{E}}_{\mathrm{2}}\mathrm{ = }\mathbf{\lambda }\mathrm{/(}\mathbf{\lambda }\mathrm{+V}{\mathrm{A}}_{\mathrm{2}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{2}}\mathrm{)}\mathrm{ for unit 2.}$$ (6)

Equation 5 states that in gas exchange unit 1, the fraction R₁ of the gas delivered to that unit in the pulmonary arterial blood which remains in the end-capillary blood of that unit after undergoing pulmonary gas exchange is the ratio of the partition coefficient of the gas to the sum of the partition coefficient and the V̇a/$\dot{\text{Q}}$ ratio of the unit. Equation 6 makes the identical statement for the second unit. The equations show that R₁ and R₂ will be lower for a poorly soluble gas (with low λ) than for a highly soluble gas (with high λ) in any gas exchange unit, and higher for any gas when the unit’s V̇a/$\dot{\text{Q}}$ ratio is low compared with when its V̇a/$\dot{\text{Q}}$ ratio is high.

Referring to Fig. 1, suppose the two V̇a/$\dot{\text{Q}}$ compartments are connected in parallel by both airways and blood vessels as shown. Their exhaled airstreams will mix and their end-capillary blood streams will also mix as ventilation and perfusion continue.

Because of this, the mixed exhaled gas will have a ventilation-weighted average partial pressure, normalized to Pv, (and termed PE) given by:

$$\mathrm{PE = }\left({\mathrm{E}}_{\mathrm{1}}\mathrm{ \times }\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{+}{\mathrm{E}}_{\mathrm{2}}\mathrm{ \times }\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\right)\mathrm{/}\left(\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\right)$$ (7)

Symmetrically, because the two bloodstreams also mix to form the systemic arterial blood after leaving the alveolar region, the mixed arterial blood will have a perfusion-weighted average partial pressure (Pa), also normalized to Pv, given by:

$$\mathrm{Pa = }\left({\mathrm{R}}_{\mathrm{1}}\mathrm{ \times }{\dot{\text{Q}}}_{\mathrm{1}}\mathrm{+}{\mathrm{R}}_{\mathrm{2}}\mathrm{ \times }{\dot{\text{Q}}}_{\mathrm{2}}\right)\mathrm{/}\left({\dot{\text{Q}}}_{\mathrm{1}}\mathrm{+}{\dot{\text{Q}}}_{\mathrm{2}}\right)$$ (8)

Just as for the alveolar-arterial difference for O₂, the difference between Pa and PE expresses the degree of interference to gas exchange (of a gas with partition coefficient λ in this particular two-unit lung with ventilation and blood flow distributed as described). Hence:

$$\mathrm{Pa-PE = }\left({\mathrm{R}}_{\mathrm{1}}\mathrm{ \times }{\dot{\text{Q}}}_{\mathrm{1}}\mathrm{+}{\mathrm{R}}_{\mathrm{2}}\mathrm{ \times }{\dot{\text{Q}}}_{\mathrm{2}}\right)\mathrm{/}\left({\dot{\text{Q}}}_{\mathrm{1}}\mathrm{+}{\dot{\text{Q}}}_{\mathrm{2}}\right)\mathrm{ }-\mathrm{ }\left({\mathrm{E}}_{\mathrm{1}}\mathrm{ \times }\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{+}{\mathrm{E}}_{\mathrm{2}}\mathrm{ \times }\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\right)\mathrm{/}\left(\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\right)$$ (9)

The terms on the right side of Eq. 9 contain R₁ and E₁, both of which equal

$$\lambda \mathrm{/(}\lambda \mathrm{+}\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{1}}\mathrm{) }$$

and also R2 and E2, both of which equal

$$\lambda \mathrm{/(}\lambda +\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{2}}\mathrm{)}\mathrm{.}$$

In sum, the unique terms in Eq. 9 are only five in number: V̇a₁, V̇a₂, $\dot{\text{Q}}$₁, $\dot{\text{Q}}$₂, and λ. Therefore, for a given set of values of V̇a₁, V̇a₂, $\dot{\text{Q}}$₁, and $\dot{\text{Q}}$₂, the arterial-alveolar gas partial pressure difference, Pa − PE, is a unique function of λ.

In fact, when V̇a₁, V̇a₂, $\dot{\text{Q}}$₁, and $\dot{\text{Q}}$₂ are nonzero themselves, the equations show that if λ were zero, the arterial-alveolar gas partial pressure difference must be zero as both R₁ and R₂ fall to zero. Similarly, when λ is infinitely high, the arterial-alveolar gas partial pressure difference must also be zero, because R₁ = R₂ = 1.0. In between these extremes, differential calculus can be used to show that there is a unique value of λ for which the arterial-alveolar gas partial pressure difference will be at a maximum. This requires differentiating Eq. 9 with respect to λ and solving for the value of λ that makes the differentiated equation zero. That process defines the value of λ at which Pa − PE is maximal (λ_max ).

This unique value of λ_max must be a function of the values of V̇a₁, V̇a₂, $\dot{\text{Q}}$₁, and $\dot{\text{Q}}$₂ because they are the only other terms than λ in Eq. 9. When this calculus is performed, the outcome is remarkably simple in that the arterial-alveolar gas partial pressure difference will be at a maximum when:

$${\mathrm{\lambda }}_{\max }\mathrm{ = square root }\left[\left(\dot{\text{V}}{\mathrm{A}}_{\mathrm{1}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{1}}\right)\mathrm{ \times }\left(\dot{\text{V}}{\mathrm{A}}_{\mathrm{2}}\mathrm{/}{\dot{\text{Q}}}_{\mathrm{2}}\right)\right]$$ (10)

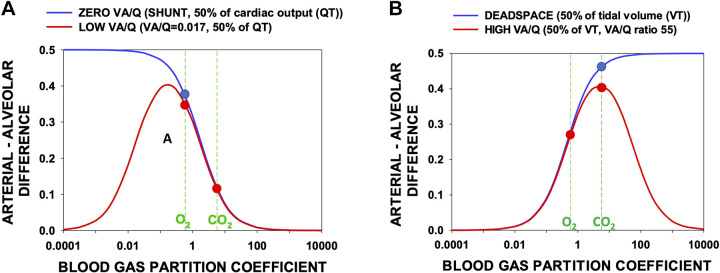
This result was mentioned in Ref. 13. Figure 2 shows the arterial-alveolar gas partial pressure difference calculated using Eq. 9 over a wide range of λ for four model lungs, two in each panel. Figure 2A describes alveolar-arterial difference outcomes using Eq. 9 for a wide range of partition coefficients for two models having 1) 50% shunt (V̇a/$\dot{\text{Q}}$ = 0) perfusion and 50% perfusion of normal lung (V̇a/$\dot{\text{Q}}$ = 1; blue line) and 2) 50% low V̇a/$\dot{\text{Q}}$ (0.017) perfusion and 50% normal perfusion (V̇a/$\dot{\text{Q}}$ = 1; red line).

Figure 2.

The relative arterial-alveolar partial pressure differences arising from shunt and deadspace (blue curves) and from low or high V̇a/$\dot{\text{Q}}$ ratio regions (red curves) as a function of gas partition coefficient (λ, abscissa). The ordinate cannot be less than zero nor greater than 1.0. The vertical dashed lines indicate the average values of the O₂ and CO₂ dissociation curves slopes expressed as partition coefficients (see text). A: the greatest impediment to gas exchange in the examples of low V̇a/$\dot{\text{Q}}$ regions and shunt occurs for gases of λ = 0.17 and 0, respectively. The O₂-equivalent gas has a more than threefold higher arterial-alveolar difference than the CO₂-equivalent gas. B: for the high V̇a/$\dot{\text{Q}}$ and deadspace models, the most affected gases have λ = 5 and infinity, respectively. The CO₂-equivalent gas has an arterial-alveolar difference about 50% greater than that of the O₂-equivalent gas. Whether the lungs have low and high V̇a/$\dot{\text{Q}}$ regions (red) or zero and infinitely high V̇a/$\dot{\text{Q}}$ regions (blue) is seen to not be important for O₂ or CO₂ in each case (compare red and blue circles). $\dot{\text{Q}}$, blood flow; V̇a, alveolar ventilation.

The values of the average slopes of the O₂ and CO₂ dissociation curves expressed as partition coefficients as discussed above are indicated by the vertical green dashed lines. Although the red and blue curves can be seen to differ markedly at very low partition coefficients, at the partition coefficients representing O₂ and CO₂, there is little difference between them: whether the lung has low V̇a/$\dot{\text{Q}}$ areas or shunt makes little difference to O₂ or CO₂ exchange (when ambient air is breathed, as proposed in this paper).

Figure 2B describes alveolar-arterial difference outcomes using Eq. 9 for a wide range of partition coefficients for two models having 1) 50% deadspace (V̇a/$\dot{\text{Q}}$ = infinitely high) ventilation and 50% ventilation of remaining normal lung (V̇a/$\dot{\text{Q}}$ = 1; blue line) and 2) 50% high V̇a/$\dot{\text{Q}}$ (55) ventilation and 50% ventilation of remaining normal (V̇a/$\dot{\text{Q}}$ = 1; red line).

The values of the average slopes of the O₂ and CO₂ dissociation curves are again expressed as partition coefficients and are indicated by the vertical green dashed lines. Although the red and blue curves can be seen to differ markedly at very high partition coefficients, for O₂ and CO₂ there is, as with Fig. 2A, little difference between them: whether the lung has high V̇a/$\dot{\text{Q}}$ areas or actual unperfused deadspace makes little difference to O₂ or CO₂ exchange.

It is thus evident (by the solid circles) that a lung with low—or zero— V̇a/$\dot{\text{Q}}$ ratios affects a gas with partition coefficient equivalent to that of O₂ more than one with partition coefficient equivalent to that of CO₂, and that a lung with high—or infinite— V̇a/$\dot{\text{Q}}$ areas affects CO₂ more than O₂. It should also be emphasized that either a shunt or a lesion with low V̇a/$\dot{\text{Q}}$ areas will affect both O₂ and CO₂, whereas high V̇a/$\dot{\text{Q}}$ regions and deadspace also affect both gases. This means that O₂ cannot be used alone to define shunt (or low V̇a/$\dot{\text{Q}}$ areas) and CO₂ cannot be used alone to define deadspace (or high V̇a/$\dot{\text{Q}}$ areas). The power of this analysis lies in the simultaneous use of the two gases, as will be further developed below.

This fundamental concept—that the relative interference to exchange of a gas in any pattern of V̇a/$\dot{\text{Q}}$ inequality is dependent on the (effective) solubility or partition coefficient of the gas—is now the basis of using O₂ and CO₂ to identify the presence of areas of both low/zero and high/infinitely high V̇a/$\dot{\text{Q}}$ ratio in the lungs of patients with pulmonary disease such as COVID-19.

The ensuing section exploits these principles to apportion shunt and deadspace in the lungs of any individual subject by measuring the alveolar-arterial partial pressure differences for both O₂ and CO₂ and calculating the size of the shunt and deadspace necessary to explain those differences. The framework for this approach is the seven decades old three-compartment analysis proposed by Riley and Cournand in the middle of the last century (16) whereby the lung is divided into three virtual compartments: one contains all of the shunt, the second contains all of the deadspace, and the third contains all of the nonshunt blood flow and nondeadspace ventilation. In this model, perfusion of low (but nonzero) V̇a/$\dot{\text{Q}}$ regions is expressed as equivalent shunts. Correspondingly, ventilation of high (but not infinitely high) V̇a/$\dot{\text{Q}}$ regions is expressed as equivalent deadspace. Even though both shunt and low V̇a/$\dot{\text{Q}}$ areas may be present, the analysis provides a value for the size of the shunt required to fully explain arterial Po₂ and Pco₂, and the size of the deadspace required to fully explain the expired Po₂ and Pco₂. To accomplish this, the quantitative relationships between 1) deadspace and shunt and 2) arterial-alveolar partial pressure differences for O₂ and CO₂ must first be established.

The Alveolar-Arterial Po₂ Difference and the Arterial-Alveolar Pco₂ Differences in Lungs with Shunt and Deadspace

Although the preceding analysis provides an analytical explanation of why the exchange of any gas becomes differentially affected depending on the type of V̇a/$\dot{\text{Q}}$ inequality present in the lungs and the partition coefficient of the gas, the approximation of the carriage of both O₂ and CO₂ in blood by a single hypothetical average “partition coefficient” must be addressed to better reflect the fact that both O₂ and CO₂ possess nonlinear dissociation curves. This means using their actual dissociation curves, rather than their average dissociation curve slopes. Fortunately, this can readily be accomplished, as follows.

In 1969, West published a seminal paper (17) describing a sophisticated set of algorithms that would calculate the mixed (systemic) arterial and mixed exhaled alveolar Po₂ and Pco₂ values in a lung of any selected degree of V̇a/$\dot{\text{Q}}$ inequality. The actual O₂ and CO₂ dissociation curves described by Kelman (18–20) were employed in this computer program, which allows for their chemical interaction. In this way, the linear approximation to their dissociation curves used in the preceding theoretical section, while conceptually essential, was avoided in the application. Factors affecting the shape and position of both dissociation curves (in particular, hemoglobin concentration and P50, base excess and temperature) are accounted for quantitatively.

Moreover, although West depicted inequality by means of a log-normal multicompartmental V̇a/$\dot{\text{Q}}$ distribution model, his algorithm is easily pared down to the simpler Riley and Cournand three-compartment model of shunt, deadspace, and a normal compartment, which was used in the present study. The reason for our choosing this simplification is that from a single measurement of alveolar and arterial Po₂ and Pco₂ with the patient breathing ambient air, the information available is insufficient to describe the shape and position of the entire V̇a/$\dot{\text{Q}}$ distribution but is sufficient to determine shunt and deadspace in the Riley construct. Karbing et al. recognized this and used multiple measurements over a range of inspired O₂ concentrations to discriminate better areas of low V̇a/$\dot{\text{Q}}$ ratio from shunt areas of zero V̇a/$\dot{\text{Q}}$ ratio (21–23).

The key inputs to West’s algorithm are the values of ventilation and blood flow in each compartment (and hence their sums, i.e., total alveolar ventilation and pulmonary blood flow). Ancillary input data are O₂ consumption, CO₂ production, inspired O₂ and CO₂ concentrations, [Hb], Hb P50, barometric pressure, body temperature, and base excess. The key outputs from West’s algorithm are the alveolar-arterial differences for O₂ and CO₂, and the corresponding values of shunt and deadspace that in combination account for both alveolar-arterial Po₂ and Pco₂ differences.

To show the relationships between arterial-alveolar differences for O₂ and CO₂ and the corresponding values of shunt and deadspace, 3 three-compartmental models of V̇a/$\dot{\text{Q}}$ inequality were constructed, and West’s algorithm was utilized. One—modeling only the expected development of regions of deadspace from diffuse microvascular obstruction—employed a lung with a compartment of normal V̇a/$\dot{\text{Q}}$ (∼1) plus a second compartment of infinitely high V̇a/$\dot{\text{Q}}$ ratio, with its ventilation ranging from 0% to 50% of tidal volume. Here, for the third compartment (shunt), perfusion was set to zero to determine how deadspace alone affected the arterial-alveolar difference for both gases. A second model performed the mirror-image calculations using a normal compartment and one with V̇a/$\dot{\text{Q}}$ ratio = 0. Here, the third compartment (deadspace) was assigned zero ventilation so as to model the pure effects of a shunt on alveolar-arterial differences. The third model combined various amounts of shunt plus deadspace and determined the alveolar-arterial differences over these ranges.

It is critical to understand that the alveolar-arterial Po₂ difference depicted in the above is not the classical difference commonly derived from the alveolar gas equation. Such an approach would not be valid in the present context, because the alveolar gas equation specifically assumes that the alveolar Pco₂ can be approximated by the arterial Pco₂, which is clearly untrue whenever there is V̇a/$\dot{\text{Q}}$ inequality (see Fig. 2). The appropriate alveolar values to compare to arterial are the mixed alveolar values of both O₂ and CO₂, which are the ventilation-weighted averages of the compartmental values.

Figure 3A plots the arterial-mixed alveolar Pco₂ differences provided by West’s algorithm against those for O₂ for the three models (shunt only, red; deadspace only, blue; both shunt and deadspace, green). Results for values of shunt and deadspace from 0% to 50% are shown. This figure provides the fundamental framework of the proposed approach to determining the existence of areas of high V̇a/$\dot{\text{Q}}$ ratio in patients with COVID. The key concept is that where a patient’s measured Po₂ and Pco₂ alveolar-arterial differences lie on this framework figure enables quantification of the amounts of shunt and deadspace, singly or in combination. If the sole gas exchange defect is vascular obstruction causing deadspace, the data should lie somewhere along the blue line, depending on the extent of the obstruction. If the sole defect is the existence of shunt, the patient data should lie along the red line; when both types of lesions coexist, the data would lie in between these two lines. The green line shows the example of what would be seen if there were equal amounts of shunt and deadspace present. Importantly, in each of the three models, both gases are affected, but it is the relative amount by which each gas is affected that provides the key insight. This diagram therefore allows for estimates of both shunt and deadspace simultaneously. It recognizes that shunt affects CO₂ and must be allowed for. Correspondingly it recognizes that deadspace affects O₂ which must also be allowed for.

Figure 3.

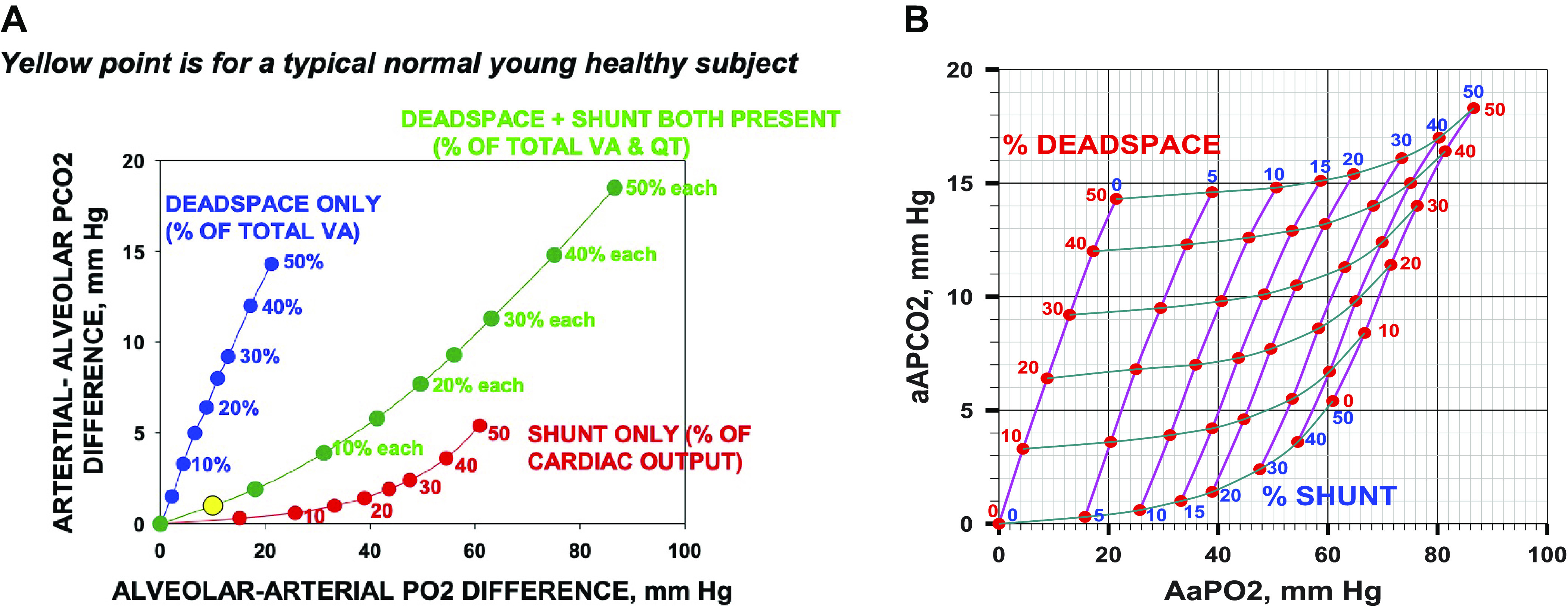
A: the arterial-alveolar partial pressure differences for CO₂ (ordinate) plotted against the alveolar-arterial partial pressure differences for O₂ (abscissa). Red points: differences due to shunt alone (from 0% to 50% of the cardiac output); blue points: differences due to deadspace alone (from 0% to 50% of the ventilation); and green points: differences due to shunt plus deadspace (each from 0% to 50%). It is evident that although both O₂ and CO₂ are affected by shunt, by deadspace, and by their combination, the relationships between O₂ and CO₂ for each type of abnormality are very different. A normal young subject, with a typical alveolar-arterial Po₂ difference of 10 mmHg and arterial-alveolar Pco₂ difference of 1 mmHg is shown by the yellow solid circle. B: the plots of A extended into a complete grid showing alveolar arterial differences for O₂ and CO₂ as a function of the range of combinations of shunt and deadspace, each from 0% to 50%. This grid can be used for any measured pair of alveolar-arterial differences for O₂ and CO₂ to estimate the percentage of pulmonary blood flow perfusing unventilated regions (shunt) and percentage of alveolar ventilation associated with unperfused regions (deadspace). aAPco₂, arterial-alveolar Pco₂ difference; AaPo₂, alveolar-arterial Po₂ difference.

Figure 3B extends the calculations of Fig. 3A to form a complete grid depicting how any combination of shunt and deadspace affects the alveolar-arterial partial pressure differences for O₂ and CO₂. This grid may then be used in reverse to identify the amounts of shunt and deadspace corresponding to any measured pair of values of alveolar-arterial differences for O₂ and CO₂.

To apply these concepts to individual patients as accurately as possible, the above-mentioned ancillary variables (O₂ consumption, CO₂ production, inspired O₂ and CO₂ concentrations, [Hb], Hb P50, barometric pressure, body temperature and base excess) are used in executing West’s algorithm, along with total alveolar ventilation, pulmonary blood flow (assumed equal to cardiac output). This means that the grid of Fig. 3B is in effect calculated uniquely for each patient using measured values of the ancillary variables. All of these variables are available from the proposed measurements, either from the expired gas or the arterial blood samples, with the exception of Hb P50 and cardiac output. In the majority of patients without hemoglobinopathy, Hb P50 lies within a narrow range around 27 mmHg (24–26), and the sensitivity of the estimated shunt and deadspace to variation in P50 given the measured alveolar-arterial differences was explored. Similarly, absent its direct measurement, cardiac output was estimated using a round-number formula (cardiac output = 5 × O₂ consumption + 5, with both O₂, consumption and cardiac output in l/min) that has been shown to closely describe how cardiac output varies linearly with O₂ consumption (27, 28) so that sensitivity to this variable could also be explored. The results will be presented later in this article using the data from one normal subject and two subjects with COVID-19.

The Determination of Mixed Alveolar Po₂ and Pco₂ Values from Exhaled Breath Profiles

As mentioned, the alveolar-arterial Po₂ and Pco₂ differences used in the present approach are not those derived from the standard alveolar gas equation, because the difference for CO₂ is explicitly assumed to be zero when that equation is used. Rather, the arterial values for each gas are compared with their mixed alveolar values. This raises the question of how to determine mixed alveolar values, averaged over the whole breath.

In 1952, Arthur DuBois and his coworkers addressed the issue of how alveolar Po₂ and Pco₂ varied throughout the respiratory cycle (29–32). They showed that alveolar Pco₂ fell and Po₂ rose during inspiration, and then reversed direction during expiration, as would be expected from tidal inspiration of air high in O₂ and low in CO₂. This led to the notion of an oscillating alveolar (and blood) Po₂ and Pco₂ about their means during steady state breathing. When sampling arterial blood, we ensure that the aspiration procedure is intentionally prolonged over at least 2–4 breaths so as to obtain a de facto mean arterial blood level for each gas. This in turn requires that if alveolar gas is to be compared with arterial blood in terms of both Po₂ and Pco₂, the best estimates of alveolar Po₂ and Pco₂ for this comparison would be their mean values averaged over the entire respiratory cycle.

There is an immediate practical problem with this logical conclusion: One can only observe alveolar gas during expiration, and even then, only after the anatomic deadspace gas has been washed out. During inspiration, sampling at the mouth records only inspired air. It would require a probe in the alveoli to record alveolar Po₂ and Pco₂ over the whole cycle. However, the observable portion of the alveolar gas (after anatomic deadspace washout during expiration) is well known to follow a straight, almost flat, trajectory in health (33, 34). Figure 4 portrays (green tracings) two exhalations, with an inhalation in between, for both O₂ and CO₂ from a normal subject to illustrate the issues. The first ∼100 mL of expirate is low in CO₂ and high in O₂, reflecting “anatomic deadspace” gas exhaled first from the conducting airways (i.e., gas at or near inspired levels), transitioning over the next ∼200 mL to the alveolar plateau, which is in this case a linear, slightly sloped line (up for CO₂, down for O₂) continuing until the end of the expiration. The slope in healthy subjects, such as that in Fig. 4, is due mostly to continuing gas exchange as CO₂ keeps moving from blood to gas as expiration continues, causing alveolar Pco₂ to rise. The opposite holds for O₂ being moved from alveolar gas into capillary blood, causing Po₂ to fall.

Figure 4.

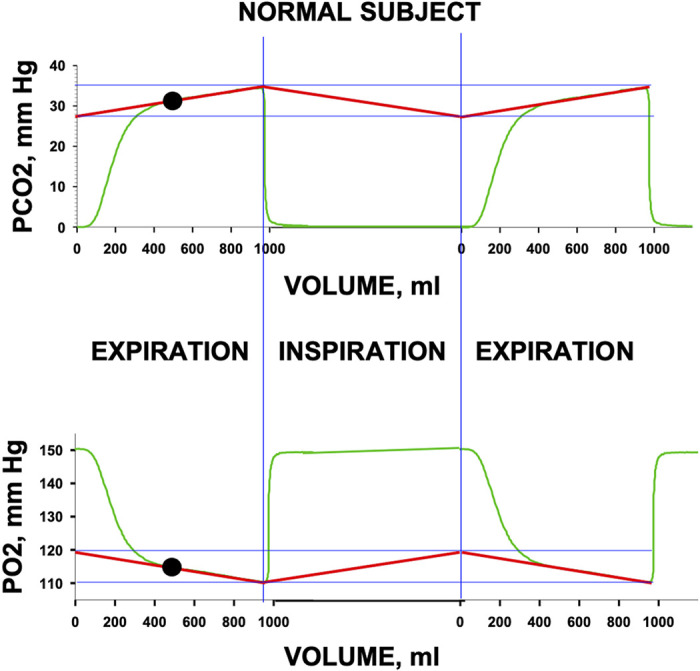
The figure shows an expiration (left), an inspiration (middle), and another expiration (right) for a normal subject (green tracings). For this conceptual example, the second expiration is a reproduction of the first. Tidal volume is a little less than 1,000 mL. Top panel shows Pco₂ and bottom panel shows Po₂. Vertical blue lines separate expirations from inspirations. The regression lines (red) for the alveolar plateau for each gas are linearly projected to the start of expiration and connected by the presumed linear return pathway for the inspiratory portion, highlighting the oscillation in alveolar gas levels between inspiration and expiration, marked by the horizontal blue lines drawn at the high and low points on the regression lines. The inspiratory segment shows inspired Po₂ and Pco₂. The expirations show initial exhalation of previously inspired conducting airway gas (first ∼100 mL), the transition toward alveolar gas (next ∼200 mL) and the linear, sloping, alveolar plateau (remainder of breath). The solid black circle indicates the mean alveolar Po₂ and Pco₂, which are the values at the midpoint of expiration.

The key observation is that the alveolar plateau is essentially linear over the entire post-deadspace washout portion. This allows the reasonable inference that in a steady state with constant tidal volume, breathing frequency, metabolic rate, and cardiac output, linearity in actual alveolar Po₂ and Pco₂ change would continue throughout the respiratory cycle, even though it cannot be seen at the mouth. This notion is illustrated in Fig. 4 where both the visible and invisible but presumed alveolar values are indicated by the straight red lines drawn as a tangent to the alveolar plateau for each gas. As long as the alveolar gas levels change linearly, the mean alveolar values are, by simple geometry, those values at the volume midpoint of the exhalation (solid black circles in Fig. 4). It is therefore proposed to use the alveolar Po₂ and Pco₂ at the midpoint of exhalation as the best estimate of the mixed alveolar values of Po₂ and Pco₂ averaged over the respiratory cycle. It is these values that would then be compared with the measured arterial Po₂ and Pco₂ values, so as to derive the alveolar-arterial differences to plot on the framework of Fig. 3B. Note that end-tidal Po₂ and Pco₂ values would be inappropriate for such a comparison because they provide the highest rather than the mean Pco₂ and lowest rather than the mean Po₂ throughout the respiratory cycle.

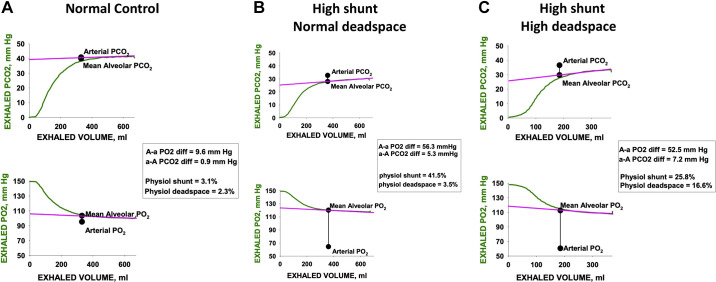
Figure 5 shows the application of this methodology for one normal subject (Fig. 5A) and two patients with COVID-19 (Fig. 5, B and C). These single, expired gas, tracings indicate proof of concept, showing an essentially linear alveolar plateau for both gases in each case, enabling estimation of the mean alveolar Po₂ and Pco₂. The three examples were drawn from a larger study of patients with COVID-19 and normal controls whose data were obtained by Swedish collaborators (Drs. Harbut and Hedenstierna) after obtaining IRB approval and written informed consent from the subjects.

Figure 5.

Expired gas tracings from three subjects (A: normal subject; B and C: two patients with COVID-19) analyzed by the proposed methodology. For both O₂ and CO₂, a single expiration is shown (green) with the least squares best-fit line to the latter portion of the exhalation (pink). Solid black circles indicate the measured arterial Po₂ and Pco₂ and mean alveolar Po₂ and Pco₂. Alveolar arterial differences, shunt, and deadspace are indicated on the figure for each subject. The normal subject has minimal shunt and deadspace whereas both patients with COVID-19 have substantial shunt. However, only patient (C) has a large alveolar deadspace in which the arterial-alveolar Pco₂ difference cannot be explained by the coexisting shunt.

Figure 5 raises the questions of sensitivity and specificity of the proposed approach. Sensitivity requires knowing the 95% upper confidence limit of normal for both physiological shunt and deadspace. Based on data from the multiple inert gas elimination technique used in subjects breathing ambient air (35), the 95% upper confidence limits for physiological shunt and physiological deadspace are 5% and 10%, respectively. The upper limit for shunt is less than for deadspace because of the flatness of the O₂-Hb dissociation curve in the normal range and because there is slightly more dispersion of ventilation than blood flow. Values above these limits are therefore highly unlikely to be false-positive results, whereas values below those limits are considered to be within the normal range. On the other hand, specificity requires an independent method for assessing the presence of pulmonary vascular obstruction causing high V̇a/$\dot{\text{Q}}$ regions, and in the current context, we are unaware of any adequate approach when the vascular lesions are likely many and small. This makes specificity unable to be addressed currently. That said, it is well established that areas of high V̇a/$\dot{\text{Q}}$ ratio interfere especially with CO₂ exchange, and so the inference of such regions from elevated arterial-alveolar Pco₂ values should not be in question.

As mentioned, West’s algorithm was executed using each patient’s own measured ancillary variables. Both Hb P50 and cardiac output however were not measured and were thus estimated. Hb P50 was assumed to be 26.8 mmHg, and cardiac output as 5 × O₂ consumption + 5 (27, 28) with both O₂ consumption and cardiac output in l/min. Because these variables had to be estimated, sensitivity of derived shunt and deadspace to variation in Hb P50 and to variation in cardiac output was determined.

Sensitivity analysis based on the three example cases shown in Fig. 5 was performed with varying cardiac output by ±25% from its assumed value and varying Hb P50 by ±2 mmHg. There was an insignificant sensitivity of deadspace to either condition. Shunt showed a small degree of sensitivity to Hb P50 that increased as shunt fraction increased. For example, the case in Fig. 5C showed a variation in shunt of 3 percentage points at the extremes of the Hb P50 range around a value of 26% shunt. Shunt estimates were affected more by uncertainty in cardiac output, but when shunt was modest, the uncertainty is small. Although there is evident sensitivity to cardiac output when shunt is large (e.g., Fig. 5C), even this was modest. In this case, there was a variation of approximately ±4 percentage points for a 25% change in cardiac output (i.e., when cardiac output was almost doubled from 6 to 10 L/min).

DISCUSSION

The purpose of this article has been to provide a firm theoretical foundation and practical method for the use of simultaneous measurements of Po₂ and Pco₂ in alveolar gas and arterial blood to estimate both the percentage shunt and the percentage deadspace using the framework of the 70-yr-old Riley and Cournand three-compartment model of pulmonary gas exchange. The new analyses point out how both shunt and deadspace affect both O₂ and CO₂ in their exchange, so that using O₂ measurements alone to define shunt and CO₂ measurements alone to define deadspace (as is common practice) is insufficient. Rather, the present analysis points out that O₂ and CO₂ measurements together are needed to simultaneously estimate shunt and deadspace. A further critical issue is recognizing that equating arterial and alveolar Pco₂, as is the norm when using the conventional alveolar gas equation, would completely undermine the proposed approach. This is because with either shunt or deadspace, the arterial-alveolar Pco₂ difference is significant and forms a key input to the analysis.

The drive to accomplish this methodology is not to analyze the lung physiologically. It is to answer the question of whether in patients with lung disease, especially COVID-19, their hypoxemia and arterial Pco₂ can be explained fully by shunt, or whether there must be additional gas exchange defects. In particular, is the deadspace determined by this approach in excess of that expected from shunt alone, or not? This is potentially clinically important, because deadspace in excess of that expected from shunt alone in spontaneously breathing patients suggests the presence of high V̇a/$\dot{\text{Q}}$ areas indicative of pulmonary vascular obstruction. Imaging and catheter-based approaches to determining small vessel obstruction are problematic in the context of clinical COVID-19.

The decision to use the respiratory gases O₂ and CO₂ rather than more comprehensive tools such as the multiple inert gas elimination technique (13) arose from the desire to develop a methodology that would both answer the fundamental question posed in the preceding paragraph and be feasible at the bedside, even in the patient with COVID-19. Measurement of arterial blood gas levels is clinically commonplace; measurement of exhaled gas concentrations requires the patient to provide no more than 10 breaths (over ∼30 s) under steady-state conditions, with collection of a single arterial blood sample during this time. During this period, continuous measurement of O₂ and CO₂ at the mouth provides for subsequent calculation of O₂ and CO₂ levels at mid-expiration (see Fig. 4) along with total alveolar ventilation, O2 consumption, and CO₂ production. Note that measurement of inhaled and exhaled O₂ and CO₂ at the mouth at high frequency (100 Hz) is done routinely in cardiopulmonary exercise testing (CPET). With the raw data, mean alveolar O₂ and CO₂ levels then are determined as the values of [O₂] and [CO₂] at the point halfway through exhalation.

There are assumptions and thus limitations to the proposed methodology. Since the derivation of shunt and deadspace from alveolar and arterial Po₂ and Pco₂ is based on steady-state relationships among these variables, it is important to ensure a steady state during data collection. We suggest (and use) a metronome to encourage a constant respiratory rate, and monitor constancy (±1 mmHg) of end-tidal Pco₂ as an indicator of an adequate steady state. It is important that tidal volume be sufficient in size to produce an alveolar plateau adequate in length for inscribing a least-squares best-fit line to its linear portion. A subject who cannot conform to these requirements will not be able to be studied by the proposed approach. We choose to include only patients who are not so ill that they cannot be safely studied while breathing ambient air for the ∼5–10 min required for making the measurements. In theory there is no barrier to using the approach at a higher $\text{F}{\text{I}}_{{\text{O}}_2}$, as did Karbing et al. in a related technique for assessing V̇a/$\dot{\text{Q}}$ inequality (21–23), but it should be recognized that as $\text{F}{\text{I}}_{{\text{O}}_2}$ is raised, areas of low V̇a/$\dot{\text{Q}}$ ratio that have an alveolar Po₂ close to mixed venous when $\text{F}{\text{I}}_{{\text{O}}_2}$ is 0.21 will develop a progressive increase in alveolar Po₂ as $\text{F}{\text{I}}_{{\text{O}}_2}$ is raised. This will render them invisible in the current approach despite their remaining poorly ventilated. It also increases experimental complexity because $\text{F}{\text{I}}_{{\text{O}}_2}$ needs to be known to employ the methodology. In addition, the method of Karbing employs sequentially different $\text{F}{\text{I}}_{{\text{O}}_2}$ levels, which could be difficult to implement in the acutely ill patient. We also choose to study patients who are spontaneously breathing. Although mechanically ventilated patients could be studied, in some ways more easily than those breathing spontaneously, it is well-known that mechanical ventilation itself can lead to regional overinflation and alveolar capillary compression, causing reduction in alveolar blood flow with increased functional alveolar deadspace. Thus, if the proposed approach in a ventilated patient shows a high alveolar deadspace, it would be difficult to know if that represents pulmonary vascular obstruction or only a functional outcome of the ventilatory strategy. However, even if the distinction cannot be made, it would still be a potentially useful parameter of the presence of high V̇a/$\dot{\text{Q}}$ ratio regions in the lung.

Another limitation is that the relationship between alveolar-arterial differences and shunt/deadspace is modulated by factors such as body temperature, [Hb], and acid-base status. However, these are routinely available from the blood gas sample (noting that body temperature is required for proper interpretation of arterial Po₂ and Pco₂) and are readily incorporated into the calculation of shunt and deadspace (via the algorithm of West that we use). Although cardiac output and Hb P50 are both not commonly measured (but can each affect the calculated shunt for a given pair of alveolar-arterial differences), they can be determined experimentally and relatively noninvasively from standard techniques. But even without their measurement, uncertainty in shunt is generally small and there is no discernible effect on deadspace.

In summary, we present a bedside approach applicable in health and pulmonary diseases such as COVID-19 and other acute (or chronic) respiratory illnesses that simultaneously samples exhaled gas and arterial blood over several breaths to determine the alveolar-arterial differences for both Po₂ and Pco₂. The methodology employs commonly available instrumentation for expired gas and arterial blood analysis. The Po₂ and Pco₂ differences are then used to determine shunt and deadspace, which reflect the extent of poorly ventilated (or unventilated) regions subject to alveolar filling and poorly perfused (or unperfused) regions subject to vascular obstruction.

DISCLOSURES

A. Malhotra has NIH funding outside the scope of this study. He also reports income related to medical education from LIvanova, Equillium, Corvus and Jazz. ResMed provided a philanthropic donation to UC San Diego. No conflicts of interest, financial or otherwise, are declared by the other authors.

AUTHOR CONTRIBUTIONS

P.D.W., A.M., and G.K.P. conceived and designed research; G.K.P. analyzed data; P.D.W., A.M., and G.K.P. interpreted results of experiments; P.D.W. and G.K.P. prepared figures; P.D.W. drafted manuscript; P.D.W., A.M., and G.K.P. edited and revised manuscript; P.D.W., A.M., and G.K.P. approved final version of manuscript.