Bayesian sequential data assimilation for COVID-19 forecasting

Abstract

We introduce a Bayesian sequential data assimilation and forecasting method for non-autonomous dynamical systems. We applied this method to the current COVID-19 pandemic. It is assumed that suitable transmission, epidemic and observation models are available and previously validated. The transmission and epidemic models are coded into a dynamical system. The observation model depends on the dynamical system state variables and parameters, and is cast as a likelihood function. The forecast is sequentially updated over a sliding window of epidemic records as new data becomes available. Prior distributions for the state variables at the new forecasting time are assembled using the dynamical system, calibrated for the previous forecast. Epidemic outbreaks are non-autonomous dynamical systems depending on human behavior, viral evolution and climate, among other factors, rendering it impossible to make reliable long-term epidemic forecasts. We show our forecasting method’s performance using a SEIR type model and COVID-19 data from several Mexican localities. Moreover, we derive further insights into the COVID-19 pandemic from our model predictions. The rationale of our approach is that sequential data assimilation is an adequate compromise between data fitting and dynamical system prediction.

1. Introduction

The current COVID-19 pandemic is a major challenge to the world population. Reliable model-based forecasts are required to assist healthcare authorities in decision-making and planning. Compartmental epidemic models have proven to be adequate to assimilate epidemic data and making forecasts (Asher, 2018, Bertozzi et al., 2020). However, epidemic dynamics is a non-autonomous dynamical system in which model parameters, e.g. contact rates, evolve in time. Indeed, epidemic outbreak predictability is limited due to the influence of human behavior, incomplete knowledge of the virus’s evolution, and weather (Castro et al., 2020, Wilke and Bergstrom, 2020), as well as delay and under-reporting of new cases and deaths (Krantz and Rao, 2020, Lau et al., 2021), and the size of the initial susceptible population.

For a non-autonomous dynamical system inference problem, we may introduce time-dependent parameters for the entire evolution and try to fit their values for all times (Capistran et al., 2021). However, the complexity of the resulting inference increases with the amount of data and may make the inference process infeasible. Moreover, fitting the whole of the epidemic to infer initial state values for an epidemic lasting several months ceases to be useful. For instance, in Capistran et al. (2021) only the contact rate varies with time, and the resulting Markov Chain Monte Carlo (MCMC) is cumbersome and challenging to run. In fact, given the generation interval of COVID-19, data beyond one month in the past should start to have less importance for nowcasting and predictions. A practical compromise is to make probabilistic epidemic forecasts a few weeks ahead in a moving window (Brooks et al., 2020, Engbert et al., 2021) and recalibrate regularly. Consequently, all model parameters evolve in time, and the inference problem splits into smaller ones. In this approach, the method should account explicitly for data delay and under-reporting.

In this paper, we introduce a Bayesian sequential data assimilation and forecasting method for non-autonomous dynamical systems. We applied this method to the current COVID-19 pandemic. We assume that transmission, epidemic, and observation models are properly postulated and previously validated. The transmission and epidemic models are coded into a dynamical system following the mathematical epidemiology theory (Hethcote, 2000, Van den Driessche and Watmough, 2002). In this case, we postulate a SEIR type epidemic model with Erlang (Champredon et al., 2018) residence times in the exposed and infected compartments to model non-exponential residence times. The observation model, cast as a likelihood function, depends on the dynamical system state variables and parameters (Held et al., 2019). We elicit prior distributions on the susceptible population size, the dynamical system initial conditions, and the infectious contact rates. With a MCMC we infer parameters and predict quantities of interest (QoI), such as hospital occupancy in a metropolitan area during the epidemic outbreak. The inference begins when the community transmission starts, and we infer parameters and predict QoI for a couple of weeks into the future. As new data becomes available, we update the forecast sequentially over a sliding window in time. New prior models are defined from the current parameters and state variables posterior distributions. New posterior distributions are computed within each new window beyond the available epidemic records to produce the forecasts. Moreover, we constrain changes in the contact rate and susceptible population size naturally through auto-regressive models on the corresponding parameters. We argue that this is a natural approach to data assimilation and forecasting with an epidemic. To sustain this claim, we show our forecasting method’s performance using a SEIR type model and COVID-19 data from several Mexican localities.

1.1. Related work

Real time epidemic forecasting is an emerging research field (Desai et al., 2019). Many forecast modeling efforts study how to address data under-reporting and delays (Gibson et al., 2020, Engbert et al., 2021). Other efforts are directed at exploring what sources of information can be incorporated as covariates to make better forecasts. McGough et al. (2017) incorporate traditional surveillance with social media data to forecast Zika in Latin America. The RAPIDD ebola forecasting challenge (Viboud et al., 2018) explored how to integrate different sources of data for Ebola forecasting. Hii et al. (2012) use temperature and rainfall to forecast dengue incidence.

In a related work, Capistran et al. (2021) present a COVID-19 prediction model. Using a SEIR type dynamical model, and including hospital dynamics and Erlang compartments (Champredon et al., 2018) to properly model residence times, Capistran et al. (2021) model and predict the COVID-19 epidemic in the Mexican 32 states and several metropolitan areas, from the epidemic onset in Mexico in March 2020 (and until February 2021, see Conacyt (2020a), in Spanish; model ama2).

1.2. Contributions and limitations

The probabilistic forecasting method introduced in this paper allows to reliably predict the incidence of new cases and deaths one to four weeks ahead of time. Once we are near or after a local incidence maximum, our forecasting method disentangles the role of infectious contact rate and effective population size. Other quantities of interest such as hospital occupancy can be calculated as a byproduct of the forecast using suitable renewal equations.

More general data analysis, e.g. by age groups, is not presented in this work. However, our results may be applicable on those cases, provided suitable transmission and epidemic models are available. The estimation of the time varying effective population size obtained in this paper has a large variance, provided we use a mean field equations to represent the underlying epidemics’ dynamics, which is a stochastic process on a network. Finally, it is not straightforward to compute the accumulated number of cases nor the accumulated number of deaths using our approach.

This manuscript is organized as follows. In Section 2 we make a summary of the modeling decisions taken to implement our forecasting method. In Section 3 we apply our method to COVID-19 epidemic data. Finally, in Section 4 we present the analysis of the Mexico City data. Other examples are provided in the Supplementary material (SM).

2. BayesIan sequential forecasting method

Let $L$ be the length in days of the period used to train our model to make a forecast. Let $D$ denote the delay in days taken by a laboratory to confirm an infection. Let us assume that community transmission starts at time $t=t_0-L-D$ at the metropolitan area where the outbreak is being analyzed. Set $k=0$ and denote by $[t_k-L-D,t_k-D]$ the learning period. Namely, the period when we collect epidemic records $z^{\left(k\right)}$ to create a forecast. In the example presented in Section 3, these epidemic records are new hospital admittances and deaths. The delay period is $[t_k-D,t_k]$, i.e. the period when epidemic records are not mature and may include delays in reporting. The forecasting day, from which forecasting starts, is $t_k$. We refer to $[t_k,t_k+F]$ as the forecasting period, and $[t_k-L-D,t_k+F]$ is the forecasting window as illustrated in Fig. 1.

Fig. 1.

Bayesian Sequential data assimilation. We propose a Bayesian filtering method that predicts along the dynamical system (1). The model is fitted with data in the training period and this is used to make predictions during the reporting delay period (nowcasting) and a forecasting period. The training window is updated and moved $n$ days forward, to update all forecasts and the former posterior becomes the prior, in the next window. Further details are described in Algorithm 1.

Let $x\left(t\right)={(S\left(t\right),E\left(t\right),I\left(t\right),\dots )}^T$ denote the time-dependent vector of state variables. We shall assume that the epidemic and transmission models are posed as an initial value problem for a nonlinear system of ordinary differential equations

$$\dot{x}\left(t\right)=f(x\left(t\right),{\theta }_k)$$$$x(t_k-L-D)=x_k,$$ (1)

where $t_k-L-D$ and $x_k$ denote respectively the initial time and state in the forecasting window $[t_k-L-D,t_k+F]$, and ${\theta }_k$ is a vector of model parameters (e.g. contact rate $\beta$, etc.) used to calibrate model (1). We shall denote $p^{\left(k\right)}=(x_k,{\theta }_k)$ the joint vector of initial conditions and model parameters to be inferred, and $x(t,p^{\left(k\right)})$ is the solution of problem (1) at time $t$ with parameters $p^{\left(k\right)}$. Note that, from the start, $p^{\left(k\right)}$ is assumed to be changing in time with each forecast window $k$.

If $k=0$, we postulate a prior distribution ${\pi }_{P^{\left(k\right)}}\left(p^{\left(k\right)}\right)$, a likelihood ${\pi }_{Z^{\left(k\right)}|P^{\left(k\right)}}\left(z^{\left(k\right)}\right|p^{\left(k\right)})$ and use Eq. (1) and samples obtained through Markov Chain Monte Carlo of the corresponding posterior distribution ${\pi }_{P^{\left(k\right)}|Z^{\left(k\right)}}\left(p^{\left(k\right)}\right|z^{\left(k\right)})$ to make a probabilistic prediction of $x\left(t\right)$ in the forecasting period $t\in [t_k-L-D,t_k+F]$. Afterwards, we update the forecasting window by setting $t_{k+1}=t_k+n$, where $n$ is the number of days until the next forecast (commonly, weekly updates $n=7$ are performed). We assemble a new prior distribution ${\pi }_{P^{(k+1)}}\left(p^{(k+1)}\right)$ for the model parameters $p^{k+1}$ in the new forecasting window $[t_{k+1}-L-D,t_{k+1}+F]$ using the predicted values of $x\left(t\right)$ at $t=t_{k+1}-L-D$ obtained with Eq. (1) and samples of the posterior distribution ${\pi }_{P^{\left(k\right)}|Z^{\left(k\right)}}\left(p^{\left(k\right)}\right|z^{\left(k\right)})$ of the previous forecast. Model parameters ${\theta }_{k+1}$ have an autoregressive prior distribution in terms of ${\theta }_k$. Finally, we set $k\leftarrow k+1$ and repeat the above process to create a new forecast. In passing, note that this fits correctly with the inherent sequential nature of Bayesian inference in which “today’s posterior is tomorrow’s prior” (D. Lindley, Lindley (1972), p. 2).

The Bayesian sequential data assimilation method consists of three parts , a dynamical system that codes the transmission and epidemiological models, a probabilistic model for the observed incident cases and deaths, and an informed prior distribution for the parameter space in each forecasting period. In Section 3, we show how to postulate each model component for a forecasting model of COVID-19 using data from several Mexico localities.

3. Example: A SEIR type model

3.1. Dynamical model

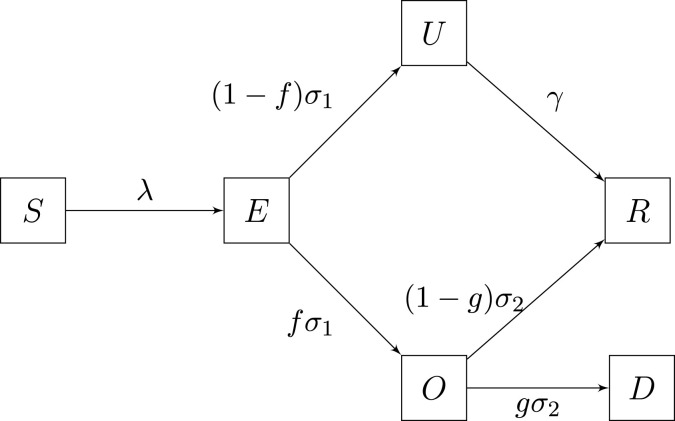
We consider a variation on the SEIRD epidemic model for susceptible, exposed, infectious, removed, and dead individuals. We have added a compartment for unobserved infectious individuals.

We assume that the total population of the metropolitan area being analyzed is $N$. We assume further that there is only a few infected individuals at the onset of community transmission. Susceptible individuals $S$ become exposed $E$ with force of infection $\lambda$. The transmission model is coded into $\lambda$ as follows. We assume that only unobserved ($U$) and observed ($O$) infectious individuals spread the infection, that is

$$\lambda =\frac{(U+\kappa O)\beta }{\omega \cdot N},$$

where $\beta$ is the infectious contact rate and the effective population size is $\omega =\frac{N-A}{N}$, where $N$ is the total population size and the number of isolated individuals $A$ comprises all individuals that due to their behavior have a negligible probability of encountering an infected individual. In $A$, we include individuals separated from infected ones due to their typical network of social contacts and all self-isolating individuals, regardless whether they were already infected or not. We have assumed that the contact rate for observed infectious is a factor ($\kappa$) of the contact rate for unobserved infectious. A fraction $f$ of exposed individuals proceeds to the observed infected class ($O$) at rate ${\sigma }_1$, while the remainder goes directly to an unobserved ineffective stage ($U$), also at rate ${\sigma }_1$. Individuals leave the infectious class at rate ${\sigma }_2$, with a fraction $1-g$ recovering and going to the removed class ($R$) and the remainder ($g$) dying of infection. Unobserved individuals go to the removed stage at rate $\gamma$. We split the $E$, $I$, and $O$ compartments into two sub-compartments to model residence rates explicitly as Erlang distributions (Champredon et al., 2018), see Table 1.

Table 1.

Average times and Erlang shape parameters for sub-compartments.

Variable	Rates	Average time	Erlang shape	Reference
$S$	$\beta$	Inferred	1
$E$	$1/{\sigma }_1$	5 days	2	Lauer et al., 2020, Jiang et al., 2020
$A$	$1/\gamma$	7 days	2	Long et al. (2020)
$I$	$1/{\sigma }_2$	14 days	2	Verity et al., 2020, Bi et al., 2020

The dynamics of the epidemic process is governed by the following nonlinear system of ordinary differential equations

$$\dot{S}=-\lambda S$$

$$\dot{E}=\lambda S-{\sigma }_{1}E$$

$$\dot{O}=f{\sigma }_{1}E-{\sigma }_{2}O$$

$$\dot{U}=(1-f){\sigma }_{1}E-\gamma U$$

$$\dot{R}=(1-g){\sigma }_{2}O+\gamma U$$

$$\dot{D}=g{\sigma }_{2}O,$$

with initial conditions $E\left(0\right)=E_0,O\left(0\right)=O_0,U\left(0\right)=U_0,R_0=R\left(0\right),D_0=D\left(0\right)$, and $S\left(0\right)=N-E_0-O_0-U_0-R_0-D_0$. Here $N=S+E+O+U+R+D$. A flow diagram for the model is shown in Fig. 2.

Fig. 2.

A SEIR type model that into account both observed and unobserved infections.

In general, the components of the epidemic and contagion models, from exposition time to clinical outcome, should be posed taking into account the distribution of the residence time in each compartment, see Flaxman et al. (2020) and its supplementary material. In this work, the contact rate ($\beta$) pertains to the time-varying reproduction number. On the other hand, the serial interval distribution, the symptoms to death distribution, and infection to symptoms distribution are judiciously set using hospital records and references, see Capistran et al. (2021) and Table 1. Finally, a proxy of the population-averaged infection fatality rate is represented through the product $f\cdot g$, where $f$ is set using records of the number of infected individuals seeking help at the hospital and $g$ is an estimated parameter that accounts for hospital fatality rate of COVID-19 patients. In this work, we infer a time-varying effective population size ($\omega$), which is the fraction of the total population having contact that may lead to contagion at a given time.

Despite its simplicity, this model captures the essential features of what we can learn from the available data (at least with Mexico’s records). Namely, the observed infected individuals and deaths. After the inference, we can use offline linear observation operators – based on renewal equations – at the appropriate compartments to extract more valuable and applicable information. We derived the linear observation operators approach from the equivalence between Erlang waiting times in renewal equations and Erlang boxes introduced in Champredon et al. (2018). We can apply this approach to any subset of compartments without nonlinear terms. In our case, after the first exposed individuals’ Erlang box. Therefore, the linear part of the system can be as complex as needed and treated separately from the inference procedure where only a minimal complexity is required. See the SM for an application on the hospital pressure estimates.

3.2. Model parameters

The model has two kinds of parameters that have to be calibrated or inferred, respectively. Namely, those related to COVID-19 disease (such as residence times and proportions of individuals that split at each bifurcation of the model) and those associated with the public response to mitigation measures such as the contact rate ($\beta$) and the proportion of effective population size during the outbreak ($\omega$). Some of these parameters can be found in recent literature (see Table 1) or inferred from reported cases and deaths, but some remain mostly unknown and not possible to infer from such data (Capistran et al., 2021). In the latter category, we have the fraction $1-f$ of unobserved infections. We assume $1-f=0.2$, which means that 80% of cases of symptomatic/asymptomatic infectious go unreported.

3.3. Observational model and data

The observed data used to fit the model is based on time series of incident confirmed cases and deaths. We consider daily deaths counts $d_i$ and its theoretical expectation that is estimated in terms of the dynamical model as

$${\mu }_D\left(t_i\right)=D\left(t_i\right)-D\left(t_{i-1}\right).$$

Analogously, we consider daily cases $c_i$ and its corresponding theoretical expectation ${\mu }_c\left(t_i\right)$ given by the daily flux entering the $O$ compartment (Capistran et al., 2021), namely

$${\mu }_c\left(t_i\right)={\int }_{t_{i-1}}^{t_i}f{\sigma }_1{E}_2\left(t\right)dt,$$

where $E_2\left(t\right)$ is the last state variable in the $E$ Erlang series. We calculate the above integral using a simple trapezoidal rule with 10 points.

3.4. Estimating model parameters with MCMC

We consider daily confirmed cases $c_i$ of patients with a positive test ($O$) and daily reported deaths $d_i$, for the area being analyzed. To account for over dispersed counts, we use a negative binomial (NB) distribution $NB(\mu ,\omega ,\theta )$ with mean $\mu$ and over dispersion parameters $\theta$ and $\omega$ (Capistran et al., 2021). For data $y_i$, we let

$$y_i\sim NB(p\mu \left(t_i\right),\omega ,\theta ),$$

with fixed values for the over dispersion parameters $\omega ,\theta$ and the reporting probability $p$. We assume conditional independence in the data and therefore from the NB model we obtain a likelihood.

The parameters to be inferred are the contact rate ($\beta$), the proportion of the effective population ($\omega$), the fraction of infected dying ($g$), and crucially we also infer the initial conditions for $E\left(0\right)$, $O\left(0\right)$, $U\left(0\right)$, $R\left(0\right)$, $D\left(0\right)$, letting $S\left(0\right)=\omega \cdot N-(E\left(0\right)+O\left(0\right)+U\left(0\right)+R\left(0\right))$. We have all initial conditions defined and the model can be solved numerically to obtain ${\mu }_D$ and ${\mu }_c$ to evaluate our likelihood. To sample from the posterior, we resort to MCMC using the t-walk generic sampler (Christen and Fox, 2010). The MCMC runs semi-automatic, with consistent performances in most data sets.

Table 2.

Parameters and prior distributions for the initial window used for Bayesian inference. These prior distributions are only used at the start and are not used in the rest of the sequential inference, where in each window, the prior is an over dispersed version of the posterior in the previous window (see Sub-Section 3.5). The prior for $\beta$ is a diffuse long-tail log normal centered at $\beta =1$. The prior for $g$ and $\omega$ are nearly uniform, also non-informative, but avoiding the unexpected a prior values of zero and one, Capistran et al. (2021).

Parameter	Prior distribution
Contact rate $\beta$	$log\left(\beta \right)\sim N(0,1)$
Fraction of infected dying ($g$)	$Beta(1+1/6,1+1/3)$
Proportion of the effective population ($\omega$)	$Beta(1+1/6,1+1/3)$

3.5. BayesIan filtering design

Regarding the elicitation of the parameters’ prior distribution for the first forecast, at $k=0$, we use Gamma distributions for the initial conditions $E_0$, $O_0$, and $U_0$, with scale $1$ and shape parameter $10$. This for modeling the low, near to $10$, and close to zero counts for the number of initial infectious conditions. For the initial conditions $R_0$ and $D_0$, we also use Gamma distributions with scale and shape parameters equal to $1$. This because at the beginning of the outbreak, both parameters are close to zero. The prior distributions for the remaining parameters are summarized in Table 2. Note that, the above prior distributions are only used at the first learning window. From $k=1$ onwards, the MCMC posterior sample from window $k$ is used to create a prior for window $k+1$, as previously mentioned and explained in Algorithm 1.

Regarding how the MCMC posterior sample is used to create a prior, we proceed as follows. For each parameter, the MCMC sample mean is used to match the mean of a Gamma distribution, with over dispersion, making the standard deviation of the Gamma prior equal to 0.9 of the mean. This allows for reduced dependence on the previous period, permitting more learning in the current window. Matching all moments will signify that a single parameter (e.g. $\omega$) is assumed in all windows, nonetheless a time dependent scheme was envisaged from the onset. We found this scheme to be a reasonable compromise between utilizing the previous window information and learning from the current. We tested other options for this updating scheme. We tested using a kernel density estimation for the posterior sample of each parameter to be used as a prior. This resulted into reduced variance, since this implies independence and equal weight of past data. Another choice tested was to match any positive density, as a Beta, Log-Normal or Gamma. Over dispersion needs to be introduced, to down weight the past data information into the future. The pragmatic choice we took was the over dispersed Gamma moment fit as explained.

Setting the lengths $L$, $D$ and $F$ of the learning, delay and forecasting periods should be also an evidence-based modeler decision. In the example presented in this paper, we set $L$ to twice the length from symptoms onset to mild disease clinical outcome, namely 28 days. The length of the delay period is set to 11 days, corresponding to roughly the mean of the delay in Mexican clinical laboratory reports. Finally, $F$ is chosen to be 1,2,3 and 4 weeks.

4. Results

In this section, we present the results of Algorithm 1 applied to the COVID-19 pandemic for Mexico’s city metropolitan area. We solve the initial value problem for the dynamical system using the function scipy.integrate.odeint of Python. The convergence of the MCMC is presented in the SM for some forecasting cones. We provide further examples of other Mexican states in the SM. The method is applied to the daily reports on the incident number of confirmed cases and deaths starting in early 2020.

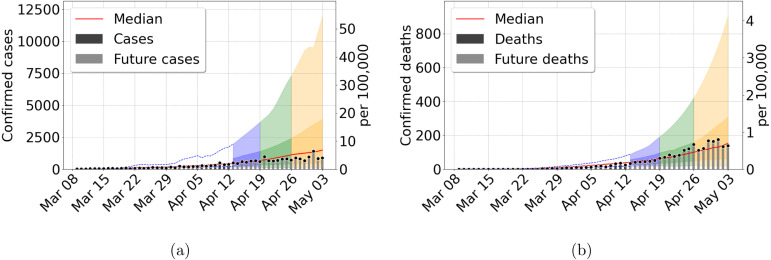
We use the Bayesian Sequential Forecasting Method to predict trajectories, given weekly updates. The model starts with inaccurately predicted trajectories, where the median of the trajectories overestimate the future data (See Fig. 3), and the initial prediction cones are rather wide. Early forecast uncertainty is high because we do not know yet the effective population size participating in the epidemic, namely $\omega$ in our model. Furthermore, forecasts at this stage are prone to additional errors due to the uncertainty in disease parameters such as the transmission rate $\beta$ and the initial state of the epidemic outbreak.

Fig. 3.

Forecast results for Mexico city metropolitan area, using data from March 8 to April 12, 2020. (a) Confirmed cases (b) Confirmed deaths. Central red lines indicate the median incidence forecast. The darker shaded region indicates the interquartile forecast range, and the lighter shaded region indicates the 5–95th percentile range. The colors blue, green, and orange represent the forecast 1, 2, and 3 weeks ahead, respectively. Total population 21,942,666 inhabitants. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

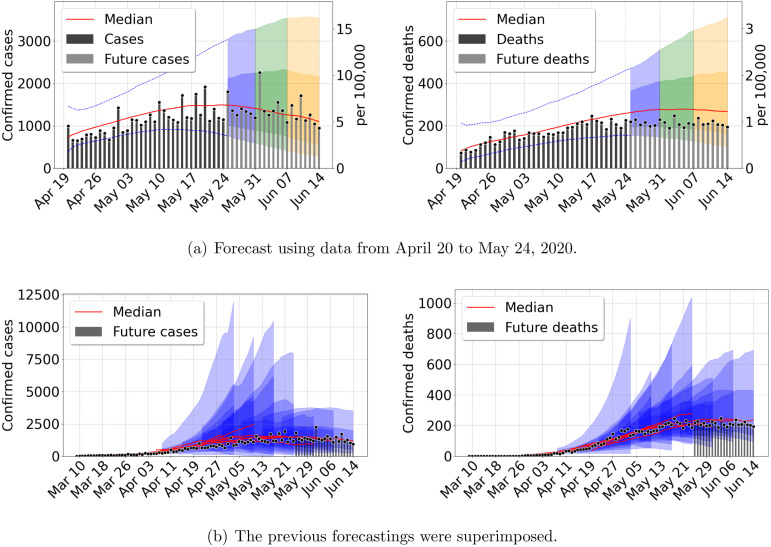
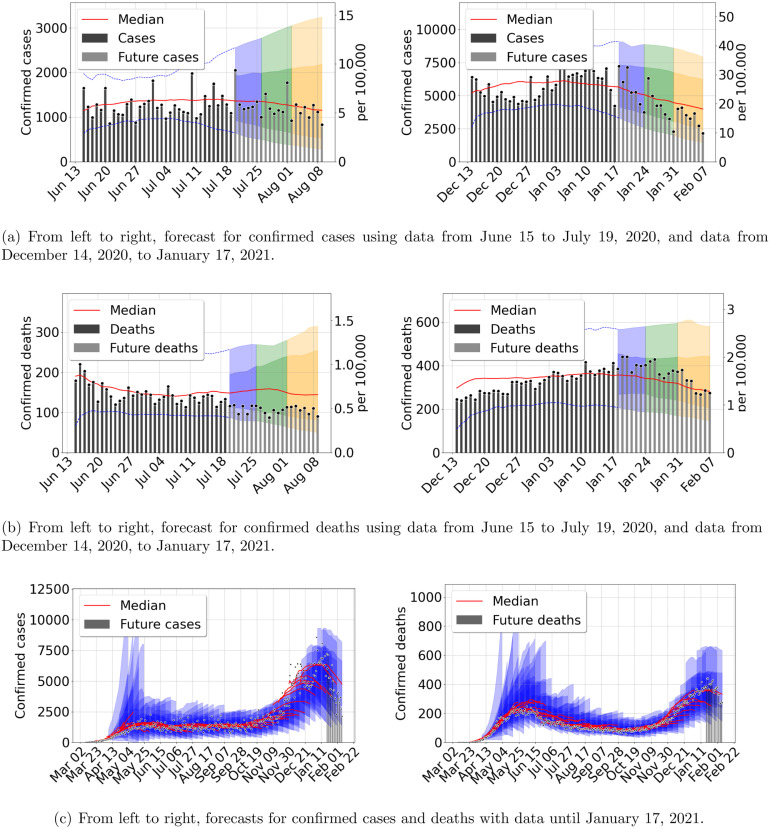
As we combine previous information with new incoming data into the next predictions, accuracy increases quickly. The median of the forecast becomes closer to future data, and the prediction cone uncertainty shrinks. In Fig. 3 we presented the early stages of the epidemic outbreak, and in Fig. 4, Fig. 5 we present three later times. First, after the initial outbreak wave peak, second during late summer, where the outbreak was decreasing slowly, and third in the middle of a second intense wave in December. The results show rather uniform prediction cones during the entire evolution, increasing cone size at the onset of the second outbreak wave. Despite the larger intensity of the second wave, the prediction cones never become as large as at the early stages. We can explain this behavior by looking at the other model parameter included in our inference process.

Fig. 4.

Outbreak analysis for Mexico City metropolitan area. From left to right, confirmed cases and deaths. Central red lines indicate the median incidence forecast. The darker shaded region indicates the interquartile forecast range, and the lighter shaded region indicates the 5–95th percentile range. All displayed forecast durations are 21 days from the point of prediction. We stress that nowcasting is very accurate throughout examples presented here and in the SM. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

Outbreak analysis for Mexico City metropolitan area. From left to right, confirmed cases and deaths. Central red lines indicate the median incidence forecast. The darker shaded region indicates the interquantile forecast range, and the lighter shaded region indicates the 5–95th percentile range. All displayed forecast duration are 20 days from the point of prediction. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

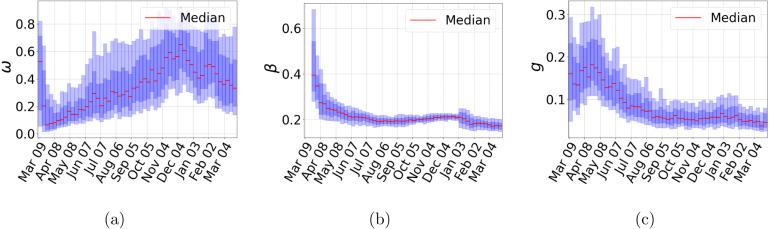
In Fig. 6, we present the weekly estimates of the infection contact rate $\beta$, the effective population size (or available pool of susceptible individuals) $\omega$, and the hospital fatality rate $g$. The figure shows that after an initial period where the estimates of $\beta$ have considerable uncertainty, its median value becomes relatively stable around 0.2. At the second wave, we observe an increase in uncertainty, but $\beta$’s mean value remains almost constant with a slight decrease afterward. Regarding $g$, we also observe an initial uncertainty period, but its mean value is relatively stable, and its uncertainty becomes smaller. Finally, the effective population size behavior is somewhat different since $\omega$ is a proxy of the complex network of people’s contacts in a metropolitan area. Its estimates show a significant uncertainty for almost all times. We observe the minimum value of $\omega$ in the early months of the pandemic with a slow increase afterward and another peak during the second wave. After the initial period, our inference method “learned” reasonable parameter values for $\beta$ and $g$, and we can trace back most changes in our prediction cones to $\omega$. These observations explain the difference between the prediction cones between the first and second waves. In the SM, we present our estimates for all 32 Mexican states where almost all the above analysis apply.

Fig. 6.

Outbreak analysis for Mexico City metropolitan area. (a) Proportion of the effective population ($\omega$), (b) contact rate ($\beta$), and (c) fraction observed infected individuals dying ($g$). Central red lines indicate median incidence forecast. Darker shaded region indicates forecast interquartile range, and lighter shaded region indicates 5–95th percentile range. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.1. Model parameters, mobility index and mask usage

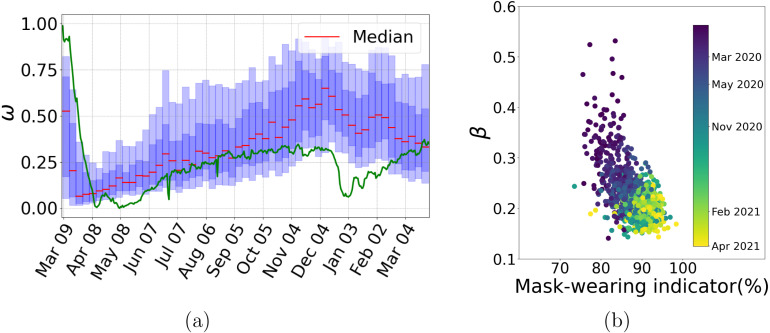
Changes in $\omega$ are an accurate proxy of the population’s response to mobility lockdown and release measures. To support our claim, we include in Fig. 6 the plot of a mobility index derived from social media tracking, see Graff et al. (2021) and the associate website (Conacyt, 2020b) (In Spanish). The correlation between both quantities is unmistakable.

Mask-wearing is widely accepted as a primary measure to prevent contagion. In our model, changes in this behavior should be reflected in the transmission rate $\beta$. In Fig. 7, we compare mask-wearing indicator practices with the transmission rate $\beta$ for all states over time. The mask-wearing practices indicator is part of the University of Maryland Social Data Science Center Global COVID-19 Trends and Impact Survey in partnership with Facebook (UMD Global CTIS) (Social data science center, 2020) and measures the percentage of respondents who report wearing a mask almost all of the time in the past five days. The UMD Global CTIS survey data for the Mexican States and the country starts in May 2020. The color code in Fig. 7 represents the time evolution; we conclude that mask-wearing practices were accepted early in the pandemic and have been maintained relatively constant afterward. The correlation between $\beta$ and the mask-wearing indicator is also evident from the figure.

Fig. 7.

In panel (a), we present a plot of the predicted effective population proportion ($\omega$) together with the social media-based unique mobility index (green line). Correlation between changes in both quantities is evident. Panel (b), we plot weekly estimated contact rates ($\beta$) for all 32 states against the UMD Global CTIS mask-wearing index (Social data science center, 2020) for available data. Color code represents time evolution starting in May 2020. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.2. Forecast performance

This paper presents the probabilistic one to four-week ahead forecasts of the total number of confirmed cases and deaths due to COVID-19 from early-mid March 2020 to February 2021 for all Mexican states. In our forecasting algorithm, we take into account reporting delays of 11 days in the past. Therefore, the earliest forecasts are, in fact, nowcasting (“predictions of the past present”). This becomes important to sense the most recent infection trends and could be a deciding factor in managing social distancing policies.

We evaluated our forecast performance using prediction interval coverage for two metrics; the 25% to 75% and the 10% to 90% interquantile. We call them the 50%, or interquartile and 80% forecast cones, respectively. The prediction interval coverage is calculated by counting the frequency with which the prediction interval contains the eventually observed outcome. In a model that accurately characterizes uncertainty, the prediction interval level will correspond closely to the frequency of eventually observed outcomes that fall within that prediction interval. For example, finally, observed values should be within the interquartile prediction interval approximately 50% of the time.

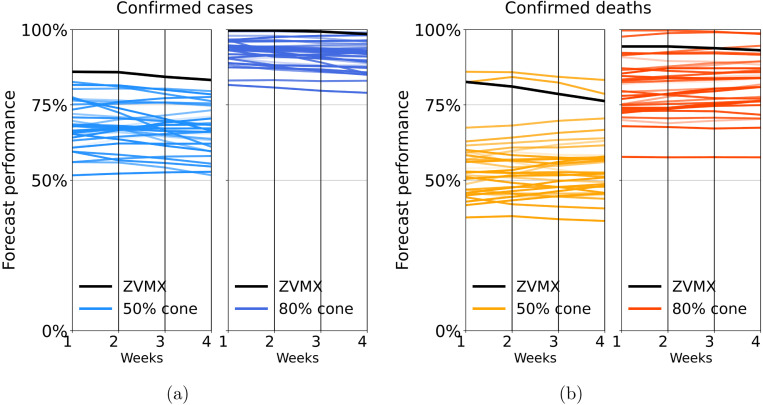
In Fig. 8 we shows a slope-graph of the weekly performance average of the one to four-week forecasts measured for the 50% and 80% cones metrics. In this figure, we included the performance measured for all 32 states as a comparison. The performance measure shows variability among the different states (see also Figures S14 to S17 in SM), but in every case, the performance is above 50 and 40 percent for confirmed cases and deaths, respectively. Therefore, we are confident to say that our model characterizes uncertainty accurately in all cases.

Fig. 8.

We present a slope-graph of the average weekly forecast performance for all 32 states in Mexico. Panel (a) and panel (b) correspond to confirmed cases and confirmed deaths, respectively. Each line connects a state’s average performance for 1 to 4 weeks forecast. Darker and lighter colors correspond to the performance measured for the 50% and 80% prediction cones, respectively. We also include ZVMX performance in black color. In all cases, the forecast’s performance decreases slightly with the prediction length. The 50% cone has a performance value between 50 and 80 percent, and the 80% cone has a corresponding value between 80% and 100% for confirmed cases. In the case of deaths, the 50% and 80% cones have performance values between 40% and 60% and between 60% and 100%, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the SM we present the result of our weekly analysis of the 1–4 week forecast performance for all Mexican states and Mexico City metropolitan area (ZVMX).

5. Discussion and conclusions

The current COVID19 pandemic has posed significant challenges in scientific research. In mathematics, forecasting and modeling an ongoing epidemic outbreak is a major problem. Although some general modeling methods are available, such as Bayesian inference and data assimilation schemes, thought-out modeling decisions are needed for specific cases. Clear-cut methodologies in the modeling processes remain unclear. Identification of general principles and modeling strategies will improve our forecasting capabilities.

In many studies (Capistran et al., 2021, Asher, 2018, Bertozzi et al., 2020), inference schemes assume constant model parameters, failing to recognize the non-autonomous nature of the prolonged COVID19 pandemic outbreak. Public behavior, such as mask-wearing, changes model transmission parameters, while lockdown measures shift the pool of susceptible individuals. Moreover, the case and hospital fatality rates also depend on the health workers’ learning curve to treat the disease. In addition, long-time series epidemiological records pose a hard inference problem. Some authors (e.g., Capistran et al. (2021)) address this issue using models with more parameters and complex dynamical systems structures that try to capture the changing landscape. Other studies (Gibson et al., 2020, Ray et al., 2020) considering time-dependent parameters lack a well-designed moving-in-time data assimilation scheme that balances long and short-term information usage.

Our first contribution is a general Bayesian sequential data assimilation method that effectively captures parameter’s time evolution, achieving an information balance between the outbreak’s entire history and its latest short-term behavior. Our prediction scheme updates and continuously refine model parameters (such as $\beta$ and $\omega$) as information about new cases is incorporated in a sliding time window. Simulations are then computed beyond the available epidemic records within each sliding window to produce forecasts.

The second contribution in this paper is to recognize that a simplified SEIRD model is enough to capture the actual inference problem with the available data. Namely, the observed infected individuals and deaths. After the inference, we can use offline linear observation operators – based on renewal equations – at the appropriate compartments to extract information from a more complex model featuring additional compartments. Note that the latter is a record-keeping and counting problem, as long as the extra compartments in the complex model remain linear, as is the case in many SEIRD type models. Model complexity must depend on the original questions and modeling goals. We maintain that our model strategy poses a sensible alternative to an approach where complex systems are considered and multiple parameters must be tuned, making the inference problem harder due to a possible lack of parameter identifiability or ambiguous interpretation.

Meaningful insights into the recent COVID19 epidemic outbreak also rose from the proposed modeling strategy. In SEIRD type models, there exists a confounding effect between susceptible individuals’ pool and the infections contact rate (Capistran et al., 2021). Our model disentangles these parameters after the first wave’s exponential growth periods. The balance of long and short-term information usage implies that part of these parameters are “learned” at first waves, and our method produces more accurate estimates in later second waves. The evidence we have gathered for more than 32 states in Mexico, included in the SM, shows a clear difference between the time-dependent behavior of the infection contact rate $\beta$ and the susceptible pool represented by $\omega$. The correlations between $\omega$ and the social media mobility index support our interpretation of $\omega$ as a proxy to people’s response to mobility restrictions such as lockdown and lockdown-release measures. As a mobility proxy, we notice that $\omega$ represents the complex network of people’s contacts in a metropolitan area with a single number. Hence, significant uncertainty in $\omega$ and the forecast is expected. Nevertheless, we have shown that the forecasting performance is acceptable and almost constant up to four weeks into the future.

The relatively constant value of $\beta$ in all cases implies that this quantity does not depend on people’s mobility. Our results also show a clear correlation between our estimates on $\beta$ and the UMD Global CTIS’s mask-wearing index. This correlation is consistent with the interpretation of $\beta$ in the proposed model and the impact of behavioral practices to prevent contagion. The relationship between mask-wearing practices and model’s transmission rate is not in question, but deriving its quantitative relationship is challenging. Our results may be helpful to calibrate models that have mask-wearing as an adjustable parameter but should be used carefully. Other personal hygiene measures and social distancing practices also imply changes in the model’s transmission rate $\beta$. A more comprehensive study beyond the present paper’s scope is needed to address this question. Nevertheless, our results show that the Mexicán population adopted these hygiene and social distancing practices early in the pandemic and has maintained them relatively constant afterward. Finally, the hospital fatality rate $g$ (the proportion of COVID19 in-patients that eventually die) is also inferred as part of the model. Note that observed cases and deaths come from a biased sample due to Mexico’s testing policy. Thus, our estimate of $g$ is also biased concerning the whole outbreak (observe and unobserved infection). Interestingly, its value shown a steady decline in some states after February 2021. These declines are consistent with the start of local vaccination campaigns on the elderly population.

A reliable stream of information is essential in a forecasting algorithm like the one presented here, and well-defined epidemiological data records are necessary for reliable inferences. In Mexico, the federal testing policy has been consistent throughout the pandemic. Starting on April 2020, only positive tests at hospital admissions are reported (Dirección General de Epidemiología, 2020), while open population tests belong to separate records. Therefore, the data used in the model has a constant and consistent bias, as can be observed from the almost constant in-time positivity test rate (see Figure S1 in SM). Applying the present model to other countries and cities would require a careful analysis of the corresponding testing policies that may affect forecast and inferred parameters due to non-constant in-time biases.

Our well-designed Bayesian data assimilation scheme for nonlinear dynamical systems such as the epidemiological model presented in the current paper produces reliable forecasts. Key to our approach is the balance between the short and long-term information usage, and its application to a simplified dynamical model that completely defines the inference problem. Beyond epidemiology, the introduced principles and methods apply to other non-autonomous dynamical systems models. The present study is a step towards a more comprehensive understanding of mathematical forecasting methods.

Data reporting

The databases necessary for the estimation of parameters and the codes implemented for the study are available in the github repository (Daza-Torres et al., 2021). Analyses were carried out using Python version 3.

Data sources

Daily COVID-19 confirmed cases and deaths for all Mexican states and Mexico City’s metropolitan area. All data are publicly available at Covid-19 México (2020), and therefore did not require ethical approval of an institutional review board nor written informed consent. All analyses were conducted with data updated to January, 2021.

CRediT authorship contribution statement

Maria L. Daza-Torres: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Visualization. Marcos A. Capistrán: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Writing – review & editing, Visualization, Supervision, Funding acquisition. Antonio Capella: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Writing – review & editing, Visualization, Supervision, Funding acquisition. J. Andrés Christen: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Writing – review & editing, Supervision, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

The supplementary material contains forecast results for all Mexican states and Mexico City’s metropolitan area and a section dedicated to linear observations operators.