Prediction of Bleb Formation in Intracranial Aneurysms using Machine Learning Models Based on Aneurysm Hemodynamics, Geometry, Location, and Patient Population

Abstract

Background:

Bleb presence in intracranial aneurysms (IAs) is a known indication of instability and vulnerability. Our objective was to develop and evaluate predictive models of bleb development in IAs based on hemodynamics, geometry, anatomical location, and patient population.

Methods:

Cross-sectional data (one time-point) of 2395 IAs was used for training bleb formation models using machine learning (random forest, support vector machine, logistic regression, k-nearest neighbor, and bagging). Aneurysm hemodynamics and geometry were characterized using image-based computational fluid dynamics. A separate dataset with 266 aneurysms was used for model evaluation. Model performance was quantified by the area under the receiving operating characteristic (AUC), true positive rate (TPR), false positive rate (FPR), precision, and balanced accuracy.

Results:

The final model retained 18 variables including hemodynamic, geometrical, location, multiplicity, and morphology parameters, and patient population. Generally, strong and concentrated inflow jets, high speed, complex and unstable flow patterns, and concentrated, oscillatory, and heterogeneous wall shear stress patterns as along with larger, more elongated, and more distorted shapes were associated with bleb formation. The best performance on the validation set was achieved by the random forest model (AUC=0.82, TPR=91%, FPR=36%, misclassification error=27%).

Conclusions:

Based on the premise that aneurysm characteristics prior to bleb formation resemble those derived from vascular reconstructions with their blebs virtually removed, ML models are capable of identifying aneurysms prone to bleb development with good accuracy. Pending further validation with longitudinal data, these models may prove valuable for assessing the IAs propensity of progressing to vulnerable states and potentially rupturing.

Introduction

Blebs or secondary outpouchings have been identified as an important risk factor for intracranial aneurysm (IA) rupture.^1–3 They are thought to be the result of focalized damage and remodeling of the aneurysm wall and are indicative of wall instability.^3,4 Approximately 30-35% of aneurysms harbor one or more blebs.⁵ As such, identifying aneurysms that at the time of evaluation are prone to developing blebs is important for early assessment of the future instability of the aneurysm, which could, in turn, predispose the aneurysm for rupture.

Previous studies have found associations between the presence of blebs in IAs and patient characteristics.⁵ Additionally, significant differences in hemodynamic and geometric characteristics of aneurysms that developed blebs and aneurysms without blebs have been reported.⁶ Presumably, these distinguishing characteristics could be used to discriminate between aneurysms prone to develop blebs and those not likely to develop blebs. Recently, artificial intelligence and machine learning (ML) techniques have seen tremendous advances and have been widely applied in diverse fields. In particular, several prediction models based on ML techniques have been developed to predict the risk of aneurysm development,^7,8 rupture risk of aneurysms,^9,10 and prognosis of aneurysm after flow diverter implantation.¹¹

Thus, the purpose of this work was to develop and evaluate predictive models of bleb development in intracranial aneurysms using the aneurysm features mentioned above to train machine learning algorithms. The current study is based on the hypothesis that bleb development is faster than typical aneurysm growth, and therefore it is reasonable to approximate the shapes of aneurysms prior to bleb formation by virtually deleting blebs from 3D vascular reconstructions. Further discussion and support for this hypothesis can be found in the Supplementary material accompanying Suppl. Fig. 1.

Methods

Strategy

The study was carried out in three steps: 1) identify the distinguishing characteristics between aneurysms with blebs (prior to bleb formation) and aneurysms without blebs, 2) construct predictive models of bleb development using machine learning techniques, and 3) validate the ML model predictions on a separate dataset. To accomplish these goals, two independent datasets were used. The first dataset was used for identifying differences between aneurysms with and without blebs and to train ML models. The second dataset was used to validate the predictions of these models and characterize their predictive power. Protocols for consent, data handling, and analysis were approved by the institutional review boards at the University of Pittsburg and George Mason University.

Datasets

A total of 2395 aneurysms in 1614 patients were used for ML model development (training set). These aneurysms correspond to patients referred for diagnostic angiography and imaged with 3D rotational angiography (3DRA) or computer tomographic angiography (CTA). This set contains data from different populations, including the United States (US), South America (SA), Europe (EU, other than Finland), Finland (FIN), and Japan (JAP). The second dataset (validation set) contained 266 aneurysms in 195 patients selected for surgical clipping and imaged with 3DRA or CTA prior to surgery. This set includes data from the US and FIN populations. For this study, deidentified vascular geometries and patient demographic information were obtained from our database. More details about these datasets are provided in Suppl. Table 1. Supplementary Table 2 lists the number of aneurysms in the testing set with and without blebs imaged with 3DRA and CTA, respectively. The p-value of the Fisher’s test provided (p=1.0) indicating that the presence of blebs is independent of the imaging modality. This supports the combination of both modalities since it implies that associations between hemodynamic and geometric parameters and bleb presence are not affected by the imaging modality.

Aneurysm Characterization

Patient-specific 3D vascular models were constructed for all aneurysms in the training and testing sets from the available 3DRA or CTA images as previously described.¹² Blebs were then identified (see Suppl. Fig. 2) by visual inspection of the vascular reconstruction, volume-rendered 3D images, and surface Gaussian curvature maps (a measure of the local bending of the aneurysm surface). In these curvature maps, the blebs generally appear as red regions of positive curvature surrounded by a blue ring of negative curvature.⁵ Blebs were then interactively marked (painted) on the vascular reconstructions using a previously developed tool (ChePen3D).¹⁴ Once blebs were identified, in order to approximate the aneurysm characteristics prior to bleb development, the marked blebs were automatically removed and the surface locally retriangulated as previously described (see Suppl. Fig. 3).⁶

Computational fluid dynamics (CFD) simulations were carried out to characterize the aneurysm hemodynamic environment. As in previous studies,^13,14 blood was modeled as a Newtonian incompressible fluid with a density of 1.0 g/cm³ and viscosity of 0.04 Poise, and the unsteady Navier-Stokes equations were numerically solved using finite elements. Vascular walls were approximated as rigid. Pulsatile inflow conditions were imposed by scaling a representative flow waveform with an empirical law relating flow rate and cross-sectional vessel area in internal carotid and vertebral arteries. Outflow conditions were imposed by dividing flows consistent with Murray’s law. No-slip boundary conditions were imposed at the walls and wall compliance was neglected. Simulations were computed for two cardiac cycles with a heart-beat rate of 60 beats per minute using 100 time-steps per cardiac cycle, and data from the second cycle was used to characterize the flow conditions in the aneurysm.

The aneurysm hemodynamics and geometry were characterized by computing 15 flow variables and 10 geometric parameters defined on the aneurysm region.^15,16 The aneurysm anatomical characteristics (location, morphology, and multiplicity) and patient demographics (population, sex, and age) were described by 6 additional categorical variables (numerical in the case of age).

Post-Processing and Dimensionality Reduction

Aneurysm characteristics associated with the presence of blebs were identified by performing contingency table analysis and Pearson’s Chi-squared test for categorical variables. For continuous variables, tests for differences in the median of the two groups defined by the bleb presence were performed using the two-sample unpaired Wilcoxon (Mann-Whitney) test. All statistical analysis and ML modeling were performed in R. The p-values were adjusted for multiple testing using the Bonferroni method available in R, and associations were considered significant if p<0.05 after adjustment.

To improve model interpretability and performance, the variable reduction was performed to detect and remove variables that were redundant or irrelevant before training the model. The correlation matrix of the predictor variables was analyzed to remove highly correlated variables (i.e. with an absolute correlation of 0.75 or higher). Among pairs of variables with correlation > 0.75, the variable that exhibited the strongest association with bleb status as measured by the p-value of the univariate association was retained. Moreover, variables were ranked according to their variance inflation factor (VIF), in decreasing magnitude, and multicollinear variables with VIF of 10 or higher were removed in a recursive fashion, one at a time, and then the VIF was re-evaluated, to prevent redundancy between predictor variables and to obtain more accurate and easier to interpret variable importance rankings.

Construction of Predictive Models of Bleb Development

Several ML methods for supervised binary classification were used to have a good representation of algorithm types (linear, non-linear, trees, etc.) and to identify the best predictive approach. This includes logistic regression (LR), support vector machine (SVM), K – nearest neighbor (KNN), random forest (RF), and bagging or bootstrap aggregating (BG). These ML models were trained with data of all 2395 aneurysms of the training set.

The columns of the feature matrix of the continuous predictor variables were standardized so that the attributes would have a mean value of 0 and a standard deviation of 1. Categorical variables were encoded as dummy variables. One hundred repetitions of ten-fold (internal) cross-validation, yielding 100 random partitions of the original training sample were used to train the models, estimate the tuning parameters, and identify the important predictor variables. In this step, the data were split into training and testing sub-sets for each of the ten folds, and the optimal value of each tuning parameter related to the training process was determined via a grid search to achieve the largest area under the curve (AUC) of the receiver operating characteristic (ROC). The 100 results were combined (averaged) to produce a single estimation.

Feature Selection

In order to identify features to be used to predict the bleb presence in aneurysms, the recursive feature elimination (RFE)¹⁷ technique was performed. Briefly, an initial model was built based on the entire set of predictors and an importance score was computed for each predictor. Then, the least important predictor(s) were removed. The optimal subset of features was then used to train the final model.

Since only about one-third of aneurysms harbor blebs, the datasets are inherently unbalanced, which can negatively impact the model fitting and performance. Therefore, during the internal cross-validation of the model training process a down-sampling approach was used, where data from the majority class (aneurysms without blebs) were randomly removed to achieve a balanced class distribution and thus mitigate this issue.

Model Evaluation and Validation

First, the performance of the different ML models of bleb development was evaluated internally (i.e. on the same training dataset) and compared. For this purpose, the AUC of the ROC, the true positive rate (TPR), the false positive rate (FPR), and the misclassification error were calculated. 95% confidence intervals of the AUC were estimated based on 2000 bootstrap repetitions. Pairwise comparisons of these performance metrics between ML models were carried out using the built-in summary function of the CARET package available in R (based on one-sample t-test) to determine if the differences in performance of the various models were statistically significant, and thus allows us to identify the model with the best predictive power.

Secondly, the predictive ML models were externally validated on the independent validation dataset containing data from 266 aneurysms, which was not used during training, parameter tuning, and model selection. In addition to the AUC, the accuracy of the model was assessed in terms of true positive rate (TPR or recall), false positive rate (FPR), positive predictive value (PPV or precision), NPV (negative predictive value), F1 score (harmonic mean of precision and recall), and balanced accuracy.

Results

Aneurysm Characteristics Associated with Bleb Development

A total of 1131 blebs were identified in 735 (31%) aneurysms in 603 patients of the 2395 aneurysms in the training dataset. The remaining 1660 (69%) aneurysms in 1011 patients were classified as having no blebs.

Statistical comparisons between patient and aneurysm characteristics between aneurysms with and without blebs are presented in Table 1. No significant associations were observed between bleb presence and patient sex (p=1) and age (p=1). The presence of blebs was significantly associated with aneurysm rupture status (p<0.01), as well as aneurysm multiplicity (p<0.01), morphology (p<0.01), and location (p<0.01), and patient population (p<0.01).

Table 1:

Patient and aneurysm characteristics associated with blebs.

Characteristics	Values	Aneurysms with blebs	Aneurysms without blebs	p-value	Adjusted p-value
Patient characteristics
Age	Mean ± SD	56.7 ± 13.8 y	57.2 ± 14.2 y	0.50	1
Sex	Female	364 (35%)	673 (65%)	0.86	1
	Male	141 (36%)	255 (64%)
	Unknown	98	83
Population	US	451 (38%)	741 (62%)	<0.01*	<0.01*
	EU	84 (43%)	113 (57%)
	SA	2 (15%)	11 (85%)
	FIN	30 (42%)	41 (58%)
	JAP	36 (26%)	105 (74%)
Aneurysm characteristics
Rupture Status	Ruptured	341 (53%)	307 (47%)	<0.01*	<0.01*
	Unruptured	375 (22%)	1304 (78%)
	Unknown	19	49
Multiplicity	Multiple	283 (23%)	936 (77%)	<0.01*	<0.01*
	Single	452 (38%)	724 (62%)
Morphology	Bifurcation	603 (37%)	1025 (63%)	<0.01*	<0.01*
	Lateral	132 (17%)	635 (83%)
Location	ACA	24 (29%)	60 (71%)	<0.01*	<0.01*
	ACOM	175 (48%)	192 (52%)
	BA	40 (31%)	88 (69%)
	ICA	161 (18%)	723 (82%)
	MCA	168 (32%)	352 (68%)
	PCOM	164 (41%)	239 (59%)
	PICA	3 (33%)	6 (67%)

ACA, anterior cerebral artery; ACOM, anterior communicating artery; BA, basilar artery; ICA, internal carotid artery; MCA, middle cerebral artery; PCOM, posterior communicating artery; PICA, posterior inferior cerebellar artery. The ‘Adjusted p-value’ column lists the p-values after adjustment for multiple testing using the Bonferroni method.

Statistical comparisons between hemodynamic and geometric parameters of aneurysms with blebs (prior to bleb formation, i.e. with their blebs virtually removed) and aneurysms without blebs are presented in Suppl. Table 3. Hemodynamically, aneurysms in which blebs developed had stronger (Q, p<0.01) and more concentrated inflow jets (ICI, p<0.01), higher intra-aneurysmal flow velocity (VE, p<0.01), more complex (corelen, p<0.01) and unstable (podent, p<0.01) flow patterns than aneurysms where blebs did not form. They also had larger maximum wall shear stress (WSSmax, p<0.01; MaxWSSnorm, p<0.01), more concentrated (SCI, p<0.01) and oscillatory (OSImax, p<0.01; OSImean, p<0.01) WSS distribution, and a larger number of critical points of the WSS field (nCrPoints, p<0.01). Geometrically, aneurysms that developed blebs were larger (Asize, p<0.01; SR, p<0.01; GAA, p<0.01), more elongated (AR, p<0.01; VOR, p<0.01; BF, p<0.01), had wider necks (Nsize, p<0.01), larger shape distortion (CR, p<0.01, NSI, p<0.01) and more surface irregularity (UI, p<0.01) than aneurysms without blebs.

Variables Retained in the Model

After removing variables correlated to other variables and multicollinear variables, 25 variables were used to build the models and select the optimal set of predictive features. The final model retained the following 18 predictive variables from the four different domains: 1) hemodynamic: Q, ICI, corelen, MWSSnorm, OSImax, nCrPoints; 2) geometric: Asize, SR, GAA, AR, VOR, BF, NSI, CR; 3) aneurysm: location, multiplicity, morphology; and 4) patient: population. As illustrated in the Suppl. Fig. 4, accuracy reached the maximum level when 18 variables were retained in the model, without noticeable improvement beyond 18 variables. See Suppl. Table 4 for the complete list of the variables considered and retained.

Predictive Models Internal Evaluation and Comparison

The ML model with the best performance during the internal cross-validation phase was the random forest (RF) with a mean AUC=0.80, TPR=0.80, FPR=0.33, and misclassification error=0.28 (see Suppl. Table 5 for internal evaluation metrics for all ML models considered, and Suppl. Fig. 5 to visualize the spread of their AUC, specificity, and sensitivity). The difference in performance between RF and the other ML models as measured by the AUC was statistically significant (p<0.01) (see Suppl. Table 6), confirming that RF was indeed the best classifier.

The optimal parameters for RF were determined after experimenting with different hyper-parameters such as the number of decision trees in the forest and the number of features considered by each tree when splitting a node during the training process. AUC was used as a criterion for determining the best model. The optimal hyper-parameters were set to 1000 trees in the forest, a maximum depth of 1 and 2 random variables used in each tree.

External Validation

The performance of the different ML classifiers when applied to the independent external testing dataset is presented in Table 2. It can be seen that the best performance was achieved by the RF classifier, with consistently the largest AUC=0.82 (Mean and 95% bootstrap confidence interval AUC, 0.8186 [0.7732, 0.8710]), TPR=0.91, PPV=0.58, NPV=0.92, F1=0.71, balanced accuracy=0.77, and the smallest misclassification error=0.27 and FPR=0.36. The performance of different ML models on the external dataset is graphically presented in Figure 1, which shows the ROC and the precision-recall (PR) curves.

Table 2:

Performance measures for each ML model applied to the external testing dataset.

Model	AUC	TPR	FPR	PPV	NPV	F1 Score	Balanced Accuracy	Misclassification Error
BG	0.79	0.82	0.38	0.55	0.86	0.66	0.72	0.31
RF	0.82	0.91	0.36	0.58	0.92	0.71	0.77	0.27
SVM	0.78	0.87	0.52	0.48	0.87	0.62	0.68	0.38
KNN	0.76	0.89	0.53	0.49	0.91	0.63	0.69	0.37
LR	0.79	0.90	0.47	0.52	0.91	0.66	0.72	0.34

AUC=area under the ROC curve. TPR=true positive rate (sensitivity or recall = number of true positives divided by all positives). FPR=false positive rate (1-specificity = number of false positives divided by all negatives). PPV=positive predictive value (precision = number of true positives divided by number of true and false positives). NVP=negative predictive value (=number of true negatives divided by the number of true and false negatives). F1=2*PPV*TPR/(PPV+TPR)=harmonic mean of precision and recall. Balanced accuracy=accuracy accounting for class imbalance (=(sensitivity + specificity)/2). Misclassification error=number of incorrect classifications divided by sample size.

Figure 1:

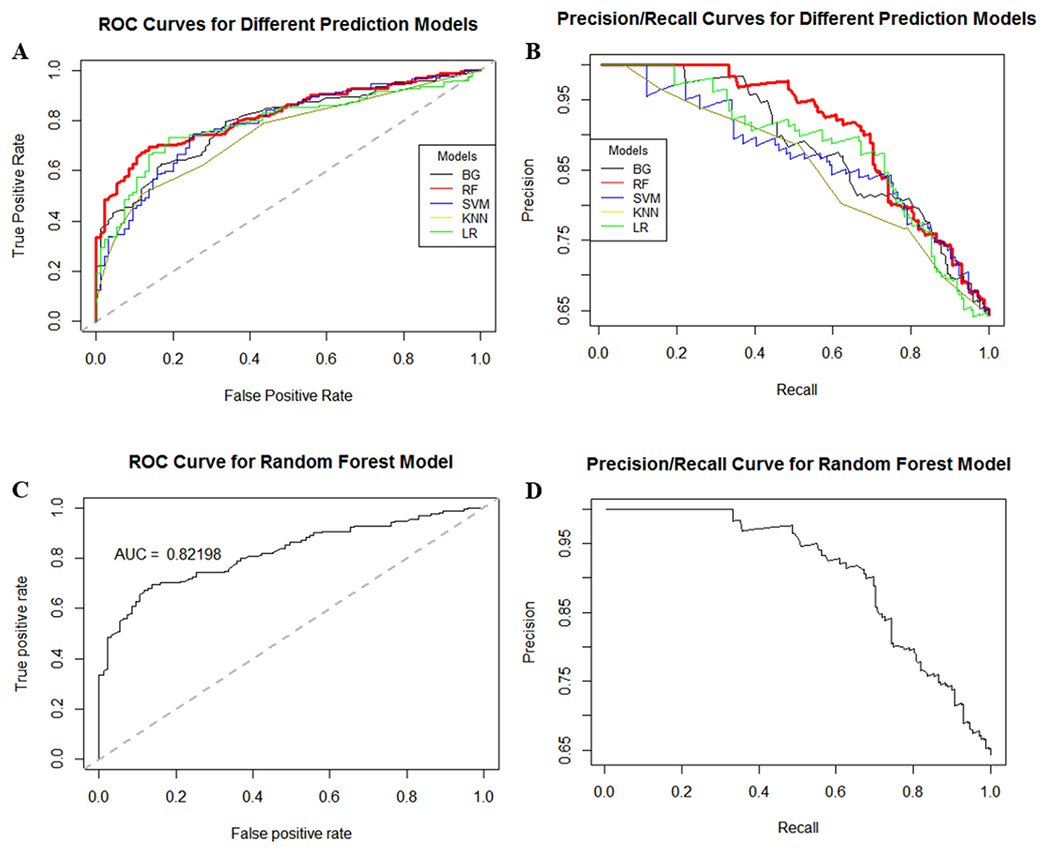
Performance of different ML models on independent external validation dataset: A) ROC curves, B) precision/recall curves. The best performance is achieved by the RF model (red curves).

In the external validation dataset, 35% of aneurysms had blebs, therefore the accuracy of a baseline (null) model, which corresponds to a non-informative model that always predicts the largest class (no blebs), is 65%. The results presented in Table 2 indicate that the performance of the RF model was better than this baseline accuracy, and Cohen’s Kappa statistics gave a value of 0.47, confirming that its accuracy was 47% better than random predictions.

The most important variables (n=18) for discriminating between aneurysms prone to bleb development and aneurysms less likely to develop blebs, as determined by the mean decrease in Gini measure (Suppl. Fig. 6), included geometric shape and size factors, hemodynamic inflow, flow complexity, and wall shear stress parameters, as well as aneurysm location and morphology type and patient population. As shown in Suppl. Fig. 4, the accuracy of the RF model trained with the increasing number of variables (in order of importance) continues to improve until these 18 most important variables are included, indicating that in general multivariate ML models outperform individual metrics.

Examples of aneurysms from the external validation dataset that were correctly classified by the RF model are presented in Figure 2. Column 1 of this figure shows an ACOM aneurysm with two blebs and the corresponding hemodynamic environment prior to bleb formation, characterized by a strong inflow jet, elevated WSS, and a complex flow structure. The RF model assigned to this aneurysm a probability of 92% of developing blebs. Column 2 shows an ACOM aneurysm without blebs and its hemodynamics characterized by slow, smooth, and simple flow pattern with uniformly low WSS. This aneurysm was assigned a probability of 87% of not developing blebs. Column 3 shows an MCA aneurysm with a bleb and the corresponding hemodynamics prior to bleb formation, characterized by a strong inflow jet, elevated and heterogeneous WSS, and a complex flow structure. The RF model assigned to this aneurysm a probability of 80% of developing blebs. Column 4 shows an MCA aneurysm without blebs and its hemodynamics characterized by a simple flow pattern with fairly uniform WSS. This aneurysm was assigned a probability of 84% of not developing blebs.

Figure 2:

Examples of flow visualizations (at peak systole) in MCA (left two columns) and ACOM (right two columns) aneurysms with and without blebs that were correctly classified by the RF model. Columns from left to right: MCA aneurysm with bleb (removed as indicated in insert), MCA aneurysm without bleb, ACOM aneurysm with bleb (removed), and ACOM aneurysm without blebs. Rows top to bottom: vascular geometry, inflow jet (velocity iso-surfaces), wall shear stress magnitude, flow pattern (streamlines). Stronger inflow jets and flow impingement, higher and more heterogeneous WSS, and more complex flow structures can be observed in aneurysms that developed blebs.

Discussion

The current study confirmed, with a large (n=2395), and independent dataset, previous associations between hemodynamic and geometric parameters and bleb development.⁶ Specifically, blebs developed in aneurysms with stronger flow conditions characterized by larger and more concentrated inflow jets, faster, more complex, and unstable flow patterns, and higher, more concentrated, heterogeneous, and oscillatory wall shear stress distributions compared to aneurysms that did not develop blebs. Blebs also developed more frequently in larger aneurysms, with wider necks, more elongated, distorted, and irregular shapes. In addition, the current study found new significant associations between blebs and aneurysm location, morphology and multiplicity, and patient population; and confirmed, in agreement with the previous study,⁵ that patient sex and age were not associated with the presence of blebs.

Secondly, our study showed that predictive models based on machine learning techniques are capable of identifying aneurysms prone to bleb development with good accuracy (91%). These models showed good predictive power in both internal (the same dataset using cross-validation) and external (independent testing dataset) evaluations. It must be emphasized that during the model training phase it is important to account for class imbalance, which in this case it was accomplished with down-sampling without compromising the model accuracy since the training dataset was large enough. We found that the best ML model was the random forest and that this model retained several hemodynamic and geometry parameters, as well as aneurysm location, and patient population. This highlights the multi-factorial nature of aneurysm disease and suggests that perhaps additional parameters from other domains such as aneurysm wall characteristics could improve the predictive power of these models even further.

Previous studies have suggested that blebs form in regions of the aneurysm wall exposed to high WSS at or adjacent to the flow impingement points and aligned with the main flow stream within the aneurysm.^18,19 Once a bleb develops, presumably under the influence of focalized flow impingement forces, the local flow conditions progress to a state of low WSS and high OSI, which has been speculated to increase its rupture risk.²⁰ In contrast, another study found low WSS and high OSI in regions of focalized aneurysm growth, while aneurysms exhibiting a uniform growth pattern were exposed to higher WSS conditions in a short series of 6 IAs.²¹ As suggested in a recent study,²² blebs with different wall characteristics (e.g. translucent ultra-thin vs atherosclerotic thick) may develop under different hemodynamic conditions, which could explain these apparent disagreements. Nevertheless, our current study indicates that aneurysm flow conditions together with aneurysm shape characteristics and anatomical location can be used to identify aneurysms prone to bleb development which could be used clinically as an early indicator of future aneurysm instability.

The RF model was able to correctly identify 91% (TPR) of aneurysms that developed blebs. In our sample, these comprise about 35% of all aneurysms (a relatively rare event), so in a sample of 100 aneurysms, the model would correctly identify 32 of the 35 aneurysms likely to develop blebs. This is a clinically valuable result because it is important to identify early on and with good accuracy aneurysms likely to progress to a more vulnerable state and potentially rupture, and therefore recommend preventive treatment. This high accuracy for detecting “high risk” aneurysms comes at the cost of a relatively high 36% (FPR) misclassification of aneurysms less likely to develop blebs. In our sample, these comprise about 65% of all aneurysms, which implies that in a sample of 100 aneurysms the model would correctly classify 42 (and misclassify 23) out of the 65 aneurysms not likely to develop blebs. Thus, in this case, the model suggests conservative monitoring of 42 stable aneurysms, and preventive treatment or more aggressive monitoring of 23 aneurysms that were not likely to progress to a more vulnerable state. Given a combined treatment complication rate of approximately 10%,²³ the use of this model would result in about 2 unnecessary complications (when treating the 23 misclassified stable aneurysms), which would be lower than the approximately 6 complications expected if all 65 stable aneurysms are preventively treated.

To further analyze the impact of using a limited number of predictive variables, the model was re-trained using only the three most important variables (BF, NSI, and VOR). The results that are presented in Suppl. Table 7 show that TPR declined from 91% to 84%, indicating that this model would correctly identify 29 of the 35 aneurysms which developed blebs (compared to 32/35 of the full model). Additionally, the FPR increased from 36% to 41% indicating that 27 stable aneurysms would be misclassified (compared to 23/65 with the full model), which could increase the number of treatment complications by one. Given that the effort of quantifying these 3 variables or the 18 variables of the full model is essentially the same, this comparison suggests that it may not be worth using predictions based on a reduced set of variables.

The current study has several limitations. In addition to the usual limitations of the CFD modeling approach (Newtonian flow, rigid walls, estimated flow rates, etc.), as mentioned before, the flow conditions and geometric characteristics prior to bleb development were approximated by virtually removing the blebs, therefore the results of this study are conditional to the validity of this assumption. Additionally, the internal and external validations were carried out using retrospective cross-sectional datasets, and image data included two modalities, 3DRA and CTA. Thus, further evaluation and validation with longitudinal datasets are needed and will be the focus of future studies. Moreover, factors characterizing the aneurysm wall structure and biology, genetic factors, and disease status were not included and could substantially improve the predictive power of models of aneurysm instability.

Conclusions

Predictive bleb formation models based on aneurysm hemodynamic and geometric characteristics as well as aneurysm location and patient population are capable of identifying aneurysms prone to develop blebs. This may prove to be important for early assessment of the risk of future aneurysm instability and rupture.