Hierarchical confounder discovery in the experiment-machine learning cycle

Summary

The promise of machine learning (ML) to extract insights from high-dimensional datasets is tempered by confounding variables. It behooves scientists to determine if a model has extracted the desired information or instead fallen prey to bias. Due to features of natural phenomena and experimental design constraints, bioscience datasets are often organized in nested hierarchies that obfuscate the origins of confounding effects and render confounder amelioration methods ineffective. We propose a non-parametric statistical method called the rank-to-group (RTG) score that identifies hierarchical confounder effects in raw data and ML-derived embeddings. We show that RTG scores correctly assign the effects of hierarchical confounders when linear methods fail. In a public biomedical image dataset, we discover unreported effects of experimental design. We then use RTG scores to discover crossmodal correlated variability in a multi-phenotypic biological dataset. This approach should be generally useful in experiment-analysis cycles and to ensure confounder robustness in ML models.

Highlights

• •Hierarchical confounder effects in complex datasets can bias ML models
• •RTG scoring identifies confounding variables in real-world biomedical data
• •RTG scoring can be used to guide model debiasing and inform experimental design

The bigger picture

The promise of using machine learning (ML) to extract insights from high-dimensional data is tempered by the frequent presence of confounding variables. For example, models attempting to identify biomarkers of disease can be severely biased by disease-irrelevant features, such as the physical site where an experiment is performed. While we have many tools to grapple with known confounders, we lack a general method to identify which of a set of potential confounders warrant debiasing. Here, we present a simple non-parametric statistical method called the rank-to-group (RTG) score, which identifies hierarchical confounder effects in raw data and ML-derived data embeddings. We show that RTG scoring identifies previously unreported effects of experimental design in a public dataset and uncovers cross-model correlated variability in a multi-phenotypic biological dataset. This approach should be of general use in experiment-analysis cycles and to ensure confounder robustness in ML models.

Machine learning (ML) models may be biased by hierarchically organized confounding variables, which are frequently present in complex datasets. We present a statistical method, the rank-to-group (RTG) score, that can identify confounding variables in any dataset. Using RTG scoring, we find previously unreported effects of experimental design in a public dataset and uncover crossmodal correlated variability in a multi-phenotypic biological dataset. This approach should be of general use in experiment-analysis cycles and to ensure confounder robustness in ML models.

Introduction

The practice of training a model that maps high-dimensional input objects (such as biomedical images) to target labels (e.g., diseased versus healthy) and subsequently quantifying model performance to identify biomarkers or disease phenotypes is of substantial interest in multiple fields of diagnostic medicine.1, 2, 3, 4, 5, 6 However, recent studies have shown that disease-irrelevant features, such as the physical site where an experiment is performed⁶ or the sample preparation protocol,⁷ can severely bias these models. In these examples, “site” and “protocol” are potentially confounding discrete variables (confounders), whose values are additional confounder labels that accompany the target labels for each data point.

Many debiasing strategies exist to mitigate confounding effects on machine learning (ML) models including methods for (1) a priori balancing of datasets with respect to confounders (e.g., matching),⁸ (2) post hoc correction of datasets to reduce bias (e.g., restriction, stratification, harmonization, decorrelation),9, 10, 11 and (3) incorporating bias resilience during model training.12, 13, 14, 15 However, while we have many tools to grapple with known confounders, we are lacking a general method to identify which variables in a set of potential confounders warrant debiasing.

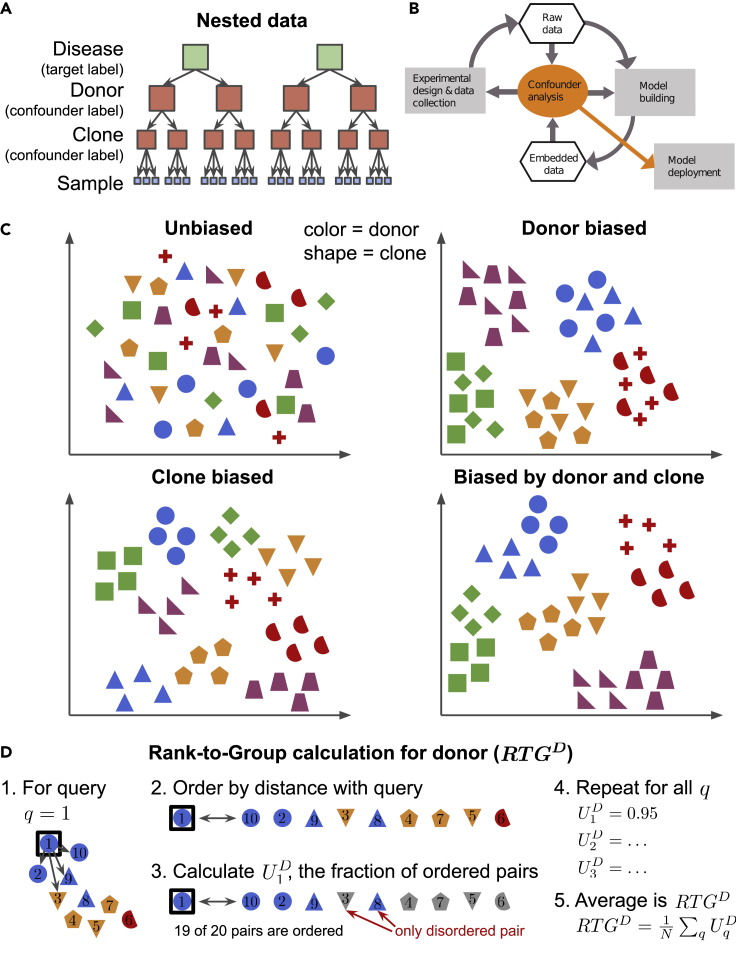
A particular challenge is the attribution of bias to hierarchically organized nested confounders—confounders for which all data points that share a lower-level confounder label also share the same higher-level confounder label. For example, in induced pluripotent stem cell (iPSC) culture, multiple stem cell lines (“clones”) can be derived from the same human subject (“donor”) (Figure 1A). Donors differ due to genetic variation; clones are also known to differ through the biological underpinnings of clone-to-clone variability, which remain an active area of research.16, 17, 18 Such a confounder hierarchy is nested because each clone can only belong to a single donor. A typical linear approach to isolating the effect of a specific confounder is to compare models that fit the data with and without using the confounder of interest, i.e., by subtracting the variance explained by a model that excludes the confounder from the variance explained by a full model. However, for nested confounders this quantity will always be zero, because the lower-level label (e.g., clone) confers perfect knowledge of the higher-level label (e.g., donor), rendering this technique useless (Figure S1A). Alternatively, one can assess for bias by computing the performance of linear decoders that predict confounder labels from data. This approach can work in the setting of nested confounders, but—unlike with calculations of variance explained—provides no concept of effect size: the prediction accuracy of two different confounders may be unmoored from the amount of structure they confer to the data (Figure S1B). Beyond linear methods, probabilistic graphical models are in theory purpose built for characterizing the effects of an interacting set of variables, including hierarchically organized ones, but they require assumptions about the data-generating process as well as advanced Bayesian inference methods in non-conjugate settings which may not scale well to high dimensions.¹⁹ Other nonlinear techniques, such as neural networks, may be able to determine the effects of nested confounders, but they are sensitive to hyperparameter settings that may work for establishing the bias conferred by one confounder but not another, and thus cannot be deployed as a general method. One solution to dealing with a set of potential confounders is simply to apply debiasing strategies with respect to all such variables and test for improved model performance. However, if data are limited, model building expensive, or the relationships between confounders complex—and all three are often true in biology—this brute force approach is infeasible. Instead, a technique that does not suffer from the limitations articulated above and that can be used to quickly score the importance of potential confounders, including nested confounders, is needed.

Figure 1.

Hierarchical confounders and the RTG score

(A) An example data hierarchy drawn from the field of stem cell biology. A typical modeling goal would be to predict the target label (healthy versus diseased) of a data sample. However, every data point would also be accompanied by potential confounder labels “clone” (i.e., stem cell line) and “donor” (i.e., human subject from whom a clone is derived). Clone and donor are organized in a nested hierarchy: all data points that share the same clone label also share the same-donor label.

(B) Role of confounder analysis in the iterative cycle of experimental data collection and model building with ML. The degree to which potential confounders confer structure to the raw data or data embeddings can inform both the experimental design used to collect more data and the modeling framework used to analyze the data. Model deployment should depend on confirmation of successful debiasing.

(C) Schematized data where donor is represented by color and clone by shape. The data are either unbiased by these variables (top left), biased by donor alone (top right), biased by clone alone (bottom left), or biased by both donor and clone (bottom right). Confounders can group the data. For example, for donor-biased data (top right), the data are clustered by color, but within a cluster no structure is conferred by shape.

(D) Steps illustrating the computation of the rank-to-group (RTG) score for donor (i.e., color), which we notate as RTG^D. See algorithm 1 in experimental procedures for full details. Step 1: a query data point q is selected and the distances from the query to all other data points are calculated (as schematized by the arrows). Step 2: the data are ordered by their distances to the query. Step 3: pairs of points are evaluated where one point shares the same donor as the query and the other does not. The query score $U_q^D$ for query q is the fraction of such pairs for which the same-donor point is closer to the query than the different donor point. In this example, four points (in blue) share the same donor as the query, while five (in gray) do not, yielding 20 possible pairs. Of these, one is out of order—the pair marked with the red arrows—giving a query score of $U_q^D=0.95$. Finally, repeating steps 1–3 for all possible queries and then averaging all query scores $U_q^D$ gives the value of RTG^D (steps 4 and 5).

Consider Figure 1C, which shows datasets with and without biasing by donor, clone, or both. Linear analysis would correctly declare that the data in the top right panel are biased by donor, but would also identify the data in the bottom left panel as donor dependent despite those data being constructed to be biased by clone alone. This is because the combined set of blue circles and triangles in this panel has substantially lower variance than the data as a whole as a result of the nested dependency between clone and donor. To correctly determine if donor confers structure beyond that determined by clone alone, we require a method that can disambiguate nested confounders. We could then use such a method to (1) inform the design of the next round of experiments to minimize bias, (2) guide data debiasing methods, or (3) build models that explicitly account for known biases (Figure 1B).

Here, we provide a novel non-parametric statistical method for scoring the degree to which data is structured by a potential confounder, the rank-to-group (RTG) score, which relies solely on similarity measures between data points. Thus, the RTG score is applicable both to raw data and to the embeddings that result from ML models. This method has a natural extension for handling nested confounders.

In the following sections, we describe the details of the RTG score method, provide analytic results for simple scenarios, compare it with linear analysis, and demonstrate how RTG analysis can be used to guide data collection and modeling decisions. We then apply our approach to two real-world datasets. First, we analyze a large public dataset of images of cultured cells²⁰ and reveal that some features of the experimental design strongly bias the results. We furthermore show that linear techniques fail to discover these confounding effects. Next, we compare RTG analyses of a multi-modal dataset from patient-derived iPSC cultures²¹ to interrogate the effects of donor, clone, and batch, as well as their interactions. We show that these potential confounders differentially bias the data, but that their relative effects are conserved across three highly disparate modalities of biological measurement: quantitative PCR, bright-field microscopy, and single-cell RNA sequencing. The general applicability of our approach to datasets with complex confounder hierarchies makes it of potentially broad utility when using ML techniques to interrogate large-scale real-world datasets.

Results

The RTG score is a measure of the degree to which a potential confounder confers structure on—or biases—a dataset. A score of 0.5 means that a potential confounder has no effect on the data, while a score of 1.0 means complete confounding. The name “rank-to-group” derives from the score’s computation, which determines the relationship between the rank ordering of the distances among data points and their confounder group memberships. RTG scoring is non-parametric, which simplifies its application, and it is computable whenever the following two conditions are met. First, the data live in a metric space with any valid distance measure between data points x and y. For example, for N-dimensional vector data in ${\mathbb{R}}^N$, the Euclidean distance ${\left|\mathbf{x}\mathbf{–}\mathbf{y}\right|}_2$ is a natural metric. Other data types that can live in metric spaces include reals, non-negative reals, natural numbers, text, discrete labels, tree structures, and event times, among many others. Not only can RTG scoring be applied for any choice of distance metric, it is identical for any two distance metrics that preserve the order of all pairs of distances in the dataset. The second constraint is that each data point must be associated with a set of labels corresponding to potential confounders.

To compute the RTG score RTG^A for a dataset with N samples with respect to a potential confounder A, we proceed as follows. First, for some “query” data point q, all other points are considered in pairs where one member of each pair shares confounder label identity with the query point and the other does not. The query score $U_q^A$ is the fraction of these pairs for which the distance from the query to the same-confounder data point is less than the distance to the different-confounder data point (see Figure 1D for an example calculation and algorithm 1 in experimental procedures for details). Thus, the query score measures the likelihood that a random data point that shares the same-confounder label as the query is closer to it than a random data point that does not. We use the variable “U” because the query score is identical to the area under the curve of the receiver-operator characteristic curve (ROC AUC) computed via the U statistic of an ordinal statistical test (Mann-Whitney U test²²) that compares two sets of distance measurements: (1) from the query to data that share the query’s confounder label and (2) from the query to data with different-confounder labels. (Of note the ROC AUC interpretation requires that the distances between a query point and all others can be ordered. This adds an additional mild constraint on the choice of distance metric. Namely, that $d\left(\mathbf{x},\mathbf{a}\right)<d\left(\mathbf{x},\mathbf{b}\right)$ and $d\left(\mathbf{x},\mathbf{b}\right)<d\left(\mathbf{x},\mathbf{c}\right)$ implies $d\left(\mathbf{x},\mathbf{a}\right)<d\left(\mathbf{x},\mathbf{c}\right)$. Euclidean distances in ${\mathbb{R}}^N$, for example, meet this constraint.) The average of the query scores over all possible queries gives the RTG score for the confounder in question: $RT{G}^A=\frac{1}{N}\sum _q{U}_q^A$. This score has a maximum of 1 when all data points that share the same-confounder label are closer to each other than they are to any other data point. On the other hand, if the confounder confers no structure on the data, RTG^A will approach 0.5.

The RTG score has several useful properties. First, it is well suited to high-dimensional data because it depends on a distance measure alone. Second, as a non-parametric rank order-based score, it is insensitive to low noise levels that do not change the order of data distances relative to the query, and, for the same reason, is largely insensitive to outliers. More generally, it provides useful results whenever distances are preserved locally even if they are less reliable over long length scales—as is the case for embeddings via UMAP, t-SNE, and other nonlinear techniques²³—since misorderings far from the query will likely have negligible impact on the calculated RTG score. Third, it can be applied to any embedding, regardless of interpretability. Finally, and most importantly, this technique is easily extended to the case of nested confounders.

When confounders are hierarchically nested (e.g., donor and clone) the RTG score for the higher level will include effects of the lower level, obscuring the effects of the higher level alone. To disambiguate the effects of two hierarchically related confounders, we can compute a restricted RTG score RTG^A\B, which isolates the effects of higher-level confounder A by removing the influence of lower lever confounder B. For example, during the evaluation of the RTG score for “donor-exclude-same-clone” (RTG^D\C), the computation of each query score is modified to exclude all data points that share the same clone label as the query (see Figure S2 for an example calculation and algorithm 1 in experimental procedures for details). This means that the query score $U_q^{D\mathrm{\backslash }C}$ measures the degree to which, for data points that do not share the same clone label as the query, distance to the query can sort those data into same-donor and different-donor groups. If an apparent confounding effect of donor is entirely attributable to clone as in the bottom left panel of Figure 1C, RTG^D\C will be at the chance level of 0.5. Thus, the restricted RTG score allows us to disambiguate clone-confounder effects from (donor and clone)-confounder effects (bottom left and right panels of Figure 1C).

While we only consider examples of discrete valued confounding variables in this article, the RTG and restricted RTG scores can be extended to the setting of continuous valued confounders as described in the supplemental notes.

Analytic RTG scores for hierarchical Gaussian mixture data

We now illustrate how RTG scores can disambiguate between three scenarios of confounder-introduced variability by applying them to synthetic data. We specify a three-level clone-donor-sample hierarchical Gaussian mixture model governed by three parameters, the variances ${\sigma }_D^2$, ${\sigma }_C^2$, and ${\sigma }_X^2$ (Figure 2A). The relative sizes of these variances define the structure of the data. We consider three extreme scenarios: (1) data fully biased by both donor and clone, (2) data biased by donor only, and (3) data biased by clone only (Figure 2B). For these scenarios, we can compute simple analytic expressions for the RTG scores of clone (RTG^C) and donor (RTG^D), and for the restricted RTG score of donor-exclude-same-clone (RTG^D\C). These depend only on D and C, the number of donors and clones per donor, respectively, assuming large numbers of samples per clone (Figure 2C). If we interpolate from the scenario when biased by both donor and clone to the donor-only and clone-only scenarios, we observe that the RTG scores indeed change according to the analytic expressions (Figure 2D).

Figure 2.

Confounder analysis of hierarchical Gaussian synthetic data

(A) Data-generation scheme. The means for each donor and clone are sampled from Gaussian distributions as ${\mu }^d\sim N(0,{\sigma }_D^{2}I)$ and ${\mu }^{cd}\sim N({\mu }^d,{\sigma }_C^{2}I)$, respectively. Then, the i^th data point for each clone is sampled as $x_i^{cd}\sim N({\mu }^{cd},{\sigma }_X^{2}I)$. D, C, and N are the number of donors, clones per donor, and data points per clone.

(B) Three extreme confounder scenarios for two-dimensional data. Each circle represents a single clone whose radius represents σ_X (i.e., the scale of the data distribution for that clone). Each color represents a donor. In scenario 1, the variance differentiating donors dominates the variance differentiating the clones within a donor, which in turn dominates the variance of the data for each clone (i.e., ${\sigma }_X^2\ll {\sigma }_C^2\ll {\sigma }_D^2$). Thus, the data are completely biased by both donor and clone. With variances ordered as ${\sigma }_C^2\ll {\sigma }_X^2\ll {\sigma }_D^2$ (scenario 2) and ${\sigma }_X^2\ll {\sigma }_D^2\ll {\sigma }_C^2$ (scenario 3), the data are instead biased by donor alone or clone alone, respectively.

(C) The analytic expressions for the RTG scores for donor, clone, and donor-exclude-same-clone for scenarios 1, 2, and 3 from (B) when assuming many samples per clone.

(D) The evolution of RTG scores as datasets change from scenario 1 to scenarios 2 (left) and 3 (right). RTG scores are plotted against the ratios σ_X/σ_C (left) and σ_C/σ_D (right) while ensuring that the other constraints from (B) remain in place (i.e., that σ_D is large for the left panel and σ_X is small for the right panel). The RTG score for donor (green) is plotted with a thin line since it does not isolate the confounding effects of a single potential confounder as opposed to the restricted RTG score for donor-exclude-same-clone (orange) which does.

(E) Leave-one-out cross-validated R² values of linear models fit using clone and donor identities, and—to isolate donor effects—the leave-clone-out cross-validated R² values for models fit using donor but only trained on C−1 clones and tested on the held-out clone. Other conventions as in (D).

Left panels in (D and E): D = 2; C = 10; σ_D = 400σ_C. Right panels: D = 50; C = 2; σ_X = 10⁻⁴σ_D. All panels: N = 100; data are ten dimensional; error bars are standard deviations over five random samples of the data

Our analytic results illustrate the importance of restricted RTG scores for distinguishing between single or multiple confounder effects. For example, for data biased only by clone (i.e., when ${\sigma }_X^2\ll {\sigma }_D^2\ll {\sigma }_C^2$), the analytic expression for the RTG score for donor (RTG^D) is $1/2+1/2C$, which for small C can significantly exceed 0.5 even though in truth there is no donor effect (right panel of Figure 2D, green curve). However, while RTG^D may be misleading, the restricted RTG score for donor-exclude-same-clone (RTG^D\C) reports a score of 0.5, consistent with no donor effect. If, on the other hand, donor does structure the data beyond the effects of clone (i.e., when ${\sigma }_D^2$ is similar to or greater than ${\sigma }_C^2$), then RTG^D\C will exceed 0.5, confirming the effect (right panel of Figure 2D, orange curve).

Linear-model confounder analysis approaches fail on hierarchical data

Confounder discovery via linear analysis is a reasonable baseline against which to compare the RTG method. However, as discussed in the Introduction, the standard approach of comparing full and partial models to isolate the effect of a potential confounder—i.e., by computing the difference in data variance explained by models that use and do not use the confounder of interest—fails for nested hierarchies (see Figure S1A). An alternative linear approach that avoids this pitfall is “leave-confounder-out” cross validation. To isolate the confounding effects of a variable higher in a confounder hierarchy-like donor, a model can be constructed from donor labels using only a subset of the data that holds out one or more clones. This model can then be tested, in terms of the variance explained, on the held-out data. This approach is similar to K-fold cross validation except that the data folds, rather than being random, are defined by the lower-level label identities (e.g., clone).

Comparison of the left panels of Figures 2D–2E shows the utility of RTG scoring versus linear analysis. Data that are biased by both donor and clone or by donor alone are indistinguishable by R² values but clearly differentiated when using the RTG method. In contrast, leave-confounder-out linear analysis is useful for disambiguating clone-biased data from data biased by both donor and clone (Figures 2D–2E, right). Note that if the number of labels for a held-out lower-level confounder (e.g., clone) is two and if the structure of the data is dominated by that lower lever confounder, then the leave-confounder-out R² for the higher-level variable will reach a minimum of −1 for hierarchical Gaussian data (as seen for the orange line in Figure 1E, right).

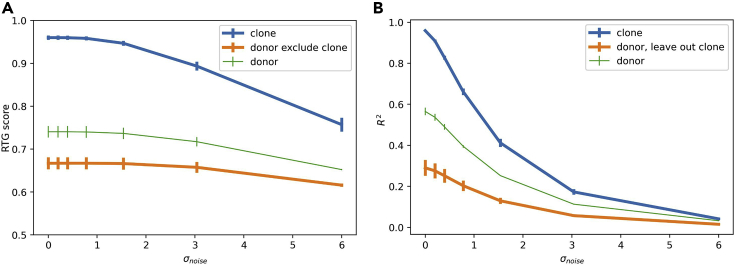
We next consider the consequences of noise in synthetic data with mixed donor and clone effects (Figure 3). For increasing noise values, RTG scores are largely stable while R² values drop precipitously. This is because RTG scoring—a rank order-based method—is unaffected by noise unless distances to the query for data points that share and do not share confounder labels change order (see Figure 1D; and algorithm 1 in experimental procedures). In other words, as long as noise does not result in mixing of clusters in the data that are defined by confounder labels, RTG analysis will reveal the confounder-dependent structure in the data. R² values, on the other hand, only report the structure of the data indirectly through their measurement of explained variance, and thus are guaranteed to drop as data noise increases even when the underlying clustered structure in the data remains intact.

Figure 3.

Analysis of robustness to noise

(A and B) Comparison between RTG scores (A) and R² values (B) as a function of noise. The data were generated as per Figure 2A, but then randomly projected to a much higher dimensional space before being corrupted by white noise with scale σ_noise. Conventions are as in Figures 2D–2E except: D = 14; C = 2–6 (different for each donor); σ_D = σ_C = 1; σ_X = 0.25; N = 25; data are two dimensional before being projected to 512 dimensions; error bars are standard deviations over three random samples of the data

Model debiasing example

We can consider a simple example of using RTG analysis to guide decision making around data collection and modeling when building classifiers to predict disease state (as per Figure 1B). We first generate synthetic data from a mixture model according to Figure 2A, but with the modification that half of all donors—representing healthy human subjects—have the vector [1, 0, …, 0]^T added to their means. The other half of the donors have their means shifted by [–1, 0, …, 0]^T and represent diseased patients. As before, the confounder structure of the generated data depends on the relative values of the variances of donor, clone given donor, and data sample given clone (${\sigma }_D^2$, ${\sigma }_C^2$, and ${\sigma }_X^2$).

First, we consider the case of analyzing small datasets—two donors per disease state and two clones per donor—to determine whether or not more donors or clones should be collected to improve the disease state prediction accuracy of a logistic regression model. When the data are biased by donor but not clone, adding more donors while keeping the number of clones per donor fixed improves model performance, while adding clones confers no benefit (Figure 4A). Conversely, for data biased by clone but not donor, adding either clones or donors improves model performance equally (Figure 4B). These results demonstrate the power of RTG analysis for informing data collection strategy. In a real-world setting, new samples of lower-level variables (e.g., more clones) may be cheaper to obtain than samples of higher-level variables (e.g., donors). The confounder structure as measured by RTG scoring can dictate how best to use resources for data collection by clarifying when sampling more higher-level confounders is necessary or when adding new lower-level examples to a dataset is sufficient.

Figure 4.

Using RTG scores to inform data collection and debiasing

(A) Effect of training data quantity on model performance for donor confounded data. Left: RTG scores for donor, clone, and donor-exclude-same-clone before adding new donors or clones. Right: accuracy of logistic regression models on test data. Models are trained while either increasing the number of donors in the training dataset when holding the number of clones per donor fixed (D = 2–10 and C = 2, red) or while increasing the number of clones per donor when holding the number of donors fixed (D = 2 and C = 2–10, purple). σ_D = 1; σ_C = 0.1.

(B) Same as (A) for clone confounded data. σ_D = 0.1; σ_C = 1.

(A and B): σ_X = 0.1; N = 10 for training; 10,000 test data points each with a unique donor and clone; 20-dimensional data; error bars are standard errors of the mean over 20 random samples of the training data.

(C) Effect of data debiasing on model performance for donor confounded data. Left: RTG scores prior to debiasing. Right: changes in model performance when debiasing by donor or by clone. Debiasing procedure described in the text. Red lines show mean changes due to debiasing over 100 sample datasets; black lines show 20 example datasets. The mean change due to donor debiasing was significantly different from the mean change due to clone debiasing (p < 10⁻⁴ via resampling). σ_D = σ_C = σ_X = 0.3 in all dimensions except three dimensions with σ_D = 100; D = 4, N = 10.

(D) Same as (C) for clone confounded data.

σ_D = σ_C = σ_X = 0.3 except three dimensions with σ_C = 100; D = 2, N = 20.

(C and D): C = 2; 10,000 test data points; 10-dimensional data

Next, we consider the case of using RTG analysis to inform how best to improve model quality when no further data collection is possible. For this example, during data generation, we confine ${\sigma }_D^2$ and ${\sigma }_C^2$ to only be large in a subset of data dimensions (3 of 10) when biasing by donor and clone, respectively. Then, to debias with respect to donor, for example, we determine directly from the training data which dimensions correspond most strongly to donor and project the data out of those dimensions before model fitting. In particular, for each donor, the centroid of all the data with the same disease state was subtracted from that donor’s centroid to obtain that donor’s specific direction. Principal-component analysis was performed on the set of donor-specific directions and the top two principal components were identified as the donor-specific subspace. The data were then linearly projected out of that subspace before constructing our logistic regression classifier. Debiasing by clone was analogous to debiasing by donor except that each clone’s specific direction was computed from the difference between that clone’s centroid and the centroid of the corresponding donor. Test data were also projected out of the donor-specific and clone-specific subspaces when debiasing by donor and clone, respectively.

For donor-biased data, debiasing by donor improved the average prediction accuracy on test data from 72% before debiasing to 81% after debiasing, while debiasing by clone showed a small negative effect (70% post-debiasing accuracy; Figure 4C). The difference between these mean changes was highly significant (p < 10⁻⁴ by resampling; Figure S3A). For clone-biased data, average prediction accuracy improved from 71% before debiasing by clone to 83% afterward, while debiasing by donor showed a smaller, although meaningful effect (79% post-debiasing accuracy; Figure 4D). The difference between these mean changes was also highly significant (p < 10⁻⁴; Figure S3B). These results demonstrate that, in the data-constrained regime, identification of confounders with large effects can inform strategies for building higher-performing models.

Identification of confounding effects in a hierarchical biomedical dataset

Next, we applied RTG analysis to identify confounders in a dataset of biomedical image embeddings released in the public domain by Recursion Pharmaceuticals.²⁰ The raw images are of cell cultures in 1,536-well plates. The data consist of 2 experimental batches of 12 plates each. Each well is imaged at four sites. The wells along the edges of the plates were not used. Many of the wells in this dataset were treated with pharmacologic agents; but, for our analysis, we chose to look only at untreated control wells, which were randomly dispersed across each plate. This left a dataset of approximately 8,000 image embeddings that we analyzed for the confounding effects of batch ID (1 or 2), plate ID (1–12), well position (e.g., C4), unique well ID (e.g., C4 on plate 3 in batch 1), camera field of view within a well or “imaging site” (1–4), and whether or not an image came from a well on the “subedge”—the outer rim of wells that remain after excluding the edge wells themselves.

In Figure 5A we calculated RTG scores and restricted RTG scores for these potential confounders, and confirmed via subsampling that our calculated scores are precise enough to facilitate comparison between them (Figure S4). Our analysis reveals that the Recursion data are largely free of obvious experimental pitfalls. For example, imaging site does not bias the data (RTG 0.5) while unique well ID nearly completely biases the data (RTG 0.95), meaning that the four images within each well are essentially interchangeable. Furthermore, well position alone strongly biases the data (RTG 0.76), but well-position-exclude-same-plate (i.e., equivalent to well-position-exclude-same-unique-well) drops the RTG score to 0.58, supporting the notion that similarity between images within the same well primarily drives the embedded data structure. Next, we observe that the confounding effects of plate ID (RTG 0.55) can be entirely explained by batch ID (plate-exclude-same-batch RTG 0.5). Batch ID, on the other hand, confers significant structure to the data (RTG 0.87), suggesting some difference in conditions between experimental batches.

Figure 5.

RTG scores and R² values calculated from the analysis of Recursion Pharmaceuticals' public dataset

(A) RTG and restricted RTG scores for potential confounders: batch, plate, well position, imaging site, unique well, and whether or not a data point is from a subedge well. Each confounder is considered without (top row) and with (other rows) the exclusion of each other confounder (except if the would-be excluded confounder is strictly higher in the confounder hierarchy, making exclusion impossible).

(B) RTG and restricted RTG scores after the data have been collapsed along the dimension defined by the line between the centroids of the subedge well data and the non-subedge well data. Conventions as in (A). Errors in (A and B) are bootstrapped 95% CIs obtained by resampling with replacement.

(C) Five-fold cross-validated R² values (top row) and leave-confounder-out cross-validated R² values (other rows) for the same potential confounders as in (A and B). Negative values mean that models built while leaving out data with a particular confounder label and then tested on that left-out data are worse than a naive model that simply predicts the mean of the whole dataset

However, we found that whether or not an image comes from a well on the subedge strongly structures the data (RTG 0.73). Indeed, subedge membership is a strong influence even across batches (subedge-exclude-same-batch RTG 0.68). These results suggest that, despite not using the edge wells—presumably to mitigate a common issue with well plates—the data embeddings remain highly influenced by whether or not a well is on the outer rim of the in-use wells. To confirm this finding, we debiased the data with respect to the subedge well effect and then recomputed the RTG scores. More precisely, we linearly projected the data out of the dimension defined by the line that connects the centroids of the data points from subedge and non-subedge wells. The debiased data showed improved RTG scores (Figure 5B). The residual effect of well-position-exclude-same-plate is largely eliminated (RTG from 0.58 to 0.53) with the remaining confounding effect attributable to batch (well-position-exclude-same-batch RTG 0.51). The confounding effects of batch become slightly more pronounced (RTG from 0.87 to 0.9), including when excluding the effects of subedge membership (batch-exclude-same-subedge-group RTG from 0.67 to 0.84), suggesting that simple manipulations of the data, such as linear projections, can mitigate certain confounding effects while amplifying the effects of other confounders.

We also used this dataset to demonstrate that RTG analysis is highly data efficient. With a random subsampling of the data, we showed that the Spearman’s rank correlation between RTG scores for full (100%) and partial (10%) datasets was 0.985 (Figure S4).

We can compare the results of RTG and linear analysis to demonstrate the power of the RTG approach (Figures 5A and 5C). Although some of the conclusions are the same (e.g., that images in the same well are more correlated than any other grouping), others differ. For example, well position accounts for more variance than batch; although, per RTG analysis, batch confers more clustered structure to the data. Furthermore, the highest R² values only reach about half of their maximum while the highest RTG scores are nearly maxed out. RTG analysis specifically measures the degree to which a confounder clusters data, while R² captures this only indirectly through a measurement of variance explained. Thus, the Recursion data demonstrate that real-world data embeddings can be both highly clustered and noisy, suggesting the risk of a faulty conclusion if relying on a low R² value as a surrogate for low bias.

Most importantly, linear analysis fails to unambiguously identify the confounding effects of the subedge. The raw cross-validated R² for subedge is near zero (0.07, last value in first row of Figure 5C), which is in conflict with the negative R² values obtained when performing leave-subedge-group-out cross validation (bottom row). These negative values suggest that a model fit with data from the subedge is poor at predicting the data off the subedge and vice versa (à la the negative values in the right panel of Figure 2E). Such conflicting results may impede discovery of the importance of subedge if using linear confounder analysis. Of note, leave-batch-out cross validation also results in negative values (next to bottom row); but, unlike for the subedge, the raw cross-validated R² for batch is well above zero (0.20, first value in first row).

RTG analysis yields modality-independent confounder effects in multi-phenotypic data

Next, we applied RTG analysis to our own multi-phenotypic dataset collected from human iPSC-derived brain organoids.²¹ These data consist of three kinds of measurements: gene expression via qPCR, morphology via bright-field microscopy, and cell-type distribution via single-cell RNA sequencing. For each modality, multiple donors and clones per donor were used and data collection occurred in several experimental batches. We analyzed 21 donors, 58 clones, and 17 batches for qPCR; 10 donors, 20 clones, 7 batches for bright-field; and 14 donors, 29 clones, and 3 batches for scRNA-seq.

Our analysis (Figure 6) detects substantial confounder effects. Both the RTG score for clone and restricted RTG score for donor-exclude-same-clone are elevated with clone showing a somewhat stronger effect than donor. Batch shows a weak effect on its own, but a confounder defined as the intersection of batch and clone (i.e., where each confounder label is the union of a batch label and a clone label) strongly biases the data. Similar, although weaker, confounding effects are seen with the intersection of batch and donor. These results illustrate the utility of RTG scoring in the cycle of experimentation and data analysis (Figure 1B). They suggest that future data collection can be targeted at increasing the number of clones, which is typically less resource intensive than increasing donors. Furthermore, both clones and donors should be distributed across batches to reduce the bias conferred by these variables. Finally, these results clarify the need to use ML techniques that can generate data embeddings that are insensitive to donor, clone, and batch effects to aid biological interpretation.

Figure 6.

RTG scores when evaluating different aspects of our previously published multi-modal dataset

For each modality, potential confounders batch, donor, and clone are evaluated, as well as the intersections of batch plus donor and batch plus clone. Restricted RTG scores excluding batch, donor, and clone are also presented (unless they are higher in the data hierarchy than the confounder being evaluated).

(A–C) RTG scores computed from gene transcriptional data via qPCR, image data via bright-field microscopy, and cell-type distribution data via scRNA-seq for iPSC-derived brain organoid cultures. Errors are bootstrapped 95% CIs obtained by resampling with replacement.

Strikingly, we see that the RTG scores for gene expression, imaging, and cell-type distribution (Figures 6A–6C) are consistent across modalities (average pairwise Spearman’s rank correlation of 0.924). These results suggest that there is a common biological origin of these phenotypic modalities; thus, the use of cost-efficient, scalable modalities (e.g., imaging) for the characterization of variability may be sufficient without the need to scale-up highly resource-intensive techniques, such as single-cell sequencing.²¹ This demonstrates another use for confounder analysis in the experiment-analysis cycle: in addition to informing how to balance future data collection (e.g., more clones), RTG scores can also inform resource allocation toward specific types of assays.

Discussion

Strategies for confounder analysis are currently lacking. Standard linear methods suffer from outlier sensitivity, are blind to complex structure in data, and cannot disambiguate hierarchically nested confounders; matching and stratification strategies suffer on high-dimensional data due to combinatorial scaling of unmatched dimensions, and matching is impossible for a lower-level confounder in a nested hierarchy; and Bayesian models suffer from poor performance in high dimensions.¹⁹ In this article we present a novel non-parametric method, the RTG score, that addresses these issues and is easily deployable in settings where data interpretability is limited (e.g., neural network embeddings) and confounder sensitivity of great concern (e.g., models of biomedical data that are intended to support disease diagnosis or treatment). Our method only requires (1) distance measurements between data points and (2) confounder labels for each data point. We have demonstrated that RTG scoring is robust to noise and can identify the level in a confounder hierarchy from which a confounding effect arises even when the structure conferred by the confounder is nonlinear.

RTG scoring presents some significant advantages with respect to leave-confounder-out model comparison using regression-based methods. First, as with rank-based tests, which are only sensitive to the order of univariate quantities, RTG scoring is ideal for ordinal distance comparisons between samples within and across groups. Therefore, it inherits all the benefits of methods for ordinal statistics. For instance, RTG scoring is insensitive to outliers unlike regression methods (unless they have been specifically adapted to be outlier robust). Second, additive noise or random ablations, such as a few incorrect, missing, or imputed pairwise distances, will not alter the rank order of most samples, rendering RTG scoring more robust than alternatives. Third, RTG scoring is designed to be agnostic to the data manifold and the distance metric employed, and therefore makes fewer assumptions about the dataset than linear methods, which expect a linear relationship between confounders and data features. Fourth, unlike linear methods, RTG scoring is non-parametric and therefore has no parameters to tune (such as the specific choice of regression model, model regularization, or stratification for cross validation), rendering it robust to researcher-introduced bias when assessing for confounding effects (i.e., through the biased selection of model parameters).

An alternative to RTG scoring for the analysis of nested dependency structures is hierarchical modeling (HM). However, RTG scoring provides a number of practical benefits and differences. First, HM requires the user to make a number of modeling assumptions: for example, prior distributions, their hyperparameters, and the dependency structure of interactions between variables. In practice, this means that, before undertaking HM confounder analysis, the user needs to have considerable insight into the data-generation process, and how confounds might interact with each other and influence the observed data. In contrast, RTG scoring only requires the user to specify a sensible distance metric between observations. In addition, the parameters of HM must be appropriately fit to data as a prerequisite to assessing the contributions of potentially confounding variables. This often limits HM to only consider linear relationships between confounding variables and data due to the practical difficulties of fitting nonlinear models. In contrast, the RTG score is easy to compute with no restrictions on the relationship between putative confounders and data. These requirements of HM pose substantial barriers to widespread adoption as a confounder quality-control procedure.

When we apply our method to real-world biomedical datasets, we find that it can identify confounders such as batch, edge, donor, and clone, a point of critical importance when attempting to derive general results from these kinds of data. Batch effects—which arise when some experimental conditions shift despite the intention of repeating them exactly—is an example of a confounder that iterative experimental design and careful data collection may be able to mitigate. Donor effects may be reduced by matching certain variables across disease and healthy groups (e.g., gender and age), but may also require strict protocols (e.g., sample collection and handling) to mitigate fully. Edge effects can be partially managed by randomization and clone effects by increasing the numbers of clones per donor, but each of these confounders also likely requires specific computational solutions to mitigate. Recent methods that force data embeddings to be insensitive to certain potential confounders^14,15 may be of particular value for debiasing data with respect to confounders such as edge and clone. However, they rely on minimizing the decodability of a confounder in data embeddings, which does not address the importance of that confounder in structuring the data (i.e., one confounder may be more decodable than another while structuring the data more weakly; see Figure S1B). In all of these cases, a method such as RTG scoring is needed to identify the critical confounders and thus inform experimental and data analysis choices that can ultimately improve models of the data.

The RTG score is based on non-parametric ordinal tests in the classical statistical hypothesis testing literature. Specifically, the query score $U_q^A$ is identical to the ROC AUC computed from the Mann-Whitney U statistic. The U test evaluates the null hypothesis that, for two random samples x and y from two independent populations, the probabilities of x > y and y > x are equal. The query score is the effect size of a U test comparing two populations corresponding to the distances from the query to data from either same-confounder or different-confounder groups. To obtain a single scalar describing the whole dataset, the RTG score is computed as the mean of the ROC AUCs of each U test over all possible queries. An alternative method for obtaining a single score for an entire dataset would be to pool all distances between pairs of data points that share a same-confounder label and pairs that do not, and then compute a single ROC AUC comparing these two pooled distributions. However, this approach is limited by both non-independence (two distances that share a sample are correlated) and adverse selection (over-represented confounder labels in the dataset lead to over-represented pairwise distances in both same-confounder and different-confounder groups). These correlations violate the independence assumptions required for the U test. Attempts to grapple with them have been reported in the literature—e.g., Gilbert et al.²⁴ have proposed some adjustments to standard two-sample tests to correct for these effects—but here we benefit from the fact that, at a per-query level, distances to the query for each group are independent, and therefore both of these limitations are mitigated. Hence we use the average of query-conditional Mann-Whitney U statistics to construct our RTG score.

RTG scoring is more than just a post hoc tool for comparing whether one data embedding is better—more confounder resilient—than another. Rather, we envision that the utility of our approach will be best realized as part of a virtuous cycle of experimental design, data collection, model building, and confounder analysis (Figure 1B). Careful attribution of confounding effects can give confidence as to an ML model’s likely performance after deployment. If, as in the example used throughout this article, a model’s ability to identify disease state is simply due to the fact that it has separated every clone in embedding space, there may be considerable concern that this model has not learned anything about disease per se. In this case, RTG analysis can guide how best to improve confounder robustness through both new experiments (i.e., by suggesting the highest-value new data to collect) and updated model training approaches (i.e., that are specifically designed to counter the effects of certain confounders) so as to mitigate confounder influences in the next cycle of development. The general applicability of this approach to high-dimensional datasets with complex, potentially nested, confounder hierarchies makes it of broad utility when using ML techniques to interrogate large-scale real-world datasets.

Experimental procedures

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, G. Sean Escola (gse3@columbia.edu).

Materials availability

This study did not generate new unique reagents.

Published: February 22, 2022

Data and code availability

In Figure 5, this paper analyzes existing data available at https://www.rxrx.ai/. Data for Figure 6 have been deposited at Zenodo under https://doi.org/10.5281/zenodo.5893469 and are publicly available as of the date of publication. All original code has been deposited at Zenodo under https://doi.org/10.5281/zenodo.5893469 and is publicly available as of the date of publication. All original code has also been deposited in GitHub at https://github.com/herophilus/rtg_score. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Algorithm 1: RTG score

We start with (1) the items in our dataset x_i for i = 1, …, N; (2) an included group variable I whose confounding effect we want to estimate; and (3) possibly an excluded group variable E whose confounding efforts we wish to ensure are not misattributed to I. Using the notation introduced in the main text, we want to calculate the RTG score RTG^I or, if E is present, the restricted RTG score RTG^I\E. For notational simplicity we use RTG^I for both scores here. Each item x_i has a label for the included group I_i and—optionally, when excluding another confounder—a label for the excluded group E_i.

We compute $U_q^I$, the query score for item q, as follows:

• 1Define two sets: S_q consisting of the indices of the items that share the same included group label I_q with item q, and D_q consisting of the indices of the items whose included group labels do not equal I_q. When excluding another potential confounder, the indices of the items that share the same excluded group label E_q with item q are removed from S_q and D_q.

$$S_q=\left\{i:i\ne qand{I}_i=I_q\left(\text{and optionally}{E}_i\ne E_q\right)\right\}$$

$$D_q=\left\{i:i\ne qand{I}_i\ne I_q\left(\text{and optionally}{E}_i\ne E_q\right)\right\}.$$

• 2Then, $U_q^I$ is defined as the fraction of pairs of items with indices in sets S_q and D_q, where the distance from the query item to the item whose index is in set S_q is less than it is to the item whose index is in set D_q (with half attribution in the case of equal distances): $U_q^I=\frac{1}{\left|S_q\right|\times \left|D_q\right|}{\sum }_{i\in S_q}{\sum }_{j\in D_q}\mathbb{1}\left[d\left({\mathbf{x}}_q,{\mathbf{x}}_i\right)<d\left({\mathbf{x}}_q,{\mathbf{x}}_j\right)\right]+0.5\times 1\left[d\left({\mathbf{x}}_q,{\mathbf{x}}_i\right)=d\left({\mathbf{x}}_q,{\mathbf{x}}_j\right)\right],$

where $\left|S_q\right|$ and $\left|D_q\right|$ are the number of elements in the sets S_q and D_q, and d(x_q,x_i) is any chosen distance measure that is valid for comparing items of our dataset.

This definition is identical to the ROC AUC computed when (1) all the items whose indices are in the set S_q∪D_q are sorted by their distance to the query item and labeled with 1 and 0s if their indices are members of S_q and D_q, respectively, and (2) the 1 and 0s are treated as true and false positives as in standard ROC analysis. Thus we can efficiently compute $U_q^I$ from a single pass through S_q∪D_q after sorting.

The RTG score RTG^I is simply the average of the scores $U_q^I$ over all possible query items in the dataset (i.e., for q = 1, …, N). Of note, for some queries, $U_q^I$ may be undefined because either set S_q or D_q is empty. These queries are excluded from averaging.