A Heterogenous, Time Harmonic, Nearly Incompressible Transverse Isotropic Finite Element Brain Simulation Platform for MR Elastography

Abstract

In this study, we describe numerical implementation of a heterogenous, nearly incompressible, transverse isotropic (NITI) finite element (FE) model with key advantages for use in MR elastography of fibrous soft tissue. MR elastography (MRE) estimates heterogenous property distributions from MR-measured harmonic motion fields based on assumed mechanical models of tissue response. Current MRE property estimation methods usually assume isotropic properties, which cause inconsistencies arising from model-data mismatch when anisotropy is present. In this study, we use a NITI model parameterized by a base shear modulus, shear anisotropy, tensile anisotropy, and an isotropic bulk modulus, which describes the mechanical behavior of tissues with aligned fiber structures well. Property and fiber direction heterogeneity are implemented at the level of FE Gauss points, which allows high-resolution diffusion tensor imaging (DTI) data to be incorporated easily into the model. The resulting code was validated against analytical solutions and a commercial FEM package, and is suitable for incorporation into nonlinear inversion MRE algorithms. Simulations of MRE in brain tissue with heterogeneous properties and anisotropic fiber tracts, which produced wavefields similar to experimental MRE, were generated from anatomical, DTI and MRE image data, allowing investigation of MRE inversion performance in a realistic setting where the ground truth and underlying mechanical behavior are known. Two established isotropic inversion algorithms – nonlinear inversion (NLI) and local direct inversion (LDI) – were applied to simulated MRE data. Both algorithms performed well in simple isotropic homogenous cases; however, heterogeneity cased substantial artifacts in LDI arising from violation of local homogeneity assumptions. NLI was able to recover accurate heterogenous displacement fields in the presence of measurement noise. Isotropic NLI inversion of simulated anisotropic data (generated using the NITI model) produced maps of isotropic mechanical properties with (undesirable) dependence on the wavefield. Local anisotropy also caused wavefield-dependent errors of 7% in nearby isotropic structures, compared to 10% in the anisotropic structures.

Introduction

Many biological tissues are composed of aligned fibrous structures, including skeletal muscle and brain white matter. In these cases, strong heterogeneities are also present in both mechanical properties and fiber directions due to networks of brain white matter tracts or multiple muscle bundles in a limb. The mechanical behavior of these tissues in response to applied loading is well described by nearly incompressible transverse isotropic equations of motion (Schmidt et al. 2016). Most mechanical property estimation techniques, such as MR elastography (MRE), assume mechanical isotropy, which causes model-data mismatches. These mismatches provoke wavefield dependencies in resulting mechanical property estimates in tissues that are strongly anisotropic. Anisotropic MRE approaches have been reported previously (Sinkus et al. 2005, Qin et al. 2013, Romano et al. 2012, Namani et al. 2009, Guo et al. 2016, Chatelin, el al 2016, Miller et al 2018), but, to date, they have required assumptions of local homogeneity that do not hold in complex organs such as the brain where heterogeneity is present in both mechanical properties and fiber directions. Nonlinear inversion (NLI) methods exploit models that are fully heterogeneous and capture reflection and mode conversion effects that are present in tissue, and an anisotropic formulation of NLI may prove advantageous for examining mechanical properties of brain and muscle tissue.

Adapting NLI to anisotropic models requires numerical implementation of the heterogenous anisotropic equations, which are well-suited to the finite element (FE) method, if computational challenges associated with large differences in shear and bulk moduli are addressed for nearly incompressible materials. A 4^th order elasticity tensor has 81 components in three-dimensions (3D), but symmetries reduce this number to 21 independent parameters for the general anisotropic case. Assuming further symmetries affords additional parameter reductions. Orthotropic models involve 3 orthogonal axes with different shear moduli, tensile moduli, and Poisson ratios which are represented by 9 independent parameters. Transverse isotropy (TI) is a special case in which properties are invariant as the coordinate system is rotated around a single axis (that typically corresponds to the direction of aligned fibers) and involves 5 independent parameters. Incompressible materials provide further simplification and reduce the number of free parameters to 3. Full incompressibility must be handled numerically with care; hence, nearly incompressible (NI) assumptions achieve “isotropic compressibility” through a bulk modulus term with a large value, which results in 4 free parameters in the transverse isotropic case (Itskov and Askel 2002), and allows models to include the fast p-wave (longitudinal wave) in nearly incompressible tissue.

In this paper, a reduced-parameter heterogenous, nearly incompressible (mixed displacement/pressure, u-p) transverse isotropic (NITI) FE model is described, which is parameterized by an in-plane shear modulus, shear anisotropy, tensile anisotropy, and bulk modulus. To the best of our knowledge, details associated with a heterogenous FE implementation of the 4-parameter NITI model have not been published previously. Other transverse isotropic options in the literature include five parameter compressible TI models (Kaliske 2000, Rouze et al. 2013), 5–7 parameter hyperelastic TI models (Weiss et al. 1996, Rüter et al. 2000), and 7-parameter biphasic TI models (Almeida et al. 1998). However, the NITI model has been proposed as the simplest case which reproduces experimentally confirmed shear and tensile anisotropy differences (Schmidt et al. 2016). Models with the minimum number of parameters needed to reproduce observed phenomena are advantageous for inversion algorithms, where obtaining estimates of many properties accurately can be difficult from limited, noisy data. In this implementation of the NITI model, property and fiber direction heterogeneity are accommodated in the FE model at the level of FE Gauss points, which allows high-resolution data on fiber direction to be incorporated to define axes of symmetry. The implementation is validated against analytical solutions and commercial software but is more modular and flexible than the latter, especially for MRE research studies because it enables relatively simple assimilation of patient specific imaging data. The source code and precise form of the FEM terms are also available, which is necessary for advanced FEM applications that require manipulation of individual stiffness matrix contributions, such as NLI for NITI MRE (Tan et al. 2016).

Combining this FE model with MRI anatomical atlases, diffusion tensor imaging (DTI) fiber directions, and MRE displacement maps also provides a simulation platform capable of generating realistic patient specific synthetic MRE data with which to test the performance of inversion algorithms in cases where the ground truth is known. MRE-focused simulations often fail to test major assumptions underpinning the inversion algorithms they are being used to validate. Direct inversion MRE relies on assumptions of local homogeneity and encounters problems with reflected waves which are unavoidable in practice. Simulations used to validate the approach often involve homogeneous properties configured in simple geometries that minimize reflections (Papazoglou et al. 2008, Jiang and Nakamura 2011, Hamhaber et al. 2007, Manduca et al. 2002, Clayton et al. 2011, Green et al 2008), and thus do not capture critical behavior of heterogeneous tissues. Simulations with simple spatial variations, for example discrete inclusions (Ou et al. 2007, Pattison et al 2014, Sanchez et al. 2010, Barnhill et al. 2017), have been investigated, although the zones of stiffness change have been small compared to a large homogenous background and inclusion center. Recent publications have presented simulations based on realistic geometries derived from imaging data which reveal inaccuracies in direct inversion MRE near mechanical property variations (Murphy et al. 2013, Barnhill et al. 2019, McGrath et al. 2016.). These simulations typically involved only a few homogeneous tissue classes, whereas in vivo MRE images suggest continuous spatial variations and distinct mechanical properties occur in a wide range of brain structures (Johnson et al. 2013, Guo et al. 2013). Thus, specification and treatment of heterogeneity are vital for simulations that replicate conditions associated with in vivo MRE, which is especially true when considering anisotropy where spatial variation in both properties and fiber directions are present.

In this study, we use the proposed NITI FE model to create realistic representations of brain tissue mechanics with a reduced number of parameters. Simulated wavefields with known properties, including heterogeneity and anisotropy, were generated to understand better the performance of MRE inversion algorithms in the brain. In particular, we examine the relative performance of NLI and local direct inversion (LDI) in recovering properties in homogenous and heterogenous simulated data, with and without measurement noise. We also apply isotropic NLI to anisotropic heterogenous data generated with the NITI model, and quantify the wavefield-dependent errors that occur in the resulting mechanical property estimates, which have been observed in vivo (Anderson et al. 2016). By validating the NITI FE model and replicating previous experimental results in simulation, we demonstrate utility of the model as a MRE simulation platform, and for use in development of anisotropic inversion algorithms in the future.

Nearly Incompressible Transverse Isotropic Model

The constitutive equation in Voigt notation (6×1 vector representation of the 2^nd order tensors) for the relationship between the stress, {σ}, and strain, {ϵ}, in a NITI material, where the axis of symmetry aligns with one of the coordinate directions (this orientation is denoted by σ′ and ϵ′) is given by (Feng et al. 2013, Tweten et al. 2015)

$$\left\{\begin{array}{l}{\sigma }_{11}^{\prime }\hfill \\ {\sigma }_{22}^{\prime }\hfill \\ {\sigma }_{33}^{\prime }\hfill \\ {\sigma }_{12}^{\prime }\hfill \\ {\sigma }_{23}^{\prime }\hfill \\ {\sigma }_{13}^{\prime }\hfill \end{array}\right\}=\left[\begin{array}{cccccc}{c}_{11}& c_{12}& c_{13}& 0& 0& 0\\ c_{21}& c_{22}& c_{23}& 0& 0& 0\\ c_{31}& c_{32}& c_{33}& 0& 0& 0\\ 0& 0& 0& c_{44}& 0& 0\\ 0& 0& 0& 0& c_{55}& 0\\ 0& 0& 0& 0& 0& c_{66}\end{array}\right]\left\{\begin{array}{c}{ϵ}_{11}^{\prime }\\ {ϵ}_{22}^{\prime }\\ {ϵ}_{33}^{\prime }\\ 2{ϵ}_{12}^{\prime }\\ 2{ϵ}^{\prime }{}_{23}\\ 2{ϵ}_{13}^{\prime }\end{array}\right\}.$$ (1)

In Equation 1, shear components are rearranged to match common numerical notation (Zienkiewicz et al. 1977). Defining the fiber axis as the x₁ direction, the components of the 6×6 elasticity matrix, [C], are given by

$$\begin{array}{l}{c}_{11}=\kappa +\frac{4}{3}\mu \left(1+\frac{4}{3}\zeta \right),c_{22}=c_{33}=\kappa +\frac{4}{3}\mu \left(1+\frac{1}{3}\zeta \right),c_{44}=c_{66}=\mu (1+\varphi ),\\ c_{12}=c_{13}=c_{21}=c_{31}=\kappa -\frac{2}{3}\mu \left(1+\frac{4}{3}\zeta \right),c_{32}=c_{23}=\kappa -\frac{2}{3}\mu \left(1-\frac{2}{3}\zeta \right),c_{55}=\mu \end{array}$$ (2)

where μ is the shear modulus in the plane normal to the fiber axis, ϕ is the shear anisotropy, ζ is the tensile anisotropy, and κ is the isotropic bulk modulus. Terms in Equation 2 involve sums of κ and μ, which are problematic numerically when κ ≫ μ, i.e. near incompressibility. If we define the material pressure to be,

$$P=\kappa \left({ϵ}_{11}+{ϵ}_{22}+{ϵ}_{33}\right),$$ (3)

κ can be removed from the terms in Equation 2 to produce an analogous system in Voigt notation

$$\left\{{\sigma }^{\prime }\right\}=[\overline{\mathit{C}}]\left\{{\mathit{ϵ}}^{\prime }\right\}+\left\{\begin{array}{l}P\hfill \\ P\hfill \\ P\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right\},$$ (4)

where terms in $[\overline{\mathit{C}}]$ are the same as those in [C] with κ removed. P becomes an additional degree of freedom, and Equation 3 is used as a penalty that enforces the near incompressibility condition. Separation of deviatoric and volumetric strains is common when implementing mixed u-p FEM for nearly incompressible materials (Zienkiewicz et al. 1977).

The simplified structure of the elasticity matrix in Equations 1 and 2 is lost when one of the coordinate directions is not aligned with the fiber axis. The 6×1 Voigt representation of the strain tensor, {ϵ}, with the fiber axis in the local x₁-direction, can be rotated into another coordinate system using a Bond transformation (Zienkiewicz et al. 1977), {ϵ′} = [B_ϵ]{ϵ}, where

$$\left[B_{ϵ}\right]=\left[\begin{array}{cccccc}{t}_{11}{t}_{11}& t_{12}{t}_{12}& t_{13}{t}_{13}& {\text{t}}_{11}{t}_{12}& {\text{t}}_{12}{t}_{13}& {\text{t}}_{13}{t}_{11}\\ t_{21}{t}_{21}& t_{22}{t}_{22}& t_{23}{t}_{23}& {\text{t}}_{21}{t}_{22}& {\text{t}}_{22}{t}_{23}& {\text{t}}_{23}{t}_{21}\\ t_{31}{t}_{31}& t_{32}{t}_{32}& t_{33}{t}_{33}& {\text{t}}_{31}{t}_{32}& {\text{t}}_{32}{t}_{33}& {\text{t}}_{33}{t}_{31}\\ 2{\text{t}}_{11}{t}_{21}& 2{\text{t}}_{12}{\text{t}}_{22}& 2{\text{t}}_{13}{\text{t}}_{23}& \left(t_{12}{t}_{23}+t_{13}{t}_{22}\right)& \left({\text{t}}_{12}{t}_{23}+t_{13}{t}_{22}\right)& \left({\text{t}}_{13}{t}_{21}+t_{11}{t}_{23}\right)\\ 2{\text{t}}_{21}{t}_{31}& 2t_{22}{t}_{32}& 2{\text{t}}_{23}{\text{t}}_{33}& \left(t_{21}{t}_{32}+t_{22}{t}_{31}\right)& \left({\text{t}}_{22}{t}_{33}+t_{23}{t}_{32}\right)& \left({\text{t}}_{23}{t}_{31}+t_{21}{t}_{33}\right)\\ 2t_{31}{t}_{11}& 2t_{32}{t}_{12}& 2{\text{t}}_{33}{t}_{13}& \left(t_{31}{t}_{12}+t_{32}{t}_{11}\right)& \left({\text{t}}_{32}{t}_{13}+t_{33}{t}_{12}\right)& \left({\text{t}}_{33}{t}_{11}+t_{31}{t}_{13}\right)\end{array}\right].$$ (5)

Here, the rotation matrix, T, expresses a vector in the global x-coordinate direction in the fiber axis, i.e. x′ =Tx. The elasticity matrix is similarly transformed via [𝐶′]=[B_ϵ]^T[𝐶][B_ϵ]. P is invariant to rotation so this transformation can be applied to either [𝐶] or $[\overline{C}]$. For the generalized case with arbitrary fiber alignment relative to the coordinate system, [𝐶] and $[\overline{C}]$ are fully populated 6×6 matrices. Physically, these relationships ensure uniaxial stress in a material where angled fibers produces axial and shear strains in all orientations, unless the fiber and stress directions are aligned.

Methods

Implementation of NITI model in FE framework

The governing equation of solid mechanics is written as

$${\partial }_i{\sigma }_{ij}=\rho {\ddot{u}}_J+F_j$$ (6)

where u is the displacement vector and F is an applied body force. In Equation 6, stress and strain appear as standard rank two tensors, rather than in the Voigt notation used above. MRE typically uses steady state vibration at a set frequency, ω, with no internal forces at the vibration frequency, i.e. u(x, t) = Re{U(x)e^iωt}, and F = 0. Assuming the complex-valued displacement amplitude, U, is supported on a set of finite element basis functions such that $U(x)={\sum }_{a=1}^N{u}^{(a)}{\psi }^{(a)}(x)$, the a^th Galerkin weighted residual statement in Eq. 6 is

$$\langle {\partial }_i{\sigma }_{ij}{\psi }^{(a)}\rangle =\langle -\rho {\omega }^2{U}_j{\psi }^{(a)}\rangle ,$$ (7)

where ⟨…⟩ = ∭(…) dV (Lynch 2004). Assuming a right-handed coordinate system and applying an appropriate integration by parts, ∮(ψn_iσ_ij)ds = ∭(∂_iσ_ij +σ_ij∂_iψ)dV, to the LHS gives

$$\langle {\sigma }_{ij}{\partial }_i{\psi }^{(a)}\rangle -\langle \rho {\omega }^2{u}_j{\psi }^{(a)}\rangle =\oint \left(n_i{\sigma }_{ij}{\psi }^{(a)}\right)dS,$$ (8)

Assuming a full 6×6 $[\overline{C}]$ matrix after rotation with respect to an arbitrary fiber orientation, and substituting terms into Equation 8, three components of ⟨σ_ij∂_iψ_a⟩ can be written as

$$\begin{array}{l}\langle \begin{array}{l}\left({\overline{c}}_{11}{ϵ}_{11}+{\overline{c}}_{12}{ϵ}_{22}+{\overline{c}}_{13}{ϵ}_{33}+2{\overline{c}}_{14}{ϵ}_{12}+2{\overline{c}}_{15}{ϵ}_{23}+2{\overline{c}}_{16}{ϵ}_{13}+P\right)\frac{d{\psi }^{(a)}}{dx}\\ +\left({\overline{c}}_{41}{ϵ}_{11}+{\overline{c}}_{42}{ϵ}_{22}+{\overline{c}}_{43}{ϵ}_{33}+2{\overline{c}}_{44}{ϵ}_{12}+2{\overline{c}}_{45}{ϵ}_{23}+2{\overline{c}}_{46}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dy}\\ +\left({\overline{c}}_{61}{ϵ}_{11}+{\overline{c}}_{62}{ϵ}_{22}+{\overline{c}}_{63}{ϵ}_{33}+2{\overline{c}}_{64}{ϵ}_{12}+2{\overline{c}}_{65}{ϵ}_{23}+2{\overline{c}}_{66}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dz}\end{array}\rangle \\ \langle \begin{array}{l}\left({\overline{c}}_{41}{ϵ}_{11}+{\overline{c}}_{42}{ϵ}_{22}+{\overline{c}}_{43}{ϵ}_{33}+2{\overline{c}}_{44}{ϵ}_{12}+2{\overline{c}}_{45}{ϵ}_{23}+2{\overline{c}}_{46}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dx}\\ +\left({\overline{c}}_{21}{ϵ}_{11}+{\overline{c}}_{22}{ϵ}_{22}+{\overline{c}}_{23}{ϵ}_{33}+2{\overline{c}}_{24}{ϵ}_{12}+2{\overline{c}}_{25}{ϵ}_{23}+2{\overline{c}}_{26}{ϵ}_{13}+P\right)\frac{d{\psi }^{(a)}}{dy}\\ +\left({\overline{c}}_{51}{ϵ}_{11}+{\overline{c}}_{52}{ϵ}_{22}+{\overline{c}}_{53}{ϵ}_{33}+2{\overline{c}}_{54}{ϵ}_{12}+2{\overline{c}}_{55}{ϵ}_{23}+2{\overline{c}}_{56}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dz}\end{array}\rangle \\ \langle \begin{array}{l}\left({\overline{c}}_{61}{ϵ}_{11}+{\overline{c}}_{62}{ϵ}_{22}+{\overline{c}}_{63}{ϵ}_{33}+2{\overline{c}}_{64}{ϵ}_{12}+2{\overline{c}}_{65}{ϵ}_{23}+2{\overline{c}}_{66}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dx}\\ +\left({\overline{c}}_{51}{ϵ}_{11}+{\overline{c}}_{52}{ϵ}_{22}+{\overline{c}}_{53}{ϵ}_{33}+2{\overline{c}}_{54}{ϵ}_{12}+2{\overline{c}}_{55}{ϵ}_{23}+2{\overline{c}}_{56}{ϵ}_{13}\right)\frac{d{\psi }^{(a)}}{dy}\\ +\left({\overline{c}}_{31}{ϵ}_{11}+{\overline{c}}_{32}ϵs_{22}+{\overline{c}}_{33}{ϵ}_{33}+2{\overline{c}}_{34}{ϵ}_{12}+2{\overline{c}}_{35}{ϵ}_{23}+2{\overline{c}}_{36}{ϵ}_{13}+P\right)\frac{d{\psi }^{(a)}}{dz}\end{array}\rangle \end{array}$$ (9)

Support of heterogeneities

FEM implementations often model heterogeneity with constant properties over each element, and use specialized meshes to define regional boundaries. Brain tissue contains few sharp interfaces in properties; smoothly varying properties and fiber directions are common between structures and along tracts; hence, high-resolution continuous basis support of model parameters is advantageous. Additionally, the specialized meshing required for elementally-constant properties is not practical for MRE inversion since the property interfaces are not known in advance.

The FE system is implemented on 27-node quadratic hexahedral elements for which integrals over elements are evaluated with Gaussian integration. Thus, the finest level of heterogeneity which can be accommodated occurs at Gauss points. Orientation of fiber axes is defined by diffusion tensor imaging (DTI) data, which are nearest-neighbor-interpolated to Gauss point locations. Heterogenous material property values, (μ, ϕ, ζ), are interpolated to Gauss points from independent property meshes using the appropriate basis functions (McGarry et al. 2012). The elasticity matrix is assembled in local fiber coordinates through Equation 1 for each Gauss point, and then transformed to the global coordinate system through Equation 5 for FEM stiffness matrix assembly via Gaussian integration. Clinical DTI data resolution is approximately 1–3 mm, whereas the highest resolution MRE acquisitions reported to date on a clinical system are 1.25 mm, with 2 mm being more typical (Johnson et al. 2013, Johnson et al. 2019). Imaging time usually dictates the resolution achieved in each scan; the Gauss point approach to heterogeneity maximizes the value of any high-resolution data when acquired.

Finite element support of displacement and pressure

To avoid volume locking, the pressure variable is supported on basis functions of lower order than the displacements. Displacement is expressed on standard quadratic FE basis functions, ψ, defined on isoparametric 27-node hexahedral elements (Zienkiewicz et al. 1977) and written as

$$U(x)={\sum }_{b=1}^{27}{U}^{(b)}{\psi }^{(b)}(x)$$ (10)

Pressure is represented on linear basis functions, χ, defined as χ₁ = 1, χ₂ = x_r, χ₃ = y_r, χ₄ = z_r, where the subscript r refers to the reference, or ‘parent’ coordinate system of the isoparametric element, written as

$$P(x)={\sum }_{n=1}^4{P}^{(n)}{\chi }^{(n)}(x)$$ (11)

These forms are often referred to as Q²-P¹ Nicolaides-Boland elements. For a FE mesh with N_n nodes and N_e elements, the vector of unknown values to be computed during the solution process, {u}, is of length 3N_n +4N_e, and is structured as

$$\{U\}={\left[U_1^{(1)}{U}_2^{(1)}{U}_3^{(1)}{U}_1^{(2)}{U}_2^{(2)}\cdots U_3^{\left(N_n\right)}{P}_1^{(1)}{P}_2^{(1)}{P}_3^{(1)}{P}_4^{(1)}{P}_1^{(2)}{P}_2^{(2)}\cdots P_4^{\left(N_e\right)}\right]}^T$$ (12)

where the superscripts refer to the node number for displacements, and element number for pressures.

Finite element matrix contributions

Substituting the definition of the strain tensor,

$${ϵ}_{ij}=\frac{1}{2}\left({\partial }_j{u}_i+{\partial }_i{u}_j\right)$$ (13)

into Equation 9, then using Equations 8, 10 and 11 allows the first 3 × N_n equations of the FE system to be generated. The remaining 4 × N_e equations required to solve the FE system for {U} are generated through Equation 3, enforced as a penalty term. The weighted residual form for the m^th pressure basis, χ^(m), serving as a weighting function can be written

$$\langle \left(-\frac{P}{\kappa }+\left({ϵ}_{11}+{ϵ}_{22}+{ϵ}_{33}\right)\right){\chi }^{(m)}\rangle =0$$ (14)

Specific forms of the FE stiffness matrix components are provided in the Appendix.

Viscoelasticity

In this study, time harmonic viscoelasticity is implemented through complex-valued moduli, μ. ϕ, ζ, and κ are real-valued parameters, and includes an isotropic form of damping through the material property definitions. Allowing ϕ and ζ to have non-zero imaginary contributions would achieve anisotropic damping, where shear waves attenuate differently depending on their propagation direction and wave polarization. Complex-valued κ causes phase lag between an applied hydrostatic stress and the resulting volumetric strain, which approximates p-wave damping when κ ≫ μ.

Model validation

The Fortran FE NITI model implemented with the MUMPS matrix solver (Amestoy et al. 2001) was validated against an analytic prediction of wavelength and exponential attenuation coefficient. The NITI model results in two shear waves, which depend on the propagation direction, $\overrightarrow{n}$, and the fiber direction, $\overrightarrow{f}$, and the angle, θ, between them (Tweten et al. 2015). In the undamped case with real-valued μ, The slow shear wave with wavespeed

$$c_{slow}^2=\frac{\mu }{\rho }\left(1+\varphi {\cos }^2\theta \right)$$ (15)

occurs when fibers are not stretched, i.e. when the wave polarization direction, m_s, is perpendicular to the plane defined by the propagation and polarization direction, i.e. ${\overrightarrow{m}}_s=\overrightarrow{n}\times \overrightarrow{f}$. Note that c_slow has no dependence on tensile anisotropy, ζ. When fibers are stretched, the fast shear wave appears, with wavespeed

$$c_{fast}^2=\frac{\mu }{\rho }\left(1+\varphi {\cos }^{2}2\theta +\zeta {\sin }^{2}2\theta \right).$$ (16)

Note that the maximum effect of ζ occurs when θ = 45°. The wave polarization direction in this case is ${\overrightarrow{m}}_f={\overrightarrow{m}}_s\times \overrightarrow{n}$. For harmonic viscoelasticity, the damped wavelength depends on both real and imaginary components (Guidetti and Royston, 2018). Defining the complex-valued slow modulus as ${\mu }_s=\frac{\mu }{\rho }\left(1+\varphi {(cos\theta )}^2\right)$ and the fast modulus as μ_f = μ(1 + ϕ(cos 2θ)² + ζ(sin 2θ)²), the expected shear wavelength at frequency F (Hz) is

$$L_{s\mid f}=\frac{1}{F}\sqrt{\frac{2}{\rho }\frac{{\left|{\mu }_{s_{\mid f}}\right|}^2}{Re\left({\mu }_{s_{\mid f}}\right)+\left|{\mu }_{s_{\mid f}}\right|}},$$ (17)

The damping ratio is ${\xi }_{s\mid f}=\frac{Im\left({\mu }_{s\mid f}\right)}{2Re\left({\mu }_{s\mid f}\right)}$, which gives an exponential attenuation coefficient of

$${\alpha }_{s\mid f}=\frac{2\pi }{L_{s\mid f}{\xi }_{s\mid f}}.$$ (18)

A 90×90×180 mm block geometry was created (long axis defined as the z direction), and shear displacement boundary conditions were applied on the XY face, in either the X or Y directions, resulting in shear waves propagating along the long axis of the block. Displacement amplitudes in other directions are small as the wave is nearly completely damped prior to reflection from the end face. Four fiber orientations were considered: X direction, Y direction, Z direction, and at an angle of 60 degrees from the Z axis in the XZ plane. The choices of fiber orientations and BC direction isolated either the slow or the fast shear wave to avoid the complication of the double damped sine wave fit required when both waves are present with significant amplitude. Material properties were μ = 2900 + 1200i, and 4 different combinations of the anisotropies were specified: (ϕ = 0.5, ζ = 0.5), (ϕ = 0, ζ = 0.5), (ϕ = 0.5, ζ = 0), and (ϕ = 0, ζ = 0). These parameter selections generate 8 simulations for each fiber orientation. Displacement profiles were extracted from the central axis of the block, which were fit to a decaying sinusoid via nonlinear least squares.

$$u_{fit}(z)=A{e}^{-\alpha z}sin\left(\frac{2\pi }{L}z+P\right)$$ (19)

The wavelength, L, and exponential attenuation coefficient, α, for each of the 32 block simulations were compared to the theoretical predictions in equations 17 and 18.

As an additional check, we compared our computations with a model evaluated previously within the commercial finite element package, (COMSOL Inc, Stockholm, Sweden) (Tweten et al. 2015, Tweten et al. 2017). A 50 mm cube of NITI material was generated and meshed at 2 mm. Material properties were assigned as μ = 3 + 0.3ikPa, ρ = .1000kgm⁻³, κ = 1000kPa, and boundary conditions obeyed 50–100 Hz x-directed shear vibration with 1 mm amplitude of the z = 0 face (all other faces were stress free). Validation was performed through isotropic (ϕ = 0, ζ = 0) and anisotropic cases with ϕ = 1, ζ = 2 and fibers in the x direction, at 30 degrees in the xz plane, and 45 degrees in the xy plane.

Brain model with DTI defined fiber directions

MRE data from a previous study was used to construct a patient-specific NITI brain model and investigate the performance of isotropic MRE inversion under conditions of known and controllable anisotropy. Full-brain MRE displacement data at 60 Hz were acquired with 2.0 mm isotropic resolution using a 3D multiband, multishot spiral MRE sequence (Johnson et al. 2019). Imaging parameters included: TR/TE = 2134/70 ms; field-of-view = 240×240 mm²; matrix = 120×120; 64, 2.0 mm thick slices; field inhomogeneity correction with auxiliary fieldmap. Two separate MRE datasets were recorded sequentially over the same field-of-view and resolution: one with vibration in the anterior-posterior (AP) direction and the other with vibration in the left-right (LR) direction (Smith et al. 2020). T₁-weighted anatomical images informed atlas-based segmentation of 10 white matter tracts (WMT) and 6 subcortical grey matter regions (SGM) using standard-space atlases (Hua et al. 2008, Makris et al. 1999). Segmentations were registered to MRE image space using FLIRT in FSL (Jenkinson et al. 2002, Jenkinson et al. 2012). DTI data provided fiber directions and fractional anisotropy (FA) maps. DTI imaging data were collected with a simultaneous multislice EPI sequence with same field-of-view and matrix as the MRE data with the following parameters: TR/TE = 3000/73.8 ms; b-value = 1000 s/mm²; multiband factor = 4; two acquisitions performed with reverse phase-encoding direction for distortion correction. Fiber directions and FA maps were determined using DTIfit in FSL (Jenkinson et al. 2012).

A mask generated from the MRE and DTI data was used to construct a model with realistic tissue classes and fiber orientations. Bulk white and grey matter were segmented by thresholding the T₂-weighted anatomical image, and the 10 WMT and 6 SGM regions were assigned homogenous properties based on global and regional properties we have published previously (Hiscox et al. 2019). Structures which were not included in the previous study were extracted from the underlying data using the same methods. Property values from literature were originally generated from 50 Hz MRE experiments, so we performed simulations at 50 Hz as well. WMTs were assigned baseline ϕ and ζ values, estimated from their average diffusion fractional anisotropy (FA), to encode different shear and tensile anisotropy in each structure. The diffusion FA for three diffusion eigenvalues, λ₁, λ₂, λ₃ is given by

$$FA=\sqrt{\frac{1}{2}}\frac{\sqrt{{\left({\lambda }_1-{\lambda }_2\right)}^2+{\left({\lambda }_2-{\lambda }_3\right)}^2+{\left({\lambda }_3-{\lambda }_1\right)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$ (15)

An equivalent mechanical FA, μ_FA, can be derived by assuming mechanical anisotropy is identical to diffusion anisotropy: $\frac{{\lambda }_1}{mean\left({\lambda }_2,{\lambda }_3\right)}=\frac{{\mu }_{12}}{{\mu }_{23}}=(1+\varphi )$, λ₂ ≈ λ₃. Applying this definition of ϕ to Eq. 15 leads to

$${\mu }_{FA}=\frac{\left|\varphi \right|}{\sqrt{3+2\varphi +{\varphi }^2}}$$ (16)

Equivalent ϕ values can then be computed by using

$$\varphi =\frac{-1\pm \sqrt{-2+\frac{3}{{\mu }_{FA}^2}}}{\left(1-\frac{1}{{\mu }_{FA}^2}\right)}$$ (17)

with the assumption that μ_FA = αFA, where the coefficient can be used to scale the relationship between mechanical and diffusion anisotropy. The tensile anisotropy parameter, ζ, can be estimated under the same assumption. Values of ϕ and ζ from Eq. 17 were multiplied by a random value in the range [0.8 1.2] to avoid the special case where ϕ = ζ. Although evidence suggests that gray matter regions have some mechanical anisotropy (Prange and Margulies 2002), gray matter was assumed to be isotropic to create a model with both perfectly isotropic and transverse isotropic tissue classes. Structures and their assigned NITI property values are summarized in Table 1.

Table 1:

Properties from the literature or subject-specific imaging used in the NITI brain simulation. Columns indicate the structure name/number (#), Gray/white matter classification (GW), the number of 2x2x2 mm voxels (N), fractional anisotropy from DTI (FA), and assigned NITI properties: real/imaginary shear modulus (μ, units of kPa), and the baseline shear and tensile anisotropy, ϕ and ζ. Regions of cerebrospinal fluid (including the ventricles) were not segmented for these simulations and were assigned the same properties as unspecified gray matter.

Structure	#	GW	N	FA	Re(μ)	Im(μ)	ϕ	ζ
Unspecified gray matter	1	G	61144	0.190	2.300	1.012	0	0
Unspecified white matter	2	W	52165	0.302	2.875	1.265	0.643	0.755
Anterior thalamic radiation	3	W	1312	0.355	3.152	1.351	0.838	0.665
Corticospinal tract	4	W	1624	0.512	2.886	1.242	1.720	1.461
Cingulum (cingulate gyrus)	5	W	554	0.412	3.497	0.910	0.964	0.823
Cingulum (hippocampus)	6	W	223	0.335	2.950	0.538	0.611	0.613
Forceps major/minor	7	W	3560	0.345	2.794	1.246	0.766	0.725
Inferior fronto-occipital fasciculus	8	W	1515	0.400	3.031	1.314	1.124	0.928
Inferior longitudinal fasciculus	9	W	1824	0.422	2.832	1.247	1.166	1.008
Superior longitudinal fasciculus	10	W	1879	0.340	2.732	1.306	0.841	0.641
Uncinate fasciculus	11	W	560	0.363	2.868	1.334	0.971	0.810
Superior longitudinal fasciculus	12	W	1020	0.445	2.922	1.361	1.261	0.945
Thalamus	13	G	1534	0.351	3.535	1.308	0	0
Caudate	14	G	539	0.172	3.381	1.460	0	0
Putamen	15	G	983	0.228	3.434	1.449	0	0
Pallidum	16	G	296	0.234	3.406	1.355	0	0
Hippocampus	17	G	606	0.182	3.022	1.070	0	0
Amygdala	18	G	297	0.156	3.256	1.290	0	0

Two sets of displacement boundary conditions were defined using boundary values from AP and LR MRE measurements (McGarry et al. 2015), which provided two realistic displacement fields that represent published experiments (Anderson et al. 2016) investigating the effects of wave propagation direction on isotropic inversions in the brain. The bottom surface was left stress-free to avoid high pressures arising from a boundary fully constrained with noisy measurement data. Figure 1 illustrates the process of creating the subject-specific NITI simulation. A 132,000 node, full-brain computational problem required 1032 seconds to run on a single core of an Intel Xeon Gold 6148 2.40 GHz processor with 384 GB of RAM.

Figure 1:

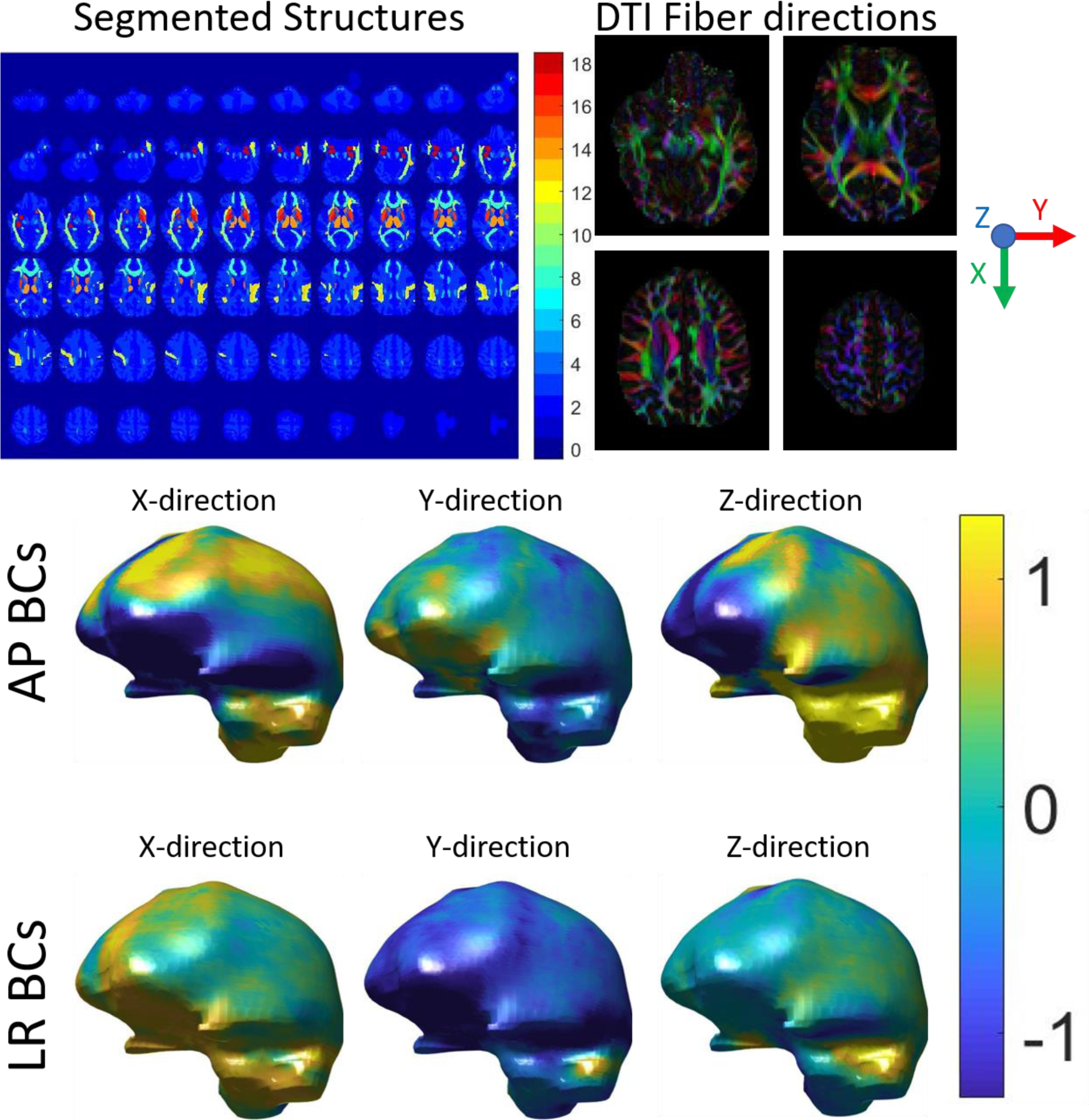
Subject-specific NITI FEM brain model. Top Left: Atlas-based segmentation of brain regions used to construct the model, where the region number correspond to structures detailed in Table 1. Top Right: DTI-defined fiber directions. Bottom: Two sets of boundary conditions (BCs) taken from MRE displacement measurements with AP and LR vibration, units of mm.

Isotropic inversion of simulated NITI data

Output from the NITI FE model was used as input for MRE inversion in order to investigate performance in an idealized situation where “true” properties are known. Isotropic simulated data (ϕ = ζ = 0) which were noise free, as well as with simulated added Gaussian noise (standard deviation equal to 5% of the mean absolute displacement value) were inverted with two commonly used isotropic MRE inversions – nonlinear inversion (NLI), and local direct inversion (LDI). Further analysis of the effect of anisotropy was investigated with NLI only.

NLI inversion parameters were the same as those applied in clinical brain studies, and included 100 global iterations with 3 conjugate gradient and 2 line search iterations per subzone, Gaussian smoothing between global iterations, 25 mm subzones with 15% overlap, and equal resolution for material property and input data (2 mm) (Hiscox et al. 2018). Real and imaginary shear modulus maps were recovered starting from an initial homogeneous estimate of μ = 3.3 + 1.188i kPa. Density was ρ = 1000 kgm⁻³ (same as the simulation), and bulk modulus was held constant at κ = 1649kPa to enforce near-incompressibility (simulations used κ = 1000kPa).

Details of the implementation of the LDI algorithm are available in the literature (Okamoto et al. 2011). Briefly, the curl of the data was taken using a 2^nd order Savitzky-Golay filter on 3×3×3 blocks of data to reduce compressional wave contributions. The curl data were smoothed with a 1 mm Gaussian filter, and the Laplacian of the curl was estimated using a central difference approximation. An assumption of local homogeneity of mechanical properties is then invoked to solve for an estimate of the complex-valued μ in Equation 6 at the center of 5×5×5 blocks of data via total Least Squares and the singular value decomposition. At the boundaries, data outside of the mask was given a weight of zero, and if less than 50% of the 5×5×5 block was present, the stiffness was not computed.

Presumably, mechanical and diffusion anisotropy have the same principal direction, since these effects are determined by the axes of anisotropy which are dominated by the fiber tract geometry. However, the magnitude of diffusion and mechanical anisotropy are governed by different physical mechanisms; therefore, the level of anisotropy is not expected to be the same for the two processes (in fact, they may provide distinct diagnostic signatures). Simulated data were generated by scaling ϕ and ζ between diffusion and mechanical anisotropy through the scalar $\alpha =\frac{{\mu }_{FA}}{FA}$, and differences between NLI inversions of AP and LR motions were investigated and compared to a previously published in vivo study (Anderson et al. 2016).

Results

Model validation

Agreement between theoretical and numerical values of the damped wavelength and exponential attenuation coefficient was found. Of the 32 combinations of fiber direction, boundary conditions and NITI parameter values investigated, two outliers occurred in which errors in the least squares fit were evident, which generated deviations greater than 12% in L and 29% in α. Excluding these two outliers, mean absolute difference between predicted and numerically estimated values of L and α in the 30 remaining cases were 0.53% and 2.8%, respectively. Examples of numerical and fitted curves for representative cases are shown in figure 2.

Figure 2:

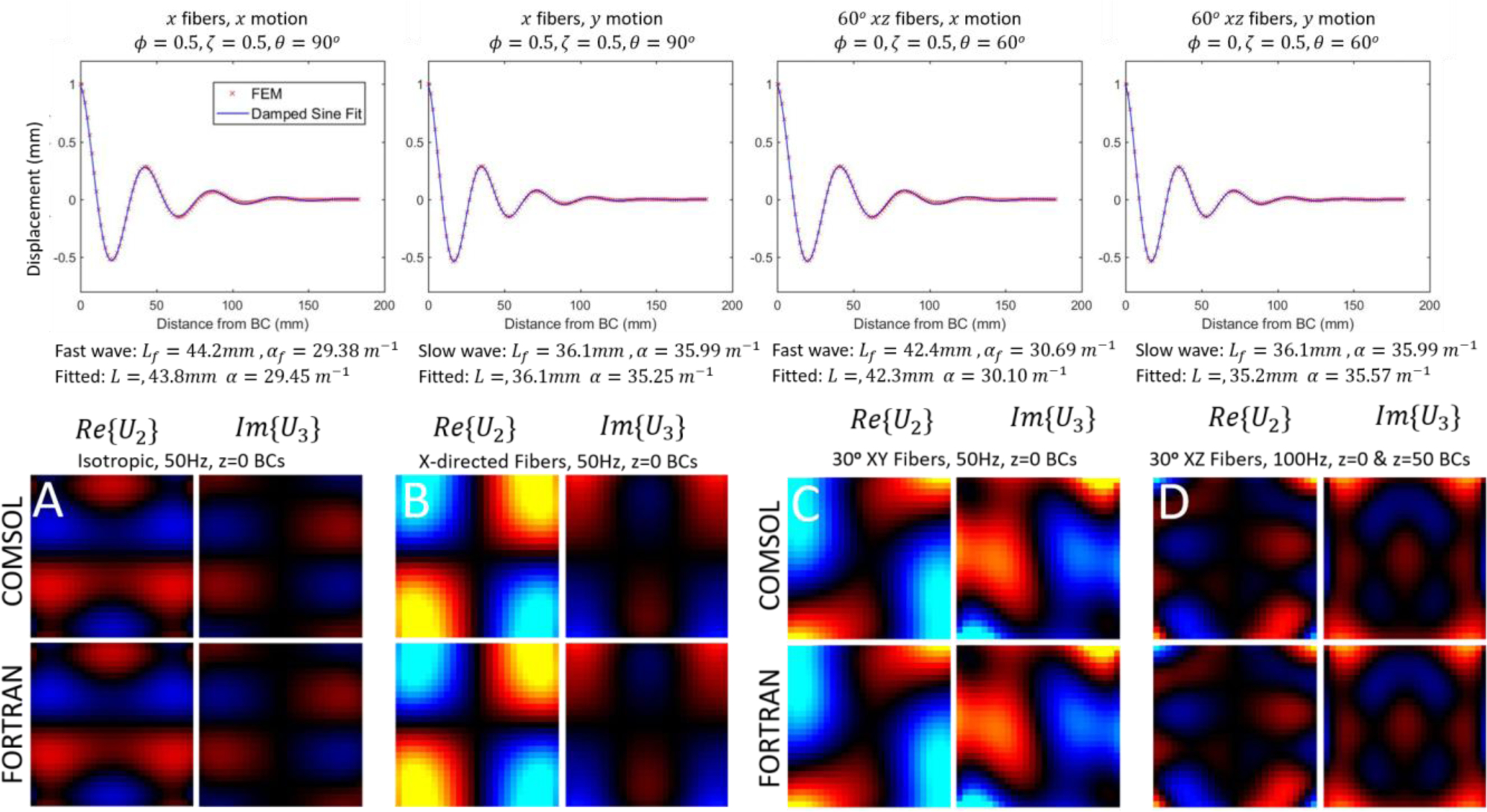
Verification of NITI implementation. Top row: Displacements along the central axis of an elongated block simulation. The parameters fit to a damped sinusoid (Eq. 19) are compared to theoretical predictions of wavelength, L, and attenuation, α (Eqs. 17–18). Bottom row: comparison of displacement field images of the simulation platform (Fortran), against a previously validated COMSOL implementation for A) isotropic case (ϕ = ζ = 0), B) Anisotropic with x-directed fibers (no rotation), C) and D), 30 degree fibers in the XY and XZ planes. Two arbitrary components for the central slice are shown in units of mm, as well as the RMS percentage difference for all components. RMS differences for the whole volume were: A=1.36%, B=0.87%, C=3.24%, D=1.93%.

Comparison of the Fortran-based NITI implementation described here and its COMSOL counterpart is also shown in Figure 2. The FE model reproduced the COMSOL results for isotropic cases, as well as for cases with arbitrarily aligned fibers in the xy- and xz-planes with RMS errors of 0–3%. The COMSOL mesh was a 25×25×26 grid of quadratic hexahedral elements, whereas the NITI implementation used a 13×13×13 nodal grid of quadratic-27 node hexahedral elements, small differences between solutions of this order are expected due to discretization errors. The elemental property support of COMSOL relative to the Gauss point support in the Fortran implementation describe here are identical in homogenous cases; hence, these differences are not expected to contribute to disagreement between models. The COMSOL model was previously validated through comparisons of plane wave solutions in the simulation to analytic solutions governing slow and fast shear waves in NITI materials (Tweten et al. 2015, Hou et al. 2020).

Example displacement fields from the subject-specific NITI brain model with AP and LR displacement boundary conditions are shown in Figure 3, and compared to experimental MRE measurements. We also compare displacement fields simulated with isotropic material properties. Differences between the NITI model and the isotropic model are 25% and 19% RMS for AP and LR boundary conditions, respectively. Difference images reveal local variations up to 100% between NITI and isotropic models.

Figure 3:

Comparison of experimentally measured MRE data (column 1) with predictions from the NITI model (column 2), and an isotropic model (column 3). Differences between NITI and isotropic model predictions appear in column 4. All components of the complex-valued amplitude are shown for the same slice in units of mm.

Isotropic inversions of isotropic data (ϕ = ζ = 0) based on NLI and LDI are compared in Figures 4 and 5 (homogeneous case), and Figures 6 and 7 (heterogenous case), for both AP and LR boundary conditions, with and without noise. Ideally, estimated parameter maps are independent of displacement field patterns. NLI performs well in all cases since the major assumption of isotropic elasticity is not violated, and NLI correctly models heterogenous materials. LDI performs well in the central region of homogenous data where the local homogeneity assumption is valid; however, it suffers from substantial artifacts near boundary and stiffness interfaces.

Figure 4:

Plots of Re(μ) in kPa. Single slice of NLI and LDI isotropic inversions of simulated heterogenous isotropic data. True Re(μ) assigned in the simulation appears on the left, and inversions of noise-free and 5% added Gaussian noise motion data are on the right. The first row reports data generated with BCs from AP actuated MRE data, whereas the second row presents results with BCs from LR actuation. The third row shows absolute differences in estimated properties between the two cases.

Figure 5:

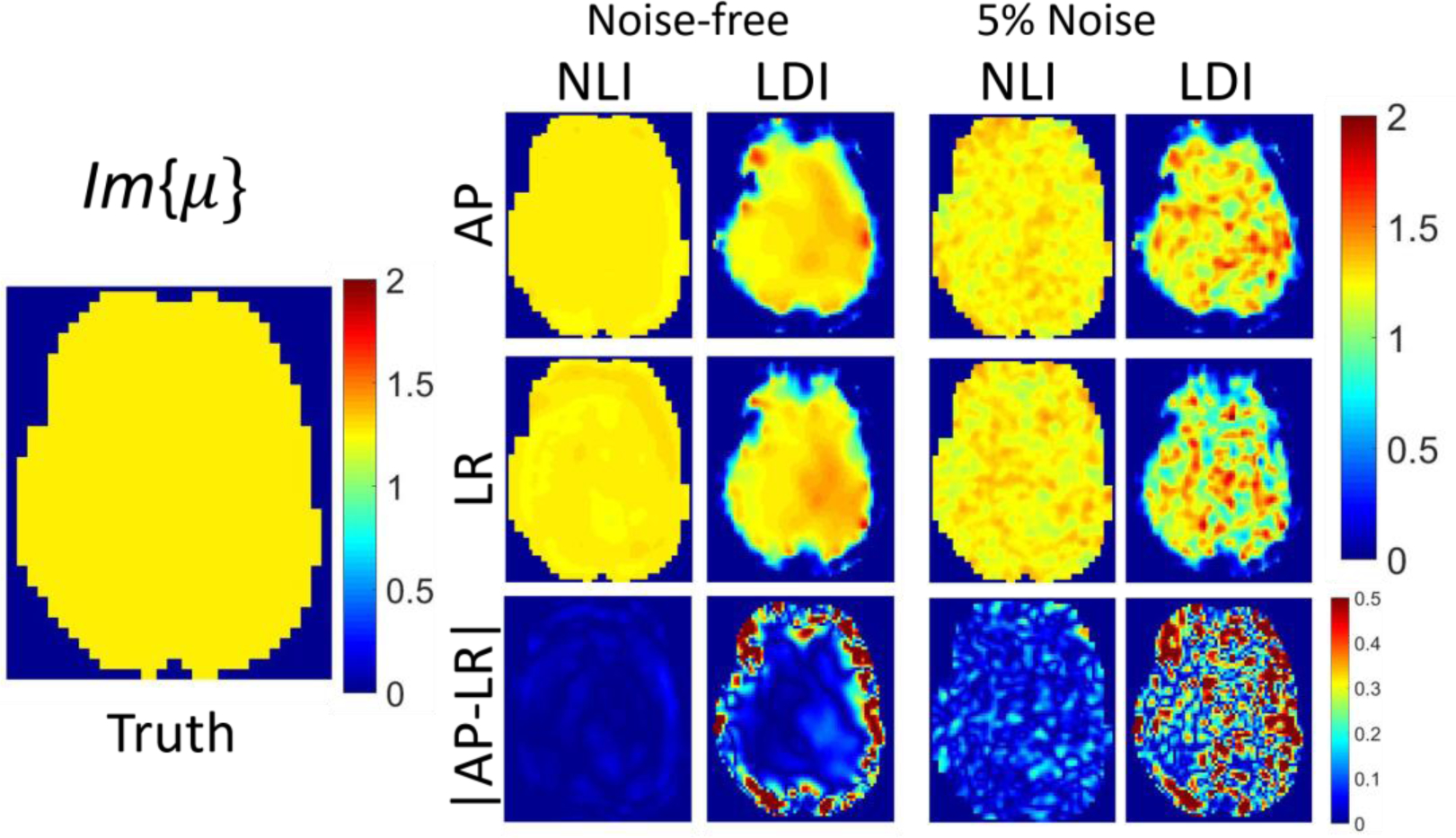
Plots of Im(μ) in kPa. Single slice of NLI and LDI isotropic inversions of simulated homogenous isotropic data. True Im(μ) assigned in the simulation appears on the left, and inversions of noise-free and 5% added Gaussian noise motion data are displayed on the right. The first row reports data generated with BCs from AP actuated MRE data, whereas the second row presents results with BCs from LR actuation. The third row shows absolute differences in estimated properties between the two cases.

Figure 6:

Plots of Re(μ) in kPa. Single slice of NLI and LDI isotropic inversions of simulated heterogenous isotropic data. True Re(μ) assigned in the simulation appears on the left, and inversions of noise-free and 5% added Gaussian noise motion data are on the right. The first row reports data generated with BCs from AP actuated MRE data, whereas the second row presents results with BCs from LR actuation. The third row shows absolute differences in estimated properties. between the two cases.

Figure 7:

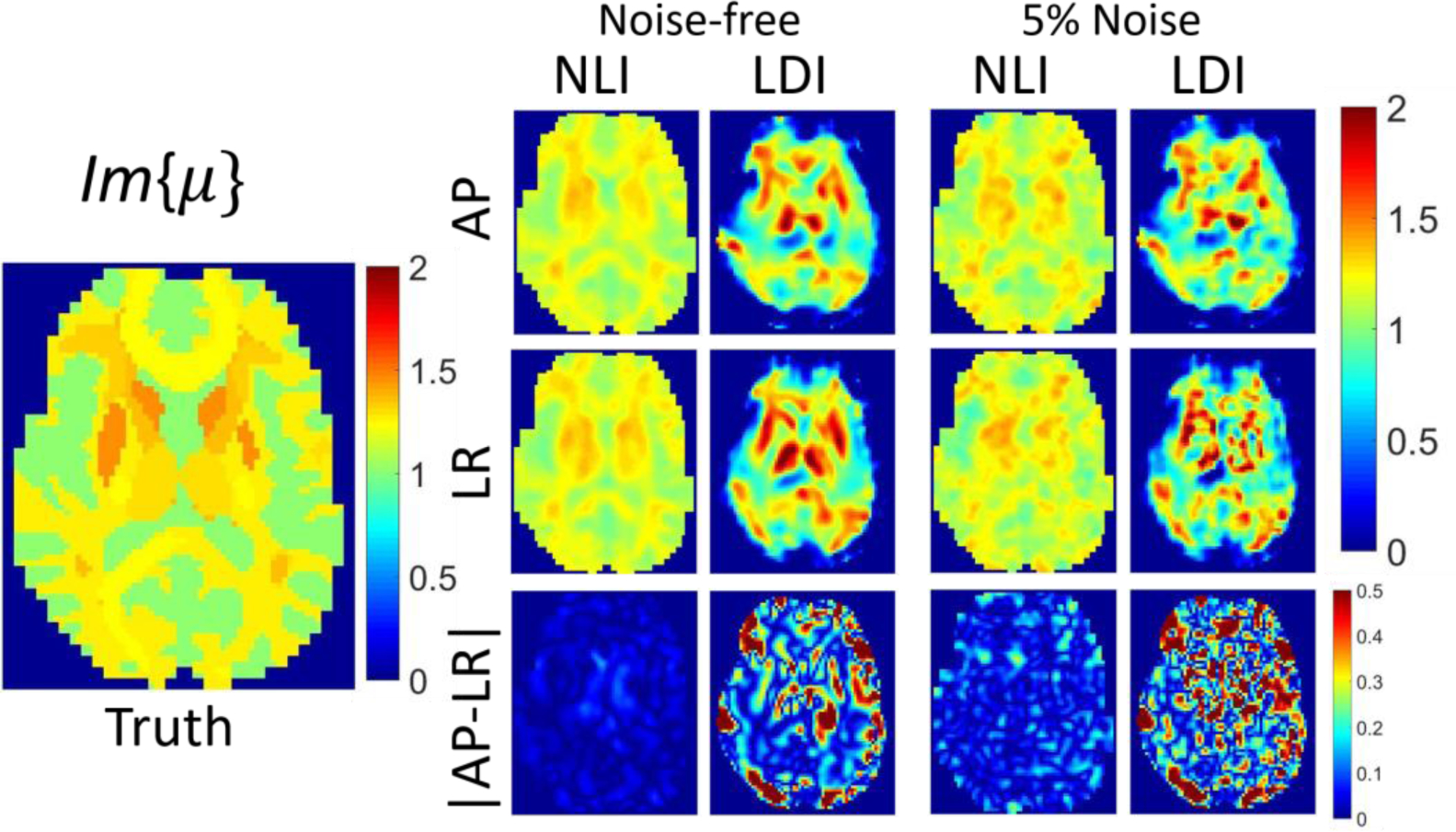
Plots of Im(μ) in kPa. Single slice of NLI and LDI isotropic inversions of simulated heterogenous isotropic data. True Im(μ) assigned in the simulation appears on the left, and inversions of noise-free and 5% added Gaussian noise motion data are on the right. The first row reports data generated with BCs from AP actuated MRE data, whereas the second row presents results with BCs from LR actuation. The third row shows absolute differences in estimated properties.

Isotropic NLI inversions of anisotropic data appear in Figure 8. The shear modulus estimate falls between the perpendicular and parallel shear moduli, and RMS difference between inversions of AP and LR motions increases to 8.6%, compared to 1.7% for inversions of isotropic data.

Figure 8:

Isotropic Inversion of simulated data generated with the anisotropic NITI model. A single central slice is shown, the true values used in the simulation are provided on the left, μ, ϕ and ζ values from Table 1, along with the shear modulus parallel to the fibers, μ_f = μ(1 + ϕ), and the Young’s modulus along the fibers, E_f = μ(3 + 4ζ). Images recovered by isotropic NLI are shown on the right. Inversions of AP and LR motion fields appear in rows 1 and 2, and row 3 reports the absolute difference, |μ_AP − μ_LR|. All units are kPa, other than ϕ and ζ, which are dimensionless.

Table 2 summarizes RMS errors with respect to the ground truth values for noise-free inversions, and RMS differences between AP and LR inversions for the cases illustrated in figures 4–8. Isotropic NLI inversions of isotropic displacement data had low RMS errors for both homogenous and heterogenous stiffness distributions (0.7–6.9% for Re(μ), 1.6–12% for Im(μ)). Consistency between NLI inversions using AP and LR displacement fields was also observed: RMS difference 1.0–1.7% for Re(μ), 1.8–3.0% for Im(μ). LDI inversion performed well in the central region of inclusions in the homogenous case, with RMS errors 4.6% for Re(μ) and 12% for Im(μ). Substantial artifacts occurred near the boundaries and at stiffness interfaces in heterogenous model cases, causing errors of 12–30% for Re(μ) and 22–70% for Im(μ) under these conditions. Despite the property estimation errors, consistency of LDI for AP and LR vibration fields was relatively good, even in heterogenous case: RMS differences of 3.7% for Re(μ), 7.1% for Im(μ). NLI inversion of anisotropic data increased RMS differences between AP and LR inversions to 8.6% and 15% for Re(μ) and Im(μ), respectively (relative to 1.7% and 3.0% for the isotropic case).

Table 2:

RMS differences for NLI and LDI inversions between ground truth parameters and values recovered from inversion of noise-free data (average of AP and LR inversions), and RMS differences between the AP and LR inversions. NLI differences are computed from the full field solution, whereas LDI results use a mask eroded by seven serial erosions with a 3x3x3 kernel to avoid the artifacts near the boundary evident in figures 4–8. The last row presents values from isotropic NLI inversions of anisotropic data; RMS differences with the truth are not given since three moduli are supplied to the forward simulation, but only one is recovered by inversion.

	Re(μ): truth	Im(μ): truth	Re(μ): AP-LR	Im(μ) – AP-LR
NLI: homogeneous isotropic simulation	0.74%	1.6%	1.04%	1.76%
LDI: homogeneous isotropic simulation	4.6%	11.9%	8.5%	20.3%
NLI: heterogenous isotropic simulation	6.9%	11.8%	1.7%	3.0%
LDI: heterogenous isotropic simulation	12.3%	22.9 %	3.0%	7.13%
NLI: heterogeneous anisotropic simulation	N/A	N/A	8.6%	15.0%

The NITI brain model was also used to investigate the effect of anisotropic structures on nearby isotropic regions for isotropic NLI inversion. Weak correlation was found between property variability and AP and LR boundary conditions (Figure 5), and some isotropic structures exhibited errors as large as those observed in the most strongly anisotropic regions – for example, the isotropic pallidum had an AP-LR difference of 0.32 kPa, which was almost as high as the largest differences in anisotropic WM tracts, such as the uncinate fasciculus at 0.33 kPa, and the corticospinal tract at 0.39 kPa. GM and WM structures had AP-LR RMS differences of 1.8% and 1.7%, respectively, when both were defined as isotropic, and 7.2% and 9.8%, respectively, for NITI simulated data when gray matter was isotropic, and white matter was defined as TI. These results suggest that neglecting anisotropy will increase the wavefield dependent error for in vivo MRE by a factor of 4 to 5 (assuming μ_FA =FA).

A plot of AP-LR RMS differences for Re(μ) of isotropic NLI inversions, where the level of mechanical anisotropy in the simulated data was scaled to be lower than the diffusion anisotropy from FA measurements is shown in Figure 10. As expected, lower anisotropy resulted in smaller RMS differences between AP and LR motions. In vivo results from (Anderson et al. 2016) reported average white matter differences of 2.2% and maximum differences of 23% in highly aligned white matter tracts, which corresponds to a scaling factor in the range 0.2–0.25 in Figure 10, as indicated by the dashed lines.

Figure 10:

Effect of setting the mechanical anisotropy by scaling the diffusion anisotropy. Simulated data were generated by computing ϕ and ζ through equation 17, and while adjusting the scalar multiplier, α, that maps diffusion anisotropy to mechanical anisotropy. Mean (left axis) and maximum (right axis) difference between isotropic NLI inversions of simulated data with AP and LR displacement fields are plotted. Dashed lines indicate in vivo results reported in (Anderson et al. 2016).

Discussion

Many tissues in the human body consist of aligned fibers, resulting in transverse isotropic mechanical properties (e.g. skeletal muscle and brain white matter). Importantly, both fiber directions and mechanical properties have strong spatial variation in vivo, as evidenced by the structure maps and DTI images shown in Figure 1. The majority of MRE inversions currently used in practice assume isotropic properties and many also assume local homogeneity. The consequences of violating these assumptions have not been investigated thoroughly. The finite element (FE) implementation of a heterogenous, NITI material presented here is capable of modeling wave propagation in fibrous tissues, such as brain and muscle. The model accommodates heterogeneity in both properties and fiber directions at FE Gauss points, which achieves the highest possible discretization on a given FE mesh. DTI data with resolution higher than the MRE acquisitions can be incorporated into the model. Reflections and wave propagation are modeled appropriately, which ensures the simulated data are representative of wave behavior observed in heterogenous elastic solids such as tissue.

The nearly incompressible behavior of tissue is evidenced by the vastly different propagation speeds of sound (~1540 m s⁻¹), and shear waves (~1–2 m s⁻¹). The FE NITI implementation presented here takes advantage of the structure of the elasticity matrix (Tweten et al. 2015) to separate shear and bulk moduli, and enforces low compressibility through a penalty equation. This strategy introduces an extra, unknown, pressure variable into the FEM system that incurs increased computation costs, however, implementation is relatively straightforward, and models p-wave and associated mode conversions at boundaries and stiffness interfaces in the computations. We have used this approach successfully in our previous isotropic NLI routines (McGarry, et al, 2012), and have adopted it for the NITI material here. In a general compressible TI material, bulk moduli will also be anisotropic, which generates 5 independent mechanical parameters. In our model, we have assumed isotropic compressibility, which is expected to be accurate provided κ ≫ μ, and has the benefit of reducing the number of unknown material property parameters to 4. Nearly incompressible formulations are available with accurate treatment of bulk modulus anisotropy (Taylor et al. 1968); however, they involve much more complicated FE stiffness matrix terms, which are not ideal for methods that exploit FEM in other techniques (such as model-based MRE inversions) because these terms must be differentiated with respect to the mechanical property parameters in order to generate iterative property updates (Van Houten et al. 2001). The FEM terms in this model are linear in μ, ϕ, and ζ, which makes differentiation straightforward.

The model can be used to generate forward-simulated data to test MRE inversion algorithms under idealized conditions where “ground truth” properties are known. The brain model illustrated in Figure 1 incorporates subject-specific maps of brain structures with properties taken from the literature, fiber directions from DTI data, and fractional anisotropy maps to approximate mechanical anisotropy. Realistic wavefields are generated through simulations by using measured MRE data as boundary conditions. Although the goal of the simulations was not to match MRE experiments exactly, Figure 3 shows that the simulated data resemble the experimentally measured MRE results in terms of wavelength and major features of the wave pattern. Noticeable differences between measured and simulated data are evident around the falx, which is a stiff membrane-like structure that is not included in this model explicitly, and the ventricles, which are modeled as a solid tissue continuum rather than true fluid-filled spaces. Accurately modeling these structures would further improve the simulation platform and will be addressed in future work. Properties used in simulations were average literature values from isotropic MRE at 50 Hz and were assumed to be constant over each structure. Applying subject-specific MRE maps and anisotropic mechanical testing data collected under controlled conditions for these properties would likely yield a closer match between the model and these 60 Hz MRE displacements, but would be less appropriate for testing the spatial accuracy of MRE inversions. Although appreciable differences between the NITI and isotropic models occur in these simulations, applying measured data as boundary conditions around most of the exterior give results which are more similar than would be expected for a simulation with free boundary conditions. Modeling the true boundary conditions on the surface of the brain from skull vibration is difficult due to the surrounding CSF, arachnoid trabeculae and cerebral meninges. Using MRE measured displacements to define brain surface boundary conditions produces realistic wave fields in simulation and ensures that conclusions drawn from simulated inversions are relevant to common experimental MRE conditions.

Experiments where isotropic simulated data were inverted with isotropic NLI (based on a heterogenous FE model) and LDI (assuming locally homogenous mechanical properties) showed that NLI outperformed LDI in all cases, particularly near the boundaries and at tissue stiffness interfaces where shear wave reflections are generated. The assumption of local homogeneity of μ required to simplify Equation 6 and allow direct solutions through LDI means that shear wave reflections are not modeled correctly, leading to the artifacts visible in Figures 4–7. Despite the artifacts in the heterogenous LDI inversions, the AP and LR inversions were similar, which demonstrates that LDI is reasonably independent of wavefield patterns. NLI was also less sensitive to noise than LDI, although the inversion parameters in NLI and LDI can be modified to trade off accuracy and spatial resolution with noise sensitivity, so this result should be considered valid only for the particular parameters used in this study. The LDI model we implemented has been applied in the literature; however, other direct inversion algorithms are available that use techniques such as directional filtering to reduce reflections which are not included in our simulations. Data generated here from simulations are available for testing with more sophisticated direct inversion algorithms from other research groups in the future.

Effects of NITI materials on isotropic inversions were investigated by applying anisotropic properties to white matter structures while keeping gray matter isotropic. In recent MRE literature, isotropic inversions are speculated to have larger errors in anisotropic white matter due to model-data mismatch while more isotropic gray matter will be less affected (Johnson et al. 2013, Guo et al. 2013). In the isotropic NLI inversions in Figure 8, anisotropy in the simulated data results in an isotropic MRE approximation which is a weighted average of the two shear moduli; the weighting is likely to be proportional to the energy of waves propagating parallel and transverse to the local fiber axes, respectively (Schmidt et al. 2016). Differences between inversions using AP and LR boundary conditions are 4–5 times as large for the NITI model relative to the isotropic case, as different wavefields yield different primary wave propagation directions. A weak correlation is apparent (Figure 9) between local anisotropy and wavefield-dependence of properties, which indicates that the presence of anisotropy also causes errors in nearby isotropic structures. Accordingly, a spatially accurate NITI NLI approach can be expected to improve parameter estimates in both gray and white matter structures, and an advantage of the relatively simple form of the FEM terms in the NITI model presented here is ideal for future implementation in advanced FE model-based inversions such as NLI. The differences in AP and LR motions indicate the sensitivity of MRE results to wavefield and likely propagation direction. While solving for all 4 parameters in the NITI model is theoretically possible given a single wavefield, it has been hypothesized that including two or more wavefields may improve the estimation (Anderson et al. 2016, Smith et al. 2020), and overcome potential limitations associated with insufficient wave propagation relative to fiber direction (Tweten et al., 2017).

Figure 9:

Effect of local anisotropy on wave direction dependence of isotropic MRE inversion of NITI simulated data. The y-axis represents the difference in average recovered property values for each structure defined in Table 1, in kPa. The x-axis is the average anisotropy, $\frac{\varphi +\zeta }{2}$.

Figure 10 suggests that scaling the mechanical anisotropy to be 4 to 5 times lower than the diffusion anisotropy measured with DTI approximately matches published in vivo results Anderson et al. (2016), where experimentally demonstrated differences of 2.2% in bulk white matter and larger differences (up to 23%) in highly aligned WM structures were reported. This finding indicates mechanical anisotropy may be lower than diffusion anisotropy, and provides an approximate scaling relationship for assigning realistic anisotropic ϕ and ζ parameters in future simulations. This further suggests anisotropy on the order of ~10–30% present in brain WM tracts, which is similar to previous in vivo and ex vivo assessments, although more direct evidence from in vivo anisotropic MRE would be required to provide more reliable estimates.

Conclusions

A finite element model based on an NITI material was developed and details of the FEM implementation in heterogenous materials were presented for the first time. The model was used to perform subject-specific simulations of shear wave behavior in the brain. MRE, DTI, and anatomical MRI data were collected to generate realistic wavefields in a full-brain geometry, which were then used to quantify error and wavefield dependencies in estimated properties for two commonly used inversion algorithms under idealized conditions. Analysis of simulated data demonstrated that local anisotropy affects parameter estimates in both anisotropic structures (white matter tracts) and nearby isotropic regions, motivating development of model-based heterogenous NITI inversions. The approach, which makes the stiffness matrix terms accessible within the FEM model, provides the foundation for implementing NLI-based MRE inversion.

Appendix: Finite element stiffness matrix terms.

Replacing ϵ_ij in equation 9 with equation 13 and substituting equations 10 and 11 for U and P allows the finite element stiffness matrix contribution from each gauss point to be calculated.

Equation 9 contributes a 3×3 submatrix, A_dd, for each weighting function, ψ^a, and each nodal basis function supporting the displacements, χ^(b). The terms are given by

$$\begin{gathered} A_{dd}(1,1)=\langle \left({\overline{c}}_{11}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{14}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{16}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{41}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{44}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{46}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{61}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{64}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{66}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}-\rho {\omega }^2{\psi }^b{\psi }^a\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(1,2)=\langle \left({\overline{c}}_{12}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{14}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{15}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{42}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{44}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{45}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{62}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{64}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{65}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(1,3)=\langle \left({\overline{c}}_{13}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{15}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{16}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{43}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{45}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{46}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{63}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{65}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{66}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(2,1)=\langle \left({\overline{c}}_{41}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{44}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{46}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{21}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{24}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{26}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{51}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{54}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{56}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(2,2)=\langle \left({\overline{c}}_{42}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{44}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{45}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{22}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{24}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{25}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{52}\frac{\partial {\psi }^{(b)}}{\partial v}+{\overline{c}}_{54}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{55}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle -\rho {\omega }^2{\psi }^b{\psi }^a \end{gathered}$$

$$\begin{gathered} A_{dd}(2,3)=\langle \left({\overline{c}}_{43}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{45}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{46}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{23}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{25}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{26}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{53}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{55}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{56}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(3,1)=\langle \left({\overline{c}}_{61}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{64}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{66}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{51}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{54}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{56}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{31}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{34}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{36}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(3,2)=\langle \left({\overline{c}}_{62}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{64}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{65}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{52}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{54}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{55}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial y} \\ +\left({\overline{c}}_{32}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{34}\frac{\partial {\psi }^{(b)}}{\partial x}+{\overline{c}}_{35}\frac{\partial {\psi }^{(b)}}{\partial z}\right)\frac{\partial {\psi }^{(a)}}{\partial z}\rangle \end{gathered}$$

$$\begin{gathered} A_{dd}(3,3)=\langle \left({\overline{c}}_{63}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{65}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{66}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial x}+\left({\overline{c}}_{53}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{55}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{56}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial x} \\ +\left({\overline{c}}_{33}\frac{\partial {\psi }^{(b)}}{\partial z}+{\overline{c}}_{35}\frac{\partial {\psi }^{(b)}}{\partial y}+{\overline{c}}_{36}\frac{\partial {\psi }^{(b)}}{\partial x}\right)\frac{\partial {\psi }^{(a)}}{\partial x}-\rho {\omega }^2{\psi }^b{\psi }^a\rangle \end{gathered}$$

There is also a 3×1 submatrix, A_dp, for every weighting function, ψ^(a), and pressure basis support function, χ⁽ⁿ⁾, and these terms are given by

$$A_{dp}(1)=\langle {\chi }^{(n)}\frac{d{\psi }^{(a)}}{dx}\rangle$$

$$A_{dp}(2)=\langle {\chi }^{(n)}\frac{d{\psi }^{(a)}}{dy}\rangle$$

$$A_{dp}(3)=\langle {\chi }^{(n)}\frac{d{\psi }^{(a)}}{dz}\rangle$$

Substituting Equation 13 and Equation 10 into Equation 14 generates the FE system

$$\langle \left(\sum _{n=1}^4\left(\frac{1}{\kappa }{P}^{(n)}{\chi }^{(n)}\right)-\sum _{b=1}^{27}\left(u_1^{(b)}\frac{\partial {\psi }^{(b)}}{dx}+u_2^{(b)}\frac{\partial {\psi }^{(b)}}{dy}+u_3^{(b)}\frac{\partial {\psi }^{(b)}}{dz}\right)\right){\chi }^{(m)}\rangle =0$$ (15)

This expression produces a 1×3 submatrix, A_pd, for each pressure basis weighting function, χ_m, and displacement basis function, ψ^(b),

$$A_{pd}(1)=\langle \frac{\partial {\psi }^{(b)}}{dx}{\chi }^{(m)}\rangle ,A_{pd}(2)=\langle \frac{\partial {\psi }^{(b)}}{dy}{\chi }^{(m)}\rangle ,A_{pd}(3)=\langle \frac{\partial {\psi }^{(b)}}{dz}{\chi }^{(m)}\rangle$$ (16)

and a 1×1 submatrix, A_pp, for each pressure basis weighting function, χ^(m), and pressure basis support function, χ⁽ⁿ⁾,

$$A_{pp}=\langle \frac{1}{\kappa }{\chi }^{(n)}{\chi }^{(m)}\rangle$$ (17)

Comparison of A_pd with terms in A_dp confirms that the approach maintains FE stiffness matrix symmetry, which offers storage and computation speed benefits to the mixed nearly incompressible implementation.

The volume integrals indicated by the 〈⋯〉 notation are computed by Gaussian integration, so these terms just need to be evaluated at each Gauss point and included in the weighted sum. The submatrices are inserted into the global stiffness matrix based on the global location of a, b and n in the solution vector, {U} defined in equation 12. Standard isoparametric mappings are also used to transform basis functions and their derivatives from the parent to global coordinate systems (Zienkiewicz et al. 1977).