Abstract
Linezolid is an efficacious medication for the treatment of drug-resistant tuberculosis but has been associated with serious safety issues that can result in treatment interruption. The objectives of this study were thus to build a population pharmacokinetic model and to use the developed model to establish a model-informed precision dosing (MIPD) algorithm enabling safe and efficacious dosing in patients with multidrug- and extensively drug-resistant tuberculosis. Routine hospital therapeutic drug monitoring data, collected from 70 tuberculosis patients receiving linezolid, was used for model development. Efficacy and safety targets for MIPD were the ratio of unbound area under the concentration versus time curve between 0 and 24 h over minimal inhibitory concentration (fAUC0–24h/MIC) above 119 and unbound plasma trough concentration (fCmin) below 1.38 mg/L, respectively. Model building was performed in NONMEM 7.4.3. The final population pharmacokinetic model consisted of a one-compartment model with transit absorption and concentration- and time-dependent auto-inhibition of elimination. A flat dose of 600 mg once daily was appropriate in 67.2% of the simulated patients from an efficacy and safety perspective. Using the here developed MIPD algorithm, the proportion of patients reaching the efficacy and safety target increased to 81.5% and 88.2% using information from two and three pharmacokinetic sampling occasions, respectively. This work proposes an MIPD approach for linezolid and suggests using three sampling occasions to derive an individualized dose that results in adequate efficacy and fewer safety concerns compared to flat dosing.
Keywords: tuberculosis, population pharmacokinetics, linezolid, auto-inhibition of linezolid elimination, model-informed precision dosing, simulation
1. Introduction
Rifampicin-resistant (including multidrug-resistant (MDR)) tuberculosis (TB) is still a global health threat, with close to half a million new cases annually [1]. MDR-TB is defined as resistant to both isoniazid and rifampicin and extensively drug-resistant (XDR) as resistant to isoniazid and rifampicin, plus any fluoroquinolone and at least one Group A drug (levofloxacin, moxifloxacin, bedaquiline, or linezolid). Treatment of these infections requires the use of second-line treatment, which is longer, associated with higher costs, increased toxicity, and has a success rate of merely 59% [2,3]. Currently, one of the core second-line anti-TB drugs used for the treatment of MDR- and XDR-TB is linezolid, a synthetic antibiotic from the oxazolidinone class, inhibiting the bacterial protein synthesis by binding to the 23S rRNA of 50S ribosomal subunit [4]. Its two main inactive metabolites are hydroxyethyl glycine and aminoethoxy acetic acid, excreted both renally (unchanged) and non-renally [4]. The efficacy of linezolid has been suggested to be related to the ratio of unbound area under the concentration versus time curve between 0 and 24 h over minimal inhibitory concentration (fAUC0–24h/MIC) with a threshold above 119 [5,6]. As a potential safety target for linezolid in TB treatment, it has been suggested that the unbound plasma trough concentration (fCmin) should be below 1.38 mg/L [6,7] since the time above fCmin is assumed to be related to mitochondrial toxicity [8,9].
Treatment of MDR- and XDR-TB with linezolid (nowadays usually in combination with one of the later generation fluoroquinolones, bedaquiline, and another second-line anti-TB drug) [10] is much longer than the standard treatment of other indications with linezolid that have a maximum treatment length of 28 days, which has been shown to lead to more serious adverse events [6,10]. A common adverse event, especially during longer treatment, is myelosuppression (mainly thrombocytopenia, but also leukopenia and anemia). Peripheral and optic neuropathy, lactic acidosis, hepatotoxicity, and hypoglycemia occur more seldom but can be severe and irreversible (neuropathies) [6,11]. Linezolid’s high toxicity during longer treatment contributes to a treatment discontinuation rate of 22.6% (141/624, based on 11 studies conducted between 2009 and 2018) [12]. One approach to reduce the risk of developing serious adverse events and minimize the risk of early treatment discontinuation is model-informed precision dosing (MIPD) [13]. MIPD is guided by patient characteristics, individual plasma drug concentrations, and a population pharmacokinetic (PK) or combined pharmacokinetic-pharmacodynamic (PKPD) model. The approach can be used in TB treatment to reduce the risk of treatment failure as well as toxicity [13,14,15,16]. The challenge in the treatment of MDR- and XDR-TB is to administer a linezolid dose that is highly efficacious with limited toxicity. MIPD can be used to support individual dose selection using a population PK model and targets for efficacy and safety.
The objectives of this work were to develop a population PK model, which, together with pre-set efficacy and safety targets, can be used to develop an MIPD algorithm enabling safe and efficacious dosing on an individual level.
2. Materials and Methods
2.1. Patients and Pharmacokinetic Data
Routine therapeutic drug monitoring (TDM) data from 70 MDR- or XDR-TB patients receiving linezolid was collected at the TB center Beatrixoord in Haren, University Medical Center Groningen (UMCG), The Netherlands, between 2007 and 2019. Due to the retrospective nature of this study and because TDM was already part of the routine treatment protocol in the TB center, the need for subjects to provide informed consent was waived by the Medical Ethical Review Board UMCG (METC 2013.492, ethical clearance date: 3 December 2013). Patient demographics, patient characteristics, linezolid total plasma concentrations, and linezolid dosing regimens were retrieved from the medical charts. A summary of patient demographics and characteristics is provided in Table 1. Linezolid was administered in combination with other anti-TB drugs for up to 542 days with oral daily doses (once daily (QD) or twice daily (BID)) ranging from 150 to 1200 mg. A summary of all regimens included in the analysis can be found in Table S1 (Supplementary Materials). Linezolid plasma concentrations were obtained at varying time points at up to seven independent sampling occasions in each patient. In most instances, a pre-dose sample was taken before drug administration. Plasma total linezolid concentrations were quantified using validated liquid chromatography coupled with the mass spectrometry (LC-MS/MS) (ThermoFisher, San Jose, CA, USA) method with a lower limit of quantification (LLOQ) of 0.05 mg/L [17].
Table 1.
Demographics and covariates for patients included in the data set used for population pharmacokinetic model building.
| Parameter | Unit | All Patients |
|---|---|---|
| N | 70 | |
| Mean weight (range) | kg | 61.2 (35.3–88.9) |
| Mean height (range) | m | 1.70 (1.50–1.93) |
| Mean creatinine clearance (range) | mL/min | 116.1 (40.7–150.0) a |
| Mean age (range) | years | 32 (15–70) |
| Mean body mass index (range) | kg/m2 | 21.2 (15.5–32.6) |
| No. of male sex | n (%) | 38 (54.5) |
| No. with HIV | n (%) | 5 (7.1) |
| No. with diabetes | n (%) | 9 (12.9) |
| No. smoking | n (%) | 26 (37.1) |
| No. alcohol abuse | n (%) | 6 (8.6) |
| No. pregnancy | n (%) | 3 (4.3) |
| No. from indicated WHO region | n (%) | |
| African region | 10 (14.3) | |
| Region of the Americas | 2 (2.9) | |
| Southeast Asia region | 6 (8.6) | |
| European region Eastern |
27 (38.6) | |
| Mediterranean region | 15 (21.4) | |
| Western Pacific region | 10 (14.3) |
a Calculated using the Cockcroft-Gault equation [18], using lean body weight instead of regular body weight for patients with BMI higher than 25 and with creatinine clearance truncated at 150 mL/min (13 patients had a calculated creatinine clearance above 150 mL/min). Age, bodyweight, body mass index, and creatinine plasma concentration were registered on the day of admission. WHO region–region based on World Health Organization (WHO) region classification describing origin of birth; ART–antiretroviral therapy; alcohol–alcohol abuse characterized by more than 1 or 2 glasses of alcohol/day and less than 2 days/week with no alcohol; n–number of patients.
2.2. Population Pharmacokinetic Model
A population pharmacokinetic model was developed based on data from 70 patients (811 observations). One individual’s second sampling occasion was excluded from the analysis as the treatment with linezolid was stopped one day before sampling. There were two observations below LLOQ, which were set to LLOQ/2 since the usage of likelihood-based methods such as the M3 and M4 method [19] did not seem necessary in light of the sparseness of LLOQ data.
Model comparison during the modeling process was performed by comparing the objective function value (OFV) of two nested hierarchical models, where a decrease in OFV of 3.84 for one degree of freedom (addition or removal of one parameter) is considered to be statistically significant at a 5% significance level according to the chi-squared distribution (χ2-distribution).
2.2.1. Structural Model Building
Different disposition models were evaluated, including one- and two-compartment models. In order to describe absorption, a first-order absorption with and without lag-time and a transit absorption model [20,21] were tested. Transit absorption was hard-coded with an increasing number of transit compartments (NN) until the most optimal number of compartments was reached [20,21], as described in Equations (1) and (2). Equation (1) represents the first absorption transit compartment, while Equation (2) represents all other transit compartments.
| (1) |
| (2) |
ktr is the transit rate constant calculated as ktr = (NN + 1)/MTT, and MTT is the mean transit time (estimated). The amount of drug in a certain transit compartment is described by An, where n is the absorption compartment.
For drug elimination, linear elimination, Michaelis–Menten elimination kinetics, as well as different approaches to account for drug-induced auto-inhibition of elimination [22,23,24] were explored. The first evaluated approach describing auto-inhibition of elimination was developed for linezolid by Plock et al. [22], where an empirical inhibition compartment is introduced, i.e., the drug concentration in the inhibition compartment drives the auto-inhibition. Different previously published rate constant into the inhibition compartment (kIC) and concentration in the inhibition compartment yielding half of clearance inhibition (IC50) values [22,25,26] were evaluated, and the ones providing the best fit were fixed and retained in the model. The second approach, initially developed for itraconazole [23], describes clearance inhibition dependent on dose with an exponential function. Lastly, in a model originally developed for auto-induction of rifampicin elimination [24], the formation of an enzyme is described by a first-order enzyme degradation and zero-order formation rate in which enzyme formation is stimulated by the presence of the drug via a nonlinear (Emax) model. For description of linezolid elimination auto-inhibition, the approach was reversed by inhibiting the enzyme formation.
2.2.2. Stochastic Model Building
Different residual error models on a normal scale were explored, including additive, proportional and combined additive plus proportional models. All possible combinations of inter-individual variability (IIV) and inter-occasion variability (IOV) were tested on all structural parameters. IIVs and IOVs were modeled exponentially, assuming that individual parameter values are log-normally distributed. Correlations were tested between IIVs of absorption parameters.
2.2.3. Covariate Model Building
Allometric scaling of apparent clearance (CL/F) and apparent volume of distribution (V/F) was introduced using bodyweight as a descriptor for body size [27,28,29]. The exponents for the allometric relationships were fixed to 0.75 and 1 for CL/F and V/F, respectively [30], and the terms were scaled to 70 kg. The impact of additional covariates including age, sex, origin of birth (WHO region), HIV co-infection, diabetes, smoking, alcohol abuse, pre-emptive use of erythropoietin, creatinine clearance (calculated using the Cockcroft-Gault equation [18]) and the effects of concomitant P-glycoprotein (P-gp) inhibitors, P-gp inducers, CYP3A4 inhibitors, and CYP3A4 inducers were assessed using the automated stepwise covariate modeling (SCM) procedure in Perl-speaks-NONMEM (PsN) [31]. Values of calculated creatinine clearance above 150 mL/min were truncated to 150 mL/min. Only clinically plausible covariate relationships were explored (see Table S2, Supplementary Materials). Missing covariate information was handled by imputing the mean value of a covariate for continuous covariates and the mode for categorical covariates. Covariates were selected in a forward inclusion step at a statistical significance level of p < 0.05 and retained following a backward deletion step (p < 0.01). Statistically significant covariate relationships from the SCM were also assessed for clinical significance. Clinical significance was defined as a change in the typical parameter by more than 20% caused by the covariate effect for categorical covariates and 20% change from the median for the 10% and 90% percentiles of the continuous covariate. The covariates pregnancy, anti-retroviral therapy, and therapeutic use of erythropoietin were not evaluated since only 3, 4, and 0 patients, respectively, exhibited the particular covariate.
2.2.4. Model Evaluation
Prediction-corrected visual predictive checks (pcVPCs), goodness-of-fit (GOF) plots, scientific plausibility, and precision of model parameter estimates were evaluated. A 1000 sample sampling importance resampling (SIR) procedure was performed in PsN for the final model to obtain the 90% nonparametric confidence interval for all parameters in order to assess parameter uncertainty.
2.3. Model-Informed Precision Dosing Algorithm
An MIPD algorithm originally developed for dose individualization of rifampicin [15] was adapted for dose optimization of linezolid treatment in patients with MDR- and XDR-TB.
A simulated population of 1000 hypothetical patients was created by bootstrapping patient covariates, as well as individual MIC values from the original study population (patient characteristics, see Table 1).
For the MIPD algorithm, the fAUC0–24h/MIC > 119 and fCmin < 1.38 mg/L were used as efficacy and safety targets [5,7], respectively, and the individualized dose should meet both the efficacy and the safety target.
In order to obtain observed linezolid plasma concentrations for the simulated patient population, the exposure following an initial dose of 600 mg QD was simulated for the first day of treatment. In the next step, these concentrations were used to compute individual PK parameters (empirical Bayes estimates (EBEs)), such as individual clearance or mean transit time. Based on the individual PK parameters, the individual fAUC0–24h/MIC and fCmin were derived following doses of 150 mg to 1200 mg QD and 150 mg to 600 mg BID (increments of 150 mg). The MIPD algorithm was then used to select the individual dose that meets the efficacy and safety target. In case both the efficacy and safety were reached, the lowest efficacious dose was selected. If two dosing regimens resulted in the same fAUC0–24h/MIC, which is the case for the same daily dose administered once versus twice daily, the dosing regimen leading to the lower fCmin was chosen, ensuring safety. If efficacy but not safety was reached, the lowest efficacious dose was selected, and a warning was given regarding safety. If safety but not efficacy was attained, the highest dose was chosen, and an efficacy warning was given. If neither efficacy nor safety could be achieved, the highest dose was selected (1200 mg QD), and warnings regarding efficacy and safety were reported. The selected individual dose was then used for simulation of further sampling occasions using an adaptive dosing strategy. Using this workflow, in total, three PK sampling occasions on days 1, 8, and 15 of treatment were simulated using a sparse sampling (0, 2, and 5 h post dose) [32], updating the individual PK parameters at every occasion using the newly obtained linezolid plasma concentrations.
For transformation of simulated total AUC0–24h and Cmin to fAUC0–24h and fCmin, respectively, linearity in protein binding across the simulated plasma concentration range was assumed, and AUC0–24h and Cmin were multiplied by the fraction unbound (assumed to be 0.69) [33].
In order to evaluate the performance of the MIPD algorithm, the true individual doses were derived using information from all sampling occasions and a rich PK sampling for EBE estimation.
To compare the performance of the MIPD algorithm using different amounts of information for computation of the individual PK parameters, the relative bias (rBias) Equation (3) and relative root mean squared error (rRMSE) Equation (4) were calculated for fAUC0–24h/MIC and fCmin as follows:
| (3) |
| (4) |
The relative dose prediction error (rDPE), evaluating the accuracy in dose prediction, was computed as follows Equation (5):
| (5) |
where DD is the total daily dose.
2.4. Software
The data were analyzed with the non-linear mixed-effects modeling software NONMEM (v.7.4.3; Icon Development Solutions, Ellicott City, MD, USA) [34] using conditional estimation with interaction (FOCE-I). Data handling and visualization were performed in R (v.3.6.1; R Foundation for Statistical Computing, Vienna, Austria) [35]. Model diagnostics were generated using Xpose4 (v.4.6.1) [31] and prediction-corrected visual predictive checks (pcVPCs) were created with PsN (v.4.9.5) [31].
3. Results
3.1. Population Pharmacokinetic Model
The final population PK model consisted of a one-compartment disposition model since a two-compartment model did not describe the data statistically significantly better (p > 0.05). A transit absorption model including five transit compartments was statistically significantly superior to an absorption lag-time model. The addition of a sixth transit compartment did not improve the fit significantly. Incorporating Michaelis–Menten elimination kinetics did not improve the model fit (OFV: 1978.5) compared to a model with first-order elimination (OFV: 1974.9), and thus first-order kinetics were chosen for the description of linezolid elimination. Based on goodness-of-fit plots (GOF) plots and prediction-corrected visual predictive checks (pcVPCs), a slight underestimation at higher concentrations was observed, suggesting the need to explore concentration-dependent auto-inhibition of linezolid elimination. For that purpose, different models, including dose- and time-dependency [23] as well as concentration- and time-dependency [22,24], were tested to describe auto-inhibition of linezolid elimination. In the final model, the structure of a previously developed concentration- and time-dependent elimination model developed by Plock et al. [22] was implemented. The incorporated auto-inhibition model [22] consists of an empirical inhibition compartment. Depending on the concentration in the inhibition compartment (Ci), clearance (CL) from the central compartment (Ac) is inhibited, where CL is a fraction of the original uninhibited value at the first dose. Equations (6) and (7) describe the CL auto-inhibition:
| (6) |
| (7) |
where CL is the uninhibited clearance (L/h), Aa the linezolid amount in the absorption compartment (mg), Ac the linezolid amount in the central compartment (mg), Ci the linezolid concentration in the inhibition compartment (mg/L), ka the absorption rate constant (h−1), Vd the central volume of distribution (L), kIC the rate constant into the inhibition compartment (1/h), RCLF the remaining CL fraction, and IC50 the concentration in the inhibition compartment leading to half of the maximum clearance inhibition (mg/L). The kIC was fixed to the best fitting literature value of 0.0005 h−1 [25] and IC50 to 0.38 mg/L [25] due to the fact that most of the patient data in this study were captured in steady state, thus not enabling estimation of the inhibition parameters with sufficient precision.
The residual error model was a combined additive and proportional error on a normal scale. IIV in CL/F and mean transit time (MTT) were statistically significant, as well as IOV in CL/F, V/F, MTT, and ka. Covariances were not found to be statistically significant between any of the parameters.
The parameters CL/F and V/F were allometrically scaled using bodyweight. Out of all explored covariates, HIV on CL/F, sex on ka, administration of P-gp inhibitors on MTT were found to be both statistically and clinically significant.
The NONMEM code for the final model is given in Text S1 (Supplementary Materials). Goodness-of-fit plots are shown in Figure S1 (Supplementary Materials). The structure of the final model is schematically represented in Figure 1, and the final parameter estimates are provided in Table 2. The final model described the observed data well in all dose groups based on the precision in parameter estimates, GOFs, individual plots (not shown), and pcVPCs showing both the whole population (Figure 2) as well as strata for the different patient covariates (Figure S2, Supplementary Materials).
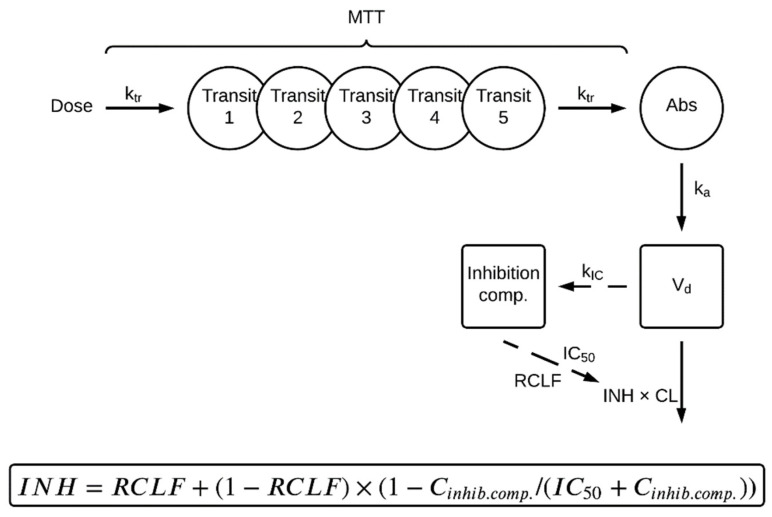
Figure 1.
Schematic representation of the final linezolid population pharmacokinetic model. First, the dose is transferred into an absorption compartment (Abs) via five transit compartments (Transit 1–5), where ktr is the transit rate constant describing the transfer between transit compartments, calculated as the number of transit compartments (NN) + 1 divided by the mean transit time (MTT). The drug is absorbed from Abs to the central compartment (indicated by Vd, the distribution volume of the central compartment), described by the absorption rate constant (ka). Clearance (CL) from the central compartment is inhibited based on the linezolid plasma concentration (Cinhib.comp) in an empirical inhibition compartment (Inhibition comp.). The concentration- and time-dependency of the inhibition (INH) is described by the Cinhib.comp leading to half of the maximum possible inhibition (IC50) and a rate constant (kIC) representing the transfer from the central into the inhibition compartment. The fraction of clearance remaining uninhibited is described by the parameter RCLF. The elimination of the drug is described by first-order kinetics, which is inhibited by INH.
Table 2.
Parameter estimates from the final linezolid population pharmacokinetic model.
| Parameter | Description | Estimate | 90% CI c | RSE% d |
|---|---|---|---|---|
| CL/F (L/h/70 kg) | Apparent clearance (uninhibited) | 6.3 | 5.6–7.0 | 6.4 |
| Vd/F (L/70 kg) | Apparent volume of distribution | 50.6 | 48.5–53.1 | 3.1 |
| ka (h−1) | Absorption rate constant | 1.8 | 1.5–2.1 | 13.8 |
| MTT (h) | Mean transit time | 0.53 | 0.44–0.61 | 10.6 |
| kIC (h−1) | Rate constant into the inhibition compartment | 0.0005 FIX e | - | - |
| IC50 (mg/L) | Concentration in the inhibition compartment yielding half of clearance inhibition | 0.38 FIX e | - | - |
| RCLF | Remaining clearance fraction uninhibited | 0.798 | 0.69–0.92 | 11.3 |
| Covariates | ||||
| HIV co-infection on CL/F | Effect of HIV co-infection on CL/F | 0.43 | 0.07–0.90 | 122.0 |
| Sex on ka | Effect of sex on ka | 0.95 | 0.78–1.10 | 14.0 |
| P-gp inhibitor on MTT | Effect of P-gp inhibitor on MTT | 0.96 | 0.84–1.09 | 9.0 |
| Inter-individual variability | ||||
| IIVCL/F (%CV) a | Inter-individual variability in apparent clearance (uninhibited) | 0.26 | 0.21–0.31 | 13.0 |
| IIVMTT (%CV) a | Inter-individual variability in mean transit time | 0.62 | 0.40–0.80 | 19.9 |
| Inter-occasion variability | ||||
| IOVCL/F (%CV) b | Inter-occasion variability in apparent clearance (uninhibited) | 0.27 | 0.23–0.30 | 9.0 |
| IOVV/F (%CV) b | Inter-occasion variability in apparent volume of distribution | 0.26 | 0.23–0.30 | 8.5 |
| IOVka (%CV) b | Inter-occasion variability in absorption rate constant | 0.93 | 0.71–1.16 | 15.2 |
| IOVMTT (%CV) b | Inter-occasion variability in mean transit time | 0.69 | 0.53–0.85 | 13.4 |
| Residual variability | ||||
| Proportional error (%) | Proportional residual error | 0.054 | 0.045–0.065 | 12.5 |
| Additive error (mg/L) | Additive residual error | 0.53 | 0.483–0.570 | 7.0 |
a Inter-individual variability expressed as the standard deviation and in % of the parameter estimate. b Inter-occasion variability expressed as the standard deviation and in % of the parameter estimate. c 90% CI is the 90% percentile confidence interval obtained from a sampling importance resampling (SIR) procedure. d Standard errors expressed as relative standard errors (standard errors for omegas relative to their variance estimates). e Values obtained by a publication by Keel et al. [25]. IIV, inter-individual variability; IOV, inter-occasion variability; RSE, residual standard error.
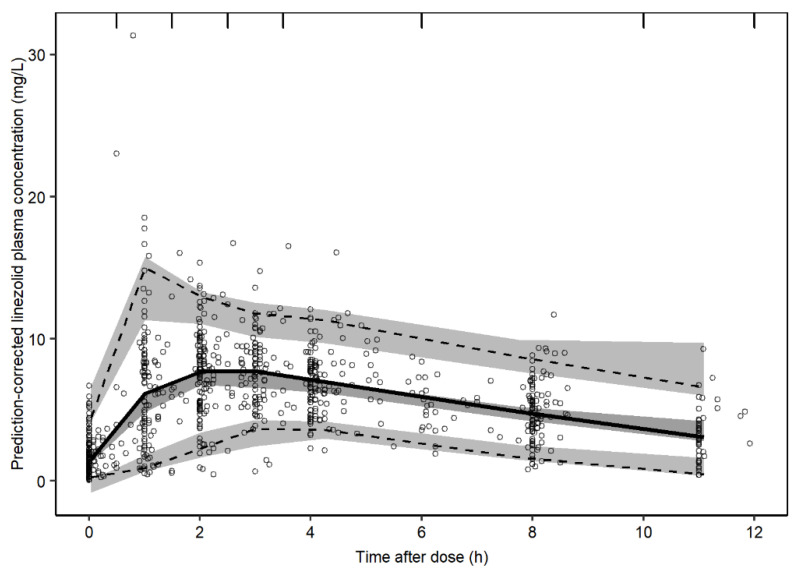
Figure 2.
Prediction-corrected visual predictive check (pcVPC) of the final linezolid population pharmacokinetic model. The solid and dashed lines are the median, 2.5th and 97.5th percentiles of the observed data, respectively. The shaded areas (top to bottom) are the 95% confidence intervals of the 97.5th (light gray), median (gray), and 2.5th (light gray) percentiles of the simulated data based on 1000 simulations. Open circles are prediction-corrected observation points.
3.2. MIPD Algorithm
An MIPD algorithm incorporating adaptive dosing was developed for individualized linezolid dosing in patients with MDR- and XDR-TB. The proposed MIPD workflow is illustrated in Figure 3.
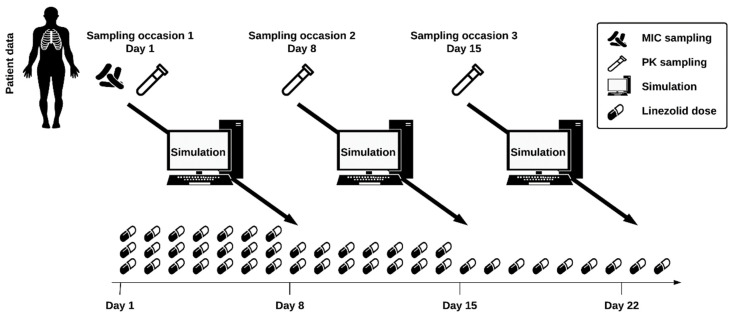
Figure 3.
Model-informed precision dosing workflow. MIC determination is performed on day 1 of treatment and PK sampling on days 1, 8, and 15. A Bayesian forecast is then performed using the population PK model, patient characteristics, and individual linezolid plasma concentrations. Taking efficacy and safety into account, the dose is adjusted one week after PK sampling. MIC, minimal inhibitory concentration; PK, pharmacokinetics.
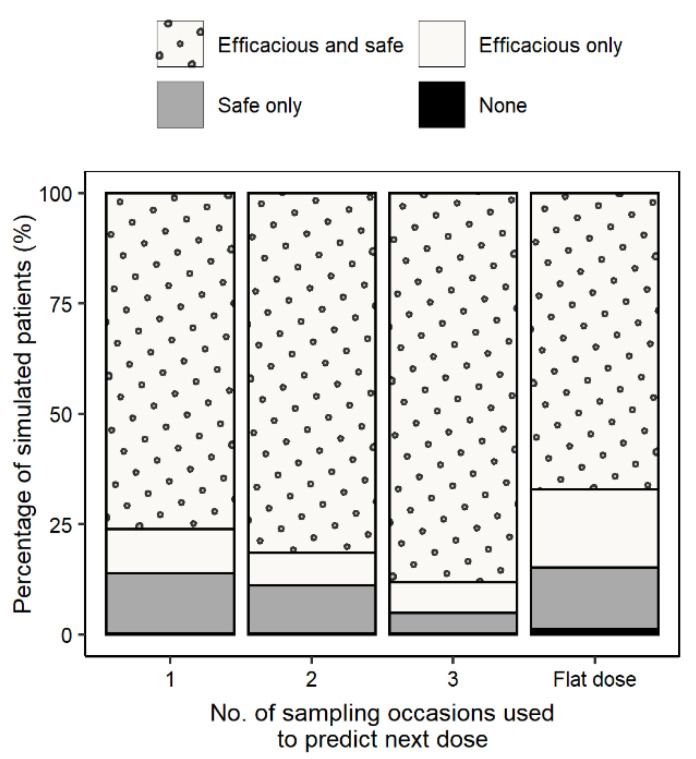
A flat dose of 600 mg QD led to efficacious and safe (fAUC0–24h/MIC > 119 and fCmin < 1.38 mg/L) exposures in 67.2% of the simulated patients (17.6% of the patients did not meet the safety, 14.0%, not the efficacy, and 1.2% neither the efficacy nor the safety target) (Figure 4). Using the MIPD approach, both the efficacy and safety targets were met in 76.1%, 81.5%, and 88.2% of the simulated patients following dosing regimens derived based on information from one, two, or three PK sampling occasions, respectively. Using information from three occasions, 6.9% of the simulated patients did not meet the safety target, 4.6% did not meet the efficacy target, and 0.3% did not meet the safety nor the efficacy target (Figure 4). A Sankey plot (Figure S3, Supplementary Materials) was created showing individual dose adjustments for three consecutive PK sampling occasions, indicating that a significant part of the simulated patients received the appropriate dose when adjusted based on information from the first sampling occasion. All doses selected by the MIPD algorithm were QD doses since BID dosing would lead to a higher fCmin.
Figure 4.
Percentage of patients reaching both efficacy and safety, only efficacy, only safety, and neither efficacy nor safety using information from one, two, and three sampling occasions to derive individual PK parameters. The true individual PK parameters were obtained from a rich sampling in order to derive the true optimal dose for comparison.
In order to determine how many sampling occasions are necessary to compute the individual PK parameters and subsequently predict the fAUC0–24h/MIC and fCmin with sufficient accuracy and precision, the rRMSE and rBias were calculated for fAUC0–24h/MIC and fCmin predictions based on information from one, two and three sampling occasions. Both the accuracy and precision in predictions of fAUC0–24h/MIC (rBias: −5.0%, −2.1%, and −1.8%; rRMSE: 19.3%, 12.4%, and 8.1% for one, two, and three occasions) and fCmin (rBias: −8.9%, −2.7%, and −2.1%; rRMSE: 44.8%, 30.5%, and 20.2% for one, two and three occasions) improved when additional information was added.
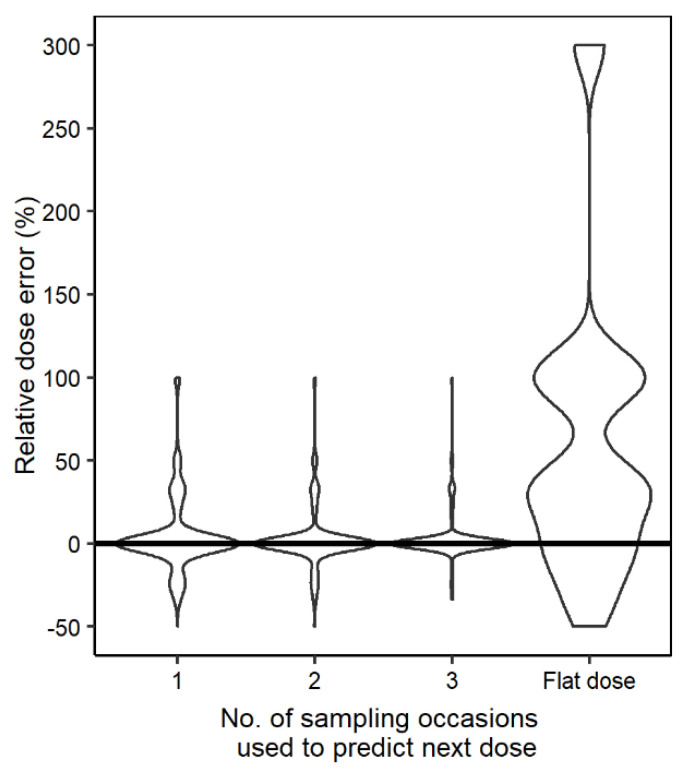
The relative dose prediction error decreased with increasing information used to obtain individual parameters from sparse sampling (Figure 5), indicating that a higher percentage of simulated individuals received a dose closer to the true dose.
Figure 5.
Violin plot showing the dose prediction error comparing the true dose to the individualized dose derived based on information from one, two, and three sampling occasions, as well as flat dosing of 600 mg QD for comparison.
4. Discussion
An MIPD workflow, using the here developed population PK model, was established, enabling safe and efficacious dosing on an individual level.
Several studies have shown that linezolid clearance decreases with increasing doses. This phenomenon has previously been described with either Michaelis–Menten elimination kinetics [36,37] or concentration- and time-dependent auto-inhibition of elimination [22,25,26]. In this work, Michaelis–Menten elimination kinetics was not supported by the data; however, the inclusion of a concentration- and time-dependent auto-inhibition of elimination described the data well, and its incorporation is crucial to be able to use the population PK model for MIPD before steady state is reached. The mechanism behind the auto-inhibition of linezolid elimination is not fully known yet. It is suggested that for the metabolite’s hydroxyethyl glycine formation, reduced nicotinamide adenine dinucleotide phosphate (NADPH) is needed [22,38]. As linezolid inhibits cytochrome c-oxidase activity, it interrupts the synthesis of adenosine triphosphate (ATP), which is needed for nicotinamide adenine dinucleotide phosphate (NADP) reduction to NADPH [22]. Lack of NADPH results in decreased hydroxylinezolid formation, and thus, linezolid elimination is inhibited.
In this work, both statistical and clinical significance were considered when incorporating covariates in the model. Three covariates fulfilled both criteria, HIV co-infection on CL/F, sex on ka, and coadministration of P-gp inhibitors on MTT (Table 2). Typical CL/F was 43% higher in patients with HIV co-infection, and the effect of the covariate on the apparent clearance could be explained by changes in kidney function or concomitant medication (Table 2). Typical ka was 95% higher in females, possibly due to biological differences between men and women, such as differences in gastric pH, gastric fluid flow, intestinal motility, and gastric emptying [39]. Typical MTT was 96% higher in patients who received P-gp inhibitors. The imprecision in the estimated effect of HIV on CL/F was high, with a 90% confidence interval of 7–90% (Table 2), which is probably due to the low number of HIV patients in the study population (n = 5/70). The covariate was kept in the model since clearance is a parameter that can greatly influence plasma concentration. However, the effect of HIV on CL/F estimated here should be interpreted with caution and studied further. Allometric scaling, besides improving the model fit, was implemented in order to be able to apply the population PK model to a pediatric population.
Linezolid has high efficacy for the treatment of MDR- and XDR-TB and a low resistance development rate but is one of the most frequently reported anti-TB drugs to cause severe adverse events, which might require early termination of treatment [40]. A recent clinical trial investigating long-term linezolid treatment showed that toxicity was high, with 81% of the patients suffering from peripheral neuropathy and 48% from myelosuppression [8]. According to our simulations, a flat dosing regimen of 600 mg QD led to efficacious and safe exposures in 67.2% of the simulated patients, which is comparable to previous findings [5,6,41]. While some work suggests that 600 mg BID is needed to reach efficacy [42], other studies are in accordance with the here described findings. In the work by Millard et al. [6], the majority of simulated patients reached the safety target following doses of 300 mg QD, 300 mg BID, and 600 mg QD, but almost all subjects were above the safety threshold with a dose of 600 mg BID. Alghamdi et al. [41] also suggested that 600 mg QD is preferred in most patients with respect to safety. Furthermore, recent results from the ZeNix trial presented in Berlin 2021 [43] highlight that cure is achievable with 600 mg QD for 6 months, leading to less frequent adverse events compared to 1200 mg QD (38% vs. 24% for peripheral neuropathy and 22% vs. 2% for anemia) [43].
Besides studying the use of lower doses to increase safety, as in the ZeNix trial (NCT03086486), individualizing a patient’s dose based on individual characteristics and drug exposure with MIPD can be used as a tool to increase efficacy and safety [13,14,15,16]. MIPD provides individual dose suggestions, which is different from classical TDM, where the achieved PK exposure after a dose is compared to a target without a precise dose suggestion apart from the information that a dose is too high or too low. The here proposed MIPD approach (Figure 3) ensures efficacy and safety on an individual level and can be applied at any time during treatment. Simulations of 1000 virtual patients showed that by using the MIPD approach, 88.2% reached efficacious and safe linezolid concentrations with an individualized dose obtained using information from three sampling occasions. After three sampling occasions, 6.9% of all simulated patients would get an efficacious but not safe dose (17.6% following a flat dose of 600 mg QD), 4.3% would get a safe but not efficacious dose (versus 14% for 600 mg QD flat dosing), and for 0.3% of the simulated patients, the dose would be considered neither safe nor efficacious (versus 1.2% for 600 mg QD flat dosing) (see Figure 4). Using information from three occasions resulted in 88.2% of simulated patients reaching both the efficacy and safety target (improvement of 6.7% compared to using information from two occasions), thus highlighting the importance of the third occasion (Figure 4). In all simulated patients, a QD dosing strategy was superior compared to BID due to the fact that the fCmin is lower following QD dosing. The superiority of a QD dosing strategy over BID has been shown previously [5,6,41] and could be advantageous to increase patient adherence.
There are some limitations to this work. Firstly, since retrospective TDM data from routine clinical care was analyzed and because patients were in their intensive phase of TB infection, selection bias might have been introduced. In addition, it was only possible to derive the dose prediction error for the total daily dose; thus, there was no distinction between QD and BID dosing. However, since a QD strategy was superior to BID in all simulated patients, it was not necessary here to compare the dose prediction error between QD versus BID strategies. Furthermore, the parameters describing the auto-inhibition of elimination were not identifiable in this work as the majority of samples were taken at steady state, and thus the parameters related to elimination auto-inhibition had to be fixed to values obtained from earlier studies [25]. In this work, efficacy and safety targets from earlier defined PKPD indices were used for dose selection. A simulation study by Kristoffersson et al. [44] showed that the use of longitudinal PKPD models can be more appropriate in certain situations than using PKPD indices. PKPD indices can further be influenced by uncertainty in the obtained MIC value, both due to intra- and inter-laboratory variability [45,46]. Since the MIC is determined in two-fold dilution steps, an error may lead to a substantial change in the PKPD index and, subsequently, dose selection. These findings indicate that MIPD based on a PKPD model might be more appropriate than based on PKPD indices, which should be investigated in further studies. Furthermore, the safety target has only been evaluated in one study with 38 participants [7], and the authors merely explored fCmin as a potential driver for toxicity. Other PK parameters such as AUC or Cmax were not explored, and there is, therefore, a need to derive an updated individualized safety target based on PK data combined with clinical safety outcome data. Lastly, the developed MIPD approach should be validated in the clinic.
5. Conclusions
In conclusion, a linezolid population PK model for MDR- and XDR-TB patients was successfully developed. This work presents an MIPD workflow for linezolid, which can be used on any day of treatment, proposes to use three sparse sampling occasions to derive the individualized dose, and suggests that an individualized dose would be beneficial from an efficacy and safety perspective compared to a flat dose of 600 mg QD.
Acknowledgments
The computations were enabled by resources in project SNIC 2020-5-524 provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX, partially funded by the Swedish Research Council through grant agreement no. 2018-05973.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pharmaceutics14040753/s1, Text S1 NONMEM model code for the final population pharmacokinetic model; Figure S1 Goodness-of-fit plots for the final population pharmacokinetic model; Figure S2 Prediction corrected visual predictive checks (pcVPC) for the final linezolid population pharmacokinetic model stratified on covariates; Figure S3 Sankey plot showing individual dose adjustments for three consecutive PK sampling occasions, each one week apart; Table S1 Summary of the different regimens included in the analysis dataset; Table S2 Covariate relationships evaluated in the population pharmacokinetic analysis.
Author Contributions
Conceptualization, L.K., L.M., L.M.G.H., M.G.G.S., M.S.B., O.W.A. and U.S.H.S.; methodology, L.K., L.M., L.M.G.H., M.G.G.S., M.S.B., O.W.A. and U.S.H.S.; software, L.K., L.M. and U.S.H.S.; validation, L.K., L.M., L.M.G.H., M.G.G.S., M.S.B., O.W.A. and U.S.H.S.; formal analysis, L.K., L.M. and U.S.H.S.; data curation, L.K., L.M. and U.S.H.S.; writing—original draft preparation, L.K. and L.M.; writing—review and editing, L.K., L.M., L.M.G.H., M.G.G.S., M.S.B., O.W.A. and U.S.H.S.; visualization, L.K. and L.M.; supervision, U.S.H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Medical Ethical Review Board UMCG (METC 2013.492, ethical clearance date: 3 December 2013).
Informed Consent Statement
Due to the retrospective nature of this study and because TDM was already part of the routine treatment protocol in the TB center, the need for subjects to provide informed consent was waived by the Medical Ethical Review Board UMCG (METC 2013.492, ethical clearance date: 3 December 2013).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons, as this is sensitive personal patient data.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Global Tuberculosis Report 2019. World Health Organization; Geneva, Switzerland: 2019. Licence: CC BY-NC-SA 3.0 IGO. [Google Scholar]
- 2.Meeting Report of the WHO Expert Consultation on the Definition of Extensively Drug-Resistant Tuberculosis, 27–29 October 2020. World Health Organization; Geneva, Switzerland: 2021. CC BY-NC-SA 3.0 IGO. [Google Scholar]
- 3.Global Tuberculosis Report 2021. World Health Organization; Geneva, Switzerland: 2021. Licence: CC BY-NC-SA 3.0 IGO. [Google Scholar]
- 4.Hashemian S.M., Farhadi T., Ganjparvar M. Linezolid: A review of its properties, function, and use in critical care. Drug Des. Dev. Ther. 2018;12:1759–1767. doi: 10.2147/DDDT.S164515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Srivastava S., Magombedze G., Koeuth T., Sherman C., Pasipanodya J.G., Raj P., Wakeland E., Deshpande D., Gumbo T. Linezolid Dose That Maximizes Sterilizing Effect While Minimizing Toxicity and Resistance Emergence for Tuberculosis. Antimicrob. Agents Chemother. 2017;61:e00751-17. doi: 10.1128/AAC.00751-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Millard J., Pertinez H., Bonnett L., Hodel E.M., Dartois V., Johnson J.L., Caws M., Tiberi S., Bolhuis M., Alffenaar J.-W.C., et al. Linezolid pharmacokinetics in MDR-TB: A systematic review, meta-analysis and Monte Carlo simulation. J. Antimicrob. Chemother. 2018;73:1755–1762. doi: 10.1093/jac/dky096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Song T., Lee M., Jeon H.-S., Park Y., Dodd L.E., Dartois V., Follman D., Wang J., Cai Y., Goldfeder L.C., et al. Linezolid Trough Concentrations Correlate with Mitochondrial Toxicity-Related Adverse Events in the Treatment of Chronic Extensively Drug-Resistant Tuberculosis. EBioMedicine. 2015;2:1627–1633. doi: 10.1016/j.ebiom.2015.09.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Conradie F., Diacon A.H., Ngubane N., Howell P., Everitt D., Crook A.M., Mendel C.M., Egizi E., Moreira J., Timm J., et al. Treatment of Highly Drug-Resistant Pulmonary Tuberculosis. N. Engl. J. Med. 2020;382:893–902. doi: 10.1056/NEJMoa1901814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Maartens G., Benson C.A. Linezolid for Treating Tuberculosis: A Delicate Balancing Act. EBioMedicine. 2015;2:1568–1569. doi: 10.1016/j.ebiom.2015.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.WHO Consolidated Guidelines on Drug-Resistant Tuberculosis Treatment. World Health Organization; Geneva, Switzerland: 2019. Licence: CC BY-NC-SA 3.0 IGO. [PubMed] [Google Scholar]
- 11.Rao G.G., Konicki R., Cattaneo D., Alffenaar J.-W., Marriott D.J.E., Neely M. Therapeutic Drug Monitoring Can Improve Linezolid Dosing Regimens in Current Clinical Practice: A Review of Linezolid Pharmacokinetics and Pharmacodynamics. Ther. Drug Monit. 2020;42:83–92. doi: 10.1097/FTD.0000000000000710. [DOI] [PubMed] [Google Scholar]
- 12.Singh B., Cocker D., Ryan H., Sloan D.J. Linezolid for drug-resistant pulmonary tuberculosis. Cochrane Database Syst. Rev. 2019;3:CD012836. doi: 10.1002/14651858.CD012836.pub2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Keizer R.J., ter Heine R., Frymoyer A., Lesko L.J., Mangat R., Goswami S. Model-Informed Precision Dosing at the Bedside: Scientific Challenges and Opportunities. CPT Pharmacomet. Syst. Pharmacol. 2018;7:785–787. doi: 10.1002/psp4.12353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.van Beek S.W., ter Heine R., Keizer R.J., Magis-Escurra C., Aarnoutse R.E., Svensson E.M. Personalized Tuberculosis Treatment Through Model-Informed Dosing of Rifampicin. Clin. Pharmacokinet. 2019;58:815–826. doi: 10.1007/s40262-018-00732-2. [DOI] [PubMed] [Google Scholar]
- 15.Svensson R.J., Niward K., Davies Forsman L., Bruchfeld J., Paues J., Eliasson E., Schön T., Simonsson U.S. Individualised dosing algorithm and personalised treatment of high-dose rifampicin for tuberculosis. Br. J. Clin. Pharmacol. 2019;85:2341–2350. doi: 10.1111/bcp.14048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Keutzer L., Simonsson U.S.H. Individualized Dosing With High Inter-Occasion Variability Is Correctly Handled With Model-Informed Precision Dosing-Using Rifampicin as an Example. Front. Pharmacol. 2020;11:794. doi: 10.3389/fphar.2020.00794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Harmelink I.M., Alffenaar J.-W., Wessels A.M.A. A rapid and simple liquid chromatography-tandem mass spectrometry method for the determination of linezolid in human serum. Eur. J. Hosp. Pharm. 2008;14:3–7. [Google Scholar]
- 18.Cockcroft D.W., Gault M.H. Prediction of creatinine clearance from serum creatinine. Nephron. 1976;16:31–41. doi: 10.1159/000180580. [DOI] [PubMed] [Google Scholar]
- 19.Beal S.L. Ways to fit a PK model with some data below the quantification limit. J. Pharmacokinet. Pharmacodyn. 2001;8:481–504. doi: 10.1023/A:1012299115260. [DOI] [PubMed] [Google Scholar]
- 20.Rousseau A., Léger F., Le Meur Y., Saint-Marcoux F., Paintaud G., Buchler M., Marquet P. Population Pharmacokinetic Modeling of Oral Cyclosporin Using NONMEM: Comparison of Absorption Pharmacokinetic Models and Design of a Bayesian Estimator. Ther. Drug Monit. 2004;26:23–30. doi: 10.1097/00007691-200402000-00006. [DOI] [PubMed] [Google Scholar]
- 21.Savic R.M., Jonker D.M., Kerbusch T. Evaluation of a Transit Compartment Model Versus a Lag Time Model for Describing Drug Absorption Delay. Population Approach Group Europe; Uppsala, Sweden: 2004. Abstr 513. [Google Scholar]
- 22.Plock N., Buerger C., Joukhadar C., Kljucar S., Kloft C. Does linezolid inhibit its own metabolism? Population pharmacokinetics as a tool to explain the observed nonlinearity in both healthy volunteers and septic patients. Drug Metab. Dispos. 2007;35:1816–1823. doi: 10.1124/dmd.106.013755. [DOI] [PubMed] [Google Scholar]
- 23.Abuhelwa A.Y., Foster D.J.R., Mudge S., Hayes D., Upton R.N. Population pharmacokinetic modeling of itraconazole and hydroxyitraconazole for oral SUBA-itraconazole and sporanox capsule formulations in healthy subjects in fed and fasted states. Antimicrob. Agents Chemother. 2015;59:5681–5696. doi: 10.1128/AAC.00973-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Smythe W., Khandelwal A., Merle C., Rustomjee R., Gninafon M., Bocar Lo M., Sow O.B., Olliaro P.L., Lienhardt C., Horton J., et al. A semimechanistic pharmacokinetic-enzyme turnover model for rifampin autoinduction in adult tuberculosis patients. Antimicrob. Agents Chemother. 2012;56:2091–2098. doi: 10.1128/AAC.05792-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Keel R.A., Schaeftlein A., Kloft C., Pope J.S., Knauft R.F., Muhlebach M., Nicolau D.P., Kuti J.L. Pharmacokinetics of Intravenous and Oral Linezolid in Adults with Cystic Fibrosis. Antimicrob. Agents Chemother. 2011;55:3393–3398. doi: 10.1128/AAC.01797-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Minichmayr I.K., Schaeftlein A., Kuti J.L., Zeitlinger M., Kloft C. Clinical Determinants of Target Non-Attainment of Linezolid in Plasma and Interstitial Space Fluid: A Pooled Population Pharmacokinetic Analysis with Focus on Critically Ill Patients. Clin. Pharmacokinet. 2017;56:617–633. doi: 10.1007/s40262-016-0463-7. [DOI] [PubMed] [Google Scholar]
- 27.West G.B., Brown J.H., Enquist B.J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science. 1997;276:122–126. doi: 10.1126/science.276.5309.122. [DOI] [PubMed] [Google Scholar]
- 28.West G., Brown J., Enquist B. The Fourth Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms. Science. 1999;284:1677–1679. doi: 10.1126/science.284.5420.1677. [DOI] [PubMed] [Google Scholar]
- 29.Holford N.H. A size standard for pharmacokinetics. Clin. Pharmacokinet. 1996;30:329–332. doi: 10.2165/00003088-199630050-00001. [DOI] [PubMed] [Google Scholar]
- 30.Holford N.H.G., Anderson B.J. Allometric size: The scientific theory and extension to normal fat mass. Eur. J. Pharm. Sci. 2017;109:S59–S64. doi: 10.1016/j.ejps.2017.05.056. [DOI] [PubMed] [Google Scholar]
- 31.Keizer R.J., Karlsson M.O., Hooker A. Modeling and Simulation Workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT Pharmacomet. Syst. Pharmacol. 2013;2:e50. doi: 10.1038/psp.2013.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kamp J., Bolhuis M.S., Tiberi S., Akkerman O.W., Centis R., de Lange W.C., Kosterink J.G., van der Werf T., Migliori G.B., Alffenaar J.-W.C. Simple strategy to assess linezolid exposure in patients with multi-drug-resistant and extensively-drug-resistant tuberculosis. Int. J. Antimicrob. Agents. 2017;49:688–694. doi: 10.1016/j.ijantimicag.2017.01.017. [DOI] [PubMed] [Google Scholar]
- 33.Pawsey S.D., Daley-Yates P.T.R., Wajszczuk C.P. Abstracts of the First European Congress of Chemotherapy, Glasgow UK. Federation for the Societies for European Chemotherapy and Infection; London, UK: 1996. U-1007666 safety, toleration and pharmacokinetics after oral and intravenous administration. Abstract F151. [Google Scholar]
- 34.Beal S., Sheiner L., Boeckmann A., Bauer R. NONMEM 7.4 Users Guides. ICON plc.; Gaithersburg, MD, USA: 1989. [Google Scholar]
- 35.R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. [Google Scholar]
- 36.Cojutti P., Pai M.P., Pea F. Population Pharmacokinetics and Dosing Considerations for the Use of Linezolid in Overweight and Obese Adult Patients. Clin. Pharmacokinet. 2018;57:989–1000. doi: 10.1007/s40262-017-0606-5. [DOI] [PubMed] [Google Scholar]
- 37.Beringer P., Nguyen M., Hoem N., Louie S., Gill M., Gurevitch M., Wong-Beringer A. Absolute bioavailability and pharmacokinetics of linezolid in hospitalized patients given enteral feedings. Antimicrob. Agents Chemother. 2005;49:3676–3681. doi: 10.1128/AAC.49.9.3676-3681.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.De Vriese A.S., Van Coster R., Smet J., Seneca S., Lovering A., Van Haute L.L., Vanopdenbosch L.J., Martin J.-J., Groote C.C.-D., Vandecasteele S., et al. Linezolid-Induced Inhibition of Mitochondrial Protein Synthesis. Clin. Infect. Dis. 2006;42:1111–1117. doi: 10.1086/501356. [DOI] [PubMed] [Google Scholar]
- 39.Soldin O.P., Mattison D.R. Sex differences in pharmacokinetics and pharmacodynamics. Clin. Pharmacokinet. 2009;48:143–157. doi: 10.2165/00003088-200948030-00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Guidelines for Treatment of Drug-Susceptible Tuberculosis and Patient Care. World Health Organization; Geneva, Switzerland: 2017. Licence: CC BY-NC-SA 3.0 IGO; 2017 Update. [Google Scholar]
- 41.Alghamdi W.A., Al-Shaer M.H., An G., Alsultan A., Kipiani M., Barbakadze K., Mikiashvili L., Ashkin D., Griffith D.E., Cegielski J.P., et al. Population Pharmacokinetics of Linezolid in Tuberculosis Patients: Dosing Regimens Simulation and Target Attainment Analysis. Antimicrob. Agents Chemother. 2020;64:e01174-20. doi: 10.1128/AAC.01174-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tietjen A.K., Kroemer N., Cattaneo D., Baldelli S., Wicha S.G. Population pharmacokinetics and target attainment analysis of linezolid in multidrug-resistant tuberculosis patients. Br. J. Clin. Pharmacol. 2021;88:1835–1844. doi: 10.1111/bcp.15102. [DOI] [PubMed] [Google Scholar]
- 43.New Trial Results Show Effectiveness of BPaL Regimen for Highly Drug-Resistant TB Can Be Maintained with Reduced Dosing of Linezolid. TB Alliance n.d. [(accessed on 19 November 2021)]. Available online: https://www.tballiance.org.za/news/zenix-press-release-english.
- 44.Kristoffersson A.N., David-Pierson P., Parrott N.J., Kuhlmann O., Lave T., Friberg L.E., Nielsen E.I. Simulation-Based Evaluation of PK/PD Indices for Meropenem Across Patient Groups and Experimental Designs. Pharm. Res. 2016;33:1115–1125. doi: 10.1007/s11095-016-1856-x. [DOI] [PubMed] [Google Scholar]
- 45.Mouton J.W., Meletiadis J., Voss A., Turnidge J. Variation of MIC measurements: The contribution of strain and laboratory variability to measurement precision. J. Antimicrob. Chemother. 2018;73:2374–2379. doi: 10.1093/jac/dky232. [DOI] [PubMed] [Google Scholar]
- 46.Mouton J.W., Muller A.E., Canton R., Giske C.G., Kahlmeter G., Turnidge J. MIC-based dose adjustment: Facts and fables. J. Antimicrob. Chemother. 2018;73:564–568. doi: 10.1093/jac/dkx427. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons, as this is sensitive personal patient data.