Abstract
Theoretical considerations suggest that the strength of carbon nanotube (CNT) fibers be exceptional; however, their mechanical performance values are much lower than the theoretical values. To achieve macroscopic fibers with ultrahigh performance, we developed a method to form multidimensional nanostructures by coalescence of individual nanotubes. The highly aligned wet-spun fibers of single- or double-walled nanotube bundles were graphitized to induce nanotube collapse and multi-inner walled structures. These advanced nanostructures formed a network of interconnected, close-packed graphitic domains. Their near-perfect alignment and high longitudinal crystallinity that increased the shear strength between CNTs while retaining notable flexibility. The resulting fibers have an exceptional combination of high tensile strength (6.57 GPa), modulus (629 GPa), thermal conductivity (482 W/m·K), and electrical conductivity (2.2 MS/m), thereby overcoming the limits associated with conventional synthetic fibers.
Fibers with ultrahigh mechanical, electrical, and thermal properties are prepared.
INTRODUCTION
High-performance synthetic fibers feature a common basic structure consisting of long, elongated macromolecules that are highly aligned along the fiber axis (1). Since their discovery, carbon nanotubes (CNTs) have been considered as the ultimate building block for ultrahigh-performance fibers owing to their high strength. The tensile strength (130 GPa) and modulus (1 TPa) of the monolayer graphene shell of CNTs are higher than those of any other material, including polymeric building blocks (2). Unlike polymers, CNTs offer extremely high electrical (3) and thermal conductivities (4); unlike carbon fibers (CFs), they are flexible and withstand bending and compressional stresses (5). Owing to this unique combination of properties, CNT fibers have received considerable interest for advanced applications ranging from military equipment, sensors, actuators, and energy storage devices to the space elevator (6).
Since the initial reports on the production of CNT fibers, their properties have been continuously improved (7). However, the bulk properties of the best realized CNT fibers, particularly their strength, remain comparable to those of high-performance macromolecular fibers, indicating that only a small fraction (~10%) of the performance potential has been realized. Depending on the spinning method, the bulk properties of CNT fibers are generally limited by their degree of alignment and/or the interactions between adjacent graphitic layers (8, 9). Extremely high alignments can be achieved by producing CNT fibers from nematic liquid crystalline solutions (10). The resulting fibers have good orientation, similar to reference synthetic fibers, with an azimuthal breadth of 5°. Although the alignment of CNT fibers is superior to that of polyacrylonitrile (PAN)–based CFs, these fibers have comparable properties. The limiting factor in highly aligned CNT fibers is weak interactions between the adjacent elements, originating from the limited load transfer between single-walled CNTs that are hexagonally packed in bundles (11)—strong interactions are developed during the graphitization phase in PAN-based CFs. The interaction area between nanotubes can be maximized by collapsing the nanotube structure, similar to stacked ribbons. Flattened tube surfaces from collapsed CNT (C-CNT) structures may also enhance the intertube shear strength (12). Theoretically, collapsed tube structures experience extended pairwise Lennard-Jones interactions, which provide an advantage for dislocation stacking over regular and dislocation dipole stacking (13).
In this work, to realize CNT fibers with high-performance bulk properties, we produced highly aligned fibers by macromolecular assembly, followed by thermal treatment to increase the interactions between graphitic layers through CNT collapse, coalescence, and, ultimately, graphitization (Fig. 1A). This approach was based on the previous observation that single-walled nanotubes (SWNTs) in tightly bound bundles can form interconnected networks through coalescence and polymerization via sp3 bonding at vacancies and other defects of the graphitic structure (14, 15). These structural transformations in the large-diameter tubes could be directly induced at high pressures or temperatures. According to Monte Carlo models, SWNT bundles can be rearranged into multiwalled nanotubes or more complex graphitic nanoribbons (GNRs) via coalescence under high pressure and high temperature (16). López et al. (17) reported that the coalescence of CNT bundles is caused by the polymerization between CNTs, resulting in the formation of cylindrical and C-CNTs at high temperatures. In the present work, the increased interactions between layers following thermal treatment led to an unprecedented combination of longitudinal mechanical, electrical, and thermal properties, with simultaneous improvements in strength and modulus to levels beyond those of traditional CFs. Rationalization of the mechanical properties using a shear lag model, orientations measured using synchrotron wide-angle x-ray scattering (WAXS), and molecular dynamics (MD) simulations revealed that thermal treatment increased the shear strength between CNTs and limited embrittlement through a moderate increase in the shear modulus.
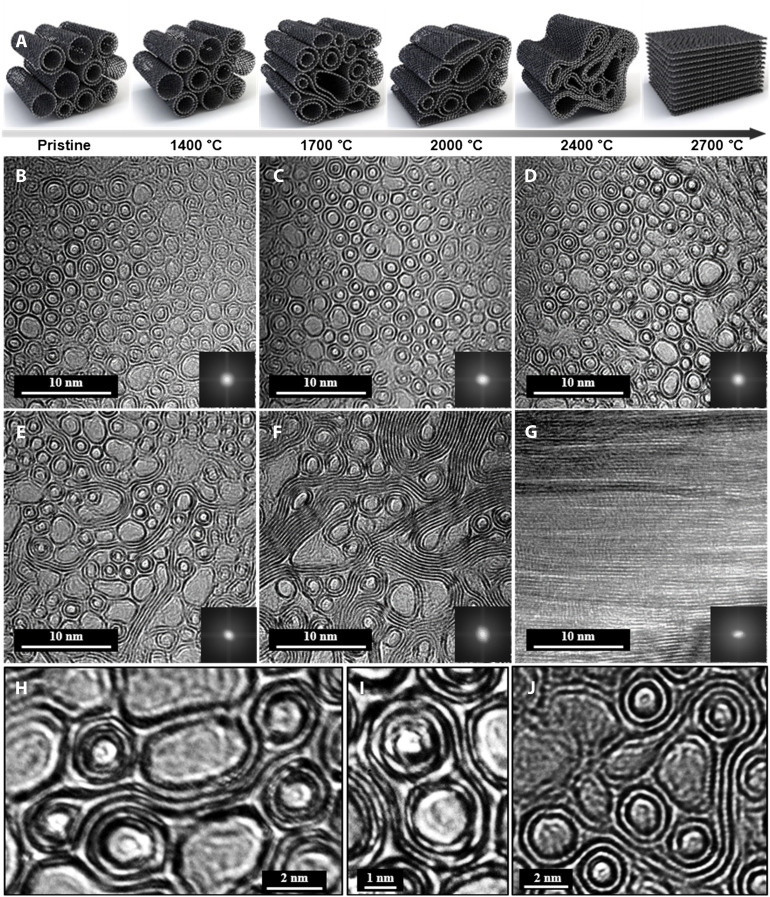
Fig. 1. Development of CNT fibers through the coalescence of nanotubes.
(A) The schematic illustration of CNT coalescence via annealing temperature. (B) Cross-sectional transmission electron microscopy (TEM) image of as-prepared CNT fibers with S·DWNT bundles. Cross-sectional TEM images of CNT fibers with MIW-CNT and C-CNT hybrid structures after annealing at (C) 1400, (D) 1700, (E) 2000, and (F) 2400°C. (G) TEM image of CNT fibers with a highly aligned GNR structure after annealing at 2700°C. High-resolution TEM images of (H) collapsed DWNT, (I) MIW-CNT, and (J) DWNT bundles wrapped with a collapsed SWNT.
RESULTS
We prepared wet-spun CNT fiber arrays directly from the nematic liquid crystal phase. The liquid crystalline dopes were prepared using CNTs (98% pure) and extruded through an optimized wet-spinning process using a single spinneret (fig. S1) (18). Figure 1 shows the distributions (fig. S2) and microstructures (fig. S3) of CNT fibers spun from a mixture (S·DWNT) of SWNT and double-walled nanotube (DWNT) (55:45) liquid crystalline dopes followed by heat treatment at different temperatures. The diameter of the CNTs increased after annealing at 1400°C (fig. S2) compared with that of the pristine S·DWNT fiber (Fig. 1B), indicating the coalescence of CNTs. The generation of defects at high temperatures or the presence of reactive sites such as ends, dangling bonds, and Stone-Wales defects in CNTs results in the formation of linkages between tubes and induces coalescence by the zipping mechanism (Fig. 1, C to E) (14). After annealing at 2400°C, unzipping of the CNT bundles into planar structures was initiated (Fig. 1F). Planarization by grain growth and orientation during graphitization were complete after annealing at 2700°C (Fig. 1G), resulting in an AB stacking GNR structure, which is generally reported in other graphitic CFs (19, 20).
Compared with tubular structures [d-spacing of 0.35 nm for the (002) plane], the d-spacing of AB stacked GNR decreased to 0.338 nm. During the coalescence of the CNT bundles, various multidimensional tube structures were observed. As the diameter of the tube increased in a limited area, favoring their collapse induced by contact with adjacent nanotube structures (Fig. 1H). Furthermore, during coalescence of the CNT bundles, multiple nanotubes sharing a single outer wall structure were formed, which we named multi-inner wall (MIW)–CNTs (Fig. 1I). In extreme cases, multiple nanotubes wrapped with a single collapsed structure appeared to fill the voids between the tubes (Fig. 1J). The average diameter of the CNTs increased by 6 to 20% up to 2000°C (fig. S2), and the ratio of C-CNTs to MIW-CNTs was up to 10%. We found that the SWNTs with smaller diameter were more likely to undergo coalescence than the DWNTs with larger diameter. This coalescence process led to an increase in the tube diameter, polygonization and flattening of tubes, and formation of C-CNT and MIW-CNT structures (figs. S2 and S3). According to an MD simulation incorporating the Berendsen thermostat scheme (21), the ability of CNTs with smaller diameters to withstand thermal loads is less than those with larger diameters because they have a greater tendency to bend, and thus, the end-to-end distance shrinks.
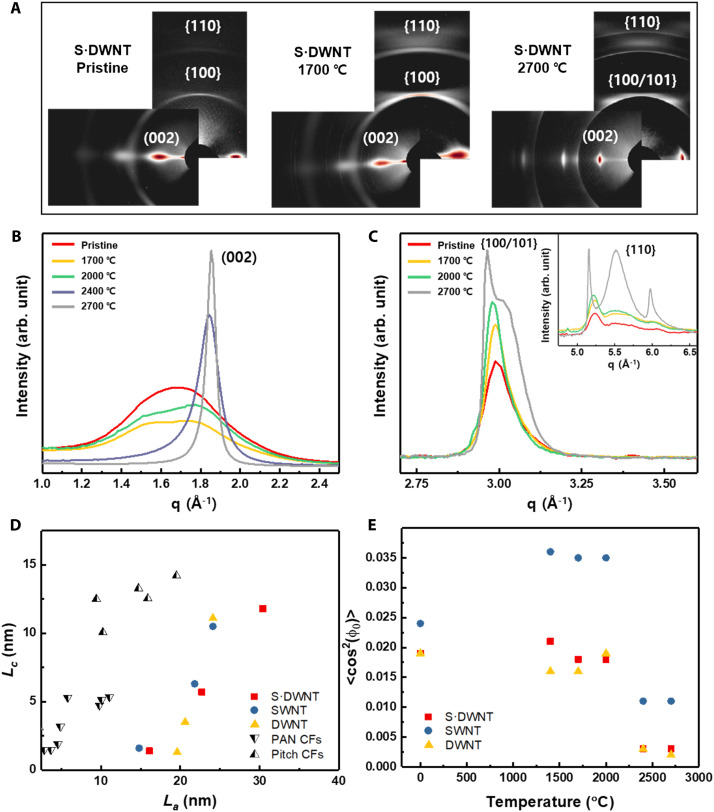
WAXS measurements show the evolution of the main structural features that control the longitudinal fiber properties upon thermal annealing. Figure 2A shows the two-dimensional (2D) WAXS patterns of S·DWNT fibers in pristine form and after annealing at 1700 and 2700°C (others in fig. S4). As inferred from the equatorial (Fig. 2B) and meridional (Fig. 2C) radial profiles, these annealing temperatures mark the main transformations. The starting material comprises highly aligned CNTs [full width at half maximum (FWHM) < 9°] in bundles with limited order and residual acid molecules. The acid molecules were removed, and CNT compaction was induced when annealing was carried out up to 1700°C, thereby resulting in stronger interplanar {hk0} reflections and smaller interlayer spacing; in contrast, annealing above 1700°C resulted in a transition from CNT bundles to flat, elongated graphitic domains, similar to ribbons, observed by the sharpening of the (002) interlayer reflection and the emergence of strong {100} and {110} reflections. After annealing at 2700°C, the material was highly graphitic, with interlayer spacing of 0.338 nm and {101} reflections indicating stacking order. Since the annealed fibers are considered as a network of crystallites, they are unique compared to traditional CFs in combining a small crystallite thickness (Lc) with an exceptionally large crystallite length (La) (Fig. 2D and fig. S5). The 2D WAXS measurements also show high alignment after annealing at various temperatures (fig. S6), with FWHM values (6° to 7°) comparable to those of high-performance polymer fibers (22). Upon annealing, the contributions of less-aligned elements disappeared from the azimuthal profile, changing the orientation distribution function and orientation parameter, ⟨cos2(ϕ)⟩ (Fig. 2E)
| (1) |
Fig. 2. Structural evolution of CNT fibers after annealing.
(A) 2D WAXS patterns of representative S·DWNT fibers. (B) Equatorial and (C) meridional radial profiles showing the transition from bundles to highly crystalline graphitic domains upon high-temperature annealing. (D) Plot of crystal sizes transversal (Lc) and parallel (La) to the fiber axis for CNT fibers as well as conventional graphitic CFs from different precursors (48). (E) Orientation parameters ⟨cos2(ϕ)⟩ calculated from the interlayer reflections (Eq. 1).
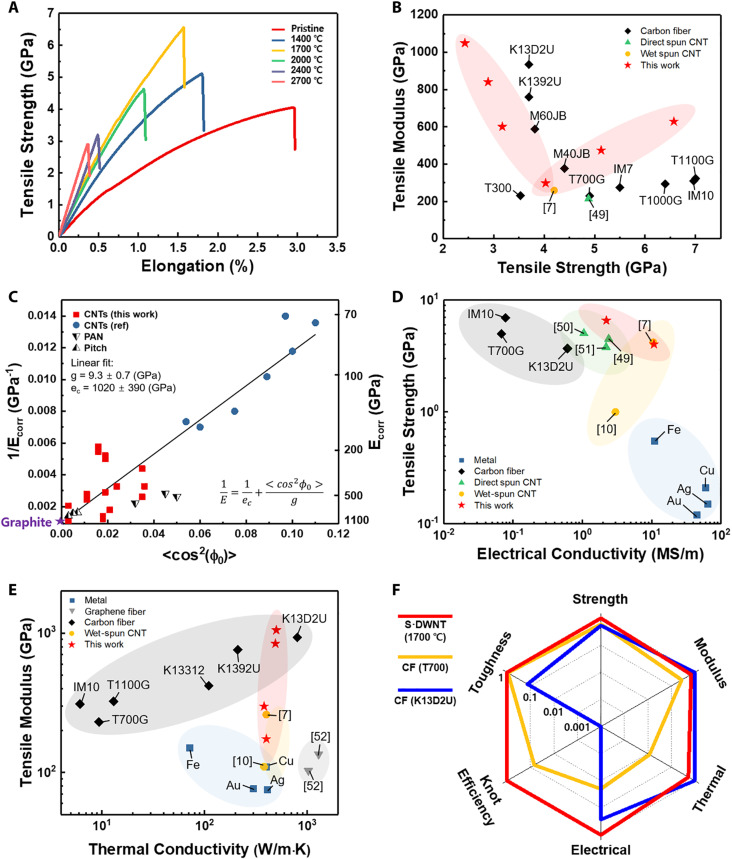
Although no significant differences were observed in the fiber cross sections (fig. S7), the changes in internal crystallite network structure produced upon annealing had a strong effect on the tensile properties. When annealing was carried out at 1700°C, tensile strength increased to 6.57 ± 0.43 GPa (best value: 7.0 GPa), and modulus to 629 ± 49 GPa (Fig. 3A). At higher annealing temperatures, the modulus increased up to 840 ± 19 GPa at 2700°C; however, the tensile strength decreased to 2.89 ± 0.1 GPa. Similar behavior was observed for the SWNT and DWNT fibers (figs. S8 and S9). Furthermore, after annealing at 2700°C, the DWNT fiber was fully transformed into a graphitic structure with a tensile modulus of 1049 ± 105 GPa, which is near the theoretical limit for graphite fibers (23). Typical fibrillary fracture surface was observed at annealing temperatures below 2000°C, whereas brittle fracture tended to occur at annealing temperatures above 2000°C (fig. S10), indicating that the transformation from a multidimensional tube structure to a graphitic structure reduces the extent of CNT sliding. Compared with previous CNT-, graphene-, PAN-, and pitch-based CFs, the tensile strength and modulus of these multidimensional structures were enhanced simultaneously (Fig. 3B).
Fig. 3. Properties of high-performance CNT fibers.
(A) Stress-strain curves of S·DWNT fibers after annealing at various temperatures. (B) Comparison of mechanical properties with other CNT fibers and CFs (7, 49). (C) Relationship between longitudinal compliance and the orientation parameter 〈cos2(ϕ)〉, and comparison with other CNT fibers and CFs, showing an apparent internal crystal shear modulus that is substantially lower that than for CFs. (D) Comparison of electrical conductivity as a function of tensile strength with other CNT fibers and CFs (7, 10, 49–51). (E) Comparison of thermal conductivity as a function of tensile modulus with other CFs, CNT, and graphene fibers (7, 10, 52). (F) A radar chart of properties for CNT fiber and CFs. Each property is normalized to the highest value within this set of fibers.
These tensile properties can be rationalized on the basis of shear lag theory (24), considering the fiber as a network of highly aligned bundles, similar to a fiber surrounded by a continuous matrix of secondary bonds that transfer stress through shear. Axial stress builds up along the bundle length and reaches a maximum in the middle of it. The magnitudes of the shear and axial stresses increase as matrix deformation increases, until the shear stress exceeds the interfacial shear strength (τC) and sliding occurs. As an estimate of fiber strength, we use the average bundle axial stress, which, for high-aspect-ratio load–bearing elements, can be obtained approximately as follows
| (2) |
where μ is related to the ratio of CNT axial (ec) and shear moduli (g), (), and c is a constant related to the bundle volume fraction Vf () (25). This equation is consistent with the observation of failure through slippage of load-bearing elements rather than fracture. Such failure mode implies that a low shear modulus is beneficial: A high shear modulus would produce a rapid buildup of a shear stress above the limiting shear strength, thereby resulting in premature failure before substantial axial stress could build up in the bundle (fig. S11). From the relationship between fiber compliance and the orientation parameter , we obtained a shear modulus of 9.3 GPa for CNT fibers (Fig. 3C), which is substantially lower than that for high-strength CFs (46 ± 10 GPa) (26). In addition, an increase in shear strength results from the reduction in interlayer separation (27) and increased crystallographic order upon annealing, as observed in Fig. 2. The simulation of pull-out energy further confirmed that annealing increases the shear strength (fig. S12). For the MD simulations, four different models were constructed to describe the CNT fibers produced (fig. S12). Compared with the SWNT bundles, C-CNT and MIW-CNT exhibited larger interfacial areas, i.e., between those of the pull-out CNTs and other CNTs, resulting in strong van der Waals interactions with 58 and 46% higher pull-out energies, respectively, than the SWNT bundles. Furthermore, the pull-out energy of the GNR structure was approximately 180% higher than that of the SWNT bundles.
CNTs are hexagonal sp2-bonded carbon structures with exceptionally high in-plane electrical (1 to 10 MS/m) and thermal conductivities (25 to 4500 W/m·K) (7, 28). However, their out-of-plane electrical (1 to 104 S/m) and thermal conductivities (0.10 to 19 W/m·K) are relatively low (28, 29). Therefore, the electrical and thermal conductivities of CNT fibers depend on the degree of alignment (7, 30). Figure S9 shows electrical conductivity versus annealing temperature, which mostly factors in dedoping for the lower temperatures and then fusing of carbon sheets for the higher temperatures. Highly oriented S·DWNT fibers with MIW and C-CNT structures annealed at 1700°C exhibited high strength (6.57 ± 0.43 GPa; best value: 7 GPa) and high electrical conductivity (2.2 ± 0.3 MS/m) (Fig. 3D and table S1). According to previous report, the thermal conductivity of graphitic fibers is often influenced by their structural defects (31–34) and domain boundaries (35, 36). Therefore, the highest thermal conductivity (496 ± 6 W/m·K) and the highest modulus (1049 ± 105 GPa) (table S1) were achieved for DWNT fibers that were prepared by annealing at 2700°C and exhibited a comparatively large longitudinal crystallite size (La = 30.4 nm) (Fig. 3E and fig. S13). The high thermal conductivity has been attributed to a very high degree of La and the corresponding reduction in phonon scattering (37). The development of La exhibited a proportional relationship with the thermal conductivity (fig. S13). Effectively, the multidimensional CNT fibers synthesized via coalescence simultaneously exceeds all the properties of previous CFs with superior knot efficiency (45%) (fig. S14) and toughness (34 J/g) (table S2). The combination of high-performance mechanical, electrical, and thermal properties is above most of PAN- and pitch-based CFs (Figs. 3, D to F).
DISCUSSION
We introduced a previously unknown CNT fiber structure by annealing process, wherein CNTs with high degree of structural perfection were first organized into superaligned fibers and then compacted by annealing to form coalesced domains with strong interactions between graphitic planes. The multidimensional CNT fiber structures were found to consist of macromolecular structures with a high shear strength and low shear modulus for effective stress transfer of the load-bearing elements. As a result, the proposed CNT fibers exhibited an ultrahigh strength (~7 GPa) or a high modulus (>1,000 GPa), close to the mechanical properties of individual nanotubes. Furthermore, these structures were highly oriented, which is favorable for designing macromolecular structures for effective phonon and electron transfer. Moreover, these new fibers exhibited high thermal (482 ± 63 W/m·K) and electrical conductivities (2.2 ± 0.3 MS/m). These multifunctional CNT fibers could be invaluable in existing and emerging applications, including aerospace vehicles, robot arms, satellites, and electronic devices, which require simultaneously high mechanical, thermal, and electrical properties.
MATERIALS AND METHODS
Materials
SWNTs (TUBALL) were purchased from OCSiAl. The SWNT content is more than 90%, and the purity is more than 95% (figs. S1A and S2). The average diameter of SWNT is 1.87 nm (fig. S2D).
Single-walled and double-walled carbon nanotube mixtures (S∙DWNT) were prepared from Meijo Nano Carbon Co. Ltd. The ratio of SWNT and DWNT is 55:45. The purity of S∙DWNT is more than 98% (fig. S1A). The average diameter of S·DWNT is 1.94 nm (fig. S2B).
Wet-spun DWNT fibers were purchased from DexMat (Houston, TX). The average diameter of DWNT is 2.42 nm (fig. S2F).
Preparing liquid crystal CNT dopes
In order to remove the amorphous carbon, SWNTs (TUBALL) were treated at 400°C for 1 hour under air atmosphere (18, 38). In addition, SWNTs were purified with piranha solution. SWCNTs (600 mg) were dispersed in 200 ml of the piranha solution [mixture of 98 weight % (wt %) sulfuric acid and 28 wt % hydrogen peroxide in a ratio of 7:3] for 5 hours at room temperature (39). The solution was washed with deionized (DI) water until it became pH 7. It was dried at 100°C in vacuum oven for 12 hours.
The S∙DWNTs (Meijo Nano Carbon Co. Ltd.) were heat treated at 400°C for 1 hour under air atmosphere without any purification process. The SWNT and S∙DWNT dopes at concentrations of 1 to 3 wt % were prepared by dispersion in chlorosulfonic acid (Sigma-Aldrich) for at least 3 days.
Wet-spinning process
The CNT dopes were extruded into an acetone (99.5%, Daejung) bath using a 24-hole spinneret or needle (fig. S1D). We spun 350 m of fiber at a time, and the spinning process could be continued as long as the liquid crystalline dope was available. The spun fibers had a minimum diameter of 8 μm (needle) and a maximum diameter of 80 μm (24-hole nozzle). Both the fibers obtained from the spinneret and needle have similar mechanical and electrical properties. The draw ratio was controlled by flow rate and winding rate in wet-spinning process. The wet-spun CNT fibers were washed in DI water for 6 hours and dried overnight in the vacuum oven at 170°C.
Heat treatment of CNT fibers
Wet-spun CNT fibers were tightly fixed to the graphite sheet using carbon tapes. The samples were heat treated at temperatures of 1400, 1700, 2000, 2400, and 2700°C, respectively. The heat treatment at 1400°C was performed using a tube-type carbonization furnace. The heat treatment at the other temperature was performed using a graphitization furnace. The temperature was raised at a heating rate of 10°C/min up to 1400°C, 5°C/min up to 1700°C, 3°C/min up to 2400°C, and 2°C/min up to 2700°C. Under the Ar atmosphere, each sample was kept at each temperature for 30 min.
Measurement of mechanical properties and linear density
Mechanical properties were measured using a FAVIMAT+ with 210 cN load cell. The sample was prepared by setting the gauge length of 25 mm onto a square frame. A weight of 100 mg was hung to measure the correct linear density. A linear density was measured by a known method (40). This is a method of calculating the resonance frequency measured with a vibroscope. The frequency of the CNT fibers was obtained by increasing the pretension from 1 to 2 cN at a rate of 2 mm/min. The linear density was calculated according to Mersenne’s law
| (3) |
where f is the frequency of the CNT fibers, L is the gauge length, T is the pretension of the CNT fiber, and μ is the linear density. Each sample was measured at least 30 times.
WAXS measurements and data analysis
WAXS measurements of individual CNT fiber filaments (~10 μm in diameter) were obtained under microfocus configuration at the NCD-SWEET beamline of ALBA synchrotron. Multiple patterns were collected in each measurement in order to reduce noise. These patterns were summed and background subtracted. The 2D patterns shown correspond to measurements at two different angles of the fiber relative to the WAXS detector, combined into a single image only for visualization. Coherent lengths, which are equivalent to crystal sizes, are calculated with the Scherrer equation using the proportionality factors used in graphite. No instrumental broadening correction is required because of the high coherence of synchrotron radiation. In-plane crystal size, La, is obtained with the FWHM of the (100) peak, fitted with a split Pearson VII function (41). For the DWNT fiber annealed at 2700°C, there is evidence of an additional peak, identified as the (101) reflection (vide supra). For those samples, La is calculated from the (100) after deconvolution. Out-of-plane crystal size, Lc, is obtained through the Scherrer equation using the (002) peak, fitted with a pseudo-Voigt function. This method for determination of crystal size is most commonly applied to synthetic fibers, thus enabling a direct comparison of CNTFs and other graphitic fibers using equivalent microstructural and mechanical characterization methods. Estimating the crystal size using the Scherrer equation usually gives a lower limit. There are alternative, more rigorous methods to calculate coherent sizes in graphitic systems, for example, by full fitting of experimental data using the model of Ruland and Smarsly (42) for coherent scattering from inter- and intralayer interference. While more accurate, this model is substantially more difficult to apply, hence less commonly related to bulk fiber properties, and produces small increases in crystal size, which are approximately constant for nongraphitizable carbons, PAN-based CF, and pitch-based CF processed at different temperatures from 500° to 2500°C (43). Azimuthal profiles were obtained after radial integration at the (002) reflection or at the maximum for the interlayer diffraction peak. For pristine samples and fiber annealed up to 2000°C, the azimuthal profile was fitted with pseudo-Voigt functions. For samples annealed at higher temperatures, a PearsonVII function was used.
Thermal conductivity measurement using a steady-state dc thermal bridge method
The thermal conductivity of suspended CNT fibers is measured using an established steady-state dc thermal bridge method that has been previously applied to CNT fibers (44). Electrical dc currents are used to heat a suspended fiber, and four-point resistance thermometry measurements are used to measure the average temperature rise. Both convection and radiation losses are negligible because the measurements are carried in high vacuum (~10−6 Torr), the suspended length of the sample is relatively small (lengths ranging from 3.9 to 5.92 mm) (45), and the temperature difference between the heated sample and substrate is maintained below 10 K. Thermal contact resistances at the sample-substrate interface are mitigated via silver paste contacts.
Briefly summarizing the analysis, the governing 1D heat conduction equation is written as
| (4) |
where x is position, T is temperature, P is the total Joule heat generation in the sample, A is the cross-sectional area of the sample, L is the suspended length, and k is the longitudinal thermal conductivity of the sample. After solving Eq. 4 and applying the boundary conditions (46), the average temperature rise of the sample above the substrate temperature can be written as
| (5) |
Equation (5) is used to extract the thermal conductivity k. The temperature of the sample was controlled using a thermoelectric module with a Pt-100 thermometer. To measure the heat generation P in Eq. 5, the current was applied using a source meter (Keithley 6221), and the voltage was measured by a nanovoltmeter (Keithley 2182A). The length of the sample was measured with optical microscopy, and the cross-sectional area was measured by scanning electron microscopy (SEM).
Simulation methods
The MD simulation was performed to investigate the effect of the structures of the CNT bundle on the pull-out energy of the CNT fiber using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS). The steered MD simulation (46) was conducted to predict the potential energy required for pulling a pull-out CNT or layer from a CNT bundle (from case 1 to case 3) or graphitic sheets (case 4) in the four models with the different structure (fig. S11A). Figure S11B shows the stabilized CNT bundle and graphitic sheets after the equilibration process of MD simulation models. The pull-out simulation was conducted using the stabilized simulation models. The one end of the other CNTs (or the other layers) except for the pull-out CNT (or pull-out layer) in the model was fully fixed in a longitudinal direction of CNTs. The pull-out CNT (or pull-out layer) was pulled out at a constant velocity during the pulling process. The pull-out energy (W), which is the calculated potential of mean force during the pull-out simulation, is expressed as
| (6) |
| (7) |
where U is the potential energy, k is the spring force constant, v is the pull-out velocity, t is the time, and n is the vector direction. r and r0 are the position of atoms at time t and the initial position of atoms, respectively (47).
Characterizations
The cross sections and surface morphology of CNT fibers were observed by SEM (FEI-Helios). High-resolution transmission electron microscopy (TEM; FEI-Titan G3) was used to observe the diameter and structural evolutions of CNTs. Specimens for TEM imaging of fiber cross sections were prepared using the focused ion beam of the FEI-Helios scanning electron microscope. The thermogravimetric analysis was performed using a Q50 (TA Instruments) at a heating rate of 10°C/min under air atmosphere. The liquid crystal phase of the CNT dope was obtained using an optical microscopy with cross-polarizing filter (L150, Nikon). The electrical conductivity of CNT fibers was measured by a four-point probe method using a probe station (MST-4000A, MS Tech). The G/D ratios of raw CNTs and CNT fibers were measured by a Raman spectrometer (InVia Reflex, RENISHAW) with 514-nm excitation wavelengths.
Acknowledgments
Funding: This work was funded by KIST ORP Program (2E31332), Korean National Research Foundation (2019R1A5A8080326), European Union Horizon 2020 Framework Program (678565, ERC-STEM), Air Force Office of Scientific Research of the United States (NANOYARN FA9550-18-1-7016), The Carbon Hub, The Robert A. Welch Foundation (grants C-1668 and C-1509), the Department of Energy (DOE) of the United States award DE-AR0001015 (Advanced Research Projects Agency Energy), the Department of Energy (DOE) of the United States, the Basic Energy Science (BES) program (grant no. DE-FG02-06ER46308), and Department of Defense through a National Defense Science and Engineering Graduate (NDSEG) Fellowship (32CFR 168a).
Author contributions: Conceptualization: D.L. and S.G.K. Methodology: D.L., S.G.K., S.H., C.M., Y.O., M.P., N.K., L.W.T., B.C., and J. Kim Investigation: J.Y.H., J.Y., D.S.L., H.S.J., N.H.Y., N.D.K., D.-Y.K., H.S.L., J. Kono, G.W., and M.P. Project administration: K.-H.L. Supervision and writing: J.J.V., S.R., and B.-C.K.
Competing interests: B.-C.K., J.Y.H., H.S.J., N.H.Y., N.D.K., D.-Y.K., D.L., S.G.K., S.K.H., and S.R. are inventors on patent application related to this work (10-2021-0006762) submitted by ENVISION that covers (Carbon nanotube fiber having improved property and preparing method thereof). B.-C.K., D.L., S.K.H., J.Y.H., H.S.J., N.H.Y., and S.R. are inventors on a patent related to this work filed by Y.P. Lee, MOCK & Partners (patent number 10-2322833; submitted 15 May 2020; published 01 November 2021). M.P. has a financial interest in DexMat, which commercializes solution-spun CNT fibers. The authors declare that they have no other competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S14
Tables S1 and S2
References
REFERENCES AND NOTES
- 1.Chae H. G., Kumar S., Making strong fibers. Science 319, 908–909 (2008). [DOI] [PubMed] [Google Scholar]
- 2.Lee C., Wei X., Kysar J. W., Hone J., Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008). [DOI] [PubMed] [Google Scholar]
- 3.Javey A., Guo J., Wang Q., Lundstrom M., Dai H., Ballistic carbon nanotube field-effect transistors. Nature 424, 654–657 (2003). [DOI] [PubMed] [Google Scholar]
- 4.Yu C., Shi L., Yao Z., Li D., Majumdar A., Thermal conductance and thermopower of an individual single-wall carbon nanotube. Nano Lett. 5, 1842–1846 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Adnan M., Pinnick R. A., Tang Z., Taylor L. W., Pamulapati S. S., Carfagni G. R., Pasquali M., Bending behavior of CNT fibers and their scaling laws. Soft Matter 14, 8284–8292 (2018). [DOI] [PubMed] [Google Scholar]
- 6.M. Miao, Carbon Nanotube Fibres and Yarns: Production, Properties and Applications in Smart Textiles (Elsevier, Cambridge, 2019). [Google Scholar]
- 7.Taylor L. W., Dewey O. S., Headrick R. J., Komatsu N., Peraca N. M., Wehmeyer G., Kono J., Pasquali M., Improved properties, increased production, and the path to broad adoption of carbon nanotube fibers. Carbon 171, 689–694 (2021). [Google Scholar]
- 8.Gupta N., Alred J. M., Penev E. S., Yakobson B. I., Universal strength scaling in carbon nanotube bundles with frictional load transfer. ACS Nano 15, 1342–1350 (2021). [DOI] [PubMed] [Google Scholar]
- 9.Zhang X., Lu W., Zhou G., Li Q., Understanding the mechanical and conductive properties of carbon nanotube fibers for smart electronics. Adv. Mater. 32, 1902028 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Behabtu N., Young C. C., Tsentalovich D. E., Kleinerman O., Wang X., Ma A. W. K., Bengio E. A., ter Waarbeek R. F., de Jong J. J., Hoogerwerf R. E., Fairchild S. B., Ferguson J. B., Maruyama B., Kono J., Talmon Y., Cohen Y., Otto M. J., Pasquali M., Strong, light, multifunctional fibers of carbon nanotubes with ultrahigh conductivity. Science 339, 182–186 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Vilatela J. J., Elliott J. A., Windle A. H., A model for the strength of yarn-like carbon nanotube fibers. ACS Nano 5, 1921–1927 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Jensen B. D., Kim J.-W., Sauti G., Wise K. E., Dong L., Wadley H. N. G., Park J. G., Liang R., Siochi E. J., Toward ultralight high-strength structural materials via collapsed carbon nanotube bonding. Carbon 156, 538–548 (2020). [Google Scholar]
- 13.Qian D., Liu W. K., Ruoff R. S., Load transfer mechanism in carbon nanotube ropes. Compos. Sci. Technol. 63, 1561–1569 (2003). [Google Scholar]
- 14.Terrones M., Terrones H., Banhart F., Charlier J.-C., Ajayan P. M., Coalescence of single-walled carbon nanotubes. Science 288, 1226–1229 (2000). [DOI] [PubMed] [Google Scholar]
- 15.Elliott J. A., Sandler J. K. W., Windle A. H., Young R. J., Shaffer M. S. P., Collapse of single-wall carbon nanotubes is diameter dependent. Phys. Rev. Lett. 92, 095501 (2004). [DOI] [PubMed] [Google Scholar]
- 16.Kim U. J., Gutiérrez H. R., Kim J. P., Eklund P. C., Effect of the tube diameter distribution on the high-temperature structural modification of bundled single-walled carbon nanotubes. J. Phys. Chem. B 109, 23358–23365 (2005). [DOI] [PubMed] [Google Scholar]
- 17.López M. J., Rubio A., Alonso J. A., Lefrant S., Méténier K., Bonnamy S., Patching and tearing single-wall carbon-nanotube ropes into multiwall carbon nanotubes. Phys. Rev. Lett. 89, 255501 (2002). [DOI] [PubMed] [Google Scholar]
- 18.Jeong H. D., Kim S. G., Choi G. M., Park M., Ku B.-C., Lee H. S., Theoretical and experimental investigation of the wet-spinning process for mechanically strong carbon nanotube fibers. Chem. Eng. J. 412, 128650 (2021). [Google Scholar]
- 19.Jin S., Chung B., Park H. J., Cunning B. V., Lee J.-H., Yoon A., Huang M., Seo H., Lee D., Lee Z., Ruoff R. S., Ryu S., Ultrahigh strength and modulus graphene-based hybrid carbons with AB-stacked and turbostratic structures. Adv. Funct. Mater. 30, 2005381 (2020). [Google Scholar]
- 20.D. D. L. Chung, Carbon Composites: Composites with Carbon Fibers, Nanofibers, and Nanotubes (Elsevier, Cambridge, 2016). [Google Scholar]
- 21.Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., Dinola A., Haak J. R., Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690 (1984). [Google Scholar]
- 22.Northolt M. G., den Decker P., Picken S. J., Baltussen J. J. M., Schlatmann R., The Tensile strength of polymer fibres. Adv. Polym. Sci. 178, 1–108 (2005). [Google Scholar]
- 23.B. T. Kelly, The Physics of Graphite (Applied Science Publishers, 1981). [Google Scholar]
- 24.Wei X., Ford M., Soler-Crespo R. A., Espinosa H. D., A new Monte Carlo model for predicting the mechanical properties of fiber yarns. J. Mech. Phys. Solids 84, 325–335 (2015). [Google Scholar]
- 25.Yoon H. N., Strength of fibers from wholly aromatic polyesters. Colloid Polym. Sci. 268, 230–239 (1990). [Google Scholar]
- 26.Behr M. J., Landes B. G., Barton B. E., Bernius M. T., Billovits G. F., Hukkanen E. J., Patton J. T., Wang W., Wood C., Keane D. T., Rix J. E., Weigand S. J., Structure-property model for polyethylene-derived carbon fiber. Carbon 107, 525–535 (2016). [Google Scholar]
- 27.Shibuta Y., Elliott J. A., Interaction between two graphene sheets with a turbostratic orientational relationship. Chem. Phys. Lett. 512, 146–150 (2011). [Google Scholar]
- 28.Kumanek B., Janas D., Thermal conductivity of carbon nanotube networks: A review. J. Mater. Sci. 54, 7397–7427 (2019). [Google Scholar]
- 29.Fairchild S. B., de Assis T. A., Park J. H., Cahay M., Bulmer J., Tsentalovich D. E., Ang Y. S., Ang L. K., Ludwick J., Back T. C., Pasquali M., Strongly anisotropic field emission from highly aligned carbon nanotube films. J. Appl. Phys. 129, 125103 (2021). [Google Scholar]
- 30.Tsentalovich D. E., Headrick R. J., Mirri F., Hao J., Behabtu N., Young C. C., Pasquali M., Influence of carbon nanotube characteristics on macroscopic fiber properties. ACS Appl. Mater. Interfaces 9, 36189–36198 (2017). [DOI] [PubMed] [Google Scholar]
- 31.Hao F., Fang D., Xu Z., Mechanical and thermal transport properties of graphene with defects. Appl. Phys. Lett. 99, 041901 (2011). [Google Scholar]
- 32.Xie G., Shen Y., Wei X., Yang L., Xiao H., Zhong J., Zhang G., A bond-order theory on the phonon scattering by vacancies in two-dimensional materials. Sci. Rep. 4, 5085 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fthenakis Z. G., Zhu Z., Tománek D., Effect of structural defects on the thermal conductivity of graphene: From point to line defects to haeckelites. Phys. Rev. B 89, 125421 (2014). [Google Scholar]
- 34.Anno Y., Imakita Y., Takei K., Akita S., Arie T., Enhancement of graphene thermoelectric performance through defect engineering. 2D Mater. 4, 025019 (2017). [Google Scholar]
- 35.Yasaei P., Fathizadeh A., Hantehzadeh R., Majee A. K., El-Ghandour A., Estrada D., Foster C., Aksamija Z., Khalili-Araghi F., Salehi-Khojin A., Bimodal phonon scattering in graphene grain boundaries. Nano Lett. 15, 4532–4540 (2015). [DOI] [PubMed] [Google Scholar]
- 36.Liu H. K., Lin Y., Luo S. N., Grain boundary energy and grain size dependences of thermal conductivity of polycrystalline graphene. J. Phys. Chem. C 118, 24797–24802 (2014). [Google Scholar]
- 37.Qiu L., Zhang X., Guo Z., Li Q., Interfacial heat transport in nano-carbon assemblies. Carbon 178, 391–412 (2021). [Google Scholar]
- 38.Davis V. A., Ericson L. M., Parra-Vasquez A. N. G., Fan H., Wang Y., Prieto V., Longoria J. A., Ramesh S., Saini R. K., Kittrell C., Billups W. E., Adams W. W., Hauge R. H., Smalley R. E., Pasquali M., Phase behavior and rheology of SWNTs in superacids. Macromolecules 37, 154–160 (2004). [Google Scholar]
- 39.Datsyuk V., Kalyva M., Papagelis K., Parthenios J., Tasis D., Siokou A., Kallitsis I., Galiotis C., Chemical oxidation of multiwalled carbon nanotubes. Carbon 46, 833–840 (2008). [Google Scholar]
- 40.Park J., Lee S.-H., Lee J., Lee D.-M., Yu H., Jeong H. S., Kim S. M., Lee K.-H., Accurate measurement of specific tensile strength of carbon nanotube fibers with hierarchical structures by vibroscopic method. RSC Adv. 7, 8575–8580 (2017). [Google Scholar]
- 41.Milev A., Wilson M., Kannangara G. S. K., Tran N., X-ray diffraction line profile analysis of nanocrystalline graphite. Mater. Chem. Phys. 111, 346–350 (2008). [Google Scholar]
- 42.Ruland W., Smarsly B., X-ray scattering of non-graphitic carbon: An improved method of evaluation. J. Appl. Cryst. 35, 624–633 (2002). [Google Scholar]
- 43.Zickler G. A., Smarsly B., Gierlinger N., Peterlik H., Paris O., A reconsideration of the relationship between the crystallite size La of carbons determined by X-ray diffraction and Raman spectroscopy. Carbon 44, 3239–3246 (2006). [Google Scholar]
- 44.Moon J., Weaver K., Feng B., Chae H. G., Kumar S., Baek J.-B., Peterson G. P., Note: Thermal conductivity measurement of individual poly(ether ketone)/carbon nanotube fibers using a steady-state dc thermal bridge method. Rev. Sci. Instrum. 83, 016103 (2012). [DOI] [PubMed] [Google Scholar]
- 45.Qiu L., Wang X., Tang D., Zheng X., Norris P. M., Wen D., Zhao J., Zhang X., Li Q., Functionalization and densification of inter-bundle interfaces for improvement in electrical and thermal transport of carbon nanotube fibers. Carbon 105, 248–259 (2016). [Google Scholar]
- 46.S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers, K. Schulten, Steered Molecular Dynamics, Computational Molecular Dynamics: Challenges, Methods, Ideas (Springer, 1998), pp. 39–65. [Google Scholar]
- 47.Park S., Schulten K., Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 120, 5946–5961 (2004). [DOI] [PubMed] [Google Scholar]
- 48.Takaku A., Shioya M., X-ray measurements and the structure of polyacrylonitrile- and pitch-based carbon fibres. J. Mater. Sci. 25, 4873–4879 (1990). [Google Scholar]
- 49.Lee J., Lee D.-M., Jung Y., Park J., Lee H. S., Kim Y.-K., Park C. R., Jeong H. S., Kim S. M., Direct spinning and densification method for high-performance carbon nanotube fibers. Nat. Commun. 10, 2962 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tran T. Q., Fan Z., Liu P., Myint S. M., Duong H. M., Super-strong and highly conductive carbon nanotube ribbons from post-treatment methods. Carbon 99, 407–415 (2016). [Google Scholar]
- 51.Wang J. N., Luo X. G., Wu T., Chen Y., High-strength carbon nanotube fibre-like ribbon with high ductility and high electrical conductivity. Nat. Commun. 5, 3848 (2014). [DOI] [PubMed] [Google Scholar]
- 52.Xin G., Yao T., Sun H., Scott S. M., Shao D., Wang G., Lian J., Highly thermally conductive and mechanically strong graphene fibers. Science 349, 1083–1087 (2015). [DOI] [PubMed] [Google Scholar]
- 53.Stuart S. J., Tutein A. B., Harrison J. A., A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486 (2000). [Google Scholar]
- 54.Yuan X., Wang Y., Zhu B., Adhesion between two carbon nanotubes: Insights from molecular dynamics simulations and continuum mechanics. Int. J. Mech. Sci. 138-139, 323–336 (2018). [Google Scholar]
- 55.Jang D., Lee S., Correlating thermal conductivity of carbon fibers with mechanical and structural properties. J. Ind. Eng. Chem. 89, 115–118 (2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S14
Tables S1 and S2
References