Common datastream permutations of animal social network data are not appropriate for hypothesis testing using regression models

Abstract

1. Social network methods have become a key tool for describing, modelling, and testing hypotheses about the social structures of animals. However, due to the non-independence of network data and the presence of confounds, specialized statistical techniques are often needed to test hypotheses in these networks. Datastream permutations, originally developed to test the null hypothesis of random social structure, have become a popular tool for testing a wide array of null hypotheses in animal social networks. In particular, they have been used to test whether exogenous factors are related to network structure by interfacing these permutations with regression models.

2. Here, we show that these datastream permutations typically do not represent the null hypothesis of interest to researchers interfacing animal social network analysis with regression modelling, and use simulations to demonstrate the potential pitfalls of using this methodology.

3. Our simulations show that, if used to indicate whether a relationship exists between network structure and a covariate, datastream permutations can result in extremely high type I error rates, in some cases approaching 50%. In the same set of simulations, traditional node-label permutations produced appropriate type I error rates (~ 5%).

4. Our analysis shows that datastream permutations do not represent the appropriate null hypothesis for these analyses. We suggest that potential alternatives to this procedure may be found in regarding the problems of non-independence of network data and unreliability of observations separately. If biases introduced during data collection can be corrected, either prior to model fitting or within the model itself, node-label permutations then serve as a useful test for interfacing animal social network analysis with regression modelling.

Introduction

Social structure, defined as the patterning of repeated interactions between individuals (Hinde 1976), represents a fundamental characteristic of many animal populations with far-reaching consequences for ecology and evolution, including for gene-flow, social evolution, pathogen transmission, and the emergence of culture (Kurvers et al., 2014). The last two decades have seen widespread adoption of social network methods in animal behaviour research to quantify social structure (Webber & vander Wal, 2019). The network framework is appealing because it explicitly represents the relationships between social entities from which social structure emerges (Hinde, 1976), and thus allows tests of hypotheses about social structure at a variety of scales (individual, dyadic, group, population). Social networks can be based on direct observations of interactions, or inferred from other data types, such as groupings of identified individuals (Franks et al., 2010), GPS tracks (Spiegel et al., 2016), proximity loggers (Ryder et al., 2012), or time-series of detections (Psorakis et al., 2012).

The analysis of animal social network data presents a statistical challenge. Specifically, two separate issues must be addressed. First, network data are inherently non-independent, thus violating the assumptions of independent observations inherent to many commonly used statistical tests. Second, factors outside of social structure, such as data structure and observation bias, may influence the structure of observed animal social networks, potentially leading to both type I and type II errors in statistical tests (Croft et al., 2011).

To address the problem of non-independence, a wide array of statistical tools have been developed, primarily in the social sciences. These methods include permutation techniques that allow for hypothesis testing in the presence of non-independence. These permutations normally test relationships between exogenous variables and network properties, such as the presence and strength of social ties, or the centrality of nodes in the network. These methods typically build empirical null distributions by randomly assigning the location of nodes in the network, while holding the network structure constant (“node-label permutations”), therefore representing the null hypothesis that the network measure serving as the response is unrelated to the predictor, while controlling for network structure and non-independence. The resulting null distribution maintains the non-independence inherent to the network while breaking any relationship that exists between network structure and potential covariates (Dekker et al., 2007).

While these methods are useful for dealing with the issue of non-independence, they do not address the second issue, from which studies of animal social systems in particular often suffer. Because the methods developed in the social sciences only permute the final constructed network, they do not inherently account for common biases in the collection of the raw observational data used to construct the final network. These biases may be introduced by the method of data collection (e.g. group-based observations), individual differences in identifiability, or demographic processes (James et al., 2009). For example, consider a situation where researchers are interested in differences in social position between sexes, but females are more cryptic and thus observed with a lower probability. This would lead to incorrect inferences due to biases in the observed network structure that are unrelated to the true social processes of interest (Farine, 2017). To deal with these problems, a suite of alternative permutation procedures has been developed. Rather than permuting the final network, these methods permute the raw data used to construct the network. These methods are therefore sometimes referred to as “pre-network permutations” or “datastream permutations.” The goal is to construct permuted datasets that maintain structures of the original data that may influence the observed network structure (e.g. the number of times individuals were observed and the sizes of observed groups), while removing the social preferences that underpin the social network (Farine & Whitehead, 2015).

The original datastream permutation technique for animal social data was proposed by Bejder et al. (1998), based on the procedure outlined by Manly (1997) for ecological presence-absence data. Bejder et al.’s procedure was designed to test whether a set of observed groupings of identified animals showed signs of non-random social preferences. This procedure permutes a group-by-individual matrix, where rows are groups and columns are individuals, with 1 representing presence and 0 indicating absence. The algorithm finds 2 by 2 “checkerboard” submatrices, with 0s on one diagonal and 1s on the other, that can be “flipped” (0s replaced with 1s and vice versa). These flips maintain row and column totals (the group size and observations per individual, respectively), but permute group membership. In biological terms, matrices generated with this procedure represent the null hypothesis that individuals associated completely at random, given the observed distribution of group sizes and the number of sightings per individual.

Refinements of this method were later developed that constrained swaps within time periods, classes of individual, or locations (Whitehead et al., 2005). One alteration also controls for gregariousness, and allows for permutation of data not constructed using group membership (Whitehead, 1999). Controlling for gregariousness and sighting history is possible when each sampling period is represented as a square matrix, where 1 indicates that individuals associated in that period and 0 indicates no association. In this format, the data can be permuted in a way that maintains the number of associates each individual had in each sampling period (Whitehead, 1999).

In recent years, datastream permutation methods have been developed that can handle more complex data structures, such as GPS tracks (Spiegel et al., 2016), time-series of detections (Psorakis et al., 2015), and focal follow data (Farine, 2017). All of these methods have in common that they essentially randomise raw observations of social association (or interactions) data and thus remove social structure while maintaining most other features of the data, including features potentially causing biased measurements of social structure. They thus provide a robust null distribution to test for non-random social structure in a dataset, which is a key step in understanding the behavioural ecology of wild populations.

Many empirical studies and methodological guides have suggested interfacing these null models with other statistical techniques, particularly regression models (including ordinary least squares, generalized linear models, and mixed-effects models), to test hypotheses about network structure. The logic of this recommendation is that permutation-based null models allow researchers to account for sampling issues when testing hypotheses using these common statistical models. However, it is important to recognize the limitations of this approach, and to think carefully about the null hypothesis that these methods specify. In common datastream permutation null models, the null hypothesis specified is that the population’s social structure is random, once we control for the structure of the data and other confounds. For a particular quantity of interest, such as edge weights or node centralities, this null hypothesis can be equivalently stated as proposing that all variance in a given network metric is due to data structure, confounds, and residual variance. In network terminology, this null hypothesis is a random graph, within a set of constraints. This is precisely the null hypothesis that these permutations were designed to test, as they were originally intended as a tool for detecting non-random social structure. However, we feel there has been a lack of consideration about whether this null hypothesis is appropriate in other contexts, such as regression modelling.

Regression models in the context of social network analysis

Most regression applications in social network analysis can be broadly considered in two broad categories: nodal regression and dyadic regression. In the case of dyadic regression, researchers are interested in determining if the strength or presence of social relationships themselves are predicted by some dyadic variable, such as kinship or similarity in some trait. Nodal regression, on the other hand, represents hypotheses linking individual level traits, such as age, sex, or personality, with the position of nodes within the network, as summarized by any number of centrality measures. Here, we will investigate whether datastream permutations specify the appropriate null hypothesis for the typical inferences in these two regression contexts.

Consider the basic linear model:

$$Y=\beta X+ϵ$$ (1)

where Y is a response variable, X is a matrix of predictor variables, ε is the error term, and β is a vector of estimated coefficients. The structure of Y, X, and ε differ between dyadic and nodal regression contexts. In dyadic regression, Y is the N x N adjacency matrix (where N is the number of individuals in the network), X is a p x N x N array of predictors (where p is the number of predictors), and ε is a square matrix. In nodal regression, Y is instead a vector of centrality measures of length N, X is a p x N matrix, and ε is a vector of length N.

We are typically interested in testing the null hypothesis ϐ = 0, representing no relationship between the response Y and the predictor(s) X. In permutation based hypothesis testing procedures, this null hypothesis is tested by calculating a test statistic (such as the coefficient ϐ or the t statistic) in the observed data, and then repeatedly shuffling either X or Y to build a null distribution of this statistic. These permutations maintain the distribution of both X and Y, but break the covariance between them (Anderson & Robinson, 2001). This is the logic behind traditional permutation tests for regression in social networks, such as node-label permutations and multiple regression quadratic assignment procedures (MRQAP) (Croft et al., 2011).

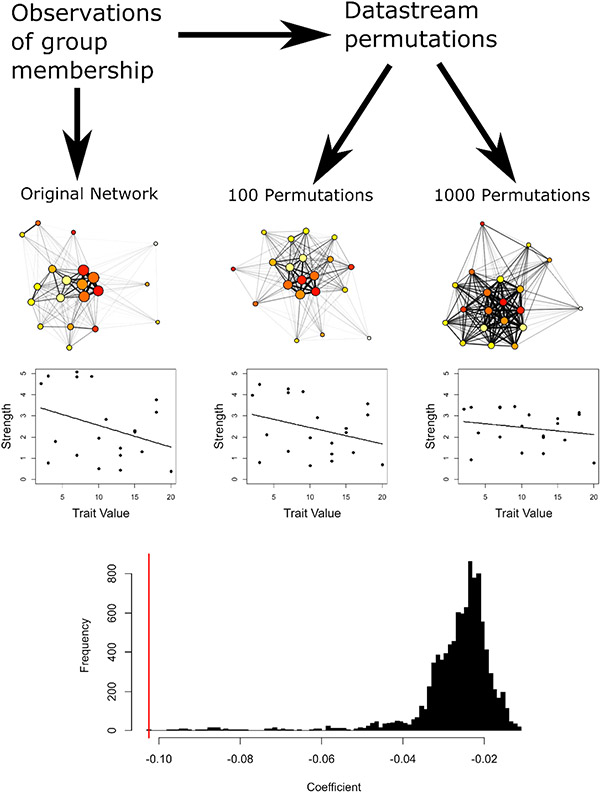
Datastream permutations, however, do something very different, which is inappropriate for testing the null hypothesis of no relationship between the response Y and the predictor(s) X. By permuting the data underlying network measures and then re-calculating the response variable, these procedures change the distribution of Y, instead of breaking relationships between the variables (Figure 1). If the network has non-random social structure, even structure entirely unrelated to X, then we will typically see a reduction in the variance of Y as we permute the raw data. When Y has a larger variance in the observed data than in the permutations, more extreme values of ϐ are more likely to occur in the observed data, even if the null hypothesis is true. This procedure is therefore likely to result in much higher rates of false-positive (type I) error than is acceptable (Figure 1).

Figure 1.

Example of the mechanism by which datastream permutations may lead to false positives in linear regression. In the original network, there is variation in strength among individuals driven by differences in gregariousness (represented by node size in the social networks). Individuals are assigned a trait value (represented by colour in the social network) unrelated to their network position. By chance, there is a slight negative relationship between network strength and trait value in the observed network. After several permutations, there is a reduction in the variance in the strength of individuals in the permuted network, and thus the magnitude of the relationship is reduced. The bottom histogram shows the distribution of null coefficients after 10,000 permutations (black), and the coefficient from the original linear model (red).

The problem here extends beyond the technical issue of reduced variance in the permuted datasets. There is a fundamental problem with this approach when it comes to testing hypotheses using regression models. When researchers fit regression models to predict network properties from exogenous variables, the null hypothesis they will typically be testing against can be stated as “the variation in network structure is not related to the exogenous variable.” This, however, is not the null hypothesis tested by the commonly used datastream permutation methods. Rather, the null hypothesis that is proposed by these datastream permutations could be stated as “the degree of variation in network structure and its relationship to the exogenous variable are both due to random interactions of individuals within constraints.” The researcher cannot disentangle the null hypothesis of no relationship between the network and the predictor from the null hypothesis of random social structure. In other words, a significant result from this procedure could be due to a relationship between the predictor and the network, or because individuals do not interact at random, whether or not the true social structure is related to the predictor. This fundamental mismatch between the null hypothesis of interest and that tested by the datastream permutation algorithm makes tests of regression models using this procedure nearly uninterpretable.

To further illustrate the problems that occur when combining datastream permutations of animal social network data with regression we provide two simulated scenarios. In these scenarios, we generate datasets with simple, but non-random social structure. We then introduce a random exogenous variable that has no relationship to social structure, and test for a relationship between network structure and this variable with linear models, using datastream permutations to determine statistical significance. We show that even in the absence of any true relationship between exogenous variables and social structure, datastream permutations are highly prone to producing significant p-values when social structure is non-random. We caution against using these datastream permutations to test the coefficients of regression models, and we discuss possible solutions and alternative methods for regression analysis in social networks.

Materials and Methods

General framework

We carried out simulations across two different scenarios, reflecting common research questions in animal social network analysis. The first scenario simulates a case in which researchers are interested in whether dyadic covariates (e.g. kinship or phenotypic similarity) influences the strength of social bonds, which we will refer to as a case of “dyadic regression”. The second scenario simulates a case when researchers are interested in how a quantitative individual trait (e.g. age or personality) influences individual network position, which we refer to as “nodal regression.”

While the methods of network generation differ slightly for each scenario, the general steps are the same:

1. Generate observations of a network in which the quantity of interest (edge weight or node centrality) has inherent variation.

2. Generate values for a trait that are unrelated to this variation.

3. Fit a linear model with the network property as the response variable and the trait as the predictor.

4. Create permuted versions of the observed network via a common datastream permutation.

5. Compare the original model’s test statistics to those from the permuted data sets to calculate a p-value.

For each simulation, we perform 200 runs, with varying parameter values (Table 1). For each run of both simulations, we produce six outputs. The first two outputs are the p-values from the datastream permutation test when using either the coefficient or t-value as the test statistic. We additionally calculate the p-values for the same two test statistics using node-label permutations, although further analysis showed that the t statistic and coefficient always produced identical results in these cases. The final two outputs give information about the characteristics of the dataset not given by the initial inputs. The first is the standard deviation of the response variable (either the edge weights or strengths), indicating the degree of non-randomness in the social structure, and the second is the average number of sightings per individual, a common measure of sampling effort in social network studies.

Table 1.

Ranges for varied parameters used in simulations

Parameter	Meaning	Dyadic	Nodal	Range
N	Number of individuals in population	✓	✓	20 – 100
μ	Mean association probability	✓		0.01 – 0.5
t	Number of sampling periods	✓		20 – 200
ϕ	Precision of beta distribution for association probabilities	✓		1 – 10
o	Observation probability per sampling period	✓		0.1 – 1
G	Number of observed groupings		✓	20 – 500
M	Maximum grouping size		✓	5 – 10
σ	Standard deviation of group size preference		✓	0.1 – 2.0

All simulations and subsequent analyses were performed in R (R Core Team 2020), using the packages asnipe (Farine 2019), lhs (Carnell 2019), and truncnorm (Mersmann et al. 2018).

Dyadic regression: Does similarity in a trait predict the strength of social relationships?

In our first simulation, we investigate the case in which the researcher is interested in the influence of a dyadic predictor (such as similarity in phenotype or kinship) on the rates at which dyads associate or interact. Our simulation framework is heavily inspired by those of Whitehead & James (2015) and Farine & Whitehead (2015). We simulate a population of N individuals, and assign each dyad an association probability p_ij from a beta distribution with mean μ and precision ϕ (α = μϕ, ϐ = (1-μ) ϕ). By assigning association probabilities in this way, we create non-random social preferences in the network, and thus larger variance in edge weights than would be expected given random association (Whitehead et al., 2005).

We then simulate τ sampling periods. For simplicity, individuals are sighted in each sampling period with a constant probability o, and associations between dyads where both individuals are sighted occur with probability p_ij. We then build the observed association network by calculating dyadic simple ratio indices (SRI):

$$SR{I}_{ij}=\frac{X_{ij}}{D_{ij}}$$ (2)

Where X_ij is the total number of sampling periods in which i and j were observed associating, and D_ij is the total number of periods in which either i or j was observed (including periods where they were observed, but did not associate with any individuals).

We then assign each individual a trait value from a uniform distribution (0,1). We do not need to specify what this trait represents for our simulation, but it could represent any quantitative trait used as a predictor in social network studies (age, personality, cognitive ability, dominance rank, parasite load, etc.). Note that the trait value is generated after the observations of association and has no influence on any network property.

We then fit the linear model:

$$SR{I}_{ij}={\beta }_0+{\beta }_1\mid trai{t}_i-trai{t}_j\mid +{\epsilon }_{ij}$$ (3)

and save the estimate of β₁ and the associated t statistic. We compare this coefficient and t statistic to a null model generated using the sampling period permutation method proposed by Whitehead (1999). There are several algorithms available to perform these swaps. We use the “trial swap” procedure described by Miklós & Podani (2004) and suggested for social network studies by Krause et al. (2009). For each trial, this procedure chooses an arbitrary 2 by 2 submatrix of the lower triangle within a random sampling period. If a swap is possible, it is performed (and symmetrized), otherwise the matrix stays at its current state. These steps when the matrix is not changed are referred to as “waiting steps.” This algorithm is ideal because it ensures that the Markov chain samples the possible matrices uniformly, while other algorithms that do not include waiting steps exhibit biases in their sampling of the possible matrices (Miklós & Podani, 2004). We generate 10,000 permuted datasets for each simulation, with 1,000 trial swaps between each permutation, and re-fit our linear model to each permuted dataset, recording the coefficient and t statistic. We then use these distributions to calculate p-values for the linear model’s coefficient. Across the 200 runs, we vary the parameters of the simulation by drawing μ, ϕ, N, o, and τ randomly using Latin hypercube sampling (Table 1).

Nodal regression: Do individual traits influence network centrality?

We next investigate the same concept in the context of nodal regression. This form of analysis tests whether some individual attribute is related to variation in network position. This is perhaps the most common use of datastream permutation null models for testing the significance of linear regression coefficients in animal social networks (e.g. Cowl et al., 2020; Poirier & Festa-Bianchet, 2018; Zeus et al., 2018). For simplicity, we focus on strength, which is simply the sum of an individual’s edge weights.

In this simulation, we consider the case where networks are derived from patterns of shared group membership (“gambit of the group”). This form of data collection is extremely common in animal social network studies, and was the basis for the original datastream null model developed by Bejder et al. (1998).

The framework for this simulation is based on that used by Firth et al. (2017). We simulate G observations of groupings in a population of N individuals. Each group is assigned a group size 5 from a discrete uniform distribution on [1,M]. We assign each individual a preference for a particular group size P from a truncated normal distribution with mean (1+M)/2, standard deviation σ, lower bound 0, and upper bound M. Higher values of σ will therefore lead to higher variation in gregariousness in the population. For each group g, membership is determined by sampling S_g individuals without replacement, with individual sampling probability determined by the size of group g and each individual’s group size preference:

$$P(i\text{in}g)\propto \frac{1}{(S_g-P_i{)}^2}$$ (4)

This gives the simulation the property that individuals with higher assigned gregariousness scores tend to occur in larger groups, and vice versa. This leads to non-random differences in gregariousness (and thus strength centrality) between individuals. We then calculate the association network, again using the SRI:

$$SR{I}_{ij}=\frac{X_{ij}}{X_{ij}+Y_i+Y_j}$$ (5)

Where X_ij is the number of groups in which the dyad was seen together, and Y_i and Y_j are the number of groups in which only i or only j were seen, respectively. After calculating the network, we determine each individual’s strength. We again generate a trait value for each individual at random from a uniform distribution on (0,1) and fit the linear model

$${\sum }_{j}SR{I}_{ij}={\beta }_0+{\beta }_{1}trai{t}_i+{\epsilon }_i$$ (6)

and again save the estimate of β₁, along with the associated t statistic. We compare these statistics to those derived from networks generated using the group-based permutation procedure proposed by Bejder et al. (1998). This procedure again sequentially permuted the observed dataset, while maintaining the size of each group and the number of groups per individual. We again use the trial swap method to perform these permutations, generating 10,000 permuted datasets with 1,000 trials per permutation, and derived p-values in the same way as above. We vary the parameters of this simulation by using Latin hypercube sampling to draw values of N, M, G, and V (see Table 1 for ranges).

Analysis

We use the outputs of the simulations primarily to derive overall type I error rates (calculated as the portion of runs in which a p-value less than 0.05 was obtained) when using either regression coefficient or t-value as the test statistic. We further investigated the sensitivity of these results to non-random social structure, sampling effort, and population size. Previous work suggests that the sensitivity of datastream permutation techniques are highly dependent on variation in social structure and sampling intensity (Whitehead, 2008). We use binomial generalized linear models to summarize how population size, response variance, and sampling intensity influence the probability of false positives. We further analyse these relationships qualitatively using conditional probability plots. We compare these results to those derived from node-label permutation tests on the same simulated datasets.

Results

Dyadic regression

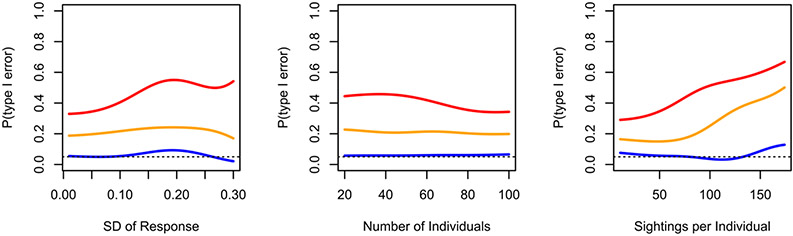
The overall type I error rate for the dyadic regression case was high, with 41% (81/200) of runs giving false positives when using the coefficient as the test statistic, and 21% (42/200) when using the t-value. When using the regression coefficient as the test statistic, the false positive rate increased with greater sampling effort (ϐ = 0.012 ± 0.004, z = 2.82, p = 0.005) and variance in SRI values (ϐ = 6.35 ± 3.04, z = 2.09, p = 0.03), but was not strongly influenced by the network size (ϐ −0.007 ± 0.006, z = −1.085, p = 0.278). When the t-value was used as the test statistic, only the sampling effort significantly influenced the false positive rate (ϐ = 0.014 ± 0.004, z = 3.00, p = 0.003), while neither the number of individuals (ϐ = 0.0007 ± 0.008, z = 0.091, p = 0.927) or variance in edge weights (ϐ = −0.59 ± 3.72, z = −0.177, p = 0.859) were significantly correlated with the false positive rate. In contrast, the node-label permutation method had a much lower false positive rate of 6% (12/200) and was unaffected by sampling effort (ϐ = −0.004 ± 0.008, z = −0.443, p = 0.658), network size (ϐ = 0.001 ± 0.013, z = 0.086, p = 0.931), or edge weight variance (ϐ = 3.574 ± 5.438, z = 0.657, p = 0.511).

Nodal regression

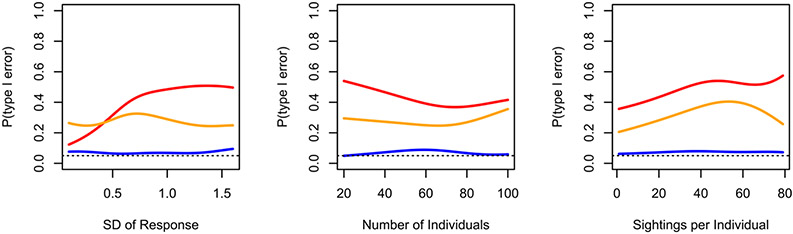
In the case of nodal regression, type I errors were once again high when using datastream permutations. When using the regression coefficient as the test statistic, our simulation resulted in a type I error rate of 43.5% (87/200), and when using the t-value the type I error rate was 28% (56/200). When using the regression coefficient as the test statistic, both sampling effort (ϐ = 0.029 ± 0.012, z = 2.434, p = 0.015) and variance in centrality (ϐ = 1.444 ± 0.479, z = 3.017, p = 0.003) were positively correlated with type I errors, while the number of individuals was not related to type I errors (ϐ = −0.005 ± 0.007, z = −0.732, p = 0.464). When using the t-statistic, sampling effort was still positively related to type I error rate (ϐ = 0.042 ± 0.013, z = 3.265, p = 0.001), however the variance in centrality was not (ϐ = −0.287 ± 0.498, z = −0.577, p = 0.564), and, interestingly, the size of the network appears to be positively correlated with type I error (ϐ = 0.017 ± 0.009, z = 1.990, p = 0.047). As in the case of dyadic regression, the node-label permutations produced an acceptable false positive rate of 7% (14/200), which was unaffected by sampling (ϐ = 0.014 ± 0.021, z = 0.663, p = 0.507) network size (ϐ = 0.008 ± 0.015, z = 0.579, p = 0.562) or variance in centrality (ϐ = 0.194 ± 0.868, z = 0.224, p = 0.823).

Discussion

These two simple simulated scenarios show that the commonly used datastream permutation procedures for animal social network data produce extremely high and thus unacceptable false-positive rates when used as a test of regression models. This is because datastream permutations represent a null hypothesis that is different from the typical null hypothesis that researchers are interested in testing when fitting regression models (that the model coefficients are 0).

It is important here to stress that the permutation procedure is not doing anything “wrong” in these examples. The permutations are in fact generating a distribution of statistics that is correct for the null hypothesis that the algorithm is designed to test, which is that the social structure is random. The “type I errors” that we discuss here are introduced when the rejection of this null hypothesis is taken as evidence that a relationship exists between the non-random structure of the network and an exogenous variable, when in fact these rejections in our simulations are simply indicating that social structure is not in fact random. For this reason, we recommend against datastream permutations as a test for regression models with social network data. Datastream permutations, however, will continue to play an important role in animal social network analysis; the results of datastream permutations can tell us whether a given dataset shows signs of non-random social structure. This is key, not just for social analyses generally but for regression analyses in particular. If a dataset does not show signs of non-random social structure, it likely does not make sense to continue with regression analyses that attempt to uncover the correlates of social network structure.

In this study, we focused on the case where network measures are the response variable in a linear model. A different, but related scenario is when we try to predict individual attributes (such as measures of fitness or personality) using network measures as a predictor. The statistical problems presented by this scenario are slightly different than those of the network response case. Here, the non-independence of the network data are not a problem, as linear models do not make any assumptions about the distribution or covariance structure of the predictors (n.b. there can still be covariance in the attribute used as a response variable related to network position that, if present, would need accounting for in the statistical model). The issue of data unreliability, however, may still be present. As in the simulations used here, datastream permutations alone would not serve as an adequate test. These models would test the null hypothesis that the relationship between the response and the network arose due to random social structure, when in fact the researcher is likely interested in whether the non-random social structure influences the individual attributes. A significant result from the datastream permutation method could simply indicate that the social structure is not random, rather than serving as an indicator that a relationship exists between the network and the response.

The high false-positive rate we describe here is the result of decreased variance in the response variable after permuting the raw data, as the variation due to social processes has been removed. A potential “quick fix” that might be mooted is to simply standardize the response variable in the observed network so that all subsequent permutations to have a constant variance, for example by using Z-scores. This may reduce the type I error rate. However, we strongly recommend against this as a solution to the problem. Standardizing the variance does not address the inconsistency at the heart of the problem. The null hypothesis being specified by the null model, that the social structure is random, is still not the same as the null hypothesis of interest in the regression.

In the following sections, we highlight some potential ways forward for the application of regression in animal social network analyses, and give some general recommendations for researchers. We hope that this discussion will encourage further work that may provide an extended toolkit for ecologists interested in these kinds of problems.

Carrying out regression in social networks by separating non-independence and bias

If datastream permutations alone cannot be used to test regression models in animal social network analyses, how should we conduct these analyses? While there are numerous potential solutions, and a full accounting of them is beyond the scope of this paper, we suggest that a general way forward is to recognize that the two issues of non-independence and unreliability of the data are separate problems requiring distinct statistical solutions.

Not all animal network data will be subject to the issue of unreliability (e.g., in cases where sampling is balanced across subjects and relevant contexts) and in some instances data may be complete and unbiased. In these cases, node permutations or other statistical network models will be appropriate (Croft et al. 2011). When structure or bias in the observations need to be controlled for, we propose two general approaches that may be useful; other solutions are certainly possible, and we encourage further work on this matter.

The first method (Figure 4A) would first attempt to remove the bias from the network using generalised affliliation indices (GAIs; Whitehead & James, 2015) or similar corrections to account for confounding variables that may influence observed edge weights. GAIs fit the observed associations or interactions as the response in a binomial or Poisson generalized linear model, with confounding factors such as space use, sightings frequency, or joint gregariousness as predictors. The residuals of this model are then used as measures of affiliation, as they reflect the difference between observed and expected association rates given the confounding factors. While a flexible and appealing approach, GAIs require that potential confounds be properly specified in terms of dyadic covariates, and that the relationship between confounds and edge weights be linear. This second issue could be solved by deriving affiliations from generalized additive models (GAMs), where the relationship between covariates and the response can be represented by smooth functions. While GAIs represent the most well developed method for correcting social network edge weights, other methods are certainly possible. Once corrections are made, researchers can use the corrected social network to derive responses to use in the statistical model. A potential drawback of GAIs is that avoidance between individuals is represented as negative edge weights. While this is not a problem for dyadic regression (in fact it better conforms to the assumptions of traditional linear models), this complicates the calculation of some centrality measures, requiring that negative edge weights be ignored or set to zero (Whitehead & James 2015). Inference would be carried out using post-network permutation methods, such as node-label permutations or MRQAP.

Figure 4.

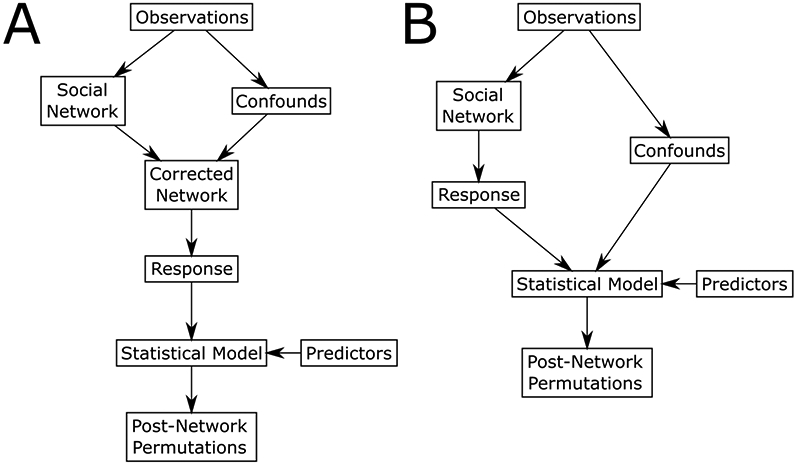
Flowcharts of two approaches for regression analysis in animal social networks. In the first (A), a network is generated that attempts to adjust for confounding effects (through e.g. GAIs) which is then used to derive the response. In the second (B), the original network is used to derive the response variable, with confounds instead being incorporated as covariates in the inferential model. In both methods, inference is based on post-network permutations (such as MRQAP or node-label permutations).

A second, different approach (Figure 4B) would be to incorporate confounds in the inferential model itself. If researchers identify likely confounds and summarize them quantitatively at the same level as the hypothesis being tested (e.g. dyadic or nodal), these could be used directly in the statistical model. Where potential non-linearity between confounds and responses exist, data transformations, polynomials, and smooth functions may present a possible solution. Again, post-network permutation methods would be employed for inference to correct for the non-independence of the data. Franks et al. (2020) explore this method in detail.

We feel that these approaches have the potential to address the current issue that we have identified and we strongly encourage new work to explore and validate these approaches. These suggestions are general, identifying the ways in which we might approach separately address non-independence and bias. It is important to note that the methods we propose are only useful if the question of interest is about the structure of social affinity, rather than the empirical pattern of encounters between individuals. If, instead, researchers are interested in the actual rates of contact (as is the case in disease research and studies of social learning), this approach may not be appropriate. Extensions of recent work using hidden state modelling may be more appropriate for disentangling true association patterns when detections are potentially biased or imperfect (Gimenez et al., 2019).

Building better null models

The problems we have identified here arise because the commonly used null models for animal societies do not generate datasets representing the null hypothesis of interest in a regression setting. These models were specifically designed to test the null hypothesis of random social structure, not the null hypothesis that aspects of social structure are unrelated to exogenous factors. An obvious way forward would be the development of permutation procedures that generate datasets that correctly represent the relevant null hypothesis. In the case of dyadic regression, these datasets would maintain the structure of the data (e.g. sightings per individual, associations per sampling period, spatial patterns of observations), randomise identities of associated individuals, and simultaneously preserve the variance in edge weights. In the case of nodal regression, permuted datasets would maintain the same (or at least a similar) distribution of individual centrality within the network, in addition to structural confounds such as the size of groups, sightings per individual, and timing of sightings. The design of such procedures is far from trivial, and is beyond the scope of this paper, but we suspect that the development of algorithms that simultaneously maintain aspects of data structure and features of the social system will be an important area of methodological research going forward. This area of research is still in its early days, although there has been some potentially applicable work in other sub-fields of network science (e.g. Chodrow 2019).

Conclusions

The development of permutation techniques that control for sampling biases while maintaining temporal, spatial, and structural aspects of the raw data is an important development in the study of animal social systems, and we suspect that these procedures will remain a key tool for hypothesis testing in ecology and evolution. These techniques are particularly crucial when it is not clear whether a dataset shows signs of non-random social structure. However, a lack of consideration regarding the matching up of the null hypothesis being tested with the null model being generated using datastream permutations has led to unwarranted application of these techniques, particularly in the context of hypothesis testing using regression models. Here, we have shown that significant p-values from applying datastream permutations to regression models cannot be used as evidence of a relationship between the social network and exogenous predictors.

We recommend that researchers think critically and carefully about the null hypothesis they wish to test using social network data, and ensure that the null model they specify does in fact represent that hypothesis (Table 2). We suspect that in most cases, the null hypothesis of random social structure will clearly not be appropriate in regression analysis, and therefore traditional datastream permutations will not be a viable approach. We hope that our discussion of this issue and the results of our simulations will result in reconsideration of how researchers employ null models when analysing animal social networks, promote further research and discussion in this area, and lead to the development of procedures that correctly specify null hypotheses and allow robust inference in animal social network studies.

Table 2.

Comparison of datastream and node-label permutations

	Datastream permutations	Node-label permutations
Dyadic H0	There is no variation in the strength of social ties once data structure, sampling noise, and constraints (time, location, etc.) are accounted for.	The observed variation in the strength of social ties is unrelated to dyadic covariates (e.g. kinship, trait similarity)
Nodal H0	There is no variation in centrality once data structure, sampling noise, and constraints are accounted for.	Observed variation in centrality is unrelated to node characteristics (e.g. age, sex, personality)
Applications	Testing for the presence of social preferences Testing for non-random variation in social position	Testing relationships between observed social ties and dyadic predictors Testing relationships between centrality and node attributes
Benefits	Corrects for bias in data collection from differences in detection probability and demographic processes Accounts for complex data structures such as focal follows and gambit of the group	Corrects for the structure of the observed network Specifies the null distribution of interest for most regression applications
Drawbacks	Results in a decrease in variance in network measures compared to observed data when social structure is non-random Cannot be used to test regression models against the null hypothesis of zero effect	Does not account for data collection method or complex data structures Does not correct for bias or uncertainty due to sampling

Figure 2.

Conditional probability plots from dyadic regression simulation. Lines indicate smoothed conditional probabilities of a type I error (a p-value less than 0.05) for datastream permutations using the coefficient (red) or t-value (orange), and node-label permutations (blue) in relation to three covariates. Dotted line indicates target type I error rate of 0.05.

Figure 3.

Conditional probability plots from nodal regression simulation. Lines indicate smoothed conditional probabilities of a type I error (a p-value less than 0.05) for datastream permutations using the coefficient (red) or t-value (orange), and node-label permutations (blue) in relation to three covariates. Dotted line indicates target type I error rate of 0.05.

Data availability

This study used no empirical data. The R code to run the simulations presented here is archived on Zenodo (https://doi.org/10.5281/zenodo.4048094 ).