Sequence to Sequence ECG Cardiac Rhythm Classification using Convolutional Recurrent Neural Networks

Abstract

This paper proposes a novel deep learning architecture involving combinations of Convolutional Neural Networks (CNN) layers and Recurrent neural networks (RNN) layers that can be used to perform segmentation and classification of 5 cardiac rhythms based on ECG recordings. The algorithm is developed in a sequence to sequence setting where the input is a sequence of five second ECG signal sliding windows and the output is a sequence of cardiac rhythm labels. The novel architecture processes as input both the spectrograms of the ECG signal as well as the heartbeats’ signal waveform. Additionally, we are able to train the model in the presence of label noise. The model’s performance and generalizability is verified on an external database different from the one we used to train. Experimental result shows this approach can achieve an average F1 scores of 0.89 (averaged across 5 classes). The proposed model also achieves comparable classification performance to existing state-of-the-art approach with considerably less number of training parameters.

I. INTRODUCTION

AN electrocardiogram (ECG) contains information on the electrical signal activities of the heart. It can be used to produce various measures such as heart rate as well as to diagnose a condition like arrhythmia. Discerning an arrhythmia such as Atrial Fibrillation (AF) from other common cardiac rhythms with continuous monitoring is of high value because, if left undetected, those with silent AF (estimated to be about 1/3 of AF patients) experience the same risk for stroke as symptomatic AF patients [1] and AF is associated with an estimated 5-fold increase in risk of stroke [2]. Since AF is implicated in over 454,000 hospital admissions [2] and 158,000 deaths each year [3], improved automated methods to passively identify AF may significantly reduce associated morbidity and mortality for those unaware they are at risk. Diagnosis often depends on patients’ first recognizing symptoms (e.g., elevated heart rate, palpitations, fatigue) [4] and seeking care where careful clinical assessment and expert cardiologist review of electrocardiogram (ECG) data remains the goal standard to confirmed diagnosis and select intervention [5]. Although the American Heart Association treatment guidelines fail to mandate a minimum threshold of AF burden (i.e, number of minutes in 24 hours) that require treatment [5] recent studies note significant increase in stroke risk as AF burden increases (i.e., 2.5 hours in 24 hours) (see [6]–[8]) suggesting the importance of early identification methods.

Machine learning based detection methods, where a model is trained using an existing database with annotated ECG records to learn the task of classifying arrhythmias, have had a long history of research mostly on the task of heartbeat classification. Deep learning based models has also emerged as successful in this task. [9]–[13] Most approaches focus on the beat-level classification problem where each beat is classified into various types rather than on the classification of cardiac rhythms. These algorithms are trained mostly using the publicly available MIT-BIH arrhythmia database [14], whose small size and data imbalance in terms of cardiac rhythm classes may have hindered the ability to train machine learning based model for cardiac rhythm detection. The detection of cardiac rhythms especially Atrial Fibrillation(AF) using machine learning methods has also gained recent interests. These includes deep learning approaches such as [15], [16] for AF detection as well as the deep learning model in [17] which can classify 12 rhythm classes. The detection of cardiac rhythms such as Atrial Fibrillation(AF) where segments in a ECG recording are given rhythm labels is the focus of this work. Each cardiac rhythm has distinct characteristics. For instance, AF is characterized by fast irregular rhythm and the absence of P waves in ECG.

The contributions of the current paper are as follow. First, we propose a novel architecture depicted in Fig. 1 that incorporates each heartbeat’s waveform morphology and the spectrogram-based pattern of heartbeats over time. This is specifically designed for the cardiac rhythm detection task that requires both beat-level information as well as the temporal pattern of the heart beats and their relationships. Second, the proposed approach works in a sequence to sequence setting where the input is a sequence of signal segments and the output is a sequence of cardiac rhythm labels. This allows both segmentation and classification of cardiac rhythm within an ECG recording of varying lengths. On the clinical side, this means that the burden of AF, i.e., the frequency and duration of the episode can be measured, and therefore help inform clinical decision making [18]. Third, we demonstrates the ability to train the model robustly in the presence of noisy labels (i.e., labels are not ground-truth annotations) by using an existing Holter monitor database with labels supplied by the manufacturer’s automatic classifier. This is inspired by previous works outside of the healthcare domain that uses large datasets with noisy annotations instead of laboriously collected clean annotations to train neural networks [19]–[21]. Finally, we assess model performance on samples from an external database with ground-truth annotations to verify that the model generalizes beyond the database we use to train the model.

Fig. 1.

Overview diagram of the proposed model

Related works with details on other existing approaches to arrhythmia detection are presented in Section II. Section III describes our proposed methodology. The experimental setup is given in Section IV, and the details on how we train the model is given in Section V. Finally, Section VI, VII, VIII contains the results, discussion, and conclusion respectively.

II. RELATED WORKS

Much of the previous work in arrhythmia detection that uses deep learning approaches (for review, see [22], [23]) has focused on the heartbeat recognition/classification problem. Other proposed machine learning based approaches include Support Vector Machine based systems [24], [25]. These approaches rely on hand-crafted features, unlike deep learning approaches, where feature extraction is learned by the model. Successful deep learning approaches include, for instance, using artificial neural networks with a Kohonen layer [9], a 1-D convolutional neural network [10], [11], convolutional denoising autoencoders [26], and an LSTM-based algorithm [12]. A sequence to sequence model has also been proposed at the beat-level classification [13]. Similar to others, a part of our work includes extracting each heartbeat’s features from ECGs using Convolutional Neural Networks (CNNs). The focus of our work is on the task of cardiac rhythm detection (not on beat level classification), a task that requires incorporating these features with the timing and the context of the surrounding beats in order to detect the rhythm class.

Because Atrial Fibrillation is the most common form of cardiac arrhythmia, the detection of this rhythm has been an active area of research. Some studies use RR interval analysis for this task. These include studying sample entropy measures [27] as well as scatterplots of RR intervals versus change of RR intervals [28]. These detection methods rely only on the temporal characteristics of cardiac rhythms. In recent years, deep learning approaches have also gained popularity. For example CNN [15], as well as LSTM [16], [29], have been used for the classification task. More recently, the 2017 PhysioNet Challenge [30] resulted in many methods successful in classifying short (9s - 60s) single-lead ECG recordings to 4 classes: 1) Normal sinus rhythm, 2) AF, 3) Other rhythm, or 4) Noise. Some of the top performing methods include using a combination of expert generated features and features from neural networks [31]; Recurrent Neural Networks (RNN) [32], [33]; Convolutional Recurrent Neural Networks (CRNN) [34]; and Random Forests based on engineered features [35]. One limitation of the aforementioned methods and the PhysioNet Challenge methods is that the algorithms only produce as output a single label for each input ECG recording. Unlike real-world ECG signals, the 2017 Physio-Net Challenge data were segmented to contain only one rhythm class. Our approach allows the input to contain more than one rhythm class and performs segmentation as well as classification. One way to perform segmentation and classification at the same time is for the output of the algorithm to be a sequence of labels. This is proposed in [17] where a 34-layers CNN takes as input a 30 s record and outputs a sequence of 23 rhythm labels. The deep architecture allows the model to reduce the 30 s 200 Hz record to a sequence of output labels. We take a different approach allowing the input to be a sequence of sliding (much shorter) windows of signal that then generate a sequence of rhythm label outputs. This allows the Convolutional Neural Network part of our architecture to have fewer layers while Recurrent Neural Network layers are used to process the signal windows sequentially and generate a sequence of labels as output. This approach also allows the input recording to be of varying length, unlike, the CNN in [17] that requires a fixed length input.

III. PROPOSED METHODOLOGY

The high-level overview of the proposed methodology is illustrated in Fig. 1. The algorithm takes as input a sequence of 5 seconds ECG signal segments and outputs a sequence of ECG arrhythmia rhythm labels. 5 second ECG signal segments are fed into two parts of the model to generate two different sets of features that represent the segment: 1. heartbeat waveform features and 2. spectrogram features. This architecture is uniquely designed to synthesize two sources of information from ECG signals specifically for the rhythm classification task: morphology of each heart beat as well as the pattern of heart beats underlying the rhythm over a longer period of time.

Note that the parameter values given in this section are in the context of ECG recordings with a sampling rate of 200 Hz.

A. Pre-processing

Only minimal pre-processing transformation is applied to the raw ECG signal. For each segment of ECG signal, the signal is demeaned and rescaled so that the range is 1 as described by the function

$$f(x)=\frac{x-\overline{x}}{\max (x)-\min (x)},$$

where x is a vector of the raw values of a segment ECG signal.

In addition, the two pre-processing steps described below are applied for each of the two main feature sets of the model.

1). R-peak detection:

A QRS complex detection algorithm is executed to detect the QRS complex so that the R peaks can be located in the ECG signal segment. There are many accurate and reliable algorithms available for this task (see [36] for comparison). Tools, for example [37], that analyze ECG signals often start with this QRS detection step in order to extract useful information such as the RR interval time series. For our method, we need the R peak locations to extract the beat waveform features of the signal values surrounding these locations.

2). Spectrogram:

A spectrogram is often used in end-to-end automatic speech recognition systems (ASRs), for instance in [38]–[41], to generate numerical input features for neural networks from raw audio signal. To produce a spectrogram, a Short-Time Fourier Transform (STFT) of the ECG signal is first computed with the following parameter: size of FFT window = 64 samples with Hann window function, stride length = 20 samples. The power spectrum is then computed and transformed to the decibel scale.

B. Heartbeat Waveform Features

The objective of this feature set is to extract information about the waveform of each heartbeat from a given segment of ECG signal. The morphology around the QRS complex helps distinguish between types of beats, for instance, determining a premature ventricular contraction beat from a normal sinus beat. Using the locations of detected R peaks, we extract 0.7 seconds of signal surrounding each location (0.3 seconds before and 0.4 seconds after). This means that for each segment of ECG signal, we have a sequence of 0.7 second signal chunks (one for each heartbeat). Note that different segments of ECG signal will have different numbers of beats and therefore the sequences may be of different lengths.

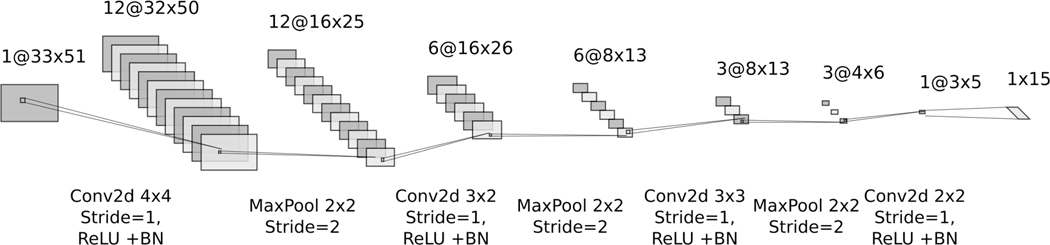
Each 0.7 second signal chunk is passed through a 4-layer Convolutional Neural Network (CNN) to be encoded into 10 features. Each convolutional layer is followed by a Rectified Linear Unit (ReLU) activation function [42] and Batch Normalization (BN) [43]. Downsampling is done directly by each convolutional layer with a stride of 2. Moreover, the number of filters is also halved at every convolutional layer. The architecture of this CNN is shown in Fig. 2.

Fig. 2.

Diagram of the Convolutional Layers used to process each heart beat’s signal

The 10 features output from the Beat CNN is then fed into a unidirectional Long Short-term Memory (LSTM) [44] with 1 hidden layer and 10 features in the hidden states. To obtain a fixed-dimensional feature set for the varying length sequence of beats, we adopt a many-to-one sequence modelling structure. Therefore, only the 10-features output from the last beat’s LSTM is passed to the integrating LSTM (described in Section III-D).

C. Spectrogram Features

A two-dimensional spectrogram with time on the x-axis and frequency on the y-axis is fed into another Convolutional Neural Network (CNN) to produce 15 features. Two-dimensional convolution is performed at each layer followed by a Rectified Linear Unit (ReLU) activation function [42] and Batch Normalization (BN) [43]. Downsampling is then performed by maxpooling. This architecture is illustrated in Fig. 3. This CNN extracts the local features of the spectrogram of a 5 seconds ECG signal segment.

Fig. 3.

Diagram of the convolutional layers used to process a spectrogram of a 5s ECG signal segment

D. Integrating LSTM and Output Layers

Feature sets from section III-B (15 features) and section III-C (10 features) are then combined to form the local representation of the 5 seconds ECG signal segment. This combined set of features is then fed into a 2-layer bidirectional LSTM with 10 hidden units. The bidirectional LSTM serves as an aggregator of information across the surrounding ECG signal segments so that both the local features of the ECG signal segment as well as the surrounding context of that segment can be summarized and fed as input to the output layers. Note that we adopt the many-to-many RNN sequence structure so that a label is generated for each 5s window. Finally, 20 features (10 from each direction) are passed to the 2 output layers. The first output layer has 10 hidden units with ReLU activation function [42], and in the last layer the number of hidden units equals the number of ECG rhythm classes with the softmax functions as activation at the output nodes.

IV. EXPERIMENTAL SETUP

The ECG cardiac rhythm detection model with the proposed architecture described above is trained with a database of Holter Recording and its performance is evaluated on an external database.

A. Datasets

1). UVA Holter Recordings:

Training a neural network from scratch requires a large dataset. We first use a subset of a large dataset which contains 24 hours of Holter recordings sampled at 200 Hz collected at University of Virginia (UVA) Heart Station and used in previous studies on heart rate dynamics [45], [46]. We restrict the dataset to patients of age 25 years or older. The age restriction is chosen to resemble patients in the MIT-BIH Arrhythmia Database [14] which is the external database we use to test the model. The total number of patients in the subset we used is 1928. The included patients are primarily female (54.41%) and range in age from 25 to 91 (mean=59). Twenty percent (n= 386) of these patients are then reserved for the test set. The remaining 1542 patients are used in the training phase. Since most of the sample sections contain only Normal Sinus Rhythm (NSR), we only include 10 percent of these NSR sections for training. However, for the test set, all the sections are used. ECG signal sections from the 1542 patients reserved for training are then split 80 percent for the training set and 20 percent for the validation set. The original data collection [45] was carried under the University of Virginia’s Institutional Review Board; however, this analysis is performed on de-identified Holter recordings.

2). MIT-BIH Arrhythmia Database:

To test how well the model generalizes, an external database: MIT-BIH Arrhythmia Database [14] is used as a test set. This database contains 48 half-hour two-channel ambulatory ECG recordings. The recording is sampled at 360 Hz. To be consistent with the UVA Philips Holter recordings, we resample these recordings to 200 Hz. Moreover, only lead II is used in this experiment. The annotations in this database were verified by two cardiologists with discrepancies resolved by consensus [14]. For the experiment in this paper, we consider these annotations ground-truth.

The ECG signal from both datasets are then set up according to the formulation described below in section IV-B. Sections of the ECG are also filtered out if their Signal Quality Index (SQI) is below 0.7 as measured by the Physio-Net Cardiovascular Signal Toolbox [37]. In addition, based on data availability, only five rhythm classes are used in both training and testing of this experiment: 1. Normal Sinus Rhythm (NSR), 2. Atrial Fibrillation (AF), 3. Supraventricular Tachyarrhythmia (SVTA), 4. Ventricular Bigeminy (B), 5. Ventricular Trigeminy (T). Sections of ECG recordings with rhythm labels other than these 5 classes are excluded.

B. Problem Formulation

We formulate arrhythmia detection as a sequence-to-sequence learning task since this allows ECG recordings to be both segmented and classified to various rhythms. The input to our algorithm is a sequence of ECG signal segments and the output is a sequence of ECG cardiac rhythm labels. In our experiment, a sliding window (length: 5s, stride: 2s) is used to generate a sequence of ECG signal segments within an ECG section of length 123s (about 2 min). Each 5s window is then assigned to one rhythm label and the algorithm produces a label output every 2 seconds. Therefore, in this setup, a 123s ECG signal section contains 60 rhythm labels.

During training, the labels and the timing of rhythm changes from an automatic classifier from Philips Holter Software is used as supervision to train the neural network. As such, we implement learning paradigms previously proposed to train the network in the presence of noisy labels, i.e., some proportion of the labels for the supervised learning are misclassified. The training with noisy labels is described in section V-B.

V. TRAINING PROCEDURE

We train the neural networks from scratch in mini batches of size 50 samples with the oversampling scheme described in Section V-A. Each epoch contains 100,000 samples drawn from our training set. We also implement two recently proposed learning paradigms: Co-teaching [47] and PENCIL [48] described below during training to account for the fact that we are training the model in the presence of label noise. The number of epochs is 20 for both the model trained under the Co-teaching paradigm and the model trained under the PENCIL paradigm.

A. Dataset Imbalance

The number of ECG signal sample sections of length 123s used in the training set is 174,956 samples (n = 174,956). Although this is a relatively large training dataset, the dataset is imbalanced in terms of the rhythm classes as shown in Table I (Note that each sample can contain more than one rhythm classes). To address this imbalance, during training we sample these sections into each mini batch with different sampling weights assigned according to which rhythm class the sample contains. The last column of Table I shows the value of the weight w_i for each class. Since each ECG signal sample section can contain more than one rhythm class, the maximum of the weights w_i assigned for each class in that section is used. Each mini batch is a weighted random sample of size 50 drawn with replacement from the training set of size n where the sampling probability is $w_i/{\sum }_{j=1}^n{w}_j$ for each sample.

TABLE I.

CLASS IMBALANCE

Class	Number of samples containing the rhythm	wi
NSR	93,997	1
AF	80,757	1
SVTA	20,418	4
B	13,649	5
T	15,699	5

B. Noisy Label

Because our model is trained under the supervision of labels obtained from an automatic classifier, we assume that there is a certain level of noise in the label. It is known that deep neural network has the capacity to overfit random labels [49]. Therefore, the presence of noisy labels can negatively affect the training of the model and may result in poor generalization. To address this issue, we implemented two previously proposed learning methods described below to ensure robustness during the training of our model.

1). Co-teaching [47]:

Co-teaching is a learning paradigm that utilizes two peer networks to select instances for each other to train. This sample selection is an attempt to try to select clean instances to train on so that the training data that each network uses is less noisy in terms of the label. Thus, large loss instances aren’t used when updating the parameter of the network. In our experiment, R(T) which controls the proportion of instances to keep during training for each epoch is set to $R(T)=1-0.1\cdot \min \left(\frac{T}{10},1\right)$ where T = 1,...,20 is the epoch number.

2). PENCIL [48]:

Probabilistic end-to-end noise correction (PENCIL) is another framework that deals with noisy labels in a different way. In the PENCIL framework, noisy labels are used to initialize a label distribution which is then allowed to be updated during training. The proposed loss function in PENCIL is comprised of 3 components: classification loss (${\mathcal{L}}_c$), compatibility loss (${\mathcal{L}}_o$), and entropy loss (${\mathcal{L}}_e$). There are two hyperparameters in this loss function, α which controls the weight of ${\mathcal{L}}_o$ and β which controls weight of ${\mathcal{L}}_e$. In our experiment, we set α to 0.1 and β to 0.4. Additionally, λ = 10000 is used to update the label distribution. The number of epochs for the three steps are 3 epochs (backbone learning), 10 epochs (PENCIL learning), 7 epochs (final fine-tuning). Following examples in [48], we also halve the learning rate at the beginning of the second and third step.

C. Optimization and Hyperparameters

Optimization of all the weights in our proposed neural network is done by the Adam [50] optimizer with default parameters (β₁ = 0.9, β₂ = 0.999) as set by Pytorch. Various initial learning rates (0.001, 0.01, and 0.1) were tried and the learning rate of 0.01 works best based on the validation set. We also choose a relatively small batch size of 50 as findings from [51] suggest that smaller batch sizes tend to lead to better generalization.

D. Evaluation of Classification Performance

To evaluate the performance of the proposed algorithm, four measures commonly used to evaluate classification algorithm are reported: sensitivity (SEN; also known as recall), positive predictive value (PPV; also known as precision), specificity (SPEC), and F1 score which is the harmonic mean of SEN and PPV. The performance is evaluated at the “sequence-level” (as in [17]) where a sequence of predicted rhythm label outputs is compared against a sequence of rhythm labels from a reference annotation. In our setup, the sequence of labels is generated every two seconds based on a 5s sliding window of ECG signal.

VI. RESULTS

First, we test both the model trained under the Co-teaching and PENCIL paradigm on the UVA Holter recordings test set we reserved. The test set consists of 195,849 sample sections. Note that since the annotations come from the Philips Holter Software, the results shown in Table II and III are a comparison of our trained model labels and the labels generated by the system we used to supervise the training. For comparison with ground-truths annotation, we rely on the samples from the MIT-BIH Arrhythmia Database.

TABLE II.

UVA HOLTER RESULTS FOR MODEL A: CO-TEACHING

Class	SPEC (%)	SEN (%)	PPV (%)	F1 score (%)
NSR	96.39	97.91	99.48	98.69
AF	98.11	95.32	85.25	90.00
SVTA	99.77	90.64	81.00	85.54
B	99.88	89.86	81.56	85.51
T	99.95	87.59	90.24	88.89

TABLE III.

UVA HOLTER RESULTS FOR MODEL B: PENCIL

Class	SPEC (%)	SEN (%)	PPV (%)	F1 score (%)
NSR	96.43	97.68	99.48	98.58
AF	97.88	95.78	83.80	89.39
SVTA	99.81	92.36	84.08	88.02
B	99.91	87.77	84.23	85.96
T	99.96	88.16	90.75	89.44

Second, samples from the MIT-BIH Arrhythmia Database are used to test both models. After restricting to just 5 classes, the test set size from the MIT-BIH arrhythmia database consists of 386 sample sections. There are 60 labels in each section based on the experimental setup described in section IV-B and, therefore, 23,160 labels in total in the test set. The overall test accuracy is 97.60 percent for Model A (Co-teaching) and 97.43 percent for Model B (PENCIL). Because of the class imbalance, we examine the models’ performance for each class as shown in Table IV and Table V. This result shows that both models perform similarly well and that the models trained can generalize beyond the database that was used for training.

TABLE IV.

MIT-BIH RESULTS FOR MODEL A: CO-TEACHING

Class	SPEC (%)	SEN (%)	PPV (%)	F1 score (%)
NSR	95.85	98.01	99.24	98.62
AF	99.13	98.83	92.94	95.79
SVTA	99.98	70.37	88.37	78.35
B	99.20	91.40	78.09	84.22
T	99.81	85.34	89.20	87.22

TABLE V.

MIT-BIH RESULTS FOR MODEL B: PENCIL

Class	SPEC (%)	SEN (%)	PPV (%)	F1 score (%)
NSR	95.12	97.92	99.10	98.51
AF	98.98	99.62	91.88	95.59
SVTA	99.95	70.37	77.55	73.79
B	99.27	85.53	78.35	81.78
T	99.85	85.34	91.49	88.31

Next, we compare the two models trained under the two learning paradigms for noisy labels described in Section V.B against a baseline model trained with the same hyperparameters but without the implementation of those learning methods. The baseline model was trained with early stopping. When the average F1 score across 5 classes on the validation set stopped improving for 5 epochs, the training ended and we save the best model in terms of the average F1 score as evaluated on the validation set. The performance of the models in the MIT-BIH test set is reported in Table VI and the comparison shows that the two learning methods that account for noisy labels have helped the training of our proposed model.

TABLE VI.

COMPARISON AGAINST BASELINE MODEL WITHOUT NOISY LABEL LEARNING PARADIGMS

Model	NSR	AF	SVTA	B	T
Baseline	96.51	83.57	76.36	76.74	80.92
Model A: Co-teaching	98.62	95.79	78.35	84.22	87.22
Model B: PENCIL	98.51	95.59	73.79	81.78	88.31

For comparison against existing approaches, we cannot directly compare the sequence of outputs from our model which consists of one label for each signal interval and do segmentation for samples with more than one class against other works. Therefore, we slightly modified our model to perform only one classification for each recording by replacing the bidirectional LSTM with 10 hidden-units with a unidirectional LSTM with 20 hidden-units as the integrating LSTM. The many-to-one RNN structure is adopted in this case instead to perform only one classification from the entire sample. We evaluate our proposed CRNN architecture against another CRNN [34] which achieved second best average F1 score (0.82 vs the highest 0.83) in the PhysioNet/CinC Challenge 2017(for details, see [30]). Note also that the method in [34] is the top ranked end-to-end deep learning approach that does not rely on any feature engineering. Table VII shows the comparison reporting the F1 scores estimated using the same 5-folds cross validation experiment in [34] to ensure fair comparison. We believe the proposed method achieves comparable results with much fewer number of trainable parameters in the model (∼10,000 vs ∼5 millions parameters). This suggests that our model may be easier to train as well as potentially less prone to overfitting to the training data which can lead to poor generalizability.

TABLE VII.

COMPARISON AGAINST RECENT WORK USING F1 SCORES(%) ESTIMATED BY 5-FOLDS CROSS VALIDATION

Model	NSR	AF	Other	Noisy	Overall
Proposed†	87.3	71.4	67.8	55.6	75.5
Zihlmann et al.† [34]	87.4	69.9	66.5	54.9	74.6
Proposed*	88.2	74.6	69.5	58.1	77.4
Zihlmann et al.* [34]	88.8	76.4	72.6	64.5	79.2

F1 score averaged across NSR,AF,Other is reported as Overall following [30]

^†denotes training without any data augmentation

^*denotes training with data augmentation described in [34]

VII. DISCUSSION

The model complexity of our proposed model is relatively lightweight with 8,042 parameters (864 in spectrogram CNN; 513 in Beat CNN; 880 in Beat LSTM; 5,520 in Integrating LSTM; and 265 in Output Layers).

Next, an ablation study is conducted to examine the value of the two blocks in the proposed models which generate two features sets: 1. Spectrogram Features 2. Heartbeat waveform features from a sequence of beats. Table VIII shows the experimental results of removing each of the two feature sets from the model while keeping the rest of the training procedure constant. All three models in Table VIII are trained using the Co-teaching learning schemes and the test dataset is the MIT-BIH Arrhythmia Dataset. ”Beat Sequence Only” model removes the spectrogram features block from the model while the “Spectrogram Only” model removes the heartbeat waveform features. Compared to the proposed model, we see that there is a degradation in model performance across the 5 rhythm classes for the “Beat Sequence Only” model which relies only on the sequences of beat waveform morphology. This suggests that the 5s window spectrogram contains useful additional information for classifying these cardiac rhythms. With regards to the “Spectrogram Only” model, the F1 scores are lower only for AF and T. This suggests that explicitly extracting heartbeat waveform as a sequence can help in detecting for instance trigeminy where every third heartbeat is a premature ventricular contraction (PVC).

TABLE VIII.

F1 SCORES (%) AFTER REMOVING COMPONENTS IN THE MODEL

Model	NSR	AF	SVTA	B	T
Proposed Model	98.62	95.79	78.35	84.22	87.22
Beat Sequence Only	95.87	79.27	48.64	70.81	64.45
Spectrogram Only	97.17	91.49	79.61	85.85	43.28

Lastly, we examine some common mistakes made by the model. The confusion matrix for Model A (Co-Teaching) using ground-truth annotations from the MIT-BIH Arrhythmia Database is shown in Fig. 4. The most common mistake is that Supraventricular Tachyarrhythmia (SVTA) is mistaken as Normal Sinus Rhythm (NSR). The model also sometimes misses very short segments of SVTA. Less common mistakes include slightly shifted locations of the onsets and offsets of Bigeminy (B) and Trigeminy (T) and, therefore, some B and T labels are still labelled as NSR by the model.

Fig. 4.

Normalized Confusion Matrix for Model A: Co-teaching

VIII. CONCLUSION

To conclude, we present in this work a novel architecture that uniquely combines the morphology of each heart beat and the overall pattern of heart beats over a period of time. While other previous deep learning approaches have mostly focused on beat classifications or AF classification, our approach demonstrates the ability to differentiate various cardiac rhythms and the sequence to sequence learning setting allows our model to do both segmentation and classification of rhythms from variable-length ECG recordings. This can aid cardiologists in locating a specific rhythm within a long recording to confirm a heart arrhythmia and estimate its burden. We also demonstrate the ability to train this model in the presence of noisy labels. The use of existing databases to train deep learning models even with some noise in the labels can be helpful especially in healthcare settings where large datasets can be hard or expensive to obtain. The training with noisy labels is in contrast to other work in arrhythmia detection which often relies on databases with expert annotated labels such as the MIT-BIH arrhythmia database [14] and the much larger database used in [17]. We also show that the performance of the learned model generalizes beyond the database we used to train.

One area to expand in this research is to include other rhythms such as Atrial Flutter. Atrial Flutter is not in our analysis mainly due to data availability. However, the distinction between Atrial Flutter and Atrial Fibrillation can be challenging due to their similarities [27], [52] and often result in mislabeling by current automated systems. Further work to discern between these arrhythmias has important clinical treatment implications as most interventions come with patient risk of harm and side effect [5]. Additionally, since the experiment in this work was done only after filtering out sections of the ECG with low signal quality index, another issue to explore is to test the robustness of the method to detecting cardiac rhythms under different levels of noise and presence of artefacts in the ECG signal due to various sources such as the movement of patients.

Wearable devices hold promises for continuous health monitoring including heart activity [12], [53]–[55]. Recent innovations in wearable technology and their increasing acceptance may provide opportunities to better advise patients of potential lethal arrhythmias, such as AF [56], [57]. Our approach may lead to improved effectiveness of personal wearable devices as well as electrocardiogram (ECG) monitoring in intensive care units where AF may go undetected, contributing to increased length of ICU stay and in-hospital mortality [58]. Improvement in monitoring and diagnostics tools for heart health would have a significant public health benefit as cardiovascular disease burden remains a significant global issue.