Abstract
A new modification of the SIR epidemic model incorporating vaccination is proposed in the present paper. The recent trend of vaccinating against COVID-19 pandemic reveals a strong control of infectious disease. On the other hand, it is observed in some countries that, the vaccine application offers less control over the spread of virus, since some portion of vaccinated people is not totally protected/immuned and viable to infection again after a while due to weak/loss immunity offered by the vaccine. This requires transition from vaccinated department to infected for COVID-19. This character of COVID-19 helps us reconsideration of the vaccinated department by letting some part of it being exposed to the infection again. Taking this into account, as a result of modification of the SIR model, the epidemiology is now governed with three main epidemic dimensionless parameters, having provided an initial fraction of infected individuals. The dimensionless model with these parameters is analyzed initially from the stability point of view. The effects of weak immunity are then illustrated numerically on some chosen parameter range. How some of the countries applying the COVID-19 vaccine programs affected by weak/loss immunity is eventually examined with the modified model. The rate of vaccination as well as the basic Reproduction number are found to affect the epidemic demography of the population subject to weak or loss of immunity. In the case of a high vaccination rate, the countries are not anticipated to be highly influenced by the weak immunity of low level, whereas weak immunity prolongs the contagious disease by appearance of secondary multiple peaks in the epidemic compartments with relatively small vaccination rates and basic Reproductive numbers.
Keywords: Compartmental epidemic model (SIR), Vaccination, Weak-immunity, Stability, COVID-19, Simulations
1. Introduction
The epidemic compartmental SIR model originally proposed in the pioneering paper [1] for the beginning, spread and end of a disease in a population, despite the fact of being an approximate rough approach without considering dynamical ingredients of the infection, keeps still illuminating the knowledge worldwide with the main trends of globally effective infectious diseases, like the COVID-19 pandemic [2] of nowadays. A number of variations of SIR mathematical model is present now taking into account new physiological, social and economical demands [3]. A strong control of spread of illness can only be achieved through vaccination programs [4]. However, the vaccination does not always provide full immunity as current research in some countries clearly exhibited and temporal/weak immunity as a result of vaccination is still an open problem. The present attempt is to modify the vaccine SIR model in [4] (SIRV) to account for the weak/loss immune vaccination impacts.
Owing to its simplicity and easy access with many numerical schemes, most of the infective diseases are still preferred to study with the well-documented SIR epidemic model, if not with the latency-based SEIR model [5]. Thus, scholars are continuing their interest to investigate the SIR model via theoretical and computational tools with deterministic versus stochastic aspects. Chronically, some epidemic diseases including Tuberculosis, HIV and Fever were analyzed numerically within the SIR framework in [6]. The theoretical analysis in [7] proved from an optimal control problem approach that the optimal vaccination policies are not unique as studied from the extended SIR model. The finale size of an epidemic was computed for a two-group SIR epidemic model in [8]. In order to completely eradicate an infectious disease, pulse vaccination was suggested in [9], which was also pointed out in [7]. In [10], the SIR model was extended to vaccinated and reinfected after vaccinated in order to simulate the direct and indirect effects of influenza vaccination within a population exposed to seasonal transmission of four influenza strains, and it was concluded that when the reproduction number is close to the endemic value, indirect vaccination effects are stronger. A modified SIR model accounting for nonlinear incidence and recovery rates was given in [11]. The results were reported in [12] for the SIR model under a stochastic perturbation term with vaccination.
To focus on the very recent literature on the SIR mathematical model, Crowley–Martin type functional response in the fractional SIR epidemic model was investigated in [13]. The time homogeneity in the SIR model was introduced in the methodology and applied to COVID-19 data in the United States in [14]. A time-independent reproduction number was involved in [15] with potential approximate analytical solutions. How the peak time of infection can be forecasted accurately without a full simulation was formulated in [16], [17]. With the effects of health system, the fractional SIR model was analyzed in [18]. Prediction of the outbreak of COVID-19 in Iran/Isfahan in the long run was shown to be failure with the traditional SIR model in [19]. The effect of vaccination on an epidemic with a constant removal from the susceptible population was modeled in [20]. Social distancing was imbedded into SIR model in [21]. A diffusive age-structured SIR epidemic model was studied in [22] to search for traveling wave solutions. [23] applied both variational iteration and successive methods to estimate the time history of disease for a constant vaccination SIR epidemic model. A mathematical analysis was implemented in [24] on a diffusive SIR epidemic model with new treatments. [25] proposed a stochastic SIR epidemic model considering Markov jump and low medical equipments. Numerical simulations were performed in [26] considering a two patch setting of variable population SIR epidemic model.
Quite new variants of SIR can be further be encountered recently in the research papers [27] (ISIR), [28] (SIRS), [29] (Neuro-SIR), [30] (GSIR) and [31] (ASIR), amongst many others. The successful epidemic model with vaccination (SIRV) recently presented in [4] (adhering the theoretical bases established in [7] and [10]) assumes a full immunity long-lasting in the society if a person in the susceptible compartment is vaccinated. However, the recent updates of COVID-19 program in certain countries justifies that the vaccines developed so far are not fully protective, meaning that some vaccinated are likely to be contracted the disease again. This necessitates the modification of the epidemic model with vaccination in [4], taking into account the weak or loss immunity offered and possible transition between the vaccinated and infected compartments. Hence, the motivation here is to embed this feature of the vaccination into the epidemic model of [4]. Although such a modification was previously offered in [10], it was approached to quantify the direct and indirect effects of vaccination to the seasonal influenza. Interaction of vaccinated with infected brings a new weak/loss-immunity term into the model, leading to a new SIR model named as SIRVI in the present research. Impacts of this term on the time evolution of SIRV quantities are analyzed both theoretically and numerically. Finally, some countries applying the COVID-19 vaccine program are analyzed with the newly proposed epidemic model SIRVI to conceive the changes in their epidemic demography during COVID-19.
2. The compartmental SIRVI model
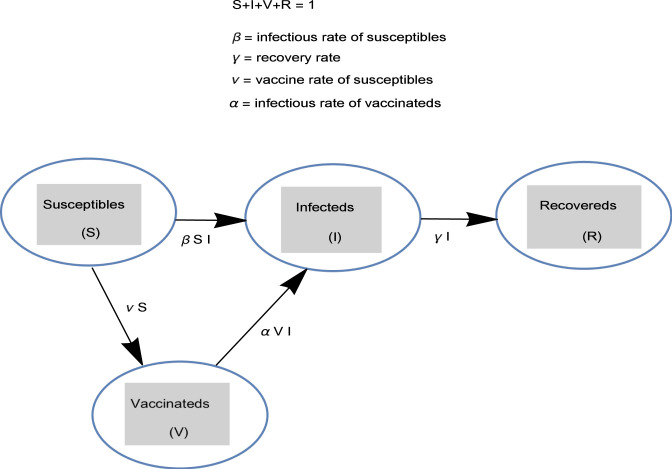
Although there are other variants of SIR model with vaccination as cited in the Introduction, the recent SIRV model in [4] is adopted here. As shown in Fig. 1, the SIRV model consists of fractions of susceptible , infected , vaccinated and removed/recovered . According to the model in [4] (without birth and death rates), an adaptive immunity to the hosts can be given by vaccine administration into the body reducing the number of susceptible and also preventing later infection and transmission. However, the SIRV model in [4] requires modification in the case of weak/loss of immune so that some portion of the vaccinated should be transferred back into infected class , resulting in the following new variant SIRVI
| (1a) |
| (1b) |
| (1c) |
| (1d) |
It is noted that Eq. (1d) is redundant, since can be solved from the fact that the cumulative time rate of the population is zero, hence
| (2) |
Fig. 1.
The SIRVI epidemic model with essential parameters.
In (1a)–(1d), is the parameter leading to illness transmission through an infected individual contacting with susceptible population, immunity to the susceptible is gained to combat the disease with the parameter , is the parameter of reinfection disease transmit via weak or loss immune host in contact with the infected population and is the effective recovery rate of infected arising both from susceptible and vaccinated. Although a general initial condition set can be imposed, the overall character of the SIRVI model can be captured from the initial fractions of infective and of suspected . Additionally, the reproduction number for the epidemic model (1a)–(1d), identifying the die out or persistence of an infective disease is defined through
| (3) |
which coincides with the Reproduction number of the classical SIR owing to the no vaccinated fraction assumption in (1c).
3. The stability analysis
After a sufficient time span, the disease dynamics can be understood from the stability analysis of equilibria. We provide the following Theorems for this purpose for the present SIRVI epidemic model.
Theorem 1
With non-zero (positive) infection parameters, the points leading to equilibria are given by
(4) Such equilibria in (4) are seen to occur at the extinct of disease within the presence of vaccination/removed combination, hence they can be termed as disease-free vaccination/removed equilibrium points.
Proof
Equating the right hand sides of (1a)–(1d) to zero together with (2) yields the equilibrium points (4). ♢
Theorem 2
For stability of the disease-free vaccination/removed equilibrium points (4) , it should hold true
(5)
Proof
Indeed, the Jacobian matrix corresponding to the system (1a)–(1d) with dying disease can computed in the form
(6) Two of the eigenvalues of (6) are already zero, and the other two eigenvalues are
(7) On account of the equilibria in (4), the eigenvalues in (7) are negative (if not zero), which implies stability when (5) holds. ♢
Theorem 3
The disease-free vaccination/removed equilibria (4) is globally asymptotically stable under the constraint (5) .
Proof
Establishing the Lyapunov formalism
(8) and differentiating it with respect to time yields on the account of (1a)–(1b)
(9) It is clear that at the equilibria in (4). Moreover, it turns out to be strictly negative accounting for the positiveness of the epidemic quantities as well as the constraint (5). This completes the proof. ♢
4. Reduction to dimensionless form
With the assist of a dimensionless time , the system (1d) can be written in the subsequent reduced form
| (10a) |
| (10b) |
| (10c) |
| (10d) |
where the epidemiology is affected by the physical parameters
| (11) |
which controls the effective vaccination rate , the recovery rate and the loss immunity rate (or the reinfective rate of vaccinated).
Corollary
Note that the initial rate of infection plays vital role in spread of disease; epidemic outburst (termed as epidemic persistence in[3]) occurs with initially rising rates of infection, i.e. , so from (10b) we have , meaning that the Reproductive number from (3) .
It is also remarked that, no exact solutions to (10a) – (10d) are likely, except that we have
(12)
5. Numerical simulation results and discussions
It is anticipated from (12) that when , decays to zero in the presence of vaccination. The final size of vaccination, though, will be apparent as a limit of indefinite form . Actually, there is no a specific restriction on the admissible range of epidemic parameters, except that lies in the interval . and are also maintained in the intervals and , respectively, to comply with the COVID-19 data supplied in [4].
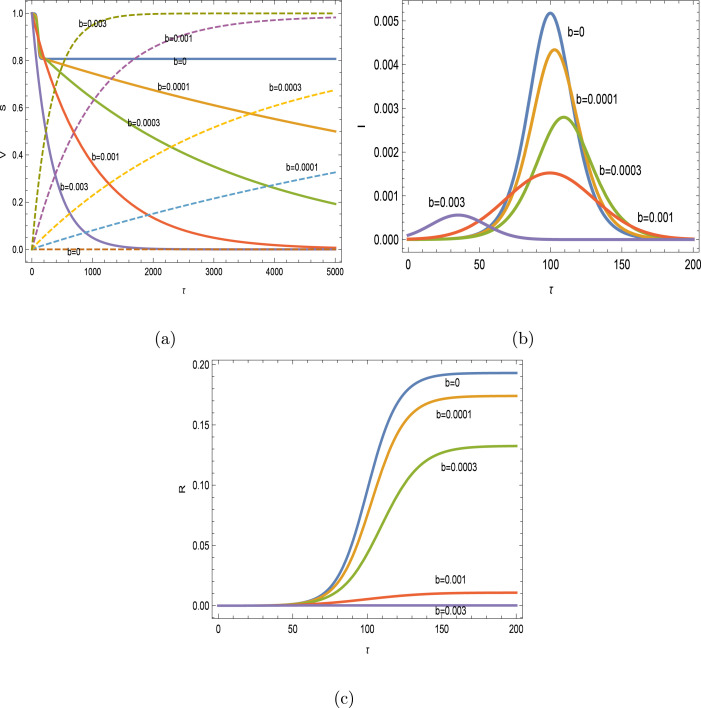
Numerical simulations are performed on the platform Mathematica. Initially, for and with Reproductive number , the impacts of vaccination are depicted on the SIR variables in Figs. 2(a–c) with . In this case, the vaccinating is fully protective. The vaccination helps to reduce the level of infected individuals in time; the more the people are vaccinated, the peak of infected dramatically decreases and the final peak time is also decreased, after an initial increase with smaller vaccination rates. This behavior of vaccination is in full agreement with the analytical results in [4]. Susceptible hosts are rapidly transferred to vaccinated class, and it is seen that the disease free vaccinated/removed equilibria in (4) are converged.
Fig. 2.
Impacts of vaccination with and . (a) , (b) (magnified 10 times when and 100 times when ) and (c) .
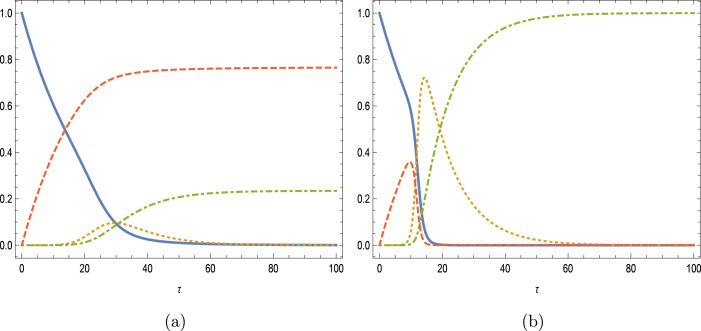
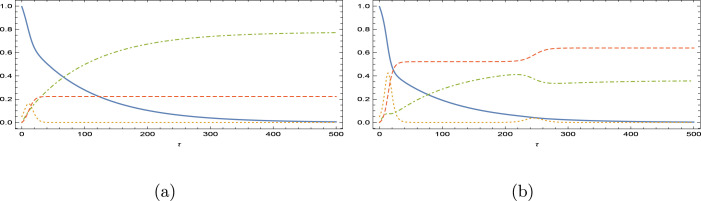
The influences of , loss immunity are next demonstrated in Fig. 3(a–d) for , with the level of vaccination rate and of initial infected . The main observations are that as the immunity gets weaker, infected and removed compartments are filled with more hosts, while susceptible and vaccinated classes are decreased. The more the vaccinated is prone to the reinfection, secondary peak (lower than the first) is reinforced in the infected people leading to oscillatory character of the overall infectious disease. It is worthy to mention that although the effectiveness of the vaccination at this low Reproduction number is in line with the simulations of [10], no such vibrational phenomena were observed in the latter during vaccination study in influenza disease.
Fig. 3.
Impacts of weak-immune vaccination with and . (a) , (b) (c) and (d) .
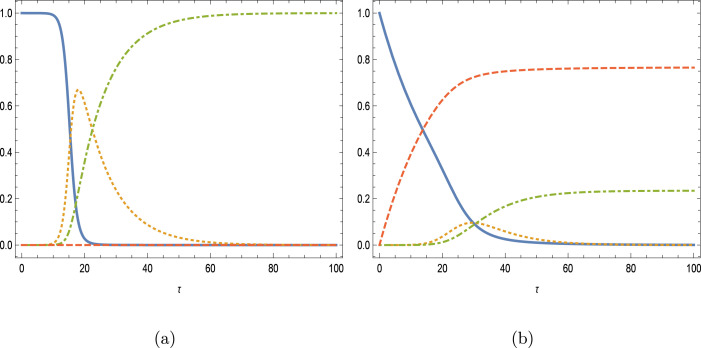
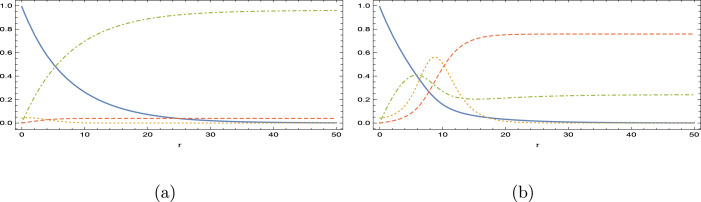
In the case of a larger Reproduction number with , and the mutual parameters with full immunity, the impacts of vaccination are depicted later on the SIR variables in Figs. 4(a,b) with . Curves correspond to unbroken , dashed , dotted and dot–dashed . The prevention of epidemic disease is seen to be very successful again, with reduced infection peaks, declined removed and increased vaccinated curves. The inflective property of susceptible class is gradually turned into a monotonic decrease with higher vaccination rates.
Fig. 4.
Impacts of vaccination with and . (a) and (b) .
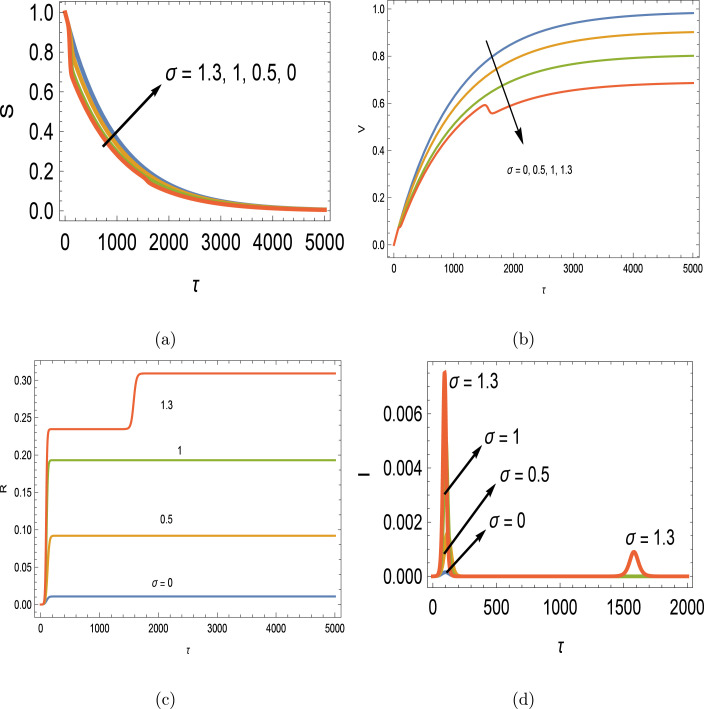
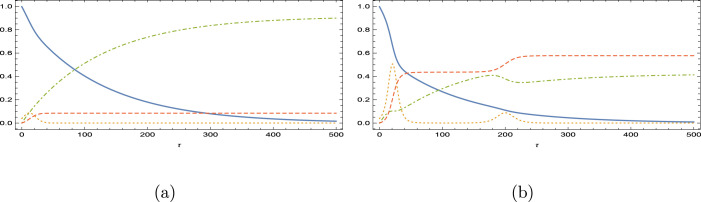
The influences of are then revealed in Figs. 5(a,b) for , and . The effects with the high Reproductive number here are much distinct from those with close epidemic Reproductive number in Figs. 3(a–d). Loss of immunity of vaccinated with higher rates results in reduction in susceptible and vaccinated, followed by boost in infected and removed. Interestingly, the monotonic increase character of vaccinated department replaces its character with inflective one, and after , the vaccinated is totally emptied in the long run with fully removed remaining, refer to the equilibria (4). Even with a larger , no oscillatory behavior is encountered, unlike the epidemic behavior in Figs. 3(a–d).
Fig. 5.
Impacts of weak-immune vaccination with and . (a) and (b) .
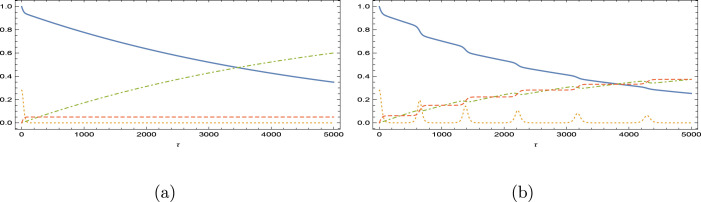
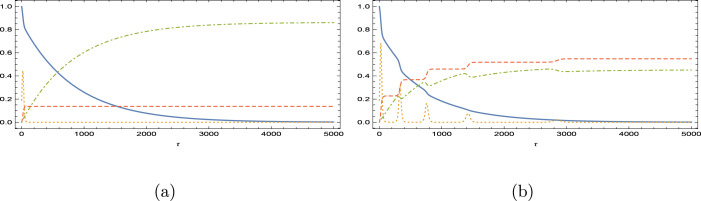
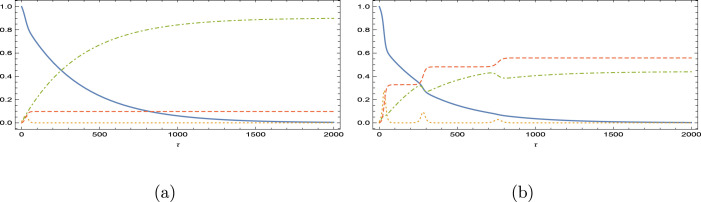
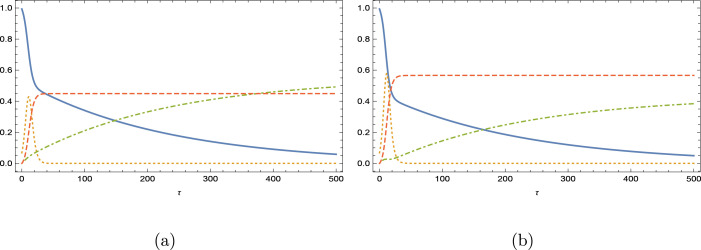
We now explore the impacts of our model on some selected countries, whose COVID-19 parameters with vaccinating [4] are listed in Table 1. The list is formed in accordance with increasing Reproductive number, rather than increasing vaccination rates. The aim is to predict how the loss of immunity due to vaccination can lead to alteration in the response of epidemiology in the population. For this purpose, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12 demonstrate the effects of , where the curves correspond to unbroken , dot–dashed , dotted and dashed . Because countries have distinct epidemiological parameters and Reproductive numbers, time evolution of epidemic variables are naturally different under vaccine program. It can be commonly deduced from the analysis that the populations are slightly affected when the loss immunity rate is less than or equal to unity with a fair increase in the infected people at the peak time, while vaccinated people decreasing and removed people increasing. Literally, the reinfection is more stringent when the loss immunity rate is bigger than unity; in particular, for Finland, Germany and French, where already vibrating response of model epidemic quantities are observed. Notice that these three countries possess comparatively small Reproduction numbers and vaccination rates in Table 1. This behavior is in consistence with the previous findings shown in Figs. 3(a–d).
Table 1.
COVID-19 data with vaccination in some selected countries [4].
| FINLAND | 0.997 | 0.0002 | 0.00140 | 1.00160 |
| GERMANY | 0.915 | 0.0012 | 0.00190 | 1.09082 |
| FRENCH | 0.886 | 0.0027 | 0.00065 | 1.12793 |
| USA | 0.868 | 0.0081 | 0.00195 | 1.14983 |
| ISRAEL | 0.855 | 0.1283 | 0.00835 | 1.15982 |
| BRAZIL | 0.790 | 0.0099 | 0.00505 | 1.25943 |
| MEXICO | 0.712 | 0.0044 | 0.00680 | 1.39494 |
Fig. 6.
Immunity loss scenario for the vaccination program in Finland. is magnified 200 times. (a) and (b) .
Fig. 7.
Immunity loss scenario for the vaccination program in Germany. is magnified 100 times. (a) and (b) .
Fig. 8.
Immunity loss scenario for the vaccination program in French. is magnified 20 times. (a) and (b) .
Fig. 9.
Immunity loss scenario for the vaccination program in USA. is magnified 20 times. (a) and (b) .
Fig. 10.
Immunity loss scenario for the vaccination program in Israel. is magnified 5 times. (a) and (b) .
Fig. 11.
Immunity loss scenario for the vaccination program in Brazil. is magnified 10 times. (a) and (b) .
Fig. 12.
Immunity loss scenario for the vaccination program in Mexico. is magnified 10 times. (a) and (b) .
With a higher reinfective rate at , now USA and Brazil (see Figs. 9(b) and 11(b)) also gives response with an oscillatory behavior, and the oscillations in Germany and Finland are now more severe. Still no oscillations yet appeared in Israel and Mexico as inferred from Figs. 10(b) and 12(b); Israel having the best vaccination rate and Mexico having the highest Reproductive number. Unexpectedly, Brazil in between the countries yields oscillations. Overall, it can be concluded that the appearance of oscillations in the epidemic model is highly dependent on the rate of vaccination as well as the basic Reproduction number. Persistence against the oscillatory epidemiology is anticipated when these two epidemic parameters are high.
As a final remark, the present modification of SIR epidemic model with vaccination can be adapted for the countries in order to guess how the program will be successful when these happens weak or loss of immunity in the vaccinated portion of the people.
6. Conclusions
To control and reduce the effects of a contagious outbreak of an infectious disease, one of an effective strategy is to apply vaccination programs. Vaccinating a population, on the other hand, modifies the well-known epidemic SIR model, as implemented very recently in [4] with the SIRV model.
The SIRV model of vaccination in [4] assumes a 100% immunity in an infected disease. However, this is almost impossible, for instance in the case of COVID-19, since some countries applying vaccine programs still report uncontrolled reinfection of vaccinated individuals ending with higher rates of death. Keeping this in view, the present motivation is to improve the SIRV epidemic model in [4] by plugging the weak–loss immunity influences. Hence, a modification is proposed to reduce the number of vaccinated hosts introducing a reinfection parameter. Therefore, the effects of vaccination and infection of vaccinated individuals in an extension of the SIRV model introduced in [4] are the main goals and motivations inspiring the current investigation.
The stability of equilibria for the new model is analyzed first. Then it is applied to the COVID-19 disease data of some countries (refer to Table 1), wherein ambitious vaccination programs were started to fight against the pandemic. From the presented model, how the epidemic demography of populations will be affected by loss of immunity can be estimated efficiently from country to country, since each has its own inherent parameters. As a consequence, the rate and dose of vaccination can be readjusted.
The main conclusion from the current work is that populations are slightly affected when the loss immunity rate is less than or equal to unity with a fair increase in the infected people at the peak time, while vaccinated people decreasing and removed people increasing. Relying on the rate of vaccination as well as the basic Reproduction number, oscillations appear in the epidemic variables. Persistence against the oscillatory epidemiology is anticipated when these two epidemic parameters are high, for instance in Israel and Mexico.
Simulations with more actual data gathered from more reliable/current resources would warrant further future work. Also the problem of how would one gauge the predictive power of the SIRVI model over the SIRV or even a regular SIR, SIRS, SEIRS, models can be further research activity.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1927;115:700–721. [Google Scholar]
- 2.Tolles J., Luong T. Modeling epidemics with compartmental models. JAMA. 2020;323:2515–2516. doi: 10.1001/jama.2020.8420. [DOI] [PubMed] [Google Scholar]
- 3.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- 4.Schlickeiser R., Kröger M. Analytical modeling of the temporal evolution of epidemics outbreaks accounting for vaccinations. Physics. 2021;3:386–426. [Google Scholar]
- 5.Heng K., Althaus C.L. The approximately universal shapes of epidemic curves in the susceptible-exposed-infectious-recovered (seir) model. Sci. Rep. 2020;10:19365. doi: 10.1038/s41598-020-76563-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ergen K., Cilli A., Yahnioglu N. Predicting epidemic diseases using mathematical modelling of SIR. Acta Phys. Polonica A. 2015;128:273–275. [Google Scholar]
- 7.Laguzet L., Turinici G. Global optimal vaccination in the SIR model: Properties of the value function and application to cost-effectiveness analysis. Math. Biosci. 2015;263:180–197. doi: 10.1016/j.mbs.2015.03.002. [DOI] [PubMed] [Google Scholar]
- 8.Magal P., Seydi O., Webb G. Final size of an epidemic for a two-group SIR model. SIAM J. Appl. Math. 2016;76:2042–2059. [Google Scholar]
- 9.Zhou A., Sattayatham P., Jiao J. Dynamics of an SIR epidemic model with stage structure and pulse vaccination. Adv. Difference Equ. 2016;2016:140. [Google Scholar]
- 10.Eichner M., Schwehm M., Eichner L., Gerlier L. Direct and indirect effects of influenza vaccination. BMC Infect. Dis. 2017;17(308):2–8. doi: 10.1186/s12879-017-2399-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li G.-H., Zhang Y.-X. Dynamic behaviors of a modified SIR model in epidemic diseases using nonlinear incidence and recovery rates. PLoS ONE. 2017;12 doi: 10.1371/journal.pone.0175789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang Y., Li Y., Zhang Q., Li A. Behavior of a stochastic SIR epidemic model with saturated incidence and vaccination rules. Physica A. 2018;501:178–187. [Google Scholar]
- 13.Naik P.A. Global dynamics of a fractional-order SIR epidemic model with memory. Int. J. Biomath. 2020;13 [Google Scholar]
- 14.Yang H.-C., Xue Y., Pan Y., Liu Q., Hu G. Time fused coefficient SIR model with application to COVID-19 epidemic in the United States. J. Appl. Stat. 2021 doi: 10.1080/02664763.2021.1936467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kröger M., Schlickeiser R. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part a: time-independent reproduction factor. J. Phys. A. 2021;53 [Google Scholar]
- 16.Turkyilmazoglu M. Explicit formulae for the peak time of an epidemic from the SIR model. Physica D. 2021;422 doi: 10.1016/j.physd.2021.132902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kröger M., Turkyilmazoglu M., Schlickeiser R. Explicit formulae for the peak time of an epidemic from the SIR model. Which approximant to use? Physica D. 2021;425 doi: 10.1016/j.physd.2021.132981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Alqahtani R.T. Mathematical model of SIR epidemic system (COVID-19) with fractional derivative: stability and numerical analysis. Adv. Difference Equ. 2021;2021 doi: 10.1186/s13662-020-03192-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Moein S., Nickaeen N., Roointan A., Borhani N., Heidary Z., Javanmard S.H., Ghaisari J., Gheisari Y. Inefficiency of SIR models in forecasting COVID-19 epidemic: a case study of isfahan. Sci. Rep. 2021;11:4725. doi: 10.1038/s41598-021-84055-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nakamura G., Grammaticos B., Badoual M. Vaccination strategies for a seasonal epidemic: a simple SIR model. Open Commun. Nonlinear Math. Phys. 2021;1:20–40. [Google Scholar]
- 21.Gounane S., Barkouch Y., Atlas A., Bendahmane M., Karami F., Meskine D. An adaptive social distancing SIR model for COVID-19 disease spreading and forecasting. Epidemiol. Methods. 2021 doi: 10.1515/em-2020-0044. [DOI] [Google Scholar]
- 22.Wu S.-L., Chen L., Hsu C.-H. Traveling wave solutions for a diffusive age-structured SIR epidemic model. Commun. Nonlinear Sci. Numer. Simul. 2021;98 [Google Scholar]
- 23.Mungkasi S. Variational iteration and successive approximation methods for a SIR epidemic model with constant vaccination strategy. Appl. Math. Model. 2021;90:1–10. [Google Scholar]
- 24.Avila-Vales E., Garcia-Almeida G.E., Perez A.G.C. Qualitative analysis of a diffusive SIR epidemic model with saturated incidence rate in a heterogeneous environment. J. Math. Anal. Appl. 2021;503 [Google Scholar]
- 25.Wei W., Xu W., Song Y., Liu J. Bifurcation and basin stability of an SIR epidemic model with limited medical resources and switching noise. Chaos Solitons Fractals. 2021;152 [Google Scholar]
- 26.Liu L., Jiang D., Hayat T. Dynamics of an SIR epidemic model with varying population sizes and regime switching in a two patch setting. Physica A. 2021;574 [Google Scholar]
- 27.Zhu W.-j., Shen S.-f. An improved SIR model describing the epidemic dynamics of the COVID-19 in China. Results Phys. 2021;25 doi: 10.1016/j.rinp.2021.104289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu C., Cui R. Qualitative analysis on an SIRS reaction–diffusion epidemic model with saturation infection mechanism. Nonlinear Anal. RWA. 2021;62 [Google Scholar]
- 29.Lymperopoulos I.N. #Stayhome to contain Covid-19: Neuro-SIR – neurodynamical epidemic modeling of infection patterns in social networks. Expert Syst. Appl. 2021;165 doi: 10.1016/j.eswa.2020.113970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Singh P., Gupta A. Generalized SIR (GSIR) epidemic model: An improved framework for the predictive monitoring of COVID-19 pandemic. ISA Trans. 2021 doi: 10.1016/j.isatra.2021.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gaeta G. A simple SIR model with a large set of asymptomatic infectives. Math. Eng. 2020;3:1–39. [Google Scholar]