Abstract
Dye molecules that absorb light in the visible region are key components in many applications, including organic photovoltaics, biological fluorescent labeling, super-resolution microscopy, and energy transport. One family of dyes, known as squaraines, has received considerable attention recently due to their favorable electronic and photophysical properties. In addition, these dyes have a strong propensity for aggregation, which results in emergent materials properties, such as exciton delocalization. This will be of benefit in charge separation and energy transport along with fundamental studies in quantum information. Given the high structural tunability of squaraine dyes, it is possible that exciton delocalization could be tailored by modifying the substituents attached to the π-conjugated network. To date, limited theoretical studies have explored the role of substituent effects on the electronic and photophysical properties of squaraines in the context of DNA-templated dye aggregates and resultant excitonic behavior. We used ab initio theoretical methods to determine the effects of substituents on the electronic and photophysical properties for a series of nine different squaraine dyes. Solvation free energy was also investigated as an insight into changes in hydrophobic behavior from substituents. The role of molecular symmetry on these properties was also explored via conformation and substitution. We found that substituent effects are correlated with the empirical Hammett constant, which demonstrates their electron donating or electron withdrawing strength. Electron withdrawing groups were found to impact solvation free energy, transition dipole moment, static dipole difference, and absorbance more than electron donating groups. All substituents showed a redshift in absorption for the squaraine dye. In addition, solvation free energy increases with Hammett constant. This work represents a first step toward establishing design rules for dyes with desired properties for excitonic applications.
Squaraine dyes are candidates for DNA-templated excitonic interactions. This work presents substituent effects on the electronic and photophysicalproperties of squaraine dyes and a correlation between empirical Hammettconstant and those properties.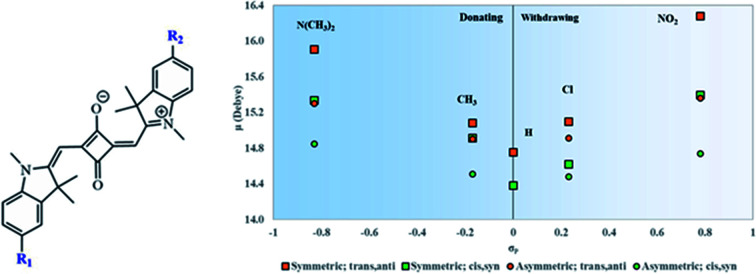
1. Introduction
The aggregation of dyes gives rise to Frenkel exciton delocalization in molecular composite systems.1,2 The study of dye aggregates can provide insight into the implementation of aggregate systems, such as organic photovoltaics,3,4 near infrared medical imaging5 and molecular photoswitch applications6 that draw from a well-established theoretical framework exploiting unique exciton transfer properties.7 Dye aggregate behavior is well described by the molecular exciton model, formulated by Davydov and Kasha, in which intermolecular dipole–dipole interactions lead to the mixing of excited-state wavefunctions to access nondegenerate states.2,8,9 When dye monomers aggregate, the monomeric excited-state energy levels split into the excited states of the aggregate, in which excitons are distributed in a wave-like fashion, called exciton delocalization.10–12 The new excited-state behavior (i.e., exciton delocalization) in the dye aggregate generally manifests as an energy shift.13,14 The inclusion of a double-body exciton interaction introduces a second order molecular excitation interaction, i.e., the exciton–exciton interaction energy Km,n,which is crucial for modeling exciton–exciton interaction behavior in the dye aggregate.14–16
It is pertinent to also discuss the environment, in which dyes may aggregate. DNA is an attractive choice for dye templating due to its customization at the nanoscale and an ability to promote the exciton delocalization of dyes.17–34 DNA has been shown to negligibly change the electronic properties of visible-light absorbing dye monomers.35 As such, the electronic properties of the dye monomers can be evaluated as free-dyes to screen their potential utility as DNA-templated dyes. The customizability of DNA templates and the options for binding dyes to different sites are further enhanced via DNA origami methods to construct multidimensional scaffolds.31,36
Expanding the number of dyes that can potentially be incorporated will no doubt increase the functional capabilities of DNA templating.27,29,35,37–48 Squaraine (SQ) dyes, a family of dyes similar to the widely used cyanine dyes, but with a central squaraine ring, have advantageous properties, such as strong absorption in the visible spectrum49 and resistance to photobleaching.50 They can potentially be structurally tailored for a wide variety of applications.51–53 First synthesized by Treibs and Jacobs,54 the central feature of SQ dyes includes an electron-deficient squaric moiety, combined with electron-rich groups in a symmetric manner by means of a methine bridge.52 The photophysical features and extensive structural tunability make squaraines well-suited candidates for the investigation of exciton delocalization when assembled.18,24,28,55 Although the dipole–dipole coulombic coupling between dyes must be considered to accurately predict aggregate absorption spectra, monomer transition dipole moments provide estimates of the strength of exciton delocalization for various dye configurations via the extended dipole approximation, which can be used as a guide for exciton applications.15,56
There is also a robust body of work demonstrating the customizability of squaraine dyes, offering opportunities for the tunability of dye properties through the engineering of functional groups to yield desired properties.50,52,57–59 Previous work on photophysical property engineering of squaraine dyes via substitution is present in the literature with an emphasis on the changing of the donor groups that flank the central squaraine group or the finetuning of dyes largely for efficient light-to-electrical conversion and imaging.52,60,61 In the context of promoting stronger exitonic interaction, customizing squaraine dyes enables the introduction of substituents that may alter their electronic structures to make them more favorable for dipole interactions without detrimentally affecting photophysical properties.62–64 There has also been a research interest in manipulating two key excitonic coupling factors, including exciton hopping (or exchange) energy, Jm,n, and exciton–exciton interaction energy, Km,n, by controlling the transition dipole μ and static dipole difference Δd of a dye monomer.56,65–67 The maximization of μ within a single absorption band is also benefitted by the minimization of vibronic coupling of dyes.68 Maximizing exciton–exciton interaction energy depends upon the maximization of Δd. This should be concomitant with maintaining or increasing μ and is a primary target for the selection of dyes and their substituents in this study. The maximization of these quantities increases Jm,n and Km,n, leading to a larger excitation energy.56
Substituent effects may also alter the propensity for dye aggregation by changing dye solubility.35,39 Local environment impacts the orientation of the dye by introducing steric effects when hydrophobic substituents are added. In the case of DNA-templated squaraines, the local environment can consider both a solvent environment as well as DNA. The balance of substituents' ability to influence electronic, photophysical, and hydrophobic behaviors is key to the promotion of ideal dyes for excitonic device performance. To further investigate the effect of substituents, this study focuses on substituents that can increase the hydrophobicity of a squaraine dye, because this is expected to promote dye packing in order to influence dipole interactions.39 The study of substituent effects on the electronic, photophysical, and solubility properties of monomers can therefore provide information on candidates for aggregation.
In this work, first-principles methods were used to address the potential for indolenine-based squaraine dyes to be tuned for excitonic applications. Specifically, we used density functional theory (DFT)-based methods to calculate the ground- and excited-state properties of nine squaraine dyes, i.e., SQ-H2, SQ-N(CH3)2, SQ-(N(CH3)2)2, SQ-CH3, SQ-(CH3)2, SQ-Cl, SQ-(Cl)2, SQ-NO2, and SQ-(NO2)2. A range of substituents on a free squaraine dye were studied to evaluate their influence on μ, Δd, absorbance, and hydrophobicity, which were subsequently validated against experimental data for DNA-templated squaraine monomers. By adding functional groups to an unsubstituted squaraine, i.e., SQ-H2, its μ, Δd, absorbance, and hydrophobicity could be altered. In addition, three different conformers were investigated for each dye to examine the impact of structural changes.
2. Methodology
2.1. Computational methods
The Gaussian 16 software package69 was used to perform density functional theory (DFT) and time-dependent density functional theory (TD-DFT) calculations. DFT has proven to provide insight in the investigation of dye properties,65–67,70 and there has been extensive work addressing best practices in employing this method, such as appropriate exchange-correlation functionals to represent electron–electron interactions in the fluorescing dyes similar to squaraine dyes.71–74 The dyes were built and initially relaxed with the molecular editing software Avogadro75 using the UFF76 method. All calculations were performed using the 6-31+G(d,p) basis set with the M06-2X77 exchange-correlation functional, because this showed a good agreement with experimental results in comparison with sets of similar fluorescent dyes.72,73 M06-2X is a hybrid meta-generalized gradient approximation exchange-correlation functional. This nonlocality denotes an inclusion of Hartree–Fock (HF) exchange energy, which is advantageous for non-metal systems. The term “meta” indicates that the functional is constrained to be optimized using empirical data. Specifically, for dipole and absorption calculations, M06-2X was found to be the most reliable in comparison with other popular pure and hybrid exchange-correlation functionals.72,74,78 Jacquemin et al. also conducted an extensive survey of exchange-correlation functionals applicable to different dyes, including squaraine and so-called push–pull dyes.71,73,78–80 Molecules were built according to the structures in Fig. 1. Comparisons were made to monomers incorporated to DNA. DNA was found to negligibly affect the absorbance data of a monomer.18,35
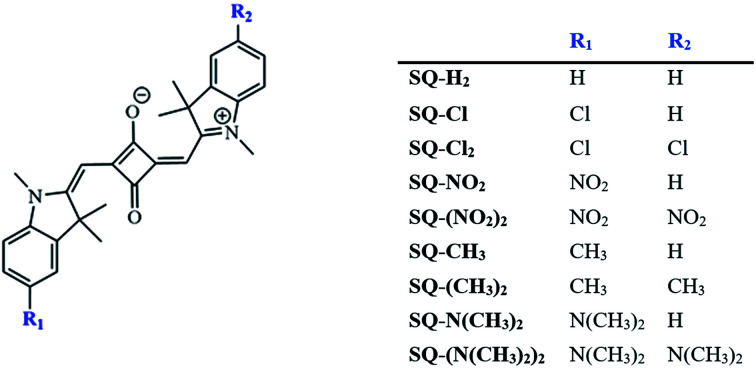
Fig. 1. Indolenine-based squaraines. H atoms are located at the R1 and R2 positions, forming SQ-H2. If H is replaced with substituents, it forms either symmetric (R1 = R2 = substituent) or asymmetric (R1 = H and R2 = substituent). Substituents this study focuses on include N(CH3)2, CH3, Cl, and NO2.
Atomic structures were optimized using a tight root mean square residual force of 1 × (10)−5 Hartree/Bohr and an ultra-fine integration grid of 99 radial shells and 590 angular points per shell. The ground-state optimization of these molecules was verified by ground-state frequency calculations to ensure that no imaginary frequencies were present, because imaginary frequencies represent unstable geometry. Dyes exhibiting desirable Δd (i.e., large Δd) were selected for further calculations to determine vibrationally-resolved absorption spectra. To do so, the optimized first excited-state geometry was used to calculate the excited-state frequency to ensure that an optimized structure was achieved. This procedure resulted in an adiabatic transition by including the zero-point vibrational energies, which accounted for vibrational energies at the states' respective minima.80 The ground- and excited-state frequencies were then used to calculate an absorption spectrum for each molecule with the Franck–Condon (FC) approximation. The FC approximation assumes that nuclear motion is frozen on the timescale of the electronic transition. Our previous studies showed that the calculated absorption spectra of cyanine dyes with the FC approximation agreed well with experiments.35 Here, the changes in the bond lengths of ground and excited states of squaraine dyes were analyzed. We found that the bond lengths among the squaric moiety carbons elongated. The methine chain lengths, connecting the trimethylindolenine groups, and the carbon–oxygen bonds of the squaric moiety shortened. However, all the changes between ground and excited states were on the order of 0.01 Å. This finding indicated that the FC approximation was adequate for squaraine dyes, and agreed well with Bassal et al.74 The vertical excitation was expected to be indicative of the excitation behavior of the squaraine dyes. For dyes in solution, nonequilibrium solvent–solute conditions were considered. Permanent dipole information was generated by taking the vertical excitation from the optimized ground state. This vertical excitation could result in a difference between ground- and excited-state static dipoles, i.e. Δd, written as:72
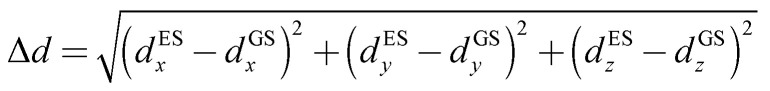 |
1 |
where dji is the Cartesian component of the permanent dipole moment, i, in either the excited ES or ground GS state, j.
Solvation energy, ΔGsolv, has been shown to correspond to hydrophobic behavior and qualitatively imply the stability of dye aggregate.35 To investigate the likelihood of dye aggregation, the solvation free energy ΔGsolv was calculated by taking a difference in the ground state energies calculated using SMD (i.e., Solvation Model based on Density) water and vacuum given as:35,81
| ΔGsolv = Esolv − Ev | 2 |
where Esolv is the ground-state energy calculated in solvent and Ev is the vacuum or gas-phase ground-state energy. Previous studies have introduced squaraine conformers present in solution. Their population percentages were calculated using the Boltzmann distribution.58 The energies used to compare likely populations were the ground-state energies of each system in vacuum and in a water environment at 25 °C. In addition to water solvent, pyridine, quinoline, and isoquinoline were also investigated to approximate a DNA environment. In order to reduce computational time, nitrogen heterocycle solvents were used as suitable analogs to nitrogenous purine and pyrimidine nucleobases in a DNA scaffold.
2.2. Experimental methods
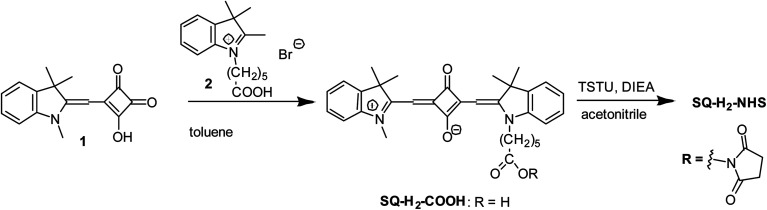
N-Hydroxysuccinimide ester of 2-((1-(5-carboxypentyl)-3,3-dimethylindolin-2-ylidene)methyl)-3-oxo-4-((1,3,3-trimethyl-3H-indol-1-ium-2-yl)methylene)cyclobut-1-en-1-olate (SQ-H2-NHS) was synthesised similar to the procedure described in Kolosova et al.58 (Fig. 2).
Fig. 2. Synthesis of SQ-H2.
3-Hydroxy-4-((1,3,3-trimethylindolin-2-ylidene)methyl)cyclobut-3-ene-1,2-dione (1) (150 mg, 0.56 mmol) and 1-(5-carboxypentyl)-2,3,3-trimethyl-3H-indolium bromide (2) (200 mg, 0.56 mmol) were heated under reflux in toluene (10 mL) for 10 h. The solvent was removed under reduced pressure by a rotary evaporator. The residue was purified by a column chromatography (Silica gel 60, 0–8% methanol–chloroform) to give SQ-H2-COOH (190 mg, 65%) as a dark blue solid with a golden sheen. 1H-NMR (200 MHz, DMSO-d6), δ, ppm: 7.52 (2H, d, 7.3 Hz, arom.), 7.44–7.25 (4H, m, arom.), 7.25–7.04 (2H, m, arom.), 5.79 (1H, s, CH), 5.76 (1H, s, CH), 4.06 (2H, t, 7.4 Hz, NCH2), 3.57 (3H, s, NCH3), 2.21 (2H, t, 6.7 Hz, CH̲2COOH), 1.68 (12H, s, (CH3)2), 1.80–1.29 (6H, m). MALDI-TOF MS, m/z calcd. for [C33H36N2O4] 524.27, found: 525.32 [M + H]+. Anal. calcd. (%) for C33H36N2O4: C, 75.55; H, 6.92; N, 5.34. Found C, 75.43; H, 6.89; N, 5.31. UV-Vis: λmax (Abs) 630 nm (methanol); λmax (Em) 639 nm (methanol); λmax (Abs) 622 nm, ε 285 000 M−1 cm−1 (phosphate buffer); λmax (Em) 632 nm (phosphate buffer).
SQ-H2-COOH (30 mg, 57 mmol), N,N,N′,N′-tetramethyl-O-(N-succinimidyl)uronium tetrafluoroborate (TSTU) (26 mg, 86 μmol), and N,N-diisopropylethylamine (DIEA) (16 mL, 92 mmol) were dissolved in acetonitrile (3 mL). The solution was stirred at room temperature for 20 min. The solvent was removed under reduced pressure by a rotary evaporator. The residue was purified by a column chromatography (Silica gel 60, 0–3% methanol–chloroform) to give SQ-H2-NHS. Yield: 18 mg (51%). 1H-NMR (200 MHz, DMSO-d6), δ, ppm: 7.53 (2H, d, 7.4 Hz, arom.), 7.46–7.24 (4H, m, arom.), 7.24–7.01 (2H, m, arom.), 5.79 (1H, s, CH), 5.76 (1H, s, CH), 4.06 (2H, t, 7.4 Hz, NCH2), 3.58 (3H, s, NCH3), 2.81 (4H, s, CH2 (NHS)), 2.67 (2H, t, 6.0 Hz, CH̲2COONHS), 1.68 (12H, s, (CH3)2), 1.80–1.29 (6H, m).
For computation-experiment validation, we assembled a four-arm DNA Holliday junction with the unsubstituted squaraine SQ-H2 covalently attached to one of the oligonucleotides. Three unlabeled oligonucleotides and one oligonucleotide labeled with SQ-H2 (SETA BioMedicals, Urbana-Champaign, IL) via the nucleosidic sequence modifier C6 dT were obtained from Integrated DNA Technologies (Coralville, IA). Squaraine-labeled and unlabeled DNA oligonucleotides were rehydrated in ultrapure water (Barnstead Nanopure, Thermo Scientific) to prepare a 100 μM stock solution. Concentrations of DNA samples were determined spectroscopically on NanoDrop One Microvolume UV-Vis (Thermo Scientific) using a calculated extinction coefficient. DNA Holliday junctions were prepared by combining equimolar amounts of complimentary functionalized and non-functionalized oligonucleotides in 1× TBE 15 mM MgCl2 buffer solution, to a final DNA concentration 1.5 μM. Samples were annealed in a Mastercycler Nexus PCR cycler (Eppendorf) according to the following protocol: 4 min at 94 °C, followed by a cooling rate: 0.1 °C per 15 s from 94 °C to 64 °C, and 10 °C per minute from 64 °C to room temperature. UV-Vis spectra were recorded in duplicates at room temperature on a dual-beam Cary 5000 UV-Vis-NIR spectrophotometer (Agilent Technologies) in a cuvette with a 10 mm pathlength. Absorbance spectra were monitored over a wavelength range of 230–800 nm. Spectra were normalized at dye absorption maximum in UV-Vis range using OriginPro 2019.
3. Results
3.1. Boltzmann populations of conformers
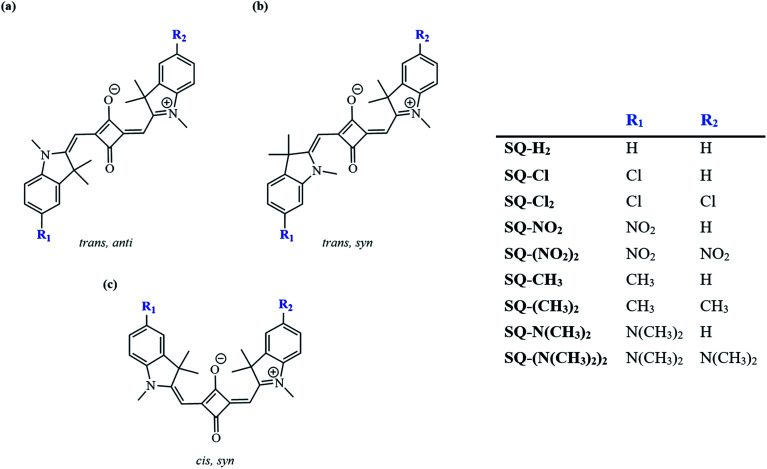
To further complement changes associated with composition via substitution, this study considered three conformers of the indolenine-based squaraine, including trans,syn with Cs symmetry; cis,syn with C2v symmetry; and trans,anti with C2h symmetry using a Boltzmann distribution calculation at room temperature.58 The conformations of dyes were considered based on previously reported indolenine-based squaraines via photoisomerization.58,82 The energies of the optimized ground-state squaraine dyes were used to calculate the energy differences and corresponding Boltzmann populations of three conformers of the indolenine-based squaraine dyes, as shown in Fig. 3. The energy differences between the optimized ground-state conformers are shown in Table 1. For all dyes, a more stable conformer is represented by a more negative total energy. Comparing the differences of total energies of different conformers shows that the trans,anti conformer is about 5 kJ mol−1 more stable than the cis,syn conformer (trans,anti–cis,syn) and about 8 kJ mol−1 more stable than the trans,syn conformer (trans,anti–trans,syn). The energy difference results, when used as states for a Boltzmann distribution, demonstrate that the two major conformers of indolenine-squaraines are trans,anti and cis,syn. The trans,anti conformer is the most energetically favorable for all the indolenine-based squaraine dyes with the most negative total energy. These energy differences have been described as a result of steric strain from the dimethyl group of the indolenine rings in agreement with previous computational and experimental studies.58,83,84 The trans,anti conformer further benefits from a staggered conjugation, favoring minimized steric effects.85,86 However, we found that substituents have a minor effect on the Boltzmann populations with respect to the unsubstituted trans,anti squaraine (SQ-H2) at most by only 3%. The greatest variation of conformer population from the unsubstituted cis,synSQ-H2 conformer occurs from SQ-Cl by 3%. The Boltzmann populations of different trans,syn conformers are lower than 4% and have the greatest variation with respect to the unsubstituted trans,synSQ-H2 is also from SQ-Cl by 1%. Computational results show that the cis,syn and trans,anti conformers are popular, so our further studies focus on these conformers.
Fig. 3. Three possible indolenine squaraine conformers: (a) trans,anti, (b) trans,syn, and (c) cis,syn. Substituents this study focuses on include N(CH3)2, CH3, Cl, and NO2.
Ground-state total energy differences between trans,anti and cis,syn conformers and between trans,anti and trans,syn conformers, as well as associated Boltzmann populations calculated from the energy differences at 25 °C in vacuum.
| Dye | Energy difference (kJ mol−1) | Boltzmann populations (%) | |||
|---|---|---|---|---|---|
| trans,anti–cis,syn | trans,anti–trans,syn | trans,anti | trans,syn | cis,syn | |
| SQ-(N(CH3)2)2 | −4.81 | −8.39 | 84.93 | 2.88 | 12.2 |
| SQ-N(CH3)2 | −4.78 | −8.18 | 84.58 | 3.12 | 12.3 |
| SQ-(CH3)2 | −4.77 | −8.33 | 82.14 | 1.31 | 16.54 |
| SQ-CH3 | −4.76 | −8.32 | 84.65 | 2.95 | 12.39 |
| SQ-H2 | −4.81 | −8.31 | 82.69 | 2.57 | 14.74 |
| SQ-Cl | −4.70 | −8.18 | 80.49 | 1.49 | 18.02 |
| SQ-(Cl)2 | −4.72 | −8.46 | 83.02 | 2.54 | 14.44 |
| SQ-NO2 | −4.69 | −8.85 | 84.84 | 2.38 | 12.78 |
| SQ-(NO2)2 | −4.95 | −8.73 | 85.83 | 2.53 | 11.63 |
3.2. Comparison of SQ-H2 with experiment
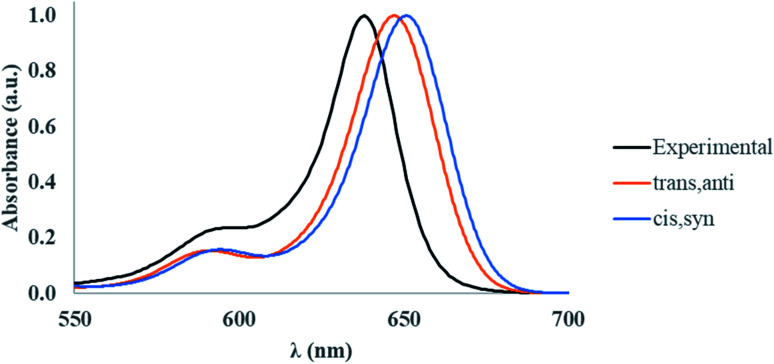
To validate our approach for the calculations of ground- and excited-state properties of substituted squaraines, the vibrationally-resolved absorption spectra of SQ-H2 were generated using the Franck–Condon (FC) method in the TD-DFT framework for the trans,anti and cis,syn conformers. The calculated absorption spectra are shown in Fig. 4 along with the experimental absorption profile.
Fig. 4. Experimental and calculated vibrationally-resolved absorption spectra for SQ-H2. The calculated absorption spectra were obtained using the FC approach with the optimized ground- and excited-state structures of a free dye in a water solvent. The experimental spectrum was obtained for SQ-H2 covalently attached to a DNA HJ; the concentration of SQ-H2 – DNA HJ construct was 1.5 μM in 1× TBE 15 mM MgCl2 aqueous buffer solution.
TD-DFT satisfactorily reproduces the lineshape of the experimental absorption spectrum, which exhibits a strong absorption peak at 638 nm and a smaller vibrionic shoulder around 590 nm. The TD-DFT calculated peak absorption λmax is found to be 647 nm for the trans,anti conformer and 651 nm for the cis,syn conformer. Compared to the experimental data, the absorbance data calculated by TD-DFT exhibits a peak absorption λmax within 0.027 eV of experiment (as calculated for the trans,anti conformer). Furthermore, the calculated trans,anti peak absorption λ is closest to experiment, which suggests that the trans,anti conformer dominates the dye populations, agreeing well with the Boltzmann population results (Table 1). The deviation from the theoretical calculation is a known artifact in TD-DFT calculations when computing absorption spectra for dyes. This is due to small perturbations in the excited electronic density that the hybrid exchange-correlation functional cannot adequately model in the TD-DFT scheme.87
3.3. Solvation free energy calculations
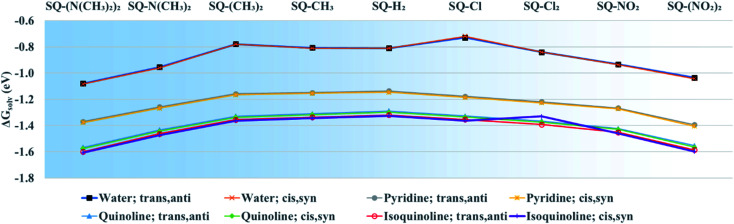
To determine the effects of electron donating and withdrawing substituents on the solvation energies of squaraine dyes, DFT ground-state optimization calculations were performed in vacuum and solvent. From the solvated and vacuum energies, the solvation free energy, ΔGsolv, was determined using eqn (2) for each dye, as shown in Fig. 5. As with other studies,88,89 the values of ΔGsolv were calculated to estimate the solubility of the dyes in the given solvent. As shown in Fig. 1, the substituted dye structures consist of symmetrically substituted dyes (R1 = R2) and asymmetrically substituted dyes (R1 = H ≠ R2).
Fig. 5. Solvation free energy (ΔGsolv) of unsubstituted and symmetrically substituted squaraine dyes in water, pyridine, quinoline, and isoquinoline calculated using eqn (2). Geometry optimizations were done using the M06-2X functional. The lines added to the data are to highlight trends of the data and are not meant to infer quantitative behavior. The x-axis is in order of increasing donating and withdrawing strength as its position away from SQ-H2.
Unsubstituted squaraine has a ΔGsolv of −0.81 eV in water for both the trans,anti and cis,syn conformers. For all dyes, the conformer does not affect ΔGsolv, and, overall, the values of ΔGsolv are only slightly affected by substitution. Upon substitution, most dyes exhibit more negative ΔGsolv values in water, except for SQ-Cl, which has the least negative ΔGsolv value, indicating being the most hydrophobic. In contrast, SQ-(N(CH3)2)2 has the most negative ΔGsolv for the water solvated dyes and so is taken to be the most hydrophilic. The ΔGsolv for the dyes in pyridine, quinoline, and isoquinoline follow similar trends as those in water. The values of ΔGsolv in pyridine, quinoline, and isoquinoline are also unaffected by conformers. ΔGsolv for the dyes in water are less negative, indicating that it is more energetically favorable for the dyes to form solutes in pyridine, quinoline, and isoquinoline. These three solvents are taken to mimic the molecular structure of DNA bases.
3.4. Excited-state calculations
The optimized water-solvated ground-state structures of unsubstituted and substituted squaraines were used for single-step TD-DFT calculations in the first excited singlet state to determine the effects that electron donating and electron withdrawing substituents have on electronic excited-state properties (i.e., μ and Δd). We introduced the empirically derived Hammett constant (σp), which could quantify the strength of a substituent as electron withdrawing (positive) or electron donating (negative).90,91 A list of these constants is provided in Table 2. N(CH3)2 and NO2 are strong donating and withdrawing substituents, respectively. CH3 and Cl are weak donating and withdrawing substituents, respectively. The Hammett constant has been shown to relate to the characteristics of an electronic structure.67,92 To establish a relationship between the strengths of the electron donating and electron withdrawing substituents (as quantified with σp) and calculated properties, μ, Δd, and Δλmax are plotted against the σp of attached substituents, as discussed in the following sections.
Substituents used in this study and their corresponding Hammett constants,90,91σp. The empirically derived Hammett constant (σp) is used to quantify the strength in which a substituent is electron withdrawing (positive) or electron donating (negative).
| Substituent | Hammett constant (σp) | Classification |
|---|---|---|
| N(CH3)2 | −0.83 | Donating |
| CH3 | −0.17 | |
| H | 0 | |
| Cl | 0.23 | Withdrawing |
| NO2 | 0.78 |
3.4.1. Transition dipole moments
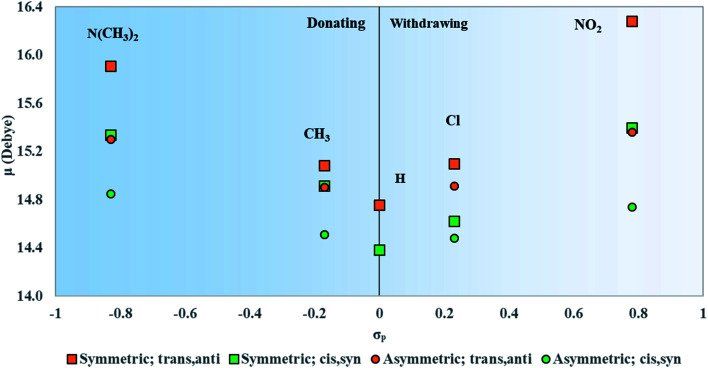
Compared to unsubstituted squaraine, Fig. 6 shows that substituents with the larger magnitudes of σp yield dyes with larger μ. The calculated values of μ for unsubstituted squaraine (SQ-H2) are 14.7 D for the trans,anti conformer and 14.4 D for the cis,syn conformer and were determined to be along the long axis of the dye. The dyes exhibiting the largest values of μ are trans,antiSQ-(N(CH3)2)2 (15.9 D) and SQ-(NO2)2 (16.3 D), which are the dyes with the strongest electron donating and electron withdrawing substituents, respectively. In general, symmetrically substituted dyes have the larger values of μ than asymmetrically substituted ones. Furthermore, the trans,anti conformers exhibit the larger values of μ than cis,syn conformers. In comparison with the unsubstituted squaraine, the largest change is SQ-(NO2)2 with 1.6 D, and all substituents contribute an increase in μ.
Fig. 6. Transition dipole moment magnitudes (μ) for symmetrically and asymmetrically substituted squaraines plotted against the Hammett constant of the substituent(s) attached to the dye.
3.4.2. Static dipole differences
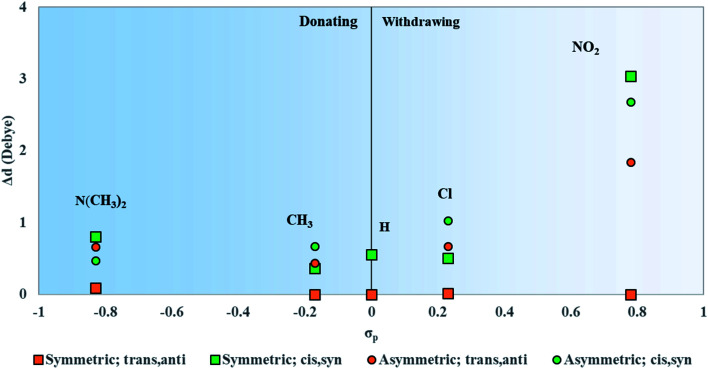
Similar to μ, the Δd of squaraine increases with the magnitude of σp, as shown in Fig. 7. Substitution type and conformation also influence Δd. Symmetrically substituted SQ-N(CH3)2 and SQ-NO2 dyes have the higher Δd than their asymmetrical ones. Symmetrically substituted SQ-(CH3) and SQ-Cl dyes have the lower Δd than their asymmetrical ones. Furthermore, symmetrically substituted dyes in the trans,anti conformations all have Δd values of nearly 0 D while others have non-zero Δd. In general, trans,anti conformers, characterized by C2h type symmetry, have the lower values of Δd compared to cis,syn conformers, characterized by C2v symmetry. The largest values of Δd belong to cis,synSQ-Cl (0.8 D) in the asymmetrically substituted dyes and cis,synSQ-NO2 (3.0 D) in the symmetrically substituted dyes. This indicates that electron withdrawing substituents have the larger impact on Δd than electron donating substituents.
Fig. 7. Static dipole difference magnitudes (Δd) for symmetrically and asymmetrically substituted squaraines plotted against the Hammett constant of the substituent(s) attached to the dye.
3.4.3. Absorption spectra of asymmetric squaraines
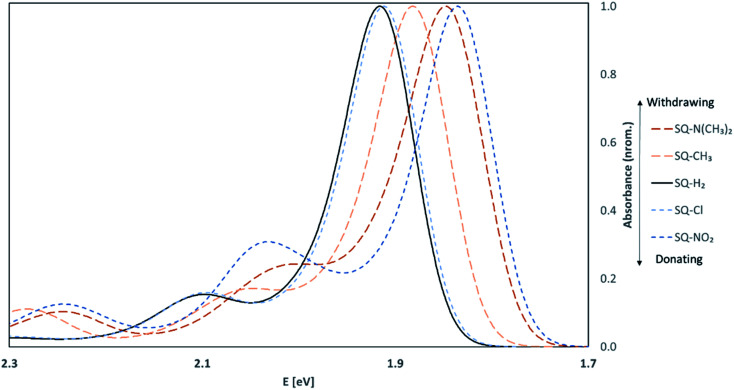
To further test the effects of substituents on the excited-state properties of dyes, vibrationally-resolved absorption spectra were calculated. The asymmetrically substituted dyes in the trans,anti conformations with the larger Δd values were chosen for further studies with the FC method. The normalized results are shown in Fig. 8.
Fig. 8. Vibrationally-resolved absorption spectra for trans,anti asymmetrically substituted squaraine dyes calculated using the FC method in implicit water. The solid black line is the unsubstituted squaraine (SQ-H2) absorbance spectrum.
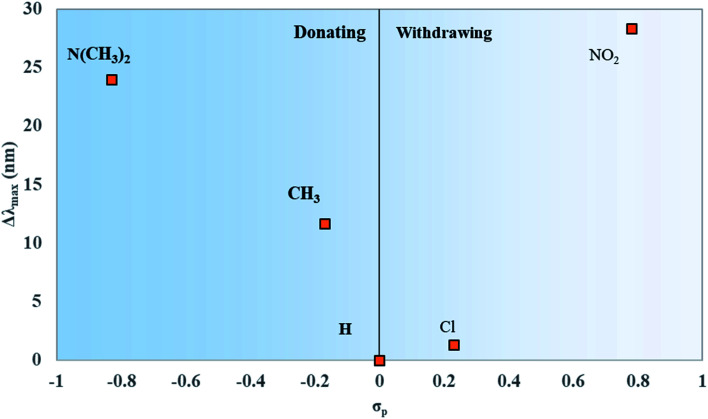
Upon asymmetric substitution, the lineshapes of the spectra remain relatively unaffected, with a main absorption peak between 1.97 and 1.84 eV (630 and 675 nm) and a smaller vibrionic shoulder around 2.1 eV (600 nm). However, the λmax values for asymmetrically substituted dyes are redshifted compared to the unsubstituted squaraine dye. SQ-Cl has the smallest redshift of 0.04 eV. The largest redshifts of 0.08 eV and 0.09 eV belong to SQ-N(CH3)2 and SQ-NO2, indicating that the stronger electron donating or electron withdrawing substituents have a larger effect on λmax.
Like μ and Δd, the values for Δλmax were plotted against the values of σp for the substituents attached to the dyes. Δλmax is defined as the redshift of the λmax of the dyes in Fig. 8 from unsubstituted squaraine (SQ-H2). As shown in Fig. 9, the larger σp values of the substituents promote the larger Δλmax.
Fig. 9. Maximum absorption wavelength differences from unsubstituted squaraine (Δλmax) for asymmetrically substituted squaraines plotted against the Hammett constant of the substituent(s) attached to the dye.
4. Discussion
In regard to the changes to Δd and μ upon substitution, all substituents lead to changes in electronic structures as compared with the reference squaraine SQ-H2. In the frame of treating the squaraine as a donor–acceptor–donor dye, the substituents modify the donating behavior of the trimethylindolenine groups attached to the accepting squaric moiety. The electron withdrawing substituents in this study appear to have a stronger effect on the change of Δd and μ. Electronically, this may be the result of decreasing the donating ability of the indolenine groups towards the squaraine center. In contrast to the withdrawing substituents, the donating substituents are expected to increase the donating strength of the indolenine groups. The contribution of the electron donating substituents to an increase in Δd and μ is relatively smaller than that of the electron withdrawing substituents (Fig. 6 and 7).
ΔGsolv is sensitive to solvent and becomes more negative with the nitrogen heterocyclic solvents pyridine, quinoline, and isoquinoline, as shown in Fig. 5. This trend increases from pyridine to quinoline and isoquinoline and can be attributed to π–π interactions between the solvent and the solute.93 The magnitude of ΔGsolv also increases with σp. An increase in the magnitude of ΔGsolv indicates a greater stability in a solvent environment. This would suggest that the dyes have a propensity for a DNA environment and are more likely to aggregate in a DNA template rather than dissolve in aqueous solution.
Recent squaraine dye applications have revealed the effect of conformers on device performance. These effects are due to the alteration of energy transfer pathways.53,82,94–97 Conformers have also been shown to change transition dipole orientation, further potentially affecting exciton delocalization.98 Certain applications may benefit from different conformers, such as dye-sensitized solar cells in part because of accommodation of different anchoring options on substrates.53 Boltzmann distribution calculations have been used to predict the population of conformers existing in solution.58 Squaraine dyes with unaltered central squaric moieties have been found most likely to exist in a trans,anti (C2h) symmetry state.
Upon both symmetric and asymmetric substitution, μ is relatively unaffected by the type of substitution. Because of this, the exciton hopping interaction occurring between dyes in an aggregate should remain unchanged and may be slightly augmented with substituents. For symmetric substitution, most dyes in the trans,anti conformations exhibit a Δd of ∼0 D. As shown in Fig. 3, dyes in the trans,anti conformations have C2h symmetry, which, along with the donor–acceptor–donor electronic pattern of squaraine, results in small changes in Δd. In contrast, dyes in the cis,syn conformations are characterized by C2v symmetry and exhibit a non-zero Δd. By only including a single substituent on the dye (i.e. asymmetric substitution), the structural symmetry is distorted. Furthermore, substituents with non-zero σp would increase Δd. Specifically for the subsituents studied in this work, the electron withdrawing substituent NO2 increases Δd the most. Our computational results suggest that σp can guide the selection of dye candidates with desired electronic and photophysical properties.
Based on the results of this study, the substitution of the squaraine indolenine rings can enhance the dye's excitonic properties. Upon substitution, μ is slightly increased for most dyes, indicating that the excitonic hopping interaction between dyes in an aggregate should be enhanced rather than diminished. Similarly, substituents can promote an increase in Δd, which could improve the exciton-exciton interaction energy of the squaraine aggregate.
5. Conclusion
Squaraine dyes with varied substituents were investigated to compare their solvation free energy ΔGsolv, static dipole difference Δd, transition dipole moment μ, and absorption wavelength λmax using DFT and TD-DFT. Changes in these values upon substitution were compared to the empirically derived Hammett constant σp and experimental absorption profiles for the unsubstituted squaraine dye. It was found that the magnitude of σp correlated with ΔGsolv, μ, Δd,and λmax. ΔGsolv becomes more negative with a larger σp value in water and in solvents similar to a DNA environment. μ increases with σp for symmetric substitution patterns. Δd increases with asymmetric substitution and σp. λmax also increases with σp. These findings on the electronic, photophysical, and hydrophobic properties of squaraine dyes can guide the selection of substituted dyes. The ability to control dye properties, when coupled with DNA scaffolding, may make it possible to tailor the performance of dye aggregate materials for excitonic systems and applications.
Author contributions
German Barcenas: investigation (lead), writing – original draft (lead), methodology (equal), formal analysis (lead), data curation (lead). Austin Biaggne: investigation (supporting), writing – original draft (supporting), methodology (equal), formal analysis (supporting), data curation (supporting). Olga A. Mass: conceptualization (equal), validation (lead), writing – review and editing (equal), supervision (supporting). Christopher K. Wilson: validation (supporting). Olena M. Obukhova: resources (supporting). Olga S. Kolosova: resources (supporting). Anatoliy L. Tatarets: resources (supporting). Ewald Terpetschnig: resources (supporting), writing – review and editing (equal). Ryan D. Pensack: conceptualization (equal), writing – review and editing (equal). Jeunghoon Lee: conceptualization (equal), writing – review and editing (equal). William B. Knowlton: conceptualization (equal), project administration (supporting), writing – review and editing (equal). Bernard Yurke: conceptualization (equal), writing – review and editing (equal), supervision (supporting). Lan Li: conceptualization (equal), project administration (lead), writing – review and editing (equal), supervision (lead).
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This research was supported wholly by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Materials Sciences and Engineering Division, and DOE's Established Program to Stimulate Competitive Research (EPSCoR) (Award DE-SC0020089), except for the following. This research also made use of the resources of the High Performance Computing Center at Idaho National Laboratory, which is supported by the Office of Nuclear Energy of the DOE and Nuclear Science User Facilities under Contract No. DE-AC07-05ID14517.
References
- Cannon B. L. et al., Large Davydov Splitting and Strong Fluorescence Suppression: An Investigation of Exciton Delocalization in DNA-Templated Holliday Junction Dye Aggregates. J. Phys. Chem. A. 2018;122:2086–2095. doi: 10.1021/acs.jpca.7b12668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasha M., Energy Transfer, Charge Transfer, and Proton Transfer in Molecular Composite Systems, in Physical and Chemical Mechanisms in Molecular Radiation Biology, Springer US, 1991, pp. 231–255. 10.1007/978-1-4684-7627-9_8 [DOI] [PubMed] [Google Scholar]
- Wei G. et al., Functionalized Squaraine Donors for Nanocrystalline Organic Photovoltaics. ACS Nano. 2012;6:972–978. doi: 10.1021/nn204676j. [DOI] [PubMed] [Google Scholar]
- Chen J. et al., Density functional theory investigations of D-A-D′ structural molecules as donor materials in organic solar cell. Front. Chem. 2018;6:200. doi: 10.3389/fchem.2018.00200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strassel K. et al., Squaraine Dye for a Visibly Transparent All-Organic Optical Upconversion Device with Sensitivity at 1000 nm. ACS Appl. Mater. Interfaces. 2018;10:11063–11069. doi: 10.1021/acsami.8b00047. [DOI] [PubMed] [Google Scholar]
- Lubbe A. S. Szymanski W. Feringa B. L. Recent developments in reversible photoregulation of oligonucleotide structure and function. Chem. Soc. Rev. 2017;46:1052–1079. doi: 10.1039/C6CS00461J. [DOI] [PubMed] [Google Scholar]
- Kasha M. Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates. Radiat. Res. 1963;20:55. doi: 10.2307/3571331. [DOI] [PubMed] [Google Scholar]
- Kasha M. Rawls H. R. Ashraf El-Bayoumi M. The exciton model in molecular spectroscopy. Pure Appl. Chem. 1965;11:371–392. [Google Scholar]
- Davydov A. S. S. The theory of molecular excitons. Usp. Fiz. Nauk. 1964;82:393–448. doi: 10.3367/UFNr.0082.196403a.0393. [DOI] [Google Scholar]
- Banal J. L. Kondo T. Veneziano R. Bathe M. Schlau-Cohen G. S. Photophysics of J-Aggregate-Mediated Energy Transfer on DNA. J. Phys. Chem. Lett. 2017;8:5827–5833. doi: 10.1021/acs.jpclett.7b01898. [DOI] [PubMed] [Google Scholar]
- Abramavicius D. Mukamel S. Exciton Delocalization and Transport in Photosystem I of Cyanobacteria Synechococcus elongates: Simulation Study of Coherent Two-Dimensional Optical Signals. J. Phys. Chem. B. 2009;113:6097–6108. doi: 10.1021/jp811339p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelley E. E. Exchange narrowing and exciton delocalization in disordered J aggregates: simulated peak shapes in the two dimensional spectra. Nature. 1936;139:034313. doi: 10.1063/1.4812927. [DOI] [PubMed] [Google Scholar]
- Hestand N. J. Spano F. C. Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 2018;118:7069–7163. doi: 10.1021/acs.chemrev.7b00581. [DOI] [PubMed] [Google Scholar]
- Abramavicius D. Voronine D. V. Mukamel S. Double-quantum resonances and exciton-scattering in coherent 2D spectroscopy of photosynthetic complexes. Proc. Natl. Acad. Sci. U. S. A. 2008;105:8525–8530. doi: 10.1073/pnas.0802926105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madjet M. E. Abdurahman A. Renger T. Intermolecular Coulomb Couplings from Ab Initio Electrostatic Potentials: Application to Optical Transitions of Strongly Coupled Pigments in Photosynthetic Antennae and Reaction Centers. J. Phys. Chem. B. 2006;110:17268–17281. doi: 10.1021/jp0615398. [DOI] [PubMed] [Google Scholar]
- Brüggemann B. May V. Ultrafast laser pulse control of exciton dynamics: a computational study on the FMO complex. J. Phys. Chem. B. 2004;108:10529–10539. doi: 10.1021/jp040096+. [DOI] [Google Scholar]
- Cannon B. L. et al., Coherent Exciton Delocalization in a Two-State DNA-Templated Dye Aggregate System. J. Phys. Chem. A. 2017;121:6905–6916. doi: 10.1021/acs.jpca.7b04344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mass O. A. et al., Exciton Delocalization in Indolenine Squaraine Aggregates Templated by DNA Holliday Junction Scaffolds. J. Phys. Chem. B. 2020;124:9636–9647. doi: 10.1021/acs.jpcb.0c06480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikeda S. Okamoto A. Hybridization-sensitive on-off DNA probe: application of the exciton coupling effect to effective fluorescence quenching. Chem.–Asian J. 2008;3:958–968. doi: 10.1002/asia.200800014. [DOI] [PubMed] [Google Scholar]
- Kashida H. Asanuma H. Komiyama M. Alternating hetero H aggregation of different dyes by interstand stacking from two DNA-dye conjugates. Angew. Chem., Int. Ed. 2004;43:6522–6525. doi: 10.1002/anie.200460870. [DOI] [PubMed] [Google Scholar]
- Kringle L. et al., Temperature-dependent conformations of exciton-coupled Cy3 dimers in double-stranded DNA. J. Chem. Phys. 2018;148:85101. doi: 10.1063/1.5020084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazuski R. J. et al., Ultrafast Excitation Transfer in Cy5 DNA Photonic Wires Displays Dye Conjugation and Excitation Energy Dependency. J. Phys. Chem. Lett. 2020;11:4163–4172. doi: 10.1021/acs.jpclett.0c01020. [DOI] [PubMed] [Google Scholar]
- Ruedas-Rama M. J. et al., Interaction of YOYO-3 with different DNA templates to form H-aggregates. J. Phys. Chem. B. 2014;118:6098–6106. doi: 10.1021/jp5022888. [DOI] [PubMed] [Google Scholar]
- Barclay M. S. Rotaxane rings promote oblique packing and extended excited-state lifetimes in DNA-templated squaraine dye aggregates. Commun. Chem. 2021;4:19. doi: 10.1038/s42004-021-00456-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kashida H. et al., Covalent incorporation of methyl red dyes into double-stranded DNA for their ordered clustering. Chem.–Eur. J. 2006;12:777–784. doi: 10.1002/chem.200500111. [DOI] [PubMed] [Google Scholar]
- Asanuma H. Shirasuka K. Takarada T. Kashida H. Komiyama M. DNA-dye conjugates for controllable H* aggregation. J. Am. Chem. Soc. 2003;125:2217–2223. doi: 10.1021/ja021153k. [DOI] [PubMed] [Google Scholar]
- Huff J. S. et al., DNA-Templated Aggregates of Strongly Coupled Cyanine Dyes: Nonradiative Decay Governs Exciton Lifetimes. J. Phys. Chem. Lett. 2019;10:2386–2392. doi: 10.1021/acs.jpclett.9b00404. [DOI] [PubMed] [Google Scholar]
- Markova L. I. Malinovskii V. L. Patsenker L. D. Häner R. Synthesis and properties of squaraine-modified DNA. Org. Biomol. Chem. 2012;10:8944–8947. doi: 10.1039/C2OB26787J. [DOI] [PubMed] [Google Scholar]
- Adeyemi O. O. Malinovskii V. L. Biner S. M. Calzaferri G. Haner R. Photon harvesting by excimer-forming multichromophores. Chem. Commun. 2012;48:9589–9591. doi: 10.1039/C2CC34183B. [DOI] [PubMed] [Google Scholar]
- Albinsson B. Hannestad J. K. Börjesson K. Functionalized DNA nanostructures for light harvesting and charge separation. Coord. Chem. Rev. 2012;256:2399–2413. doi: 10.1016/j.ccr.2012.02.024. [DOI] [Google Scholar]
- Cunningham P. D. Díaz S. A. Yurke B. Medintz I. L. Melinger J. S. Delocalized Two-Exciton States in DNA Scaffolded Cyanine Dimers. J. Phys. Chem. B. 2020;124:8042–8049. doi: 10.1021/acs.jpcb.0c06732. [DOI] [PubMed] [Google Scholar]
- Fujii T. Kashida H. Asanuma H. Analysis of coherent heteroclustering of different dyes by use of threoninol nucleotides for comparison with the molecular exciton theory. Chem.–Eur. J. 2009;15:10092–10102. doi: 10.1002/chem.200900962. [DOI] [PubMed] [Google Scholar]
- Garo F. Häner R. A DNA-based light-harvesting antenna. Angew. Chem., Int. Ed. 2012;51:916–919. doi: 10.1002/anie.201103295. [DOI] [PubMed] [Google Scholar]
- Hara Y. et al., Coherent quenching of a fluorophore for the design of a highly sensitive in-stem molecular beacon. Angew. Chem., Int. Ed. 2010;49:5502–5506. doi: 10.1002/anie.201001459. [DOI] [PubMed] [Google Scholar]
- Fothergill J. W. Hernandez A. C. Knowlton W. B. Yurke B. Li L. Ab Initio Studies of Exciton Interactions of Cy5 Dyes. J. Phys. Chem. A. 2018;122:8989–8997. doi: 10.1021/acs.jpca.8b05237. [DOI] [PubMed] [Google Scholar]
- Zhang F. Nangreave J. Liu Y. Yan H. Structural DNA nanotechnology: state of the art and future perspective. J. Am. Chem. Soc. 2014;136:11198–11211. doi: 10.1021/ja505101a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitus M. Ranjit S. Cyanine dyes in biophysical research: the photophysics of polymethine fluorescent dyes in biomolecular environments. Q. Rev. Biophys. 2011;44:123–151. doi: 10.1017/S0033583510000247. [DOI] [PubMed] [Google Scholar]
- Nicoli F. et al., Proximity-Induced H-Aggregation of Cyanine Dyes on DNA-Duplexes. J. Phys. Chem. A. 2016;120:9941–9947. doi: 10.1021/acs.jpca.6b10939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler A. L. Renikuntla B. R. Yaron D. Fang A. S. Armitage B. A. Substituent effects on the assembly of helical cyanine dye aggregates in the minor groove of a DNA template. Langmuir. 2011;27:1472–1479. doi: 10.1021/la104329c. [DOI] [PubMed] [Google Scholar]
- Hart S. M. et al., Engineering couplings for exciton transport using synthetic DNA scaffolds. Chem. 2021;7(3):752–773. [Google Scholar]
- Mathur D. et al., Can a DNA Origami Structure Constrain the Position and Orientation of an Attached Dye Molecule? J. Phys. Chem. C. 2021;125:1509–1522. doi: 10.1021/acs.jpcc.0c09258. [DOI] [Google Scholar]
- Cunningham P. D. et al., Resonance energy transfer in DNA duplexes labeled with localized dyes. J. Phys. Chem. B. 2014;118:14555–14565. doi: 10.1021/jp5065006. [DOI] [PubMed] [Google Scholar]
- Würthner F. Kaiser T. E. Saha-Möller C. R. J-aggregates: from serendipitous discovery to supramolecular engineering of functional dye materials. Angew. Chem., Int. Ed. 2011;50:3376–3410. doi: 10.1002/anie.201002307. [DOI] [PubMed] [Google Scholar]
- Moreira B. G. You Y. Owczarzy R. Cy3 and Cy5 dyes attached to oligonucleotide terminus stabilize DNA duplexes: predictive thermodynamic model. Biophys. Chem. 2015;198:36–44. doi: 10.1016/j.bpc.2015.01.001. [DOI] [PubMed] [Google Scholar]
- Cunningham P. D. et al., Optical Properties of Vibronically Coupled Cy3 Dimers on DNA Scaffolds. J. Phys. Chem. B. 2018;122:5020–5029. doi: 10.1021/acs.jpcb.8b02134. [DOI] [PubMed] [Google Scholar]
- Iqbal A. et al., Orientation dependence in fluorescent energy transfer between Cy3 and Cy5 terminally attached to double-stranded nucleic acids. Proc. Natl. Acad. Sci. U. S. A. 2008;105:11176–11181. doi: 10.1073/pnas.0801707105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustroph H. Towns A. Fine Structure in Electronic Spectra of Cyanine Dyes: Are Sub-Bands Largely Determined by a Dominant Vibration or a Collection of Singly Excited Vibrations? ChemPhysChem. 2018;19:1016–1023. doi: 10.1002/cphc.201701300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markova L. I. Malinovskii V. L. Patsenker L. D. Haner R. J- vs. H-type assembly: pentamethine cyanine (Cy5) as a near-IR chiroptical reporter. Chem. Commun. 2013;49:5298–5300. doi: 10.1039/C3CC42103A. [DOI] [PubMed] [Google Scholar]
- Funabiki K. et al., Design of NIR-absorbing simple asymmetric squaraine dyes carrying indoline moieties for use in dye-sensitized solar cells with Pt-free electrodes. Org. Lett. 2012;14:1246–1249. doi: 10.1021/ol300054a. [DOI] [PubMed] [Google Scholar]
- Markova L. I. Terpetschnig E. A. Patsenker L. D. Comparison of a series of hydrophilic squaraine and cyanine dyes for use as biological labels. Dyes Pigm. 2013;99:561–570. doi: 10.1016/j.dyepig.2013.06.022. [DOI] [Google Scholar]
- Sreejith S. Carol P. Chithra P. Ajayaghosh A. Squaraine dyes: a mine of molecular materials. J. Mater. Chem. 2008;18:264–274. doi: 10.1039/B707734C. [DOI] [Google Scholar]
- Ilina K. et al., Squaraine Dyes: Molecular Design for Different Applications and Remaining Challenges. Bioconjugate Chem. 2020;31:194–213. doi: 10.1021/acs.bioconjchem.9b00482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Punitharasu V. Mele Kavungathodi M. F. Singh A. K. Nithyanandhan J. π-Extended cis-Configured Unsymmetrical Squaraine Dyes for Dye-Sensitized Solar Cells: Panchromatic Response. ACS Appl. Energy Mater. 2019;2:8464–8472. doi: 10.1021/acsaem.9b01341. [DOI] [Google Scholar]
- Treibs A. Jacob K. Cyclotrimethine Dyes Derived from Squaric Acid. Angew. Chem., Int. Ed. Engl. 1965;4:694. doi: 10.1002/anie.196506941. [DOI] [Google Scholar]
- Zhong C. Bialas D. Collison C. J. Spano F. C. Davydov Splitting in Squaraine Dimers. J. Phys. Chem. C. 2019;123:18734–18745. doi: 10.1021/acs.jpcc.9b05297. [DOI] [Google Scholar]
- Abramavicius D. Palmieri B. Mukamel S. Extracting single and two-exciton couplings in photosynthetic complexes by coherent two-dimensional electronic spectra. Chem. Phys. 2009;357:79–84. doi: 10.1016/j.chemphys.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beverina L. Sassi M. Twists and Turns Around a Square: The Many Faces of Squaraine Chemistry. Synlett. 2014;25:477–490. doi: 10.1055/s-0033-1340482. [DOI] [Google Scholar]
- Kolosova O. S. et al., Molecular structure and spectral properties of indolenine based norsquaraines versus squaraines. Dyes Pigm. 2019;163:318–329. doi: 10.1016/j.dyepig.2018.12.007. [DOI] [Google Scholar]
- Mayerhöffer U. Fimmel B. Würthner F. Bright near-infrared fluorophores based on squaraines by unexpected halogen effects. Angew. Chem., Int. Ed. 2012;51:164–167. doi: 10.1002/anie.201107176. [DOI] [PubMed] [Google Scholar]
- Law K.-Y. Wilson J. C. Squaraine Chemistry. Absorption, Fluorescence Emission, and Photophysics of Unsymmetrical Squaraines. J. Phys. Chem. 1995;99:9818–9824. doi: 10.1021/j100024a024. [DOI] [Google Scholar]; , https://pubs.acs.org/sharingguidelines
- Wang S. et al., N,N-Diarylanilinosquaraines and Their Application to Organic Photovoltaics. Chem. Mater. 2011;23:4789–4798. doi: 10.1021/cm2020803. [DOI] [Google Scholar]
- Menke S. M. Holmes R. J. Exciton diffusion in organic photovoltaic cells. Energy Environ. Sci. 2014;7:499–512. doi: 10.1039/C3EE42444H. [DOI] [Google Scholar]
- Xia G. et al., Controlling Crystal Structures and Multiple Thermo- and Vapochromic Behaviors of Benzimidazole-Based Squaraine Dyes by Molecular Design and Solvent Adjustment. Chem.–Eur. J. 2018;24:13205–13212. doi: 10.1002/chem.201801518. [DOI] [PubMed] [Google Scholar]
- Ros-Lis J. V. et al., Squaraines as reporter units: insights into their photophysics, protonation, and metal-ion coordination behaviour. Chem.–Eur. J. 2008;14:10101–10114. doi: 10.1002/chem.200800300. [DOI] [PubMed] [Google Scholar]
- Cervantes-Navarro F. Glossman-Mitnik D. DFT study of the effect of substituents on the absorption and emission spectra of Indigo. Chem. Cent. J. 2012;6:70. doi: 10.1186/1752-153X-6-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rode M. F. Sobolewski A. L. Effect of chemical substituents on the energetical landscape of a molecular photoswitch: an Ab initio study. J. Phys. Chem. A. 2010;114:11879–11889. doi: 10.1021/jp105710n. [DOI] [PubMed] [Google Scholar]
- Abou-Hatab S. Spata V. A. Matsika S. Substituent Effects on the Absorption and Fluorescence Properties of Anthracene. J. Phys. Chem. A. 2017;121:1213–1222. doi: 10.1021/acs.jpca.6b12031. [DOI] [PubMed] [Google Scholar]
- Uejima M. Sato T. Yokoyama D. Tanaka K. Park J.-W. Quantum yield in blue-emitting anthracene derivatives: vibronic coupling density and transition dipole moment density. Phys. Chem. Chem. Phys. 2014;16:14244–14256. doi: 10.1039/C4CP01428F. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.,et al., Gaussian 16, 2016
- Biaggne A. Knowlton W. B. Yurke B. Lee J. Li L. Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations. Molecules. 2021;26:524. doi: 10.3390/molecules26030524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquemin D. Planchat A. Adamo C. Mennucci B. TD-DFT Assessment of Functionals for Optical 0–0 Transitions in Solvated Dyes. J. Chem. Theory Comput. 2012;8:2359–2372. doi: 10.1021/ct300326f. [DOI] [PubMed] [Google Scholar]
- Jacquemin D. Excited-State Dipole and Quadrupole Moments: TD-DFT versus CC2. J. Chem. Theory Comput. 2016;12:3993–4003. doi: 10.1021/acs.jctc.6b00498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquemin D. Duchemin I. Blase X. 0–0 Energies Using Hybrid Schemes: Benchmarks of TD-DFT, CIS(D), ADC(2), CC2, and BSE/GW Formalisms for 80 Real-Life Compounds. J. Chem. Theory Comput. 2015;11:5340–5359. doi: 10.1021/acs.jctc.5b00619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassal F. Laurent A. D. Le Guennic B. Jacquemin D. Exploring the excited-states of squaraine dyes with TD-DFT, SOS-CIS(D) and ADC(2) Dyes Pigm. 2017;138:169–175. doi: 10.1016/j.dyepig.2016.11.046. [DOI] [Google Scholar]
- Hanwell M. D. et al., Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 2012;4:17. doi: 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappé A. K. Casewit C. J. Colwell K. S. Goddard W. A. Skiff W. M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992;114:10024–10035. doi: 10.1021/ja00051a040. [DOI] [Google Scholar]
- Zhao Y. Truhlar D. G. Zhao Y. Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- Charaf-Eddin A. Planchat A. A. Mennucci B. Adamo C. Jacquemin D. Choosing a functional for computing absorption and fluorescence band shapes with TD-DFT. J. Chem. Theory Comput. 2013;9:2749–2760. doi: 10.1021/ct4000795. [DOI] [PubMed] [Google Scholar]
- Jacquemin D. Mennucci B. Adamo C. Excited-state calculations with TD-DFT: from benchmarks to simulations in complex environments. Phys. Chem. Chem. Phys. 2011;13:16987–16998. doi: 10.1039/C1CP22144B. [DOI] [PubMed] [Google Scholar]
- Adamo C. Jacquemin D. The calculations of excited-state properties with time-dependent density functional theory. Chem. Soc. Rev. 2013;42:845–856. doi: 10.1039/C2CS35394F. [DOI] [PubMed] [Google Scholar]
- Marenich A. V. Cramer C. J. Truhlar D. G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B. 2009;113:6378–6396. doi: 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Paternò G. M. et al., Excited state photophysics of squaraine dyes for photovoltaic applications: an alternative deactivation scenario. J. Mater. Chem. C. 2018;6:2778–2785. doi: 10.1039/C7TC05078J. [DOI] [Google Scholar]
- Borrelli R. Ellena S. Barolo C. Theoretical and experimental determination of the absorption and emission spectra of a prototypical indolenine-based squaraine dye. Phys. Chem. Chem. Phys. 2014;16:2390–2398. doi: 10.1039/C3CP54298J. [DOI] [PubMed] [Google Scholar]
- Dirk C. W. et al., Squarylium Dyes: Structural Factors Pertaining to the Negative Third-Order Nonlinear Optical Response. J. Am. Chem. Soc. 1995;117:2214–2225. doi: 10.1021/ja00113a011. [DOI] [Google Scholar]
- Pophristic V. Goodman L. Hyperconjugation not steric repulsion leads to the staggered structure of ethane. Nature. 2001;411:565–568. doi: 10.1038/35079036. [DOI] [PubMed] [Google Scholar]
- Quijano-Quiñones R. F. Quesadas-Rojas M. Cuevas G. Mena-Rejón G. J. The rotational barrier in ethane: a molecular orbital study. Molecules. 2012;17:4661–4671. doi: 10.3390/molecules17044661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Guennic B. Jacquemin D. Taking Up the Cyanine Challenge with Quantum Tools. Acc. Chem. Res. 2015;48:530–537. doi: 10.1021/ar500447q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Md. Abdur Rauf S. et al., The effect of N-methylation of amino acids (Ac-X-OMe) on solubility and conformation: a DFT study. Org. Biomol. Chem. 2015;13:9993–10006. doi: 10.1039/C5OB01565K. [DOI] [PubMed] [Google Scholar]
- Mananghaya M. R. Santos G. N. Yu D. N. Solubility of amide functionalized single wall carbon nanotubes: a quantum mechanical study. J. Mol. Liq. 2017;242:1208–1214. doi: 10.1016/j.molliq.2017.07.107. [DOI] [Google Scholar]
- Brown H. C. Okamoto Y. Electrophilic Substituent Constants. J. Am. Chem. Soc. 1958;80:4979–4987. doi: 10.1021/ja01551a055. [DOI] [Google Scholar]
- Hansch C. Leo A. Taft R. W. A Survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991;91:165–195. doi: 10.1021/cr00002a004. [DOI] [Google Scholar]
- Mao Y. Head-Gordon M. Shao Y. Unraveling substituent effects on frontier orbitals of conjugated molecules using an absolutely localized molecular orbital based analysis. Chem. Sci. 2018;9:8598–8607. doi: 10.1039/C8SC02990C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahman M. H. et al., Aggregation of Conjugated Polymers in Aromatic Solvent. Langmuir. 2009;25:1667–1674. doi: 10.1021/la802526d. [DOI] [PubMed] [Google Scholar]
- Qin C. et al., A near-infrared cis-configured squaraine co-sensitizer for high-efficiency dye-sensitized solar cells. Adv. Funct. Mater. 2013;23:3782–3789. doi: 10.1002/adfm.201203384. [DOI] [Google Scholar]
- Völker S. F. et al., Singlet-singlet exciton annihilation in an exciton-coupled squaraine-squaraine copolymer: a model toward hetero-J-aggregates. J. Phys. Chem. C. 2014;118:17467–17482. doi: 10.1021/jp5055809. [DOI] [Google Scholar]
- Pedersen T. G. Johansen P. M. Pedersen H. C. Characterization of azobenzene chromophores for reversible optical data storage: molecular quantum calculations. J. Opt. A: Pure Appl. Opt. 2000;2:272–278. doi: 10.1088/1464-4258/2/4/305. [DOI] [Google Scholar]
- Etherington M. K. et al., Regio- and conformational isomerization critical to design of efficient thermally-activated delayed fluorescence emitters. Nat. Commun. 2017;8:14987. doi: 10.1038/ncomms14987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brand C. Meerts W. L. Schmitt M. How and why do transition dipole moment orientations depend on conformer structure? J. Phys. Chem. A. 2011;115:9612–9619. doi: 10.1021/jp200492s. [DOI] [PubMed] [Google Scholar]