Abstract
A growing number of nonsynonymous mutations in the human HCN4 channel gene, the major component of the funny channel of the sinoatrial node, are associated with disease but how they impact channel structure and function, and, thus, how they result in disease, is not clear for any of them. Here, we study the S672R mutation, in the cyclic nucleotide-binding domain of the channel, which has been associated with an inherited bradycardia in an Italian family. This may be the best studied of all known mutations, yet the underlying molecular and atomistic mechanisms remain unclear and controversial. We combine measurements of binding by isothermal titration calorimetry to a naturally occurring tetramer of the HCN4 C-terminal region with a mathematical model to show that weaker binding of cAMP to the mutant channel contributes to a lower level of facilitation of channel opening at submicromolar ligand concentrations but that, in general, facilitation occurs over a range that is similar between the mutant and wild-type because of enhanced opening of the mutant channel when liganded. We also show that the binding affinity for cGMP, which produces the same maximum facilitation of HCN4 opening as cAMP, is weaker in the mutant HCN4 channel but that, for both wild-type and mutant, high-affinity binding of cGMP occurs in a range of concentrations below 1 μM. Thus, binding of cGMP to the HCN4 channel may be relevant normally in vivo and reduced binding of cGMP, as well as cAMP, to the mutant channel may contribute to the reduced resting heart rate observed in the affected family.
Significance
A growing number of nonsynonymous mutations in the human pacemaker channel of the sinoatrial node are associated with disease but how they impact channel structure and function, and how they result in disease, is not clear for any of them. Here, we study a mutation in a domain that binds the second messenger cAMP, which is associated with an inherited bradycardia in an Italian family. We show that this mutation reduces the ability of cAMP to bind, but also modifies the opening process such that the effect of reduced binding is minimized. This is because the mutation may enhance opening of cAMP-bound channels. Finally, we show that the effect of cGMP is reduced, which may also contribute to bradycardia in this family.
Introduction
HCN channels underlie the hyperpolarization-activated current, so designated Ih (hyperpolarization-activated) or If (funny), which is a critical for spontaneous action potential firing in the sinoatrial node (SAN) of the heart (1,2). Hyperpolarization of the membrane potential opens HCN channels and permits the inward flow of sodium, and lesser outflow of potassium, which contributes to the slow depolarization during diastole that leads to action potential firing.
The funny current If is modulated by β-adrenergic and muscarinic stimulation, which, respectively, stimulates or inhibits cAMP production by adenylyl cyclase (3, 4, 5, 6). Facilitation of If channel opening occurs by the direct action of cAMP on the cytoplasmic side of the channel with a half-maximal cAMP concentration (EC50) of 0.2 μM (6). Facilitation by cAMP is marked by a depolarizing shift in the range of voltages over which the channel opens, ranging from ∼11 to 14 mV in the SAN and accounting for most of the additive shift of ∼18 mV seen upon maximal stimulation with β-adrenergic and muscarinic agonists (7,8). Both cAMP and cGMP bind to sinoatrial HCN, and facilitate opening to the same extent, but the former has an EC50 that is >30-fold lower (0.2 vs. 7.85 μM) (6). The direct action of cAMP on the cytoplasmic side of patches excised from SAN myocytes (6) suggested that the channel itself contained a region to which this cyclic nucleotide binds. Direct binding by cyclic nucleotides was confirmed when the four mammalian HCN isoforms (HCN1-4) were cloned, each containing a cyclic nucleotide-binding domain (CNBD) in the cytosolic C-terminal region (9, 10, 11, 12).
A preponderance of evidence supports a critical role for the HCN4 gene, and the CNBD specifically, in cardiac pacemaking. Unstable and/or low heart rates were noted in mice with overexpression of HCN4 channels that are insensitive to cAMP due to either a mutation within the CNBD (13) or a deletion of the CNBD altogether (14). Second, several mutations in the HCN4 CNBD are associated with cardiac disease (15, 16, 17, 18, 19, 20, 21). However, like most of the more than 20 disease-associated mutations in HCN4 channel (19), how they impact the HCN4 channel at the molecular and atomistic level remains unclear.
Perhaps the best-studied disease-associated mutation in the human HCN4 gene is S672R, in the CNBD, which was shown to associate with a bradycardia phenotype in an Italian family (18). Yet, even for this mutation, how channel function is impacted, and how altered channel function results in resting bradycardia, is uncertain. The initial study showed that the mutant HCN4 channel responded to cAMP in a manner that was not much different than the wild-type channel but that it was not as easily opened by hyperpolarization (18). By contrast, another study showed that the affinity of a monomeric version of the C-linker and CNBD of the HCN4 channel for cAMP was greatly reduced, as was its potency in the chimeric channel containing the HCN2 transmembrane regions and the HCN4 C-linker and CNBD (22).
In his review of HCN4 mutations (23), DiFrancesco states that “the results from the two studies cannot apparently be reconciled, although several significant differences exist in the experimental settings.” He also points out that there are differences in the channels used by his group and the Zhou group. He states that “clearly more experimental data are required to investigate these differences.”
The unusual data and uncertainty surrounding this mutation provided an incentive for our group to investigate using different approaches. We measure the affinity of cAMP to a naturally occurring tetrameric form of the wild-type and S672R HCN4 C-terminal region using isothermal titration calorimetry (ITC). This approach is novel and previously suggested that cAMP binds to the HCN2 and HCN4 channels, but not HCN1 channels, with negative cooperativity (24). We have combined measurements of cAMP binding affinities and previous data on channel function obtained by electrophysiology in a mathematical model of facilitation of channel opening by this ligand (25). Our results suggest that the S672R mutation reduces the binding affinity of cAMP for the HCN4 channel but it may also enhance the opening of the cAMP-bound channel which limits the functional defect. We also show that the binding affinity of cGMP, which binds to the wild-type and mutant channel with negative cooperativity, as does cAMP, is reduced by the mutation. We propose that the reduction in binding affinity for cAMP and cGMP by the mutation reduces channel activity under resting conditions, which contributes to the resting bradycardia observed in this family.
Methods
Cloning, site-directed mutagenesis, expression, and purification
The C-terminal region used here (C-linker and CNBD) of HCN4 was cloned into a modified pEt28 vector. A His-tag, maltose binding protein, and TEV cleavage site was inserted in the N-terminal side of the construct of interest. Site-directed mutagenesis was performed using the QuikChange protocol (Agilent, Santa Clara, CA, USA). Expression and purification were done the same way as previously by our group. Protein are expressed at 37°C in E. coli Rosetta (DE3) pLacI cells (MilliporeSigma, Burlington, MA, USA), induced at OD600 of 0.6 with 0.4 M IPTG, and inoculated for another 4 h before harvesting. The cell pellets were resolubilized and lysed with sonication in 250 mM KCl and 10 mM HEPES at pH 7.4 (buffer A), and the addition of glycerol, 25 μg/mL DNase I and lysozyme, 0.4 mM EDTA, and 10 mM PMSF. The constructs were applied to Talon (cobalt-bound-resin) columns and eluted with 250 mM KCl and 500 mM imidazole at pH 7.4. The eluent was dialyzed with TEV protease in buffer A for 2 h. The content was run on another Talon column and the flow through was collected. The protein was then charged in dialysis buffer with 10 mM KCl + 20 mM MES at pH 6.0 for 2 h and applied to a ResourceS column (GE Healthcare, Chicago, IL, USA) at an increasing KCl concentration from 0 to 50%. The protein was confirmed on an SDS-PAGE gel and was dialyzed in 150 mM KCl and 10 mM HEPES at pH 7.4. The protein was concentrated to 20 mg/mL, determined with spectrophotometry and the Edelhoch method.
ITC
ITC was performed, in general, as described in our previous publications (24, 25, 26). Each protein was diluted to 200 μM in dialysis buffer (150 mM KCl + 10 mM HEPES [pH 7.4]). At this concentration, we found that the wild-type and mutant HCN4 C-terminal protein is present mainly in tetrameric form (24) (see Fig. 2). Cyclic AMP and cGMP were utilized at 2 mM and injected into the sample cell 1 μL at a time, for a total of 40 injections. The experiments were performed at 25°C and five to eight replicates were compiled for each protein-ligand combination. The heat needed to compensate for the temperature difference between the sample and reference cell was recorded for each injection, and heat was integrated to obtain kilocalories per mole of injectant. Fitting was carried out using a two-independent site binding model in Origin 7.0 (MicroCal ITC add-on, Malvern Panalytical, Malvern, UK). From fitting, binding affinity, the thermodynamics of binding and stoichiometry of the interaction were determined. The procedure we utilized here has been described in more detail previously (27, 28, 29), as well as in the MicroCal tutorial guide and in a recent publication from our lab (25).
Figure 2.
Cyclic AMP and cGMP promote oligomerization of the wild-type and S672R mutant HCN4 C-linker/CNBD. Plots of average apparent molecular mass versus concentration of the wild-type (left) and S672R (right) HCN4 C-linker/CNBD without ligand (open square/circle) or with a saturating concentration of cAMP (black) or cGMP (gray) as determined by DLS. The population of tetramers (∼90 kDa) increases with increasing amount of wild-type or mutant protein. The addition of the ligand promotes formation of tetramers at lower concentration, indicated by an increase in average MW on top of self-oligomerization. Values represent mean ± SE.
Dynamic light scattering
To determine the oligomerization state of the HCN4 C-linker/CNBD, we used dynamic light scattering (DLS). The HCN4 protein was diluted to 12.5, 25, 50, 100, or 200 μM in a 50 μL mixture, in the absence or presence of ligand (at a 10:1 ratio of ligand/protein). The mixture was spun for 2 min at 6000 rpm to get rid of debris, before applying it to a 384-multiwell microtiter plate. The hydrodynamic radii were measured at 22°C using a DynaPro plate reader II (Wyatt Technology, Santa Barbara, CA, USA), and autocorrected and converted to molecular weights based on parameters of a globular protein. Five readings were averaged per acquisitions, and ten acquisitions were again averaged per well. Acquisitions with values of polydispersity over 30% were discarded.
Thermal melting experiments
Melting curves were done either in the absence or presence of cAMP or cGMP. The HCN4 protein was diluted to 50 μM, and the ligand to 500 μM (if any). Samples for the experiments were 50 μL in total, containing the protein, ligand, and 1× SYPRO Orange solution (Invitrogen, Waltham, MA, USA) according to the manufacturer's instructions. The samples were inserted and fluorescence was detected in a DNA Engine Opticon 2 Real-Time PCR machine (Bio-Rad, Hercules, CA, USA) with SYBR green filter. The dye fluoresced upon binding to hydrophobic residues, which were exposed during thermal denaturation. The temperature increased from 25 to 95°C at 0.5°C intervals, and each temperature was held for 15 s. The y axis of the melting curve was the normalized fluorescence, which is related to the fraction of unfolded protein. Negative control (dye in buffer) was subtracted from individual trials. Maximal fluorescence was obtained when the protein was completely unfolded, and it decreased when the dye dissociated from the protein. Residual signal could be due to the dye binding to aggregated protein. The inflection point on the melting curve corresponds to Tm (mid-unfolding temperature) and was alternatively determined with the first derivative (dRFU/dT) of the fluorescence intensities.
A model of the cAMP-induced depolarizing shift in the channel activation curve
The steady-state model developed here for the HCN4 channel is adapted from that which we used to examine cAMP-induced facilitation of the HCN2 channel (25). Here, we briefly describe the model and how it has been adapted for the HCN4 channel. This model uses the Boltzmann equation with a slope that is unaltered by cAMP, which was shown previously for both the wild-type and mutant HCN4 channels (18). For one active binding site, the model is described by the following diagram.
The open and shaded squares represent a site that is available or not for cAMP binding, respectively, while an open circle is a subunit that is bound by cAMP. The solid and open small circles in the center represent a channel that is closed and open, respectively. are the rate constants of channel opening and closing, respectively, when the channel is bound with cAMP molecules, where for the one binding site scheme and in the full model. are the association (binding) and dissociation (unbinding) rate constants, respectively, of cAMP bound to a channel in state . The superscript represents a channel in an open state () or a closed state ().
In the above scheme, on the right, a channel in open and closed state is represented, by and , respectively. The subscript is number of cAMP molecules bound to the channel and cAMP is represented by the letter .
The top two states exist only in the absence of cAMP and at steady state,
| (1) |
This comes from the Boltzmann expression of channel opening , where it is assumed that voltage is fixed at or (i.e., ) in the absence of cAMP and, therefore, . Square brackets represent the number of channels in each state. The differential equations that describe the time evolution of the four channel states satisfy the constraint = constant.
Cyclic AMP binding is assumed to be much faster than the change in structure associated with channel opening and closing, and therefore
| (2) |
Thus, the cAMP binding process is expected to reach a steady state relatively quickly and
| (3) |
where are the dissociation constants for the closed and open channels, respectively.
The numbers of channels in closed and open states, respectively, are,
| (4) |
Similarly,
| (5) |
Because is a constant, the differential equations governing the time evolution of yields the following fraction of open channels
| (6) |
where
| (7) |
are, respectively, the rate constants of channel opening and closing in the presence of cAMP at the dose of .
The Boltzmann expression of the HCN activation curve is:
| (8) |
where V is the test voltage (mV), Vh is the half-activation voltage (mV) and q is the slope factor (mV).
If is the shift of the activation curve induced by the addition of cAMP, then the shifted curve is described by
| (9) |
at ,
| (10) |
Therefore,
| (11) |
The following predictions can be made.
For ,
| (12) |
For ,
| (13) |
Therefore, if , , i.e., is necessary to produce a positive shift in the activation curve.
The model may be extended to the case where all four subunits are available for cAMP binding.
| (14) |
| (15) |
Above, the dissociation constants are defined as
| (16) |
We then may introduce the following dimensionless quantities
thus and
| (17) |
| (18) |
Notice that ≠ (αc)2 if ≠ . Thus, the powers in these expressions are not powers in the ordinary sense. We use these unusual definitions to make the long expressions appear simpler. However, when all of the binding constants ( and ) are identical, they become real powers. Therefore,
| (19) |
| (20) |
where . is the i-combination of a set of four, i.e., the number of distinct ways of picking i objects out of a set of four without repetition.
When , there is a shift as a function of cAMP concentration for channels with four active binding subunits:
| (21) |
It can be confirmed that, at , for all . In this case, .Whereas at , i.e., at saturating levels of cAMP,
| (22) |
The following,
| (23) |
measures the bias between the rate of channel opening and that of channel closing after the channel is bound to cAMP molecules.
In most known instances to date, for all . Also, .
Thus, binding of cAMP to the channel facilitates the opening of the channel. When more cAMP molecules are bound, the ratio between the opening rate and the closing rate is higher and a stronger bias toward channel opening exists. This bias is estimated quantitatively by the model.
To fit the HCN4 channel, we began with the parameters used for the HCN2 channel and used the binding data for the wild-type HCN4 C-terminal tetramer. We adjusted the closing rates of the bound channel relative to the closing rate of the unbound channel, mainly for the fourth site bound, while keeping K1 < K2 < K3 < K4.
This model assumes that the binding affinity of cAMP is the same for both the closed and open states of the HCN4 channel. In the experiments carried out measuring activity and the effect of cyclic nucleotides in excised patches, we consider the HCN4 channels to have reached a steady state and not a thermodynamic equilibrium. Therefore, we did not apply detailed balance to the model.
Results
Location of the S672R mutation in the HCN4 C-terminal region
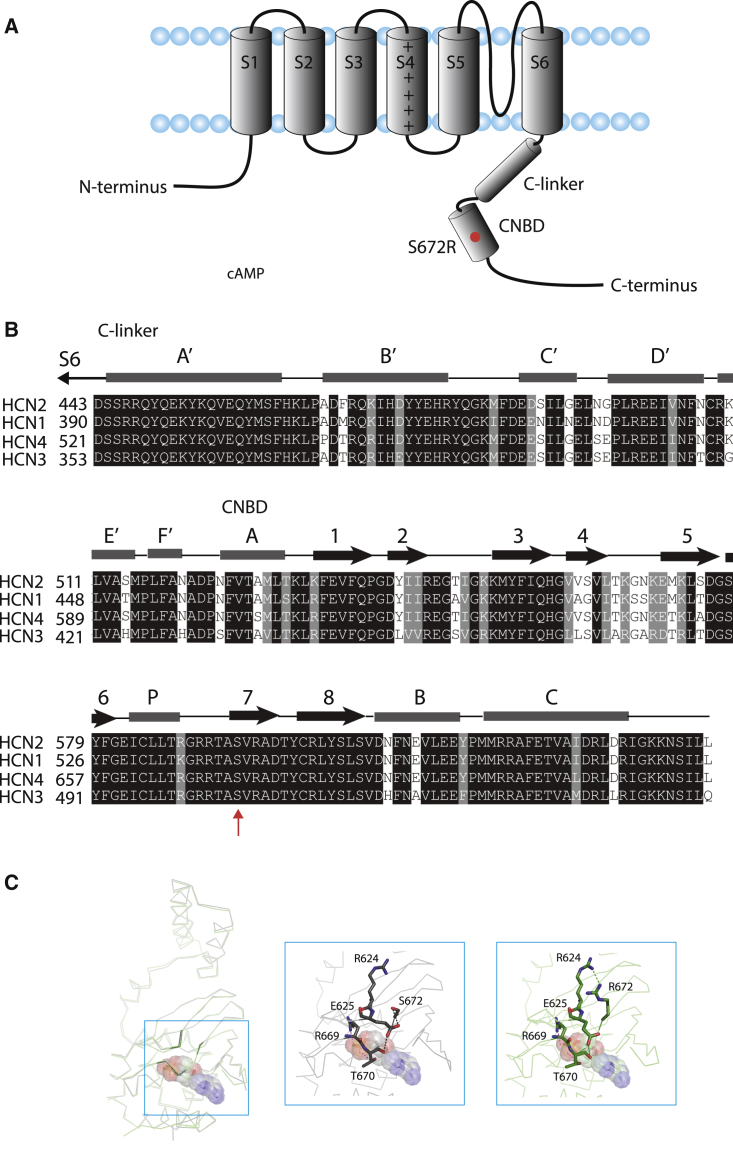
Alterations in the regions surrounding the ligand in the mutant structure suggest potential modifications to cAMP binding or to allosteric events that are downstream of ligand binding. Serine 672 is a highly conserved residue among HCN isoforms that is located in the seventh β sheet of the CNBD, which resides in the C-terminal cytoplasmic region of the HCN2 channel (Fig. 1, A and B). A previously solved structure of the HCN4 S672R C-terminal region showed that the structure of the region surrounding the residue is disrupted by the mutation (22) (Fig. 1 C). This part of the C-terminal region contains the CNBD and C-linker, which connects the CNBD to the pore. The mutant and wild-type structures are shown in this figure. Although not in direct contact with the ligand, residue 672 is near the ligand and close to other residues, e.g., two well-conserved residues, arginine 669 and threonine 670, which make contacts with the phosphate group of the cyclic nucleotide and are likely important for tight binding as seen in the HCN2 isoform (25,30,31). Other examples are the positions of two other residues, R624 and E625, which are modified as shown here, and the β4-β5 loop, which is disordered.
Figure 1.
Location of serine 672 in the HCN4 C-terminal region. (A) Cartoon of the HCN4 channel showing one of the four HCN subunits. Each contains six transmembrane segments (S1-S6), including voltage sensor (S4), along with the S5 and S6 segments that are proposed to form the ion conducting pore. The C-terminal end comprises the C-linker and the cyclic nucleotide-binding domain. The red dot shows the approximate location of the S672R mutation studied here. (B) Sequence alignment of the C-terminal region of the four mammalian HCN isoforms. Gray horizontal bars and black arrows represent α helices and β strands, respectively. Residues highlighted in black and dark gray represent those that are identical and conserved, respectively. The red arrow shows the serine residue that is mutated to arginine in the patients who exhibit bradycardia. (C) The fragment of HCN4 C-linker/CNBD (i.e., 521–739) of HCN4 co-crystallized with cAMP (PDB: 3OTF, dark gray) and represented with a stick backbone. On the left, this is overlaid with the same ligand but for the S672R mutant construct (PDB: 4HBN, light gray) after aligning the peptide main chain atoms. In both cases, cAMP is displayed with molecules as spheres. The middle and right structures are of the wild-type and mutant, respectively, and shows the location and alteration of specific residues and regions, and the overall differences between them more closely. To see this figure in color, go online.
The region of the HCN4 channel shown here is used for subsequent experiments (below).
Cyclic AMP and cGMP promote oligomerization of both the wild-type and mutant HCN4 C-linker/CNBD
Previously, oligomerization of the HCN2 C-linker/CNBD was found to occur as a function of its concentration and it was markedly promoted by cAMP binding (24,32,33). The promotion of oligomerization of this C-terminal region by cAMP binding led to the proposal that, in the full-length channel, cAMP promoted intersubunit interactions just below the pore facilitated opening (32). Using DLS, we previously found that an increase in oligomerization of this C-terminal region of HCN2 and HCN4 is dependent upon the concentration of the protein as well as the presence of cAMP (24). We found that molecules that promoted oligomerization of this C-terminal region of HCN2 were full agonists, whereas molecules that did not oligomerize this region acted as partial agonists (26).
Here, we compared the oligomeric nature of the wild-type and S672R HCN4 C-linker/CNBD, and the effect of cAMP and cGMP on its oligomerization using DLS. In the HCN2 channel, this region provides tonic inhibition to the pore which is relieved by the binding of cAMP and facilitates opening (34). We found that saturating concentrations of both cyclic nucleotides increased the estimated molecular weight of the C-terminal region for both the wild-type and mutant HCN4 channels (Fig. 2). The maximum value of the estimated molecular weight for both wild-type and mutant protein reflects the predominance of tetramers at the higher concentrations. Because we found that oligomerization by cAMP correlates with facilitation of opening in the HCN2 channel (26), our data are consistent with the original study showing that the maximum effect of cAMP on the HCN4 channel, a depolarizing shift of the activation curve of about 15 mV, was unaltered by the S672R mutation (18). We did not find that oligomerization as a function of protein concentration, and in the absence of cyclic nucleotide, was affected by the mutation.
Cyclic AMP and cGMP bind to the wild-type and mutant HCN4 C-terminal tetramer with negative cooperativity but with lower affinity to the mutant
To determine if the mutant HCN4 C-terminal region has altered ligand binding, ITC was used to measure and compare the binding affinity of cAMP to the C-terminal region between the wild-type and mutant HCN4 channel. As shown above, this region forms mainly a tetramer in solution when present in high concentrations (24). Using a high concentration of wild-type protein (200 μM), we found that cAMP produced a two-phase pattern in the binding isotherm that could be best fitted with a two-independent binding site model (Fig. 3 A); this yielded high- and low-affinity binding values of 0.06 and 0.69 μM, respectively (Fig. 3 B). We also noted that the stoichiometry of binding (N), which also arises from the fitting, is lower for the high-affinity binding event than for the low-affinity binding event. Thus, we suggest a ratio of 1:3 for cAMP binding to the high-affinity versus low-affinity sites. These results are similar to what we found for the HCN4 C-linker and CNBD previously (24).
Figure 3.
cAMP and cGMP bind to the mutant C-linker/CNBD with negative cooperativity but with lower binding affinity than to the wild-type. (A) Plots of heat produced upon progressive injections of cAMP and cGMP to 200 μM HCN4 C-terminal region, measured by ITC. The inflections in the top plot arise from injections of cNMP where each inverted peak shows the heat difference between the sample and reference compartment. The peaks decrease in magnitude as binding sites become saturated. The lower plot shows values determined by integration of the area under the peaks from the upper plot versus the ratio of injected ligand to protein. The solid line through the values represents a two-independent binding site model, which yielded values for affinity and thermodynamics. (B) Bar plot of dissociation constant (Kd) for the high- and low-affinity binding events for cAMP and cGMP. The values represent the mean ± SE. (C) A bar graph showing the changes in enthalpy, entropy and free energy upon binding of the wild-type and mutant HCN4 C-terminal region tetrameric protein to cAMP or cGMP. The values represent the mean ± SE. A significant difference between the wild-type and mutant values e free energy (ΔG) of cAMP and cGMP binding is represented by two stars (∗∗) and one star (∗), respectively, for both high- and low-affinity binding events.
For the mutant C-terminal protein, cAMP also produced a two-phase binding pattern with negative cooperativity, but lower values for binding affinity were obtained; 0.53 and 5.05 μM for the high- and low-binding affinities, respectively. The biphasic pattern is apparent because the release of heat for each of two binding events differs in magnitude and saturates over separate ranges of cyclic nucleotide concentration. For both the high- and low-affinity binding of cAMP, the decrease in affinity produced by the mutation is about sixfold (Fig. 3 B).
We next examined cGMP binding to the wild-type and mutant HCN4 channel C-terminal tetramer. For cGMP binding to wild-type HCN4, a two-phase pattern in the binding isotherm was again best fitted with a two-independent binding site model (Fig. 3 A); this yielded high- and low-affinity binding Kd values of 0.16 and 1.74 μM, respectively. These Kd values for cGMP binding in the wild-type HCN4 channel suggest that this molecule may be an important facilitator of HCN4 opening in vivo. For the mutant C-terminal region, cGMP also produced a two-phase binding pattern with negative cooperativity, but higher Kd values, 0.88 and 9.95 μM (Fig. 3 B; Table 1). These data suggest that a reduction of cGMP binding to the HCN4 channel may also contribute to the resting bradycardia in patients carrying the S672R HCN4 mutation.
Table 1.
Values obtained from binding and stability experiments
| Isothermal titration calorimetry |
Low affinity |
Thermofluor |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High affinity |
|||||||||||||
| Kd (μM) | ΔH (kcal/mol) | –TΔS (kcal/mol) | ΔG (kcal/mol) | N | Kd (μM) | ΔH (kcal/mol) | –TΔS (kcal/mol) | ΔG (kcal/mol) | N | n | Tm (°C) | n | |
| Wild-type apo | 39.56 ± 0.21 | 12 | |||||||||||
| Wild-type + cAMP | 0.06 ± 0.02 | −7.64 ± 0.66 | −2.36 ± 0.66 | −10.00 ± 0.17 | 0.11 ± 0.006 | 0.69 ± 0.10 | −14.30 ± 0.86 | 5.86 ± 0.78 | −8.44 ± 0.09 | 0.60 ± 0.01 | 7 | 39.26 ± 0.20 | 12 |
| Wild-type + cGMP | 0.16 ± 0.02 | −4.94 ± 0.61 | −4.35 ± 0.61 | −9.29 ± 0.05 | 0.11 ± 0.01 | 1.74 ± 0.23 | −13.64 ± 1.38 | 5.75 ± 1.35 | −7.89 ± 0.07 | 0.64 ± 0.02 | 6 | 38.95 ± 0.22 | 12 |
| S672R apo | 39.21 ± 0.22 | 12 | |||||||||||
| S672R + cAMP | 0.53 ± 0.10 | −3.83 ± 0.99 | −4.81 ± 0.90 | −8.64 ± 0.12 | 0.15 ± 0.003 | 5.05 ± 0.56 | −16.60 ± 0.60 | 9.34 ± 0.61 | −7.25 ± 0.07 | 0.85 ± 0.02 | 8 | 39.70 ± 0.23 | 12 |
| S672R + cGMP | 0.88 ± 0.27 | −4.55 ± 0.59 | −3.81 ± 0.59 | −8.36 ± 0.18 | 0.18 ± 0.003 | 9.95 ± 0.58 | −19.03 ± −2.85 | 12.19 ± 2.85 | −6.83 ± 0.04 | 0.85 ± 0.07 | 5 | 39.38 ± 0.19 | 12 |
The table summarizes the dissociation constants (Kd) in μM for comparison of the wild-type and mutant S672R, which were obtained by ITC. The stoichiometry of the interaction (N) and the associated thermodynamic parameters (ΔG, ΔH, and TΔS) obtained by fitting are also shown here. For ITC and thermofluor experiments, the number of replicates is represented by “n” and, for the latter, the melting temperature is represented by Tm. The values represent the mean ± s.e.m.
The thermodynamics of the interaction of cAMP and cGMP with the wild-type and mutant channel were also determined from the measurements of heat by ITC (Fig. 3 C). Here, the low-affinity binding of cAMP to both the wild-type and mutant HCN4 C-terminal tetramer was associated with favorable enthalpy and unfavorable entropy, whereas both were favorable for the high-affinity binding event. This pattern is similar to what we found previously for cAMP binding to the wild-type HCN2 and HCN4 C-terminal region (24) and to what we found for cGMP binding to this region of HCN2 (26).
A comparison of cAMP and cGMP binding to the wild-type HCN4 C-terminal tetramer shows differences. For high-affinity binding, the change in favorable enthalpy was smaller for cGMP than for cAMP but the change in favorable entropy was larger for the former. The resulting change in free energy of binding was less for cGMP than for cAMP. The mutation reduced the favorable change in enthalpy and increased the favorable change in entropy for cAMP binding but, overall, reduced the free energy of binding. By contrast, the mutation did not have an effect on the change in enthalpy for cGMP binding, but reduced the favorable change in entropy; thus, the free energy of binding was reduced. The difference between cAMP and cGMP high-affinity binding may be due to the difference in configuration when bound, as observed in the solved HCN4 C-terminal structures; cAMP binds in the anti-configuration, whereas cGMP binds in the syn-configuration (33,35,36).
For low-affinity binding to the wild-type, the favorable change in enthalpy and unfavorable change in entropy were a bit smaller for cGMP, which resulted in a smaller free energy of binding compared with cAMP. The mutation had similar effects on cAMP and cGMP low-affinity binding; it increased the favorable change in enthalpy but increased the unfavorable change in entropy, which reduced the free energy of binding compared with the wild-type fragment.
The thermal stability is similar between the wild-type and mutant HCN4 C-linker/CNBD and between the ligand-bound and unbound forms of this region
Thermal melting experiments were performed to determine and compare the mid-unfolding temperature between the wild-type and S672R C-terminal proteins. We found that thermal stability was similar between the wild-type and mutant C-linker/CNBD; unfolding temperatures Tm, which were determined from the inflection points, were ∼39°C for both constructs (Fig. 4). Furthermore, the addition of either cAMP or cGMP did not greatly alter the unfolding. Different concentration ratios of proteins to ligands were examined, but the temperature was always in the same range regardless of the combination. These data suggest that the mutation, and ligand binding, do not greatly impact the thermal stability of the protein.
Figure 4.
The mutant and wild-type HCN4 C-termini have similar thermal stability, which is not greatly altered by cAMP and cGMP. Plots of normalized fluorescence versus temperature. The melting curve is sigmoidal and is correlated to the fraction of unfolded protein. The mid-unfolding temperature (Tm) is determined at the inflection point; the values are included in Table 1. Wild-type data are presented in squares and mutant data in circles; open symbols represent protein in apo condition, while solid black or gray symbols are proteins bound with saturating cAMP or cGMP, respectively. The Tm is not largely changed by the mutation or by adding ligand.
A mathematical model suggests that the mutation promotes opening of the HCN4 channels bound to cAMP
We next used a mathematical model to determine how the mutation might affect the facilitation of HCN4 opening by cAMP. The model was developed initially for the HCN2 channel by our group (25) and is also discussed in greater detail in the Methods sections of this paper. In brief, the model is made up of ten states that represent the tetrameric HCN4 channel in the closed and open state either without cAMP or bound by one to four molecules of ligand (Fig. 5 A). This model uses the dissociation constants determined by ITC from cAMP binding to the HCN4 C-terminal tetramer.
Figure 5.
The S672R mutation promotes opening of the liganded HCN4 channel. (A) A diagram of the model used for the facilitation of channel opening by cAMP binding to the HCN4 channel. The closed and open states are on the left (solid center circles) and right (open center circles), respectively. (B) Plots of the shift in the HCN4 channel activation curve versus the concentration of cAMP. The individual data points represent data published previously (18), which were obtained by patch-clamp electrophysiology, for the wild-type (solid blue squares) and mutant (solid red circles) HCN4 channel, which were overexpressed in HEK cells by transient transfection. The solid green line is the theoretical fit to the experimental shifts in current activation for the wild-type HCN4 channel, using values for cAMP binding to the wild-type C-terminal region and values for the closed to open rates that were adjusted to fit the wild-type experimental data points. The solid red line is the theoretical curve using values for binding that were determined for the mutant C-terminal region and using the rates for the gating transitions that were determined from the wild-type fit. The solid purple line represents the theoretical fit to the experimental shifts in current activation for the mutant channel using the values for binding of cAMP to the mutant C-terminal region and rate values for the gating transitions that were adjusted to fit the mutant experimental data points. The solid blue line represents the theoretical curve using the wild-type values of cAMP binding but the gating transition parameters obtained from the fit to the mutant data. The two sets of values of the parameters of the model for this set of four curves are shown in Table 2. (C) Plots of the shift in the mHCN2-h4 channel activation curve versus the concentration of cAMP. The individual data points represent data published previously, which were obtained by patch-clamp electrophysiology, for the wild-type (solid blue squares) and mutant (solid red circles) HCN4 channel, which were injected in Xenopus oocytes. The solid green line is the theoretical fit to the experimental shifts in current activation for the mHCN2-h4 channel, using values for cAMP binding to the wild-type C-terminal region and values for the closed to open rates that were adjusted to fit the wild-type experimental data points. The solid red line is the theoretical curve using values for binding that were determined for the mutant HCN4 C-terminal region and using the rates for the gating transitions that were determined from mHCN2-h4 fit. The solid purple line represents the theoretical fit to the experimental shifts in current activation for the mutant mHCN2-h4 channel using the values for binding of cAMP to the mutant C-terminal region and rate values for the gating transitions that were adjusted to fit the mutant experimental data points. The two sets of values of the parameters of the model for this set of four curves are shown in Table 3. The green dash-dotted line is the theoretical curve for the wild-type HCN4 channel redrawn here for direct comparison. Note the smaller maximum effect and reduced slope of the concentration response curve for the wild-type HCN4 channel. To see this figure in color, go online.
We originally developed the model (25) for the HCN2 channel that possessed one, two, three, or four functional binding sites for which data describing the relationship between concentration and depolarizing shift in the activation curve were available (30). Because we used binding affinities obtained by ITC, we carried out the fitting in a less conventional way.
We first fit the model to the shift versus cAMP concentration data that were obtained from a HCN2 channel with one binding site. We used the high-affinity value obtained by ITC. The equilibrium constant for opening and closing of the ligand-bound channel (K1) was constrained by the maximum effect of cAMP binding on the shift of the activation curve. To fit the data, the closing rate of the single-site channel, bound to one molecule of cAMP, was adjusted relative to the closing rate of the unbound channel.
We next used the model to fit the shift versus cAMP concentration data that were obtained for the HCN2 channel containing two functional sites. The closing rate for the channel with one ligand bound was already determined (above) and the closing rate for the second site channel was adjusted relative to the closing rate of the unbound channel to fit the shift versus cAMP concentration data for a HCN2 channel with two functional sites. In this case, the low binding affinity value was used. Here, too, the equilibrium constant (K2) for opening and closing of the doubly bound channel was constrained by the maximum effect of cAMP binding to the two-site channel. However, the maximum effect of cAMP for the HCN2 channel with one binding site was smaller than for the HCN2 channel with two sites; therefore, K2 > K1. The opening and closing rates for the second site were then fixed and the data were fit using the model in the same way as for the HCN2 channel with three functional sites. The entire process was then repeated for the last time to fit the shift versus concentration data for the channel with four functional sites. The equilibrium constants (K3 and then K4) were constrained by the maximum effect of cAMP for the channel with three and four functional sites, respectively. Thus, the relative values for the equilibrium constants for opening were K4 > K3 > K2 > K1. The low binding affinity for cAMP was used for the third and fourth site, as for the second site. The one high-affinity site and three low-affinity sites in the model arises from the stoichiometry of cAMP binding to the HCN2 C-terminal tetramer in the ITC experiments.
The model predicted the effects of a subset of mutations in the CNBD of the HCN2 channel on the relation between the concentration of cAMP and the depolarizing shift in the activation curve. The mutations were notable in that they did not affect the gating of the channel in the absence of ligand and, because the model predicted the concentration response relations using ITC-determined values of Kd, they appeared to impact mainly the binding affinity of cAMP and not the opening and closing of the liganded channel. The model also suggested that the difference in potency between cAMP and cGMP, both of which produce a similar maximum effect, was due to differences in their effects on the opening and closing of the HCN2 channel as well as to differences between them in binding affinity.
Here, we use the model to estimate the difference in how binding and gating contribute to the actions of cAMP between the mutant and wild-type HCN4 channel.
In Fig. 5 B, the model is first used to fit concentration response data for the wild-type HCN4 channels (solid blue squares), which were obtained from patches excised from HEK cells that were transiently transfected with the HCN4 channel and measured using patch-clamp electrophysiology (18). The fitting was carried out by adjusting the closing rates of the bound channel relative to the unbound channel. We used the values of cAMP binding to the tetrameric HCN4 C-terminal region, which were determined by ITC (Fig. 3; Table 1). Importantly, we assumed that the values for binding affinity determined by ITC approximate those that occur under steady-state measurements of channel activity in the excised patch experiments. The high-affinity value was used for binding of cAMP to the first site and the low-affinity value was used for the binding of cAMP to the second, third, and fourth sites. This comes from the stoichiometry of the interaction that was obtained by ITC, which suggests that one site binds with high affinity and three sites bind with low affinity. The value for q (the slope factor from the Boltzmann equation) was set at 8.7 mV for the wild-type and mutant channel, which was obtained from the original study of the S672R mutation for the experimental data that were fit here (18). This slope factor is a determinant of the maximum shift produced by cAMP or cGMP in our model (see Methods). We also assumed that this value of q was not affected by cyclic nucleotide binding. By adjusting the closed to open transitions, we were able to fit the wild-type data using the experimentally determined binding values (Fig. 5 B, green solid line; Table 2).
Table 2.
Parameters of the mathematical model used to simulate concentration response data for the HCN4 channel expressed in HEK cells
| cAMP | Wild-type | S672R |
|---|---|---|
| q | 8.7 | 8.7 |
| Kd site 1 | 0.06 |
0.53 |
| Kd site 2 | 0.69 | 5.05 |
| Kd site 3 | 0.69 | 5.05 |
| Kd site 4 | 0.69 | 5.05 |
| k0c | 1 | 2.85 |
| K0 | 1 | 0.35 |
| 0.05 | 2 | |
| K1 | 1.11 | 1.11 |
| 0.07 | 0.8 | |
| K2 | 1.5 | 1.5 |
| 0.07 | 14 | |
| K3 | 1.7 | 1.7 |
| 0.03 | 100 | |
| K4 | 3.08 | 3.08 |
The table summarizes the sets of parameters of the mathematical model used for data and curves shown in Fig. 5B, showing the concentration of cAMP versus the depolarizing shift of the activation curve. The units of “q” are in mV, Kd values are in μM, while k and K are dimensionless. The value for q comes from the experimental data which were fit with the Boltzmann relation in (18).
To assess the effect of the mutation on the channel, we first substituted the values for the mutant channel binding affinity into the model without altering the wild-type values for the closed to open transitions of the channel bound to cAMP or other parameters. We did adjust the transition between the closed and open channel in the absence of cAMP because the original functional studies showed that, without ligand, the range of activation and opening was shifted to more negative potentials by ∼9 mV, with no change in slope (18). The theoretical concentration response curve generated by the model (Fig. 5 B, red solid line) is shifted well to the right of the mutant channel experimental data (solid red circles) as well as the wild-type data. This suggests that the mutation may alter the opening and closing rates of the ligand-bound channel as well as reducing the binding affinity of the channel for cAMP.
Based on the above findings, we next adjusted the closed to open transitions, but still using the mutant binding affinities, to fit the mutant concentration response data. The mutant data are well fitted by these adjustments (Fig. 5 B, purple solid line; Table 2), which suggests, perhaps surprisingly, that the mutation promotes opening from the bound closed states even though it reduces the binding affinity of the channel for cAMP and inhibits the opening of the channel in the absence of cAMP. This result provides a possible explanation for the similarity in the range of concentrations over which cAMP promotes opening between the mutant and wild-type channels. Nevertheless, it is notable that the two concentration response relations are not identical but differ in steepness. In particular, the mutant channel relation is steeper and, at 0.3 μM, the value for the shift is twice as large for the wild-type channel as it is for the mutant channel (18). The smaller effect at lower concentrations of cAMP fits with the larger high-affinity value for Kd, which was measured for the mutant channel by ITC.
Next, we utilized the wild-type binding values in the mathematical model with the mutant gating parameters. This produced a concentration response curve (Fig. 5 B, blue line; Table 2) that was left shifted compared with the experimental data for the wild-type and mutant channels as well as to the theoretical relations fitted to those data (Fig. 5 B, green and purple lines). Notably, this curve was left shifted by an absolute amount that is similar to the right shift of the theoretical relation, which was determined using the wild-type gating parameters and the mutant binding affinities (Fig. 5 B, red line; Table 2). These two curves (the red and blue lines) help to visualize how both binding affinity and gating transitions contribute to the position of the cAMP concentration response relation in the HCN4 channel, without altering the maximum shift produced by this ligand.
The curves using the mutant gating parameters (blue and purple) are steeper than those using the wild-type gating parameters (green and red), which suggests that the mutation has a larger effect on the gating parameters at the higher concentrations of cAMP. This is borne out by the values of in Table 2, which show that they are larger than those for the wild-type channel, and larger for the third and fourth binding sites than for the first and second binding sites.
The equilibrium constants were not different between the mutant and wild-type gating parameters. Thus, the model predicts that the maximum effect of cAMP on HCN4 channels with one, two, or three binding sites would be the same. The model also predicts that the differences in the concentration response relations between the wild-type and mutant channels are due to differences in the relative rates of closing and opening of the HCN4 channels bound to cAMP.
A mathematical model suggests that the mutation inhibits the opening of an HCN2 channel containing the C-linker and CNBD of the HCN4 channels bound to cAMP
We next used the model to fit concentration response data for mouse HCN2 channels that have the HCN4 C-linker and CNBD (mHCN2-h4) (22,35). These data were obtained from patches excised from Xenopus oocytes that were injected with the mHCN2-h4 channel and measured using patch-clamp electrophysiology. The values of cAMP binding to the tetrameric HCN4 C-terminal region, which were determined by ITC, were utilized in the same way as for the HCN4 channel data (Fig. 3; Table 1). By adjusting the closed to open transitions, as well as the equilibrium constants for the opening of the bound channel, we were able to fit the data for the chimera (purple squares) using the experimentally determined binding values (Fig. 5 C, green line; Table 3). The equilibrium constants for the opening and closing of the channel bound to cAMP were also adjusted because of the larger maximum cAMP-induced shift in the activation curve when all four sites were occupied, which was obtained by experiment.
Table 3.
Parameters of the mathematical model used to simulate concentration response data for the HCN2-h4 channel expressed in Xenopus oocytes
| cAMP | Zhou_JBC mHNC2-H4 | Zhou_Cell S672R |
|---|---|---|
| q | 8.7 | 8.7 |
| Kd site 1 | 0.06 | 0.53 |
| Kd site 2 | 0.69 | 5.05 |
| Kd site 3 | 0.69 | 5.05 |
| Kd site 4 | 0.69 | 5.05 |
| k0c | 1 | 2.85 |
| K0 | 1 | 0.35 |
| 2 | 2 | |
| K1 | 1.1 | 1.05 |
| 0.8 | 1.5 | |
| K2 | 1.5 | 2 |
| 8 | 0.3 | |
| K3 | 3 | 4 |
| 100 | 1 | |
| K4 | 6 | 10 |
The table summarizes the sets of parameters of the mathematical model used for the curves in Fig. 5C, showing the concentration of cAMP versus the depolarizing shift of the activation curve. The units of “q” are in mV, Kd values are in μM, while k and K are dimensionless. Because the values of q were not available for the chimera, we used the same value for q as for the full-length HCN4 channel from (18).
To assess the effect of the mutation on the mHCN2-h4 channel, the values for the mutant channel binding affinity were substituted into the model without altering the wild-type mHCN2-h4 values for the closed to open transitions of the channel bound to cAMP. Here, as above, the transition between the closed and open channel in the absence of cAMP was also considered because the range of activation and opening was shifted to more negative potentials by ∼ 6 mV. The theoretical concentration response curve is shifted to the right of the wild-type channel data (Fig. 5 C, red line) but not as far to the right as the experimental data for the mutant (red solid circles). To fit those data, further adjustments to the closed to open transitions, which inhibit opening, were necessary to fit the mutant data (Fig. 5 C, purple line). Together, these changes suggest that the mutation may alter the opening and closing rates of the ligand-bound mHCN2-h4 channel as well as the binding affinity for cAMP as for the human HCN4 channel. However, the effect of the mutation is opposite in the two types of channels; it inhibits the opening of the ligand-bound mHCN2-h4 channel, when expressed in Xenopus oocytes, and promotes opening of the ligand-bound human HCN4 channel, when expressed in HEK cells. This can be seen in the values of and in Table 2, which are smaller for the mutant channel than for the wild-type channel.
The height of the mHCN2-h4 mutant data and curve is also higher than that for the mHCN2-h4 data and curve, by about 5 mV. In the model, we simulated this by increasing the equilibrium constants of opening and closing of the bound channel (K1-4). This also suggests an effect of the mutation on gating.
Fig. 5C also shows the theoretical concentration response curve for the wild-type human HCN4 channel (green dash-dotted line), which is the green line in Fig. 5 B. This line does not reach the same height as the mouse HCN2-h4 line (green line), indicating a smaller maximum effect of cAMP; it is also less steep and shifted to larger concentrations of cAMP. According to the model, these differences can be explained by differences in the rate and equilibrium constants between the open and closed states of the ligand-bound channel. The differences between the curves for the human HCN4 and mHCN2-h4, together with the difference in the effect of the mutation on these two HCN channels, suggest that the transmembrane domains or the expression system (oocytes versus mammalian cells) influence the cAMP-induced shift in the activation curve and the interaction of cAMP with the binding site.
Discussion
A previous study (18) identified a mutation in the CNBD of the HCN4 channel, S672R, which was associated with bradycardia in an Italian family. In that study, this mutation caused a hyperpolarizing shift in the activation curve of the channel without greatly affecting the potency or maximum effect of cAMP. It was proposed that the hyperpolarizing shift of the activation curve would lessen the contribution of the funny current to the sinoatrial pacemaker, which results in bradycardia. A subsequent study (22) suggested that the mutation reduced the binding affinity and potency of cAMP. However, the lower potency was observed in a chimera of mouse HCN2 and human HCN4, whereas potency was not greatly affected when wild-type and mutant HCN4 channels were expressed in HEK cells and the cAMP concentration response curves were compared in the original study (18). Furthermore, it was suggested that the large reduction in potency observed in the HCN2-HCN4 chimera would result in chronotropic incompetence, a feature that was not observed in those patients with bradycardia (23).
To address the apparent discrepancy of previous results on the S672R mutant HCN4 channel, and to understand its effects in the context of negatively cooperative binding of cAMP, we carried out binding on a tetrameric HCN4 C-terminal region and applied a mathematical model of cAMP-induced facilitation of channel opening. We found that cAMP and cGMP bind to both the wild-type and mutant tetrameric HCN4 C-terminal regions with negative cooperativity, as we found previously for cAMP binding to the wild-type HCN4 as well as for the binding of cGMP and cAMP to the corresponding HCN2 channel region (24,26). We also found that the high- and low-binding affinity of both cAMP and cGMP for the tetrameric HCN4 C-terminal region is reduced by the S672R mutation by about sixfold. A reduction in binding affinity is not surprising given the location of the residue, which is a region that engulfs the nucleobase (adenine or guanine) and is also near the phosphate-binding cassette, which binds strongly to the phosphate group of the cyclic nucleotide. A previous study that solved the structure of the HCN4 S672R C-terminal region showed that the structure of the protein surrounding the residue is disrupted by the mutation (22) (see Fig. 1).
To determine how the mutation affects the response of the channel to cAMP, we applied a mathematical model for HCN4 channel opening, using the concentration response relations which were determined previously for the human channel expressed in HEK cells (18). We show that the model, which incorporates negatively cooperative binding, fits the concentration response for the wild-type HCN4 channel. By substituting cAMP binding affinities of the mutant HCN4 channel, but using the values for closed to open transition rates determined for the wild-type, the curve is shifted to the right and does not fit the concentration response data for the mutant channel. To fit the mutant data, the closed to open transition rates were adjusted in a manner that suggests that the mutation promotes opening when cAMP is bound to a greater extent than in the wild-type channel. Thus, the concentration response data for the wild-type and mutant channels span a similar range of cAMP concentrations. An effect of the mutation on how the channel opens and closes when bound to cAMP suggests a role for this residue in transmitting and transducing information from the C-terminal ligand binding region to the pore. Such a role is also supported by the effect of the mutation on opening in the absence of ligand, although it inhibits, rather than promotes, opening of the pore when cAMP is not bound.
Interestingly, the fitted curve for the mutant channel is steeper and the effect of cAMP on the shift in channel activation at 0.3 μM is approximately twice as large in the wild-type channel compared with the mutant. This difference could alter the contribution of the HCN4 channel to pacemaking but more detailed analysis and modeling would be required to determine how action potential firing might be affected. We also applied the mathematical model to a second set of data, namely concentration response relations that were determined from a chimeric HCN channel, mHCN2-h4 (22,35). This channel is made up of the mouse HCN2 channel N-terminal region, including the transmembrane domains, and the mouse HCN4 C-terminal regions, consisting of the C-linker and CNBD. This chimera was expressed in Xenopus oocytes, either with or without this bradycardia-associated mutation in the CNBD, and the effect of cAMP on the activation curve was determined from excised patches by patch-clamp electrophysiology.
The mathematical model was fitted to the mHCN2-h4 channel data using the binding affinities that were determined for the wild-type HCN4 C-linker and CNBD and by adjusting the gating parameters. Substitution of the mutant binding affinities, but keeping the values for closed to open transition rates determined for the mHCN2-h4 channel, resulted in a curve that is shifted to larger concentrations of cAMP. However, this curve, again, does not fit the experimental data for the mutant mHCN4-h4 channel. But, in this case, the closed to open transition rates were adjusted in a manner that suggests that the mutation inhibits opening when cAMP is bound. This is the opposite effect of the mutation on cAMP-induced facilitation of opening compared with its action on the human HCN4 channel expressed in HEK cells.
There are also other differences in the action of cAMP on these two channels without the mutation. The maximum effect of cAMP is larger, and the concentration response relation is steeper, for the mHCN2-h4 channel than for the human HCN4 channel. Our model suggests that these differences are also linked to the actions of cAMP on gating. Thus, it may not be surprising that the effects of the mutation are different between the two channels although the underlying mechanism is not clear. Nevertheless, in both cases, the effects of the mutation suggest a role for this residue in connecting the binding of cAMP with the opening of the pore. Also, the mutation shifts the activation curve to more negative voltages in a way that is independent of cAMP in the human HCN4 channel and this is probably true for the mHCN2-h4 channel. More studies, where the two channels are examined side-by-side in the same expression system, will be required to compare the actions of cAMP and to determine if these differences might be attributed to the interaction of the C-linker and CNBD with the transmembrane domains or if the difference is due to the expression system.
Both the isoform and expression system are thought to influence the opening and closing of HCN channels. For example, the position of the If activation curve is more positive when the HCN2 and HCN4 isoforms are expressed in neonatal ventricular myocytes compared with HEK cells (37). Those authors also showed that the position of the activation curve is more positive for HCN4 compared with HCN2 in both cardiomyocytes and HEK cells, evidence that the structure of the isoform is also important. Findings from various labs have suggested that the effect of cAMP on a given HCN isoform may or may not depend on the expression system and recording conditions. For example, the maximum shift in the activation curve of about ∼18 vs. ∼19 mV, and a potency for the shift in the mid-point of about 0.1 and 0.07 μM, were found when measured in patches excised from HCN2-expressing Xenopus oocytes and HEK cells, respectively (31,38). Notably, in these two studies, cAMP increased the amplitude of current as well shifting the activation curve to less-negative voltages, which may be a characteristic of the HCN2 channel but not of the other isoforms. By contrast, cAMP, delivered at 1 mM via the pipette solution in the whole-cell configuration or at 100 μM applied directly in excised patches, shifted the activation curve by about 17 and 11 mV, respectively, when measured in HCN4-expressing HEK cells but it had no effect when applied in the same ways to HCN4-expressing CHO cells (39). A strong effect on the activation curve was also observed when cAMP was applied to HCN2-expressing CHO cells, which was comparable with its effect on HCN4-expressing HEK cells. The absence of an effect of cAMP on the HCN4 isoform expressed in CHO cells may be due to isoform-specific interactions with proteins expressed in one cell type but not another (40).
The influence of the C-linker and more distal regions of the C-terminus on the maximum effect of cAMP has been studied (34,41,42), but transmembrane and N-terminal domains may also play a role. The data we modeled here showing the difference in effect of cAMP on the HCN2-h4 chimeric channel and the HCN2 channel when measured in patches excised from Xenopus oocytes (35) suggest that the interaction of the C-linker and CNBD with the transmembrane domain may be important. Using a HCN2 channel with a HCN4 transmembrane domain, it was shown that the position of the activation curve without influence from cAMP is more negative than the wild-type HCN2 channel (43). Thus, both the degree of autoinhibition of opening and its relief by cAMP may be regulated by transmembrane domains. An interaction of the voltage-sensing regions with the C-terminus has also been proposed based on signals from a fluorescent analog of cAMP when bound to the HCN2 channel, which occur before current onset during a hyperpolarizing pulse delivered by patch-clamp electrophysiology (44).
Reports of recent structures (solved by cryoelectron microscopy) and functional data have identified two novel regions that may control the maximum effect of cAMP in an HCN isoform-specific manner. The HCN domain is a region in the N-terminus, just before the first transmembrane domain, and was originally shown to be critical for functional expression of the HCN2 channel in mammalian cells (45,46). This region, consisting of three helices, makes contacts with voltage-sensing transmembrane regions and the C-linker and contributes to both voltage-dependent and cyclic nucleotide-dependent gating (47, 48, 49, 50). Specific interaction of the HCN domain with residues in the A′ and B′ helices were found to regulate the maximum effect of cAMP in HCN1, HCN2, and HCN4 isoforms, as well as the potency of this ligand on the HCN2 channel. The HCN domain, like the voltage-sensing region and C-linker/CNBD, is not conserved between isoforms and, thus, it may contribute to gating differently between them. A second region that may control the effect of cAMP is formed by residues in the S4-S5 linker and B′ helix of the C-linker and, together, may coordinate a magnesium ion in the HCN4 channel but not in the HCN1 channel (50). Mutation of certain residues abolishes the effect of cAMP in the HCN4 channel but not the HCN1 channel, while removal of magnesium appears to abolish the effect of cAMP in HCN4 but not in HCN1 or HCN2. Thus, this ion coordination site, which connects the transmembrane regions and the C-linker/CNBD, may provide a contribution to cAMP action that is unique to the HCN4 channel isoform. Notably, another residue in the A′ helix of the HCN4 channel has also been shown to control cAMP potency (20), while a residue triplet located in the A′ helix can reverse the effect of cAMP on the HCN2 channel (51). Together, the findings suggest that a mutation, such as S672R in the CNBD, which affects both binding and gating, could produce variable, or even opposite, effects that depend on the sequence of the N-terminus and transmembrane domains, including the HCN domain and tetrad formed by the S4-S5 linker and proximal C-linker.
The different effect of the S642R mutation on the potency and maximum shift of cAMP between the HCN4 channel in HEK cells and the HCN2-h4 chimera in Xenopus oocytes could be further examined by keeping in mind the possible roles of isoform structure and expression system. For example, by expressing the HCN2-h4 channel in HEK cells, it would be possible to compare the effects of the S672R mutation on the action of cAMP between this chimera and the HCN4 channel. If the potency and maximum effect of cAMP on the HCN2-h4 channel were also unchanged by the mutation, then it is probable that the reduction of potency and increase in maximum effect observed by Xu et al. in this chimera were due to its expression in Xenopus oocytes. If, however, the potency of cAMP was reduced and the maximum effect increased by the mutation on the chimera in HEK cells, as it was in Xenopus oocytes, then further experiments could be undertaken in HEK cells to understand what specific differences in the N-terminus and transmembrane regions between HCN2 and HCN4 channels were responsible for the different effects of cAMP on the wild-type HCN4 and the HCN2-h4 chimera. To understand the roles of regions outside of the C-linker and CNBD on regulation by cAMP and the effect of mutations, it would be helpful to carry out experiments that can account for the expression system and experimental conditions where possible.
Our model was originally developed using the HCN2 channel (25). The rates of opening and closing were determined using concentration response data for channels containing one, two, three, or four binding sites (30). The equilibrium constant for each of the four binding sites was also determined using concentration response data for HCN2 channels containing one, two, three, or four binding sites. Importantly, the math model was able to predict the concentration response curves for single alanine substitutions that were shifted to higher concentrations of cAMP. These substitutions reduced the binding affinity as determined by ITC and, in the absence of ligand, had no effect on gating. Thus, the cAMP-induced shift in the activation curve could be explained, and predicted, by reduced binding affinity only.
Here, we have determined theoretical values for the equilibrium constant, and rates of opening and closing, for HCN4 channels with one, two, or three of sites bound with cAMP. These numbers offer predictions that can be tested in the future by determining the concentration response relation for mutant HCN4 channels containing one, two, or three binding sites. The mutation studied here in HCN4 differs from the alanine mutations studied in the HCN2 channel in that it causes a shift in the activation curve in the absence of ligand. Hence, it is perhaps not surprising that this mutation may have a direct effect on cAMP gating as well as an effect on its binding. The nature of how gating is modified by the mutation, and the role of the wild-type residue in gating, remains to be determined.
The Kd values for cGMP binding in the wild-type HCN4 channel are approximately 0.16 and 1.74 μM for the high- and low-affinity binding events, respectively (Fig. 3; Table 1). These values suggest that cGMP is an important modulator of the channel in the human SAN under normal conditions in vivo. The binding affinity of cGMP is a bit weaker than that for cAMP (with Kd values = 0.06 and 0.69 μM for the high and low binding events, respectively), which might make it difficult for the former to compete for the binding site when cAMP levels are high. However, cGMP may be elevated in pacemaker cells when cAMP is scarce and it could help to prevent excessive bradycardia under these conditions, e.g., at rest where vagal tone is dominant and acetylcholine levels are elevated (52, 53, 54). Cholinergic stimulation in sinoatrial pacemaker cells has been shown to increase HCN activity via nitric oxide formation (55).
Our study also shows that the S672R mutation reduces the binding affinity of cGMP for the HCN4 channel. Given the potential role of cGMP in facilitating wild-type HCN4 opening in vivo, as mentioned above, it seems reasonable to suggest that the reduced ability of the mutant channel to bind cGMP may contribute to reduced channel activity and bradycardia under resting conditions in patients carrying the S672R HCN4 mutation. It would be interesting, in the future, to determine the concentration response relation for the effect of cGMP on the HCN4 channel expressed in different systems.
The data in this study support an asymmetric functional and structural model for the facilitation of the HCN4 channel, which we recently proposed also for the HCN2 channel (25). In this model, the initial binding of cAMP and cGMP occurs with a distinct thermodynamic signature (24,26), which was also observed here for both ligands and for both the mutant and wild-type HCN4 channel. The high-affinity binding of cAMP and cGMP occurs with favorable changes in entropy and enthalpy, whereas the change in entropy is unfavorable for the low-affinity binding event despite an even larger change in enthalpy. Thus, negatively cooperative binding of ligand to the HCN2 and HCN4 C-terminal region is driven by the change in entropy. A similar pattern of thermodynamics has been observed for the dimeric catabolite activator protein, which may have distinct structural consequences (56,57). It is interesting that high-affinity cAMP binding is driven by a smaller change in entropy than cGMP, whereas the S672R mutation impacts the change in entropy for high-affinity binding of cAMP but not cGMP. Thus, it will be of great interest to determine the impact of the mutations on the structure of a full-length HCN4 channel that is intermediately liganded as well as fully liganded.
Our data show that the mutation, and binding of cAMP or cGMP, do not greatly impact the stability of this protein in response to temperature, nor do they impact oligomerization as a function of protein concentration or in response to either cyclic nucleotide. This corresponds to alterations in function that might be considered modest, e.g., hyperpolarization-activated opening of the channel occurs but is shifted to more negative voltages and the maximum effect of cAMP, as well as the impact of cAMP on the oligomerization of the C-terminal region, are not altered, although the binding affinity of this ligand is reduced and the opening of the liganded channel is promoted. Likewise, the crystal structure of the identical HCN4 protein studied here shows local perturbations but conformation is not greatly modified globally. Nevertheless, NMR analyses of a monomeric version of this protein (58,59) have shown that this mutation alters the dynamics of the bound and apo states beyond the local region of this residue. These changes in dynamics are more extensive than the alterations observed in the crystal structure, and favor an inactive conformation and an increase in the rate of cAMP unbinding and, overall, are thought to reflect remodeling of the free energy landscape by the mutation (60).
In summary, our data and modeling lead us to propose that the S672R mutation reduces cAMP binding but promotes the opening of the liganded HCN4 channel, such that the shift in the activation curve by this ligand spans a range of concentrations that is similar to that of the wild-type channel. We also noted that the effect of cAMP may be modestly reduced in the submicromolar range of concentrations, which may impact channel opening under resting conditions in the SAN. Thus, we propose that both inhibition of channel opening, as shown previously (18), and reduced binding of cAMP, contribute to mutant HCN4 channel dysfunction and contribute to the bradycardia observed in patients with this mutation. Our data also suggest that cGMP may modulate HCN4 channel function in the SAN and limit bradycardia at rest but that it does so to a lesser extent in patients who possess the S672R mutation. Finally, our study shows that combining measurements of channel activity with direct measures of ligand binding and mathematical analysis of gating can deepen understanding of how HCN channels, and ligand-gated ion channels in general, function, and are impacted by disease-associated mutations, at the molecular and atomistic level.
Author contributions
L.N. and E.A.A. designed the study, with feedback from F.V.P. L.N. conducted the experiments and, with E.A.A., analyzed and interpreted the experimental data, and prepared the associated figures. F.V.P. also helped to design the experiments, and interpret the experimental data and their analysis. Y.X.L. developed the mathematical model in collaboration with E.A.A. and L.N., who also prepared the associated figures. L.N. and E.A.A. wrote the manuscript, which was reviewed and edited by all of the authors. This work was supported by operating funds from the Canadian Institutes of Health Research (MOP-106655) and the Natural Sciences and Engineering Research Council of Canada (RGPIN-203288) to E.A. Accili. L.C.T. Ng was supported by a CIHR Graduate Studentship.
Editor: Christopher A. Ahern.
References
- 1.DiFrancesco D. Pacemaker mechanisms in cardiac tissue. Annu. Rev. Physiol. 1993;55:455–472. doi: 10.1146/annurev.ph.55.030193.002323. [DOI] [PubMed] [Google Scholar]
- 2.Pape H.C. Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annu. Rev. Physiol. 1996;58:299–327. doi: 10.1146/annurev.ph.58.030196.001503. [DOI] [PubMed] [Google Scholar]
- 3.Brown H.F., DiFrancesco D., Noble S.J. How does adrenaline accelerate the heart? Nature. 1979;280:235–236. doi: 10.1038/280235a0. [DOI] [PubMed] [Google Scholar]
- 4.DiFrancesco D., Ferroni A., et al. Tromba C. Properties of the hyperpolarizing-activated current (if) in cells isolated from the rabbit sino-atrial node. J. Physiol. 1986;377:61–88. doi: 10.1113/jphysiol.1986.sp016177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.DiFrancesco D., Ducouret P., Robinson R.B. Muscarinic modulation of cardiac rate at low acetylcholine concentrations. Science. 1989;243:669–671. doi: 10.1126/science.2916119. [DOI] [PubMed] [Google Scholar]
- 6.DiFrancesco D., Tortora P. Direct activation of cardiac pacemaker channels by intracellular cyclic AMP. Nature. 1991;351:145–147. doi: 10.1038/351145a0. [DOI] [PubMed] [Google Scholar]
- 7.DiFrancesco D., Mangoni M. Modulation of single hyperpolarization-activated channels (i(f)) by cAMP in the rabbit sino-atrial node. J. Physiol. 1994;474:473–482. doi: 10.1113/jphysiol.1994.sp020038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Accili E.A., Robinson R.B., DiFrancesco D. Properties and modulation of if in newborn versus adult cardiac SA node. Am. J. Physiol. 1997;272(3 Pt 2):H1549–H1552. doi: 10.1152/ajpheart.1997.272.3.H1549. [DOI] [PubMed] [Google Scholar]
- 9.Gauss R., Seifert R., Kaupp U.B. Molecular identification of a hyperpolarization-activated channel in sea urchin sperm. Nature. 1998;393:583–587. doi: 10.1038/31248. [DOI] [PubMed] [Google Scholar]
- 10.Ludwig A., Zong X., et al. Biel M. A family of hyperpolarization-activated mammalian cation channels. Nature. 1998;393:587–591. doi: 10.1038/31255. [DOI] [PubMed] [Google Scholar]
- 11.Santoro B., Liu D.T., et al. Tibbs G.R. Identification of a gene encoding a hyperpolarization-activated pacemaker channel of brain. Cell. 1998;93:717–729. doi: 10.1016/s0092-8674(00)81434-8. [DOI] [PubMed] [Google Scholar]
- 12.Ishii T.M., Takano M., et al. Ohmori H. Molecular characterization of the hyperpolarization-activated cation channel in rabbit heart sinoatrial node. J. Biol. Chem. 1999;274:12835–12839. doi: 10.1074/jbc.274.18.12835. [DOI] [PubMed] [Google Scholar]
- 13.Harzheim D., Pfeiffer K.H., et al. Seifert R. Cardiac pacemaker function of HCN4 channels in mice is confined to embryonic development and requires cyclic AMP. Embo J. 2008;27:692–703. doi: 10.1038/emboj.2008.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Alig J., Marger L., et al. Isbrandt D. Control of heart rate by cAMP sensitivity of HCN channels. Proc. Natl. Acad. Sci. U S A. 2009;106:12189–12194. doi: 10.1073/pnas.0810332106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Duhme N., Schweizer P.A., Koenen M. Altered HCN4 channel C-linker interaction is associated with familial tachycardia-bradycardia syndrome and atrial fibrillation. Eur. Heart J. 2013;34:2768–2775. doi: 10.1093/eurheartj/ehs391. [DOI] [PubMed] [Google Scholar]
- 16.Schulze-Bahr E., Neu A., et al. Isbrandt D. Pacemaker channel dysfunction in a patient with sinus node disease. J. Clin. Invest. 2003;111:1537–1545. doi: 10.1172/JCI16387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ueda K., Nakamura K., et al. Kimura A. Functional characterization of a trafficking-defective HCN4 mutation, D553N, associated with cardiac arrhythmia. J. Biol. Chem. 2004;279:27194–27198. doi: 10.1074/jbc.M311953200. [DOI] [PubMed] [Google Scholar]
- 18.Milanesi R., Baruscotti M., et al. DiFrancesco D. Familial sinus bradycardia associated with a mutation in the cardiac pacemaker channel. N. Engl. J. Med. 2006;354:151–157. doi: 10.1056/NEJMoa052475. [DOI] [PubMed] [Google Scholar]
- 19.Verkerk A.O., Wilders R. Pacemaker activity of the human sinoatrial node: an update on the effects of mutations in HCN4 on the hyperpolarization-activated current. Int. J. Mol. Sci. 2015;16:3071–3094. doi: 10.3390/ijms16023071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baruscotti M., Bucchi A., et al. DiFrancesco D. A gain-of-function mutation in the cardiac pacemaker HCN4 channel increasing cAMP sensitivity is associated with familial Inappropriate Sinus Tachycardia. Eur. Heart J. 2017;38:280–288. doi: 10.1093/eurheartj/ehv582. [DOI] [PubMed] [Google Scholar]
- 21.Campostrini G., DiFrancesco J.C., et al. DiFrancesco D. A loss-of-function HCN4 mutation associated with familial benign myoclonic epilepsy in infancy causes increased neuronal excitability. Front. Mol. Neurosci. 2018;11:269. doi: 10.3389/fnmol.2018.00269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xu X., Marni F., et al. Zhou L. Local and global interpretations of a disease-causing mutation near the ligand entry path in hyperpolarization-activated cAMP-gated channel. Structure. 2012;20:2116–2123. doi: 10.1016/j.str.2012.09.017. [DOI] [PubMed] [Google Scholar]
- 23.DiFrancesco D. Funny channel gene mutations associated with arrhythmias. J. Physiol. 2013;591(Pt 17):4117–4124. doi: 10.1113/jphysiol.2013.253765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chow S.S., Van Petegem F., Accili E.A. Energetics of cyclic AMP binding to HCN channel C terminus reveal negative cooperativity. J. Biol. Chem. 2012;287:600–606. doi: 10.1074/jbc.M111.269563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ng L.C.T., Zhuang M., et al. Accili E.A. Binding and structural asymmetry governs ligand sensitivity in a cyclic nucleotide-gated ion channel. J. Gen. Physiol. 2019;151:1190–1212. doi: 10.1085/jgp.201812162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ng L.C., Putrenko I., et al. Accili E.A. Cyclic purine and pyrimidine nucleotides bind to the HCN2 ion channel and variably promote C-terminal domain interactions and opening. Structure. 2016;24:1629–1642. doi: 10.1016/j.str.2016.06.024. [DOI] [PubMed] [Google Scholar]
- 27.Leavitt S., Freire E. Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr. Opin. Struct. Biol. 2001;11:560–566. doi: 10.1016/s0959-440x(00)00248-7. [DOI] [PubMed] [Google Scholar]
- 28.Velazquez-Campoy A., Ohtaka H., et al. Freire E. Isothermal titration calorimetry. Curr. Protoc. Cell Biol. 2004;17:17.8. doi: 10.1002/0471143030.cb1708s23. [DOI] [PubMed] [Google Scholar]
- 29.Velazquez Campoy A., Freire E. ITC in the post-genomic era...? Priceless. Biophys. Chem. 2005;115:115–124. doi: 10.1016/j.bpc.2004.12.015. [DOI] [PubMed] [Google Scholar]
- 30.Ulens C., Siegelbaum S.A. Regulation of hyperpolarization-activated HCN channels by cAMP through a gating switch in binding domain symmetry. Neuron. 2003;40:959–970. doi: 10.1016/s0896-6273(03)00753-0. [DOI] [PubMed] [Google Scholar]
- 31.Zhou L., Siegelbaum S.A. Gating of HCN channels by cyclic nucleotides: residue contacts that underlie ligand binding, selectivity, and efficacy. Structure. 2007;15:655–670. doi: 10.1016/j.str.2007.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zagotta W.N., Olivier N.B., et al. Gouaux E. Structural basis for modulation and agonist specificity of HCN pacemaker channels. Nature. 2003;425:200–205. doi: 10.1038/nature01922. [DOI] [PubMed] [Google Scholar]
- 33.Lolicato M., Nardini M., et al. Moroni A. Tetramerization dynamics of C-terminal domain underlies isoform-specific cAMP gating in hyperpolarization-activated cyclic nucleotide-gated channels. J. Biol. Chem. 2012;286:44811–44820. doi: 10.1074/jbc.M111.297606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wainger B.J., DeGennaro M., et al. Tibbs G.R. Molecular mechanism of cAMP modulation of HCN pacemaker channels. Nature. 2001;411:805–810. doi: 10.1038/35081088. [DOI] [PubMed] [Google Scholar]
- 35.Xu X., Vysotskaya Z.V., et al. Zhou L. Structural basis for the cAMP-dependent gating in the human HCN4 channel. J. Biol. Chem. 2010;285:37082–37091. doi: 10.1074/jbc.M110.152033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lolicato M., Bucchi A., et al. Moroni A. Cyclic dinucleotides bind the C-linker of HCN4 to control channel cAMP responsiveness. Nat. Chem. Biol. 2014;10:457–462. doi: 10.1038/nchembio.1521. [DOI] [PubMed] [Google Scholar]
- 37.Qu J., Altomare C., et al. Robinson R.B. Functional comparison of HCN isoforms expressed in ventricular and HEK 293 cells. Pflugers Arch. 2002;444:597–601. doi: 10.1007/s00424-002-0860-7. [DOI] [PubMed] [Google Scholar]
- 38.Kusch J., Thon S., et al. Benndorf K. How subunits cooperate in cAMP-induced activation of homotetrameric HCN2 channels. Nat. Chem. Biol. 2011;8:162–169. doi: 10.1038/nchembio.747. [DOI] [PubMed] [Google Scholar]
- 39.Liao Z., Lockhead D., et al. Proenza C. Cellular context and multiple channel domains determine cAMP sensitivity of HCN4 channels: ligand-independent relief of autoinhibition in HCN4. J. Gen. Physiol. 2012;140:557–566. doi: 10.1085/jgp.201210858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Peters C.H., Myers M.E., et al. Proenza C. Isoform-specific regulation of HCN4 channels by a family of endoplasmic reticulum proteins. Proc. Natl. Acad. Sci. U S A. 2020;117:18079–18090. doi: 10.1073/pnas.2006238117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Viscomi C., Altomare C., et al. DiFrancesco D. C terminus-mediated control of voltage and cAMP gating of hyperpolarization-activated cyclic nucleotide-gated channels. J. Biol. Chem. 2001;276:29930–29934. doi: 10.1074/jbc.M103971200. [DOI] [PubMed] [Google Scholar]
- 42.Wang J., Chen S., Siegelbaum S.A. Regulation of hyperpolarization-activated HCN channel gating and cAMP modulation due to interactions of COOH terminus and core transmembrane regions. J. Gen. Physiol. 2001;118:237–250. doi: 10.1085/jgp.118.3.237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Page D.A., Magee K.E.A., et al. Young E.C. Cytoplasmic autoinhibition in HCN channels is regulated by the transmembrane region. J. Membr. Biol. 2020;253:153–166. doi: 10.1007/s00232-020-00111-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kusch J., Biskup C., et al. Benndorf K. Interdependence of receptor activation and ligand binding in HCN2 pacemaker channels. Neuron. 2010;67:75–85. doi: 10.1016/j.neuron.2010.05.022. [DOI] [PubMed] [Google Scholar]
- 45.Proenza C., Tran N., et al. Accili E.A. Different roles for the cyclic nucleotide binding domain and amino terminus in assembly and expression of hyperpolarization-activated, cyclic nucleotide-gated channels. J. Biol. Chem. 2002;277:29634–29642. doi: 10.1074/jbc.M200504200. [DOI] [PubMed] [Google Scholar]
- 46.Tran N., Proenza C., et al. Accili E.A. A conserved domain in the NH2 terminus important for assembly and functional expression of pacemaker channels. J. Biol. Chem. 2002;277:43588–43592. doi: 10.1074/jbc.M208477200. [DOI] [PubMed] [Google Scholar]
- 47.Lee C.H., MacKinnon R. Structures of the human HCN1 hyperpolarization-activated channel. Cell. 2017;168:111–120.e11. doi: 10.1016/j.cell.2016.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Porro A., Saponaro A., et al. Moroni A. The HCN domain couples voltage gating and cAMP response in hyperpolarization-activated cyclic nucleotide-gated channels. Elife. 2019;8:e49672. doi: 10.7554/eLife.49672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Z.J., Blanco I., et al. Brelidze T.I. The HCN domain is required for HCN channel cell-surface expression and couples voltage- and cAMP-dependent gating mechanisms. J. Biol. Chem. 2020;295:8164–8173. doi: 10.1074/jbc.RA120.013281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Saponaro A., Bauer D., et al. Moroni A. Gating movements and ion permeation in HCN4 pacemaker channels. Mol. Cell. 2021;81:2929–2943.e26. doi: 10.1016/j.molcel.2021.05.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhou L., Olivier N.B., et al. Siegelbaum S.A. A conserved tripeptide in CNG and HCN channels regulates ligand gating by controlling C-terminal oligomerization. Neuron. 2004;44:823–834. doi: 10.1016/j.neuron.2004.11.012. [DOI] [PubMed] [Google Scholar]
- 52.Han X., Shimoni Y., Giles W.R. An obligatory role for nitric oxide in autonomic control of mammalian heart rate. J. Physiol. 1994;476:309–314. doi: 10.1113/jphysiol.1994.sp020132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Han X., Shimoni Y., Giles W.R. A cellular mechanism for nitric oxide-mediated cholinergic control of mammalian heart rate. J. Gen. Physiol. 1995;106:45–65. doi: 10.1085/jgp.106.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Shimoni Y., Han X., et al. Giles W.R. Mediation by nitric oxide of the indirect effects of adenosine on calcium current in rabbit heart pacemaker cells. Br. J. Pharmacol. 1996;119:1463–1469. doi: 10.1111/j.1476-5381.1996.tb16059.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Musialek P., Lei M., et al. Casadei B. Nitric oxide can increase heart rate by stimulating the hyperpolarization-activated inward current, I(f) Circ. Res. 1997;81:60–68. doi: 10.1161/01.res.81.1.60. [DOI] [PubMed] [Google Scholar]
- 56.Popovych N., Sun S., et al. Kalodimos C.G. Dynamically driven protein allostery. Nat. Struct. Mol. Biol. 2006;13:831–838. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Cui Q., Karplus M. Allostery and cooperativity revisited. Protein Sci. 2008;17:1295–1307. doi: 10.1110/ps.03259908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Akimoto M., Zhang Z., et al. Melacini G. A mechanism for the auto-inhibition of hyperpolarization-activated cyclic nucleotide-gated (HCN) channel opening and its relief by cAMP. J. Biol. Chem. 2014;289:22205–22220. doi: 10.1074/jbc.M114.572164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Boulton S., Akimoto M., et al. Melacini G. Free energy landscape remodeling of the cardiac pacemaker channel explains the molecular basis of familial sinus bradycardia. J. Biol. Chem. 2017;292:6414–6428. doi: 10.1074/jbc.M116.773697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tsai C.J., Nussinov R. Allostery modulates the beat rate of a cardiac pacemaker. J. Biol. Chem. 2017;292:6429–6430. doi: 10.1074/jbc.H116.773697. [DOI] [PMC free article] [PubMed] [Google Scholar]