Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2021 Jun 30;11(37):23122–23135. doi: 10.1039/d1ra03246a

A comprehensive study on lithium-based reactive hydride composite (Li-RHC) as a reversible solid-state hydrogen storage system toward potential mobile applications†

Fahim Karimi 1,✉, Philipp Klaus Pranzas 1, Julián Atillio Puszkiel 1,2, María Victoria Castro Riglos 3, Chiara Milanese 4, Ulla Vainio 5, Claudio Pistidda 1, Gökhan Gizer 1, Thomas Klassen 1, Andreas Schreyer 6, Martin Dornheim 1
PMCID: PMC9034372  PMID: 35480441

Abstract

Reversible solid-state hydrogen storage is one of the key technologies toward pollutant-free and sustainable energy conversion. The composite system LiBH4–MgH2 can reversibly store hydrogen with a gravimetric capacity of 13 wt%. However, its dehydrogenation/hydrogenation kinetics is extremely sluggish (∼40 h) which hinders its usage for commercial applications. In this work, the kinetics of this composite system is significantly enhanced (∼96%) by adding a small amount of NbF5. The catalytic effect of NbF5 on the dehydrogenation/hydrogenation process of LiBH4–MgH2 is systematically investigated using a broad range of experimental techniques such as in situ synchrotron radiation X-ray powder diffraction (in situ SR-XPD), X-ray absorption spectroscopy (XAS), anomalous small angle X-ray scattering (ASAXS), and ultra/small-angle neutron scattering (USANS/SANS). The obtained results are utilized to develop a model that explains the catalytic function of NbF5 in hydrogen release and uptake in the LiBH4–MgH2 composite system.

Superb dehydrogenation/hydrogenation kinetic enhancement of the LiBH4–MgH2 reactive hydride composite system by addition of NbB2 nano-particles as nucleation agents for MgB2.graphic file with name d1ra03246a-ga.jpg

Introduction

The global energy demand is currently covered mainly by fossil fuels and nuclear power. By following this path, it will be a question of when these limited resources will be exhausted. Moreover, massive exploitation/consumption of these resources can lead to irreversible ecological disasters. Considering these facts, strategies and concepts for clean and sustainable energy solutions are urgently needed. A widely recognized candidate for sustainable and pollutant-free energy conversion is considered to be hydrogen. This is due to its high energy density per mass unit (33.3 kW h kg−1) in comparison to natural gas (13.9 kW h kg−1) and liquid fossil fuels (12.4 kW h kg−1),1,2 and because its combustion product is just water: 2H2 + O2 → 2H2O, using a fuel cell. By using sustainable energy sources (such as sun, wind, biomass energy, etc.) to produce hydrogen, a renewable energy circuit can be created. The main obstacles hindering hydrogen being used as an energy carrier in a wide variety of industrial applications is its low volumetric energy density (∼0.003 kW h dm−3) and its low ignition energy (∼0.02 MJ at hydrogen/air volume ratio ≈ 29%; a spark could ignite it) in comparison to gasoline (∼9 kW h dm−3, 0.24 ml gasoline vapor) at standard conditions.3 In order to enhance the volumetric energy density of gaseous hydrogen, two alternative approaches are probed so far: (1) gaseous hydrogen is pressurized up to ∼700 bar at 15 °C (1.2 kW h dm−3), and (2) gaseous hydrogen is liquefied at cryogenic temperatures (2.4 kW h dm−3).4 Although these methods do improve the volumetric energy density of gaseous hydrogen, the safety issue remains still challenging. A more convenient alternative approach is to store hydrogen chemically in metal hydrides. This concept not only improves the volumetric energy density of the gaseous hydrogen significantly, but it also avoids the above-mentioned safety issues. Since hydrogen atoms are chemically bonded (stored) in the host metal, an energy barrier has to be overcome before hydrogen can be released. Especially, light metal hydrides are of great interest for hydrogen storage in mobile applications due to their high gravimetric- and volumetric energy densities. In particular, borohydrides of alkaline and alkaline earth metals show exceptionally high gravimetric hydrogen storage capacity. LiBH4 has one of the highest volumetric energy densities (4.0 kW h dm−3)5 and one of the highest gravimetric hydrogen capacities (∼13 wt%).6 However, its decomposition starts at temperatures above 700 K according to reaction (1),5,7,8 due to its thermodynamic stability (67–74 kJ mol−1 H2),9–12 that is very high relative to the reference stability window (30–50 kJ mol−1 H2) defined by the DOE.13

LiBH4 → LiH + B + Created by potrace 1.16, written by Peter Selinger 2001-2019 H2 1

A partial rehydrogenation of reaction (1) can be achieved only at temperatures above 900 K and at hydrogen pressures of ∼15 MPa,14,15 which makes this complex hydride unsuitable for a possible mobile and/or stationary application. An alternative approach that avoids a dramatic degradation in hydrogen capacity and simultaneously reduces the reaction enthalpy is the concept of so-called “reactive hydride composite” (RHC).16–18 In this approach, one or more metal hydride is added to the complex metal hydride forming a high hydrogen storage capacity composite system with a lower thermodynamic stability and enhanced reversibility.12,19 The reaction-enthalpies of various systems were altered by using the this concept.20–29 In this work, MgH2 is used to stabilize the dehydrogenation products of LiBH4. Indeed, the overall reaction enthalpy of the LiBH4–MgH2 reactive hydride composite system (Li-RHC) is reduced to 46 kJ mol−1 H2,12 in comparison to the respective values of each single metal hydride (LiBH4 (67 kJ mol−1 H2), MgH2 (75 kJ mol−1 H2)),5,30 according to the following reaction path:

2LiBH4 + MgH2 ↔ 2LiH + MgB2 + 3H2 2

Experimentally, however, this composite system can take different reaction paths depending on the applied hydrogen backpressures and temperatures.31 At applied hydrogen backpressures lower than 3 bar and at temperatures about 400 °C, the system's components decompose independently:

2LiBH4 + MgH2 → 2LiH + Mg + B + 4H2 3

In this case, the overall reaction enthalpy of this composite system is not altered, and it is only partially reversible (due to its possible stable decomposition products such as amorphous boron). Though reaction (2) is thermodynamically more stable compared to reaction (3), independent decomposition of the hydrides is kinetically favored in latter case. By applying hydrogen backpressures greater than 3 bar at temperatures around 400 °C, the decomposition of LiBH4 is thermodynamically prevented, however not that of MgH2. Thus, after decomposition of MgH2 to metallic magnesium, subsequently Mg reacts with LiBH4 to form MgB2.31,32 In this case, the dehydrogenation reaction can be described as follows:33

2LiBH4 + MgH2 → 2LiBH4 + Mg + H2 4.1
2LiH + MgB2 + 3H2 4.2

Upon the dehydrogenation reaction, an amount of roughly 11.5 wt% hydrogen is released. The first reaction step proceeds endothermic, while the second reaction step takes place exothermic, which causes a reduction in the overall reaction enthalpy of the system. Hence, the formation of MgB2 is crucial to ensure the reversibility of Li-RHC. This is, due to a graphite-like layered structure of MgB2, compared to the closo-structure of boron (Fig. S1, ESI†).19 The rehydrogenation of 2LiH + MgB2 proceeds in one step under moderate thermodynamic conditions (50 bar H2, 350 °C), according to reaction (5):

2LiH + MgB2 + 3H2 → 2LiBH4 + MgH2 5

Although thermodynamics and reversibility of LiBH4 can be tuned applying the RHC concept, the de/rehydrogenation reaction kinetics of the system remains rather slow. In this work, the dehydrogenation and rehydrogenation reaction kinetics of this composite system could be significantly improved (∼ 96%) by an addition of a small amount of NbF5. The catalytic role of NbF5 in enhancing the dehydrogenation/rehydrogenation reaction kinetics of Li-RHC is studied in the following in detail using advanced experimental methods such as small-angle X-ray scattering (SAXS), anomalous small-angle X-ray scattering (ASAXS), small-angle neutron scattering/ultra-small-angle neutron scattering (SANS/USANS), in situ synchrotron radiation X-ray powder diffraction (in situ SR-XPD), and high-resolution transmission electron microscopy (HR-TEM).

Experimental

The raw material were purchased from Sigma-Aldrich, (with degree of purity of: LiBH4 ≥ 97.0%, MgH2 ≥ 90.0%, and NbF5 ≥ 98.0%), and the isotope containing materials (Li11BH4, and 7Li11BH4 with purities of ≥95%) were purchased from KAT-Chem Ltd. All samples were prepared by ball-milled in a Spex 8000 mill/shaker. The Spex 8000 mill/shaker was placed in a glove box (MB-BRAUN, Germany) under a continuously purified argon atmosphere with less than 10 ppm oxygen and moisture, respectively. The milling vial and the milling balls were made of stainless steel. The utilized ball-to-powder ratio was 10 : 1. MgH2 was premilled for 5 h before mixing it with LiBH4/NbF5. Volumetric measurements were performed using the Sievert's type apparatus Hydro Quebec, Canada,34 in order to study the dehydrogenation/hydrogenation properties of the composite systems and prepare cycled samples for further measurements. Coupled manometric-calorimetric desorption measurements were performed by connecting a PCT-Pro instrument (Setaram and Hy-Energy, France) with a Sensys high-pressure DSC (Setaram, HP-DSC, France). For each measurement, the mass of the samples was chosen to be about 30 mg. The measurements were performed by heating the samples from room temperature up to 500 °C at 3 °C min−1 under a H2 pressure of 4 bar. In situ SR-XPD measurements were carried out at the powder diffraction beamline D3 at the DORIS III synchrotron storage ring (at DESY in Hamburg, Germany). For in situSR-XPD measurements, samples were loaded into single-crystal sapphire tubes in a glove box filled with argon atmosphere. The sapphire tubes were subsequently mounted in a gas pressure cell.25 Thereafter, the cell unit was transferred into the experimental hutch, where it was mounted to a goniometer and subsequently exposed to the synchrotron beam. The incident photon wavelength was set to 0.5 Å. A MarCCD-165 area detector was applied to collect the diffracted intensities. The diffraction intensities from the sample were collected after each 30 seconds, and the sample-to-detector distance (SDD) was kept at about 125 mm. The sample was heated up by a ceramic oven placed underneath the capillary while the sample temperature was measured by a thermocouple positioned close to the sample in the capillary and controlled via a PID regulator. The temperature and pressure parameters were set to the same values as they were chosen for the volumetric measurements. The acquired 2D-patterns were further processed to a 1D diffractogram using the Fit2D program,35 and the program FindIt (ICSD-database)36 was used for phase identification. X-ray absorption spectroscopy (XAS) measurements were performed at the C-beamline at DORIS III. The ideal amount of the samples for the measurements was calculated by using the program XAFSMASS.37 Samples were mixed with dry cellulose (∼50 mg) in a mortar and pressed (5 bar) into pellets of 10 mm in diameter. The pellets were placed then in an aluminum sample holder and sealed with Kapton tape (55 µm, in thickness) to avoid sample's oxidation. Niobium was measured in its various oxidation states (metallic Nb, NbF5, and NbB2) as reference material. All measurements were recorded in transmission mode as well as in fluorescence mode at the K-edge of metallic Nb (18.99 keV). For each sample, three XAS-spectra were acquired. After removing the spikes, the spectra were aligned, calibrated, and subsequently averaged. XAS data processing and analysis were conducted by using the “IFEFFIT” software package.38 Anomalous small-angle X-ray scattering (ASAXS) measurements were performed at the beamline B1 at DORIS III (DESY in Hamburg, Germany). All measurements were carried out near the K absorption edge of niobium (18.99 keV) to characterize the Nb-containing structures in the samples upon dehydrogenation/rehydrogenation cycles. Samples were mounted in an aluminum sample holder with a circular hole (5 mm in diameter and a thickness of 0.25 mm). All samples were sealed with Kapton tape to avoid any possible oxidation. The ASAXS intensities were acquired at four different energies at two SDD (Dmin = 885 mm and Dmax = 3585 mm), respectively, to cover the maximum experimental q-range available. Here, q is the magnitude of the scattering vector defined as: q = (4π/λ)sin θ, where λ is the incident X-ray wavelength and 2θ is the respective scattering angle. The beamline was equipped with a Pilatus 300 K detector and a Si (311) double crystal monochromator with a wavelength resolution of Δλ/λ < 10−4. All selected energies with their corresponding anomalous dispersion factors are listed in Table 1 (the calculated dispersion values are based on the theory of Cromer & Lieberman).39 Small-Angle Neutron Scattering (SANS) measurements were performed at the SANS-1 instrument at FRM II of Heinz Maier-Leibnitz Zentrum (MLZ, Bavaria, Germany).40 The thermal neutrons were from a source with a maximum flux of 8 × 1014 n cm−2 s−1. The incident neutron wavelength could be monochromated in the range of 3.4–30 Å by applying an array of two mechanical velocity selectors with a wavelength resolution of 10% and 6%, respectively. The SDD could be set in the range of 1.1–21 m, with a maximum q range of 0.001–2 Å−1. For the performed experiments in this work, three sample to detector distances (1.6, 8, 20 m) and two wavelengths (6 Å for 1.6 and 8 m, 12 Å for 20 m) were applied, respectively, to cover the maximum q-range available at the high q values and to cover a reasonable q-range in the low q region in order to have a good overlapping with the USANS measurements.

Selected energies for the ASAXS-measurements at the K-edge of Nb and the corresponding anomalous dispersion factors41.

# Energy [eV] f′ f″
E1 18 522 −3.097 0.557
E2 18 822 −4.078 0.542
E3 18 924 −5.035 0.542
E4 18 926 −5.068 0.543
E5 18 976 −6.907 0.668
Open in a new tab

The scattering intensities were measured by using a 128 3He proportional counter detector with an area of 1000 × 1020 mm2 with a count rate of 1 MHz. Silverbehenate (AgBe) was measured at a short distance (1.6 m) to calibrate the q-axis. A water standard was measured in order to set the scattering intensities onto an absolute scale. All SANS data were processed by using BerSANS software.42 In addition to SANS measurements, USANS measurements were carried out to evaluate the larger structures present in the samples. USANS measurements were performed at the BT5-Instrument at the National Institute of Standard and Technology (NIST) in Gaithersburg (Maryland, USA).43 TEM characterization was performed on a FEI TECNAI G2 machine using 200 kV, point resolution: 0.12 nm, and a field emission gun (FEG). Dark Field imaging technique (DF) was used to distinguish different phases by their diffraction. Size measurements of the particles were performed by means of an interpolated polygon tool from iTEM software,44 and the values that took into account were those from mean diameter measurements. High-resolution transmission electron microscopy (HR-TEM) images were obtained with a magnification higher than M > 300k×. In HR-TEM images, Fast Fourier Transform (FFT) was performed by Digital Micrograph software45 to obtain the diffraction patterns. These were compared with the simulated ones obtained by JEMS software.46 Samples for TEM were prepared by dispersing a small amount of powder in hexane and then ultrasonicated the suspension for 10 min. A drop of this suspension was deposited over a commercial copper grid for TEM coated with a Formvar support film. In this procedure, the samples were exposed to air for a short period.

Results

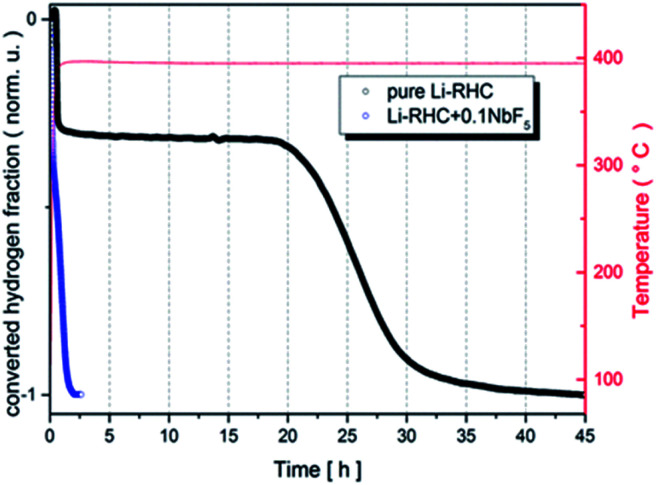
The first dehydrogenation reactions of pure Li-RHC and the doped Li-RHC + 0.1NbF5 sample are presented in Fig. 1, where the normalized converted fraction of desorbed hydrogen is plotted over the corresponding elapsed time in hours. The overall dehydrogenation process of the pure Li-RHC system is completed after approximately 45 h. This reaction proceeds in two distinct steps, which are separated by a plateau region. The first reaction step is finished after 0.75 h, followed by the plateau phase, which extends nearly up to 18 h, before the second reaction step starts. The second reaction step is completed after roughly 20 h.

Fig. 1. Dehydrogenation reaction kinetics of pure and doped Li-RHC under 4 bar of hydrogen back pressure. The samples were heated up (5 K min−1) to about 390 °C and were kept isothermal for the rest of the measurement.

Fig. 1

Open in a new tab

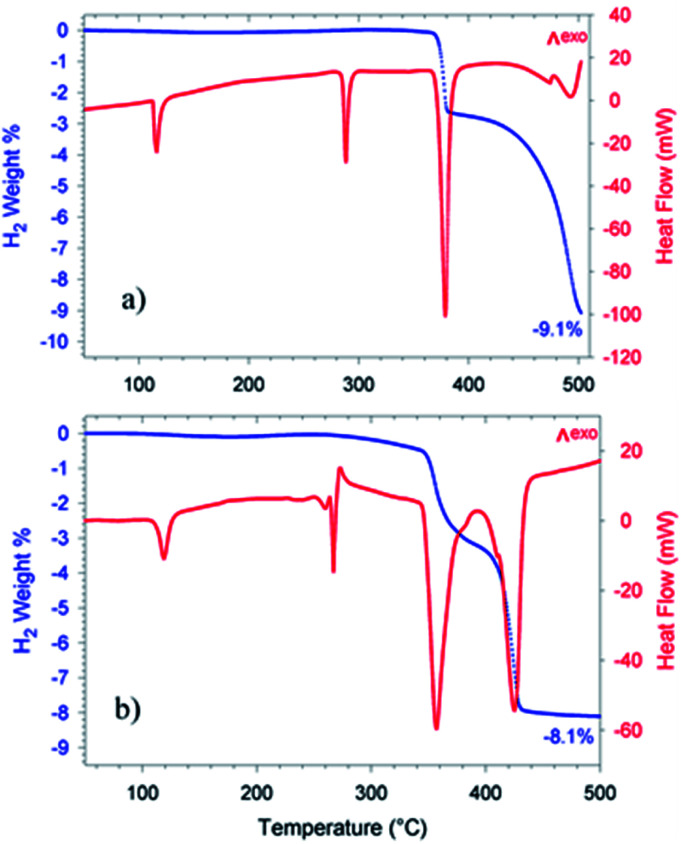
The dehydrogenation reaction of the doped Li-RHC + 0.1NbF5 composite system shows significantly improved kinetics in comparison to the pure Li-RHC system. In contrary to the dehydrogenation process of the pure Li-RHC, the plateau region is not observed in this sample. For both composite systems, the first reaction step's kinetics is very similar and is completed roughly after 0.25 h. However, the second reaction step of the doped system is improved by a factor of ∼20, relative to the pure Li-RHC system. To further investigate the influence of NbF5 on Li-RHC, coupled manometric- and DSC measurements were carried out on the pure and on the doped Li-RHC samples, and the results are shown in Fig. 2. The desorption curves were acquired using a manometric instrument in the coupled measurements confirm the results obtained by volumetric measurements. This is further confirmed by the analysis of the onset temperatures of the different peaks evolving during dehydrogenation. Apart from the first peak, due to the polymorphic transition of Li borohydride, that takes place at identical onset temperature in the two samples (113 °C), the onset temperatures of the other peaks are lower in the doped sample in comparison to the pure Li-RHC system (see Table 2). The temperature differences between the samples' peaks increase by moving from the second (ΔT = 21 °C) to the last (ΔT = 67 °C) one. Moreover, the dehydrogenation of the RHC is completed at 500 °C, with an induction time for the Li borohydride phase smaller than for the undoped sample. The peak with a small shoulder at lower T represents this step when the fluoride is present, instead of several less intense peaks (two visible before 500 °C in Fig. 2a). Concerning the second peak in the undoped sample, it is a sharp and single event. In the doped sample, it seems that a pre-melting takes place at lower T and an exothermic reaction occurs at the end of melting. This is coupled with a slow decrease of the sample mass, i.e. to a minor hydrogen release. The kinetics of this step is very slow. The reaction rate accelerates only when the Mg hydride dehydrogenation starts (under the 3 peak). By considering the dehydrogenation enthalpies, for MgH2 (3rd peak), values of 61 ± 2 kJ mol−1 H2 and 58 ± 2 kJ mol−1 H2 are obtained for the undoped and doped sample, respectively, which means a slight destabilization due to the presence of NbF5. This value is in agreement with the values obtained in other studies under similar conditions.47,48 A more significant destabilization effect, however, is evident for the LiBH4 dehydrogenation enthalpy (4th peak): at 4 bar the process is not completed for the undoped sample, while it is completed for the NbF5 containing system (characterized by an enthalpy of 13 ± 1.5 kJ mol−1 H2). This value is lower than the one reported for the dehydrogenation at 3 bar of the undoped system, i.e. 20 ± 3 kJ mol−1 H2.47

Fig. 2. Coupled manometric- DSC measurements of the first dehydrogenation reaction of pure (a) and doped Li-RHC (b) under 4 bar of hydrogen backpressure.

Fig. 2

Open in a new tab

Pure- and doped Li-RHC samples after first desorption with different isotopes.

Sample/state Pure Li-RHC Description Li-RHC + 0.1NbF5 Description
First-desorption 2LiH + MgB2 1D-L 2LiH + MgB2 + 0.1NbF5 1D-LN
2LiH + Mg11B2 1D-11L 2LiH + Mg11B2 + 0.1NbF5 1D-11LN
27LiH + Mg11B2 1D-7L 27LiH + Mg11B2 + 0.1NbF5 1D-7LN
Open in a new tab

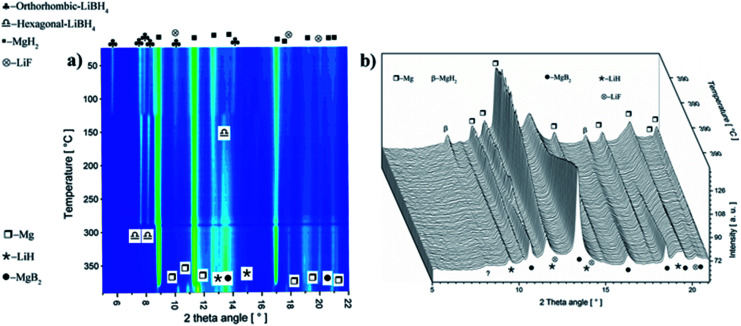
To understand the effect of NbF5 on the reaction mechanism of Li-RHC, in situ SR-XPD was applied as a function of temperature. The result of these measurements is presented in Fig. 3. For the sake of a better overview, the in situ diffraction patterns are plotted in non-isothermal (Fig. 3a) and isothermal (Fig. 3b) conditions, respectively. Fig. 3a shows the in situ diffraction patterns of the doped sample from room temperature up to 390 °C (isothermal temperature). Intensities of the diffracted beam are plotted (in color code) over the temperature (in °C) and 2-theta diffraction angle (in degrees ). As can be seen, the initial crystalline phases of the as-milled sample consist of MgH2, orthorhombic LiBH4 (o-LiBH4), and LiF. However, no diffraction peaks of any Nb-containing phase are detected. By raising the sample's temperature, simultaneous narrowing and shifting of the diffraction peaks are observed toward smaller angles. The narrowing of diffraction peaks can be inferred to a higher degree of recrystallization of the high-energy ball-milled material. The shift toward lower angles is due to the thermal expansion of the crystalline unit cells. The first change in the diffraction pattern occurs at about 120 °C. This is caused by the structural phase transformation of LiBH4 from orthorhombic o-LiBH4 (space group Pnma)49 to hexagonal h-LiBH4 (space group P63mc),50 and matches with the first endothermal peak in the coupled volumetric-DSC measurement in Fig. 2b. At about 370 °C, the intensities of the Bragg-peaks of MgH2 start to diminish, and those of metallic Mg start to emerge. This corresponds to the second endothermic peak of the coupled volumetric-DSC curves, which is correlated to the dehydrogenation of MgH2 → Mg + H2. Shortly after that, diffraction peaks of MgB2 phase are detected. The immediate appearance of MgB2 after decomposition of MgH2 implies a reaction between metallic Mg and molten LiBH4, which corresponds to the third DSC signal in Fig. 2b. At isothermal conditions (Fig. 3b), the diffraction intensities of metallic Mg decreases rapidly, whereas the diffraction peaks of MgB2 and LiH are increasing correspondingly. This further confirms the assumption of a mutual reaction between metallic Mg and liquid LiBH4 phase. However, over the entire in situ SR-XPD measurement time, the state of niobium remains unknown. This could be due to the amorphous or/and nanoscale nature of Nb containing phase/s in the Li-RHC matrix.

Fig. 3. (a) In situ SR-XPD plot of the first desorption of the doped Li-RHC + 0.1NbF5 composite system collected at a temperature ramp of 3 °C min−1 up to a maximum temperature of 390 °C. (b) In situ SR-XPD plot at the isothermal condition (390°) and at 4 bar H2 backpressure.

Fig. 3

Open in a new tab

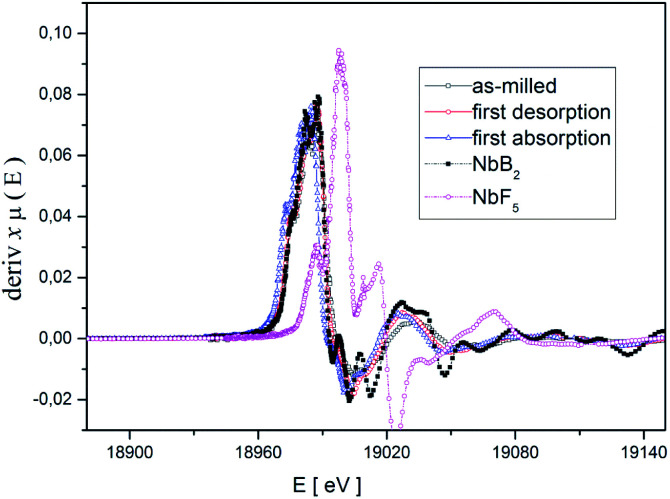
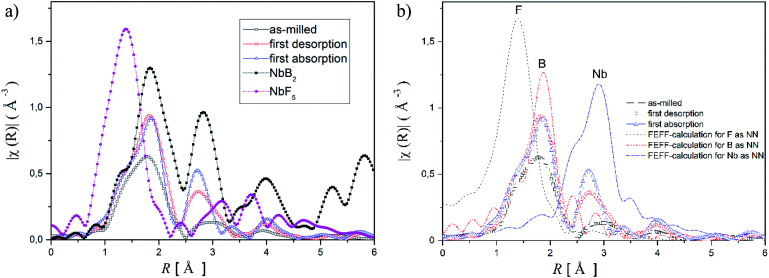
For obtaining detailed information about these phases, X-ray absorption spectroscopy (XAS) was applied. Because XAS method allows to detect elements in very small quantities in any environment, (in crystalline, or in an amorphous state). Hence, XAS measurements were carried out at the K-edge of niobium (18.98 keV) to determine the chemical state and the local environment of niobium in the hydride matrix at different hydrogenation cycle. Near edge structure of the XAS-spectra (XANES) was used to determine niobium's valance state in the Li-RHC system at different hydrogenation states. Additionally, pure NbF5 and NbB2 samples were measured as reference samples. In Fig. 4, the first derivatives of XANES of samples and references are presented. A comparison between the XANES spectra of the doped Li-RHC samples reveals that niobium has the same oxidation states at different hydrogenation states of the hydride matrix. On the other hand, a comparison between XANES spectra of samples and the NbB2 reference shows a great accordance in all details, which suggests an oxidation change in niobium valance from Nb5+ to Nb2+. To determine the local environment of Nb in the hydride matrix at different hydrogenation state, the EXAFS region of XAS spectra of the samples- and references (NbB2 and NbF5) were extracted and Fourier transformed (FT). The resulting radial distribution functions (RDF) are shown in Fig. 5a.

Fig. 4. Derivatives of XANES spectra of the Li-RHC samples and NbF5 and NbB2 references.

Fig. 4

Open in a new tab

Fig. 5. (a) Unweighted Radial Distribution Function (RDF) of Li-RHC samples and references in the k-range of 2–12 Å, FT from the EXAFS spectra, (b) RDFs of the samples and their corresponding calculated backscattering amplitude for the nearest neighbours for NbF5 and NbB2.

Fig. 5

Open in a new tab

A comparison between the RDF patterns of the as-milled sample and the cycled samples shows that the local environment of Nb does not change upon dehydrogenation/hydrogenation procedure of the hydride matrix, after the milling process. Nevertheless, the width and size of the RDF amplitudes of the samples are differing at different cycling stages. However, their peak positions remain unchanged over the cycles. The RDF amplitudes of the samples increase with increasing hydrogenation cycles. This indicates that the degree of order around Nb (in the hydride matrix) is increased with increasing hydrogenation cycles of the sample. The comparison between the RDF patterns of the samples and NbF5 reference shows considerably changes in the local environment of Nb in the sample already after the ball milling process relative to NbF5 confirming the observation made by XANES.

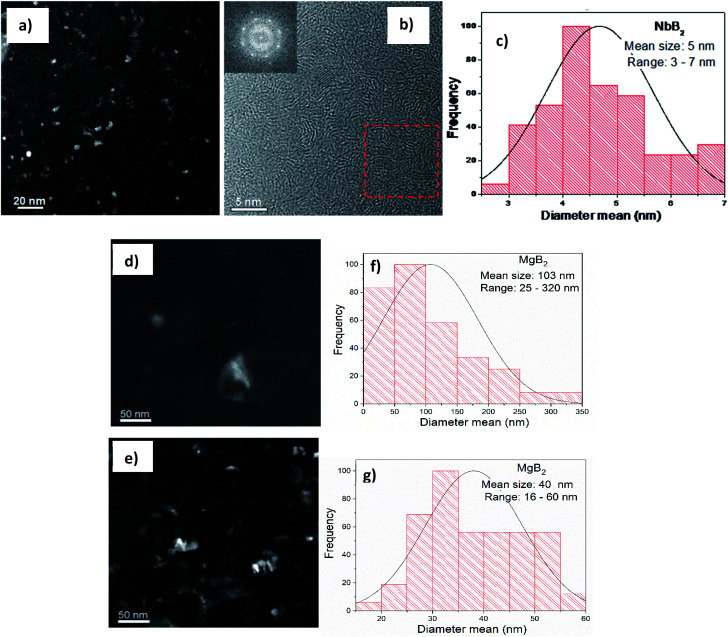
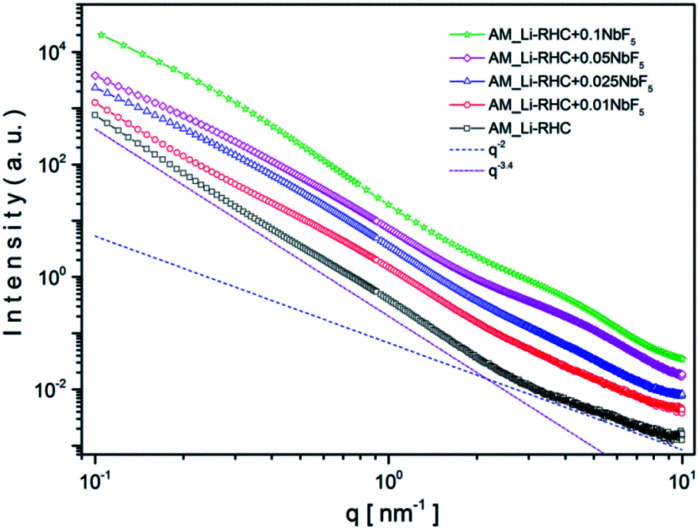
Comparing the RDF patterns of the samples and the RDF pattern of NbB2 reference shows an excellent agreement between them in overall details. This again strongly suggests the formation of NbB2 phase in the sample after the ball-milling process which remains stable upon cycling. To further confirm this observation, ab initio calculations were carried out using FEFF6 program.38 Results of these calculations and experimentally observed RFD patterns of the doped sample at different hydrogenation states are shown in Fig. 5b. In the calculation, the magnitudes of the scattering amplitudes were not included for electron relaxation processes since only the phase's existence was at the center of interest. FEFF-calculations were performed assuming NbF5 and NbB2 in crystalline state (space group C12/m1; Cryst. Sys. monoclinic (ICSD #26647)), (space group P6/mmm; Cryst. Sys. hexagonal (ICSD #30328)), respectively. As can be seen in Fig. 5b, the amplitude around 1 Å could be identified as the backscattering amplitude of fluorine. Moreover, the first- and second RDF amplitudes of the samples are well described by the backscattering amplitudes of boron and Nb, respectively. This confirms the formation of NbB2 phase in the as-milled and cycled Li-RHC + 0.1NbF5 samples. Therefore, Nb's local environment in the hydride matrix can be identified as NbB2. Further comparison between the RAD patterns of NbB2 reference and those of the samples shows that the RAD amplitudes of the samples drop significantly with increasing distance in comparison to those of the NbB2 reference. This indicates the presence of nanosized NbB2 crystalline particles in the samples, which explains the absence of any Nb containing diffraction signals in the in situ SR-XPD patterns above. To cross-check the chemical state of Nb containing phase(s) in the doped Li-RHC, and to investigate the microstructural effects of NbF5 on the hydride matrix, HR-TEM measurements were carried out. The results of these investigations are shown in Fig. 6. HR-TEM image of doped Li-RHC sample confirms the presence of nano-sized niobium-containing particles in the Li-RHC matrix. The length of each reflection (|ghkl|) could be measured using the FFT images (Fig. 6b) for these particles, and based on that, the inter-planar distances (dhkl = 1/|ghkl|) could be calculated. The values for |ghkl| were in excellent agreement with those from the JEMS simulations for NbB2, thus confirming that for each case, indeed, NbB2 particles were formed. From dark field (DF) images, particle size measurements were carried out from which a local size distribution of NbB2 particles could be extracted (Fig. 6c). According to this distribution, the mean size of NbB2 particles is about 5 nm within the range between 3 and 7 nm. Additionally, HR-TEM micrographs (in DF mode) of MgB2 particles of pure- and doped Li-RHC samples in the desorbed state were taken (Fig. 6d and e). From the micrographs, size distributions of MgB2 particles in both samples were calculated, and the results are shown in Fig. 6f and g, respectively. As can be seen, the particle sizes of MgB2 in pure Li-RHC range from 25 up to 320 nm with an average particle size of 103 nm. In the doped Li-RHC sample, the corresponding particle sizes range from 16 nm up to 60 nm with a mean particle size of 40 nm. This clearly shows that the MgB2 particles in the doped Li-RHC sample (desorbed state) are much finer compared to the corresponding sizes in the Li-RHC sample. In order to characterize the size distribution of NbB2 particles in the hydride matrix in more detail, SAXS and ASAXS measurements were carried out. For SAXS measurements, samples with increasing NbF5 additive content (Li-RHC + xNbF5 with x being: 0, 0.01, 0.025, 0.05, 0.1) were prepared to investigate the effect of the additive on the hydride matrix. The results of SAXS measurements are shown in Fig. 7.

Fig. 6. (a) TEM dark field image shows a homogeneous distribution of NbB2 particles. (b) Calculations based on inter-planar distances (dhkl = 1/|ghkl|) of FFT images confirm the presence of NbB2 particles. (c) Calculated size distribution of NbB2 particles from TEM DF images. (d) DF image of MgB2 particles in the desorbed pure Li-RHC sample, (e) DF image of MgB2 particles in the desorbed doped Li-RHC sample. (f) Calculated size distribution of MgB2 particles from DF images of the desorbed pure Li-RHC sample. (g) Calculated size distribution of MgB2 particles of the desorbed doped Li-RHC sample.

Fig. 6

Open in a new tab

Fig. 7. SAXS curves of as-milled Li-RHC sample with increasing NbF5 additive content (Li-RHC + xNbF5 with x being: 0, 0.1, 0.025, 0.05, 0.1 mol%) measured at 18.5 keV. Additional q−α power-law lines are included to clarify the fractal character of the samples.

Fig. 7

Open in a new tab

The y-axis represents the scattering intensities in arbitrary units, and the x-axis represents the scattering vector q in the inverse space (Å−1), where q = (4π/λ)sin θ and 2θ is the scattering angle. All SAXS measurements were carried out at the energy (18.54 keV) below the K-edge absorption energy of Nb (18.99 keV), to minimize the incoherent scattering. The SAXS curve of the sample without additive content (pure Li-RHC) exhibits a small and very broad shoulder around 1 nm−1 (which corresponds to structures of 4–7 nm in size), but otherwise, it is featureless over the entire observed q-range. This indicates a highly disordered material with a lack of morphological features over the measured size range. Nevertheless, the scattering curves can be divided into two main regions, which are well described by a simple q−α power-law (dotted lines), respectively. This suggests a fractal morphology of the samples over the observed length scale.51 At the high q-region, between approximately 3 nm−1 and 10 nm−1, the power-law exponent is roughly α = 2, which corresponds to the scattering from a mass fractal structure. The length scale of these structures is between 1–3 nm, which is typical for distances in the grain boundaries. In the q-region between 0.1 nm−1 and 1 nm−1, the scattering curve follows a power-law behavior with an exponent of α = 3.4, which can be associated with scattering from particles with rough surfaces. The size scale of these particles lies in between 5 and 60 nm and larger. The fractal regions of the scattering curve gain morphological features with increasing NbF5 content in the Li-RHC sample. The very broad structure at the lower q-region around 0.3 nm−1 is observed first with an increment of 1 mol% NbF5 content. It becomes more prominent with increasing NbF5 content, while its peak center shifts toward lower angles and the width of its amplitude become extremely broad while its magnitude becomes larger. The second structure at higher q-region is centered around 3 nm−1 and becomes noticeable only after a NbF5 content of 2.5 mol%, but it becomes rapidly very pronounced with further addition of NbF5. In contrast to the first structure at the lower q region, the second structure becomes clearly visible only after adding of 5 mol% of NbF5.

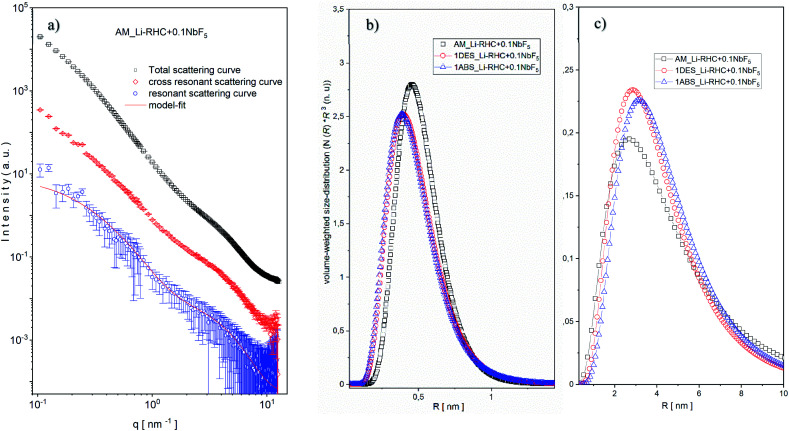
This is due to the length scale of the structures in this region (1–3 nm) in comparison to structures found at the low q region (5–60 nm). Since the intensity of SAXS is ∼V2 ∼ R6 (where V is the volume, and R is the sphere's radius). Therefore, structures with relative small sizes are well discriminated by their SAXS intensities. It should also be noted that the overall fractal character of the scattering curves in both regions remain approximately valid. Interestingly, in the lower q region, the power-law decreases from 3.4 to roughly 2.9 with increasing NbF5 content. This indicates an increase in surface roughness (∼increase in surface area) of particles in this region with increasing NbF5 content. In contrast, the power-law exponent rises in the higher q region from 2.0 to approximately 2.5 with increasing NbF5 content, which implies a higher degree of compactness or increasing order of structures in this region with increasing NbF5 content. Although a systematic relation between NbF5 content and structures formed in the SAXS curves can be recognized, no specific statement about the size distribution of Nb-containing structures can be made due to the overlapping signal between the matrix and Nb containing structures. In order to extract the scattering intensities of Nb-containing structures, ASAXS measurements were carried out. Details about the ASAXS method can be found in the referred literature.52–55 One of the obtained results of an ASAXS measurement (Li-RHC + 0.1NbF5 after the milling procedure) is exemplary shown in Fig. S2a (ESI).† The peak scattering, located at around 4–5 nm−1, belongs to the scattering of the Kapton foil, which was used to seal the samples. In the inset figure, the sample's resonant behavior is emphasized with respect to variation in energy of the incident beam (near the K absorption edge of Nb). As the energy of the incident photons approaches the K absorption edge of the resonant atoms, the scattering intensities increase at the very high q region (Porod region) considerably. This effect is caused by fluorescence and inelastic Raman scattering of the resonant atoms, which leads to an additional (energy-dependent) constant scattering. However, the contribution of this constant scattering (relative to total structural scattering) becomes significant only in the Porod-region and at energies close to the absorption edge of a scattering element.56 Fig. S2b (ESI)† shows the background-corrected ASAXS scattering curves of Fig. S2a.† The shape of the scattering curves gives evidence of two structures in the sample (see inset figures). At the large q values of around 4 nm−1 the structures are rather resonant, and their estimated average size is approximately 2 nm (using the rule of thumb: d ≈ 2π/q). The structures located at about 0.3 nm−1 are less resonant in comparison to structures located at smaller q values, and their average size can be estimated to be around 10 nm. In order to isolate the pure resonant scattering of NbB2 structures from the total scattering, the Stuhrmann method (dispersion analysis) was applied (eqn (6)).57

I(q,E) = I0(q) + 2f′(E)I0R(q) + [f′2(E) + f″2(E)]IR(q) 6

Here, I0(q) is the non-resonant scattering contribution to the overall scattering intensity, which equals the SAXS curve observed far from any resonant absorption edges. I0R(q) is the of-resonant (or mixed resonant) scattering contribution of superposed intensities of, both, resonant and non-resonant scattering. Using the dispersion analysis, the pure resonant scattering contribution of NbB2 structures could be isolated. In Fig. 8a, as an example, a result of this procedure is shown for the as-milled sample. As can be seen, the two structures discussed above are maintained in the pure resonant scattering curve, as well. Based on this fact, a bimodal spherical size distribution (eqn (1) and (2) in ESI†) was fitted to the pure resonant scattering curves (red line in Fig. 8a), assuming a lognormal distribution. The calculated bimodal size distributions for all samples are shown in Fig. 8b and c, respectively. As shown in Fig. 8b, the size of small NbB2 particles in the as-milled sample has an average size of ∼1 nm, which decreases slightly in number and in size (0.8 nm) after the first desorption and remains stable. In contrast to smaller particles, the bigger particles (Fig. 8c) grow after the first desorption in number and in size from 5 nm to ∼6 nm and remain roughly stable over the hydrogenation cycle. The bimodal size distribution and the evolution of small and larger NbB2 particles during cycling can be understood if one assumes that the NbB2 particles formed during the milling procedure are located in the grain boundaries of the hydride matrix as loosely linked mass fractals, as was suggested by SAXS results. During the 5 hours of high-energy ball milling, some clusters are merged to larger NbB2 nanoparticles (coarsening effect). That would explain the significantly lower number of larger NbB2 nanoparticles in the size range of 5 nm. Over the cycling procedure, some of the smaller NbB2 nanoparticles could migrate and agglomerate to/with larger particles; this can explain the decreasing amount of smaller NbB2 nanoparticles and the aggregate of larger NbB2 nanoparticles over the cycling procedure.

Fig. 8. (a) Pure resonant scattering curve (blue circles) of as-milled sample and its model fit (red line), mixed resonant scattering curve (red diamonds), and the total scattering curve (black squares). Evolution of isolated bimodal size distributions of (b) small and (c) large NbB2 particles over a hydrogenation cycle of the doped Li-RHC system.

Fig. 8

Open in a new tab

To study the structural effects of NbB2 nanoparticles on the hydride matrix (ultra) small-angle neutron scattering (SANS/USANS), measurements were carried out. For this reason, samples with and without additive after the first dehydrogenation process were measured. To determine the composition differences between particles of pure Li-RHC and doped Li-RHC + 0.1NbF5 systems, samples with different contrast were prepared by using lithium (7Li)- and boron (11B) isotopes, respectively. A list of samples for these measurements is given in Table 2.

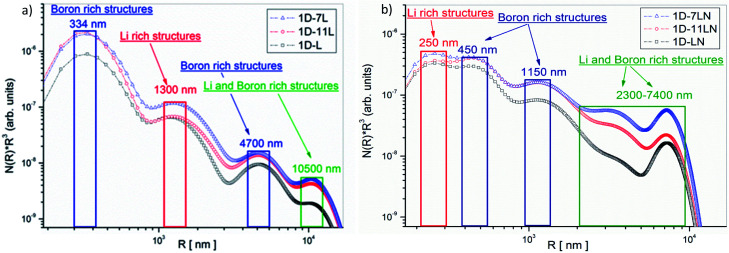
All samples were measured with SANS and USANS, respectively, in order to cover all matrix structures from the nm- to the µm-range in all samples. After calibration to absolute units, SANS and USANS curves were merged. An exemplary combined SANS/USANS result is shown in Fig. S3 (ESI).† To uncover the structural features depending only on the isotope effect, all SANS/USANS scattering curves of each sample with different isotopes were fitted simultaneously. Since contrast and number density of particles are directly correlated, only the number density of particles was fitted to pronounce the effect of isotope-containing structures. By applying this procedure and assuming spherical particles, size distributions of pure and doped Li-RHC systems were calculated. The calculated size distributions of pure and doped hydride matrices are presented in Fig. 9a and b. Both figures are plotted in a double logarithmic scale, where the x-axis represents the radii of spheres and the y-axis the volume-weighted number density of particles. The first observation of both size distributions shows that much smaller structures are present in the doped sample compared to the pure sample. Moreover, the size distributions of pure and doped Li-RHC sample, respectively, with different isotopes vary in their number densities. This can be attributed to different scattering length densities of the respective isotopes in each sample, which allow a qualitative interpretation of specific structures present in both isotope-containing samples. Due to higher coherent scattering and lower absorption cross-section of 7Li and 11B, the scattering intensities, hence the number density, of scattering structures in 7LiH–Mg11B2 and LiH–Mg11B2 should be comparable, in contrast to LiH–MgB2. Therefore, the size region around 334 nm (Fig. 9a) can be assigned to predominantly boron-containing structures. In the region at about 1300 nm the number densities of LiH–Mg11B2 and LiH–MgB2 samples are similar, however, smaller than the one of 7LiH–Mg11B2. This indicates that structures in this size range contain significantly less boron since the LiH–Mg11B2 and 7LiH–Mg11B2 samples have the same boron isotope. Thus, it can be deduced that these structures are predominantly lithium-containing structures. Likewise, it can be concluded that structures in the region at about 4700 nm are boron rich, whereas in the region at around 10 500 nm none of the size distribution curves cover each other entirely. Hence, it can be inferred that structures within this range are both lithium- and boron-containing structures. Size distributions of doped Li-RHC systems with different isotopes show a different behavior (Fig. 9b). The largest structures are much smaller (∼30%) in comparison to those found in the pure Li-RHC system. Moreover, for the above-mentioned reason, structures in the size range of 250 nm are predominantly lithium-containing, whereas structures at about 450 nm and 1150 nm are mainly boron rich. Particles in the range between 2300 nm and 7400 nm are lithium- and boron-containing, indicating a significantly better phase mixture in the Li-RHC + NbF5 sample in comparison to the pure Li-RHC sample.

Fig. 9. Size distribution of (a) pure Li-RHC and (b) doped Li-RHC + 0.1NbF5 with different isotopes after the first dehydrogenation reaction.

Fig. 9

Open in a new tab

Discussion

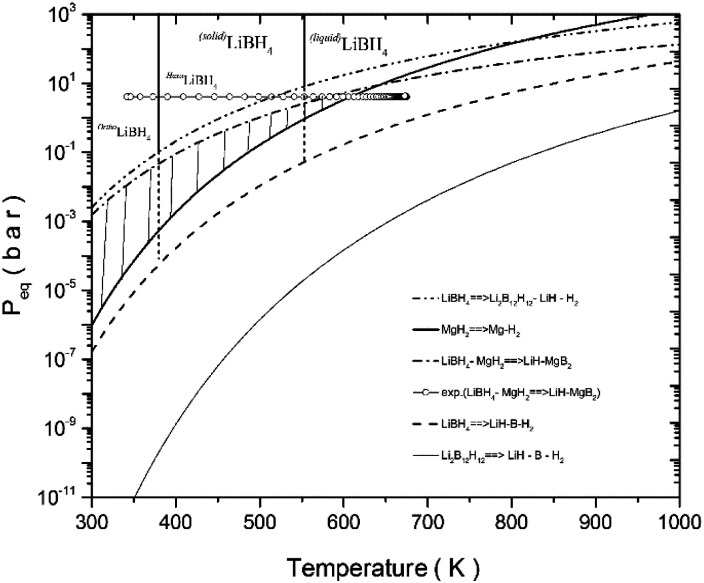
Volumetric- and calorimetric measurements have shown that the addition of NbF5 to the LiBH4–MgH2 reactive hydride composite system enhances its dehydrogenation/rehydrogenation reaction kinetics by one order of magnitude, in comparison to its pristine state (see Fig. 1). Prior to its second dehydrogenation reaction step, the pure LiBH4–MgH2 composite system undergoes an extended plateau region where no reaction occurs. This plateau period, however, is not observed in the NbF5 doped system. Nonetheless, the dehydrogenation processes of both systems proceed in two steps. This can be explained by the phase diagram of LiBH4–MgH2, MgH2, and LiBH4, as is shown in Fig. 10. The experimental dehydrogenation reaction of Li-RHC is also plotted as supportive information, using volumetric measurements. The phase region, in which the composite system could react in one step to form LiH–MgB2, is restricted by the hatched area. In this region, the equilibrium pressure of the Li-RHC system is higher than that of both individual hydrides (LiBH4 and MgH2); hence, a one-step reaction is preferred. However, most of this dashed area lies in the solid phase region of LiBH4, where the reaction kinetic is highly constrained by mass diffusion and low surface contact area of both single hydrides. These kinetic limitations are minimized by applying experimental conditions where LiBH4 is in its liquid phase. The experimental conditions applied here lie outside the hatched area (open circles, see Fig. 10). Hence, the equilibrium pressure is lower than MgH2 but higher than LiBH4, which leads to a two-step reaction. Although the pure- and doped Li-RHC system follow a two-step dehydrogenation reaction, their reaction paths are very different, as shown by in situ SR-XPD measurements (see Fig. 3).

Fig. 10. Phase diagram of orthogonal LiBH4, hexagonal LiBH4, liquefied LiBH4, Li2B12H12, MgH2, and LiBH4–MgH2 and LiBH4 with its different reaction paths. As an illustration, a volumetric desorption measurement of as-milled LiBH4–MgH2 sample. The hatched area displays the RHC phase. The values for enthalpy and entropy for the compounds and for the hydride composites were taken from ref. 30, 31 and 58–62.

Fig. 10

Open in a new tab

The doped Li-RHC follows a more complex reaction mechanism than the pure Li-RHC (reaction (4)). One difference is the formation of LiF in the as-milled state, which remains stable over the entire reaction path. The presence of LiF in the as-milled material also implies a reaction between NbF5 and the hydride matrix. However, no trace of any Nb containing phases could be detected by in situ XPD. Using the XAS, TEM, and ASAXS method, the chemical state and the local environment were determined, which indicated the presence of nano sized NbB2 particles, that remains stable over the dehydrogenation and rehydrogenation cycling processes. To understand the impact of NbB2 on the dehydrogenation/hydrogenation reaction mechanisms on the LiBH4–MgH2 composite system, kinetic models on volumetric data of the pure and doped systems are applied in order to find the rate-limiting steps for the desorption reaction of each system.63–67 Since the first desorption reaction step is the same for both systems, the second dehydrogenation reaction for both systems is examined using kinetic models listed in Table S1 (ESI).† For the fitting procedure, a transformed fraction of a maximum of 0.6 was chosen to describe the growth mechanism of MgB2 phase in both systems. The results of the transformed fraction α(t) of the pure Li-RHC and the doped Li-RHC + 0.1NbF5 systems are shown in Fig. S4 (see ESI†). Kinetics of both systems are well described by using a common model. The best fit suggests a two-dimensional growth of MgB2 phase with constant interface velocity of existing nuclei. The second best fit, which converges the curve with delay and diverges roughly two hours before the final state of the system, is obtained by a three-dimensional growth of MgB2 phase with constant interface velocity. Therefore, it can be concluded that the growth mechanisms of MgB2 in both systems are very similar. Based on these results, it can be assumed that the growth process of the MgB2 phase begins in a plate-like manner and at later stages the three-dimensional growth process becomes more dominant. Although the growth mechanisms of MgB2 in the pure and in the doped system are very similar, their respective rate conversion differs considerably. Therefore, it is worth focusing on the details of the second reaction step. After the decomposition of MgH2, metallic magnesium (Mg) remains in the solid phase, which is surrounded by the liquid phase of LiBH4. Thus, a reaction between these two phases can only occur at the solid–liquid interface by the formation of small nuclei of MgB2. However, the formation of these nuclei requires certain amount of energy, which has to be delivered by the system in order to initiate a heterogeneous nucleation and growth process of MgB2 phase. Here, the classical nucleation theory (CNT) can help to understand the underlying principles of nucleation and growth of MgB2 in this complex system as a very rough approximation. A very simple model for a heterogeneous nucleation process in CNT is given by a spherically shaped nuclei and its Gibbs free energy is:

ΔGhet = [−(4/3)πΔGvr3 + 4πγar2]S(θ) 7

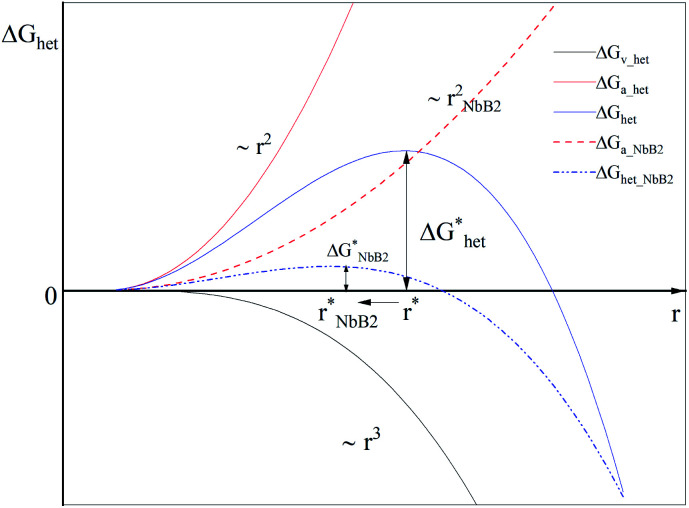
where, r represents the radius of the nucleus. ΔGv stands for the energy decrease per converted unit volume, γa represents the increased interfacial energy per converted unit area between the nucleus and the matrix, and S(θ) is the shape factor, which describes the dependency of the “wetting” angle θ over the nucleus. For the sake of simplicity, it can be assumed that S(θ) ≈ 1. Then, eqn (7) (with its two contributors (solid lines)) can be plotted over the nucleus's radius, as shown in Fig. 11.

Fig. 11. The change in Gibbs free energy required for heterogeneous nucleation for a spherical nucleus without- (blue solid line) and with NbB2 seeds (blue dashed-dotted blue line).

Fig. 11

Open in a new tab

In the beginning, the nucleus is formed by a few atoms. Consequently, there are more atoms on its surface relative to its volume. Therefore, the nucleus bulk properties are dominated by surface characteristics (∼r2) of the nucleus. At a specific nucleus size, the volume properties (∼r3) of the nucleus start to determine its bulk properties. Therefore, the Gibbs free energy undergoes a maximum point 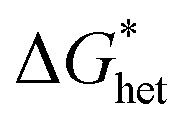Inline graphic, where both effects are mutually balanced, and the corresponding r-value is denoted as “critical nucleus size”: r*. Therefore, nuclei formed with radii less than r* are likely to decay, whereas nuclei with radii greater than r* are more likely to overcome this energy barrier and remain stable with significantly higher probabilities. Consequently, the plateau phase in the pure Li-RHC system can be assigned to the nucleation period of MgB2 phase. NbB2 and MgB2 have the same hexagonal crystal structure. Furthermore, NbB2 provides two possible matching planes for the MgB2 phase to grow on, namely: MgB2 {1011} ‖ NbB2 {1011} and MgB2 {1010} ‖ NbB2 {1010} with d-mismatch values of 2.3% and 0.7%, respectively, which are well below the critical value of 6%.68,69 As was deduced from the SAXS/ASAXS results, NbB2 nanoparticles are distributed in the grain boundaries of the matrix and, therefore, NbB2 nanoparticles provide pre-existing stable nucleation centres for the formation of the MgB2 phase. This can lead to a significant reduction in the interfacial energy γa (see Fig. 11, dashed red line) and reduction in lattice strains between NbB2 and MgB2, promoting the nucleation and growth of MgB2 phase in the doped Li-RHC system. As a consequence, not only the energy barrier 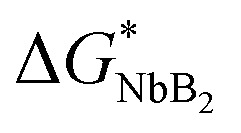Inline graphic for building stable NbB2 nuclei can be considerably reduced but also its corresponding critical nucleus size: 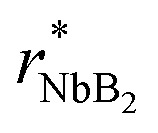Inline graphic (dashed-dotted blue line in Fig. 11), in comparison to pure Li-RHC. Since the thermodynamic driving forces are approximately the same in both systems, the volume contribution can be assumed to be comparable. Also, Mg provides a possible nucleation plane for MgB2 (MgB2 {0001} ‖ Mg {0001}); however, its directional misfit in the altitude 〈0001〉 of the hexagonal unit cell amounts up to about 48%. Taking into account that nucleation favorably does not occur on flat surfaces but along the ledges, this huge misfit (48%) would considerably increase the interfacial energy γa, which in turn increases 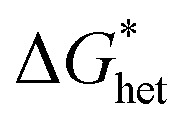Inline graphic, and r* hence hindering the nucleation and growth of MgB2 phase significantly. Moreover, since the formation of MgB2 nuclei is energy-consuming, the nucleation centers built in the pure Li-RHC system are scarcely and inhomogeneously distributed in the matrix compared to the doped system. This leads to a much slower reaction kinetics and larger MgB2 structures, which is observed in the pure Li-RHC system. In contrast, in the doped system abundant stable nuclei are provided (by the NbB2 nanoparticles) for nucleation and growth of MgB2. In addition, Zener pinning may also limit the growth of MgB2 structures in the doped system.70 Therefore, in the doped system much smaller MgB2 structures is expected, which is indeed observed by HR-TEM measurements. This is further supported by SANS/USANS results where the overall structures are observed to be smaller in the doped system in comparison to the pure system. This in turn creates significantly larger reaction surface areas in the doped Li-RHC and noticeably shorter diffusion paths relative to the pure Li-RHC system. The following schematic patch shows the key steps of the transformation of the additive, NbF5, and its role in improving the kinetic behavior of the Li-RHC: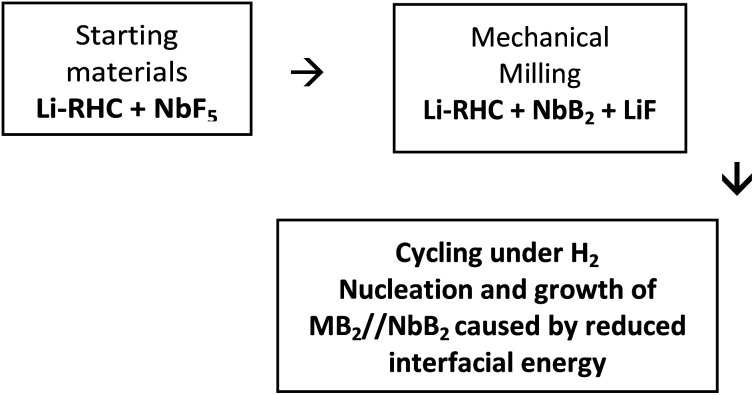graphic file with name d1ra03246a-u1.jpg

Conclusions

In this study, LiBH4–MgH2 (Li-RHC) composite system was investigated. The dehydrogenation process of the pure LiBH4–MgH2 system proceeded in two steps which were separated by an incubation period and the overall reaction was completed after roughly 45 hours. The dehydrogenation/hydrogenation kinetics of this system could significantly be enhanced by an addition of small amount of NbF5.Here, the dehydrogenation process took place in reaction steps as well, however, the overall desorption reaction was completed after only 1.5 hours. Various experimental methods were applied to shed some light onto the catalytic function of NbF5 in dehydrogenation/hydrogenation reaction of Li-RHC system. X-ray absorption spectroscopy (XAS) investigation revealed that the local environment of NbF5 is changed during the milling process to NbB2, which remained stable upon further hydrogen desorption/absorption cycles. The results of SAXS/ASAXS investigation showed a nano-size distribution of NbB2 particles in the grain boundaries of the hydride matrix which are organized as loosely bounded clusters. The model also allowed concluding that NbB2 act as nucleation seeds for nucleation and growth of MgB2 phase, as no incubation period was observed in the doped system. Therefore, it was concluded that the presence of NbB2 nanoparticles considerably lowers the interfacial tension between the matrix and MgB2 nuclei, which can lead to a smaller energy barrier for the nucleation and growth process for MgB2 phase in the doped Li-RHC system. Indeed, noticeably smaller matrix structures were observed by SANS/USANS and high-resolution transmission electron microscopy (HR-TEM) measurements in the doped system in comparison to those in the pure Li-RHC system.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-011-D1RA03246A-s001

Acknowledgments

The authors thank the great support from the BT5-Instrument staff at NIST center for Neutron Research. In particular, the authors are thankful to Dr David Mildner and Dr Steve Kline for the fruitful discussions and help for the USANS data evaluation and interpretation. The authors thank also CONICET (Consejo Nacional de Inve-tigaciones Científicas y Técnicas), ANPCyT – (Agencia Nacional de Promoción Científica y Tecnológica), for financial support to carry out this work. We would also like to thank the Metals Physics Division at Helmoltz-Zentrum Hereon for providing the TEM devices. The research leading to these results has received funding from Alexander von Humboldt Foundation, Fellowship number: ARG-1187279-GF-P.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03246a

References

  1. Züttel A., Borgschule A. and Schlapbach A., Hydrogen as a Future Energy Carrier, New York, 2008 [Google Scholar]
  2. Schlapbach L. Züttel A. Nature. 2001;414:353. doi: 10.1038/35104634. [DOI] [PubMed] [Google Scholar]
  3. U. S. D. o. Energy, Hydrogen Data Book, 2001, http://hydrogen.pnl.gov/hydrogen-data/hydrogen-properties [Google Scholar]
  4. C. o. t. Desert, Hydrogen Properties, College of the Desert, 2001 [Google Scholar]
  5. Züttel A. Wenger P. Rentsch S. Sudan P. Mauron P. Emmenegger C. J. Power Sources. 2003;118:1–7. doi: 10.1016/S0378-7753(03)00054-5. [DOI] [Google Scholar]
  6. Züttel A. Borgschulte A. Orimo S.-I. Scr. Mater. 2007;56:823–828. doi: 10.1016/j.scriptamat.2007.01.010. [DOI] [Google Scholar]
  7. Orimo S.-I. Nakamori Y. Ohba N. Miwa K. Aoki M. Towata S.-i. Züttel A. Appl. Phys. Lett. 2006;89:021920. doi: 10.1063/1.2221880. [DOI] [Google Scholar]
  8. Orimo S.-i. Nakamori Y. Eliseo J. R. Züttel A. Jensen C. M. Chem. Rev. 2007;107:4111–4132. doi: 10.1021/cr0501846. [DOI] [PubMed] [Google Scholar]
  9. Davis W. D. Mason L. S. Stegeman G. J. Am. Chem. Soc. 1949;71:2775–2781. doi: 10.1021/ja01176a052. [DOI] [Google Scholar]
  10. Hallett N. C. Johnston H. L. J. Am. Chem. Soc. 1953;75:1496–1497. doi: 10.1021/ja01102a521. [DOI] [Google Scholar]
  11. Mauron P. Buchter F. Friedrichs O. Remhof A. Bielmann M. Zwicky C. N. Züttel A. J. Phys. Chem. B. 2008;112:906–910. doi: 10.1021/jp077572r. [DOI] [PubMed] [Google Scholar]
  12. Vajo J. J. Skeith S. L. Mertens F. J. Phys. Chem. B. 2005;109:3719–3722. doi: 10.1021/jp040769o. [DOI] [PubMed] [Google Scholar]
  13. Klebanoff L. and Keller J., Final Report for the DOE Metal Hydride Center of Excellence, U.S. Department of Energy, Livermore, CA, 94551-0969, 2012 [Google Scholar]
  14. Orimo S. Nakamori Y. Kitahara G. Miwa K. Ohba N. Towata S. Züttel A. J. Alloys Compd. 2005;404–406:427–430. doi: 10.1016/j.jallcom.2004.10.091. [DOI] [Google Scholar]
  15. Puszkiel J. Gasnier A. Amica G. Gennari F. Molecules. 2020;25:163. doi: 10.3390/molecules25010163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Vajo J. J. Olson G. L. Scr. Mater. 2007;56:829–834. doi: 10.1016/j.scriptamat.2007.01.002. [DOI] [Google Scholar]
  17. Barkhordarian G. Jensen T. R. Doppiu S. Bösenberg U. Borgschulte A. Gremaud R. Cerenius Y. Dornheim M. Klassen T. Bormann R. J. Phys. Chem. C. 2008;112:2743–2749. doi: 10.1021/jp076325k. [DOI] [Google Scholar]
  18. Vajo J. J., Mertens F. O., Skeith S. L., and Balogh M. P., WO 2005/097671 A2, 2004
  19. Barkhordarian G. Klassen T. Dornheim M. Bormann R. J. Alloys Compd. 2007;440:L18–L21. doi: 10.1016/j.jallcom.2006.09.048. [DOI] [Google Scholar]
  20. Carrillo-Bucio J. L. Saldan I. Pistidda C. Karimi F. Suárez-Alcántara K. Dornheim M. Klassen T. J. Phys. Chem. C. 2017;121:4093–4102. doi: 10.1021/acs.jpcc.6b09776. [DOI] [Google Scholar]
  21. Cao H. Zhang W. Pistidda C. Puszkiel J. Milanese C. Santoru A. Karimi F. Castro Riglos M. V. Gizer G. Welter E. Bednarcik J. Etter M. Chen P. Klassen T. Dornheim M. Phys. Chem. Chem. Phys. 2017;19:32105–32115. doi: 10.1039/C7CP06826C. [DOI] [PubMed] [Google Scholar]
  22. Karimi F. Klaus Pranzas P. Pistidda C. Puszkiel J. A. Milanese C. Vainio U. Paskevicius M. Emmler T. Santoru A. Utke R. Tolkiehn M. Minella C. B. Chaudhary A.-L. Boerries S. Buckley C. E. Enzo S. Schreyer A. Klassen T. Dornheim M. Phys. Chem. Chem. Phys. 2015;17:27328–27342. doi: 10.1039/C5CP03557K. [DOI] [PubMed] [Google Scholar]
  23. Karimi F. Pranzas P. K. Hoell A. Vainio U. Welter E. Raghuwanshi V. S. Pistidda C. Dornheim M. Klassen T. Schreyer A. J. Appl. Crystallogr. 2014;47:67–75. doi: 10.1107/S1600576713031567. [DOI] [Google Scholar]
  24. Bergemann N. Pistidda C. Milanese C. Emmler T. Karimi F. Chaudhary A. L. Chierotti M. R. Klassen T. Dornheim M. Chem. Commun. 2016;52:4836–4839. doi: 10.1039/C5CC09991A. [DOI] [PubMed] [Google Scholar]
  25. Bösenberg U. Pistidda C. Tolkiehn M. Busch N. Saldan I. Suarez-Alcantara K. Arendarska A. Klassen T. Dornheim M. Int. J. Hydrogen Energy. 2014;39:9899–9903. doi: 10.1016/j.ijhydene.2014.02.068. [DOI] [Google Scholar]
  26. Puszkiel J. Gennari F. C. Arneodo Larochette P. Troiani H. E. Karimi F. Pistidda C. Gosalawit-Utke R. Jepsen J. Jensen T. R. Gundlach C. Tolkiehn M. Bellosta von Colbe J. Klassen T. Dornheim M. J. Power Sources. 2014;267:799–811. doi: 10.1016/j.jpowsour.2014.05.130. [DOI] [Google Scholar]
  27. Puszkiel J. Gennari F. Larochette P. A. Karimi F. Pistidda C. Gosalawit-Utke R. Jepsen J. Jensen T. R. Gundlach C. von Colbe J. B. Klassen T. Dornheim M. Int. J. Hydrogen Energy. 2013;38:14618–14630. doi: 10.1016/j.ijhydene.2013.08.068. [DOI] [Google Scholar]
  28. Santoru A. Pistidda C. Sørby M. H. Chierotti M. R. Garroni S. Pinatel E. Karimi F. Cao H. Bergemann N. Le T. T. Puszkiel J. Gobetto R. Baricco M. Hauback B. C. Klassen T. Dornheim M. Chem. Commun. 2016;52:11760–11763. doi: 10.1039/C6CC05777B. [DOI] [PubMed] [Google Scholar]
  29. Pistidda C. Karimi F. Garroni S. Rzeszutek A. Bonatto Minella C. Milanese C. Le T. T. Rude L. H. Skibsted J. Jensen T. R. Horstmann C. Gundlach C. Tolkiehn M. Pranzas P. K. Schreyer A. Klassen T. Dornheim M. J. Phys. Chem. C. 2014;118:28409–28417. doi: 10.1021/jp508780b. [DOI] [Google Scholar]
  30. El Kharbachi A. Pinatel E. Nuta I. Baricco M. Calphad. 2012;39:80–90. doi: 10.1016/j.calphad.2012.08.005. [DOI] [Google Scholar]
  31. Pinkerton F. E. Meyer M. S. Meisner G. P. Balogh M. P. Vajo J. J. J. Phys. Chem. C. 2007;111:12881–12885. doi: 10.1021/jp0742867. [DOI] [Google Scholar]
  32. Schulz J. H. R. and Boily S., Can. Patent, Ser. No. 2207149, 1999
  33. Bösenberg U. Ravnsbæk D. B. Hagemann H. D'Anna V. Minella C. B. Pistidda C. van Beek W. Jensen T. R. Bormann R. Dornheim M. J. Phys. Chem. C. 2010;114:15212–15217. doi: 10.1021/jp104814u. [DOI] [Google Scholar]
  34. Schulz J. H. R., Boily S., Can. Patent, Ser. e Nr. 2207149, 1999
  35. Hammersley A. P., FIT2D: An Introduction and Overview, ESRF Internal Report, ESRF97HA02T, FIT2D: An Introduction and Overview, 1997
  36. Allmann R. Hinek R. Acta Crystallogr., Sect. A: Found. Crystallogr. 2007;63:412–417. doi: 10.1107/S0108767307038081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Klementiev K. V., XAFSmass, freeware:www.cells.es/Beam-lines/CLAESS/software/xafsmass.html2012:2012, [15-May-2012]
  38. Ravel B. Newville M. J. Synchrotron Radiat. 2005;12:537–541. doi: 10.1107/S0909049505012719. [DOI] [PubMed] [Google Scholar]
  39. Cromer D. T. Liberman D. A. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1981;37:267–268. doi: 10.1107/S0567739481000600. [DOI] [Google Scholar]
  40. Gilles R. Ostermann A. Petry W. J. Appl. Crystallogr. 2007;40:s428–s432. doi: 10.1107/S0021889807006310. [DOI] [Google Scholar]
  41. Cromer D. T. J. Chem. Phys. 1970;53:1891. doi: 10.1063/1.1674266. [DOI] [Google Scholar]
  42. Keiderling U. Appl. Phys. A. 2002;74:s1455–s1457. doi: 10.1007/s003390201561. [DOI] [Google Scholar]
  43. Barker J. G. Glinka C. J. Moyer J. J. Kim M. H. Drews A. R. Agamalian M. J. Appl. Crystallogr. 2005;38:1004–1011. doi: 10.1107/S0021889805032103. [DOI] [Google Scholar]
  44. Goerigk G. Huber K. Mattern N. Williamson D. L. Eur. Phys. J.: Spec. Top. 2012;208:259–274. [Google Scholar]
  45. Micrograph Digital (License No. 90294175)
  46. JEMs (License No. Ieb59ybdflumh)
  47. Jepsen J. Milanese C. Puszkiel J. Girella A. Schiavo B. Lozano G. A. Capurso G. Bellosta von Colbe J. M. Marini A. Kabelac S. Dornheim M. Klassen T. Energies. 2018;11:1081. doi: 10.3390/en11051081. [DOI] [Google Scholar]
  48. Karimi F. Riglos M. V. C. Santoru A. Hoell A. Raghuwanshi V. S. Milanese C. Bergemann N. Pistidda C. Nolis P. Baro M. D. Gizer G. Le T.-T. Pranzas P. K. Dornheim M. Klassen T. Schreyer A. Puszkiel J. J. Phys. Chem. C. 2018;122:11671–11681. doi: 10.1021/acs.jpcc.8b02258. [DOI] [Google Scholar]
  49. Hartman M. R. Rush J. J. Udovic T. J. Bowman Jr R. C. Hwang S.-J. J. Solid State Chem. 2007;180:1298–1305. doi: 10.1016/j.jssc.2007.01.031. [DOI] [Google Scholar]
  50. Kang J. K. Kim S. Y. Han Y. S. Muller R. P. Goddard W. A. Appl. Phys. Lett. 2005;87:111904. doi: 10.1063/1.2042632. [DOI] [Google Scholar]
  51. Cherny A. Y. Anitas E. M. Osipov V. A. Kuklin A. I. Phys. Chem. Chem. Phys. 2019;21:12748–12762. doi: 10.1039/C9CP00783K. [DOI] [PubMed] [Google Scholar]
  52. Stuhrmann H. B., Resonance scattering in macromolecular structure research, 1985, pp. 123–163 [Google Scholar]
  53. Guilleaume B. Blaul J. Ballauff M. Wittemann M. Rehahn M. Goerigk G. Eur. Phys. J. E: Soft Matter Biol. Phys. 2002;8:299–309. doi: 10.1140/epje/i2001-10105-8. [DOI] [PubMed] [Google Scholar]
  54. Simon J.-P. J. Appl. Crystallogr. 2007;40:s1–s9. doi: 10.1107/S0021889806055579. [DOI] [Google Scholar]
  55. Goerigk G. Haubold H.-G. Lyon O. Simon J.-P. J. Appl. Crystallogr. 2003;36:425–429. doi: 10.1107/S0021889803000542. [DOI] [Google Scholar]
  56. Brumberger H., Modern Aspects of Small-Angle Scattering, Springer Science & Business Media, Como, Italy, 2013 [Google Scholar]
  57. Stuhrmann H. B. Q. Rev. Biophys. 1981;14:433–462. doi: 10.1017/S0033583500002365. [DOI] [PubMed] [Google Scholar]
  58. Stampfer J. F. Holley C. E. Suttle J. F. J. Am. Chem. Soc. 1960;82:3504–3508. doi: 10.1021/ja01499a006. [DOI] [Google Scholar]
  59. Dematteis E. M. Roedern E. Pinatel E. R. Corno M. Jensen T. R. Baricco M. RSC Adv. 2016;6:60101–60108. doi: 10.1039/C6RA09301A. [DOI] [Google Scholar]
  60. Ozolins V. Majzoub E. H. Wolverton C. J. Am. Chem. Soc. 2009;131:230–237. doi: 10.1021/ja8066429. [DOI] [PubMed] [Google Scholar]
  61. Dornheim M. Eigen N. Barkhordarian G. Klassen T. Bormann R. Adv. Eng. Mater. 2006;8:377–385. doi: 10.1002/adem.200600018. [DOI] [Google Scholar]
  62. Ohba N. Miwa K. Aoki M. Noritake T. Towata S.-i. Nakamori Y. Orimo S.-i. Züttel A. Phys. Rev. B. 2006;74:075110. doi: 10.1103/PhysRevB.74.075110. [DOI] [Google Scholar]
  63. Burbelko A. A. Fraś E. Kapturkiewicz W. Mater. Sci. Eng., A. 2005;413–414:429–434. doi: 10.1016/j.msea.2005.08.161. [DOI] [Google Scholar]
  64. Burger M., Capasso V. and Micheletti A., in Math Everywhere: Deterministic and Stochastic Modelling in Biomedicine, Economics and Industry. Dedicated to the 60th Birthday of Vincenzo Capasso, ed. G. Aletti, A. Micheletti, D. Morale and M. Burger, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 63–76, 10.1007/978-3-540-44446-6_6 [DOI] [Google Scholar]
  65. Avrami M. J. Chem. Phys. 1939;7:1103–1112. doi: 10.1063/1.1750380. [DOI] [Google Scholar]
  66. Avrami M. J. Chem. Phys. 1940;8:212–224. doi: 10.1063/1.1750631. [DOI] [Google Scholar]
  67. Avrami M. J. Chem. Phys. 1941;9:177–184. doi: 10.1063/1.1750872. [DOI] [Google Scholar]
  68. Zhang M. X. Kelly P. M. Scr. Mater. 2005;52:963–968. doi: 10.1016/j.scriptamat.2005.01.040. [DOI] [Google Scholar]
  69. Zhang M. X. Kelly P. M. Acta Mater. 2005;53:1073–1084. doi: 10.1016/j.actamat.2004.11.007. [DOI] [Google Scholar]
  70. Zhou J. Li C. Guan M. Ren F. Wang X. Zhang S. Zhao B. Modell. Simul. Mater. Sci. Eng. 2017;25:065008. doi: 10.1088/1361-651X/aa6cfb. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-011-D1RA03246A-s001
RA-011-D1RA03246A-s001.pdf (532.5KB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES