Abstract
False negative rates of severe acute respiratory coronavirus 2 diagnostic tests, together with selection bias due to prioritized testing can result in inaccurate modeling of COVID‐19 transmission dynamics based on reported “case” counts. We propose an extension of the widely used Susceptible‐Exposed‐Infected‐Removed (SEIR) model that accounts for misclassification error and selection bias, and derive an analytic expression for the basic reproduction number as a function of false negative rates of the diagnostic tests and selection probabilities for getting tested. Analyzing data from the first two waves of the pandemic in India, we show that correcting for misclassification and selection leads to more accurate prediction in a test sample. We provide estimates of undetected infections and deaths between April 1, 2020 and August 31, 2021. At the end of the first wave in India, the estimated under‐reporting factor for cases was at 11.1 (95% CI: 10.7,11.5) and for deaths at 3.58 (95% CI: 3.5,3.66) as of February 1, 2021, while they change to 19.2 (95% CI: 17.9, 19.9) and 4.55 (95% CI: 4.32, 4.68) as of July 1, 2021. Equivalently, 9.0% (95% CI: 8.7%, 9.3%) and 5.2% (95% CI: 5.0%, 5.6%) of total estimated infections were reported on these two dates, while 27.9% (95% CI: 27.3%, 28.6%) and 22% (95% CI: 21.4%, 23.1%) of estimated total deaths were reported. Extensive simulation studies demonstrate the effect of misclassification and selection on estimation of and prediction of future infections. A R‐package SEIRfansy is developed for broader dissemination.
Keywords: compartmental models, infection fatality rate, R package SEIRfansy , reproduction number, selection bias, sensitivity, undetected infections
1. INTRODUCTION
The COVID‐19 pandemic, caused by severe acute respiratory coronavirus 2 (SARS‐CoV‐2), first identified in Wuhan, China in December 2019, escalated to a global pandemic leading to more than 220 million cases and more than 4.5 million reported deaths worldwide as of September 6, 2021. 1 While rapid testing for COVID‐19 is an important component of nonpharmaceutical intervention strategies 2 using either a reverse transcription polymerase chain reaction (RT‐PCR) test, rapid antigen tests or the less frequently used computed tomography imaging of the chest, 3 concerns about false negative test results remain a practical and methodological challenge. Evidence‐based clinical understanding supported by robust statistical tools to identify such misclassification errors is a critical step for mitigating COVID‐19 transmission risk through effective contact tracing and isolation. 4
Extant literature on false negative results include Yang et al 5 who describe a study of 213 hospitalized patients, where 11% of sputum‐, 27% of nasal‐ and 40% of throat‐based samples were declared false negatives after a week. Studying publicly available time‐series data of laboratory tests, Burstyn et al 6 develop Bayesian methods for understanding misclassification errors. A systematic review 7 of five studies (covering 957 patients) reports a false negative rate range of 2% to 29% . Existing studies focus more on false negative RT‐PCR results because they might provide a false sense of security to truly infected and infectious individuals and lead to further spread of the disease. In addition, false positive rates of diagnostic tests appear to be much lower than the corresponding false negative rates. 8 , 9
Models for infectious disease spread such as the ones proposed by the Institute of Health Metrics and Evaluation‐ University of Washington, Seattle 10 and the Imperial College London 11 have become widely popular as forecasting tools. Such multicompartment epidemiological models, based on the daily time series of infected, recovered, and fatal cases, have been effectively used to model the full course of disease transmission owing to their generalizability, robustness, and accuracy. 12 The extended Susceptible‐Infected‐Removed (SIR) model, 13 building on the standard SIR 14 model, provides a tool to directly incorporate various types of time‐varying interventions. Another extension, the SAPHIRE model, 15 accounts for the infectiousness of asymptomatic 16 and presymptomatic 17 individuals in the population, time‐varying ascertainment rates, transmission rates and population movement. Despite these extensions, there is essentially no statistical methodology to formally address the key issue of false negatives in tests in these mechanistic models, which could lead to a larger number of unreported cases, bias the model estimates and subsequent inference.
An additional concern surrounding testing is the selection bias resulting from prioritized testing for individuals or sub‐groups, driven by a combination of severity of symptoms and types of occupation as a requirement prior to undergoing medical procedures, travel requirements or preexisting health conditions. As a result, predicted case‐counts and estimated parameters deviate from the population truth. Estimating the underlying selection model and sensitivity analyses are feasible when we have extensive information available on why someone got tested. 18 , 19 In the context of COVID‐19 testing, such biases impact estimates of disease prevalence and the effective reproduction number unless a random sample of the population is tested and/or testing becomes abundantly available for everyone. Moreover, false positive/negative rates of tests interact with selection bias in complex ways: Dempsey 20 notes the inability of current methods to simultaneously account for selection bias and measurement error, and makes several suggestions on addressing these two issues.
In this paper, we propose a Bayesian compartmental epidemiological model which accounts for false negatives in diagnostic tests by adding extra compartments for false negatives to the standard SEIR model 21 , 22 assuming a known value of the test sensitivity (). Our method provides estimated numbers of total cases and deaths, both reported and unreported, characterizes uncertainty in estimation via posterior sampling. To facilitate decision‐making and public use, we have contributed an r‐package SEIRfansy (faLSE nEGATIVE rate and syMPTOM) to implement these methods.
We illustrate our methods by analyzing the transmission patterns of COVID‐19 in India from April 1, 2020 to August 31, 2021. While our method can be applied more generally, we have focused on India for three main reasons—first, the devastating second wave has caused an unprecedented catastrophe in India, with more than 440 000 reported deaths on September 6, 2021 and an worst case estimate of roughly 4.2 million deaths. 23 Second, different stages of nonpharmaceutical interventions in India are well‐documented and the public health policies were roughly uniform throughout the country in Wave 1, but not in Wave 2, providing two different test cases for our methods. Third, India is one of the few countries where there has been four national serosurveys, providing an empirical estimate of the prevalence of past infections, this helps us to calibrate our estimates for latent infections. 24
The rest of the paper is organized as follows. In Section 2, we introduce the method used for data analysis and simulation, accompanied by key metrics for evaluation. We also describe extensions to incorporate (i) time‐varying fatality rates (ii) symptom‐based testing and general selection bias with details of extensions relegated to Appendix S1. Section 3 contains the results for analysis of the data from India. Section 4 contains extensive simulation studies to assess the performance of our model under misclassification and symptom‐driven selection. Section 5 provides a summary discussion. We note here that earlier contributions by a subset of the current authors 25 , 26 focused on the serosurvey data from Delhi, India and a systematic comparison of five different epidemiological models, respectively. In contrast, this paper provides an extensive analysis of the two waves of COVID‐19 pandemic in India (vide Section 3), and delineates the effect of misclassification and selection via extensive simulation study.
2. METHODS
2.1. Developing the SEIR‐fansy model
Compartmental epidemiological models such as the SEIR model 21 , 22 for studying the spread of an infectious disease divides the entire population into various compartments per their current status (e.g., SEIR: Susceptible‐S, Exposed‐E, Infectious‐I, Removed‐R), and model the flow patterns between these compartments over time.
We propose an extension of the SEIR model (Figure 1) that directly incorporates false negative rates of the diagnostic tests and untested infectious compartments into the model. We assume that the untested compartment primarily consists of asymptomatic individuals and divide the tested individuals into “Tested Positive” (which consists of true positives) and negative (“False Negative”) compartments. Further, as in the base‐model, exposed individuals are included in the E compartment. Our model specification excludes a small fraction of people who are diagnosed directly based on only symptoms, without ever having a diagnostic test. After virus exposure (with or without subsequent testing), infectious people will then either recover from disease or die. Compartments for these two outcomes are defined separately for reported and unreported cases. Thus, compared to the standard SEIR model, 21 we have retained the S and E compartments but have split the I compartment into U, and F compartments. The removed (R) compartment in the SEIR model has been further split into four compartments ‐ RU, DU, RR, and DR, respectively. The precise definitions for the compartments and parameters as shown in Figure 1 are described below. Note that in our model, we consider two different types of unreported infectious individuals—untested (U) and false negatives (F). These two compartments, along with the the tested positive individuals, constitute the infectious component and play a crucial role in the disease transmission dynamics. On the other hand, the exposed (E) individuals, although themselves infected, do not transmit the disease to other (susceptible) individuals during the latent incubation period. Furthermore, the “tested” compartment (T) does not include the tested individuals who truly do not carry the virus (ie, true negatives). The reason that we do not model truly negative individuals explicitly is that they do not have any impact on the disease transmission dynamics and hence, can be treated same as the individuals in the S compartment.
FIGURE 1.
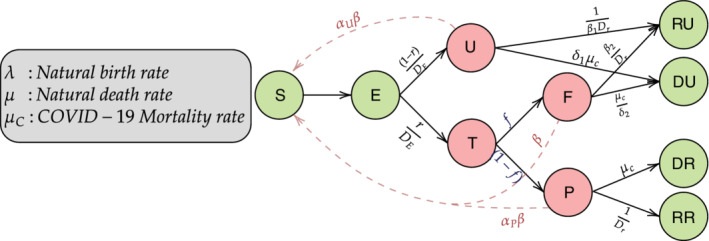
Compartmental model incorporating false negative test results. There are total 10 compartments in this model. The S and E compartments corresponds to Susceptible (who have not been infected till now) and Exposed (who are infected with the virus but are still not infectious). There are three infectious compartments, namely, U (Untested infectious), P (Tested Positive), and F (Tested False Negative). Finally the four compartments RU, RR, DU, and DR denote the Recovered Unreported, Recovered Reported, Deceased Unreported, and Deceased Reported, respectively. corresponds to the rate of transmission by false negative (F) individuals, while for U and P, it is multiplied by scaling factors and . Other parameters include which corresponds to the incubation period, f which is the false negative rate (= 1‐sensitivity) and r which denotes the rate of ascertainment. , , and correspond to recovery period for P, and F, respectively, while , , , and denote the death rates for P, U, and F, respectively
2.2. Compartmental parameters
We model the duration of stay in a particular compartment by an exponential distribution with a specified rate parameter, and the system of differential equations given by (1) describes the underlying transmission dynamics. Although transitions between compartments happen in continuous time, we adopt the standard practice 16 of considering a discretized system to implement our model as data are collected at a daily level. Below, we define the main parameters of our model (vide Figure 1) that specify the underlying transmission dynamics:
: Rate of transmission of infection by false negative individuals.
: Ratio of rate of transmission by tested positive patients relative to false negatives. We assume , since patients who are tested positive are likely to adopt isolation measures, where the chance of spreading the disease is less than that of false negative patients who are mostly unaware of their infectious status.
: Scaling factor for the rate of transmission by untested individuals. is assumed to be < 1 as compartment U mostly consists of asymptomatic or mildly symptomatic cases who are on average likely to be less contagious than those having symptoms.
: Incubation period (in number of days).
: Mean number of days till recovery for those who test positive.
: Mean number of days for the return of test result.
: Death rate due to COVID‐19 infection, equivalent to the inverse of the average number of days from disease onset to death multiplied by the true infection fatality rate.
, : Natural birth and death rates in the population. These are assumed to be equal for the sake of simplicity.
r: Probability of being tested for infection, akin to the ascertainment rate used in other comparable SEIR‐type models.
f: False negative probability of RT‐PCR test.
and : Scaling factors for rate of recovery for undetected and false negative individuals, respectively. Both and are assumed to be less than 1. The severity of symptoms in untested individuals is assumed to be less than those tested positive. Consequently, untested individuals are assumed to recover faster than those who tested positive. The time to recovery for false negatives is assumed to be larger than those who tested positive since their absence of diagnosis and consequently formal hospital treatment.
and : Scaling factors for death rate for untested and false negative individuals, respectively. Both and are assumed to be less than 1. The untested individuals are assumed to have a smaller probability of dying relative to those who test positive, since untested people are mostly asymptomatic. False negatives are assumed to have a higher probability of dying relative to those who test positive due to absence of diagnosis and consequently seek hospital treatment.
In the following sections we assume and r to be time‐varying quantities, with and being their respective values at time t. We briefly describe the transmission dynamics of our model. First, the susceptible (S) individuals come in contact with any infected individual at a given time at the four infectious compartments/nodes U, T, F, and P with rates , , , and , respectively. After getting infected, susceptible people transition to the exposed node, and after the incubation period, become infectious and move into either the untested (U) or the tested (T) node with rates and , respectively. It is important to note that the E node contains only infected people, and so if they are tested after the subclinical latency period they should all be positives with a perfect test. However, due to limited testing and asymptomatic diseases, only those who are tested are reported to be positive or negative after days with rate and , respectively. Those in the untested compartment (U) move to the recovered unreported node (RU) and the death unreported node (DU) with rates and while the tested positive people move to the recovered reported node (RR) and death reported node (DR) with rates and , respectively. Finally, the tested false negative people (F) move to the the recovered unreported (RU) and death unreported (DU) with rates and , respectively. We shall use , , , , , , , and to denote the number of people in the aforementioned compartments on the tth day.
2.2.1. Differential equations
The number of individuals at time t at each node in Figure 1 follows the set of differential equations described below. Here we make a simplifying assumption that the time required from getting tested to obtaining the result or is hard to identify and to estimate when treated as a separate parameter. In the main text, we assume , implying that the T node is instantaneous, that is, individuals do not spend any time at that node and move to either F or P immediately. This assumption makes the system of equations simpler and leads to more stable estimates. We describe the case of noninstantaneous testing in section S.1.3 in Appendix S1. The following are the differential equations corresponding to instantaneous testing.
| (1) |
The individuals in the exposed compartment are not infectious yet, as the virus is in subclinical latency and not contagious. In fact, the number of days for an individual in the E compartment to become infectious (ie, to enter either P, or U) is assumed to follow an exponential distribution with mean days. The first term in the differential equation for S compartment, that is, denotes the incoming infected individuals which depends on the infection/transmission rate , the number of susceptible individuals , and the number of infectious individuals and . These three compartments are the only that can spread infection. The system of differential equations in (1) provides the evolution dynamics of the compartmental counts over time. It is worth pointing out that while our assumption of mean incubation period is consistent with extant literature 27 for the ancestral, alpha and delta variants, the reduced generation interval for Omicron does not affect our data analysis as it ends in August 2021 before Omicron emerged. To investigate the effect of on key metrics, we have performed a new sensitivity analysis by varying the latency period from 2 to 6 days (section S.7.2 in Appendix S1). We observe that the predicted number of active cases and estimates of exhibit small but observable variation with changing values of , with the overall trend remaining similar. Thus, while our assumptions are guided by the values reported for the ancestral, alpha, and delta variants predominant during our observation period in India, the latency and incubation periods are subject to change with emerging variants of COVID‐19 like Omicron with shorter incubation period. Future studies would need to incorporate this external information using reliable and accurate estimates 28 of . Different periods of the pandemic will need different values of based on the dominant variant.
To obtain predictions for derived quantities of interest, such as the reported and total active case counts starting from the primary compartmental counts, we refer to the formulae given in Table 1.
TABLE 1.
Variables of interest and their expressions in terms of model compartments as functions of time
| Counts of interest | Notation (at time t) | |
|---|---|---|
| Reported active cases |
|
|
| Unreported active cases |
|
|
| Total active cases |
|
|
| Reported cumulative cases |
|
|
| Unreported cumulative cases |
|
|
| Total cumulative cases |
|
|
| Reported deaths |
|
|
| Unreported deaths |
|
|
| Total deaths |
|
The basic reproduction number under these set of differential equations is given by
| (2) |
where,
The derivation of has been deferred to Section S.1.1.1 of Appendix S1. With the system of differential equations governing our compartmental model and the expression of , we describe the estimation strategy for the key parameters in our model. We fix the values of most parameters guided by previous studies (details in Section S.3.1 of Appendix S1), and use data‐based estimates for the time‐varying parameters and for each of the predetermined time intervals. Toward this, we assume a multinomial likelihood for the compartmental counts (see Section 2.3.2) and use a Metropolis‐Hastings algorithm (Section 2.3.4) to draw samples from the posterior distribution of the parameters and .
2.3. Estimation
Typically, one can solve the system of equations by assuming initialization constraints/values, then fixing certain key parameters and allowing parameters of interest to be estimated based on data. We assume there are two key time‐varying parameters—the transmission rate and ascertainment rate . For our analysis, we have split the time period of interest (training period) into smaller subintervals, within which the values of and do not change. However, as we move from one sub‐interval to another, we allow the parameter values to vary. This assumption reflects the natural progression of the pandemic coupled with changes in intervention strategies in the population under study. In this context, it is natural to ask if only two unknown parameters are sufficient to describe a complex model like the one at hand. Here, we are only estimating the parameters and because the other parameters like , , , etc. have been studied extensively using data across the world, and reliable estimates have been obtained by various studies on different populations (see the references in Section 3.1 of Appendix S1). The effect of changing the fixed parameter values or initial values on our analysis has been studied in Section S.7 of Appendix S1. The steps for estimating the parameters are outlined as follows. The brief outline of the procedure is provided in Figure 2.
FIGURE 2.
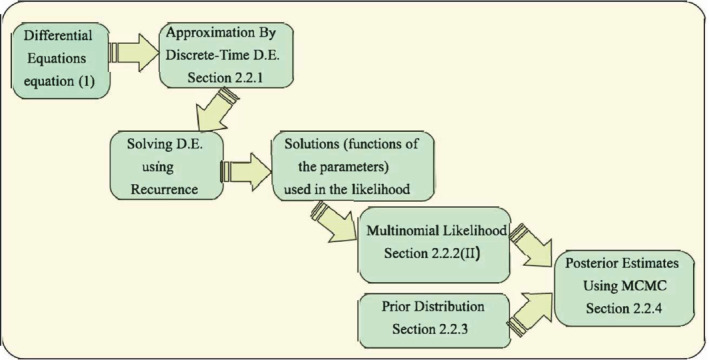
Flowchart showing the estimation process of misclassification model using a Metropolis‐Hastings Markov chain Monte Carlo algorithm
2.3.1. Solving the system of differential equations
Since it is difficult to obtain analytical solutions to this set of differential equations, we use approximations to solve them. Further, we only need the compartmental values at discrete time points (daily values, in our case). One can use discrete time approximations of the continuous time differential equations. Such approximations are common in epidemiological applications and have been empirically shown to be quite accurate. The differential equations presented in Section 2.3.1 are replaced by a set of difference equations. That is, the derivative (instantaneous rate of change) of number of cases for any compartment X with respect to time t given by is approximated by the difference between that compartment counts on the th day and the tth day, . The discrete time recurrence relations are provided below:
| (3) |
An examination of (3) reveals that the state variables at time depend not only on the state space at time t but also the transmission parameters at time t. As before, some of these parameters are assumed to be fixed, while others (viz., and ) are the unknown parameters of interest. Knowing the initial compartment values (at ) along with the entire set of parameters (including initial values and ) allows us to generate compartmental values for the entire time period under investigation (say, d days) in an iterative manner using the system of difference equations (3) above. This enables us to calculate the likelihood function at any given value of and using one of the underlying functions (discussed in Section 2.3.2).
We use a Bayesian inferential framework via Markov chain Monte Carlo (MCMC) sampling for estimating the key parameters and . Our choice of a Bayesian paradigm over a frequentist one is motivated by two main concerns. First, iterated algorithms for finding the maximum likelihood estimate are more prone to returning a local optimum rather than the global maxima in presence of multiple parameters in a nonlinear model. 30 , 31 In our context, for wave 1, we have divided the entire time period into 12 time intervals, based on the different nonpharmaceutical interventions by the government. This necessitates estimating 24 parameters (transmission rate and ascertainment rate ) corresponding to the 12 periods. Properly designed posterior sampling algorithms are more likely to converge to more stable estimates in such cases. Second, Bayesian methods allow automatic uncertainty quantification and inference on complex functions of the underlying parameters without resorting to large sample approximations like the delta theorem.
Since the full conditional distributions for and do not have analytically tractable conjugate forms, posterior computation can proceed via a Metropolis‐Hastings algorithm using the likelihood as a function of and and the prior specification in Section 2.3.3. We observe good computational efficiency for our sampler indicated by rapid convergence, adequate mixing and low autocorrelation, and point estimates are obtained via summary statistics based on the posterior draws.
Before writing the skeletal algorithm, let us introduce some notation for the rest of the estimation procedure. Let s denote the total number of time periods. Then for , let and denote the values of parameters and r in the jth period (since, parameters are assumed to remain constant within each time period). Define and and . Also, let and denote the posterior samples of and drawn at the ith iteration of the MCMC algorithm. Algorithm 1 presents an outline of the iterative estimation algorithm.
Algorithm 1. Estimation algorithm.
1.

The following sections discuss how the likelihood is formulated and choice of priors in greater detail.
2.3.2. Distributional assumptions and likelihood
We assume that the joint distribution of the counts transitioning to each compartment at a given time follows a multinomial distribution. For example, from the exposed node, one can move to the positive, false negative, or untested nodes, or they may die due to natural causes. Let denote the number of individuals moving from X to Y compartment at time t with denoting the number of individuals in compartment X dying at time t. Similarly denote the probability of an individual moving from X to Y compartment at time t and denotes the probability of an individual in compartment X dying at time t.
| (4) |
The complete model with the distributions of latent nodes have been described in details in Section S.2.3.2 of Appendix S1, and we describe the likelihood next.
Case I: Only using data on daily new cases: For this situation, we assume that given the parameters, the number of new confirmed cases on the the tth day depends only on the number of exposed individuals on the previous day. Let the number of newly reported cases on day t, , say, follow a distribution with probability mass function (pmf) . Then, we can write the likelihood of and , where s denotes the number of disjoint time periods, as:
Here, d denotes the last day used in model‐fitting. We assume that follows a Binomial distribution with size and probability . This is a natural corollary of the assumption that counts corresponding to all the compartments jointly follow a multinomial distribution. Thus the daily number of positive cases marginally will follow a binomial distribution. Alternatively one can assume that follows a Poisson distribution with rate , where is the conditional expectation of the number of exposed at day .
Case II: When daily data on new cases, recoveries and deaths are available. Marginally, the distribution for the daily number of positive cases remains the same as before. For the recovered and death nodes, the joint distribution is again a multinomial distribution given . Let , , and denote the number of new reported cases, recoveries and deaths, respectively, on the tth day. If , , and follow the distribution with pmf . Then, we can write the likelihood of and where s denotes the number of time periods as follows:
The number of daily new reported positive cases depends only on the number of exposed individuals on the previous day, while the number of new reported recoveries and the new reported deaths depend on only the number of reported active cases on the previous day. This leads to the following calculation.
From (4),
The values of and are required for formulating the likelihood, as and depend on them. and are used as the size parameters in the binomial and multinomial distributions respectively. These size parameters are obtained as deterministic functions of and by applying the discrete time differential equations (3) recursively (see Section 2.3.1). These deterministic functions of and are then plugged into the likelihood used in our Metropolis‐Hastings algorithm to draw posterior samples of the parameters as well as the compartmental counts derived as functions of and as described in Table 1.
In case of lack of reliable data on recoveries and deaths, a simpler Poisson or Binomial likelihood might be a more pragmatic modeling choice compared to the multinomial likelihood. Note that in order to write the likelihood of the observed data we first need to represent the observed variables in terms of the compartmental counts which can be done according to Table 1. It is important to remember that we are modeling the number of active cases, recoveries and deaths first and using these quantities we obtain estimates of cumulative cases and deaths. We will assess our models primarily based on their performance in predicting active cases as the other case‐counts are largely dependent on this estimated value.
2.3.3. Choice of priors
For the parameter , we assume a prior distribution while for , we assume an improper noninformative flat prior:
Alternatively, one may consider a log‐normal prior for and . This will induce an implicit prior distribution on the ascertainment rate by virtue of the relationship between , , and . Our choice of noninformative priors reflects the lack of substantive a priori knowledge about these parameters.
2.3.4. Posterior sampling
Having specified the likelihood and the prior distribution, we draw samples for and from the corresponding posterior distributions using a Metropolis‐Hastings sampling algorithm with a Gaussian random walk proposal distribution. With new draws of and , we approximate the expected number of individuals in each compartment at each time point t conditioned on the drawn values of and using (3). This enables us to express the likelihood according to Section 2.3.2. We ran the MH sampling algorithm for 200 000 iterations with a burn‐in of 100 000 and retained every 100th draw to reduce autocorrelation. We assessed the convergence and adequate mixing of the chain by using the Gelman and Rubin diagnostic measure 31 and trace plots. The thinning bins were determined based on the autocorrelation plot to ensure successive MCMC draws used for estimation are moderately uncorrelated. The diagnostic analysis is presented in Section S.6 in Appendix S1. Finally, the mean of the draws of and are used as Bayesian posterior mean‐based estimates of and . For every posterior draw of and , we use (3) to generate counts of the different compartments at each time point t. The generated counts serve as parameters for generating posterior estimates of the compartmental counts, using the sampling distributions specified in Section S.2.3.2 of Appendix S1. All compartmental counts are rounded off to the nearest integer. We repeat this for all time points t. The 95% Bayesian credible interval for all parameters are calculated using the 2.5% quantile and 97.5% quantile of the posterior draws (after thinning). The same is done for the estimated counts in each compartment for all time points. The model obtained using the likelihood described in the Section 2.3.2 and the priors will be hereby referred to as the multinomial‐2‐parameter model.
Extensions: With the above structure as our primary analytic foundation, we extend the model in three primary directions to better adapt to real data and allow more flexibility. Details are deferred to Section S.2 of Appendix S1.
- Extension 1. Time‐varying case‐fatality rate (mCFR) To address the ever‐changing nature of the case‐fatality rates during the course of this pandemic, we propose the modified CFR or mCFR which includes only the removed cases in the denominator.
Figure S2 shows variation of mCFR across across time observed in real data. Hence, we hypothesize that modeling mCFR as a time‐varying quantity will improve the prediction of active cases and deaths, and introduce a third time‐varying parameter called the mCFR along with and in the previous multinomial likelihood. Extension 2. Testing of infectious people based on symptoms As the probability of an infected individual getting tested depends largely on the symptoms, we split the Exposed (E) compartment into three nodes: Severe Symptomatic (Se), Mild Symptomatic (Mi), and Asymptomatic (As). The new set of differential equations (particularly for the nodes nodes P, U, and F), schematic diagram as well as parameter choices are discussed in great details in the Section S.2.2 of Appendix S1. This model is nearly equivalent to the multinomial‐2‐parameter model described in Section S.2.2 in Appendix S1, and a similar estimation strategy will apply as this is a simple reparameterization of our original model. We shall refer to extensions 1 and 2 as multinomial‐3‐parameter and Multinomial Symptoms models, respectively.
Extension 3. Selection model: Who is getting tested? Considering only testing of truly infected individuals cannot tell us the complete story, to understand the selection bias in testing we have to consider the probability of being tested in susceptible and unexposed individuals as well due a variety of other causes. We extend the multinomial‐2‐parameter model to incorporate the testing mechanism. Here the key ideas is that individuals with severe symptoms are always tested provided sufficient tests are available, and then the remaining tests are divided among those with mild symptoms and asymptomatics according to some given allocation rule that is independent of their true disease status given observed symptoms. The schematic model and other analytic details are given in Section S.2.3 of Appendix S1.
2.4. Data sources and analytic strategy for COVID‐19 in India
We analyze the COVID transmission dynamics in India from a period of April 1, 2020 to August 31, 2021, focusing primarily on misclassification using the multinomial‐2‐parameter model, given the lack of disaggregated testing data for India. Further, we divide this period into two parts corresponding to wave 1 and wave 2. For wave 1, we consider the period from April 1, 2020 to January 31, 2021 while for wave 2, we consider the training period February 1, 2021 to June 30, 2021. We also consider the period July 1 to August 31, 2021 as a test period for the model corresponding to wave 2. For each of the waves, we set the initial compartmental counts according to Tables S2 and S3. Then, we fit the multinomial‐2‐parameter model for both these waves and obtain estimates of basic reproduction number as well as case counts. We provide the countrywide analysis in the main text, and defer analysis for two major Indian cities—Delhi and Mumbai to Section S.4 of Appendix S1.
The data are sourced from https://www.covid19india.org. We check the accuracy of model predictions with reported counts for cumulative cases, deaths, and active cases, since there is no reported data for the other compartments. The training period is divided into subintervals based on public health interventions in India (see Table S4). Values of and are assumed to be piece‐wise constant, with between‐subinterval variation allowed, which reflects the variations in transmission dynamics over each of the lockdown and unlock periods in India. We have performed a comparison of models (see Section S.3.2 of Appendix S1). Based on the results, we have chosen the multinomial‐2‐parameter model for all of the subsequent analysis.
3. RESULTS OF DATA ANALYSIS: COVID‐19 IN INDIA
3.1. Basic reproduction number
Using the multinomial‐2‐parameter model we obtain the estimates of for both waves 1 and 2. For wave 1, we observe that though the estimated values of were very high (reaching 4.06 for Lockdown 3), it decreased progressively and Unlock 4 onward, the value of remained less than 1. For wave 2, we observe a similar pattern where the value of first increased, reaching a peak value of 2.47 in April 2021, and then remained under 1 from May 2021 onward. For the detailed results on the estimates of (with CIs), refer to Figure 3.
FIGURE 3.
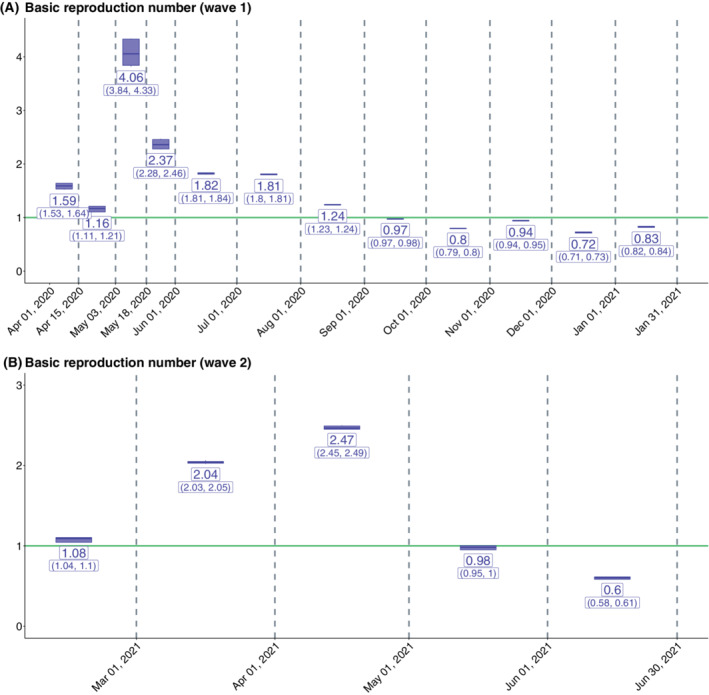
Estimates of in India across phases for (A) wave 1 and (B) wave 2. The mean and 95% credible intervals (in parentheses) are provided under the multinomial‐2‐parameter model. The reproduction numbers are estimated for the training periods corresponding to each of the two waves: April 1, 2020 to January 31, 2021 for the first wave and February 1, 2021 to June 30, 2021 for the second wave
3.2. Prediction accuracy for reported counts
We use a scale‐independent metric, mean squared relative prediction error (MRPE) or relative mean square error or RMSE, 32 defined as follows:
for observed data and predicted vector . Here we only discuss the case , and report the MRPE of the reported cumulative cases, reported deaths, and reported active cases. Prediction of reported active cases is especially important, since accurate prediction of this crucially helps inform policy makers and administrators about health care needs on a daily basis. For the first wave, the training MRPE for reported cumulative cases, reported deaths and reported active cases came out to be 0.002, 0.24, and 0.26, respectively, while for the second wave, the three training MRPE were 0.0006, 0.92, and 0.0003. For calculating the test set error for wave 2, we have used only the period of July 1, 2021 to July 31, 2021 and the three test MRPEs came out to be , 0.0003 and 1.2, respectively. These results substantiate that the model is performing quite well in terms of prediction, especially for reported cumulative cases.
We also note that the reported number of cases not only exhibit an overall trend but also a day‐of‐the‐week effect. This is because test centers in most countries do not operate uniformly on all days of the week and typically have one or two “off days” when relatively lower number of tests are reported. We introduce an extra parameter which is a day‐specific modifier for the outgoing rate from the E compartment. This in turn influences the estimation of daily reported cases. Details of this approach are provided in Section S.3.4 of Appendix S1. Figure S7 details how this modification results in more accurate predictions.
3.3. Prediction of unreported or latent counts
Figures 4 and 5 present the daily composition of active and cumulative COVID cases in India in terms of both reported and unreported infections for waves 1 and 2, respectively. The subfigures show the counts (left) and proportion (right) of cases who are reported, results from false negatives, or remain untested.
FIGURE 4.
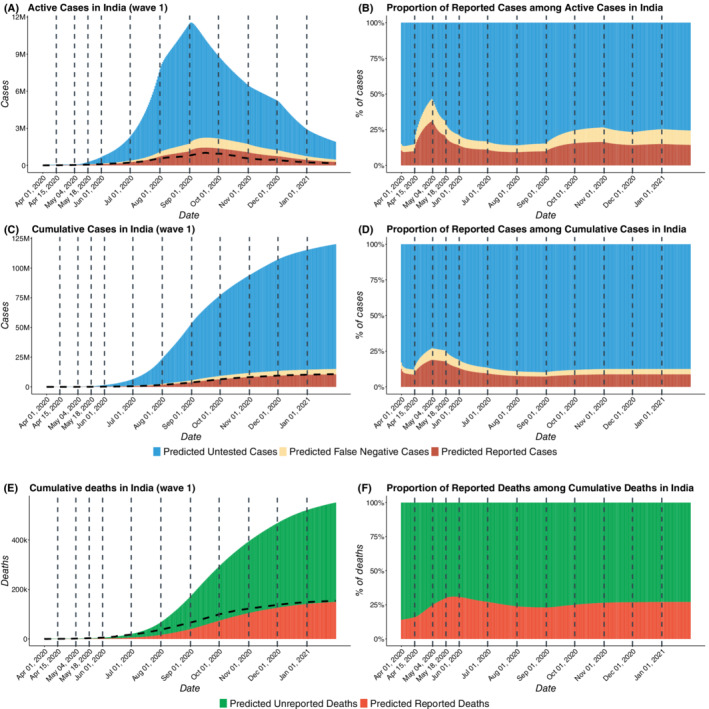
COVID‐19 cases in India for wave 1 with estimated number of reported, false negative, and untested cases. We have taken April 1, 2020 to January 31, 2021 as the first wave training period and in the first wave, we have not taken any testing period. (A) Total active COVID cases in India from April 1, 2020 to January 31, 2021 including reported active cases, false negatives active, and untested active cases. (B) Proportion of reported active cases among Active COVID cases in India (C) Total cumulative cases in India from April 1, 2020 to January 31, 2021 including reported cumulative cases, cumulative false negatives and untested cumulative cases. (D) Proportion of reported cases among total cumulative COVID cases in India . (E) Total deaths in India from April 1, 2020 to January 31, 2021 including reported and unreported deaths. (F) Proportion of reported deaths among total deaths in India. The dotted curves in subfigures A, C, and E represent the observed data
FIGURE 5.
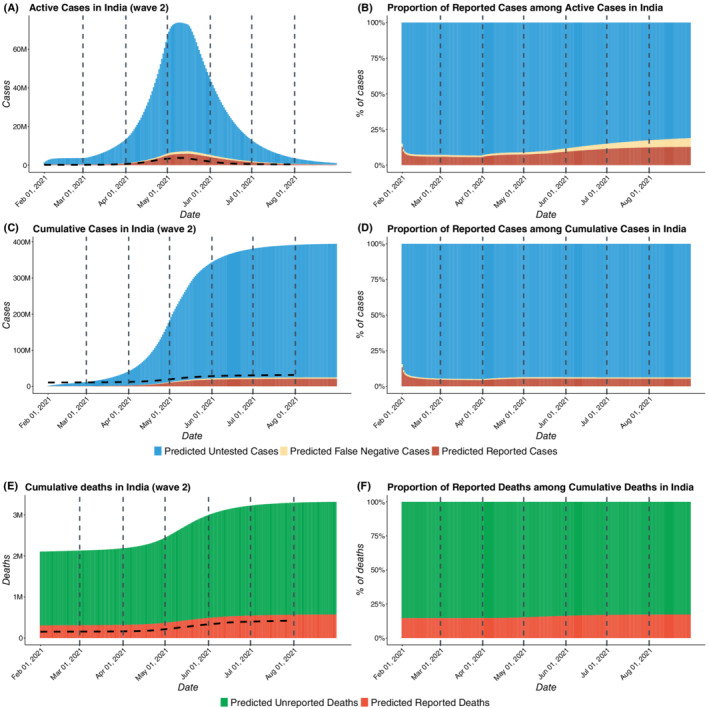
COVID‐19 cases in India for wave 2 with estimated number of reported, false negative, and untested cases. In the wave 2, we have taken February 1, 2021 to June 30, 2021 as the training period, while, July 1, 2021 to August 31, 2021 was taken to be the test period. (A) Total active COVID cases in India from February 1, 2021 to August 31, 2021 including reported active cases, false negatives active, and untested active cases. (B) Proportion of reported active cases among active COVID cases in India (C) Total cumulative cases in India from February 1, 2021 to August 31, 2021 including reported cumulative cases, cumulative false negatives, and untested cumulative cases. (D) Proportion of reported cases among total cumulative COVID cases in India . (E) Total deaths in India from February 1, 2021 to August 31, 2021 including reported and unreported deaths. (F) Proportion of reported deaths among total deaths in India. The dotted curves in subfigures A, C, and E represent the observed data
From Figure 4B,D, we note that the proportion of reported active cases among total active cases rises initially, reaching a peak value of 0.31 on May 3, 2020 and then decreases for 4 months before increasing again slightly from September 2020 onward. For wave 2, Figure 5B, D, we observe that there is an increasing trend in capture rates from March to August, 2021, in the proportion of detected cases and deaths. The predicted proportion of reported cases among active cases has increased from 0.06 on March 1 to 0.13 on August 31, 2021. This suggests widespread testing when the case‐counts are growing, around the peaks of the curve which is consistent with known patterns of human behavior. In spite of enhanced testing and contact‐tracing, our estimates suggest that more than 90% of the cases in India remain unreported as of February 1, 2021, while in July 1, 2021 approximately 94.7% of cases in India remain unreported. As evident from the Table 2, the underreporting factors for cases came out to be 11.1 (95% CI: 10.7,11.5) as of February 1, 2021 and 19.2 (95% CI: 17.9, 19.9) as of July 1, 2021. This means that the predicted proportion of reported cases is roughly 0.09 (95% CI: on February 1, 2021 and 0.052 (95% CI: 0.05, 0.056) of true infections on July 1, 2021. For the deaths, the estimated underreporting factor is 3.58 (95% CI: 3.5, 3.66) as of February 1, 2021 and 4.55 (95% CI: 4.32, 4.68) as of July 1, 2021. This implies that the predicted proportion of reported deaths is roughly 0.279 (95% CI: 0.273, 0.286) on February 1, 2021 and 0.22 (95% CI: 0.214, 0.231) on July 1, 2021. Thus, about 95% infections and 78% deaths remained unreported in India according to the model‐based estimation. For further discussion on the CI's of the predicted case counts please refer to Section S.3.3 of Appendix S1.
TABLE 2.
Predicted cumulative cases and deaths (reported and total) of India along with observed counts and predicted under‐reporting factors for cases and deaths in India across the two waves. The training period for the first wave was taken to be April 1, 2020 to January 31, 2021 with no testing period. Wave 2 training period was taken to be February 1, 2021 to June 30, 2021 with July 1, 2021 to August 31, 2021 as the test period. For both of the waves, reported numbers are based on the day just after the end of training periods
| February 1, 2021 | July 1, 2021 | ||
|---|---|---|---|
| Cases | Predicted reported (millions) | 10.5 (10.4, 10.6) | 30.9 (30.8 , 30.9) |
| Predicted total (millions) | 120 ( 115, 124) | 452 ( 426, 466) | |
| Observed (millions) | 10.8 | 30.4 | |
| Under‐reporting factor | 11.1 (10.7, 11.5) | 19.2 ( 17.9, 19.9) | |
| Deaths | Predicted reported (millions) | 0.15 (0.148, 0.152) | 0.393 (0.393, 0.395) |
| Predicted total (millions) | 0.55 (0.54, 0.56) | 2.2 (2.1, 2.2) | |
| Observed (millions) | 0.154 | 0.399 | |
| Under‐reporting factor | 3.58 (3.5, 3.66) | 4.55 (4.32, 4.68) |
3.4. Effect of misclassification on prediction
For both the waves, we assumed the false negative rate of RT‐PCR tests to be 15%, while acknowledging variation in this rate across the various tests being used in India. 33 In light of this uncertainty, we study how the predictions change for different values of false negative rates (, and ). From Figure 6B,D, we note that predictions for reported active cases from all three models with different values of f concur for both waves 1 and 2. We also note that each of the fits agrees closely with the observed data quite well. Figure 6A,C shows how the estimates of total active cases (sum of reported, false negative, and untested cases) vary substantially across the three assumed values of f for waves 1 and 2, respectively. As expected, the model with leads to the highest estimate of unreported cases as it assumes the highest false negative rate while the model with leads to the lowest estimate of unreported cases. It is also worthy of mention that for both the waves, the difference between predicted number of unreported cases between models with and is lower than the same for models with and .
FIGURE 6.
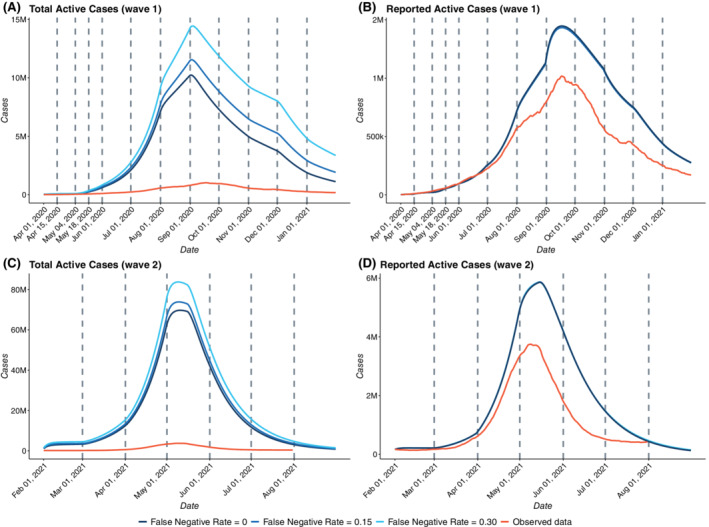
Effect of misclassification on estimates for India (A) Estimates of Total Active Cases for wave 1 with f = 0, 0.15 and 0.3 (B) Estimates of Reported Active Cases for wave 1 with f = 0, 0.15 and 0.3 with the observed data (C) Estimates of Total Active Cases for wave 2 with f = 0, 0.15 and 0.3 (D) Estimates of Reported Active Cases for wave 2 with f = 0, 0.15, and 0.3 with the observed data. April 1, 2020 to January 31, 2021 was taken as the first wave training period and there was no test period for the first wave. In the wave 2, February 1, 2021 to June 30, 2021 was taken as the training period, while July 1, 2021 to August 31, 2021 was taken to be the test period for the second wave
4. SIMULATION STUDIES
Since the underlying truth is unknown in an actual study and the number of true infections are latent counts, we study the effect of selection bias and misclassification on the estimation of and the predicted case counts via simulation studies where we know the true values of the parameters. Each simulation is repeated 1000 times and average values are reported by means of tables and figures.
4.1. Effect of misclassification
4.1.1. Simulation design
We quantify the effect of incorporating false negative tests in our model by characterizing the differences in estimated transmission dynamics with and without accounting for false negatives in our simulation study. We first simulate count data from a model where the tests have a true false negative rate and we then estimate the parameters of interest using three models: and 0.
For this part of the simulation study, we do not consider selection bias and assume that all individuals are equally likely to be tested.
For details regarding the simulation data generation procedure, refer to Section S.5.1 of Appendix S1.
4.1.2. Results
Estimation of : The values of for the five periods used to generate the data (using ) were 3.99, 3.65, 2.12, 1.59, and 1.69. The mean of predicted values of for the model with across the 1000 iterations were 3.64, 3.51, 1.97, 1.48, and 1.65 for the five periods while those for model with were 3.52, 3.64, 2.01, 1.51, and 1.69 and for model with were 3.83, 3.73, 2.04, 1.53, and 1.71, respectively. Now in this simulation, we have generated the data using . This shows that ignoring misclassification can lead to bias in estimating .
Prediction accuracy for total active case‐counts: Figure 7A shows the variation of predicted values of total active cases across different models with varying rates of false negatives in one iteration of the simulation The true value of f used to generate the data was 0.3. After fitting the three models (with , and 0.3), we observe that the model with performs best in predicting the total active cases followed by the model with . As expected, the model which does not consider false negatives, that is, with performs worst. We calculate the mean of MRPE of the predicted number of reported active cases (relative to that of the simulated true data) across 1000 simulation iterations and the model with performs best as expected. The mean MRPEs for the models with and 0.3 are 0.13, 0.068, and 0.012, respectively. We note the significant improvement in prediction accuracy if one incorporates the false negative rate of the test. We also note that the MRPE for reported active cases are considerably less after incorporating this correction. We see a similar trend in other counts as well. For cumulative cases, we have mean MRPE of 0.13, 0.066, and 0.012 for models with 0, 0.15, and 0.3, respectively. Finally, for total deaths, we have MRPE of 0.06, 0.01, and 0.02 for models with f = 0, 0.15, and 0.3, respectively.
FIGURE 7.
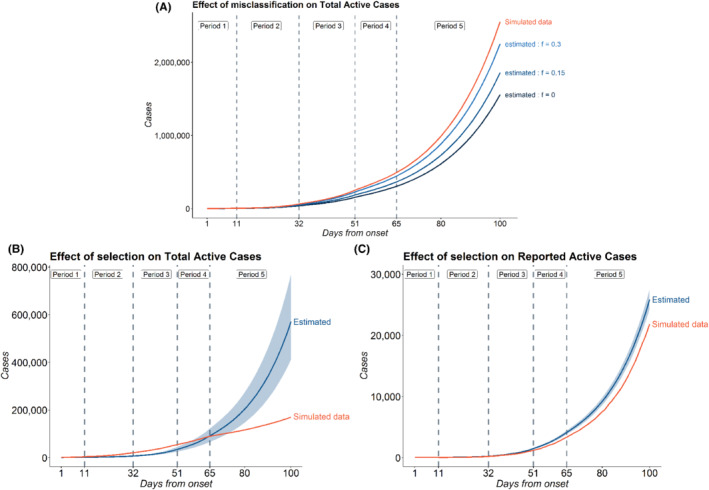
(A) Effect of misclassification on Total Active Cases; (B) Effect of selection on Total Active Cases; and (C) Effect of selection on Reported Active Cases: simulations were carried out in order to assess the effect of misclassification, selection on Reported Active and Total Active Cases. For misclassification, the data was generated for a period of 101 days which was divided into five time periods: days , , , , . The values of across the five periods were set at 0.8, 0.65, 0.4, 0.3, 0.3 and the corresponding values of were set at 0.1, 0.2, 0.15, 0.15, 0.2. For selection model, additional parameters were set as and . As before, the data are generated for a period of 101 days with five periods , , , and while the values of used to generate the data were and 0.2 for the five periods, respectively. Predictions are based on the multinomial‐2‐parameter model, where the probability of being tested is assumed to be independent of symptoms with (the simulation truth)
4.2. Effect of selection
4.2.1. Simulation design
In Section 2.1, extension 3, we propose an extended model incorporating symptom‐dependent testing. To study the effect of ignoring this biased testing mechanism, we generate data following this and estimate model parameters using our misclassification model which incorrectly ignores selection/testing. The choice of parameters are described in Section S.5.2 of Appendix S1.
4.2.2. Results
Estimation of : The true values of for the five periods used to generate the data were 2.22, 2.51, 1.89, 0.52, and 1.29. In presence of selection, we find that the estimated values of differ substantially from the actual values. The means (and 95% percentile‐based CI) of estimated values across all the 1000 simulations for the five periods were 0.24 (0.02, 0.78), 2.40 (1.57, 3.08), 2.92 (2.64, 3.18), 2.56 (2.37, 2.80), and 2.10 (2.06, 2.20). Compared to the effect of misclassification, the effect of selection is more evident on estimated .
Prediction accuracy of active case‐counts: Figure 7B,C shows the predictions for total and reported active cases in a random iteration among the 1000 simulations. The blue band indicates the 95% CI of estimated counts in that particular simulation. The figure indicates that under selective testing, the predicted counts from the model may be very different from the true simulated counts. The model incorporating misclassification and ignoring selection failed to capture the overall trend in the simulated data for the total active cases. As a result we obtain a high MRPE of 0.56 for total active cases, the 95% CI being (0.32, 1.54). For reported active cases, however, the misclassification model obtained fairly accurate predictions and successfully captured the trend in the data. The mean MRPE for the reported active cases came out to be 0.085 (95% percentile‐based CI: 0.044, 0.150) which is much lower than the same for total active cases. This simulation demonstrates that selection bias has substantial impact on our estimates, and ignoring selection could lead to erroneous inference, particularly for predicting total number of true infections.
The effect of number of tests has also been studied using the selection model. We observe that with higher number of tests, the pandemic ends faster as expected. For more details on this, please refer to Section S.5.3 of Appendix S1.
5. CONCLUSION
In this paper, we have undertaken a principled modeling effort to understand the effect of selection bias and misclassification in test results in compartmental models and analyzed the COVID‐19 data in India from April 1, 2020–August 31, 2021. The SEIR‐fansy method has broader methodological significance for modeling any infectious disease transmission where diagnostic strategies are prone to misclassification errors. Our Bayesian approach allows for direct uncertainty quantification of all policy‐relevant estimands.
The standard SEIR model considers a removed compartment which comprises of both recovered and deceased individuals. In the present model, we have split this into two nodes namely recovered (R) and deceased (D) and have modeled them using a multinomial likelihood function. We have further divided each of these two nodes into two subnodes‐based on whether the counts are reported (RR, DR) or unreported (RU, DU). As a result, we are able to estimate the underreporting factors for deaths as well. We also model the undetected and false negative individuals as two new compartments compared to the standard SEIR model which enables us to estimate the number of active/cumulative undetected cases/deaths at any given time point more accurately. Section 3.3 contains the predicted proportion of unreported counts which is substantial for a country like India. 35 , 36 This helps us in understanding the true extent of the disease beyond the reported figures which is important from a policy making perspective. RT‐PCR tests are well known to have a substantial false negative rate. 8 We study the effect of misclassification on the predicted counts. We observe in Section 3.4 that accounting for misclassification has a substantial influence on the predicted number of total cases/deaths. This is crucial because even though there are many models for estimating the number of untested infectious individuals, many of them overlook the contribution of false negatives which might lead to underestimation of the true number of cases. Such modifications enable us to arrive at a more accurate estimate of the infection fatality rates than a naïve one based on reported cases and deaths. We have illustrated our methods using data from India and two of its states, Delhi and Mumbai. During the first wave on February 1, 2021, we estimate that the under‐reporting factors for cumulative cases and cumulative deaths in India are approximately 11.1 and 3.58, respectively (Table 2), while during the second wave on July 1, 2021, they came out out to be 19.2 and 4.55. This indicates the actual death toll in India is approximately four times higher than what is observed. Any reasonable calculation of infection fatality rates will need to incorporate this undercounting into account. A recent paper by Zimmermann et al 36 calculates the Infection Fatality Rate for India to be around 0.1% using observed death counts and 0.4% after incorporating underreporting of deaths and discusses the range of problems associated with underreporting of deaths and cases.
In addition, we have also conducted extensive simulation studies to characterize the effects of misclassification and selection on estimated counts and other model parameters. We observe that misclassification alone does not have a substantial effect on estimates of but has a strong effect on projected future counts. Selection bias, on the other hand, has a strong effect on estimates of both and estimated counts. Additional simulation studies showing the effect of number of tests on the predicted total number of active cases are deferred to Section S.5.3 of Appendix S1 for the sake of brevity.
It is worth pointing out the limitations of our study. Like all compartmental models, our model makes a number of assumptions about the modeling framework and the transmission dynamics, and the accuracy of estimates depend on these. For example, we assume that the probability of infection is the same for all individuals in a particular compartment, which might be unrealistic where contact happens within individualized local networks. When this assumption is not tenable, it is better to apply the model to smaller subpopulations and aggregate the results. Alternatively, one could decompose each compartment into subcompartments based on age‐sex‐job‐specific contact networks and impose a hierarchical structure. One of the major limitations of this method is to assume that f or the false negative rate is known, which may be a realistic assumption when a single approved test with known error rates is used. In reality, different tests with varying error rates are used and a model will need to adapt to their composite nature. We also ignore the false positives here as the SEIR model focuses only on the “truly exposed.” But an extended model (eg, our selection model) that includes a component for tested unexposed individuals will need to consider false positives. Our model also assumes that the values of infection transmission rate and ascertainment rate remain constant over periods of time and that other parameters remain constant through the entire course of the pandemic. However, such an assumption might not hold in reality. One possible solution is to replace by as done by Ray et al. 37 Here, is a time‐varying intervention modifier which takes values in for stricter lockdown relative to the last period in the training data. The credible intervals observed in our procedure are extremely narrow, indicating underestimation of uncertainties inherent in the predictions. This stems from two reasons, one is due to choosing the starting values of and at the MLEs and not accounting for that data‐driven choice. The other is from ignoring the hierarchical uncertainty in the parameters governing the distribution of the incubation and infectious periods. Future work needs to accommodate another layer of hierarchy in these choices. Lastly, instead of the standard SEIR model based on the daily time series of cases, recoveries and fatalities and the first‐order differential equations, one can extend these to second‐order equations. 39 , 40
We have focused on the accuracy of predicted reported cases and active cases with an underlying premise that improving these predictions also improves predictions of all other compartments, including death counts, as long as the other fixed parameters are compatible with the data. Existing literature 11 adopts the reverse strategy by starting from the death data, and future comparison of our method with this genre of work is warranted. Despite the limitations, we hope that this generalized framework and the r package will serve as useful tools to assess robustness of emerging disease transmission models and elsewhere.
CONFLICT OF INTEREST
The author declares that there is no conflict of interest that could be perceived as prejudicing the impartiality of the research reported.
Supporting information
Appendix S1. Supporting information
ACKNOWLEDGEMENTS
This research is supported by the Michigan Institute of Data Science (MIDAS), Precision Health Initiative and Rogel Scholar Fund at the University of Michigan. The research of Bhramar Mukherjee was supported by NSF DMS 1712933, NIH R01 HG008773, and NIH P30 CA046592. The research of Jyotishka Datta was supported by NSF DMS 2015460.
Bhaduri R, Kundu R, Purkayastha S, et al. Extending the susceptible‐exposed‐infected‐removed (SEIR) model to handle the false negative rate and symptom‐based administration of COVID‐19 diagnostic tests: SEIR‐fansy . Statistics in Medicine. 2022;41(13):2317–2337. doi: 10.1002/sim.9357
Ritwik Bhaduri and Ritoban Kundu are co‐first authors.
Funding information Division of Cancer Prevention, National Cancer Institute, 5P30CA046592‐27; Michigan Institute of Data Science (MIDAS), Precision Health Initiative and Rogel Scholar Fund at the University of Michigan, Division of Mathematical Sciences, 1712933; National Human Genome Research Institute, 5R01HG008773‐05; P30 CA046592; National Science Foundation, 2015460; 1712933
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available, and are sourced from https://covid19india.org. All correspondence should be directed to Bhramar Mukherjee (bhramar@umich.edu). Codes for R package SEIRfansy are available at https://cran.r‐project.org/web/packages/SEIRfansy/index.html.
REFERENCES
- 1. Johns Hopkins University . COVID‐19 dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU); 2020. https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6. Accessed April 7, 2020.
- 2. Sharfstein JM, Becker SJ, Mello MM. Diagnostic testing for the novel coronavirus. Jama. 2020;323(15):1437‐1438. doi: 10.1001/jama.2020.3864 [DOI] [PubMed] [Google Scholar]
- 3. Ai T, Yang Z, Hou H, et al. Correlation of chest CT and RT‐PCR testing in coronavirus disease 2019 (COVID‐19) in China: a report of 1014 cases. Radiology. 2020;200642. doi: 10.1148/radiol.2020200642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. West CP, Montori VM, Sampathkumar P. COVID‐19 testing: the threat of false‐negative results. Mayo Clinic Proceedings. Vol 95. 2020(6):1127‐1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Yang Y, Yang M, Yuan J, et al. Laboratory diagnosis and monitoring the viral shedding of SARS‐CoV‐2 infection. Innovation. 2020;1(3):100061. doi: 10.1016/j.xinn.2020.100061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Burstyn I, Goldstein ND, Gustafson P. Towards reduction in bias in epidemic curves due to outcome misclassification through Bayesian analysis of time‐series of laboratory test results: case study of COVID‐19 in Alberta, Canada and Philadelphia, USA. BMC Med Res Methodol. 2020;20:(1). 10.1186/s12874-020-01037-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Arevalo‐Rodriguez I, Buitrago‐Garcia D, Simancas‐Racines D, et al. False‐negative results of initial RT‐PCR assays for COVID‐19: a systematic review. medRxiv; 2020. 10.1101/2020.04.16.20066787 [DOI] [PMC free article] [PubMed]
- 8. Woloshin S, Patel N, Kesselheim AS. False negative tests for SARS‐CoV‐2 infection–challenges and implications. New Engl J Med. 2020. doi: 10.1056/NEJMp2015897 [DOI] [PubMed] [Google Scholar]
- 9. Krüttgen A, Cornelissen CG, Dreher M, Hornef MW, Imöhl M, Kleines M. Comparison of the SARS‐CoV‐2 rapid antigen test to the real star Sars‐CoV‐2 RT PCR kit. J Virolog Methods. 2021;288:114024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Murray CJ, IHME COVID‐19 health service utilization forecasting team . Forecasting COVID‐19 impact on hospital bed‐days, ICU‐days, ventilator‐days and deaths by US state in the next 4 months. MedRxiv; 2020. 10.1101/2020.03.27.20043752
- 11. Flaxman S, Mishra S, Gandy A, et al. Estimating the effects of non‐pharmaceutical interventions on COVID‐19 in Europe. Nature. 2020;1‐5. doi: 10.1038/s41586-020-2405-7 [DOI] [PubMed] [Google Scholar]
- 12. Tang L, Zhou Y, Wang L, et al. A review of multi‐compartment infectious disease models. Int Stat Rev. 2020. doi: 10.1111/insr.12402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Song PX, Wang L, Zhou Y et al. An epidemiological forecast model and software assessing interventions on the COVID‐19 epidemic in China. J Data Sci 2021;18(3):409‐432. 10.6339/jds.202007_18(3).0003 [DOI] [Google Scholar]
- 14. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 1927;115(772):700‐721. 10.1098/rspa.1927.0118 [DOI] [Google Scholar]
- 15. Hao X, Cheng S, Wu D, Wu T, Lin X, Wang C. Reconstruction of the full transmission dynamics of COVID‐19 in Wuhan. Nature. 2020;1‐5. doi: 10.1038/s41586-020-2554-8 [DOI] [PubMed] [Google Scholar]
- 16. Bai Y, Yao L, Wei T, et al. Presumed asymptomatic carrier transmission of COVID‐19. JAMA. 2020;323(14):1406‐1407. doi: 10.1001/jama.2020.2565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Tong ZD, Tang A, Li KF, et al. Potential presymptomatic transmission of SARS‐CoV‐2, Zhejiang province, China, 2020. Emerg Infect Diseases. 2020;26(5):1052. doi: 10.3201/eid2605.200198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Griffith GJ, Morris TT, Tudball MJ, et al. Collider bias undermines our understanding of COVID‐19 disease risk and severity. Nature Commun. 2020;11(1). doi: 10.1038/s41467-020-19478-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Beesley LJ, Mukherjee B. Statistical inference for association studies using electronic health records: handling both selection bias and outcome misclassification. medRxiv; 2019. 10.1101/2019.12.26.19015859 [DOI] [PubMed]
- 20. Dempsey W. The hypothesis of testing: paradoxes arising out of reported coronavirus case‐counts; arXiv preprint arXiv:2005.10425.
- 21. Aron JL, Schwartz IB. Seasonality and period‐doubling bifurcations in an epidemic model. J Theor Biol. 1984;110(4):665‐679. [DOI] [PubMed] [Google Scholar]
- 22. Li MY, Muldowney JS. Global stability for the SEIR model in epidemiology. Math Biosci. 1995;125(2):155‐164. [DOI] [PubMed] [Google Scholar]
- 23. Gamio L & Glanz J Just how big could India's true Covid toll be? The New York Times; 2021.
- 24. Murhekar MV, Clapham H. COVID‐19 serosurveys for public health decision making. Lancet Global Health. 2021;9(5):e559‐e560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Bhattacharyya R, Kundu R, Bhaduri R, et al. Incorporating false negative tests in epidemiological models for SARS‐CoV‐2 transmission and reconciling with seroprevalence estimates. Sci Rep. 2021;11(1):1‐14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Purkayastha S, Bhattacharyya R, Bhaduri R, et al. A comparison of five epidemiological models for transmission of SARS‐CoV‐2 in India. BMC Infect Dis. 2021;21(1):1‐23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Wang L, Zhou Y, He J, et al. An epidemiological forecast model and software assessing interventions on the COVID‐19 epidemic in China. J Data Sci. 2020;18(3):409‐432. [Google Scholar]
- 28. Xin H, Li Y, Wu P, et al. Estimating the latent period of coronavirus disease 2019 (COVID‐19). Clin Infect Dis. 2021. [DOI] [PubMed] [Google Scholar]
- 29. Abbott S, Sherratt K, Gerstung M, Funk S. Estimation of the test to test distribution as a proxy for generation interval distribution for the Omicron variant in England. medRxiv; 2022. 10.1101/2022.01.08.22268920 [DOI]
- 30. Zou Y, Heath WP. Conditions for attaining the global minimum in maximum likelihood system identification. IFAC Proc Vol. 2009;42(10):1110‐1115. [Google Scholar]
- 31. Horbelt W, Timmer J, Voss H. Parameter estimation in nonlinear delayed feedback systems from noisy data. Phys Lett A. 2002;299:513‐521. doi: 10.1016/S0375-9601(02)00748-X [DOI] [Google Scholar]
- 32. Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Stat Sci. 1992;7(4):457‐472. [Google Scholar]
- 33. Despotovic M, Nedic V, Despotovic D, Cvetanovic S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew Sustain Energy Rev. 2016;56:246‐260. 10.1016/j.rser.2015.11.058 [DOI] [Google Scholar]
- 34. Sethuraman N, Jeremiah SS, Ryo A. Interpreting diagnostic tests for SARS‐CoV‐2. Jama. 2020. [DOI] [PubMed] [Google Scholar]
- 35. Zimmermann L, Bhattacharya S, Purkayastha S, et al. SARS‐CoV‐2 infection fatality rates in India: systematic review, meta‐analysis and model‐based estimation. Stud Microecon. 2021;23210222211054324. [Google Scholar]
- 36. Purkayastha S, Kundu R, Bhaduri R, et al. Estimating the wave 1 and wave 2 infection fatality rates from SARS‐CoV‐2 in India. medRxiv; 2021. [DOI] [PMC free article] [PubMed]
- 37. Zimmermann LV, Salvatore M, Babu GR, Mukherjee B. Estimating COVID‐19‐ related mortality in India: an epidemiological challenge with insufficient data. Am J Public Health. 2021;111(S2):S59‐S62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Ray D, Salvatore M, Bhattacharyya R, et al. Predictions, role of interventions and effects of a historic national lockdown in India's response to the COVID‐19 pandemic: data science call to arms. Harvard Data Sci Rev. 2020. https://hdsr.mitpress.mit.edu/pub/r1qq01kw10.1162/99608f92.60e08ed5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Beretta E, Breda D. An SEIR epidemic model with constant latency time and infectious period. Math Biosci Eng. 2011;8(4):931. [DOI] [PubMed] [Google Scholar]
- 40. Sharma VK, Nigam U, Sharma VK, Nigam U. Modeling and Forecasting of COVID‐19 Growth Curve in India. Transactions of the Indian National Academy of Engineering. 2020;5:(4):697–710. 10.1007/s41403-020-00165-z [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Supporting information
Data Availability Statement
The data that support the findings of this study are openly available, and are sourced from https://covid19india.org. All correspondence should be directed to Bhramar Mukherjee (bhramar@umich.edu). Codes for R package SEIRfansy are available at https://cran.r‐project.org/web/packages/SEIRfansy/index.html.


