Longitudinal K-means approaches to clustering and analyzing EHR opioid use trajectories for clinical subtypes

Abstract

Identification of patient subtypes from retrospective Electronic Health Record (EHR) data is fraught with inherent modeling issues, such as missing data and variable length time intervals, and the results obtained are highly dependent on data pre-processing strategies. As we move towards personalized medicine, assessing accurate patient subtypes will be a key factor in creating patient specific treatment plans. Partitioning longitudinal trajectories from irregularly spaced and variable length time intervals is a well-established, but open problem. In this work, we present and compare k-means approaches for subtyping opioid use trajectories from EHR data. We then interpret the resulting subtypes using decision trees, examining how each subtype is influenced by opioid medication features and patient diagnoses, procedures, and demographics. Finally, we discuss how the subtypes can be incorporated in static machine learning models to improve their performance in predicting opioid overdose and adverse events. The proposed methods are general, and can be extended to other EHR prescription dosage trajectories.

Introduction

Electronic Health Records (EHRs) are recognized as a readily available data source for analyzing complex patient cohorts. The typical EHR system contains a rich source of observational longitudinal data that spans many patient attributes. These properties make EHR data ideal for identification of patient subtypes. Clustering longitudinal observational data into patient subtypes can be difficult due to the inherent issues of missing data and varying length of observations per patient (1, 2). Methods for clustering quantitative trajectories to assess patient subpopulations have been applied to EHR data for vital signs, laboratory values, and other calculated measures (3–6). However, use of prescription dosage information in longitudinal models necessitates a large amount of pre-processing and standardization that is not only time and cost intensive, requiring a deep knowledge in EHR data structure, terminologies, and clinical expertise, but decisions made during preprocessing can have a large impact on the choice of clustering method and the extracted subtypes (7–9). Prescription dosage data in an EHR is often missing not at random, meaning that the probability of an observation being missing depends on unobserved data (10). For instance, in chronic disease patients, gaps between observations can be representative of medication non-adherence (9). Therefore, typical imputation methods, such as mean imputation, do not work. Prescription dosage data also extends over a longer period of time with patients that have an inciting incident, such as a surgery, receiving a prescription for a few days, to patients that are receiving the prescription for a chronic disease that lasts years.

Methods for clustering these types of trajectories are either data-adaptive, using the data directly such as k-means, or model-based, assuming that the data can be described by a probabilistic model, such as mixture models (3). Model-based techniques are widely used and provide high-quality subtypes for sparse data and short trajectories (11–13). However, they tend to involve computationally complex statistical inference, which is difficult to scale (3, 6, 11, 14, 15). For instance, Gaussian Processes suffer from cubic complexity in data size compared to quadratic complexity of k-means, a method that identifies a set of centroids and groups patients to the nearest centroid. (16). While great strides have been made to improve scalable gaussian processes and mixture models in high-dimensionality in terms of number of patients, these methods tend to lose efficiency when the number of time points exceeds a few dozen. (14–16).

Longitudinal k-means clustering offers an alternative to model-based. In the study, we explore three different longitudinal k-means methods, varying in how they deal with the outlined medication trajectory issues, using a prescription opioid cohort. Prescription opioids are used by a large heterogeneous population affected by acute and chronic pain and addiction with irregular trajectory lengths across patient. Increases in opioid prescriptions over the last few decades has led to opioid-related adverse effects, ranging from gastrointestinal problems, endocrine disorders, and opioid-induced hyperalgesia to dependency, abuse and overdose (17, 18). Identification of opioid prescription use subtypes may offer critical information to design personalized treatment regimens for opioid patients (19–21). For instance, previous prospective research has shown that opioid use subtypes can capture non-response to treatment at an early stage and offer insights into effectiveness of drug prescription policies (22–24). In the context of opioid subtype identification and trajectory clustering, EHR data use has been limited (25). While previous research has identified opioid use subtypes using group-based trajectory and mixed model approaches, to date, studies have not assessed the methodologies for applying high-dimensional EHR prescription data to scalable k-means algorithms (24–26).

We outline here how to carefully pre-process, apply, and transform EHR data to computationally tractable longitudinal k-means methods to get both efficient and clinically meaningful clusters (3). First, we used k-means for longitudinal data to create subtypes using the raw morphine milligram equivalent (MME) medication data with the assumption of no opioid use when missing (27). Second, we found subtypes using k-means with a b-spline transformation on the raw non-imputed data and irregular sequences (6). Finally, we used long short-term memory variational autoencoders to map the trajectories to latent vector representations, followed by k-means clustering (28). Examining the longitudinal clusters using interpretable decision trees based on external and summary data, we found the three methods capture different aspects of the trajectories with the B-spline transformation and the variational autoencoder capturing more complex and clinically relevant subtypes. In addition, these methods performed better as predictors in machine learning models to predict opioid overdose and adverse events compared to only using static summary statistics like mean MME of the trajectories, showing the importance of prescription data transformation and pre-processing to create patient subtypes.

Materials and Methods

Sample

We analyzed an EHR database of individuals from an inpatient hospital (Erie County Medical Center) and an outpatient practice (UBMD) in Buffalo, NY. To identify patients across hospital and outpatient data, we performed exact matching using social security number, birth date, last name, and first three letters of the first name. We set the study period to cover January 2013 to December 2017, with 2013 showing a significant increase in opioid deaths involving synthetic opioids in the United States (29). We selected patients 12 to 90 years old, eliminating children and infants who typically show different use patterns than the general population. We excluded patients diagnosed with cancer, with the exception of non-melanoma skin cancers (Table 1), due to the differing guidelines for opioid use to treat cancer pain (30). Furthermore, only patients who were given an opioid prescription for seven or more days during the study period were included. Our final cohort consisted of 3,997 individuals, where 306 patients overlapped both facilities and 3,691 patients only had prescription data from the outpatient practice EHR.

Table 1.

Inclusions and Exclusions.

Inclusion	Prescription Medications
Opioids Indicated for Pain Treatment	Codeine, Fentanyl, Hydromorphone, Butorphanol, Dihydrocodeine, Hydrocodone, Levomethadyl, Levorphanol, Meperidine, Morphine, Opium, Oxycodone, Oxymorphone, Pentazocine, Propoxyphene, Tapentadol, Tramadol
Opioids Indicated for Abuse Treatment	Buprenorphine, Buprenorphine/Naloxone, Methadone
Exclusion	Codes
Cancer/Palliative Care	ICD-10 C category cancers except C44, Z51.5, 172, 174, 140, 141, 152, 147, 142, 153, 148, 143, 154, 149, 144, 155, 150, 145, 156, 151, 146, 157, 164, 171, 158, 165, 225, 159,166,209.7, 160, 167, 230, 161, 168, 231, 162, 169, 232, 163, 170, 233, 234, 247, 238.7, V66.7, 209.36, 173.00, 173.09, 173.10, 173.19, 173.20, 173.29, 173.30, 173.39, 173.40, 173.49, 173.50, 173.59, 173.60, 173.69, 173.70, 173.79, 173.89, 173.80, 173.99, 173.90, 227.3, 227.4, 228.02, 228.1 237.5, 237.6, 237.9, 238.4, 239.6, 239.7

Non-prescription related clinical variables

For the downstream analysis tasks, we identified overdose and abuse events based on available ICD codes (Table 2). For each patient, we created a binary outcome variable of whether or not an overdose or abuse event occurred within the 5-year study window. Since a single patient may have multiple event encounters, we defined the first recorded case of overdose or abuse as a patient’s endpoint. In total, we found 3.73% of patients with a positive outcome variable (i.e., overdose or abuse events).

Table 2.

Diagnostic codes for outcomes and predictors.

Variable	Codes
Overdose and abuse (Outcome)	96500, 96501, 96502, 96509, 9701, E8500, E8501, E8502, E9350, E9351, E9352, T400X1, T400X2, T400X3, T400X4, T401, T402X1, T402X2, T402X3, T402X4, T404X1, T404X2, T404X3, T404X4, T403X1, T403X2, T403X3, T403X4, T40601, T40602, T40603, T40604, T40691, T40692, T40693, T40694, 30550, 30551, 30552, F1110, F11120, F11121, F11122, F11129, F1114, F11150, F11151, F11151, F11159, F11181, F11182, F11188, F1119
Opioid Dependence	30400, 30401, 30402, 30470, 30471, 30472, F1120, F1122, F1123, F1124, F11250, F11241, F11259, F11281, F11282, F11288, F1129, F11220
Surgeries	CPT: 10030 – 69990
Cardiovascular System Surgeries	CPT: 33010 – 37799
Abdominal/Gynecological Surgeries	CPT: 38100 –38999, 54000 –55899, 55920, 55970 –55980, 56405–58999, 59000–59899, 38100 –38999
Anxiety	F064,F4000,F4001,F4002,F4010,F4011,F40210,F40218,F40220,F40228,F40230,F40231,F40232,F40233,F40240,F40241,F40242,F40243,F40248,F40290,F40291,F40298,F408,F409,F410,F411,F413,F418,F419,F42,F422,F423,F424,F428,F429,F430,F4310,F4311,F4312,F488,F489,R452,R453,R454,R455,R456,R457,R4581,R4582,R4583,R4584
Attention deficit	F11920, F11921, F11922, F11929, F1193, F1194, F11950, F11951, F11959, F11988, F1199
Counseling	V65.42, Z71.41, Z71.51, Z71.6, 99406, 99407, 99408, 99409

We assessed other known opioid-related clinical variables defined by structured EHR data including patient demographics, addictive behavior and mental illness indicators, and other comorbid conditions (Table 3) (31). Additionally, we included patient socio-demographic variables: age of first recorded prescription, race, gender, ethnicity, insurance category, and marital status. We categorized race as White, Black, and Other. Ethnicity was coded as Hispanic or Non-Hispanic. As a socio-demographic indicator, we broke insurance into Commercial, Medicare, Medicaid, No Insurance, and Other. Addictive behavior variables included other types of substance abuse and dependence, opioid-related counseling, and a history of urine drug screens. Other health factors included history of surgery, chronic pain diagnoses, injury, mental illness, and typical comorbid conditions. Our sample was majority female (64.3%) with a median age of 51.68. The distribution of race was 58.9 % White, 40.1% Black, and 1% Other. There were 3.67% Hispanic or Latinos.

Table 3.

Demographic, clinical, and trajectory characteristics for a general opioid cohort from two sites.

Variable		Full Dataset (n=3,997)
Demographic and Clinical Characteristics
Age (years)	<30	442 (11.1%)
	30–65	2754 (68.9%)
	65+	801 (20.0%)
Opioid Adverse Event		149 (3.7%)
Female		2570 (64.3%)
Race	Black	1555 (40.1%)
	White	2283 (58.9%)
	Other	39 (1%)
Insurance	Commercial	1098 (27.5%)
	Medicaid	1172 (29.4%)
	Medicare	1636 (41%)
	No Insurance	41 (1%)
	Other	43 (1.1%)
Number of Surgeries	Multiple	248 (6.2%)
	One	260 (6.5%)
	None	3489 (87.3%)
Injury		1022 (25.6%)
Buprenorphine		454 (11.4%)
Methadone		162 (4.1%)
Opioid Dependence		528 (13.2%)
Mentall Illness		1432 (35.8%)
Non-Opioid Substance Abuse		751 (18.8%)
MME Trajectories (Mean 7-day Measurements)
		Mean (SD)
Mean MME over entire trajectory		40.56 (47.8)
Change from first recorded MME to last		21.86 (43.82)/11.43 (21.85)
Observations		29.95 (50.53)
		N (%)
Starting MME	<20	1403 (35.1%)
	20–49	1625 (40.7%)
	50–89	383 (9.6%)
	>90	585 (12.6%)

Prescription data

For each patient in the cohort, we obtained a list of opioid prescriptions directly from the EHR record. To ensure that all opioid prescriptions are captured, we mapped opioid-related National Drug Codes (NDC) in the EHR data to RxNorm codes. We queried the local prescription labels when NDC codes were not present for both generic and proprietary opioid drug names, mapping those to RxNorm codes. We excluded prescriptions for which there was an error flag, or if it was voided, unauthorized, or canceled. For outpatient prescriptions, we observed that in some cases multiple prescriptions for the same generic drug and in the same time frame were registered in the EHR, even though only one of them was realized. In such cases, we retained only the latest prescription. In certain instances, the quantity of a drug was representative of a full packet or box as defined by their NDC. To handle such cases, we adjusted the quantity to the number within the product description, e.g., the number of pills in a packet, the number of patches in a box, etc. Finally, we removed prescriptions with null or 0 quantity dispensed, or missing prescription starting and ending date. We used 12,387 outpatient prescriptions and 26,141 hospital administrations. This led to a total of 875,906 days of prescribed opioids with a median of 25 days (IQR=51) per patient and an average of 117 days (sd=272.32) of prescription per patient.

In addition to quantity and days supply for each prescription, we extracted prescription variables including opioid treatment, indicated by methadone, buprenorphine, or buprenorphine-naloxone, whether first recorded prescription was a long or short-acting opioid, and the first recorded prescription generic drug category, e.g., hydrocodone, methadone, etc. For our sample, 11.4% were on buprenorphine within the 5-year time window and 4.1% were on Methadone.

Conversion to Morphine Milligram Equivalent (MME)

To render different opioid prescriptions comparable across patients and timelines, we performed the Morphine Milligram Equivalent (MME) conversion using guidelines provided in “CDC compilation of benzodiazepines, muscle relaxants, stimulants, zolpidem, and opioid analgesics with oral morphine milligram equivalent conversion factors, 2018 version” (32).

Each prescription was converted into MME, which determines a patient’s cumulative intake of any opioid drugs within a 24-hour interval, and is defined as:

$$\frac{MME}{day}=\left(StrengthperUnit\right)\left(\frac{NumberofUnits}{DaysSupply}\right)\left(MMEconversionfactor\right).$$ (1)

We obtained Strength per Unit and MME conversion factor from the CDC specifications (24). We derived Number of Units from the prescription quantity in tablet, capsule, film, solution, or suspension. We defined Days Supply as the total number of days between the prescription start date and the prescription end date for outpatient prescriptions. For inpatient administrations, each administration was calculated as a separate prescription and then aggregated to find the total MME per day (32).

We decided to include Buprenorphine, a semi-synthetic opioid antagonist drug, in this analysis. Despite the hypothesis that buprenorphine, a partial agonist with strong affinity for the mu receptor, is not expected to be associated with overdose risk in the same dose-dependent manner as a full agonist opioid medication, patients on buprenorphine still experience opioid related adverse effects and a potential for overdose (33–35). Therefore, prescriptions with Buprenorphine film, tablet, or patch extended-release were assigned corresponding MMEs from the CDC’s 2016 file (36).

Creation of Patient MME Trajectories

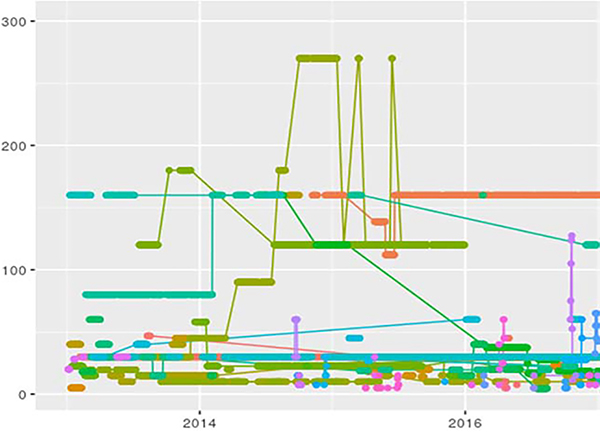
For each patient in the cohort, we identified vector $x_i={\left[x_{\left\{i1\right\}},x_{\left\{i2\right\}},...,x_{\left\{{in}_i\right\}}\right]}^{\text{'}}$ representing their MME trajectory. Here, n_i is the total number of weeks in the period between the first and the last opioid prescription for patient i, and x_{ij} represents MME exposure of patient i in week j calculated as the weekly average. We decided to use weekly average since current New York State policies limit acute pain prescriptions to seven days. Moreover, weekly intervals are sufficiently long to mitigate effects of a non-uniform distribution in time. In addition, they are short enough to provide insights into the dynamics of long-term opioid use as compared to using a longer time interval like a month, since changes for even a few days of use can lead to addiction and overdose (37). Figure 1 shows a random sample of patients’ weekly MME trajectories. We had a mean of 29.95 (sd=50.53) weekly observations in our cohort and a mean of 40.56 (sd=47.8) for weekly MME across each patient’s trajectory (Table 3).

Figure 1.

Raw Patient Morphine Milligram Equivalent (MME) Trajectories for 50 Randomly Sampled Patients

Clustering Trajectories

We divided our trajectories into a 70% training set and a 30% validation set. We used a stratified sampling method to ensure that the proportion of opioid overdose and abuse events in both subsets closely matched the distribution across the entire cohort (Train: 3.79%, Test 3.56%). Stratified sampling was done using R 3.6.1 package caret ‘createDatapartition.’ The median starting MME of the initial prescription in the time frame was 27.7 (IQR=30) for the training set, 30 (IQR=42.972) for the testing set, and 28.6 (IQR=30) for the entire dataset (Table 3). The mean starting MME of the initial prescription was 45.599 (sd=56.72) for the training set, 45.929 (sd=51.776) for the testing set, and 45.623 (sd=55.34) for the entire cohort. Substance use disorder was coded with ICD for 13.2% of the sample (13.6% of training, 13.2% of testing). To perform clustering, we considered three methods. All methods were run on a machine with 24 CPUS, 128 GB of mem, and 4 Nvidia 2080Tis with 11 GB.

1. Longitudinal k-means with imputation (kml)

We used R package kml to cluster the training set trajectories (27). Kml uses Euclidean distance with Gower adjustment as its distance measure, and the Calinski and Harabasz criterion for choosing optimal k (27). Kml, like most data-adaptive longitudinal clustering algorithms, requires missing values to be filled. Due to the nature of prescription data, unlike laboratory values and other measurements, we cannot rely on typical imputation methods, such as mean imputation, especially when there are long gaps in prescriptions or there is a surgical or acute pain clinical indication. Therefore, we ran kml assuming that 0 MME dosages were given when data was missing for the 7-day period. The training time for the final model was 39 seconds when the ‘Fast’ procedure is used.

2. Longitudinal k-means with B-splines (b-spline)

In (6), Luong and Chandola proposed a method to use B-spline basis representations of the data to learn clusters of individual trajectories with k-means clustering. This methodology allows for different vector lengths and missing data without the need for imputation or assigning 0s. It assumes that time series within a cluster can be approximated using a weighted sum over a collection of splines or polynomial functions (5, 6, 38, 39). The basis matrix for representing the family of splines is evaluated with boundary points of 0, corresponding to the first 7-day prescription, and 261 (maximum weeks in 5 years) with the specified interior knots defined by quantiles. Each patient is then assigned to one of k clusters, where each cluster represents the joint MME trajectory of all patients belonging to the cluster with a curve fitted to all of the observations of the patients assigned. We assessed the k clusters running 5-fold cross validation and selecting the lowest BIC values. To encourage convergence towards the global maximum, we initialized the k-means algorithm 10 times and trained on 500 iterations. The training time for the final model was 157 seconds.

3. K-means on Variational Recurrent Autoencoders (VRAE)

Variational recurrent autoencoders combine recurrent neural networks (RNNs) with stochastic gradient variational Bayes to map time series data to a latent vector representation (28). Since variational autoencoders are generative models, they attempt to learn the underlying distribution so that trajectories not seen in the training dataset can still be assessed with higher accuracy. We used long short-term memory (LSTM) to mitigate the exploding gradient problem encountered with traditional RNNs. We trained the variational recurrent autoencoder using Python 3 and PyTorch. The architecture of the model from (28) was maintained with one hidden layer using the Adam optimizer, gradient normalized clipping, and a batch-size of 32. The LSTM hidden layer size 90. We trained the model with 500 epochs and a latent length of 20. A dropout layer (0.2) is included to help prevent overfitting. With a small sample space such as this one, we risked not being able to capture the distribution; therefore, the maximized loss term is the summation of two terms. The first term is the reconstruction loss (MSE) and the second term is the KL-divergence, which is the amount of compression or information that is contained within the latent space. (40). A set of learning rates, [0.005,0.0005, 0.00005], and a set of latent lengths [5, 10, 20, 30], was assessed minimizing reconstruction loss as the objective with the final model having a learning rate of 0.0005 and latent length of 20. The final average loss of our model was 163,591.49 (KL-divergence= 5.26), implying that even though the sample size was small for deep learning methodology, the VRAE learned a latent pattern. In order to model missing data, we padded vectors with 0s and masked them by setting the loss generated by the pad tokens to zero. We then employed non-longitudinal k-means with Euclidean distance on the embedded representation. We used the silhouette score and elbow method to decipher how many clusters should be used. The training time for the final model was 7329 seconds.

Optimal Number of Clusters k and Stability

The problem of choosing k for k-means cluster analysis has been well studied an many methods have been proposed (27, 40, 41). Given the unsupervised nature of the problem, meaning that subtypes do not have gold standard labels, there is no standard way to use prediction ability to drive model selection (41). To select the number of clusters k for each method, we approach the problem based on the idea of cluster ‘stability,’ meaning that if multiple independent samples from the population find the same k, the clusters are meaningful (42, 43). Therefore, on our training set of 70%, we select k by running 5-fold cross-validation. First, we shuffled our training dataset, then we split our dataset into 5 folds for cross-validation, where for each fold j=[1,2,3,4,5], j is the ‘testing’ set and the remaining folds become the ‘training’ set. For VRAE, dimensionality reduction is applied on the ‘training’ set to create the latent embedded representation of the trajectories with the hyperparameters fixed as described in section__. Then, clusters are generated on the ‘training’ set. Finally, we predict each ‘testing’ observation’s ‘training’ set membership as defined by each method. We report the mean internal criterion measures that are suggested by each package for each fold’s training set (i.e. the combination of the four folds with one fold left out), such as BIC (B-spline) (6), Calinski-Hararanski (kml) (27), and the silhouette score combined with the elbow method (VRAE). In addition, we provide profile analysis showing the comparison of the held-out testing set verses the other four-folds training set across all five runs to show the robustness of the clusters regardless of fold and the ability of the found clusters to be used to assign new, unseen, patient trajectories to a subtype.

After choosing the most appropriate value of k for each method using cross-validation, we re-ran each method for the selected value of k on the full 70% training set. In addition, we compared the profiles of the training set and test set clusters to see if individual training cluster trajectories and predicted cluster trajectories form similar patterns. For kml, to predict the test set’s cluster assignment, a person is assigned, based on Euclidean distance, to the training set’s cluster with the closest center. For the test set in b-spline, patients are assigned to the training set’s closest cluster that produces the smallest error given the training set basis coefficients for each cluster. For the test set in VRAE, we obtained latent vectors by passing the vectors into the encoder and obtaining the intermediate latent vector. We predicted the k-means cluster estimating the vector closest to the cluster center (40).

Content Validity

To assess the content validity of the clusters, we used external clinical variables and drug prescription variables in a decision tree analysis with cluster as the outcome variable (44). Decision trees can provide insight into the clusters by generating interpretable rules and visualizations for how the cluster was formed. Inspired by Leffondré et al. (45), we extracted various summary measures that describe features of the trajectories, e.g., MME mean, standard deviation, regressed linear slope, change in MME from first to last prescription, maximum MME, and minimum MME. We then used those extracted features, combined with additional clinical variables and medication features, to produce a decision tree for each of the three methods. We used the Gini index to determine splits in the decision tree and a minimum number of 20 observations in a node for a split to occur. The tree is described by the number of nodes, which determine its complexity, and the accuracy of the tree, i.e., the ratio of elements not correctly explained by the resulting tree. We then pruned the trees to avoid overfitting to outliers in the data and chose the complexity parameter associated with minimum cross-validated error, following typical convention. For kml, the complexity parameter with minimized cross-validated error was chosen to be 0.01. The b-spline and VRAE decision trees had a higher complexity with the complexity parameters associated with minimum error set at 0.0007 and 0.0007, respectively.

Predictive Validity

To assess the predictive validity of the clustered temporal data in predicting the outcome measure opioid poisoning and abuse events, we used the clusters as features in machine learning models. Since our outcome is highly imbalanced, we modeling techniques that are known to offer sufficient robustness. First, we employed ensemble methods, random forest and XGBoost, since they have been shown to have the highest accuracy for imbalanced class sizes (41, 46, 47). We used synthetic Minority Over-sampling Technique (SMOTE) to over-sample the minority class using nearest neighbors (48). SMOTE was applied solely on the training set at each fold using the R package caret. The testing set was left highly imbalanced to mirror the true percentage of opioid overdoses in the population. Finally, we used the area under the precision-recall curve as our accuracy metric. We handled missing data for race, gender, and ethnicity by encoding the missing data with the category ‘MISS’ and allowing the model to estimate this pattern. We trained the models with R package caret using 5-fold cross validation repeated 5 times with grid-search for hyperparameter optimization. Each model used the best hyperparameter combination. We set the random number seed for all models to ensure that the algorithm gets the same data partitions and repeats, allowing us to compare models using resampling techniques(49). To provide a comparison to using temporal clusters as features for MME, we ran the models with aggregated patient features: number of 7-day prescription observations and mean MME.

Results

Optimal choice of k using cross-validation

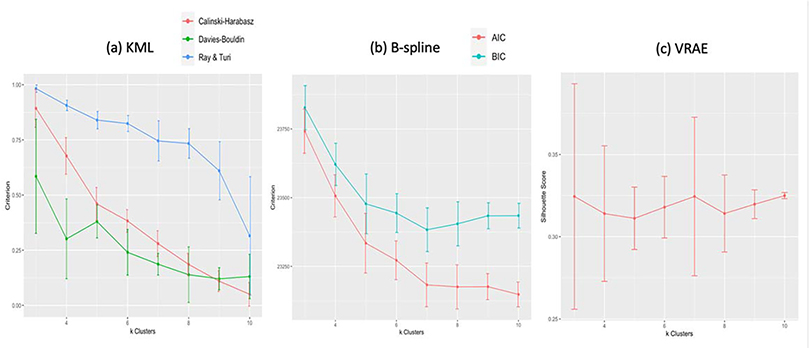
Since we allowed the number of clusters to be chosen by each method’s criteria, the first difference between the methods lies here: kml criterion selected 3 clusters as optimal, longitudinal k-means using b-splines (b-splines) selected 7 clusters, and k-means variational autoencoder (VRAE) selected 7 clusters (Figure 2). Plotting the sum of squared errors for k-means, also produced an elbow at 7 clusters. Since the optimal choice of k will try to balance the maximum compression of the data using a single cluster and the maximum accuracy by assigning each data point to its own cluster, the differing number of clusters is representative of how the data was pre-processed and transformed.

Figure 2.

Selecting optimal k using cross-validation and method suggested internal criterion. The plots show the mean criterion value with error bars across the five folds. In (a), the KML method shows all criterion (Calinski-Harabasz, Davies-Bouldin, and Ray and Turi) maximized for k=3 clusters. For B-spline (b), the BIC is minimized for k=7 clusters and AIC plateaus at k=7 as well. Finally, (c) shows the silhouette score is highest for k=7 clusters in VRAE.

Assessing the smoothed trajectory subtypes for each fold with k=3 subtypes for KML, k=7 subtypes for B-spline and k=7 subtypes for VRAE, we see robust representations regardless of training set (Figure 3). The most volatile subtype, characterized by high MME in each graph, changes shape across the folds. This could be representative of the small number of patients (4.8%) in the entire cohort who have an overall mean greater than 150.

Figure 3.

Profile analysis of 5-fold cross validation for clusters selected by method criterion. Other than for the highest, smallest, and most erratic clusters (represented by the top curves in all plots), the profile analysis shows stable clusters across all folds for each method.

Subtypes on 70% Training Set

After re-running each method on the full training set (n=2,846) for the selected optimal value of k found by cross-validation, we plotted the patient trajectory subtypes using a linear smoothing function and confidence interval band can be found (Figure 4). Due to the way kml deals with irregular sequences and the addition of 0s where missing values were present, we only found a small number of subtypes that suffer from highly unequally-sized clusters (Figure 4(a)). The profile analysis of the test cohort shows that prediction of the clusters is stable (Figure 4(b)). However, the majority of cases clustered into cluster 1 (89.6%), which has a low starting MME and consists primarily of patients with less than 2 opioid prescriptions. Since this cluster contains approximately 90% of the patients, this allows no clinically relevant discernment between the trajectories. The remaining two clusters formed a trajectory that has a higher starting MME which starts to taper off across time (8.3%) and a trajectory which consists of high MME and continuous prescriptions (2.1%).

Figure 4.

Profile analysis and trajectories found using the three k-means methods on the full 70% training set (n=2,846) compared to the 30% testing set (n=1,151).

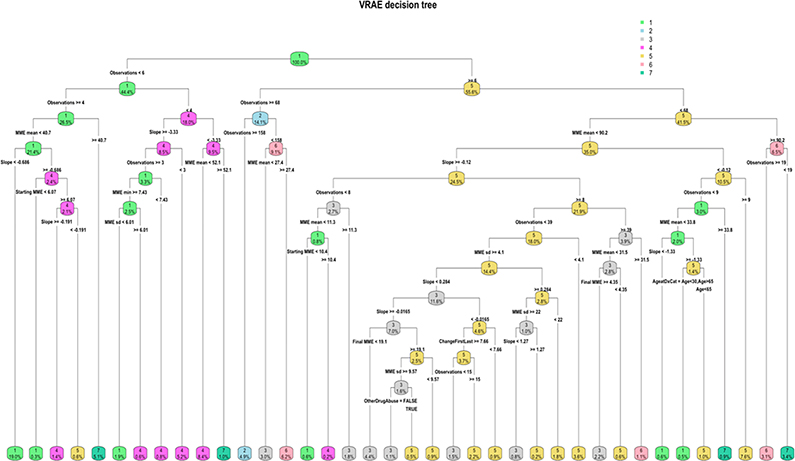
Therefore, by pre-processing the data into this form, we may have underestimated the number of true subtypes, forcing disjoint groups of data into one larger cluster, namely cluster 1. Examining the decision tree for kml, which has a training misclassification error of 0.021, a macro-F1 of 0.91, and a weighted-F1 of 0.979, implying that the chosen trajectory summary variables can highly accurately predict the clusters. Additional exploratory analysis of how robust the method is at classifying new data to clusters, shows that the error on the test set is only slightly higher (0.034) with a weighted-F1 score of 0.965 and a macro-F1 score of 0.86. We see that 77.4% of the cohort has only two primary splits: the number of observations is less than 82 and the mean MME is less than 88.1 (Figure 5(a)). Since CDC guidelines recommend prescriptions less than 90 MME/day, and furthermore, caution increasing dosages to greater than 50 MME per day, this cluster provides very little insight that would be useful in clinical practice (50).

Figure 5.

Decision tree analysis for KML and B-spline extracted k-means clusters

B-splines and VRAE on the other hand, do not require these same pre-processing methods, and therefore, have found a higher number of subtypes that appear informative and relevant to patient treatment. For b-splines, the majority (50.3%, cluster 6) of cases clustered to a low starting MME and static across time (Figure 2(c)). We see that this coincides with the decision tree, which, like kml, has a low misclassification training error of 0.0225, a macro-F1 of 0.94, and a weighted-F1 of 0.978 meaning these features represent the clusters well (Figure 5(b)).Applying this decision tree again to our test set, gives a slightly higher misclassification error (0.04) with a weighted-F1 score of 0.96 and a macro-F1 score of 0.89. It shows cluster 6 characterized by at least 2 observations and a low MME. Interestingly, cluster 6 is associated with chronic pain, containing 49% of patients with rheumatoid arthritics and chronic joint pain, 60% of patients with other long-term chronic pain, and 54.7% of patients with migraines and headaches. Cluster 2 (23.2%) is stagnant across time with a higher baseline MME than cluster 6 and cluster 7 (8.4%) follows the same pattern with a higher baseline MME. Cluster 3 (5.5%) and cluster 4 (3.8%) have different baseline MME and increase initially and then decrease. The decision tree shows cluster 3 having a high MME mean between 126 and 207, which is characteristic of how MME for buprenorphine is calculated, making it unsurprising that 31% of buprenorphine users are in this cluster. Cluster 5 (4.5%) also has a high starting MME that tapers down and consists of the other buprenorphine users (29.5%). Cluster 1 (4.2%) has a very high baseline MME, decreases initially, and then increases. All of the clusters are stable when looking at the profile analysis of the test cohort (Figure 4(d)).

For VRAE, the majority of patients (24.9%) were clustered to the lowest MME trajectory similar to kml and b-spline transformation (Cluster 1, Figure 4(e)). The decision tree shows that these patients primarily (19%) also have only 4 to 6 observations and a negative slope, meaning that the prescriptions have tapered off across time (Figure 5).

For this cluster, the initial prescriptions in the time period were short-acting (91.1%) and 81% of the cluster has as an initial prescription hydrocodone or tramadol. Clusters 3,4, and 5 had differing starting MMEs with cluster 5 increasing and then tapering off and clusters 3 and 4 initially decreasing (Figure 4(e)). Examining the decision tree, cluster 4 primarily has less than four observations. Cluster 5 is primarily female (67.5%) and 74.6% are between the ages of 30 and 65, which is used as a primary node split in the decision tree. Cluster 6 (9.4%) has a high starting MME and then decreasingly tapers. Cluster 7 (9.6%) has the highest starting MME and is the most erratic of the clusters. Like b-splines, the profile analysis for this erratic cluster is also the only one that is not stable for the test set (Figure 4(f)). For cluster 7, 72.5% of the initial prescriptions in the time frame were longacting opioids. Clusters 6 and 7 characterize dependence, containing 65.66% of Buprenorphine users and 48% have are recorded to have opioid use disorder (Figure 6 (c)).

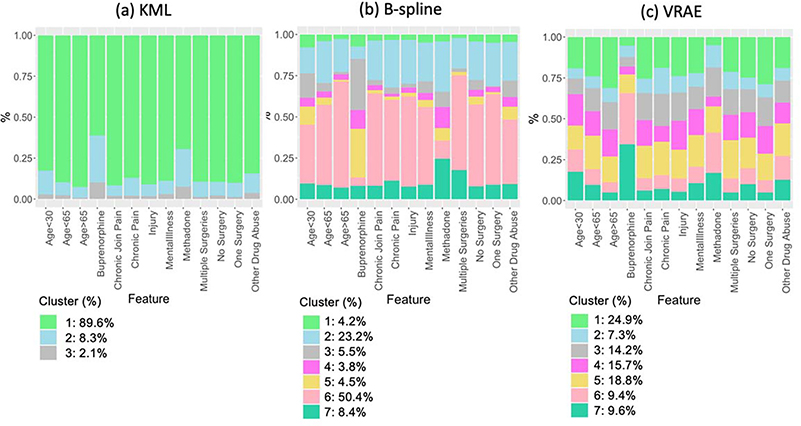
Figure 6.

Proportion of cases for clinical features by cluster. For kml (a), since the majority of patients have clustered to cluster 1 (89.6%), they also make up a large portion of the clinical features. Cluster 2 has a high proportion of opioid treatment patients. For B-spline (b), clusters 3 and 5 contain a large portion of patients on buprenorphine. For VRAE (c), the majority of buprenorphine patients come from clusters 6 and 7.

Mapping time sequences of MME to one latent vector of engineered features as compared to directly applying over timeseries vectors such as with kml and b-splines, led to a much higher misclassification training error (0.159), a macro-F1 of 0.834, and a weighted-F1 of 0.841 for the VRAE clusters. This implementation has attempted to build a latent structure of the time series, and therefore, summary statistics and other patient features collected here are not fully able to explain the clusters. Variable importance for the VRAE decision tree, unlike for b-spline and kml which relied heavily on number of observations and mean MME as features, was high for slope. In addition, the VRAE decision tree found other patient features, ‘Other Drug Abuse’ and ‘Age,’ important for distinguishing between clusters. Finally, our exploratory analysis of the test set shows a misclassification error rate of 0.277, with a weighted-F1 score of 0.725, and a macro-F1 score of 0.705. This decrease in accuracy is expected, since the trained decision tree had a higher misclassification error rate.

Predictive Validity

Using the clusters as features in a downstream prediction task to assess risk of opioid poisoning and abuse, our three clustering methods did better than the static model with overall mean MME and number of exposure observations in terms of the area under the precision-recall curve and other accuracy metrics for the test set (Table 4). The B-spline clusters did the best, followed by the VRAE clusters. In terms of scaled variable importance by model, VRAE cluster 7 and 6, characteristic of the highest starting MME and a steep decline in MME dosage, were the most important features for predicting the overdose (XGBoost:100 and 91.93, RF: 98.5 and 94.06). On the contrary, the clusters that have the most variable importance for b-spline and kml are the static, low starting MME clusters. This could be due to the imbalanced nature of the clusters, where the majority of patients have clustered to these two clusters. However, for B-spline’s cluster 6, which is characteristic of chronic use of opioids and chronic pain, this importance is much higher than kml’s Cluster 1 importance (XGBoost: 100 and RF:100 compared to XGBoost:29.9 and RF: 19.9). This makes intuitive sense since approximately 20% of chronic pain patients have experienced a life-time overdose (51). Finally, while VRAE and b-spline clusters were highly important features, the three kml clusters all had importance, regardless of model, less than 20.

Table 4.

Random Forest and XG Boost algorithms with SMOTE for predicting Opioid Overdose and Abuse. AUC refers to area under the receiver-operating curve. PrAUC refers to area under the precision-recall curve.

Model	Cluster	Recall		Precision		F1-Score		AUC		PrAUC
		Train	Test	Train	Test	Train	Test	Train	Test	Train	Test
Random Forest	KML	0.207	0.268	0.141	0.157	0.163	0.198	0.771	0.734	0.108	0.132
	B-Spline	0.245	0.244	0.14	0.161	0.175	0.194	0.798	0.76	0.118	0.194
	VRAE	0.3	0.317	0.128	0.125	0.178	0.179	0.776	0.748	0.12	0.165
	Static	0.205	0.244	0.145	0.179	0.165	0.206	0.8	0.72	0.125	0.123
XGBoost	KML	0.31	0.39	0.113	0.123	0.165	0.187	0.746	0.73	0.097	0.104
	B-Spline	0.332	0.439	0.111	0.126	0.166	0.196	0.778	0.748	0.103	0.096
	VRAE	0.305	0.439	0.11	0.439	0.161	0.213	0.763	0.72	0.101	0.123
	Static	0.29	0.342	0.1	0.108	0.792	0.164	0.76	0.735	0.08	0.086

Discussion

Our ultimate goal was to inform precision medicine by assessing longitudinal k-means methods for varying and irregular medication trajectory subtypes. In addition, we have explored visualization techniques like decision trees which can help to further analyze the resulting subtypes. Each of the three methods extracted certain information from the trajectories and used that to form the subtypes. For kml, three easily observed clinical opioid trajectories were found with the majority of patients having a low level of MME. These subtypes mirror what was found in Elmer et al. (25), which focused on prescribing patterns. Due to the highly imbalanced cluster sizes and the use of 0s when no dosage information was present, additional clinical attributes could not be extracted from the trajectories (Figure 6). Even when we force the kml method to extract 7 clusters like for B-splines and VRAE, the majority (79.6%) are still clustered into one cluster, meaning that given the opportunity to stratify the largest cluster further, the method chooses instead to stratify the smaller clusters with the smallest cluster resulting in only 0.1% of the data.

However, the methods (b-spline and VRAE) that dealt with missing time points by not electing to fill them with 0s, allowed for different sequence lengths, and transformed the raw data, ultimately clustered the trajectories into more clinically interpretable and useful subtypes. Seen in the profile analysis and the high F1 scores associated with the decision tree for B-splines, this method extracts more evenly distributed clusters that can be primarily explained by extracted trajectory features, such as number of MME observations, mean and standard deviation of MME over the trajectory, and the change in MME from the first observation to the last. However, the deep latent representation derived from the trajectories in VRAE could not fully be explained by extracted descriptive statistics. While the lower trajectories for B-splines and kml in Figure 4 tend to be static, the lower trajectories for VRAE are dynamic, picking up different potential global patterns. In addition, both of these methods showed clusters that were associated with other clinical features, such as dependence and chronic pain. In addition, our clusters for VRAE and B-spline provided meaningful temporal information to the model, increasing how accurate the model was in predicting opioid overdose and addiction in a highly imbalanced class setting, where even small increases in precision and recall on the test set are relevant. The question of how to handle temporality of medications in a standard risk prediction model is an important one, and clustering temporal data for feature creation may be a viable option, as it is presented here.

The application of machine learning to find subgroups that may not be inherently visible in a heterogenous general population is important to furthering biomedical research. For our use case, finding good opioid subtypes can have clinical implications. Very few people have assessed opioid trajectories in a general population that includes all payer types, even though arguably addiction and overdose can affect all people with initialized opioid use (16). In the general population, patients who are started on an opioid prescription with a high MME and then are subsequently tapered off of opioids, based on the VRAE clusters, tend to be highly predictive of opioid overdose or abuse.

Furthermore, integrating opioid trajectory subtype modeling into clinical decision support tools, may allow clinicians to more accurately predict which patients are at an increased risk of adverse opioid events. Risk stratification that incorporates an individual’s history of opioid use pattern, diagnoses, procedures, and other prescription medications may facilitate earlier interventions to prevent or detect abuse, or identify patients who would benefit from having an opioid overdose reversal agent such as naloxone readily available at home. This type of clinical decision support may also serve to encourage safer prescribing patterns. For example, in cluster 6, 65.5% of patients receiving opiates had a corresponding diagnosis of migraines and headaches. Best practice guidelines discourage opiates for the treatment of migraine and headache (52, 53). In addition to the risk of dependency with long term use, opiates commonly worsen headache symptoms and are not as effective as other agents (54).

In addition to modeling MME dosages, temporal clustering pre-processing strategies based on discrete EHR data, such as laboratory values or medication dosages, may enhance individualized prognostication in other disease states such as diabetes or congestive heart failure. Increasingly patients are using home monitoring systems which transmit clinical data directly to the EHR for clinician interpretation. Quantitating the influence of known clinical patterns in these and other disease states may enhance clinical decision making and enhance individualized medicine.

While we only explore three longitudinal k-means methods for dealing with high-dimensional and irregular medication trajectories, there are many alternative methods outside of these methods that should be assessed. For instance, VADER also uses a variational autoencoder with two LSTMs to cluster potentially sparse multivariate trajectories with imputation for missing not at random data. (4) However, they similarly have to estimate an optimal number of clusters and their model requires equal-length time series (4). In addition functional data analysis, such as functional PCA, is especially good at dimensionality reduction when the number of observations is less than the number of time points(55). These methods have been used to model growth patterns and cognitive development and could potentially be extended to medication trajectories (56). Finally, while we chose to use variational recurrent autoencoders to create our deep trajectory representations, there are other deep learning methods that could be used.

Limitations

While this paper aims to model subtypes of opioid use, there are several limitations to the data and modeling with k-means. The database only contains EHR data from two outpatient clinic sites and a patient may have obtained an opioid prescription at a different practice within WNY and this external information is not always reflected in a practice’s EHR system. However, this is less likely since New York state uses a prescription monitoring system to track prescriptions. Conversely, this sample is likely representative of the type of data available to one provider at the time of care. Currently, efforts are being made to integrate state prescription drug monitoring programs (PDMP) data into EHR systems with one in three hospital systems already doing so (37). PDMPs give a patient’s history of opioids, calculates total MME/day, and identifies patients who are obtaining opioids from multiple providers. However, these systems do not currently incorporate clinical decision support or provide clinicians with proactive alerts (38). As integration becomes a reality, the methodology of these types of models can still be applied, yielding more generalizable results. The presence of gaps in medication usage data means that our time zero, or entry into the cohort, could contain both patients being initiated on opioid therapy and chronic opioid users with inconsistent use. Without a complete record detailing a patient’s opioid prescription history it is not possible to accurately identify initial prescribing events. Despite this limitation, it is often a reality in a clinical setting where clinicians lack access to concise historical data from external sources about their patients.

While k-means provides an efficient and computationally tractable alternative to model-based clustering algorithms, it does have limitations. K-means relies on a given set of initial parameters’ start values and then attempts to converge towards the maximum; however, there is no way to be sure whether this is a global maximum or a local maxima. Therefore, as was done in this study, k-means should be run multiple times with different starting points to encourage convergence towards the global maximum. In addition, estimating the optimal number of clusters remains an open problem for k-means, although statistical heuristics exist and were employed (39).

Conclusion

Leveraging EHR data with machine learning has a tremendous potential to enhance clinical decision making and provide more granular risk stratification techniques. Temporal irregularities, including sequence length and missing data, can make it challenging to extract features for use as input in supervised machine learning models, often requiring deep expertise in the medical domain. As shown here, missing values methods, feature selection, scaling, transforming, and latent mappings can create very different subtypes that extract disparate information from the trajectories and create meaningful clinical clusters. The use of these clusters in downstream prediction tasks offer a way to incorporate this temporal information into a standard static machine learning model with higher accuracy. Our b-spline and VRAE clusters were highly important variables for predicting opioid overdose, compared to both a method that disregarded the longitudinal nature of the trajectory and a method that did not account for the temporal irregularities well. In addition, with decision tree visualization, we were able to characterize these clusters into clinically meaningful opioid use subtypes, accounting for both the dynamics of MME usage and relevant patient clinical features. While we applied these methods to an opioid cohort, these methods are universal and can be applied to any EHR laboratory or medication measure.