Addressing Heterogeneous Populations in Latent Variable Settings through Robust Estimation

Abstract

Individuals routinely differ in how they present with psychiatric illnesses and in how they respond to treatment. This heterogeneity, when overlooked in data analysis, can lead to misspecified models and distorted inferences. While several methods exist to handle various forms of heterogeneity in latent variable models, their implementation in applied research requires additional layers of model crafting, which might be a reason for their underutilization. In response, we present a robust estimation approach based on the expectation-maximization (EM) algorithm. Our method makes minor adjustments to EM to enable automatic detection of population heterogeneity and to recognize individuals who are inadequately explained by the assumed model. Each individual is associated with a probability that reflects how likely their data were to have been generated from the assumed model. The individual-level probabilities are simultaneously estimated and used to weight each individual’s contribution in parameter estimation. We examine the utility of our approach for Gaussian mixture models and linear factor models through several simulation studies, drawing contrasts with the EM algorithm. We demonstrate that our method yields inferences more robust to population heterogeneity or other model misspecifications than EM does. We hope that the proposed approach can be incorporated into the model-building process to improve population-level estimates and to shed light on subsets of the population that demand further attention.

Population heterogeneity of psychiatric illness complicates the effort to understand disease mechanisms and to treat individuals. Individual differences in clinical presentations, backgrounds and experiences, underlying causes, and treatment responses contribute to the complexity (Allsopp et al., 2019; Lanius et al., 2006; LeGates et al., 2019; Sonuga-Barke, 2002). As an example, with over 227 ways to meet the DSM-5 criteria for major depressive disorder, two individuals can be diagnosed with major depressive disorder without sharing any common symptoms (Zimmerman et al., 2015). This calls into question what generalizations one might be able to make regarding this disorder. Clinical features of major depressive disorder might differ across the population with some individuals enduring loss of appetite and disrupted sleep, while others experience weight gain and hypersomnia. (Goldberg, 2011; Lux & Kendler, 2010). On top of this, we know that cultural context can shape how a person perceives and communicates their symptoms (James & Prilleltensky, 2002; Kleinman, 2004). Disentangling the variations of psychiatric disorders across the population could have substantive implications for our ability to understand causal risk factors and to personalize treatments (Ballard et al., 2018; Nandi et al., 2009). Yet, many analyses of psychological data are not designed to handle the numerous forms of heterogeneity in the sampled population, which can lead to erroneous inferences. In this paper, we introduce a straightforward modification of certain standard analyses that automatically detects and respects population heterogeneity in an effort to recover more robust inferences.

We focus on analyses based on latent variable models, a cornerstone of psychological data analysis (c.f., Bauer & Curran, 2004; Croon & van Veldhoven, 2007; B. O. Muthén & Curran, 1997; Russell et al., 1998). There are many different classes of models that are recognized as latent variable models. Latent profile analyses and finite mixture models reveal underlying subgroups within a sample that share similar characteristics. Factor analyses, in which a few latent factors explain how item responses covary, help explore and confirm conceptual models of how well target psychological domains are measured by a psychological assessment. Similarly, latent growth models, item response theory, and structural equation models use latent variables to explain complex patterns of multidimensional observations.

Even though methods and models are available, accounting for heterogeneity within psychological data sets has yet to become ingrained within the daily practice of psychological research. Perhaps this can be partially attributed to the uncertainty in what sources of heterogeneity should be included in the latent variable model and to the complexity of the methods required to analyze latent variables within heterogeneous populations. Despite efforts to account for heterogeneity, the final model can still be misspecified. Measurement error caused by careless responses might compromise the quality of the data (Meade & Craig, 2012). Furthermore, unobserved heterogeneity can be difficult to assess in latent variable settings. Model fit diagnostics might fail to reveal poor model fit (Kelderman & Molenaar, 2007; Lai & Green, 2016; Savalei, 2012), and structural equation mixture modeling might lead to the detection of spurious latent classes among other issues (Bauer & Curran, 2004). To address some model fitting concerns, model diagnostic techniques, such as the outlier detection technique for factor analysis presented in Mavridis and Moustaki (2008), have been put forward.

Robust estimation offers another path to addressing population heterogeneity and other model misspecifications in latent variable modeling. In general, robust estimation techniques seek to provide inferences that are less sensitive than standard estimation techniques to deviations from model assumptions (Hampel et al., 2011). These techniques might be used on their own or, when combined with information about model misfit, these techniques can be incorporated into the model-building process. In latent variable settings, the expectation-maximization (EM) algorithm is commonly used to perform maximum likelihood estimation (Dempster et al., 1977). Along with having certain mathematical properties, EM is often easy to implement and available in software packages such as MPlus (L. Muthén & Muthén, 2016) and lavaan (Rosseel, 2012). Our proposed method, which we call REM (robust expectation-maximization), modifies EM in a way that addresses population heterogeneity.

REM incorporates iteratively re-estimated weighting into the EM algorithm to achieve estimates that are robust to model misspecifications. The estimated weights are probabilistic measures of model fitness and provide information on which data fit the model well and which data do not fit well. We recommend that this information be leveraged to assess heterogeneity within a data sample and inform future model-building efforts. In what follows, we set the stage with a formal background that provides necessary mathematical framing and motivates robust estimation. We present REM, its properties, and its relation to existing methods. Then, we apply REM to two commonly used latent variable models: Gaussian mixture models and linear factor models. We examine the robustness of our method relative to the EM algorithm through several simulation studies and conclude with a discussion of the benefits and limitations of REM.

Background

We start by considering multivariate data, $x_1,\dots ,x_N$, collected from N individuals. We propose a parametric model with unknown parameters $\theta \in \text{Θ}$ to describe how these data were generated; our interest is to estimate the values of the parameters given the observed data. We focus on parametric models that describe each data point as an independent realization of a random variable X that depends on a latent random variable Z. Simulation studies in this paper focus on two classes of latent variable models, mixture models and common factor models, but the concepts could be extended to other classes of models as well.

Maximum likelihood estimation is frequently employed to estimate unknown parameters $\theta$. This approach searches for an estimate, denoted by $\widehat{\theta }$, that maximizes the likelihood—or equivalently the log-likelihood—of observing the data under the assumed model (Casella & Berger, 2002). The maximum likelihood estimate, for an independent and identically distributed sample $x_1,\dots ,x_N$, can be expressed as

$$\widehat{\theta }\left(x_1,\dots ,x_N\right)=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\log f_{X\mid \theta }\left(x_n\right),$$

where $f_{X\mid \theta }(\cdot )$ is the marginal probability density function for X given parameters $\theta$, under the assumed parametric model. For discrete X, a probability mass function is used instead. If the model is correct, and observed data $x_1,\dots ,x_N$ are indeed independent realizations of X, then the maximum likelihood estimator benefits from several statistical properties. Most importantly, there is no other estimator that has lower asymptotic mean squared error under the true model than the maximum likelihood estimator.

For latent variable models, direct maximization can be computationally challenging or impossible. The EM algorithm was proposed as a procedure to perform maximum likelihood estimation for latent variable models using the complete-data likelihood, $f_{X,Z\mid \theta }(\cdot ,\cdot )$ rather than the incomplete-data likelihood, $f_{X\mid \theta }(\cdot )$ (Dempster et al., 1977). The key insight of EM is that any estimate that increases the function

$$Q(\theta \mid \widehat{\theta }):=\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right],$$

over a current estimate $\widehat{\theta }$, also increases the incomplete-data likelihood. Thus, one can improve upon an estimate $\widehat{\theta }$ by maximizing the function $Q(\cdot \mid \widehat{\theta })$. By repeatedly improving upon estimates until no more improvements can be made, EM can arrive at an estimate that (locally) maximizes the log-likelihood.

While maximum likelihood estimation, and hence EM, work well under ideal conditions, they are sensitive to departures in the data from model specifications (Moustaki & Victoria-Feser, 2006). Consider a simple example of fitting a normal distribution to data, $x_1,\dots ,x_N$, with unknown mean μ. The maximum likelihood estimate for μ is simply the empirical mean $\left(x_1+\dots +x_N\right)/N$, which is equally sensitive to each data point. If we move one point from negative to positive infinity, the empirical mean also moves from negative to positive infinity. By contrast, the median, another measure of center, does not yield as easily: if we move one point from negative to positive infinity, the median stays within a bounded interval whenever N > 2. In other words, if we get the model wrong for one individual, then the maximum likelihood estimate for μ can deteriorate.

A single individual might be poorly described by the model, but more likely several individuals are not well represented by the model. For example, pregnant women might more readily endorse changes in appetite or sleep compared to non-pregnant women. Accordingly, factor model parameters could differ between the two groups. This discrepancy is a violation of measurement invariance (Mellenbergh, 1989). Measurement invariance can be expressed mathematically as

$$f_{X\mid Z,C}(x\mid z,c)=f_{X\mid Z}(x\mid z)$$

where X denotes the observed variables, Z denotes a latent variable underlying X, and C denotes a possible unobserved or observed source of heterogeneity, such as pregnancy status. Put another way, measurement invariance requires that the observed response X is independent of possible sources of heterogeneity conditional on the latent variable Z. Lack of measurement invariance—referred to as differential item functioning—can have implications for latent variable interpretation. If differential item functioning is present, biased estimates could ensue without proper incorporation of this variation in the model.

Robust Expectation-Maximization

Robust estimation was developed to reduce the influence of violations in modeling assumptions on estimation. Considering numerous textbooks (Hampel et al., 2011; Huber, 2004) and reviews (Dixon & Yuen, 1974; Wilcox & Keselman, 2003) are devoted to the subject, a comprehensive treatment of robust estimation is beyond the scope of this paper. We highlight a class of estimators, known as M-estimators, that search for a maximum of a function of the form:

$$\sum _{n=1}^N\rho \left(x_n,\theta \right),$$

which for certain ρ amounts to solving an estimating equation:

$$\sum _{n=1}^N\psi \left(x_n,\theta \right)=0,$$

where $\psi (x,\theta )={\nabla }_{\theta }\rho (x,\theta )$. The maximum likelihood estimator is an M-estimator with $\rho (x,\theta ):=\log f_{X\mid \theta }(x)$ and $\psi (x,\theta )$ equal to the score function ${\nabla }_{\theta }\log f_{X\mid \theta }(x)$. To yield a robust M-estimator, transformations can be applied to the likelihood or score function; several approaches have been presented the literature (Basu et al., 1998; Eguchi & Kano, 2001; Fujisawa & Eguchi, 2006; Markatou, 2000; Neykov et al., 2007; Wang et al., 2017; Windham, 1995). One of the challenges is that the distribution of the noise process is generally unknown.

Building on these ideas, we propose an M-estimator that uses the likelihood, is robust to model misspecification, and lends itself to a modified EM procedure for estimation. Instead of assuming that all data were generated from the same probability model and are measured without error, we allow observed data to have been generated from our model $f_{X\mid \theta }(x)$ with probability γ and from some other distribution with probability $(1-\gamma )$. To allow for generality, we assume no knowledge of this other distribution—otherwise we could incorporate this information into our model $f_{X\mid \theta }(x)$—and replace its likelihood with a fixed value ϵ that is independent of unknown parameters $\theta$. This idea builds on Fraley and Raftery (1998), which suggests adding a component to a mixture model that captures a uniformly distributed noise process. Several concerns were raised about its robustness (Hennig et al., 2004). The issue, in part, is that the volume V can go off to infinity in unbounded domains, and hence 1/V goes to zero—returning us right back to maximum likelihood estimation. We sought to leverage the benefits of adding a uniform distribution without these drawbacks. Critically, ϵ is not a proper likelihood, since we do not presume ϵ integrates to 1 over the domain. Alternatively, ϵ serves as a hyperparameter that is used to tune our estimation (discussed later). With this viewpoint, we alter the objective function that is maximized under maximum likelihood estimation as follows:

$$\sum _{n=1}^N\log \left\{f_{X\mid \theta }\left(x_n\right)\right\}\to \sum _{n=1}^N\log \left\{\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right\}.$$

The new expression is no longer a likelihood function itself but rather a transformation of the likelihood function of interest. The substitution allows for flexibility under model misspecification. We focus on maximizing this objective function to achieve REM estimates.

Maximizing the objective function leads to the estimating equations:

$$\sum _{n=1}^{N}p\left(x_n;\theta ,\gamma \right){\nabla }_{\theta }\log f_{X\mid \theta }\left(x_n\right)=0,$$

$$\frac{\frac{1}{N}{\sum }_{n}p\left(x_n;\theta ,\gamma \right)-\gamma }{\gamma (1-\gamma )}=0,$$

where

$$p(x;\theta ,\gamma )=\frac{\gamma f_{X\mid \theta }(x)}{\gamma f_{X\mid \theta }(x)+(1-\gamma )ϵ}.$$

The first of the two estimating equations is similar, in form, to the weighted likelihood equations in Markatou et al. (1998). However, here, the weights $p(x;\theta ,\gamma )$ afford an interpretation within the modified likelihood framework. Namely, the weights describe the probability that a data point was generated from the specified model $f_{X\mid \theta }$.

With some manipulation, the objective function can be rewritten as a weighted sum containing the expression for the log-likelihood. From here, an estimation procedure can be derived from arguments similar to those used to justify the EM algorithm (detail in Appendix A). Conveniently, terms involving parameters $\theta$ and terms involving $\gamma$ can be separated and maximization steps derived independently. The result is the following set of interconnected steps:

$$\widehat{\theta }\leftarrow \underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]$$ (1)

$$\widehat{\gamma }\leftarrow \frac{1}{N}\sum _{n=1}^N{\widehat{p}}_n$$ (2)

$${\widehat{p}}_n\leftarrow \frac{\widehat{\gamma }{f}_{X\mid \widehat{\theta }}\left(x_n\right)}{\widehat{\gamma }{f}_{X\mid \widehat{\theta }}\left(x_n\right)+(1-\widehat{\gamma })ϵ},\text{for}n=1,\dots ,N$$ (3)

We iteratively update estimates $\widehat{\theta }$ and $\widehat{\gamma }$ and probabilistic weights ${\widehat{p}}_n$ until suitable convergence is achieved. Relative to the EM algorithm, we need to solve a weighted version of the maximization step, calculate a mean to get $\widehat{\gamma }$, and calculate new weights ${\widehat{p}}_n$.

The benefit of our approach rests on two things: its computational facility and the information it provides regarding individual-level model fit. As we will show for Gaussian mixture models and linear factor analysis, only minor adjustments to the EM procedure are needed. In addition to model parameter estimates, the REM procedure produces an estimate of the overall probability that individuals are represented by the original parametric model $(\widehat{\gamma })$ and an estimate of the probability that a given individual is represented by the model $\left({\widehat{p}}_n\right)$. This information can reveal both the presence of sample heterogeneity and highlight who might be poorly represented by the model.

Robustness

As demonstrated above, the modification of the likelihood function leads to a robust M-estimator. Compared to maximum likelihood estimation, the contribution of each data point to the estimating function for $\theta$ is weighted by $p(x;\theta ,\gamma )$. Critically, these weights can down-weight any data points that are unlikely under the model $f_{X\mid \theta }(x)$; weights approach zero as $f_{X\mid \theta }(x)$ goes to zero or as ϵ tends to positive infinity. Robustness is formally measured in terms of properties of the influence function, a functional derivative that measures how much an estimator changes when changing the distribution from the true model in the direction of a point mass at x (Huber, 2004). Since robustness has been well-characterized for M-estimation, we point out only that the influence function is proportional to the estimating function. Thus, the influence function benefits from the weights in the estimating function, ensuring our estimator is not strongly influenced by a single data point.

Tuning the hyperparameter

The REM procedure requires a pre-specified parameter ϵ, which we refer to as a hyperparameter. The hyperparameter ϵ acts as a tuning parameter for the sensitivity of parameter estimation to individual data points. Recall that the hyperparameter is standing in for a likelihood value, so it must take a non-negative value. When ϵ = 0, estimates of the weights ${\widehat{p}}_n$ are one, and estimates of model parameters, $\theta$, from EM and REM coincide. As ϵ increases, estimated weights move away from unity toward zero. As weight estimates approach zero, effectively none of the data provides information to estimate the model parameters.

We propose a search for the largest ϵ that satisfies the following inequality

$${\mathbb{E}}_{X\mid \widehat{\theta }}[p(X;\widehat{\theta },0.9)]\ge 1-\delta$$ (4)

where δ is a hyperparameter that effectively replaces the role of ϵ. While ϵ is on a similar scale as the likelihood, the hyperparameter δ will always lie between 0 and 1. Recall that $p(X;\widehat{\theta },0.9)$ can be interpreted as the posterior probability that a data point X drawn from a heterogeneous sample was generated by the model $f_{X\mid \widehat{\theta }}(x)$ when, on average, 10% of the data were generated by another process. Naturally, we would like data drawn from $f_{X\mid \widehat{\theta }}(x)$ to be considered likely to be drawn from this model. Assuming this with certainty, $p(X;\widehat{\theta },0.9)=1$, requires ϵ to be zero resulting in a lack of robustness. Alternatively, if we let $p(X;\widehat{\theta },0.9)$ deviate too much from one, then we down-weight data points that could help estimate $\theta$ resulting in a loss of efficiency. The inequality above attempts to strike a balance between these two competing goals by placing a lower bound on the expected value of this probability. In the end, the choice of δ should reflect how the researcher prefers to strike that balance.

The parameter δ can be thought of in a similar way as the significance level α in hypothesis testing, which specifies the probability of a Type 1 error. That is, δ captures the researcher’s tolerance of incorrectly down-weighting data from the model. Researchers with a low tolerance could choose lower values of δ compared to researchers with a higher tolerance for down-weighting data points. For example, small δ (≈ 0.001) could protect against extreme outliers without sacrificing too much efficiency. Large δ (≈ 0.05 as we use in all our simulations) could help identify and protect against sample heterogeneity and other model violations at the expense of a loss of efficiency. Empirical work will be needed to determine appropriate ranges for specifying δ.

While there may be other approaches to selecting ϵ, we draw attention to several challenges. Our modified likelihood increases monotonically with ϵ; setting ϵ to infinity would maximize the modified likelihood. Thus, the modified likelihood does not provide a suitable measure of model fit to guide selection of ϵ. More broadly, it is unclear whether ϵ should be chosen on the basis of model fit, given that we presume that not all data in our sample were generated from the same model. For example, if Akaike Information Criteria (AIC) (Akaike, 1974) or Bayesian Information Criteria (BIC) (Schwarz et al., 1978) were used, then ϵ should be zero in order to recover the maximum likelihood estimator. Further, REM does not indicate what model is appropriate for data that poorly fit the original likelihood; no model is ever investigated for these data with ϵ used instead. This hinders the use of cross-validation, which is often recommended when selecting hyperparameters but requires a measure of model fit or model prediction error upon which to evaluate generalizability. None of these challenges are unique to our method, as many robust estimation approaches include a hyperparameter and require various heuristics for selecting the hyperparameter. Similarly, we take a heuristic approach that makes use of our interpretation of the weights and leads to sensible results.

Model Selection

Researchers are often interested in selecting a model $f_{X\mid \theta }(x)$ among several choices. These choices might differ by the number of specified factors in a factor analysis or the number of groups in a mixture model. Our goal with robust estimation is to fit a model that captures the structure among the majority of the data in the sample, rather than all the data necessarily, so we recommend using a measure of model fit that reflects this goal. For the reasons described above, tuning ϵ based on standard measures of model fit (e.g., AIC or BIC) would not reflect our goal as they would tend to favor models with small values of ϵ. However, once ϵ is tuned for each candidate model $f_{X\mid \theta }(x)$, we suggest that one can utilize likelihood-based measures of model fit, such as AIC or BIC, to guide model selection. These measures would need to be evaluated at parameters estimated by REM instead of the maximum likelihood parameter values. This adjustment and how we tune ϵ helps ensure that model selection will depend on how well the model fits the majority of the data rather than the full sample. We will use this approach to guide model selection in our simulations.

Connection to other M-estimators

In addition to the aforementioned approaches in Fraley and Raftery (1998) and Markatou et al. (1998), our approach bears similarities to other robust estimation approaches. For example, Eguchi and Kano (2001) works with a transformation Ψ of the log-likelihood function but unlike our approach, they include a term $b_{\text{Ψ}}(\theta )$ to correct for bias in the estimator under the true model:

$$\rho (x,\theta ):=\text{Ψ}\left(\log f_{X\mid \theta }(x)\right)-b_{\text{Ψ}}(\theta ).$$

Proposed transformations Ψ(x) include log-logistic function log(x + η) (Eguchi & Kano, 2001), which has a similar form to our transformation of the likelihood, and a power function $\frac{1}{\beta }{f}_{X\mid \theta }{(x)}^{\beta }$ (Basu et al., 1998; Fujisawa & Eguchi, 2006). A power function is also used in Ferrari, Yang, et al. (2010) but with the bias correction term dropped, as we do. Dropping this term simplifies estimation, since this term is usually expressed as an integral without a closed form solution. The associated estimating equation becomes

$$\sum _{n=1}^N{f}_{X\mid \theta }{\left(x_n\right)}^{\beta }{\nabla }_{\theta }\log f_{X\mid \theta }\left(x_n\right)=0.$$

By tuning β, data points can be down-weighted if they are poorly represented by the model. Robust estimates can be obtained, but estimation is not a simple extension of EM.

In the specific case of a mixture of regression models, Bai et al. (2012) proposed that one could directly replace the M-step in the EM algorithm with a robust criterion instead of modifying the likelihood function. The authors note connections to weighted least squares estimation with iterative reweighting; however, weights do not carry the interpretation as probabilities of being generated from the model.

While we focus on M-estimators for situations when a researcher wants to specify a probability model (i.e. likelihood), it is important to recognize M-estimators that are not based on a likelihood function. In latent variable settings, the mean and the covariance matrix might be the only objects of interest. One can formulate SEMs as regression models and propose structural models for the first and second moments of the data without specifying a probability model for the error (Yang et al., 2012; Yuan & Bentler, 1998, 2007). Rather than minimizing the sum of squared errors, approaches like iteratively reweighted least squares with researcher-specified weighting functions can be used to estimate parameters while down-weighting outliers.

In light of these existing M-estimators, we view the contribution of our approach is its combined ability to:

1. Recover likelihood-based estimates that are robust to sample heterogeneity and other violations of modeling assumptions.

2. Incorporate easily in latent variable settings due to its similarity to EM.

3. Return meaningful information about population heterogeneity in the form of an estimate of the overall probability that individuals are represented by the original parametric model $(\widehat{\gamma })$ and an estimate of the probability that a given individual is represented by the model $\left({\widehat{p}}_n\right)$.

Robust Mixture Modeling

Mixture modeling is a common approach for breaking down a sample into distinct groups based on observed variables such as individual behavior, symptoms, and/or physiology. After collecting self-ratings of depressive symptoms within a sample of individuals with major depressive disorder or bipolar disorder, we could use a mixture model to determine if the sample divides along diagnostic groups based on their depressive symptoms. Formally, we collect a vector of P observations from a sample of N individuals: $\left(x_1,\dots ,x_N\right)$. Each individual in the sample is modeled as belonging to one of K underlying subgroups with their observations assumed to be drawn from a known distribution, typically multivariate normal, that depends on their group membership.

Applying EM to obtain estimates for parameters of a Gaussian mixture model would involve repeatedly updating estimates of covariance matrices ${\widehat{\text{Σ}}}_k$, means ${\widehat{\mu }}_k$, and mixture proportions ${\widehat{\pi }}_k$ associated with each latent phenotype (List 1; derivations can be found in Appendix B). These estimates are simply weighted versions of empirical covariance matrices, means, and proportions with weights ${\widehat{\omega }}_{nk}$—which can be

List 1:

Comparison of the main updates for Gaussian mixture models using EM vs. REM.

EM	REM
${\widehat{\text{Σ}}}_k\leftarrow \frac{{\sum }_n{\widehat{\omega }}_{nk}\left(x_n-{\widehat{\mu }}_k\right){\left(x_n-{\widehat{\mu }}_k\right)}^{\prime }}{{\sum }_n{\widehat{\omega }}_{nk}}$	${\widehat{\text{Σ}}}_k\leftarrow \frac{{\sum }_n{\widehat{p}}_n{\widehat{\omega }}_{nk}\left(x_n-{\widehat{\mu }}_k\right){\left(x_n-{\widehat{\mu }}_k\right)}^{\prime }}{{\sum }_n{\widehat{p}}_n{\widehat{\omega }}_{nk}}$
${\widehat{\mu }}_k\leftarrow \frac{{\sum }_n{\widehat{\omega }}_{nk}{x}_n}{{\sum }_n{\widehat{\omega }}_{nk}}$	${\widehat{\mu }}_k\leftarrow \frac{{\sum }_n{\widehat{p}}_n{\widehat{\omega }}_{nk}{x}_n}{{\sum }_n{\widehat{p}}_n{\widehat{\omega }}_{nk}}$
${\widehat{\pi }}_k\leftarrow \frac{1}{N}\sum _{n=1}^N{\widehat{\omega }}_{nk}$	${\widehat{\pi }}_k\leftarrow \frac{{\sum }_n{\widehat{p}}_n{\widehat{\omega }}_{nk}}{{\sum }_n{\widehat{p}}_n}$

interpreted as posterior probabilities of individual n belonging to latent phenotype k conditional on current estimates. Applying REM, we arrived at a slightly modified estimation procedure (List 1; derivations can be found in Appendix B). Other than the two additional REM updates (i.e. $\widehat{\gamma }$ in Eq. 2 and ${\widehat{p}}_n$ in Eq. 3), the only change was to replace weights ${\widehat{\omega }}_{nk}$ with ${\widehat{p}}_n{\widehat{\omega }}_{nk}$ which allowed for fitted parameters to be robust to outliers.

In the following subsections, we draw contrasts between how EM and REM performed in simulated scenarios of data heterogeneity. For concreteness and to enable easy visualization, we analyzed samples of individuals each contributing two observations, which might correspond to two psychological domains A and B (e.g., subscores on a positive and negative affect scale). Simulations were performed in MATLAB; source code can be found at: https://github.com/knieser/REM. Short descriptions of simulations can be found in Appendix D.

Scattered Minority Group

For context, suppose that most individuals fall into one of two distinct groups based on measurements of Domains A and B. However, within the sample, there is a minority group of individuals who are not characterized well by either of these two groups. This minority group might have a different underlying illness or might have more poorly measured responses. For example, a sample of individuals with major depressive disorder or bipolar disorder might include a minority group of misdiagnosed borderline patients or a minority group of individuals who answer survey questions at random, yielding faulty measurements. In either case, the minority group is not well-described by either of the two majority subgroup models. We conducted two simulation studies of such data, each with a sample size of 1000. Data from the two predominant majority groups were simulated from skewed bivariate Normal distributions with probabilities 0.70 and 0.20 and skew parameter set to 0.5. Minority group data were simulated with probability 0.10 from a bivariate Beta random vector scaled to cover the relevant domain. Further simulation specifications can be found in Appendix D. The REM hyperparameter was selected based on the heuristic method described with δ = 0.05.

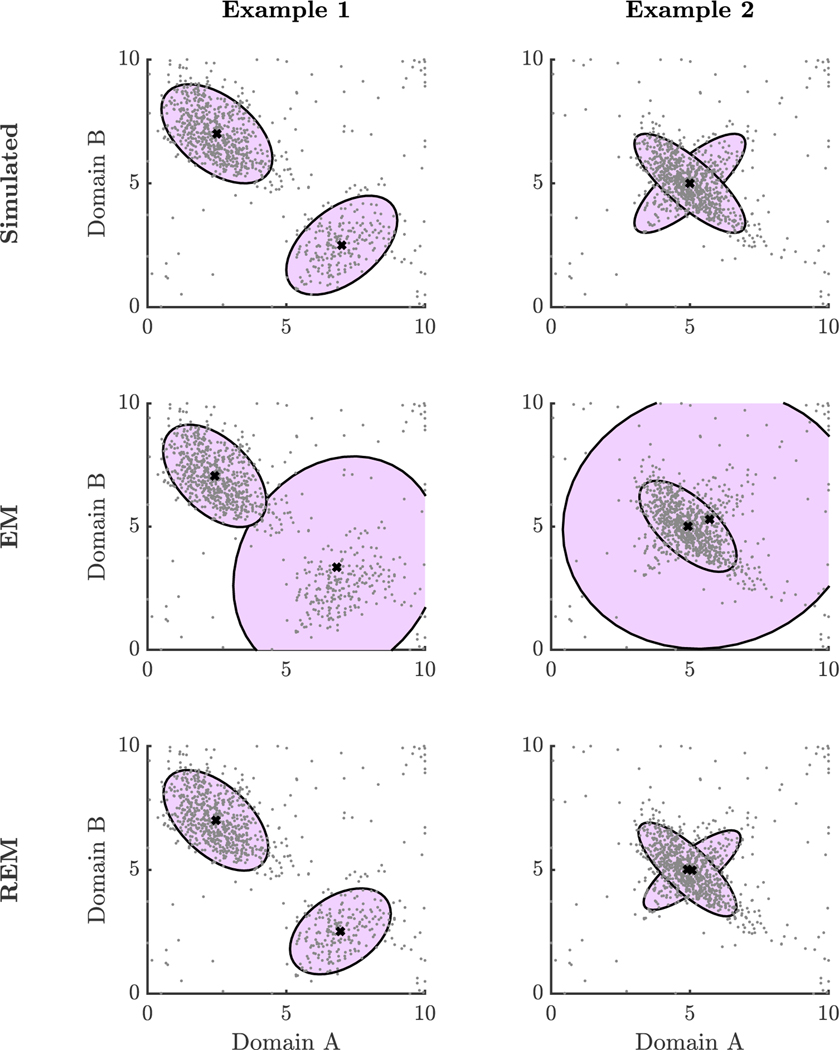
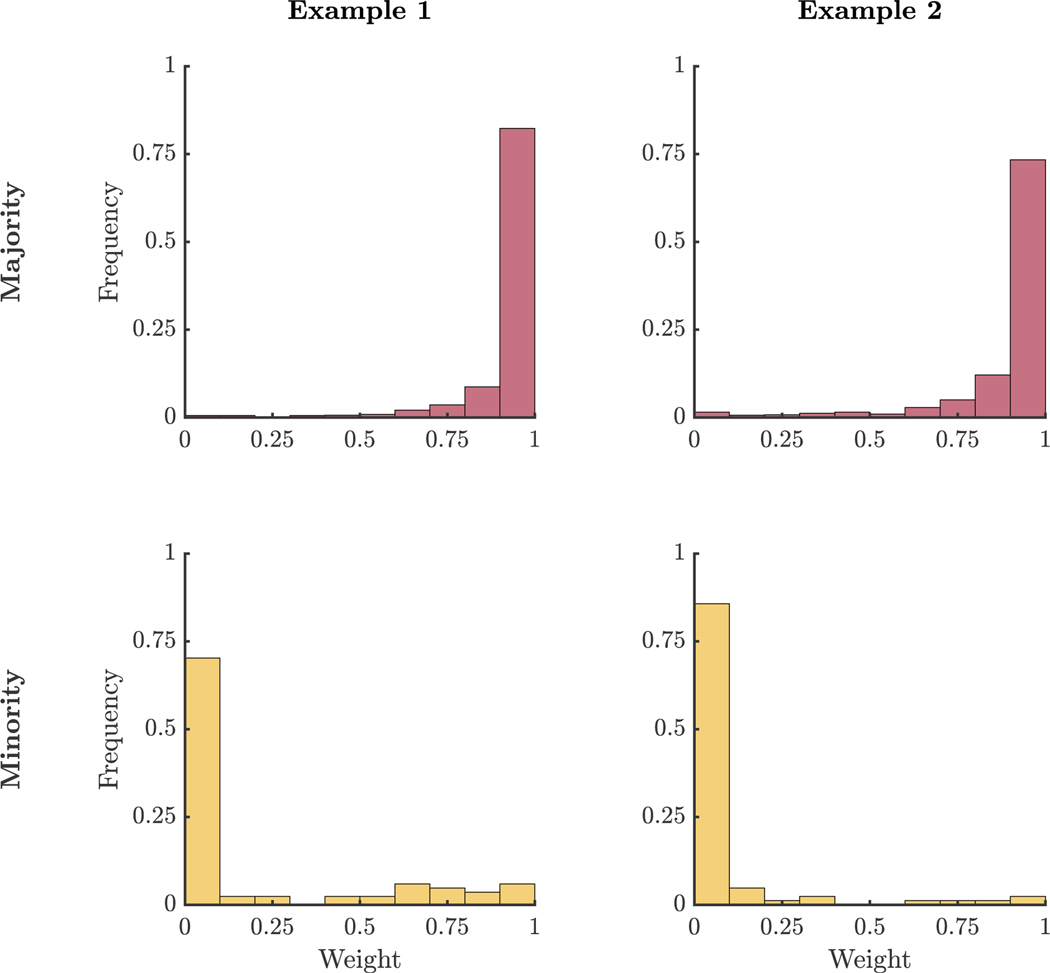
In Example 1, EM resulted in visibly inaccurate models for the two majority groups, because it tried to fit the scattered minority group into one of the two majority groups (Figure 1). By contrast, REM resulted in more accurate models for the majority groups, because it used p_n to down-weight the scattered minority group during model estimation. The REM estimated parameters for the smaller latent group align more closely with the true underlying sample estimates (Table E1). Comparing the estimated means and population means, the root mean square error (RMSE) was 0.44 based on the EM estimates and 0.03 based on the REM estimates. We compared the Frobenius norm of the difference between the estimated and population covariance matrices. The norm difference was 1.69 for the EM estimated covariance matrix and 0.15 for the REM estimated covariance matrix. Estimated weights provided a mechanism for clearly differentiating individuals that fit the model well (majority groups) and those that were not well-described by the model (minority group) (Figure 2).

Figure 1. Simulations of Scattered Minority Group.

Note: This figure shows scatter plots of simulated data and approximate 95% confidence ellipses for ground truth parameter values, EM estimates, and REM estimates.

Figure 2. REM Estimated Weight Distributions.

In Example 2, the two majority groups overlap (Figure 1). In one group, Domain A and B are positively correlated and in the other, Domain A and B are negatively correlated. Nonetheless, we found similar results to Example 1. REM yielded model estimates that more closely aligned with the two underlying groups compared to EM (Table E2); the REM estimated parameters were unperturbed by the minority group whereas the EM estimated parameters for one of the groups recovered was affected by the data from individuals in the minority group. Comparing the estimated means and population means, the RMSE was 0.39 based on the EM estimates and 0.06 based on the REM estimates. The norm difference between the estimated and population covariance matrices was 2.98 for the EM estimates and 0.22 for the REM estimates.

To further examine how EM and REM compare under other finite mixture scenarios, we include three additional examples in Appendix G. In short, when majority and minority groups both have large within-group variability, they can be more difficult to distinguish. In these situations, REM estimation will not necessarily outperform EM estimation in terms of the metrics we examined.

Determining the Number of Groups

Considering the previous two examples, if the minority individuals truly formed a separate, third group, a researcher might consider fitting three groups based on model fit criteria. On the other hand, if minority individuals are truly scattered or their observations poorly measured, their identification as a singular group might be spurious. However, various fit criteria might fail to suggest three groups or might disagree on the number of groups that would be appropriate. Model fit criteria, such as Akaike Information Criteria (AIC) (Akaike, 1974) or Bayesian Information Criteria (BIC) (Schwarz et al., 1978), are generally used to select an appropriate number of groups. However, the AIC and BIC do not always agree and tend to perform well under different scenarios (Vrieze, 2012). Consequently, some judgement is needed to settle on the number of groups, which can influence what groups are identified.

For Examples 1 and 2, we computed AIC and BIC for models with $K=1,\dots ,9$. In Example 1, the minimum value of AIC was 7072.9 and the minimum value of BIC was 7303.5, both corresponding to K = 8. For comparison, values of the AIC were 8574.4, 7520.5, 7253.2, 7198.1 and values of the BIC were 8598.9, 7574.5, 7336.7, 7311.0 for K = 1,2,3,4, respectively. In Example 2, the minimum value of AIC was 5946.4 corresponding to K = 8 and the minimum value of BIC was 6133.9 corresponding to K = 6. Values of the AIC were 7100.7, 6237.1, 6105.8, 6049.7, and values for BIC were 7125.3, 6291.1, 6189.2, 6162.6 for K = 1,2,3,4, respectively. The number of clusters K would be at least 6 in either example if we wanted to minimize AIC or BIC. There was not an indication, in either example, that K = 2 or K = 3 was the appropriate choice. Rather than attempting to force every individual toward a subgroup, REM allows for greater flexibility and recognizes that the designated model might not be appropriate for the entire sample.

As described above, we suggest using the AIC and BIC information criteria evaluated at the REM estimated parameter values, which we denote by $\text{AIC}\left({\theta }_{REM}\right)$ and $\text{BIC}\left({\theta }_{REM}\right)$, to select a model. For Example 1, we computed $\text{AIC}\left({\theta }_{REM}\right)$ values of 25958.2, 8896.3, 8888.6, 8985.0, 9089.8 and $\text{BIC}\left({\theta }_{REM}\right)$ values of 25982.8, 8950.3, 8972.0, 9097.9, 9232.1 for K = 1,2,3,4,5, respectively. In Example 2, we computed $\text{AIC}\left({\theta }_{REM}\right)$ values of 12574.5, 7753.9, 8228.4, 8134.6, 8375.6 and $\text{BIC}\left({\theta }_{REM}\right)$ values of 12599.0, 7807.9, 8311.9, 8247.4, 8517.9 for K = 1,2,3,4,5, respectively. In Example 1, the K = 3 case provides the lowest $\text{AIC}\left({\theta }_{REM}\right)$ but the K = 2 case provides the lowest $\text{BIC}\left({\theta }_{REM}\right)$. In Example 2, the K = 2 case provides the lowest $\text{AIC}\left({\theta }_{REM}\right)$ and lowest $\text{BIC}\left({\theta }_{REM}\right)$.

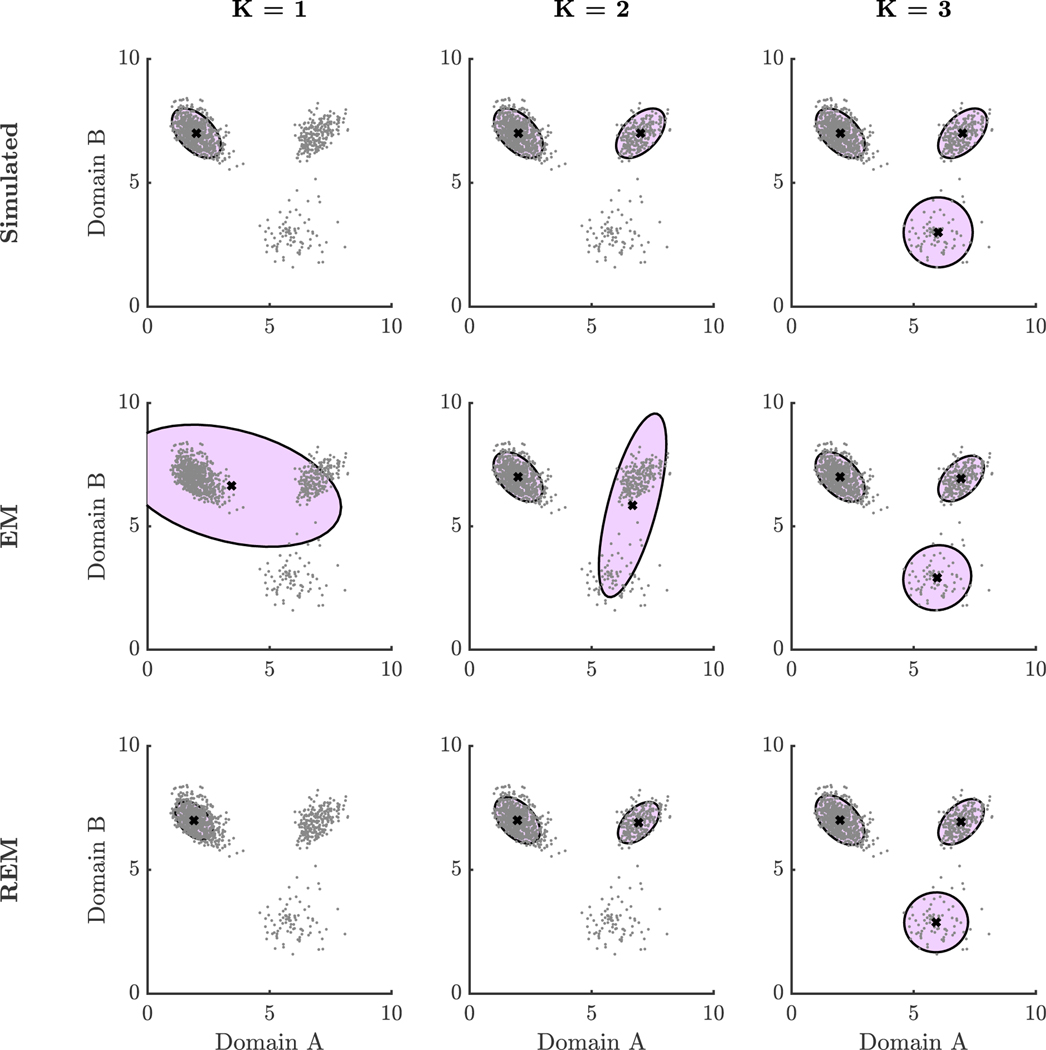
For further illustration, we simulated a sample of three distinct groups (Figure 3). Data were simulated from three different skewed bivariate Normal distributions with probability 0.70, 0.20, and 0.10 and skew parameter set to 0.5 (further detail in Appendix D). Again, the REM hyperparameter was selected based on the heuristic method described with δ = 0.05. We obtained EM and REM parameter estimates for a varying number of groups K fit to the data. We found that the estimated means and covariances from EM moved around as the algorithm attempted to put every data point into one of the groups (Table E3). Estimated means were also unrepresentative of the observations if K was underspecified in that very few individuals were near the estimated means. By contrast, estimated means and covariances from REM were relatively more consistent when changing K in the following sense. Comparing the estimated means to the population means of the closest clusters, the RMSE was 1.05 based on the EM estimates and 0.07 based on the REM estimates when K = 1. The norm difference between estimated and population covariance matrices of the closest clusters was 2.54 for the EM estimates and 0.08 for the REM estimates. In the case of K = 2, the RMSE was 0.60 based on the EM estimates and 0.07 based on the REM estimates. The norm difference between estimated and population covariance matrices was 1.60 for the EM estimates and 0.05 for the REM estimates. In the case of K = 3, the RMSE was 0.05 based on the EM estimates and 0.07 based on the REM estimates. The norm difference between estimated and population covariance matrices was 0.03 for the EM estimates and 0.05 for the REM estimates. In terms of these metrics, EM slightly outperformed REM when the number of latent groups was correctly specified, but REM provided estimates substantially closer to the underlying parameters when the number of latent groups was misspecified. While a suitable number of groups can easily be determined in this example by visually inspecting the data, we presented this example to give insight into how REM can provide estimates of underlying groups even if the number of latent groups is misspecified in the model.

Figure 3. Model Fits with Varying Number of Latent Groups.

Note: This figure shows scatter plots of simulated data and approximate 95% confidence ellipses for ground truth parameter values, EM estimates, and REM estimates.

Robust Factor Analysis

Factor analysis is a method for modeling correlations among observed variables as a result of underlying latent factors within individuals. For example, we might theorize that there is a latent psychological construct that explains observed correlations between symptoms of a psychiatric illness. Formally, in the linear factor model, we relate a P-dimensional vector of observations X to a K-dimensional latent variable Z, where P > K, in the following way

$$X=\text{Λ}Z+U$$

for some unknown P × K matrix Λ, referred to as the loading matrix or factor structure, and P-dimensional multivariate normal random variable U with mean 0 and unknown diagonal covariance Ψ. Typically, the factors in Z are referred to as common factors, while factors in U are referred to as unique factors. We can intuit U as an error term; U captures the additional variation in each observed variable in X that is not explained by one or more of the common factors represented in Z. We assume that U

List 2:

Comparison of the main updates for factor analysis using EM vs. REM.

EM	REM
$\widehat{\text{Λ}}\leftarrow \left(C_{xx}{\widehat{\beta }}^{\prime }\right){\left(\mathbb{I}-\widehat{\beta }\widehat{\text{Λ}}+\widehat{\beta }{C}_{xx}{\widehat{\beta }}^{\prime }\right)}^{-1}$	$\widehat{\text{Λ}}\leftarrow \left(C_{xx}{\widehat{\beta }}^{\prime }\right){\left(\mathbb{I}-\widehat{\beta }\widehat{\text{Λ}}+\widehat{\beta }{C}_{xx}{\widehat{\beta }}^{\prime }\right)}^{-1}$
$\widehat{\text{Ψ}}\leftarrow \text{diag}\left[(\mathbb{I}-\widehat{\text{Λ}}\widehat{\beta })C_{xx}\right]$	$\widehat{\text{Ψ}}\leftarrow \text{diag}\left[(\mathbb{I}-\widehat{\text{Λ}}\widehat{\beta })C_{xx}\right]$
$C_{xx}\leftarrow \frac{1}{N}\sum _{n=1}^N{x}_n{x}_n^{\prime }$	$C_{xx}\leftarrow \frac{{\sum }_n{\widehat{p}}_n{x}_n{x}_n^{\prime }}{{\sum }_n{\widehat{p}}_n}$
$\widehat{\beta }\leftarrow {\widehat{\text{Λ}}}^{\prime }{\left(\widehat{\text{Ψ}}+{\widehat{\text{Λ}}\widehat{\text{Λ}}}^{\prime }\right)}^{-1}$	$\widehat{\beta }\leftarrow {\widehat{\text{Λ}}}^{\prime }{\left(\widehat{\text{Ψ}}+{\widehat{\text{Λ}}\widehat{\text{Λ}}}^{\prime }\right)}^{-1}$

and Z are independent and that Z follows a multivariate normal distribution with mean 0 and covariance matrix $\mathbb{I}$—the identity matrix. Together, Λ and Ψ make up unknown parameters $\theta$ that need to be estimated.

Various methods exist for estimating the unknown parameters. Among these, maximum likelihood estimation is one of the most common methods. Again, given that direct maximization of the likelihood function can be challenging, the EM algorithm is often applied (Rubin & Thayer, 1982). In this section, we demonstrate the application of REM to the linear factor model. Aside from the estimation of $\widehat{\gamma }$ in Eq. 2 and ${\widehat{p}}_n$ in Eq. 3, REM resulted in an estimation procedure very similar to the EM algorithm with the modification of estimating an iteratively re-weighted empirical correlation matrix C_xx (List 2; details can be found in Appendix C).

We studied how estimates recovered using REM differed from estimates recovered from the EM approach in several simulations of data samples taken from a population with a mixture of factor structures, which we describe in the following subsections. To simulate realistic factor structures with control over the level of sparsity and of communality, we used the simulation method described in Tucker et al. (1969) (details in Appendix F). Simulations were performed in MATLAB; source code can be found at: https://github.com/knieser/REM.

We focused on the loading matrix (Λ), which relates the observed variables to the common factors uniquely up to a rotation. The choice of rotation has an effect on the interpretation of the results, and various rotation approaches exist with different advantages and disadvantages (Fabrigar et al., 1999). To circumvent the dependency of the solution on factor rotation, we calculated the R_V coefficient to obtain a measure of congruence between the estimated factor structure and the simulated factor structure of the majority group (Abdi, 2007; Robert & Escoufier, 1976). The R_V coefficient is invariant to rotations of the loading matrices. R_V coefficients were calculated as

$$R_V=\frac{\text{tr}\left({\text{Λ}}_0{\text{Λ}}_0^{\prime }\times {\widehat{\text{Λ}}\widehat{\text{Λ}}}^{\prime }\right)}{\sqrt{\text{tr}\left({\text{Λ}}_0{\text{Λ}}_0^{\prime }\right)\times \text{tr}\left({\widehat{\text{Λ}}\widehat{\text{Λ}}}^{\prime }\right)}},$$

where tr is the matrix trace, Λ₀ is the loading matrix for the majority group, and $\widehat{\text{Λ}}$ is either the EM or REM estimated loading matrix.

Minority Group with Different Factor Structure

As discussed earlier, factor structures might differ across a data sample. Underlying psychopathology might vary across subtypes of a psychiatric illness. Moreover, expression of symptoms can differ across cultures and languages (Kleinman, 2004). Both of these situations can result in differing factor structures. That is, the relationships between observed symptoms and underlying psychological constructs are not consistent across the sample. Without proper accounting of this heterogeneity, these differences could lead to biased inferences.

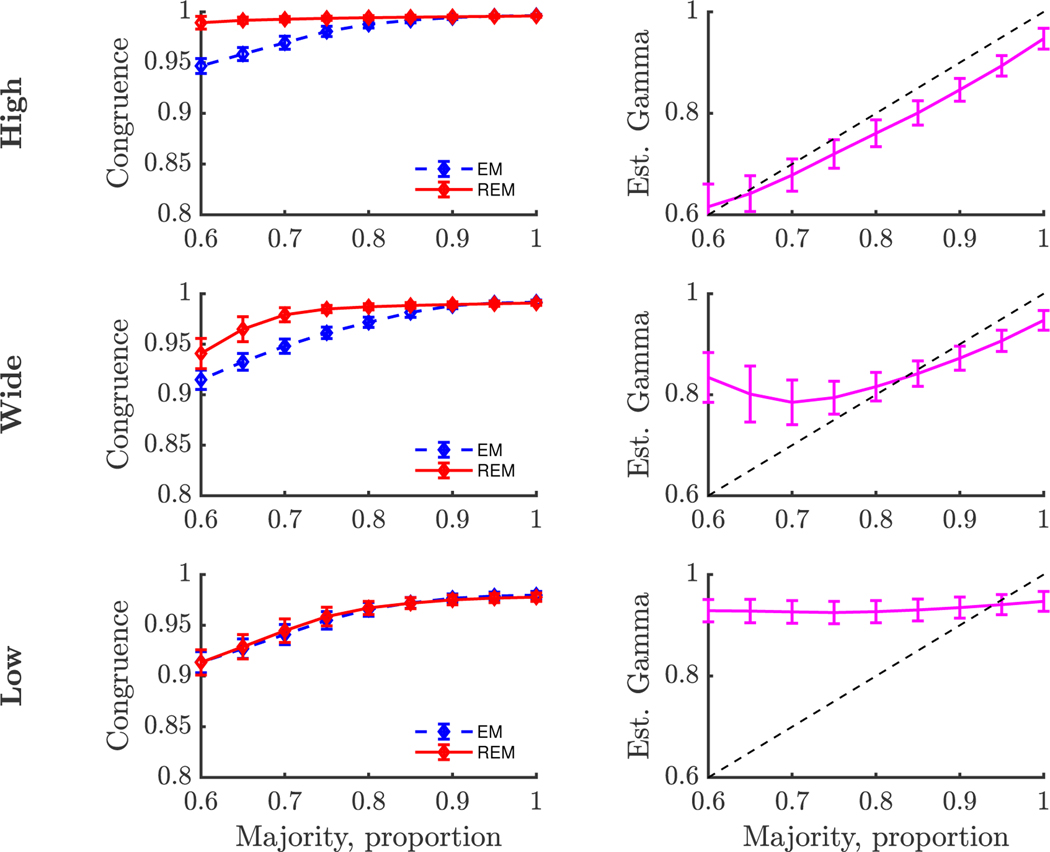
To emulate this issue, we simulated samples from two populations with different factor structures. From each population, data samples were drawn from a multivariate Normal distribution with dimension P = 30, mean of zero, and covariance matrix $\text{Σ}=\text{Λ}{\text{Λ}}^{\prime }+\text{Ψ}$, where Λ and Ψ were generated according to the method described in Tucker et al. (1969). We combined samples from the two populations at varying rates to simulate varying percentages of majority and minority proportions, fixing the total sample size to N = 500. The percentage from the minority population varied from 0% to 40% in increments of 5%. In addition, we simulated Λ and Ψ at three different levels of communality: high ($h_p^2$=0.6, 0.7 or 0.8); wide ($h_p^2$=0.2, 0.3, 0.4, 0.5, 0.6, 0.7 or 0.8); and low ($h_p^2$=0.2, 0.3 or 0.4), similar to MacCallum et al. (1999) and Hogarty et al. (2005). This led to 27 (9 mixture levels × 3 communality levels) total simulation scenarios. In each scenario, we computed a measure of congruence (R_V coefficient) between the estimated factor structures from EM and REM to the true, simulated factor structure of the majority group (Figure 4). The REM hyperparameter was selected based on the heuristic method described with δ = 0.05. We conducted 400 Monte Carlo simulations for each scenario to recover estimated means and standard deviations of the R_V coefficients.

Figure 4. Simulations of Minority Group with Different Factor Structure.

Note: Congruence was measured between estimated factor structure and simulated majority factor structure with the R_V coefficient. Error bars represent standard deviations. Communality values were set to high (0.6–0.8), wide (0.2–0.8), or low (0.2–0.4).

In the heterogeneous samples, we found that the estimated loading matrix from the EM procedure became less congruent with the simulated majority factor structure as the sample proportion of the minority group increased (Figure 4). Conversely, the estimates from the REM procedure maintained a greater or equal (in the low communality case) degree of congruence to the majority structure compared to the EM procedure. As communality declined, the separation between REM and EM lessened. Simultaneously, the parameter $\gamma$ was estimated (Figure 4). While the estimated $\gamma$ did vary with changing mixture percentages, there was some discrepancy between the true proportion of the majority group and the estimated value from $\gamma$. In the case of high communality, the estimated value of $\gamma$ was near, but slightly lower, than the true proportion. The gap was approximately 0.05 when the true proportion was large (> 0.85) and narrowed for smaller proportions. This gap reflects how much data from the majority group were allowed to be down-weighted in our choice of hyperparameter δ. In the case of the wide communality, the estimated value of $\gamma$ was slightly lower than the true proportion by about 0.05, but only for the large proportions (> 0.85). For the smaller proportions, the estimated $\gamma$ was overestimated. In the case of low communality, the estimated value of $\gamma$ remains relatively constant regardless of the true proportion of the majority group. In general, overestimates of $\gamma$ indicate that the REM estimates are fitting both the majority and minority group data, which leads to a loss of congruence between the estimated and majority structures.

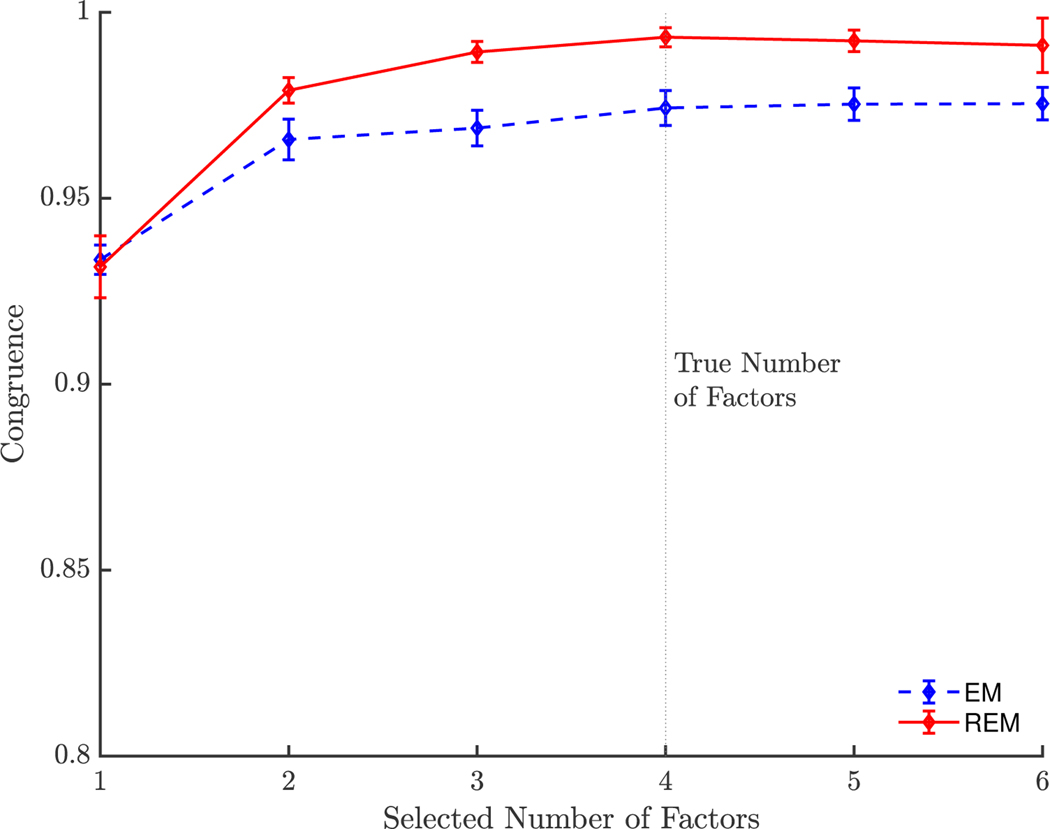
Determining the Number of Factors

Choosing the appropriate number of factors to specify is a crucial step in factor analysis. There are many methods to inform the choice of number of factors and different methods might disagree (Fabrigar et al., 1999). For a fixed level of heterogeneity, we explored the effect of factor number misspecification on the degree of congruence to the true factor structure (Figure 5). Using the same approach, we fixed the minority group percentage to 30%, the communality values to high, and varied the number of estimated factors from 1 to 6. For each scenario, we conducted 400 Monte Carlo simulations to recover estimated means and standard deviations of the R_V coefficients. The REM hyperparameter was selected based on the heuristic method described with δ = 0.05. Relative to the EM estimates, the REM estimates showed higher congruence to the true, underlying factor structure. Other than the extreme case of specifying just one factor, when in fact there are four, the misspecification of the number of factors had little influence on the estimated factor structures.

Figure 5. Varying Number of Factors.

Note: Congruence was measured between estimated factor structure and simulated majority factor structure with R_V coefficient. Error bars represent standard deviations. Communality values were selected from the high range (0.6–0.8).

Discussion

Individuals differ in many substantive ways that are not always captured through the assumed data-generating model. In an effort to address this reality of modeling of psychological data, we have proposed a robust estimation method that offers several benefits for analysis of data from heterogeneous populations. This method builds off of the familiar EM algorithm, which performs maximum likelihood estimation for latent variable models. For two frequently used models—Gaussian mixture models and linear factor models—we have shown that REM leads to an estimation procedure not that different from the EM algorithm, yet provides robustness from and insight into heterogeneous populations.

One of the distinguishing features of REM is that we take into account that not all individuals in our sample are equally well-explained by the assumed model. We accomplish this by assigning probabilistic weights to each individual, which can be interpreted as individual-level measures of model fitness. Weighting data points according to the level of information they supply is not in itself a novel concept. Consider, for example, weighted least squares regression methods, where data are typically weighted inversely to their variance, leading to a down-weighting of noisy data points. Recently, Wang et al. (2017) presented a robust Bayesian re-weighting approach that involves modifying the likelihood function by raising each term to its own latent weight. REM takes a similar, but distinct, approach; we down-weight data, at the level of the likelihood function, with less likelihood of originating from the assumed data-generating model. Weights are estimated simultaneously with model parameters and can be analyzed a posteriori. Methods, such as regression analysis or machine learning algorithms, could be applied to build models of the assigned probabilistic weights and learn more about the nature of the heterogeneity within the sample. In some cases, these measures might bring to light sources of heterogeneity in the sample that warrant further investigation.

When population heterogeneity is suspected, there are several approaches a researcher might currently take. If sources of heterogeneity are observed, a researcher could build their model to incorporate these sources of heterogeneity, such as through multiple-group models (Jöreskog, 1971), multiple-indicator multiple-cause (MIMIC) models (Jöreskog & Goldberger, 1975), or moderated non-linear factor analysis (Bauer & Hussong, 2009). If sources of heterogeneity are missing or unobserved, structural equation mixture models (SEMM) are a potential solution (Bauer & Curran, 2004). However, SEMM might become unwieldy considering that modeling all possible sources of heterogeneity that exist within a psychiatric population can prove to be a formidable task. Spurious latent groups might be identified. In addition, factor mixture models have yet to become widely adopted, potentially due to the complexity in their interpretation (Clark et al., 2013).

Despite direct modeling of possible sources of heterogeneity, modeling psychological data is never perfect, nor should it be. In statistical modeling, there is always a trade-off. When the sample size is small, we might not have ample data to adjust for all known sources of heterogeneity. While analyzing data from multiple sites can be one solution, which also helps to increase statistical power, heterogeneity between sites can threaten the validity and reliability of analyses. Curran et al. (2014) presented a carefully crafted approach to building a moderated non-linear factor analysis model within the context of integrative data analysis. As the authors noted, these models can be computationally demanding, sometimes requiring hours or days to fit to data. Moreover, like any model-building exercise, there are subjective decisions that need to be made, and each decision opens up opportunity for misspecification. For this reason, we propose that our approach can be used to supplement existing efforts for combating the issues that arise from heterogeneous populations.

Our approach uses ideas from an established area of statistics known as robust estimation (Huber, 2004). Robust estimation seeks to ensure estimation is more robust to inevitable violations in modeling assumptions and often works by ensuring that estimation is relatively insensitive to a single data point. In the case of mixture models, various robust estimation approaches have been presented in the literature. For example, a researcher estimating parameters of a finite normal mixture model could substitute t-distributions (Lo & Gottardo, 2012; Peel & McLachlan, 2000) or skew-normal distributions (Basso et al., 2010) to increase the robustness of their estimates to outliers. The minimum covariance determinant (MCD) estimator is a robust covariance estimator which is resistant to outliers in multivariate data (Rousseeuw, 1984) and can be incorporated into robust factor analysis (Pison et al., 2003). A review of the MCD estimator and its extensions have been presented previously (Hubert et al., 2018). In general, psychological data analysis might benefit from more widespread testing of the usefulness of various robust methods with empirical data.

In contrast to some of the alternate robust approaches discussed above, REM is widely applicable and computationally manageable, especially for those already familiar with EM. REM enables a comprehensive approach to handling misspecification by considering heterogeneity in the assumed data-generating process. The approach to modifying the likelihood function could, in theory, be applied to many situations beyond those covered in this paper: latent class analysis, item response theory, and more complex structural equation models. Moreover, REM relies on a commonly used estimation procedure, the EM algorithm. Although other methods have been suggested to improve upon the convergence speed of EM (Liu & Rubin, 1998; Zhao et al., 2008), the EM algorithm remains as the core concept within these alternative maximum likelihood estimation procedures. Thus, the adjustment of current estimation procedures to REM should be straightforward.

In the case of mixture models, REM estimators for the latent group means, covariances, and mixture proportions were probability-weighted versions of the estimators derived from the EM algorithm. In linear factor models, the EM estimators rely on the observed data only through the empirical covariance matrix. We showed that REM followed the same EM algorithm with the exception of a probability-weighted version of the covariance matrix in place of the empirical covariance matrix. Thus, the modifications to the estimators from the EM algorithm—for both mixture models and linear factor models—were minimal; the main difference was the incorporation of probabilistic weights that allow for flexibility in model fit.

An added benefit of REM was its ability to maintain robust inferences even in the presence of misspecified number of latent groups or latent factors. For both mixture models and factor models, several criteria are available for evaluating the number of appropriate latent groups or factors. In both cases, we have shown that even with misspecification, REM recovered model fits that correspond to true, underlying data structures. We have not been the first to consider estimators robust to this type of misspecification. Yang et al. (2012) present a robust EM estimator for finite mixture models that is designed to automatically select an optimal number of latent groups. The estimator adds a penalty term to the likelihood function to minimize the information-theoretic entropy. While this method could be useful for avoiding misspecification of the number of latent groups, the authors did not test robustness to outliers or other model misspecifications. In the case of factor analysis, there is not a clear consensus on the optimal process for selecting the appropriate number of factors. A discussion of various approaches for factor number selection can be found in Fabrigar et al. (1999); a model selection perspective is provided in Preacher et al. (2013). Despite previous discussion of the sensitivity of analyses to factor number specification, we found in our simulation studies that misspecification of the number of factors can still yield estimated factor structures that are largely congruent, in terms of the R_V coefficient, to the true factor structures. This point does not appear to have received discussion in the current literature.

Limitations

There were several limitations to our approach that suggest future areas of improvement. In REM, we shifted the original parametric model to a semiparametric one in a somewhat unconventional way. We modified the likelihood function by adding an improper density—specifically, a constant value ϵ. While simulation studies gave evidence for the utility of REM, more work will be needed to develop its theoretical grounds. We are unable to explicitly quantify the conditions under which REM outperforms EM and vice versa. From the examples we have studied, it does appear that EM can outperform REM in terms of RMSE of the mean and covariance matrix norm difference in a mixture model analysis when the model is correctly specified. This follows from choosing δ > 0, which allows some chance that data from the specified model are down-weighted.

A consequential limitation, resulting from our modification of the likelihood function, was that REM relies on a user-specified hyperparameter. It was unclear on what metric the hyperparameter should have been optimized. For the simulations in this paper, our heuristic approach yielded reasonable results, but there were a few issues. First, this method required specification of another hyperparameter, denoted by δ. However, this hyperparameter does allow for flexibility of our algorithm; a researcher can select a hyperparameter that aligns with their degree of belief that there is potential model misspecification. A researcher might run the estimation algorithm multiple times with varying choices of the hyperparameter to examine sensitivity of the results. Second, while the parameter, γ, should capture an average measure of model fitness, we found that scenarios with large within-group variability or noise processes that closely resembled the specified model resulted in overestimates of γ.

Another limitation, of lesser concern, was that like the EM algorithm, REM was sensitive to the starting values. Neither EM nor REM can guarantee achieving a global maximum of the objective function. Consequently, we used a global optimization procedure which tested multiple starting points to increase the chances of reaching a global maximum. We recommend that a global optimization procedure should be implemented in practice.

Lastly, we recognize that simulations in this paper do not address all situations that might arise in empirical data. For the finite mixture model simulations, we studied simulations with only two dimensions so that we could visually illustrate the performance of REM and EM. For factor analysis simulations, we purposefully employed the method from Tucker et al. (1969) to simulate factor loadings with a limited number of cross-loadings. We felt this was representative of a more typical factor analysis of psychological data which seeks to provide a relatively sparse representation of the complex multivariate data.

Conclusion

Heterogeneous populations are, in some sense, unavoidable. Ideally, all known sources of individual variation—particularly those that threaten the validity and reliability of an analysis—would be properly accounted for in models; however this is not always feasible. Moreover, pertinent points of variation might be unknown at the outset. To contribute to addressing the population heterogeneity of psychological constructs and psychiatric disorders, we offer an estimation approach that aims to provide robust inferences under model misspecification and a mechanism for detecting individuals who might be inadequately explained by the model.

Appendix A. Robust Expectation-Maximization

We are interested in building statistical models of an observed p-dimensional random vector X that depends on an unobserved k-dimensional random vector Z, which we refer to as a latent variable. Models belong to a parametric family $\mathcal{P}:=\left\{f_{X,Z\mid \theta }(\cdot ):\theta \in \text{Θ}\subset {ℝ}^d\right\}$ of probability density functions (pdf) for X and Z. If X and Z are discrete, then $f_{X,Z\mid \theta }(\cdot )$ denotes the joint probability mass function (pmf). Note we use the notation $f_V(\cdot )$ to denote the probability density (mass) function of any continuous (discrete) random variable V.

Suppose we observe a random sample $x_1,\dots ,x_N$. We assume observations are realizations of the random vector X and that the observations are independent and identically distributed. Our goal is to infer $\theta$ from the observations $x_1,\dots ,x_N$. Maximum likelihood estimation is a common estimation approach, resulting in a variety of advantageous statistical properties. Notably, the maximum likelihood estimator (MLE) is consistent and asymptotically efficient under the squared error loss function.

Formally, the MLE can be defined as:

$${\widehat{\theta }}_{MLE}\left(x_1,\dots ,x_N\right)=\underset{\theta \in \text{Θ}}{\arg \max }\log L\left(\theta \mid x_1,\dots ,x_N\right),$$

where $\log L\left(\theta \mid x_1,\dots ,x_N\right)$ is the log-likelihood function. In the case of observations that are independent and identically distributed, the MLE can be expressed as:

$${\widehat{\theta }}_{MLE}\left(x_1,\dots ,x_N\right)=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\log L\left(\theta \mid x_n\right)\mathit{\text{(independence)}}$$

$$=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\log f_{X\mid \theta }\left(x_n\right)\mathit{\text{(identical distributions)}}.$$

In practice, this optimization problem can be difficult in the case of latent variable models. For example, the MLE in latent variable models is often expressed in terms of expectation:

$${\widehat{\theta }}_{MLE}\left(x_1,\dots ,x_N\right)=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\log {\mathbb{E}}_Z\left[f_{X,Z\mid \theta }\left(x_n,Z\right)\right].$$

We can use the Expectation-Maximization (EM) algorithm to solve a sequence of easier optimization problems that converges to the MLE. The EM algorithm entails repeatedly solving the following optimization problem until convergence is achieved:

$${\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right].$$

Derivation of this algorithm can be found elsewhere.

With robust expectation-maximization (REM), we maintain that observations are independent but address the possibility that observations are not all identical draws of the random vector X. In other words, our assumed parametric data-generating model might be incorrect for a subset of the observed data. In this case, we could use the law of total probability to write the likelihood of an observed data point as:

$$L\left(\theta \mid x_n\right)=\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )g_X\left(x_n\right),$$

where $\gamma \in [0,1]$ is the probability that data are generated from the model $f_{X\mid \theta }(\cdot )$ and $g_X(\cdot )$ represents the alternate pdf of the data. Of course, if we knew (or assumed) what the alternate pdf was, we could proceed with the typical EM approach. However, in many cases, this alternate pdf would be unknown. Without a more informed guess, we replace the unknown pdf with a constant ϵ > 0, which will act as a hyperparameter that tunes parameter estimation:

$$L\left(\theta \mid x_n\right)=\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ.$$

We can express our modified optimization problem as

$$\widehat{\theta }=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\log \left\{\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right\}$$

With an argument similar to the justification for the EM estimator, we will show that this optimization problem can be solved with a sequence of easier optimization problems. To facilitate this, we introduce a quantity

$$p(x;\gamma ,\theta ):=\frac{\gamma f_{X\mid \theta }(x)}{\gamma f_{X\mid \theta }(x)+(1-\gamma )ϵ},$$

and the shortened notation: $p_n:=p\left(x_n;\gamma ,\theta \right)$, and ${\widehat{p}}_n:=p\left(x_n;\widehat{\gamma },\widehat{\theta }\right)$. This quantity is bounded by 0 and 1 and will be interpreted as the probability that the data point is generated from the assumed parametric model $f_{X\mid \theta }(\cdot )$.

With some algebra, we can write each term in the sum as:

$$\begin{gathered} \log \left\{\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right\}={\widehat{p}}_n\log \left\{\frac{\gamma f_{X\mid \theta }\left(x_n\right)}{\gamma f_{X\mid \theta }\left(x_n\right)}\left(\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right)\right\} \\ +\left(1-{\widehat{p}}_n\right)\log \left\{\frac{(1-\gamma )ϵ}{(1-\gamma )ϵ}\left(\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right)\right\} \\ ={\widehat{p}}_n\log \left\{\frac{\gamma f_{X\mid \theta }\left(x_n\right)}{p_n}\right\}+\left(1-{\widehat{p}}_n\right)\log \left\{\frac{(1-\gamma )ϵ}{1-p_n}\right\} \\ ={\widehat{p}}_n\left(\log \gamma -\log p_n+\log f_{X\mid \theta }\left(x_n\right)\right) \\ +\left(1-{\widehat{p}}_n\right)\left(\log (1-\gamma )-\log \left(1-p_n\right)+\log ϵ\right)\text{. } \end{gathered}$$

For latent variable models, we can rewrite the term $\log f_{X\mid \theta }\left(x_n\right)$ as

$${\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X\mid \theta }\left(x_n\right)\right]={\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)-\log f_{Z\mid x_n,\theta }(Z)\right].$$

Now we can decompose our objective function into two components:

$$\sum _{n=1}^N\log \left\{\gamma f_{X\mid \theta }\left(x_n\right)+(1-\gamma )ϵ\right\}=Q(\theta ,\gamma )+H(\theta ,\gamma ),$$

where

$$\begin{gathered} Q(\theta ,\gamma )=\sum _{n=1}^N\left({\widehat{p}}_n\left[\log \gamma +{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]\right]+\left(1-{\widehat{p}}_n\right)[\log (1-\gamma )+\log ϵ]\right) \\ =N\log [1-\gamma ]+N\log ϵ+\sum _{n=1}^N{\widehat{p}}_n\left({\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]+\text{logit}\gamma -\log ϵ\right) \end{gathered}$$

and

$$H(\theta ,\gamma )=-\sum _{n=1}^N\left({\widehat{p}}_n\log p_n+\left(1-{\widehat{p}}_n\right)\log \left(1-p_n\right)+{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{Z\mid X,\theta }(Z)\right]\right).$$

By Gibb’s inequality, any $\theta$ and $\gamma$ will increase the term H over $\widehat{\theta }$ and $\widehat{\gamma }$:

$$H(\theta ,\gamma )\ge H(\widehat{\theta },\widehat{\gamma }).$$

So, choosing values of $\theta$ and $\gamma$ that increase the value of $Q(\theta ,\gamma )$ over $Q(\widehat{\theta },\widehat{\gamma })$ will also increase in our objective function $Q(\theta ,\gamma )+H(\theta ,\gamma )$ over $Q(\widehat{\theta },\widehat{\gamma })+H(\widehat{\theta },\widehat{\gamma })$.

Lastly, we note that $Q(\theta ,\gamma )$ decomposes into terms that depend on $\theta$, terms that depend on γ, and terms that depend on neither. This decomposition allows $Q(\theta ,\gamma )$ to be maximized over $\text{Θ}\otimes (0,1)$ by separately maximizing over Θ and (0,1):

$$\begin{gathered} \underset{(\theta ,\gamma )\in \text{Θ}\otimes (0,1)}{\max }Q(\theta ,\gamma )=N\log ϵ-\sum _{n=1}^N{\widehat{p}}_n\log ϵ+ \\ \underset{\gamma \in (0,1)}{\max }\left(N\log [1-\gamma ]+\sum _{n=1}^N{\widehat{p}}_n\text{logit}\gamma \right)+ \\ \underset{\theta \in \text{Θ}}{\max }\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]. \end{gathered}$$

In particular, maximization over $\gamma \in (0,1)$ can be performed directly:

$$\underset{\gamma \in (0,1)}{\arg \max }\left(N\log [1-\gamma ]+\sum _{n=1}^N{\widehat{p}}_n\text{logit}\gamma \right)=\frac{1}{N}\sum _{n=1}^N{\widehat{p}}_n.$$

These observations tell us how to improve upon an estimator $(\widehat{\theta },\widehat{\gamma })$. Applying this improvement iteratively yields the following estimation procedure:

$${\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\widehat{p}}_n^{(t)}{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]$$

$${\widehat{\gamma }}^{(t+1)}=\frac{1}{N}\sum _{n=1}^N{\widehat{p}}_n^{(t)}$$

$${\widehat{p}}_n^{(t+1)}=\frac{{\widehat{\gamma }}^{(t)}{f}_{X\mid {\widehat{\theta }}^{(t)}}\left(x_n\right)}{{\widehat{\gamma }}^{(t)}{f}_{X\mid {\widehat{\theta }}^{(t)}}\left(x_n\right)+\left(1-{\widehat{\gamma }}^{(t)}\right)ϵ}$$

In addition to the estimation of γ and p_n, the estimation step for the substantive model parameters, $\theta$, is simply a weighted version of the EM estimator, where weights are the estimated probabilities of model fitness.

Appendix B. Robust Mixture Modeling

Suppose we draw mutually independent samples $x_1,\dots ,x_N$ of a random vector $X\in {ℝ}^p$. We model the distribution of X as a mixture of K multivariate normal distributions, where the kth distribution follows $N_p\left({\mu }_k,{\text{Σ}}_k\right)$. We assume that X is drawn from the kth distribution with probability ${\pi }_k$ and introduce a latent variable $Z\in [1,2,\dots ,K]$ to specify the distribution from which X was drawn. The likelihood for $x_1,\dots ,x_N$ given the parameters of this distribution,

$$\theta =\left\{{\theta }_k:{\theta }_k=\left({\pi }_k,{\mu }_k,{\text{Σ}}_k\right),k=1,\dots ,K\right\},$$

can be expressed as:

$$\prod _{n=1}^N\sum _{k=1}^K{\pi }_k{\varphi }_k\left(x_n\right),$$

where ${\varphi }_k\left(x_n\right)$ is the density for a $N_p\left({\mu }_k,{\text{Σ}}_k\right)$ random variable.

To use the EM algorithm, we need the joint density of the observed data and the latent variables:

$$f_{X,Z\mid \theta }\left(x_n,Z\right)={\pi }_Z{\varphi }_Z\left(x_n\right).$$

Recall that the EM estimate results from iterating the following:

$${\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right].$$

So we have

$$\begin{gathered} {\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log {\pi }_Z+\log {\varphi }_Z\left(x_n\right)\right] \\ =\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N\sum _{k=1}^K{\widehat{\omega }}_{nk}^{(t)}\left\{\log {\pi }_k+\log {\varphi }_k\left(x_n\right)\right\} \end{gathered}$$

where ${\widehat{\omega }}_{nk}^{(t)}=\mathbb{P}\left[Z=k\mid x_n,{\widehat{\theta }}^{(t)}\right]$.

After maximizing the objective function, under the constraint that ${\sum }_{k=1}^K{\pi }_k=1$, we obtain the estimation procedure:

$${\widehat{\text{Σ}}}_k^{(t+1)}=\frac{{\sum }_{n=1}^N{\widehat{\omega }}_{nk}^{(t)}\left(x_n-{\widehat{\mu }}_k^{(t)}\right){\left(x_n-{\widehat{\mu }}_k^{(t)}\right)}^{\prime }}{{\sum }_{n=1}^N{\widehat{\omega }}_{nk}^{(t)}}$$

$${\widehat{\mu }}_k^{(t+1)}=\frac{{\sum }_{n=1}^N{\widehat{\omega }}_{nk}^{(t)}{x}_n}{{\sum }_{n=1}^N{\widehat{\omega }}_{nk}^{(t)}}$$

$${\widehat{\pi }}_k^{(t+1)}=\frac{1}{N}\sum _{n=1}^N{\widehat{\omega }}_{nk}^{(t)}.$$

To compute estimates, ${\widehat{\omega }}_{nk}^{(t)}$, we can use the definition of conditional probability to re-express this probability in terms of the data:

$${\widehat{\omega }}_{nk}^{(t)}=\text{ℙ}\left[Z_n=k\mid x_n,{\widehat{\theta }}^{(t)}\right]=\frac{{\widehat{\pi }}_k^{(t)}{f}_X\left(x_n\mid {\widehat{\theta }}_k^{(t)}\right)}{{\sum }_{l=1}^K{\widehat{\pi }}_l^{(t)}{f}_X\left(x_n\mid {\widehat{\theta }}_l^{(t)}\right)}.$$

Meanwhile, the REM estimate for $\theta$ is given by

$$\begin{gathered} {\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right] \\ =\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\widehat{p}}_n\sum _{k=1}^K{\widehat{\omega }}_{nk}^{(t)}\left\{\log {\pi }_k+\log {\varphi }_k\left(x_n\right)\right\}, \end{gathered}$$

with ${\widehat{\omega }}_{nk}^{(t)}$ defined as before in the EM algorithm.

Maximizing this objective function in the same manner as above, we obtain the estimation procedure

$${\widehat{\text{Σ}}}_k^{(t+1)}=\frac{{\sum }_{n=1}^N{\widehat{p}}_n^{(t)}{\widehat{\omega }}_{nk}^{(t)}\left(x_n-{\widehat{\mu }}_k^{(t)}\right){\left(x_n-{\widehat{\mu }}_k^{(t)}\right)}^{\prime }}{{\sum }_{n=1}^N{\widehat{p}}_n^{(t)}{\widehat{\omega }}_{nk}^{(t)}}$$

$${\widehat{\mu }}_k^{(t+1)}=\frac{{\sum }_{n=1}^N{\widehat{p}}_n^{(t)}{\widehat{\omega }}_{nk}^{(t)}{x}_n}{{\sum }_{n=1}^N{\widehat{p}}_n^{(t)}{\widehat{\omega }}_{nk}^{(t)}}$$

$${\widehat{\pi }}_k^{(t+1)}=\frac{1}{N}\sum _{n=1}^N{\widehat{p}}_n^{(t)}{\widehat{\omega }}_{nk}^{(t)}.$$

Appendix C. Robust Factor Analysis

Suppose we draw mutually independent samples $x_1,\dots ,x_N$ from a random vector $X\in {ℝ}^p$. We theorize that correlations of items in X are driven by an underlying latent variable $Z\in {ℝ}^k$. For $n=1,\dots ,N$, we build a common factor model for X as

$$X=\text{Λ}Z+U,$$

where Λ is a p × k loading matrix and U is an error term capturing unique variance attributable to individual items. We assume $Z\sim N_k(0,\mathbb{I}),U\sim N_p(0,\text{Ψ})$ where Ψ is a diagonal matrix, and Z is independent of U. With these assumptions and the properties of normal distributions, we have that $X\sim N_p\left(0,\text{Λ}{\text{Λ}}^{\prime }+\text{Ψ}\right)$. To simplify notation, we let $\theta =(\text{Λ},\text{Ψ})$).

To use the EM algorithm, we need the joint density of the observed data and the latent variables. For $n=1,\dots ,N$, we have

$$\begin{gathered} f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)=f_{X\mid Z,\theta }\left(x_n\mid Z,\theta \right)f_Z(Z) \\ ={(2\pi )}^{-(p+k)/2}{(\det \text{Ψ})}^{-1/2}\exp \left\{-\frac{1}{2}{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)-\frac{1}{2}{Z}^{\prime }Z\right\} \end{gathered}$$

We can express the log of this joint density as as

$$\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)=-\frac{1}{2}\det \text{Ψ}-\frac{1}{2}{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)+C$$

where C is a constant that does not depend on Λ or Ψ.

Recall that the EM estimate results from iterating the following:

$${\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)\right]$$

To solve the maximization problem, we need to simultaneously solve the following set of equations

$$\frac{\partial }{\partial \text{Λ}}\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)\right]=0$$

$$\frac{\partial }{\partial {\text{Ψ}}^{-1}}\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)\right]=0$$

Assuming we can exchange the order of the sum and conditional expectation with the partial derivative, we can focus on the following set of equations:

$$-\frac{1}{2}\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\frac{\partial }{\partial \text{Λ}}\left\{{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}\right]=0$$

$$-\frac{1}{2}\sum _{n=1}^N{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\frac{\partial }{\partial {\text{Ψ}}^{-1}}\left\{\log (\det \text{Ψ})+{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}\right]=0$$

The partial derivative with respect to $\text{Λ}$ is:

$$\begin{gathered} \frac{\partial }{\partial \text{Λ}}\left\{{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}=\frac{\partial }{\partial \text{Λ}}\left\{\text{tr}\left[{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right){\left(x_n-\text{Λ}Z\right)}^{\prime }\right]\right\} \\ =-2{\text{Ψ}}^{-1}\left(x_n{Z}^{\prime }-\text{Λ}Z{Z}^{\prime }\right) \end{gathered}$$

The partial derivative with respect to ${\text{Ψ}}^{-1}$ is:

$$\frac{\partial }{\partial {\text{Ψ}}^{-1}}\left\{\log (\det \text{Ψ})+{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}=\text{Ψ}+\left(x_n-\text{Λ}Z\right){\left(x_n-\text{Λ}Z\right)}^{\prime }$$

We can use these expressions to simplify the set of optimization equations:

$$\sum _{n=1}^N{\text{Ψ}}^{-1}{x}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[Z^{\prime }\right]+{\text{Ψ}}^{-1}{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[Z{Z}^{\prime }\right]=0$$

$$\sum _{n=1}^N\text{Ψ}+x_n{x}_n^{\prime }-x_n{\mathbb{E}}_{Z\mid x_n,\widehat{\theta }(t)}\left[Z^{\prime }\right]{\text{Λ}}^{\prime }-\text{Λ}{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}[Z]x_n^{\prime }+\text{Λ}{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[Z{Z}^{\prime }\right]{\text{Λ}}^{\prime }=0$$

From properties of multivariate normal distributions, we have that

$${\mathbb{E}}_{Z\mid x_n,\theta }[Z]=\beta x_n$$

$${\mathbb{E}}_{Z\mid x_n,\theta }\left[Z{Z}^{\prime }\right]=\mathbb{I}-\beta \text{Λ}+\beta x_n{x}_n^{\prime }{\beta }^{\prime }$$

where $\beta ={\text{Λ}}^{\prime }{\left(\text{Λ}{\text{Λ}}^{\prime }+\text{Ψ}\right)}^{-1}$. Plugging these expressions into the optimization equations and solving for Λ and Ψ, we arrive at the following estimation procedure:

$${\widehat{\text{Λ}}}^{(t+1)}=\left(C_{xx}{\widehat{\beta }}^{\prime (t)}\right){\left(\mathbb{I}-{\widehat{\beta }}^{\prime (t)}{\widehat{\text{Λ}}}^{(t)}+{\widehat{\beta }}^{(t)}{C}_{xx}{\widehat{\beta }}^{\prime (t)}\right)}^{-1}$$

$${\widehat{\text{Ψ}}}^{(t+1)}=\text{diag}\left[\left(\mathbb{I}-{\widehat{\text{Λ}}}^{(t)}{\widehat{\beta }}^{(t)}\right)C_{xx}\right]$$

$${\widehat{\beta }}^{(t+1)}={\widehat{\text{Λ}}}^{\prime (t)}{\left({\text{Λ}}^{(t)}{\text{Λ}}^{\prime (t)}+{\text{Ψ}}^{(t)}\right)}^{-1}$$

where $C_{xx}=\frac{1}{N}{\sum }_{n=1}^N{x}_n{x}_n^{\prime }$.

The REM estimate for $\theta$ is given by

$${\widehat{\theta }}^{(t+1)}=\underset{\theta \in \text{Θ}}{\arg \max }{\sum }_{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\right)\right]$$

Again, we need to simultaneously solve a set of equations:

$$\frac{\partial }{\partial \text{Λ}}\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)\right]=0$$

$$\frac{\partial }{\partial {\text{Ψ}}^{-1}}\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\log f_{X,Z\mid \theta }\left(x_n,Z\mid \theta \right)\right]=0$$

We note that the weights ${\widehat{p}}_n$ do not depend on Λ and Ψ, so once again we can move the partial derivative inside the sum and conditional expectation.

$$-\frac{1}{2}\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\frac{\partial }{\partial \text{Λ}}\left\{{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}\right]=0$$

$$-\frac{1}{2}\sum _{n=1}^N{\widehat{p}}_n{\mathbb{E}}_{Z\mid x_n,{\widehat{\theta }}^{(t)}}\left[\frac{\partial }{\partial {\text{Ψ}}^{-1}}\left\{\log (\det \text{Ψ})+{\left(x_n-\text{Λ}Z\right)}^{\prime }{\text{Ψ}}^{-1}\left(x_n-\text{Λ}Z\right)\right\}\right]=0$$

We can then proceed with the same steps presented above to arrive at the following estimation procedure:

$${\widehat{\text{Λ}}}^{(t+1)}=\left(C_{xx}^{(t)}{\widehat{\beta }}^{\prime (t)}\right){\left(\mathbb{I}-{\widehat{\beta }}^{\prime (t)}{\widehat{\text{Λ}}}^{(t)}+{\widehat{\beta }}^{(t)}{C}_{xx}^{(t)}{\widehat{\beta }}^{\prime (t)}\right)}^{-1}$$

$${\widehat{\text{Ψ}}}^{(t+1)}=\text{diag}\left[\left(\mathbb{I}-{\widehat{\text{Λ}}}^{(t)}{\widehat{\beta }}^{(t)}\right)C_{xx}^{(t)}\right]$$

$${\widehat{\beta }}^{(t+1)}={\widehat{\text{Λ}}}^{\prime (t)}{\left({\text{Λ}}^{(t)}{\text{Λ}}^{\prime (t)}+{\text{Ψ}}^{(t)}\right)}^{-1}$$

$$C_{xx}^{(t)}=\sum _{n=1}^N{\widehat{p}}_n^{(t)}{x}_n{x}_n^{\prime }/\sum _{n=1}^N{\widehat{p}}_n^{(t)}$$

For REM, the estimation steps are almost identical to those from EM with the addition of estimating a weighted covariance matrix.

Appendix D. Simulations for Mixture Modeling

We used MATLAB’s pearsrnd() function to simulate data from finite mixtures of skewed normal distributions. The skew parameter was set to 0.5. Data were scaled and shifted to specify mean and covariance parameters.

For simulations of the two majority groups with a scattered minority group in Examples 1 & 2, we sampled data from two different skewed bivariate normal distributions to represent the two majority groups with proportion 0.70 and 0.20. Population mean and covariance parameters of the skewed bivariate normal distributions are given in Tables E1 & E2. We sampled data from a bivariate random vector U ~ 10×Beta(1/2, 1/3) to represent the scattered minority group with proportion 0.10. Sample data were combined into the final mixture sample (N=1000) with probabilities: 0.70, 0.20, 0.10.

For the simulations of three distinct groups, we sampled data from three different skewed bivariate normal distributions (N=1000). Population parameters were:

Latent group	${\mu }_A$	${\mu }_B$	${\sigma }_{AA}^2$	${\sigma }_{BB}^2$	${\sigma }_{AB}^2$	π
Group 1	2.00	7.00	0.25	0.25	−0.125	0.70
Group 2	7.00	7.00	0.25	0.25	0.125	0.20
Group 3	6.00	3.00	0.50	0.50	0.00	0.10

Sample data were combined into the final mixture sample with probabilities: 0.70, 0.20, 0.10.

Appendix E. Parameter Estimates for Mixture Models

Table E1.

Example 1 Parameter Values and Estimates By Latent Group

Estimation method	${\widehat{\mu }}_A$	${\widehat{\mu }}_B$	${\widehat{\sigma }}_{AA}^2$	${\widehat{\sigma }}_{BB}^2$	${\widehat{\sigma }}_{AB}^2$	$\widehat{\pi }$
Population values	2.50	7.00	1.00	1.00	−0.50	0.78
	7.00	2.50	1.00	1.00	0.50	0.22
Sample estimates	2.51	7.00	0.99	1.06	−0.54	0.75
	7.02	2.59	1.00	0.94	0.45	0.25
EM	2.42	7.06	0.87	1.08	−0.48	0.68
	6.82	3.35	3.47	5.07	0.69	0.32
REM	2.46	7.00	0.89	1.03	−0.52	0.77
	6.95	2.52	0.82	0.75	0.32	0.23

Note: This table contains the simulated values and estimates for the simulation in Example 1 in Figure 1. The REM estimated $\widehat{\gamma }$ = 0.86.

Table E2.

Example 2 Parameter Values and Estimates by Latent Group

Estimation method	${\widehat{\mu }}_A$	${\widehat{\mu }}_B$	${\widehat{\sigma }}_{AA}^2$	${\widehat{\sigma }}_{BB}^2$	${\widehat{\sigma }}_{AB}^2$	$\widehat{\pi }$
Population values	5.00	5.00	1.00	1.00	−0.80	0.78
	5.00	5.00	1.00	1.00	0.80	0.22
Sample estimates	5.00	4.99	0.99	1.05	−0.83	0.75
	5.02	5.07	1.00	0.94	0.76	0.25
EM	4.93	5.01	0.77	0.85	−0.52	0.80
	5.71	5.29	7.00	6.90	0.54	0.20
REM	4.91	5.02	0.78	0.90	−0.66	0.78
	5.08	4.99	0.76	0.64	0.57	0.22

Note: This table contains the simulated values and parameter estimates for Example 2 in Figure 1. The REM estimated $\widehat{\gamma }$ = 0.82.

Table E3.

Varying Specified Number of Latent Groups

	Estimation method	${\widehat{\mu }}_A$	${\widehat{\mu }}_B$	${\widehat{\sigma }}_{AA}^2$	${\widehat{\sigma }}_{BB}^2$	${\widehat{\sigma }}_{AB}^2$	$\widehat{\pi }$
K = 1	Sample estimates	1.99	7.00	0.25	0.25	−0.12	1.00
	EM	3.44	6.64	5.02	1.53	−0.98	1.00
	REM	1.90	6.99	0.14	0.15	−0.07	1.00
K = 2	Sample estimates	1.99	7.00	0.25	0.25	−0.12	0.75
		6.94	6.94	0.22	0.21	0.10	0.25
	EM	1.99	7.00	0.25	0.25	−0.12	0.69
		6.67	5.85	0.48	3.47	0.86	0.31
	REM	1.96	7.00	0.22	0.22	−0.10	0.77
		6.92	6.90	0.18	0.17	0.09	0.23
K = 3	Sample estimates	1.99	7.00	0.25	0.25	−0.12	0.69
		6.94	6.94	0.22	0.21	0.10	0.23
		5.97	2.92	0.49	0.45	0.03	0.08
	EM	1.99	7.00	0.25	0.25	−0.12	0.69
		6.94	6.94	0.22	0.22	0.10	0.23
		5.96	2.92	0.48	0.44	0.03	0.08
	REM	1.98	7.00	0.25	0.25	−0.12	0.69
		6.94	6.94	0.22	0.21	0.10	0.23
		5.92	2.88	0.43	0.37	0.00	0.08

Note: This table contains parameter estimates for simulations shown in Figure 3. The REM estimated values of γ were 0.43,0.82,0.99.

Appendix F. Simulations for Factor Analysis

To simulate realistic factor structures, we follow previous work by Tucker et al. (1969). Briefly, their method decomposes common factors into major and minor, but we ignore minor factors following Hogarty et al. (2005). Major factors are generated by controlling communality, denoted by $h_p^2$, for each of the p observed variables. Communality describes the proportion of variance in an observed variable that can be explained by common factors and influences the ability to estimate the loading matrix (MacCallum et al., 1999). Similar to other studies, a value for communality is selected for each variable uniformly at random from some set. By varying this set, we tested three different levels of communality: high ($h_p^2$=0.6, 0.7 or 0.8); wide ($h_p^2$=0.2, 0.3, 0.4, 0.5, 0.6, 0.7 or 0.8); and low ($h_p^2$=0.2, 0.3 or 0.4) (Hogarty et al., 2005; MacCallum et al., 1999). After selecting values for communality, the procedure detailed in Tucker et al. (1969) was applied to generate a loading matrix Λ and diagonal covariance matrix Ψ with the specified values of communality. Based on the factor model, these matrices defined population correlation matrices $\text{Σ}=\text{Λ}{\text{Λ}}^{\prime }+\text{Ψ}$.

To create heterogeneous data samples, we sampled observations from two separate multivariate normal distributions with mean 0 and covariance matrices Σ₁,Σ₂, respectively. For all simulations, we fixed the sample size N = 600 and the number of items P = 30 and number of factors K = 4.

Appendix G. Additional Finite Mixture Scenarios

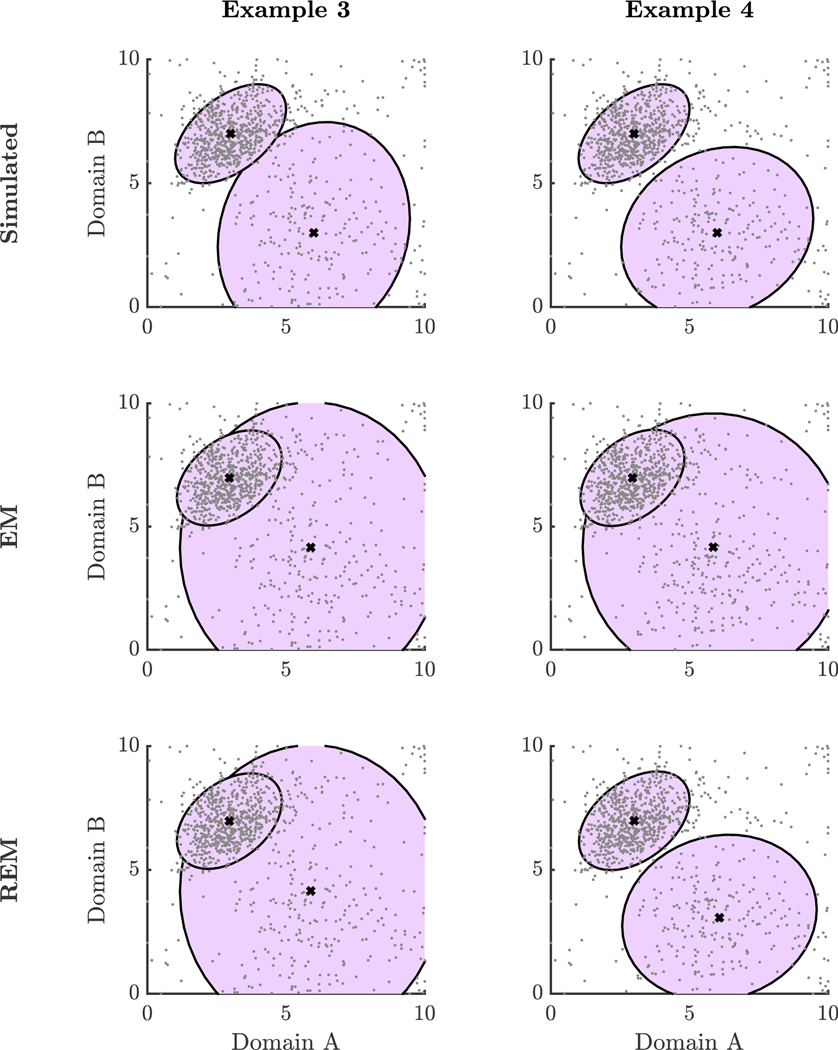
In Examples 1 & 2, majority groups were simulated with relatively small within-group variability. In Examples 3 & 4, included here, we investigated scenarios in which one of the majority groups had large within-group variability. Like Examples 1 & 2 in the subsection, Scattered Minority Group, data were sampled from two different skewed bivariate Normal distributions to represent the two majority groups with probability 0.70 and 0.20 and skew parameter set to 0.5; corresponding population mean and covariance parameters are given in Table G1. The scattered minority group was simulated by data sampled, with probability 0.10, from a bivariate random vector U ~ 10×Beta(1/2, 1/3). In Example 3, EM and REM resulted in the same estimates (Figure 6). With δ = 0.05, we estimated ${\gamma }^{\wedge }$ = 1.00. For both EM and REM, the RMSE for the mean was 0.58 and the Frobenius norm of the difference between estimated and population covariance matrices was 1.61. In Example 4, we decreased the within-group variability slightly and kept all other parameters the same as Example 3. In this situation, we found that the REM estimates improved upon the EM estimates (Figure 6). REM resulted in ${\gamma }^{\wedge }$ = 0.91 with RMSE of the mean of 0.05 and covariance norm difference of 0.13. On the other hand, EM resulted in a RMSE of the mean of 0.59 and covariance norm difference of 1.80. These examples demonstrate that large within-group variability can make it more challenging for the REM algorithm to separate the noise process from the underlying data-generating process. If δ is set too high, REM is more likely to down-weight data from the substantive data-generating process. However, as in Example 4, REM can improve upon EM when groups are, in some sense, sufficiently distinguishable. We are currently unable to quantify these limits of REM.

Figure 6. Additional Simulations of Finite Mixtures: Examples 3 & 4.

Note: This figure shows scatter plots of simulated data and approximate 95% confidence ellipses for ground truth parameter values, EM estimates, and REM estimates from Examples 3 and 4.

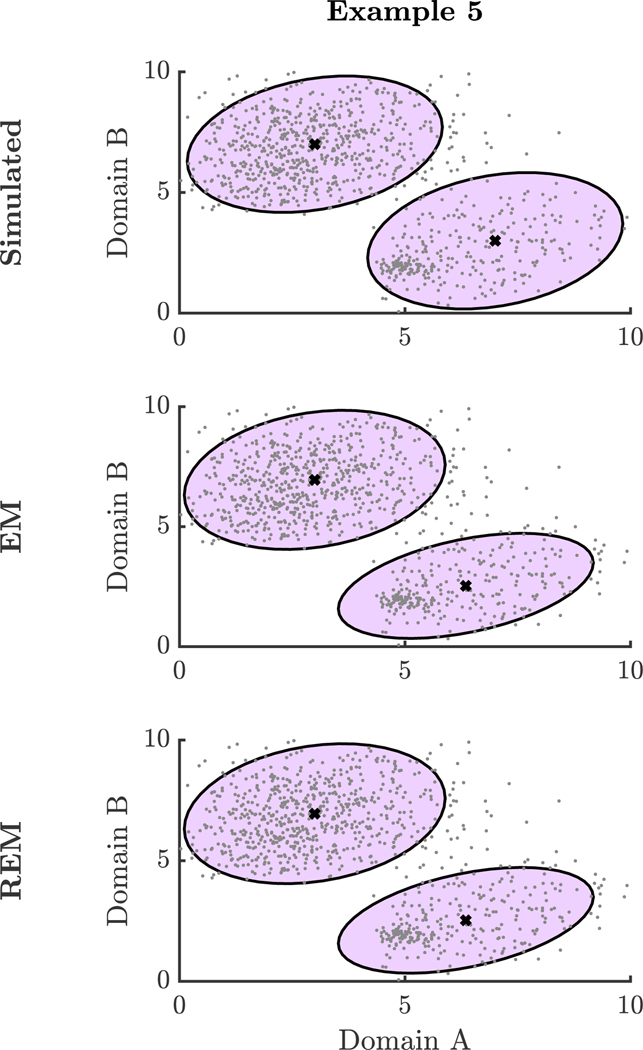
Lastly, we examined a scenario in which the minority group was located within one of the two majority groups (Example 6). Again, majority group data were sampled from two different skewed bivariate Normal distributions to represent the two majority groups with proportion 0.70 and 0.20 and skew parameter set to 0.5; corresponding population mean and covariance parameters are given in Table G1. In this scenario, the minority group had small variance and was centered near the mean of the one of the two majority groups. The minority group was simulated by a skewed bivariate Normal distribution with mean, ${\mu }_A$= 5.00 and ${\mu }_B$ = 2.00, and variance-covariance, ${\sigma }_{AA}^2={\sigma }_{BB}^2=0.10$ and ${\sigma }_{AB}^2$ = 0.00. With δ = 0.05, we estimated $\widehat{\gamma }$ = 1.00, indicating that the REM algorithm did not recognize and down-weight this anomalous process (Figure 7). At this value ofγ, the EM and REM estimates coincide. The RMSE of the mean was 0.40 and the covariance norm difference was 0.30. This is another scenario in which the REM estimates do not improve upon the EM estimates.

Figure 7. Additional Simulations of Finite Mixtures: Example 5.

Note: This figure shows scatter plots of simulated data and approximate 95% confidence ellipses for ground truth parameter values, EM estimates, and REM estimates from Example 5.

Table G1.

Example 3–5 Parameter Values for Majority Groups

Estimation method	${\mu }_A$	${\mu }_B$	${\sigma }_{AA}^2$	${\sigma }_{BB}^2$	${\sigma }_{AB}^2$	π
Example 3	3.00	7.00	1.00	1.00	0.50	0.78
	6.00	3.00	3.00	5.00	0.50	0.22
Example 4	3.00	7.00	1.00	1.00	0.50	0.78
	6.00	3.00	3.00	3.00	0.50	0.22
Example 5	3.00	7.00	2.00	2.00	0.50	0.78
	7.00	3.00	2.00	2.00	0.50	0.22

Note: This table contains the majority group population parameter values in Examples 3 & 4 in Figure 6 and Example 5 in Figure 7.